Dynamic analysis of a novel hyperchaotic system based on STM32 and application in image encryption

Abstract

This paper presents a novel 4D hyperchaotic system derived from a modified 3D Lorenz chaotic system. A key aspect of this system is the presence of a single equilibrium point, and its stability is carefully analyzed. The dynamic properties, including the Lyapunov exponent spectrum, bifurcation diagram, and chaotic attractors, are investigated using MATLAB simulations. The results reveal that the system displays hyperchaotic behavior across a wide range of the parameter $d$, with its chaotic attractor transitioning through four states: hyperchaotic, chaotic, periodic, and quasi-periodic, showcasing the system's complex dynamics. Experimental validation using STM32 embedded hardware successfully reproduces these four types of chaotic attractors, confirming the theoretical predictions. The proposed hyperchaotic system is then applied to image encryption, introducing a novel encryption method. The hyperchaotic key sequence generated by this system meets 15 tests of the NIST SP800-22 standard, and further experimental validation with STM32 hardware demonstrates the algorithm's effectiveness, simplicity, non-linearity, and high security. The encrypted images and sequences are rigorously tested key space analysis, histogram similarity analysis, information entropy analysis, statistical attack analysis, differential attack analysis, key sensitivity analysis, and correlation analysis, highlighting the robustness and reliability of the proposed system. This method is versatile and can be extended to various fields, including audio and video encryption, text encryption, IoT security, financial transaction security, and medical data protection.

Introduction

Since Rŏssler discovered the first hyperchaotic system¹ in 1979, the evolution of hyperchaotic systems from discovery to application has encompassed multiple stages, including theoretical research^2,3,4,5, numerical simulation^6,7,8,9, experimental validation^{10,11,12,13,14}, and application exploration^15,16,17,18. In recent years, the rapid proliferation of digital images containing sensitive information has heightened the need for robust encryption techniques to protect against unauthorized access and illegal copying^{19,20,21,22,23}. Traditional image encryption methods often struggle with issues such as limited parameter ranges, slow encryption speeds, and vulnerability to various attacks. To address these challenges, researchers have explored the use of hyperchaotic systems, which offer complex dynamic properties and high sensitivity to initial conditions, making them suitable for secure image encryption applications.

Several novel image encryption frameworks and algorithms have been proposed, leveraging different forms of hyperchaotic systems to enhance security and efficiency. A common approach involves multi-stage encryption processes that combine permutation and diffusion techniques. For instance, one framework²⁴ utilizes a new hyperchaotic system based on STM32 and single neuron models (SNM), involving three stages that apply a substitution box (S-box) followed by an XOR operation with encryption keys derived from the numerical solutions of hyperchaotic maps and SNM. This method significantly enhances security with a vast key space and improves encryption efficiency through optimized parallel processing.

Another approach²⁵ employs a 2D hyperchaotic map for designing an efficient pseudo-random number generator (PRNG) and a color image encryption algorithm. The hyperchaotic system generates highly random sequences validated through various analyses, with the PRNG passing all NIST tests. The encryption algorithm uses cross-channel permutation and diffusion to enhance security and speed, though the framework's complexity may require significant computational resources.

Further advancements include the use of a 6D hyperchaotic system combined with random signal insertion. This scheme²⁶ leverages the sum of all plaintext pixels to generate initial values, ensuring high key sensitivity. The encryption process involves splitting each pixel, scrambling, cycle shifting, and diffusion, resulting in robust security against various attacks. Similarly, a fast and secure image encryption algorithm²⁷ utilizes a time-delayed combinatorial hyperchaos map to enhance security and efficiency through simultaneous shuffling and diffusion processes.

Color image encryption algorithms²⁸ have also been developed, incorporating hyperchaotic maps with DNA mutation operations. These methods enhance dynamic properties and introduce additional randomness and complexity, validated through extensive simulations demonstrating robustness against various attacks. A novel image encryption algorithm²⁹ combining a seven-dimensional hyperchaotic map with stochastic signal injection further increases security, employing SHA-512 for initial value generation to ensure strong correlation with plaintext images.

Additionally, The logistic Feigenbaum nonlinear cross-coupled hyperchaotic map³⁰ with dynamic correlation of plaintext pixels offers improved chaotic properties and reduced computational complexity, validated through extensive security analyses. Reservoir computing³¹ approaches for digital image encryption and hyperchaotic finance model forecasting provide faster and more accurate long-term predictions with reduced execution times, enhancing security and efficiency.

Optical image encryption³² algorithms combining 4D memristive hyperchaotic systems with compressed sensing reduce image size and transmission burden while maintaining high security, validated through extensive simulations. Deep learning-based compression³³ combined with two-dimensional Sin-Linear-Cos hyperchaotic maps and matrix encoding ensures high-quality cipher images, fast processing speeds, and robustness against attacks.

Despite the advancements in hyperchaotic-based encryption algorithms, challenges remain in terms of implementation complexity and dependency on numerical precision. The development and application of novel four-dimensional hyperchaotic systems for image encryption demonstrate increased complexity and unpredictability, validated through extensive statistical tests and dynamic analyses^16,34,35.

Critically, the cryptanalysis of existing hyperchaotic-based encryption algorithms³⁶ reveals vulnerabilities to chosen plaintext attacks, highlighting the need for continuous improvement in algorithmic security structures. Lastly, the introduction of reservoir computing approaches and non-degenerate hyperchaotic systems for secure DNA-coding image optical communication underscores the potential for enhanced performance and security in optical access networks³⁷.

The reviewed literature illustrates significant progress in developing robust, hyperchaotic-based image encryption algorithms, each offering unique enhancements in security, efficiency, and resistance to various attacks. However, the construction of new hyperchaotic systems and the comprehensive analysis of their dynamic behavior, as well as the engineering implementation of image encryption, remain key considerations for future research and practical applications. Additionally, there are few reported studies on utilizing the high randomness and complexity of hyperchaotic systems combined with embedded hardware STM32 for image encryption.

Based on the above analysis, the research content of this paper includes the following. Firstly, a novel 4D hyperchaotic system based on a modified 3D Lorenz chaotic system is devised and analyzed for its dynamic properties, including equilibrium point stability, Lyapunov exponents’ spectrum, bifurcation diagram, and chaotic attractors. MATLAB numerical simulations confirm its hyperchaotic behavior, and experimental validation using embedded hardware STM32 demonstrates consistency between the hardware results and MATLAB simulations through oscilloscope displays of the attractor phase portrait. Secondly, leveraging the hyperchaotic key sequence generated by this system, color image pixel encryption is achieved via two bit-XOR operations, with experimental findings revealing high randomness in the hyperchaotic key sequence and the encrypted image making it impossible to discern any information about the original image, meeting 15 tests of the NIST SP800-22 standard. Thirdly, analysis against statistical attacks, differential attacks, key sensitivity, correlation, and key space demonstrates that the encrypted data sequence resembles random noise, underscoring the high complexity and nonlinearity of the hyperchaotic key sequence. Lastly, the conclusions are drawn.

Dynamical analysis of a new hyperchaotic system

An 4D hyperchaotic system³⁸ is described by (1):

$$\left\{\begin{array}{l}\dot{x}=40\left(y-x\right)+w\\ \dot{y}\text{ = 10}x+ \text{ 25} y\text{- }xz\\ \begin{array}{l}\dot{z}\text{ = }xy\text{- 3}z\\ \dot{w}\text{ = }dx\end{array}\end{array}\right.$$

(1)

where $x$, $y$, $z$ and $w$ are driving variables, and $d$ is a positive real parameter. Varying the parameter $d$ can cause system (1) to exhibit hyperchaotic, chaotic, periodic, or quasi-periodic motion. Notably, the hyperchaotic system (1) has only one equilibrium point ${\varvec{O}}\left(\text{0,0},\text{0,0}\right)$, which is unstable and acts as a saddle point.

Linearizing the system (1) and calculating the Jacobian matrix at the equilibrium point ${\varvec{O}}\left(\text{0,0},\text{0,0}\right)$ is shown as follows:

$${\text{J}}_{0}\text{=}\left(\begin{array}{cc}\begin{array}{cc}\text{-40}& {40}\end{array}& \begin{array}{cc}{0}& {1}\end{array}\\ \begin{array}{cc}\begin{array}{c}{10}\\ {0}\\ {\text{d}}\end{array}& \begin{array}{c}{25}\\ {0}\\ {0}\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}{0}\\ \text{-3}\\ {0}\end{array}& \begin{array}{c}{0}\\ {0}\\ {0}\end{array}\end{array}\end{array}\right)$$

(2)

Let $det\left( {{\varvec{J}}_{{0}} - {\uplambda }{\mathbf{I}}} \right) = 0$, the eigenvalues of system (1) in the equilibrium point ${\varvec{O}}\left(\text{0,0},\text{0,0}\right)$ is:

$${\lambda }_{1}=-40,{\lambda }_{2}=25,{\lambda }_{3}=-3, {\lambda }_{4}=0.$$

(3)

Herein, ${\lambda }_{2}=25$ is positive, ${\lambda }_{1}=-40$ and ${\lambda }_{3}=-3$ are negative. So, the equilibrium point ${\varvec{O}}\left(\text{0,0},\text{0,0}\right)$ is saddle point of system (1), and it is unstable. It indicates the new system (1) is dissipative, and can be obtained:

$$\nabla V = \frac{{\partial \dot{x}}}{\partial x} + \frac{{\partial \dot{y}}}{\partial y} + \frac{{\partial \dot{z}}}{\partial z} + \frac{{\partial \dot{w}}}{\partial w} = - 40 + 25 - 3 = - 18.$$

(4)

That is, each volume containing the system orbit shrinks to zero as $t\to \infty$ at an exponential rate $-18$. Consequently, all orbits of system (1) will ultimately be confined to a specific subset of zero volume.

Numerical simulation results

MATLAB excels in numerical simulation with advanced mathematical libraries, matrix operation advantages, a flexible programming language, and support for parallel computing. Its extensive toolbox spans multiple domains, and powerful plotting and visualization tools aid in intuitively showcasing simulation results. Therefore, this paper employs MATLAB simulation software for the numerical analysis of the hyperchaotic system.

According to chaos theory, the adjacent trajectories of a chaotic attractor in the state space separate from each other exponentially. The spectrum of Lyapunov exponents quantitatively shows the contraction or expansion of these trajectories.

Figure 1 shows the Lyapunov exponents’ spectrum of system (1) with the changing of parameter $d$. It can be observed that as the parameter $d$ changes, the four Lyapunov exponents of the constructed new system (1) also vary. The largest Lyapunov exponent remains positive over a significant range of parameter $d$, and the second-largest Lyapunov exponent exhibits positive as parameter $d$ changes. Therefore, the system (1) demonstrates hyperchaotic characteristics.

Fig. 1

Lyapunov exponents’ spectrum of system (1).

Figure 2 shows the bifurcation diagram of state variable $x$ of system (1). It is evident that as the parameter $d$ gradually changes, the bifurcation diagram reflects the instability and complexity of the system's solutions $x$, providing information about the transition from order to chaos. When the bifurcation diagram exhibits more and increasingly complex branches, it indicates that the dynamical behavior of the new system (1) becomes more intricate, potentially entering a chaotic state.

Fig. 2

Bifurcation diagram of $x$.

It is found that both of the Lyapunov exponents’ spectrum and the bifurcation diagram match, indicating that the numerical simulation results are correct. The variation of system (1) with parameter $d$ is depicted in Table 1. For $1<d\le 23.5$, system (1) exhibits hyperchaotic behavior.

Table 1 Stability of system (1) under different parameter $d$.

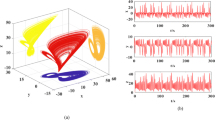
Let $d=15$, the Lyapunov exponents of system (1) is $\left(1.8451, 0.1832, 0, -19.9925\right)$, the hyperchaotic attractor is shown in Fig. 3a. Let $d=70$, the Lyapunov exponents of system (1) is $\left(1.2823, 0, -0.5963, -18.7196\right)$, the chaotic attractor is shown in Fig. 3b. Let $d=100$, the Lyapunov exponents of system (1) is $\left(0, -1.0039, -0.9961, -16.0151\right)$, the periodic orbit attractor is shown in Fig. 3c. Let $d=120$, the Lyapunov exponents of system (1) is $\left(0, 0, -2.1678, -15.8563\right)$, the quasi-periodic orbit attractor is shown in Fig. 3d.

Fig. 3

The attractors of system (1) ((a) hyperchaotic attractor ($d=15$); (b) chaotic attractor ($d=70$); (c) periodic attractor ($d=100$); (d) quasi-periodic attractor ($d=120$)).

Embedded hardware implementation results

In embedded hardware, common components include DSP and FPGA, with DSP widely applied in various embedded implementations due to its flexibility. The STM32 microcontroller, representing a typical embedded hardware, integrates numerous peripherals, prioritizes power optimization, and offers flexible configuration options. Extensively utilized in industrial control, automotive electronics, medical devices, and consumer electronics, it meets the requirements of diverse application scenarios.

In this experiment, an STM32F103ZET6 microcontroller is used to simulate and control the phase diagram of a hyperchaotic system. The results of the embedded system are displayed using a Tektronix TBS1072C digital oscilloscope. The implementation of hyperchaotic systems on STM32 has significant purposes and implications:

• a. Hyperchaotic systems are complex nonlinear dynamical systems that exhibit chaotic behavior. Implementing them on STM32 can provide valuable insights into the characteristics and behavior of hyperchaotic systems, as well as challenges related to modeling, simulation, and control of nonlinear dynamical systems.

• b. Hyperchaotic systems have wide-ranging applications in communication, encryption, control, and other fields. Implementing them on STM32 can provide a solid foundation for basic research and experimental validation in these fields.

  $$\left\{\begin{array}{l}{h}_{1}\_x\text{ = }\left({40}\times \left(y\left[\tau \right]-x\left[\tau \right]\right)\text{+}w\left[\tau \right]\right)\times h\\ {h}_{1}\_y= \text{ } \left({10}\times x\left[\tau \right]\text{+}{25}\times y\left[\tau \right]-x\left[\tau \right]\times z\left[\tau \right]\right)\times h\\ \begin{array}{l}{h}_{1}\_z\text{ = }\left(x\left[\tau \right]\times y\left[\tau \right]-{3}\times z\left[\tau \right]\right)\times h\\ {h}_{1}\_w= \text{ } \left(d\times x\left[\tau \right]\right)\times h\\ \begin{array}{l}temp\_x \, = \text{ } x\left[\tau \right]\text{+}{h}_{1}\_w/{2}\\ temp\_y \, = \text{ } y\left[\tau \right]\text{+}{h}_{1}\_y/{2}\\ \begin{array}{l}temp\_z \, = \text{ } z\left[\tau \right]\text{+}{h}_{1}\_z/{2}\\ temp\_w \, = \text{ } w\left[\tau \right]\text{+}{h}_{1}\_w/{2}\\ \begin{array}{l}{h}_{2}\_x= \text{ } \left({40}\times \left(temp\_y-temp\_x\right)\text{+}temp\_w\right)\times h\\ {h}_{2}\_y\text{ = }\left({10}\times temp\_x\text{+}{25}\times temp\_y-temp\_x\times temp\_z\right)\times h\\ \begin{array}{l}{h}_{2}\_z\text{ = }\left(temp\_x\times temp\_y-{3}\times temp\_z\right)\times h\\ {h}_{2}\_w\text{ = }\left(d\times temp\_x\right)\times h\\ \begin{array}{l}temp\_x \, = \text{ } x\left[\tau \right]\text{+}{h}_{2}\_x/{2}\\ temp\_y \, = \text{ } y\left[\tau \right]\text{+}{h}_{2}\_y/{2}\\ \begin{array}{l}temp\_z \, = \text{ } z\left[\tau \right]\text{+}{h}_{2}\_z/{2}\\ temp\_w \, = \text{ } w\left[\tau \right]\text{+}{h}_{2}\_w/{2}\\ \begin{array}{l}{h}_{3}\_x\text{ = }\left({40}\times \left(temp\_y-temp\_x\right)\text{+}temp\_w\right)\times h\\ {h}_{3}\_y\text{ = }\left({10}\times temp\_x\text{+}{25}\times temp\_y-temp\_x\times temp\_z\right)\times h\\ \begin{array}{l}{h}_{3}\_z\text{ = }\left(temp\_x\times temp\_y-{3}\times temp\_z\right)\times h\\ {h}_{3}\_w\text{ = }\left(d\times temp\_x\right)\times h\\ \begin{array}{l}temp\_x \, = \text{ } x\left[\tau \right]\text{+}{h}_{3}\_x\\ {\text{t}}emp\_y \, = \text{ } y\left[\tau \right]\text{+}{h}_{3}\_y\\ \begin{array}{l}temp\_z \, = \text{ } z\left[\tau \right]\text{+}{h}_{3}\_z\\ temp\_w \, = \text{ } w\left[\tau \right]\text{+}{h}_{3}\_w\\ \begin{array}{l}{h}_{4}\_x\text{ = }\left({40}\times \left(temp\_y-temp\_x\right)\text{+}temp\_w\right)\times h\\ {h}_{4}\_y\text{ = }\left({10}\times temp\_x\text{+}{25}\times temp\_y-temp\_x\times temp\_z\right)\times h\\ \begin{array}{l}{h}_{4}\_z= \text{ } \left(temp\_x\times temp\_y-{3}\times temp\_z\right)\times h\\ {h}_{4}\_w= \text{ } \left(d\times temp\_x\right)\times h\\ \begin{array}{l}x\left[\tau +1\right] \, = \text{ } x\left[\tau \right]\text{+}\left({h}_{1}\_x+ \text{2} \times {h}_{2}\_x+ \text{2} \times {h}_{3}\_x\text{+}{h}_{4}\_x\right)/6\\ y\left[\tau +1\right] \, = \text{ } y\left[\tau \right]\text{+}\left({h}_{1}\_y+ \text{2} \times {h}_{2}\_y+ \text{2} \times {h}_{3}\_y\text{+}{h}_{4}\_y\right)/6\\ \begin{array}{l}z\left[\tau +1\right] \, = \text{ } z\left[\tau \right]\text{+}\left({h}_{1}\_z+ \text{2} \times {h}_{2}\_z+ \text{2} \times {h}_{3}\_z\text{+}{h}_{4}\_z\right)/6\\ w\left[\tau +1\right] \, = \text{ } w\left[\tau \right]\text{+}\left({h}_{1}\_w+ \text{2} \times {h}_{2}\_w+ \text{2} \times {h}_{3}\_w\text{+}{h}_{4}\_w\right)/6\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\right.$$

  (5)

• c. Implementing hyperchaotic systems on STM32 requires overcoming technical challenges such as limited hardware resources and complex algorithm implementation, which can promote the development of embedded systems and algorithm optimization.

In experiment, the STM32 is used to verify the 4th-order Runge–Kutta method used for the discretization of the new hyperchaotic system (1), the iterative process is shown in Eq. (5). Where parameter $d=15$, iteration step $h=0.02$. τ represents the current moment, $x\left[\tau \right]$, $y\left[\tau \right]$, $z\left[\tau \right]$ and $w\left[\tau \right]$ are the values of the current moment, $temp\_x$, $temp\_y,$ $temp\_z$ and $temp\_w$ are the intermediate variables, ${h}_{1}\_x$, ${h}_{1}\_y$, ${h}_{1}\_z$ and ${h}_{1}\_w$ are the slopes at the beginning of the time period, ${h}_{2}\_x$, ${h}_{2}\_y$, ${h}_{2}\_z$ and ${h}_{2}\_w$ are the slopes of the midpoint of the time period, the slopes ${h}_{1}\_x$, ${h}_{1}\_y$, ${h}_{1}\_z$ and ${h}_{1}\_w$ are used by Euler's method to determine the values of $x\left[\tau \right]$, $y\left[\tau \right]$, $z\left[\tau \right]$ and $w\left[\tau \right]$ at the point $\tau +h/2$, ${h}_{3}\_x$, ${h}_{3}\_y$, ${h}_{3}\_z$ and ${h}_{4}\_w$ are the slopes of the midpoint, but this time the slopes ${h}_{2}\_x$, ${h}_{2}\_y$, ${h}_{2}\_z$ and ${h}_{2}\_w$ are used to determine the $x\left[\tau \right]$, $y\left[\tau \right]$, $z\left[\tau \right]$ and $w\left[\tau \right]$ values, ${h}_{4}\_x$, ${h}_{4}\_y$, ${h}_{4}\_z$ and ${h}_{4}\_w$ are the slopes of the end of the time period, and their $x\left[\tau \right]$, $y\left[\tau \right]$, $z\left[\tau \right]$ and $w\left[\tau \right]$ values are determined by ${h}_{3}\_x$, ${h}_{3}\_y$, ${h}_{3}\_z$ and ${h}_{3}\_w$. Finally, the values $x\left[\tau +1\right]$, $y\left[\tau +1\right]$, $z\left[\tau +1\right]$ and $w\left[\tau +1\right]$ of the $\tau +1$ moment are calculated.

Then, the digital signals are converted into analog signals through SPI, which is controlled by the DAC converter, and then displayed on the oscilloscope. The embedded system STM32 is depicted in Fig. 4.

Fig. 4

Experimental platform for STM32 implementation.

When $d=15$, Fig. 5a shows the phase transition trajectory of hyperchaotic signal by oscilloscope. When $d=70$, Fig. 5b shows the phase transition trajectory of chaotic signal by oscilloscope. When $d=100$, Fig. 5c shows the phase transition trajectory of periodic orbit by oscilloscope. When $d=120$, Fig. 5d shows the phase transition trajectory of quasi-periodic orbit by oscilloscope.

Fig. 5

Experimental results of STM32 implementation ((a) hyperchaotic orbit ($d=15$); (b) chaotic orbit ($d=70$); (c) periodic orbit ($d=100$); (d) quasi-periodic orbit ($d=120$)).

The alignment of simulation outcomes from MATLAB with the results derived from the hyperchaotic system implemented on the STM32, as illustrated in Figs. 3 and 5, establishes the coherence between the two datasets. This alignment not only affirms the precision and dependability of the simulation model but also underscores the efficacy of deploying the hyperchaotic system on the STM32 platform.

Image encryption

In today's digital society, image encryption, as a crucial branch of information security, plays a key role in safeguarding the privacy of image data and preventing unauthorized access. With the widespread use of images in communication, storage, and sharing, effectively encrypting them has become paramount. Image encryption aims to transform images into unintelligible forms to ensure the security of personal privacy, business secrets, and sensitive information through the utilization of complex mathematical algorithms and keys. The advancement of encryption technology provides essential tools for preventing image information leakage, safeguarding national security, and ensuring confidentiality in fields like medical imaging.

The image encryption technology based on hyperchaotic system-generated hyperchaotic keys exhibits significant necessity and superiority. The hyperchaotic system, with its high dimensionality, complexity, and nonlinear characteristics, forms the basis for generating keys with extremely high randomness, thereby enhancing the security of encryption algorithms. This technology effectively addresses modern challenges in image security by generating complex and unpredictable key sequences, protecting images from unauthorized access and information leakage. Compared to traditional encryption methods, image encryption based on hyperchaotic systems is more resilient to attacks. Supported by embedded hardware like STM32, it achieves efficient encryption and decryption processes, providing an advanced and practical solution for image encryption in the field of information security.

Encryption method

To highlight the simplicity and non-linear advantages of implementing hyperchaotic keys, as well as fully leveraging the benefits of ciphertext interleaving diffusion technology in image encryption to improve its ability to resist illegal attacks, a method of image encryption bit-XOR operation based on hyperchaotic key sequence is proposed. Characterized by suitability for image encryption, non-linear ciphertext, and easy implementation, this approach enhances the speed of ciphertext diffusion. The image encryption process based on the generation of a hyperchaotic key sequence from the hyperchaotic system is shown in Fig. 6, involves four steps:

Fig. 6

The image encryption process using the hyperchaotic key sequence.

Firstly, construct a hyperchaotic system and analyze its dynamic characteristics to demonstrate its complexity, randomness, and nonlinearity, as described in section “Dynamical analysis of a new hyperchaotic system”.

Secondly, generate hyperchaotic key sequences that meet the requirements based on the constructed hyperchaotic system, with each hyperchaotic key represented by 16 bits, as detailed in subsection “Hyperchaotic key sequence”. Next, decompose the color image to be encrypted (with each pixel represented by 8 bits) into three matrices representing the RGB channels. Convert each matrix into a column vector and concatenate them to form a complete column vector, serving as the data sequence for the image, as shown in Fig. 7.

Fig. 7

The process diagram of converting the original image into a data sequence.

Then, perform bitwise bit-XOR operations between each value of the image sequence and the corresponding value of the hyperchaotic sequence, obtaining an 8-bit encrypted sequence according to the following formula (6).

$${\varvec{R}}={\varvec{S}}\oplus {{\varvec{K}}}_{H}\oplus {{\varvec{K}}}_{L}$$

(6)

where ${\varvec{R}}$ sequence is the encrypted image sequence using bit-XOR operation, ${\varvec{S}}$ sequence is the original image sequence, and ${\varvec{K}}$ sequence is the hyperchaotic key sequence, ${{\varvec{K}}}_{H}$ and ${{\varvec{K}}}_{L}$ represent the high 8-bit and low 8-bit sub-sequences of the key sequence ${\varvec{K}}$.

Finally, output the encrypted image sequence through the serial port of the embedded hardware STM32. The decryption of the image follows the reverse process of encryption, with the decryption bit-XOR operation being consistent with the encryption process.

Hyperchaotic key sequence

Due to the inherent high randomness and complexity of the hyperchaotic system, the encryption algorithm's security is significantly strengthened. The generation of the hyperchaotic key sequence involves transforming the hyperchaotic sequence into the required key sequence through a specific quantization algorithm, outlined in the following steps:

Step 1: Pre-iterate the hyperchaotic system ${N}_{1}$ times to eliminate transient effects as it enters a hyperchaotic state.

Step 2: Iterate the hyperchaotic system ${N}_{2}$ times to obtain a new set of state values, ${\varvec{A}}=\left\{Ax, Ay, Az, Aw\right\}$, where $Ax={\{{x}_{1}, {x}_{2},{x}_{3}, {x}_{4}\}}^{T}$, $Ay={\{{y}_{1}, {y}_{2},{y}_{3}, {y}_{4}\}}^{T}$, $Az={\{{z}_{1}, {z}_{2},{z}_{3}, {z}_{4}\}}^{T}$, and $Aw={\{{w}_{1}, {w}_{2},{w}_{3}, {w}_{4}\}}^{T}$, $0<k\le {N}_{2}$. Scale down the state values ${\varvec{A}}$ to $1/p$ and take $q$ decimal places to generate new state values ${\varvec{B}}=\left\{Bx, By, Bz, Bw\right\}$, where $Bx={\{{bx}_{1}, {bx}_{2},{bx}_{3}, {bx}_{4}\}}^{T}$, $By={\{{by}_{1}, {by}_{2},{by}_{3}, {by}_{4}\}}^{T}$, $Bz={\{{bz}_{1}, {bz}_{2},{bz}_{3}, {bz}_{4}\}}^{T}$, and $Bw={\{{bw}_{1}, {bw}_{2},{bw}_{3}, {bw}_{4}\}}^{T}$, $0<k\le {N}_{2}$. The conversion formula is given by:

$$\left\{ {\begin{array}{*{20}l} {bx_{i} = x_{i} *10^{{\left( {p - q} \right)}} - \left\lfloor {x_{i} *10^{{\left( {p - q} \right)}} } \right\rfloor ,} \hfill & {if} \hfill & {x_{i} \ge 0,i = {1,2}, \cdots ,k} \hfill \\ {bx_{i} = \left\lfloor {x_{i} *10^{{\left( {p - q} \right)}} } \right\rfloor - x_{i} *10^{{\left( {p - q} \right)}} ,} \hfill & {if} \hfill & {x_{i} < 0,i = {1,2}, \cdots ,k} \hfill \\ {by_{i} = y_{i} *10^{{\left( {p - q} \right)}} - \left\lfloor {y_{i} *10^{{\left( {p - q} \right)}} } \right\rfloor ,} \hfill & {if} \hfill & {y_{i} \ge 0,i = {1,2}, \cdots ,k} \hfill \\ {by_{i} = \left\lfloor {y_{i} *10^{{\left( {p - q} \right)}} } \right\rfloor - y_{i} *10^{{\left( {p - q} \right)}} ,} \hfill & {if} \hfill & {y_{i} < 0,i = {1,2}, \cdots ,k} \hfill \\ {bz_{i} = z_{i} *10^{{\left( {p - q} \right)}} - \left\lfloor {z_{i} *10^{{\left( {p - q} \right)}} } \right\rfloor ,} \hfill & {if} \hfill & {z_{i} \ge 0,i = {1,2}, \cdots ,k} \hfill \\ {bz_{i} = \left\lfloor {z_{i} *10^{{\left( {p - q} \right)}} } \right\rfloor - z_{i} *10^{{\left( {p - q} \right)}} ,} \hfill & {if} \hfill & {z_{i} < 0,i = {1,2}, \cdots ,k} \hfill \\ {bw_{i} = w_{i} *10^{{\left( {p - q} \right)}} - \left\lfloor {w_{i} *10^{{\left( {p - q} \right)}} } \right\rfloor ,} \hfill & {if} \hfill & {w_{i} \ge 0,i = {1,2}, \cdots ,k} \hfill \\ {bw_{i} = \left\lfloor {w_{i} *10^{{\left( {p - q} \right)}} } \right\rfloor - w_{i} *10^{{\left( {p - q} \right)}} ,} \hfill & {if} \hfill & {w_{i} < 0,i = {1,2}, \cdots ,k} \hfill \\ \end{array} } \right.$$

(7)

where $\left\lfloor \cdot \right\rfloor$ denotes the floor function, $p$ and $q$ are adjustable parameters, representing scaling down the value by $1/p$ and taking $q$ decimal places as the new state value.

Step 3: Calculate the key sequence. Adjust the order of the state values ${\varvec{B}}$ based on positive and negative changes in the state values ${\varvec{A}}$ to generate the key sequence $=\left\{{K}_{1},{K}_{2},{K}_{3}, {K}_{4}\right\}$, $0<k\le {N}_{2}$, following the mapping relationship outlined in Table 2.

Table 2 The mapping relationship illustrating the sorting rule of state values ${\varvec{A}}$ and ${\varvec{B}}$ in correlation with the generation of the key sequence ${\varvec{K}}$.

The randomness of the hyperchaotic key sequence can be evaluated using the NIST SP800-22 standard. This standard, developed by the National Institute of Standards and Technology (NIST) in the United States, is one of the authoritative standards for pseudo randomness testing. It includes a total of 15 test metrics, examining the deviation of the tested sequence from ideal random sequences from different perspectives in terms of statistical characteristics. With a significance level of $0.01$, a test group number of 100, a group length of 1024000 bits, and a confidence interval of $\left[\text{0.93,1}\right]$, the test results are presented in Table 3. For items with a test frequency not less than 2, Table 3 provides P-values and the minimum values of pass rates. It can be observed that the hyperchaotic key sequence generated by the algorithm has successfully passed all 15-test metrics, further confirming its excellent randomness.

Table 3 The NIST SP 800-22 test result for hyperchaotic key sequence.

Experimental results

Since the STM32 achieves synchronized control of the encryption module and the interface module through the master clock, eliminating the need for separate control of the hyperchaotic system's encryption and decryption processes. This approach avoids the synchronization issues between the encryption and decryption modules that are commonly encountered in traditional encryption systems.

Specifically, in this experiment, image encryption based on the hyperchaotic key sequence was implemented using the embedded hardware STM32F103ZET6. Due to the absence of an integrated image acquisition and display module in the STM32F103ZET6, data input and output were facilitated in the form of a list. The resulting encrypted and decrypted image sequences were then transmitted to the PC via the serial port of the embedded hardware STM32F103ZET6. Subsequently, the data was visualized and printed using a serial port debugging tool, as shown in Fig. 8.

Fig. 8

The image encrypted and decrypted sequences printed by the serial port debugging tool.

Although the embedded hardware STM32F103ZET6 can complete the experimental process, it lacks data analysis tools, making it difficult to visually compare the information before and after image encryption. Therefore, it is necessary to transmit the data sequence generated in the embedded hardware STM32F103ZET6 to the PC through the serial port and use simulation software MATLAB for analysis. Figure 9a and d show the color image before encryption, Fig. 9b and e display the color image after encryption, Fig. 9c and f depict the color image after decryption.

Fig. 9

Image and histogram of encryption/decryption.

Comparing Fig. 9a, b, c, and d, e, f, the original images are the 256*256 color picture. After encryption with the hyperchaotic key sequences, the images are completely flooded with noise, making them impossible to discern the real information of the original image. After decryption, the images show no differences in the time domain compared to the original images. The serial port data printed by the embedded hardware STM32F103ZET6 also confirms that the image sequences before and after encryption are identical.

The real information of the original image is completely concealed after encryption, and the encrypted image sequence exhibits a Gaussian random white noise distribution, validating the high security of the image encryption method based on the hyperchaotic key sequence. The decrypted image is identical to the original image, demonstrating that image encryption based on the hyperchaotic key sequence does not have a negative impact on the original data, and using the STM32F103ZET6 embedded hardware system as the encryption device does not introduce noise. Therefore, the image encryption method based on the hyperchaotic key sequence generated by the hyperchaotic system is both secure and effective.

Performance evaluation

To evaluate the performance of this scheme, five key aspects were analyzed: key space analysis, histogram similarity analysis, information entropy analysis, statistical attack analysis, differential attack analysis, key sensitivity analysis, and correlation analysis. The performance analysis was conducted on a Windows operating system using Python software, with a PC configuration of an Intel i5-12450H 2.0 GHz CPU, 16 GB RAM, and 512 GB ROM. MATLAB 2019a was used for the analysis software.

Key space analysis

The key space size is a crucial factor in determining whether an encryption algorithm can resist brute-force attacks. Generally, an encryption algorithm is considered secure against such attacks when its key space exceeds ${2}^{100}$. For the hyperchaotic mapping, the state values $\left(x,y,z,w\right)$ range between $\left(-\text{100,100}\right)$, and six decimal places are used as the key. With double-precision floating-point data, accurate to 15 decimal places, the key space can reach approximately $2\times 1{0}^{15}\times 2\times 1{0}^{15}\times 2\times 1{0}^{15}\times 2\times 1{0}^{15}\approx {2}^{203}$, which is equivalent to a 203-bit key length. When including system parameters $d$ and pre-iteration times ${N}_{0}$, the key space expands even further, providing strong resistance against exhaustive attacks.

Table 4 presents the key space test results of different schemes, showing that the reference schemes have larger key spaces than the proposed method. However, those systems are more complex, with dimensions exceeding six, which affects encryption efficiency and storage requirements. Although the key space in this scheme is relatively smaller, it still far exceeds the minimum key space requirements for encryption systems.

Table 4 Key space of different schemes.

Histogram similarity analysis

To comprehensively demonstrate the effectiveness of the proposed hyperchaotic system for encryption, 71 images were selected from the MATLAB 2019a toolbox for encryption validation. The effectiveness of the encryption scheme was verified by analyzing the histogram similarity before and after encryption. The test results are shown in Table 5.

Table 5 Histogram similarity before and after image encryption.

Histogram similarity is an effective metric for evaluating the performance of an image encryption scheme. A lower histogram similarity indicates a significant difference between the histograms of the original and encrypted images, suggesting that the encryption algorithm has successfully altered the pixel distribution, making it difficult to find any correlation between the two. In practical applications, the histogram similarity after image encryption should generally be less than 0.3. As shown in Table 5, among the 71 images tested, the highest histogram similarity was 0.2966372, and the lowest was 0.0089738, which meets the requirements for evaluating the effectiveness of image encryption based on histogram similarity.

Information entropy analysis

Information entropy is a crucial metric for measuring the amount of information or uncertainty within an image, reflecting the complexity of the image by evaluating the randomness of pixel values. In image encryption, high entropy indicates that the encrypted image possesses a high degree of randomness and uncertainty, making it extremely difficult to reverse-engineer the original image through statistical methods. Therefore, entropy is commonly used to assess the effectiveness of encryption algorithms. Ideally, the entropy of an encrypted image should approach the maximum value (typically close to 8 for an 8-bit image), indicating a uniform pixel distribution and that the image resembles random noise, effectively safeguarding the original image information.

Table 6 presents the entropy values before and after encryption for 71 images, showing that the entropy of the encrypted images is close to 8, demonstrating the high randomness and uncertainty achieved by the proposed encryption scheme.

Table 6 Information entropy before and after image encryption.

Table 7 compares the entropy values of images after encryption using the proposed scheme with other schemes, further illustrating that the proposed method effectively confuses pixel values and enhances the security of the encrypted images.

Table 7 Information entropy of different schemes.

Statistical attack analysis

The distribution histograms of the original image and the encrypted image are shown in Fig. 10a and c, b and d respectively.

Fig. 10

Histograms distribution of images before and after encryption.

From Fig. 10, it can be observed that the distribution of the original image histogram is uneven, with a higher probability density in the low pixel segment and a lower probability density in the high pixel segment. In addition, the distribution of the encrypted image is flat and uniform, with similar probability densities in the low and high pixel segments. This indicates that the probability of pixel values in the encrypted image tends to be equal. Therefore, this encryption algorithm can effectively resist statistical analysis attacks.

Differential attack analysis

According to the principles of cryptography, the stronger the sensitivity of the key to plaintext, the stronger the resistance against differential attacks. The sensitivity of plaintext can be measured using the number of signals change rate (NSCR) and the unified average changing intensity (UACI). They respectively represent the proportion and degree of change in pixel values of the encrypted image when a pixel value of the original image is randomly altered. Assuming that the values of two ciphertext signals at point $i$ are $C\left(i\right)$ and ${C}{\prime}\left(i\right)$, if $C\left(i\right)={C}{\prime}\left(i\right)$, then $D\left(i\right)=0$; if $C\left(i\right)\ne {C}{\prime}\left(i\right)$, then $D\left(i\right)=1$. Then the definitions of NSCR and UACI are as follows Eq. (8):

$$\begin{array}{*{20}c} {NSCR = \frac{{\mathop \sum \nolimits_{i = 1}^{N} D\left( i \right)}}{N} \times 100{\text{\% }}} \\ {UACI = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \frac{{\left| {C^{\prime } \left( i \right) - C\left( i \right)} \right|}}{255} \times 100{\text{\% }}} \\ \end{array} { }$$

(8)

where $N$ is the number of image pixels. In this experiment, 256 groups were selected for encryption, with each group consisting of 2 image sequences: one original image sequence and one encrypted image sequence.

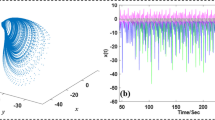
The NSCR and UACI value curves for the 256 sets of ciphertext signals obtained from the Flower image are shown in Fig. 11a and b, respectively, with average values of 99.59% for NSCR and 35.22% for UACI. Similarly, the NSCR and UACI value curves for the 256 sets of ciphertext signals obtained from the Onion image are displayed in Fig. 11c and d, with average values of 99.60% for NSCR and 33.84% for UACI. These results indicate that the bit-XOR operation causes slight changes in the lower bits of the plaintext to induce significant changes in the higher bits of the ciphertext, while changes in the higher bits of the plaintext can simultaneously affect both the higher and lower bits of the ciphertext. This enhances the overall variation magnitude of the ciphertext. Additionally, the differential attack test results from other schemes^{28,43,44,45,46,47} are summarized in Table 8, demonstrating that the proposed algorithm not only resists differential attacks but also performs stably.

Fig. 11

Plaintext sensitivity test.

Table 8 NPCR and UACI of different schemes.

Key sensitivity analysis

A good cryptographic algorithm must be highly sensitive to the key, meaning that even slight differences in encryption keys should result in significant changes in the ciphertext sequence for the same plaintext. Similarly, for the same ciphertext, slight differences in the decryption key should lead to vastly different decryption results.

In this experiment, the initial values $\left({x}_{0},{y}_{0},{z}_{0},{w}_{0}\right)$ of the system are used as the key. Initially, the encryption is performed using the key $\left(\text{1,1},\text{1,1}\right)$, followed by decryption using five sets of decryption keys with minor differences, including $\left(1+{10}^{-15},\text{1,1},1\right)$, $\left(\text{1,1}+{10}^{-15},\text{1,1}\right)$, $\left(\text{1,1},1+{10}^{-15},1\right)$, $\left(\text{1,1},\text{1,1}+{10}^{-15}\right)$, and $\left(1+{10}^{-15},1+{10}^{-15},1+{10}^{-15},1+{10}^{-15}\right)$.

Figure 12a is the original image, Fig. 12b is the decrypted image when the error in the initial decryption key ${x}_{0}$ is ${10}^{-15}$, Fig. 12c is the decrypted image when the error in the initial decryption key ${y}_{0}$ is ${10}^{-15}$, Fig. 12d is the decrypted image when the error in the initial decryption key ${z}_{0}$ is ${10}^{-15}$, Fig. 12e is the decrypted image when the error in the initial decryption key ${w}_{0}$ is ${10}^{-15}$, Fig. 12f is the decrypted image when the errors in the initial decryption keys ${x}_{0}$, ${y}_{0}$, ${z}_{0}$, and ${w}_{0}$ are all ${10}^{-15}$. Where it can be observed that the correctly decrypted signal matches the original image, indicating successful data recovery, while the remaining five sets of erroneous decryption signals resemble noise signals, demonstrating the extreme sensitivity of the algorithm to the key.

$$MSE = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \left( {P^{\prime } \left( i \right) - P\left( i \right)} \right)^{2} { }$$

(9)

Fig. 12

Correctly decrypted image and incorrectly decrypted images.

Let the original image be denoted as $P$ and the decrypted image as ${P}{\prime}$. Their mean square error is calculated using Eq. (9), and the mean square error between the erroneous decryption signal and the original image is presented in Fig. 13. It can be observed that even slight errors in the decryption key result in vastly different decryption results, thus numerically proving the sensitivity of the algorithm to the key.

Fig. 13

The mean square error of error decryption to original image.

Correlation analysis

Pixel values in images are not independent, with small differences in adjacent pixel amplitudes leading to high correlation. Therefore, one of the objectives of encryption algorithms is to reduce the correlation between adjacent pixel values. Lower correlation implies better confusion effects and higher security. Correlation can be measured using correlation coefficients, calculated between adjacent amplitude values of plaintext and ciphertext, as fallowing Eq. (10).

$$Corr = \frac{{\mathop \sum \nolimits_{i = 1}^{M} \left( {x_{i} - \overline{x}} \right)\left( {y_{i} - \overline{y}} \right)}}{{\sqrt {\left( {\mathop \sum \nolimits_{i = 1}^{M} \left( {x_{i} - \overline{x}} \right)^{2} } \right)\left( {\mathop \sum \nolimits_{i = 1}^{M} \left( {y_{i} - \overline{y}} \right)^{2} } \right)} }}{ }$$

(10)

Let ${x}_{i}$ and ${y}_{i}$ represent the i-th pair of adjacent pixel values randomly selected from the image pixel value matrix, and let $\overline{x }$ and $\overline{y }$ be their respective averages. $M$ represents the total number of pairs, with $M$ set to 8, 64, 128, and 256. The calculated results are presented in Table 9.

Table 9 Correlation of adjacent flower image pixels.

A comparison of the data reveals that adjacent original images have a high correlation $\left(Corr\to 1\right)$, while adjacent encrypted signals are almost uncorrelated $\left(Corr\to 0\right)$, indicating good confusion effects. As the correlation coefficient of plaintext increases, the correlation coefficient of ciphertext decreases. This approach effectively spreads the influence of the current ciphertext as the encryption initial parameters onto the next set, continuously enhancing the confusion performance. The correlation diagrams of adjacent pixels in the original image and the encrypted signal are shown in Fig. 14.

Fig. 14

The distributions of adjacent pixels in the original image and encrypted image.

Figure 14 illustrates the distribution of neighboring pixels in both the original and encrypted images. In the original image, pixels are clustered along a line, indicating a strong correlation between neighboring pixels. In contrast, the encrypted image displays a uniform pixel distribution across the entire range. This uniformity results from the disruption and alteration of the original image’s structure during encryption, which effectively conceals patterns and correlations. As a result, statistical attacks are unable to extract meaningful information from the encrypted image, thereby enhancing the security and robustness of the proposed encryption scheme.

The purpose of image encryption is to disrupt the strong correlation between neighboring pixels in the original image. In this study, $256\times 256$ randomly selected pixels were analyzed to compute the image correlations. Table 10 presents the calculated correlation coefficients before and after encryption. As shown in the table, the correlation between neighboring pixels is greatly diminished post-encryption, resulting in images with minimal detectable patterns or regularities.

Table 10 Correlation coefficient values of different schemes.

This section evaluates the performance of an image encryption scheme by analyzing key aspects such as key space, histogram similarity, information entropy, resistance to statistical and differential attacks, key sensitivity, and pixel correlation. The results demonstrate that the scheme effectively disrupts pixel distribution and reduces the correlation between neighboring pixels, exhibiting strong randomness and resistance to attacks, thereby ensuring the security and robustness of the encrypted images.

Conclusions

This paper introduces a novel 4D hyperchaotic system and comprehensively analyzes its fundamental dynamic behaviors, encompassing equilibrium point stability, Lyapunov exponent spectrum, bifurcation diagram, and chaotic attractors. The study reveals that the new hyperchaotic system features a single equilibrium point and can maintain two positive Lyapunov exponents across a wide parameter range, with dynamic behavior ranging hyperchaotic, chaotic, periodic, and quasi-periodic, by adjusting the parameter $d$. Experimental implementation on embedded hardware STM32 validates these dynamics, with oscilloscope displays illustrating phase trajectories, affirming the system's effectiveness.

Moreover, the paper integrates the designed hyperchaotic system with embedded hardware STM32 for image encryption. This encryption algorithm employs the hyperchaotic key sequence generated by the system, with each image pixel undergoing a bit-XOR operation with corresponding bits of the key sequence. Despite its simple implementation, the method demonstrates high algorithmic complexity. Experimental results show that all hyperchaotic key sequences pass the 15 randomness tests of the NIST SP800-22 standard, confirming their complete randomness. Key space analysis, histogram similarity analysis, information entropy analysis, statistical attack analysis, differential attack analysis, key sensitivity analysis, and correlation analysis further validates the effectiveness of the hyperchaotic key-based encryption algorithm for image encryption.

In future research, the aim is to leverage the highly random and complex nature of hyperchaotic key sequences, in conjunction with multiple embedded hardware STM32 units, to achieve secure communication for data encryption/decryption across various domains, such as audio encryption, video encryption, text encryption, IoT security, financial transaction security, and medical data protection.