A novel image encryption scheme based on 2-D logistic map and DNA sequence operations

Abstract

This paper proposes a novel image encryption scheme based on DNA sequence operations and chaotic system. Firstly, two-dimensional logistic chaotic map is employed to modify each pixel of the image, and then, the DNA encoding rules are adopted to encode and generate a DNA matrix. Secondly, pseudo-random sequences generated by two-dimensional logistic map are transformed into another DNA matrix. Thirdly, DNA addition, subtraction and complementary rules are used to control the operations between two DNA matrices for obtaining the ciphered results. Finally, the ciphered image is obtained by decoding the DNA matrix formulations into binary formulations. Experimental results and theoretical analysis show that the scheme is extraordinarily high secure to resist various attacks.

1 Introduction

Along with the rapid development in digital image processing and network communication, information security has become an increasingly serious issue [1–3]. Chaos is a definitive and similar random procedure which appears in a nonlinear system [4, 5]. In recent years, chaotic theory in cryptographic applications is a prospect research area. Many cryptographic protocols have emerged in the scientific literatures [6]. Chaotic systems have a lot of merits such as ergodicity, sensitivity to initial conditions, random-like behaviors and topological transitivity. These features are quite important in confusion and diffusion processes [7]. Therefore, encryption algorithms based on chaotic map are widely applied in cryptography fields. Britain mathematician Matthes [8] firstly adopted chaos theory for the research of encryption technology. Since then, chaos-based encryption schemes have been proposed.

Table 1 DNA encoding rules

Up to now, many chaotic cryptosystems have been proposed [9–16]. However, most of them are proved to be insecure. The most serious problem in applied chaotic systems is that the chaotic dynamics degrade rapidly when they are realized with finite precisions in digital computers [9].

Recently, lots of good characteristics of DNA computing, such as massive parallelism, huge storage and ultra-low power consumption have been infiltrated into the field of cryptography [17, 18]. Therefore, DNA cryptography is a new cryptographic resolution [19–25]. In these DNA-based cryptosystems, DNA is used as information carrier, and the DNA sequence operations and complementary rules are used to encrypt images. Zhang et al. [23] use the idea of DNA subsequence operations instead of complex biological operation for image encryptions. Liu et al. [24] employed Chebyshev maps for random series by using the DNA complementary rule for image encryptions. SaberiKamarposhti et al. [25] proposed hybrid method by using DNA sequences and logistic map for image encryptions. However, in these DNA-based schemes [23–25], the ciphered images solely depend on the secret keys. When the secret key is used repeatedly, these schemes have the risk against chosen plaintext attacks. To overcome this drawback, our scheme in this paper applies not only the 2-D logistic chaotic map but also the input plaintext image to calculate the confused DNA matrix.

The remaining of the paper is organized as follows. In Sect. 2, preliminary materials are introduced. In Sect. 3, the encryption and decryption algorithms are described. Section 4 provides simulation results. Security analysis is given in Sect. 5. Section 6 presents the extended algorithm for color images. Finally, this paper is concluded in Sect. 7.

2 Preliminary materials

2.1 2-D logistic chaotic map

2-D logistic chaotic map can be defined as follows [26]:

$$\begin{aligned} \left\{ {\begin{array}{l} x_{i+1} =x_i u_1 (1-x_i )+\lambda _1 y_i^2 \\ y_{i+1} =y_i u_2 (1-y_i )+\lambda _2 (x_i^2 +x_i y_i ) \\ \end{array}}\right. , \end{aligned}$$

(1)

where $2.75<u_1 \le 3.4, 2.75<u_2 \le 3.45, 0.15<\lambda _1 \le 0.21, 0.13<\lambda _2 \le 0.15, x_i, y_i \in (0,1]$, and the 2-D logistic chaotic map works under a chaotic state. The coefficients $u_1, u_2, \lambda _1, \lambda _2$ and the initial values of the iteration $x_0, y_0$ can be designed as the secret keys for image encryption, which makes the secret key space very large.

2.2 DNA encoding and decoding rules

A DNA sequence is composed of four nucleic acid bases (hereinafter abbreviated to base): A (adenine), C (cytosine), G (guanine) and T (thymine), where A and T are complementary, G and C are complementary. Because 0 and 1 are complementary in the binary, so 00 and 11 are complementary, and 01 and 10 are also complementary. By using four bases A, C, G and T to encode 00, 01, 10 and 11, there are 24 kinds of encoding rules. But there are only eight kinds of encoding rules satisfying the Watson–Crick complement rule [27], as listed in Table 1. DNA decoding rules are the reverse of DNA encoding rules. For example, if the grayscale value of the pixel is 177; its equivalent binary value is “10110001”, which can be encoded as a DNA sequence “CTAG” using DNA encoding Rule 1.

2.3 DNA complementary rule

The DNA complementary rule [21] must satisfy that:

$$\begin{aligned} \left\{ {\begin{array}{l} x\ne B(x)\ne B(B(x))\ne B(B(B(x))) \\ x=B(B(B(B(x)))) \\ \end{array}}\right. , \end{aligned}$$

(2)

where B(x) is the base pair of x, which can guarantee the DNA complementary rule of injective mapping. The number of legal DNA complementary rules should be considered, and there are totally six groups of legal DNA complementary rules, which are shown as follows:

$$\begin{aligned} (1) \quad B_1 (A)= & {} T, B_1 (T)=C, B_1 (C)=G, B_1 (G)=A; \\ (2) \quad B_2 (A)= & {} T, B_2 (T)=G, B_2 (G)=C, B_2 (C)=A; \\ (3) \quad B_3 (A)= & {} C, B_3 (C)=T, B_3 (T)=G, B_3 (G)=A; \\ (4) \quad B_4 (A)= & {} G, B_4 (G)=C, B_4 (C)=T, B_4 (T)=A; \\ (5) \quad B_5 (A)= & {} G, B_5 (G)=T, B_5 (T)=C, B_5 (C)=A; \\ (6) \quad B_6 (A)= & {} C, B_6 (C)=G, B_6 (G)=T, B_6 (T)=A; \end{aligned}$$

where $B_r$ is the r complement rule, $r=1,2,\ldots , 6$.

2.4 DNA addition and subtraction rules

Addition and subtraction operations for DNA sequences are performed according to traditional binary addition and subtraction. Therefore, eight kinds of DNA encoding rules can lead to corresponding eight kinds of DNA addition rules and eight kinds of DNA subtraction rules. For example, according to DNA encoding Rule 1, the DNA addition Rule 1 and DNA subtraction Rule 1 are shown in Tables 2 and 3, respectively.

Table 2 DNA addition rule 1

Table 3 DNA subtraction rule 1

3 Image encryption and decryption scheme

This section presents the proposed image encryption scheme in the framework of symmetric key cipher architecture. Without loss of generality, we employ gray-scale images with the size of $M \times N$ to present the proposed scheme for simplicity. Firstly, the image f is confused by chaotic series of 2-D logistic maps; then, the confused image G and chaotic matrix E are obtained. Secondly, the matrices of G and E are transformed into DNA format matrices D and F. Thirdly, new chaotic series of 2-D logistic maps noted as $X_{2}$ and $Y_{2}$ are calculated by new initial values which depend on the content of plaintext image. Finally, the ciphered image is generated by the results of operations between matrices D and F, and these corresponding operations solely depend on the chaotic series of $X_{2}$ and $Y_{2}$.

3.1 Secret key formulation

The proposed scheme process utilizes the secret key K, which is divided into eight components: $\mu _1 (\mu _1 \in [2.75,3.4]), \mu _2 (\mu _2 \in [2.75,3.45]), \lambda _1 (\lambda _1 \in [0.15,0.21]), \lambda _2 (\lambda _2 \in [0.13,0.15]), x_0 (x_0 \in (0,1]), y_0 (y_0 \in (0,1]), p ((p\in [1,8]))$ and $c_0 (c_0 \in \{\hbox {A, T, G, C}\})$ shown in Fig. 1. The secret keys $\mu _1, \mu _2, \lambda _1, \lambda _2, x_0$ and $y_0$ refer to the parameter $\mu _1, \mu _2, \lambda _1, \lambda _2, x_0$ and $y_0$ in Eq. (1) . The secret key p is the index of DNA encoding rules in Table 1. The secret key $c_0$ is the initial nucleic acid base value for generation of ciphered image.

Fig. 1

Secret key

3.2 Encryption and decryption algorithm

For enhancing the scheme’s sensitivity to plaintext images, the parameter $\varepsilon$ is employed and calculated by the plaintext image as follows:

$$\begin{aligned} \varepsilon =\frac{1}{(M\times N)}\sum _{x=0,y=0}^{x=M-1,y=N-1} {f(x,y)}, \end{aligned}$$

(3)

where f is the input plaintext image with the size of $M\times N$. f(x, y) is the pixel value of the coordinate (x, y). The value of $\varepsilon$ depends on the plaintext image; therefore, the proposed scheme can resist chosen plaintext attacks.

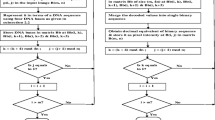
The encryption process of the proposed encryption scheme, shown in Fig. 2, can be presented as follows:

Fig. 2

The flowchart of the proposed scheme

Step 1. Compute $\varepsilon _1$ and $\varepsilon _2$, which are obtained from the sensitive parts of $\varepsilon$ as the following equations:

$$\begin{aligned} \varepsilon _1= & {} \hbox {mod} \left( \left\lfloor {\left( \varepsilon -\left\lfloor \varepsilon \right\rfloor \right) \times 10^{14}} \right\rfloor , 256\right) , \end{aligned}$$

(4)

$$\begin{aligned} \varepsilon _2= & {} \varepsilon -\left\lfloor \varepsilon \right\rfloor . \end{aligned}$$

(5)

Step 2. Assign $u_1, u_2, \lambda _1, \lambda _2, x_0, y_0$ with the corresponding value in secret key. And iterate the 2-D logistic chaotic map $M \times N$ times to obtain two following sequences:

$$\begin{aligned} X_1= & {} \left\{ {x_{200+1}, x_{200+2},\ldots , x_{200+M\times N}} \right\} , \\ Y_1= & {} \left\{ {y_{200+1}, y_{200+2},\ldots , y_{200+M\times N}} \right\} , \end{aligned}$$

where the $X_{1}$ and $Y_{1}$ start from $201^{\mathrm{st}}$ iterations of x and y, which can reduce the harm of initial value $x_{0}$ and $y_{0}$ for obtaining idea of chaotic sequences. In addition, for each element of $X_{1}$, i.e., $x_{200+k} (k \in [1, M \times N])$ and each element of $Y_{1}$, i.e., $y_{200+k} (k \in [1, M \times N])$, the random series $w_{k}$ and $v_{k}$ are calculated as follows:

$$\begin{aligned} w_k= & {} \hbox {mod} \left( \left\lfloor {x_{200+k} \times 10^{16}} \right\rfloor , 256\right) , \end{aligned}$$

(6)

$$\begin{aligned} v_k= & {} \hbox {mod} \left( \left\lfloor {y_{200+k} \times 10^{16}} \right\rfloor , 256\right) , \end{aligned}$$

(7)

where mod (x, y) returns the remainder of x divided by $y, \left\lfloor x \right\rfloor$ rounds x to the nearest integer less than or equal to x. The two random series $w_{k}$ and $v_{k}$ are employed to encrypt the pixel values of odd indexes and even indexes, respectively. The pixels’ values in even indexes and odd indexes of f are noted as f(2u) and $f(2u-1)$. $w_{2u-1}$ and $v_{2u}$ are the pixel values of odd, and even indexes of w and v, respectively, perform the following operations:

$$\begin{aligned}&G(2u-1) = w_{2u-1} \oplus f(2u-1)\oplus \varepsilon _1, \end{aligned}$$

(8)

$$\begin{aligned}&G(2u) = v_{2u} \oplus f(2u)\oplus \varepsilon _1, \end{aligned}$$

(9)

where $\varepsilon _1$ is in binary formulation, $u =1,2, \ldots , \left\lfloor {{(M\times N)}/2} \right\rfloor , \oplus$ denotes XOR operation bit by bit.

Step 3. The matrix G is encoded by the index of the DNA encoding rule p, which is one part of the secret key. Then, the $M \times (N \times 4)$ DNA matrix D is obtained. At the same time, another matrix E is constructed in the size of $M\times N$ using the random series $w_{2u}$ and $v_{2u-1}$. The $M \times (N \times 4)$ DNA matrix F is obtained by encoding matrix E with the index of the DNA encoding rule p.

Step 4. Calculate the new initial values of ${x}^{\prime }_0, {y}^{\prime }_0, {u}^{\prime }_1, {u}^{\prime }_2$ by the secret key and $\varepsilon _2$ as follows:

$$\begin{aligned} {x}^{\prime }_0= & {} \hbox {mod} (x_0 +\varepsilon _2,1), \end{aligned}$$

(10)

$$\begin{aligned} {y}^{\prime }_0= & {} \hbox {mod} (y_0 +\varepsilon _2,1), \end{aligned}$$

(11)

$$\begin{aligned} {u}^{\prime \prime }_1= & {} \hbox {mod} (u_1 +\varepsilon _2,1), \end{aligned}$$

(12)

$$\begin{aligned} {u}^{\prime \prime }_2= & {} \hbox {mod} (u_2 +\varepsilon _2,1), \end{aligned}$$

(13)

where ${u}^{\prime \prime }_1, {u}^{\prime \prime }_2$ are intermediate values for obtaining the initial values of ${u}^{\prime }_1, {u}^{\prime }_2$:

If $0\le {u}^{\prime \prime }_i <0.4$, then ${u}^{\prime }_i ={u}^{\prime \prime }_i +3$;

If $0.4\le {u}^{\prime \prime }_i \le 0.75$, then ${u}^{\prime }_i ={u}^{\prime \prime }_i +2.5$;

If $0.75<{u}^{\prime \prime }_i \le 1$, then ${u}^{\prime }_i ={u}^{\prime \prime }_i +2$.

Step 5. calculate two chaotic sequences $X_{2}$ and $Y_{2}$ by using the initial values of ${x}^{\prime }_0, {y}^{\prime }_0, {u}^{\prime }_1, {u}^{\prime }_2, \lambda _1$ and $\lambda _2$ in 2-D logistic chaotic system for $M \times N \times$ 2 iterations noted as follows:

$$\begin{aligned} X_2= & {} \left\{ {{x}^{\prime }_1, {x}^{\prime }_2,\ldots , {x}^{\prime }_{M\times N\times 2} } \right\} , \\ Y_2= & {} \left\{ {{y}^{\prime }_1, {y}^{\prime }_2,\ldots , {y}^{\prime }_{M\times N\times 2} } \right\} . \end{aligned}$$

The two chaotic sequences $X_{2}$ and $Y_{2}$ are employed to decide the specific operation rules of DNA addition, subtraction and DNA complementary for calculating the ciphered results. For each elements of $X_{2}$, i.e., ${x}^{\prime }_m(m \in [1, M])$ and $Y_{2}$, i.e.,${y}^{\prime }_n(n \in [1, N \times 4])$, the control parameters $s_i$ and $t_j$ are as follows:

$$\begin{aligned} s_i= & {} \hbox {mod} \left( \left\lfloor {{x}^{\prime }_i \times 10^{16}} \right\rfloor , 8 \right) , \end{aligned}$$

(14)

$$\begin{aligned} t_j= & {} \hbox {mod} \left( \left\lfloor {{y}^{\prime }_j \times 10^{16}} \right\rfloor , 8 \right) . \end{aligned}$$

(15)

The ciphered image in DNA formulation matrix is calculated by the addition, subtraction and complement rules according to $s_i$ and $t_j$ as follows:

If $s_i=0, c_i =D(i)+c_{i-1} +F(i)$;

If $s_i =r, c_i =B_r (D(i))+B_r (F(i))+c_{i-1}, r=1,2,\ldots ,6$;

If $s_i = 7, c_i =B_r (D(i))-B_r (F(i))-c_{i-1}$;

If $t_j = 0, c_{j+M\times N\times 2} =D(j+M\times N\times 2)-c_{j+M\times N\times 2-1} -F(j+M\times N\times 2)$;

If $t_j =r, c_{j+M\times N\times 2} =B_r (D(M\times N\times 2+j))-B_r (F(j+M\times N\times 2))-c_{j+M\times N\times 2-1}, r=1,2,\ldots ,6$;

If $t_j = 7, c_{j+M\times N\times 2} =B_r (D(M\times N\times 2+j))+B_r (F(j+M\times N\times 2))+c_{j+M\times N\times 2-1}$,

Fig. 3

The encryption and decryption results of “Lena” and “Cameraman”. a Plain image “Lena”. b Cipher image of “Lena”. c Decryption of “Lena”. d Plain image “Cameraman”. e Ciphered image of “Cameraman”. f Decryption of “Cameraman”

where the operations of “$+$” and “$-$” are the DNA addition operation and DNA subtraction operation, respectively, $B(c_{i})$ denotes the DNA rule, $c_{0}$ is one part of secret key, $B_r$ is the rth complementary rule, D(i) is the current base of matrix D and F(i) is the current base of matrix F. The DNA matrix ${D}^{\prime \prime }$ is the result of the computations of matrix D and F. The ciphered image is the equivalent binary formulation of the DNA matrix ${D}^{\prime \prime }$. The decryption algorithm is the reverse process of encryption algorithm.

4 Simulation results

We used MATLAB 7.6.0 to run the programs. Our simulation results are shown in Fig. 3. The $256\times 256$ gray-scale images “Lena” and “Cameraman” (as shown in Fig. 3a, d respectively) are used as the plaintext images. The secret key includes $u_1 = 3.3999, u_2 = 3.4499, \lambda _1 = 0.189, \lambda _2 = 0.1499, x_0 = 0.287, y_0 = 0.354, p=1$ and $c_{0}=A$. The ciphered images are shown in Fig. 3b, e respectively, which are not intelligible any longer. The recovered images are shown in Fig. 3c, f when we decrypt the ciphered images with the same key.

Fig. 4

Histograms of plain images and ciphered images. a Distribution of plain image “Lena”. b Distribution of ciphered image “Lena”. c Distribution of plain image “Cameraman”. d Distribution of ciphered image “Cameraman”

5 Security analysis

A good encryption scheme should be robust against all kinds of attacks, such as brute-force attack, statistical attack, differential attack and plaintext attack. Some theoretical analysis and numerical simulations have been performed on the proposed algorithm.

5.1 Key space analysis

A good image encryption system should be sensitive to secret keys, and the key space needs to be large enough to make the brute-force impossible. In our proposed encryption scheme, the secret keys consist of the initial values $x_0, y_0, u_1, \lambda _1, \lambda _2, u_2$ of 2-D logistic map, the DNA encoding rule $p, c_0$ of initial base. We have done many experiments to get the fact that we can decrypt the ciphered images unless we know $x_0$ within error $10^{-15}, y_0$ within error $10^{-15}, u_1$ within error $10^{-16}, u_2$ within error $10^{-16}, \lambda _1$ within error $10^{-15}, \lambda _2$ within error $10^{-15}$. So the key space is more than $10^{92}$, which is large enough to resist all kinds of brute-force attacks.

5.2 Distribution

A histogram of an image shows the distribution of pixel values. If it is not flat enough, certain amount of information can be guessed by the statistical attack opponent. This makes cipher-only attack easier through analyzing the statistic property of ciphered image. Figure 4 illustrates the histograms of plaintext images “Lena” and “Cameraman,” and their ciphered images obtained by the proposed algorithm. Figure 4a, b shows the histograms of “Lena” and ciphered “Lena”, respectively. Figure 4c, d shows the histograms of “Cameraman” and ciphered “Cameraman”, respectively. The experimental results indicate that the proposed algorithm can resist statistical attacks.

5.3 Information entropy

The information entropy is a method to test uncertainty, that is to say, entropy reflects whether gray-scale values’ distribution is random or equality. The coarser the image is, the larger the entropy is. In the contrary, the smoother the image is, the smaller the entropy is. The minimum entropy is zero while the maximum entropy is eight. Therefore, the value of entropy of encrypted image should be as higher as possible. Let m be the information source, and the equation for calculating information entropy is:

$$\begin{aligned} H(m)=\sum _{i=0}^{2^{n}-1} {p(m_i )\log _2 \frac{1}{p(m_i )}}, \end{aligned}$$

(16)

where $p(m_i)$ represents the probability of symbol $m_i$. Assume that there are $2^{8}$ states of the information source and they appear with the same probability. According to Eq. (13), the ideal information entropy is $H(m)=8$, which indicates that the information is completely random. The information entropy of the ciphered image should be close to 8 after encryption. The values of information entropy of ciphered images in the proposed scheme are higher than 7.9971, which indicate that the ciphered images obtained by the proposed algorithm could hardly divulge information.

5.4 Correlation

Ciphered images should overcome the drawback of high correlation between pixels. In general, the plain image has high correlation between two adjacent pixels, and the correlation coefficients are more than 0.9. While the ciphered image has a weak correlation between adjacent pixels, the correlation coefficients are almost less than 0.1. In order to test the correlations between two adjacent pixels of the proposed encryption scheme, we randomly select 1000 pairs of two adjacent pixels from plaintext and ciphered images in vertical, horizontal and diagonal direction, respectively. The correlation of two adjacent pixels is calculated by Eq. (17), and the results are shown in Table 4.

$$\begin{aligned} r_{xy} =\frac{\hbox {cov}(x,y)}{\sqrt{D(x)}\sqrt{D(y)}}, \end{aligned}$$

(17)

where,

$$\begin{aligned} \hbox {cov}(x,y)= & {} \frac{1}{N}\sum _{i=1}^N {(x_i -E(x))(y_i -E(y))}, \\ E(x)= & {} \frac{1}{N}\sum _{i=1}^N {x_i }, \\ D(x)= & {} \frac{1}{N}\sum _{i=1}^N {(x_i -E(x))^{2}} . \end{aligned}$$

Table 4 Correlation coefficients of two adjacent pixels in plaintext image and ciphered image of Lena

Table 4 presents that the correlation coefficients of the plaintext image are all greater than 0.9, so the plaintext image has strong correlation between adjacent pixels of each direction. In the ciphered image, these values are all smaller than 0.01.

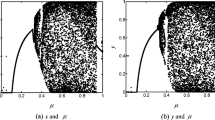
In order to demonstrate this situation clearly, we plot the correlation distributions in Fig. 5. Figure 5a–c shows the correlation distributions in the plaintext image. The strong correlation between adjacent pixels is obvious because all the dots are congregated along the diagonal. However, the dots are scattered over the entire plane in Fig. 5d–f, which indicates that the correlation is greatly reduced in the ciphered image.

Fig. 5

Correlation distribution in different directions of plaintext image and ciphered image of Lena. a Plain image, diagonal. b Plain image, vertical. c Plain image, horizontal. d Cipher image, horizontal. e Cipher image, vertical. f Cipher image, diagonal

Fig. 6

Sensitivity tests. a Cipher image using $x_{0}= 0.2780000001$. b Cipher image using $\lambda _1 =0.1890000001$. c Cipher image when one pixel changes from the plain image

Fig. 7

Histograms of Fig. 6 in different situations. a Histogram of Fig. 6a. b Histogram of Fig. 6b. c Histogram of Fig. 6c

Fig. 8

Encryption and decryption of color image Lena in the extended algorithm. a Original color image of Lena. b Encrypted color image of Lena for one round. c Decrypted color image of Lena

Fig. 9

Histograms for the color image Lena and ciphered image in the extended algorithm. a Histogram of R channel of Lena. b Histogram of G channel of Lena. c Histogram of B channel of Lena. d Histogram of R channel of ciphered image. e Histogram of G channel of ciphered image. f Histogram of B channel of ciphered image

5.5 NPCR and UACI

NPCR stands for the number of pixels change rate, while one pixel of the plain image changes. NPCR need to be close to 100 % that can lead sensitivity of the cryptosystem to the changing of the plain image and resisting plaintext attack. UACI stands for the unified average changing intensity of differences between the plain image and ciphered image. The value of UACI should be as higher as possible, which can lead the sensitivity of the cryptosystem to resist differential attacks. Here are the formulas to calculate NPCR and UACI:

$$\begin{aligned} \hbox {NPCR}= & {} \frac{\sum _{ij} {D(i,j)} }{W\times H}\times 100\,\%, \end{aligned}$$

(18)

$$\begin{aligned} \hbox {UACI}= & {} \frac{1}{W\times H} \left[ \sum _{i,j} {\frac{\left| {C_1 (i,j)-C_2 (i,j)} \right| }{255}} \right] \nonumber \\&\times 100\,\%, \end{aligned}$$

(19)

where W and H represent the width and height of the image, respectively, $C_1$ and $C_2$ are respectively the ciphered images, which are calculated from the original Lena and revised Lena image that the 34th pixel gray value is changed from 153 to 154. For the pixel at position (i, j), if $C_1 (i,j)\ne C_2 (i,j)$, assign $D(i,j)=1$; otherwise $D(i,j)=0$. NPCR = 99.65 %, UACI = 33.38 %. The results show that the proposed algorithm could resist plaintext attack and differential attack effectively.

5.6 Key sensitivity

A good cryptosystem should be sensitive to the secret keys as well as the plaintext. In this section, the key sensitivity of each part of the keys that is a little bit different from the original key is tested. Figure 6a shows the ciphered image using $x_0 =0.2780000001$ with other keys the same. Similarly, Fig. 6b shows the ciphered image using $\lambda _1 =0.1890000001$. Figure 6c shows the ciphered image when a bit data of a pixel from the plain image changes. Figure 6 shows the histograms of Fig. 4 in different situations. Comparing Figs. 6 and 7 with Figs. 3b and Fig. 4b, respectively, Figs. 6 and 7 are different from Figs. 3b and Fig. 4b, respectively; therefore, the proposed encryption algorithm provides a high key sensitivity, and the cryptosystem could resist chosen plaintext attack and differential attack effectively.

6 Extended algorithm for RGB image

Color image is an additive model that the three primary colors red, green and blue are combined to produce other colors. This is usually apportioned with eight bits each for red, green and blue, giving a range of 256 possible values, or intensities, for each color. The final displayed color is determined by these three components. In this point of view, the RGB image f can be regarded as an extended $M\times 3N$ pixels gray-level image. The Eq. (3) is extended as follows:

$$\begin{aligned} \varepsilon =\frac{1}{(M\times N)}\sum _{x=0,y=0}^{x=M-1,y=3N-1} {f(x,y)} . \end{aligned}$$

(20)

The two sequences $X_{1}$ and $Y_{1}$ in step 2 are extended as:

$$\begin{aligned} X_1= & {} \left\{ {x_{200+1}, x_{200+2},\ldots , x_{200+M\times 3N} } \right\} , \\ Y_1= & {} \left\{ {y_{200+1}, y_{200+2},\ldots , y_{200+M\times 3N} } \right\} , \end{aligned}$$

where $w_{k}$ and $v_{k}$ are extended into the size of $k \in [1, M \times 3 N]$. The two chaotic sequences $X_{2}$ and $Y_{2}$ are extended as follows:

$$\begin{aligned} X_2= & {} \left\{ {{x}^{\prime }_1, {x}^{\prime }_2,\ldots , {x}^{\prime }_{M\times 3N\times 2} } \right\} , \\ Y_2= & {} \left\{ {{y}^{\prime }_1, {y}^{\prime }_2,\ldots , {y}^{\prime }_{M\times 3N\times 2} } \right\} . \end{aligned}$$

The addition, subtraction and complement rules according to $s_i$ and $t_j$ for controlling the operations between DNA matrices D and F as follows:

If $s_i = 0, c_i =D(i)+c_{i-1} +F(i)$;

If $s_i =r, c_i =B_r (D(i))+B_r (F(i))+c_{i-1}, r=1,2,\ldots ,6$;

If $s_i = 7, c_i =B_r (D(i))-B_r (F(i))-c_{i-1}$.

If $t_j = 0, c_{j+M\times 3N\times 2} =D(j+M\times 3N\times 2)-c_{j+M\times N\times 2-1} -F(j+M\times 3N\times 2)$;

If $t_j =r, c_{j+M\times 3N\times 2} =B_r (D(M\times 3N\times 2+j))-B_r (F(j+M\times 3N\times 2))-c_{j+M\times 3N\times 2-1}, r=1,2,\ldots ,6$;

If $t_j = 7, c_{j+M\times 3N\times 2} =B_r (D(M\times 3N\times 2+j))+B_r (F(j+M\times 3N\times 2))+c_{j+M\times 3N\times 2-1}$,

where the matrices D and F are in the size of $M \times (3 N \times 4)$ in the extended algorithm. The ciphered color image is the reformed RGB image which is the equivalent of the DNA matrix. The decryption algorithm is the reverse process of encryption algorithm. Figure 8 shows the encrypted results of the color extended algorithm. Figure 9 shows the histograms for the plaintext color image Lena and ciphered image of Lena. The histograms of cipher images are fairly uniform and significantly different from that of the plain image.

7 Conclusion

In this paper, a novel image encryption scheme based on DNA sequence operations and 2-D logistic chaotic map is proposed. The plain images are confused by using 2-D logistic chaotic map and encoded by using a DNA encoding rule. Two matrices generated by plain image, chaotic mapping and DNA encoding are mutually calculated by the operation of DNA addition, subtraction and complementary rules. The binary result of calculation of the two matrices is the ciphered image. Experimental results and theoretical analysis show that the scheme is able to resist differential attack, brute-force attack, statistical attack and plaintext attack. The proposed scheme has extraordinarily high security.