Dynamical analysis, circuit realization, and applications of 4D hyperchaotic systems with bursty oscillations and infinite attractor coexistence

Abstract

A new four-dimensional chaotic system with high complexity is proposed, and the analysis of its dynamics reveals that the system shows a rare topological attractor structure symmetry phenomenon. The phenomenon of inverse multiplicative bifurcation and multistability, which changes from a quadruple period to a double period and then to a single period, are found. A complex oscillatory transformation between chaos and period can be observed, highlighting the complexity of the system. The transient hyperchaos and burst oscillations are found in the time series and Lyapunov exponential spectra of the system, and the rich dynamical behavior of the system is verified by the 0–1 test and complexity spectral entropy test. The analog circuitry of the system is simulated based on Multisim, and the actual digital circuitry of the system is implemented through a Field Programmable Gate Array. The experimental results and the numerical simulation results agree and prove the feasibility of the constructed system. An image encryption algorithm is designed by combining the disruption-diffusion algorithm with the DNA encoding algorithm, and the system is analyzed and verified to be highly sensitive to the chaotic sequence key and initial value. Moreover, the key space of the algorithm is large and the information entropy is close to the ideal value, so the new system proposed can contribute to play a role in the field of secure communication.

1 Introduction

Chaos is a form of motion unique to nonlinear dynamical systems, which is widely found in nature and many scientific fields, such as biology, physics, chemistry, geology, and so on. Chaos reveals the complexity that exists universally in nature and human society: the unity of order and disorder, the unity of certainty and probability, which opens up people's horizons and deepens their understanding of the objective world. Chaos is the inherent randomness of determinism, a world in which determinism and probability are dialectically unified. Chaotic motion is one of the most fundamental forms of motion in nature. Meteorologist Lorenz first discovered chaos in the 1960s while studying the atmosphere, and this chaos is what we know as the "butterfly effect." The 1970s was a glorious era in the history of the development of chaos science, in which chaos formally began to appear as a new independent discipline, and since then chaos science has ushered in a research boom and became a research hotspot [1,2,3,4], accompanied by the rapid development of the Internet, and chaotic systems have been widely used in pattern recognition, biomedicine, neural networks, secure communications and image encryption [5,6,7,8,9].

Image encryption is the application of encryption algorithms to clutter the target image so that the encrypted image cannot be recognized directly. In 1998, an image encryption scheme based on a chaotic mapping "disorder and diffusion" system [10, 11] was proposed by Fridrich. Image encryption based on chaotic mapping should have the operation of disorder and diffusion processing. In the process of disruption, only the position information of the pixel is changed without changing the size of the pixel, thus changing the correlation between neighboring pixels in the image, and in the process of diffusion, the operation is just the opposite. Liu [10] et al. proposed an image encryption algorithm based on segmented linear chaotic system encryption. M. Gao et al. [11] proposed a chaos-based permutation-diffusion image encryption algorithm, and P. Fang [12] et al. proposed a grouped image encryption algorithm based on an improved two-dimensional logistic chaotic mapping combined with DNA sequence operations [13].

Existing chaotic systems, with relatively simple structures and low complexity, use encryption methods that can achieve the purpose of image encryption, but they are single encryption. Moreover, most of them use low-dimensional chaotic systems, which are applied in image encryption, have the disadvantages of limited key space, low sensitivity, and undesirable information entropy, and are less secure in image encryption applications [14,15,16,17, 35, 36].

In order to improve the complexity of chaotic systems and security in image encryption, a new four-dimensional chaotic system is proposed. The system has a symmetric topology, which not only reduces the complexity of the system of differential equations and provides a way to simplify the problem, but also provides a better understanding of the behavior of the system by analyzing the symmetry of the system and the effect of symmetry transformations to infer the stability characteristics of the system.The system is found to have special dynamical properties not found in other systems. The system has excellent properties such as inverse multiplicative periodic bifurcation, transient hyperchaos phenomenon, sudden oscillation phenomenon, and coexisting attractor symmetry, and the system is more complex and can be applied to image encryption with higher security. Meanwhile, the comparison between the proposed system and the system shown in Table 1 also demonstrates the rich dynamic characteristics of the system. Compared with the chaotic systems in the literature [16, 17], the transient hyperchaos phenomenon demonstrates more diverse and rich dynamic behaviors of chaotic systems, and the complexity of the hyperchaos phenomenon makes it possible to be applied to data encryption and confidential transmission to provide higher security for information transmission.Bursty oscillations provide the system with different states and behavioral modes, expanding the variability and adaptability of the system to a wider range of conditions and environments. Coexisting attractor symmetries can be used to enhance the robustness of the system. Different attractors represent different signals or behavioral patterns, and by selecting specific attractors to suppress or filter noise components, the robustness of the system to noise interference can be improved. In this paper, the Longe-Kuta algorithm is used in analog circuit simulation, the Euler algorithm is used in FPGA, and in image encryption it is a combination of Arnold disruption and DNA dynamic encryption coding to design a new image encryption algorithm.

Table 1 Comparison of the dynamic behavior of other systems

Section 2 presents a novel four-dimensional hyperchaotic system and analyzes the phase diagram of the system. Sections 3 and 4 analyze the bifurcation diagram, Lyapunov exponential spectrum, complexity, and coexisting attractors, and find that the system has special dynamical properties not found in other systems. The system has excellent properties such as inverse multiplicative periodic bifurcation, transient hyperchaos phenomenon, sudden oscillation phenomenon, and coexisting attractor symmetry. The design and simulation of the analog circuit is carried out in Sect. 5. The chaotic circuit is constructed and simulated using Multisim circuit simulation software and the simulation results are consistent with the system phase diagram.Sect. 6 designs and implements the chaotic circuit using Field Programmable Gate Array (FPGA). Section 7 performs the image encryption analysis the new system is very sensitive to the image key and the information entropy and correlation are close to ideal values. Section 8 concludes that the new system has high complexity and excellent security performance in image encryption applications.

2 Chaotic system construction

The Lorenz system is a nonlinear dynamical model proposed by American meteorologist Edward Lorenz in 1963 to describe fluid motion in the atmosphere. It is a simplified three-dimensional dynamical system represented by three variables: x, y, and z. The Lorenz system has chaotic behavior, i.e., small changes to the initial conditions may cause the system to evolve completely different trajectories. The equations of the Lorenz system are expressed as:

$$\left\{ {\begin{array}{*{20}l} {\frac{{{\text{d}}x}}{{{\text{d}}t}} = a(y - x)} \\ {\frac{{{\text{d}}y}}{{{\text{d}}t}} = bx - y - xz} \\ {\frac{{{\text{d}}z}}{{{\text{d}}t}} - cx + xy} \\ \end{array} } \right.$$

(1)

We propose to introduce a nonlinear term and a sinusoidal function to present a new four-dimensional hyperchaotic system that consists of five parameters and four variables as follows:

$$\left\{ {\begin{array}{*{20}l} {\frac{{{\text{d}}x}}{{{\text{d}}t}} = y - ax + yz} \\ {\frac{{{\text{d}}y}}{{{\text{d}}t}} = by - xz - u} \\ {\frac{{{\text{d}}z}}{{{\text{d}}t}} = xy - cz + yu} \\ {\frac{{{\text{d}}u}}{{{\text{d}}t}} = dy + e\sin (x)} \\ \end{array} } \right.$$

(2)

where, x,y,z,u are the state variables of the system and a = 3.04, b = 1.02, c = 9.02, d = 1, e = 2.02 are the system parameters. When the system parameters are a = 3.04, b = 1.02, c = 9.02, d = 1, e = 2.02 when the initial value is (1,1,0,0), the system will have a complex chaos phenomenon, and at this time, the Lyapunov exponent is LE₁ = 0.0552 LE₂ = 0.0114 LE₃ = -0.415 LE₄ = -10.67, respectively. Simulation was carried out using Matlab keeping the parameters as a = 3.04, b = 1.02, c = 9.02, d = 1, e = 2.02 constant. The initial values are for are (1,1,0,0) Relative error tolerance and absolute error tolerance are set to le⁻⁷ after iteration 1000 times to get the 2D mapping of the system in four planes (x,y), (x,z), (x,u) and (y,z) as shown in Fig. 1a, b, c, and d. It can be observed that has a complex stretching and twisting structure, and from the overall view, the system is again very stable. The orbits in the figure have complex paths of vortices and the trajectories are very rich and dense with a relatively regular and simple form.

Fig. 1

Phase diagram of the system in each direction: a the x–y plane b the x–z plane c the x–u plane d the y–z plane

3 Analysis of the dynamics of the system

3.1 Equilibrium point

Find the equilibrium point of the system so that the right-hand side of the system equation is equal to zero. When the parameters a = 3.04, b = 1.02, c = 9.02, d = 1, e = 2.02, the equilibrium point of the system is (0,0,0,0). The Jacobi matrix obtained by linearizing the system:

$$J = \left[ {\begin{array}{*{20}{l}}{ - 3.04}&{1 + z}&y&0\\{ - z}&{1.02}&{ - x}&{ - 1}\\y&{x + u}&{ - 9.02}&y\\{e\cos (x)}&1&0&0 \end{array}} \right]$$

(3)

Let det(J − λ I) = 0, where I is the unit matrix, and find the eigenvalues λ₁ =  −9.0200, λ₂ =  −3.1807, λ₃ = 0.5803 + 1.1199i, λ₄ = 0.5803–1.1199i, at the equilibrium point S₁(0,0,0,0). Eigenvalue analysis shows that the system has two positive eigenvalues and two negative eigenvalues, which means that the equilibrium point S₁(0,0,0,0) is an unstable saddle focus.

3.2 Dissipative nature of the system

The dispersion of the system is derived from the system equation:

$$\nabla V = \frac{{\partial \dot{x}}}{\partial x} + \frac{{\partial \dot{y}}}{\partial y} + \frac{{\partial \dot{z}}}{\partial z} + \frac{{\partial \dot{u}}}{\partial u} = - a + b - c$$

(4)

Substituting a = 3.04, b = 1.02, and c = 9.02, gives ∇V = −11.04, so the system scatter is less than 0. The system is dissipative and converges according to the exponential form dv/dx = e^−11.02t. As t → ∞ there is a trajectory of the system that will finally be restricted to a volume of zero limit point set and its dynamical behavior will be fixed on an attractor, which is sufficient evidence for the existence of the attractor.

3.3 Lyapunov exponential spectrum and dimensionality

The Lyapunov exponent can quantitatively characterize the state of motion of a system and graphically describe the degree of mutual attraction and repulsion between neighboring trajectories of the system, which is one of the most important physical quantities to characterize chaotic systems. Therefore, using the Lyapunov exponential spectrum, it can be observed when the parameters of the system change, the motion state of the system changes accordingly can be observed. The bifurcation is that when the initial values of the variables of the state or the parameters of the system change, the dynamic state of the system changes as well. The system is a four-dimensional chaotic system. The curves shown in Fig. 2 are represented as LE₁, LE₂, LE₃, and LE₄ in order from top to bottom. When the parameters of the system are set to a = 3.04, b = 1.02, c = 9.02, d = 1, and e = 2.02, the Lyapunov exponents of the system are calculated as LE₁ = 3.26986, LE₂ = 2.27603, LE₃ = 0.277269 and LE₄ = −11.0299, and it can be clearly observed that the system is in a state of hyperchaos. The Lyapunov dimension of the new system is:

$$\mathop D\nolimits_{L} = j + \frac{1}{{\left| {\mathop \lambda \nolimits_{Lj} + 1} \right|}}\sum\limits_{i = 1}^{j} {\mathop \lambda \nolimits_{Li} = 3 + \frac{{\mathop \lambda \nolimits_{L1} + \mathop \lambda \nolimits_{L2} + \mathop \lambda \nolimits_{L3} }}{{\left| {\mathop \lambda \nolimits_{L4} } \right|}}} = 3.5279$$

(5)

Fig. 2

Lyapunov exponent chart

The maximum Lyapunov exponent of the four-dimensional hyperchaotic system is calculated. Since the system is four-dimensional, j = 3, the maximum Lyapunov exponent is obtained as greater than 0 and the order is not an integer, indicating that the system is chaotic. The curve of this chaotic system as the parameter changes for a =  [0, 5] can be seen in Fig. 6a. Observing the curves, it can be seen that when a ∈  [0.72,0.78], [1.2,1.26], [2.85,3.1], it can be observed that there exist two Lyapunov exponents greater than zero and the system is in a hyperchaotic state. When a = 3.02, it is in a hyperchaotic state. The super-mixing state has randomness and high unpredictability, making its encryption more effective and secure. There is a positive LE index maintained in the interval of variation of a. Chaotic attractors exist and are always in complex chaotic systems.

3.4 Poincaré cross section, power spectrum, 0–1 tests analysis

3.4.1 Poincaré cross section

The acyclic properties of chaotic systems can be well described by the Poincaré cross section. This observation highlights the disorderly and unpredictable behavior of the system. It is very effective for analyzing multivariate systems, where the motion is periodic when there is only one immobile point or few discrete points on the Poincaré cross section. When the Poincaré cross-section is a closed continuous curve, the motion is quasi-periodic. When the Poincaré section is a continuous curve or a patchwork of dense points, the motion is chaotic. The 2-dimensional Poincaré cross-sections in phase space are made as in (a), (b), and c in Fig. 3 to obtain in the x-u, x–y, and y-u planes, respectively. By looking at the cross-sectional view of the system, it can be found that the system is chaotic. It can also be observed that Fig. 3a and c are symmetric about the u-plane and Fig. 3b is symmetric about the origin. The symmetry of the Poincaré cross-section diagram allows a simpler understanding and analysis of the dynamical behavior of the system.

Fig. 3

Cross-section of Poincaré in different directions: a x-u direction with z = 0 b x–y direction with z = 0 c y-u direction with z = 0

3.4.2 0–1 tests analysis

The basic idea of the "0–1 test" [18, 19] is to create a stochastic dynamic process for the data and then study how the size of the stochastic process varies over time. The system is observed to show an unconstrained trajectory in the (p, s) plane similar to Brownian motion, and an algorithm is used to test whether the output is close to 1 to distinguish the creation of chaos. The system is proved to be chaotic by calculating the final value of K (K = 0.9798), and the trajectory maps are drawn with p(n) and s(n) as the horizontal and vertical axes, respectively, and the steps of the algorithm whose maps produce the Brownian specific algorithm are as follows.

Define the following two equations:

$$p(n) = \sum\limits_{j = 1}^{n} {\varphi (j)\cos (\theta (j)),n = 1,2...}$$

(6)

$$s(n) = \sum\limits_{j = 1}^{n} {\varphi (j){\text{sin}}(\theta (j))} ,n = 1,2...$$

(7)

When $\theta (j) = jc + \sum\nolimits_{i = 1}^{j} {\varphi (j),j = 1,2...}$

The diffusion behavior of p(n) and s(n) can be analyzed by calculating the displacement mean square error M(n), which is calculated as follows.

$$M(n) = \mathop {\lim }\limits_{N \to + \infty } \frac{1}{N}\sum\limits_{j = 1}^{N} {\left [ {p(j + n) - p(j)} \right]}^{2} ,n = 1,2...$$

(8)

The convergence of M(n) can be used to measure the convergence of p(n) and s(n). If the discrete time series is ordered, M(n) is a bounded quantity, however, if the time series is chaotic, M(n) grows linearly in n. The convergence of M(n) is a measure of the convergence of p(n) and s(n).

Finally, the linear growth rate K, the linear regression coefficient of M(n) with n, is calculated. The asynchronous growth rate is:

$$K = \mathop {\lim }\limits_{n \to + \infty } \frac{\lg M(n)}{{\lg n}}$$

(9)

By analysis, Fig. 4b shows that the motion of the system in the (p, s) plane exhibits an unbounded trajectory similar to Brownian motion, which proves that the system is a chaotic dynamical system.For example, Fig. 4a is the 0–1 test plot with initial values of (x₁, y₁, z₁, u₁) = (0, 1, 0, 0), and Fig. 4b is the 0–1 test plot with initial values of (x₂, y_2, z₂, u₂) = (1, 1, 0, 0), and the comparison between the two plots shows that (1, 1, 0, 0) is more suitable to be the initial value of this system.

Fig. 4

Different initial values: a Initial values of (x₁, y₁, z₁, u₁) = (0, 1, 0, 0), b Initial values of (x₂, y₂, z₂, u₂) = (1, 1, 0, 0)

3.4.3 Power spectrum

The power spectrum is a common method to analyze the chaotic behavior of a system, because chaotic systems produce chaotic signals that are non-periodic, so the power spectrum is also continuous. Figure 5 is obtained with initial values of (1, 1, 0, 0) parameters a = 3.04, b = 1.02, c = 9.02, d = 1, e = 2.02. From Fig. 5, it can be seen that the power spectrum is continuous, which indicates that the system is non-periodic, and therefore the system is chaotic.

Fig. 5

Power spectrum of the system

4 Dynamical behavior of chaotic systems with changing parameters

4.1 Bifurcation diagram and Lyapunov exponential spectrum with parameters

Put an as a variable, and with initial values of (1,1,0,0) and step size of 0.01, only the parameter a is changed, and the rest is kept constant to observe the change of the system state. For parameters a ∈  [0,5], keeping b = 1.02, c = 9.02, d = 1, and e = 2.02, the Lyapunov exponential spectrum and bifurcation diagram of the system are shown in Fig. 6a and b. When the parameter a is changed, periodic and chaotic regions are evident in the system. When a ∈  [0, 0.66], the system is in a periodic state, at a ∈  [0.7, 1.48], the system is chaotic, at a ∈  [1.5, 2.35], the system appears again in a periodic state, when the parameter a ∈  [2.4, 4], the system appears in a chaotic state, there are alternating chaotic and periodic changes, making its system more complex. When the parameter a ∈  [4.2,5], the system state changes as shown in Fig. 6, it is obvious that the bifurcation diagram of the system undergoes a bifurcation where the quadruple period becomes a double period and then a bifurcation where the double period becomes a period. The emergence of multiplicative bifurcation is an important phenomenon of chaotic systems, and the appearance of multiplicative bifurcation will enrich the dynamical behavior of chaotic systems and make them more diverse and complex.

Fig. 6

Lyapunov index spectrum and bifurcation diagram: a The Lyapunov index spectrum for parameter a b Bifurcation diagram for parameter a

For parameter c, take the parameter c ∈  [0, 10] and set a = 3.04, b = 1.02, d = 1, e = 2.02, and the initial values of (x₀,y₀,z₀,u₀) = (1,1,0,0), the bifurcation diagram and Lyapunov exponential spectrum of the system is shown in Fig. 7a and b. When c ∈  [2.4,4.2], the system maintains a chaotic state accompanied by a transient hyperchaotic state, and when the parameter c = 9.02, the system has two Lyapunov exponents greater than 0, which is also hyperchaotic at this moment. The hyperchaotic state is more complex than the chaotic state, with better encryption performance and higher security. In the corresponding bifurcation diagram, in which chaos and cycles alternate with each other, the chaotic state of the system is distributed in a larger parameter space, from which it can be concluded that the system has strong randomness and a larger key space, which should be better for image encryption.

Fig. 7

Lyapunov index spectrum and bifurcation diagram: a The Lyapunov index spectrum for parameter c b Bifurcation diagram for parameter c

4.2 Burst oscillations and intermittent chaos

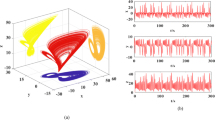
Keeping b = 1.02, c = 9.02, d = 1, e = 2.02, when a = 1.22, the timing waveform is obtained for the selected time [250,500]s as shown in Fig. 8c. In Fig. 8, we can find that the attractor appears to burst oscillation, which is not easy to appear in chaotic systems. The burst oscillation can change the flatness and monotony of the timing diagram and make it more vivid and complex. Figure 8a and b show the phase diagrams when changing the time diagrams, and it can be seen that the phase diagrams change from periodic to chaotic with rich dynamical behavior. The Lyapunov exponents at this point in Fig. 8a are LE₁ = 0, LE₂ = −0.0143, LE₃ = −0.3313, LE₄ = −8.5195, and in Fig. 8b the Lyapunov exponents at this point in time are LE₁ = 0.081, LE₂ = 0.0599, LE₃ = -0.2723, LE₄ = −9.0780, respectively. Figure 9c shows the timing diagram for selected times [500,1000]s for a = 3.3. It can be observed that the timing diagram changes from periodic to chaotic and back to periodic, with periodic and chaotic states alternating with intermittent chaotic states. Figure 9a and b show the phase diagrams that change from periodic to chaotic. The Lyapunov exponents of Fig. 9a are LE₁ = −0.1363, LE₂ = 0, LE₃ = −0.2617, LE₄ = −9.9137. The Lyapunov exponents of Fig. 9b are LE₁ = 0.0781, LE₂ = 0.0206, LE₃ = −0.4490, LE₄ = -10.9200. It is thus observed that the phase and timing diagrams of the system are very sensitive to the parameters. As the parameter changes, the topology of the attractor also changes, making the system more secure for application in image encryption.

Fig. 8

Outbreak: a Attractor diagram of the cycle b Attractor diagram of the chaos c Timing waveform at parameter a = 1.22

Fig. 9

Intermittent oscillation: a Attractor diagram of the cycle b Attractor diagram of the chaos c Timing waveform at parameter a = 3.3

The motion state of a system can change from one stable state to another, from an immobile point to a periodic state, and from a periodic state to a chaotic state. Keep the parameters b = 1.02, c = 9.02, d = 1, and e = 2.02, so that the parameter changes within (0, 5). When a ∈  [0.391,0.410], the system is in the motionless point state; when a ∈  [0.569,0.571], the system changes from an immobile point state to a periodic state; when a ∈  [0.689,0. 692], the system changes from a periodic state to a chaotic state. When a ∈  [2.429,2.433], the system changes from a chaotic state to a hyperchaotic state. The system exists in the form of jumps between immobile points, cycles, non-cycles, chaos, and hyperchaos, and has a rich dynamical behavior. As shown in Fig. 10a, b, c, and d are the phase diagrams of the different states of the system when the parameter a is varied.As shown in Fig. 10a, b, c and d the Liapunov exponents for the states are shown in Table 2.

Fig. 10

Phase diagram of the system in different states: a y–z plane at a = 0.4 b y–z plane at a = 0.57 c y–z plane at a = 0.69 d y–z plane at a = 2.43

Table 2 Lyapunov index in different states

4.3 Sensitivity to initial conditions

Initial value sensitivity means that a relatively small change in the initial state of the system can lead to a large difference in the trajectory of the system. As shown in Fig. 11, the solid blue line has an initial value of [1,1,0,0] for time-series, and the solid purple line has an initial value of [1,1,0,1] for the time-series. It can be seen that the system has a high sensitivity to initial values, and this excellent feature can be applied to confidential communications, such as image encryption.

Fig. 11

Time-series of state variables with different initial values: a Time-series of x₁ b Time-series of x₂ c Time-series of x₃ d Time-series of x₄

4.4 System coexistence attractor analysis

Chaotic systems are sensitive to changes in initial values, keeping the parameters of the system unchanged. Changing the initial values of the system will cause the system trajectories to change, with some trajectories eventually converging on the same attractor and some trajectories clustering on other attractors. These attractors are called coexisting attractors. To better analyze the state of the hyperchaotic system, the existence of multiple coexisting attractors of the system can be found by changing the initial state of the system with well-defined system parameters. When the initial parameters a = 3.04, b = 1.02, c = 9.02, d = 1, and e = 2.02, Fig. 12a, b, c, d show the attractor coexistence diagram in the x–y plane, the x–z plane, the u-z plane, and the y–z plane, respectively. When they change their initial value, their behavior changes. The initial value of the yellow track line is (-1,-1,0,0), the initial value of the red track line is (5,5,0,0), the initial value of the green track line is (0.1,0.1,0,0), and the initial value of the blue track line is (10,10,0,0). The bifurcation diagrams of the system for initial values (5,5,0,0) and (10,10,0,0) are shown in Fig. 12 in e and f, respectively, and the computation results of the coexisting attractors show that the phase diagrams and the Liapunov exponential spectra remain consistent when the initial values are changed. The initial values are the same as in the bifurcation diagram.

Fig. 12

Coexistence of attractors in different directions: a x–y coexistence attractor b x–z coexistence attractor c u-z coexistence attractor d y–z coexistence attractor d System Bifurcation Diagram e System Bifurcation Diagram

4.5 Complexity analysis

The complexity of chaotic systems is an important part of the analysis of the dynamics of the studied systems. The depth of the image color represents the complexity of the chaotic system within the parameter range, if the color is darker then it means that the complexity value of the system is higher and the corresponding sequence randomness is better, on the contrary, the lighter the color means that the complexity value of the system is lower and the random sequence of the system is worse. The results of the complexity analysis show that the complexity corresponds precisely to the randomness of the system it has the same effect as the Poincaré mapping, the bifurcation diagram, and the Lyapunov exponent. The complexity is the degree to which the chaotic sequence is close to the random sequence. The method is mainly to make the chaotic sequence close to the random sequence by using the correlation algorithm, and the closer it is to the random sequence, the greater the complexity and thus the higher the security of the system will be. This good feature can then be utilized for image encryption. There are two main types of complexity in chaotic systems, one is the SE complexity and the other is the C0 complexity, and it is verified that in continuous chaotic systems, the trends of both remain the same [33, 34].SE complexity is a measure of complexity in chaotic systems. It is often used to describe how sensitive the system is to initial conditions.C0 complexity is another measure of complexity in chaotic systems. It describes the entropy growth rate of the system's trajectory in phase space. The connection between the two is that both SE complexity and C0 complexity are used to measure the complexity of chaotic systems. They both reflect the unpredictability and nonlinear characteristics of the system behavior. The difference between the two is that SE complexity mainly focuses on the sensitivity of the system behavior to the initial conditions, while C0 complexity pays more attention to the chaotic degree of the system behavior complexity emphasizes the effect of small perturbations, while C0 complexity takes into account the entropy growth rate of the trajectories in the whole phase space.

The present analysis is based on the fixed parameters a = 3.04,b = 1.02,c = 9.02,d = 1, and e = 2.02. Figure 13a shows the 3D SE complexity of the system for the initial values (1,1, x(0),z(0)). Figure 13b shows the 3D C₀ complexity of the system for the initial values (1,x(0),0,z(0)). It can be observed that a large area of black is mixed with a small area of white and yellow, the darker the color indicates a higher complexity of the system, and the only remaining small amount of yellow and red in the darker area represents the state transfer phenomenon that exists in a chaotic system, and thus the state complexity of the hyperchaotic system. The system is more complex and its application in the field of image encryption will have higher security.

Fig. 13

Three-dimensional complexity of the system at different initial values: a C0 complexity with x(0)-z(0) as variables b SE complexity with x(0)-z(0) as variables

As shown in Fig. 14a and b plots of SE and C₀ single-parameter complexity with parameter d, respectively, it can be seen that the complexity is higher at d = 1, indicating that chaos is more pronounced. Compared to the literature [34], this system has high complexity and high security and has good properties when applied to confidential communication.

Fig. 14

Complexity: a SE complexity when d = 1 b C0 complexity when d = 1

5 Analog circuit design and simulation

In order to verify the dynamical behavior of the chaotic system, the results will be analytically verified in this section by designing a simulation circuit. It can be observed through Fig. 1 that the variable dynamic range of the phase diagram does not exceed ± 13.5 V, therefore no scaling compression transformation of the system is required. If the system exceeds ± 13.5 V, a variable proportional compression transformation must be performed. Perform proportional transformation of Eq. (2), set τ₀ = 1/(R₀C₀) = 1/(R₃C₁) = 1/(R₈C₂) = 1/(R₁₄C₃) = 1/(R₂₀C₄) to derive Eq. (10):

$$\left\{ \begin{gathered} \frac{{{\text{d}}x}}{{{\text{d}}(\tau_{0} t)}} = y - ax + {\text{yx}} \hfill \\ \frac{{{\text{d}}y}}{{{\text{d}}(\tau_{0} t)}} = by - xz - u \hfill \\ \frac{{{\text{d}}z}}{{{\text{d}}(\tau_{0} t)}} = xy - cz + - yu \hfill \\ \frac{{{\text{d}}u}}{{{\text{d}}(\tau_{0} t)}} = dy + e\sin (x) \hfill \\ \end{gathered} \right.$$

(10)

Based on the use of an inverse adder, Eq. (11) is obtained after the evolution and transformation of the equation:

$$\left\{ \begin{gathered} x = \frac{1}{{R_{0} C_{0} }}\int {\left [ { - ( - y) - ax - x( - y)} \right]} {\text{d}}t \hfill \\ y = \frac{1}{{R_{0} C_{0} }}\int {\left [ { - b( - y) - xz - u} \right]{\text{d}}t} \hfill \\ z = \frac{1}{{R_{0} C_{0} }}\int {\left [ { - x( - y) - cz - ( - y)u} \right]{\text{d}}t} \hfill \\ u = \frac{1}{{R_{0} C_{0} }}\int {\left [ { - d( - y) - e\sin ( - x)} \right]{\text{d}}t} \hfill \\ \end{gathered} \right.$$

(11)

By introducing resistance values, the circuit system equation can be derived based on the differential equation of the system circuit:

$$\left\{ \begin{gathered} x = \frac{1}{{R_{3} C_{1} }}\int {(\frac{{R_{4} }}{{R_{30} }}y - \frac{{R_{4} }}{{R_{23} }}x + \frac{{R_{4} }}{{R_{5} }}yz)} {\text{d}}t \hfill \\ y = \frac{1}{{R_{8} C_{2} }}\int {(\frac{{R_{9} }}{{R_{24} }}y - \frac{{R_{9} }}{{R_{10} }}xz - \frac{{R_{9} }}{{R_{11} }}u){\text{d}}t} \hfill \\ z = \frac{1}{{R_{14} C_{3} }}\int {(\frac{{R_{15} }}{{R_{25} }}xy - \frac{{R_{15} }}{{R_{17} }}{\text{z}} + \frac{{R_{15} }}{{R_{16} }}yu){\text{d}}t} \hfill \\ u = \frac{1}{{R_{20} C_{4} }}\int {(\frac{{R_{21} }}{{R_{33} }}y - \frac{{R_{21} }}{{R_{22} }}\sin (x)){\text{d}}t} \hfill \\ \end{gathered} \right.$$

(12)

Set C₁ = C₂ = C₃ = C₄, by comparing (10) and (12), we can get the following parameters R₃ = R₈ = R₁₄ = R₂₀ = 15KΩ, R₅ = R₁₀ = R₃ = R₂₅ = R₁₆ = 1KΩ, R₂₃ = 3.3KΩ, R₂₄ = 10.5KΩ, R₁₇ = 1.5KΩ, R₂₂ = 4.9KΩ, R₄ = R₉ = R₁₅ = R₂₁ = R₃₃ = R₃₀ = R₁₁ = 10KΩ.The circuit diagram of the system is derived from the mathematical Eq. (12) as shown in Fig. 15.The quantitative relationship between Eq. (10) and Eq. (12) is for example the ratio of the coefficients R₄/R₃₀ of y in Eq. (12) is the coefficient of y in Eq. (10) which is 1, and the ratio of R₄/R₂₃ in Eq. (12) is the coefficient a of Eq. (10). The tool used in this analog circuit is Multisim 14.0, and the models used are the AD633 multiplier, LM248 amplifier, and AD639 sine converter.

Fig. 15

System circuit schematic

The simulation is carried out through the circuit software simulation multi-simulation and the phase diagram of the system is obtained as shown in Fig. 16. By comparing this figure with the phase diagram of the system, the attractor of the circuit agrees with the theoretical attractor, so the correctness of the system is verified by numerical analysis and experimentation, and the attractor exists in the system.

Fig. 16

Circuit simulation diagram: a Phase diagram of the x–y plane b Phase diagram of the x–z plane c Phase diagram of the x-u plane d Phase diagram of the y–z plane

6 Hardware circuit implementation

Field programmable gate arrays (FPGA) are the ideal solution we chose for building chaotic circuits. Conventional chaotic circuits are constructed using analog electronic components, but the performance of these components is affected by aging and other factors, and long-term performance stability cannot be guaranteed.FPGA are used exclusively in the field of integrated circuits, successfully addressing the shortcomings of custom circuits and overcoming the shortcomings of the limited number of gates in the original programmable devices. By designing circuits using FPGA, you can reduce printed circuit board area, shorten design time, and significantly improve system reliability.FPGA is more flexible and programmable than DSP. Compared to DSP, FPGA can configure hardware circuits on demand to accommodate a variety of complex chaotic systems and different algorithms.

The XC6SLX16-2FTG256I chip is selected as the FPGA and the Texas Instruments PROGRAMMED 12-bit dual-channel TLC5618A is used as the digital-to-analog converter (DAC). The main parameters of the XC6SLX16-2FTG256I chip are the number of logic cells: 16,256, the capacity of internal memory: 49,152 bits, the number of I/O pins: 148, the internal clock management resources: 4 global clock line networks. The main parameters of the XC6SLX16-2FTG256I chip are the number of logic cells: 16,256, internal memory capacity: 49,152 bits, the number of I/O pins: 148, and the internal clock management resources: 4 global clock line networks. Quartus 15.0 was used as the development environment, and an oscilloscope with a bandwidth of 20 Hz was used to output the images with a MATRIX MOS-620 model.The XC6SLX16-2FTG256I chip offers a number of outstanding features including low static and dynamic power consumption, a maximum clock frequency of 667.0 MHZ, adjustable I/O slew rate for improved signal integrity, rich logic resources and higher logic capacity, and a highly efficient 6-input LUT that improves performance and reduces power consumption. Compared with other FPGA chips, the XC6SLX16-2FTG256I's advantageous features are more conducive to realizing chaotic digital circuits. The digital implementation circuit flow is shown in Fig. 17.

Fig. 17

Block diagram of hardware implementation of FPGA platform

The specific operation is as follows. First, connect the FPGA development board to the computer, you can generally use the USB interface to connect. Install the appropriate FPGA development tool Quartus II 15.0 on the computer to write, synthesize, and download the FPGA design. Open the FPGA development tool and create a new project, set appropriate pin constraints in the project to ensure that the input and output pins on the FPGA development board correspond to the inputs and outputs of the chaotic system phase diagram.The design is synthesized and implemented using the FPGA development tool and binary files are generated that can be burned onto the FPGA. Connect the computer to the FPGA development board and the FPGA development tool downloads the generated binary file to the FPGA development board via JTAG. Convert the input signals (initial conditions or parameters) of the chaotic system into analog signals via DA and input them to the FPGA development board.Finally, run the chaotic system design on the FPGA development board and use an oscilloscope connected to the output pins of the chaotic system to observe and record the waveforms on the oscilloscope.

Considering that the Runge Kutta algorithm would take up a lot of logic resources in the FPGA, we chose the Eulerian algorithm to convert the system to C code and discretization to obtain Eq. (13), where the step size is h = 0.001 and the parameters are a = 3.04, b = 1.02, c = 9.02, d = 1, and e = 2.02. The utilization of the chip resources in the FPGA in implementing the digital hardware circuit of the new system is shown in Table 3. Finally, the planar phase diagram of the system is obtained by a digital oscilloscope, as shown in Fig. 18, which is basically consistent with the numerical simulation results and Multisim circuit simulation results. The RTL diagram of the system is shown in Fig. 19.

$$\left\{ {\begin{array}{*{20}c} {x(n + 1) = x(n) + h(y(n) - ax(n) + y(n)z(n))} \\ {y(n + 1) = y(n) + h(by(n) - x(n)z(n) - u(n))} \\ {z(n + 1) = z(n) + h(x(n)y(n) - cz(n) + y(n)u(n))} \\ {u(n + 1) = u(n) + h(dy(n) + e\sin (x(n))} \\ \end{array} } \right.$$

(13)

Table 3 Resource utilization in the design of new four-dimensional ultra chaotic hardware

Fig. 18

Oscilloscope phase diagram: a x–y plane b x–z plane c x-u plane d y–z plane

Fig. 19

RTL schematic diagram

7 Application in image encryption

With time, image encryption algorithms based on chaotic systems have achieved rapid development [19,20,21,22,23]. Chaotic systems have the good properties of unpredictability and sensitivity to initial values, as well as the randomness of the generated sequences, so chaotic systems are widely used in image encryption. Early chaotic image encryption mainly uses some simple low-dimensional chaotic systems or only performs a single encryption. However, the image encryption algorithm proposed in this paper adopts multiple encryption strategies. Taking a grayscale image with the size of M × N as an example, Arnold transformation [24,25,26,27] was performed on the original image first, and then DNA encryption operation was performed on the transformed image. The framework diagram of the image encryption algorithm is shown in Fig. 20 [28,29,30,31,32].

Fig. 20

Encryption process

7.1 Arnold Disruption

The Arnold permutation is a transformation proposed by Russian mathematician Vladimir I. Arnold, whose transformation matrix equation is:

$$\left [ {\begin{array}{*{20}c} X \\ Y \\ \end{array} } \right] = \left [ {\begin{array}{*{20}c} 1 & A \\ B & {AB + 1} \\ \end{array} } \right]\left [ {\begin{array}{*{20}c} X \\ Y \\ \end{array} } \right]\,(\bmod N)$$

(14)

$$X = (x + By)\,\bmod N$$

(15)

$$Y = \left [ {Bx + (AB + 1)y} \right]\,\bmod N$$

(16)

x, y = {0,1 …, N-1} denotes the position before the transformation, and (X, Y) denotes the transformation position. a, b are the parameters of Arnold's transformation. a = x_i, b = y_i (i = 1, 2, 3…, MN), N denotes the side length of the square image, and mod denotes the modulus operation.A and B are pseudo-random sequences generated by vector generation X, both of size M × N, and the transformation between pixel points can be realized by pseudo-random variables A and B.

7.2 DNA encoding encryption

Watson and Crick jointly proposed the double helix structure of the DNA strand, in which each DNA sequence consists of four bases: adenine (A), cytosine (C) and guanine (G), and thymine (T), and the two DNA sequences are bonded together by the complementary pairing laws of A-T and C-G. The four bases are encoded by 00, 01, 10 and 11, and then eight coding rules can be obtained according to the principle of DNA complementarity. These four bases are encoded with 00, 01, 10 and 11, and then eight encoding rules can be obtained according to the principle of DNA base complementarity. To realize image encryption, the image data should first be converted into binary numbers, and then a DNA coding rule is randomly selected to encode two binary numbers into one base, and decoding is the inverse process of this process. Tables 4, 5 and 6 show the complete DNA algorithm.

Table 4 DNA coding rules

Table 5 DNA addition and subtraction rules

Table 6 DNA coding rule 1 when the DNA heterodyning rule

As shown in Table 4, the so-called DNA computation refers to the "different-or" or "same-or" operation between DNA codes, as well as the complementary operation of DNA codes, such as the eight DNA coding modes shown in Table 4, where DNA computation is still essentially a binary The DNA calculation here is still essentially a binary arithmetic operation.

The definition of addition and subtraction of DNA follows traditional binary addition and subtraction operations. Since there exist 8 DNA coding rules, there also exist 8 corresponding DNA rules. When using DNA coding rule 1, for example, the DNA addition and subtraction rules shown in Table 5 are obtained.

The definition of DNA dissimilarity rules follows the traditional binary dissimilarity operation. Because there are 8 DNA coding rules, there are also 8 corresponding DNA dissimilarity rules. For example, when using DNA coding rule 1, the DNA dissimilarity rules shown in Table 6 are obtained.

Using the ode45 algorithm to calculate the initial value of the chaotic system and iterate the chaotic system, four keys are obtained. To improve security and obtain better randomness, the first 3001 terms are removed to obtain four chaotic sequences, x_i, y_i, z_i, u_i, where (i = 1, 2, 3…M × N), the {u_i} chaotic sequence is converted to an integer between 0 and 255, and then u_i is converted into a random matrix R with M rows and N columns. Next, the binary matrix transformation will be performed on the matrix A and matrix R after Arnold permutation, and then every two binary numbers will be converted into a DNA base according to the DNA coding rules, and the corresponding DNA sequence matrix will be obtained, and the matrix H will be represented by DNA calculation.

7.3 Pixel-level diffusion

Firstly, the matrix H is decoded according to the rules of DNA decoding. A binary matrix is obtained, and then it is converted into a binary matrix notated as F. The pseudo-matrix sequences u_i', D_i, and L_i are the sequences after diffusion. Then the diffusion is performed, the diffusion is performed by using two-way diffusion with heterogeneous operations, and the forward and reverse diffusion are each diffused once, and the formulas for the forward and reverse operations are (17) and (18), respectively.

$$\left\{ \begin{gathered} L_{i} = L_{i - 1} \oplus D_{i} \oplus F_{i} \hfill \\ F_{i} = L_{i - 1} \oplus L_{i} \oplus D_{i} \hfill \\ \end{gathered} \right.$$

(17)

$$\left\{ \begin{gathered} L_{i} = L_{i + 1} \oplus D_{i} \oplus F_{i} \hfill \\ F_{i} = L_{i + 1} \oplus L_{i} \oplus D_{i} \hfill \\ \end{gathered} \right.$$

(18)

The standard 512 × 512 Lena image and the baboon image are chosen for the experiments of the images, and the encrypted results are shown in Fig. 21b and e, where the image features of the original image are no longer observed.

Fig. 21

Encrypted rendering: a Lena Original image b Lena Encrypted images c Lena Decrypting the image d Baboon Original image e Baboon Encrypted images f Baboon Decrypting the image

7.4 Image security analysis

7.4.1 Histogram analysis

Histogram is a statistical method to describe the distribution of images smoothly, usually, the encrypted histogram has the characteristics of uniform distribution, and the image histogram of plain text is not uniform, the implementation of this part selects the classical image Lena and orangutan image of size 512 $\times$ 512 as shown in Fig. 22. Figure 22 b and e are the histogram before encryption, Fig. 22c and f are the histograms after encryption, it can be observed that the encrypted histogram presents an overall uniform distribution, which makes it difficult for an attacker to use the statistical characteristics of the sample values to recover the original image. Therefore, it is verified that the algorithm has an excellent ability to prevent statistical analysis.

Fig. 22

Image histogram: a Lena Original image b Lena Original image histogram c Lena Histogram of the encrypted image d Baboon Original image e Baboon Original image histogram f Baboon Histogram of the encrypted image

7.4.2 Keyspace and sensitivity analysis

The set of valid keys becomes the key space, and the key space is large enough to be effective against attacks. A new four-dimensional chaotic system is proposed in this paper, the initial value of the system is k = (x₀,y₀,z₀,u₀) and the parameters of the system are a, b, c, d, and e. The computational accuracy of the computer is 10^–16, so the key space of the chaotic system in this paper is 10^–16 × 10^–16 × 10^–16 × 10^–16 × 10^–16 × 10^–16 × 10^–16 × 10^–16 × 10^–16 × 10^–16≈2⁴⁷⁸. It is generally stipulated that the reliability of an encryption system is guaranteed only when the key space is greater than 2100. According to this standard, it is obvious that the key space of the system in this paper is much larger than this requirement.

Key sensitivity is the ratio of the difference between two ciphertext images obtained by observing the encryption of the same plaintext image when the key is changed. If the difference between the two cipher images is small, it proves that the sensitivity of the key is poor. If the difference between two cipher images is large then the sensitivity of the key is proved to be good. When the key sensitivity test is performed in this paper, the key K is changed to K₁ and it is found that the image could not be decrypted as shown in (a) and b in Fig. 23, which shows that the image encryption algorithm in this paper has good key sensitivity.

Fig. 23

Key sensitivity test: a Original image b Decrypted image after key replacement

7.4.3 Correlation analysis

One of the important factors to measure the effectiveness of image encryption is the correlation property. Digital images have a strong correlation between adjacent pixel points in horizontal, vertical, diagonal, and anti-diagonal directions, close to 1. The correlation between adjacent pixels of the encrypted image becomes very small, so breaking the correlation between adjacent pixels of the image is the meaning of image encryption. The formula to calculate the correlation is as follows:

$$\left\{ \begin{gathered} E(x) = \frac{1}{n}\sum\limits_{i = 1}^{n} {x_{i} } \hfill \\ D(x) = \frac{1}{n}\sum\limits_{i = 1}^{n} {(x_{i} - E(x))^{2} } \hfill \\ {\text{cov}} (x,y) = \frac{1}{n}\sum\limits_{i = 1}^{n} {(x_{i} - E(x))(y_{i} - E(y)} \hfill \\ \tau = \frac{{{\text{cov}} (x,y)}}{{\sqrt {D(x)D(y)} }} \hfill \\ \end{gathered} \right.$$

(19)

x and y are pixel values representing adjacent pixels, E(X) is representing expectation, and D(X) is representing variance. In this paper, a classic 512 × 512 Lena image is selected to calculate the correlation coefficients before and after encryption, and the correlation coefficients are calculated from four directions. The correlation coefficients of the images before and after encryption are shown in Fig. 24, and it can be observed that the correlation of the encrypted images is evenly distributed compared with the images before encryption, thus verifying that the algorithm in this paper destroys the correlation of the original images.

Fig. 24

The correlation coefficient of images: a Plaintext horizontal direction b Plaintext vertical direction c Plaintext diagonal direction d Plaintext anti-diagonal direction e Ciphertext horizontal direction f Ciphertext vertical direction g Ciphertext diagonal direction h Ciphertext anti-diagonal direction

As shown in Table 7, the unencrypted image has a strong correlation close to 1 in 4 directions and the image has a dense pixel distribution, while the encrypted image has a small correlation close to 0 in 3 directions and the image has a uniform pixel distribution. It can also be seen from Table 5 that the correlation coefficients of all three directions of the encrypted images of the system in this paper are closer to 0 than the other compared with other methods, which indicates that the encryption effect of the new system algorithm proposed in this paper is very effective (Table 8).

Table 7 Correlation coefficient comparison

Table 8 Information entropy comparison

7.4.4 Analysis of information entropy

Information entropy can be used to measure the random distribution of image information, which is an important indicator of the random distribution. The better the random distribution, the greater the value of information entropy, which is calculated by the formula:

$$G(s) = - \sum\limits_{i = 0}^{{2^{n} - 1}} {p(s_{i} )} \log_{2} p(s_{i} )$$

(20)

All states of pixel values in the image are denoted by 2ⁿ and the probability of pixel values in the image is denoted by p(s_i), which has the information of 256 states in this paper, so the ideal information entropy is 8. The image information entropy after encryption is 7.9994, which is very close to 8. The comparison with other systems after encryption is given in the chart, and it is found that the encryption effect of this paper is better.

7.4.5 Robustness analysis

Robustness is the most important characteristic to measure the resistance of an encryption algorithm to interference. In this paper, we choose to test the robustness of the encryption algorithm by cropping attack and noise attack. After cropping a part of the image, the image is then decrypted, and the result of decryption is shown in Fig. 25c. Applying 0.03 times pretzel noise to the encrypted image, the decrypted image is shown in Fig. 26c. It is found that the key information of the graphics can still be identified using the encryption algorithm in this paper. It can be verified that this algorithm can resist the cropping attack and noise attack to a certain extent and has good robustness.

Fig. 25

Key trimming test: a Original image b Trimming test c Decrypting the image

Fig. 26

Noise Attack Test: a Original image b 0.03 times pretzel noise was applied c Decrypting the image

8 Conclusion

In this paper, a novel four-dimensional hyperchaotic system is proposed and the dynamical properties of the system are analyzed. It is found that burst oscillations appear on the time series, intermittent chaos, and inverse multiplicative period bifurcations appear in the Lyapunov exponential spectrum and bifurcation diagram. The coexisting attractor appears to have a rare symmetric structure, indicating that the system has a rich dynamical behavior and a very good topology. In addition, in the aspect of system design and verification, Multisim circuit simulation software and FPGA digital hardware circuits are used. The experimental results show that the system exhibits excellent chaotic generation capability and verifies its feasibility and effectiveness. Finally, the new image encryption algorithm is designed by combining the new chaotic system proposed in this paper and DNA encryption algorithm, and the security performance such as information entropy and correlation after image encryption is analyzed, and the system is found to have good encryption cryptographic effect. Therefore, the novel four-dimensional hyperchaotic system and encryption algorithm proposed in this paper have good prospects for application in digital image communication.