Introduction

Catadioptric cameras enable panoramic imaging and offer several advantages compared to conventional cameras based on perspective projection. Panoramic imaging also provides extensive information about the environment. The benefits of catadioptric imaging together with projection specific analysis can simplify many computer vision tasks. For example, it decreases artifacts from boundary effects in image analysis and simplifies the tracking of motion. Catadioptric cameras can more closely preserve the local shape of objects. Systems based on catadioptric cameras can also enable effective visualization and even telepresence1. Other more recent applications are for assisted vehicle driving2 and as robotic vision systems3,4.

The optical properties of reflective surfaces, mirrors, namely catoptrics, were investigated geometrically since antiquity. They were initially physically associated with burning. They examined mirrors that were shaped as conic sections. The first to discover that the ellipse, the hyperbola, and the parabola are conic sections was Menaechmus (born c.380 BC). Archimedes (287-c.212 BC) worked on both conic sections and catoptrics. Apollonius of Perga (240 BC-c.190 BC) in his books “Conic sections” and “On the burning mirrors” derived the focal and reflection properties of ellipses and hyperbolas5,6. Diocles (240 BC-c.180 BC) in his book “On burning mirrors” derived the focal property of the parabola7. Later, Anthemius of Tralles (474 AC–c534 AC) wrote a book, “On burning mirrors”, where he elaborated further on the properties of the foci of the parabola and of the ellipse as well as on their applicability to architecture8. Ptolemy (150 AD) posed the problem of reflection on a spherical surface that does not have a single viewpoint9. Alhazen (c.965–c.1040) in the “Book of optics” provided a geometrical solution to this problem.

In a large scale the reflective properties of the paraboloid are used for the focusing of parallel beams. Some examples are satellite dish antennas10 and catadioptric telescopes that avoid the chromatic aberrations from which the lenses suffer9. Omnidirectional sensors are also used in a smaller scale for various purposes. In medicine, the ellipsoid is used for lithotripsy with ultrasound11. In medical imaging they have been used for endoscopy. An example has been with a cylindrical camera that gives a flat cylindrical image12 and another example is for a system that combines forward dioptric and radial catadioptric views13. An early omnidirectional camera was implemented with a four-sided mirrored pyramid14. Also, an early system with a dodehahedral mirror enabled visualization with a single viewpoint15. A hyperboloid mirror has also been used for panoramic television16. Similarly, a catadioptric projector models the catadioptric imaging projection and inverts it to create a panoramic projection17. Also, a system for telepresence has used a hyperboloidal mirror camera1. More recently, omnidirectional sensors have been used for surveillance of traffic light intersections18 as well as for assisted vehicle driving2 and mobile robotic navigation19. Other uses have been as catadioptric stereo imaging sensors for mobile robotics3,4 and as omnidirectional sensors for aerial robotics20.

There has also been progress with analytical work on the focal properties of reflective mirror surfaces. It has been proven that any surface with a focal property both is and has to be a surface of revolution of a conic section. A proof of this result has used differential equations in polar and spherical coordinates21. Another proof of this result has been coordinate free based on the orthogonality properties of the foci22. Results along these lines were also derived and introduced to the context of computer vision by a classification of panoramic catadioptric imaging cameras with a single viewpoint constraint23,24. These derivations also describe the principles for the design of a catadioptric camera with a paraboloidal convex reflective surface and a quantification of its properties with respect to field of view, resolution, and blurring23,25,26. There have also been studies to construct an analytical model of the catadioptric projections from mirrors of different types of conic sections in a unified manner27 and further refinements of that construction28.

There has been extensive work on the calibration for catadioptric cameras in particular with a single viewpoint. This has been for paracatadioptric camera sensors29 and more generally for their calibration using images of geometric primitives such as of three parallel lines30, vanishing points31,32, or of circular sections33,34. The imaging of motion has also been investigated. A study has examined the time-to-contact with paracatadioptric sensors35. There have also been studies on the egomotion of catadioptric sensors. A simple approach first reconstructs the motion field from the 2D image to the surface of a sphere and then applies conventional methods to estimate translation and rotation36,37. Other methods process directly the image of the catadioptric projection and assume correspondence to compute the essential matrix38. Catadioptric stereo has been achieved with various arrangements of these sensors39,40,41. The corresponding models of projection from the world to the images and the respective epipolar geometries have been developed for each of these arrangements42.

The properties of catadioptric projection have been investigated for basic geometric primitives of points and parallel lines31,32, simple motions of translations and rotations, as well as early computer vision operations such as calibration and stereo. The properties of the projection of many higher order geometric features of the scene have yet to be studied. This work examines one such property. This is the maximum size of the final angle an 1D object subtends in the catadioptric image projection as a function of the distance of the object. The problem has been formulated for central projection and is known as the Regiomontanus angle maximization problem. It was posed by mathematician Johannes Mueller (1436–1476)43,44,45. This work extends the Regiomontanus angle maximization for angles of a 1D object to the case where the effective viewpoint is that of a catadioptric paraboloidal imaging sensor. It examines directly the properties of the projection in catadioptric image space.

The paraboloidal mirror shape is associated with an orthographic projection. This is called a paracatadioptric imaging sensor and implements panoramic imaging with a single viewpoint. The first step is the analytical ray tracing from a point in the world, to the intermediate mirror surface, and eventually to its vertical reflection that is recorded by the camera to form an image. Then, two points in the world are considered together that are the boundaries of a 1D world object parallel to the optical axis. The distance between the orthographic projections of these two points in the image give the length of the object in the image. This length is computed and represents the angle between the parallel rays. The optimization of the length of the projection of an object results in a third degree equation for the Regiomontanus distance. This equation can be solved explicitly. The Khayyam geometric solution of this equation provides the paracatadioptric Regiomontanus distance of the object. Applications of these results for the calibration of a paracatadioptric imaging sensor, for navigation with such an imaging sensor, and a general biomedical application are discussed.

Background

This section provides general information on paracatadioptric sensors and a formulation for Regiomontanus maximization. It also describes a catadioptric sensor with a planar mirror.

Paracatadioptric imaging sensors

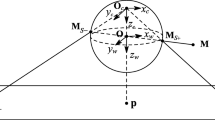
The mirror surface of a catadioptric omnidirectional sensor that has a single viewpoint has to be a surface of revolution of a conic section21,23. In this study the conic section giving the mirror is shaped as a paraboloid with the external surface convex and reflective. The reflected rays project to an orthographic telecentric lens in the camera that constrains the image projection to be orthographic and parallel to the optical axis. The parallel rays are assumed to meet at infinity under a negligible angle23. This negligible angle when measured in radians can be represented by the arc length it subtends, which is the distance between the parallel rays on the image plane. Hence, the angle difference in radians between the parallel rays is their distance on the image plane.

Regiomontanus’ angle maximization problem

It involves the angle subtended at a viewpoint directly by a 1D object that is vertical as the viewpoint moves away from the object horizontally. The coordinates in 3D space are (x, y, z). This analytical development represents the 2D plane, (x, y), with a radial coordinate \(r={(x,y) \over \Vert (x,y)\Vert _2}\). The lower point of the vertical 1D object is at height a and the higher point is at height b. The values of \(z=a\) and \(z=b\) satisfy \(b \ge a\).

The point a at distance r subtends an angle \(\alpha\). Similarly, the point b, at the same distance r, subtends an angle \(\beta\). The subtended angle of the difference \(\beta -\alpha\) as a function of r is given by43,44:

$$\begin{aligned} \tan (\beta - \alpha )=(b-a){r\over r^2+ab}. \end{aligned}$$
(1)

The geometry is in Fig. 1a. The simulation of Eq. (1) for \((a,b)=(6,12)\) and \(r=[0, 90]\) is in Fig. 2. The maximization of the subtended angle in Eq. (1) gives the condition for radial Regiomontanus distance, \(r_{RM}\). The condition can also be expressed in terms of \(\tan \alpha ={a \over r}\) and \(\tan \beta ={b \over r}\) to give

$$\begin{aligned} r_{RM}=\sqrt{ab} \Leftrightarrow \tan \alpha \tan \beta = 1 \end{aligned}$$
(2)

in trigonometric form.

Figure 1
figure 1

In (a) is a diagram with the geometry for direct Regiomontanus maximization. In (b) is a diagram with the geometry of catadioptric imaging with a planar mirror for Regiomontanus maximization.

Full size image
Figure 2
figure 2

Simulation for the geometries in Fig. 1 of subtended angle \((\beta -\alpha )\) as a function of distance r from an object. The values of the parameters are \((a, b)=(6, 12)\), and \(r=[0, 90]\).

Full size image

Angle maximization for a planar mirror catadioptric camera

A camera is placed facing down with its center of projection, its pinhole, at a distance f above a planar mirror27. The plane of the mirror is given by \(z=f\) and the camera pinhole is taken to be at (0, 2f). The result is that the effective single viewpoint is at the origin, (0, 0). Hence it follows the direct Regiomontanus analysis and satisfies its results already obtained in Sect. "Regiomontanus’ angle maximization problem" above. The catadioptric camera is in an upright position imaging a 1D object. In this case the difference between the final values of the projection angles optimized becomes \(\beta _f-\alpha _f\).

The 1D object is parallel to the optical axis with a lower point at height a and a higher point at height b. The trajectory of the object is normal to the optical axis. The 1D object and its trajectory, the rays emanating from the object that are reflected by the mirror impinging normally on the image, and the optical axis are all coplanar. The geometry is in the diagram in Fig. 1b. Due to the symmetry with respect to the mirror, Eq. (1) and its simulation in Fig. 2 still hold. The field of view of this catadioptric system with a planar mirror is limited. This work examines the use of a paraboloidal mirror that has an extended omnidirectional field of view and also preserves the single viewpoint constraint.

Methods

The geometry of a vertical catadioptric camera with a planar mirror imaging a 1D object is also used for the paracatadioptric camera considered. Rays from points of the object in the world are traced analytically to the intermediate mirror surface and are then projected to the camera to form an image. The ray tracing for two points of the object, the lower and the upper, gives the projection and length of the object in the image. The derivative of the length of the projection with distance r between the optical axis of the camera and the 1D object in the world is computed. Setting this derivative to zero gives a third degree equation for the Regiomontanus distance of maximum projection length.

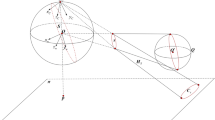
Paraboloidal catadioptric mirror

The axis of the paraboloid coincides with the vertical z-axis and its focal point is at the origin (0, 0). It is also concave down, that is, \(\left. d^2 z \over dr^2\right| _{r=0}<0\). These properties are set Without Loss Of Generality (WLOG). The resulting paraboloid has equation:

$$\begin{aligned} z=f-{1 \over 4f}r^2, \end{aligned}$$
(3)

which satisfies these properties. The paraboloid intersects the r axis at \((\pm 2f, 0)\) and the z-axis at (0, f). The geometry is in Fig. 3.

Figure 3
figure 3

Diagram with the geometry of catadioptric imaging with a paraboloidal mirror for Regiomontanus maximization.

Full size image

Intermediate projection on the paraboloidal mirror

The point at height a and distance r in the world subtends an angle \(\alpha\) at the effective viewpoint. The ray emanating from the point at a meets the paraboloidal mirror at \((r_{p_\alpha },z_{p_\alpha })\) under angle:

$$\begin{aligned} \tan {\alpha }={a \over r}={z_{p_\alpha } \over r_{p_\alpha }} \Rightarrow z_{p_\alpha }=r_{p_\alpha } \tan {\alpha }. \end{aligned}$$
(4)

The replacement of Eq. (4) in Eq. (3) of the paraboloid gives:

$$\begin{aligned} r_{p_\alpha } \tan {\alpha }=f-{1 \over 4f}r_{p_\alpha }^2 \Rightarrow {1 \over 4f}r_{p_\alpha }^2+\tan {\alpha } r_{p_\alpha }-f=0. \end{aligned}$$
(5)

The solution of Eq. (5) for \(r_{p_\alpha }\) gives:

$$\begin{aligned} r_{p_\alpha }=2f\left( -\tan {\alpha } {\mathop {\pm }\limits ^{root}} \sqrt{\tan ^2{\alpha }+1}\right) =2f\left( -\tan {\alpha } {\mathop {\pm }\limits ^{root}} {1 \over \cos {\alpha }}\right) . \end{aligned}$$
(6)

The root signs of Eq. (6) correspond to the two antipodal meeting points of the ray with the mirror surface. The positive sign corresponds to the meeting point proximal to the emanating point and the negative sign corresponds to the distal meeting point. The distal point does not satisfy physical constraints and is ignored. The positive sign that corresponds to the proximal point is selected to give:

$$\begin{aligned} r_{p_\alpha }=2f\left( -\tan {\alpha } + {1 \over \cos {\alpha }}\right) , \end{aligned}$$
(7)

with \(r_{p_\alpha }>0\). The replacement of \(\tan {\alpha }={a \over r}\) and \(\cos {\alpha }={r \over \sqrt{a^2+r^2}}\) in this equation gives:

$$\begin{aligned} r_{p_\alpha }=2f\left( {-a + \sqrt{a^2+r^2} \over r}\right) . \end{aligned}$$
(8)

Orthographic projection for the image

The point where the ray meets the surface of the paraboloidal mirror is \((r_{p_a}, z_{p_a})\). The final projection from the mirror to the camera is orthographic. Thus, the depth coordinate, \(z_{p_a}\), is ignored and the radial coordinate remains the only coordinate of interest. The radial coordinate of the projection at the mirror is the same as the radial coordinate of the projection to the camera given by Eq. (8). The derivative of the radial coordinate of the point on the mirror in Eq. (8) with respect to r in space is:

$$\begin{aligned} {d r_{p_\alpha } \over dr}= & {} 2f{r^2 (a^2+r^2)^{-1/2} +a-(a^2+r^2)^{1/2} \over r^2}. \end{aligned}$$
(9)

Length of projection of object on the image

The image projections of the two points at heights a and b give the length of the 1D object in the image. The points at the surface of the paraboloidal mirror are \((r_{p_a}, z_{p_a})\) and \((r_{p_b}, z_{p_b})\). Similarly to the radial projection of point at height a under angle \(\alpha\) in Eq. (8), the point at height b and under angle \(\beta\) has radial projection \(r_{p_\beta }\). The rays projecting on the image plane are parallel. Hence the difference between the final values of the angles, \(\beta _f-\alpha _f\), in radians, is equal to the length of the projection, l. The length of the projection in the image is the difference between the r-coordinates of the projections of points a and b in the image, \(l=r_{p_\alpha }-r_{p_\beta }\),

$$\begin{aligned} l= & {} r_{p_\alpha }-r_{p_\beta } = 2f\left( {-a + \sqrt{a^2+r^2} \over r}\right) -2f\left( {-b + \sqrt{b^2+r^2} \over r}\right) . \end{aligned}$$
(10)

Equations (9) and (10) give the derivative of the length of the projection as:

$$\begin{aligned} {d l \over dr}= & {} {d(r_{p_\alpha }-r_{p_\beta }) \over dr} ={dr_{p_\alpha } \over dr}-{dr_{p_\beta } \over dr} \nonumber \\= & {} 2f\left[ { r^2(a^2+r^2)^{-1/2} +a-(a^2+r^2)^{1/2}\over r^2} \right] - \nonumber \\- & {} 2f\left[ { r^2(b^2+r^2)^{-1/2} +b-(b^2+r^2)^{1/2}\over r^2} \right] . \end{aligned}$$
(11)

Maximization of the length of the projection of the object in the image

The condition for the maximum is \({d l (r) \over dr}=0\). Considering Eq. (11), this leads to,

$$\begin{aligned} 2f\left[ { r^2(a^2+r^2)^{-1/2} +a-(a^2+r^2)^{1/2}\over r^2} \right] - 2f\left[ { r^2(b^2+r^2)^{-1/2} +b-(b^2+r^2)^{1/2}\over r^2} \right]= & {} 0 \nonumber \\ \Rightarrow{} & {} \nonumber \\ r^2 \left[ (a^2+r^2)^{-1/2}-(b^2+r^2)^{-1/2}\right] +(a-b)-\left[ (a^2+r^2)^{1/2}-(b^2+r^2)^{1/2}\right]= & {} 0. \nonumber \\ \end{aligned}$$
(12)

The rationalization of the denominators in Eq. (12) is developed in appendix A of supplementary information to give the maximization condition as:

$$\begin{aligned} b^2(a^2+r^2)^{1/2}-a^2(b^2+r^2)^{1/2}-(b-a)(a^2+r^2)^{1/2}(b^2+r^2)^{1/2}=0. \end{aligned}$$
(13)

This equation is simplified with the removal of the radicals. The development is in appendix B of supplementary information. It gives an intermediate polynomial of eighth degree in the powers of r, \(\sum _{i=0}^{8}c_{i}'(a,b)r^i=0\). The polynomial is even in terms of the powers of r and the zeroth order term is zero. The odd terms are zero because of the symmetry of the problem around the axis \(x=0\) . The zeroth order term is zero because both the projection and its derivative are zero at \(x=0\).

The coefficients of the powers of r of the eighth degree polynomial are in turn polynomials of a and b. The coefficients are simplified by removing terms that are common to all of them. The result is an equation of the form:

$$\begin{aligned} r^2\left( c_8(a,b)r^6+c_6(a,b)r^4+c_4(a,b)r^2+c_2(a,b)\right) = 0, \end{aligned}$$
(14)

where \(c_8(a,b)\), \(c_6(a,b)\), \(c_4(a,b)\), and \(c_2(a,b)\) are polynomials of powers of a and b as computed in appendix B of supplementary information and given in Table 1. The symbolic algebraic development of the methodologies in appendix B of supplementary information and of this work in general make use of the SymPy software library46 of the Python programming language47.

Table 1 The coefficients of the eighth degree polynomial directly in terms of a and b.
Full size table

The condition in Eqs. (13) and (14) has at least a double root at \(r=0\); however, as Eq. (10) can show, this corresponds to an object projection of length \(lim_{r \rightarrow 0}l=0\). Also, the configuration with the camera located immediately above the mirror renders the solution for \(r=0\) physically impossible. Hence, this solution is ignored.

The polynomial from Eq. (14) that remains is:

$$\begin{aligned} c_8(a,b)r^6+c_6(a,b)r^4+c_4(a,b)r^2+c_2(a,b) = 0. \end{aligned}$$
(15)

The replacement:

$$\begin{aligned} w=r^2 \end{aligned}$$
(16)

gives:

$$\begin{aligned} c_8(a,b)w^3+c_6(a,b)w^2+c_4(a,b)w+c_2(a,b) = 0 \end{aligned}$$
(17)

The development of the solution of this equation is in Sect. "Geometric solution of the cubic polynomial equation" below.

Geometric solution of the cubic polynomial equation

Equation (17) is a third degree equation. The constrain \(w=r^2>0\) gives real final solutions for the Regiomontanus distance as \(r=\sqrt{w}\) in Eq. (16). The algebraic solution to the cubic equations can be computed directly with the method of Cardano48. However, that method is inconvenient. Instead, this section presents a more intuitive geometric solution of this equation provided by Omar Khayyam that conveniently provides their roots48. The solutions for w are described as intersections of conic sections. Specifically, the intersection of a parabola and hyperbola. The solution steps are given below.

Depressed form of cubic equation

A polynomial in standard form in Eq. (17) is normalized so that the coefficient of the third order becomes unity to give:

$$\begin{aligned} w^3+{c_6 \over c_8}w^2+{c_4 \over c_8}w+{c_2\over c_8} = 0 \end{aligned}$$
(18)

The substitutions for the fractions:

$$\begin{aligned} c_p={c_6 \over c_8}, \hspace{0.4cm} c_g={c_4 \over c_8}, \hspace{0.4cm} c_r={c_2 \over c_8} \end{aligned}$$
(19)

in Eq. (18) give:

$$\begin{aligned} w^3+c_pw^2+c_gw+c_r=0. \end{aligned}$$
(20)

A cubic is symmetric around its inflection point. The inflection point of Eq. (20) is located at \(w=-{c_p \over 3}\). The cubic is shifted so that the inflection point is located on the vertical axis. This gives its depressed form where the quadratic term is zero. This is achieved with the substitution,

$$\begin{aligned} \chi =w+{c_p \over 3} \Rightarrow w=\chi -{c_p \over 3} \end{aligned}$$
(21)

in Eq. (20) to give Eq. (22) and finally Eq. (23):

$$\begin{aligned} \left( \chi -{c_p \over 3}\right) ^3+c_p\left( \chi -{c_p \over 3}\right) ^2+c_g\left( \chi -{c_p \over 3}\right) +c_r= & {} 0 \Rightarrow \end{aligned}$$
(22)
$$\begin{aligned} \left( \chi -{c_p \over 3}\right) ^2\left( \chi -{c_p \over 3}+c_p\right) +c_g\left( \chi -{c_p \over 3}\right) +c_r= & {} 0 \Rightarrow \nonumber \\ \left( \chi -{c_p \over 3}\right) ^2\left( \chi +{2c_p \over 3} \right) +c_g\left( \chi -{c_p \over 3}\right) +c_r= & {} 0 \Rightarrow \nonumber \\ \left( \chi -{c_p \over 3}\right) \left[ \left( \chi -{c_p \over 3}\right) \left( \chi +{2c_p \over 3} \right) +c_g\right] +c_r= & {} 0 \Rightarrow \nonumber \\ \left( \chi -{c_p \over 3}\right) \left[ \chi ^2+{c_p\over 3}\chi -{2 \over 9}c_p^2+c_g\right] +c_r= & {} 0 \Rightarrow \nonumber \\ \chi ^3+{c_p \over 3}\chi ^2-{2 \over 9}c_p^2\chi +c_g\chi -{c_p \over 3} \chi ^2-{c_p^2 \over 9}\chi +{2 \over 27}c_p^3-{c_p \over 3}c_g+c_r= & {} 0 \Rightarrow \nonumber \\ \chi ^3+\chi \left( c_g- {c_p^2\over 3}\right) +\left( {2 \over 27}c_p^3-{c_p \over 3}c_g+c_r\right)= & {} 0 \end{aligned}$$
(23)

The substitutions of the coefficient of \(\chi\) in Eq. (23) with \(c_s\) and the zero order term in the same equation with \(c_t\) gives:

$$\begin{aligned} c_s=c_g-{c_p^2 \over 3},\hspace{0.4cm} c_t={2 \over 27}c_p^3-{c_p \over 3}c_g+c_r. \end{aligned}$$
(24)

The substitution of the relations in Eq. (24) above into Eq. (23) gives:

$$\begin{aligned} \chi ^3+c_s\chi +c_t=0. \end{aligned}$$
(25)

The substitutions of \(c_g\), \(c_p\), and \(c_r\) from Eq. (19) in Eq. (24) gives both \(c_s\) and \(c_t\) as a function of \(c_2\), \(c_4\), \(c_6\), and \(c_8\). The \(c_s\) becomes

$$\begin{aligned} c_s=c_g- {c_p^2\over 3}={c_4\over c_8}-{1\over 3}{c_6^2\over c_8^2}={3c_4c_8-c_6^2 \over 3c_8^2} \end{aligned}$$
(26)

and the \(c_t\) becomes:

$$\begin{aligned} c_t= & {} {2 \over 27}c_p^3-{c_p \over 3}c_g+c_r={2 \over 27}{c_6^3 \over c_8^3}-{c_6 \over 3c_8}{c_4\over c_8}+{c_2 \over c_8}= \nonumber \\= & {} {2c_6^3-9c_4c_6c_8+27c_8^2c_2\over 27c_8^3}. \end{aligned}$$
(27)

The substitutions of \(c_2, c_4, c_6, c_8\) from Table 1 in Eqs. (26) and (27), respectively, give

$$\begin{aligned} c_s=- \frac{4 a^{2} b^{2} \left( a^{4} + a^{3} b + a b^{3} + b^{4}\right) }{3 a^{4} - 12 a^{3} b + 18 a^{2} b^{2} - 12 a b^{3} + 3 b^{4}} \end{aligned}$$
(28)

and

$$\begin{aligned} c_t=\frac{4 a^{3} b^{3} \left( 4 a^{6} - 21 a^{5} b - 12 a^{4} b^{2} + 26 a^{3} b^{3} - 12 a^{2} b^{4} - 21 a b^{5} + 4 b^{6}\right) }{27 \left( a^{6} - 6 a^{5} b + 15 a^{4} b^{2} - 20 a^{3} b^{3} + 15 a^{2} b^{4} - 6 a b^{5} + b^{6}\right) }. \end{aligned}$$
(29)

The coefficients of the depressed polynomial in terms of a and b are also given in Table 2.

Table 2 The coefficients of the depressed polynomial directly in terms of a and b.
Full size table

These relations can more conveniently be expressed in terms of \(\frac{b}{a}\) to give:

$$\begin{aligned} c_s=- \frac{4}{3}a^{2} b^{2} \frac{ \left( 1 + \left( \frac{b}{a}\right) + \left( \frac{b}{a}\right) ^{3} + \left( \frac{b}{a}\right) ^{4}\right) }{\left( 1 - 4 \left( \frac{b}{a}\right) + 6 \left( \frac{b}{a}\right) ^{2} - 4 \left( \frac{b}{a}\right) ^{3} + \left( \frac{b}{a}\right) ^{4}\right) } \end{aligned}$$
(30)

and

$$\begin{aligned} c_t=\frac{4}{27}a^{3} b^{3} \frac{ \left( 4 - 21 \left( \frac{b}{a}\right) - 12 \left( \frac{b}{a}\right) ^{2} + 26 \left( \frac{b}{a}\right) ^{3} - 12 \left( \frac{b}{a}\right) ^{4} - 21 \left( \frac{b}{a}\right) ^{5} + 4 \left( \frac{b}{a}\right) ^{6}\right) }{\left( 1 - 6 \left( \frac{b}{a}\right) + 15 \left( \frac{b}{a}\right) ^{2} - 20 \left( \frac{b}{a}\right) ^{3} + 15 \left( \frac{b}{a}\right) ^{4} - 6 \left( \frac{b}{a}\right) ^{5} + \left( \frac{b}{a}\right) ^{6}\right) }. \end{aligned}$$
(31)

The denominator of the fraction in Eq. (30) for \(c_s\) is equal to zero for \(\frac{b}{a}=1\) and positive for \(\frac{b}{a}>1\). Hence, when \(\frac{b}{a}>1\), that is the range of interest, then \(c_s<0\). The value of \(c_t\) in Eq. (31) can be both positive and negative in the range of interest, \(\frac{b}{a}>1\).

Khayyam’s geometric solutions

The cubic equations can be classified into several Khayyam types so that the coefficients are positive. Each type is solved differently. Several of the types are either reducible to simpler ones or do not result in real solutions48. The two remaining types that are relevant in this work are in Table 3. In the range of interest, \(\frac{b}{a}>1\), the coefficient \(c_s\) satisfies \(c_s<0\) and the coefficient \(c_t\) satisfies \(c_t<0\) and \(c_t>0\). Hence, Eq. (25) can be of type 3 or of type 2 and the geometric solutions for these two types are given below.

Table 3 The two types of equations for solutions.
Full size table

Khayyam’s solutions for type 3 and type 2

The Khayyam equation of type 3 is:

$$\begin{aligned} \chi ^3=c_{3,a}\chi +c_{3,b}. \end{aligned}$$
(32)

Its geometric solution is in Fig. 4a. The Khayyam equation of type 2 is:

$$\begin{aligned} \chi ^3+c_{2,b}=c_{2,a}\chi . \end{aligned}$$
(33)

Its geometric solution is in Fig. 4a.

Figure 4
figure 4

In (a) is the solution for type 3 and in (b) is the solution for type 2.

Full size image

Khayyam treated these types in Eq. (32) and in Eq. (33) separately but by allowing negative horizontal lengths we can combine these two types and corresponding solutions into one:

$$\begin{aligned} \chi ^3 \pm c_{23,b}=c_{23,a}\chi . \end{aligned}$$
(34)

Let AB be perpendicular to BC. Two auxiliary shapes are employed. The first is a square with side AB so that:

$$\begin{aligned} (AB)^2=c_{23,a}. \end{aligned}$$
(35)

The second auxiliary shape is a solid with base equal to \((AB)^2\) and volume equal to \(c_{23,b}\):

$$\begin{aligned} (AB)^2\cdot BC=c_{23,b}. \end{aligned}$$
(36)

Place BC to the left if the sign in front of \(c_{23,b}\) is negative (Type 3) as in Fig. 4a. Place BC to the right if the sign in front of \(c_{23,b}\) is positive (Type 2) as in Fig. 4b. The first main shape is a parabola with vertex at B and parameter AB. The definition and equation of the parabola with \((BE)=\chi\) and \((BZ)=y\) becomes:

$$\begin{aligned} (BE)^2=(BZ)(AB) \Rightarrow \chi ^2=y\sqrt{c_{23,a}} \Rightarrow y={\chi ^2 \over \sqrt{c_{23,a}}}. \end{aligned}$$
(37)

The square of Eq. (37),

$$\begin{aligned} y^2={\chi ^4 \over c_{23,a}}, \end{aligned}$$
(38)

is also used for convenience. The replacement of \(c_{23,a}\) in Eq. (37) gives the parabola as

$$\begin{aligned} y=\sqrt{\frac{3 a^{4} - 12 a^{3} b + 18 a^{2} b^{2} - 12 a b^{3} + 3 b^{4}}{4 a^{2} b^{2} \left( a^{4} + a^{3} b + a b^{3} + b^{4}\right) }} \chi ^2. \end{aligned}$$
(39)

The second main shape is a hyperbola with vertices B and C and parameter BC as is shown in Fig. 4. The definition and equation of the hyperbola is:

$$\begin{aligned} (ED)^2=(BE)(CE) \end{aligned}$$
(40)

It involves the length of BC given by replacing Eq. (35) in Eq. (36) to get:

$$\begin{aligned} (AB)^2(BC)=c_{23,b} \Rightarrow c_{23,a}(BC)=c_{23,b} \Rightarrow (BC)={c_{23,b} \over c_{23,a}}. \end{aligned}$$
(41)

Khayyam’s solutions for Type 3

In type 3 the definition of the hyperbola leads to:

$$\begin{aligned} (BE)=\chi \Rightarrow (CE)=(EB)+(BC)=\chi +{c_{3,b} \over c_{3,a}} \end{aligned}$$
(42)

The definition and equation of hyperbola in Eq. (40) for relation (42) of type 3 is

$$\begin{aligned} (ED)^2=(BE)(CE) \Rightarrow y^2=\chi \left( \chi +{c_{3,b} \over c_{3,a}}\right) \Rightarrow y^2=\chi ^2+{c_{3,b} \over c_{3,a}}\chi .{} & {} \end{aligned}$$
(43)

The parameter of this equation is \({c_{3,b} \over c_{3,a}}=\frac{c_t}{c_s}.\)

The meeting point D of the parabola and hyperbola with \(\chi =(BE)\) and \(y=(ED)\) is a solution. Substitute to Eq. (43) of the hyperbola above the relation \(y^2={\chi ^4 \over c_{3,a}}\) of the square of the equation of the parabola from Eq. (38) to get:

$$\begin{aligned} y^2=\chi ^2+{c_{3,b} \over c_{3,a}}\chi \Rightarrow {\chi ^4 \over c_{3,a}}=\chi ^2+{c_{3,b} \over c_{3,a}}\chi \Rightarrow \chi ^3=c_{3,a}\chi +c_{3,b}{} & {} \end{aligned}$$
(44)

This is indeed type 3 of Khayyam’s in equation (32).

Khayyam’s solutions for type 2

In type 2 the definition of the hyperbola leads to:

$$\begin{aligned} (BE)=-\chi \Rightarrow (CE)=(BE)+(BC) \Rightarrow (CE)=-\chi +{c_{2,b} \over c_{2,a}} \end{aligned}$$
(45)

The definition and equation of hyperbola in Eq. (40) for relation (45) of type 2 is

$$\begin{aligned} (ED)^2=(BE)(CE) \Rightarrow y^2=-\chi \left( -\chi +{c_{2,b} \over c_{2,a}}\right) \Rightarrow y^2=\chi ^2-{c_{2,b} \over c_{2,a}}\chi{} & {} \end{aligned}$$
(46)

The parameter of this equation is \(-{c_{2,b} \over c_{2,a}}=\frac{c_t}{c_s}.\)

The meeting point D of the parabola and hyperbola with \(\chi =(BE)\) and \(y=(ED)\) is a solution. Substitute to Eq. (46) above of the hyperbola the relation \(y^2={\chi ^4 \over c_{2,a}}\) of the square of the equation of the parabola from Eq. (38) to get:

$$\begin{aligned} y^2=\chi ^2-{c_{2,b} \over c_{2,a}}\chi \Rightarrow {\chi ^4 \over c_{2,a}}-\chi ^2+{c_{2,b} \over c_{2,a}}\chi =0 \Rightarrow \chi ^3+c_{2,b}=c_{2,a}\chi .{} & {} \end{aligned}$$
(47)

This is indeed type 2 of Khayyam’s in equation (33).

Khayyam’s solutions for type 3 and type 2 at intersections of hyperbola and parabola

The equation of the hyperbola both on type 3 in Eq. (43) and type 2 in Eq. (46) by replacing the coefficients becomes:

$$\begin{aligned} y^2= & {} \chi ^2+\frac{a b \left( - 4 a^{4} + 29 a^{3} b - 42 a^{2} b^{2} + 29 a b^{3} - 4 b^{4}\right) }{9 \left( a^{4} - 3 a^{3} b + 4 a^{2} b^{2} - 3 a b^{3} + b^{4}\right) } \chi \nonumber \\= & {} \chi ^2+\frac{a b \left( - 4 + 29 \left( \frac{b}{a}\right) - 42 \left( \frac{b}{a}\right) ^{2} + 29 \left( \frac{b}{a}\right) ^{3} - 4 \left( \frac{b}{a}\right) ^{4}\right) }{9 \left( 1 - 3 \left( \frac{b}{a}\right) + 4 \left( \frac{b}{a}\right) ^{2} - 3 \left( \frac{b}{a}\right) ^{3} + \left( \frac{b}{a}\right) ^{4}\right) } \chi . \end{aligned}$$
(48)

Each intersection of parabola in Eq. (39) and hyperbola in Eq. (48), except of B at the origin, gives a root of the cubic48.

Recovery of roots of original polynomial

The Khayyam’s solution are for the depressed form of the cubic in Eq. (25). The solutions for the standard form of the cubic in Eq. (18) are recovered using the relation in Eq. (21) with:

$$\begin{aligned} w=\chi -{c_p \over 3}>0. \end{aligned}$$
(49)

The value of \(c_p\) as a function of a and b is obtained from Eq. (19) and Table 1:

$$\begin{aligned} c_p=\frac{c_6}{c_8}=\frac{-4ab(a^2-ab+b^2)}{(b-a)^2}=-4ab\left( 1+\frac{ab}{(b-a)^2}\right) . \end{aligned}$$
(50)

This expression for \(c_p\) in terms of a and b shows that \(c_p<0\). Hence, the term \(-{c_p \over 3} \ge 0\), in relation (49) is able to map a negative value of \(\chi\) into a positive value of w.

The value of w must be greater than zero. This is because from Eq. (16) the square root of w gives the value of r,

$$\begin{aligned} r=\pm \sqrt{w}=\pm \sqrt{\chi -{c_p \over 3}}=\pm \sqrt{\chi + \frac{4ab}{3}\left( 1+\frac{ab}{(b-a)^2}\right) }, \end{aligned}$$
(51)

that must be a real number for a meaningful physical solution. The value of r can be positive or negative due to the symmetry around the optical axis.

This shows that for type 3 it may be necessary to check one, two, or even three roots \(\chi\) if they are positive. It also shows that for type 2 it may be necessary to check two or even three roots \(\chi\) if they are positive. A solution must then also be checked to satisfy the original condition in Eq. (13).

Discussion

This work develops a method to compute the Regiomontanus distance that maximizes the length of the projection of a 1D object imaged with a paracatadioptric sensor, that is, using a paraboloidal mirror. The optical axis is assumed vertical since, in practice, catadioptric omnidirectional sensors are fixed on another object such as a wall, a vehicle, a ground robot, or an aerial robot (Unmanned Aerial Vehicle). The direction of the vertical axis can be upwards or downwards depending on the application.

The first step of the methodology is to trace rays from two world points bounding a 1D object to the mirror surface. Then, the orthographic projection on the paracatadiotric camera sensor simplifies the computation of the image projection. The expression giving the length of the projection, l, is computed as a function of the distance between the optical axis of the sensor and the 1D object. The derivative of this expression is set to zero, \({dl \over dt}=0\), to give the maximization condition through the developments in Sect. "Length of projection of object on the image", "Maximization of the length of the projection of the object in the image", and "Geometric solution of the cubic polynomial equation". This condition is a third degree equation that can be solved directly. In this work, this equation is solved geometrically with Khayyam’s method to provide in a more meaningful way the Regiomontanus distance. The solutions for the Regiomontanus distance do not depend on parameter f of the paraboloid because of the orthographic projection forming the final image.

The Regiomontanus analysis can be extended to single viewpoint catadioptric sensors with hyperboloid and ellipsoid mirrors that involve a central projection from the mirror to the camera. The derivations can also be extended to more general situations for a 1D object in 3D space. In that case a linear trajectory of an object may not be co-planar with the optical axis, in which case the projection of the trajectory will be a conic section29,30,31,32,49. The projections of the trajectories of its two end points will be two different conic sections that meet at two vanishing points that correspond to the two opposite directions along the linear trajectories30. There exist methodologies for the analysis of the projection of parallel lines on catadioptric sensors to conic sections31. The Regiomontanus approach is complementary to those in that it investigates the effect of radial motion across such projected conic sections. The extension can also be for a general projection of a 2D object in 3D space or a 3D object.

The analysis presented in this work can have direct applications in various contexts. It can be used for teleconferencing and for online remote teaching under optimal viewing angles. Notably, the Regiomontanus angle is independent of the focal length (f) or on other intrinsic camera parameter, making it applicable even for uncalibrated cameras. However, the initial portion of this study, which computes the radial length of the projection, has the potential to contribute to paracatadioptric calibration. This calibration method would be simpler than existing approaches based on images of geometric primitives such as parallel lines and vanishing points31 that require the fitting of conic sections31,33,34. Other applications of this Regiomontanus analysis can be for the navigation and positioning using paracatadioptric sensors such as those used by robots in indoor environments19 as in a museum and aerial robotics in outdoor environments. These results may extend to other contexts where the focal properties of conic sections play a role, such as ultrasound-based imaging and therapies. In those contexts, the ultrasound waves under Regiomontanus angle could potentially enhance imaging resolution.

The Regiomontanus angle maximization can be derived for other types of catadioptric sensors or even under different media. The results presented in this study can be implemented and tested experimentally in various contexts.