Common Pole–Polar Properties of Central Catadioptric Sphere and Line Images Used for Camera Calibration

Abstract

Central catadioptric cameras with a single effective viewpoint contain both mirrors and pinhole cameras that increase the imaging field of view. In this study, the common pole–polar properties of central catadioptric sphere or line images are investigated and used for camera calibration. From these properties, the pole and polar with respect to the image of absolute conic and the modified image of absolute conic, respectively, can be recovered according to the generalized eigenvalue decomposition. Moreover, these techniques are valid for paracatadioptric sensors with the degenerate conic dual to the circular points being considered. At least three images of spheres or lines are required to completely calibrate any central catadioptric camera. The intrinsic parameters of the camera, the shape of reflective mirror, and the distortion parameters can be linearly estimated using the algebraic and geometric constraints of the sphere or line images obtained by the central catadioptric camera. The obtained experimental results demonstrate the effectiveness and feasibility of the proposed calibration algorithm.

1 Introduction

Camera calibration forms a potential bridge between the two-dimensional (2D) image and three-dimensional (3D) space, which is widely used in many computer vision tasks, such as 3D reconstruction Jiménez and de Miras (2012), SLAM Durrant-Whyte and Bailey (2006), video surveillance. Generally, this process is based on a pinhole camera model Ying and Zha (2006); Yang et al. (2020); Daucher et al. (1994). However, catadioptric cameras have a wider field of view (FOV) Ying and Hu (2004) than that of traditional pinhole cameras owing to the progress in optics; therefore, camera calibration based on a catadioptric model has received significant research attention.

A catadioptric sensor uses a combination of lenses and mirrors that are carefully arranged together. Choosing the shapes of the mirrors is an important part for catadioptric sensors Baker and Nayar (1999). As noted in Baker and Nayar (1998), it is highly desirable that a catadioptric system have a single viewpoint. The reason a single viewpoint is so desirable is that it permits the generation of geometrically correct perspective images from the images captured by the catadioptric cameras Baker and Nayar (1999). Such systems are extensively used now for robotic perception Tahri and Araújo (2012) and navigation Scaramuzza and Siegwart (2008). Furthermore, the catadioptric systems are classified in two groups, central and non-central, based on the uniqueness of an effective viewpoint; those having a single effective viewpoint are central catadioptric sensors Geyer and Daniilidis (2001). There are four different types of mirrors used in the central catadioptric system including the parabolic, elliptical, hyperbolic, and plane ones. Geyer and Daniilidis (2001) unified these four cases and showed that the imaging process for all central catadioptric systems is isomorphic to the two-step projective mapping based on a unit viewing sphere. Many calibration algorithms are currently used for central catadioptric cameras, which will be introduced later.

1.1 Related Work on Central Catadioptric Camera

Self-calibration Kang (2000); Svoboda and Pajdla (2002). This approach does not require calibration objects, and its constraints are defined by the selected images. Kang (2000) presented a self-calibration algorithm using the corresponding points of multiple images as constraints. He used consistency of pairwise correspondence with the imaging characteristics of the catadioptric camera to seek the calibration parameters together with the essential matrix. However, this methods are sensitive to noise and do not yield accurate matching points.

Point-based calibration Schönbein et al. (2014); Deng et al. (2007); Puig et al. (2011). These methods use calibration patterns containing either three-dimensional (3D) or two-dimensional (2D) points. Deng et al. (2007) proposed a simple algorithm based on a 2D calibration pattern for central catadioptric cameras. In this method, the mirror parameter and FOV of the camera are used to obtain the initial intrinsic parameters, initialize the extrinsic parameters using the relationship between the pinhole and central catadioptric model, and nonlinearly optimize both the intrinsic and extrinsic parameters by minimizing the reprojection errors. Although this calibration algorithm is relatively simple and can use only one or several images containing 2D calibration patterns, it requires accurate initial values, while the mirror parameter and FOV of the camera are unknown in most cases.

Line-based calibration Zhang et al. (2011); Barreto and Araujo (2005); Ying and Hu (2004). In these methods, it is not necessary to know the relative positions of the lines with respect to that of the camera; the latter can be calibrated using only the properties of the line image. Based on the relationship between the concurrent lines, Zhang et al. (2011) proposed a rough-to-fine approach to calibrate central catadioptric cameras, where the intrinsic and mirror parameters are initialized using the line properties and further updated by varying the position of the line image on the metric plane to rectify the conic. All parameters are optimized by minimizing the reprojection errors of the corners. Although this method divides the calibration problem into several more robust solutions, it easily produces cumulative errors. Ying and Hu (2004) nonlinearly estimated the aspect ratio, principal points, and skew factor from the geometric invariants of a metric catadioptric image of lines after initializing the intrinsic parameters. They found that two line images were sufficient to determine the effective focal length and mirror parameter using the intersections of two conics. However, the use of this method to analyze some critical cases, specifically those with high noise levels, can result in a low degree of robustness.

Circle-based calibration Duan et al. (2014a, 2014b). These techniques use only the circle image in a scene without knowing the position of any circle in space. Duan et al. (2014a) demonstrated that the paracatadioptric projection of a circle was a quartic curve. Through application of these constraints, an equation of the circle image can be fitted to derive the focal length of the paracatadioptric camera; however, this method can only be used to calibrate traditional cameras with three degrees of freedom and does not allow for determination of the skew and aspect factors.

Sphere-based calibration Zhao et al. (2018, 2020); Ying and Zha (2008). These methods require only sphere images to perform camera calibration without any metric information. Zhao et al. (2018) proposed a calibration technique for catadioptric cameras using the geometric properties of the sphere and its antipodal images. They found that the vanishing point was orthogonal to the direction of its polar on such images. Moreover, Zhao et al. (2020) found that the sysmetric axis of two antipodal circles is the polar of the infinity point of the support plane with respect to the absolute conic (AC). Nevertheless, those methods were limited to paracatadioptric camera by using the properties of antipodal points Wu et al. (2008). Ying and Zha (2008) introduced the modified image of the absolute conic (MIAC) produced by the double contact with the sphere images on the central catadioptric perspective plane. This was constructed by utilizing the projective geometric properties of the sphere image and their application to calibrate the catadioptric camera.

1.2 Contributions of this Paper

Various calibration algorithms for central catadioptric cameras have been developed; however, the common pole–polar properties of multiple sphere or line images on the central catadioptric perspective plane have not been determined. In this study, we propose a novel linear calibration procedure for central catadioptric cameras based on the geometric and algebraic properties of the sphere or line images. The motivation for this study arose from the following facts background. Spheres and lines are considered important image features and have been studied widely for camera calibration Ying and Zha (2006); Liu et al. (2017). It is well known that, for conventional cameras, the occluding contour of a sphere and the projection center form a right circular cone. We find that for a catadioptric system, the sphere or line image and the virtual optical center form an oblique cone. However, the mirror boundary and projection center form a right circular cone. Previous studies Ying and Zha (2006); Daucher et al. (1994) identified an interesting phenomenon, where some special conic pairs encode an infinity point on the supporting plane. Moreover, we studied the properties of the right circular cone intensively and explored how a pair of right circular cones encapsulates an infinity point Yang et al. (2020). Based on these main principles for a pinhole, we revealed that there also exists an infinity point in the catadioptric system, which corresponds to the generalized eigenvectors of the right circular cone and oblique cone. Furthermore, we demonstrate that the vanishing point and its polar provide a pole–polar relationship with respect to the image of absolute conic (IAC) Wu et al. (2004). Moreover, we explore the algebraic properties of two oblique cones produced by two sphere or line images, which contribute to a new linear method for estimating the MIAC. According to the algebraic relationship between the IAC and MIAC, the shape of the reflective surface can be recovered. Then, the distortion coefficients are determining using rotational symmetry of a projective cone. Therefore, given an image of three or more lines or spheres, it follows that any catadioptric system can be fully calibrated, which involves recovering the intrinsic parameters of the camera, the shape of the reflective mirror, and the distortion parameters.

The main contributions of this work are fourfold:

(1) The sphere can be used as a calibration feature for central catadioptric camera. Although both lines and spheres are mapped into the conic in the catadioptric image, it is more difficult to precisely fit the conic of a line than that of a sphere Ying and Hu (2004). This is mainly because there are only small portions of the conic visible on the image plane. Moreover, a line image can be seen as a special case of a sphere image Ying and Zha (2008). Therefore, a sphere image is preferred considering the catadioptric system. Moreover, we propose a novel method for determining the type of mirror using only the sphere image, which is to the best of our knowledge, the first work to do so.

(2) Some novel geometric and algebraic properties are presented; the generalized eigenvectors of the right circular cone and oblique cone are the pole and polar with respect to the IAC.

(3) A novel approach is the recovery of the distortion parameters without using a chessboard for calibration.

(4) Our method is valid for any central catadioptric system and generalizes the pole–polar relationship for paracatadioptric sensors by considering the degenerate conic dual the circular points (CDCP).

The remainder of this paper is organized as follows. Section 2 briefly outlines the projections of a sphere and a line obtained by a central catadioptric camera and their algebraic properties. In Sect. 3, calibration algorithms based on the common pole–polar characteristics of sphere and line images are described in detail. Section 4 presents the results obtained using the proposed method on simulated and experimental data. Section 5 discusses the results of the study. Finally, Sect. 6 summarizes the conclusions of this study.

2 Preliminaries

In this section, we briefly review the imaging process of central catadioptric cameras and algebraic properties of sphere and line images.

Fig. 1

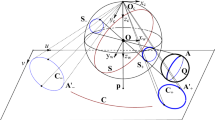
Projections of the sphere and line acquired by catadioptric camera. The green line ${\varvec{L}}$ is projected to a circle on the surface of the sphere. Further, line image ${\hat{{\varvec{C}}}_L}$ is acquired on the central catadioptric image plane through a collineation. Similarly, purple and blue represent the projection process of a sphere and the occluding contour, respectively

2.1 Imaging Process Used in Central Catadioptric Camera

Geyer and Daniilidis (2001), Geyer and Daniilidis (2000) proposed a unifying theory for all central catadioptric systems and demonstrated that the imaging model of central catadioptric camera is isomorphic to the two-step projective mapping based on the unit viewing sphere. Moreover, Barreto (2004) introduced a modified version of the aforementioned projection model, which consists of a three-step process with the non-linearity of the mapping. As shown in Fig. 1, the world coordinate system (WCS) ${\varvec{O}} - {x_w}{y_w}{z_w}$ is set up, where the center ${\varvec{O}}$ of the unit sphere serves as the origin. Let the nonhomogeneous coordinates of a space point ${\varvec{P}}$ be ${\left[ {\begin{array}{*{20}{c}} X&Y&Z \end{array}} \right] ^T}$, so that the projection of ${\varvec{P}}$ on the virtual unit sphere in the WCS is ${{\varvec{P}}_w} = \frac{{\varvec{P}}}{{\left\| {\varvec{P}} \right\| }} = \left[ {\begin{array}{*{20}{c}} {{X_w}}&{{Y_w}}&{{Z_w}} \end{array}} \right] ^T$, where $\left\| {\varvec{P}} \right\| = \sqrt{{X^2} + {Y^2} + {Z^2}}$. The WCS goes $\xi$ units along the ${z_w}$ direction to establish the mirror coordinate system (MCS) ${{\varvec{O}}_c} - {x_m}{y_m}{z_m}$, where ${{\varvec{O}}_c}$ can be considered a virtual optical center; therefore, the point ${{\varvec{P}}_w}$ can be represented by ${\left[ {\begin{array}{*{20}{c}} {{X_w}}&{{Y_w}}&{{Z_w} + \xi } \end{array}} \right] ^T}$ in the MCS. The distance $\xi = \left\| {{\varvec{O}}-{{\varvec{O}}_c}} \right\|$ $(0 \le \xi \le 1)$ between the origins ${\varvec{O}}$ and ${{\varvec{O}}_c}$ can be considered as a parameter characterizing different types of mirrors in the central catadioptric camera Geyer and Daniilidis (2000). Specifically, the mirror is a plane if $\xi = 0$, an ellipsoid or hyperboloid if $1< \xi < 1$, and a paraboloid if $\xi = 1$. Note that when $\xi > 1$, the unified projection model can approximate fisheye projections Ying and Hu (2004).

The second step is non-linear mapping described by a function $\hbar (1)$ from the MCS, where $\hbar (1)$ corresponds to re-projecting the point ${{\varvec{P}}_w}$ into a point $\bar{{\varvec{p}}} = \hbar \left( {{{\varvec{P}}_w}} \right) = {\left[ {\begin{array}{*{20}{c}} {\frac{{{X_w}}}{{{Z_w} + \xi }}}&{\frac{{{Y_w}}}{{{Z_w} + \xi }}}&1 \end{array}} \right] ^T}$ on the plane at infinity ${{\varvec{\pi }} _\infty }$ Barreto (2004). Generally, a camera exhibits radial distortion, which is dominated by the first radial components Andrew (2001). In this study, we only considered a two-degree radial distortion model

$$\begin{aligned} {{\bar{{\varvec{p}}}}_{distorted}} = \left( {1 + {k_1}{r^2} + {k_2}{r^4}} \right) {{\bar{ {\varvec{p}}}}_{undistorted}} \end{aligned}$$

(1)

where ${\bar{{\varvec{p}}}_{distorted}} = {\left[ {\begin{array}{*{20}{c}} {{x_{distorted}}}&{{y_{distorted}}} \end{array}} \right] ^T}$ are the normalized coordinates with distortion, ${\bar{{\varvec{p}}}_{undistorted}} = {\left[ {\begin{array}{*{20}{c}} {{x_{undistorted}}}&{{y_{undistorted}}} \end{array}} \right] ^T}$ are the ideal nonhomogeneous coordinates of $\bar{{\varvec{p}}}$, and ${r^2} = {x_{undistorted}}^2 + {y_{undistorted}}^2$.

Once distortion is applied, the final projection is mapping the point ${\bar{{\varvec{p}}}}_{distorted}$ onto the point $\hat{{\varvec{p}}}$ in the catadioptric image plane ${{\varvec{\pi }} _I}$ after a collineation ${{\varvec{H}}_c}$ by the following equation

$$\begin{aligned} {\lambda _p}\hat{{\varvec{p}}} = {{\varvec{H}}_c}{\left[ {\begin{array}{*{20}{c}} {{x_{distorted}}}&{{y_{distorted}}}&1 \end{array}} \right] ^T} \end{aligned}$$

(2)

where

$$\begin{aligned} {{{\varvec{H}}_c}\mathrm{{ = }}{{\varvec{K}}_c}{{\varvec{R}}_c}{{\varvec{M}}_c}} \end{aligned}$$

(3)

and ${\lambda _p}$ is a nonzero scale factor. The projection transformation ${{\varvec{H}}_c}$ depends on the calibration matrix ${{\varvec{K}}_c} = \left[ {\begin{array}{*{20}{c}} {{f_x}}&{}0&{}{{u_0}}\\ 0&{}{{f_y}}&{}{{v_0}}\\ 0&{}0&{}1 \end{array}} \right]$ of the virtual camera, the mirror parameters ${{\varvec{M}}_c} = \left[ {\begin{array}{*{20}{c}} {\eta - \xi }&{}0&{}0\\ 0&{}{\xi - \eta }&{}0\\ 0&{}0&{}1 \end{array}} \right]$ (the values for $(\xi ,\eta )$ are detailed in Barreto (2004)), and the rotation matrix ${{\varvec{R}}_c}$ between the camera and the mirror.

Definition 1

Ying and Zha (2008) For the central catadioptric system, let ${\varvec{\omega }} = {{\varvec{H}}_c}^{ - T}{{\varvec{H}}_c}^{ - 1}$ represent the IAC; in this case, $\tilde{\varvec{\omega }} = {{\varvec{H}}_c}^{ - T}\left[ {\begin{array}{*{20}{c}} {\mathrm{{1}} - {\xi ^2}}&{}\mathrm{{0}}&{}\mathrm{{0}}\\ \mathrm{{0}}&{}{\mathrm{{1}} - {\xi ^2}}&{}\mathrm{{0}}\\ \mathrm{{0}}&{}\mathrm{{0}}&{}1 \end{array}} \right] {{\varvec{H}}_c}^{ - 1} = {\tilde{{\varvec{H}}}_c}^{ - T}{\tilde{{\varvec{H}}}_c}^{\mathrm{{ - 1}}}$ corresponds to the MIAC.

Definition 2

Andrew (2001) A line $\bar{\varvec{\mu }} = \bar{{\varvec{C}}}\bar{{\varvec{v}}}$ is defined by a point $\bar{{\varvec{v}}}$ and conic $\bar{{\varvec{C}}}$. The point $\bar{{\varvec{v}}}$ is dubbed the pole of $\bar{\varvec{\mu }}$ with respect to $\bar{{\varvec{C}}}$, and the line $\bar{\varvec{\mu }}$ is the polar of $\bar{{\varvec{v}}}$ with respect to $\bar{{\varvec{C}}}$.

Definition 3

Andrew (2001) If a point $\bar{{\varvec{v}}}$ and line $\bar{\varvec{\mu }}$ satisfy both the pole–polar relationship with respect to ${\bar{{\varvec{C}}}_m}$ and $\bar{{\varvec{C}}}$, then $\bar{{\varvec{v}}}$ and $\bar{\varvec{\mu }}$ are the common poles and polar of ${\bar{{\varvec{C}}}_m}$ and $\bar{{\varvec{C}}}$, respectively.

Definition 4

Andrew (2001) A plane normal direction ${\varvec{D}}$ and the intersection line ${\bar{\varvec{\mu }}}$ of the plane with ${{\varvec{\pi }} _\infty }$ are in pole–polar relation with respect to the absolute conic ${\bar{\varvec{\Omega }} _\infty }$.

2.2 Catadioptric Projection of Sphere and Line Images

Using the central catadioptric projection model described in the previous section, a space sphere ${\varvec{S}}$ is first projected onto a small circle ${{\varvec{C}}_S}$ on the unit viewing sphere (see Fig. 1). Let the unit vector normal to the support plane ${{\varvec{\pi }} _S}$, containing circle ${\varvec{C}}_S$, be ${\varvec{N}}\mathrm{{ = }}{\left[ {\begin{array}{*{20}{c}} {{n_{{} x}}}&{{n_{{} y}}}&{{n_{{} z}}} \end{array}} \right] ^T}$ and the distance from the center ${\varvec{O}}$ of the unit sphere to the plane ${{\varvec{\pi }} _S}$ be ${d_0}$. Therefore, a central cone ${{\varvec{Q}}_S}$ is formed by the virtual optical center ${{\varvec{O}}_c}$ and circle ${{\varvec{C}}_S}$ in the MCS Ying and Zha (2008). Then the cone ${{\varvec{Q}}_S}$ maps onto the conic curve ${\bar{{\varvec{C}}}_S}$ in the plane ${{\varvec{\pi }} _\infty }$. For completeness, Table 1 lists the Euclidean parameters of the conic ${\bar{{\varvec{C}}}_S}$.

Similarly, a space line ${\varvec{L}}$ is projected onto a large circle ${\varvec{C}}_L$ on the surface of the unit sphere (see Fig. 1). Since the support plane ${{\varvec{\pi }} _L}$ passes through the unit sphere center ${\varvec{O}}$, the distance from the unit sphere center ${\varvec{O}}$ to plane ${{\varvec{\pi }} _L}$ is equal to zero (${d_0} = 0$). Hence, a unified imaging process exists for both the space line and space sphere. By assuming ${d_0} = 0$, the projection ${\bar{{\varvec{C}}_L}}$ of the line on the ${{\varvec{\pi }} _\infty }$ can be determined Barreto (2004).

$$\begin{aligned} {\bar{{\varvec{C}}}_S}= & {} \left[ {\begin{array}{*{20}{c}} {({\xi ^2} - 1){n_x}^2 + {{({d_0} - \xi {n_z})}^2}}&{}{({\xi ^2} - 1){n_x}{n_y}}&{}{(\xi {d_0} - {n_z}){n_x}}\\ {({\xi ^2} - 1){n_x}{n_y}}&{}{({\xi ^2} - 1){n_y}^2 + {{({d_0} - \xi {n_z})}^2}}&{}{(\xi {d_0} - {n_z}){n_y}}\\ {(\xi {d_0} - {n_z}){n_x}}&{}{(\xi {d_0} - {n_z}){n_y}}&{}{({d_0}^2 - {n_z}^2)} \end{array}} \right] \end{aligned}$$

(4)

$$\begin{aligned} {\bar{{\varvec{C}}}_L}= & {} \left[ {\begin{array}{*{20}{c}} {\left( {{\xi ^2} - 1} \right) {n_x}^2 + {\xi ^2}{n_z}^2}&{}{({\xi ^2} - 1){n_x}{n_y}}&{}{ - {n_x}{n_z}}\\ {({\xi ^2} - 1){n_x}{n_y}}&{}{({\xi ^2} - 1){n_y}^2 + {\xi ^2}{n_z}^2}&{}{ - {n_y}{n_z}}\\ { - {n_x}{n_z}}&{}{ - {n_y}{n_z}}&{}{ - {n_z}^2} \end{array}} \right] \end{aligned}$$

(5)

Table 1 Center, principal axes, major and minor axes of the sphere image

Notice that the projective rays, joining ${{\varvec{O}}_c}$ to the points in the mirror contour circle ${{\varvec{C}}_m}$ on the plane ${{\varvec{\pi }} _m}$ form a right circular cone ${{\varvec{Q}}_m}$ that cone projects into the conic ${\bar{{\varvec{C}}}_m}$ on the ${{\varvec{\pi }} _\infty }$, i.e., assuming ${d_0} = 0$, ${n_x} = 0$, ${n_y} = 0$, and ${n_z} = \xi$

$$\begin{aligned} {{\bar{{\varvec{C}}}_m} = \left[ {\begin{array}{*{20}{c}} 1&{}0&{}0\\ 0&{}1&{}0\\ 0&{}0&{}{ - {{{1 \big / \xi }}^2}} \end{array}} \right] } \end{aligned}$$

(6)

According to Fig. 1 , the points ${\hat{{\varvec{p}}}}$ in the central catadioptric image plane ${{\varvec{\pi }} _I}$ are linearly related to the point $\bar{{\varvec{p}}}$ through a collineation ${\varvec{H}}_c$. Hence, from Eq. (2), the sphere image equation ${\hat{{\varvec{C}}}_S}$ on the ${{\varvec{\pi }} _I}$ is derived as

$$\begin{aligned} {{\lambda _S}{\hat{{\varvec{C}}}_S} = {{\varvec{H}}_c}^{ - T}{\bar{{\varvec{C}}}_S}{{\varvec{H}}_c}^{ - 1}} \end{aligned}$$

(7)

where ${\lambda _S}$ is a nonzero scale factor. Similarly, the projection ${\hat{{\varvec{C}}}_L}$ of line ${\varvec{L}}$ on the ${{\varvec{\pi }} _I}$ can be determined using the relationship

$$\begin{aligned} {{\lambda _L}{\hat{{\varvec{C}}}_L} = {{\varvec{H}}_c}^{ - T}{\bar{{\varvec{C}}}_L}{{\varvec{H}}_c}^{ - 1}} \end{aligned}$$

(8)

By combining Eqs. (7) and (8), we prove that the line image ${\hat{{\varvec{C}}}_L}$ is a special form of the sphere image ${\hat{{\varvec{C}}}_S}$. To describe ${\hat{{\varvec{C}}}_S}$ and ${\hat{{\varvec{C}}}_L}$ conveniently, parameter $\hat{{\varvec{C}}}$ is used to express both of these images in a unified form. Similarly, $\bar{{\varvec{C}}}$ denotes conics ${\bar{{\varvec{C}}}_S}$ and ${\bar{{\varvec{C}}}_L}$, and ${\bar{{\varvec{C}}}_m}$ represents the mirror boundary.

3 Calibration

In this section, we discuss the algebraic relationship between a sphere or line image and the IAC and propose a calibration procedure for central catadioptric cameras based on these constraints. Moreover, the CDCP is used in the case of the paraboloid mirror. Here, it is assumed that the mirror parameter remains constant, and that its value can be obtained from the relationship between IAC and MIAC.

3.1 Orthogonal Constraints Related to the IAC and MIAC

Proposition 1

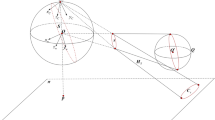
As shown in Fig. 2, considering the conics ${\bar{{\textbf {C}}}_m}$ and $\bar{{\textbf {C}}}$, their common poles $\bar{{\textbf {v}}}$ and polar $\bar{\varvec{\mu }}$ can be determined by the generalized eigenvalue decomposition of the conic pair $\left( {{{\bar{{\textbf {C}}}}_m},{{\bar{{\textbf {C}}}}}} \right)$.

Proof

For a common pole and polar of ${\bar{{\varvec{C}}}_m}$ and $\bar{{\varvec{C}}}$, according to the Definition 3, the following relationship must be satisfied

$$\begin{aligned} {\left\{ \begin{array}{l} \bar{\varvec{\mu }} = \bar{{\varvec{C}}}\bar{{\varvec{v}}}\\ \bar{\varvec{\mu }} = \lambda {{\bar{{\varvec{C}}}}_m}\bar{{\varvec{v}}} \end{array} \right. } \end{aligned}$$

(9)

where $\lambda$ is a nonzero scale factor. Subtracting the equations in Eq. (9), we obtain

$$\begin{aligned} {\left( {\lambda {\varvec{I}} - {{\bar{{\varvec{C}}}}^{ - 1}}{{\bar{{\varvec{C}}}}_m}} \right) \bar{{\varvec{v}}} = {{\textbf {0}}_{3 \times \mathrm{{1}}}}} \end{aligned}$$

(10)

Algebraically, Eq. (10) suggests that the points $\bar{{\varvec{v}}}$ correspond to the generalized eigenvector of $\left( {{{\bar{{\varvec{C}}}}_m},\bar{{\varvec{C}}}} \right)$. Given a common pole ${\bar{{\varvec{v}}}_1}$ of ${\bar{{\varvec{C}}}_m}$ and $\bar{{\varvec{C}}}$, according to the polarity principle Andrew (2001), the polar ${\bar{\varvec{\mu }} _1}$ corresponding to ${\bar{{\varvec{v}}}_1}$ passes through the two other common poles ${\bar{{\varvec{v}}}_2}$ and ${\bar{{\varvec{v}}}_3}$. Hence,

$$\begin{aligned} {{\lambda _ \mu }{\bar{\varvec{\mu }} _1}\mathrm{{ = }}{\bar{{\varvec{v}}}_\mathrm{{2}}} \times {\bar{{\varvec{v}}}_\mathrm{{3}}}} \end{aligned}$$

(11)

where ${\lambda _\mu }$ is a nonzero scale factor and $\times$ denotes the cross product operation. $\square$

Fig. 2

Common poles ${\bar{{\varvec{v}}}_k}\left( {k = 1,2,3} \right)$ of ${\bar{{\varvec{C}}}_m}$ and $\bar{{\varvec{C}}}$ on the plane ${{\varvec{\pi }} _\infty }$ determined by the generalized eigenvalue decomposition, where ${\bar{{\varvec{v}}}_1}$ is an infinity point on the intersection line ${\varvec{D}}$ of planes ${\pi _m}$ and ${\pi _S}$, and the two other points ${\bar{{\varvec{v}}}_2}$ and ${\bar{{\varvec{v}}}_3}$ are on the major axis ${\bar{\varvec{\mu }}}={\bar{\varvec{\mu }} _1}$. This property holds in the central catadioptric image plane $\pi$ after transformation ${{\varvec{H}}_c}$

Proposition 2

In Fig. 2, given a distinct pair of non-degenerate conics $\left( {{\hat{{\textbf {C}}}_m},\hat{{\textbf {C}}}} \right)$, a vanishing point ${\hat{{\textbf {v}}}_1}$ and line ${\hat{\varvec{\mu }} _1}$ exist, which correspond to the generalized eigenvectors of $\left( {{\hat{{\textbf {C}}}_m},\hat{{\textbf {C}}}} \right)$, and also exhibit a pole–polar relationship with respect to the IAC.

The proof of Proposition 2 is given in Appendix 1.

Proposition 3

For the central catadioptric system, a sphere or line image ${\hat{{\textbf {C}}}}$ can be algebraically represented by the MIAC.

Proof

By simplifying Eqs. (7) and (8) using the procedure described in Ying and Zha (2008), we obtain

$$\begin{aligned} {{\lambda _w}{\hat{{\varvec{C}}}} = \tilde{\varvec{\omega }} - {\hat{{\varvec{u}}}}{\hat{{\varvec{u}}}^T}} \end{aligned}$$

(12)

where ${\lambda _w}$ is a nonzero scale factor, and ${\hat{{\varvec{u}}}} = \frac{{\sqrt{1 - {\xi ^2}} }}{{{d_0} - \xi {m_z}}}{{\varvec{H}}_c}^{ - T}\left[ {\begin{array}{*{20}{c}} {\sqrt{1 - {\xi ^2}} {m_x}}\\ {\sqrt{1 - {\xi ^2}} {m_y}}\\ {{{ - \left( {\xi {d_0} - {m_z}} \right) } \big / {\sqrt{1 - {\xi ^2}} }}} \end{array}} \right]$. $\square$

Based on the principle of duality of projective geometry Semple (1952), the following corollary can be formulated

Corollary 1

In dual space, the dual ${\hat{{\textbf {C}}}^ * }$ of a sphere image satisfies the following condition

$$\begin{aligned} {{\lambda _w}^ * {\hat{{\textbf {C}}}}^ * = {\tilde{\varvec{\omega }} ^ * } - {\hat{{\textbf {u}}}}^ * {\hat{{\textbf {u}}}}^*}^T \end{aligned}$$

(13)

where ${\lambda _w}^ *$ is a nonzero scale factor, ${\tilde{\varvec{\omega }} ^ * } = {{\textbf {H}}_c}\left[ {\begin{array}{*{20}{c}} 1&{}0&{}0\\ 0&{}1&{}0\\ 0&{}0&{}{1 - {\xi ^2}} \end{array}} \right] {{\textbf {H}}_c}^T$ is the dual of the modified image of the absolute conic, called DMIAC, and ${\hat{{\textbf {u}}}^ * } = \frac{1}{{\sqrt{\left( {1 - {d_0}^2} \right) } }}{{\textbf {H}}_c}\left[ {\begin{array}{*{20}{c}} {{m_x}}\\ {{m_y}}\\ {\xi {d_0} - {m_z}} \end{array}} \right]$.

The corollary is valid; hence, its proof is omitted.

Proposition 4

Assuming that two $3 \times 3$ symmetric nonsingular matrices ${\hat{{\textbf {C}}}_1}$ and ${\hat{{\textbf {C}}}_2}$ represent two sphere or line images for the central catadioptric system, the eigenvectors of the matrix ${\hat{{\textbf {C}}}_2}{\hat{{\textbf {C}}}_1}^*$ can determine the line ${\hat{{\textbf {l}}}^ * }$ and point ${\hat{{\textbf {x}}}^ * }$, which also have pole–polar relationships with respect to the MIAC.

Proof

According to Corollary 1, for the two sphere (line) images ${\hat{{\varvec{C}}}_1}$ and ${\hat{{\varvec{C}}}_2}$ obtained by the central catadioptric cameras in the dual space, the following equations hold true

$$\begin{aligned} {\left\{ \begin{array}{l} {\lambda _{w1}}^ * {\hat{{\varvec{C}}}_1}^ * = {{\tilde{\varvec{\omega }} }^ * } - {\hat{{\varvec{u}}}_1}^ * {\hat{{\varvec{u}}}}{{_1^ *} ^T}\\ {\lambda _{w2}}^ * {\hat{{\varvec{C}}}_2}^ * = {{\tilde{\varvec{\omega }} }^ * } - {\hat{{\varvec{u}}}_2}^ * {\hat{{\varvec{u}}}}{{_2^ * }^T} \end{array} \right. } \end{aligned}$$

(14)

A line ${\hat{{\varvec{l}}}^ * } = {\hat{{\varvec{u}}}}_1^ * \times {\hat{{\varvec{u}}}}_2^ *$ is defined that connects the two points ${\varvec{u}}_1^ *$, ${\varvec{u}}_2^ *$. Then, the matrix ${\hat{{\varvec{C}}}_2}{\hat{{\varvec{C}}}_1}^ *$ can provide both line ${\hat{{\varvec{l}}}^*}$ and point ${\hat{{\varvec{x}}}^*}$, which are the pole and polar for $\tilde{\varvec{\omega }}$, respectively. Note that the rigorous proofs can refer to pinhole cameras Zhang et al. (2007). $\square$

3.2 Algebraic Constraints Between Sphere or Line Images and the CDCP

Generally, a paracatadioptric camera combines a parabolic mirror with an orthographic camera. In this case, the mirror parameter $\xi$ is unitary. Moreover, under the parabolic system, the optical axis of the camera must be aligned with the symmetry axis of the mirror ${{\varvec{R}}_c}\mathrm{{ = }}{\varvec{I}}$ Barreto (2004). Here, we are considering the sensor as a global device. This is particularly important for calibration, because it shows that ${f_x},{f_y}$ and $\eta$ cannot be computed independently Barreto (2004). Then, the transformation ${\varvec{H}}_c$ is rewritten as ${{\varvec{H}}_c}\mathrm{{ = }}{{\varvec{K}}_c}$. In a parabolic projection, a line or sphere is mapped to an arc of a circle, and such a projection is called a line or sphere image, respectively. In the canonical plane, the two special points (the circular points) on the infinity line play a crucial role and assume the forms ${\bar{{\varvec{I}}}_\infty } = {\left[ {\begin{array}{*{20}{c}} 1&i&0 \end{array}} \right] ^T}$ and ${\bar{{\varvec{J}}}_\infty } = {\left[ {\begin{array}{*{20}{c}} 1&{ - i}&0 \end{array}} \right] ^T}$, where ${i^2} = - 1$. In the Euclidean coordinate system, the conic $\bar{{\varvec{C}}}_\infty ^*$ is a degenerate (rank 2) line conic, called the CDCP which consists of two circular points. It is given in matrix form as

$$\begin{aligned} {\bar{{\varvec{C}}}_\infty ^* = {\bar{{\varvec{I}}}_\infty }{\bar{{\varvec{J}}}_\infty }^T + {\bar{{\varvec{J}}}_\infty }{\bar{{\varvec{I}}}_\infty }^T} \end{aligned}$$

(15)

For circles, $\bar{{\varvec{C}}}_\infty ^*$ is fixed under scale, translation and rotation transformation Andrew (2001).

Proposition 5

In paracatadioptric systems, three line or sphere images provide sufficient constraints to compute the image $\hat{{\textbf {C}}}_\infty ^*$ of the CDCP.

The proof of Proposition 5 is given in Appendix 1.

3.3 Calibration with Pole and Polar Constraints

If point ${\hat{{\varvec{v}}}_1}$ and line ${\hat{\varvec{\mu }} _1}$ are the pole and polar with respect to a conic ${\varvec{\omega }}$, respectively, the following relationship holds true

$$\begin{aligned} {{\lambda _l}{\hat{\varvec{\mu }} _1} = {\varvec{\omega }} {}{\hat{{\varvec{v}}} _1}} \end{aligned}$$

(16)

where ${\lambda _l}$ is a nonzero scale factor. This constraint can provide two independent conditions for the elements of ${\varvec{\omega }}$; hence, the complete calibration of the central catadioptric cameras would require a minimum number of three sphere or line images.

Proposition 6

once conic ${\hat{{\textbf {C}}}_\infty }^*$ has been identified on the paracatadioptric image plane, the intrinsic parameters of the camera can be determined.

Proof

Under the point transformation ${\hat{{\varvec{p}}}} = {{\varvec{H}}_c}\bar{{\varvec{p}}}$, where ${{\varvec{H}}_c}\mathrm{{ = }}{{\varvec{K}}_c}$ is the world-to-image homography, $\bar{{\varvec{C}}}_\infty ^*$ transforms to $\hat{{\varvec{C}}}_\infty ^* = {{\varvec{H}}_c}\bar{{\varvec{C}}}_\infty ^*{{\varvec{H}}_c}^T$. Further, ${\hat{{\varvec{C}}}_\infty }^*$ identified in an image plane using singular-value decomposition (SVD) can be written as

$$\begin{aligned} {\hat{{\varvec{C}}}_\infty ^* = {\varvec{U}}\left[ {\begin{array}{*{20}{c}} 1&{}0&{}0\\ 0&{}1&{}0\\ 0&{}0&{}0 \end{array}} \right] {{\varvec{U}}^T}} \end{aligned}$$

(17)

The homography is ${{\varvec{H}}_c} = {{\varvec{K}}_c}={\varvec{U}}$ up to a scale and tranlation transformation Andrew (2001). $\square$

Proposition 7

Once IAC and MIAC have been identified on the projective plane, the mirror parameter $\xi$ of the camera can be determined.

Proof

The IAC is by definition a virtual conic ${\varvec{\omega }}= {{\varvec{H}}_c}^{ - T}{{\varvec{H}}_c}^{ - 1}$.The transformation ${\varvec{H}}_c$ can be computed from the Cholesky decomposition of ${\varvec{\omega }}$. Moreover, $\xi$ is provided by $\tilde{\varvec{\omega }}$ on the basis of obtaining ${\varvec{H}}_c$. $\square$

3.4 Estimation of Distortion Coefficients

As is the case for most central catadioptric calibration methods Ying and Zha (2006); Zhang et al. (2007), it is difficult to provide a solution for the distortion coefficients compared with the calibration chessboard Andrew (2001), since the correspondence between the apparent contour point and its projection is undetermined. Here, we provide a means to solve lens distortion. Given the (distorted) points ${\hat{{\varvec{p}}}_n}\left( {n = 1,2 \cdots } \right)$ sampled from the mirror boundary and the projection (principal point) $\hat{{\varvec{O}}}$ of the equator center, the (distorted) directions of lines ${{\varvec{l}}_{pn}} = {{\varvec{H}}_c}^{ - 1}{\hat{{\varvec{p}}}_n}$ and ${{\varvec{l}}_o} = {{\varvec{H}}_\mathrm{{c}}}^{ - 1}\hat{{\varvec{O}}}$ can be obtained through back projection using the calibration results Andrew (2001), as shown in Fig. 3. From Eq. (1), the ideal (undistorted) directions of lines ${{\varvec{l}}_{pn}}^\prime$ and ${{\varvec{l}}_o}^\prime$ satisfy the following

$$\begin{aligned} {\left\{ \begin{array}{l} \left( {1 + {k_1}{r^2} + {k_2}{r^4}} \right) {{\varvec{l}}_{pn}}^\prime = {{\varvec{l}}_{pn}}\\ \left( {1 + {k_1}{r^2} + {k_2}{r^4}} \right) {{\varvec{l}}_o}^\prime = {{\varvec{l}}_o} \end{array} \right. } \end{aligned}$$

(18)

Moreover, the angle ${\vartheta _{no}}^\prime$ between ${{\varvec{l}}_{pn}}^\prime$ and ${{\varvec{l}}_o}^\prime$ is derived as

$$\begin{aligned} {{\vartheta _{no}}^\prime = \arccos \left( {\frac{{ {{{\varvec{l}}_{pn}}^\prime \cdot {{\varvec{l}}_o}^\prime } }}{{\left\| {{{\varvec{l}}_{pn}}^\prime } \right\| \cdot \left\| {{{\varvec{l}}_o}^\prime } \right\| }}} \right) } \end{aligned}$$

(19)

where $\cdot$ denotes the dot product and $\left\| \cdot \right\|$ denotes the two-norm. Further, ${{\varvec{l}}_{pn}}^\prime$ and ${{\varvec{l}}_o}^\prime$ indicate the generator lines and the revolution axis of the right circular cone ${ {\varvec{Q}}_m}$, respectively. From the properties of the right circular cone, ${\vartheta _{no}}^\prime \left( {n = 1,2 \cdots } \right)$ are all equal. Hence, the radial parameters ${k_1}$ and ${k_2}$ can be estimated by minimizing the following functional

$$\begin{aligned} { \mathop {\arg \min }\limits _{{k_1},{k_2}} \sum \limits _{n = 1}^N {{{\left\| {{\vartheta _{n + 1o}}^\prime - {\vartheta _{no}}^\prime } \right\| }^2}} } \end{aligned}$$

(20)

The final results can be obtained using the Levenberg–Marquardt algorithm Mei and Rives (2007) with the initial values ${k_1} = 0$ and ${k_2} = 0$.

Fig. 3

Properties of the right circular cone: the angles ${\vartheta _{no}}^\prime$ between the generator lines ${{\varvec{l}}_{pn}}^\prime$ and the revolution axis ${{{\varvec{l}}_o}^\prime }$ of the right circular cone ${ {\varvec{Q}}_m}$ are equal to each other

3.5 Calibration Algorithm

Based on the established relationships, the calibration algorithm comprises the following steps (see Alg. 1). Note that CDCP is a degenerate conic and IAC is a nondegenerate conic. Hence, IAC and CDCP can be distinguished by their eigenvalues Andrew (2001).

4 Experimental

To confirm the validity of the proposed calibration algorithm, a series of simulations and real experiments were performed. Additionally, the effectiveness of the calibration algorithm was validated by using the sphere images (referred to as CPS) and the line images (referred to as CPL). Our code and datasets are available at http://github.com/yflwxc/Camera-Calibration.

4.1 Simulations

In this section, the correctness of the derived expressions in the previous section was verified by using synthetic data. The operating device for this experiment was a notebook computer, the model of which was Lenovo Legion Y7000 2020 and the processor was i5-10200H. The running platform for the experiment was Matlab R2016b. This section assumes that initial calibration matrix of the simulation camera is ${\varvec{K}}_c = \left[ {\begin{array}{*{20}{c}} {800}&{}0&{}{320}\\ 0&{}{850}&{}{240}\\ 0&{}0&{}1 \end{array}} \right]$, and the mirror parameter is $\xi =0.8$. According to the analysis presented in Sect. 3, the method proposed in this work requires at least three sphere or line images to complete the calibration. Therefore, multiple images were generated to calibrate the central catadioptric cameras by randomly changing extrinsic parameters, one of which is shown in Fig. 4. For better visualization, we normalized the image data here. In the case of different noise levels $\sigma$, mirror parameters $\xi$, and numbers of images N, multiple calibration images were obtained to evaluate the performance of our algorithm. For the evaluation metrics of the algorithm, here is mainly based on the difference between the ground truth (GT) and the estimate (EST), including: the focal length errors $E_f$, the principal point errors $E_{uv0}$, the mirror parameter errors $E_{\xi }$, and the total errors $E_{total}$, which are defined as follows. Note that the intrinsic parameters range from 0 to 1000, and the mirror parameter $0 \le \xi \le 1$. Hence, they are weighted to the same magnitude.

$$\begin{aligned} {E_f}= & {} {\left\| {{f_{xGT}} - {f_{xEST}}} \right\| _2} + {\left\| {{f_{yGT}} - {f_{yEST}}} \right\| _2} \end{aligned}$$

(21)

$$\begin{aligned} {E_{uv0}}= & {} {\left\| {u_{0GT}} - {u_{0EST}} \right\| _2}+{\left\| {v_{0GT}} - {v_{0EST}} \right\| _2} \end{aligned}$$

(22)

$$\begin{aligned} {E_\xi }= & {} 1000\times {\left\| {{\xi _{GT}} - {\xi _{EST}}} \right\| _2} \end{aligned}$$

(23)

$$\begin{aligned} {E_{total} }= & {} { {E_f}+ {E_{uv0}} + {E_\xi }} \end{aligned}$$

(24)

Fig. 4

a Sphere and b line images generated by the simulated camera

As in the calibration of conventional cameras, the redundancy and accuracy of calibration data is a key factor for attenuating the effect of calibration data noise into the calibration precision. Therefore, we firstly test the performance with respect to the number of images. We vary the number of images from 3 to 21 and each images are added with Gaussian noise with zero mean and standard deviation 0.2 pixels. For each number of images, we performed 20 independent trials and then analyzed the mean errors and standard deviations of the recovered parameters. The calibration results are shown in Fig. 5. We find that the relative errors and standard deviations both decrease with the increase in the number of images. In particular, when the number of images is greater than 6, all errors are less than 2 pixels and standard deviations keep at a low level stably. The main reason is that an increase in the number of images will reduce the singularity of the proposed algorithm. The results in Fig. 5 have verified the effectiveness of the proposed calibration algorithm.

Fig. 5

Sensitivities of the proposed algorithm with different number of images N. The mean errors of f, uv0 and $\xi$ are plotted in panels (a)–(c), respectively. The size of the shadow indicates the standard deviation

Table 2 Different parameters and calibration errors for the proposed algorithm

For analyzing the influence of different noise levels on the algorithms, each points on the conic were corrupted with zero-mean Gaussian noise with different variance $\sigma$ varying from 0 to 1. For each level $\sigma$, we performed 20 independent trials by using the proposed algorithm and their errors are computed over each run. And the results were shown in Fig. 6. As can be seen from Fig. 5, high noise will make the calibration result inaccurate. However, compared with CPL, CPS obtained smaller errors under at the same noise level. This is expected because the accuracy of the obtained calibration results highly depends on the accuracy of the extracted conics. The main reason for above these results is that the more contour points (see Fig. 4) improves the performance of the conic fitting. This observation is similar to the results stated in Ying and Hu (2004).

Fig. 6

Sensitivities of the proposed algorithm with different noise levels $\sigma$. The mean errors of f, uv0 and $\xi$ are plotted in panels (a)–(c), respectively

In order to test the influence of mirror parameter change on calibration results, the mirror parameter of each image was changed to generate Sets 1–4, whose the parameters were shown in Table 2. For each set of images, 20 independent experiments were performed to analyze the errors of the estimated parameters. The experimental results were shown in Table 2. Table 2 indicates that our methods are better for calibrating hyperbolic or elliptical sensors, e.g. a smaller mirror parameter is used. The main reason for this is that we compute the pole and polar of CDCP, which is a degenerate conic.

4.2 Experimental Results with Real Data

For further performance evaluation of the proposed calibration method, we performed several experiments under different scenes:

(1) For paracatadioptric cameras: For further performance evaluation of the proposed calibration method, the public real image sets were used, which were taken by an uncalibrated paracatadioptric camera with an FOV of 180$^\circ$ Barreto and Araujo (2005), as shown in Fig. 7a. In addition, we compare CPL with the method proposed by Barreto and Araujo (2005) (denoted as CL). Generally, it is difficult to fit the line image in catadioptric systems Ying and Zha (2008). Hence, a conic fitting algorithm Barreto and Araújo (2006) was used to solve this problem. We used line images to calibrate the camera by CPL and CL. Moreover, Fig. 7b showed four pairs of pole and polar obtained from CPL. The calibration results were listed in Table 3. Table 3 showed that the calibration results for CPL were close to those for CL, and the difference of each parameter is within 2.95 pixels.

Fig. 7

Experimental images. a Several lines were taken using a paracatadioptric camera. b Four pairs of pole and polar

Table 3 The distortion and intrinsic parameters (unit: pixel) obtained from paracatadioptric images of line

(2) For hypercatadioptric cameras: The central catadioptric camera used here had a hyperbolic mirror with FOV of 217.2$^\circ$, which is designed by the Center for Machine Perception, Czech Technical University. And the camera model is Nikon D560 with an image resolution of 3898$\times$3661 pixels. Three yellow balls with a diameter of 40 mm were placed on the ruler (Note that the ruler’s boundary is marked for better extraction of lines). Here, in order to prove that the proposed algorithm is more universal, three relative positions of the ball image were considered, e.g. intersection, separation and tangent (see Fig. 8a–c). They correspond to fairly common situation in real world scenarios. A projection equation was obtained for each sphere and line image using the least square method Fitzgibbon et al. (1999). In this case, we compare CPS and CPL with the method of Ying and Zha (2008) using these images. Moreover, we mixed the sphere and line images (two spheres and a line) to evaluate the performance of this algorithm. The state-of-the-arts using the chessboard described by Puig et al. (2011); Mei and Rives (2007) and Scaramuzza et al. (2007) were used because they are highly accurate and robust. In the experiment, the chessboard had 7$\times$5 feature points, in which the horizontal or vertical spacing between two adjacent feature points was 20 mm and the target accuracy was 0.1 mm (see Fig. 8d).

As discussed in the previous section, since the correspondence between the apparent contour point and its projection is undetermined, the proposed method only provided the initial linear solution. Hence, in the experiment, we considered two stages of the calibration process: initial linear solution, the nonlinear refinement. For this comparison, the accuracy of the calibration results obtained in this study was verified by analyzing the root mean square (RMS) of the reprojection errors. Note taht, since the 3D information of the sphere and line is unknown, we computed the reprojection errors by using chessboard pattern for CPS, CPL and Ying and Zha (2008). The results are summarized in Table 4. Table 4 shows that CPS compared favorably with CPL. This is mainly because the sphere image is a closed conic, and a more accurate conic fitting can be achieved. Hence, this is understandable that mixed images provides good results comparing with CPL. Comparing the results of the CPS with the ones obtained using Ying and Zha (2008), one can see that the reprojection error of Ying and Zha (2008) is at least 2.14 times higher. This confirms that the proposed method obtains more accurate initial linear solution. Furthermore, Puig et al. (2011); Mei and Rives (2007) and Scaramuzza et al. (2007) refined the calibration parameters by using the checkerboard calibration pattern, which performed better than the proposed method. However, our methods were close to those methods, and the difference of reprojection error is within 7.45 pixels.

Fig. 8

Experimental images were taken using a hypercatadioptric camera. a Intersection, b separation, c tangent of ball images and d the chessboards

Table 4 The RMS of re-projection errors of initial parameter estimation and optimization for hypercatadioptric camera (unit: pixel)

Table 5 Recovering angles between pairs of parallel lines (unit: degree)

3) Image rectification: To further evaluate the accuracy of our method, we rectified the catadioptric image of Fig. 8a–c into a perspective image (see Fig. 9) as the calibration results are known Barreto and Araujo (2005) (the results of CPS are used). Moreover, we reconstructed several typical lines (see Fig. 9) and measured the angles between them. The results were shown in Table 5. As shown in Table 5, the mean and std of angle error was 1.47$^\circ$ and 1.60$^\circ$, respectively. It can be seen that the proposed calibration method is effective in a certain error range.

Fig. 9

The parallel lines (cyan) were determined after rectification and the angles were computed a for line images b–d for sphere images

5 Discussion

The paper presented a novel calibration algorithm for central catadioptric camera. We chose to consider the sphere under a catadioptric system since there was complete data for the sphere image for comparison with the line image. We discovered some novel geometric and algebraic properties. The algebraic relationship between the sphere or line images and the mirror is established: the common pole and polar with respect to the sphere or line images and the mirror are also the pole and polar with respect to the IAC. Furthermore, the common pole and polar of the sphere or line images can be determined from the eigenvectors of the corresponding matrix pairs. Because sphere or line images can only provide two new linear constraints for the IAC, at least three of these images are required to recover it. Similarly, the MIAC can be determined from the projective invariant properties of sphere or line image. For paracatadioptric sensors, the technique is still valid using the CDCP. These properties can be considered as extensions from the convention camera to the central catadioptric camera. However, proving the feasibility of these extensions is not trivial; it requires rigorous proofs rather than intuitive guesswork. Finally, the mirror parameter may be obtained from the algebraic relation between IAC and MIAC. In general, cameras exhibit significant lens distortion. Accordingly, we explored a method of determining the distortion parameters based on the properties of the right circular cone. However, it is not an estimate of the closed-form solution.

Moreover, the calibration process fails at certain critical conditions. First, when one of the common polar of the sphere or line images passes through or is close to the principal point, the calibration result is not highly reliable because the corresponding pole is at infinity with respect to the image plane. Second, when the three common pole–polar of any three sphere or line images are reduced to the same common pole–polar, these images may only provide two constraints; therefore, the camera cannot be calibrated. Third, when the common poles of two sphere or line images are collinear, there are no providing constraints for estimating MIAC; hence, this case is degenerate for the algorithm proposed here. However, this situation can be easily avoided in practice to obtain precise calibration data, especially when more than three spherical images are available.

6 Conclusion

In this work, we studied the common pole–polar properties of the sphere and line images obtained by a central catadioptric camera and applied them to camera calibration. In general, the developed algorithm requires only three sphere or line images to linearly calibrate a central catadioptric camera without setting the initial values of its intrinsic parameters. From the simulated noise sensitivities and reprojection errors determined experimentally, it was concluded that the proposed calibration algorithm is reliable and efficient. However, comparing with the calibration method using the chessboard, the proposed method obviously have poor accuracy. This is understandable since the corners of the chessboard can be extracted at subpixel accuracy. Howover, the extraction of the sphere or line image for catadioptric camera is well known to be a very difficult task. Hence, future work could improve the conic fitting robustness to obtain high calibration accuracy.

Appendices

Appendix A

In the MCS, the unit normal vectors of planes ${{\varvec{\pi }} _m}$ and ${{\varvec{\pi } _S}}$ are ${{\varvec{O}}_c}{\varvec{O}}\mathrm{{ = }}{\left[ {\begin{array}{*{20}{c}} 0&0&1 \end{array}} \right] ^T}$ and ${{\varvec{O}}_c}{\varvec{N}}\mathrm{{ = }}{\left[ {\begin{array}{*{20}{c}} {{n_x}}&{{n_y}}&{{n_z}} \end{array}} \right] ^T}$, respectively. Since the line ${{\varvec{O}}_c}{\varvec{O}}$ and the normal ${{\varvec{O}}_c}{\varvec{N}}$ are coplanar, the corresponding projection points $\bar{{\varvec{O}}}\mathrm{{ = }}{\left[ {\begin{array}{*{20}{c}} 0&0&1 \end{array}} \right] ^T}$ and $\bar{{\varvec{N}}}\mathrm{{ = }}{\left[ {\begin{array}{*{20}{c}} {{n_x}}&{{n_y}}&{{n_z}} \end{array}} \right] ^T}$ are collinear. Further, the intersection line ${\varvec{D}}$ of planes ${\varvec{\pi } _m}$ and ${\varvec{\pi } _S}$ is orthogonal to the plane containing both the normal ${{\varvec{O}}_c}{\varvec{N}}$ and ${{\varvec{O}}_c}{\varvec{O}}$. Considering two $3 \times 3$ symmetric matrices ${\bar{{\varvec{C}}}_m}$ and ${\bar{{\varvec{C}}}}$, and solving Eq. (9) yields the generalized eigenvalue ${\lambda _1}$ of $\left( {{{\bar{{\varvec{C}}}}_m},\bar{{\varvec{C}}}} \right)$ and the corresponding generalized eigenvector ${\bar{{\varvec{v}}}_1}$ (computed by MAPLE) as ${\lambda _1} = {\left( {{d_0} - \xi {n_z}} \right) ^2}$ and ${\bar{{\varvec{v}}}_1} = {\left[ {\begin{array}{*{20}{c}} { - {n_y}}&{{n_x}}&0 \end{array}} \right] ^T}$, respectively. Thus, the point ${\bar{{\varvec{v}}}_1} = {\left[ {\begin{array}{*{20}{c}} { - {n_y}}&{{n_x}}&0 \end{array}} \right] ^T}$ is an infinity point of the line ${\varvec{D}}$. In Fig. 2, according to Eq. (9), the common polar corresponding to ${\bar{{\varvec{v}}}_1}$ with respect to ${\bar{{\varvec{C}}}_m}$ and ${\bar{{\varvec{C}}}}$ aligns with the major axis $\bar{\varvec{\mu }} = {\bar{\varvec{\mu }} _1} = {\left[ {\begin{array}{*{20}{c}} { - {n_y}}&{{n_x}}&0 \end{array}} \right] ^T}$ (see Table 1) formed by $\bar{{\varvec{O}}}$ and $\bar{{\varvec{N}}}$ Barreto and Araujo (2005). Hence, according to the Definition 4, the infinite point ${\bar{{\varvec{v}}} _1}$ and the line ${\bar{\varvec{\mu }} _1}$ also exhibit a pole–polar relationship with respect to the absolute conic ${\bar{\varvec{\Omega }} _\infty }$(not depicted) Andrew (2001). As the projectivity ${{\varvec{H}}_c}$ preserves incidence and collinearity, the property holds in the central catadioptric image plane after the transformation ${{\varvec{H}}_c}$. Thus, the pole–polar relation between ${\hat{{\varvec{v}}}_1}$ and ${\hat{\varvec{\mu }} _1}$, which corresponds to the common pole and polar for ${\hat{{\varvec{C}}}_m}$ and ${\hat{{\varvec{C}}}}$, respectively, is preserved under the projection transformation ${{\varvec{H}}_c}$. Notably, the locus ${\hat{\varvec{\mu }} _1}$ is no longer the major axis of the catadioptric sphere or the line image ${\hat{{\varvec{C}}}}$. However, from Fig. 2, the point ${\hat{{\varvec{v}}}_1}$ and line ${\hat{\varvec{\mu }} _1}$ can be uniquely determined from the generalized eigenvectors of the conics ${\hat{{\varvec{C}}}_m}$ and ${\hat{{\varvec{C}}}}$ , as ${\hat{\varvec{\mu }} _1}$ is the only line intersecting both ${\hat{{\varvec{C}}}_m}$ and ${\hat{{\varvec{C}}}}$ at two points.

Appendix B

For a paracatadioptric camera, according to Eq. (4), replacing $\xi$ by 1 yields

$$\begin{aligned} {{\bar{{\varvec{C}}}_S} = \left[ {\begin{array}{*{20}{c}} {{{({d_0} - {m_z})}^2}}&{}\mathrm{{0}}&{}{({d_0} - {m_z}){m_x}}\\ \mathrm{{0}}&{}{{{({d_0} - {m_z})}^2}}&{}{({d_0} - {m_z}){m_y}}\\ {({d_0} - {m_z}){m_x}}&{}{({d_0} - {m_z}){m_y}}&{}{({d_0}^2 - {m_z}^2)} \end{array}} \right] } \end{aligned}$$

(B1)

Consider the dual of circle ${\bar{{\varvec{C}}}_S}^\mathrm{{*}}$, which satisfies

$$\begin{aligned} {{\bar{{\varvec{C}}}_S}^\mathrm{{*}} = \left[ {\begin{array}{*{20}{c}} {{d_0}^2 + {m_x}^2 - 1}&{}{{m_x}{m_y}}&{}{({d_0} - {m_z}){m_x}}\\ {{m_x}{m_y}}&{}{{d_0}^2 + {m_x}^2 - 1}&{}{({d_0} - {m_z}){m_y}}\\ {({d_0} - {m_z}){m_x}}&{}{({d_0} - {m_z}){m_y}}&{}{{{({d_0} - {m_z})}^\mathrm{{2}}}} \end{array}} \right] }\nonumber \\ \end{aligned}$$

(B2)

From Eq. (7), the dual of the conic curve ${\hat{{\varvec{C}}}^ * }$ is the paracatadioptric image of a line or sphere in the scene satisfying

$$\begin{aligned} {{\lambda _w}^*{\hat{{\varvec{C}}}^*} = {{\varvec{H}}_c}{\bar{{\varvec{C}}}_S}^\mathrm{{*}}{{\varvec{H}}_c}^T} \end{aligned}$$

(B3)

By simplification, equation Eq. B3 can be rearranged as

$$\begin{aligned} {{\lambda _w}^*{\hat{{\varvec{C}}}^*} = {\hat{{\varvec{C}}}_\infty ^*}+{\hat{{\varvec{v}}}}^*{\hat{{\varvec{v}}}}^*}^T \end{aligned}$$

(B4)

where ${\hat{{\varvec{C}}}_\infty }^*\mathrm{{ = }}{{\varvec{H}}_c}\left[ {\begin{array}{*{20}{c}} \mathrm{{1}}&{}\mathrm{{0}}&{}\mathrm{{0}}\\ \mathrm{{0}}&{}\mathrm{{1}}&{}\mathrm{{0}}\\ \mathrm{{0}}&{}\mathrm{{0}}&{}\mathrm{{0}} \end{array}} \right] {{\varvec{H}}_c}^T$ is the projection of the CDCP, ${\hat{{\varvec{v}}}^*} = \frac{1}{{\sqrt{\left( {1 - {d_0}^2} \right) } }}{{\varvec{H}}_c}\left[ {\begin{array}{*{20}{c}} {{m_x}}\\ {{m_y}}\\ {{d_0} - {m_z}} \end{array}} \right]$. In a similar manner, from Proposition 4, ${\hat{{\varvec{C}}}_\infty }^*$ can be computed by considering the generalized eigenvectors of any two line or sphere images. Note that, from Eq. B4 , for paracatadioptric systems, the dual of the line or sphere image is in double contact with a degenerated-line (envelope) conic $\hat{{\varvec{C}}}_\infty ^*$ consisting of the image of the circular points. Similar results can be obtained using the method presented by Ying and Zha (2008).