1 Introduction

permanent magnet synchronous motors (PMSMs) have been widely applied on electric vehicle drive systems because of their high power density, wide speed range, and high efficiency [1, 2]. However, the torque ripple, caused by slotting, non-sinusoidal back-emf, and magnetic saturation, degrades the quality of torque seriously [3]. Methods applied to reduce torque ripple can be divided into two groups: one focusing on the improvement of motor design and the other emphasizing on the active control of stator current excitations [4], and in this paper, only the latter means will be discussed.

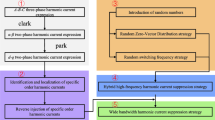
The basic principle of the harmonic current control for torque ripple reduction is shown in Fig. 1 [5]. The key of this method includes two aspects: how to select the appropriate harmonic currents for reducing torque ripple and how to inject the selected harmonic currents correctly.

Fig. 1
figure 1

Torque ripple reduction effect with active harmonic current injection [5]

Full size image

Many types of research have been done to explore how to select the appropriate harmonic currents for torque ripple reduction. Actual instantaneous torque can be obtained through torque ripple transducer or torque observer, then the difference between desired torque and actual torque is used as the input of a torque controller, and the output of torque controller is the harmonic current [6,7,8,9]; Similarly, by applying a speed harmonic suppression controller, the harmonic currents could also be updated with the output of speed controller [10,11,12]; With the software of Finite Element Model (FEM), the harmonic current for torque ripple reduction is computed offline [13, 14]. As the authors of this paper have introduced an appropriate method to compute harmonic currents for torque ripple reduction online based on an analytical model of torque ripple [5], thus this paper will only explore a harmonic currents injection method.

The relevant researches on harmonic current control are mainly focusing on harmonic currents suppression and can be divided into two main sorts. One sort of method firstly obtains harmonic current of each order via coordinate transformation and low-pass filter, then applying PI control on each harmonic current respectively [15]. The disadvantage of that method is that the phase lag caused by the filter process will lead to bad transient tracking performance. The low-pass filter structure has been optimized to solve this issue. An adaptive filter using LMS to update parameters in different working points has been proposed to improve the transient extraction performance of harmonic currents [16, 17], and a closed-loop detection system is constructed to extract the harmonics accurately [18]. Another sort of method is adding additional proportional resonant (PR) controllers in the d−q coordinate [19,20,21]. The resonant part can provide a large gain in the nearby frequency of harmonic currents, which compensate for the original PI controller's insufficient bandwidth. Compared to the multiple coordinates PI control, the phase lagging caused by the filter is eliminated, but the stability of the resonant part is relatively bad. Besides, repetitive control is also applied in harmonic current suppression [22]. But as the controller uses all the signals during one fundamental period as input, the dynamic performance cannot be guaranteed necessarily. The harmonic currents suppression performance of model predictive control is introduced and compared to traditional field-oriented control, but no specific design for harmonic currents is added and the improvement is slight [24]. Through injecting the harmonic voltage caused by the non-sinusoidal back-EMF, the harmonic current is suppressed rapidly, and its corresponding loss is reduced at the same time [23].

As for the method of harmonic currents injection, the related researches are mainly focusing on dual three-phase PMSM [25,26,27]. The applied methods are similar to the suppression of the harmonic current, with adding multiple coordinates PI or PR controllers. However, in the situation of harmonic currents injection, the needed harmonic voltages are much larger than the suppression condition, as the input harmonic voltages not only compensate the harmonics caused by dead zone, voltage-drop of inverters, or non-sinusoidal back-emf but also is used for exciting the injected harmonic currents. Thus, with the similar method applied in harmonic currents suppression, the control performance of harmonic currents will decrease.

The main contributions of our work are as follows: (1) A novel coupling model between harmonic currents and harmonic voltages is derived in multiple d-q synchronous-frames, considering the positive and negative harmonic currents simultaneously. The model reveals that either positive or negative voltage alone can induce positive and negative currents in the meantime for the IPMSM system. (2) A model-based harmonic current control method is proposed for torque ripple reduction application. Compared to the traditional PI feedback control, the proposed method can improve the dynamic tracking performance of harmonic currents significantly, and then make a better torque ripple reduction effect.

The rest of this paper is organized as the flow chart, shown in Fig. 2. We firstly deduce a harmonic voltages model in multiple synchronous-frames. Secondly, a model-based harmonic voltages feedforward control method for harmonic currents injection is added to the traditional harmonic currents feedback control system. Finally, the control performance with and without the feedforward harmonic voltages is compared with simulation and bench test. Besides, the influence of parameter uncertainties for harmonic voltages injection is discussed.

Fig. 2
figure 2

Flow chart of this paper’s structure

Full size image

2 Modelling of PMSM Harmonic Voltages in Multiple Synchronous-Frames

In this paper, the model of PMSM harmonic voltages is deduced based on two premises:

  1. 1.

    The variation of d-axis and q-axis inductances \(L_{d}\) and \(L_{q}\) with different stator excitation currents and rotor position is ignored.

  2. 2.

    The amplitude and phase of each harmonic current keep constant. Actually, the harmonic voltages model established in this paper is the corresponding steady voltage equations of harmonic currents.

2.1 Vector Description of Positive and Negative Sequence Currents/Voltages

Introduce some notations below:

  1. 1.

    \(d^{k}\) − \(q^{k}\) denotes the \(k^{th}\) synchronous-frame

  2. 2.

    \({\varvec{X}}_{{{\varvec{s}}\left( {\varvec{l}} \right)}}^{{\varvec{k}}}\) denotes \(l^{th}\) current/voltage harmonic vector in \(d^{k}\)-\(q^{k}\)

  3. 3.

    \(X_{d\left( l \right)}^{k}\) and \(X_{q\left( l \right)}^{k}\) are the components of \({\varvec{X}}_{{{\varvec{s}}\left( {\varvec{l}} \right)}}^{{\varvec{k}}}\) at \(d^{k}\)-axis and \(q^{k}\)-axis

  4. 4.

    DC values—do not change with the electric angle of the rotor \(\theta_{r}\)

  5. 5.

    AC values—change with the electric angle of rotor \(\theta_{r}\) periodically

To describe harmonic currents with different orders more effectively, we introduce multiple synchronous-frames with different rotating speeds, shown in Fig. 3.

Fig. 3
figure 3

Multiple d−q synchronous-frames

Full size image

Where \(d^{1}\)−\(q^{1}\) frame in Fig. 3. is just the traditional d−q synchronous-frame. The direction of \(d^{1}\)-axis is always the same with the magnetic field of the rotor. The angle between \(d^{1}\)-axis and A-axis is the electric angle of the rotor \(\theta_{r}\); \(d^{{\text{k}}}\)−\(q^{k}\) frame is the \(k{\text{th}}\) synchronous-frame, whose rotating speed is \(k\) times as \(d^{1}\)−\(q^{1}\)’s speed. Thereby, the angle between \(d^{{\text{k}}}\) and A-axis is \(k\theta_{r}\). \({\varvec{i}}_{{{\varvec{s}}\left( {\varvec{k}} \right)}}^{{\varvec{k}}}\) is \(k{\text{th}}\) current vector in \(d^{{\text{k}}}\)−\(q^{k}\). As the rotating speed of \({\varvec{i}}_{{{\varvec{s}}\left( {\varvec{k}} \right)}}^{{\varvec{k}}}\) is the same with \(d^{{\text{k}}}\)−\(q^{k}\), the components of \({\varvec{i}}_{{{\varvec{s}}\left( {\varvec{k}} \right)}}^{{\varvec{k}}}\) at \(d^{{\text{k}}}\)-axis and \(q^{{\text{k}}}\)-axis are DC values. Thus, \({\varvec{i}}_{{{\varvec{s}}\left( {\varvec{k}} \right)}}^{{\varvec{k}}}\) can be expressed conveniently in \(d^{{\text{k}}}\)−\(q^{k}\):

$${\varvec{i}}_{{{\varvec{s}}\left( {\varvec{k}} \right)}}^{{\varvec{k}}} = i_{d\left( k \right)}^{k} + ji_{q\left( k \right)}^{k}$$
(1)

Based on the two-axis theory of PMSM, \(L_{d}\) and \(L_{q}\) shown in voltage Eq. (6) only keep constant in \(d^{1}\)−\(q^{1}\). Thus, in order to compute the correponding harmonic voltages of harmonic currents, the expression of \({\varvec{i}}_{{{\varvec{s}}\left( {\varvec{k}} \right)}}^{{\varvec{k}}}\) in \(d^{1}\)−\(q^{1}\) should be obtained firstly. According to the vector transformation theory, the expression of \({\varvec{i}}_{{{\varvec{s}}\left( {\varvec{k}} \right)}}^{{\varvec{k}}}\) in \(d^{1}\)−\(q^{1}\) frame is:

$${\varvec{i}}_{{{\varvec{s}}\left( {\varvec{k}} \right)}}^{1} = {\varvec{i}}_{{{\varvec{s}}\left( {\varvec{k}} \right)}}^{{\varvec{k}}} e^{{j\left( {{\text{k}} - 1} \right)\theta_{r} }}$$
(2)

On account of the three-phase symmetry property of PMSM, orders of harmonic currents only consist of

$$5, 7, 11, 13, \ldots , 6k - 1, 6k + 1, \ldots \left( {k = 1, 2, 3, \ldots } \right)$$

where harmonic current vector of \(6{\text{k}} + 1\) order \({\varvec{i}}_{{{\varvec{s}}\left( {6{\varvec{k}} + 1} \right)}}^{{6{\mathbf{k}} + 1}}\) is called positive-sequence current, with the same rotation direction of the rotor. In contrast, harmonic current vector with \(6{\text{k}} - 1\) order \({\varvec{i}}_{{{\varvec{s}}\left( {6{\varvec{k}} - 1} \right)}}^{{6{\mathbf{k}} - 1}}\) is called negative-sequence current, with the contrast rotation direction of the rotor. Harmonic currents with \(6{\text{k}} + 1\) order and \(6{\text{k}} - 1\) order constitute a couple of positive and negative sequence currents, which will be the research object in the subsequent analysis.

According to (2), the expressions of \(6{\text{k}} + 1\) and \(6{\text{k}} - 1\) harmonic currents in \(d^{1}\) − \(q^{1}\) frame are:

$$\left\{ {\begin{array}{*{20}c} {{\varvec{i}}_{{{\varvec{s}}\left( {6{\varvec{k}} - 1} \right)}}^{1} = {\varvec{i}}_{{{\varvec{s}}\left( {6{\mathbf{k}} - 1} \right)}}^{{6{\varvec{k}} - 1}} e^{{j\left( { - 6k} \right)\theta_{r} }} = i_{{d\left( {6k - 1} \right)}}^{1} + ji_{{q\left( {6k - 1} \right)}}^{1} } \\ {{\varvec{i}}_{{{\varvec{s}}\left( {6{\varvec{k}} + 1} \right)}}^{1} = {\varvec{i}}_{{{\varvec{s}}\left( {6{\mathbf{k}} + 1} \right)}}^{{6{\varvec{k}} + 1}} e^{{j\left( {6k} \right)\theta_{r} }} = i_{{d\left( {6k + 1} \right)}}^{1} + ji_{{q\left( {6k + 1} \right)}}^{1} } \\ \end{array} } \right.$$
(3)

where

$$\left\{\begin{array}{c}{{i}_{d(6k-1)}}^{1}={{i}_{d(6k-1)}}^{6k-1}\mathrm{cos}\left(6k\right){\theta }_{r}+{{i}_{q(6k-1)}}^{6k-1}\mathrm{sin}\left(6k\right){\theta }_{r}\\ {{i}_{q(6k-1)}}^{1}={{-i}_{d(6k-1)}}^{6k-1}\mathrm{sin}\left(6k\right){\theta }_{r}+{{i}_{q(6k-1)}}^{6k-1}\mathrm{cos}\left(6k\right){\theta }_{r}\\ \begin{array}{c}{{i}_{d(6k+1)}}^{1}={{i}_{d(6k+1)}}^{6k+1}\mathrm{cos}\left(6k\right){\theta }_{r}-{{i}_{q(6k+1)}}^{6k+1}\mathrm{sin}\left(6k\right){\theta }_{r}\\ {{i}_{q(6k+1)}}^{1}={{i}_{d(6k+1)}}^{6k+1}\mathrm{sin}\left(6k\right){\theta }_{r}+{{i}_{q(6k+1)}}^{6k+1}\mathrm{cos}\left(6k\right){\theta }_{r}\end{array}\end{array}\right.$$
(4)

Similarly, if we define a harmonic voltage vector \({\varvec{u}}_{{{\varvec{s}}\left( {\varvec{k}} \right)}}^{{\varvec{k}}}\), it can be also expressed in \(d^{{\text{k}}}\)–\(q^{k}\) with the analogous form.

$${\varvec{u}}_{{{\varvec{s}}\left( {\varvec{k}} \right)}}^{{\varvec{k}}} = u_{d\left( k \right)}^{k} + ju_{q\left( k \right)}^{k}$$
(5)

Besides, harmonic voltages can be also divided into two different sorts according to their rotation direction: positive-sequence voltage \({\varvec{u}}_{{{\varvec{s}}\left( {6{\varvec{k}} + 1} \right)}}^{{6{\mathbf{k}} + 1}}\) and negative-sequence voltage \({\varvec{u}}_{{{\varvec{s}}\left( {6{\varvec{k}} - 1} \right)}}^{{6{\mathbf{k}} - 1}}\).

2.2 Harmonic Voltages Caused by Harmonic currents in \({\mathbf{d}}^{1}\)−\({\mathbf{q}}^{1}\) synchronous-frame

According to the voltage equations in \(d^{1}\)–\(q^{1},\)

$$\left\{ {\begin{array}{*{20}c} {{\text{u}}_{d} = R_{s} i_{d} + \frac{{d\psi_{d} }}{dt} - \omega_{r} \psi_{q} } \\ {{\text{u}}_{q} = R_{s} i_{q} + \frac{{d\psi_{q} }}{dt} + \omega_{r} \psi_{d} } \\ \end{array} } \right.$$
(6)

where \({R}_{s}\) denotes stator resistance, \({i}_{d}\) and \({i}_{q}\) the \({d}^{1}\)-axis and \({q}^{1}\)-axis current component respectively, \({\psi }_{d}\) and \({\psi }_{q}\) the \({d}^{1}\)-axis and \({q}^{1}\)-axis flux component, \({\omega }_{r}\) the space rotation speed of \({d}^{1}\)–\({q}^{1}\).

For the positive-sequence current vector \({{{\varvec{i}}}_{{\varvec{s}}(6k+1)}}^{1}\), the induced \({d}^{1}\)-axis and \({q}^{1}\)-axis flux can be expressed as:

$$\psi _{{d\left( {6k + 1} \right)}} ^{1} = L_{d} i_{{d\left( {6k + 1} \right)}} ^{1} ,\quad \psi _{{q\left( {6k + 1} \right)}} ^{1} = L_{q} i_{{q\left( {6k + 1} \right)}} ^{1} ~$$
(7)

According to (4) and (7), the derivatives of flux to time are obtained.

$$\frac{{d\psi_{{d\left( {6k + 1} \right)}}^{1} }}{dt} = - 6k\omega_{r} L_{d} i_{{q\left( {6k + 1} \right)}}^{1} ,\quad \frac{{d\psi_{{q\left( {6k + 1} \right)}}^{1} }}{dt} = 6k\omega_{r} L_{q} i_{{d\left( {6k + 1} \right)}}^{1}$$
(8)

Substitute (7) and \(\frac{{d\psi_{{q\left( {6k + 1} \right)}}^{1} }}{dt} = 6k\omega_{r} L_{q} i_{{d\left( {6k + 1} \right)}}^{1}\) (8) into (6), then the harmonic voltage of positive-sequence current of \(6\mathrm{k}+1\) order in \({d}^{1}\)-\({q}^{1}\) is represented as:

$$\left\{ {\begin{array}{*{20}c} {u_{{d\left( {6k + 1} \right)}}^{1} = R_{s} i_{{d\left( {6k + 1} \right)}}^{1} - 6k\omega_{r} L_{d} i_{{q\left( {6k + 1} \right)}}^{1} - \omega_{r} L_{q} i_{{q\left( {6k + 1} \right)}}^{1} } \\ {u_{{q\left( {6k + 1} \right)}}^{1} = R_{s} i_{{q\left( {6k + 1} \right)}}^{1} + 6k\omega_{r} L_{q} i_{{d\left( {6k + 1} \right)}}^{1} + \omega_{r} L_{d} i_{{d\left( {6k + 1} \right)}}^{1} } \\ \end{array} } \right.$$
(9)

Similarly, the harmonic voltage of negative-sequence current of \(6\mathrm{k}-1\) order is:

$$\left\{ {\begin{array}{*{20}c} {u_{{d\left( {6k - 1} \right)}}^{1} = R_{s} i_{{d\left( {6k - 1} \right)}}^{1} + 6k\omega_{r} L_{d} i_{{q\left( {6k - 1} \right)}}^{1} - \omega_{r} L_{q} i_{{q\left( {6k - 1} \right)}}^{1} } \\ {u_{{q\left( {6k - 1} \right)}}^{1} = R_{s} i_{{q\left( {6k - 1} \right)}}^{1} - 6k\omega_{r} L_{q} i_{{d\left( {6k - 1} \right)}}^{1} + \omega_{r} L_{d} i_{{d\left( {6k - 1} \right)}}^{1} } \\ \end{array} } \right.$$
(10)

Add the components of positive and negative sequence voltage in \({d}^{1}\)-axis and \({q}^{1}\)-axis respectively, and represent the expression with matrix form.

$$\left[ {\begin{array}{*{20}c} {u_{{d\left( {6k + 1} \right)}}^{1} + u_{{d\left( {6k - 1} \right)}}^{1} } \\ {u_{{q\left( {6k + 1} \right)}}^{1} + u_{{q\left( {6k - 1} \right)}}^{1} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {R_{s} } & {\text{A}} & {R_{s} } & { - {\text{B}}} \\ { - {\text{C}}} & {R_{s} } & {\text{D}} & {R_{s} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {i_{{\left. {d(6k - 1} \right)}}^{1} } \\ {i_{{\left. {q(6k - 1} \right)}}^{1} } \\ {i_{{\left. {d(6k + 1} \right)}}^{1} } \\ {i_{{\left. {q(6k + 1} \right)}}^{1} } \\ \end{array} } \right]$$
(11)

For the sake of convenient description in subsequent parts, define:

$$\left\{ {\begin{array}{*{20}c} {u_{{d\left( {6k \pm 1} \right)}}^{1} = u_{{d\left( {6k + 1} \right)}}^{1} + u_{{d\left( {6k - 1} \right)}}^{1} } \\ {u_{{q\left( {6k \pm 1} \right)}}^{1} = u_{{q\left( {6k + 1} \right)}}^{1} + u_{{q\left( {6k - 1} \right)}}^{1} } \\ \end{array} } \right.$$
(12)

Substitute (4), (11) into (12),

$$\begin{gathered} \left[ {\begin{array}{*{20}c} {u_{{d\left( {6k \pm 1} \right)}}^{1} } \\ {u_{{q\left( {6k \pm 1} \right)}}^{1} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {R_{s} \cos \left( {6k\theta_{r} } \right) - A\sin \left( {6k\theta_{r} } \right)} & {R_{s} \sin \left( {6k\theta_{r} } \right) + A\cos \left( {6k\theta_{r} } \right) \cdots } \\ { - C\cos \left( {6k\theta_{r} } \right) - R_{s} \sin \left( {6k\theta_{r} } \right)} & { - C\sin \left( {6k\theta_{r} } \right) + R_{s} \cos \left( {6k\theta_{r} } \right) \cdots } \\ \end{array} } \right. \hfill \\ \left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}c} {R_{s} \cos \left( {6k\theta_{r} } \right) - B\sin \left( {6k\theta_{r} } \right)} & { - R_{s} \sin \left( {6k\theta_{r} } \right) - B\cos \left( {6k\theta_{r} } \right)} \\ {Dcos\left( {6k\theta_{r} } \right) + R_{s} \sin \left( {6k\theta_{r} } \right)} & { - D\sin \left( {6k\theta_{r} } \right) + R_{s} \cos \left( {6k\theta_{r} } \right)} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {i_{{\left. {d(6k - 1} \right)}}^{6k - 1} } \\ {i_{{\left. {q(6k - 1} \right)}}^{6k - 1} } \\ {i_{{\left. {d(6k + 1} \right)}}^{6k + 1} } \\ {i_{{\left. {q(6k + 1} \right)}}^{6k + 1} } \\ \end{array} } \right] \hfill \\ \end{gathered}$$
(13)

where

$$\left\{ {\begin{array}{*{20}c} {A = 6k\omega_{r} L_{d} - \omega_{r} L_{q} } \\ {{\text{B}} = 6k\omega_{r} L_{d} + \omega_{r} L_{q} } \\ {{\text{C}} = 6k\omega_{r} L_{q} - \omega_{r} L_{d} } \\ {{\text{D}} = 6k\omega_{r} L_{q} + \omega_{r} L_{d} } \\ \end{array} } \right.$$
(14)

Equation (13) has described the corresponding harmonic voltages of a couple of positive and negative sequence currents in \({d}^{1}\)–\({q}^{1}\). It is obvious that the harmonic voltages are complicated AC values that varying along with rotor position \({\theta }_{r}\). Thus, it is difficult to apply this expression to system control and analysis. As shown in (5), the harmonic voltage vector can be expressed by DC values in multiple synchronous-frame whose order is the same as the harmonic voltage vector. Thereby, we will try to represent the harmonic voltages shown in (13) by DC voltage vectors in some multiple synchronous-frames.

2.3 Harmonic Voltages Model in Multiple Synchronous-Frames

Firstly, apply \(6k\) Park transformation on the harmonic voltages in \({d}^{1}\)-\({q}^{1}\), which means multiply matrix \({\mathrm{P}}_{1}\) by (13).

$$P_{1} = \left[ {\begin{array}{*{20}c} {\cos \left( {6k} \right)\theta_{r} } & {\sin \left( {6k} \right)\theta_{r} } \\ { - \sin \left( {6k} \right)\theta_{r} } & {\cos \left( {6k} \right)\theta_{r} } \\ \end{array} } \right]$$

Besides, simplify the results from the previous step with double angle formula of trigonometric function, then the harmonic voltages expressed in \(6k+1\) synchronous-frame are obtained:

$$\begin{array}{*{20}c} {\left[ {\begin{array}{*{20}c} {u_{{d\left( {6k \pm 1} \right)}}^{{6{\text{k}} + 1}} } \\ {u_{{q\left( {6k \pm 1} \right)}}^{{6{\text{k}} + 1}} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {R_{s} \cos \left( {12k\theta_{r} } \right) - \frac{A + C}{2}\sin \left( {12k\theta_{r} } \right)} & {\frac{A - C}{2} + \frac{A + C}{2}\cos \left( {12k\theta_{r} } \right) + R_{s} \sin \left( {12k\theta_{r} } \right) \cdots } \\ {\frac{A - C}{2} - \frac{A + C}{2}\cos \left( {12k\theta_{r} } \right) - R_{s} \sin \left( {12k\theta_{r} } \right)} & {R_{s} \cos \left( {12k\theta_{r} } \right) - \frac{A + C}{2}\sin \left( {12k\theta_{r} } \right) \cdots } \\ \end{array} } \right.} \\ {\left. {\begin{array}{*{20}c} {R_{s} - \frac{B - D}{2}\sin \left( {12k\theta_{r} } \right)} & { - \frac{B + D}{2} - \frac{B - D}{2}\cos \left( {12k\theta_{r} } \right)} \\ {\frac{B + D}{2} - \frac{B - D}{2}\cos \left( {12k\theta_{r} } \right)} & {R_{s} + \frac{B - D}{2}\sin \left( {12k\theta_{r} } \right)} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {i_{{\left. {d(6k - 1} \right)}}^{6k - 1} } \\ {i_{{\left. {q(6k - 1} \right)}}^{6k - 1} } \\ {i_{{\left. {d(6k + 1} \right)}}^{6k + 1} } \\ {i_{{\left. {q(6k + 1} \right)}}^{6k + 1} } \\ \end{array} } \right]} \\ \end{array}$$
(15)

Extract the DC values in (15), and define it as the positive voltage vector in \(6k+1\) synchronous-frame—\({{{\varvec{u}}}_{{\varvec{s}}(6{\varvec{k}}+1)}}^{6{\varvec{k}}+1}\). The corresponding components in \({d}^{6\mathrm{k}+1}\)-axis and \({q}^{6\mathrm{k}+1}\)-axis are:

$$\left[ {\begin{array}{*{20}c} {u_{{d\left( {6k + 1} \right)}}^{6k + 1} } \\ {u_{{q\left( {6k + 1} \right)}}^{6k + 1} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 & {\frac{A - C}{2}} & {R_{s} } & { - \frac{B + D}{2}} \\ {\frac{A - C}{2}} & 0 & {\frac{B + D}{2}} & {R_{s} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {i_{{\left. {d(6k - 1} \right)}}^{6k - 1} } \\ {i_{{\left. {q(6k - 1} \right)}}^{6k - 1} } \\ {i_{{\left. {d(6k + 1} \right)}}^{6k + 1} } \\ {i_{{\left. {q(6k + 1} \right)}}^{6k + 1} } \\ \end{array} } \right]$$
(16)

Subtract (16) form (15), then the remained harmonic voltages are obtained.

$$\begin{array}{*{20}c} {\left[ {\begin{array}{*{20}c} {\Delta u_{{d\left( {6k \pm 1} \right)}}^{{6{\text{k}} + 1}} } \\ {\Delta u_{{q\left( {6k \pm 1} \right)}}^{{6{\text{k}} + 1}} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {R_{s} \cos \left( {12k\theta_{r} } \right) - \frac{A + C}{2}\sin \left( {12k\theta_{r} } \right)} & {\frac{A + C}{2}\cos \left( {12k\theta_{r} } \right) + R_{s} \sin \left( {12k\theta_{r} } \right) \cdots } \\ { - \frac{A + C}{2}\cos \left( {12k\theta_{r} } \right) - R_{s} \sin \left( {12k\theta_{r} } \right)} & {R_{s} \cos \left( {12k\theta_{r} } \right) - \frac{A + C}{2}\sin \left( {12k\theta_{r} } \right) \cdots } \\ \end{array} } \right.} \\ {\left. {\begin{array}{*{20}c} { - \frac{B - D}{2}\sin \left( {12k\theta_{r} } \right)} & { - \frac{B - D}{2}\cos \left( {12k\theta_{r} } \right)} \\ { - \frac{B - D}{2}\cos \left( {12k\theta_{r} } \right)} & {\frac{B - D}{2}\sin \left( {12k\theta_{r} } \right)} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {i_{{\left. {d(6k - 1} \right)}}^{6k - 1} } \\ {i_{{\left. {q(6k - 1} \right)}}^{6k - 1} } \\ {i_{{\left. {d(6k + 1} \right)}}^{6k + 1} } \\ {i_{{\left. {q(6k + 1} \right)}}^{6k + 1} } \\ \end{array} } \right]} \\ \end{array}$$
(17)

Make \(12k\) IPark transformation on (17), which means multiply by matrix \({\mathrm{P}}_{2}\),

$$P_{2} = \left[ {\begin{array}{*{20}c} {\cos \left( {12k} \right)\theta_{r} } & { - \sin \left( {12k} \right)\theta_{r} } \\ {\sin \left( {12k} \right)\theta_{r} } & {\cos \left( {12k} \right)\theta_{r} } \\ \end{array} } \right]$$

Then (17) is transformed to the harmonic voltages expressed in \(6k-1\) synchronous-frame:

$$\left[ {\begin{array}{*{20}c} {\Delta u_{{d\left( {6k \pm 1} \right)}}^{{6{\text{k}} - 1}} } \\ {\Delta u_{{q\left( {6k \pm 1} \right)}}^{{6{\text{k}} - 1}} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {R_{s} } & {\frac{A + C}{2}} & 0 & { - \frac{B - D}{2}} \\ { - \frac{A - C}{2}} & {R_{s} } & { - \frac{B - D}{2}} & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {i_{{\left. {d(6k - 1} \right)}}^{6k - 1} } \\ {i_{{\left. {q(6k - 1} \right)}}^{6k - 1} } \\ {i_{{\left. {d(6k + 1} \right)}}^{6k + 1} } \\ {i_{{\left. {q(6k + 1} \right)}}^{6k + 1} } \\ \end{array} } \right]$$
(18)

Interestingly, the remained harmonic voltages in \(6k-1\) synchronous-frame only contain DC values. Thus it can be defined as the negative voltage vector in \(6k-1\) synchronous-frame—\({{{\varvec{u}}}_{{\varvec{s}}(6{\varvec{k}}-1)}}^{6{\varvec{k}}-1}\). The corresponding components in \({d}^{6\mathrm{k}-1}\)-axis and \({q}^{6\mathrm{k}-1}\)-axis are:

$$\left[ {\begin{array}{*{20}c} {u_{{d\left( {6k - 1} \right)}}^{6k - 1} } \\ {u_{{q\left( {6k - 1} \right)}}^{6k - 1} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\Delta u_{{d\left( {6k \pm 1} \right)}}^{{6{\text{k}} - 1}} } \\ {\Delta u_{{q\left( {6k \pm 1} \right)}}^{{6{\text{k}} - 1}} } \\ \end{array} } \right]$$
(19)

At present, the complicated form of harmonic voltages in \({d}^{1}\)-\({q}^{1}\) has been transformed to two voltage vectors in \(6k+1\) and \(6k-1\) multiple synchronous-frames. The voltage vector can be expressed by only DC values, so the form of harmonic voltages will be more simple. According to (14), (16), (18), and (19), the harmonic voltages model in multiple synchronous-frames is acquired, shown in Eq. (20).

$$\begin{gathered} \left[ {\begin{array}{*{20}c} {u_{{d\left( {6k - 1} \right)}}^{6k - 1} } \\ {u_{{q\left( {6k - 1} \right)}}^{6k - 1} } \\ {u_{{d\left( {6k + 1} \right)}}^{6k + 1} } \\ {u_{{q\left( {6k + 1} \right)}}^{6k + 1} } \\ \end{array} } \right]{ = }\frac{1}{2}\left[ {\begin{array}{*{20}c} {2R_{s} } & {\left( {6k - 1)\omega_{r} \left( {L_{d} + L_{q} } \right)} \right.} \\ { - \left( {6k - 1} \right)\omega_{r} \left( {L_{d} + L_{q} } \right)} & {2R_{s} } \\ {0} & {\left( {6k + 1)\omega_{r} \left( {L_{d} - L_{q} } \right)} \right.} \\ {\left( {6k + 1)\omega_{r} \left( {L_{d} - L_{q} } \right)} \right.} & 0 \\ \end{array} } \right. \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {\begin{array}{*{20}c} 0 & { - \left( {6k - 1} \right)\omega_{r} \left( {L_{d} - L_{q} } \right)} \\ { - \left( {6k - 1} \right)\omega_{r} \left( {L_{d} - L_{q} } \right)} & {0} \\ {2R_{s} } & {{ - }\left( {6k + 1)\omega_{r} \left( {L_{d} + L_{q} } \right)} \right.} \\ {\left( {6k + 1)\omega_{r} \left( {L_{d} + L_{q} } \right)} \right.} & {2R_{s} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {i_{{\left. {d(6k - 1} \right)}}^{6k - 1} } \\ {i_{{\left. {q(6k - 1} \right)}}^{6k - 1} } \\ {i_{{\left. {d(6k + 1} \right)}}^{6k + 1} } \\ {i_{{\left. {q(6k + 1} \right)}}^{6k + 1} } \\ \end{array} } \right] \hfill \\ \end{gathered}$$
(20)

From the equation (20), we can find that for the SPMSM (surface permanent magnet synchronous motor), whose d-axis inductance and q-axis inductance are the same, the positive voltage can only induce a positive current of identical order, and the negative voltage can only induce a negative current. It means that there is no coupling relationship between a positive voltage and a negative current. The control of positive or negative sequence harmonic current can be designed independently.

However, for another kind of PMSM–IPMSM (interior permanent magnet synchronous motor), whose q-axis inductance is always 2–4 times as d-axis inductance. The positive voltage can not only induce a positive current but also induce a negative current. Thus, in an IPMSM system, the control of positive and negative sequence harmonic currents must be carried out simultaneously to achieve better performance.

More importantly, with the harmonic coupling model shown in Eq. (20), the required harmonic voltages used for exciting any desired positive and negative harmonic currents can be computed advanced, which is beneficial to improve the dynamic tracking performance of harmonic currents.

3 Design of Harmonic Currents Injection System

Based on the harmonic voltages model deduced in Sect. 2, this paper puts forward a novel harmonic currents injection method. The overview of that whole control system is shown in Fig. 4. The “Harmonic current selection module” is used to select appropriate harmonic currents for torque ripple reduction. It is established based on another paper [5] of us. As the key point of this paper is exploring a harmonic currents injection method, so the “Harmonic current selection module” will not be discussed. To inject harmonic currents correctly, three parts are added to the FOC (Field oriented control) system:

  1. 1.

    Computing reference harmonic currents;

  2. 2.

    Feedback controller of harmonic currents;

  3. 3.

    Computing feedforward harmonic voltages.

Fig. 4
figure 4

Overview of whole control system of harmonic current injection

Full size image

Then we will introduce the structure and function of each part specifically.

3.1 Computing Reference Harmonic Currents

Since the basic current control is undertaken in \({d}^{1}\)–\({q}^{1}\), we must obtain the expressions of reference harmonic currents in that frame. According to (4), the specific transformation process is shown in Fig. 5. It is obvious that the new expressions of reference harmonic currents are AC values, so it is represented by \({i}_{dq\_ac}^{*}\).

Fig. 5
figure 5

Specific process of computing reference harmonic currents

Full size image

Whereas, the reference currents from the “Torque/Current Distribution” module only contain fundamental wave, which are DC values in \({d}^{1}\)-\({q}^{1}\), so it is represented by \({i}_{dq\_dc}^{*}\). Then the total reference currents are obtained by summing \({i}_{dq\_ac}^{*}\) and \({i}_{dq\_dc}^{*}\). The error between reference currents \({i}_{dq}^{*}\) and feedback currents \({i}_{dq}\) is used as the input of a PI controller. The output voltage from the PI controller is transformed to \({u}_{\alpha \beta }^{1}\), expressions in the stationary frame, because the voltage modulation method—SVPWM (space vector pulse width modulation) can only be used in that frame.

3.2 Feedback Controller of Harmonic Currents

The feedback controller of harmonic currents is widely applied to the suppression of harmonic currents. The brief structure of this controller is shown in Fig. 6. Firstly, harmonic current with each order should be extracted from the total feedback current \({i}_{dq}\). The basic method is vector transformation and lowpass filtering. Then harmonic current with different order is controlled separately by the respective PI controller in each multiple synchronous-frame. Similarly, the output voltage from every PI controller should be transformed to voltage expressions in a stationary frame. Finally, by summing all voltage expressions in stationary frame, the ultimate control voltage from the feedback controller of harmonic currents \({u}_{\alpha \beta }^{2}\) is obtained.

Fig. 6
figure 6

Specific process of feedback harmonic currents controller

Full size image

3.3 Computing Feedforward Harmonic Voltages

With the harmonic voltages model deduced in Eq. (20), the required harmonic voltages used for exciting desired positive and negative harmonic currents can be computed. As shown in Fig. 7, the feedforward harmonic voltages are obtained by inputting the reference harmonic currents. The feedforward harmonic voltages are DC values in their corresponding multiple synchronous-frame, thus vector transformation and summation are applied, then the control voltage from feedforward harmonic voltages \({u}_{\alpha \beta }^{3}\) is obtained.

Fig. 7
figure 7

Specific process of computing feedforward harmonic voltages

Full size image

At last, three control voltages (\({u}_{\alpha \beta }^{1}\) ~ \({u}_{\alpha \beta }^{3}\)) are added together, and the duty cycles of three half-bridge are calculated by SVPWM. In that harmonic currents injection system, the control effects of those three control voltages are different. The main function of \({u}_{\alpha \beta }^{1}\) is to control the DC currents while the main function of \({u}_{\alpha \beta }^{2}\) and \({u}_{\alpha \beta }^{3}\) is focusing on the tracking performance of AC currents. And the \({u}_{\alpha \beta }^{2}\) and \({u}_{\alpha \beta }^{3}\) are the feedback control voltage and feedforward control voltage in the same multiple synchronous-frames respectively. Thus, there is a small interface between those three control voltages.

Besides, please note that for expressing conveniently, only one couple of positive and negative current is shown in this harmonic current injection control system. This control system can be used for injecting several couples of harmonic currents simultaneously. We just need to duplicate the three new parts by inputting different harmonic currents, and then add all the output voltages together. In the latter simulation and experiments of this paper, two couple of positive and negative currents are injected, and the order of them are 5th, 7th, 11th, and 13th. However, at the working point of PMSM chosen in this paper, the main order of torque ripple is 12th, which is caused by cogging torque. Through FEA simulation, in the excitation of fundamental currents for the 50 Nm torque point, the amplitude of the 6th torque ripple is 0.015 Nm while the amplitude of the 12th torque ripple is 1.14 Nm. Thereby, the 5th and 7th harmonic currents used for torque ripple reduction are too small, so only the 11th and 13th harmonic currents are analyzed and compared in the subsequent simulation and experimental results.

4 Simulation Results

The control system shown in Fig. 4 is established in off-line simulation software. The tested machine is an IPMSM, the corresponding FEA (Finite element analysis) model is shown in Fig. 8. The parameters of PMSM are obtained from FEA simulation in no-load condition, represented in Table 1.

Fig. 8
figure 8

2D FEA model

Full size image

To check the harmonic currents tracking performance and torque ripple reduction effect influenced by the above three control voltages—\({u}_{\alpha \beta }^{1}\), \({u}_{\alpha \beta }^{2}\) and \({u}_{\alpha \beta }^{3}\), four different kinds of control conditions are introduced, shown in Table 2.

To compare the dynamic and steady performance of those four different control sorts, we choose a torque step at a constant speed as the test case. The frequency of harmonic currents will be close to the sampling frequency (10 kHz) when the speed of the motor goes too high, which will decrease the harmonic currents' control performance. Thus, to eliminate the effect of sampling frequency and focus on the comparison of different control sorts, we choose 1000 r/min as the test speed.

Firstly, the control performance of the previous three control sorts is compared without parameter uncertainties, which means that the parameters of the PMSM model in the simulation are the same as the values represented in Table 1. The corresponding results are shown in Fig. 9, in which plot (a) is harmonic currents signals and plot (b) is torque signals. In both two plots, colorized lines stand for reference signals while grey lines represent feedback signals. We can find during the 0–4 s, when the harmonic injection system only controlled with voltage \({u}_{\alpha \beta }^{1}\), all the feedback harmonic currents have bad tracking performance, and the instantaneous feedback torque has large torque ripple. During the 8–15 s, when the feedback controller of harmonic currents is added to the control system, although all the feedback harmonic currents can track the reference currents at last, but it takes a long time to adjust and has obvious overshoot. Thus the corresponding feedback torque has a large torque ripple at the start of the torque step, but the torque ripple can reduce gradually soon afterward. During the 4–7 s, when the feedforward harmonic voltages are added to the control system, we find that the feedback harmonic currents can track the reference currents precisely without overshoot and steady-state error. Meanwhile, the feedback torque has a small torque ripple all the time.

Table 1 Parameters of PMSM
Full size table

The results in Fig. 9 have demonstrated the strong effect of feedforward harmonic voltages for harmonic currents injection when there are no parameter uncertainties. However, the parameters of PMSM cannot keep constant in the real e-drive system because of core saturation. Thus the control effects with parameter uncertainties should be considered. Then another simulation is established, in which the parameters (\({R}_{s}\), \({L}_{d}\), \({L}_{q}\)) used for PMSM model in the simulation are 0.8 times as parameters are shown in Table 1. And the latter three control sorts in Table 2 are compared, shown in Fig. 10. As the feedback controller of harmonic currents does not rely on the parameters of PMSM, so the control effect of harmonic currents is similar to the results without parameter uncertainties. In contrast, the control effect with feedforward harmonic voltage has some decrease because of the inaccuracy parameters. A similar decrease also appears on the torque ripple reduction effect. However, during 4–8 s, when both feedback and feedforward controller is added to the system, we find that although there is some slight deviation between reference currents and feedback currents at the beginning, the feedback currents can track the reference currents well in 1.5 s. Thus, although the parameter uncertainties are existing, the torque ripple with this control sort still keeps slight in both transient process and steady-state.

Table 2 Four different control sorts
Full size table
Fig. 9
figure 9

Simulation results at 1000 r/min with three different control sorts:①, ③, ② without parameter uncertainties: (a) harmonic currents response; (b) torque response

Full size image
Fig. 10
figure 10

Simulation results at 1000 r/min with three different control sorts: ③, ④, ② with parameter uncertainties: (a) harmonic currents response; (b) torque response

Full size image

To illustrate the effectiveness at different speeds, a comparison between control sort ② and sort ④ at 200 r/min is carried out, as shown in Fig. 11. The difference of dynamic response between two control sorts is reduced. For the sort ②, only a slight overshoot appears at the response of id11th, and no large torque ripple emerges in the torque step process. But the performance of control sort ④ is still better by adding the feedforward harmonic voltages. The reason for the smaller difference is because that the feedforward harmonic voltages needed at low speed are less than the voltages at high speed. Thus, we can deduce that the feedforward harmonic voltages are more essential in the control of harmonic currents at a higher speed.

Fig. 11
figure 11

Simulation results at 200 rpm with three different control sorts: ③, ④, ② with parameter uncertainties: (a) harmonic currents response; (b) torque response

Full size image

5 Experimental Results

A test bench with a high precision torque transducer is showed in Fig. 12.

Fig. 12
figure 12

Test bench

Full size image

The real-time ripple can be obtained precisely from the torque transducer. Besides, the harmonic currents are extracted in the embedded PMSM control system and transmitted to the PC through a CAN device. The parameters of the test motor in the test bench and the control system are consistent with the values shown in Table 1. But we must know that the parameters of PMSM are variable in different operating points. Thus the control system of the experiment is a system with parameter uncertainties.

Due to the limitation of our test bench’s maximum power, the desired torque is reduced from 50 to 10 Nm and the motor’s working speed is changed from 1000 to 200 r/min. As shown in Eq. (20), with the motor speed increasing, the harmonic voltages induced by stator resistance can be ignored, and then the amplitude of harmonic voltages will be proportional to the motor speed. When injecting the same harmonic currents, the needed harmonic voltages at 1000 r/min will be almost 5 times the harmonic voltages at 200 r/min. And then the difference of control performance with or without feedforward harmonic voltages control will be larger at 1000 r/min. Thus, if the bench test can validate the effectiveness with feedforward harmonic voltages control at 200 r/min, the performance improvement at 1000 r/min must be higher and the validity can be guaranteed.

All four control sorts are tested in the experiments. The corresponding harmonic currents and torque ripple results are shown in Figs. 13 and 14. Although the working condition of experiments is different from the simulation, we can find that the trend of experiment results is consistent with the previous simulation results. With control sort ①, all the feedback harmonic currents cannot track the referenced currents. For the control sort ③, because of the parameter’s inaccuracy, only the 11th harmonic currents track their referenced value, and obvious steady tracking errors have appeared in both 13th harmonic currents. Thus, the torque ripple of control sort ③ has been reduced partially.

Fig. 13
figure 13

Experimental results of harmonic currents with four different control sorts

Full size image
Fig. 14
figure 14

Experimental results of torque signal with four different control sorts in time domain

Full size image

Both the control sort ② and ④ can eliminate the tracking errors in steady-state, leading to the torque ripple reduction obviously after 2 s. But for the dynamic response time, by adding the feedforward harmonic voltages module, the sort ④ shows an apparent advantage comparing to sort ②. In the figure of harmonic currents responses, the dynamic response times of sort ② and sort ④ are 3.43 s and 1.38 s respectively. However, in the figure of torque responses, the dynamic response time of control sort ② is almost the same as the time of harmonic currents, but the response time of control sort ④ is only 0.12 s. The reason for the difference is the delay of the lowpass filter in the harmonic currents extraction process. Thus, the response of torque ripple can describe the real dynamic tracking performance of harmonic currents, which means the tracking speed of control sort ④ is about 28 times of the control sort ②.

To analyze the torque ripple reduction results during steady-state (the last second in Fig. 14) of different control sorts more effectively, take Fast Fourier Transformation (FFT) on the torque signals above, then the bar graphs of torque in the frequency domain are obtained, shown in Fig. 15. By choosing the electric speed of PMSM as fundamental frequency, the abscissa represents the order of the harmonics of torque ripple. The 12th harmonic is the main component of torque ripple. Thereby, the results of the 12th harmonic can be used to illustrate the torque ripple reduction effect. Compared to the first control sort, the torque ripple of the second and fourth control sorts is very close, declining to about 12.7% and 8.5% respectively, and the torque ripple reduction effect of the third control sort is relatively small, about 32.4%.

Fig. 15
figure 15

Experimental results of torque signal with four different control sorts in frequency domain

Full size image

6 Conclusions

This paper proposes a novel harmonic voltages model with considering the positive and negative harmonic currents simultaneously. The model reveals the coupling relationship between positive–negative harmonic currents and voltages and lays the foundation for developing the model-based control method for harmonic currents injection. Moreover, a harmonic currents injection system by adding a feedforward harmonic voltages module is established and tested through simulation and experiments. The results show that the feedforward harmonic voltages can improve the dynamic tracking speed of harmonic currents tracking largely, with 28 times of the traditional feedback control, which improves the torque ripple reduction performance significantly in the dynamic process. Besides, the parameter uncertainties control system is discussed. At that moment, the rapid tracking of harmonic currents in the transient process is guaranteed by the feedforward harmonic voltage, while the tracking error in steady-state is eliminated by the feedback harmonic currents controller.