1 Introduction

Wind energy is receiving more and more attention as a reusable clean energy source. With the construction and advancement of a low-carbon clean, efficient and safe modern energy system, the health status of wind turbines [1, 2] and their wind energy conversion efficiency become particularly important. Among them, the blade control is closely related to the conversion efficiency of wind energy. At present, the blade control has also experienced fixed pitch stall control, to unified variable pitch control, and then to the current mainstream individual pitch control [3, 4]. Individual pitch control, as the most commonly used method, is designed to smooth the output power of wind turbines [5, 6] and reduce the cyclic load of wind turbine blades, towers and other components [7]. The individual variable pitch control system, as one of the three major control systems for wind turbines, is responsible for stabilizing the output power of the wind turbine and suppressing the vibration of blades, towers and other components. To improve the reliability of the individual pitch and reduce its failure rate, it is necessary to explore integrate scientific issues of the wind turbine's individual pitch system including the driving components, transmission structure, control system and other elements.

PMSM and its speed regulation technology have been widely used in wind turbines [8, 9], equipment manufacturing [10, 11], electric vehicles [12, 13] and marine ships [14]. Therefore, a new direct-drive variable-pitch transmission structure driven by a PMSM is proposed in this paper. The permanent magnet direct drive system has the advantages of high efficiency, energy saving, high power density, simple transmission chain, flexible regulation, low vibration and low noise [15, 16], which can effectively reduce the failure rate of the individual pitch drive system. Vector control is currently the most commonly used control scheme for PMSM. Based on vector control, the three closed-loop control structure in the PMSM position control system [17] has one more speed closed loop than the commonly used double closed-loop structure. The speed closed loop improves the accuracy of speed regulation, so the three closed loop structure is more suitable for the pitch control system that requires movement trajectory. PMSM position servo control has many control objects. The system model, load torque, etc. have an important influence on the control accuracy. Because the wind turbine blade load is relatively special, its control method is somewhat different from the common position control. At present, many scholars have conducted research in the field of individual pitch control strategies. E. A. Bossanyi [18] for the first time formally proposed a method for suppressing blade vibration using individual pitch control, thus starting the study of individual pitch control. Sandquist et al. [19] proposed an individual pitch controller based on the concept of multivariate linear quadratic Gaussian to reduce the load of megawatt wind turbines. The simulation results show that IPC control is more effective in reducing blade load. Liu et al. [20] proposed a vibration reduction strategy for large-scale variable-speed wind turbines based on pitch control and torque control. Ren et al. [21] designed an extended order and disturbance observer to estimate and compensate unknown time-varying nonlinearities and disturbances, and studied a pitch controller based on nonlinear PI. Van et al. [22] proposed an advanced pitch angle control strategy based on fuzzy logic for variable speed wind turbines. The output power and speed of the generator is used as the control input variables of the fuzzy logic controller. To overcome the uncertainty of wind turbine modeling and wind speed curve, Asgharnia et al. [23] proposed two advanced controllers, called fuzzy PID and fractional fuzzy PID, to improve the performance of pitch control. Yin et al. [24] proposed a variable displacement pump-controlled pitch system to mitigate load fluctuations in wind turbine generator power and flap direction. Lasheen A et al. [25] introduced the design of discrete-time L1 adaptive controller for centralized pitch control of variable-speed variable-pitch wind turbines. In the reference [26], a new adaptive control strategy was developed for pitch control of wind turbines. In addition, the current sliding mode control [27, 28], adaptive control of nonlinear system [29,30,31] can also provide reference for individual pitch system. Although there are many researches on independent pitch control, few of them consider the actual operation characteristics of load. On the other hand, most of the current research is still using double closed-loop control.

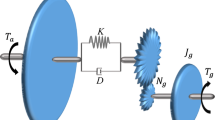
On the basis of existing research, to further improve the reliability and stability of the individual pitch system, combined with the load characteristics of the pitch, a variable-pitch transmission structure directly driven by a PMSM is proposed, and a three-closed-loop position control system that meets the requirements of variable-pitch control, especially the speed loop, is designed. The permanent magnet direct drive individual variable pitch control method is proposed. The linear auto disturbance rejection controller and the extended state observer are constructed. The permanent magnet direct drive individual variable pitch control simulation platform and experiment platform were built to explore the individual variable pitch control performance of the wind turbine directly driven by the PMSM. The control effect of the designed speed controller is verified. The research results are of great significance for improving the performance of individual pitch control, improving its dynamic performance, and improving the reliability of the individual pitch system. The individual variable-pitch transmission system of the wind turbine directly driven by the PMSM is shown in Fig. 1, which eliminates the reduction gear between the motor and the actuator.

Fig. 1
figure 1

Individual variable pitch drive system driven by PMSM

Full size image

2 Mathematical Modeling of PMSM

The mathematical model of PMSM must be established before the speed anti-interference controller and state observer are built. PMSM belongs to a complex system of multivariable, strong coupling, nonlinear and time-varying under the stator coordinate axis system. During the operation of PMSM, the stator and rotor are always in relative motion state. Permanent magnet and winding, winding and winding influence each other. The electromagnetic relationship is very complex. Coupled with nonlinear factors such as magnetic circuit saturation, it is very difficult to establish an accurate mathematical model of PMSM. To simplify the mathematical model of PMSM, it is idealized and is derived based on the following assumptions [16]. (1) Ignoring motor core saturation and parameter changes; (2) Inductance changes sinusoidally with rotor position; (3) Stator winding magnetomotive force is symmetrical sinusoidal.

Therefore, the three-phase winding voltage equation of the PMSM in the three-phase stationary coordinate system can be expressed as,

$$\left[ {\begin{array}{*{20}c} {u_{a} } \\ {u_{b} } \\ {u_{c} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {R_{s} } & 0 & 0 \\ 0 & {R_{s} } & 0 \\ 0 & 0 & {R_{s} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {i_{a} } \\ {i_{b} } \\ {i_{c} } \\ \end{array} } \right] + \frac{d}{dt}\left[ {\begin{array}{*{20}c} {\psi_{a} } \\ {\psi_{b} } \\ {\psi_{c} } \\ \end{array} } \right]$$
(1)

where ua、ub、uc are the phase voltages of the three-phase winding; Rs is the stator phase winding resistance; ia、ib、ic are the current of the three-phase winding; ψa、ψb、ψc are the flux linkage of the three-phase winding.

The calculation formula of three-phase winding flux linkage of PMSM is,

$$\left[ {\begin{array}{*{20}c} {\psi_{a} } \\ {\psi_{b} } \\ {\psi_{c} } \\ \end{array} } \right]{ = }\left[ {\begin{array}{*{20}c} {L_{aa} } & {M_{ab} } & {M_{ac} } \\ {M_{ba} } & {L_{bb} } & {M_{bc} } \\ {M_{ca} } & {M_{cb} } & {L_{cc} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {i_{a} } \\ {i_{b} } \\ {i_{c} } \\ \end{array} } \right] + \psi_{f} \left[ {\begin{array}{*{20}c} {\cos \theta_{e} } \\ {\cos \left( {\theta_{e} - 2/3\pi } \right)} \\ {\cos \left( {\theta_{e} + 2/3\pi } \right)} \\ \end{array} } \right]$$
(2)

where Laa、Lbb、Lcc are the self-inductances of the three-phase winding; Mab is the mutual inductance between the A-phase and B-phase, and the other mutual inductance variable symbols have similar meanings; ψf is the flux linkage of the permanent magnet; θe is the electrical angle of the rotor, that is, the angle between the rotor flux ψf and the A-phase winding.

According to the principle of electromechanical energy conversion, the electromagnetic torque Te is equal to the partial derivative of the magnetic field energy storage to the mechanical angular displacement θm, so there is,

$$T_{e} = \frac{1}{2}p_{n} \frac{\partial }{{\partial \theta_{m} }}\left( {i_{a} \psi_{a} + i_{b} \psi_{b} + i_{c} \psi_{c} } \right)$$
(3)

where pn is the number of pole pairs of the PMSM; The relationship between θm and θe is θe = pnθm.

According to Newton's second law, the motion equation of the system is,

$$J_{m} \frac{{d^{2} \theta_{m} }}{{dt^{2} }}{ + }B_{m} \frac{{d\theta_{m} }}{dt} + T_{L} { = }T_{e}$$
(4)

where Jm is the rotational inertia of the system. Bm is the viscous friction coefficient of the system, and TL is the load torque.

The relationship between the input, state and output of the mathematical model in the stator coordinate system is intricate, and the mathematical model in the stator coordinate system is difficult to apply to the dynamic analysis of PMSM. To this end, the coordinate transformation method can be used to transform the physical quantities such as voltage, current, inductance, and flux linkage into a rotating coordinate system, so that the three-phase stator winding is equivalent to a virtual two-phase synchronous rotating winding to realize the excitation current and torque current decoupling. After decoupling, the magnetic flux and torque of the PMSM can be individually controlled, that is, vector control. For the convenience of controller design, according to the relationship between the dq coordinate system and the ABC coordinate system, the coordinates are changed, and the voltage equation in the d-q coordinate system is obtained as,

$$\left[ {\begin{array}{*{20}c} {u_{d} } \\ {u_{q} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {R_{s} + L_{d} \frac{d}{dt}} & { - \omega_{e} L_{q} } \\ {\omega_{e} L_{d} } & {R_{s} + L_{q} \frac{d}{dt}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {i_{d} } \\ {i_{q} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} 0 \\ {\omega_{e} \psi_{f} } \\ \end{array} } \right]$$
(5)

where ud、uq are the voltage of the straight axis and the cross axis respectively; ωe is the electrical angular velocity of the rotor; Ld、Lq are the inductance of the straight axis and the cross axis respectively.

The electromagnetic torque equation in the d-q coordinate system is,

$$T_{e} = \frac{3}{2}p_{n} i_{q} \left[ {i_{d} \left( {L_{d} - L_{q} } \right) + \psi_{f} } \right]$$
(6)

3 Linear Auto Disturbance Rejection Speed Control Strategy

In order to run smoothly, a reasonable anti-interference control strategy must be established. The external input wind speed of the wind turbine is uncertain. Its actual value often deviates from the test value, so the observation of the load torque becomes particularly difficult. The disturbance of the permanent magnet direct drive variable pitch system will have a greater impact on the stable operation of the speed loop. Therefore, to improve the anti-disturbance capability and robustness of the speed control system, while taking into account the simplicity of the controller and the requirement of small calculation, linear auto-disturbance control (LADRC) is adopted to realize the speed control in the three closed-loop control structure.

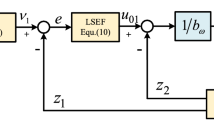
The LADRC system is composed of a linear controller and a linear expansion state observer (LESO). Proportional control can be used as a linear controller, as shown in Fig. 2. The electromagnetic time constant of the PMSM is much smaller than the mechanical time constant of the system motor. The sampling frequency of the current loop is higher than the sampling frequency of the speed loop, so the current loop can be regarded as an ideal controllable current source, that is, the tracking error of iq is not considered.

Fig. 2
figure 2

LADRC speed control block diagram

Full size image

3.1 State Observer Design

LESO is designed first. LESO is the core part of LARDC for uncertain systems. It can be used to observe the state variables and estimate the real-time values of the uncertainties and disturbances of the system model, and then convert the real-time values of the uncertainty and disturbance values of the system model into the extended state of the system. The low order differential signal is obtained by the integral of high order differential signal by using the method of extended dimension integral. The noise signal is greatly suppressed by integral processing. The state variables and their differential values of the system can be observed effectively by LESO. The information can be transmitted to the controller to realize the system stability control.

According to the motion Eq. (4), the first-order motion equation under uncertain load can be described as,

$$\dot{\omega }_{m} = - a_{0} \omega_{m} + w + bi_{q}$$
(7)

where input and output are iq and ωm, w = -TL/Jm + Δw, b = 1.5pnψf/Jm + Δb, a0 = Bm/Jm; Δw、Δb are external unknown disturbances introduced by parameter perturbations such as TL、Bm、ψf.

The actual unknown total disturbance is defined as,

$$f^{\prime} = w + \Delta bi_{q}$$
(8)

To retain the information of known objects, the model of known objects is extended to disturbances. The sum of the unknown total disturbance f’ and the known object -a0ωm is defined as the extension of the disturbance.

$$f = - a_{0} \omega_{m} + f^{\prime}$$
(9)

Therefore, Eq. (7) can be written as,

$$\dot{\omega }_{m} = f + b_{0} i_{q}$$
(10)

where b0 is the known part, and b0 = 1.5pnψf/Jm。

The system disturbance f is expanded into the state variables of the system, so that Eq. (7) can be transformed into the second-order expanded state equation of the object model.

$$\left\{ \begin{gathered} \dot{\user2{x}} = {\varvec{A}}x + {\varvec{B}}u + {\varvec{E}}f^{\prime} \hfill \\ {\varvec{y}} = {\varvec{C}}x \hfill \\ \end{gathered} \right.$$
(11)

where \(u = i_{q}\),\({\varvec{x}} = \left[ {\begin{array}{*{20}c} {\omega_{m} } \\ f \\ \end{array} } \right]\),\({\varvec{A}} = \left[ {\begin{array}{*{20}c} 0 & 1 \\ { - a_{0} } & 0 \\ \end{array} } \right], \, {\varvec{B}} = \left[ {\begin{array}{*{20}c} {b_{0} } \\ 0 \\ \end{array} } \right], \, {\varvec{E}} = \left[ {\begin{array}{*{20}c} 0 \\ 1 \\ \end{array} } \right], \, {\varvec{C}} = \left[ {\begin{array}{*{20}c} 1 & 0 \\ \end{array} } \right]\). In the state equation of the objectless model \({\varvec{A}} = \left[ {\begin{array}{*{20}c} 0 & 1 \\ 0 & 0 \\ \end{array} } \right]\). In contrast, state equations with object models are more informative.

The model-assisted second-order linear expansion state observer corresponding to Eq. (7) is as follows,

$$\left\{ \begin{gathered} \dot{\user2{z}} = \left[ {{\varvec{A}}{ - }{\varvec{LC}}} \right]{\varvec{z}} + \left[ {{\varvec{B}},{\varvec{L}}} \right]{\varvec{u}}_{{\varvec{c}}} \hfill \\ {\varvec{y}}_{{\varvec{c}}} = {\varvec{z}} \hfill \\ \end{gathered} \right.$$
(12)

where z → x, z = [z1 z2]T is the observed state vector; L is the observer error feedback gain matrix to be designed, L = [l1 l2]T; yc is the output of the observer; uc = [u y]T is the input of the observer.

To simplify the design process of LESO, through parameterization, the poles of the characteristic equation of the observer characteristic matrix [A-LC] are placed at the same position -ω0. Let the characteristic polynomial of the observer satisfy,

$$s^{2} + l_{1} s + l_{2} = \left( {s + \omega_{o} } \right)^{2}$$
(13)

Thus, we can get, l1 = 2ω0, l2 = \({\omega }_{0}^{2}\)。

3.2 Controller Design

Then the linear controller is designed. The estimation error of z2 is ignored, that is z2 → f. Thus, the system can be reduced to a first-order integral system,

$$\dot{y} = \left( {f - z_{2} } \right) + u_{0} \approx u_{0}$$
(14)

A simple proportional controller can be used to control u0.

That is,

$$u_{0} = k_{sp} \left( {\omega_{m}^{*} - z_{1} } \right)$$
(15)

where \({\omega }_{m}^{*}\) is the given value of speed. ksp is the parameter of P controller to be designed.

Through the simultaneous Eqs. (10) and (11), the final control signal expression can be obtained as,

$$u = \frac{{u_{0} - z_{2} }}{{b_{0} }}$$
(16)

The parameters l1、l2 are reduced to a parameter ω0 after parameterization, which simplifies the tuning of the gain matrix. Theoretically, the controller can be quickly adjusted through a single adjustment of Ksp. b0 is calculated using the parameters of the system, but in order to improve the control effect, b0 can also be adjusted appropriately according to the actual situation. The convergence speed of LADRC control can be adjusted by Ksp, b0 and ω0. It is found that ω0 has the most obvious effect in debugging. Larger ω0 can accelerate the convergence speed, but it will also increase overshoot.

4 Permanent Magnet Direct Drive Variable Pitch Control Simulation

To verify the effectiveness of the control method, the system is simulated. The variable-pitch load of wind turbines [19, 24] is uncertain, and there is a large sudden load during the pitch process. Therefore, it is necessary to verify the step response performance of the drive system to the sudden load. Based on the principle of vector control, the speed control simulation model was built using Matlab/Simulink, as shown in Fig. 3. The resistance of the PMSM is Rs = 4.95Ω. The inductance of the straight axis is Ld = 149Mh. The inductance of the cross axis is Lq = 180MH. The value of the rotor flux linkage is 8.7Wb, and the LADRC control module is shown in Fig. 4.

Fig. 3
figure 3

LADRC speed control simulation model

Full size image
Fig. 4
figure 4

LADRC control module

Full size image

The total duration of the LADRC control simulation is 0.5 s. The SVPWM switching frequency is 5 kHz. The target speed of the PMSM is set to 15r/min. The motor is started with no load, and a step load with an amplitude of 1000 N m is applied at 0.2 s. To analyze the performance of LADRC speed control, LADRC speed control is compared with PI speed control. The parameters of the LADRC controller are set to Ksp = Kp = 20,000, b0 = 22, ω0 = 110, a0 = 0.9, and the speed and current response curves of the motor are drawn as shown in Fig. 5. Due to the sudden step load disturbance at 0.2 s, the motor speed suddenly dropped by 30%, and then returned to the target value after about 0.1 s. Compared with PI control, LADRC control has stronger anti-abrupt load disturbance ability. It can be seen from the Fig. 5 that the cross-axis and straight-axis current tracking response is fast and the error is small. The target current \({i}_{q}^{*}\) of the cross-axis almost overlaps with the actual current curve iq. Only at the starting time, due to the limitation of the motor current loop bandwidth, there is a lag in the cross-axis current tracking phenomenon.

Fig. 5
figure 5

Speed and current response curves of speed control simulation

Full size image

On the basis of the speed control simulation model, a position controller with feed forward control is added to form a PMSM synchronous vector control simulation model, as shown in Fig. 6, and the control effect of the position controller under individual pitch load changes is simulated.

Fig. 6
figure 6

Pitch angle position following control simulation model

Full size image

Because the driving modes of the three blades are consistent and symmetrical, this section takes the pitch angle of one of the blades following the control process as the research object. Assuming that the initial value of the pitch angle of the wind turbine is 0°, the pitch control is started due to the increase in wind force. The blade moves to the 5° position, and then the individual pitch control is performed. The duration of this simulation is set to 6 s. During the first 1 s, the blades are driven from 0° to 5°. The latter 5 s is the individual pitch control. The entire process limits the pitch angle adjustment speed to no more than 10°/s. In the variable pitch drive structure, the number of teeth of the large gear is 108 teeth, and the number of teeth of the small gear is 11 teeth. Regardless of the gear transmission error and transmission power loss, the target rotation angle curve and the motor load curve of this simulation are calculated according to the transmission ratio, and the rotation angle and speed change curves of the simulation process are drawn as shown in Fig. 7.

Fig. 7
figure 7

Pitch angle position following control simulation curve

Full size image

The curves in Fig. 7 can be returned. After the motor moves to the specified position at a constant speed, it starts to follow the target rotation angle. Even at the moment of sudden torque change, the actual rotation angle maintains a good consistency with the target rotation angle. Since the electromagnetic torque Te cannot respond to the load TL in response to the speed, the motor speed fluctuates for a very short time, but this has little effect on the motor position control accuracy. It can be seen that the position tracking effect based on the speed controller is better.

5 Experimental Verification and Discussions

To further observe the effectiveness of the proposed control method in practical application, the corresponding experimental research is carried out. The change frequency of pitch angle position command is low, which does not have high requirements on the bandwidth of the position controller, but there is a sudden load in the pitch process, and the sudden load will cause the fluctuation of the speed. If the speed controller cannot quickly suppress the fluctuation, the integral of the speed fluctuation with time will bring a rotation angle deviation that cannot be ignored to the system. It can be seen that the speed controller is the most critical of the three closed-loop controllers in the PMSM position control system. Therefore, this section mainly conducts speed control experiments under step load. The permanent magnet direct-drive variable-pitch simulation experiment platform is shown in Fig. 8, which is mainly composed of a PMSM, a coupling, a torque sensor, and a magnetic powder dynamometer. The blade load is simulated by the magnetic powder dynamometer.

Fig. 8
figure 8

Physical diagram of the permanent magnet direct-drive pitch simulation experiment platform

Full size image

The target speed of the motor is set to 15r/min. After the speed is stable, a step signal of 1000 N m is applied through the magnetic particle dynamometer. Since the magnetic particle dynamometer cannot produce negative torque, the negative step is simulated by removing the load of 1000 N m torque signal, after the motor is unloaded and the speed is stable, it will stop freely. The experimental data during the experiment is read by the host computer, and the experimental curves of speed, load, and current are shown in Fig. 9.

Fig. 9
figure 9

Speed response experiment curve of permanent magnet direct-drive variable pitch motor. a Speed of PMSM, b Load toque, c dq axis current

Full size image

Through the experimental curve, it can be found that after starting the drive, the motor speed responds quickly and reaches the target speed. There is almost no overshoot in the speed, and there is a sinusoidal fluctuation after the motor reaches the rated speed. After loading, the speed drops and then quickly returns to the target speed. At this time, the motor response trend is similar to the simulation curve trend; when the unloading speed of the motor suddenly increases, it also quickly recovers; when the free stop is stopped, the motor speed tends to oscillate to zero speed. It can be seen that the speed controller has a good suppression effect on the speed fluctuation caused by the sudden load, and basically meets the control requirements.

In order to further investigate the reason of the speed fluctuation of the motor in the steady state, the FFT transformation is performed on the speed and current in the steady state, and the spectrum chart is shown in Fig. 10. In steady state, the motor speed is 15r/min, which is converted to electrical angle frequency fe = 3 Hz. There are two harmonic components of 2.93 Hz and 18.07 Hz in the speed spectrum chart, which are 1 times fe and 3 times fe, respectively. According to the number of motor slots and the number of pole pairs, the harmonic component of 18.07 Hz comes from the cogging torque ripple. The 2.93hz harmonic component is probably caused by the asymmetry of the winding, which causes the motor torque to fluctuate periodically with fe. There are also two harmonic components of 2.93 Hz and 18.07 Hz in the spectrum diagram of torque current iq. The phase difference of the harmonics of the speed and torque current at 18.07 Hz is calculated by the cross-correlation function. It is found that the speed harmonic phase leads the current iq about 113°. It can be seen that the torque ripple frequency of the PMSM is high, and the speed controller has a tendency to suppress the torque ripple, but it cannot completely suppress the torque ripple. However, due to the small amplitude and high frequency of the harmonic component of the rotating speed, the effect on the position control accuracy after integration is within the allowable range of the pitch angle error. It can provide a reference for further optimization of the speed controller.

Fig. 10
figure 10

Speed and q-axis current spectrum. a Steady state speed spectrum b Current iq spectrum

Full size image

6 Conclusion

This paper proposes a variable-pitch drive system for wind turbines driven by PMSM. In view of the abrupt changes in the pitch load of wind turbines, the control strategy of individual variable-pitch systems for wind turbines driven by PMSM is studied. Based on the LADRC control principle, a linear auto-disturbance speed controller and an extended observer are designed. A speed simulation model is built using Matlab/Simulink, and an individual variable-pitch semi-physical simulation experiment platform is also built. The response performance of the system under sudden load is verified, and the reason for the fluctuation of the motor speed is analyzed. The simulation results show that the designed controller can meet the requirements of pitch angle position follow-up control, and it shows good robustness against the sudden change of pitch load. The individual variable pitch controller designed based on this speed controller has a good position tracking effect. The experiment shows that the semi-physical simulation experiment platform can simulate the variable-pitch drive experiment. The research results can provide a reference for further optimization of the speed controller and the construction of the load simulation platform.

Although the controller has good control effect at present, the phenomenon of instantaneous loss of rotation still exists when the load changes suddenly. In future work, the relevant control algorithms such as sliding mode control and adaptive control will be combined to further optimize the pitch control.