Non-linear free periodic vibrations of variable stiffness composite laminated plates

Abstract

Steady-state free vibrations, with large amplitude displacements, of variable stiffness composite laminated plates (VSCL) are analysed. The intentions of this research are: (1) to find out how the natural frequencies and (mode) shapes evolve with the displacement amplitude in this new type of laminated composite material; (2) to describe modal interactions in VSCL due to energy interchanges under the coupling induced by non-linearity; (3) to compare the VSCL with traditional, constant stiffness, laminated plates. The VSCL of interest here have curvilinear fibres and the numerical analysis carried out is based on a recently developed p-version finite element with hierarchic basis functions. The element follows first-order shear deformation theory and considers Von Kármán’s non-linear terms. The time domain equations of motion are first reduced using the linear modes of vibration and then transformed to the frequency domain via the harmonic balance method. These frequency domain equations are solved by an arc-length continuation method.

1 Introduction

Tow-placement technology is nowadays able to place fibres along curved fibre paths [1, 2]. In this fashion, laminated composite plates with a stiffness that varies in space can be built. Although there are other ways of varying the stiffness of laminated plates [2], we will only consider here variable stiffness composite laminates (VSCL) where variations of the fibre orientation along a lamina are used to change the stiffness. This recent type of material is obviously interesting in applications like aerospace engineering, where the panels may experience vibrations with large amplitude displacements, hence geometrically non-linear.

Possibly the first publications on VSCL are those of Hyer and Lee [3] and of Gürdal and Olmedo [4], who were concerned with buckling and in-plane response. Gürdal and co-workers published a number of other works on this type of material [5–10], addressing buckling, failure and optimization. In [11], the linear modes of vibration of VSCL were investigated by a third-order shear deformation theory. Forced oscillations of VSCL were analyzed in the time domain in [12]. The former references reveal that VSCL plates can indeed show better characteristics than traditional laminates, expand the design space, and deserve attention.

The knowledge of the modes of vibration allows one to better understand and preview the dynamic behaviour of a system. In a linear and conservative system, the mode of vibration is determined by a natural frequency and a mode shape, neither of which changes with the vibration amplitude. This harmonic motion with a constant shape degenerates in a periodic motion with variable shape if one takes into account the effect of geometrical non-linearity [13–16]. Hence, in conservative, geometrically non-linear and continuous systems, free oscillations can be found that are periodic and tend to the linear modes as the displacement amplitude decreases. The natural frequency of the original linear system evolves to become the fundamental frequency of the periodic oscillations and the original “linear mode shape” becomes a shape that changes with the vibration amplitude.

There is an absence of research on non-linear free vibrations of VSCL plates, and this works endeavours to investigate these vibrations. It is here understood that the study of periodic, free non-linear oscillations of conservative VSCL plates is a natural extension of the study of modes of vibration in a conservative, linear VSCL plate. Moreover, we consider that the new, amplitude dependent, shapes, fundamental frequencies, and their harmonics define “non-linear modes of vibration” or modes of vibration of the non-linear structure.

To investigate large amplitude, periodic, free vibrations of conservative variable stiffness laminates a recently developed p-version finite element with hierarchic basis functions, based on first-order-shear deformation theory is presented. We opted for the p-version FEM, not only because of past positive experiences with p-version elements, but also because it fits rather adequately with the curvilinear fibres of the VSCL of interest here. The p-version finite element ordinary differential equations of motion are used to obtain a condensed model, based on a set of linear modes of vibration. The condensed model is then transformed to the frequency domain by the harmonic balance method and a continuation method is employed to solve the frequency domain equations.

2 Formulation

2.1 Equations of motion in the time domain

Following first-order shear deformation theory (FSDT) [14–18], the displacement components in the x, y, and z directions—which are respectively represented by u, v, and w are given by

$$ \everymath{\displaystyle} \begin{array}{@{}l} u(x,y,z,t) = u^{0}(x,y,t) + z\phi_{y}^{0}( x,y,t ), \\[2mm] v( x,y,z,t ) = v^{0}( x,y,t ) - z\phi_{x}^{0}( x,y,t ), \\[2mm] w( x,y,z,t ) = w^{0}( x,y,t ), \end{array} $$

(1)

where u ⁰, v ⁰, and w ⁰ are the values of u, v, and w at the reference surface, and $\phi_{x}^{0}$ and $\phi_{y}^{0}$ are the independent rotations about the x and y axis of lines normal to the middle surface. The origin of the Cartesian coordinate system of reference is at the centre of the undeformed plate; axis x and y define the plate’s middle reference plane. It is noted that, in order to simplify the notation, the dependence of functions on their arguments will be omitted whenever deemed convenient.

In a particular finite element, the middle plane displacement components are written as

$$ \left\{ \begin{array}{c} u^{0} ( \xi,\eta,t ) \\ v^{0} ( \xi,\eta,t ) \\ w^{0} ( \xi,\eta,t ) \\ \phi_{x}^{0} ( \xi,\eta,t ) \\ \phi_{y}^{0} ( \xi,\eta,t ) \end{array} \right\} = \left[ \begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} N^{u} ( \xi,\eta)^{T} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \mathbf{N}^{v} ( \xi,\eta)^{T} & \mathbf{0} & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \mathbf{N}^{w} ( \xi,\eta)^{T} & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{N}^{\phi_{x}} ( \xi,\eta)^{T} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{N}^{\phi_{y}} ( \xi,\eta)^{T} \end{array} \right] \left \{ \begin{array}{c} \mathbf{q}_{u} ( t ) \\ \mathbf{q}_{v} ( t ) \\ \mathbf{q}_{w} ( t ) \\ \mathbf{q}_{\phi_{x}} ( t ) \\ \mathbf{q}_{\phi{y}} ( t ) \end{array} \right\} $$

(2)

where ξ and η represent local coordinates. One p-element only will be used in the applications and, therefore, the following relations hold between local and global coordinates

$$ x = a\xi/ 2, \qquad y = b\eta/ 2 $$

(3)

with a representing the plate length and b the plate width. Vectors N ⁱ(ξ,η) contain the displacement shape functions and vectors q _i (t) the generalized displacements (with i=u,v,w,ϕ _x , and ϕ _y ). The displacement basis functions here used to form vectors N ⁱ(ξ,η) were employed before to analyse traditional isotropic and laminated plates and shells, for example in [14–17, 19], and [20]. The number of membrane, or in-plane, shape functions for each membrane displacement component is $p_{i}^{2}$, the number of transverse displacement shape functions is $p_{o}^{2}$ and the number of shape functions employed for each component of rotation is $p_{\theta}^{2}$.

Using a Von Kármán [21, 22] non-linear strain-displacement relation, one has:

(4)

$$ \begin{array}{@{}l} \boldsymbol{\varepsilon}_{0}^{\mathrm{m}} = \left\{ \begin{array}{c} u_{,x}^{0} \\ v_{,y}^{0} \\ u_{,y}^{0} + v_{,x}^{0} \\ \end{array} \right\},\qquad \boldsymbol{\varepsilon}_{0}^{\mathrm{b}} = \left\{ \begin{array}{c} - \theta_{y,x}^{0} \\ \theta_{x,y}^{0} \\ - \theta_{y,y}^{0} + \theta_{x,x}^{0} \\ \end{array} \right\}, \\[8mm] \boldsymbol{\varepsilon}^{\mathrm{nl}} = \left\{ \begin{array}{c} ( w_{,x}^{0} )^{2} / 2 \\ ( w_{,y}^{0} )^{2} / 2 \\ w_{,x}^{0}w_{,y}^{0} \\ \end{array} \right\} \end{array} $$

(5)

where ε _x ,ε _y are the membrane strain components in the x and y directions and γ _xy the membrane shear strain. Partial derivation is represented by a comma.

The transverse shear strains are given by

$$ \left\{ \begin{array}{c} \gamma_{zx} \\ \gamma_{yz} \end{array} \right\} = \left\{ \begin{array}{c} w_{,x}^{0} + \phi_{y}^{0} \\ w_{,y}^{0} - \phi_{x}^{0} \end{array} \right\} $$

(6)

In the VSCL under analysis here, the common relation between stresses and strains [18, 23, 24] also holds:

(7)

with 1, 2, and 3 representing the directions of the principal material axes x ₁,x ₂ , and x ₃. Due to the fibre curvature, the directions of axis x ₁ and x ₂ vary in each lamina.

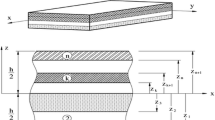
In this study, the orientation of fibres in lamina k is defined, as in [4], by

$$ \theta^{k}( x ) = \frac{2( T_{1}^{k} - T_{0}^{k} )}{a}| x | + T_{0}^{k} $$

(8)

$T_{0}^{k}$ gives the angle between the fibre and the x axis at x=0, and $T_{1}^{k}$ gives this angle at the panel ends (x=±a/2). A layer with curvilinear fibres is represented in Fig. 1. Due to the curvature of the fibres, the transformed reduced stiffnesses $\overline{Q}_{ij}^{k}$ are not constant in each lamina (contrary to traditional composite laminates); instead they are can be defined as follows:

(9)

with constants U _i obeying the following relations:

(10)

The transformed stress-strain relations now read:

$$ \everymath{\displaystyle} \begin{array}{@{}l} \left\{ \begin{array}{c} \sigma_{x} ( x,y,t ) \\ \sigma_{y} ( x,y,t ) \\ \tau_{xy} ( x,y,t ) \end{array} \right\}^{ ( k )} \\[6mm] \quad = \left[ \begin{array}{c@{\quad}c@{\quad}c} \overline{Q}_{11} ( \theta^{k} ( x ) ) & \overline{Q}_{12} ( \theta^{k} ( x ) ) & \overline{Q}_{16} ( \theta^{k} ( x ) ) \\[1mm] \overline{Q}_{12} ( \theta^{k} ( x ) ) & \overline{Q}_{22} ( \theta^{k} ( x ) ) & \overline{Q}_{26} ( \theta^{k} ( x ) ) \\[1mm] \overline{Q}_{16} ( \theta^{k} ( x ) ) & \overline{Q}_{26} ( \theta^{k} ( x ) ) & \overline{Q}_{66} ( \theta^{k} ( x ) ) \end{array} \right]^{ ( k )} \\[9mm] \qquad {}\times\left\{ \begin{array}{c} \varepsilon_{x} ( x,y,t ) \\ \varepsilon_{y} ( x,y,t ) \\ \gamma_{xy} ( x,y,t ) \\ \end{array} \right \}^{ ( k )} \\[8mm] \left\{ \begin{array}{c} \tau_{yz} ( x,y,t ) \\ \tau_{zx} ( x,y,t ) \\ \end{array} \right\}^{ ( k )} = \left[ \begin{array}{c@{\quad}c} \overline{Q}_{44} ( \theta^{k} ( x ) ) & \overline{Q}_{45} ( \theta^{k} ( x ) ) \\[1mm] \overline{Q}_{45} ( \theta^{k} ( x ) ) & \overline{Q}_{55} ( \theta^{k} ( x ) ) \\ \end{array} \right]^{ ( k )} \\[6mm] \hphantom{\left\{ \begin{array}{c} \tau_{yz} ( x,y,t ) \\ \tau_{zx} ( x,y,t ) \\ \end{array} \right\}^{ ( k )} =} {}\times \left\{ \begin{array}{c} \gamma_{yz} ( x,y,t ) \\ \gamma_{zx} ( x,y,t ) \\ \end{array} \right\}^{ ( k )} \end{array} $$

(11)

The equations of motion, in the time domain, can be obtained by the virtual work principle and have the following form:

(12)

In the former equation, superscripts 1–5 indicate the position of each sub-matrix. The mass matrix is constituted by sub-matrices $\mathbf{M}_{\mathrm{k}}^{\mathrm{ii}}$, with k=u,v,w,R _x or R _y , standing, respectively, for membrane in the direction of x, membrane in the direction of y, transverse, rotational about axis x, and rotational about y. The constant stiffness matrix is constituted by sub-matrices of the type $\mathbf{K}_{\mathrm{Lk}}^{\mathrm{ij}}$ , where ; with γ standing for shear and b for bending. Matrices of type $\mathbf{K}_{\mathrm{NL2}}^{\mathrm{ij}}( \mathbf{q}_{\mathrm{w}}( t ) )$ and $\mathbf{K}_{\mathrm{NL3}}^{\mathrm{ij}}( \mathbf{q}_{\mathrm{w}}( t ) )$ depend linearly on the transverse generalized coordinates q _w(t) and matrix $\mathbf{K}_{\mathrm{NL4}}^{33}( \mathbf{q}_{\mathrm{w}}( t ) )$ depends quadratically on these coordinates. The equations of motion have quadratic and cubic non-linear terms, and clearly the system is autonomous.

Fig. 1

Representation of layer with curved fibres

2.2 Model reduction

In periodic oscillations and in the conditions of the numerical tests that will be here carried out, the membrane inertia can usually be neglected [25]. This allows one to obtain the generalised membrane displacements q _u(t) and q _v(t) from the generalised transverse displacements q _w(t), simply using the upper part of Eq. (12). Adding to the fact that a smaller system of equations is obtained in this way, the elimination of the membrane displacements from the main equations of motion is particularly important because the present investigation is in the frequency domain. In fact, it is advisable to use higher harmonics for membrane displacements than for transverse displacements, because for every cycle in the transverse displacements there are two cycles in the membrane ones. Neglecting the membrane inertia allows us to automatically take into account the higher frequency content of the membrane displacements, via the quadratic terms in the transverse displacement (by relations as cos²(ωt)=(cos(2ωt)+1)/2).

The following condensed equations of motion are hence obtained:

(13)

with

(14)

As we will see, the method employed to solve the equations of motion requires a Jacobian matrix. This may be approximately computed numerically, but it is here opted to develop it analytically by using symbolic manipulator Maple [26]. The Jacobian matrix is then saved in a file and used by a FORTRAN code. Therefore, this matrix cannot be too large and it was decided to further reduce the equations of motion (13) by modal reduction, using a subset of the linear mode shapes as a basis.

To the latter end, the linear modes of vibration are computed and matrix Φ _n×m , whose columns are vectors that represent the first m linear mode shapes, is established. The modal coordinates q _m obey the following relation:

$$ \left\{ \begin{array}{c} \mathbf{q}_{w}( {t} ) \\ \mathbf{q}_{\theta_{x}}( {t} ) \\ \mathbf{q}_{\theta_{y}}( {t} ) \end{array} \right\} \cong\boldsymbol{\varPhi}_{{n \times m}}\mathbf{q}_{\mathrm{m}}( {t} ) $$

(15)

An error is expected from using replacement (15) because we will not take all modes into account. It was verified that this error is negligible in a few numerical tests, by carrying out computations using the modal condensed model and the full model. Hence, the subsequent analysis based on the modal reduced models is in general accurate. However, when higher modes are brought to the oscillations, we can expect precision to be lost; in these cases, and at least, the data provides qualitative information. The procedure adopted to choose the number of modes to use in (15) will be explained afterwards.

Pre-multiplying equations of motion (13) by matrix Φ _n×m transposed and using relation (15), one arrives at a reduced set of equations of motion, which will here be represented by

$$ \mathbf{M}\ddot{\mathbf{q}}_{\mathbf{m}}( {t} ) + \mathbf{K}_{\ell} \mathbf{q}_{\mathbf{m}}( {t} ) + \mathbf{K}_{\mathbf{n}\ell}\bigl(\mathbf{q}_{\mathbf{m}}( {t} )\bigr) \mathbf{q}_{\mathbf{m}}( {t} ) = \mathbf{0} $$

(16)

M, K _ℓ and K _{n ℓ} are the mass, the constant, or “linear”, stiffness and the “non-linear” stiffness matrices that result from the modal condensation. These matrices are square, with m rows and columns.

2.3 Transformation into the frequency domain and solution

The harmonic balance method is now applied in order to obtain a set of algebraic equations which depend on the fundamental frequency of vibration and on the coefficients of each harmonic. Since undamped periodic motions are of interest and travelling waves (waves that appear in axisymmetric structures, like circular plates ([27, 28]) are not expected, sine terms are not included in the Fourier expansion.

Because the non-linear terms of the condensed equations of motion (16) are of cubic type, it would be expected that the constant term, here denoted by w _c0 and the even harmonics only play a role in the case of symmetry breaking bifurcations [29]. Nevertheless, a few numerical tests were carried out with a series that included all harmonics (odd and even) until harmonic k. This series had the form

$$ \mathbf{q}_{\mathbf{m}}( {t} ) \cong\frac{1}{2}\mathbf{w}_{\mathbf{c}0} + \sum_{i = 1}^{k} \mathbf{w}_{\mathbf{c}i}\cos( {i}\omega{t} ) $$

(17)

with w _{c i} representing the coefficients of each harmonic and k the number of harmonics. Inserting the truncated Fourier series (17) into Eqs. (16) and applying the harmonic balance method, one obtains a set of algebraic equations where the unknowns are the fundamental frequency of vibration, ω, and the coefficients of each harmonic. The numerical experiments carried out using Eq. (17) indicated that in the solutions of interest in this work, the constant term and the even harmonics do not intervene. Therefore, the following series was preferred:

$$ \mathbf{q}_{\mathbf{m}}( {t} ) \cong\sum _{i = 1}^{2k-1} \mathbf{w}_{\mathbf{c}i}\cos(i \omega t) $$

(18)

and only data obtained with odd harmonics is shown in this paper.

With k=3 and adopting solution (18), the frequency domain equations of motion become

(19)

The non-linear terms, F _{c i} , in the coefficients of the harmonics are defined by Eq. (20)

$$ \mathbf{F}_{\mathbf{c}i} = \frac{2}{T}\int_{0}^{T} \mathbf{K}_{\mathbf{n}\ell} \mathbf{q}_{\mathbf{m}}( {t} )\cos(i\omega{t} ) \,\mathbf{d}t. $$

(20)

with relation (18) holding.

The frequency domain equations of motion are best solved with a continuation method. The method here used is a Newton–Raphson procedure with the distance between two points of the backbone curve employed as the governing parameter [16, 30]. The fact that there are two loops—one for prediction and another for correction—makes the method more computationally reliable then simpler alternatives and the arc-length parameterization allows passing turning points.

3 Numerical tests—variation of natural frequencies and vibration shapes

3.1 Constant stiffness laminate—validation

With the purpose of validating the present model and the computational code developed, and due to the absence of data on free non-linear oscillations of VSCL, comparisons were carried out on constant stiffness laminates. In particular, a laminated plate with the following properties was analysed: h=0.001 m, a=0.480 m, b=0.320 m, ρ=1540 kg/m³, E ₁₁=120.5×10⁹ N/m², E ₂₂=9.63×10⁹ N/m², G ₁₂=3.58×10⁹ N/m², G ₁₃=3.58×10⁹ N/m², G ₂₃=3.58×10⁹ N/m², and ν ₁₂=0.32. These geometry and material properties will be repeatedly employed in this paper. The constant stiffness composite laminated plate (CSCL) has eight layers with fibres oriented as (90,−45,45,0)_sym. The boundaries are always clamped in the numerical tests.

The fundamental frequencies of vibration computed in this work were compared with values from [19, 20], where a p-version finite element based upon classical (thin) plate theory, with 5 out-of-plane and 5 in-plane shape functions, and a one term harmonic balance procedure, was employed. To obtain the reduced models of the present approach, diverse numbers of shape functions were employed, as were different numbers of modes in the modal reduction. In addition, models with either 2 or 3 odd harmonics were used. The present results, with two and three harmonics and diverse numbers of shape functions, were in good agreement with the ones of [19, 20]. As an example, Table 1 shows the non-dimensional, non-linear fundamental frequency of vibration as a function of the amplitude of the first harmonic, W ₁(ξ,η), computed with reduced models that used 11 modes and different numbers of shape functions.

Table 1 Frequency ratios (ω/ω _ℓl ) as function of first harmonic amplitude at point ξ=η=0. CSCL plate

Table 1 indicates that the importance of the higher harmonics is small in the first main branch of solutions and for the amplitudes attained in [19, 20].

In the linear regime, the natural frequencies of VSCL computed with the present first order shear deformation model agreed quite well with frequencies published in [11] where a third-order shear deformation model was applied.

3.2 Variable stiffness composite laminates

3.2.1 VSCL properties

Now the free vibrations of VSCL are explored. The plates considered still have eight layers, are symmetric about their midplane, have the geometric properties of the CSCL plate of Sect. 3.1, and the material constituents are the same. The fibre orientations of the first VSCL plate (VSCL₁) are defined by: [〈45|0〉,〈−45|0〉,〈90|90〉,〈90|90〉]_sym. This has the peculiarity that, in the four clamped boundaries, layers with fibres perpendicular to the boundaries exist. In the second VSCL plate (VSCL₂),T ₁ (which is the fibre inclination at x=±a/2) is in all layers equal to the inclination of the respective layers on the CSCL plate, i.e. T ₁ takes values (90,−45,45,0)_sym. On the other hand, T ₀, only has the orientation of the CSCL in four layers, where the fibre orientation does not vary; in the other four layers, there is a change on the fibre orientation. Specifically, the fibres of VSCL₂ are oriented as follows: [〈90|90〉,〈45|−45〉,〈−45|45〉,〈0|0〉]_sym. In this VSCL, crossings between fibres occur at 90 degrees at the panel ends and at x=0.

Most of the following analysis is focused on VSCL₁ and VSCL₂, presented in the above paragraph; however, results on a few additional VSCL are also presented, in order to better see how the curved fibres may change (or not) the degree of hardening spring. Obviously, there is an enormous range of possible fibre variations. To limit the analysis space and with the goal of establishing a relation between these additional VSCL plates (VSCL₃–VSCL₆), two restrictions are imposed on the fibre variation: (1) all plates have the same fibre inclinations at x=±a/2 in the respective layers, i.e. the values of $T_{1}^{k}$ are the same, and these are the angles of the CSCL of Sect. 3.1; (2) $T_{0}^{k}$ changes according to a single parameter θ and when θ is 45^∘ we fall exactly on the CSCL adopted as a reference here. Therefore, it is imposed that the fibres of the variable stiffness composite laminates VSCL _i , i=3–6, are oriented as [〈(θ+45)∣90〉,〈−θ∣−45〉,〈θ∣45〉,〈(θ−45)∣0〉]_sym, with θ, respectively, taking values [0^∘,22.5^∘,67.5^∘,90^∘] for plates VSCL₃–VSCL₆, in this order.

3.2.2 Modal reduced models

In this sub-section, the procedure employed to select the number of modes and the number of shape functions is described.

The first twelve linear vibration frequencies of VSCL₁ and VSCL₂ are given in Table 2. The mode shapes computed in the linear regime with p _i =12,p _θ =9,p _o =7 (model 1) and p _i =p _θ =p _o =15 (model 2) were compared as well, although the pictures are not shown here. The mode shapes that result from the two models are the same, with the exception of the shape of mode number 9 of VSCL₁, and of the shapes of modes 9, 11, and 12 of VSCL₂, where there is some, but not large, difference.

Table 2 Linear natural frequencies of VSCL plates

We will be interested in analysing what happens with the first mode of vibration as the vibration amplitude increases, and note that in VSCL₁, the first linear natural frequency (ω _ℓ1) multiplied by 3 is about half the 11^th linear natural frequency. This means that the non-linear fundamental vibration frequency (ω _nℓ1) can range almost until 2ω _ℓ1 if only the first and third harmonics are considered and if 11 modes are used in the modal model. With such model it should be possible to correctly detect 1:3 internal resonances [31]. With an 11 modes model, but if the 5^th harmonic is also of interest, then the non-linear fundamental vibration frequency (ω _nℓ1) can go from ω _ℓ1 to almost 1.3ω _ℓ1.

In what VSCL₂ is concerned, the first linear natural frequency (ω _ℓ1) multiplied by 3 is about 1.7 times smaller than the 11^th linear natural frequency. This means that the non-linear fundamental vibration frequency (ω _nℓ1) can range to slightly above 1.7ω _ℓ1 if only the first and third harmonics are important in the analysis and if 11 modes are used in the reduced modal model. Still with the 11 modes model and if the 5^th harmonic is of interest, then the non-linear fundamental vibration frequency (ω _nℓ1) should only go from ω _ℓ1 to about 1.04ω _ℓ1.

Weighting the computational restrictions and the accuracy, it was decided to employ, for all plates, modal models with 11 modes, based on the p _i =12, p _θ =9, p _o =7 p-version finite element. This model is not error free, but the convergence studies carried out indicate that it will generally provide accurate enough information on the vibration behaviour of the diverse VSCL plates. All the following results were computed with a frequency domain model that contains the first, the third, and the fifth harmonics.

3.2.3 Variation of natural frequencies and mode shapes with the vibration amplitude

It is here understood that a “main branch” of solutions is a branch that corresponds to a set of steady-state free vibrations, which includes one solution with near zero vibration amplitude, with one harmonic only, and either occurring at a linear natural frequency or at a linear natural frequency divided by an integer. It results that the modes of vibrations in the linear regime are contained in main branches. All analysis in this paper starts on the particular main branch that contains as a solution the first linear mode associated with the first harmonic, a branch that will be designated as “first main branch”.

Figure 2 shows amplitudes of the first harmonics of the CSCL and diverse VSCL. Only solutions on the first main branch—in effect, solutions which were computed by starting the continuation procedure at the first linear mode of vibration and not following bifurcations—are shown. As expected in these conditions, all plates—either constant or variable stiffness—show hardening.

Fig. 2

Amplitudes of first harmonic at (ξ,η)=(0,0) of: — CSCL, ◊ VSCL₁, + VSCL₂, ∘ VSCL₃, ⧫ VSCL₄, × VSCL₅, ■ VSCL₆

One verifies that the degree of hardening is essentially the same in the constant stiffness laminate (CSCL) and in plate VSCL₂ until the transverse displacement amplitude reaches approximately the plate thickness. These two plates are rather similar, differing solely in T ₀ (fibre orientation at x=0) in four of their eight layers. However, at larger amplitudes, the natural frequency of the CSCL increases more with the first harmonic amplitude than the natural frequency of VSCL₂.

The backbone curve of VSCL₄ is somewhat close to VSCL₂, but with less hardening. The remaining VSCL plates (1, 3, 5, and 6) experience more hardening than the constant stiffness laminate.

To complement the non-dimensional comparison of Fig. 2, the fundamental vibration frequencies in the linear regime of the plates that have the same values of $T_{1}^{k}$ are given in Table 3 (hence the frequencies of VSCL₁ and VSCL₂, which were given in Sect. 3.2.2, are not on Table 3). The frequencies are in rad/s. It is remarkable that plates in the same materials, with the same geometric properties and with the same fibre orientation at boundaries x=±a/2 show so different fundamental frequencies in the linear regime: the variation, in percentage terms and using the lowest value as a reference, is 31 %.

Table 3 Fundamental frequencies (rad/s) in the linear regime of plates [〈(θ+45)∣90〉,〈−θ∣−45〉,〈θ∣45〉,〈(θ−45)∣0〉]_sym

Now we address in more detail plate VSCL₁. In Fig. 3, one can see the amplitudes of vibration of the first, third, and fifth harmonics, as a function of the non-dimensional, non-linear, fundamental vibration frequency of the plate. One verifies that several steady state solutions exist for the same fundamental vibration frequency. The ensuing analysis of the shapes associated with those solutions will lead us to a better understanding of the evolution of the “natural modes of vibration”—the latter designation is employed with the meaning explained in Sect. 1 of this text—and their interaction on this non-linear system.

Fig. 3

Amplitudes at (ξ,η)=(0,0) of harmonics of VSCL₁: (a) first harmonic, (b) second harmonic, (c) third harmonic

Concerning the solutions already shown in Fig. 2 (set of solutions that defines what was called the “first main branch”) of plate VSCL₁, it is verified that the shapes of the first harmonic are similar to the mode shape of the first linear mode of vibration: there is only a small change in these shapes with the vibration amplitude. The shapes of the higher harmonics change more as the natural frequency of vibration increases, but these harmonics are indeed small in this set of solutions and have a minor influence on the actual shape of the plate. Hence, in this “main branch” of the variable stiffness plate, the evolution with the amplitude of the shape assumed during a vibration period is similar to the one that is found in constant stiffness composite laminated plates [15, 19, 20, 31].

Let us now proceed to another set of solutions, pertaining to what is designated in Fig. 3 as “secondary branch 1”. This branch of solutions bifurcates from the so-called “first main branch”, because of the interaction between the first and higher vibration modes, and mainly involves the first and the third harmonic (which grows at the bifurcation point, as shown in Fig. 3(b)). An example of the outcome of this modal interaction in the non-linear regime can be seen in Fig. 4, which shows the shapes assumed by the variable stiffness plate at different instant along half a cycle, when the frequency of the first harmonic is ω=1.024ω _ℓ1. The shape at t/T=π is symmetric, about plane z=0, to the shape at t/T=0. The shapes that are not shown are symmetric to the ones at t/T=π/9, t/T=2π/9 and so on, until the oscillation cycle is completed. Still related with this solution, in Fig. 5, one can see time and phase plots at three points of VSCL₁. The large importance of the third harmonic is obvious in these plots.

Fig. 4

Shapes of VSCL₁ plate along half vibration cycle of solution on the first secondary branch at frequency ω/ω _ℓ1=1.024

Fig. 5

Time (a) and phase (b) plots of solution on the first secondary branch of VSCL₁ at frequency ω/ω _ℓ1=1.024. The original coordinates of the point are: — (x,y,z)=(0,0,0), ∘ (x,y,z)=(a/4,b/4,0), □ (x,y,z)=(a/4,−b/4,0)

The secondary branch that is here designated as “second secondary branch”, is also the result of interaction between the first and higher order modes. This turn, the 5^th harmonic becomes dominant as one proceeds along the secondary branch (see Fig. 3(c), where the sudden growth of the 5^th harmonic is clear) until the plate totally leaves the first mode, and vibrates in its 9^th mode and at the fifth harmonic.

Figure 6 compares the first harmonic of VSCL₂ with the first harmonic of the constant stiffness plate CSCL. The computations were started at the first linear mode of vibration and bifurcating branches were followed, leading to several solutions for the same fundamental frequency. As already seen in Fig. 2, in the main branch of both plates the more important harmonic is, by far, the first. In this branch and in the frequency range portrayed, the difference in the hardening degrees experienced by the two plates is minor. But there is a marked difference in the additional solutions which occur under modal interactions and associated bifurcations. The latter interactions are due to the non-linearity and involve higher harmonics and higher modes; since the higher modes of VSCL₂ differ from the ones of the CSCL, the dynamics of the two plates can become very different from each other at large amplitude vibrations. It is reminded that the fibre orientation at the boundaries x=±a are the same in the two plates; the different behaviour in the non-linear regime results solely from the fact that four layers (i.e., a half of the layers) of the variable stiffness plate have curved fibres. A large number of branches were found in VSCL₂ and these were included in Fig. 6 in order to show the rich dynamics that can occur. However, because these solutions involve higher order modes and higher harmonics, their numerical accuracy may not be guaranteed by the reduced order model employed.

Fig. 6

Amplitude of first harmonic at (ξ,η)=(0,0) of CSCL, □, and of VSCL₂, +

4 Conclusions

A reduced order model for free, periodic vibrations of variable stiffness composite plates was introduced. The model was applied with success in validation tests, where results were compared with published data. Our conclusion is that it is rather safe to use the reduced model to analyze low order modes, and that it can provide useful information in the presence of higher modes. Then an investigation on the non-linear, periodic, free vibrations of one constant and of several variable stiffness plates was carried out. The constitutive materials of all plates are the same, and all plates have the same geometry, dimensions, and number of layers. This allowed us to understand how curvilinear fibres alone can affect the evolution of the modes of vibration with the vibration amplitude.

It was verified that even small changes in the way the fibres are oriented along the layers can lead to changes not only in the linear modes, but also in the degree of hardening spring effect. In one of the numerical tests, a constant stiffness laminate (CSCL) and a variable stiffness laminate designated as VSCL₂ were compared; the only distinction between these plates is that the fibres have different orientation at x=0 (middle length) in half of the layers. The first linear natural frequency of the two plates differs less than 6 % and the rate of hardening with the vibration amplitude is very similar until about the plates’ thickness. But the way, the first harmonic amplitude increases when it exceeds the plate thickness is visibly different in the two plates. In a set of tests that complements the former, the fibres of several plates had the same orientation when x=0, but changed in different degrees until the plate borders x=±a/2 (plates CSCL and VSCL _i , i=3–6). Here, a variation of 31 % was found in the fundamental frequency in the linear regime, and different hardening degrees occurred in the diverse plates. Finally, another variable stiffness plate was the one where the hardening effect was stronger. This plate, designated as VSCL₁, had the same constitutive materials and dimensions as the other plates; its distinctive characteristic is that in the four clamped boundaries fibres perpendicular to the boundary exist.

Secondary branches that result from modal interactions were followed in the reference constant stiffness and in two variable stiffness laminated plates. It was found that apparently small design changes, like slightly changing the fibre orientation in the plate domain and not changing the orientation at the boundaries, can lead to very different dynamic behaviours in the non-linear regime. One can, for example, avoid or (if one so wishes) promote modal interactions.