1 Introduction

Plates, as one of the most practical structures, have gained great importance these days, so that their applications can be observed abundantly in engineering practices, such as aircraft and shipbuilding factories, automobiles, and train cabins. What is of much importance is to identify cracks created in the structure, since the existence of even a small crack can cause failure and reduce the permanence of the structure, dramatically. Therefore, it is necessary to be presented some models in order to inspect such defects. Many authors have presented analytical models for crack plates. For example, Rice and Levi [1] introduced line spring model for analysis of a part-through surface crack at the center of an isotropic plate. Their model was based on a two-dimensional theorem of plates and shells, which was a threshold and analytic method for solving cracked plate problems. Therefore, Israr et al. [2,3,4] developed Rice and Levi’s model [1] to investigate the nonlinear vibration of a centrally cracked plate. Both stretching and bending compliances of the crack were considered into the problem, so that stretching compliance would essentially lead to nonlinear terms. Additionally, the crack directly had a significant effect on the stiffness of the structure. Yang et al. [5], based on Reddy’s third-order shear deformation plate theory, derived governing equations in regard to linear and nonlinear vibration of an FGM plate containing only a horizontally overall surface crack. Despite the examination of the position and depth of the crack, they avoided investigating the effect of the crack angle as well as the crack size on the natural frequencies. Subsequently, in order for Israr’s method to be more practical, this method was extended by Ismail and Cartmell [6] for various crack angles at the plate center. The obtained results showed that with considering the plate under uniaxial load, the fundamental frequency of the vertical cracked plate is the same as that of an intact one. Following the previous research, Bose and Mohanty [7], based on the modified line spring model, developed nonlinear vibration of a plate including a part-through surface crack at an arbitrary position and angle by supposing that a biaxial load was exerted to the plate. Unlike the results achieved by Ismail and Cartmell [6], the fundamental frequency of the vertical cracked plate was not the same as that of intact one due to considering biaxial load. In another research, following Israr’s work, a plate having two internal perpendicular cracks was studied by Joshi et al. [8]. They indicated that maximum and minimum reduction of the plate stiffness could occur when the cracks were, respectively, internal and external. Diba et al. [9], by considering more vibration modes and the proposed model by Ismail and Cartmell [6], extended the nonlinear dynamic response of a simply supported cracked plate. Joshi et al. [10] expanded their work to present the nonlinear vibration of a cracked orthotropic plate for different boundary conditions. It was revealed that a crack parallel to the fibers had less effect on the natural frequencies in comparison with a crack perpendicular to the fibers. Moreover, Joshi et al. [11], Azizi et al. [12], and Safaei et al. [13, 14] also considered thermo-mechanical loads in the governing equations to extend their research for a micro-plate, nano-platelet, and sandwich plate, respectively.

Most of the vibration analysis is devoted to investigating structures in the absence of fluid [15, 16]. Nevertheless, dynamic responses of engineering structures are influenced by environmental fluid surrounding these structures. One of the main areas used to simulate solid–fluid interaction is the plate–cavity system which has gained extensive attention in industries. Vibroacoustic characteristics of structures via such a model have been investigated by many researchers. Pretlove [17] considered a plate coupled with a rectangular cavity. In order for the problem to be solved, he expressed the acoustic modes in terms of an arbitrary plate mode estimated by Fourier transform, thereby reducing the coupled problem into an uncoupled one. Subsequently, the first four natural frequencies of the system were obtained with a suitable precision. Moreover, he evaluated the effect of the cavity depth and revealed that the parameter was effective just for low-frequency domain. Following the previous research, Quisi [18] studied a rectangular plate interacting with an enclosure by considering a few numbers of acoustic modes in terms of the plate displacement. A reflected spherical wave off an infinite plate–cavity was studied by Nakanishi et al. [19]. In another work, Lee [20] inspected large amplitude vibration of a backed plate, by the aid of the Harmonic Balance Method. In addition, Lee et al. [21] extended the previous research for a composite plate, as one of the most practical materials in industries [22,23,24], and presented a method which did not need the nonlinear matrix to be updated. Li and Cheng [25, 26] examined acoustical behavior of a plate and enclosure comprising an inclined wall, which disclosed that such a system had different modal features. Gorman et al. [27] analyzed different geometry of a plate–cavity system. In their work, a circular plate was evaluated which was in contact with a fluid inside a cylindrical cavity. To obtain coupled natural frequencies, they applied the Galerkin method along with modal energy analysis. Sound transmission through another various structure containing a double–walled panel and a cavity was studied analytically by Xin et al. [28,29,30]. First, research was conducted for a clamped panel. Then, in another research, analytical results were compared with experimental ones. In following their research, the same procedure was also done for a triple-walled structure. Also, Xin et al. [31] presented the wave propagation analysis in a sandwich structure making up of a double plate with corrugated core. Hui et al. [32] employed the elliptical integral solution to evaluate the nonlinear vibration of a plate backed by a multi-acoustic mode cavity. They investigated the convergence criterion to obtain appropriate acoustic mode. Natural frequencies of an interacting plate–cavity system were examined differently by Tanaka et al. [33]. They presented eigenfunctions of sound pressure in terms of an infinite summation of degenerate eigenfunctions. Shen et al. [34] inspected effective parameters in order to diminish transmitted noise through a sandwich panel in contact with a fluid inside an enclosure. The obtained results showed that some parameters such as core damping, viscoelastic core density, and the plate thickness were of great importance for noise reduction. In following nonlinear problems, Sadri and Younesian [35, 36] considered the free and force nonlinear vibration of a rectangular plate inside an air cavity. First, to obtain the harmonic response of such a coupled system, they supposed an arbitrary transverse excitation force exerted to the plate. Then, the multiple-scale method was utilized to solve nonlinear equations. Furthermore, they analyzed free oscillation of such a coupled system by means of variational iteration method. In addition, they continued their work to investigate the random vibration of a platform modeled by a backed plate [37]. Through this model, it was revealed that the more irregular the track is, the more significant influence it has on the vibrational behavior and acoustical pressure inside the cabin. The interaction between a rectangular cavity and a plate containing a distributed mass was examined by Pirnat et al. [38]. They were able to reduce the complexity of obtaining mode shapes and coupled frequencies by employing some analytical models based on the Rayleigh–Ritz method. Bose and Mohanty [39] applied corner functions to model a side crack in a rectangular plate and study the transmitted sound through the structure. Sadri and Younesian [40], in another work, represented free and force responses of a sandwich panel considered as two plates connected via springy layer. Free vibration analysis of an extended cavity coupled with a nonlinear plate was investigated by Lee [41]. He determined the cavity length as an effective parameter on the nonlinear fundamental frequency, so that increasing the cavity length results in a remarkable reduction in the nonlinear frequency. Lee [42], in continuation of his research, assessed leakage effect on the nonlinear fundamental frequency at the edges of an enclosure. He concluded that with enlarging the leakage size, the higher fundamental frequency would be obtained. Vibroacoustic behavior of a plate and an acoustic irregular cavity including a tilted wall was investigated by Chen et al. [43]. Such a structure was evaluated for elastic boundary conditions by disassembling the irregular enclosure into some sub-cavities. A study on the vibration characteristics of a partially opened enclosure interacting with an isotropic plate was also conducted by Shi et al. [44]. The results showed that a considerable effect on the vibroacoustic behavior of the system was observed due to the opening size. An investigation of effective parameters on vibroacoustic behavior of a composite plate inside a cavity, such as numbers of layers, ply angles, and constitutive materials, was carried out by Sarigul and Karagozlu [45]. Additionally, their results indicated that the cavity had more effect on a plate involving elastic materials and fewer layers. Zhang et al. [46] continued the previous work and carried out linear analysis of a double composite plate for elastic boundary conditions. The authors [47] examined the linear analysis concerned with the acoustical interaction between a cracked plate and an air enclosure for different parameters. Nevertheless, in some cases, nonlinear phenomena predominate where the large deflections are of high importance. Therefore, in the present paper, the nonlinear behavior of a cracked plate–cavity is developed.

Reviewing the above literature indicates that either the vibration of cracked plates has been studied without considering solid–fluid interaction or the vibroacoustic behavior of plates without considering any defects has been investigated. As a result, it can be concluded that nonlinear analysis of a cracked plate coupled with an enclosure has not been studied so far. Herewith, in this research, a new approach is considered to inspect the nonlinear structural–acoustic coupling for a rectangular box including an arbitrary part-through surface crack. In the first step, a coupled nonlinear equation of the cracked plate surrounded by the cavity is introduced. Later, using eigenfunction expansion, the coupled nonlinear equation is converted to the time domain. Then, the Euler equation is employed in order to model the air and the cracked plate interaction. Hence, the coupled equations can be changed to uncoupled equations. By considering the linear parts of the equations, firstly linear natural frequencies are calculated. In the next step, the first iteration of VIM is used to compare such a method with available literature concerning the nonlinear vibration of an intact plate coupled with a cavity. Likewise, four steps of variational iteration method are employed for the cracked system and three different boundary conditions, in order that the convergence of the nonlinear frequencies can be obtained. Moreover, three and four-dimensional backbone curves are plotted to clarify the influence of the crack direction, position, and length on nonlinear natural frequencies for all kinds of boundary conditions. Finally, the effect of the cavity depth on the cracked frequency ratio is also evaluated.

2 Governing equation of motion

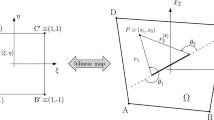
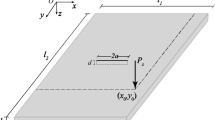
Figure 1 shows an enclosure coupled with an isotropic plate including a part–through surface crack at an arbitrary location and angle. The Cartesian coordinate is used to describe dimensions of the system, and stagnated air is considered inside the enclosure. The system is made up of five rigid walls and an elastic plate with a length of L1, width of L2, and thickness of h as well as a cavity with a depth of L3. In addition, the crack angle and length are represented by θ and 2a, and the distance between the crack center and the plate center is illustrated by dc along the x-direction. Therefore, the governing vibration equation of such a system, based on proposed relation for a cracked plate at different orientations and locations, is presented as follows [7]:

$$\begin{aligned} & \left( {1 - J_{10} } \right)\frac{{\partial^{4} W}}{{\partial x^{4} }} + \left( {2 - J_{12} } \right)\frac{{\partial^{4} W}}{{\partial x^{2} \partial y^{2} }} + \left( {1 - J_{11} } \right)\frac{{\partial^{4} W}}{{\partial y^{4} }} + \frac{\rho h}{D}\frac{{\partial^{2} W}}{{\partial t^{2} }} = \frac{{\left. {P(x,y,L_{3} ,t} \right)}}{D} \\ & \quad + \frac{{N_{x} }}{D}\left[ {\begin{array}{*{20}c} {J_{1} \frac{{\partial^{2} W}}{{\partial x^{2} }} + J_{2} \frac{{\partial^{2} W}}{{\partial y^{2} }}} \\ { + 2J_{3} \frac{{\partial^{2} W}}{\partial x\partial y}} \\ \end{array} } \right] + \frac{{N_{y} }}{D}\left[ {\begin{array}{*{20}c} {J_{5} \frac{{\partial^{2} W}}{{\partial x^{2} }} + J_{4} \frac{{\partial^{2} W}}{{\partial y^{2} }}} \\ { + 2J_{6} \frac{{\partial^{2} W}}{\partial x\partial y}} \\ \end{array} } \right] + \frac{{N_{xy} }}{D}\left[ {\begin{array}{*{20}c} {J_{8} \frac{{\partial^{2} W}}{{\partial x^{2} }} + J_{9} \frac{{\partial^{2} W}}{{\partial y^{2} }}} \\ { + 2J_{7} \frac{{\partial^{2} W}}{\partial x\partial y}} \\ \end{array} } \right] \\ & \quad - \left( {\frac{{\partial^{2} W}}{{\partial x^{2} }} + \upsilon \frac{{\partial^{2} W}}{{\partial y^{2} }}} \right)\left[ {\begin{array}{*{20}c} {J_{13} \frac{{\partial^{2} W}}{{\partial x^{2} }} + J_{14} \frac{{\partial^{2} W}}{{\partial y^{2} }}} \\ { + 2J_{15} \frac{{\partial^{2} W}}{\partial x\partial y}} \\ \end{array} } \right] - \left( {\frac{{\partial^{2} W}}{{\partial y^{2} }} + \upsilon \frac{{\partial^{2} W}}{{\partial x^{2} }}} \right)\left[ {\begin{array}{*{20}c} {J_{16} \frac{{\partial^{2} W}}{{\partial x^{2} }} + J_{17} \frac{{\partial^{2} W}}{{\partial y^{2} }}} \\ { + 2J_{18} \frac{{\partial^{2} W}}{\partial x\partial y}} \\ \end{array} } \right] \\ & \quad - \left( {1 - \upsilon } \right)\frac{{\partial^{2} W}}{\partial x\partial y}\left[ {\begin{array}{*{20}c} {J_{19} \frac{{\partial^{2} W}}{{\partial x^{2} }} + J_{20} \frac{{\partial^{2} W}}{{\partial y^{2} }}} \\ { + 2J_{21} \frac{{\partial^{2} W}}{\partial x\partial y}} \\ \end{array} } \right] + J_{22} \frac{{\partial^{4} W}}{{\partial x^{3} \partial y}} + J_{23} \frac{{\partial^{4} W}}{{\partial x\partial y^{3} }} \\ \end{aligned}$$
(1)

where Eq. (1) indicates nonlinear vibration equation of the system in which W(x, y, t), P(x, y, L3, t), ρ, and D are transverse displacement, acoustic pressure inside the cavity, density, and flexural rigidity of the plate, respectively. In addition, Nx, Ny, and Nxy are in-plane forces per unit length along x, y, and xy plane. Moreover, Jn (n = 1, 2, …23) are coefficients which are related to the presence of the crack and defined in Appendix 1. Here, in order for Eq. (1) to be achieved, it should be changed to the time domain. Hence, in order to be employed the Galerkin method, the displacement can be assumed as below:

$$W\left( {x,y,t} \right) = \mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } w_{mn} \left( t \right)X_{m} \left( x \right)Y_{n} \left( y \right)$$
(2)
Fig. 1
figure 1

A plate–enclosure system containing a surface crack

Full size image

Accordingly, by substituting Eq. (2) into Eq. (1), it can be deduced as follows:

$$\begin{aligned} & \mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } \left\{ {\left( {1 - J_{10} } \right)X_{m}^{\left( 4 \right)} Y_{n} + \left( {2 - J_{12} } \right)X_{m}^{\prime \prime } Y_{n}^{\prime \prime } + \left( {1 - J_{11} } \right)X_{m} Y_{n}^{\left( 4 \right)} } \right\}w_{mn} \left( t \right) \\ & \quad + \mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } \frac{\rho h}{D}X_{m} Y_{n} \ddot{w}_{mn} \left( t \right) = \frac{{P\left( {x,y,L_{3} ,t} \right)}}{D} + \mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } \left\{ {J_{22} X_{m}^{'''} Y_{n}^{'} + J_{23} X_{m}^{'} Y_{n}^{'''} } \right\}w_{mn} \left( t \right) \\ & \quad - \mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } \left\{ {X_{m}^{''} Y_{n} + \upsilon X_{m} Y_{n}^{''} } \right\}w_{mn} \left( t \right) \times \mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } \left\{ {\begin{array}{*{20}l} {J_{13} X_{m}^{''} Y_{n} + J_{14} X_{m} Y_{n}^{''} } \hfill \\ {\quad + 2J_{15} X_{m}^{'} Y_{n}^{'} } \hfill \\ \end{array} } \right\}w_{mn} \left( t \right) \\ & \quad - \mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } \left\{ {\upsilon X_{m}^{''} Y_{n} + X_{m} Y_{n}^{''} } \right\}w_{mn} \left( t \right) \times \mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } \left\{ {\begin{array}{*{20}l} {J_{16} X_{m}^{''} Y_{n} + J_{17} X_{m} Y_{n}^{''} } \hfill \\ {\quad + 2J_{18} X_{m}^{'} Y_{n}^{'} } \hfill \\ \end{array} } \right\}w_{mn} \left( t \right) \\ & \quad - \left( {1 - \upsilon } \right)\mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } X_{m}^{'} Y_{n}^{'} w_{mn} \left( t \right) \times \mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } \left\{ {\begin{array}{*{20}l} {J_{19} X_{m}^{''} Y_{n} + J_{20} X_{m} Y_{n}^{''} } \hfill \\ {\quad + 2J_{21} X_{m}^{'} Y_{n}^{'} } \hfill \\ \end{array} } \right\}w_{mn} \left( t \right) \\ & \quad + \frac{{N_{x} }}{D}\mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } \left\{ {\begin{array}{*{20}l} {J_{1} X_{m}^{''} Y_{n} + J_{2} X_{m} Y_{n}^{''} } \hfill \\ {\quad + 2J_{3} X_{m}^{'} Y_{n}^{'} } \hfill \\ \end{array} } \right\}w_{mn} \left( t \right) + \frac{{N_{y} }}{D}\mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } \left\{ {\begin{array}{*{20}l} {J_{5} X_{m}^{''} Y_{n} + J_{4} X_{m} Y_{n}^{''} } \hfill \\ {\quad + 2J_{6} X_{m}^{'} Y_{n}^{'} } \hfill \\ \end{array} } \right\}w_{mn} \left( t \right) \\ & \quad + \frac{{N_{xy} }}{D}\mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } \left\{ {\begin{array}{*{20}l} {J_{8} X_{m}^{''} Y_{n} + J_{9} X_{m} Y_{n}^{''} } \hfill \\ {\quad + 2J_{7} X_{m}^{'} Y_{n}^{'} } \hfill \\ \end{array} } \right\}w_{mn} \left( t \right) \\ \end{aligned}$$
(3)

In Eq. (3), Nx, Ny, and Nxy are functions of the plate mode shapes. Subsequently, in-plane forces should be rewritten in terms of the plate mode shapes. Berger [48] proposed some appropriate relations for in-plane forces as follows:

$$\begin{aligned} N_{x} & = \frac{6D}{{L_{1} L_{2} h^{2} }}\int\nolimits_{0}^{{L_{1} }} \int\nolimits_{0}^{{L_{2} }} \left[ {\left( {\frac{\partial W}{\partial x}} \right)^{2} + \upsilon \left( {\frac{\partial W}{\partial y}} \right)^{2} } \right]{\text{d}}x{\text{d}}y \\ N_{y} & = \frac{6D}{{L_{1} L_{2} h^{2} }}\int\nolimits_{0}^{{L_{1} }} \int\nolimits_{0}^{{L_{2} }} \left[ {\left( {\frac{\partial W}{\partial y}} \right)^{2} + \upsilon \left( {\frac{\partial W}{\partial x}} \right)^{2} } \right]{\text{d}}x{\text{d}}y \\ N_{xy} & = \frac{{12D\left( {1 - \upsilon } \right)}}{{L_{1} L_{2} h^{2} }}\int\nolimits_{0}^{{L_{1} }} \int\nolimits_{0}^{{L_{2} }} \left[ {\frac{\partial W}{\partial x}\frac{\partial W}{\partial y}} \right]{\text{d}}x{\text{d}}y \\ \end{aligned}$$
(4)

By substituting Eq. (2) into Eq. (4), in-plane forces result in the following equations:

$$\begin{aligned} N_{x} & = \frac{6D}{{L_{1} L_{2} h^{2} }}\mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } w_{mn}^{2} \left( t \right)\int\nolimits_{0}^{{L_{1} }} \int\nolimits_{0}^{{L_{2} }} \left[ {X_{m}^{'2} Y_{n}^{2} + \upsilon X_{m}^{2} Y_{n}^{'2} } \right]{\text{d}}x{\text{d}}y = \chi_{1mn} w_{mn}^{2} \left( t \right) \\ \chi_{1mn} & = \frac{6D}{{L_{1} L_{2} h^{2} }}\mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } \int\nolimits_{0}^{{L_{1} }} \int\nolimits_{0}^{{L_{2} }} \left[ {X_{m}^{'2} Y_{n}^{2} + \upsilon X_{m}^{2} Y_{n}^{'2} } \right]{\text{d}}x{\text{d}}y \\ \end{aligned}$$
(5-a)
$$\begin{aligned} N_{y} & = \frac{6D}{{L_{1} L_{2} h^{2} }}\mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } w_{mn}^{2} \left( t \right)\int\nolimits_{0}^{{L_{1} }} \int\nolimits_{0}^{{L_{2} }} \left[ {\upsilon X_{m}^{'2} Y_{n}^{2} + X_{m}^{2} Y_{n}^{'2} } \right]{\text{d}}x{\text{d}}y = \chi_{2mn} w_{mn}^{2} \left( t \right) \\ \chi_{2mn} & = \frac{6D}{{L_{1} L_{2} h^{2} }}\mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } \int\nolimits_{0}^{{L_{1} }} \int\nolimits_{0}^{{L_{2} }} \left[ {\upsilon X_{m}^{'2} Y_{n}^{2} + X_{m}^{2} Y_{n}^{'2} } \right]{\text{d}}x{\text{d}}y \\ \end{aligned}$$
(5-b)
$$\begin{aligned} N_{xy} & = \frac{{12D\left( {1 - \upsilon } \right)}}{{L_{1} L_{2} h^{2} }}\mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } w_{mn}^{2} \left( t \right)\int\nolimits_{0}^{{L_{1} }} \int\nolimits_{0}^{{L_{2} }} X_{m}^{'} Y_{n}^{'} {\text{d}}x{\text{d}}y = \chi_{3mn} w_{mn}^{2} \left( t \right) \\ \chi_{3mn} & = \frac{{12D\left( {1 - \upsilon } \right)}}{{L_{1} L_{2} h^{2} }}\mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } \int\nolimits_{0}^{{L_{1} }} \int\nolimits_{0}^{{L_{2} }} X_{m}^{'} Y_{n}^{'} {\text{d}}x{\text{d}}y \\ \end{aligned}$$
(5-c)

Now, by means of orthogonality of plate modes, each side of Eq. (3) should be multiplied by XiYj and then integrated over the plate dimensions. Thus, the following relation is concluded:

$$M_{ij} \ddot{w}_{ij} \left( t \right) + K_{ij} w_{ij} \left( t \right) + H_{ij} w_{ij}^{2} \left( t \right) + G_{ij} w_{ij}^{3} \left( t \right) = \frac{1}{D}\int\nolimits_{0}^{{L_{1} }} \int\nolimits_{0}^{{L_{2} }} P\left( {x,y,L_{3} ,t} \right) X_{i} Y_{j } {\text{d}}x{\text{d}}y$$
(6)

where

$$M_{ij} = \frac{\rho h}{D}\mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } \int\nolimits_{0}^{{L_{1} }} \int\nolimits_{0}^{{L_{2} }} X_{m} Y_{n} X_{i} Y_{j} {\text{d}}x{\text{d}}y$$
(7-a)
$$K_{ij} = \mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } \int\nolimits_{0}^{{L_{1} }} \int\nolimits_{0}^{{L_{2} }} \left\{ {\left( {1 - J_{10} } \right)X_{m}^{\left( 4 \right)} Y_{n} + \left( {2 - J_{12} } \right)X_{m}^{\prime \prime } Y_{n}^{\prime \prime } + \left( {1 - J_{11} } \right)X_{m} Y_{n}^{\left( 4 \right)}-\left( { J_{22} } \right)X_{m}^{\prime \prime\prime } Y_{n}^{\prime }-\left( { J_{23} } \right)X_{m}^{\prime } Y_{n}^{\prime\prime\prime } } \right\}X_{i} Y_{j} {\text{d}}x{\text{d}}y$$
(7-b)
$$H_{ij} = \sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 1}^{\infty } {\int\nolimits_{0}^{{L_{1} }} {\int\nolimits_{0}^{{L_{2} }} {\left[ {\begin{array}{*{20}l} {\left\{ {X_{m}^{''} Y_{n} + \upsilon X_{m} Y_{n}^{''} } \right\}\left\{ {{\text{J}}_{13} X_{m}^{''} Y_{n} + {\text{J}}_{14} X_{m} Y_{n}^{''} + 2{\text{J}}_{15} X_{m}^{'} Y_{n}^{'} } \right\}} \hfill \\ {\quad + \left\{ {\upsilon X_{m}^{''} Y_{n} + X_{m} Y_{n}^{''} } \right\}\left\{ {{\text{J}}_{16} X_{m}^{''} Y_{n} + {\text{J}}_{17} X_{m} Y_{n}^{''} + 2{\text{J}}_{18} X_{m}^{'} Y_{n}^{'} } \right\}} \hfill \\ {\quad + \left( {1 - \upsilon } \right)X_{m}^{'} Y_{n}^{'} \left\{ {{\text{J}}_{19} X_{m}^{''} Y_{n} + {\text{J}}_{20} X_{m} Y_{n}^{''} + 2{\text{J}}_{21} X_{m}^{'} Y_{n}^{'} } \right\}} \hfill \\ \end{array} } \right]} } } } X_{i} Y_{j} {\text{d}}x{\text{d}}y$$
(7-c)
$$G_{ij} = - \frac{1}{D}\mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } \int\nolimits_{0}^{{L_{1} }} \int\nolimits_{0}^{{L_{2} }} \left[ {\begin{array}{*{20}l} {\chi_{1mn} \left\{ {J_{1} X_{m}^{''} Y_{n} + J_{2} X_{m} Y_{n}^{''} + 2J_{3} X_{m}^{'} Y_{n}^{'} } \right\}} \hfill \\ {\quad + \chi_{2mn} \left\{ {J_{5} X_{m}^{''} Y_{n} + J_{4} X_{m} Y_{n}^{''} + 2J_{6} X_{m}^{'} Y_{n}^{'} } \right\}} \hfill \\ {\quad + \chi_{3mn} \left\{ {J_{8} X_{m}^{''} Y_{n} + J_{9} X_{m} Y_{n}^{''} + 2J_{7} X_{m}^{'} Y_{n}^{'} } \right\}} \hfill \\ \end{array} } \right]X_{i} Y_{j} {\text{d}}x{\text{d}}y$$
(7-d)

2.1 Linear analysis of the cracked plate–cavity

First, in order for the linear natural frequencies of Eq. (6) to be obtained, the acoustic pressure should be computed. Therefore, partial differential equation corresponding to the acoustic wave pressure exerted on the plate can be written as follows:

$$\frac{{\partial^{2} P}}{{\partial x^{2} }} + \frac{{\partial^{2} P}}{{\partial y^{2} }} + \frac{{\partial^{2} P}}{{\partial z^{2} }} - \frac{1}{{c_{a}^{2} }}\frac{{\partial^{2} P}}{{\partial t^{2} }} = 0$$
(8)

where ca is the sound speed inside the air. Equation (2) can be attained by the aid of the separation of variables. As a result, the acoustic pressure is considered as below:

$$\left. {P\left( {x,y,z,t} \right) = X\left( x \right)\,Y\left( y \right)\,Z\left( z \right)\,T(t} \right)$$
(9)

Related acoustic boundary conditions for such a system are expressed by:

$$\begin{aligned} & \frac{\partial P}{\partial x}|_{{x = 0,L_{1} }} = 0,\quad \frac{\partial P}{\partial y}|_{{y = 0,L_{2} }} = 0 \\ & \frac{\partial P}{\partial z}|_{z = 0} = 0,\quad \frac{\partial P}{\partial z}|_{{z = L_{3} }} = - \rho_{a} \frac{{\partial^{2} \,W}}{{\partial t^{2} }} \\ \end{aligned}$$
(10)

Therefore, by replacing Eq. (9) into Eq. (8) and then, with the aid of the acoustic boundary conditions represented in Eq. (10) along the x and y directions, the acoustic wave inside the cavity is achieved in the form of below equation:

$$\begin{aligned} & P\left( {x,y,z,t} \right) = \mathop \sum \limits_{k = 0}^{\infty } \mathop \sum \limits_{l = 0}^{\infty } T_{kl} \left( t \right)\cosh \left( {g_{kl} z} \right)\cos \left( {\frac{k\pi }{{L_{1} }}x} \right)\cos \left( {\frac{l\pi }{{L_{2} }}y} \right) \\ & g_{kl} = \sqrt {\left( {\frac{k\pi }{{L_{1} }}} \right)^{2} + \left( {\frac{l\pi }{{L_{2} }}} \right)^{2} - \left( {\frac{\omega }{{c_{a} }}} \right)^{2} } \\ \end{aligned}$$
(11)

where ω is the coupled linear natural frequency of the system, and Tkl(t) is an unknown coefficient that can be determined via the acoustic boundary condition at z = L3. In this work, three modes of the plate for converging the problem are taken into account, namely mode numbers of (1, 1), (1, 2), and (2, 1). Now, by substituting Eq. (2) into Eq. (10) at z = L3 as well as considering the three modes, the following equation can be found:

$$\mathop \sum \limits_{k = 0}^{\infty } \mathop \sum \limits_{l = 0}^{\infty } T_{kl} \left( t \right)g_{kl} \sinh \left( {g_{kl} L_{3} } \right)\cos \left( {\frac{k\pi }{{L_{1} }}x} \right)\cos \left( {\frac{l\pi }{{L_{2} }}y} \right) = - \rho_{air} \left\{ {\left. {\ddot{w}_{11} \left( t \right)X_{1} \left( x \right)Y_{1} \left( y \right) + \ddot{w}_{12} \left( t \right)X_{1} \left( x \right)Y_{2} \left( y \right) + \ddot{w}_{21} \left( t \right)X_{2} \left( x \right)Y_{1} (y} \right)} \right\}$$
(12)

Three different boundary conditions can be introduced as below:

  1. (1)

    For fully simply supported edges, related boundary conditions are defined-SSSS:

    $$\begin{aligned} & X_{m} \left( x \right) = \sin \left( {\alpha_{m} x} \right),\quad \alpha_{m} = \frac{m\pi }{{L_{1} }},\quad m = 1,2, \ldots \\ & Y_{n} \left( y \right) = \sin \left( {\beta_{n} y} \right),\quad \beta_{n} = \frac{n\pi }{{L_{2} }},\quad n = 1,2, \ldots \\ \end{aligned}$$
    (13-a)
  2. (2)

    Fully clamped edges can be defined as (CCCC):

    $$\begin{aligned} & X_{m} \left( x \right) = \cosh \left( {\alpha_{m} x} \right) - \cos \left( {\alpha_{m} x} \right) - \gamma_{m} \left( {\sinh \left( {\alpha_{m} x} \right) - \sin \left( {\alpha_{m} x} \right)} \right) \\ & \alpha_{1} = \frac{4.730041}{{L_{1} }},\quad \alpha_{2} = \frac{7.853205}{{L_{1} }},\quad \alpha_{3} = \frac{10.995607}{{L_{1} }} \\ & Y_{n} \left( y \right) = \cosh \left( {\beta_{n} y} \right) - \cos \left( {\beta_{n} y} \right) - \lambda_{n} \left( {\sinh \left( {\beta_{n} y} \right) - \sin \left( {\beta_{n} y} \right)} \right) \\ & \beta_{1} = \frac{4.730041}{{L_{2} }},\quad \beta_{2} = \frac{7.853205}{{L_{2} }},\quad \beta_{3} = \frac{10.995607}{{L_{2} }} \\ \end{aligned}$$
    (13-b)
  3. (3)

    For simply supported edges along the x-direction and clamped edges along the y-direction, boundary conditions are expressed as (SSCC):

    $$\begin{aligned} & X_{m} \left( x \right) = \sin \left( {\alpha_{m} x} \right),\quad \alpha_{m} = \frac{m\pi }{{L_{1} }},\quad m = 1,2, \ldots \\ & Y_{n} \left( y \right) = \cosh \left( {\beta_{n} y} \right) - \cos \left( {\beta_{n} y} \right) - \lambda_{n} \left( {\sinh \left( {\beta_{n} y} \right) - \sin \left( {\beta_{n} y} \right)} \right) \\ & \beta_{1} = \frac{4.730041}{{L_{2} }},\quad \beta_{2} = \frac{7.853205}{{L_{2} }},\quad \beta_{3} = \frac{10.995607}{{L_{2} }} \\ \end{aligned}$$
    (13-c)

In Eqs. (13-b) and (13-c), the coefficients γm and λn are equal to \(\gamma_{m} = \frac{{\cosh \left( {\alpha_{m} L_{1} } \right) - \cos \left( {\alpha_{m} L_{1} } \right)}}{{\sinh \left( {\alpha_{m} L_{1} } \right) - \sin \left( {\alpha_{m} L_{1} } \right)}}\) and \(\lambda_{n} = \frac{{\cosh \left( {\beta_{n} L_{2} } \right) - \cos \left( {\beta_{n} L_{2} } \right)}}{{\sinh \left( {\beta_{n} L_{2} } \right) - \sin \left( {\beta_{n} L_{2} } \right)}}\). Thus, substituting each type of these boundary conditions into Eq. (12), and afterward by using orthogonality of eigenfunctions related to the acoustic pressure, the unknown coefficients are acquired in terms of the plate time modes. Finally, the acoustic pressure can be introduced as:

$$\left. {P\left( {x,y,L_{3} ,t} \right) \cong \psi_{11} \ddot{w}_{11} \left( t \right) + \psi_{12} \ddot{w}_{12} \left( t \right) + \psi_{21} \ddot{w}_{21} (t} \right)$$
(14)

where ψ11, ψ12, and ψ21 are defined in Appendix 2 for all kinds of boundary conditions. Here, Eq. (14) is substituted in Eq. (6), and then, neglecting nonlinear parts of Eq. (6) leads to the linear differential equation of the coupled system as:

$$M_{ij} \ddot{w}_{ij} \left( t \right) + K_{ij} w_{ij} \left( t \right) = \frac{1}{D}\int\nolimits_{0}^{{L_{1} }} \int\nolimits_{0}^{{L_{2} }} \left\{ {\left. {\psi_{11} \ddot{w}_{11} \left( t \right) + \psi_{12} \ddot{w}_{12} \left( t \right) + \psi_{21} \ddot{w}_{21} (t} \right)} \right\} X_{i} Y_{j } {\text{d}}x{\text{d}}y$$
(15)

Equation (15) can be rewritten as below:

$$M_{ij} \ddot{w}_{ij} \left( t \right) + K_{ij} w_{ij} \left( t \right) = \beta_{ij}^{11} \,\ddot{w}_{11} \left( t \right) + \beta_{ij}^{12} \,\ddot{w}_{12} \left( t \right) + \beta_{ij}^{21} \,\ddot{w}_{21} \left( t \right)$$
(16)

where \(\beta_{ij}^{mn} = \frac{1}{D}\int\nolimits_{0}^{{L_{1} }} \int\nolimits_{0}^{{L_{2} }} \psi_{mn} X_{i} Y_{j } {\text{d}}x{\text{d}}y\). By using \(\left. {w_{ij} \left( t \right) = a_{ij} \cos (\omega t} \right)\), substituting such a relation into Eq. (16) results in

$$\begin{array}{*{20}l} { - \omega^{2} M_{11} \,a_{11} + K_{11} \,a_{11} = - \omega^{2} \{ \beta_{\,11}^{11} \,a_{11} + \beta_{\,11}^{12} \,a_{12} + \beta_{\,11}^{21} \,a_{21} \} } \hfill \\ { - \omega^{2} M_{12} \,a_{12} + K_{12} \,a_{12} = - \omega^{2} \{ \beta_{\,12}^{11} \,a_{11} + \beta_{\,12}^{12} \,a_{12} + \beta_{\,12}^{21} \,a_{21} \} } \hfill \\ { - \omega^{2} M_{21} \,a_{21} + K_{21} \,a_{21} = - \omega^{2} \{ \beta_{\,21}^{11} \,a_{11} + \beta_{\,21}^{12} \,a_{12} + \beta_{\,21}^{21} \,a_{21} \} } \hfill \\ \end{array}$$
(17)

Equation (17) can be rearranged in matrix form as

$$\begin{aligned} & \left[ C \right]\left\{ {\begin{array}{*{20}c} {a_{11} } \\ {a_{12} } \\ {a_{21} } \\ \end{array} } \right\} = 0 \\ & \left[ C \right] = \left[ {\begin{array}{*{20}c} {\left. {K_{11} - \omega^{2} (M_{11} - \beta_{\,11}^{11} } \right)} & {\omega^{2} \beta_{\,11}^{12} } & {\omega^{2} \beta_{\,11}^{21} } \\ {\omega^{2} \beta_{\,12}^{11} } & {\left. {K_{12} - \omega^{2} (M_{12} - \beta_{\,12}^{12} } \right)} & {\omega^{2} \beta_{\,12}^{21} } \\ {\omega^{2} \beta_{\,21}^{11} } & {\omega^{2} \beta_{\,21}^{12} } & {\left. {K_{21} - \omega^{2} (M_{21} - \beta_{\,21}^{21} } \right)} \\ \end{array} } \right] \\ \end{aligned}$$
(18)

Finally, the natural frequencies of the coupled cracked plate and cavity are determined by considering the fact that determination of matrix [C] is zero.

2.2 Nonlinear analysis of cracked plate–cavity system

In the previous section, the acoustic pressure and linear natural frequencies of the coupled system were computed. Now, it is possible to analyze the nonlinear equation of the system, namely Eq. (6). By substituting the coupled linear natural frequencies resulting from Eq. (18) into the acoustic pressure represented in Eq. (11) and then replacing into Eq. (6), it can be changed as follows:

$$\left( {M_{ij} + \mu_{ij} } \right)\ddot{w}_{ij} \left( t \right) + K_{ij} w_{ij} \left( t \right) + H_{ij} w_{ij}^{2} \left( t \right) + G_{ij} w_{ij}^{3} \left( t \right) = 0$$
(19)

where in Eq. (19), μij is the added effective mass due to the acoustic pressure. Equation (19) is a well-known nonlinear equation named Duffing equation. Herewith, to solve such a nonlinear problem, variational iteration method (VIM) is employed as a semi-analytical method.

Researchers have been utilized different numerical methods, such as harmonic balance method [49], perturbation method [50, 51], generalized differential quadrature method (GDQ) [52,53,54], domain decomposition method [55], in order to analyze nonlinear problems. Among available numerical methods, VIM is introduced as one of the fast convergent methods for numerical problems. VIM was firstly introduced by He [56, 57] in order to solve linear and nonlinear problems analytically. Accordingly, it is supposed that the following relation is available [58, 59]:

$$Lu + Nu = g\left( x \right)$$
(20)

where L and N represent linear and nonlinear operators. Then, it is assumed that u0(x) is the solution of Lu = 0, thereby being employed as the first approximation. Subsequently, correction functional is introduced in order to correct the solution of Eq. (20) as follows [60, 61]:

$$u_{n + 1} \left( x \right) = u_{n} \left( x \right) + \int\nolimits_{0}^{x} \lambda \left\{ {Lu_{n} \left( \xi \right) + Nu_{n} \left( \xi \right) - g\left( \xi \right)} \right\} {\text{d}}\xi$$
(21)

where λ, known as Lagrange multiplier, is a function of x and ξ, and it is found optimally via variational theory. Such a procedure is a repetitive method and stopped at an appropriate precision. Here, VIM can be handled in order for Eq. (19) to be solved. Firstly, both sides of Eq. (19) are divided by (Mij + μij), and the outcome will be as:

$$\ddot{w}_{ij} \left( t \right) + \omega_{ij}^{2} w_{ij} \left( t \right) + \varUpsilon_{ij} w_{ij}^{2} \left( t \right) + \varphi_{ij} w_{ij}^{3} \left( t \right) = 0$$
(22)

where \(\omega_{ij}^{2}\), \(\varUpsilon\)ij and φij are defined

$$\omega_{ij}^{2} = \frac{{K_{ij} }}{{M_{ij} + \mu_{ij} }},\quad \varUpsilon_{ij} = \frac{{H_{ij} }}{{M_{ij} + \mu_{ij} }},\quad \varphi_{ij} = \frac{{G_{ij} }}{{M_{ij} + \mu_{ij} }}$$
(23)

Correction functional for Eq. (22) is presented as follows so that VIM can be started:

$$\left( {w_{ij} \left( t \right)} \right)_{n + 1} = \left( {w_{ij} \left( t \right)} \right)_{n} + \int\nolimits_{0}^{t} \lambda_{ij} \left\{ {\left( {(\ddot{w}_{ij} \left( \tau \right)} \right)_{n} + \omega_{ij}^{2} \left( {(w_{ij} \left( \tau \right)} \right)_{n} + \varUpsilon_{ij} \left( {\tilde{w}_{ij} \left( \tau \right)} \right)_{n}^{2} + \varphi_{ij} \left( {\tilde{w}_{ij} \left( \tau \right)} \right)_{n}^{3} } \right\} {\text{d}}\tau$$
(24)

The Lagrange multiplier is determined by using the variational theory. Therefore, applying variation on both sides of Eq. (24), and knowing δwij(t) = 0, the following relation is deduced as:

$$0 = \delta \left( {w_{ij} \left( t \right)} \right)_{n} + \lambda_{ij} \delta \left( {\dot{w}_{ij} \left( \tau \right)} \right)_{n} |_{\tau = t} - \lambda_{ij}^{'} \delta \left( {w_{ij} \left( \tau \right)} \right)_{n} |_{\tau = t} + \int\nolimits_{0}^{t} \left[ {\lambda_{ij}^{\prime \prime } + \omega_{ij}^{2} \lambda_{ij} } \right]\delta \left( {w_{ij} \left( \tau \right)} \right)_{n} {\text{d}}\tau$$
(25)

Stationary conditions are concluded from Eq. (25) as follows:

$$\left\{ {\begin{array}{*{20}l} {\lambda_{ij}^{\prime \prime } + \omega_{ij}^{2} \lambda_{ij} = 0} \hfill \\ {1 - \lambda_{ij}^{'} = 0\quad \tau = t} \hfill \\ {\lambda_{ij} = 0\quad \tau = t} \hfill \\ \end{array} } \right.$$
(26)

Finally, the Lagrange multiplier is obtained as:

$$\lambda_{ij} = \frac{1}{{\omega_{ij} }}\sin \left( {\omega_{ij} \left( {\tau - t} \right)} \right)$$
(27)

Now, the obtained Lagrange coefficient is replaced into Eq. (24). Finally, the correction functional can be written as:

$$\left( {w_{ij} \left( t \right)} \right)_{n + 1} = \left( {w_{ij} \left( t \right)} \right)_{n} + \int\nolimits_{0}^{t} \frac{1}{{\omega_{ij} }}\sin \left( {\omega_{ij} \left( {\tau - t} \right)} \right)\left\{ {\left( {(\ddot{w}_{ij} \left( \tau \right)} \right)_{n} + \omega_{ij}^{2} \left( {(w_{ij} \left( \tau \right)} \right)_{n} + \varUpsilon_{ij} \left( {w_{ij} \left( \tau \right)} \right)_{n}^{2} + \varphi_{ij} \left( {w_{ij} \left( \tau \right)} \right)_{n}^{3} } \right\} {\text{d}}\tau$$
(28)

As it was declared, VIM starts by an initial approximation. Thus, by assuming that initial conditions are \(w_{ij} \left( t \right)|_{t = 0} = A_{ij}\) and \(\dot{w}_{ij} \left( t \right)|_{t = 0} = 0\), the first approximation is presented as:

$$\left( {(w_{ij} \left( t \right)} \right)_{0} = A_{ij} \cos \left( {\alpha_{ij} t} \right)$$
(29)

where Aij is the vibration amplitude and αij is the nonlinear frequency of the coupled system, so that it is found by the following procedure. By replacing Eq. (29) into Eq. (28), and knowing that the structure vibrates with limited amplitude, it must be eliminated a secular term appearing at each iteration, which appears in form of cos(ωijt).

3 Numerical results

3.1 Validation

In the previous section, variational iteration method was introduced as an appropriate technique for linear and nonlinear problems. In order to prove the accuracy of the present method, the outcomes are compared with those of Lee [20] as listed in Table 1. Hence, the first iteration of VIM is applied to obtain the ratio of nonlinear and linear coupled fundamental frequency for an intact aluminum plate under simply supported boundary conditions with dimensions of 0.3048 m × 0.3048 m × 1.2192 mm. The inspection of Table 1 shows that there is a proper validity between the two outcomes, which indicates the reliability of the present method.

Table 1 Comparison of frequency ratio between the present method and those of harmonic balance method (Lee [20])
Full size table

For further verification, the results are also compared with Lee [41] by considering another value for the cavity depth as L3 = 0.1524 m, as shown in Fig. 2. Comparing the present results with those of Lee [41] indicates an excellent agreement, particularly in high-frequency ranges more than frequency ratio of \(\frac{{\alpha_{11} }}{{\omega_{11} }} = 1.8\).

Fig. 2
figure 2

Comparison of backbone curve between the present study (VIM) and multi-level residue harmonic balance method (HBM), offered by Lee [41] for an intact simply supported plate surrounded by an air cavity

Full size image

3.2 Nonlinear natural frequencies of the cracked plate–cavity system

In this section, the solution procedure is followed to obtain the nonlinear natural frequencies of the cracked plate–cavity system. For this purpose, the geometrical characteristics and physical properties of the present model are assumed to be L1 = 0.18 (m), L2 = 0.38 (m), h = 0.8 (mm), L3 = 0.866 (m), E = 206 (GPa), and \(\rho = 7900\,\left( {\frac{\text{kg}}{{{\text{m}}^{3} }}} \right)\). Besides, the following values are used for the specifications of the air cavity as \(c_{a} = 340\, \left( \frac{\hbox{m}}{\hbox{s}} \right)\) and \(\rho_{a} = 1.21 \,\left( {\frac{\text{kg}}{{{\text{m}}^{3} }}} \right)\). In order to demonstrate the defect on the plate, arbitrary amounts are chosen for parameters of the crack. In fact, it is assumed that the crack is located parallel to the x-axis at non-dimensional distance of ξc = 0.2 and length of Γ = 0.3, respectively. By considering these characteristics, variational iteration method is carried out for such a system by four iterations. It is noteworthy that applying this method leads to create some terms at each iteration which are a function of the nonlinear frequencies, known as secular terms causing to intensify the vibration amplitude. Since the amplitude of vibration is a certain amount, it can be deduced that these terms must be equal to zero at each iteration. Hence, by eliminating the secular terms at each iteration, the nonlinear frequencies are computed. Therefore, it is carried out four iterations, and the nonlinear frequency at each iteration is extracted. In order to show the accuracy and convergence of the present method, three mode numbers are arbitrarily taken into account, including mode (1, 1) of fully simply supported, (1, 2) of fully clamped and (2, 1) of simply supported-clamped boundary conditions. However, due to the complexity of displaying all of the iterations, only the secular term associated with the first iteration is displayed for the above mode numbers, respectively, as follows:

$$\begin{aligned} & \frac{{10^{12} A_{11} \left\{ {\begin{array}{*{20}l} {\left( {13.33 \cdot 10^{ - 11} A_{11} + 5.63 \cdot 10^{ - 12} } \right)\alpha_{11}^{6} + \left( { - 1.67A_{11}^{2} + 0.00 \cdot A_{11} - 16.03 \cdot 10^{ - 7} } \right)\alpha_{11}^{4} } \hfill \\ {\quad + \left( {137501.09A_{11}^{2} + 3.9A_{11} + 0.10} \right)\alpha_{11}^{2} - 68175.53A_{11} - 2.62 \cdot 10^{9} A_{11}^{2} - 1437.69} \hfill \\ \end{array} } \right\}}}{{9.61 \cdot 10^{10} \alpha_{11}^{2} - 1.44 \cdot 10^{15} - 1.6 \cdot 10^{6} \alpha_{11}^{4} + 5.63\alpha_{11}^{6} }} \\ & \frac{{10^{12} A_{12} \left\{ {\begin{array}{*{20}l} {\left( {18.85 \cdot 10^{ - 15} A_{12} + 36.01 \cdot 10^{ - 13} } \right)\alpha_{12}^{6} + \left( { - 35.36 \cdot 10^{ - 9} A_{12} - 9.33A_{12}^{2} - 57.10 \cdot 10^{ - 7} } \right)\alpha_{12}^{4} } \hfill \\ {\quad + \left( {42.64 \cdot 10^{5} A_{12}^{2} + 0.00 \cdot A_{12} + 1.87} \right)\alpha_{12}^{2} - 45.16 \cdot 10^{10} A_{12}^{2} - 1655.42A_{12} - 157902.22} \hfill \\ \end{array} } \right\}}}{{ - 5.71 \cdot 10^{6} \alpha_{12}^{4} - 1.58 \cdot 10^{17} + 1.90 \cdot 10^{12} \alpha_{12}^{2} + 1.00 \cdot 10^{5} \alpha_{12} + 3.6\alpha_{12}^{6} }} \\ & \frac{{10^{12} A_{21} \left\{ {\begin{array}{*{20}l} {\left( {4.00 \cdot 10^{ - 13} - 15.52 \cdot 10^{ - 29} A_{21} } \right)\alpha_{21}^{6} + \left( { - 13.81 \cdot 10^{ - 7} - 3.36A_{21}^{2} + 6.25 \cdot 10^{ - 22} A_{21} } \right)\alpha_{21}^{4} } \hfill \\ {\quad + \left( {1.01 + 33.53 \cdot 10^{5} A_{21}^{2} - 6.65 \cdot 10^{ - 16} A_{21} } \right)\alpha_{21}^{2} - 181705.27 - 7.73 \cdot 10^{11} A_{21}^{2} 14.11 \cdot 10^{ - 11} A_{21} } \hfill \\ \end{array} } \right\}}}{{4.00\alpha_{21}^{6} - 1.82 \cdot 10^{18} - 1.38 \cdot 10^{7} \alpha_{21}^{4} + 1.00 \cdot 10^{13} \alpha_{21}^{2} - 1.00 \cdot 10^{6} \alpha_{21} + 1.00 \cdot \alpha_{21}^{3} }} \\ \end{aligned}$$
(30)

As observed clearly in Eq. (30), the numerator of each fraction must be equal to zero in order that the nonlinear frequencies for the first iteration can be obtained. A similar procedure is also followed by four iterations to prove the convergence of the nonlinear frequencies for the mode numbers (1, 1), (1, 2) and (2, 1), and the results are listed in Tables 2, 3 and 4. The achieved outcomes display that the integral part of each nonlinear frequency for an arbitrary vibration amplitude ratio converges. This issue also implies a high convergence rate for nonlinear problems. In addition, it should be noted that the first iterations reported in Tables 2, 3 and 4 are computed by the aid of Eq. (30). Accordingly, since the fourth iteration of these tables represents the convergence of the frequencies, four iterations of VIM are also implemented for the other modes of the boundary conditions, and finally the nonlinear frequencies associated with the fourth iteration of all modes are reported in Table 5.

Table 2 Convergence of nonlinear frequency related to mode number (1, 1) of the fully simply supported cracked plate–cavity system
Full size table
Table 3 Convergence of nonlinear frequency related to mode number (1, 2) of fully clamped cracked plate–cavity system
Full size table
Table 4 Convergence of nonlinear frequency related to mode number (2, 1) of simply supported-clamped cracked plate–cavity system
Full size table
Table 5 The nonlinear frequencies related to three modes of cracked plate–cavity systems for different boundary conditions
Full size table

Figures 3, 4 and 5 present the influence of the crack orientation with respect to various boundary conditions. It is shown that by increasing the crack angle, the frequency ratio for mode numbers of (1, 1) and (2, 1) is continually reduced. Still, an opposite behavior is seen for mode number of (1, 2). It is worth to note that the enhancement of such a factor at each amplitude ratio presents an extremum value. Additionally, for low amplitude ratio, although the frequency ratio is approached to the unit, the increase of the crack angle cannot remarkably affect it. Meanwhile, when the amplitude ratio is increased, not only is the frequency ratio raised due to increase of nonlinearities, but the effect of the crack orientation is also easily seen. According to this fact that the maximum stiffness of the structure corresponds to clamped boundary conditions, it is inferred that the frequency ratio for mode numbers of (1, 1) and (2, 1) decreases with lower rate compared to the other boundary conditions.

Fig. 3
figure 3

Three-dimensional configurations for the frequency ratio versus crack angle and amplitude ratio for simply supported boundary conditions at various mode numbers a (1, 1), b (1, 2) and c (2, 1)

Full size image
Fig. 4
figure 4

Three-dimensional configurations for the frequency ratio versus crack angle and amplitude ratio for clamped boundary conditions at various mode numbers a (1, 1), b (1, 2) and c (2, 1)

Full size image
Fig. 5
figure 5

Three-dimensional configurations for the frequency ratio versus crack angle and amplitude ratio for simply supported-clamped boundary conditions at various mode numbers a (1, 1), b (1, 2) and c (2, 1)

Full size image

In the following, in order to highlight the simultaneous effect of the non-dimensional distance of the crack and amplitude ratio on the frequency ratio, some other three dimensional configurations are plotted. Accordingly, Fig. 6 is presented, including some subfigures from (a) to (c). As it is obvious, each of these figures is shown for the fundamental frequency ratio with respect to various boundary conditions. Based on the outcomes, it is concluded that when the crack is approached to the edges of the plate, the frequency ratio reduces. This trend is due to the fact that the closer the crack is to the plate edges, the more rigid the plate is, which subsequently the difference between the nonlinear and linear frequency decreases. It is worth to emphasize that this matter for the other modes are similarly affected; therefore, they are neglected for avoiding repetitive plots.

Fig. 6
figure 6

Investigation of simultaneous effect of amplitude ratio and non-dimensional distance on fundamental frequency ratio for a cracked plate–cavity system with respect to various boundary conditions a simply supported, b clamped and c simply supported-clamped

Full size image

Following the discussed issues, some other four-dimensional configurations involving Figs. 7, 8 and 9 are demonstrated to remark the simultaneous influences of the crack angle, non-dimensional length, and amplitude ratio on the frequency ratio for the mode numbers (1, 1) of fully simply supported (Fig. 7), (1, 2) of fully clamped (Fig. 8) and (2, 1) of simply supported-clamped boundary conditions (Fig. 9). As perceived from the outcomes, it is easily seen that the crack length does not have any effect on the results, so that by increasing this factor, no variation is created in all four-dimensional figures. Hence, the influence of such a parameter is negligible on the frequency ratio. However, as previously concluded from Figs. 3, 4 and 5, it can be deduced that enhancing the crack angle parameter makes the frequency ratio decrease for both the mode numbers (1, 1) and (2, 1). Meanwhile, the trend of the figure for the mode number (1, 2) is different. In fact, by increasing this parameter, although the frequency ratio has increasing trend to a certain angle, it decreases after this angle.

Fig. 7
figure 7

Frequency ratio plotted versus amplitude ratio, crack length, and crack angle for a cracked plate–enclosure with respect to various boundary conditions a simply supported, b clamped and c simply supported-clamped

Full size image
Fig. 8
figure 8

Cracked coupled nonlinear frequency and intact plate linear frequency ratio plotted versus cavity depth and amplitude ratio for simply supported boundary conditions

Full size image
Fig. 9
figure 9

Cracked coupled nonlinear frequency and intact plate linear frequency ratio plotted versus cavity depth and amplitude ratio for clamped boundary conditions

Full size image

Here, the aim is to show the effect of the cavity depth on the ratio of the cracked coupled nonlinear frequency and the intact plate linear frequency. Hence, a specific crack is assumed with characteristics ξc = 0.2, Γ = 0.3 and θ = 30°. Subsequently, the frequency ratio is plotted versus the cavity depth and amplitude ratio, represented in Figs. 8, 9 and 10 for the three boundary conditions. Inspection of these figures presents that the cavity depth has a remarkable influence on the frequency ratio, so that with increasing the cavity depth at an arbitrary amplitude ratio, the frequency ratio continuously decreases. Additionally, as clearly observed, it can be inferred that increasing the cavity depth for a low amplitude ratio causes the amount of the cracked coupled nonlinear frequency to become less than the plate intact linear frequency, namely less than the unit. Furthermore, the effect of the cavity depth is seen more obvious by increasing the amplitude ratio.

Fig. 10
figure 10

Cracked coupled nonlinear frequency and intact plate linear frequency ratio plotted versus cavity depth and amplitude ratio for simply supported-clamped boundary conditions

Full size image

4 Conclusion

In this paper, the nonlinear vibration of a plate, as well as a surrounding cavity, was studied. The plate included a part-through surface crack considered at an arbitrary position and direction, modeled by the modified line spring model. In the first step, the Euler equation was employed to introduce solid–fluid interaction. Subsequently, the linear analysis of the cracked plate–cavity system could be analyzed. In the next step, in order for the nonlinear part of the problem to be solved, variational iteration method (VIM) was introduced as a practical method with high precision. Therefore, by implementing such a method by four iterations, the convergence of nonlinear frequencies of all boundary conditions was indicated. Additionally, the examination of the crack direction, as the most effective parameter on the frequency ratio, revealed that the frequency ratio of modes (1, 1) and (2, 1) decreased continuously as the crack angle increased, and the reduction was more obvious for a higher vibration amplitude. However, the frequency ratio related to mode (1, 2) increased to a specific angle and then decreased. Also, the inspection of the crack position indicated that the closer the crack is to the plate edges, the less the amount of the frequency ratio is. Further, presenting four-dimensional backbone curves for studying the effect of the crack length on the frequency ratio proved that this crack parameter had less effect on the frequency ratio than the other parameters. At last, the examination of the cavity depth showed that increasing this parameter resulted in diminishing the frequency ratio.