1 Introduction

Targeted energy transfer (TET) or “energy pumping” from a linear oscillator to an attached nonlinear energy sink (NES) has been an object of extensive recent studies. It was shown for a single degree-of-freedom (SDOF) NES that it can efficiently and irreversibly draw energy from a linear oscillator under various forms of excitation including impulse [1–6], periodic [7–12], and quasiperiodic forcing [13]. Its efficiency has been demonstrated numerically and experimentally for seismic excitations [14] and it has also been applied for passive suppression of aeroelastic instabilities [15, 16] in reducing oscillations of the primary system to a more desirable level for a wide range of excitations and frequencies. It was shown that such attachment can be more efficient than a traditional linear solution (a tuned mass damper) under harmonic forcing [9]. Recent developments in the field were summarized in the review paper [17].

It was revealed, however, that a strategy of vibration absorption based on the SDOF NES displays some limitations in terms of excitation amplitude, especially in the most interesting vicinity of 1:1 resonance [8, 13]. Under stronger excitation, instead of the simple periodic response observed for low forcing, the primary mass exhibits a strongly modulated response (SMR) [7–13, 17]. For even stronger forcing, the mitigation capability of the NES almost disappears, since the system exhibits periodic responses with very high amplitudes. One possible solution is an inclusion of nonlinear damping in the system [18, 19].

It was shown that the NES with few degrees-of-freedom (multiple-DOF, MDOF) has an advantage over the SDOF NES in terms of the TET efficiency [20–22]. It was demonstrated that this type of the NES exhibits enhanced TET abilities for impulse excitations—both efficient energy pumping and wide effective work diapason [23]. These results motivated us to investigate the system with single primary mass and the 2DOF NES under periodic external forcing. Although such system eventually suffers from the same drawbacks as the SDOF NES system, we demonstrate that the external forcing threshold under which there is effective energy pumping is considerably wider in the system with the 2DOF NES.

In addition, the study of the possible response regimes in the 2DOF NES system shows that apart from behaviors already discussed in the context of the SDOF NES system, such as coexistence of simple periodic responses and the SMRs under the same parameters [7, 8] or the existence of nontrivial quasiperiodic regimes [9], we also find coexisting periodic, quasiperiodic, and chaotic regimes, sometimes differing from one another by an order of magnitude in terms of resulting amplitudes. These patterns and response regimes are also discussed in the paper.

2 Description of the system

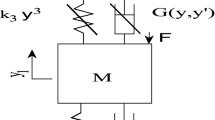
We consider a system that comprises a SDOF linear oscillator coupled to a 2DOF NES as shown in Fig. 1. The NES consists of two relatively small masses connected by a cubic spring with relatively small stiffness and weak linear damping The primary mass is connected to the NES via cubic spring and weak linear dashpot. In general, the system is similar to one discussed in [23].

Fig. 1
figure 1

Sketch of the dynamical system with 2DOF NES

Full size image

This system is allowed to move only in the horizontal direction ignoring any possible bending forces or perpendicular vibration. Equations of motion of this system are written as follows:

$$ \left \{ \begin{array}{l}\bar{M}\ddot{U} + {{\bar{\lambda}}_0}\dot{U} + {{\bar{k}}_1}U + {{\bar{\lambda}}_1}({\dot{U} - {{\dot{V}}_1}} )\\[4pt]\quad {} + \frac{4}{3}{{\bar{k}}_2}{( {U - {V_1}} )^3} =\bar{A}\cos({\bar{t} \cdot\bar{\omega}({1 - \bar{\sigma}})} )\\[4pt]{{\bar{m}}_1}{{\ddot{V}}_1} - {{\bar{\lambda}}_1}({\dot{U} - {{\dot{V}}_1}} ) - \frac{4}{3}{{\bar{k}}_2}{({U - {V_1}} )^3}\\[4pt]\quad {} +{{\bar{\lambda}}_2}( {{V_1} - {V_2}} ) + \frac{4}{3}{{\bar{k}}_3}{({{V_1} - {V_2}} )^3}= 0\\[4pt]{{\bar{m}}_2}{{\ddot{V}}_2} - {{\bar{\lambda}}_2}( {{{\dot{V}}_1} -{{\dot{V}}_2}} ) - \frac{4}{3}{{\bar{k}}_3}{( {{V_1} - {V_2}} )^3}= 0\end{array} \right .$$
(1)

where U,V 1,V 2 are displacements of the primary system, the first NES and the second NES, respectively, \(\bar{M}\) is a value of the primary mass, \(\bar{m}_{1}, \bar{m}_{2}\) are masses of the first and the second NES, respectively, \({{\bar{\lambda}}_{0}}, \bar{k}_{1}\) are the linear oscillator’s damping and stiffness coefficient, respectively, \({{\bar{\lambda}}_{1}}, \bar{k}_{2}\) are a damping and a cubic stiffness coefficients of the first NES, \({{\bar{\lambda}}_{2}}, \bar{k}_{3}\) are the damping and the cubic stiffness coefficients of the second NES, \(\bar{A}\) is the excitation amplitude, \(\omega = \sqrt{{{{{\bar{k}}_{1}}}\mathord{/{\vphantom{{{{\bar{k}}_{1}}} {\bar{M}}}}\kern-\nulldelimiterspace} {\bar{M}}}} \) is the undamped eigenfrequency of the primary oscillator and \(\bar{\sigma}\) is a relative frequency detuning of the external force.

System (1) is then reduced to nondimensional variables and yields

$$ \left \{ \begin{array}{l}\ddot{u} + \varepsilon{\lambda_0}\dot{u} + u + \varepsilon{\lambda_1}( {\dot{u} - {{\dot{v}}_1}} )\\[4pt]\quad {} + \frac {4}{3}{k_2}\varepsilon{( {u - {v_1}} )^3} = \varepsilon A\cos( {t( {1 - \varepsilon\sigma} )} )\\[4pt]{m_1}{{\ddot{v}}_1} - {\lambda_1}( {\dot{u} - {{\dot{v}}_1}} )- \frac{4}{3}{k_2}{( {u - {v_1}} )^3}\\\quad {} + {\lambda_2}({{{\dot{v}}_1} - {{\dot{v}}_2}} ) + \frac{4}{3}{k_3}{( {{v_1}- {v_2}} )^3} = 0\\[4pt]{m_2}{{\ddot{v}}_2} - {\lambda_2}( {{{\dot{v}}_1} - {{\dot{v}}_2}}) - \frac{4}{3}{k_3}{( {{v_1} - {v_2}} )^3} = 0\end{array} \right .$$
(2)

Detailed expressions for the nondimensional parameters are presented in Appendix A. Note that in the most general form all of the parameters are independent and the NESs not necessarily have equal mass or any other parameter. Small parameter ε is related to relative mass of the NESs with respect to the mass of the primary oscillator. We adopt that the same small parameter defines the scale of the excitation amplitude, all damping coefficients, and the frequency detuning. The scale of the nonlinear stiffness has been tuned to the same order by appropriate choice of the characteristic displacement (see Appendix A).

For the purpose of numeric analysis, the parameters were set arbitrarily but within practical limits. Unless otherwise stated, ε=0.05, σ=1.0044, both m 1 and m 2 are set to be 1 so that each NES is 5 % of the primary mass, λ 1,2=0.2, λ 0=0, k 2=1, and k 3=k=0.01. In addition, unless otherwise stated, all initial conditions (displacements and velocities) are considered to be 0.

3 Numerical analysis

3.1 Performance and comparison to SDOF NES system

In order co compare the performance of the system with the 2DOF NES to that with the single degree-of-freedom, we use the SDOF NES system with the mass doubled so that the total NES mass is the same for both systems. Both systems are simulated in the most interesting regime of 1:1 resonance. The frequency detuning is chosen in order to get as close as possible to the resonant peak. The comparison reveals very similar phenomena in both systems. Perhaps, the most interesting is effective “locking” of the NES and growth of the response amplitude by orders of magnitude when the excitation amplitude achieves certain critical value. Such response indicates that the NES completely ceases to be efficient for the vibration absorption. This “explosion” is discussed more thoroughly in Sect. 3.2. Here, we are going to mention that such response exists both in the systems with the SDOF NES and with the 2DOF NES; these results are presented in Fig. 2. One can mention that the 2DOF NES system can withstand much higher excitation amplitudes while keeping low primary mass’ displacement magnitudes (Fig. 3) and also have a wide region where the NES efficiently channels the energy away from the primary mass (Fig. 4). The energy of each mass is defined here as the time average of the sum of its kinetic energy and the potential energy stored in the spring that couples it to the previous element in the chain in the steady state. So, one can see that the 2DOF NES demonstrates obvious superiority over the SDOF NES with respect to the TET in this forced system.

Fig. 2
figure 2

Primary mass’ displacement after “explosion” of SDOF NES system (a) with A=4,σ=0.4668 and 2DOF NES system (b) with A=16,σ=1.001

Full size image
Fig. 3
figure 3

Primary mass’ displacement of SDOF NES system (a) with A=2,σ=0.4668 and 2DOF NES system (b) with A=12,σ=1.001

Full size image
Fig. 4
figure 4

Total system energy and total NES energy with respect to excitation amplitude for a set of initial conditions

Full size image

Another testimony of the efficiency of the 2DOF system can be found looking at the energy distribution between the primary mass and the NES. As seen in Fig. 5, while the total energy in the system grows with the increase in excitation amplitude, nearly all of it is concentrated in the NES. However, as mentioned earlier, this is true only up to certain threshold amplitude at which the NES “locks” to the primary mass (i.e., the relative displacements of the NES elements become lower by an order of magnitude than those of the primary mass) and ceases to be effective as in Fig. 6 where the oscillations of the primary mass has about 10 times larger amplitude than the relative displacements of the NES elements.

Fig. 5
figure 5

Energy levels with respect to excitation amplitude for a set of initial conditions

Full size image
Fig. 6
figure 6

An example of the NES “locking” (A=16)

Full size image

3.2 Response regimes of the system with varying frequency and amplitude

In order to investigate possible response regimes of this system, a number of simulations with changing amplitude and frequency detuning of the forcing has been performed. Other system parameters were kept fixed, as we have mentioned in Sect. 2. All simulations were run near the 1:1 resonance, where maximum resulting displacement amplitudes were observed.

The results suggest four distinct types of possible response, depending on the forcing amplitude. In Fig. 7, we depict the time series for the displacements of the main mass for different response types.

Fig. 7
figure 7

Response regimes for σ=1.0044: (a) Periodic response (A=4), (b) WMR (A=1), (c) SMR (A=10), (d) High Amplitude WMR (A=16)

Full size image

In Fig. 7a, which depicts the system’s response to relatively low forcing amplitude, one observes a constant-amplitude vibration, i.e., a simple periodic response. On the other hand, in Fig. 7b, which depicts the system’s response to even lower forcing amplitude, we see a quasiperiodic response although it seems to be a Weakly Modulated Response (WMR) [17]. Meanwhile, in Fig. 7c, which depicts the system’s response to higher forcing amplitude, we see the SMR—a quasiperiodic response with much stronger modulations. Another response regime, which appears very suddenly at high forcing amplitudes, includes very slow modulations, which usually decay over time, i.e., the transient of this system is longer than the time span of these figures (see Fig. 8b which depicts a longer time span for a similar case). After the transient ends, we observe a high-amplitude WMR as in Fig. 7d.

Fig. 8
figure 8

Time series before (A=14.8) (a) and after (A=14.9) (b) bifurcation

Full size image

Note that for the first three figures the maximal amplitude of the displacement is of the same order of magnitude as the forcing amplitude, while in the last case the magnitude is more than 20 times the excitation amplitude. In the examples above, the forcing amplitude varies considerably; even under small variations this change is very sudden.

As it is demonstrated in Fig. 8, increasing the forcing amplitude by about 0.7 % causes an increase in the displacement amplitude by over 2000 %. It seems that one observes here a transition from the SMR to the high-amplitude WMR. This transition is clearly visible when determining the amplitude of the primary mass while varying the detuning with constant forcing amplitude as we depict in Fig. 9.

Fig. 9
figure 9

Maximal displacement of the primary mass versus the frequency detuning for A=15

Full size image

Note that the transition is not “smooth” but very sudden and that the high amplitudes continue to characterize the response regime as the excitation amplitude grows. The discrepancies around the bifurcation point are presumably related to high sensitivity to initial conditions, as discussed later on. It was also determined that this transition depends both on the frequency and the amplitude of the external forcing. Defining the “transition amplitude” as the forcing amplitude at which the system displays a 10-fold growth in the displacement amplitude and plotting it versus forcing frequency shows it clearly.

In Fig. 10 also, the variations are likely caused by the sensitivity to the initial conditions. We also see that there is no clear bifurcation point here, as there is a “band” in which the system can stabilize on one of the two response regimes depending on initial conditions, implying fractal boundaries between the different response regimes in the state-space.

Fig. 10
figure 10

Bifurcation amplitude versus the frequency detuning

Full size image

3.3 Spectral analysis

In order to further study the observed response regimes, we have produced a frequency spectrum using Fast Fourier Transform (FFT) on a span of the time series after the initial transient, i.e., when the system reaches the steady-state. Under certain weak forcing, as one should expect, the response consists primarily of the component frequency equal to that of the excitation.

In Fig. 11, we present the FFT spectrum of the time series in Fig. 7a. The majority of the energy in this signal is concentrated around the 1:1 peak, and rapidly decays as frequency grows. Quite expectable peaks at the following odd multipliers of the primary frequency are present but barely notable. Still, even in these conditions, the spectrum of the NES, corresponding to the relative displacement between the NES components (Fig. 12) displays much more significant peaks at the odd multipliers.

Fig. 11
figure 11

Single-sided amplitude spectrum of the primary mass displacement for A=4 (the response in Fig. 7a)

Full size image
Fig. 12
figure 12

Single-sided amplitude spectrum of the relative displacements for A=4

Full size image

However, further simulations show that, again as one should expect, for both weaker and stronger forcing amplitudes, the spectrum may consist of many additional harmonics, as demonstrated here for forcing amplitudes of A=1 and A=8, respectively.

The spectra in Fig. 13 describe the motion of the primary mass, but both nonlinear energy sinks behave in rather similar fashion. In both cases, the significant responses are still concentrated around the first few odd multipliers, and due to the difference in magnitude, the system’s behavior is still determined mainly by the first peak cluster around the 1:1 resonance.

Fig. 13
figure 13

Primary mass displacement and its single-sided amplitude spectrum for A=1 (a) and A=8 (b)

Full size image

Under higher forcing amplitudes, the spectrum is different. Near the transition amplitude, the spectrum of the main mass shows additional peaks (Fig. 14a), at even multipliers, while the spectra of the NES (Fig. 14b–c) resemble that expected of an impact-like response, i.e., a relatively strong excitation of all the multiplies of the excitation frequency.

Fig. 14
figure 14

Single-sided amplitude spectrum of the primary mass (a) and the relative displacements (b–c) for A=14.5—an example of an impulse-like spectra

Full size image

Under these conditions, both NESs almost “lock” to the primary mass, their relative displacement being more than an order of magnitude smaller than that of the primary mass as mentioned in Sect. 3.1. Further evidence is found in comparison between the behavior of the NES before and after the critical amplitude. Shown in Fig. 15 are the relative displacements of the primary mass and the first NES.

Fig. 15
figure 15

Relative displacements before (a) (A=14.6) and after (b) (A=14.7) bifurcation, respectively, and their single-sided amplitude spectrum

Full size image

The spectrum before the transition in Fig. 15a shows much noisier peaks than the one after the bifurcation in Fig. 15b. The time series show that while the displacement amplitude of the NES is about 20 % that of the primary mass before the transition (see Fig. 8 for time series of the primary mass in corresponding cases), it is only about 3 % after it. These differences can be attributed to “locking” of the NES to the main mass over certain amplitudes, thus considerably limiting relative oscillations and drastically reducing the performance of the NES.

The implications of these results on the possible analytical approximations are discussed in more detail below.

3.4 Stability

As discussed earlier, the system can be very sensitive both to small changes in the parameters and in the initial conditions. This sensitivity cannot only be discussed in terms of modulations, but also in terms of periodicity.

In Fig. 16a, we see a time series of the system for some given parameters and its stroboscopic map with respect to the period of the external excitation. The response regimes presented in the map reveal seemingly quasiperiodic nature with relatively neat orbits. In the map obtained for the same system under slightly stronger excitation at Fig. 16b, the random scatter implies a very complex quasiperiodic response or even a chaotic response as investigated in Sect. 3.5. Note that although the time series seem similar at first glance, additional focus on the beat reveals a small difference between the two responses.

Fig. 16
figure 16

The primary mass displacement and the stroboscopic map of A=9.9, σ=0.9 (a) and A=10, σ=0.9 (b)

Full size image

It is important to note that the aforementioned response regimes can also coexist as can be seen in Fig. 17 where we can see a quasiperiodic response and what seems to be a chaotic one for the same parameters, differing only in initial condition. This is most interesting since even though the stroboscopic maps reveals essentially different response regimes; the time series shows that these are two close attractors that coexist there.

Fig. 17
figure 17

The primary mass displacement and the stroboscopic map for A=9 and σ=0.9 with u(0)=0 (a) and u(0)=18 (b)

Full size image

The coexistence of very close attractors along with the similarity of the responses in both Fig. 16 and Fig. 17 was quite suspicious and, therefore, an additional simulation was ran for a much longer time series; the stroboscopic map remained the same, thus denying the possibility of transient influence.

3.5 Chaotic regimes

“Scattered” character of the observed stroboscopic maps (Figs. 16, 17) gives a clue of some chaotic-like behavior of the system. To validate this assumption, we use the algorithm developed by Wolf et al. [24, 25] of computing Lyapunov exponents from a time series. The Lyapunov exponents describe the exponential rate of separation of trajectories with infinitesimal initial separation, i.e., a positive exponent means divergence and therefore chaos. The results are presented in Fig. 19.

It is quite interesting that for all responses with the excitation amplitude over critical value A=0.7 we observe positive Lyapunov exponents. This result holds even for the responses similar to one in Fig. 17b, which demonstrate seemingly “regular” stroboscopic map and their time series also look quite regular. It means that the chaotic behavior can be observed on quite a large time span, whereas the dynamics on a smaller span seems just “quasiperiodic.” As for the critical amplitude of the external excitation, it is possible to reveal its nature by a simple analytic procedure. This analysis is presented in the next section.

4 Theoretical analysis

4.1 Harmonic balance approximation for the case of low amplitudes

In general, known analytic procedures cannot say much about the behavior of this strongly nonlinear and highly degenerate system. We use here a version of common harmonic balance approach in order to study the transition from steady-state to weakly modulated response (Neimark–Sacker bifurcation) which occurs at relatively low amplitude of the external forcing. In this section, we use slightly modified equations of motion so that the detuning is not in the forcing but in the linear oscillator’s resonant frequency as in Eq. (3). This change introduces the discrepancy of order O(ε 2) and does not affect the qualitative behavior of this system.

$$ \left \{ \begin{array}{l}\ddot{u} + \varepsilon{\lambda_0}\dot{u} + ( {1 + \varepsilon \sigma} )u + \varepsilon{\lambda_1}( {\dot{u} - {{\dot{v}}_1}} )\\[3pt]\quad {} + \frac{4}{3}{k_2}\varepsilon{{( {u - {v_1}})}^3} = \varepsilon A\cos(t)\\[3pt]{m_1}{{\ddot{v}}_1} - {\lambda_1}( {\dot{u} - {{\dot{v}}_1}} )- \frac{4}{3}{k_2}{{( {u - {v_1}} )}^3}\\[3pt]\quad {} + {\lambda_2}( {{{\dot{v}}_1} - {{\dot{v}}_2}} ) + \frac{4}{3}{k_3}{{({{v_1} - {v_2}} )}^3} = 0\\[3pt]{m_2}{{\ddot{v}}_2} - {\lambda_2}( {{{\dot{v}}_1} - {{\dot{v}}_2}}) - \frac{4}{3}{k_3}{{( {{v_1} - {v_2}} )}^3} = 0\end{array} \right .$$
(3)

Simple change of variables in Eq. (3) brings about more convenient set of equations (See Eq. (4).)

$$ \left \{ \begin{array}{l}{{\ddot{x}}_1} + \frac{{{\lambda_0}\varepsilon( {{{\dot{x}}_1} +\varepsilon( {{m_1} + {m_2}} ){{\dot{x}}_2} + \varepsilon {m_2}{{\dot{x}}_3}} )}}{{1 + \varepsilon( {{m_1} + {m_2}})}}\\[5pt]\quad {}+ \frac{{( {1 + \varepsilon\sigma} )( {{x_1} +\varepsilon( {{m_1} + {m_2}} ){x_2} + \varepsilon {m_2}{x_3}} )}}{{1 + \varepsilon( {{m_1} + {m_2}} )}}= \varepsilon A\cos( t )\\[5pt]{{\ddot{x}}_2} - {{\ddot{x}}_1} + ( {\varepsilon + \frac {1}{{{m_1}}}} ){\lambda_1}{{\dot{x}}_2} + \frac {{4}}{3}{x_2^3}( {\varepsilon + \frac{1}{{{m_1}}}} )\\[5pt]\quad {} -\frac{1}{{{m_1}}}{{\lambda_2}{{\dot{x}}_3}} - \frac {{4}}{{3{m_1}}}{kx_3^3} = 0\\[5pt]{{\ddot{x}}_3} - \frac{1}{{{m_1}}}{{\lambda_1}{{\dot{x}}_2}} - \frac {{4}}{{3{m_1}}}{x_2^3} + ( {\frac{{{m_1} + {m_2}}}{{{m_1}{m_2}}}}){\lambda_2}{{\dot{x}}_3}\\[5pt]\quad {} + \frac{{4}}{3}{kx_3^3}( {\frac {{{m_1} + {m_2}}}{{{m_1}{m_2}}}} ) = 0\end{array} \right .$$
(4)

with

This still leaves us with second-order differential equations, therefore, further simplification is necessary. To reduce the order of our differential equations, we use complexification-averaging approach [19]. At the first stage, we replace \({\varphi_{n}} = \frac{{{{\dot{x}}_{n}} + i{x_{n}}}}{2}\) in Eq. (4) and obtain:

$$ \left \{ \begin{array}{l}2{{\dot{\varphi}}_1} - ( {{\varphi_1} + \varphi_1^*} )i +{( {1 + \varepsilon( {{m_1} + {m_2}} )} )^{ -1}}\\[5pt]\quad {}\times \left (\begin{array}{l}\varepsilon{\lambda_0}\left (\begin{array}{l}{\varphi_1} + \varphi_1^*\\[2pt]- \varepsilon({{m_1} + {m_2}} )( {{\varphi_2} +\varphi_2^*} )\\[2pt]- \varepsilon{m_2}({{\varphi_3} + \varphi_3^*} )\end{array} \right )\\[20pt]- i({1 + \sigma\varepsilon} )\left ( \begin{array}{l}{\varphi_1} - \varphi_1^*\\[2pt]- \varepsilon( {{m_1} + {m_2}} )( {{\varphi_2} -\varphi_2^*} )\\[2pt]- \varepsilon{m_2}( {{\varphi_3} - \varphi_3^*} )\end{array} \right ) \end{array} \right )\\[35pt]\quad = \varepsilon A\cos( t )\\[5pt]2{{\dot{\varphi}}_2} - ( {{\varphi_2} +\varphi_2^*} )i - 2{{\dot{\varphi}}_1} + ( {{\varphi_1} + \varphi_1^*} )i\\[5pt]\quad {}+ {\lambda_1} \bigl( {\varepsilon + \frac{1}{{{m_1}}}} \bigr)( {{\varphi_2} + \varphi_2^*} ) +\frac{{4i{{( {{\varphi_2}- \varphi_2^*} )}^3}}}{3} ( {\varepsilon + \frac {1}{{{m_1}}}} )\\[5pt]\quad {}- \frac{{{\lambda_2}( {{\varphi_3} + \varphi_3^*})}}{{{m_1}}} - \frac{{4ki{{( {{\varphi_3} - \varphi_3^*})}^3}}}{{3{m_1}}} = 0\\[5pt]2{{\dot{\varphi}}_3} - ( {{\varphi_3} +\varphi_3^*} )i - \frac{{{\lambda_1}( {{\varphi_2} + \varphi_2^*})}}{{{m_1}}}\\[5pt]\quad {}- \frac{{4i{{( {{\varphi_2} - \varphi_2^*})}^3}}}{{3{m_1}}} + {\lambda_2} \bigl( {\frac{{{m_1} +{m_2}}}{{{m_1}{m_2}}}} \bigr) ( {{\varphi_3} + \varphi_3^*}) \\[5pt]\quad {}+ \frac{{4ki{{( {{\varphi_3} - \varphi_3^*} )}^3}}}{3} \cdot \bigl( {\frac{{{m_1} + {m_2}}}{{{m_1}{m_2}}}} \bigr) = 0\end{array} \right .$$
(5)

Then we assume that the system is close to 1:1 resonance and only one frequency component should be taken into account. Consequently, we look for a harmonic solution with the excitation frequency φ n =ψ n exp(t⋅i) then averaging in Eq. (6).

$$ \left \{ \begin{array}{l}2{{\dot{\psi}}_1} + i{\psi_1}\\[6pt]\quad {}+ \frac{{\varepsilon{\lambda_0} -( {1 + \sigma\varepsilon} )i}}{{1 + \varepsilon({{m_1} + {m_2}} )}}\left (\begin{array}{l}{\varphi_1} - \varepsilon( {{m_1} + {m_2}} ){\psi_2}\\[4pt]- \varepsilon{m_2}{\psi_3}\end{array} \right ) =\frac{{\varepsilon A}}{2}\\[22pt]2{{\dot{\psi}}_2} + i{\psi_2} + \frac{{\varepsilon{\lambda_0} -( {1 + \sigma\varepsilon} )i}}{{1 + \varepsilon( {{m_1} +{m_2}} )}}\left (\begin{array}{l}{\psi_1} - \varepsilon( {{m_1} + {m_2}} ){\psi_2}\\[4pt]- \varepsilon{m_2}{\psi_3}\end{array} \right )\\[22pt]\quad {}+ \bigl( {\varepsilon + \frac{1}{{{m_1}}}} \bigr) ( {{\lambda_1} {\psi_2} - 4i{{|{{\psi_2}}|}^2} {\psi_2}} )\\[12pt]\quad {}+ \frac{1}{{{m_1}}}\left ( \begin{array}{l}4ik{| {{\psi_3}} |^2}{\psi_3}\\[4pt]- {\lambda_2}{\psi_3}\end{array} \right )= \frac{{\varepsilon A}}{2}\\[18pt]2{{\dot{\psi}}_3} + i{\psi_3} + \frac{1}{{{m_1}}}({4i{{| {{\psi_2}} |}^2} {\psi_2} - {\lambda_1} {\psi_2}} )\\[12pt]\quad {}+ \bigl( {\frac{{{m_1} + {m_2}}}{{{m_1}{m_2}}}} \bigr) ( {{\lambda_2} {\psi_3} - 4ik{{|{{\psi_3}} |}^2} {\psi_3}}) = 0 \end{array} \right .$$
(6)

Steady-state responses of the initial system correspond to fixed points of Eq. (6). Algebraic equations for these points may be written as

$$ \left \{ \begin{array}{l}{\psi_{10}}( {{\lambda_0} + i( {{m_1} + {m_2} - \sigma})} )\\[4pt]\qquad {}+ {\psi_{20}}( {\varepsilon{\lambda_0} - i( {1 + \sigma \varepsilon} )} )( {{m_1} + {m_2}} )\\[4pt]\qquad {}+ {\psi_{30}}{m_2}({\varepsilon{\lambda_0} - i( {1 +\sigma\varepsilon} )} )\\[4pt]\quad = \frac{A}{2}( {1 + \varepsilon( {{m_1} + {m_2}} )} )\\[4pt]i{\psi_{10}}{m_1} + {\psi_{20}}\left (\begin{array}{l}{\lambda_1}({\varepsilon{m_1} + 1} )+ i{m_1}\\[4pt]- 4i( {\varepsilon{m_1} + 1} ){| {{\psi_{20}}} |^2}\end{array} \right )\\[15pt]\quad + {\psi_{30}}( {4ik{{| {{\psi_{30}}} |}^2}- {\lambda_2}} ) = 0\\[4pt]{\psi_{20}}( {4i{m_2} {{|{{\psi_{20}}}|}^2} - {\lambda_1} {m_2}} )\\[4pt]\quad + {\psi_3}\left ( \begin{array}{l}i{m_1}{m_2}\\- 4ik( {{m_1} + {m_2}} ){|{{\psi_{30}}} |^2}\\[4pt]+ {\lambda_2}({{m_1} + {m_2}} )\end{array} \right ) = 0\end{array} \right .$$
(7)

For a more comfortable presentation of the equations, we replace q n =|ψ n |2 in Eq. (7) with some algebraic manipulations.

$$ \left \{ \begin{array}{l}{\psi_{10}}{h_1} + {\psi_{20}}{h_2} + {\psi_{30}}{m_2}{h_3} = H\\[4pt]{\psi_{10}}{g_1} + {\psi_{20}}{g_2} ( {{q_2}} ) + {\psi_{30}}{g_3} ( {{q_3}} ) = 0\\[4pt]{\psi_{20}}{f_2} ( {{q_2}} ) + {\psi_{30}}{f_3} ({{q_3}} ) = 0\end{array} \right .$$
(8)

where the new functions are defined in Appendix B.

From Eq. (8), we can derive two functions, presented below:

$$ \left \{ \begin{array}{l}F = {q_2}\bigl \vert {\frac{{{f_2}}}{{{f_3}}} \cdot\frac {{{g_3}}}{{{g_1}}}{h_1} - \frac{{{g_2}}}{{{g_1}}}{h_1} + {h_2} - \frac {{{f_2}}}{{{f_3}}}{h_3}} \bigr \vert - {H^2}\\[4pt]G = {q_2}\vert {{f_2}} \vert - {q_3}\vert {{f_3}} \vert \end{array} \right .$$
(9)

Requesting nullification of both these functions, and using Eqs. (4), (8), we find the steady state amplitudes for u, v 1, and v 2 and compare them with the numerical results in Fig. 20.

4.2 Stability of steady-state responses

To determine the stability, we add a small perturbation to the results found in the previous subsection, i.e., ψ n =ψ n0+δ n (δ n ≪ψ n ), and replace it in Eq. (6) to result in Eq. (10).

$$ \begin{array}{l}{{\dot{\delta}}_1} + {C_1}{\delta_1} + {C_2}{\delta_2} + {C_3}{\delta_3} = 0\\[4pt]{{\dot{\delta}}_2} + {D_1}{\delta_1} + {D_2}{\delta_2} + {D_3}{\delta_3} + {D_4}\delta_2^* + {D_5}\delta_3^* = 0\\[4pt]{{\dot{\delta}}_3} + {E_1}{\delta_2} + {E_2}{\delta_3} + {E_3}\delta_2^* + {E_4}\delta_3^* = 0\end{array} $$
(10)

Coefficients in these equations are defined in Appendix C.

Putting Eq. (10) in matrix form in Eq. (11) so we can look for positive eigenvalues implying instability.

(11)

Results for particular set of parameters are presented in Fig. 20. Even without looking further into the response, we can immediately see that there exists a transition in the numerical result very close to the Hopf bifurcation where the response becomes unstable.

It is also interesting to note that the loss of stability is more or less in accordance with the appearance of positive Lyapunov exponents as shown in Fig. 18.

Fig. 18
figure 18

Largest Lyapunov exponent with respect to excitation amplitude for σ=0.9

Full size image
Fig. 19
figure 19

A sample of the intersections of F and G for some arbitrary parameters

Full size image
Fig. 20
figure 20

Analytical and numerical displacement magnitudes in respect to excitation amplitude for σ=0.9

Full size image

Figure 21 indeed verifies the loss of stability; moreover, we can see that the loss of stability brings about weak modulation of the steady-state response.

Fig. 21
figure 21

Primary mass’ displacement before (A=0.55, σ=0.9) and after (A=0.65, σ=0.9) loss of stability, respectively

Full size image

However, for larger excitation amplitudes, the harmonic balance becomes unusable, as expected for this simple approximation.

5 Concluding remarks

The results presented above demonstrate that the 2DOF NES can have significantly better performance as for the amplitude range of vibration absorption than the SDOF NES with equal mass. In other terms, the enhanced TET abilities [23] of the 2DOF NES exist for the periodic excitation as well. However, additional complications also appear. The system with 2DOF NES exhibits a multitude of possible dynamical responses; even for moderate excitation amplitudes most of them appear to have chaotic nature. There are many interesting phenomena in this system, such as existence of a multitude of rather close attractors and the “locking” of the strongly nonlinear attachment; needless to say, these phenomena deserve additional study. As for engineering applications, further investigations are required to establish whether dynamical systems with that complicated behavior can be feasible as the vibration absorbers.