Introduction

High-strength and lightweight composites were applied effectively in numerous fields of material science engineering. The nonlinear vibration of laminated composite plates has obtained a huge deal of attention since they are suitable for use in harsh environments. To fit a variety of material applications, it is critical to determine the frequency of the nonlinear vibration accurately.

The nonlinear vibration behavior of plates was extensively assessed utilizing different approximation methods. Several authors studied the plates’ nonlinear vibration behavior for laminated and isotropic composite plates.

Large deflection vibration of cross-ply laminated plates with certain edge conditions. Journal of Sound and Vibration studied by Chandra [1]. Chandra et al. analyzed Large deflection vibration of angle ply laminated plates [2]. Singh et al. investigated Non-linear vibrations of simply supported rectangular cross-ply plates. Journal of Sound and Vibration [3]. Singh et al. presented Large amplitude free vibration of simply supported antisymmetric cross-ply plates [4]. Nonlinear vibrations of rectangular laminated composite plates with different boundary conditions. Was reviewed by Amabili et al. [5]. Analytical Nonlinear Elasto-Plastic Impact Response of a Moderately Thick Rectangular Plate has been studied by Khorshidi [6].

The Homotopy Perturbation Method (HPM) for nonlinear vibration behavior of functionally graded plates analyzed by Yazdi [7]. The HPM was further used to analyze the geometrical nonlinear vibrations of thin rectangular laminated plates made of functionally graded material (FGM). Using Von Karman's strain displacement relations, the structural nonlinearity of the system has been modeled. Quan and Duc studied Nonlinear vibration and dynamic response of shear deformable imperfect functionally graded double curved shallow shells resting on elastic foundations in thermal environments [8]. Vibration and nonlinear dynamic response of imperfect sandwich piezoelectric auxetic plate were reviewed by Quan et al. [9].

Andrianov et al. presented An artificial small perturbation parameter and nonlinear plate vibrations. Journal of Sound and Vibration [10]. Duc and Tung investigated Nonlinear analysis of stability for functionally graded cylindrical shells under axial compression [11]. An analytical approach for nonlinear thermo-electro-elastic forced vibration of piezoelectric penta-graphene plates has been done by Quan Quyen and Duc [12]. Differential quadrature method for nonlinear vibration of orthotropic plates with finite deformation and transverse shear effect provided by Li and Cheng [13]. These authors assessed the nonlinear free vibration behavior by the differential quadrature technique, using the harmonic balance process to derive the equations of motion. Lal et al. [14] presented Nonlinear free vibration of laminated composite plates on elastic foundation with random system properties. Typical numerical results (second-order statistics) were obtained for the composite plates resting on Winkler and Pasternak elastic foundations with different support conditions. Quan et al.presented Vibration and nonlinear dynamic response of imperfect sandwich piezoelectric auxetic plate [9]. Nonlinear buckling and postbuckling of imperfect piezoelectric S-FGM circular cylindrical shells with metal-ceramic–metal layers in thermal environment using Reddy's third-order shear deformation shell theory Was reviewed by Khoa et al. [15].

Tian et al. [16] presented A new higher-order analysis model for sandwich plates with flexible core.

The Vibration Controllability of Sandwich Structures with Smart Materials of Electrorheological Fluids and Magnetorheological Materials was explored by Kolekar et al. [17]. Nonlinear stability of eccentrically stiffened S-FGM elliptical cylindrical shells in thermal environment has been studied by Duc et al. [18]. Malekzadeh et al. [19] investigated the dynamic response of in-plane pre-stressed sandwich panels with a viscoelastic flexible core and various boundary conditions. A Three-Layer Quasi-3D Finite Element Analysis for Smart Actuation on Sandwich Plates has been studied by Nabarrete [20]. Lv et al. presented The Dynamic Models, Control Strategies and Applications for Magnetorheological Damping Systems: A Systematic Review [21]. Duc investigated Nonlinear thermo-electro-mechanical dynamic response of shear deformable piezoelectric Sigmoid functionally graded sandwich circular cylindrical shells on elastic foundations [22]. Nonlinear analysis of stability for functionally graded cylindrical shells under axial compression has been done by Tungand and Duc [23].

For moderately thick laminated plates, applying classical theories can result in imprecise data. In anisotropic materials, a coupling exists between the stretching and bending of laminated composite plates. It is caused by overlooking the rotary inertia and shear strains effects. Hence, both the first-order shear deformation and higher-order SDT theories have been used to assess the laminated plates’ nonlinear vibration behavior. Frostig [24] developed the higher-order sandwich panel theory. Malekzadeh et al. [25]introduced the enhanced higher-order sandwich plate theory using the first-order shear deformation theory to the face sheets. Most studies conducted in recent years, focused on the Vibration of a sandwich plate equipped with an electrorheological fluid core. the concepts of ER adaptive structures based on materials for the first time were introduced by Carlson [26]. Yeh and Chen investigated the dynamic stability problems of an ER sandwich beam and explained the dynamic behavior of a variety of sandwich plates (annular, orthotropic, orthotropic annular, and rotating polar orthotropic annular plates) with various thicknesses of the ER layer and electric field strength [27,28,29,30,31,32]. high-order linear vibration behavior of moderately thick sandwich panel equipped with an ER core evaluated by Keshavarzian et al. [33].

Despite the fact that wide studies have been conducted on the vibration performance of sandwich panels equipped with ER fluid cores, fewer studies have been published on the nonlinear vibration behavior of sandwich panels consisting of ER fluid cores. Therefore, there is a definite need for research to elucidate this subject further. Considering these facts, this study was designed for deriving the nonlinear equations of motion for sandwich panels with multi-layer face sheets and an ER fluid core. For this purpose, we used the first-order shear deformation theory, including rotary inertia. Our primary focus was to examine the impacts of geometric aspect ratio, electric field magnitude, and ER core layer thickness versus the sandwich panels dynamic properties in terms of Galerkin’s method. These equations were decreased to some coupled nonlinear partial differential equations (PDEs) plus a compatibility equation after the introduction of a force function. This was accomplished after establishing the validity of our study on isotropic and investigating the laminated rectangular panels, nonlinear and linear free vibration of a panel. Moreover, we studied the impacts of the system’s parameters on the nonlinear vibration frequency.

Theoretical Formulation

Basic Assumptions

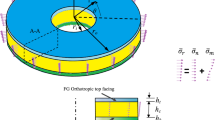
The basic assumption was having a thick composite sandwich panel comprising two composite laminated face sheets and a core layer, in which the thickness of the bottom and top covers, and the core material were as follows: ht, hb, hc. The proposed sandwich panel would have its length “a”, width “b” and total thickness as “h”. In addition, the orthogonal coordinates (xi, yi, zii = t, b, c) would be as represented in Fig. 1. In that model, the “t” index represents the upper sheet, “b” shows the lower sheet, and “c” represents the core.

Fig. 1
figure 1

A sandwich panel with laminated face sheets, an ER core and orthogonal coordinates

Full size image

Mathematical Formulations

The “u, v and w” of the face sheets plus the “x, y (longitudinal) and z (thickness) axes” are stated as:

$$\begin{aligned}{u}_{i}\left(x,z,y,t\right)&={u}_{0}^{i}\left(x,y,t\right)+{f}_{1}\left({z}_{i}\right)\frac{\partial {w}_{0}\left(x,y,t\right)}{\partial x}+{f}_{2}\left({z}_{i}\right){\phi }_{x}^{i}\left(x,y,t\right)\\ {v}_{i}\left(x,z,y,t\right)& ={v}_{0}^{i}\left(x,y,t\right)+{f}_{1}\left({z}_{i}\right)\frac{\partial {w}_{0}\left(x,y,t\right)}{\partial y}+{f}_{2}\left({z}_{i}\right){\phi }_{y}^{i}\left(x,y,t\right); \left(i=t,b\right)\\ {w}_{i}\left(x,z,y,t\right)& ={w}_{0}^{i}\left(x,y,t\right), \end{aligned}$$
(1)

where “zi” represents the vertical coordinate of each face sheet (i = t, b), which was measured upward from each face sheet mid-plane. Regarding the first-order shear deformation theory, \({f}_{1}\left({z}_{i}\right)=0\), \({f}_{2}\left({z}_{i}\right)={z}_{i}\), the kinematic equations for the face sheets are:

$${\varepsilon }_{xx}^{i}={\varepsilon }_{0xx}^{i}+{f}_{1}\left({z}_{i}\right){L}_{xx}^{i}+{f}_{2}\left({z}_{i}\right){k}_{xx}^{i} , {\varepsilon }_{yy}^{i}={\varepsilon }_{0yy}^{i}+{f}_{1}\left({z}_{i}\right){L}_{yy}^{i}+{f}_{2}\left({z}_{i}\right){k}_{yy }^{i}, {\varepsilon }_{zz}^{i}=0,$$
$$\begin{aligned}& {\gamma }_{xy}^{i}=2{\varepsilon }_{xy}^{i}={\gamma }_{0xy}^{i}+{f}_{1}\left({z}_{i}\right){L}_{xy}^{i}+{f}_{2}\left({z}_{i}\right){k}_{xy}^{i}\\ & {\gamma }_{xz}^{i}=2{\varepsilon }_{xz}^{i}={\gamma }_{0xz}^{i}+\frac{d{f}_{1}\left({z}_{i}\right)}{d{z}_{i}}{G}_{xz}^{i}+\frac{d{f}_{2}\left({z}_{i}\right)}{d{z}_{i}}{T}_{xz}^{i}; \left(i=t,b\right)\\ & {\gamma }_{yz}^{i}=2{\varepsilon }_{yz}^{i}={\gamma }_{0yz}^{i}+\frac{d{f}_{1}\left({z}_{i}\right)}{d{z}_{i}}{G}_{yz}^{i}+\frac{d{f}_{2}\left({z}_{i}\right)}{d{z}_{i}}{T}_{yz}^{i}\end{aligned}$$
(2)

where

$$\begin{aligned}{\varepsilon }_{0xx}^{i}& =\frac{\partial {u}_{0}^{i}}{\partial x}+{\frac{1}{2}\left(\frac{\partial {w}_{0}^{i}}{\partial x}\right)}^{2}, {\varepsilon }_{0yy}^{i}=\frac{\partial {v}_{0}^{i}}{\partial y}+{\frac{1}{2}\left(\frac{\partial {w}_{0}^{i}}{\partial y}\right)}^{2} , {\gamma }_{0xy}^{i}=\frac{\partial {v}_{0}^{i}}{\partial x}+\frac{\partial {u}_{0}^{i}}{\partial y}+\frac{\partial {w}_{0}^{i}}{\partial x} \frac{\partial {w}_{0}^{i}}{\partial y} \\{\gamma }_{0xz}^{i}&=\frac{\partial {w}_{0}^{i}}{\partial x}, {\gamma }_{0yz}^{i}=\frac{\partial {w}_{0}^{i}}{\partial y}, {L}_{xx}^{i}=\frac{{\partial }^{2}{w}_{0}^{i}}{\partial {x}^{2}}, {k}_{xx}^{i}=\frac{\partial {\phi }_{x}^{i}}{\partial x}, {L}_{yy}^{i}=\frac{{\partial }^{2}{w}_{0}^{i}}{\partial {y}^{2}}, {k}_{yy}^{i}=\frac{\partial {\phi }_{y}^{i}}{\partial y}, \\ {L}_{xy}^{i}&=2\frac{{\partial }^{2}{W}_{0}^{i}}{\partial x\partial y}, {k}_{xy}^{i}=\frac{\partial {\phi }_{x}^{i}}{\partial y}+\frac{\partial {\phi }_{y}^{i}}{\partial x} , {G}_{xz}^{i}=\frac{\partial {w}_{0}^{i}}{\partial x} , {T}_{xz}^{i}={\phi }_{x}^{i} , {G}_{yz}^{i}=\frac{\partial {w}_{0}^{i}}{\partial y} , {T}_{yz}^{i}={\phi }_{y}^{i}.\end{aligned}$$
(3)

Displacement fields are oriented by the second Frostig’s model for the thick core layer, as follows [24]:

$$\begin{aligned}{u}_{c}\left(x,y,z,t\right)&={u}_{0}^{c}\left(x,y,t\right)+{z}_{c}{u}_{1}^{c}\left(x,y,t\right)+{z}_{c}^{2}{u}_{2}^{c}\left(x,y,t\right)+{z}_{c}^{3}{u}_{3}^{c}\left(x,y,t\right),\\{v}_{c}\left(x,y,z,t\right)&={v}_{0}^{c}\left(x,y,t\right)+{z}_{c}{v}_{1}^{c}\left(x,y,t\right)+{z}_{c}^{2}{v}_{2}^{c}\left(x,y,t\right)+{z}_{c}^{3}{v}_{3}^{c}\left(x,y,t\right),\\ {w}_{c}\left(x,y,z,t\right)&={w}_{0}^{c}\left(x,y,t\right)+{z}_{c}{w}_{1}^{c}\left(x,y,t\right)+{z}_{c}^{2}{w}_{2}^{c}\left(x,y,t\right).\end{aligned}$$
(4)

The kinematic relations of the core layer are:

$$\begin{aligned}{\varepsilon }_{xx}^{c}& =\frac{\partial {u}_{c}}{\partial x}, {\varepsilon }_{yy}^{c}=\frac{\partial {v}_{c}}{\partial y} ,{\varepsilon }_{zz}^{c}=\frac{\partial {w}_{c}}{\partial z}\\ {\gamma }_{xy}^{c}&=2{\varepsilon }_{xy}^{c}= \frac{\partial {v}_{c}}{\partial x}+\frac{\partial {u}_{c}}{\partial y} , { \gamma }_{xz}^{c}=2{\varepsilon }_{xz}^{c}= \frac{\partial {w}_{c}}{\partial x}+\frac{\partial {u}_{c}}{\partial z}, {\gamma }_{yz}^{c}=2{\varepsilon }_{yz}^{c}=\frac{\partial {w}_{c}}{\partial y}+\frac{\partial {v}_{c}}{\partial z}.\end{aligned}$$
(5)

By placing the (4) in the relations (5) the strains in terms of the displacement of the mid-plane can be obtained as follows:

$$\begin{aligned}{\varepsilon }_{xx}^{c}&=\left({\varepsilon }_{0xx}+{z}_{c}{x}_{0xx}+{{z}_{c}}^{2}{\varepsilon }_{0xx}^{*}+{{z}_{c}}^{3}{x}_{0xx}^{*}\right), {\varepsilon }_{yy}^{c}=\left({\varepsilon }_{0yy}+{z}_{c}{x}_{0yy}+{{z}_{c}}^{2}{\varepsilon }_{0yy}^{*}+{{z}_{c}}^{3}{x}_{0yy}^{*}\right)\\{\varepsilon }_{zz}^{c}&={\varepsilon }_{0zz}+{z}_{c}{x}_{0zz}\\{\gamma }_{xy}^{c}&={\varepsilon }_{0xy}+{z}_{c}{x}_{0xy}+{{z}_{c}}^{2}{\varepsilon }_{0xy}^{*}+{{z}_{c}}^{3}{x}_{0xy}^{*}+{\varepsilon }_{0yx}+{z}_{c}{x}_{0yx}+{{z}_{c}}^{2}{\varepsilon }_{0yx}^{*}+{{z}_{c}}^{3}{x}_{0yx}^{*}\\{\gamma }_{xz}^{c}&={\varepsilon }_{0xz}+{z}_{c}{x}_{0xz}+{{z}_{c}}^{2}{\varepsilon }_{0xz}^{*}+{{z}_{c}}^{3}{x}_{0xz}^{*}+{\varepsilon }_{1xz}+{{z}_{c}}{x}_{1xz}+{{z}_{c}}^{2}{\varepsilon }_{1xz}^{*}\\ {\gamma }_{yz}^{c}&={\varepsilon }_{0yz}+{z}_{c}{x}_{0yz}+{{z}_{c}}^{2}{\varepsilon }_{0yz}^{*}+{{z}_{c}}^{3}{x}_{0yz}^{*}+{\varepsilon }_{1yz}+{{z}_{c}}{x}_{1yz}+{{z}_{c}}^{2}{\varepsilon }_{1yz}^{*},\end{aligned} $$
(6)

where

$$\begin{aligned}{\varepsilon }_{0xx}& =\frac{\partial {u}_{0}^{c}}{\partial x}, {\chi }_{0xx}=\frac{\partial {u}_{1}^{c}}{\partial x} ,{\varepsilon }_{0xx}^{*}=\frac{\partial {u}_{2}^{c}}{\partial x}, {\chi }_{0xx}^{*}=\frac{\partial {u}_{3}^{c}}{\partial x} ,{\varepsilon }_{0yy}=\frac{\partial {v}_{0}^{c}}{\partial y},\\ {\chi }_{0yy}&=\frac{\partial {v}_{1}^{c}}{\partial y} ,{\varepsilon }_{0yy}^{*}=\frac{\partial {v}_{2}^{c}}{\partial y}, {\chi }_{0yy}^{*}=\frac{\partial {v}_{3}^{c}}{\partial y} ,{\varepsilon }_{0zz}={w}_{1}^{c}, {\chi }_{0zz}=2{w}_{2}^{c}\\ {\varepsilon }_{0xy}&=\frac{\partial {v}_{0}^{c}}{\partial x} , {\chi }_{0xy}=\frac{\partial {v}_{1}^{c}}{\partial x} , {\varepsilon }_{0xy}^{*}=\frac{\partial {v}_{2}^{c}}{\partial x} , {\chi }_{0xy}^{*}=\frac{\partial {v}_{3}^{c}}{\partial x} ,{\varepsilon }_{0yx}=\frac{\partial {u}_{0}^{c}}{\partial y} , {\chi }_{0yx}=\frac{\partial {u}_{1}^{c}}{\partial y}\\ {\varepsilon }_{0yx}^{*}&=\frac{\partial {u}_{2}^{c}}{\partial y} , {\chi }_{0yx}^{*}=\frac{\partial {u}_{3}^{c}}{\partial y} ,{\varepsilon }_{0xz}=\frac{\partial {w}_{0}^{c}}{\partial x} , {\chi }_{0xz}=\frac{\partial {w}_{1}^{c}}{\partial x} , {\varepsilon }_{0xz}^{*}=\frac{\partial {w}_{2}^{c}}{\partial x} ,{\chi }_{0xz}^{*}=0\\ {\varepsilon }_{1xz}&={u}_{1}^{c} , {\chi }_{1xz}=2{u}_{2}^{c} , {\varepsilon }_{xz}^{*}=3{u}_{3}^{c} {\varepsilon }_{0yz}=\frac{\partial {w}_{0}^{c}}{\partial y} , {\chi }_{0yz}=\frac{\partial {w}_{1}^{c}}{\partial y} , {\varepsilon }_{0yz}^{*}=\frac{\partial {w}_{2}^{c}}{\partial y}\\ {\chi }_{0xy}^{*}& =0 , {\varepsilon }_{1yz}={v}_{1}^{c} , {\chi }_{1yz}=2{v}_{2}^{c} , {\varepsilon }_{yz}^{*}=3{v}_{3}^{c}. \end{aligned}$$
(7)

The following compatibility circumstances are obtained assuming a perfect bonding between the bottom and top face sheets and core interfaces:

$$\left\{\begin{array}{l}{u}_{c}\left(z={z}_{ci}\right)={u}_{0}^{i}+\frac{1}{2}{\left(-1\right)}^{k}{h}_{i}{\phi }_{x}^{i}\\ {v}_{c}\left(z={z}_{ci}\right)={v}_{0}^{i}+\frac{1}{2}{\left(-1\right)}^{k}{h}_{i}{\phi }_{y}^{i}\\ {w}_{c}\left(z={z}_{ci}\right)={w}_{0}^{i}\end{array}\right. \left\{\begin{array}{l}\text{For}\quad i=t\to \left(k=1;{z}_{ct}=\frac{{h}_{c}}{2}\right)\\ \text{For} \quad i=b\to \left(k=0; {z}_{cb}=-\frac{{h}_{c}}{2}\right)\end{array}\right..$$
(8)

Applying Eqs. (4) and (6) with some simplifications, the compatibility circumstances may be expressed as:

$$\begin{aligned}{u}_{2}^{c}&=\frac{2\left({u}_{0}^{t}+{u}_{0}^{b}\right)-{h}_{t}{\phi }_{x}^{t}+{h}_{b}{\phi }_{x}^{b}-4{u}_{0}^{c}}{{h}_{c}^{2}}, {u}_{3}^{c}=\frac{4\left({u}_{0}^{t}-{u}_{0}^{b}\right)-2\left({h}_{t}{\phi }_{x}^{t}+{h}_{b}{\phi }_{x}^{b}\right)-4{h}_{c}{u}_{1}^{c}}{{h}_{c}^{3}}\\{v}_{2}^{c}& =\frac{2\left({v}_{0}^{t}+{v}_{0}^{b}\right)-{h}_{t}{\phi }_{y}^{t}+{h}_{b}{\phi }_{y}^{b}-4{v}_{0}^{c}}{{h}_{c}^{2}} ,{v}_{3}^{c}=\frac{4\left({v}_{0}^{t}-{v}_{0}^{b}\right)-2\left({h}_{t}{\phi }_{y}^{t}+{h}_{b}{\phi }_{y}^{b}\right)-4{h}_{c}{v}_{1}^{c} }{{h}_{c}^{3}}\\ {w}_{1}^{c}& =\frac{\left({w}_{0}^{t}+{w}_{0}^{b}\right)}{{h}_{c}}, {w}_{2}^{c}=\frac{2\left({w}_{0}^{t}+{w}_{0}^{b}\right)-4{w}_{0}^{c}}{{h}_{c}^{2}}\end{aligned}$$
(9)

According to Eq. (7), the number of unknown elements in the core layer is decreased to five items as: \(u_{0}^{c} ,u_{1}^{c} ,v_{0}^{c} ,v_{1}^{c} \;{\text{and}}\;w_{0}^{c}\). Therefore, the unknowns for a flat composite sandwich panel consist of fifteen items as follows:

$$\left\{{u}_{0}^{t} , {v}_{0}^{t},{w}_{0}^{t},{\psi }_{x}^{t},{\psi }_{y}^{t},{u}_{0}^{b},{v}_{0}^{b},{w}_{0}^{b},{\psi }_{x}^{b},{\psi }_{y}^{b},{u}_{0}^{c} , {u}_{1}^{c},{v}_{0}^{c} , {v}_{1}^{c},{w}_{0}^{c}\right\}.$$

resultants of the Stress for the Core

The stress has the following results on core:

$$\begin{aligned} & \left\{\begin{array}{c}\begin{array}{c}\begin{array}{c}{N}_{xx}^{c}\\ {N}_{yy}^{c}\end{array}\\ {N}_{xy}^{c}\end{array}\end{array}\right\}=\underset{-{h}_{c}/2}{\overset{{h}_{c}/2}{\int }}\left\{\begin{array}{c}\begin{array}{c}\begin{array}{c}{\sigma }_{xx}^{c}\\ {\sigma }_{yy}^{c}\end{array}\\ {\sigma }_{xy}^{c}\end{array}\end{array}\right\}d{z}_{c} ,\left\{\begin{array}{c}\begin{array}{c}\begin{array}{c}{M}_{nxx}^{c}\\ {M}_{nyy}^{c}\end{array}\\ {M}_{nxy}^{c}\end{array}\end{array}\right\}=\underset{-{h}_{c}/2}{\overset{{h}_{c}/2}{\int }}{z}_{c}^{n}\left\{\begin{array}{c}\begin{array}{c}\begin{array}{c}{\sigma }_{xx}^{c}\\ {\sigma }_{yy}^{c}\end{array}\\ {\sigma }_{xy}^{c}\end{array}\end{array}\right\}d{z}_{c}, \left\{\begin{array}{c}\begin{array}{c}\begin{array}{c}{N}_{xz}^{c}\\ {N}_{yz}^{c}\end{array}\\ {M}_{nxz}^{c}\end{array}\\ {M}_{nyz}^{c}\end{array}\right\}=\underset{-{h}_{c}/2}{\overset{{h}_{c}/2}{\int }}{z}_{c}^{n}\left\{\begin{array}{c}\begin{array}{c}\begin{array}{c}{\sigma }_{xz}^{c}\\ {\sigma }_{yz}^{c}\end{array}\\ {z}_{c}^{n}{\sigma }_{xz}^{c}\end{array}\\ {z}_{c}^{n}{\sigma }_{yz}^{c}\end{array}\right\}d{z}_{c}\\ & \quad \left\{{R}_{z}^{c},{M}_{z}^{c}\right\}=\underset{-{h}_{c}/2}{\overset{{h}_{c}/2}{\int }}\left(1,{z}_{c}\right){\sigma }_{zz}^{c}d{z}_{c} , \quad n=\mathrm{1,2},3.\end{aligned}$$
(10)

Resulting Stress per Unit Length of the Face Sheets

resultant stress per unit length of the face sheets is defined as follows:

$$\begin{aligned}&\left\{\begin{array}{c}\begin{array}{c}\begin{array}{c}{N}_{xx}^{i}\\ {N}_{yy}^{i}\end{array}\\ {N}_{xy}^{i}\end{array}\end{array}\right\}=\underset{-{h}_{i}/2}{\overset{{h}_{i}/2}{\int }}\left\{\begin{array}{c}\begin{array}{c}\begin{array}{c}{\sigma }_{xx}^{i}\\ {\sigma }_{yy}^{i}\end{array}\\ {\sigma }_{xy}^{i}\end{array}\end{array}\right\}d{z}_{i} , \left\{\begin{array}{c}\begin{array}{c}\begin{array}{c}{M}_{xx}^{i}\\ {M}_{yy}^{i}\end{array}\\ {M}_{xy}^{i}\end{array}\end{array}\right\}=\underset{-{h}_{i}/2}{\overset{{h}_{i}/2}{\int }}{f}_{1}\left({z}_{i}\right)\left\{\begin{array}{c}\begin{array}{c}\begin{array}{c}{\sigma }_{xx}^{i}\\ {\sigma }_{yy}^{i}\end{array}\\ {\sigma }_{xy}^{i}\end{array}\end{array}\right\}d{z}_{i }, \left\{\begin{array}{c}\begin{array}{c}\begin{array}{c}{P}_{xx}^{i}\\ {P}_{yy}^{i}\end{array}\\ {P}_{xy}^{i}\end{array}\end{array}\right\}=\underset{-{h}_{i}/2}{\overset{{h}_{i}/2}{\int }}{f}_{2}\left({z}_{i}\right)\left\{\begin{array}{c}\begin{array}{c}\begin{array}{c}{\sigma }_{xx}^{i}\\ {\sigma }_{yy}^{i}\end{array}\\ {\sigma }_{xy}^{i}\end{array}\end{array}\right\}d{z}_{i}\\ & \quad {N}_{xz}^{i}={k}_{s}\underset{-{h}_{i}/2}{\overset{{h}_{i}/2}{\int }}{\sigma }_{xz}^{i}d{z}_{i}, {R}_{xz}^{i} ={k}_{s}\underset{-{h}_{i}/2}{\overset{{h}_{i}/2}{\int }}{\left(\frac{d{f}_{1}\left({z}_{i}\right)}{dz}\right)\sigma }_{xz}^{i}d{z}_{i},{S}_{xz}^{i} ={k}_{s}\underset{-{h}_{i}/2}{\overset{{h}_{i}/2}{\int }}{\left(\frac{d{f}_{2}\left({z}_{i}\right)}{dz}\right)\sigma }_{xz}^{i}d{z}_{i,}i=t,b\\ & \quad {N}_{yz}^{i} ={k}_{s}\underset{-{h}_{i}/2}{\overset{{h}_{i}/2}{\int }}{\sigma }_{yz}^{i}d{z}_{i},{R}_{yz}^{i} ={k}_{s}\underset{-{h}_{i}/2}{\overset{{h}_{i}/2}{\int }}{\left(\frac{d{f}_{1}\left({z}_{i}\right)}{dz}\right)\sigma }_{yz}^{i}d{z}_{i},{S}_{yz}^{i} ={k}_{s}\underset{-{h}_{i}/2}{\overset{{h}_{i}/2}{\int }}{\left(\frac{d{f}_{2}\left({z}_{i}\right)}{dz}\right)\sigma }_{yz}^{i}d{z}_{i,}i=t,b,\end{aligned}$$
(11)

where \({k}_{s}\) is the shear correction factor.

Equations of Motion

The Hamilton’s principle was used for extracting the sandwich panel motion equations. Analytically, the principle may be expressed as:

$$\underset{0}{\overset{t}{\int }}\delta \mathrm{Ldt}=\underset{0}{\overset{t}{\int }}\left(\delta K-\delta U+\delta {W}_{\mathrm{ext}}\right)dt=0,$$
(12)

where, δK and δU denote variations in the kinetic and strain energies, respectively. Also, \(\delta {W}_{\mathrm{ext}}\) potential energy variation is caused by external forces and “t” is the duration between times “t1 and t2”, and “δ” represents the variation operator. Hence, the first variation equation of the kinetic energy (presuming homogeneous circumstances for velocity and displacement regarding time coordinate) is:

$$\begin{aligned}& \begin{array}{c}\delta K=-\sum_{i=t,b,c}\left[\underset{{A}_{i}}{\overset{}{\iint }}\underset{-{h}_{i}/2}{\overset{{h}_{i}/2}{\int }}{\rho }_{i}\left({\ddot{u}}_{i}\delta {u}_{i}+{\ddot{v}}_{i}\delta {v}_{i}+{\ddot{w}}_{i}\delta {w}_{i}\right)d{z}_{i} d{A}_{i}\right]\end{array}\\ & \quad d{A}_{c}=d{x}_{c}d{y}_{c}, d{A}_{i}=d{x}_{i}d{y}_{i}, \left(i=t,b\right).\end{aligned}$$
(13)

The total strain energy stored in the sandwich panel cases and core is expressed as follows:

$$\begin{aligned}\delta U&=\sum_{i=t,b}\left(\underset{{V}_{i}}{\overset{}{\int }}\left({\sigma }_{xx}^{i}\delta {\varepsilon }_{xx}^{i}+{\sigma }_{yy}^{i}\delta {\varepsilon }_{yy}^{i}+{\gamma }_{xy}^{i}\delta {\gamma }_{xy}^{i}+{\gamma }_{xz}^{i}\delta {\gamma }_{xz}^{i}+{\gamma }_{yz}^{i}\delta {\gamma }_{yz}^{i}\right)d{V}_{i}\right) \\& \quad+\underset{{V}_{c}}{\overset{}{\int }}\left({\sigma }_{xx}^{c}\delta {\varepsilon }_{xx}^{c}+{\sigma }_{yy}^{c}\delta {\varepsilon }_{yy}^{c}+{\gamma }_{xy}^{c}\delta {\gamma }_{xy}^{c}+{\gamma }_{xz}^{c}\delta {\gamma }_{xz}^{c}+{\gamma }_{yz}^{c}\delta {\gamma }_{yz}^{c}\right)d{V}_{c},\end{aligned}$$
(14)

where: dVc = dAcdZc = dxcdycdzc, dVi = dAidzi = dxidyidzi; (i = t, b).

Ultimately, we must substitute the relations of both the displacement fields and strain–displacement in the kinetic energy variations and system potentials. Using the Hamilton's principle, the motion equations are obtained. Given the long equations, only one equation is given as an example:

$$\begin{aligned}{\delta u}_{0}^{t}& :\frac{\partial {N}_{xx}^{t}}{\partial x}+\frac{\partial {N}_{xy}^{t}}{\partial y}+\frac{2}{{h}_{C}^{2}}\frac{\partial {M}_{2xx}^{C}}{\partial x}+\frac{4}{{h}_{C}^{3}}\frac{\partial {M}_{3xy}^{C}}{\partial y}+\frac{2}{{h}_{C}^{2}}\frac{\partial {M}_{2xy}^{C}}{\partial y}-\frac{4{M}_{1xz}^{C}}{{h}_{C}^{2}}-\frac{12{M}_{2xz}^{C}}{{h}_{C}^{3}}+\frac{4}{{h}_{C}^{3}}\frac{\partial {M}_{3xx}^{C}}{\partial x}\\ & =\left(-\frac{16{I}_{5}^{c}}{{h}_{c}^{5}}\right.\left.-\frac{8{I}_{4}^{C}}{{h}_{c}^{4}}+\frac{4{I}_{3}^{C}}{{h}_{c}^{3}}+\frac{2{I}_{2}^{C}}{{h}_{c}^{2}}\right){\ddot{u}}_{0}^{C}+\left(\frac{2{I}_{3}^{C}}{{h}_{c}^{2}}\right.\left.-\frac{8{I}_{5}^{C}}{{h}_{c}^{4}}-\frac{16{I}_{6}^{C}}{{h}_{c}^{5}}+\frac{4{I}_{4}^{C}}{{h}_{c}^{3}}\right){\ddot{u}}_{1}^{C}+\left(\frac{4{I}_{4}^{C}}{{h}_{c}^{4}}-\frac{16{I}_{6}^{C}}{{h}_{c}^{6}}\right){\ddot{u}}_{0}^{b}+ \left(\frac{16{I}_{6}^{C}}{{h}_{c}^{6}}\right.+\frac{4{I}_{4}^{C}}{{h}_{c}^{4}}\left.+\frac{16{I}_{5}^{C}}{{h}_{c}^{5}}+{I}_{0}^{t}\right){\ddot{u}}_{0}^{t}\\ & \quad +\left(\frac{2{I}_{4}^{C}{h}_{b}}{{h}_{c}^{4}}-\frac{8{{h}_{b}I}_{6}^{C}}{{h}_{c}^{6}}\right){\ddot{\varnothing }}_{x}^{b}+\left.\left(-\frac{8{{h}_{t}I}_{5}^{C}}{{h}_{c}^{5}}\right.+{I}_{2}^{t}-\frac{2{I}_{4}^{C}{h}_{t}}{{h}_{c}^{4}}-\frac{8{{h}_{t}I}_{6}^{C}}{{h}_{c}^{6}}\right){\ddot{\varnothing }}_{x}^{t} +{I}_{1}^{t}{\ddot{W}}_{0,x}^{t}. \end{aligned}$$
(15)

The moment of inertia of the core is defined by the following equations:

$${I}_{n}^{c}=\underset{-\frac{{h}_{c}}{2}}{\overset{\frac{{h}_{c}}{2}}{\int }}{\rho }_{c}{z}_{c}^{n}d{z}_{c}\mathrm{ n}=\mathrm{0,1},\dots ,6$$
(16)

Moreover, the moment of the face sheets inertia in relation is derived by the following equations:

$$\begin{aligned}{I}_{0}^{t}& =\underset{-\frac{{h}_{t}}{2}}{\overset{\frac{{h}_{t}}{2} }{\int }}{\rho }_{t}d{z}_{t} ,{I}_{1}^{t}=\underset{-\frac{{h}_{t}}{2}}{\overset{\frac{{h}_{t}}{2}}{\int }}{\rho }_{t}{f}_{1}\left({z}_{i}\right)d{z}_{t} , {I}_{2}^{t}=\underset{-\frac{{h}_{t}}{2}}{\overset{\frac{{h}_{t}}{2}}{\int }}{\rho }_{t}{f}_{2}\left({z}_{i}\right)d{z}_{t} , {I}_{3}^{t}=\underset{-\frac{{h}_{t}}{2}}{\overset{\frac{{h}_{t}}{2}}{\int }}{\rho }_{t}{f}_{1}\left({z}_{i}\right){f}_{2}\left({z}_{i}\right)d{z}_{t}\\{I}_{4}^{t}& = \underset{-\frac{{h}_{t}}{2}}{\overset{\frac{{h}_{t}}{2}}{\int }}{\rho }_{t}{[{f}_{2}\left({z}_{i}\right)]}^{2}d{z}_{t}\\ {I}_{0}^{b}&=\underset{-\frac{{h}_{b}}{2}}{\overset{\frac{{h}_{b}}{2}}{\int }}{\rho }_{b}d{z}_{b} , {I}_{1}^{b}=\underset{-\frac{{h}_{b}}{2}}{\overset{\frac{{h}_{b}}{2}}{\int }}{\rho }_{b}{f}_{1}\left({z}_{i}\right)d{z}_{b} , {I}_{2}^{b}=\underset{-\frac{{h}_{b}}{2}}{\overset{\frac{{h}_{b}}{2}}{\int }}{\rho }_{b}{f}_{2}\left({z}_{i}\right)d{z}_{b}, {I}_{3}^{b}=\underset{-\frac{{h}_{b}}{2}}{\overset{\frac{{h}_{b}}{2}}{\int }}{\rho }_{b}{f}_{1}\left({z}_{i}\right){f}_{2}\left({z}_{i}\right)d{z}_{b},\\ {I}_{4}^{b}& =\underset{-\frac{{h}_{b}}{2}}{\overset{\frac{{h}_{b}}{2}}{\int }}{\rho }_{b}{[{f}_{2}\left({z}_{i}\right)]}^{2}d{z}_{b}.\end{aligned}$$
(17)

Lamina Constitutive Relations

For kth orthotropic Lamina, the linear constitutive relations in the principal material coordinates are:

$$\left[\begin{array}{c}{\sigma }_{xx}\\ {\sigma }_{yy}\\ {\sigma }_{xy}\end{array}\right]={\left[\begin{array}{c}{\mathrm{Q}}_{11 } {\mathrm{Q}}_{12 } {\mathrm{Q}}_{16 }\\ {\mathrm{Q}}_{12 } {\mathrm{Q}}_{22 } {\mathrm{Q}}_{26 }\\ {\mathrm{Q}}_{16 } {\mathrm{Q}}_{26 } {\mathrm{Q}}_{66}\end{array}\right]}^{\left(k\right)}\left[\begin{array}{c}{\varepsilon }_{xx}\\ {\varepsilon }_{yy}\\ {\varepsilon }_{xy}\end{array}\right] , \left[\begin{array}{c}{\sigma }_{yz}\\ {\sigma }_{xz}\end{array}\right]={\left[\begin{array}{c}{\mathrm{Q}}_{44 } {\mathrm{Q}}_{45 }\\ {\mathrm{Q}}_{45 } {\mathrm{Q}}_{55 }\end{array}\right]}^{(k)}\left[\begin{array}{c}{\varepsilon }_{yz}\\ {\varepsilon }_{xz}\end{array}\right] ,$$
(18)

where \({Q}_{ij}^{(k)}\) are the plane stress-reduced stiffness. For \({Q}_{ij}\) of each layer, relations (19) are also available:

$${Q}_{11}=\frac{{E}_{1}}{1-{v}_{12}{v}_{21}},{Q}_{12}=\frac{{v}_{12}{E}_{1}}{1-{v}_{12}{v}_{21}},{Q}_{22}=\frac{{E}_{2}}{1-{v}_{12}{v}_{21}} , {Q}_{66}={G}_{12}, {Q}_{44}={G}_{23}, {Q}_{55}={G}_{13}$$
(19)

The stress–strain relations in the direction of the sandwich panel geometrical axes are derived as follows:

$$\left[\begin{array}{c}{\sigma }_{xx}\\ {\sigma }_{yy}\\ {\sigma }_{xy}\end{array}\right]={\left[\begin{array}{c}{\overline{Q} }_{11 } {\overline{Q} }_{12 } {\overline{Q} }_{16 }\\ {\overline{Q} }_{12 } {\overline{Q} }_{22 } {\overline{Q} }_{26 }\\ {\overline{Q} }_{16 } {\overline{Q} }_{26 } {\overline{Q} }_{66}\end{array}\right]}^{(k)}\left[\begin{array}{c}{\varepsilon }_{xx}\\ {\varepsilon }_{yy}\\ {\varepsilon }_{xy}\end{array}\right]. \left[\begin{array}{c}{\sigma }_{yz}\\ {\sigma }_{xz}\end{array}\right]=\left[\begin{array}{cc}{\overline{Q} }_{44}& {\overline{Q} }_{45}\\ {\overline{Q} }_{45}& {\overline{Q} }_{55}\end{array}\right]\left[\begin{array}{c}{\varepsilon }_{yz}\\ {\varepsilon }_{xz}\end{array}\right],$$
(20)

where, \({\overline{Q} }_{ij}\) represents the transmitted stiffness in the geometric axis of the sandwich panel.

The association between the transferred stiffness and axial stiffness is derived by the following equation:

$$\begin{aligned}{\overline{Q} }_{11}&={Q}_{11}{\mathrm{cos}}^{4}\theta +2\left({Q}_{12}+2{Q}_{66}\right){\mathrm{sin}}^{2}\theta {cos}^{2}\theta +{\mathrm{Q}}_{22}{\mathrm{sin}}^{4}\theta \\{\overline{Q} }_{12}& =\left({Q}_{11}+{Q}_{22}-{4Q}_{66}\right){\mathrm{sin}}^{2}\theta {\mathrm{cos}}^{2}\theta +{Q}_{12}\left({\mathrm{sin}}^{4}\theta +{\mathrm{cos}}^{4}\theta \right)\\ {\overline{Q} }_{22}& ={Q}_{11}{\mathrm{sin}}^{4}\theta +2\left({Q}_{12}+2{Q}_{66}\right){\mathrm{sin}}^{2}\theta { \mathrm{cos}}^{2}\theta +{\mathrm{Q}}_{22}{\mathrm{cos}}^{4}\theta \\{\overline{Q} }_{16}& =\left({Q}_{11}-{Q}_{12}-{2Q}_{66}\right)\mathrm{sin}\theta {\mathrm{cos}}^{3}\theta +\left({Q}_{12}-{Q}_{22}+{2Q}_{66}\right){\mathrm{sin}}^{3}\theta \mathrm{cos}\theta\\ {\overline{Q} }_{26}& =\left({Q}_{11}-{Q}_{12}-{2Q}_{66}\right){\mathrm{sin}}^{3}\theta \mathrm{cos}\theta +\left({Q}_{12}-{Q}_{22}+{2Q}_{66}\right)\mathrm{sin}\theta {\mathrm{cos}}^{3}\theta \\{\overline{Q} }_{66}& =\left({Q}_{11}+{Q}_{22}-{2Q}_{12}-{2Q}_{66}\right){\mathrm{sin}}^{2}\theta {\mathrm{cos}}^{2}\theta +{Q}_{66}\left({\mathrm{sin}}^{4}\theta +{\mathrm{cos}}^{4}\theta \right)\\ {\overline{Q} }_{44}& ={Q}_{44}{\mathrm{cos}}^{4}\theta +{Q}_{55}{\mathrm{sin}}^{4}\theta \\{\overline{Q} }_{45}& =\left({Q}_{55}-{Q}_{44}\right)\mathrm{cos}\theta \mathrm{sin}\theta \\{\overline{Q} }_{55}& ={Q}_{55}{\mathrm{cos}}^{4}\theta +{Q}_{44}{\mathrm{sin}}^{4}\theta.\end{aligned}$$
(21)

By placing relation (21) in relations (11) and (10) and using relation (4), the multi-layered and thick core layer constitutive relations related to face sheets are written as follows in terms of in-plane displacements. Due to a large number of equations, the most relevant ones were placed in Appendices A, B and C.

Model of ER Material

The complex modulus of the utilized ER fluid was measured by a previous study experimentally[34] and can be stated as follows. They are called fluid types 2a and 2b, and the relations have been presented previously by [35].

$$\begin{aligned}{G}_{2a(xz)}^{C}& ={G}_{2a(xz)}^{\mathrm{^{\prime}}C}+i{G}_{2a(xz)}^{^{\prime\prime} C} , {G}_{2a(yz)}^{C}={G}_{2a(yz)}^{\mathrm{^{\prime}}C}+i{G}_{2a(yz)}^{^{\prime\prime} C}\\ {G}_{2a(xz)}^{\mathrm{^{\prime}}C}& ={G}_{2a(yz)}^{\mathrm{^{\prime}}C}=\mathrm{15,000}{E}^{2}, {G}_{2a(xz)}^{^{\prime\prime} C}={G}_{2a(yz)}^{^{\prime\prime} C}=6900,\end{aligned}$$
(22)
$$\begin{aligned}{G}_{2b(xz)}^{C}&={G}_{2b(xz)}^{\mathrm{^{\prime}}C}+i{G}_{2b(xz)}^{^{\prime\prime} C} , {G}_{2b(yz)}^{C}={G}_{2b(yz)}^{\mathrm{^{\prime}}C}+i{G}_{2b(yz)}^{^{\prime\prime} C}\\{G}_{2b(xz)}^{\mathrm{^{\prime}}C}&={G}_{2b(yz)}^{\mathrm{^{\prime}}C}=\mathrm{50,000}{E}^{2}, {G}_{2b(xz)}^{^{\prime\prime} C}={G}_{2b(yz)}^{^{\prime\prime} C}=2600 E+1700,\end{aligned}$$
(23)

no normal stress exists in the ER layer and there exist only transverse shear stresses as follows:

$${\sigma }_{xz}^{c}={G}_{2b(xz)}^{C}{\gamma }_{xz}^{c}={G}_{2b(xz)}^{C}\left[\frac{\partial {w}_{0}^{C}}{\partial x}+z\frac{\partial {w}_{1}^{C}}{\partial x}+{z}^{2}\frac{\partial {w}_{2}^{C}}{\partial x}\right]+{G}_{2b(xz)}^{C}\left[{u}_{1}^{c}+2z{u}_{2}^{c}+3{z}^{2}{u}_{3}^{c}\right],$$
(24)
$${\sigma }_{yz}^{c}={G}_{2b(yz)}^{C}{\gamma }_{yz}^{c}={G}_{2b(yz)}^{C}\left[\frac{\partial {w}_{0}^{C}}{\partial y}+z\frac{\partial {w}_{1}^{C}}{\partial y}+{z}^{2}\frac{\partial {w}_{2}^{C}}{\partial y}\right]+{G}_{2b(yz)}^{C}\left[{v}_{1}^{c}+2z{v}_{2}^{c}+3{z}^{2}{v}_{3}^{c}\right].$$
(25)

The assumed responses of the relationship satisfy simply supported boundary conditions, as shown by the following relations:

$$\left[\begin{array}{c}{u}_{0}^{j}\left(x,y,t\right)\\ {v}_{0}^{j}\left(x,y,t\right)\\ {w}_{0}^{j}\left(x,y,t\right)\\ {\phi }_{x}^{j}\left(x,y,t\right)\\ {\phi }_{y}^{j}\left(x,y,t\right)\\ {u}_{k}^{c}\left(x,y,t\right)\\ {v}_{k}^{c}\left(x,y,t\right)\\ {w}_{0}^{c}\left(x,y,t\right)\end{array}\right]=\sum_{n=1}^{\infty }\sum_{m=1 }^{\infty }\left[\begin{array}{c}{U}_{0mn}^{j}cos({\alpha }_{m}x)sin\left({\beta }_{n}y\right)\\ {V}_{0mn}^{j}sin({\alpha }_{m}x)cos\left({\beta }_{n}y\right)\\ {W}_{0mn}^{j}sin({\alpha }_{m}x)sin\left({\beta }_{n}y\right)\\ {\phi }_{xmn}^{j}cos({\alpha }_{m}x)sin\left({\beta }_{n}y\right)\\ {\phi }_{ymn}^{j}sin({\alpha }_{m}x)cos\left({\beta }_{n}y\right)\\ {U}_{kmn}^{c}cos({\alpha }_{m}x)sin\left({\beta }_{n}y\right)\\ {V}_{kmn}^{c}sin({\alpha }_{m}x)cos\left({\beta }_{n}y\right)\\ {W}_{lmn}^{j}sin({\alpha }_{m}x)sin\left({\beta }_{n}y\right)\end{array}\right]{e}^{i\omega t}, \left(k=\mathrm{0,1},\mathrm{2,3}\right),\left(l=0, 1, 2\right),$$
(26)

where \({\alpha }_{\mathrm{m}}=\frac{\mathrm{m\pi }}{\mathrm{a}}\) and \({\beta }_{n}=\frac{\mathrm{n\pi }}{\mathrm{b}}\)

In Eq. (26), \({U}_{0mn}^{j}\), \({V}_{0mn}^{j}\), \({W}_{0mn}^{j}\), \({\psi }_{xmn}^{j}\), \({\psi }_{ymn}^{j}\), \({U}_{kmn}^{c}\), \({V}_{kmn}^{c}\) and\( {W}_{lmn}^{j}\), represent the Fourier coefficients while “m” and “n” representing half wave numbers along “x” and “y” directions, respectively. The nonlinear ordinary-differential equation may be obtained by substituting Eq. (26) into equations of motion, in displacement terms and applying Galerkin’s process. To solve these equations of motion of nonlinear ordinary differential, each of the equations of motion can be obtained according to one of the unknowns:

$$\left\{{u}_{0}^{t} , {v}_{0}^{t},{w}_{0}^{t},{\psi }_{x}^{t},{\psi }_{y}^{t},{u}_{0}^{b},{v}_{0}^{b},{w}_{0}^{b},{\psi }_{x}^{b},{\psi }_{y}^{b},{u}_{0}^{c} , {u}_{1}^{c},{v}_{0}^{c} , {v}_{1}^{c},{w}_{0}^{c}\right\}.$$

Given that transverse oscillations are considered in this paper, all time-dependent variables of relations (26) are obtained using the equation of motion, in terms of \(w\left(t\right)\).the nonlinear equation of motion can be obtained symbolically as:

$$\ddot{w}\left(t\right)+{\omega }_{L}^{2}w\left(t\right)+{\alpha }_{2}{w\left(t\right)}^{2}+{\alpha }_{3}{w\left(t\right)}^{3}=0.$$
(27)

In the above relation, \({\omega }_{L}\) is the natural linear frequency,\({\alpha }_{2}\) and \({\alpha }_{3}\) coefficient of nonlinear stiffness.

Solving the Equation of Motion

The obtained nonlinear equation of motion (27) can be solved, using perturbation techniques including the harmonic balance method as described by a previous study [36].

Hardening/Softening Behavior in Nonlinear Oscillations

According to the same study[36], the effective nonlinearity coefficient δ is obtained by:

$$\delta =\frac{10{a}_{2}^{2}-9{a}_{3}{\omega }_{L}^{2}}{24{\omega }_{L}^{2}}.$$
(28)

Hence, “δ” represents the extent of the resonance curves bending. When the value of δ > 0, the frequency response curves are declined to the right where the type of effective nonlinearity becomes hardening. Conversely, when the value of δ < 0, the frequency–response curves are bent to the left and the effective nonlinearity becomes a softening type. Also, when δ = 0, the frequency–response curves are not bent to either right or left and, by the second approximation, the system’s response becomes linear in nature.

Considering Eq. (28), it follows that the quadratic nonlinearity possesses a softening effect. When a3 is positive, the effective nonlinearity “δ” may be negative or positive, based on the relative magnitudes of “a2” and “a3”.

Results and Discussion

Validation of the Equations

The following examples justify our research approach.

Example 1

The non-linear free vibration analysis of a flat rectangular panel with SSSS B.C.

In this case, a flat square panel without a core was considered, for which the findings of the present study were compared with those of another work. Please review the details described by Ref. [37]. References [37, 38] the components of the nonlinear strains are taken on the basis proposed by two old studies. The Geometry and mechanical properties of a square panel are selected based on the following definitions:

$$ \begin{gathered} a = {1},b = {1},h = a/{1}0,E_{{1}} = E_{{2}} = E_{{3}} = { 322}.{\text{2 GPa}}, \hfill \\ G_{{{12}}} = G_{{{13}}} = G_{{{23}}} = E/{2 }({1} + v),v = \, 0.{32}, \, \rho \, = { 237}0{\text{ Kg}}/{\text{m}}^{3} . \hfill \\ \end{gathered} $$

As shown in Table 1, the results of the current theory with harmonic balance and von Karman’s nonlinear strains methods were compared with those obtained from the first order and nonlinear strains, described previously by Ref. [38]. Our results were also in good consistency with those reported by an older study [37].

Table 1 First dimensionless period of the flat square panel with H = h/a = variable, a = b = 1, m, n = 1 \(({T}_{N}={\overline{T} }_{N} {\left(E/p\right)}^{1/2}/a)\)
Full size table

Example 2

Nonlinear Free vibration analysis of laminated panel via SSSS B.C.

Since there was no available literature for validating the results of the current study, we had to reduce the core thickness to zero and compare the data with those reported by other references. In this case, we considered a flat sandwich panel with multi-layer face sheets and an ER core under simply supported boundary conditions (SSSS) via First-order shear deformation theory for the face sheets. For face sheets, the lay-up sequences were [90/0/core/0/90] and the sandwich panel was symmetrical about the mid-plane. The following material properties were used for computation:

$${E}_{1}=412\mathrm{GPa },{E}_{2}={E}_{3}=10.3\mathrm{ GPa},{G}_{12}={G}_{13}=6.18\mathrm{ GPa },{G}_{23}=5015\mathrm{ GPa}, ={v}_{12}=0.25, \rho =1\frac{\mathrm{Kg}}{{\mathrm{m}}^{3}}.$$

As deduced from Table 2, it may be found that out results are reasonably in good consistency with those reported by previous studies [4, 14, 39]. Table 2 shows the results of the current investigation for a flat sandwich panel with ER core utilizing the revised high-order theory of sandwich panel, as well as comparisons with results from older multilayer sheet theories. As can be shown, the current theory was able to forecast lower frequency ratios with a small error margin.

Table 2 Comparison of the frequency ratio of laminated composite square panel with SSSS boundary condition, a/b = 1, hc/ht = 1, m, n = 1, a/h = 10
Full size table

Influence of Hardening/Softening Behavior in Nonlinear Vibrations

The mechanical features of the face sheets for the ER core are shown in Table 3. Based on the data presented in Table 4, the hardening effects were much greater than the softening effects.

Table 3 Mechanical and geometrical properties of the composite sandwich panel with multi-layer face sheets and an ER core
Full size table
Table 4 The Values of a3 and a2 for flat sandwich panel with aluminum face sheet and ER core based on first shear Deformation theory
Full size table

Nonlinear Free Vibration Analysis

The effects of altering the electric field intensity and the thickness of the ER layer were also assessed on the nonlinear frequencies of the sheets. The sandwich panel was symmetrical around the mid-plane and the lay-up sequences for face sheets were [0/0/0/core/0/0/0]. Table 5 presents the comparison of the nonlinear frequency ratios for the first vibration modes of a square sandwich panel with ER core, based on first-order shear deformation theory.

Table 5 Comparison of nonlinear frequency ratios for the first vibration modes of a square sandwich panel with ER core based on first-order shear deformation theory
Full size table

Comparison of Linear and Nonlinear Frequency of Flat Sandwich Panel with an ER Core

Figure 2, shows the effect of electric field intensity on the nonlinear frequency. Figure 3 represents the variations in the modal loss factor as a function of electric field intensity.

Fig. 2
figure 2

Diagrammatic changes in the a nonlinear and b linear frequency of the sheet for different electric field intensities

Full size image
Fig. 3
figure 3

Comparison of the damping coefficient in terms of vibrational modes and different electric fields for a nonlinear and b linear frequency of the sheet for different electric field intensities

Full size image

Influence of the Core Thickness Ratio to Total Sheet Thickness on the First Natural Frequency

As reflected in Fig. 4, the nonlinear frequency increases by increasing the ratio of core thickness relative to the total sheet thickness. However, an earlier study [33] suggests that increases in the ratio of core thickness to total sheet thickness reduce the natural frequency of the sheet. Regarding the nonlinear vibration, increases in the ER core thickness the ratio of the natural nonlinear frequency to the linear counterpart increases initially, then progressively declines.

Fig. 4
figure 4

Diagrams of the a first nonlinear (E = 2 kV/mm) and b linear frequency changes of the sheet in different ratios of the core to sheet thickness, for electric field intensities

Full size image

Effect of Electric Field Intensity on the Nonlinear Frequency

Figure 5 illustrates the diagrammatic variations in the first nonlinear frequency of the flat sandwich panel with the ER core relative to the electric field intensity for varying aspect ratio coefficients.

Fig. 5
figure 5

Diagram of the a nonlinear (E = 2 kV/mm) and b linear frequency ratio variations of the sheet versus the electric field intensity for different aspect ratios

Full size image

Effect of Length-to-Thickness Ratio on the Natural Frequency

Figure 6 illustrates the diagram of the nonlinear frequency ratio variations of the first flat sandwich panel with an ER core based on the length to thickness ratio (ℎc/ℎt = 1, a/b = 1, E = 2 kVmm − 1).

Fig. 6
figure 6

The diagram of the(a) nonlinear (E = 2 kV/mm) and (b) linear frequency ratio variations of the sheet in terms of electric field intensity for different length to thickness ratios

Full size image

Highlights

To Control the Sandwich Panel’s Nonlinear Vibration Behavior

  • By increasing the electric field intensity, the nonlinear frequency of the panel decreases.

  • By increasing the aspect ratio, the nonlinear frequency of the panel increases.

  • By increasing the length-to-thickness ratio, the nonlinear frequency decreases.

  • During the rise in the electric field intensity, if damping is applied, the vibration amplitude declines consistently.

  • With an increase in the panel’s ratio, it becomes thinner while the vibration amplitude gradually increases.

  • Within the ER core, the ratio of nonlinear to linear frequency increases initially, then declines consistent with increases in the core thickness.

  • As the sandwich panel’s thickness grows, the hardening behavior also rises.

Conclusions

This study was undertaken for the first time to investigate the nonlinear vibration behaviors of sandwich panel with multi-layer face sheets and an ER fluid core, using an improved first-order shear deformation theory. Based on the findings, the following conclusions can be drawn:

  1. 1.

    With an increase in the electric field intensity, the nonlinear vibration frequency of the panel decreases and the structure hardens, leading to improvement in the structure’s stability.

  2. 2.

    With increased damping simultaneously with a rise in the electric field intensity, the vibration amplitude declines significantly.

  3. 3.

    The findings enable us to develop a controllable electric field, thereby controlling the natural frequency and amplitude of the vibration in structures.

  4. 4.

    The contribution of the core thickness is such that by increasing it relative to the panel’s thickness at a fixed electric field intensity, the ratio of nonlinear to linear vibration frequency initially rises, then declines over time.

  5. 5.

    As the ratio of core thickness to that of the whole panel increases, the panel’s stiffness declines.

  6. 6.

    By injecting more oil into the core layer, the panel’s weight increases, thereby reducing the ratio of the panel’s density to its stiffness.

  7. 7.

    With an increase in the panel’s dimensional ratio, it becomes thinner while the vibration amplitude gradually increases.

  8. 8.

    By adjusting the above parameters, it is possible to achieve the optimal and desired nonlinear vibration frequency and amplitude in a variety of structures.