1 Introduction

Lightweight sandwich structures which adopt a high stiffness–weight ratio and a high strength–weight ratio have been manufactured and used for engineering applications such as in the aircraft industry [1,2,3,4,5,6,7,8]. However, classic sandwich plates are incapable of withstanding high-temperature environments. A new class of composite materials that has drawn extensive attention is functionally graded materials (FGMs) [1, 9]. A typical FGM is an inhomogeneous composite structure made up of different phases of material constituents (usually ceramic and metal) with a high bending–stretching coupling effect. By gradually varying the volume fraction of the constituent materials, their material properties show a smooth and continuous change from one surface to another, consequently eliminating interface problems and mitigating thermal stress concentrations [10,11,12]. By merging the extraordinary behavior of FGM in conjunction with the sandwich plate, researchers have tried to investigate the behavior of an FGM “sandwich plate” (FGSP). Moreover, as the FGSP uses three layers, this opens the door to studying the plate with a range of different possibilities. Considering FG face sheets and a homogeneous core is one case that is investigated from different perspectives [13,14,15,16,17,18,19,20,21,22,23]. On the other hand, FGM could be placed in the core of an FGSP, and the other two faces could be comprised of either FGM or homogeneous sheets [13, 16, 24,25,26,27,28]

Nguyen [29] proposed a “high-order shear deformation theory” (HSDT) to evaluate the dynamic behavior of an FG sandwich beam; moreover, HSDT is used frequently to solve composite problems as it reaches the solution accurately and efficiently compared to others [30]. An analytical solution was developed using a method employing Lagrange multipliers for three different boundary conditions (simply supported–simply supported, clamped–clamped, and clamped–free). Zenkour investigated the effect of trigonometric shear deformation theory on a “sandwich plate” behavior with FG faces in terms of buckling and natural frequency [31]. Meksi et al. [32] proposed an HSDT and impeded an indeterminate integral term in the displacement field to evaluate the bending, buckling, and vibrational behavior of an FGSP with a homogeneous core and FG face sheets. Di Sciuva [33] investigated the vibration and buckling behavior of an FG carbon nanotube reinforced sandwich plate using an extended refined Zigzag theory in parallel with the Ritz method. The mechanical behavior of FGSP resting on an elastic foundation and subjected to a thermal environment while using refined quasi-3D shear deformation theory was studied by Mahmoudi et al. [34]. Ghumare et al. [35] considered a new fifth-order shear deformation theory accounting for transverse shear and normal deformations to analyze the bending behavior of an FG plate subjected to a hygro-thermal environment and resting on an elastic foundation. Fu [27] utilized a two-dimensional differential quadrature (DQ) method developed by Bellman [36] in the calculation of an nth order shear deformation theory to evaluate the free vibrational response of an FGSP resting on an elastic foundation. Madenci [37] extended the method of Mixed Finite Element Method (MFEM) to account for static and vibrational analysis, while other works continued evolving numerical techniques to optimize the solution using methods such as Artificial Neural Networks (ANN) [38,39,40]. Nebab et al. [36] considered a nonlinear elastic foundation in deriving the dynamic behavior of FG plates using the four-unknown shear deformation theory. Akbas et al. [37] investigated the case of an FG thick beam resting on a viscoelastic foundation focusing on the dynamic responses under a dynamic sine pulse load. The case of FG nanobeams resting on a viscoelastic foundation was further investigated by Ebrahimi et al. [41]. They studied the effect of a hygrothermal environment on the dynamic behavior of FG nanobeams using nonlocal strain gradient theory.

The increase of temperature and moisture concentration exposure on the structures has a very strong adverse impact on its performance. Therefore, the dynamic properties of an FGSP resting on a viscoelastic foundation will be affected when subjected to this type of exposure. In addition, the literature review showed that no research work is conducted on the vibrational behavior of the FGSP resting on a viscoelastic foundation and subjected to a hygrothermal environment. Therefore, the impact of the damping coefficient for the viscoelastic foundation of the plate using an efficient “four-unknown” HSDT with sine function is explored, along with the effect induced by hygro-thermal conditions on the FGSP. FGSP will be modeled as a continuous variation of material constituents along the thickness using a “power law variation.” Therefore, the material properties would change gradually. The analytical solutions for the “fundamental frequency” of an FGSP resting on a viscoelastic foundation can be obtained using Navier’s procedure.

1.1 Sandwich assembly

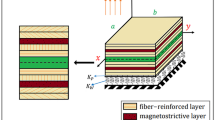
This study considers a rectangular FGSP. Cartesian coordinate (x, y, z) systems are utilized to describe the infinitesimal deformations of a typical plate. The origin of a “sandwich plate” with respect to z \((z=0)\) is considered to be at the middle surface of the plane. The top and bottom surfaces are defined at \(=\pm h/2\). The material properties vary along the z-direction continuously based on the following power law equation:

$$P((n))(z) = P_{{\text{m}}} + \left( {P_{{\text{c}}} - P_{{\text{m}}} } \right)V_{n} ,$$
(1)

where \(n\) denotes the number of each layer \(n=\left(\mathrm{1,2},3\right),\) while \({P}_{\mathrm{c}} and {P}_{\mathrm{m}}\) denote the properties of ceramic and metal of the FGSP, respectively. The volume fraction \(\left({V}_{n}\right)\) of the material is defined below for each FGSP. The effective change of the material properties in the direction of Z, such as Young’s modulus \((E)\), thermal expansion coefficient \(\left(\alpha \right)\), moisture expansion coefficient \((\beta )\) and mass density (\(\rho )\) are considered in Eq. (1). We consider in this work three types of FG Sandwich Plate as shown in Figs. 1, 2 and 3.

1.2 Types of FG sandwich plate

Type A: sandwich plate with homogeneous ceramic core and FG face sheets.

This type of sandwich plate has a ceramic core, and the top and bottom layers are FGM sheets. The top layer is metallic on its upper surface and ceramic on the lower side. In contrast, the bottom layer is metallic on its lower surface and ceramic on its upper surface. The volume fraction \(\left({V}_{n}\right)\) of the ceramic in this type can be determined by the following formulas [42]:

$$\begin{gathered} V_{1} = \left( {\frac{{1 + 2\overline{z}}}{1 + 2H1}} \right)^{r} ,\quad - \frac{1}{2} \le \overline{z} \le H_{1} , \hfill \\ V_{2} = 1,\quad H_{1} \le \overline{z} \le H_{2} , \hfill \\ V_{3} = \left( {\frac{{1 - 2\overline{z}}}{1 - 2H2}} \right)^{r} ,\quad H_{2} \le \overline{z} \le 1/2 \hfill \\ \end{gathered}$$
(2)

where \(\overline{z }=z/h\) and \({H}_{j}={h}_{j}/h\) \((j=\mathrm{1,2})\). \((r\ge 0)\) represents the material index. A fully homogeneous ceramic plate is in the case of \(r=0.\) However, it is a metal–ceramic–metal plate (m–c–m) when \(r\to \infty\).

Type B: sandwich plate with homogeneous metal core and FG face sheets.

This type of sandwich plate has a metallic core, whereas the top and bottom layers are FG. The upper surface of the top layer is ceramic, and it is graded to be metallic on its lower face. However, the bottom layer is metallic on the upper face and ceramic on the lower one. The formulation of the volume fraction in this type is defined as follows [42]:

$$\begin{gathered} V_{1} = \left( {\frac{{2H_{1} - 2\overline{z}}}{{2H_{1} + 1}}} \right)^{r} ,\quad - \frac{1}{2} \le \overline{z} \le H_{1} , \hfill \\ V_{2} = 0,\quad H_{1} \le \overline{z} \le H_{2} , \hfill \\ V_{3} = \left( {\frac{{2H_{2} - 2\overline{z}}}{{2H_{2} - 1}}} \right)^{r} ,\quad H_{2} \le \overline{z} \le 1/2. \hfill \\ \end{gathered}$$
(3)

A plate represents the case of ceramic–metal–ceramic (c–m–c) when \(r\to 0\), and its fully homogeneous metallic plate when \(r\to \infty\).

Type C: sandwich plate with homogeneous face sheets and FG core.

The top layer is fully ceramic, followed by a core layer, which is functionally graded as ceramic on the upper face and metallic on the lower face. The bottom layer is fully metallic in this type of sandwich plate. The formulation of the volume fraction, in this case, is given by [42]

$$\begin{gathered} V_{1} = 0,\quad \frac{1}{2} \le \overline{z} \le H_{1} , \hfill \\ V_{2} = \left( {\frac{{\overline{z} - H_{1} }}{{H_{2} - H_{1} }}} \right)^{r} ,\quad H_{1} \le \overline{z} \le H_{2} , \hfill \\ V_{3} = 1,\quad H_{2} \le \overline{z} \le 1/2. \hfill \\ \end{gathered}$$
(4)

2 Problem formulation

2.1 Kinematics and constitutive equations

For the plate in x-, y-, and z-directions, the \(u,v,\) and \(w\) terms represent the displacement components, respectively. They can be expressed as

$$u\left(x,y,z,t\right)={u}_{0}\left(x,y,t\right)-z\frac{\mathrm{d}{w}_{0}\left(x,y,t\right)}{dx}+{k}_{1}f(z)\int \theta \left(x,y,t\right)\mathrm{d}x,$$
(5)
$$v\left(x,y,z,t\right)={v}_{0}\left(x,y,t\right)-z\frac{\mathrm{d}{w}_{0}\left(x,y,t\right)}{dy}+{k}_{2}f\left(z\right)\int \theta \left(x,y,t\right)\mathrm{d}y,$$
(6)
$$w(x,y,z,t) = w_{0} (x,y,t),$$
(7)

where \({u}_{0}\) and \({v}_{0}\) represent the displacement of the mid-plane of the plate in both directions \(z\) and \(y\), respectively. While \({w}_{0}\) and \(\theta\) are the bending and shear components of transverse displacement (\(z\)-direction). \({k}_{1}\) and \({k}_{2}\) are geometry-dependent constants. In this study, a novel shape function \(f\left(z\right)\) is proposed to satisfy the boundary conditions of zero transverse shear stresses at the top and bottom faces and written as

$$f\left(z\right)=\frac{h}{\pi }\mathrm{sin}\left(\frac{\pi z}{h}\right).$$
(8)

Considering infinitesimal deformation theory for the plate, the displacements in Eqs. (5)–(7) are evaluated in terms of strains as follows:

$${\epsilon }_{x}={\epsilon }_{x}^{0}+z {\epsilon }_{x}^{1}+f\left(z\right) {\epsilon }_{x}^{2},$$
(9)
$${\epsilon }_{y}={\epsilon }_{y}^{0}+z {\epsilon }_{y}^{1}+f\left(z\right) {\epsilon }_{y}^{2},$$
(10)
$${\epsilon }_{xy}={\epsilon }_{xy}^{0}+z {\epsilon }_{xy}^{1}+f\left(z\right) {\epsilon }_{xy}^{2},$$
(11)
$${\gamma }_{xz}=g\left(z\right) {\gamma }_{xz,}^{0}$$
(12)
$$\gamma_{yz} = g(z)\gamma_{yz}^{0} ,$$
(13)

where

$$\left\{ {\begin{array}{*{20}c} {\epsilon_{x}^{0} } \\ {\epsilon_{x}^{1} } \\ {\epsilon_{x}^{2} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\frac{{\partial u_{0} }}{\partial x}} \\ { - \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}} \\ {k_{1} \theta } \\ \end{array} } \right\},\left\{ {\begin{array}{*{20}c} {\epsilon_{y}^{0} } \\ {\epsilon_{y}^{1} } \\ {\epsilon_{y}^{2} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\frac{{\partial v_{0} }}{\partial x}} \\ { - \frac{{\partial^{2} w_{0} }}{{\partial y^{2} }}} \\ {k_{2} \theta } \\ \end{array} } \right\},\left\{ {\begin{array}{*{20}c} {\epsilon_{xy}^{0} } \\ {\epsilon_{xy}^{1} } \\ {\epsilon_{xy}^{2} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\frac{{\partial u_{0} }}{\partial y} + \frac{{\partial v_{0} }}{\partial y}x} \\ { - 2\frac{{\partial^{2} w_{0} }}{\partial x\partial y}} \\ {k_{1} \frac{\partial }{\partial y}\int {\theta \;{\text{d}}x} + k_{2} \frac{\partial }{\partial x}\int {\theta \;{\text{d}}y} } \\ \end{array} } \right\},$$
$$\left\{ {\begin{array}{*{20}c} {\gamma_{xz}^{0} } \\ {\gamma_{yz}^{0} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {k_{1} \int {\theta \;{\text{d}}x} } \\ {k_{2} \int {\theta \;{\text{d}}y} } \\ \end{array} } \right\},g(z) = \frac{{{\text{d}}f(z)}}{{{\text{d}}z}}.$$

The shear part, which includes the integrals, has been evaluated using the analogy of the Navier method in which a sinusoidal behavior of transverse displacement is assumed as follows:

$$\frac{\partial }{\partial y}\int {\theta \;{\text{d}}x} = A^{\prime}\frac{{\partial^{2} \theta }}{\partial x\partial y},\;\frac{\partial }{\partial x}\int {\theta \;{\text{d}}y} = B^{\prime}\frac{{\partial^{2} \theta }}{\partial x\partial y},\;\int {\theta \;{\text{d}}x} = A^{\prime}\frac{\partial \theta }{{\partial x}},\;\int {\theta \;{\text{d}}y} = B^{\prime}\frac{\partial \theta }{{\partial y}},$$
(14)

where

$$A^{\prime} = - \frac{1}{{\lambda^{2} }},\;B^{\prime} = - \frac{1}{{\mu^{2} }},\;k_{1} = \lambda^{2} ,\;k_{2} = \mu^{2} ,$$

and

$$\lambda = m\pi /a,\;\mu = \frac{n\pi }{b}.$$

The constitutive relation considered in the formulation of a linear-elastic sandwich plate is as follows:

$${\left\{\begin{array}{c}{\sigma }_{x}\\ {\sigma }_{y}\\ \begin{array}{c}{\tau }_{xy}\\ \begin{array}{c}{\tau }_{yz}\\ {\tau }_{xz}\end{array}\end{array}\end{array}\right\}}^{\left(n\right)}={\left[\begin{array}{c}{C}_{11}\\ {C}_{12}\\ \begin{array}{c}0\\ 0\\ 0\end{array}\end{array}\begin{array}{c}{C}_{12}\\ {C}_{22}\\ \begin{array}{c}0\\ 0\\ 0\end{array}\end{array}\begin{array}{c}0\\ 0\\ \begin{array}{c}{C}_{66}\\ 0\\ 0\end{array}\end{array}\begin{array}{c}0\\ 0\\ \begin{array}{c}0\\ {C}_{44}\\ 0\end{array}\end{array}\begin{array}{c}0\\ 0\\ \begin{array}{c}0\\ 0\\ {C}_{55}\end{array}\end{array}\right]}^{\left(n\right)}{\left\{\begin{array}{c}{\epsilon }_{x}-\alpha \Delta T-\beta \Delta C\\ {\epsilon }_{y}-\alpha \Delta T-\beta \Delta C\\ \begin{array}{c}{\gamma }_{xy}\\ {\gamma }_{yz}\\ {\gamma }_{xz}\end{array}\end{array}\right\}}^{\left(n\right)}.$$
(15)

Considering \({C}_{11}^{\left(j\right)}={C}_{22}^{\left(j\right)}=\frac{{E}^{\left(j\right)}\left(z\right)}{1-{\nu }^{2}}\),\({C}_{66}^{\left(j\right)}={C}_{44}^{\left(j\right)}={C}_{55}^{\left(j\right)}=\frac{{E}^{\left(j\right)}\left(z\right)}{2\left(1+\nu \right)}\), where \(\Delta T\mathrm{ and }\Delta C\) represent the temperature and moisture differences, respectively, such as

$$\Delta k=k-{k}_{0}, \left(k=T,C\right),$$
(16)

\({T}_{0},{C}_{0}\) are the reference temperature and moisture, respectively.

2.2 Governing equation

The governing equation used in this paper is developed with the help of Hamilton’s Principle, which is stated as follows:

$${\int }_{0}^{T}\left(\delta U-\delta K+\delta V\right)=0,$$
(17)

where \(\delta U\) is the variant of strain energy, \(\delta K\) is the variant of kinetic energy, and \(\delta V\) is the variant of the external work implied by the reaction force of the foundation. The following equation represents the variant of the strain energy of the plate:

$$\begin{aligned} \delta U & = \mathop \smallint \limits_{ - h/2}^{h/2} \int\limits_{A} {\left[ {\sigma_{x} \delta \epsilon_{x} + \sigma_{y} \delta \epsilon_{y} + \tau_{xy} \delta \gamma_{xy} + \tau_{yz} \delta \gamma_{yz} + \tau_{xz} \delta \gamma_{xz} } \right]} {\text{d}}A{\text{d}}z \\ & = \int\limits_{A} {\left[ {N_{x} \delta \epsilon_{x}^{0} + N_{y} \delta \epsilon_{y}^{0} + N_{xy} \delta \gamma_{xy}^{0} + M_{x}^{b} \delta k_{x}^{b} } \right.} \\ & \quad + \left. {M_{y}^{b} \delta k_{y}^{b} + M_{xy}^{b} \delta k_{xy}^{b} + M_{x}^{s} \delta k_{x}^{s} + M_{y}^{s} \delta k_{y}^{s} + M_{xy}^{s} \delta k_{xy}^{s} + S_{yz}^{s} \delta \gamma_{yz} + S_{xz}^{s} \delta \gamma_{xz} } \right]{\text{d}}A. \\ \end{aligned}$$
(18)

Considering \((A)\) as the plane surface of the plate in the \((x,y)\) directions, and the terms \(N, M,\) and \(S\) are defined as

$$\left\{\begin{array}{ccc}{N}_{x}& {N}_{y}& {N}_{xy}\\ {M}_{x}^{b}& {M}_{y}^{b}& {M}_{xy}^{b}\\ {M}_{x}^{s}& {M}_{y}^{s}& {M}_{xy}^{s}\end{array}\right\}={\int }_{-h/2}^{h/2}\left({\sigma }_{x},{\sigma }_{y},{\tau }_{xy}\right)\left\{\begin{array}{c}1\\ z\\ f\left(z\right)\end{array}\right\}\mathrm{d}z,$$
(19)
$$\left( {S_{xz} , S_{yz} } \right) = \mathop \smallint \limits_{ - h/2}^{h/2} \left( {g\left( z \right)\left( {\tau_{xz} ,\tau_{yz} } \right)} \right.{\text{d}}z.$$

Thereafter, the variation of kinetic energy \((\delta K)\) is expressed as

$$\delta K={\int }_{-h/2}^{h/2}{\int }_{A}\rho \left(z\right)\left[\frac{\delta u}{\delta t} \delta \left(\frac{\delta u}{\delta t}\right)+\frac{\delta v}{\delta t}\delta \left(\frac{\delta v}{\delta t}\right)+\frac{\delta w}{\delta t}\delta \left(\frac{\delta w}{\delta t}\right)\right]\mathrm{d}A \mathrm{d}z.$$
(20)

The variation of external energy caused by the reaction force of the foundation is given by

$$\delta V={\int }_{A}{R}_{f}\delta w \mathrm{d}A,$$
(21)

where \({R}_{f}\) represents the density of the reaction force of the visco-elastic foundation:

$${R}_{f}=\left({k}_{w}-{k}_{s}{\nabla }^{2}+{c}_{t}\frac{\partial }{\partial t}\right)w\left(x,y\right),$$
(22)

\({K}_{w}\) represents Winkler parameter, while \({K}_{s}\) and \({C}_{t}\) are the shear layer foundation stiffness and viscosity parameter, respectively.

The governing equation would be a result of solving Eq. (17) using the principle of variational calculus. Thereafter, the solution would be expressed in terms of \(\delta {u}_{0}, \delta {v}_{0}, \delta {w}_{0}\) and \(\delta \theta\) as

$$\delta u_{0} : \frac{{\partial N_{x} }}{\partial x} + \frac{{\partial N_{xy} }}{\partial y} - I_{1} \frac{{\partial^{2} u_{0} }}{{\partial t^{2} }} + I_{2} \frac{{\partial^{3} w_{0} }}{{\partial x\partial t^{2} }} - I_{3} k_{1} A^{\prime}\frac{{\partial^{3} \theta }}{{\partial x\partial t^{2} }} = 0,$$
(23)
$$\delta v_{0} : \frac{{\partial N_{y} }}{\partial y} + \frac{{\partial N_{xy} }}{\partial x} - I_{1} \frac{{\partial^{2} v_{0} }}{{\partial t^{2} }} + I_{2} \frac{{\partial^{3} w_{0} }}{{\partial y\partial t^{2} }} - I_{3} k_{2} B^{\prime}\frac{{\partial^{3} \theta }}{{\partial y\partial t^{2} }} = 0,$$
(24)
$$\begin{aligned} \delta w_{0} & : \frac{{\partial^{2} M_{x}^{b} }}{{\partial x^{2} }} + \frac{{\partial^{2} M_{y}^{b} }}{{\partial y^{2} }} + 2\frac{{\partial^{2} M_{xy}^{b} }}{\partial x\partial y} - K_{w} w_{0} + K_{s} \nabla^{2} w_{0} - c_{t} \frac{{\partial w_{0} }}{\partial t} - I_{1} \frac{{\partial^{2} w_{0} }}{{\partial t^{2} }} \\ & \quad - I_{2} \left( {\frac{{\partial^{3} u_{0} }}{{\partial x\partial t^{2} }} + \frac{{\partial^{3} v_{0} }}{{\partial y\partial t^{2} }}} \right) + I_{4} \left( {\frac{{\partial^{4} w_{0} }}{{\partial x^{2} \partial t^{2} }} + \frac{{\partial^{4} w_{0} }}{{\partial y^{2} \partial t^{2} }}} \right) - I_{5} \left( {k_{1} A^{{\prime}{\frac{{\partial^{4} \theta }}{{\partial x^{2} \partial t^{2} }}}} + k_{2} B^{{\prime}{\frac{{\partial^{4} \theta }}{{\partial y^{2} \partial t^{2} }}}} } \right) = 0, \\ \end{aligned}$$
(25)
$$\begin{aligned} \delta \theta_{0} : & - k_{1} A^{\prime}\frac{{\partial^{2} M_{xs} }}{{\partial x^{2} }} - k_{2} B^{\prime}\frac{{\partial^{2} M_{ys} }}{{\partial y^{2} }} - \left( {k_{1} A^{\prime} + k_{2} B^{\prime}} \right)\frac{{\partial^{2} M_{xy}^{s} }}{\partial x\partial y} + k_{1} A^{\prime}\frac{{\partial S_{xz} }}{\partial x} \\ & + k_{2} B^{\prime}\frac{{\partial S_{yz} }}{\partial y} + I_{3} \left( {k_{1} A^{\prime}\frac{{\partial^{3} u_{0} }}{{\partial x\partial t^{2} }} + k_{2} B^{\prime}\frac{{\partial^{3} v_{0} }}{{\partial y\partial t^{2} }}} \right) - I_{5} \left( {k_{1} A^{\prime}\frac{{\partial^{4} w_{0} }}{{\partial x^{2} \partial t^{2} }} + k_{2} B^{\prime}\frac{{\partial^{4} w_{0} }}{{\partial y^{2} \partial t^{2} }}} \right) \\ & + I_{6} \left( {k_{1}^{2} A^{^{\prime}2} \frac{{\partial^{4} \theta }}{{\partial x^{2} \partial t^{2} }} + k_{2}^{2} B^{^{\prime}2} \frac{{\partial^{4} \theta }}{{\partial y^{2} \partial t^{2} }}} \right) = 0, \\ \end{aligned}$$
(26)

where \(\left({I}_{1},{I}_{2}, {I}_{3}, {I}_{4}, {I}_{5}, {I}_{6}\right)\) are mass inertias, and written as

$$\left({I}_{1},{I}_{2}, {I}_{3}, {I}_{4}, {I}_{5}, {I}_{6}\right)={\int }_{-h/2}^{h/2}\rho \left(z\right) \left(1,z,f,{z}^{2},zf,{f}^{2}\right)\mathrm{d}z.$$
(27)

Using the constitutive equation in Eq. (15) and incorporate Eq. (19), the resultant forces of the FG plate including the effect of both temperature and moisture would be evaluated as follows:

$$\left\{\begin{array}{c}N\\ {M}^{b}\\ {M}^{s}\end{array}\right\}=\left[\begin{array}{ccc}\left[A\right]& \left[B\right]& \left[{B}^{s}\right]\\ \left[B\right]& \left[D\right]& \left[{D}^{s}\right]\\ \left[{B}^{s}\right]& \left[{D}^{s}\right]& \left[{H}^{s}\right]\end{array}\right]\left\{\begin{array}{c}{\epsilon }^{0}\\ {\epsilon }^{1}\\ {\epsilon }^{2}\end{array}\right\}+\left\{\begin{array}{c}{N}^{T}\\ {M}^{bT}\\ {M}^{sT}\end{array}\right\}+\left\{\begin{array}{c}{N}^{C}\\ {M}^{bC}\\ {M}^{sC}\end{array}\right\},$$
(28)
$$\left\{\begin{array}{c}{S}_{xz}\\ {S}_{yz}\end{array}\right\}=\left[\begin{array}{cc}{A}_{44}^{s}& 0\\ 0& {A}_{55}^{s}\end{array}\right]\left\{\begin{array}{c}{\gamma }_{xz}^{0}\\ {\gamma }_{yz}^{0}\end{array}\right\},$$

where

$$\left[\begin{array}{ccc}\left[A\right]& \left[B\right]& \left[{B}^{s}\right]\\ \left[B\right]& \left[D\right]& \left[{D}^{s}\right]\\ \left[{B}^{s}\right]& \left[{D}^{s}\right]& \left[{H}^{s}\right]\end{array}\right]=\left[\begin{array}{ccc}\begin{array}{ccc}{A}_{11}& {A}_{12}& 0\\ {A}_{12}& {A}_{22}& 0\\ 0& 0& {A}_{66}\end{array}& \begin{array}{ccc}{B}_{11}& {B}_{12}& 0\\ {B}_{12}& {B}_{22}& 0\\ 0& 0& {B}_{66}\end{array}& \begin{array}{ccc}{B}_{11}^{s}& {B}_{12}^{s}& 0\\ {B}_{12}^{s}& {B}_{22}^{s}& 0\\ 0& 0& {B}_{66}^{s}\end{array}\\ \begin{array}{ccc}{B}_{11}& {B}_{12}& 0\\ {B}_{12}& {B}_{22}& 0\\ 0& 0& {B}_{66}\end{array}& \begin{array}{ccc}{D}_{11}& {D}_{12}& 0\\ {D}_{12}& {D}_{22}& 0\\ 0& 0& {D}_{66}\end{array}& \begin{array}{ccc}{D}_{11}^{s}& {D}_{12}^{s}& 0\\ {D}_{12}^{s}& {D}_{22}^{s}& 0\\ 0& 0& {D}_{66}^{s}\end{array}\\ \begin{array}{ccc}{B}_{11}^{s}& {B}_{12}^{s}& 0\\ {B}_{12}^{s}& {B}_{22}^{s}& 0\\ 0& 0& {B}_{66}^{s}\end{array}& \begin{array}{ccc}{D}_{11}^{s}& {D}_{12}^{s}& 0\\ {D}_{12}^{s}& {D}_{22}^{s}& 0\\ 0& 0& {D}_{66}^{s}\end{array}& \begin{array}{ccc}{H}_{11}^{s}& {H}_{12}^{s}& 0\\ {H}_{12}^{s}& {H}_{22}^{s}& 0\\ 0& 0& {H}_{66}^{s}\end{array}\end{array}\right],$$
$$\epsilon^{0} = \left\{ {\begin{array}{*{20}c} {\epsilon_{x}^{0} } \\ {\epsilon_{y}^{0} } \\ {\epsilon_{xy}^{0} } \\ \end{array} } \right\},\epsilon^{1} = \left\{ {\begin{array}{*{20}c} {\epsilon_{x}^{1} } \\ {\epsilon_{y}^{1} } \\ {\epsilon_{xy}^{1} } \\ \end{array} } \right\},\epsilon^{1} = \left\{ {\begin{array}{*{20}c} {\epsilon_{x}^{2} } \\ {\epsilon_{y}^{2} } \\ {\epsilon_{xy}^{2} } \\ \end{array} } \right\},$$
$$N = \left\{ {\begin{array}{*{20}c} {N_{11} } \\ {N_{22} } \\ {N_{12} } \\ \end{array} } \right\},M_{b} = \left\{ {\begin{array}{*{20}c} {M_{11}^{b} } \\ {M_{22}^{b} } \\ {M_{12}^{b} } \\ \end{array} } \right\},M^{s} = \left\{ {\begin{array}{*{20}c} {M_{11}^{s} } \\ {M_{22}^{s} } \\ {M_{12}^{s} } \\ \end{array} } \right\},$$
$$N^{k} = \left\{ {\begin{array}{*{20}c} {N_{11}^{k} } \\ {N_{22}^{k} } \\ 0 \\ \end{array} } \right\},M^{bk} = \left\{ {\begin{array}{*{20}c} {M_{11}^{bk} } \\ {N_{22}^{bk} } \\ 0 \\ \end{array} } \right\},M^{sk} = \left\{ {\begin{array}{*{20}c} {M_{11}^{sk} } \\ {M_{22}^{sk} } \\ 0 \\ \end{array} } \right\},\quad k = \left\{ {T,C} \right\}.$$

Stiffness elements are evaluated as

$$\left( {A_{ij} ,A_{ij}^{s} ,B_{ij} ,B_{ij}^{s} ,D_{ij} ,D_{ij}^{s} ,H_{ij}^{s} } \right) = \int_{( - h/2)}^{(h/2)} {\left( {1,g(z)^{2} ,z,f(z),z^{2} ,zf(z),f(z)^{2} C_{ij} {\text{d}}z} \right),\;(i,j = 1,2\;{\text{and}}\;6)}$$
$$A_{ij}^{s} = \int_{ - h/2 }^{h/2} {C_{ij} \left[ {g\left( z \right)} \right]^{2} } {\text{d}}z,\;(i,j = 4,5)$$

and

$$\left\{\begin{array}{c}{N}_{jj}^{T}\\ {M}_{jj}^{bT}\\ {M}_{jj}^{sT}\end{array}\right\}=-\sum_{i=1}^{3}{\int }_{{h}_{i}-1}^{{h}_{i}}\left({C}_{11}+{C}_{12}\right)T\left(z\right)\left\{\begin{array}{c}1\\ z\\ f\left(z\right)\end{array}\right\}\mathrm{d}z, \left(j=\mathrm{1,2}\right),$$
$$\left\{\begin{array}{c}{N}_{jj}^{C}\\ {M}_{jj}^{bC}\\ {M}_{jj}^{sC}\end{array}\right\}=-\sum_{i=1}^{3}{\int }_{{h}_{i}-1}^{{h}_{i}}\left({C}_{11}+{C}_{12}\right)C\left(z\right)\left\{\begin{array}{c}1\\ z\\ f\left(z\right)\end{array}\right\}\mathrm{d}z, \left(j=\mathrm{1,2}\right).$$

The applied temperature \(T\) and moisture \(C\) are assumed to vary along with the thickness of the FGSP, while the variation depends on the exponent \(P.\) In the case where \(P=1\), the variation would be linear along with the thickness, while it is nonlinear when \(P>1\) according to the following relation:

$$k(z) = \Delta k\left( {\frac{z}{h} + \frac{1}{2}} \right)^{p} + k_{b} ,\quad k = (T,C),$$
(29)

where \(\Delta T={T}_{t}-{T}_{b}\) and \(\Delta C={C}_{t}-{C}_{b}\) are the temperature and moisture differences, respectively. The subscript \(t\) denotes the top surface, while the subscript \(b\) is for the bottom surface of the sandwich plate.

3 Analytical solution

The analytical solution for the natural frequency of an FGSP resting on a viscoelastic foundation would be resolved based on a Navier’s type solution. The solution only considers the case of simply supported “boundary conditions” by expanding the displacement as a double trigonometric Fourier series as functions of unknown parameters. Therefore, the displacement could be represented as

$$\left\{\begin{array}{c}{u}_{0}\\ {v}_{0}\\ {w}_{0}\\ \theta \end{array}\right\}=\sum_{m=1}^{\infty }\sum_{n=1}^{\infty }\left\{\begin{array}{c}{U}_{mn}\mathrm{cos}\left(\lambda x\right)\mathrm{sin}(\mu y)\\ {V}_{mn}\mathrm{sin}\left(\lambda x\right)\mathrm{cos}(\mu y)\\ {W}_{mn}\mathrm{sin}\left(\lambda x\right)\mathrm{sin}\left(\mu y\right)\\ {\theta }_{mn}\mathrm{sin}\left(\lambda x\right)\mathrm{sin}\left(\mu y\right)\end{array}\right\} {e}^{{i \omega }_{mn} t,}$$
(30)

where \({U}_{mn}, {V}_{mn}, {W}_{mn}\) and \({\theta }_{mn}\) are unknown coefficients, \(\lambda =m \pi /a\), \(\mu =n \pi /b\). Also, \(\omega\) represents the eigenfrequency of the plate at each \(m\) and \(n\) half wave numbers. The equation of motion would be a result of substituting the Eqs. (30) into (23–29). Therefore, it would appear in the form of an Eigen-value problem as

$$\left\{\left[K\right]-{\omega }^{2}\left[M\right]\right\}\left\{\Delta \right\}=0,$$
(31)

where

$$\left\{\Delta \right\}=\left\{\begin{array}{c}{U}_{mn}\\ {V}_{mn}\\ {W}_{mn}\\ {\theta }_{mn}\end{array}\right\}.$$

Solving Eq. (31) would lead to the following analytical solution:

$$\left(\left[\begin{array}{cccc}{k}_{11}& {k}_{12 }& {k}_{13}& {k}_{14}\\ {k}_{12}& {k}_{22}& {k}_{23}& {k}_{24}\\ {k}_{13}& {k}_{23}& {k}_{33}& {k}_{34}\\ {k}_{14}& {k}_{24}& {k}_{34}& {k}_{44}\end{array}\right]-{\omega }^{2}\left[\begin{array}{cccc}{m}_{11}& {m}_{12}& {m}_{13}& {m}_{14}\\ {m}_{12}& {m}_{22}& {m}_{23}& {m}_{24}\\ {m}_{13}& {m}_{23}& {m}_{33}& {m}_{34}\\ {m}_{14}& {m}_{24}& {m}_{34}& {m}_{44}\end{array}\right]\right)\left\{\begin{array}{c}{U}_{mn}\\ {V}_{mn}\\ {W}_{mn}\\ {\theta }_{mn}\end{array}\right\}=\left\{\begin{array}{c}0\\ 0\\ 0\\ 0\end{array}\right\},$$

where

$$k_{1} 1 = - \lambda^{2} A_{11} - \mu^{2} A_{66} ,\;k_{12} = - \lambda \mu \left( {A_{12} + A_{66} } \right),\;k_{13} = \lambda \mu^{2} B_{12} + 2\lambda \mu^{2} B_{66} + \lambda^{3} B_{11} ,$$
$$k_{14} = \lambda \mu^{2} B_{12}^{s} + \lambda^{3} B_{11}^{s} + 2\lambda \mu^{2} B_{66}^{s} ,\;k_{22} = - \mu^{2} A_{22} - \lambda^{2} A_{66} ,$$
$${k}_{24}={\mu }^{3}{B}_{22}^{s}+{\lambda }^{2}\mu {B}_{12}^{s}+2{\lambda }^{2}\mu {B}_{66}^{s},$$
$$k_{23} = \mu^{3} B_{22} + 2\lambda^{2} \mu B_{66} + \lambda^{2} \mu B_{12} ,$$
$${k}_{33}=-0.5{c}_{t}-{K}_{w}-{K}_{s}\left({\lambda }^{2}+{\mu }^{2}\right)-2{\lambda }^{2}{\mu }^{2}{D}_{12}--{\lambda }^{4}{D}_{11}-{\mu }^{4}{D}_{22}-4{\lambda }^{2}{\mu }^{2}{D}_{66},$$
$${k}_{34}=2{\lambda }^{2}{\mu }^{2}{D}_{12}^{s}-4{D}_{66}^{s}{\lambda }^{2}{\mu }^{2}-{\mu }^{4}{D}_{22}^{s}-{\lambda }^{4}{D}_{11,}^{s}$$
$${k}_{44}=-{\lambda }^{2}{A}_{55}^{s}-{\mu }^{2}{A}_{44}^{s}-4{\lambda }^{2}{\mu }^{2}{H}_{66}^{s}-{\lambda }^{4}{H}_{11}^{s}-2{\lambda }^{2}{\mu }^{2}{H}_{12}^{s}-{\mu }^{4}{H}_{22,}^{s}$$
$$m_{11} = m_{22} = I_{1} ,\;m_{12} = 0,\;m_{13} = - I_{2} \lambda ,\;m_{14} = - I_{3} \lambda ,$$
$$\begin{gathered} m_{23} = - I_{2} \mu ,\;m_{24} = - I_{3} \mu ,\;m_{33} = I_{1} + \left( {\lambda^{2} + \mu^{2} } \right)I_{4} ,m_{34} = \left( {\lambda^{2} + \mu^{2} } \right)I_{5} \hfill \\ m_{44} = \left( {\lambda^{2} + \mu^{2} } \right)I_{6} . \hfill \\ \end{gathered}$$

4 Numerical results

The following parameters have been considered in this study:

$$T_{b} - T_{0} = 25\;^\circ {\text{C}},\quad C_{b} - C_{0} = 0\%$$

and the sandwich plate is composed of metal (aluminum) and ceramic (alumina) material.

  • The material properties of Alumina are

    \({E}_{c}=380\) Gpa, \({\rho }_{c}=3800\) kg/m3,\({\alpha }_{c}=7\times {10}^{-6}(1/^\circ{\rm C} ),\)

    \({\beta }_{c}=0.001\) (wt % H2O)−1, \({\nu }_{c}=0.3\)

  • The material characteristics of Aluminum are

    \({E}_{m}=70\) Gpa, \({\rho }_{m}=2707\) kg/m3, \({\alpha }_{m}=23\times {10}^{-6}(1/^\circ{\rm C} ),\)

    \({\beta }_{m}=0.44\) (wt % H2O)−1, \({\nu }_{c}=0.3.\)

The solutions in the graphs are shown in non-dimensional units that are proposed as

\(\overline{\omega }=\omega h\sqrt{\frac{{\rho }_{c}}{{G}_{c}{\alpha }_{c}\Delta T}}\),\({k}_{w}=\frac{{K}_{w}{a}^{4}}{{D}_{c}}\),\({k}_{s}=\frac{{K}_{s}{a}^{2}}{{D}_{c}}\), \({D}_{c}=\frac{{E}_{c}{h}^{3}}{12\left(1-{\nu }^{2}\right)}\), \({G}_{c}=\frac{{E}_{c}}{2\left(1+\nu \right)}\),\({\overline{k} }_{w}=\frac{{K}_{w}{a}^{4}}{{D}_{m}}\), \({\overline{k} }_{s}=\frac{{K}_{s}{a}^{2}}{{D}_{m}}\),\({D}_{m}=\frac{{E}_{m}{h}^{3}}{12\left(1-{\nu }^{2}\right)}.\)

The novel proposed shear deformation theory is proved in the first place in Table 1 by comparing the natural frequency of a homogeneous square plate excluding a visco-elastic foundation with the exact result published by Sirivas et al. [43]. Furthermore, the proposed theory is also compared with the results obtained by Sobhy [16], in which several theories were used, such as the refined plate theory (RPT), Third-order Plate Theory (TPT), sinusoidal plate theory (SPT), hyperbolic plate theory (HPT1), exponential plate theory (EPT) and HPT2. The comparison concludes that the proposed theory is functioning properly and matches the results of the other previously puplished papers mentioned above. Thereafter, Table 2 includes the effect elastic foundation. The newly proposed theory is compared with Hellal’s [42] results for an elastic foundation by considering that the damping coefficient \({c}_{t}\) is equal to zero, where the table shows a very good agreement between both theories.

Table 1 Comparison of non-dimensional natural frequencies \(\omega h\sqrt {\rho _{{\text{c}}} /G_{{\text{c}}} }\) of a homogeneous square plate without viscoelastic foundations \(\mathrm{a}/\mathrm{h}=10,\upnu =0.3\)
Full size table
Table 2 Comparison of non-dimensional natural frequencies \(\omega h \sqrt{{\rho }_{m}/{E}_{m}}\) of FGM square plate resting on elastic foundation
Full size table
Fig. 1
figure 1

Illustration of FGSP resting on the viscoelastic foundation: Type A

Full size image
Fig. 2
figure 2

Illustration of FGSP resting on the viscoelastic foundation: Type B

Full size image
Fig. 3
figure 3

Illustration of FGSP resting on the viscoelastic foundation: Type C

Full size image

The effect of the damping coefficient (\({c}_{t})\) is tabulated in Table 3, where a non-dimensional natural frequency is calculated for an FGM square plate considering different scenarios of visco-elastic foundation. The effect over the natural frequency is examined among ten different foundation models (two columns representing the elastic part with five rows imitating the viscosity in the foundation). Furthermore, each natural frequency is controlled with respect to the effect of the thickness to length ratio \((h/a)\) and the power-law index; as the value of the damping coefficient increases, the natural frequency increases. The effect would be more significant as the \((h/a)\) and power-index \((r)\) are increasing.

Table 3 Non-dimensional natural frequencies \(\omega h \sqrt{{\rho }_{m}/{E}_{m}}\) of FGM square plate resting on a viscoelastic foundation
Full size table

The effect of the damping coefficient of a viscoelastic foundation with respect to the power index \(r\) over the natural frequencies is shown in Figs. (4, 5 and 6). Each figure considers one type of FGSP out of the three that were explained earlier with specific geometries. Natural frequency looks to increase as the damping coefficient increases, which would lead to enhancing the rigidity of the plate. The effect of the power index, which varies upon the plate type, is also examined. The natural frequency decreases as the power index increases up to a point where \(r=1\), thereafter the decrement of the natural frequency is minimal. The slope of the first portion of the graph is affected by the ratios between the three layers: as we increase the density of the core (ceramic), the slope tends to decrease. In the case of Type B, the natural frequency behaves similar to Type A. However, the natural frequency in Type B is the maximum among all of the other three types. The plate acquires more rigidity when its core is metal, and the other two faces are FG sheets. Furthermore, the damping coefficient enhances the vibrational response of the plate regardless of the type of the plate.

Fig. 4
figure 4

Effect of the power-law index and damping coefficient on the Eigen frequency \(\overline{\upomega }\) of FGSP (Type A): \((a/h=10,b/a=1, p=1, \Delta T=50 ^\circ \mathrm{C}, \Delta C=10\mathrm{ \%},{k}_{w}=100, {k}_{s}=20)\), a: the (1–1–1) FGSP, b the (1–2–1) FGSP, c the (2–1–2) FGSP

Full size image
Fig. 5
figure 5

Effect of the power-law index and damping coefficient on the eigenfrequency \(\overline{\upomega }\) of FGSP (Type B): \(\left({k}_{w}=100, {k}_{s}=20\right), \left(a/h=10, b/a=1, p=1, \Delta T=50 ^\circ \mathrm{C}, \Delta C=10\mathrm{ \%}\right),\) a the (1–1–1) FGSP, b the (1–2–1) FGSP, c the (2–1–2) FGSP

Full size image
Fig. 6
figure 6

Effect of the power-law index and damping coefficient on the eigenfrequency \(\overline{\omega }\) of FGSP (Type C): \(({k}_{w}=100, {k}_{s}=20)\),\()\); \(\left(a/h=10,b/a=1, p=1, \Delta T=50^\circ \mathrm{C}, \Delta C=10 \%\right),\) a the (1–1–1) FGSP, b the (1–2–1) FGSP, c the (2–1–2) FGSP

Full size image

Figure 7 shows the effect of temperature difference over the natural frequency with respect to the aspect ratio. The results emphasize the fact that the increase in temperature difference reduces the rigidity of the plate significantly. Furthermore, the increase in the aspect ratio reduces the natural frequency. The decrement in the natural frequency for reducing the aspect ratio is less significant when the ratio b/a reaches 1, where the geometry of the plate is square. Whereas an increase in the damping coefficient would enhance the sustainability of the plate linearly in terms of the natural frequency, as in Fig. 8.

Fig. 7
figure 7

Effect of the temperature difference \(\Delta T\) on the eigen frequency \(\overline{\upomega }\) of various types of FGSP; \(\left(a/h=10, r=p=1, \Delta C=10\%, {k}_{w}=100, {k}_{s}=20\right),\) a Type A, b Type B, c Type C

Full size image
Fig. 8
figure 8

Effect of the temperature difference \(\Delta T\) and damping coefficient on the eigenfrequency \(\overline{\upomega }\) of various types of FGSP; \((a/h=10, r=p=1, \Delta C=10\mathrm{ \%}, {k}_{w}=100, {k}_{s}=20)\): a Type A, b Type B, c Type C

Full size image

The effect of moisture concentration works in a similar way to temperature. The rigidity of the plate is reduced as the moisture concentration increases, as in Fig. 9, where a comparison is carried out using four different moisture concentrations with respect to two different parameters: the aspect ratio and the damping coefficient.

Fig. 9
figure 9

Effect of the a moisture concentration \(\Delta C\) and b damping coefficient on the eigenfrequency \(\overline{\upomega }\) of FGSP (TypeA) \((a/h=10, r=p=1, {k}_{w}=100, {k}_{s}=20)\)

Full size image

The effect of the temperature study is further extended in Fig. 10 to include the temperature variation. This led to the conclusion that an increase in the temperature variation would elevate the free vibration; a uniform temperature is more severe than the case of linear and nonlinear variation. Finally, the effect of the elastic foundation coefficient \(({K}_{w}, {K}_{s})\) along with the damping coefficient \({c}_{t}\) is examined in Fig. 11. The natural frequency increases as the coefficient of the viscoelastic foundation increases. The increment is linear along with the damping coefficient.

Fig. 10
figure 10

The variation of the eigenfrequency \(\overline{\upomega }\) of FGSP (Type A) under various types of hygrothermal with respect to a the aspect ratio and b the damping coefficient \((a/h=10, r=p=1, \Delta T=50 ^\circ \mathrm{C}, \Delta C=10\mathrm{ \%}, {k}_{w}=100, {k}_{s}=20)\)

Full size image
Fig. 11
figure 11

Effect of the elastic foundation parameters and damping coefficient on the eigenfrequency \(\overline{\omega }\) of FGSP of Type A \((a/h=10,b/a=1, r=p=1, \Delta C=10 \%)\)

Full size image

5 Conclusions

This work studies for the first time the vibrational behavior of a simply supported FGSP resting on a viscoelastic foundation subjected to a hygro-thermal environment using a newly proposed “four-unknown shear deformation plate theory.” This theory assumes a trigonometric distribution of the shear stress along with the thickness of the plate. Furthermore, a comparison carried out with previously published papers shows a very good agreement. The FGSP is examined considering three different scenarios of the panel’s arrangement. This work enhanced the understanding of the impact of the damping coefficient and drew the following conclusions:

  • The increase in damping coefficient \(({c}_{t})\) as a property of the viscoelastic foundation would enhance the free-vibrational response of the plate in the same manner among all types of FGSP: Type A, Type B, and Type C.

  • The effect of the damping coefficient \(({c}_{t})\) over the natural frequency is not influenced by the plate’s configuration.

  • The natural frequency of FGSP is enhanced by the increase in damping coefficient value more significantly when the temperature difference \((\Delta T)\) is at low levels.

  • At high moisture concentrations, the damping coefficient tends to enhance the rigidity of the plate.

  • The change of temperature profile would affect the natural frequency of the plate.

This paper has examined the FGSP in many different aspects considering all of the stated variations, including temperature variation, moisture, aspect ratio, power index, and plate type with different geometries. The analytical solution is obtained with the help of Navier’s solution, whereas Hamilton’s principle is used in the case of the governing equation derivation.