1 Introduction

The applications and advantages of nanoscience and nanosystems are rapidly increasing in wide range from medical diagnosis to energy harvesting. Some of the new researches on micro- and nanostructures which consist nano-/microbeams as important element are done Guo et al. [1], Kim et al. [2], Kima and Fana [3] and Xu et al. [4]. Since every technological growth needs a firm theoretical background, a considerable part of researches is allocated to nanosystems in the recent decade. Bounouara et al. [5] developed a zeroth-order shear deformation theory to study the vibration behavior of functionally graded nanoplates resting on elastic foundation. Belkorissat et al. [6] studied a new nonlocal hyperbolic plate model to perform analysis on the vibration characteristics of functionally graded plate nanotubes. Tounsi et al. [7] studied the thermal buckling of double-walled carbon nanotubes based on nonlocal Timoshenko beam model. They also considered the effects of transverse shear deformation and rotary inertia. Besseghier et al. [8] studied the nonlinear vibration of an embedded zigzag single-walled carbon nanotube. Benguediab et al. [9] analyzed the buckling of a zigzag double-walled carbon nanotube with both chirality and small-scale effects. In addition, vibrational properties of nanobeams are also put into attention by many authors. Ke et al. [10] studied the nonlinear vibration behavior of the piezoelectric nanobeams based on the nonlocal theory and Timoshenko beam model. Murmu and Adhikari [11] studied the vibration of double-nanobeam systems. Berrabah et al. [12] presented a unified nonlocal shear deformation theory to study bending, buckling and free vibration of nanobeams. Gheshlaghi and Hasheminejad [13] studied the nonlinear flexural vibrations of micro- and nanobeams considering the surface effects. Malekzadeh and Shojaee [14] studied the surface and nonlocal effects on the nonlinear flexural vibrations behavior of nonuniform nanobeams. In addition, vibration behavior of nanobeams was also considered by [15–17], etc.

Functionally graded materials which were introduced in 1980s are rapidly becoming well known and widely used in different micro- and nanostructures such as beams, plates, shells, and a lot of researches have been conducted on the mechanical behavior of micro- and nanosystems made of FGMs. Using Eringen’s relations, Zemri et al. [18] proposed a nonlocal shear deformation beam theory to study the bending, buckling and vibration of FG nanobeams. Chaht et al. [19] studied the bending and buckling behaviors of size-dependent nanobeams made of functionally graded materials (FGMs) including the thickness stretching effect. Ahouel et al. [20] studied the nonlocal trigonometric shear deformation beam theory on the basis of neutral surface position for bending, buckling and vibration of FG nanobeams. Al-Basyouni et al. [21] studied a unified beam formulation that considers a variable length scale parameter in conjunction with the neutral axis concept to study bending and dynamic behaviors of FG microbeam. In addition, FGMs using higher-order theories are also used in studies specifically in macro-scales. Bourada et al. [22] studied a simple and refined trigonometric higher-order beam theory for bending and vibration of functionally graded beams. Hebali et al. [23] presented a new quasi-three-dimensional hyperbolic shear deformation theory for the bending and vibration of functionally graded plates. Bennoun et al. [24] proposed a five-variable refined plate theory for the free vibration behavior of functionally graded sandwich plates. Yahia et al. [25] studied various higher-order shear deformation plate theories for wave propagation in functionally graded plates. Belabed et al. [26] studied a simple higher-order shear and normal deformation theory for functionally graded plates. Mahi and Tounsi [27] developed a hyperbolic shear deformation theory for bending and free vibration of isotropic, functionally graded, sandwich and laminated composite plates. Meziane et al. [28] presented a simple refined shear deformation theory for the vibration and buckling of exponentially graded sandwich plate resting on elastic foundations. Bousahla et al. [29] investigated a trigonometric higher-order theory including the stretching effect for the static analysis of advanced composite plates such as FG plates. Bellifa et al. [30] presented a first-order shear deformation theory for bending and dynamic behaviors of functionally graded plates.

Thermal analysis on structures made of FGMs is of great interest among researchers. Hamidi et al. [31] studied a sinusoidal plate theory for the thermo-mechanical bending behavior of functionally graded sandwich plates. Tounsi et al. [32] studied a refined trigonometric shear deformation theory for the thermo-elastic bending of FG sandwich plates. Zidi et al. [33] studied the bending response of FG plate resting on elastic foundation and subjected to hygro-thermo-mechanical loading. Bouderba et al. [34] presented the thermo-mechanical bending response of FG plates resting on Winkler–Pasternak elastic foundations.

As a different kind of new material, porous materials are also taken into consideration in many studies on mechanical behavior of micro- or nanostructures. Magnucki and Stasiewicz [35] studied the buckling of a straight porous beam pivoted at both ends and loaded with a lengthwise compressive force. Leclaire et al. [36] studied the vibrational behavior of a rectangular porous plate. Leclaire et al. [37] presented a simple model of the transverse vibrations of a thin rectangular porous plate saturated by a fluid.

Rotating mechanical systems find its vast usage in micro- and nanoscales such as micro- and nanomotors. For example, Zhang et al. [38] presented an electromagnetic micromotor which is controlled by independent coils and capacitance structure. Ayers et al. [39] designed a micro- actuator system for precise transmission and reception of bio-optical signals. These applications have made researchers to study the rotary micro- and nanobeams as a main element of rotating micro- and nanosystems. Ghadiri and Shafiei [40] and Ghadiri et al. [41] studied the vibration of simple and FG nanobeams. Ramezani and Alasty [42] studied the large amplitude vibration of a doubly clamped microbeam. Shafiei et al. [43] studied the small-scale effect on the nonlinear flapwise bending vibration of rotating cantilever and propped cantilever nanobeams. Shafiei et al. [44] studied the flapwise bending vibrations of a rotating nanoplate which is the model of the blades of nanoturbines. Ghadiri et al. [45] studied the thermal vibration of rotary nanobeams. It is seen that the thermal vibration of the AFG nanobeams with cantilever boundary condition has not been studied. Thus, it motivated us to consider this problem in this paper. The nanobeam is modeled as Timoshenko nanobeam, and the governing equations are derived using the nonlocal Eringen’s theory. The material composition and mechanical properties of the temperature-dependent nanobeam are considered to vary through thickness and axis of the nanobeam separately based on the power-law function. The boundary conditions are supposed to be cantilever. The numerical results present analysis on the effects of the nonlocal small-scale parameter, angular velocity, hub radius, FG and AFG indexes and also thermal effects on the first two frequencies of the porous nanobeams.

2 Formulation

2.1 Functionally graded materials

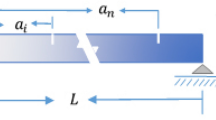
Consider an FG nanobeam which is composed of metal and ceramic with varying material composition along x and z directions (Fig. 1). The material composition can be varied along length (Fig. 1a) and along thickness (Fig. 1b). It is clear that the mechanical properties of the nanobeam, i.e., Young’s modulus ‘E’, Poisson’s ratio ‘ν’, shear modulus ‘G’ and mass density ‘ρ’, vary with the material composition. The modified rule of mixture for the FG (z) or AFG (x) nanobeam becomes:

$$P\left( {z\;{\text{or}}\;x} \right) = P_{\text{m}} V_{\text{m}} + P_{\text{c}} V_{\text{c}}$$
(1)

where the subscripts of ()c and ()m are used to define the ceramic and metal, respectively. The power-law of the volume fraction of ceramic is [46, 47]:

$$V_{\text{c}} \left( {z\;{\text{or}}\;x} \right) = \left( {\frac{1}{2} + \frac{z}{h}} \right)^{nz} \;{\text{or}}\;\left( {\frac{x}{L}} \right)^{nx}$$
(2)

Here, ‘nx’ and ‘nz’ are the AFG (axially functionally graded) and FG (functionally graded) power indexes, respectively, which are related to the volume fraction change in the material composition.

Fig. 1
figure 1

Schematic of the rotating beam with different material distributions, a AFG, b FG

Full size image

Hence, the material properties of the nanobeam are obtained as [46–48]:

$$P\left( {z\;{\text{or}}\;x} \right) = P_{\text{m}} + \left( {P_{\text{c}} - P_{\text{m}} } \right)\left( {\frac{1}{2} + \frac{z}{h}} \right)^{nz} \;{\text{or}}\;\left( {\frac{x}{L}} \right)^{nx}$$
(3)

where nz and nx are FG and AFG power indexes and z and x are the distance from the mid-plane and left end of the FG beam, respectively. The material of the beam is pure ceramic when nx and nz are set to be zero, and increment of nx and nz increases the metal volume fraction. Thus, Young’s modulus ‘E’, Poisson’s ratio ‘ν’, the thermal distribution ‘α’, mass density ‘ρ’ and shear modulus ‘G’ equations of the FGM nanobeam are defined as:

$$E\left( {z\;{\text{or}}\;x} \right) = E_{\text{m}} + \left( {E_{\text{c}} - E_{\text{m}} } \right)\left( {\frac{1}{2} + \frac{z}{h}} \right)^{nz} \;{\text{or}}\;\left( {\frac{x}{L}} \right)^{nx}$$
(4a)
$$\nu \left( {z\;{\text{or}}\;x} \right) = \nu_{\text{m}} + \left( {\nu_{\text{c}} - \nu_{\text{m}} } \right)\left( {\frac{1}{2} + \frac{z}{h}} \right)^{nz} \;{\text{or}}\;\left( {\frac{x}{L}} \right)^{nx}$$
(4b)
$$\alpha \left( {z\;{\text{or}}\;x} \right) = \alpha_{\text{m}} + \left( {\alpha_{\text{c}} - \alpha_{\text{m}} } \right)\left( {\frac{1}{2} + \frac{z}{h}} \right)^{nz} \;{\text{or}}\;\left( {\frac{x}{L}} \right)^{nx}$$
(4c)
$$\rho \left( {z\;{\text{or}}\;x} \right) = \rho_{\text{m}} + \left( {\rho_{\text{c}} - \rho_{\text{m}} } \right)\left( {\frac{1}{2} + \frac{z}{h}} \right)^{nz} \;{\text{or}}\;\left( {\frac{x}{L}} \right)^{nx}$$
(4d)
$$G\left( {z\;{\text{or}}\;x} \right) = \frac{{E\left( {z\;{\text{or}}\;x} \right)}}{{2 + 2\nu \left( {z\;{\text{or}}\;x} \right)}}$$
(4e)

For the nonlinear thermo-elasticity equation, the temperature-dependent material properties can be obtained at temperature T as [49]:

$$P = P_{0} \left( {P_{ - 1} T^{ - 1} + P_{1} T + P_{2} T^{2} + P_{3} T^{3} + 1} \right)$$
(5)

here P 0, P −1, P 1, P 2 and P 3 are the temperature-dependent coefficients of material properties which are given in Table 1.

Table 1 Temperature-dependent coefficients of Young’s modulus, thermal expansion coefficient and mass density [50]
Full size table

2.2 The governing equation and boundary conditions

As there is no slipping between upper and down layers and the underlying material, the displacement is unified in the beam. The displacements of an arbitrary point along the x- and z-axes based on the Timoshenko beam theory are defined as:

$$u_{x} \left( {x,z,t} \right) = u\left( {x,t} \right) + z\varphi \left( {x,t} \right)$$
(6a)
$$u_{z} \left( {x,z,t} \right) = w\left( {x,t} \right)$$
(6b)

where t is time, φ is the total bending rotation of the cross section, and u and w are the displacement components of the mid-plane along x and z directions, respectively. Therefore, according to the Timoshenko beam theory (TBT), the strain–displacement relations are obtained as:

$$\varepsilon_{xx} = \frac{\partial u}{\partial x} + z \frac{\partial \varphi }{\partial x}$$
(7)
$$\gamma_{xz} = \frac{\partial w}{\partial x} + \varphi$$
(8)

Hamilton’s principle is employed to derive the governing equation of motion and the associated boundary conditions as:

$$\int\limits_{0}^{1} {\delta \left( {U - T + V} \right){\text{d}}t} = 0$$
(9)

where T, U and V denote the virtual kinetic energy, virtual strain energy and potential energy due to applied loads, respectively. The virtual kinetic energy of the nanobeam can be expressed as

$$\delta U = \int\limits_{V} {\sigma_{ij} \delta \varepsilon_{ij} {\text{d}}V} = \int\limits_{V} {\left( {\sigma_{xx} \delta \varepsilon_{xx} + \sigma_{xz} \delta \gamma_{xz} } \right){\text{d}}V}$$
(10)

Substituting Eqs. (8) and (9) into Eq. (10) yields:

$$\delta U = \int\limits_{0}^{L} {\left( {N\left( {\delta \frac{\partial u}{\partial x}} \right) + M\left( {\delta \frac{\partial \varphi }{\partial x}} \right) + Q\left( {\delta \frac{\partial w}{\partial x} + \delta \varphi } \right)} \right){\text{d}}x}$$
(11)

in which N is the axial force, M is the bending moment, and Q is the shear force. These stress resultants are defined as:

$$N = \int\limits_{A} {\sigma_{xx} {\text{d}}A} ,\quad M = \int\limits_{A} {\sigma_{xx} z{\text{d}}A} ,\quad Q = \int\limits_{A} {K_{S} \sigma_{xz} {\text{d}}A}$$
(12)

where K S = 5/6 is the shear correction factor. The kinetic energy of Timoshenko beam can be written as:

$$T = \frac{1}{2}\int\limits_{0}^{L} {\int\limits_{A} {\rho \left( {x\;{\text{or}}\;z,T} \right)\left( {\left( {\frac{{\partial u_{x} }}{\partial t}} \right)^{2} +\, \left( {\frac{{\partial u_{z} }}{\partial t}} \right)^{2} } \right){\text{d}}A{\text{d}}x} }$$
(13)

Also the virtual kinetic energy can be expressed as:

$$\delta T = \int\limits_{0}^{L} {\left[ {\begin{array}{*{20}l} {I_{0} \left( {\frac{\partial u}{\partial t}\frac{\partial \delta u}{\partial t} + \frac{\partial w}{\partial t}\frac{\partial \delta w}{\partial t}} \right) + I_{1} \left( {\frac{\partial \varphi }{\partial t}\frac{\partial \delta u}{\partial t} + \frac{\partial u}{\partial t}\frac{\partial \delta \varphi }{\partial t}} \right)} \hfill \\ { +\, I_{2} \left( {\varOmega^{2} \varphi \delta \varphi + \frac{\partial \varphi }{\partial t}\frac{\partial \delta \varphi }{\partial t}} \right)} \hfill \\ \end{array} } \right]{\text{d}}x}$$
(14)

where (I 0, I 1, I 2) are the mass moments of inertia defined as follows:

$$\left( {I_{0} ,I_{1} ,I_{2} } \right) = \int\limits_{A} {\rho \left( {x\;{\text{or}}\;z,T} \right)\left( {1,z,z^{2} } \right){\text{d}}A}$$
(15)

Now, rotation effect on the governing equation is evaluated. The variation of the work done corresponding to angular velocity change can be obtained by:

$$\delta V = \int\limits_{0}^{L} {\bar{N}\frac{\partial w}{\partial x}\frac{\partial \delta w}{\partial x}{\text{d}}x}$$
(16)

and

$$\bar{N} = N^{\text{Rotation}} + N^{\text{Thermal}} = \int\limits_{A} {\int\limits_{x}^{L} {\rho \left( {x\;{\text{or}}\;z,T} \right)\varOmega^{2} \left( {\xi + r} \right){\text{d}}\xi } + \left[ {E\left( {x\;{\text{or}}\;z,T} \right)\alpha \left( {x\;{\text{or}}\;z,T} \right)\left( {T - T_{0} } \right)} \right]{\text{d}}A}$$
(17)

where ρ, Ω, r, x and T 0 are beam density at certain point z, angular velocity, hub radius (Fig. 1), beam length variation along x direction and reference temperature, respectively. Substituting Eqs. (11), (15) and (17) into Eq. (9) and setting the coefficients of δu, δw and δφ to zero, the following Euler–Lagrange equation can be obtained:

$$\frac{\partial N}{\partial x} = I_{0} \frac{{\partial^{2} u}}{{\partial t^{2} }} + I_{1} \frac{{\partial^{2} \varphi }}{{\partial t^{2} }}$$
(18a)
$$\frac{\partial Q}{\partial x} - \bar{N}\frac{{\partial^{2} w}}{{\partial x^{2} }} = I_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }}$$
(18b)
$$\frac{\partial M}{\partial x} - Q = I_{1} \frac{{\partial^{2} u}}{{\partial t^{2} }} + I_{2} \frac{{\partial^{2} \varphi }}{{\partial t^{2} }}$$
(18c)

Under the following boundary conditions:

$$N = 0\quad {\text{or}}\quad u = 0\quad {\text{at}}\quad x = 0\quad {\text{and}}\quad x = L$$
(19a)
$$Q = 0\quad {\text{or}}\quad w = 0\quad {\text{at}}\quad x = 0\quad {\text{and}}\quad x = L$$
(19b)
$$M = 0\quad {\text{or}}\quad \varphi = 0\quad {\text{at}}\quad x = 0\quad {\text{and}}\quad x = L$$
(19c)

2.3 The nonlocal elasticity model for FG nanobeam

The classic continuum theories do not consider the spaces between the atoms and also define the state of each point as a function of strain at that very point. These assumptions lead to erroneous results in studies of nanosystems which lack strong scientific assumptions in nanoscales. Eringen's nonlocal elasticity theory [51] is a strong and accurate theory for studying nanobeams, and the reason is that this theory considers a point dependent to the state of the whole body. In addition, Eringen's theory considers the small scale parameter which is not negligible comparing to the size of the nanostructures.

Unlike the classic elasticity theory, the nonlocal Eringen’s elasticity theory expresses the stress tensor at point x of mass environment (Ω) to the tensor of the strain (ɛ) of the whole body by a differential equation. Thus, the nonlocal stress tensor at point x can be expressed as:

$$\sigma_{ij} \left( x \right) = \int\limits_{\varGamma } {\alpha \left( {\left| {x^{{\prime }} - x} \right|,\tau } \right)t_{ij} \left( {x^{{\prime }} } \right){\text{d}}\varGamma \left( {x^{{\prime }} } \right)}$$
(20)

where σ ij , τ ij are local and nonlocal stress tensor, respectively, and \(\alpha \left( {\left| {x^{\prime } - x} \right|} \right)\) is nonlocal kernel. The macroscopic stress σ at point x in a Hookean solid is related to the strain ε at the point by generalized Hooke’s law.

$$t_{ij} = C_{ijkl} \varepsilon_{kl}$$
(21)
$$\tau = \frac{{e_{0} a}}{l}$$
(22)

where \(\tau = \frac{{e_{0} a}}{l}\) is a material constant that puts the effect of the small-scale parameter, e 0 is material constant which can be obtained by experiments, and a and l are also the internal (e.g., lattice parameter) and external characteristic lengths (e.g., crack length, wave length) of the nanobeam, respectively. As a result of the difficulty in using the integral constitutive relation, Eringen [52] introduced:

$$\left( {1 - \left( {e_{0} a} \right)^{2} {\nabla }^{2} } \right)\sigma_{kl} = t_{kl}$$
(23)

When the local stress tensor is defined according to the displacement gradients by using the generalized Hooke’s law, the nonlocal displacements are obtained using the strain and temperature–strain as below:

$$\sigma_{xx} - \left( {e_{0} a} \right)^{2} \frac{{\partial^{2} \sigma_{xx} }}{{\partial x^{2} }} = E\varepsilon_{xx}$$
(24)
$$\sigma_{xz} - \left( {e_{0} a} \right)^{2} \frac{{\partial^{2} \sigma_{xz} }}{{\partial x^{2} }} = G\gamma_{xz}$$
(25)

Equations (24) and (25) are in fact the displacement on the right-hand side of Eq. (23), and σ and ε are the nonlocal stress and strain, respectively. E is the Young’s modulus, and G = E/2(1 − υ) is the shear modulus (υ denotes the Poisson’s ratio). For Timoshenko nonlocal 2D-FG beam, Eqs. (24) and (25) can be rewritten as:

$$\sigma_{xx} - \left( {e_{0} a} \right)^{2} \frac{{\partial^{2} \sigma_{xx} }}{{\partial x^{2} }} = E\left( {x\;{\text{or}}\;z,T} \right)\varepsilon_{xx}$$
(26)
$$\sigma_{xz} - \left( {e_{0} a} \right)^{2} \frac{{\partial^{2} \sigma_{xz} }}{{\partial x^{2} }} = G\left( {x\;{\text{or}}\;z,T} \right)\gamma_{xz}$$
(27)

The force–strain and the moment–strain of the nonlocal Timoshenko 2D-FG beam can be obtained as follows:

$$N - \left( {e_{0} a} \right)^{2} \frac{{\partial^{2} N}}{{\partial x^{2} }} = A_{xx} \frac{\partial u}{\partial x} + B_{xx} \frac{\partial \varphi }{\partial x}$$
(28a)
$$M - \left( {e_{0} a} \right)^{2} \frac{{\partial^{2} M}}{{\partial x^{2} }} = B_{xx} \frac{\partial u}{\partial x} + D_{xx} \frac{\partial \varphi }{\partial x}$$
(28b)
$$Q - \left( {e_{0} a} \right)^{2} \frac{{\partial^{2} Q}}{{\partial x^{2} }} = C_{xz} \left( {\frac{\partial w}{\partial x} + \varphi } \right)$$
(28c)

and the cross-sectional rigidities are:

$$\left( {A_{xx} ,B_{xx} ,D_{xx} } \right) = \int\limits_{A} {E\left( {x\;{\text{or}}\;z,T} \right)\left( {1,z,z^{2} } \right){\text{d}}A}$$
(29a)
$$C_{xz} = K_{\text{S}} \int\limits_{A} {G\left( {x\;{\text{or}}\;z,T} \right){\text{d}}A}$$
(29b)

The explicit equation of the nonlocal normal force is obtained by the substitution of the second derivative of N from Eq. (19a) into Eq. (28a) as:

$$N = A_{xx} \frac{\partial u}{\partial x} + B_{xx} \frac{\partial \varphi }{\partial x} + \left( {e_{0} a} \right)^{2} \frac{\partial }{\partial x}\left( {I_{0} \frac{{\partial^{2} u}}{{\partial t^{2} }} + I_{1} \frac{{\partial^{2} \varphi }}{{\partial t^{2} }}} \right)$$
(30a)

Similarly, the nonlocal bending moment can be calculated by substituting the second derivative of M from Eq. (19b) into Eq. (28b) as:

$$M = B_{xx} \frac{\partial u}{\partial x} + D_{xx} \frac{\partial \varphi }{\partial x} + \left( {e_{0} a} \right)^{2} \left( {I_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }} + I_{1} \frac{{\partial^{3} u}}{{\partial x\partial t^{2} }} + I_{2} \frac{{\partial^{3} \varphi }}{{\partial x\partial t^{2} }} + \frac{\partial }{\partial x}\left( {\bar{N}\frac{\partial w}{\partial x}} \right)} \right)$$
(30b)

By substituting for the second derivative of Q from Eq. (19c) into Eq. (28c), the nonlocal shear force is obtained as:

$$Q = C_{xz} \left( {\frac{\partial w}{\partial x} + \varphi } \right) + \left( {e_{0} a} \right)^{2} \frac{\partial }{\partial x}\left( {I_{0} \frac{{\partial^{3} w}}{{\partial x\partial t^{2} }} + \frac{\partial }{\partial x}\left( {\bar{N}\frac{\partial w}{\partial x}} \right)} \right)$$
(30c)

The motion equation is obtained based on nonlocal displacements ‘u’, ‘φ’ and ‘w’ by substituting N, Q and M into Eqs. (18); similarly, the boundary conditions are expressed in terms of displacement.

$$\delta u:\frac{\partial }{\partial x}\left( {A_{xx} \frac{\partial u}{\partial x}} \right) + \frac{\partial }{\partial x}\left( {B_{xx} \frac{\partial \varphi }{\partial x}} \right) = I_{0} \frac{{\partial^{2} u}}{{\partial t^{2} }} + I_{1} \frac{{\partial^{2} \varphi }}{{\partial t^{2} }} - \left( {e_{0} a} \right)^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}\left( {I_{0} \frac{{\partial^{2} u}}{{\partial t^{2} }} + I_{1} \frac{{\partial^{2} \varphi }}{{\partial t^{2} }}} \right)$$
(31a)
$$\delta \varphi :\frac{\partial }{\partial x}\left( {B_{xx} \frac{\partial u}{\partial x}} \right) + \frac{\partial }{\partial x}\left( {D_{xx} \frac{\partial \varphi }{\partial x}} \right) - C_{xz} \left( {\varphi + \frac{\partial w}{\partial x}} \right) = I_{1} \frac{{\partial^{2} u}}{{\partial t^{2} }} + I_{2} \frac{{\partial^{2} \varphi }}{{\partial t^{2} }} - \left( {e_{0} a} \right)^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}\left( {I_{1} \frac{{\partial^{2} u}}{{\partial t^{2} }} + I_{2} \frac{{\partial^{2} \varphi }}{{\partial t^{2} }}} \right)$$
(31b)
$$\delta w:\frac{\partial }{\partial x}\left[ {C_{xz} \left( {\varphi + \frac{\partial w}{\partial x}} \right)} \right] - \frac{\partial }{\partial x}\left( {\bar{N}\frac{\partial w}{\partial x}} \right) + \left( {e_{0} a} \right)^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}\left[ {\frac{\partial }{\partial x}\left( {\bar{N}\frac{\partial w}{\partial x}} \right)} \right] = I_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }} - \left( {e_{0} a} \right)^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}\left( {I_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }}} \right)$$
(31c)

2.4 Type of temperature rise

Consider an FG nanobeam with top surface of temperature T c and with nonlinear temperature gradient along thickness from T c to T m (bottom temperature). Therefore, in this case, the temperature distribution through the thickness is given according to the following approach [53]:

$$T = T_{0} +\Delta T\left( {\frac{1}{2} + \frac{z}{h}} \right)^{{\alpha^{T} }}$$
(32)

where T 0 = T m = 300 k and ΔΤ = T c − T m and α T is the nonnegative power index of temperature variation function. When α T = 1, the temperature variation is linear.

3 Solution procedure

Differential quadrature method (DQM) which is proved to obtain accurate results is used for solving the governing equations. Simple formulation and low computational cost are the advantages of DQM which was introduced by Bellman and Casti [54], Bellman et al. [55]. The weighting coefficients of DQM depend on the grid spacing. Therefore, using these coefficients, every partial differential equation can be simplified to a set of algebraic equations [56]. Thus, the rth-order derivative of function f(x) can be written as linear sum of the function values

$$\frac{{\partial^{r} f\left( x \right)}}{{\partial x^{r} }}\left| {_{{x = x_{p} }} } \right. = \sum\limits_{j = 1}^{n} {C_{ij}^{\left( r \right)} } f\left( {x_{i} } \right)$$
(33)

It is clear that the weighting coefficients are of great importance in this method. Here \(C_{ij}^{\left( 1 \right)}\), M(x) and C (r) are defined as:

$$C_{ij}^{\left( 1 \right)} = \frac{{M\left( {x_{i} } \right)}}{{\left( {x_{i} - x_{j} } \right)M\left( {x_{j} } \right)}}\quad i,\, j = 1,2, \ldots ,n\quad {\text{and}}\quad i \ne j$$
(34a)
$$C_{ii}^{\left( 1 \right)} = - \sum\limits_{j = 1,i \ne j}^{n} {C_{ij}^{\left( 1 \right)} } \quad i = j$$
(34b)
$$M\left( {x_{i} } \right) = \prod\limits_{j = 1,i \ne j}^{n} {\left( {x_{i} - x_{j} } \right)}$$
(34c)
$$C_{ij}^{\left( r \right)} = r\left[ {C_{ij}^{{\left( {r - 1} \right)}} C_{ij}^{\left( 1 \right)} - \frac{{C_{ij}^{{\left( {r - 1} \right)}} }}{{\left( {x_{i} - x_{j} } \right)}}} \right]\quad i,\, j = 1,\, 2, \ldots ,n,\;i \ne j\quad {\text{and}}\quad 2 \le r \le n - 1$$
(34d)
$$C_{ii}^{\left( r \right)} = - \sum\limits_{j = 1,i \ne j}^{n} {C_{ij}^{\left( r \right)} } \quad i,\, j = 1,2, \ldots ,n\quad {\text{and}}\quad 1 \le r \le n - 1$$
(34e)

where n and r, respectively, are the number of grid points along axis and the order of the derivative. Also, \(C_{ij}^{\left( r \right)}\) is the weighing coefficient along axis. Using the Chebyshev–Gauss–Lobatto approach, the speed of the convergence increases:

$$\zeta_{i} = \frac{1}{2}\left( {1 - \cos \left( {\frac{{\left( {i - 1} \right)}}{{\left( {N - 1} \right)}}\pi } \right)} \right)\quad i = 1,2,3, \ldots ,n$$
(35)

Applying the GDQM in Eqs. (31) yields the following equations:

$$\sum\limits_{s = 1}^{n} {C_{rs}^{\left( 1 \right)} } \left( {A_{xx} \sum\limits_{s = 1}^{n} {C_{rs}^{\left( 1 \right)} u_{s} } } \right) + \sum\limits_{s = 1}^{n} {C_{rs}^{\left( 1 \right)} } \left( {B_{xx} \sum\limits_{s = 1}^{n} {C_{rs}^{\left( 1 \right)} } \varphi_{s} } \right) = \omega^{2} \left[ {m_{0} u_{s} + m_{1} \varphi_{s} - \left( {e_{0} a} \right)^{2} \sum\limits_{s = 1}^{n} {C_{rs}^{\left( 2 \right)} } \left( {m_{0} u_{s} + m_{1} \varphi_{s} } \right)} \right]$$
(36a)
$$\sum\limits_{s = 1}^{n} {C_{rs}^{\left( 1 \right)} } \left( {B_{xx} \sum\limits_{s = 1}^{n} {C_{rs}^{\left( 1 \right)} } u_{s} } \right) + \sum\limits_{s = 1}^{n} {C_{rs}^{\left( 1 \right)} } \left( {D_{xx} \sum\limits_{s = 1}^{n} {C_{rs}^{\left( 1 \right)} } \varphi_{s} } \right) - C_{xz} \left( {\varphi_{s} + \sum\limits_{s = 1}^{n} {C_{rs}^{\left( 1 \right)} } w_{s} } \right) = \omega^{2} \left[ {m_{1} u_{s} + m_{2} \varphi_{s} - \left( {e_{0} a} \right)^{2} \sum\limits_{s = 1}^{n} {C_{rs}^{\left( 2 \right)} } \left( {m_{1} u_{s} + m_{2} \varphi_{s} } \right)} \right]$$
(36b)
$$\sum\limits_{s = 1}^{n} {C_{rs}^{\left( 1 \right)} } \left[ {C_{xz} \left( {\varphi_{s} + \sum\limits_{s = 1}^{n} {C_{rs}^{\left( 1 \right)} } w_{s} } \right)} \right] - \sum\limits_{s = 1}^{n} {C_{rs}^{\left( 1 \right)} } \left( {\bar{N}\sum\limits_{s = 1}^{n} {C_{rs}^{\left( 1 \right)} w_{s} } } \right) + \left( {e_{0} a} \right)^{2} \sum\limits_{s = 1}^{n} {C_{rs}^{\left( 2 \right)} \left[ {\sum\limits_{s = 1}^{n} {C_{rs}^{\left( 1 \right)} } \left( {\bar{N}\sum\limits_{s = 1}^{n} {C_{rs}^{\left( 1 \right)} w_{s} } } \right)} \right]} = \omega^{2} \left[ {m_{0} w_{s} - \left( {e_{0} a} \right)^{2} \sum\limits_{s = 1}^{n} {C_{rs}^{\left( 2 \right)} } \left( {m_{0} w_{s} } \right)} \right]$$
(36c)

Using the boundary conditions of nanobeam (Eq. 19) and by assembling the related matrixes to the boundary conditions and governing equations, the linear fundamental vibration of nanobeam can be calculated as below [57]:

$$\left[ {\begin{array}{*{20}c} {\left[ {K_{dd} } \right]} & {\left[ {K_{db} } \right]} \\ {\left[ {K_{bd} } \right]} & {\left[ {K_{bb} } \right]} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\left\{ {\lambda_{d} } \right\}} \\ {\left\{ {\lambda_{b} } \right\}} \\ \end{array} } \right\} = \omega^{2} \left[ {\begin{array}{*{20}c} {\left[ {M_{dd} } \right]} & {\left[ {M_{db} } \right]} \\ {\left[ {M_{bd} } \right]} & {\left[ {M_{bb} } \right]} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\left\{ {\lambda_{d} } \right\}} \\ {\left\{ {\lambda_{b} } \right\}} \\ \end{array} } \right\}$$
(37)

where b and d indexes indicate the boundary and domain, respectively, and λ is the mode shape.

4 Results

The obtained results using the GDQM are presented for the parametric study considering different effects such as small-scale effects, power-law index of functionally graded nanobeam, nondimensional angular velocity, hub radius, nanobeam’s thickness and temperature changes. The aim is to determine best properties of nanobeams for different temperature change (ΔT) ranges and determine critical temperature change (ΔT critical) for different beam properties which is applicable to design rotating nanostructures. L/h is set to be 100 in Figs. 2, 3, 4, 5, 6 and 7, and the boundary condition is considered as cantilever.

Fig. 2
figure 2

Nondimensional fundamental frequency of FG and AFG nanobeams versus nondimensional annular velocity

Full size image
Fig. 3
figure 3

Nondimensional second frequency of FG and AFG nanobeams versus nondimensional annular velocity

Full size image
Fig. 4
figure 4

Nondimensional fundamental frequency of pure ceramic, metal and AFG nanobeams versus temperature change

Full size image
Fig. 5
figure 5

Nondimensional second frequency of pure ceramic, metal and AFG nanobeams versus temperature change

Full size image
Fig. 6
figure 6

Nondimensional fundamental frequency of AFG nanobeam versus temperature change when Φ = 1, δ = 0.4, nx = 1 and L/h = 50

Full size image
Fig. 7
figure 7

Nondimensional second frequency of AFG nanobeam versus temperature change when Φ = 1, δ = 0.4, nx = 1 and L/h = 50

Full size image

In order to have better judgment on results, nondimensional parameters are defined as following:

$$\begin{array}{*{20}l} {x = \xi L;} \hfill & {r = \delta L} \hfill \\ {\varPhi^{2} = \left( {\frac{{m_{0} }}{EI}} \right)_{\text{ceramic}} L^{4} \varOmega^{2} ;} \hfill & {\varPsi^{2} = \left( {\frac{{m_{0} }}{EI}} \right)_{\text{ceramic}} L^{4} \omega^{2} } \hfill \\ {\left( {\frac{{m_{0} }}{EI}} \right)_{\text{ceramic}} = \frac{{12\rho_{\text{ceramic}} }}{{E_{\text{ceramic}} h_{1}^{2} }};} \hfill & {\mu = \frac{{e_{0} a}}{L}} \hfill \\ \end{array}$$
(38)

in which Ψ, Φ, μ and δ indicate nondimensional frequency, nondimensional angular velocity, nondimensional nonlocal parameter and nondimensional hub radius, respectively.

In special case (i.e., Φ = 0), comparison of results for first two nondimensional frequencies of cantilever nanobeam (Table 2) presents good agreement with results of Wang et al. [58]. In addition, Table 3 depicts the comparison of the natural frequency of nanobeams made of pure metal, pure ceramic FGM in different values of L/h.

Table 2 Comparison of results for nondimensional frequency, Ψ of cantilever nanobeam (nonFG)
Full size table
Table 3 Comparison of the natural frequency of pure ceramic, metal and FG nanobeams with the results of local beam, Φ = 2, δ = 0
Full size table

Bold values represent distinguishable results

Figures 2 and 3, respectively, show the fundamental and second frequencies of FG and AFG nanobeams versus nondimensional angular velocity and for different values of hub radius. Figure 2 shows that the increment of angular velocity decreases the dependency of nondimensional fundamental frequency of nanobeams on FG and AFG power indexes. Figures 2 and 3 also show that the nondimensional fundamental and second frequencies of nanobeams increase with the angular velocity and decrease with the increment of FG or AFG power indexes. In addition, it is seen that the increment of hub radius increases the first and second frequencies.

Figures 4 and 5 represent the effects of temperature change, nondimensional angular velocity and AFG power index on fundamental and second nondimensional frequencies, respectively. Figure 4 shows that by increasing temperature changes, fundamental frequency increases continuously. A transition temperature change ΔT transition can be defined to explain the fundamental frequency of cantilever nanobeam’s thermal behavior. For example, this transition region can be defined in Fig. 4c (nx = 0.5) in the range of 85 < ΔT transition < 150, where nanobeam response to different parameters varies. For temperature changes below ΔT transition, by increasing nondimensional angular velocity, nondimensional frequency increases for other certain parameters, while for temperature changes over ΔT transition, by increasing nondimensional angular velocity, nondimensional frequency decreases. Moreover, it is comprehended from Fig. 4a–d that increasing AFG index causes ΔT transition to occur earlier. Also, it is seen that by increasing AFG index, nondimensional fundamental frequency increases more intensively after ΔT transition.

Figure 5 shows that increasing temperature change in AFG nanobeam decreases the nondimensional frequency up to a relative zero point which is called critical point ΔT critical, where increasing temperature changes over critical point increases second nondimensional frequency. This relative zero point is close to real zero for boundary conditions containing simply supported condition [59], while for other boundary conditions, this relative zero value increases. Moreover, Fig. 5 shows that increasing AFG index decreases the nondimensional frequency and critical temperature changes ΔT critical. On the other hand, increasing nondimensional angular velocity would increase the ΔT critical.

Figures 6 and 7 represent temperature change, nondimensional nonlocal parameter (μ) and gradient temperature rise (α T) of nanobeam effects on fundamental and second nondimensional frequencies.

Figure 6 shows that by increasing temperature changes, fundamental frequency increases continuously. Similar to Fig. 4, transition zones of temperature can be observed in Fig. 6 too. For temperature changes below ΔT transition, by increasing nondimensional small-scale parameter, nondimensional frequency increases, while for temperature changes over ΔT transition, by increasing small-scale parameter, nondimensional frequency decreases. Moreover, Fig. 6a–d shows that decreasing thickness of nanobeam causes ΔT transition to occur earlier. Also, it is seen that by decreasing α T, the dependency of nondimensional fundamental frequency on temperature change after ΔT transition increases.

Figure 7 represents temperature changes, small-scale parameter and gradient temperature rise (α T) of nanobeam effects on nondimensional second frequency. Figure 7 shows that increasing temperature changes for a AFG nanobeam decreases the nondimensional frequency up to a relative zero point which is called critical point ΔT critical, where increasing temperature changes over critical point increases second nondimensional frequency. Moreover, Fig. 7 shows that increasing thickness increases the nondimensional frequency and critical temperature changes ΔT critical. On the other hand, increasing small-scale parameter would decrease the ΔT critical.

Tables 4 and 5 show the nondimensional fundamental frequency of local and nonlocal nanobeams, respectively, when nx has very high value to set the material of the nanobeam as metal. The nondimensional frequency is derived for various values of power index of temperature variation function, temperature change and L/h. Comparing Tables 4 and 5 shows that increment of nonlocal value increases the fundamental frequency of nanobeams. Tables 4 and 5 also show that the increment of α T decreases the nondimensional frequency. Also, the frequency increases with the temperature change and L/h. It should also be noted that the effect of ΔΤ and α T is more significant in higher values of L/h.

Table 4 Nondimensional fundamental frequency of nanobeam when Φ = 3, μ = 0 and nx = ∞
Full size table
Table 5 Nondimensional second frequency of nanobeam when Φ = 3, μ = 0.1 and nx = ∞
Full size table

5 Conclusions

Studied herein is the thermal vibrational behavior of FG and AFG rotating nanobeams. The material volume fraction of the nanobeam is variable along thickness or axis based on the power-law function. The equations are developed according to the Eringen’s nonlocal theory and solved using the generalized differential quadrature method (GDQM). The vibration characteristics of the FG and AFG nanobeams are explored by studying effects of nonlocal value, temperature gradient, FG and AFG power indexes, temperature change, nonlocal value and angular velocity. These results yielded the important conclusions mentioned below:

  • The nondimensional fundamental frequencies increase with the temperature change.

  • Before ΔT transition, the fundamental frequency of AFG nanobeam increases with nonlocal value. But after ΔT transition, increment of nonlocal value decreases the frequency.

  • Before ΔT transition, the fundamental and second frequencies of AFG nanobeam increase with the angular velocity. But after ΔT transition, increasing the angular velocity decreases the frequencies.

  • Decrement of thickness makes ΔT transition to occur in lower temperatures.

  • Increment of hub radius increases the first and second frequencies.

  • Increasing L/h, angular velocity and also temperature change increases the first and second frequencies.

  • Increment of angular velocity decreases the effect of FG and AFG power indexes.