Introduction

In recent years, nanomaterials and nanotechnology have been widely used in biological monitoring and microelectronics, such as micro-drug transporters, nano-blood detection robots, microscopes, and nanofunctional coatings [1,2,3]. However, nanostructures have special small-scale effects compared with macro-scale mechanical structures. Three approaches have been used to investigate the mechanics of nanostructures, namely experimental, molecular dynamics simulation and the nonlocal continuum theory [4]. Due to the complexity of experiments at nanoscale and time consumption of molecular dynamics simulation, mechanical properties of nanostructures have been investigated mainly by the nonlocal continuum theory during the past decades [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27]. The nonlocal elasticity theory [4,5,6], proposed by Eringen and his assistants, can well capture and explain the nonlocal scale effect of nanostructures. Lim et al. [9] investigated the free vibration of nanobeams with axial variable velocity using the nonlocal elasticity theory. The natural frequency and critical velocity were obtained by complex mode method, and the effects of nonlocal parameter and axial speed on the natural frequencies were analyzed. Liu et al. [15] studied the principal harmonic resonance response of simply supported nanobeams based on the nonlocal elasticity theory. It was found that the nonlocal parameter reduces natural frequency of nanobeams compared with the macro-structures. Li et al. [17] studied the bending of cantilever nanobeams subjected to transverse loads based on the nonlocal elasticity theory and found that the effect of nonlocal scale would disappear in the cantilever beams. Zhang et al. [20] analyzed the vibration characteristics of Euler nanobeams resting on viscoelastic foundation and obtained the closed solutions of the natural frequencies and vibration modes under different boundary conditions using the method of transfer function. Yang et al. [21] investigated the free vibration behavior of nanobeams, based on the nonlocal elasticity theory. The natural frequencies of vibration were solved using the symplectic approach. Zhou et al. [23] provided a rigorous analytical method to find the exact solutions for free vibration and steady-state forced vibration of the double-nanobeam systems embedded in an elastic medium using the Hamiltonian system in conjunction with Eringen’s nonlocal Euler beam theory and Timoshenko beam theory. Zhang et al. [25] studied the free vibration of functionally graded nanobeams based on the nonlocal elasticity theory and Timoshenko beam theory.

Moreover, elastic waves are generated with a vibrating nanostructure. If elastic waves propagate in structures with obstacles such as holes, cracks or interfaces, scattering will occur near them, which results in dynamic stress concentration. Thus, the study on the propagation characteristics of elastic waves in nanostructures is helpful for us to understand and master the wave propagation law of nanobeams, and it has theoretical significance for flaw detection, as well as the study of inverse dynamics problems. At present, the literature on wave propagation in nanobeams is scarce. Narendar and Gopalakrishnan [28] investigated the wave dispersion characteristics of rotating nanotubes using the nonlocal elasticity theory and Euler–Bernoulli beam theory, and the relationship between the spectral and dispersion curves with rotational speed and nonlocal scale parameter was obtained. Narendar et al. [29] studied the wave propagation of Euler nanobeams in magnetic field using nonlocal elasticity theory, and the effects of stiffness, magnetic field strength and nonlocal parameter on wave velocity were analyzed. It was found that the existence of magnetic field strength increases the propagation velocity of elastic wave.

With the development of science and technology, the traditional homogeneous nanomaterials cannot meet the requirement of actual engineering. New composite nanomaterials, functionally graded nanomaterials (FGNM), were invented, such as functionally graded nanocomposite Ti (C, N) based on cermet [30]. However, the research on the mechanical properties of functionally graded nanostructures was still insufficient, and most literature studies neglected the effect of material inhomogeneity on the axial displacement of functionally graded beams [31]. In this paper, free vibration and wave propagation of functionally graded Euler nanobeam with constant axial velocity are presented based on the nonlocal elasticity theory. To this end, the concept of neutral plane is introduced, which is used to express the axial displacement of geometry plane, caused by inhomogeneity of functionally graded materials. Moreover, natural frequency and wave propagation velocity of functionally graded nanobeams are obtained by the methods of the complex mode and Newton iteration. After that, the effects of nonlocal parameter, axial velocity and gradient index on natural frequency and wave propagation are analyzed in detail.

Mechanical Model and Governing Equations

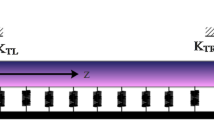
For a functionally graded nanobeam as shown in Fig. 1, the nanobeam travels at an axial velocity \(v\) between two boundaries separated by distance \(l\). The cross section is a rectangle with thickness h and width b. The x-axis is taken along the middle plane, which is \(z_{0}\) from the neutral plane.

Fig. 1
figure 1

Mechanical model of functionally graded nanobeam with axial motion

Full size image

Power-Law Functionally Graded Material

The physical parameters of functionally graded material (FGM) are assumed to vary along the thickness direction according to power index law, and they are made of two basement materials: ceramic and metal. Consequently, the material parameters can be described by [32, 33]

$$P\left( z \right) = \left( {P_{c} - P_{m} } \right)\left( {\frac{z}{h} + \frac{1}{2}} \right)^{k} + P_{m} ,\quad - \frac{h}{2} \le z \le \frac{h}{2},$$
(1)

where \(P\left( z \right)\) represents the modulus of elasticity E and density \(\rho\). \(P_{c}\) and \(P_{m}\) stand for physical parameters of pure ceramics and pure metals, respectively. The bottom surface (z = − h/2) of a FGM beams is pure metal, whereas its top surface (z = h/2) is pure ceramics. k represents gradient index.

Kinematic Relations

Firstly, the distance from middle plane to neutral plane \(z_{0}\) is given by [34]

$$z_{0} = \frac{{\int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {zE\left( z \right){\text{d}}z} }}{{\int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {E\left( z \right){\text{d}}z} }} = h\alpha a_{1} ,$$
(2)

where \(a_{1} = \frac{k}{{2\left( {k + 2} \right)\left( {\alpha + k + 1} \right)}}\), \(\alpha = E_{c} /E_{m} - 1\).

Using the Euler–Bernoulli beam model and introducing the neutral plane, the displacement field at any point of the nanobeam can be written as [34]

$$u\left( {x,z,t} \right) = - \left( {z - z_{0} } \right)\frac{{\partial w\left( {x,t} \right)}}{\partial x},\quad w\left( {x,z,t} \right) = w_{0} \left( {x,t} \right),$$
(3)

where \(u\left( {x,z,t} \right)\) and \(w\left( {x,z,t} \right)\) represent the axial displacement and transverse displacement of nanobeam, respectively. \(w_{0}\) stands for the transverse displacement of middle plane. In accordance, the linear strain–displacement relationship is

$$\varepsilon_{xx} = \frac{{\partial u\left( {x,z,t} \right)}}{\partial x} = - \left( {z - z_{0} } \right)\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }},$$
(4)
$$\sigma_{xx} = E\left( z \right)\varepsilon_{xx} = - E\left( z \right)\left( {z - z_{0} } \right)\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }},$$
(5)

where \(\varepsilon_{xx}\) and \(\sigma_{xx}\) represent strain and stress of FGM nanobeam, respectively.

Using Eq. (5), the local bending moment \(M\) can be determined after some mathematical manipulation, written as

$$M = \int_{A} {\left( {z - z_{0} } \right)\sigma_{xx} {\text{d}}A} = - I_{2} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }},$$
(6)

where

$$I_{ 2} = \int_{A} {E\left( z \right)} \left( {z - z_{0} } \right)^{ 2} {\text{d}}A = E_{m} Ia_{2} ,$$
(7)

in which \(a_{2} = \frac{{3\alpha \left( {k^{2} + k + 2} \right)}}{{\left( {k + 1} \right)\left( {k + 2} \right)\left( {k + 3} \right)}} - \frac{{6\alpha^{2} a_{1} k}}{{\left( {k + 1} \right)\left( {k + 2} \right)}} + 1\), \(I = \frac{{bh^{3} }}{12}.\)

Using Eqs. (4) and (5), the variation of potential energy U is given by

$$\delta U = \int_{ 0}^{l} {\int_{A} {\sigma_{xx} \delta \varepsilon_{xx} {\text{d}}A{\text{d}}x = } } I_{2} \int_{0}^{l} {\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}\frac{{\partial^{2} \delta w_{0} }}{{\partial x^{2} }}} {\text{d}}x.$$
(8)

Secondly, kinetic energy can be described by

$$T = \frac{1}{2}\int_{0}^{l} {\int_{A} {\rho \left( z \right)} \left[ {\left( {\frac{{\partial w_{0} }}{\partial t} + v\frac{{\partial w_{0} }}{\partial x}} \right)^{2} + \, \left( { - \left( {z - z_{0} } \right)\frac{{\partial^{2} w_{0} }}{\partial x\partial t} + v} \right)^{2} } \right]{\text{d}}A{\text{d}}x} ,$$
(9)

where \(\left( {\frac{{\partial w_{0} }}{\partial t} + v\frac{{\partial w_{0} }}{\partial x}} \right)\) and \(\left[ { - \left( {z - z_{0} } \right)\frac{{\partial^{2} w_{0} }}{\partial x\partial t} + v} \right]\) represent transverse and axial speeds of nanobeam, respectively. Therefore, the variation of kinetic energy is given by

$$\delta T = S_{0} \left( {\int_{0}^{l} {\frac{{\partial w_{0} }}{\partial t}\frac{{\partial \delta w_{0} }}{\partial t}} {\text{d}}x + \int_{0}^{l} {v\frac{{\partial w_{0} }}{\partial t}\frac{{\partial \delta w_{0} }}{\partial x}} {\text{d}}x + \int_{0}^{l} {v\frac{{\partial w_{0} }}{\partial x}\frac{{\partial \delta w_{0} }}{\partial t}} {\text{d}}x + \int_{0}^{l} {v^{2} \frac{{\partial w_{0} }}{\partial x}\frac{{\partial \delta w_{0} }}{\partial x}} {\text{d}}x} \right) - S_{1} \int_{0}^{l} {v\frac{{\partial^{2} \delta w_{0} }}{\partial x\partial t}} {\text{d}}x + S_{2} \int_{0}^{l} {\frac{{\partial^{2} w_{0} }}{\partial x\partial t}\frac{{\partial^{2} \delta w_{0} }}{\partial x\partial t}} {\text{d}}x,$$
(10)

where

$$S_{0} = \int_{A} {\rho \left( z \right)} {\text{d}}A = \rho_{m} Aa_{3} ,$$
(11)
$$S_{ 1} = \int_{A} {\rho \left( z \right)} \left( {z - z_{0} } \right){\text{d}}A = \rho_{m} bh^{2} a_{4} ,$$
(12)
$$S_{2} = \int_{A} {\rho \left( z \right)} \left( {z - z_{0} } \right)^{ 2} {\text{d}}A = \rho_{m} Ia_{5} ,$$
(13)

in which

$$a_{3} = \frac{\gamma + k + 1}{k + 1},$$
(14)
$$a_{4} = \frac{\gamma }{k + 2} - \frac{{\gamma \left( {1 + 2\alpha a_{1} } \right)}}{{2\left( {k + 1} \right)}} - \alpha a_{1} ,$$
(15)
$$a_{5} = \frac{{3\gamma \left( {k^{2} + k + 2} \right)}}{{\left( {k + 1} \right)\left( {k + 2} \right)\left( {k + 3} \right)}} - \frac{{6\gamma^{2} a_{1} k}}{{\left( {k + 1} \right)\left( {k + 2} \right)}} + 1,$$
(16)

\(\gamma = \rho_{c} /\rho_{m} - 1,\;A = bh.\)

Substituting Eqs. (8) and (10) into the Hamilton’s principle

$$\delta \int_{{t_{1} }}^{{t_{2} }} {\left( {U - T} \right)} {\text{d}}t = 0,$$
(17)

the governing equation of FGM beams with axially motion can be derived as

$$I_{2} \frac{{\partial^{4} w_{0} }}{{\partial x^{4} }} + S_{0} \frac{{\partial^{2} w_{0} }}{{\partial t^{2} }} + 2S_{0} v\frac{{\partial^{2} w_{0} }}{\partial x\partial t} + S_{0} \frac{{{\text{d}}v}}{{{\text{d}}t}}\frac{{\partial w_{0} }}{\partial x} + S_{0} v^{2} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} - S_{2} \frac{{\partial^{4} w_{0} }}{{\partial x^{2} \partial t^{2} }} = 0.$$
(18)

Substituting Eq. (6) into Eq. (18), the governing equation can be rewritten as

$$\frac{{\partial^{2} M}}{{\partial x^{2} }} = S_{0} \frac{{\partial^{2} w_{0} }}{{\partial t^{2} }} + 2S_{0} v\frac{{\partial^{2} w_{0} }}{\partial x\partial t} + S_{0} \frac{{{\text{d}}v}}{{{\text{d}}t}}\frac{{\partial w_{0} }}{\partial x} + S_{0} v^{2} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} - S_{2} \frac{{\partial^{4} w_{0} }}{{\partial x^{2} \partial t^{2} }}.$$
(19)

Nonlocal Elasticity Theory

The nonlocal elasticity theory [4,5,6] holds that stress at a reference point in a body is considered as a function of strains of all points in the near region. For Euler–Bernoulli nonlocal FGNM beams, nonlocal constitutive relations can be simplified as [8]

$$t_{xx} - \left( {e_{0} a} \right)^{2} \frac{{\partial^{2} t_{xx} }}{{\partial x^{2} }} = \sigma_{xx} = E\left( z \right)\varepsilon_{xx} ,$$
(20)

where \(\left( {e_{0} a} \right)\) stands for the nonlocal parameter that incorporates the nonlocal scale effect. Note that a is the internal characteristic length (e.g., lattice parameter, C–C bond length and granular distance) and e0 is a constant appropriate to each material [8]. \(t_{xx}\) and \(\sigma_{xx}\) represent the nonlocal stress and local stress of FGNM nanobeam, respectively.

By integrating Eq. (20) over the cross-sectional area of the nanobeam, we obtain that

$$M - \left( {e_{0} a} \right)^{2} \frac{{\partial^{2} M}}{{\partial x^{2} }} = - I_{2} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }},$$
(21)

where \(M\) represents the nonlocal bending moment when the nonlocal elasticity theory is introduced.

Substituting Eq. (19) into Eq. (21), the bending moment of nonlocal Euler–Bernoulli FGM beam can be derived as

$$M = \left( {e_{0} a} \right)^{2} \left( {S_{0} \frac{{\partial^{2} w_{0} }}{{\partial t^{2} }} + 2S_{0} v\frac{{\partial^{2} w_{0} }}{\partial x\partial t} + \, S_{0} \frac{{{\text{d}}v}}{{{\text{d}}t}}\frac{{\partial w_{0} }}{\partial x}} \right.\left. { + S_{0} v^{2} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} - S_{2} \frac{{\partial^{4} w_{0} }}{{\partial x^{2} \partial t^{2} }}} \right) - I_{2} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}.$$
(22)

Substituting Eq. (22) into Eq. (19), the governing equation of nonlocal Euler–Bernoulli FGM nanobeam with axial motion can be established as

$$\begin{aligned} \left( {e_{0} a} \right)^{2} \left( {S_{0} \frac{{\partial^{4} w_{0} }}{{\partial x^{2} \partial t^{2} }} + 2S_{0} v\frac{{\partial^{4} w_{0} }}{{\partial x^{3} \partial t}} + \, S_{0} \frac{{{\text{d}}v}}{{{\text{d}}t}}\frac{{\partial^{3} w_{0} }}{{\partial x^{3} }} + S_{0} v^{2} \frac{{\partial^{4} w_{0} }}{{\partial x^{4} }} - S_{2} \frac{{\partial^{6} w_{0} }}{{\partial x^{4} \partial t^{2} }}} \right) - I_{2} \frac{{\partial^{4} w_{0} }}{{\partial x^{4} }} \hfill \\ = S_{0} \left( {\frac{{\partial^{2} w_{0} }}{{\partial t^{2} }} + 2v\frac{{\partial^{2} w_{0} }}{\partial x\partial t} + \frac{{{\text{d}}v}}{{{\text{d}}t}}\frac{{\partial w_{0} }}{\partial x} + v^{2} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}} \right) - \quad S_{2} \frac{{\partial^{4} w_{0} }}{{\partial x^{2} \partial t^{2} }}. \hfill \\ \end{aligned}$$
(23)

In particular, when the nanobeam travels at a constant axial speed, the governing equation can be rewritten as

$$\begin{aligned} \left( {e_{0} a} \right)^{2} \left( {S_{0} \frac{{\partial^{4} w_{0} }}{{\partial x^{2} \partial t^{2} }} + 2S_{0} v\frac{{\partial^{4} w_{0} }}{{\partial x^{3} \partial t}} + S_{0} v^{2} \frac{{\partial^{4} w_{0} }}{{\partial x^{4} }} - S_{2} \frac{{\partial^{6} w_{0} }}{{\partial x^{4} \partial t^{2} }}} \right) - I_{2} \frac{{\partial^{4} w_{0} }}{{\partial x^{4} }} \hfill \\ = S_{0} \left( {\frac{{\partial^{2} w_{0} }}{{\partial t^{2} }} + 2v\frac{{\partial^{2} w_{0} }}{\partial x\partial t} + v^{2} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}} \right) - S_{2} \frac{{\partial^{4} w_{0} }}{{\partial x^{2} \partial t^{2} }}. \hfill \\ \end{aligned}$$
(24)

Frequency and Velocity of Wave Propagation

For a linear problem, the solution of the axially moving FGM nanobeam with the steady vibration waves by Eq. (24) can be expressed as

$$w_{0} = We^{{i\left( {\beta x - \omega t} \right)}} ,$$
(25)

where \(W\) is the wave amplitudes, \(\beta\) and \(\omega\) are the wave number and the circular frequency, respectively. i is the imaginary unit. Substituting Eq. (25) into Eq. (24), the dispersion equation of nonlocal Euler–Bernoulli FGM beam with axial motion can be obtained as

$$b_{1} \omega^{2} - b_{2} \omega + b_{3} = 0,$$
(26)

in which

$$b_{1} = \eta^{2} \beta^{4} \frac{{h^{2} a_{ 5} }}{{12a_{ 3} }} + \left( {\eta^{2} + \frac{{h^{2} a_{ 5} }}{{12a_{ 3} }}} \right)\beta^{2} + 1,\quad b_{2} = 2\left( {\eta^{2} \beta^{2} + 1} \right)v\beta ,\quad b_{3} = \left( {\eta^{2} v^{2} - \frac{{h^{2} E_{m} a_{ 2} }}{{12\rho_{m} a_{ 3} }}} \right)\beta^{4} + \eta^{2} \beta^{2} ,\eta^{2} = \left( {e_{0} a} \right)^{2} .$$

Equation (26) is the analysis of wave propagation of nonlocal Euler–Bernoulli FGM beam with axial motion. In accordance, the velocity of wave propagation can be arrived as

$$C_{p} = \frac{\omega }{\beta }.$$
(27)

By solving Eq. (26), the circular frequency can be obtained as

$$\omega_{ 1 , 2} { = }\frac{{12v\beta a_{ 3} }}{{12a_{ 3} + a_{ 5} h^{2} \beta^{2} }} \pm \frac{{h\beta^{2} \sqrt {a_{ 2} E_{m} (12a_{ 3} + a_{ 5} h^{2} \beta^{2} )/\rho_{m} - 12a_{ 5} a_{ 3} v^{2} \left( {1 + \beta^{2} \mu^{2} } \right)} }}{{\sqrt {1 + \beta^{2} \mu^{2} } \left( {12a_{ 3} + a_{ 5} h^{2} \beta^{2} } \right)}}.$$
(28)

Since the value of \(\omega_{2}\) is always negative, this paper only analyzes the relationship between \(\omega_{1}\) and wave number.

Frequency of Vibration

By introducing the following non-dimensional terms:

$$\xi = x/l,\quad W = w_{0} /l,\quad \delta = h/l,\quad \tau { = }\left( {e_{0} a} \right)/l,\quad V = v\sqrt {\frac{{\rho_{m} l^{2} A}}{{E_{m} I}}} ,\quad T = t\sqrt {\frac{{E_{m} I}}{{\rho_{m} l^{4} A}}} ,\quad \bar{M} = \frac{Ml}{{E_{m} I}},$$
(29)

where \(\xi\), \(W\), \(\delta\), \(\tau\), V, \(\bar{M}\) and \(T\) represent the non-dimensional axial coordinate value, non-dimensional deflection, slenderness ratio, non-dimensional nonlocal parameter, non-dimensional axial velocity, non-dimensional nonlocal bending moment and non-dimensional time, respectively.

Substituting Eq. (29) into Eq. (24), the non-dimensional governing equation can be obtained as

$$\begin{aligned} \tau^{2} \left( {\frac{{\partial^{4} W}}{{\partial \xi^{2} \partial T^{2} }} + 2V\frac{{\partial^{4} W}}{{\partial \xi^{3} \partial T}} + V^{2} \frac{{\partial^{4} W}}{{\partial \xi^{4} }} - \frac{{a_{5} \delta^{2} }}{{12a_{3} }}\frac{{\partial^{6} W}}{{\partial \xi^{4} \partial T^{2} }}} \right) \hfill \\ - \frac{{a_{2} }}{{a_{3} }}\frac{{\partial^{4} W}}{{\partial \xi^{4} }} = \frac{{\partial^{2} W}}{{\partial T^{2} }} + 2V\frac{{\partial^{2} W}}{\partial \xi \partial T} + V^{2} \frac{{\partial^{2} W}}{{\partial \xi^{2} }} - \frac{{a_{5} \delta^{2} }}{{12a_{3} }}\frac{{\partial^{4} W}}{{\partial \xi^{2} \partial T^{2} }}. \hfill \\ \end{aligned}$$
(30)

Since the mode of FGNM beam is harmonic to time, the transverse vibration displacement of FGNM beam is assumed to be as

$$W\left( {\xi ,T} \right) = W_{n} \left( \xi \right)e^{{i\omega_{n} T}} ,$$
(31)

where \(W_{n}\) and \(\omega_{n}\) represent the nth-order dimensionless mode and natural frequency of free vibration, respectively.

Substituting Eq. (31) into Eq. (30), we can get

$$d_{1} \frac{{{\text{d}}^{4} W_{n} }}{{{\text{d}}\xi^{4} }} + d_{2} \frac{{{\text{d}}^{3} W_{n} }}{{{\text{d}}\xi^{3} }} - d_{3} \frac{{{\text{d}}^{2} W_{n} }}{{{\text{d}}\xi^{2} }} - d_{4} \frac{{{\text{d}}W_{n} }}{{{\text{d}}\xi }} + d_{5} W_{n} = 0,$$
(32)

in which

$$d_{1} = \tau^{2} V^{2} + \frac{{\delta^{2} a_{5} \tau^{2} }}{{12a_{3} }}\omega_{n}^{2} - \frac{{a_{2} }}{{a_{3} }},\quad d_{2} = 2iV\tau^{2} \omega_{n} ,\quad d_{3} = \tau^{2} \omega_{n}^{2} + V^{2} + \frac{{\delta^{2} a_{5} }}{{12a_{3} }}\omega_{n}^{2} ,\quad d_{4} = 2iV\omega_{n} ,\quad d_{5} = \omega_{n}^{2} .$$

Equation (32) is a fourth-order ordinary differential equation, so the dimensionless mode of transverse vibration of FGNM beam with axial motion can be assumed to be

$$W_{n} \left( \xi \right) = C_{1} e^{{\lambda_{1} \xi }} + C_{2} e^{{\lambda_{2} \xi }} + C_{3} e^{{\lambda_{3} \xi }} + C_{4} e^{{\lambda_{4} \xi }} ,$$
(33)

where \(C_{j} \left( {j = 1,2,3,4} \right)\) is integral constant, and \(\lambda_{j} \left( {j = 1,2,3,4} \right)\) is the characteristic root of Eq. (32).

Simply Supported (S–S) FGNM Beam

The boundary conditions of simply supported FGNM beams at both ends can be described as

$$W\left( 0 \right) = 0,\quad \bar{M}\left( 0 \right) = 0,\quad W\left( 1 \right) = 0,\quad \bar{M}\left( 1 \right) = 0.$$
(34)

Substituting Eqs. (22) and (33) into Eq. (34), we can obtain a set of algebraic equations. To make the original problem have non-zero solution, the determinant of coefficient matrix in algebraic equations is required to be zero, that is,

$$\left| {\begin{array}{*{20}l} 1 \hfill & 1 \hfill & 1 \hfill & 1 \hfill \\ {e^{{\lambda_{1} }} } \hfill & {e^{{\lambda_{2} }} } \hfill & {e^{{\lambda_{3} }} } \hfill & {e^{{\lambda_{4} }} } \hfill \\ {f(\lambda_{1} )} \hfill & {f(\lambda_{2} )} \hfill & {f(\lambda_{3} )} \hfill & {f(\lambda_{4} )} \hfill \\ {f(\lambda )e^{{\lambda_{1} }} } \hfill & {f(\lambda_{2} )e^{{\lambda_{2} }} } \hfill & {f(\lambda_{3} )e^{{\lambda_{3} }} } \hfill & {f(\lambda_{4} )e^{{\lambda_{4} }} } \hfill \\ \end{array} } \right| = 0,$$
(35)

where \(f(\lambda ) = d_{1} \lambda^{2} + d_{2} \lambda + d_{ 6}\), \(d_{6} = - \tau^{2} d_{5} .\)

Clamped–Clamped (C–C) FGNM Beam

The boundary conditions of clamped–clamped FGNM beams at both ends can be described as

$$W\left( 0 \right) = 0,\quad W^{\prime}\left( 0 \right) = 0,\quad W\left( 1 \right) = 0,\quad W^{\prime}\left( 1 \right) = 0.$$
(36)

Substituting Eq. (33) into Eq. (36), we can obtain the condition of non-zero solution similarly, expressed by

$$\left| {\begin{array}{*{20}l} 1 \hfill & 1 \hfill & 1 \hfill & 1 \hfill \\ {e^{{\lambda_{1} }} } \hfill & {e^{{\lambda_{2} }} } \hfill & {e^{{\lambda_{3} }} } \hfill & {e^{{\lambda_{4} }} } \hfill \\ {\lambda_{1} } \hfill & {\lambda_{2} } \hfill & {\lambda_{3} } \hfill & {\lambda_{4} } \hfill \\ {\lambda_{1} e^{{\lambda_{1} }} } \hfill & {\lambda_{2} e^{{\lambda_{2} }} } \hfill & {\lambda_{3} e^{{\lambda_{3} }} } \hfill & {\lambda_{4} e^{{\lambda_{4} }} } \hfill \\ \end{array} } \right|{ = 0} .$$
(37)

Equations (35) and (37) are transcendental equations, which can be recorded as \(g\left( {\omega_{n} } \right) = 0\). The Newton iteration method is applied to solve them, and the flowchart is shown in Fig. 2. In Fig. 2, \(\Delta \omega { = 3}\) and \(\varepsilon { = 10}^{ - 4}\) stand for the increment of frequency and the convergence accuracy to judge the root of transcendental equation, respectively.

Fig. 2
figure 2

Flowchart for solving transcendental equation

Full size image

Numerical Results and Analysis

In the following numerical examples, it is assumed that the FGNM beam is made of steel metal (k = \(\infty\)) and alumina ceramics (k = 0), and several parameters are chosen to be [35]

$$\begin{aligned} l = & 10{\text{ nm}}, \, b = 1{\text{ nm}}, \, \delta = 0.1 \\ E_{m} = & 210\;{\text{GPa}}, \, \rho_{m} = 7800{\text{ kg/m}}^{3} , \, E_{c} = 390{\text{ GPa}}, \, \rho_{c} = 3960{\text{ kg/m}}^{3} . \\ \end{aligned}$$
(38)

Validity and Accuracy of Present Analysis

In this sub-section, a numerical verification is performed to check the validity and accuracy of present analysis. The axially moving functionally graded nanobeam model is degenerated into a macro-beam model with uniform material without axial speed, with setting k = 0 (or k = \(\infty\)), \(\delta\) = 0.1, V = 0, and \(\tau = 0\). As is shown in Table 1, the first three order dimensionless natural frequencies of macroscopically simply supported beams are performed, compared with the exact solutions of Ref. [35].

Table 1 Non-dimensional natural frequency of simply supported uniform macro-beams
Full size table

From Table 1, it can be seen that the calculation results are very close to the exact solutions of Ref. [35], and the relative error is within 3.5%. It proves that the presented theoretical derivation and calculation method are correct and effective. Moreover, with the introduction of neutral plane, results are very close to the exact solutions of Ref. [35], where the axial displacement of middle plane is considered.

Effects of Axial Velocity, Small-Scale Parameters and Gradient Index on Natural Frequencies of Vibration

Figure 3 illustrates the effect of non-dimensional axial velocity V on the first three natural frequencies for different non-dimensional nonlocal parameter with k = 2. As observed, with the increase of axial velocity, the three order natural frequencies decrease. Moreover, the existence of nonlocal parameter leads to the decrease of natural frequencies (\(\tau { = 0} . 1\)), compared with local elasticity theory (\(\tau { = 0}\)). Especially, the natural frequencies of C–C FGNM beams vary rapidly when axial velocity V is more than 3. It can also be observed that the natural frequencies of C–C FGNM beams are more than the natural frequencies of S–S FGNM beams.

Fig. 3
figure 3

Relationship between natural frequency of FGNM beams and non-dimensional axial velocity (k = 2)

Full size image

In the present work, the square of nonlocal parameter \(\left( {e_{0} a} \right)^{2}\) is assumed to be in the range of 0–5 (nm)2 [36]. After calculation, \(\tau \left( { = e_{0} a/l} \right)\) varies from 0 to 0.223, so \(\tau\) is given to vary from 0 to 0.2 in this paper. Figure 4 shows the effect of non-dimensional nonlocal parameter \(\tau\) on natural frequencies of FGNM beams for different gradient index k with V = 1. It can be found from Fig. 4 that with the increase of non-dimensional nonlocal parameter, all of the three order natural frequencies decrease. Besides, natural frequencies decrease rapidly with \(\tau\) varying from 0 to 0.1, while they decrease slowly with \(\tau\) varying from 0.1 to 0.2. It also reflects that non-dimensional nonlocal parameter has more significant effect on the third-order natural frequency than the first-order natural frequency.

Fig. 4
figure 4

Relationship between natural frequency and non-dimensional nonlocal parameter (V = 1)

Full size image

Figure 5 shows the effect of gradient index k on natural frequencies for different non-dimensional nonlocal parameter with V = 1. Figure 6 illustrates the effect of gradient index k on natural frequencies of FGNM beams for different non-dimensional axial velocity with \(\tau = 0.1\). In Figs. 5 and 6, it can be seen that increasing the gradient index causes a decrease in natural frequencies. Moreover, the three order natural frequencies reduce rapidly when k varies from 0 to 2, while they reduce tardily with k varying from 2 to \(\infty\). Comparing Fig. 5 with Fig. 6, it is implied that the influence of non-dimensional nonlocal parameter on the natural frequencies is more obvious, compared with non-dimensional axial velocity. It means that the nonlocal scale effect, instead of the axial motion, dominates the dynamic behaviors of nanobeams at nanoscale.

Fig. 5
figure 5

Relationship between natural frequency and gradient index (V = 1)

Full size image
Fig. 6
figure 6

Relationship between natural frequency and gradient index (\(\tau\) = 0.1)

Full size image

Effects of Wave Number on Wave Propagation Frequency and Wave Propagation Velocity

Figure 7 shows the effect of wave number \(\beta\) on the wave propagation frequency \(f = \omega_{1} /\left( {2\pi } \right)\) for different nonlocal parameter, axial velocity and gradient index. As observed, with the increase of wave number from 0 to 1 (/nm), frequencies of wave propagation increase rapidly. However, they increase slowly until reaching a stable value when \(\beta\) varies from 1 to 5 (/nm). This phenomenon is called the escape phenomenon of wave propagation. Moreover, increasing the gradient index causes a decrease in frequencies of wave propagation, increasing the axial velocity causes an increase in frequencies of wave propagation, and increasing the nonlocal parameter causes an increase in frequencies of wave propagation. In addition, the nonlocal parameter has the greatest influence on wave propagation frequency. Although the axial velocity also influences the wave propagation frequency, its effect is relatively small.

Fig. 7
figure 7

Relationship between wave propagation frequency of FGNM beams and wave number

Full size image

Figure 8 displays the relationship between the velocity and wave number of wave propagation. In Fig. 8, with the increase of wave number from 0 to 2 (/nm), velocity of wave propagation decreases rapidly. However, the speed of descent becomes slow when \(\beta\) varies from 2 to 5(/nm), and then reaches a stable value. Moreover, increasing the gradient index causes a decrease in velocity of wave propagation, increasing the axial velocity causes an increase in velocity of wave propagation, and increasing the nonlocal parameter causes a decrease in velocity of wave propagation.

Fig. 8
figure 8

Relationship between wave propagation velocity of FGNM beams and wave number

Full size image

Conclusions

This paper is devoted to the transverse free vibration and wave propagation of axially moving Euler nanobeam made of functionally graded materials, based on the nonlocal elasticity theory. Neutral plane is introduced to express the axial displacement of geometry surface caused by non-uniformity of functionally graded materials. Complex mode method and Newton iteration method are applied to obtain the natural frequency of free vibration and the wave propagation velocity. Numerical examples are presented to demonstrate the validity and accuracy of present analyses, and the effects of some parameters including axial velocity, nonlocal parameter and gradient index on the natural frequencies are investigated. The calculations are very close to the exact solutions of reference. For free vibration, with the increase of non-dimensional axial velocity, natural frequencies decrease. Increasing the non-dimensional nonlocal parameter causes a decrease in natural frequencies, and non-dimensional nonlocal parameter has greater impact on the third-order natural frequency than the first-order natural frequency. Increasing the gradient index causes a decrease in natural frequencies. In addition, the influence of non-dimensional nonlocal parameter on the natural frequencies is more obvious, compared with non-dimensional axial velocity. For wave propagation, with the increase of wave number, frequency of wave propagation increases. However, with the increase of wave number, velocity of wave propagation decreases. Moreover, increasing the gradient index causes a decrease in frequency and velocity of wave propagation, increasing the axial velocity causes an increase in frequency and velocity of wave propagation, and increasing the nonlocal parameter causes a decrease in frequency and velocity of wave propagation. The results reported could be useful for designing and optimizing the FGNM Euler beam-like structures with axial motion.