Introduction

Aerospace equipment, high-precision instruments, vehicles and construction machines, etc., are inevitably accompanied by various vibrations during operation which generate from self-excitation or their surroundings [1,2,3,4]. Most of vibrations are undesirable and destructive to the precision and safety of mechanical equipment. They can aggravate wear and fatigue of structures, cause discomfort and even mental/physical damages to the drivers of vehicles and the operators of construction machines.

It is known that there are two ways to protect equipment from vibration hazards: (1) eliminating vibration sources, and (2) isolating vibrations during propagation. Limited by the accuracy of equipment manufacturing and the complexity of the surroundings, it is difficult to eliminate the vibration source thoroughly. Therefore, isolating the equipment from the vibration source by installing a vibration isolator becomes an alternative and effective way to protect the equipment from vibration hazards. In general, the vibration isolators are not effective until the excitation frequencies are larger than \(\sqrt{2}\) times of the isolators’ natural frequency (\({\omega }_{n}=\sqrt{k/m}\)), which are mainly affected by the stiffness (k) of the isolator and the mass (m) of payload [5]. This feature makes it difficult for traditional linear mass-spring-damper vibration isolators to realize low-frequency isolation while maintaining sufficient load capacity with small deformation.

Fortunately, the nonlinear isolators with beneficial high static and low dynamic stiffness (HSLDS), namely quasi-zero stiffness vibration isolators (QZS-VI), have emerged to cope with the dilemma along with linear isolator, in which low dynamic stiffness causes lower resonant frequency, while high static stiffness means large load capacity with small deformation. The obvious advantages of nonlinear isolators have attracted widespread attention in numerous studies of vibration isolation systems [6].

As a typical case of using inherent geometric nonlinearity of structures to realize the characteristics of high static and low dynamic stiffness, the vibration isolator with X-shaped structure has been widely concerned and studied in many researches. Sun and Jing et al. [7,8,9,10,11] conducted a series of researches on the vibration isolation performance of X-shaped structure isolators. The results indicate that the X-shaped structure isolator with inherent nonlinearity of equivalent stiffness and damping can achieve superior vibration isolation performance and have the potential to be employed in various engineering practices. In addition, in order to take full use of the nonlinear stiffness, damping and inertia characteristics, a lever-type isolation system was connected in parallel with an X-shaped supporting structure to constitute a new isolator. The new isolator can achieve adjustable ultra-low resonant frequency and profitable anti-resonance properties [12,13,14].

Another more common and attractive method of constructing the QZS-VI is adding negative stiffness structure (NSS) to positive stiffness supporting platform. Up to now, a variety of QZS-VI containing NSS have been constructed and studied. Waters et al. [15, 16] conducted the static and dynamic analysis of a passive QZS-VI, in which two oblique springs acting as NSS were connected in parallel with one vertical positive stiffness spring. Similarly, Hu et al. [17] developed another QZS-VI, in which the above mentioned two oblique springs were replaced by two oblique rigid rods which were hinged with two horizontal springs. Yang et al. [18] designed and analyzed a QZS system, in which the NSS was constructed by connecting four horizontal springs with nonlinear lever-shaped structure. Zhou et al. [19] and Liu et al. [20] constructed the physical prototype of the QZS-VI with the cam–roller–spring mechanisms that served as NSS and conducted analytical, simulation and experimental studies on its vibration isolation performance. The results showed that the QZS-VI outperforms the linear counterpart, specifically the QZS-VI’s peak transmissibility and starting frequency of isolation were lower than those of the linear counterpart. Furthermore, Sun et al. [21] developed the QZS-VI with parabolic-cam-roller that served as NSS and the asymmetric X-shaped structure as positive stiffness supporting platform. The research results indicated that adding a NSS to the support platform with asymmetric stiffness characteristics can improve the vibration isolation effect.

The nonlinear isolators mentioned above are all constructed by combining various geometrically nonlinear structures and linear elastic elements such as linear springs. The physical nonlinear elements such as magnetic springs and Euler buckled beams can also be used to construct nonlinear vibration isolators. Zhou et al. [22] proposed a HSLDS vibration isolator, which is constructed by connecting a mechanical spring in parallel with a magnetic spring. Specifically, the mechanical spring is a structural beam which exhibits stiffness hardening characteristic, and the magnetic spring is constructed by a permanent magnet and a pair of electromagnets which exhibit variable stiffness characteristic. Yan et al. [23] developed a bi-stable nonlinear vibration isolator consisting of several permanent magnet elements and a linear mass-spring-damper, in which the permanent magnet elements provide nonlinear magnetic force and act as a negative stiffness corrector. Xu et al. [24], Wu et al. [25] and Su et al. [26] also presented the QZS-VI with the magnetic spring served as the negative stiffness element. Except the above mentioned magnetic springs, Euler buckled beams are another common physical nonlinear elements in QZS-VI. Huang et al. [27] utilized Euler buckled beams as negative stiffness corrector to construct the nonlinear isolator, which makes the starting frequency of isolation lower than that of the linear counterpart. Fulcher et al. [28] and Oyelade et al. [29] presented different types of nonlinear vibration isolators where Euler bending beams served as the NSS.

Numerous studies have proven that the nonlinear QZS-VI with HSLDS exhibits superior vibration isolation performance than linear counterpart in terms of isolation frequency and vibration transmissibility. Inspired by the above researches, we design a vibration isolation platform by combining V-shaped lever, plate spring and cross-shaped structure (VL-PS-CS), and build a nonlinear QZS-VI by parallel connecting VL-PS-CS with coil spring. In the QZS-VI, the stiffness of VL-PS-CS platform changes nonlinearly from positive to negative with the increase of its deformation, and the coil spring serves as positive stiffness component to offset the negative stiffness of VL-PS-CS platform so as to maintain the stability of the isolation system. The nonlinearity of the VL-PS-CS platform is produced by combining the physical nonlinear stiffness of plate spring and the geometrical amplification effect of V-shaped lever, which fully explores the nonlinear advantages of each component and renders the QZS-VI achieving excellent high-static and low-dynamic stiffness.

Considering the physical and geometrical nonlinearity of plate spring and V-shaped lever, the static and dynamic modeling of the isolator is established and the effects of different parameters on the static mechanical and nonlinear friction properties of the isolator are thoroughly investigated. The average method is used to seek the analytical solution of dynamic equation of QZS-VI. The superior isolation performance of the proposed QZS-VI is validated by comparing with another QZS-VI of buckled beam mechanism and traditional linear mass–spring-damper isolator. The main contributions of this study are as follows: (a) A novel passive QZS-VI with the VL-PS-CS is proposed for the first time, which exhibits profitable high-static and low-dynamic stiffness and advantageous vibration isolation performance compared to another QZS-VI of buckled beam mechanism and traditional linear isolator; (b) the nonlinear properties of the VL-PS-CS platform are very beneficial to vibration isolation, which can be designed easily by tuning structure parameters; (c) the effects of different structural parameters on the mechanical properties of the nonlinear isolator are thoroughly investigated, which provides useful guidance for engineering practices.

The rest of this paper is organized as follows: First, the design of QZS-VI with VL-PS-CS is introduced in section “Design of QZS-VI”. Second, the static mechanical and dynamic modeling of the isolator based on physical and geometrical nonlinearity is established in section “The Modeling of QZS-VI”. Third, the effect of different parameters on the static mechanical and nonlinear friction properties of the QZS-VI is analyzed in sections “Effect of Different Parameters on Static Mechanical Properties” and Effect of Different Parameters on Equivalent Friction Properties”. Then, the superior vibration isolation performance of the proposed QZS-VI is validated by comparing with another QZS-VI of buckled beam mechanism and traditional linear vibration isolator in section “Performance Comparison with Existing Isolators”. Finally, for verification of analytical method, the simulation study subject to harmonic excitation is conducted in section “Simulation Study Subject to Harmonic Excitation” and a conclusion is given in section“Conclusion”.

Design of QZS-VI

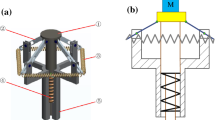
The QZS-VI subject to base excitation is designed as shown in Fig. 1, which mainly comprised one VL-PS-CS and one positive stiffness coil spring. The VL-PS-CS is composed of two V-shaped levers, one plate spring, one cross-shaped structure (CS) and one payload platform, which is expected to combine the benefits of nonlinear stiffness of plate spring and the advantages of geometrical nonlinearity of V-shaped lever. As shown in Fig. 1, the CS is composed of one vertical guiding shaft and two horizontal supporting shafts, which provide support and guidance for the operation of the isolator. Among them, two parallel horizontal shafts are fixedly connected with the vertical shaft by cross hinges. To improve the stiffness of the horizontal shafts, both ends of the horizontal shafts are connected to the top end of vertical shaft by two square pipes, respectively. The two square pipes are redundant which can be designed with other shapes. The bottom end of vertical shaft is fixed to the midpoint of the plate spring and then fixed to the base. Two V-shaped levers are symmetrically mounted on both sides of the CS. Each long-arm end of two levers is hinged to the bottom of payload platform which can slide along the vertical shaft of the CS through one linear bearing. Correspondingly, each short-arm end of two levers is hinged to each connector, which can slide along the horizontal shafts of the CS through four linear bearings. Each middle fulcrum of two levers is supported on the upper surface of the plate spring through rolling bearings.

Fig. 1
figure 1

Physical model of the vibration isolator

Full size image

The plate spring can be made up of a linear elastic material such as spring steel with a uniform rectangular cross section, which is easy to be manufactured. Both sides of the plate spring are in cantilever states. In initial state, the working surface of the plate spring is parallel to the horizontal shafts of the CS. While after bearing payload, the plate spring undergoes large deflection which exhibits nonlinear stiffness characteristic. Combine with the V-shaped lever, the nonlinear stiffness of the plate spring is magnified, which shows fascinating characteristics of high-static and low-dynamic stiffness. To offset the negative stiffness of the VL-PS-CS, a coil spring with positive stiffness is mounted vertically between the payload platform and the cross hinges of CS. The coil spring can be chosen to make its stiffness equal to the absolute value of VL-PS-CS’s minimum stiffness, so as to achieve the quasi-zero dynamic stiffness of QZS-VI.

The Modeling of QZS-VI

The flat schematic of the QZS-VI is depicted in Fig. 2, with clear designation of the structural parameters. To facilitate discussion, the upper parts of the CS including the upper part of vertical shaft (acting as guidance) and two oblique square pipes (acting as reinforcement) are ignored and not drawn in the flat schematic. As depicted in Fig. 2, the lengths of the long and short arms of the V-shaped levers are \({l}_{1}\) and \({l}_{2}\), respectively. The angle between the long arm and the short arm of the V-shaped lever is \(\theta\). The effective distance between the undeformed plate spring and the horizontal shafts of CS is \({l}_{3}\). The stiffness of the coil spring is marked as \({k}_{l}\). The absolute displacement of the isolated mass and the base excitation are defined as z and y, respectively, with the downward positive direction.

Fig. 2
figure 2

Flat schematic of QZS-VI

Full size image

In Fig. 2, the highest position (dashed line) of the payload platform represents the initial state of the isolator with no payload. After loading the mass M, the coil spring is compressed, while the payload platform combining with the endpoints of two levers’ long arms moves down along the vertical shaft, and the endpoints of two levers’ short arms move away from the symmetry center of CS along two horizontal shafts. At the same time, the V-shaped levers rotate around the endpoints of the short arms, and the plate spring is forced to bend. When the total reaction force of coil spring and the VL-PS-CS are balanced with the weight of payload, the isolator reaches the static equilibrium position (solid line) as shown in Fig. 2.

The VL-PS-CS

It is profitable to start with establishing the static modeling of the VL-PS-CS. Benefit from the structural symmetry of VL-PS-CS, only one side of the center of symmetry is drawn to illustrate the relationship between the acting force and the deformation of the VL-PS-CS, as shown in Fig. 3 (Figs. 4, 5):

  1. (1)

    The deformation of VL-PS-CS

    The O- × 1- × 2 coordinate system is defined as shown in Fig. 3, in which the origin of the coordinate system is on the working surface of the plate spring and vertically below the end point of the lever’s long arm, and the positive directions of horizontal (\({x}_{1}\)) and vertical (\({x}_{2}\)) axes are defined as right and downward, respectively. In the initial state, no payload is acted on the platform of VL-PS-CS and the plate spring is not bent as shown (dotted line) in Fig. 3. The endpoints of two arms of the V-shaped lever are marked as A and D, and the middle fulcrum of V-shaped lever is marked as C. When the isolated mass M is loaded, the isolator reaches the static equilibrium position, while the V-shaped lever slides and rotates, plate spring bends to supporting payload, two endpoints and the middle fulcrum of the V-shaped lever move to new position, marked as A’, D’ and C’, respectively. The angle between the long arm of the lever and the vertical direction changes from \(\varphi\) to \({\varphi }^{{\prime}}\). The relative displacement between payload and the base is defined as \(\widehat{z}=\mathrm{z}-\mathrm{y}\). The coordinates of point C’ in the coordinate system of O − × 1 − × 2 are set to be (\({x}_{1\mathrm{c}}\), \({x}_{2\mathrm{c}}\)).

    According to the geometric trigonometric relationship of VL-PS-CS, as shown in Fig. 3, it can be derived that

    $${l}_{1}\mathrm{sin}{\varphi }^{{\prime}}={\mathrm{x}}_{1c}$$
    (1)
    $${l}_{2}\mathrm{cos}(\uptheta -{\varphi }^{{\prime}})={l}_{3}+{\mathrm{x}}_{2c}$$
    (2)
    $${l}_{1}\mathrm{cos}{\varphi }^{{\prime}}={\mathrm{x}}_{2c}+{l}_{1}\mathrm{cos}\varphi -\widehat{\mathrm{z}}$$
    (3)
    $${l}_{2}\mathrm{sin}(\uptheta -{\varphi }^{{\prime}})=\sqrt{\mathrm{A}-{(\mathrm{B}-\widehat{z})}^{2}}-{\mathrm{x}}_{1c},$$
    (4)

    where \({\mathrm{A}=l}_{1}^{2}+{l}_{2}^{2}-2{l}_{1}{l}_{2}\mathrm{c}\mathrm{o}\mathrm{s}\theta\), \(\mathrm{B}={l}_{1}\mathrm{cos}{\varphi }-{l}_{3}\).

    For the convenience of expression, we define that

    $${f}_{3}=\sqrt{\mathrm{A}-{(\mathrm{B}-\widehat{z})}^{2}}$$
    (5)

    Combining Eqs. (1)–(5), the horizontal and vertical coordinates of point C’ can be, respectively, expressed as follows.

    .

    $${\mathrm{x}}_{1c}={f}_{2}=\frac{1}{2{f}_{3}}[\mathrm{C}-2\left(\mathrm{B}-\widehat{z}\right){f}_{1}-{\left({l}_{1}\mathrm{cos}\varphi -\widehat{z}\right)}^{2}-{\left(\mathrm{B}-\widehat{z}\right)}^{2}]$$
    (6)

    where \(\mathrm{C}={l}_{1}^{2}-{l}_{2}^{2}+{l}_{3}^{2}+\mathrm{A}\).

    $${{\mathrm{x}}_{2c}=f}_{1}=-\frac{1}{\mathrm{A}}\left({l}_{1}\mathrm{cos}\varphi -\widehat{z}\right){f}_{3}^{2}+\frac{1}{2\mathrm{A}}\left(\mathrm{B}-\widehat{z}\right)\left[\mathrm{C}-\mathrm{A}+{f}_{3}^{2}-{\left({l}_{1}\mathrm{cos}\varphi -\widehat{z}\right)}^{2}\right]+ \frac{1}{2A}{{\{[2\left({l}_{1}\mathrm{cos}\varphi -\widehat{z}\right){f}_{3}^{2}-\left(\mathrm{B}-\widehat{z}\right)\left[\mathrm{C}-\mathrm{A}+{f}_{3}^{2}-{\left({l}_{1}\mathrm{cos}\varphi -\widehat{z}\right)}^{2}\right]]}^{2}-\mathrm{A}{\left[\mathrm{C}-\mathrm{A}+{f}_{3}^{2}-{\left({l}_{1}\mathrm{cos}\varphi -\widehat{z}\right)}^{2}\right]}^{2}-4\mathrm{A}\left[{\left({l}_{1}\mathrm{cos}\varphi -\widehat{z}\right)}^{2}-{l}_{1}^{2}\right]{f}_{3}^{2}\}}^\frac{1}{2}$$
    (7)
  2. (2)

    Moment balance of V-shaped lever

    According to the moment balance principle, the equation which represents the moment acting on the endpoint (\({D}^{{^{\prime}}}\)) of V-shaped lever’s short arm can be derived as follows:

    $$\frac{1}{2}{F}_{n}[{l}_{1}\mathrm{s}\mathrm{i}\mathrm{n}{\varphi }^{{\prime}}+{l}_{2}\mathrm{sin}\left(\uptheta -{\varphi }^{{\prime}}\right)]+{F}_{\mathrm{c}}\mathrm{sin}{\upbeta }_{\mathrm{c}}{l}_{2}\mathrm{c}\mathrm{o}\mathrm{s}(\uptheta -{\varphi }^{{\prime}})={F}_{\mathrm{c}}\mathrm{cos}{\upbeta }_{\mathrm{c}}{l}_{2}\mathrm{s}\mathrm{i}\mathrm{n}(\uptheta -{\varphi }^{{\prime}})$$
    (8)

    where \({F}_{n}\) is the force acting on the VL-PS-CS, \({F}_{\mathrm{c}}\) is the force from the bending of the plate spring, \({\beta }_{\mathrm{c}}\) is the angle between the remaining uncurved surface of plate spring and the horizontal direction, as depicted in Fig. 4a.

  3. (3)

    Large deflection of plate spring

    The plate spring with large deflection forced by the V-shaped lever can be approximated as a cantilever beam. The Bernoulli–Euler bending moment–curvature relationship for the plate spring can be written as follows [30,31,32]:

    $$EI\frac{\mathrm{d}\upbeta }{\mathrm{d}\mathrm{s}}=M$$
    (9)

    where \(E\) is the elastic modulus of the plate spring, I is the moment of inertia of the leaf spring cross section about the neutral axis, \(\frac{\mathrm{d}\upbeta }{\mathrm{d}\mathrm{s}}\) and M are the curvature and the bending moment at any point of the plate spring, respectively.

    As shown in Fig. 4b, the coordinates of an arbitrary point E of the plate spring are set as (\({x}_{1}\), \({x}_{2}\)), the arc length of the plate spring between the fixed end O and point E is set as s, the force acting on the plate spring at \({\mathrm{C}}^{{^{\prime}}}\) is \({F}_{\mathrm{c}}^{{\prime}}\). Using the Newton’s third law of motion, regardless of the direction of the force, we can get \({F}_{\mathrm{c}}^{{\prime}}={F}_{\mathrm{c}}\). Differentiating Eq. (9) with respect to s, getting that

    $$EI\frac{{\mathrm{d}}^{2}\upbeta }{\mathrm{d}{\mathrm{s}}^{2}}=\frac{\mathrm{d}M}{\mathrm{d}s}$$
    (10)

    Among Eq. (10), the bending moment of the plate spring at point E is

    $$M={F}_{\mathrm{c}}^{{\prime}}\mathrm{c}\mathrm{o}\mathrm{s}{\upbeta }_{\mathrm{c}}\left({\mathrm{x}}_{1\mathrm{c}}-{\mathrm{x}}_{1}\right)+{F}_{\mathrm{c}}^{{\prime}}\mathrm{s}\mathrm{i}\mathrm{n}{\upbeta }_{\mathrm{c}}\left({x}_{2\mathrm{c}}-{x}_{2}\right),$$
    (11)

    where \({\upbeta }_{\mathrm{c}}\) is the angle between the free end of plate spring and the horizontal direction. Substituting Eq. (11) into Eq. (10), we can get that

    $$EI\frac{{\mathrm{d}}^{2}\upbeta }{\mathrm{d}{\mathrm{s}}^{2}}+{F}_{\mathrm{c}}^{{\prime}}\mathrm{c}\mathrm{o}\mathrm{s}{\upbeta }_{\mathrm{c}}\mathrm{c}\mathrm{o}\mathrm{s}\upbeta +{F}_{\mathrm{c}}^{{\prime}}\mathrm{s}\mathrm{i}\mathrm{n}{\upbeta }_{\mathrm{c}}\mathrm{s}\mathrm{i}\mathrm{n}\upbeta =0$$
    (12)

    Equation (12) can be written as another form

    $$\frac{\mathrm{d}}{\mathrm{d}s}\left[\frac{1}{2}EI{\left(\frac{\mathrm{d}\beta }{\mathrm{d}s}\right)}^{2}+{F}_{\mathrm{c}}^{{\prime}}\mathrm{c}\mathrm{o}\mathrm{s}{\upbeta }_{c}\mathrm{s}\mathrm{i}\mathrm{n}\upbeta -{F}_{\mathrm{c}}^{{\prime}}\mathrm{s}\mathrm{i}\mathrm{n}{\upbeta }_{\mathrm{c}}\mathrm{c}\mathrm{o}\mathrm{s}\upbeta \right]=0$$
    (13)

    Equation (13) can be directly integrated, considering that at free end \(\beta \left(L\right)={\upbeta }_{\mathrm{c}}\), and

    $${\left(\frac{\mathrm{d}\beta }{\mathrm{d}s}\right)}_{s=L}=0,$$
    (14)

    where L is the arc length of plate spring between points O and \({\mathrm{C}}^{{\prime}}\). Definite integrating Eq. (13) with respect to s, in which the integral interval is s-L, it can be obtained that

    $$\mathrm{d}s=\sqrt{\frac{EI}{2{F}_{\mathrm{c}}^{{\prime}}}}\frac{\mathrm{d}\upbeta }{\sqrt{\mathrm{s}\mathrm{i}\mathrm{n}({\upbeta }_{c}-\upbeta )}}$$
    (15)

    Project the arc length ds to the horizontal and vertical coordinates, respectively, getting that

    $$\mathrm{d}{x}_{1}=\sqrt{\frac{EI}{2{F}_{\mathrm{c}}^{{\prime}}}}\frac{\mathrm{c}\mathrm{o}\mathrm{s}\upbeta \mathrm{d}\upbeta }{\sqrt{\mathrm{s}\mathrm{i}\mathrm{n}({\upbeta }_{\mathrm{c}}-\upbeta )}}$$
    (16)
    $$\mathrm{d}{\mathrm{x}}_{2}=\sqrt{\frac{EI}{2{F}_{\mathrm{c}}^{{\prime}}}}\frac{\mathrm{s}\mathrm{i}\mathrm{n}\upbeta \mathrm{d}\upbeta }{\sqrt{\mathrm{s}\mathrm{i}\mathrm{n}({\upbeta }_{\mathrm{c}}-\upbeta )}}$$
    (17)

    Equations (16) and (17) can be integrated with respect to \(\upbeta\) from 0 to \({\upbeta }_{\mathrm{c}}\), respectively, for finding the coordinate values of free end point \({\mathrm{C}}^{{^{\prime}}}\) of plate spring.

    $${x}_{1\mathrm{c}}=\sqrt{\frac{EI}{2{F}_{\mathrm{c}}^{{\prime}}}}\left(2\mathrm{c}\mathrm{o}\mathrm{s}{\upbeta }_{\mathrm{c}}\sqrt{\mathrm{s}\mathrm{i}\mathrm{n}{\upbeta }_{\mathrm{c}}}+\mathrm{s}\mathrm{i}\mathrm{n}{\upbeta }_{\mathrm{c}}{\int }_{0}^{{\upbeta }_{\mathrm{c}}}\sqrt{\mathrm{sin}\upbeta }\mathrm{d}\upbeta \right)$$
    $$\approx \sqrt{\frac{\mathrm{E}\mathrm{I}}{2{F}_{\mathrm{c}}^{{\prime}}}}\left(2\mathrm{c}\mathrm{o}\mathrm{s}{\upbeta }_{\mathrm{c}}\sqrt{\mathrm{sin}{\upbeta }_{\mathrm{c}}}+\frac{2}{3}{\upbeta }_{\mathrm{c}}^\frac{3}{2}\mathrm{sin}{\upbeta }_{\mathrm{c}}\right)$$
    (18)
    $$x_{{2{\text{c}}}} = \sqrt {\frac{{EI}}{{2F_{{\text{c}}}^{\prime } }}} (2{\text{sin}}\upbeta _{{\text{c}}} \sqrt {{\text{sin}}\upbeta _{{\text{c}}} } - {\text{cos}}\upbeta _{{\text{c}}} \int _{0}^{{\upbeta _{{\text{c}}} }} \sqrt {{\text{sin}}\upbeta } {\text{d}}\upbeta {\text{)}}$$
    $$\approx \sqrt{\frac{EI}{2{F}_{\mathrm{c}}^{{\prime}}}}\left[2{\left(\mathrm{sin}{\upbeta }_{\mathrm{c}}\right)}^\frac{3}{2}-\frac{2}{3}{\upbeta }_{\mathrm{c}}^\frac{3}{2}\mathrm{cos}{\upbeta }_{\mathrm{c}}\right],$$
    (19)

    where \(\sqrt{\mathrm{sin}\upbeta }\) is approximated to be \(\sqrt{\upbeta }\), in the expression of definite integral \({\int }_{0}^{{\upbeta }_{\mathrm{c}}}\sqrt{\mathrm{sin}\upbeta }\mathrm{d}\upbeta\). The function values of \(\sqrt{\mathrm{sin}\upbeta }\) and \(\sqrt{\upbeta }\) with respect to \(\upbeta\) in the whole integral range are depicted in Fig. 5. From the figure, it can be seen that the errors between two function values along the whole integral range are small enough, which can guarantee the accuracy of calculation results.

  4. (4)

    Summarize

Fig. 3
figure 3

The schematic of half of VL-PS-CS

Full size image
Fig. 4
figure 4

The force and deformation of (a) V-shaped lever and (b) plate spring

Full size image
Fig. 5
figure 5

The function values of \(\sqrt{\mathrm{sin}\upbeta }\) and \(\sqrt{\upbeta }\) with respect to \(\upbeta\)

Full size image

Combining Eqs. (6) (7) (8) (18) and (19), the relationship between the applied force (\({F}_{n}\)) and the relative displacement (\(\widehat{z}\)) can be obtained.

$${F}_{n}\left(\widehat{z}\right)=\frac{1}{{f}_{3}}\left[-{2F}_{c}({\upbeta }_{\mathrm{c}}-\frac{1}{6}{\upbeta }_{\mathrm{c}}^{3})({l}_{3}+{f}_{1})+2{F}_{\mathrm{c}}(1-\frac{{\upbeta }_{\mathrm{c}}^{2}}{2})({f}_{3}-{f}_{2})\right],$$
(20)

where

$${\upbeta }_{\mathrm{c}}=-2\frac{{f}_{2}}{{f}_{1}}+\sqrt{{4(\frac{{f}_{2}}{{f}_{1}})}^{2}+6}$$
(21)
$${F}_{\mathrm{c}}=\frac{{\mathrm{E}\mathrm{I}\upbeta }_{\mathrm{c}}}{2{{f}_{2}}^{2}}{(2-\frac{1}{3}{\upbeta }_{\mathrm{c}}^{2}-\frac{1}{9}{\upbeta }_{\mathrm{c}}^{4})}^{2}$$
(22)

Furthermore, the nonlinear stiffness (\({k}_{n}\)) of VL-PS-CS can be obtained by differentiating the force (\({F}_{n}\)) with respect to the relative displacement (\(\widehat{\mathrm{z}}\)):

$${k}_{n}=-2\frac{1}{{f}_{3}}\frac{\partial {F}_{\mathrm{c}}}{\partial \widehat{z}}\left({\upbeta }_{\mathrm{c}}-\frac{{\upbeta }_{\mathrm{c}}^{3}}{6}\right)\left({l}_{3}+{f}_{1}\right)+2\frac{1}{{f}_{3}}\frac{\partial {F}_{c}}{\partial \widehat{z}}\left(1-\frac{{\upbeta }_{\mathrm{c}}^{2}}{2}\right)\left({f}_{3}-{f}_{2}\right)-\frac{2}{{f}_{3}}{F}_{\mathrm{c}}\frac{\partial {\upbeta }_{\mathrm{c}}}{\partial \widehat{z}}\left(1-\frac{{\upbeta }_{\mathrm{c}}^{2}}{2}\right)\left({l}_{3}+{f}_{1}\right)-\frac{2}{{{f}_{3}}^{2}}{F}_{\mathrm{c}}\left({\upbeta }_{\mathrm{c}}-\frac{{\upbeta }_{\mathrm{c}}^{3}}{6}\right)\left[{f}_{3}\frac{\partial {f}_{1}}{\partial \widehat{z}}-\left({l}_{3}+{f}_{1}\right)\frac{\partial {f}_{3}}{\partial \widehat{z}}\right]-\frac{2}{{f}_{3}}{F}_{\mathrm{c}}\frac{\partial {\upbeta }_{\mathrm{c}}}{\partial \widehat{z}}{\upbeta }_{\mathrm{c}}\left({f}_{3}-{f}_{2}\right)+\frac{2}{{f}_{3}}{F}_{\mathrm{c}}\left(1-\frac{{\upbeta }_{\mathrm{c}}^{2}}{2}\right)\left(-\frac{\partial {f}_{2}}{\partial \widehat{z}}+\frac{{f}_{2}}{{f}_{3}}\frac{\partial {f}_{3}}{\partial \widehat{z}}\right),$$
(23)

where

$$\frac{\partial {F}_{\mathrm{c}}}{\partial \widehat{z}}=-EI\frac{1}{{f}_{2}^{3}}\frac{\partial {f}_{2}}{\partial \widehat{z}}{\left(2\sqrt{{\upbeta }_{\mathrm{c}}}-\frac{1}{3}{\upbeta }_{\mathrm{c}}^\frac{5}{2}-\frac{1}{9}{\upbeta }_{\mathrm{c}}^\frac{9}{2}\right)}^{2}+\frac{EI}{{{f}_{2}}^{2}}\frac{\partial {\upbeta }_{\mathrm{c}}}{\partial \widehat{z}}\left(2\sqrt{{\upbeta }_{\mathrm{c}}}-\frac{1}{3}{\upbeta }_{\mathrm{c}}^\frac{5}{2}-\frac{1}{9}{\upbeta }_{\mathrm{c}}^\frac{9}{2}\right)\left(\frac{1}{\sqrt{{\upbeta }_{\mathrm{c}}}}-\frac{5}{6}{\upbeta }_{\mathrm{c}}^\frac{3}{2}-\frac{1}{2}{\upbeta }_{\mathrm{c}}^\frac{7}{2}\right)$$
(24)
$$\frac{\partial {\upbeta }_{\mathrm{c}}}{\partial \widehat{z}}=-2\left(\frac{\partial {f}_{2}}{\partial \widehat{z}}\frac{1}{{f}_{1}}-\frac{\partial {f}_{1}}{\partial \widehat{z}}\frac{{f}_{2}}{{f}_{1}^{2}}\right)+\frac{4}{\sqrt{{4\left(\frac{{f}_{2}}{{f}_{1}}\right)}^{2}+6}}\left(\frac{\partial {f}_{2}}{\partial \widehat{z}}\frac{{f}_{2}}{{f}_{1}^{2}}-\frac{\partial {f}_{1}}{\partial \widehat{z}}\frac{{f}_{2}^{2}}{{f}_{1}^{3}}\right)$$
(25)
$$\frac{\partial {f}_{1}}{\partial \widehat{z}}=\frac{1}{A}{f}_{3}^{2}-\frac{2}{A}\left({l}_{1}\mathrm{cos}\varphi -\widehat{z}\right){f}_{3}\frac{\partial {f}_{3}}{\partial \widehat{z}}-\frac{1}{2\mathrm{A}}\left[\mathrm{C}-\mathrm{A}+{f}_{3}^{2}-{\left({l}_{1}\mathrm{cos}\varphi -\widehat{z}\right)}^{2}\right]+\frac{1}{A}\left(\mathrm{B}-\widehat{z}\right)({f}_{3}\frac{\partial {f}_{3}}{\partial \widehat{\mathrm{z}}}+{l}_{1}\mathrm{cos}\varphi -\widehat{z})+\frac{1}{2\mathrm{A}\sqrt{{f}_{4}}}{{f}_{5}f}_{6}-\frac{1}{\sqrt{{f}_{4}}}\left[\mathrm{C}-\mathrm{A}+{f}_{3}^{2}-{\left({l}_{1}\mathrm{cos}\varphi -\widehat{z}\right)}^{2}\right]({f}_{3}\frac{\partial {f}_{3}}{\partial \widehat{z}}+{l}_{1}\mathrm{cos}\varphi -\widehat{z})+\frac{2}{\sqrt{{f}_{4}}}\left({l}_{1}\mathrm{cos}\varphi -\widehat{z}\right){f}_{3}^{2}-\frac{2}{\sqrt{{f}_{4}}}\left[{\left({l}_{1}\mathrm{cos}\varphi -\widehat{z}\right)}^{2}-{l}_{1}^{2}\right]{f}_{3}\frac{\partial {f}_{3}}{\partial \widehat{z}}$$
(26)
$${f}_{4}={\left\{2\left({l}_{1}\mathrm{cos}\varphi -\widehat{z}\right){f}_{3}^{2}-\left(\mathrm{B}-\widehat{z}\right)\left[\mathrm{C}-\mathrm{A}+{f}_{3}^{2}-{\left({l}_{1}\mathrm{cos}\varphi -\widehat{z}\right)}^{2}\right]\right\}}^{2}-A{\left[\mathrm{C}-\mathrm{A}+{f}_{3}^{2}-{\left({l}_{1}\mathrm{cos}\varphi -\widehat{z}\right)}^{2}\right]}^{2}-4\mathrm{A}\left[{\left({l}_{1}\mathrm{cos}\varphi -\widehat{z}\right)}^{2}-{l}_{1}^{2}\right]{f}_{3}^{2}$$
(27)
$${f}_{5}=2\left({l}_{1}\mathrm{cos}\varphi -\widehat{z}\right){f}_{3}^{2}-\left(\mathrm{B}-\widehat{z}\right)\left[\mathrm{C}-\mathrm{A}+{f}_{3}^{2}-{\left({l}_{1}\mathrm{cos}\varphi -\widehat{z}\right)}^{2}\right]$$
(28)
$${f}_{6}=-2{f}_{3}^{2}+4\left({l}_{1}\mathrm{cos}\varphi -\widehat{z}\right){f}_{3}\frac{\partial {f}_{3}}{\partial \widehat{\mathrm{z}}}+\left[\mathrm{C}-\mathrm{A}+{f}_{3}^{2}-{\left({l}_{1}\mathrm{cos}\varphi -\widehat{z}\right)}^{2}\right]-\left(\mathrm{B}-\widehat{z}\right)\left[2{f}_{3}\frac{\partial {f}_{3}}{\partial \widehat{z}}+2\left({l}_{1}\mathrm{cos}\varphi -\widehat{z}\right)\right]$$
(29)
$$\frac{\partial {f}_{2}}{\partial \widehat{\mathrm{z}}}=\frac{1}{{f}_{3}}\left[-\frac{\partial {f}_{1}}{\partial \widehat{\mathrm{z}}}\left(\mathrm{B}-\widehat{z}\right)+{f}_{1}+{l}_{1}\mathrm{cos}\varphi -2\widehat{z}+\mathrm{B}\right]-\frac{1}{{2f}_{3}^{2}}\left[\mathrm{C}-2{f}_{1}\left(\mathrm{B}-\widehat{z}\right)-{\left({l}_{1}\mathrm{cos}\varphi -\widehat{z}\right)}^{2}-{\left(\mathrm{B}-\widehat{z}\right)}^{2}\right]\frac{\partial {f}_{3}}{\partial \widehat{z}}$$
(30)
$$\frac{\partial {f}_{3}}{\partial \widehat{z}}=\frac{\mathrm{B}-\widehat{z}}{\sqrt{\mathrm{A}-{(\mathrm{B}-\widehat{z})}^{2}}}$$
(31)

The QZS-VI

The VL-PS-CS serving as supporting structure is unstable due to its negative stiffness characteristic. So it is necessary to add a positive stiffness coil spring to the VL-PS-CS to obtain a stable QZS-VI. Based on the superposition principle of forces acting on parallel elastic structure, the relationship between the total exerting force and the deformation of the QZS-VI becomes

$$F\left(\widehat{z}\right)={k}_{l}\widehat{z}+{F}_{n}\left(\widehat{z}\right),$$
(32)

where \({k}_{l}\) is the stiffness of coil spring, \(F\left(\widehat{\mathrm{z}}\right)\) is the total force acting on the QZS-VI and \({F}_{n}\left(\widehat{\mathrm{z}}\right)\) is the component force acting on the VL-PS-CS, whose exact expression is showed in Eq. (20).

Differentiating Eq. (32), the total equivalent stiffness of the isolator becomes

$$k\left(\widehat{z}\right)={k}_{l}+{k}_{n}(\widehat{z})$$
(33)

where \({k}_{n}(\widehat{z})\) is the nonlinear stiffness of VL-PS-CS, which is described in Eq. (23).

Dynamic modeling of the QZS-VI

It is worth mentioning that the moving parts of the isolator, including two V-shaped levers and two connectors, can be constructed of low-density, high-strength materials (e.g., aluminum alloy or carbon fiber, etc.). In addition, two arms of each V-shaped lever can be designed with hollow rods to reduce potential inertia and flexibility influence on dynamic response of the system. During dynamic analysis of the isolator, the inertia impacts of two V-shaped levers and two connectors are ignored, and only viscous friction force is considered. The equivalent vertical friction forces of one vertical slider of payload platform, two horizontal sliders and four rotation joints of both ends of two V-shaped levers are considered and, respectively, represented as \({F}_{\mathrm{c}1}\), \({F}_{\mathrm{c}2}\) and \({F}_{\mathrm{c}3}\). \({F}_{\mathrm{c}1}\) is the linear viscous friction force which can be expressed as Linear viscous friction

$${F}_{\mathrm{c}1}={\mathrm{c}}_{1}\dot{\widehat{z}},$$
(34)

where \(\dot{\widehat{z}}=d(\widehat{z})/d\mathrm{t}\) and \({\mathrm{c}}_{1}\) is the friction resistance constant of the vertical slider.

The horizontal friction force of each horizontal slider can be obtained as follows:

$${F}_{h}={\mathrm{c}}_{2}\frac{\mathrm{B}-\widehat{z}}{\sqrt{{\mathrm{A}-\left(\mathrm{B},-\widehat{z}\right)}^{2}}}\cdot\dot{\widehat{z}}$$
(35)

where \({\mathrm{c}}_{2}\) is the friction resistance constant of each horizontal slider. So the equivalent vertical friction force \({F}_{c2}\) can be deduced as follows:

$${F}_{c2}=2\mathrm{t}\mathrm{a}\mathrm{n}{\alpha }{F}_{h}=2{\mathrm{c}}_{2}\frac{{\left(\mathrm{B}-\widehat{z}\right)}^{2}}{{\mathrm{A}-\left(\mathrm{B}-\widehat{z}\right)}^{2}}\dot{\widehat{z}}$$
(36)

The rotational friction force of each rotation joint can be expressed as follows:

$${F}_{\varphi }={c}_{3}\left(\frac{\mathrm{d}{{\varphi }}^{{^{\prime}}}}{\mathrm{d}\widehat{z}}\right)\cdot \dot{\widehat{z}}$$
(37)

where \({\mathrm{c}}_{3}\) is the friction resistance constant of each rotation joint.

From Eq. (1), it can be derived that

$${\varphi }^{{\prime}}=\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{s}\mathrm{i}\mathrm{n}\frac{{\mathrm{x}}_{1\mathrm{c}}}{{l}_{1}}$$
(38)

Then

$${F}_{\varphi }={\mathrm{c}}_{3}\frac{1}{\sqrt{{l}_{1}^{2}-{{\mathrm{x}}_{1\mathrm{c}}}^{2}}}\frac{\partial {f}_{2}}{\partial \widehat{z}}. \dot{\widehat{z}},$$
(39)

where the exact expressions of \({\mathrm{x}}_{1\mathrm{c}}\) and \(\frac{\partial {f}_{2}}{\partial \widehat{\mathrm{z}}}\) are showed in Eqs. (6) and (30), respectively. The equivalent horizontal friction force acting on two horizontal sliders which derived from the rotational friction of long arm end of two V-shaped levers is \({F}_{\varphi h}=2{F}_{\varphi }(\mathrm{B}-\widehat{z})\), and the equivalent vertical friction force acting on vertical slider which derived from the rotational friction of short arm end of two V-shaped levers is \({F}_{\varphi v}=2{F}_{\varphi }\sqrt{{\mathrm{A}-\left(\mathrm{B}-\widehat{z}\right)}^{2}}\). So the equivalent vertical friction force \({F}_{\mathrm{c}3}\) can be obtained as follows:

$${F}_{\mathrm{c}3}={F}_{\varphi v}+{\frac{\mathrm{B}-\widehat{z}}{\sqrt{{\mathrm{A}-\left(\mathrm{B}-\widehat{z}\right)}^{2}}}F}_{\varphi h}=\frac{2\mathrm{A}}{\sqrt{{\mathrm{A}-\left(\mathrm{B}-\widehat{z}\right)}^{2}}}\frac{{\mathrm{c}}_{3}}{\sqrt{{l}_{1}^{2}-{{\mathrm{x}}_{1\mathrm{c}}}^{2}}}\frac{\partial {f}_{2}}{\partial \widehat{z}}\bullet \dot{\widehat{z}},$$
(40)

where \({\mathrm{A}=l}_{1}^{2}+{l}_{2}^{2}-2{l}_{1}{l}_{2}cos\theta\), \(\mathrm{B}={l}_{1}\mathrm{cos}{\varphi }-{l}_{3}\). Then, the total equivalent vertical friction force is obtained and defined as follows:

$${F}_{\mathrm{c}}={f}_{\mathrm{c}}\dot{\widehat{z}}$$
(41)

where \({f}_{\mathrm{c}}={f}_{\mathrm{c}1}+{f}_{\mathrm{c}2}+{f}_{\mathrm{c}3}\), \({f}_{\mathrm{c}1}={\mathrm{c}}_{1}\), \({f}_{\mathrm{c}2}=2{\mathrm{c}}_{2}\frac{{\left(\mathrm{B}-\widehat{z}\right)}^{2}}{{\mathrm{A}-\left(\mathrm{B}-\widehat{z}\right)}^{2}}\), \({f}_{\mathrm{c}3}=\frac{2\mathrm{A}}{\sqrt{{\mathrm{A}-\left(\mathrm{B}-\widehat{z}\right)}^{2}}}\frac{{\mathrm{c}}_{3}}{\sqrt{{l}_{1}^{2}-{{\mathrm{x}}_{1\mathrm{c}}}^{2}}}\frac{\partial {f}_{2}}{\partial \widehat{z}}\) .

The QZS-VI with payload and under base excitation is simplified as a second-order nonlinear system with one degree of freedom, as depicted in Fig. 6. Using the Newton’s second law of motion, the dynamic equation of the isolator’s payload mass can be expressed as follows:

Fig. 6
figure 6

The simplified dynamic model of QZS-VI

Full size image
$$M\ddot{\mathrm{z}}+{f}_{\mathrm{c}}\dot{\widehat{z}}+F\left(\widehat{z}\right)=\mathrm{M}\mathrm{g}$$
(42)

where M is the mass of payload, \(z\) is the absolute displacement of payload mass, \(\widehat{z}=z-y\) is the relative displacement between payload platform and the base. \(F\left(\widehat{z}\right)\) is the equivalent spring force provided by the nonlinear stiffness of the QZS-VI, whose exact expression is showed in Eq. (32).

Introducing the base excitation, both hand sides of Eq. (42) are simultaneously subtracted by \(M\ddot{\mathrm{y}}\):

$$M\ddot{\widehat{z}}+{f}_{\mathrm{c}}\dot{\widehat{z}}+F\left(\widehat{z}\right)-\mathrm{M}\mathrm{g}=-M\ddot{\mathrm{y}}$$
(43)

where y is the absolute displacement of base excitation.

Assuming that under the gravity of payload, the vibration isolator reaches the static equilibrium position with the deformation of \({\widehat{\mathrm{z}}}_{0}\), it can be obtained that \(\mathrm{M}\mathrm{g}=F\left({\widehat{z}}_{0}\right)\). \(F\left(\widehat{z}\right)\) and \({f}_{\mathrm{c}}\) are highly nonlinear functions of \(\widehat{z}\), which can be expanded by Taylor series at static equilibrium position \({\widehat{z}}_{0}\) as

$$F\left(\widehat{z}\right)=F\left({\widehat{z}}_{0}\right)+{F}^{{\prime}}\left({\widehat{z}}_{0}\right)\left(\widehat{z}-{\widehat{z}}_{0}\right)+\frac{{F}^{\prime\prime}\left({\widehat{z}}_{0}\right)}{2}{\left(\widehat{z}-{\widehat{z}}_{0}\right)}^{2}+\frac{{F}^{\prime\prime\prime}\left({\widehat{z}}_{0}\right)}{6}{\left(\widehat{z}-{\widehat{z}}_{0}\right)}^{3}+o$$
(44)
$${f}_{\mathrm{c}}={f}_{\mathrm{c}}\left({\widehat{z}}_{0}\right)+{{f}_{\mathrm{c}}}^{{\prime}}\left({\widehat{z}}_{0}\right)\left(\widehat{z}-{\widehat{z}}_{0}\right)+\frac{{{f}_{\mathrm{c}}}^{\prime\prime}\left({\widehat{z}}_{0}\right)}{2}{\left(\widehat{z}-{\widehat{z}}_{0}\right)}^{2}+o,$$
(45)

where \({F}^{{\prime}}\left({\widehat{z}}_{0}\right)=k={k}_{l}+{k}_{n}\left({\widehat{z}}_{0}\right)\), \({F}^{\prime\prime}\left({\widehat{z}}_{0}\right)=\frac{\partial k}{\partial \widehat{z}}\left|({\widehat{z}}_{0})\right.\), \({F}^{\prime\prime\prime}\left({\widehat{z}}_{0}\right)= \frac{{\partial }^{2}k}{\partial {\widehat{z}}^{2}}\left|({\widehat{z}}_{0})\right.\), \({{f}_{\mathrm{c}}}^{{\prime}}\left({\widehat{z}}_{0}\right)=\frac{\partial {f}_{\mathrm{c}}}{\partial \widehat{z}}\left|({\widehat{z}}_{0})\right.\), \({{f}_{\mathrm{c}}}^{\prime\prime}\left({\widehat{z}}_{0}\right)=\frac{{\partial }^{2}{f}_{\mathrm{c}}}{\partial {\widehat{z}}^{2}}\left|({\widehat{z}}_{0})\right.\), \(o\) is the sum of higher order infinitesimal terms greater than the third order. The detailed expressions of \(\frac{\partial k}{\partial \widehat{z}}\) and \(\frac{{\partial }^{2}k}{\partial {\widehat{z}}^{2}}\) are listed in “Supplementary Material”.

For the case \({l}_{3}\)=100 mm, \({l}_{2}\)=175 mm, \({l}_{1}\)=350 mm, \(\theta{=}{75}^{\circ }\), h = 1.5 mm, \({k}_{l}=2.44\) N cm−1, \({\mathrm{c}}_{1}=0.6 \mathrm{N}\mathrm{s} {\mathrm{m}}^{-1}\), \({\mathrm{c}}_{2}=0.8 \mathrm{N}\mathrm{s} {\mathrm{m}}^{-1}\) and \({\mathrm{c}}_{3}=0.2 \mathrm{N}\mathrm{s} {\mathrm{m}}^{-1}\), the approximated third-order Taylor series expansion and exact solutions of the function \({f}_{\mathrm{c}}\) and the total restoring force \(F\left(\widehat{z}\right)\) are compared in Fig. 7a, b. It can be revealed that the approximate curve of \({f}_{\mathrm{c}}\) can fit the exact curve along the whole displacement range very well, and the approximate curve of \(F\left(\widehat{z}\right)\) can fit the exact curve very well near the static equilibrium position (\({\widehat{z}}_{0}\)=58 mm), while the error between the approximate force and the exact force increases as the displacement from the static equilibrium position increased. This can be quantified by the relative error \(\updelta\) which defined as follows:

Fig. 7
figure 7

Comparisons of the approximate and exact solutions of function \({f}_{\mathrm{c}}\) (a) and restoring force \(F\left(\widehat{z}\right)\) (b)

Full size image
$$\updelta =\left|1-\frac{{F}_{\mathrm{a}\mathrm{p}\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{x}\mathrm{i}\mathrm{m}\mathrm{a}\mathrm{t}\mathrm{e}}}{{F}_{\mathrm{e}\mathrm{x}\mathrm{a}\mathrm{c}\mathrm{t}}}\right|\times 100\mathrm{\%},$$
(46)

where \({F}_{\mathrm{a}\mathrm{p}\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{x}\mathrm{i}\mathrm{m}\mathrm{a}\mathrm{t}\mathrm{e}}\) is given by Eq. (44) and \({\mathrm{F}}_{\mathrm{e}\mathrm{x}\mathrm{a}\mathrm{c}\mathrm{t}}\) is given by Eq. (32). The relative error is plotted in Fig. 8. It can be seen that when the distance from the equilibrium position is small, the error value is correspondingly small enough. So it is reasonable to analyze the vibration isolation characteristics of the isolator through Taylor approximation, when the amplitude of vibration near the static equilibrium position is small.

Fig. 8
figure 8

The relative error between the approximate force and the exact force

Full size image

Substitute Eqs. (44) and (45) into Eq. (43), where \(o\) is omitted, and specify the equilibrium position \(\widehat{z}={\widehat{z}}_{0}\) as the origin of a new relative displacement coordinate \(\widehat{\mathrm{u}}\) (\(\widehat{\mathrm{u}}=\widehat{z}-{\widehat{z}}_{0}\)). By introducing the following parameters: \({\varepsilon }_{0}={f}_{c}\left({\widehat{z}}_{0}\right)\), \({\varepsilon }_{1}={{f}_{c}}^{{\prime}}\left({\widehat{z}}_{0}\right)\), \({\varepsilon }_{2}=\frac{{{f}_{c}}^{\prime\prime}\left({\widehat{z}}_{0}\right)}{2}\), \({\mu }_{1}={F}^{{\prime}}\left({\widehat{z}}_{0}\right)\), \({\mu }_{2}=\frac{{F}^{\prime\prime}\left({\widehat{z}}_{0}\right)}{2}\) and \({\mu }_{3}=\frac{{F}^{\prime\prime\prime}\left({\widehat{z}}_{0}\right)}{6}\), the dynamic Eq. (43) can be rewritten as

$$\mathrm{M}\ddot{\widehat{\mathrm{u}}}+({\varepsilon }_{0}+{\varepsilon }_{1}\widehat{\mathrm{u}}+{\varepsilon }_{2}{\widehat{\mathrm{u}}}^{2})\dot{\widehat{\mathrm{u}}}+{\mu }_{1}\widehat{\mathrm{u}}+{\mu }_{2}{\widehat{\mathrm{u}}}^{2}+{\mu }_{3}{\widehat{\mathrm{u}}}^{3}=-\mathrm{M}\ddot{\mathrm{y}}$$
(47)

where \(\dot{\left(\cdot \right)}=d(\cdot )/d\mathrm{t}\). Using average method [33] for approximated analytical results, the displacement of base excitation and the solution of Eq. (47) can be, respectively, set as follows:

$$\mathrm{y}={Y}_{e}\mathrm{c}\mathrm{o}\mathrm{s}\upomega \mathrm{t}$$
(48)
$$\left\{\begin{array}{c}\widehat{\mathrm{u}}=a cos(\omega t+\varphi )\\ \dot{\widehat{\mathrm{u}}}=-a\omega \mathrm{sin}\left(\upomega \mathrm{t}+\varphi \right),\end{array}\right.$$
(49)

where \({Y}_{e}\) is the displacement amplitude of excitation, \(\omega\) is the angular frequency of excitation, a is the amplitude of harmonic terms and \(\varphi\) is the phase angle. a and \(\varphi\) are slowly varying functions of time t. Differentiating Eq. (49) with respect to t, the following can be obtained:

$$\left\{\begin{array}{c}\dot{\widehat{\mathrm{u}}}=\frac{\mathrm{d}\mathrm{a}}{\mathrm{d}t}\mathrm{cos}\left(\omega t+\varphi \right)-a(\omega +\frac{\mathrm{d}\varphi }{\mathrm{d}t})sin(\omega t+\varphi )\\ \ddot{\widehat{\mathrm{u}}}=-\frac{\mathrm{d}\mathrm{a}}{\mathrm{d}t}\omega sin(\omega t+\varphi )-a\omega (\omega +\frac{\mathrm{d}\varphi }{\mathrm{d}t})\mathrm{cos}\left(\omega t+\varphi \right)\end{array}\right.$$
(50)

Combining Eqs. (49) and (50), and substituting them into Eq. (47), we can get that the following:

$$\frac{\mathrm{da}}{\mathrm{d}t}=-\frac{1}{M\upomega }\mathrm{sin}\left(\omega t+\varphi \right)\Pi$$
(51)
$$\frac{\mathrm{d}\varphi }{\mathrm{d}t}=-\frac{1}{{Ma\omega }}\mathrm{cos}\left(\omega t+\varphi \right)\Pi ,$$
(52)

where

$$\Pi =Ma{\omega }^{2}\mathrm{cos}\left(\omega t+\varphi \right)+M{Y}_{e}{\omega }^{2}\mathrm{c}\mathrm{o}\mathrm{s}\omega t+\left[{\varepsilon }_{0}+{\varepsilon }_{1}a\mathrm{cos}\left(\omega t+\varphi \right)+{\varepsilon }_{2}{a}^{2}{\mathrm{cos}}^{2}\left(\omega t+\varphi \right)\right]a\omega \mathrm{sin}\left(\omega t+\varphi \right)-{\mu }_{1}a\mathrm{cos}\left(\omega t+\varphi \right)-{\mu }_{2}{a}^{2}{\mathrm{cos}}^{2}\left(\omega t+\varphi \right)-{\mu }_{3}{\mathrm{a}}^{3}{\mathrm{c}\mathrm{o}\mathrm{s}}^{3}(\upomega \mathrm{t}+\varphi )$$

Assuming that a and \(\varphi\) remain constant in one cycle, Eqs. (51) and (52) can be averaged as follows:

$$\frac{\mathrm{da}}{\mathrm{d}t}=-\frac{\omega }{2\pi }{\int }_{0}^{\frac{2\pi }{\omega }}\frac{1}{{M\omega }}{\Pi }\mathrm{sin}\left(\omega t+\varphi \right)\mathrm{d}t=-\frac{1}{2M}(M{Y}_{e}\omega \mathrm{s}\mathrm{i}\mathrm{n}\varphi +a{\varepsilon }_{0}+\frac{1}{4}{\varepsilon }_{2}{a}^{3})$$
(53)
$$\frac{\mathrm{d}\varphi }{\mathrm{d}t}=-\frac{\omega }{2\pi }{\int }_{0}^{\frac{2\pi }{\omega }}\frac{1}{{Ma\omega }}\Pi\mathrm{ cos}\left(\omega t+\varphi \right)\mathrm{d}t=-\frac{1}{2Ma\omega }\left[\left(Ma{\omega }^{2}-{\mu }_{1}\mathrm{a}\right)+M{Y}_{\mathrm{e}}{\upomega }^{2}\mathrm{c}\mathrm{o}\mathrm{s}\varphi -\frac{3}{4}{\mu }_{3}{a}^{3}\right]$$
(54)

Therefore, derived from Eqs. (53) and (54), and the condition \({\mathrm{s}\mathrm{i}\mathrm{n}}^{2}\varphi +{\mathrm{c}\mathrm{o}\mathrm{s}}^{2}\varphi =1\), the amplitude-frequency equation can be achieved as follows:

$${{\omega }^{2}(a{\upvarepsilon }_{0}+\frac{1}{4}{\varepsilon }_{2}{a}^{3})}^{2}+{(-Ma{\omega }^{2}+{\mu }_{1}a+\frac{3}{4}{\mu }_{3}{a}^{3})}^{2}={M}^{2}{{Y}_{\mathrm{e}}}^{2}{\omega }^{4}$$
(55)

The absolute displacement transmissibility \({T}_{\mathrm{d}}\) of the isolator can be obtained as follows:

$${T}_{\mathrm{d}}=\left|\frac{\sqrt{{a}^{2}+{Y}_{\mathrm{e}}^{2}+2a{Y}_{\mathrm{e}}\mathrm{cos}{\varphi }}}{{Y}_{\mathrm{e}}}\right|$$
(56)

Effect of Different Parameters on Static Mechanical Properties

The structural parameters of the QZS-VI can be designed for different nonlinear stiffness characteristics. The parameters (including the lengths of long arm \({l}_{1}\) and short arm \({l}_{2}\) of V-shaped lever, the angle between two arms of each lever \(\theta\), the distance between the undeformed plate spring and the horizontal shaft of CS \({l}_{3}\), the thickness of plate spring h, the stiffness of coil spring \({k}_{l}\)) are considered as structural parameters to be designed for different nonlinear stiffness. And other parameters are supposed to be fixed in this research such as the width of plate spring settings b = 45 mm. In addition, the flexibility of the V-shaped lever and the CS is ignored. For the facility of analysis, the minimum stiffness of VL-PS-CS is marked as \({k}_{\mathrm{m}\mathrm{i}\mathrm{n}}\), which occurs on the static equilibrium position \({\widehat{z}}_{0}\). And the dimensionless parameters which reflect the structural size relationship of different components of the QZS-VI are defined as follows: (1) ζ = \({l}_{2}\)/\({l}_{3}\), the ratio of the short-arm length of each lever to its initial vertical maximum moving distance; (2) ξ = \({l}_{1}\)/\({l}_{2}\), depicts the length ratio of the long arm to the short arm of each V-shaped lever. It is worth noting that for successful implementation of the designed nonlinear QZS-VI, the boundary conditions of the structural parameters are \({{l}_{3}<l}_{2}<{l}_{1}\) and \({\mathrm{cos}}^{-1}(\frac{{l}_{3}}{{l}_{2}}\text{)} \, {<} \, \theta \, {<}\frac{\pi }{2}\). The force–displacement relationships obtained by Eqs. (20) and (32), and the stiffness–displacement relationships obtained by Eqs. (23) and (33) can be used to reflect the static mechanical properties of VL-PS-CS and QZS-VI, respectively.

Effect of ζ

For \({l}_{3}\)= 100 mm, ξ = 2, \(\theta {=}{ 75}^{\circ }\) and \(h= 1.5 \mathrm{m}\mathrm{m}\), the static force and stiffness properties of VL-PS-CS with different ζ are shown in Fig. 9a, b, respectively. It is known from Fig. 9a that to reach the same deformation of VL-PS-CS, the larger ζ is, the greater the force is needed to act on the VL-PS-CS. From Fig. 9b, it can be seen that with the ratio ζ increasing, the deformation of VL-PS-CS becomes smaller when the stiffness reaches zero, and the value of minimum stiffness becomes smaller. The specific static equilibrium position \({\widehat{z}}_{0}\) and the minimum stiffness of VL-PS-CS with different ζ are shown in Table 1.

Fig. 9
figure 9

The static force–displacement (a) and stiffness-displacement (b) curves of VL-PS-CS with different ζ; the static force–displacement (c) and stiffness-displacement (d) curves of QZS-VI with different ζ and \({k}_{l}\)

Full size image
Table 1 The static equilibrium position and the minimum stiffness with different ζ
Full size table

Parallel connecting the coil spring whose stiffness is equal to the absolute value of \({k}_{min}\) as shown in Table 1, the QZS-VI can achieve high-static and low-dynamic stiffness characteristic. The static force and stiffness characteristics of QZS-VI with different ζ and \({k}_{l}\) are shown in Fig. 9c, d, respectively. From Fig. 9c, d, it can be deduced that the larger ζ, the higher the static bearing capacity of the isolator, and the smaller the quasi zero stiffness displacement range. In a word, the larger the ζ, the stronger the nonlinear stiffness of the VL-PS-CS and the QZS-VI. In order to improve the static bearing capacity with small deformation, while achieving high-static and low-dynamic stiffness, improving ζ is helpful.

Effect of ξ

For \({l}_{3}\)=100 mm, ζ = 1.75, \(\theta {=} \, {75}^{\circ }\) and h = 1.5 mm, the static force and stiffness properties of VL-PS-CS with different ξ are shown in Fig. 10a, b, respectively. It is known from Fig. 10a that to reach the same deformation of VL-PS-CS, the smaller the ξ, the greater the force is needed to act on the VL-PS-CS. From Fig. 10b, it can be seen that with the ratio ξ increasing, the deformation of VL-PS-CS becomes larger when the stiffness reaches zero, and the value of minimum stiffness becomes larger. The specific static equilibrium position \({\widehat{z}}_{0}\) and the minimum stiffness of VL-PS-CS with different ξ are shown in Table 2.

Fig. 10
figure 10

The static force–displacement (a) and stiffness–displacement (b) curves of VL-PS-CS with different ξ; the static force–displacement (c) and stiffness–displacement (d) curves of QZS-VI with different ξ and \({k}_{l}\)

Full size image
Table 2 The static equilibrium position and the minimum stiffness with different ξ
Full size table

Parallel connecting the coil spring whose stiffness is equal to the absolute value of \({k}_{\mathrm{m}\mathrm{i}\mathrm{n}}\) as shown in Table 2, the QZS-VI can achieve high-static and low-dynamic stiffness characteristic. The static force and stiffness characteristics of QZS-VI with different ξ and \({k}_{l}\) are shown in Fig. 10c, d, respectively. From Fig. 10c, d, it can be inferred that the smaller theξ, the higher the static bearing capacity of the isolator, and also the smaller the quasi zero stiffness displacement range. In a word, the smaller ξ, the stronger the nonlinear stiffness of the VL-PS-CS and the QZS-VI. To improve the static bearing capacity with small deformation, while achieving high-static and low-dynamic stiffness, reducing ξ is beneficial.

Effect of \(\theta\)

For \({l}_{3}\)=100 mm, ζ = 1.75, ξ = 2 and h = 1.5 mm, the static force and stiffness characteristics of VL-PS-CS with different \(\theta\) are shown in Fig. 11a, b, respectively. It is known from Fig. 11a that to reach the same deformation of VL-PS-CS, the smaller the \(\theta\), the greater the force is needed to act on the VL-PS-CS. From Fig. 11b, it can be seen that with the angle \(\theta\) increasing, the deformation of VL-PS-CS becomes larger when the stiffness reaches zero, and the value of minimum stiffness becomes larger. The specific static equilibrium position \({\widehat{z}}_{0}\) and the minimum stiffness of VL-PS-CS with different \(\theta\) are shown in Table 3.

Fig. 11
figure 11

The static force–displacement (a) and stiffness–displacement (b) curves of VL-PS-CS with different \(\theta\); the static force–displacement (c) and stiffness–displacement (d) curves of QZS-VI with different \(\theta\) and \({k}_{l}\)

Full size image
Table 3 The static equilibrium position and the minimum stiffness with different \(\theta\)
Full size table

Parallel connecting the coil spring whose stiffness is equal to the absolute value of \({k}_{\mathrm{m}\mathrm{i}\mathrm{n}}\) as shown in Table 3, the QZS-VI can achieve high-static and low-dynamic stiffness properties. The static force and stiffness characteristics of QZS-VI with different \(\theta\) and \({k}_{l}\) are shown in Fig. 11c, d, respectively. From Fig. 11c, d, it can be deduced that the smaller the \(\theta\), the higher the static bearing capacity of the isolator, and the smaller the quasi zero stiffness displacement range. In a word, the smaller the \(\theta\), the stronger the nonlinear characteristics of the VL-PS-CS and the QZS-VI. In order to improve the static bearing capacity with small deformation, while achieving high-static and low-dynamic stiffness, reducing \(\theta\) is profitable.

Effect of h

It is noted that the moment of inertia (I) is the function of the thickness (h) and width (b) of plate spring’s cross section, whose specific expression is \(I=\frac{1}{12}b{h}^{3}\). In this section, the width (b) of plate spring is set to be 45 mm and the thickness (h) is chosen to be of different values, which reflect the equivalent bending stiffness of plate spring.

For \({l}_{3}\)=100 mm, ζ = 1.75, ξ = 2 and \(\theta {=}{75}^{\circ }\), the static force and stiffness characteristics of VL-PS-CS with different \({\text{h}}\) are shown in Fig. 12a, b, respectively. It is known from Fig. 12a that to reach the same deformation of VL-PS-CS, the larger h, the greater the force needed to act on the vibration isolator; From Fig. 12b, it is observed that the larger h, the smaller the value of minimum stiffness. It is worth noting that the deformations of VL-PS-CS keep constant when the zero stiffness and the minimum stiffness occur. The specific static equilibrium position \({\widehat{z}}_{0}\) and the minimum stiffness of VL-PS-CS with different h are shown in Table 4.

Fig. 12
figure 12

The static force–displacement (a) and stiffness–displacement (b) curves of VL-PS-CS with different h; the static force–displacement (c) and stiffness–displacement (d) curves of QZS-VI with different h and \({k}_{l}\)

Full size image
Table 4 The static equilibrium position and the minimum stiffness with different \({\text{h}}\)
Full size table

Parallel connecting the coil spring whose stiffness is equal to the absolute value of \({k}_{\mathrm{m}\mathrm{i}\mathrm{n}}\) as shown in Table 4, the QZS-VI can achieve high-static and low-dynamic stiffness properties. The static force and stiffness characteristics of QZS-VI with different h and \({k}_{l}\) are shown in Fig. 12c, d, respectively. It can be inferred from Fig. 12c, d that the larger the h, the higher the static bearing capacity of the isolator. In a word, the larger the h, the stronger the nonlinear characteristics of the VL-PS-CS and the QZS-VI. In order to improve the static bearing capacity with small deformation, while achieving high-static and low-dynamic stiffness, increasing h is instructive.

Based on above results, it can be concluded that the QZS-VI can be well designed by properly tuning several structural parameters to obtain practical nonlinear high-static and low--dynamic stiffness. For example, if one wants to increase the bearing capacity, while keeping the shape and size of the QZS-VI unchanged, the thickness of plate spring and the stiffness of coil spring should be increased, respectively; if one wants to achieve quasi-zero dynamic stiffness with smaller deformation of isolator, decreasing the ratio ξ and/or decreasing the assembly angle \(\theta\) and/or increasing the ratio ζ are helpful; if one wants to reduce structural size, while remaining the vibration isolation performance and loading capacity unchanged, decreasing effective distance \({l}_{3}\), and lengths of long-arm \({l}_{1}\) and short-arm \({l}_{2}\) of V-shaped lever, and maintaining the parameter ζ, ξ, \(\theta\) and h unchanged is profitable. Overall, redundant structural parameters can be used to tune the vibration isolation performance of QZS-VI in practice, which has a wide range of options in practical applications.

Effect of Different Parameters on Equivalent Friction Properties

In the designed QZS-VI, there are one vertical slider, two horizontal sliders and some rotation joints of V-shaped levers which provide nonlinear friction force to the vibration isolation structure. It is essential to analyze the nonlinear friction properties and their effect on the vibration isolation performance. This section focuses on the effect of different structural parameters on the equivalent friction coefficients of VL-PS-CS. The length ratioζ and ξ, and the angle between two arms of each lever \(\theta\) are changed to investigate the effect of different structure on the friction coefficients of the designed vibration isolation structure. Other parameters are set to be \({l}_{3}\)=100 mm and \(h= 1.5 \mathrm{m}\mathrm{m}\). The physical meanings of \({f}_{\mathrm{c}2}\), \({f}_{\mathrm{c}3}\) and \({f}_{\mathrm{c}}\) are described in Eq. (41). \({f}_{\mathrm{c}2}\) and \({f}_{\mathrm{c}3}\) are related to the friction damping effect of the horizontal sliders and the rotational joints, respectively. \({f}_{\mathrm{c}}\) is the total nonlinear friction coefficient. Setting \({\mathrm{c}}_{1}=0.6\), \({\mathrm{c}}_{2}=0.8\) and \({\mathrm{c}}_{3}=0.2\) (ensuring friction coefficients \({f}_{\mathrm{c}2}\), \({f}_{\mathrm{c}3}\) and \({f}_{\mathrm{c}}\) in the same scale) for comparison, the relationship between different coefficients and relative displacement \(\widehat{z}\) can be seen in Figs. 13–15.

Fig. 13
figure 13

Friction coefficients \({f}_{\mathrm{c}}{2}\), \({f}_{\mathrm{c}3}\) and \({f}_{\mathrm{c}}\) with different length ratio ζ when ξ = 2 and \(\theta {=}{75}^{\circ }\)

Full size image

Figure 13 shows that the friction coefficients \({f}_{\mathrm{c}2}\), \({f}_{\mathrm{c}3}\) and \({f}_{\mathrm{c}}\) change differently when the value of \(\widehat{z}\) changes from 0 to 100 mm. The values of \({f}_{\mathrm{c}2}\), \({f}_{\mathrm{c}3}\) and \({f}_{\mathrm{c}}\) are always positive and decrease nonlinearly as the increase of \(\widehat{z}\). A bigger length ratio ζ leads to a larger nonlinear friction effect \({f}_{\mathrm{c}2}\) and \({f}_{\mathrm{c}3}\), which causes the increase of the total friction coefficient \({f}_{\mathrm{c}}\), \(\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{p}\mathrm{o}\mathrm{n}\mathrm{d}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{l}\mathrm{y}\). The total friction coefficient \({f}_{\mathrm{c}}\) can be changed from a very small value to a much bigger value around the equilibrium position, which means the QZS-VI can dissipate more energy in the resonant amplitude peak.

Figure 14 displays the effect of the length ratio ξ on the friction coefficients. The nonlinear friction properties are displacement-dependent with respect to different length ratio. It is noticed that increasing ξ leads to the increasing of all friction coefficients \({f}_{\mathrm{c}2}\), \({f}_{\mathrm{c}3}\) and \({f}_{\mathrm{c}}\). The effect of the assembly angle \(\theta\) of the V-shaped lever is shown in Fig. 15. It can be seen that a bigger assembly angle leads to a much smaller friction effect in the QZS-VI, and the total friction effect tends to be a constant as the assembly angle enlarged, while a smaller assembly angle yields much more nonlinear friction effect and a significant varying range.

Fig. 14
figure 14

Friction coefficients \({f}_{\mathrm{c}2}\), \({f}_{\mathrm{c}3}\) and \({f}_{\mathrm{c}}\) with different length ratio ξ when ζ = 1.75 and \({\theta =}{75}^{\circ }\)

Full size image
Fig. 15
figure 15

Friction coefficients \({f}_{\mathrm{c}2}\), \({f}_{\mathrm{c}3}\) and \({f}_{\mathrm{c}}\) with different angle \(\theta\) when ζ = 1.75 and ξ = 2

Full size image

In general, by increasing ζ and/or ξ, and/or decreasing \(\theta\), the total friction coefficient \({f}_{\mathrm{c}}\) can be increased rapidly. To obtain nonlinear and significant damping effect, the angle \(\varphi\) between the long arm of the lever and the vertical direction should be smaller. Therefore, by adjusting structural parameters \({l}_{1}\), \({l}_{2}\), \({l}_{3}\) and \(\theta\), and designing friction constant \({\mathrm{c}}_{1}\), \({\mathrm{c}}_{2}\) and \({\mathrm{c}}_{3}\), the friction properties of the QZS-VI can be tuned for better vibration isolation performance.

Performance Comparison with Existing Isolators

As the designed quasi-zero stiffness vibration isolator (D-QZS-VI) is the combination of nonlinear geometrical structure with plate spring (acting as buckled beam), it is beneficial to reveal the vibration isolation performance of our designed isolator by comparing its performance with existing quasi-zero stiffness vibration isolator which is equipped with buckled beam. An existing quasi-zero stiffness vibration isolator (E-QZS-VI) with Euler buckled beam as negative stiffness corrector is studied in [25, 34]. The dynamic modeling of the E-QZS-VI in [25, 34] is given as follows:

$$m\ddot{y}+c\dot{y}+kL\left(\alpha {\stackrel{\sim }{y}}^{3}+\sqrt{1-{\gamma }^{2}}\right)-\mathrm{m}\mathrm{g}=m{\omega }^{2}{Z}_{0}\mathrm{c}\mathrm{o}\mathrm{s}\omega t,$$
(57)

where m is the mass of payload, c is the linear damping constant, k is the stiffness of linear spring, y is the relative displacement between the payload and the base, \(\stackrel{\sim }{y}=y/L\) is the non-dimensional relative displacement, L is the length of the beam before buckling, \(\gamma =\frac{a}{L}=\mathrm{c}\mathrm{o}\mathrm{s}\theta\) reflects the initial inclined angle of the beam, \(kL(\alpha {\stackrel{\sim }{y}}^{3}+\sqrt{1-{\gamma }^{2}})\) is the Taylor approximation of the restoring force and \(\alpha\) is the coefficient of the cubic term about \(\stackrel{\sim }{y}\), whose exact expression is listed as follows:

$${\alpha }=\left(\left(\frac{1}{2{\gamma }^{2}}+\frac{2}{\gamma \left({\left(\pi {\stackrel{\sim }{q}}_{0}\right)}^{2}-4\gamma +12\right)}\right)+\frac{\pi {\stackrel{\sim }{q}}_{0}}{{\gamma \left({\left(\pi {\stackrel{\sim }{q}}_{0}\right)}^{2}-4\gamma +12\right)}^{(3/2)}-\pi {\stackrel{\sim }{q}}_{0}\left({\left(\pi {\stackrel{\sim }{q}}_{0}\right)}^{2}-4\gamma +12\right)}\right)$$

where \({\stackrel{\sim }{q}}_{0}={q}_{0}/L\), \({q}_{0}\) is the initial imperfection of the beam.

To compare the vibration isolation performance between two kinds of QZS-VI, the parameters of two isolators are chosen to make them possess the same bearing capacity with the specific deformation. Given the mass of payload as 3.4 kg, the two isolators all reach equilibrium position with the deformation of \(58 \mathrm{m}\mathrm{m}\). The structural parameters of the E-QZS-VI are set to be: k = 5.745 N cm−1, \(\gamma =0.9862\), L = 350 mm, \({\stackrel{\sim }{q}}_{0}=0.03\), c = 1.6364 \(\mathrm{N}\mathrm{s} {\mathrm{m}}^{-1}\). Similarly, the structural parameters of the D-QZS-VI are specified as: \({k}_{l}=2.44\) N cm−1, \({l}_{3}\)=100 mm, ζ = 1.75, ξ = 2, \(\theta {=}{75}^{\circ }\), h = 1.5 mm, \({c}_{1}=0.6 \mathrm{N}\mathrm{s} {\mathrm{m}}^{-1}\), \({c}_{2}=0.8 \mathrm{N}\mathrm{s} {\mathrm{m}}^{-1}\), \({c}_{3}=0.2 \mathrm{N}\mathrm{s} {\mathrm{m}}^{-1}\).

For comparison, a typical linear mass-spring-damper vibration isolator (MSD-VI) with similar parameter setting is

$$\mathrm{m}\ddot{y}+\mathrm{c}\dot{y}+ky=\mathrm{m}{\omega }^{2}{Z}_{0}\mathrm{c}\mathrm{o}\mathrm{s}\omega t$$
(58)

For the three isolation systems, the linear components of passive damper are set to be equal. For the D-QZS-VI, the friction force is \({F}_{\mathrm{c}}=(1.6364-9.8\widehat{\mathrm{u}}+65{\widehat{\mathrm{u}}}^{2})\dot{\widehat{\mathrm{u}}}\) and the restoring force is \(\mathrm{F}=33.32+0.17\widehat{\mathrm{u}}-17{\widehat{\mathrm{u}}}^{2}+35474{\widehat{\mathrm{u}}}^{3}\). For the E-QZS-VI, the friction force is \({F}_{\mathrm{c}}=1.6364\dot{y}\) and the restoring force is \(F=33.32+2041{y}^{3}\). For the MSD-VI, the friction force is \({F}_{\mathrm{c}}=1.6364\dot{y}\) and the restoring force is \(F=33.32+574.5y\). The equivalent restoring force and stiffness properties of the three isolators are shown in Fig. 16. From Fig. 16, the equivalent stiffness property of D-QZS-VI is very close to or even better than that of E-QZS-VI, both of which exhibit much softer than the MSD-VI.

Fig. 16
figure 16

The equivalent restoring force and stiffness properties of three isolators

Full size image

The absolute displacement transmissibility of the D-QZS-VI solved

by Eq. (56) is used to reflect the vibration isolation performance. The same method is used to obtain the displacement transmissibility of E-QZS-VI and MSD-VI. Under the same displacement amplitude (\({Z}_{0}=5 \mathrm{m}\mathrm{m}\)) of harmonic excitation, the comparison of displacement transmissibility is shown in Fig. 17. It can be obtained that the dynamic property of the designed QZS-VI (without any extra dampers) behaves much better than other two isolators due to its special nonlinear friction and stiffness properties (lower peak value, smaller resonant frequency and more stability property at the peak frequency). By adjusting proper structural parameters of the designed QZS-VI, the amplitude of displacement transmissibility can be suppressed obviously compared with the other two isolators.

Fig. 17
figure 17

Displacement transmissibility of three isolators with respect to different exciting frequency

Full size image

In Fig. 17, the comparison of displacement transmissibility between the designed QZS-VI and the existing QZS-VI is conducted with the same restoring force and the same linear components of damper. It is depicted that the designed QZS-VI and the existing QZS-VI have the same resonant frequency which is much smaller than that of MSD-VI. Due to the friction of links and sliders, the displacement transmissibility of D-QZS-VI is larger than that of E-QZS-VI at lower frequency, while being smaller than that of E-QZS-VI at resonant frequency. Although the rigid motion of the D-QZS-VI caused by equivalent nonlinear friction force cannot be avoided, the resonant peak is suppressed and the stability is improved, which largely improves the performance of vibration isolation.

Simulation Study Subject to Harmonic Excitation

In order to verify the vibration isolation property of the QZS-VI more intuitively, the nonlinear dynamic modeling is solved by 4-order Runge–Kutta algorithm and the time domain response of the designed QZS-VI with payload under fixed-frequency harmonic excitation are simulated. In the simulation, the parameters of QZS-VI are set to be \({l}_{3}\)=100 mm, ζ = 1.75, ξ = 2, \(\theta {=}{75}^{\circ }\), h = 1.5 mm, \({k}_{l}=2.44\) N cm−1, M = 3.4 kg, \({\mathrm{c}}_{1}=0.6 \mathrm{N}\mathrm{s} {\mathrm{m}}^{-1}\), \({\mathrm{c}}_{2}=0.8 \mathrm{N}\mathrm{s} {\mathrm{m}}^{-1}\) and \({\mathrm{c}}_{3}=0.2 \mathrm{N}\mathrm{s} {\mathrm{m}}^{-1}\), which are same as the settings in Sect. 6. Under the harmonic vibration excitation with the fixed displacement amplitude (5 mm) and different forcing frequencies, the absolute displacement response of QZS-VI is researched and the results are shown in Fig. 18. It can be seen that under the frequency of 0.1 Hz, the displacement response slightly amplifies the displacement of vibration excitation due to the resonance effect. When the forcing frequencies are, respectively, set to be 0.2 Hz, 0.5 Hz and 1 Hz, vibration isolation phenomenon occurs and the isolation effect becomes more and more prominent with the increase of forcing frequency. The numerical simulation results are consistent with the approximated solution of displacement transmissibility obtained in Sect. 6, which verifies the accuracy of analytical solution based on average method.

Fig. 18
figure 18

The absolute displacement response (dashed line) of QZS-VI under the base excitation (solid line) with frequency of (a) 0.1 Hz, (b) 0.2 Hz, (c) 0.5 Hz and (d) 1 Hz

Full size image

Conclusion

A novel passive nonlinear QZS-VI with VL-PS-CS is proposed and studied. The VL-PS-CS takes an ingenious combination of plate spring and V-shaped lever and facilitates the QZS-VI achieving quasi-zero stiffness property and superior nonlinear vibration isolation performance. The isolator can be well designed by properly tuning several structural parameters (e.g., \({l}_{1}\), \({l}_{2}\), \({l}_{3}\), \(\uptheta ,\) h, \({k}_{l}\)) to obtain practical high-static and low-dynamic stiffness, which presents the possibility for different stiffness and damping design. It also indicates that some optimization process can be employed for a detailed engineering practice (taking into account the actual requirements on performance, weight, size, loading capacity and others). Compared with another QZS-VI of buckled beam mechanism and traditional linear vibration isolator, the designed QZS-VI exhibits smaller resonant frequency, lower peak value and more stable property at the peak frequency while possessing the same loading capacity. The innovative structure provides novel insights into the design of passive vibration isolators and has great potential for application in engineering practice.

The QZS-VI can be further developed by considering mass and moment of inertia of V-shaped levers in system modeling and verifying the theoretical results with a practical experimental prototype. Moreover, the application of the innovative structure to many practical engineering issues can also be investigated.