Introduction

Mechanical vibration is an important issue often raised in the field of engineering technology which is mainly caused by excitation resonance resulting from noise. From literature review, we found that long-term exposure to noisy environment will endanger human life and health. For example, it damages cardiovascular, nervous system disease and leads to hearing loss. Too much noise even results in life-threatening conditions [1,2,3]. The internal organs of humans produce resonances when the vibration frequency reached in the range of 4–8 Hz. When it reaches the range of 8–12.5 Hz, the human spine will be greatly affected [4]. Therefore, it is particularly important to control vibration and noise, and controlling mechanical vibration can indirectly control noise. In the control of mechanical vibration, vibration isolation is an effective means to control vibration, and it is widely used in engineering. When the source of vibration is the device itself, to reduce the influence of the device on the surrounding objects, the vibration isolation between the source and the foundation is called the active vibration isolation. When the source of vibration comes from the foundation, it is necessary to reduce the impact of the base vibration on the equipment, namely, the passive vibration isolation. However, in the traditional linear vibration isolation system, the isolation effect can be motivated only when the excitation frequency is \( \sqrt 2 \) times greater than the natural frequency. Therefore, to improve the low-frequency vibration isolation effect, the natural frequency of the system must be reduced, which will lead to a decrease of the system stiffness [5]. Meanwhile, the more the stiffness reduced, the worse the stability of the vibration isolation system [6]. After an in-depth study for the vibration isolation system, we found that a nonlinear quasi-zero-stiffness (QZS) vibration isolation mechanism can be realized by linear positive stiffness spring in parallel with negative stiffness mechanism and that a higher static rigidity as well as a lower dynamic stiffness can be achieved a better low-frequency vibration isolation performance which based on the bearing capacity [7].

Alabuzhev [8] took the lead in elaborating the theory of QZS vibration isolation system. Later, he came up with multiple structural design forms. Platus [9] first proposed that as a negative stiffness mechanism, the Euler column spring can obtain a QZS vibration isolation mechanism in parallel with the vertical spring, which stiffness can be nearly zero. Carrella [10,11,12,13] proposed a classical form of the QZS systems, as well studied a QZS isolator with a single linear spring in parallel with two linear oblique springs. Zhang et al. [14] and Liu [15,16,17] developed a new type of nonlinear ultra-low-frequency vibration isolation system and used it in vibration isolation for precision instruments. Thus, it is obvious that the QZS mechanism has great application prospects in precision instrument areas.

In recent years, Shi [18] designs a new mechanical adjustable type with QZS characteristic. Thanh et al. [19, 20] studied a QZS isolator using a horizontal compression spring parallel vertical spring and applied it to the vehicle seat for vibration isolation. Robertson et al. [21] succeeded in low-frequency vibration isolation using a permanent magnet QZS isolator though analyzed the azimuth and cross-sectional area of the permanent magnets at both ends. Cheng [22] researched the QZS structure of one horizontal tension spring with two vertical positive stiffness springs. Wang [23] studied the performance of QZS vibration isolator under mistuned mass. Meng et al. [6] designed a new QZS mechanism using two negative stiffness tension springs in parallel with a linear positive stiffness spring, which has been applied it to the structure of a rehabilitation robot. However, most QZS vibration isolators designed by scholars are more complicated with higher cost and requirements for greater precision. Besides, studies are insufficient on the relationship between the structural parameter ratio and the vibration isolation effect, and on dynamic characteristics and vibration isolation under ordinary excitation. Thus, a QZS mechanism with simple structure, compact structure, and good vibration isolation effect was designed, and the structural parameters were studied in depth. Moreover, this research also contains several simulations on the vibration isolation effect under different excitations.

In this paper, by statics calculations, the appropriate structural parameters were selected for the QZS vibration isolation mechanism. Meanwhile, a better low-frequency vibration isolation effect at the equilibrium position has been achieved. The paper mainly consists of several parts. First, the design of the model was introduced in the second part. In the third part, the static characteristics of the mechanism were analyzed, and the stiffness error and stiffness ratio error were compared by adding the disturbance variable at the quasi-equilibrium position. In the fourth part, the influences of excitation amplitude, damping ratio, and nonlinear term on force transmissibility and displacement transmissibility were analyzed. The fifth part mainly is the numerical simulation of the system under sine wave, single shock, and multi-frequency excitation. Finally, the conclusion was given in the sixth section.

3D Modeling of Vibration Isolator

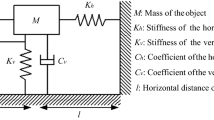
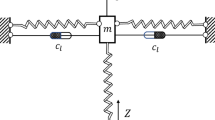
The QZS systems designed in this paper are shown in Fig. 1. Its three-dimensional structure is shown in Fig. 1a. It mainly includes: (1) loading support; (2) connecting rods; (3) horizontal springs; (4) vertical springs; and (5) bases. The horizontal spring is installed on the bar, the loading support and the base are connected with the bar through the cylindrical pin, and the vertical spring is installed the spring mounting hole in the base. The structural principle of the QZS mechanism is shown in Fig. 1b. When the load is not applied, the loading support is in the initial position. After the load is applied, the loading support is subjected to the force of the vertical spring and the horizontal extension spring at the same time. After the load in equilibrium position, it is only related to the restoring force of the vertical spring and has nothing to do with the force of the horizontal spring. For the QZS vibration isolation system, the vertical spring is mainly used to bear the static mass, and the symmetrical horizontal stretching spring is the negative stiffness mechanism, which can offset each other with the vertical positive stiffness spring at the balance position.

Fig. 1
figure 1

QZS isolator model: a three-dimensional structure of vibration isolation system; b structure principle of vibration isolation system

Full size image

Research on Static Properties

Negative Stiffness Mechanism

First, the structural part of negative stiffness was calculated. The force analysis of the negative stiffness mechanism is shown in Fig. 2.

Fig. 2
figure 2

QZS system force diagram

Full size image

When the platform is loaded, the thrust T in the vertical direction will cause the platform to generate a downward displacement x, stretching four horizontal tension springs, which also produces an upward restoring force F. According to the geometric relationship, the force analysis was carried out on the 1/2 part of two adjacent springs and the force provided by the vertical negative stiffness spring was obtained:

$$ F = 4F_{\text{h}} \tan \left( \theta \right) $$
(1)
$$ F_{\text{h}} = 2K_{\text{h}} \lambda \cos \left( {45^\circ } \right). $$
(2)

Among them, Fh is the horizontal force of 1/2 part of the adjacent two horizontal tension springs, Kh is the stiffness of the horizontal tension spring, λ is the distance that the horizontal stretch spring 1/2 is stretched, and θ is an included angle made up with the connecting rod and the horizontal spring.

The angle θ at any position can be given as

$$ \tan \left( \theta \right) = \frac{{h_{0} - x}}{{\sqrt {L^{2} - \left( {h_{0} - x} \right)^{2} } }}, $$
(3)

by geometric relations, the equation can be expressed as

$$ \lambda = \sqrt 2 \left( {\sqrt {L^{2} - \left( {h_{0} - x} \right)^{2} } - L_{0} } \right) $$
(4)
$$ h_{0} = \sqrt {L^{2} - L_{0}^{2} } . $$
(5)

Substituting Eqs. (3), (4), and (5) into Eq. (1), relationship between restoring force and displacement is as follows:

$$ F = 8K_{\text{s}} \left( {1 - \frac{{L_{0} }}{{\sqrt {L^{2} - \left( {\sqrt {L^{2} - L_{0}^{2} } - x} \right)^{2} } }}} \right)\left( {\sqrt {L^{2} - L_{0}^{2} } - x} \right). $$
(6)

It is convenient to define the following dimensionless parameters:

$$ \hat{F} = F/K_{\text{s}} L_{0} ,\,\hat{x} = x/L_{0} ,\,m = L/L_{0} ,\,\hat{h}_{0} = \sqrt {m^{2} - 1} , $$

wherein \( \hat{F} \) represents the dimensionless restoring force, \( \hat{x} \) is the dimensionless displacement, Ks is the stiffness of the horizontal spring, L0 is the original length of horizontal spring, L is the length of the bar, m is the configurative parameter, and \( \hat{h}_{0} \) is the dimensionless initial deformation of the vertical spring. In terms of these dimensionless parameters, the dimensionless restoring force can be derived from Eq. (6):

$$ \hat{F} = 8\left( {1 - \frac{1}{{\sqrt {m^{2} - \left( {\hat{h}_{0} - \hat{x}} \right)^{2} } }}} \right)\left( {\hat{h}_{0} - \hat{x}} \right). $$
(7)

Equation (7) is the dimensionless force–displacement expression of the negative stiffness mechanism of the vibration isolation system, and these curves are shown in Fig. 3.

Fig. 3
figure 3

Dimensionless force–displacement

Full size image

Figure 3 shows that only when the m > 1, the mechanism is a negative stiffness mechanism. The area between the two extreme points of the curve is a zone of negative stiffness. The restoring force in the zone decreases with displacement increasing, and the stiffness is negative. If the stiffness of the mechanism is less than zero, the sense of isolation will be lost. Therefore, adding a positive stiffness spring to achieve the effect of QZS is very necessary.

QZS Vibration Isolation System

As can be seen from Fig. 1 that the relationship between the dimensionless restoring force and the dimensionless displacement of the QZS systems can be expressed as

$$ \hat{F} = \hat{x} + 8\alpha \left( {1 - \frac{1}{{\sqrt {m^{2} - \left( {\hat{h}_{0} - \hat{x}} \right)^{2} } }}} \right)\left( {\hat{h}_{0} - \hat{x}} \right) - \hat{h}_{0} , $$
(8)

wherein \( \alpha = K_{\text{S}} /K_{\text{V}} \) represents the stiffness ratio, the dimensionless restoring force of the system is zero when \( \hat{h}_{0} = \hat{x} \), and the relationship between force and displacement of the system is a cubic polynomial and \( \hat{x} \in \left( {0\sim \mathop 2\limits_{{}} \hat{h}\mathop {_{0} }\limits_{{}} } \right) \):when \( \hat{u} = \hat{x} - \hat{h}\mathop {_{0} }\limits_{{}} \), the dimensionless force–displacement expression of the system can be shown as

$$ \hat{F} = \hat{u} - 8\alpha \left( {1 - \frac{1}{{\sqrt {m^{2} - \hat{u}^{2} } }}} \right)\hat{u}. $$
(9)

The relationship between the dimensionless stiffness and displacement of the system is shown in Fig. 3:

$$ \hat{K} = 1 + 8\alpha \left( {\frac{{m^{2} }}{{\left( {m^{2} - \hat{u}^{2} } \right)^{{\frac{3}{2}}} }} - 1} \right) $$
(10)
$$ \gamma = \frac{m}{{8\left( {m - 1} \right)}}. $$
(11)

In Eq. (11), γ represents the geometric ratio of the mechanism. When α = γ, the corresponding relationship between the two is shown in Fig. 4, and when m gradually increases, the stiffness ratio α gradually decreases. It can be seen from Fig. 4 that when the bar is inclined to the horizontal plane, the negative stiffness characteristics are more obvious and the nonlinearity is stronger, but the saltation phenomenon may occur in this case.

Fig. 4
figure 4

Relationship between α and m

Full size image

When α and γ are equal, the mechanism achieves a QZS at the equilibrium position. It can be verified from Fig. 5 that when in the equilibrium position, the stiffness of the system is zero at the \( \hat{u} = 0 \) moment, and when α = 0.5γ, the system will exhibit positive stiffness near the equilibrium position. If α = 1.5γ, the system will exhibit negative stiffness near the equilibrium position. Therefore, to achieve a wider vibration isolation frequency domain, it is necessary to ensure that the average stiffness is small enough in the range near the equilibrium position. Similarly, it can be seen from Fig. 6 that the curvature of the dimensionless stiffness curve is gradually increasing with the increase of α.

Fig. 5
figure 5

Dimensionless force–displacement curve

Full size image
Fig. 6
figure 6

Stiffness curves for different α values

Full size image

As shown in Fig. 7, in conjunction with Eqs. (9), (10), and (11), it can be seen that \( \hat{K} \) is mainly determined by α and γ when at the equilibrium position. When α = γ, as m increases, α gradually decreases, and control the size of α and γ to maintain better QZS characteristics.

Fig. 7
figure 7

Relationship between m and α at equilibrium

Full size image

The QZS isolator has better vibration isolation effect than the conventional linear system, but the above analysis is based on Eqs. (10) and (11) to ensure the accuracy. In the process of actual processing, it is inevitable that there will be some processing errors, so it is difficult to ensure that the relationship between m and α is completely accurate during the actual experiment. Therefore, it is necessary to analyze the static stability of the vibration isolator. By introducing a small disturbance variable ε, the dimensionless stiffness expression is

$$ \hat{K} = \hat{K}_{{\text{QZS}}} \pm 8\alpha \varepsilon \left( {\frac{{m^{2} }}{{\left( {m^{2} - \widehat{u}^{2} } \right)^{{\frac{3}{2}}} }} - 1} \right), $$
(12)

wherein \( \hat{K}_{{\text{QZS}}} \) represents the stiffness of the system. In the static equilibrium position,\( \hat{K}_{{\text{QZS}}} = 0 \), \( \hat{u} = 0 \) the stiffness error near the static equilibrium position is

$$ \hat{K}= \mp \varepsilon . $$
(13)

That is, the error in stiffness and stiffness ratios at the static equilibrium point of the system is of the same order of magnitudes and is opposite in sign.

Approximate Replacement of Force and Stiffness Characteristics

When the vibration isolator displacement is small, to analyze the characteristics of the QZS isolator more clearly, the restoring force of the system can be developed using the Taylor formula. That is, when \( \hat{u} = 0 \), Taylor formula can be obtained:

$$ \hat{F} = \hat{F}\left( 0 \right) + \hat{F}^{\prime}\left( 0 \right)\hat{u} + \frac{{\hat{F}^{\prime\prime}\left( 0 \right)}}{2!}\hat{u}^{2} + \frac{{\hat{F}^{\prime\prime\prime}\left( 0 \right)}}{3!}\hat{u}^{3} . $$
(14)

According to Eqs. (9)–(11) and Fig. 8

$$ \hat{F}^{\prime}\left( {\hat{u}} \right) = 1 + 8\alpha \left( {\frac{{m^{2} }}{{\left( {m^{2} - \hat{u}^{2} } \right)^{{\frac{3}{2}}} }} - 1} \right) $$
(15)
$$ \hat{F}^{\prime\prime}\left( {{\hat{\text{u}}}} \right) = 24\alpha m^{2} \frac{{\hat{u}}}{{\left( {m^{2} - \hat{u}^{2} } \right)^{{\frac{5}{2}}} }} $$
(16)
$$ \hat{F}^{\prime\prime\prime}\left( {\hat{u}} \right) = 24\alpha m^{2} \frac{{m^{2} - 7\hat{u}^{2} }}{{\left( {m^{2} - \hat{u}^{2} } \right)^{{\frac{7}{2}}} }} $$
(17)

when \( \hat{u} = 0 \), Eq. (14) can be simplified as

$$ \hat{F} = \frac{4\alpha }{{m^{3} }}\hat{u}^{3} . $$
(18)

It can be seen from the above equation that the elastic restoring force has a cubic term, so the QZS isolator is a nonlinear vibration isolator. Take m = 1.5, α = 0.375, the dimensionless restoring force–displacement exact solution and approximate solution of the system, and the dimensionless stiffness–displacement exact solution and approximate solution are shown in Figs. 8 and 9, respectively. Near the equilibrium position, the exact curve of the force coincides with the approximate curve, the corresponding stiffness curve, superposition and the degree of superposition is high. Therefore, it is feasible to replace the exact expression with the approximate expression in the range of small amplitude. In addition, the mechanism can guarantee a lower stiffness value near the equilibrium position. The larger the distance from the static equilibrium point, the greater the error between the approximate result and the exact result.

Fig. 8
figure 8

Comparison of exact force and approximate force

Full size image
Fig. 9
figure 9

Comparison of exact stiffness and approximate stiffness

Full size image

When the geometric parameters and stiffness ratio of the system meet the characteristics of QZS, the approximate stiffness can be written as

$$ \hat{K}_{{\text{app}}} = \frac{12\alpha }{{m^{3} }}\hat{u}^{2} , $$
(19)

which \( \hat{K}_{{\text{app}}} \) represents approximate dynamic stiffness of system. It can be seen from Fig. 9 that the error between the approximate stiffness and the accurate stiffness increases with the distance from the equilibrium point, and the error between the approximate stiffness and the accurate stiffness can be measured by the relative error calculation. Defining the relative error δ between the two can be expressed as

$$ \delta = \left| {1 - \frac{{\hat{K}_{{\text{app}}} }}{{\hat{K}}}} \right| \times 100\% . $$
(20)

It can be seen from Fig. 10 that when the distance from the equilibrium point is small, the error value between the approximate stiffness and the accurate stiffness obtained by the Taylor expansion formula is correspondingly getting small, so in this case, it is reasonable and compared to be easier analyzing the QZS characteristics of the isolator through approximate stiffness method, but the expression of the approximate stiffness would be ineffective due to the relative error will increases with the offset distance. While in practical situations, the deviation of the system’s vibration displacement relative to the equilibrium point is relatively smaller, so it is feasible to use the Taylor polynomial to analyze the performance of the vibration isolator.

Fig. 10
figure 10

Relative error δ between approximate stiffness and precision stiffness

Full size image

Dynamic Analysis

Dynamic Modeling

The QZS isolator is a single-degree-of-freedom nonlinear vibration isolation system. According to Eq. (9), the relationship between the bearing quality M and the system parameters is given by

$$ \text{Mg} = \hat{F} = K_{\text{v}} h_{0} = K_{\text{v}} \hat{h}_{0} L_{0} . $$
(21)

The harmonic force excitation \( f = F\cos (\mathop \omega \limits_{{}} t) \) and harmonic displacement excitation \( z = Z\cos \left( {\omega t} \right) \) are applied to the base. According to Newton’s second law, the nonlinear motion differential equation of the system can be established as

$$ {M\ddot{u}} + {c\dot{u}} + F_{r1} - \text{Mg} = F\cos \left( {\omega t} \right) $$
(22)
$$ \varvec{M\ddot{y}} + {c\dot{y}} + F_{r2} - \text{Mg} = M\omega^{2} Z\cos \left( {\omega t} \right), $$
(23)

among them, y = u − z is the relative displacement between the vibration-isolated object and the base under the harmonic displacement excitation condition, and \( F_{{\text{r}1}} \) and \( F_{{\text{r}2}} \) are the restoring forces of the system under excitation conditions of harmonic force and harmonic wave excitation, respectively. Then:

$$ F_{{\text{r}1}} = \text{Mg} + \frac{4\alpha }{{m^{3} }}\hat{u}^{3} $$
(24)
$$ F_{{\text{r}2}} = \text{Mg} + \frac{4\alpha }{{m^{3} }}\hat{y}^{3} . $$
(25)

Introducing dimensionless parameters

$$ \tau = \omega t,\,\,\varOmega = \frac{\omega }{{\omega_{\text{n}} }},\,\,\omega_{\text{n}} = \sqrt {\frac{{K_{\text{v}} }}{m}} ,\,\,\hat{y} = \frac{y}{{L_{0} }},\,\,\hat{z} = \frac{z}{{L_{0} }},\,\,\xi = \frac{c}{{2M\omega_{\text{n}} }},\,\,\hat{F} = \frac{F}{{K_{\text{v}} L_{0} }}. $$

Substituting Eqs. (24) and (25) into Eqs. (22) and (23), respectively, the system dimensionless motion differential equations are

$$ \hat{u}^{\prime \prime } + 2\xi \hat{u}^{\prime } + \chi \hat{u}^{3} = \hat{F}\cos \left( {\varOmega \tau } \right) $$
(26)
$$ \hat{y}^{\prime \prime } + 2\xi \hat{y}^{\prime } + \chi \hat{y}^{3} = \varOmega^{2} \hat{Z}\cos \left( {\varOmega \tau } \right). $$
(27)

Simplified as

$$ \hat{v}^{\prime \prime } + 2\xi \hat{v}^{\prime } + \chi \hat{v}^{3} = \eta \rho \cos \left( {\varOmega \tau } \right), $$
(28)

wherein ρ is the amplitude of the harmonic excitation and when the system is excited by the harmonic force, \( \eta = 1 \), \( \rho = \hat{F} \); when the system is excited by harmonic displacement, \( \eta = \varOmega^{2} \), \( \rho = \hat{Z} \). The nonlinear motion differential equation shown in Eq. (28) is the Duffing equation under symmetric excitation conditions. The average method can be used to solve the equation. The steady-state solution to Eq. (28) is supposed to be

$$ \hat{v} = A_{1} \cos \left( {\varOmega \tau + \varphi } \right) $$
(29)
$$ \hat{v}^{\prime } = - \varOmega A_{1} \sin \left( {\varOmega \tau + \varphi } \right). $$
(30)

The harmonic term amplitude \( A_{1} \) and phase angle φ are slowly varying functions of time τ. Taking the changes in \( A_{1} \) and φ into account, substituting Eqs. (29) and (30) into Eq. (28) can obtain

$$ A_{1}^{\prime } = - \frac{1}{\varOmega }\prod {\sin \left( {\varOmega \tau + \varphi } \right)} $$
(31)
$$ \varphi^{\prime}= - \frac{1}{{A_{1} \varOmega }}\prod {\cos \left( {\varOmega \tau + \varphi } \right)} $$
(32)

\( \prod {= \gamma \rho \cos \left( {\varOmega \tau } \right) + 2\xi \varOmega A_{1} } \sin \left( {\varOmega \tau + \varphi } \right) + \varOmega^{2} A_{1} \cos \left( {\varOmega \tau + \varphi } \right) + \chi A_{1}^{3} \cos^{3} \left( {\varOmega \tau + \varphi } \right) \) and \( \left( {\varOmega \tau + \varphi } \right) \) can be approximately replaced by the mean value in one period. Assuming that \( A_{1} \) and φ remain constant in one cycle, and the averaged equation can be obtained:

$$ A_{1}^{\prime } = - \frac{\varOmega }{2\pi }\int_{0}^{{\frac{2\pi }{\varOmega }}} {\frac{1}{\varOmega }} \prod {\sin \left( {\varOmega \tau + \varphi } \right)d\tau } $$
(33)
$$ \varphi^{\prime}= - \frac{\varOmega }{2\pi }\int_{0}^{{\frac{2\pi }{\varOmega }}} {\frac{1}{{A_{1} \varOmega }}} \prod {\cos \left( {\varOmega \tau + \varphi } \right)\text{d}\tau } . $$
(34)

Equations (33) and (34) can be simplified as

$$ - \frac{\eta \rho \sin \left( \varphi \right)}{2\varOmega } - \xi A_{1} = 0 $$
(35)
$$ - \frac{\eta \rho \cos \left( \varphi \right)}{{2\varOmega A_{1} }} - \frac{\varOmega }{2} + \frac{{3\chi A_{1}^{2} }}{8\varOmega }= 0. $$
(36)

Sum the squares of the two equations to obtain the system’s amplitude–frequency response function:

$$ \left( {\frac{3}{4}\chi A_{1}^{3} - \varOmega^{2} A_{1} } \right)^{2} + 4\xi^{2} \varOmega^{2} A_{1}^{2} = \eta^{2} \rho^{2} . $$
(37)

According to Eq. (37), two solutions can be obtained in harmonic force and harmonic displacement excitation; the expressions are

$$ \varOmega_{1,2}^{\text{f}} = \frac{1}{2}\sqrt {3\chi A_{1}^{2} - 8\xi^{2} \pm \frac{4}{{A_{1} }}\sqrt {4\xi^{4} A_{1}^{2} - 3\chi \xi^{2} A_{1}^{4} + \rho^{2} } } $$
(38)
$$ \varOmega_{1,2}^{\text{z}} = \frac{1}{2}\sqrt {\frac{{3\chi A_{1}^{4} - 8\xi^{2} A_{1}^{2} \pm A_{1}^{2} \sqrt {64\xi^{4} - 48\chi \xi^{2} A_{1}^{2} + 9\chi^{2} \rho^{2} A_{1}^{2} } }}{{A_{1}^{2} - \rho^{2} }}} . $$
(39)

The peak amplitude of the responses \( A_{\hbox{max} }^{\text{f}} \) and \( A_{\hbox{max} }^{\text{z}} \) and the frequencies corresponding to the peak responses \( \varOmega_{\hbox{max} }^{\text{f}} \) and \( \varOmega_{\hbox{max} }^{\text{z}} \) for the two types of excitations can be achieved as

$$ A_{\hbox{max} }^{\text{f}} = \sqrt {\frac{{2\xi^{3} + \sqrt {4\xi^{6} + 3\chi \rho^{2} } }}{3\chi \xi }} $$
(40)
$$ A_{\hbox{max} }^{\text{z}} = \frac{{8\xi^{2} }}{{\sqrt {48\chi \xi^{2} - 9\chi^{2} \rho^{2} } }} $$
(41)
$$ \varOmega_{\hbox{max} }^{\text{f}} = \frac{1}{{\sqrt {2\xi } }}\sqrt {\sqrt {\xi^{6} + \frac{3}{4}\chi \gamma^{2} } - 3\xi^{3} } $$
(42)
$$ \varOmega_{\hbox{max} }^{\text{z}} = \xi^{3} \sqrt {\frac{{24\chi \rho^{2} - 64\xi^{2} }}{{64\xi^{6} - 60\chi \xi^{4} \rho^{2} + 18\chi^{2} \xi^{2} \rho^{4} - 27\chi^{3} \rho^{6} }}} . $$
(43)

System Transmissibility

Force transmissibility and absolute displacement transmissibility are two crucial factors for evaluating the performance of the isolator. The force transmissibility is the ratio of the dynamic force transmitted to the base and the amplitude ratio of the excitation force, and the absolute displacement transmissibility is the ratio of the absolute displacement of the object to be isolated and the amplitude of the base excitation displacement.

When the QZS systems is excited by the harmonic force excitation, the dimensionless force \( \hat{f}_{\text{t}} \) transmitted to the base includes the dimensionless damping force \( \hat{f}_{{\text{td}}} \) and the dimensionless elastic force \( \hat{f}_{{\text{te}}} \), which can be expressed as

$$ \hat{f}_{\text{t}} = \hat{f}_{{\text{td}}} + \hat{f}_{{\text{te}}} = 2\xi \hat{v}^{\prime } + \chi \hat{v}^{3} . $$
(44)

Substituting Eq. (29) into it can obtain:

$$ \hat{f}_{\text{t}} = - \hat{F}_{{\text{td}}} \sin \left( {\varOmega \tau + \varphi } \right) + \hat{F}_{{\text{te}}} \cos \left( {\varOmega \tau + \varphi } \right), $$
(45)

among them, \( \hat{F}_{{\text{td}}} = 2\mathop \xi \limits_{{}} \varOmega A_{1} \) is the amplitude of the dimensionless damping force \( \hat{f}_{{\text{td}}} \), \( \hat{F}_{{\text{te}}} = 3\chi A_{1}^{3} /4 \) is the amplitude of the dimensionless elastic force \( \hat{f}_{{\text{te}}} \), and the amplitude \( \hat{F}_{\text{t}} \) of the dimensionless force \( \hat{f}_{\text{t}} \) transmitted to the base can be expressed as

$$ \hat{F}_{\text{t}} = \sqrt {\hat{F}_{{\text{td}}}^{2} + \hat{F}_{{\text{te}}}^{2} } = \sqrt {\left( {2\xi \varOmega A_{1} } \right)^{2} + \left( {\frac{3}{4}\chi A_{1}^{3} } \right)^{2} } . $$
(46)

The system’s force transmissibility is

$$ T_{\text{f}} = \frac{{\hat{F}_{\text{t}} }}{{\hat{F}}}. $$
(47)

When the QZS systems is excited by a harmonic displacement, the absolute displacement transmissibility expression of the system is

$$ T_{\text{z}} = \frac{{\left| {\hat{u}} \right|}}{{\left| {\hat{z}} \right|}} = \frac{{\sqrt {A_{1}^{2} + \rho^{2} + 2A_{1} \rho \cos \left( \varphi \right)} }}{{\hat{z}}}, $$
(48)

wherein \( \cos \left( \varphi \right) = \frac{{\frac{3}{4}\chi A_{1}^{3} - A_{1} \varOmega^{2} }}{{\mathop \rho \limits_{{}} \varOmega^{2} }}. \)

Effect of the Damping Ratio, Excitation Amplitude, and Nonlinear Term on the Transmissibility

The effect of the damping ratio on the force transmissibility is shown in Fig. 11. When the excitation force amplitude and the nonlinear term are fixed, the damping ratio ξ gradually increases, and the peak value of the displacement transmissibility gradually decreases. As can be seen from Fig. 12, the initial vibration isolation frequency is the maximum when the damping ratio is the minimum value, which means that the damping effect of the system is poor when the damping ratio is too small. When the damping ratio is the minimum, there is a jump phenomenon. When the damping ratio takes the maximum value, the jumping phenomenon disappears, the initial vibration isolation frequency is the minimum, and the effective vibration isolation range is the largest.

Fig. 11
figure 11

Force transmissibility for various ξ

Full size image
Fig. 12
figure 12

Displacement transmissibility for various ξ

Full size image

As can be seen from Fig. 13, there are two states in the system. The steady state is the upper branch and the lower branch, the middle branch is unstable, and the frequency of the downward jump and the frequency of the upward jump are the bifurcation points of the frequency response of the system. With the decrease of the excitation amplitude, the resonance frequency corresponding to the maximum transmissibility is reduced. Therefore, under the effect of the smaller excitation amplitude, the system can obtain better vibration isolation effect when the excitation amplitude increases sequentially, as shown in Fig. 14. The system’s displacement transmissibility increases with the increase of the excitation amplitude, and when the excitation amplitude is the minimum, the peak of transmissibility is the smallest, and its unstable solution is also the shortest, and the starting frequency of vibration isolation is also smaller.

Fig. 13
figure 13

Force transmissibility for various ρ

Full size image
Fig. 14
figure 14

Displacement transmissibility for various ρ

Full size image

As shown in Figs. 15 and 16, the influence of the nonlinear term χ and the excitation amplitude ρ on the transmissibility of the system are basically the same, and it is mainly concentrated in the vicinity of its resonant frequency. The lower the starting frequency, the larger the isolation frequency range, the smaller the maximum transmissibility of the system, the smaller the unstable area is, and the less harmful it is to the isolated objects, the better the low-frequency vibration isolation performance of the system.

Fig. 15
figure 15

Force transmissibility for various χ

Full size image
Fig. 16
figure 16

Displacement transmissibility for various χ

Full size image

Numerical Simulation

Time Response to a Sinusoidal Wave Excitation

In the previous section, it has been able to get the curve of the transfer rate image. Then, the fourth-order Runge–Kutta method was used for simulation MATLAB. When the input signal is a sine wave, the excitation amplitude is 10 mm and the frequency is 2.5 Hz, and the response curve of the displacement relative to time can be obtained, as shown in Fig. 17. After a short time, the output curve stabilizes. It can be seen that the displacement response curve of the QZS is significantly lower than the excitation wave.

Fig. 17
figure 17

System response under sinusoidal excitation

Full size image

Time Response to an Excitation of Displacement Pulse

By impact to the system [24], the response of this system is shown in Fig. 18. The impact force is 20 N, the bearing mass is 50 kg, and the damping ratio is 0.05. It was found that the QZS systems and the linear system produce approximately the same amplitude when the shock is received under the same conditions, but the amplitude of the QZS system will stabilize after a short time, and tend to zero. Therefore, the QZS isolator is more suitable than the traditional linear isolator in the case of shock vibration.

Fig. 18
figure 18

System response under pulse excitation

Full size image

Time Responses to a Multi-Frequency Wave Excitation

The vibrations to which humans and machinery are subjected often contain multiple frequency components, and the frequency of a single frequency is relatively less. By giving the model a multi-frequency excitation, to observe the response of the system, the following excitation form has been into consideration:

$$ z_{\text{e}} = 5\sin \left( {2\pi \times 1.1t} \right) + 3.5\sin \left( {2\pi \times 1.6t} \right) + 2\cos \left( {2\pi \times 1.2t} \right) + 4\cos \left( {2\pi \times 1.8t} \right). $$
(49)

In this response, the displacement response comparison between the QZS system denoted by the solid line and the traditional system denoted by the dashed line. It can be seen from the Fig. 19 that the QZS systems have a small amplitude; with the time growth, it gradually stabilizes and keeps vibrating at a lower amplitude, but the amplitude of the traditional system increases remarkably.

Fig. 19
figure 19

Displacement response comparison between the QZS system and the traditional system

Full size image

Conclusions

Based on the impact of low-frequency vibration isolation in all aspects of life, a new QZS system was proposed in this paper, and this vibration isolator can control low-frequency vibration effectively. The conclusions are as follows:

  1. 1.

    The stability of the structure can be improved using the spring in the damping mechanism. Therefore, this structure has more flexible operation mode and is more suitable for installation in the mechanical structure with small space. In addition, the QZS system is simple in structure and easy to manufacture, which is beneficial to engineering.

  2. 2.

    In the vibration isolation system, the smaller the transmissibility, the better the vibration isolation performance of the system. By calculating the statics and dynamics, under the excitation of force and displacement, the system transmissibility was found to increase as the excitation amplitude and nonlinear term increase. Meanwhile, when damping ratio is increased, the transmissibility of the system can be reduced.

  3. 3.

    The vibration isolation mechanism designed in this paper is more suitable for low-frequency vibration isolation. Because the numerical simulations show that the QZS systems have faster response and smaller amplitude for sine wave and multi-frequency excitations, which is a more ideal candidate for low-frequency vibration isolation. In addition, compared with the linear system, the QZS system’s amplitude can be quickly weakened under the impulse excitation, so it can play a role in cushioning and damping.

At the same time, this structure provides a reference for the development and promotion of medical rehabilitation machinery and precision vibration damping equipment.