Theoretical Design and Analysis of a Nonlinear Electromagnetic Vibration Isolator with Tunable Negative Stiffness Characteristic

Abstract

Background

A novel tunable negative stiffness nonlinear electromagnetic isolator is presented, it includes a vertical positive stiffness spring, an electromagnetic spring constructed by two permanent magnets and an electromagnet. The electromagnetic isolator can act as a passive isolator or a semi-active control one.

Method

The mathematical expression of system stiffness-current-displacement is derived by analyzing the mechanical characteristics. The motion differential equation under an external harmonic excitation force is established. The amplitude-frequency relationship of the system is deduced by the averaging method. The global dynamic behavior on the Van der pol plane and the force transmissibility are researched.

Results

The results show that the nonlinear electromagnetic isolator with appropriate parameters can enlarge the low frequency isolation range and make the system have better isolation performance in the low frequency band.

Conclusions

The nonlinear electromagnetic isolator with suitable system parameters has the advantages of widening the vibration isolation range and improving the low-frequency vibration isolation effect.

Introduction

In recent years, it is urgent to meet the requirement of low-frequency vibration isolation in the engineering field to reduce waterborne noise. According to the vibration theory, the lower limit of effective vibration isolation frequency of linear vibration isolation system is $\sqrt 2$$\omega_{\text{n}}$, where $\omega_{\text{n}}$ is the natural frequency, which requires that $\omega_{\text{n}}$ of isolation system should be deceased greatly [1]. However, to reduce the system natural frequency of the system means to reduce the system stiffness, and thus a large static deformation will be produced. So it is difficult to meet the needs of low-frequency vibration isolation for the general linear vibration isolation system. To restrain low-frequency vibration effectively, a high-static-low-dynamic stiffness vibration isolator (HSLDS-VI) is studied. The design of the HSLDS-VI structure includes a positive and a negative stiffness mechanism. The negative stiffness mechanism plays a key role in the HSLDS-VI. Many different types of the HSLDS-VI structure are proposed in the literature. A typical structure with oblique springs as a negative stiffness is connected to a vertical spring as a positive stiffness researched in [2,3,4,5]. The Platus [6] used two poles hinged to each other under axial load as a negative stiffness mechanism. The results showed that the negative stiffness mechanisms could cancel the stiffness of power cables connected with payloads. Le et al. [7] designed a new quasi-zero-stiffness vibration isolation system in which the connecting rod acted as a negative stiffness, and it was applied to the vibration reduction of the car seat successfully. Huang et al. [8] proposed a method for designing a quasi-zero stiffness system through connecting a linear spring with a negative stiffness Euler flex beam. Zhou et al. [9] designed a high-static–low-dynamic stiffness vibration isolator (HSLDS-VI) with a cam roller. The design of a quasi-zero-stiffness isolator with equal thickness and variable thickness butterfly spring was proposed in the recent paper [10, 11], and the influence of system parameters on the transmission rate of vibration isolator was studied by the averaging method. Xu et al. [12] used the magnetic spring as a negative stiffness mechanism, and designed a low-frequency vibration isolator with quasi-zero-stiffness characteristics. Sun [13] proposed a high-static–low-dynamic stiffness vibration isolator with scissor-like structure. Carrella et al. [14] put forward a three-magnet negative stiffness mechanism. The basic principle was that two permanent magnets were fixed at the ends of the poles, and the other one which generated negative stiffness was put in the middle of the structure.

The above-mentioned negative stiffness structures belong to the passive pattern of vibration isolation, and their parameters cannot be adjusted. Xu et al. [15] introduced a mechanical device to change the pre-compression of the horizontal spring on the basis of the conventional spring, and obtained an online adjustable negative stiffness mechanism. Zhou et al. [16] designed a tunable negative stiffness vibration isolator using a set of electromagnets and a permanent magnet. The negative stiffness could be adjusted by changing the current. Although these structures can achieve the self-adaptive negative stiffness, the load can only be installed in the fixed position, and its operating range is limited.

The averaging method is an important analysis method for a nonlinear dynamic system [17]. Wang et al. studied the robustness problem of nonlinear systems with state delayed feedback control by this method. The infinite dimensional delay differential equations were reduced to ordinary differential equations so that the periodic solutions of nonlinear vibration systems were solved. It could be extended to a class of linear control systems with small perturbations and weakly bounded nonlinear delay systems [18]. Atay used the average method to study the delay feedback control of the van der Pol equation. The relationship between the limit cycle and the delay time of the system was derived [19]. Stroucken et al. applied the average method to investigate the problem of solving the partial differential equation with small parameters under certain boundary conditions [20]. Bogoliubov et al. investigated the modified method in practical nonlinear oscillators [21, 22]. To improve the calculation effect of the averaging method, Okabe et al. used the elliptic function as the generating function of the method to analyze the Duffing equation with catastrophe and obtained the amplitude–frequency curve. Compared with the shooting method, it is concluded that this method has higher accuracy [23].

In this paper, a new design of a nonlinear electromagnetic vibration isolator with a tunable negative stiffness characteristic is proposed. The isolator can act as a passive or semi-active pattern isolator. It depends on the variation of current. The paper is organized as follows. In the section “Isolator Stiffness Characteristics”, the model of nonlinear electromagnetic vibration isolator is introduced. In the section “Dynamic System Behavior”, the isolator stiffness characteristics are analyzed. The dynamical equation of the system is established and the influence of system parameters on the dynamic characteristics is discussed in the section “Conclusions”. Finally, the conclusions are presented.

Isolator Stiffness Characteristics

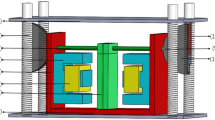
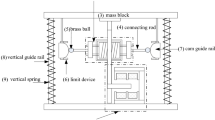
The structure of the nonlinear electromagnetic isolator is shown in Fig. 1. As a negative stiffness mechanism, the electromagnetic spring is composed of three magnets. Three permanent magnets repel each other, and their polarity is shown in Fig. 1. The middle of the permanent magnet is wound around the coil, and its position is fixed. The left and right permanent magnets can slide on the horizontal guide rod. The vertical springs are fixed on the base as a positive stiffness mechanism, and the top is connected with a ringer. Each spring has a vertical guide with a diameter less than the diameter of the spring. The ringer can be slid on the vertical guide through rollers. The supporting platform is connected with the ringer by three supporting rods. The connecting rod connects the electromagnetic spring to the vertical springs.

Fig. 1

Schematic of electromagnetic vibration isolator

The electromagnetic spring force depends on the magnetic flux density, current and distance between the permanent magnets. Although the electromagnetic spring contains the coupling problem between the electromagnetic field and the permanent magnetic field inevitably, this paper only focuses on the dynamic characteristics of vibration isolation system. The coupling between the magnetic fields is not the main content of this study. Therefore, the electromagnetic force is measured by experiment. The experimental conditions are set such that the current changes from 0 A to 2 A at a step size of 0.4 A, and the current direction is shown in Fig. 1. The distance between the permanent magnet and the electromagnet is gradually changed, and the curve of the electromagnetic force with distance is obtained. Repeat this procedure to get a series of data curves as shown in Fig. 2. According to the curve, the approximate formula of the electromagnetic force can be obtained by the application of curve fitting based on Matlab:

$$f_{\text{E}} = w_{1} {\text{e}}^{{\left( {\frac{i}{{w_{2} }} - \frac{d}{{w_{3} }}} \right)}} ,$$

(1)

where i is the current, d is air gap between permanent magnet and electromagnet,$w_{1} = 46.5$, $w_{2} = 2.6$, and $w_{3} = 0.0128 .$

Fig. 2

Measured force curves between PE and EM

The isolator modeling when the system is excited is shown in Fig. 3. When the system reaches the static equilibrium position, the compression amount of the positive stiffness spring element is h and the air gap spacing is $d_{0}$. The coordinate y defines the displacement from the static balance in the vertical direction, and the downward direction is positive. The vertical spring stiffness is k and the connecting rod length is L. The relationship between the system force and the displacement can be expressed as

$$f = - 2k(h + y) + 2f_{\text{E}} \frac{y}{{\sqrt {L^{2} - y^{2} } }}.$$

(2)

Fig. 3

Schematic of isolator when system is excited

Noting that $x = L - \sqrt {L^{2} - y^{2} }$, $d = x + d_{0}$, and substitute Eq. (1) into Eq. (2):

$$f = - 2k(h + y) + 2w_{1} {\text{e}}^{{\left( {\frac{i}{{w_{2} }} - \frac{{d_{0} + L - \sqrt {L^{2} - y^{2} } }}{{w_{3} }}} \right)}} \frac{y}{{\sqrt {L^{2} - y^{2} } }}.$$

(3)

Differentiating Eq. (3), the stiffness $K$ can be obtained:

$$K = - \;2k + \frac{{2w_{1} y^{2} {\text{e}}^{{\left( {\frac{i}{{w_{2} }} - \frac{{d_{0} + L - \sqrt {L^{2} - y^{2} } }}{{w_{3} }}} \right)}} }}{{(L^{2} - y^{2} )^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} }} + \frac{{2w_{1} {\text{e}}^{{\left( {\frac{i}{{w_{2} }} - \frac{{d_{0} + L - \sqrt {L^{2} - y^{2} } }}{{w_{3} }}} \right)}} }}{{\sqrt {L^{2} - y^{2} } }} - \frac{{2w_{1} y^{2} {\text{e}}^{{\left( {\frac{i}{{w_{2} }} - \frac{{d_{0} + L - \sqrt {L^{2} - y^{2} } }}{{w_{3} }}} \right)}} }}{{(L^{2} - y^{2} )w_{3} }}.$$

(4)

Let $y = 0$ and $K = 0$, the relationship between the vertical spring stiffness and the current can be obtained:

$$k = \frac{{2w_{1} {\text{e}}^{{\left( {\frac{i}{{w_{2} }} - \frac{{d_{0} }}{{w_{3} }}} \right)}} }}{{\sqrt {L^{2} - y^{2} } }}.$$

(5)

When the parameters of the vibration isolator meet the Eq. (5), the system will work in a quasi-zero stiffness state at the equilibrium position. The system parameters selected in this article are: $k = 450\;{\text{N/m}}$, $L = 0.15\;{\text{m}}$, $h = 0.05\;{\text{m}}$, and $d_{0} = 0.01\;{\text{m}}$. The current range of the coil is: $0 \le i \le 5\;{\text{A}}$.The relationship between stiffness, current and displacement of vibration isolator given by Eq. (4) is shown in Fig. 4. It can be seen from the figure, under the same displacement, the stiffness increases with the current increasing. The variation of the negative stiffness will change the stiffness of the vibration isolator so that the isolator exhibits different vibration isolation performance.

Fig. 4

Stiffness–current–displacement curves

When the displacement range of the system at the static equilibrium position is narrow, Eq. (3) can be expanded by the Taylor series:

$$f = - \;2kh + \frac{{w_{1} }}{{L^{2} }}\left( {\frac{1}{L} - \frac{1}{{w_{3} }}} \right){\text{e}}^{{^{{\left( {\frac{i}{{w_{2} }} - \frac{{d_{0} }}{{w_{3} }}} \right)}} }} y^{3} .$$

(6)

Differentiating Eq. (6), an approximate expression of the stiffness is obtained:

$$K = 3\frac{{w_{1} }}{{L^{2} }}\left( {\frac{1}{L} - \frac{1}{{w_{3} }}} \right){\text{e}}^{{^{{\left( {\frac{i}{{w_{2} }} - \frac{{d_{0} }}{{w_{3} }}} \right)}} }} y^{2} .$$

(7)

The comparison of force displacement curves between the exact expressions given by Eqs. (3) and (4) and the approximate expressions given by Eqs. (4) and (5) are shown in Fig. 5. It can be seen from the figure that the error between the exact expression and approximate expression increases with the increase of displacement. When the displacement is small, the error is neglected, so the third-order Taylor series expansion can fit the exact expression in the vicinity of the static equilibrium position.

Fig. 5

Comparison between approximate and exact expressions of force and stiffness

Dynamic System Behavior

Dynamic Modeling

The dynamical model of the system under a vertical harmonic force is shown in Fig. 6, and the dynamical equation of the system is:

$$M\ddot{Z} + c\dot{Z} - f = F_{h} \cos (\varOmega T).$$

(8)

Fig. 6

Dynamical system model

Introducing the non-dimensional parameters, $\varOmega_{0} = \sqrt {{k \mathord{\left/ {\vphantom {k M}} \right. \kern-0pt} M}}$, $\varOmega = \varOmega_{0} \omega$, $\xi = {c \mathord{\left/ {\vphantom {c {\sqrt {Mk} }}} \right. \kern-0pt} {\sqrt {Mk} }}$, $t = \varOmega_{0} T$, and $F = {{F_{h} } \mathord{\left/ {\vphantom {{F_{h} } {(kh)}}} \right. \kern-0pt} {(kh)}}$: $\gamma = \frac{{w_{1} h^{2} }}{{kL^{2} }}\left( {\frac{1}{{w_{3} }} - \frac{1}{L}} \right){\text{e}}^{{^{{\left( {\frac{i}{{w_{2} }} - \frac{{d_{0} }}{{w_{3} }}} \right)}} }}$.

Equation (8) becomes:

$$\ddot{z} + \xi \dot{z} + \gamma z^{3} = F\cos (\omega t).$$

(9)

Assuming that the basic solution of the system under linear condition is

$$z(t) = a\cos (\omega t) + b\sin (\omega t).$$

(10)

Differentiating Eq. (10):

$$z^{\prime}(t) = b\omega \cos (\omega t) - a\omega \sin (\omega t).$$

(11)

In the nonlinear condition, due to the complexity of vibration, the amplitude and phase of the system are considered as time-varying parameters. The expression is:

$$z(t) = a(t)\cos (\omega t) + b(t)\sin (\omega t).$$

(12)

At the same time, it is assumed that the vibration velocity of the vibration system has the same form as Eq. (11):

$$z^{\prime}(t) = \omega b(t)\cos (\omega t) - \omega a(t)\sin (\omega t).$$

(13)

Differentiating Eq. (12):

$$z^{\prime}(t) = a^{\prime}(t)\cos (\omega t) - \omega a(t)\sin (\omega t) + b^{\prime}(t)\sin (\omega t) + \omega b(t)\cos (\omega t).$$

(14)

Combining Eqs. (13) and (14), we get:

$$a^{\prime}(t)\cos (\omega t) + b^{\prime}(t)\sin (\omega t) = 0.$$

(15)

Differentiating Eq. (13), the second derivative form is obtained:

$$z^{\prime\prime}(t) = - \;\omega a^{\prime}(t)\sin (\omega t) - \omega^{2} a(t)\cos (\omega t) + \omega b^{\prime}(t)\cos (\omega t) - \omega^{2} b(t)\sin (\omega t).$$

(16)

Inserting Eqs. (13) and (16) into Eq. (9), we obtain:

$$\begin{aligned} & \cos (\omega t)\left( \xi \right.a^{\prime}(t) - \omega^{2} a(t) + \omega b^{\prime}(t) + \xi \omega b(t) - \left. F \right) + \gamma b^{3} (t)\sin^{3} (\omega t) \\ & \quad + \sin (\omega t)\left( \xi \right.b^{\prime}(t) - \omega a^{\prime}(t) - \xi \omega a(t) - \omega^{2} \left. {b(t)} \right) + \gamma a^{3} (t)\cos^{3} (\omega t) \\ & \quad + \;3\gamma a^{2} (t)b(t)\sin (\omega t)\cos^{2} (\omega t) + 3\gamma a(t)b^{2} (t)\sin^{2} (\omega t)\cos (\omega t) = 0. \\ \end{aligned}$$

(17)

Combining Eqs. (15) and (17), the two equations are obtained:

$$\begin{aligned} a^{\prime}(t) & = \frac{1}{\omega }\sin (\omega t)(a(t)(\gamma a^{3} (t)\cos^{3} (\omega t) + 3\gamma b^{2} (t)\sin^{2} (\omega t)\cos (\omega t) - \xi \omega \sin (\omega t) - \omega^{2} \cos (\omega t)) \\ & \quad + \;3\gamma a^{2} (t)b(t)\sin (\omega t)\cos^{2} (\omega t) + \gamma b^{3} (t)\sin^{3} (\omega t) - F\cos (\omega t) + b(t)(\xi \omega \cos (\omega t) - \omega^{2} \sin (\omega t))), \\ \end{aligned}$$

(18)

$$\begin{aligned} b^{\prime}(t) & = - \frac{1}{\omega }\cos (\omega t)(a(t)(\omega^{2} \cos (\omega t) - \xi \omega \sin (\omega t) + 3\gamma b^{2} (t)\sin^{2} (\omega t)\cos (\omega t)) + \gamma b^{3} (t)\sin^{3} (\omega t) \\ & \quad + \;3\gamma a^{2} (t)b(t)\sin (\omega t)\cos^{2} (\omega t) - F\cos (\omega t) + \gamma a^{3} (t)\cos^{3} (\omega t) + b(t)(\xi \omega \cos (\omega t) - \omega^{2} \sin (\omega t))). \\ \end{aligned}$$

(19)

To facilitate the analysis, transforming the non-autonomous system into an autonomous system, let $\omega t = \varphi_{0}$:

$$\begin{aligned} a^{\prime}(t) & = \frac{1}{\omega }\sin (\varphi_{0} )(a(t)(\gamma a^{3} (t)\cos^{3} (\varphi_{0} ) + 3\gamma b^{2} (t)\sin^{2} (\varphi_{0} )\cos (\varphi_{0} ) - \xi \omega \sin (\varphi_{0} ) - \omega^{2} \cos (\varphi_{0} )) \\ & \quad + \;3\gamma a^{2} (t)b(t)\sin (\varphi_{0} )\cos^{2} (\varphi_{0} ) + \gamma b^{3} (t)\sin^{3} (\varphi_{0} ) - F\cos (\varphi_{0} ) + b(t)(\xi \omega \cos (\varphi_{0} ) - \omega^{2} \sin (\varphi_{0} ))), \\ \end{aligned}$$

(20)

$$\begin{aligned} b^{\prime}(t) & = - \frac{1}{\omega }\cos (\varphi_{0} )(a(t)(\omega^{2} \cos (\varphi_{0} ) - \xi \omega \sin (\varphi_{0} ) + 3\gamma b^{2} (t)\sin^{2} (\varphi_{0} )\cos (\varphi_{0} )) + \gamma b^{3} (t)\sin^{3} (\varphi_{0} ) \\ & \quad + \;3\gamma a^{2} (t)b(t)\sin (\varphi_{0} )\cos^{2} (\varphi_{0} ) - F\cos (\varphi_{0} ) + \gamma a^{3} (t)\cos^{3} (\varphi_{0} ) + b(t)(\xi \omega \cos (\varphi_{0} ) - \omega^{2} \sin (\varphi_{0} ))). \\ \end{aligned}$$

(21)

Assuming that the amplitude $a(t)$ and $b(t)$ are slow variation parameters, the right side of the Eqs. (20) and (21) is integrated at [0, 2π] and averaged over the interval. We get:

$$\left\{ \begin{array}{l} a^{\prime}(t) = - \frac{{3\gamma a^{2} (t)b(t)}}{8\omega } + \frac{\xi a(t)}{2} + \frac{{3\gamma b^{3} (t)}}{8\omega } - \frac{\omega b(t)}{2} \hfill \\ b^{\prime}(t) = - \frac{{3\gamma a(t)b^{2} (t)}}{8\omega } + \frac{\omega a(t)}{2} - \frac{{3\gamma a^{3} (t)}}{8\omega } - \frac{\xi b(t)}{2} + \frac{F}{2\omega } \hfill \\ \end{array} \right..$$

(22)

To facilitate analysis, $a(t)$ and $b(t)$ are expressed in polar coordinates: $a(t) = A\cos \varphi$, $b(t) = A\sin \varphi$, and they are inserted into Eq. (12). The following equations are obtained:

$$\frac{A\xi \cos (\varphi )}{2} + \frac{A\omega \sin (\varphi )}{2} - \frac{{3A^{3} \gamma \cos^{2} (\varphi )\sin (\varphi )}}{8\omega } - \frac{{3A^{3} \gamma \sin^{3} (\varphi )}}{8\omega } + A^{\prime}\cos (\varphi ) - A\varphi^{\prime}\sin (\varphi ) = 0,$$

(23)

$$\begin{aligned} & - \frac{F}{2\omega } - \frac{A\omega \cos (\varphi )}{2} + \frac{{3A^{3} \gamma \cos^{3} (\varphi )}}{8\omega } + \frac{A\xi \sin (\varphi )}{2} + \frac{{3A^{3} \gamma \cos (\varphi )\sin^{2} (\varphi )}}{8\omega } \\ & \quad + \;A^{\prime}\sin (\varphi ) + A\varphi^{\prime}\cos (\varphi ) = 0. \\ \end{aligned}$$

(24)

So $A^{\prime}$ and $\varphi^{\prime}$ are found to be

$$\left\{ \begin{array}{l} A^{\prime} = \frac{ - \;A\xi \omega + F\sin (\varphi )}{2\omega } \hfill \\ \varphi^{\prime} = \frac{{ - \;3A^{3} \gamma + 4A\omega^{2} + 4F\cos (\varphi )}}{8A\omega } \hfill \\ \end{array} \right..$$

(25)

The equilibrium point on the van der Pol plane should be satisfied:

$$\left\{ \begin{array}{l} \frac{ - \;A\xi \omega + F\sin (\varphi )}{2\omega } = 0 \hfill \\ \frac{{ - \;3A^{3} \gamma + 4A\omega^{2} + 4F\cos (\varphi )}}{8A\omega } = 0 \hfill \\ \end{array} \right..$$

(26)

Removing $\varphi$ and using $\sin^{2} (\varphi ) + \cos^{2} (\varphi ) = 1$, the amplitude–frequency expression $A - \omega$ can be obtained:

$$\frac{{A^{2} (3\gamma A^{2} - 4\omega^{2} )^{2} }}{{16F^{2} }} + \frac{{\xi^{2} A^{2} \omega^{2} }}{{F^{2} }} = 1.$$

(27)

Amplitude–Frequency Characteristic

Based on the above derivation, the change influence of the system parameters on the amplitude–frequency characteristic curve can be analyzed.

• 1. When parameters $\xi = 0.4$ and $\gamma = 4$, the excitation parameter F is increased from 0.5 to 2, the amplitude–frequency curve is plotted using Eq. (27) shown in Fig. 7. It can be seen that the system exhibits obvious nonlinearity and the response amplitude increases as the excitation force amplitude F increases.

  Fig. 7

  

  Amplitude–frequency curve of system when parameter F is varied

• 2. When parameters $\gamma = 4$, $F = 1$, and the damping ratio $\xi$ is increased from 0.1 to 0.4, the amplitude–frequency characteristic given by Eq. (27) is plotted in Fig. 8. It can be seen that the resonance amplitude of the curve is restrained as the damping ratio increases.

  Fig. 8

  

  Amplitude–frequency curve of system when parameter $\xi$ is varied

• 3. When parameters $\xi = 0.1$ and $F = 1$, the system parameter $\gamma$ is increased from 1 to 4, and the amplitude–frequency curves are shown in Fig. 9. With the increase of parameter $\gamma$, the system nonlinearity is gradually enhanced, and the response peak is obviously reduced.

  Fig. 9

  

  Amplitude–frequency curve of system when parameter $\gamma$ is varied

The Force Transmissibility Analysis

In the vibration isolation system, the force transmission rate index is generally used to evaluate the vibration isolation effect. The transmitted force as shown in Fig. 6 is given as

$$F_{t} = \xi \dot{z} + \gamma z^{3} .$$

(28)

The magnitude of the transmitted force is obtained:

$$\left| {F_{\text{t}} } \right| = \sqrt {\left( {\xi \omega A} \right)^{2} + \left( {\frac{3}{4}\gamma A^{3} } \right)^{2} } .$$

(29)

Thus we get the force transmissibility:

$$T = {\raise0.7ex\hbox{${\sqrt {\left( {\xi \omega A} \right)^{2} + \left( {\frac{3}{4}\gamma A^{3} } \right)^{2} } }$} \!\mathord{\left/ {\vphantom {{\sqrt {\left( {\xi \omega A} \right)^{2} + \left( {\frac{3}{4}\gamma A^{3} } \right)^{2} } } {F_{h} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${F_{h} }$}}.$$

(30)

The force transmissibility of the linear system is given by [24]

$$T_{\text{L}} = \sqrt {\frac{{1 + 4\xi^{2} \varOmega^{2} }}{{(1 - \varOmega^{2} )^{2} + 4\xi^{2} \varOmega^{2} }}} .$$

(31)

It can be seen from the Eq. (30) that the expression of the force transmissibility of the electromagnetic vibration isolation system is different from that of the linear system. Besides the parameters of the system, it changes under the effect of an external excitation force. This is because in the nonlinear system, the relationship between the response amplitude and the external excitation force is nonlinear. The influence of system parameters and external excitation parameters on the system force transmissibility will be described by a numerical simulation.

• 1. When the system parameters $\xi = 0.1$ and $\gamma = 4$, the force transmissibility given by Eq. (30) for several values F is plotted in Fig. 10. When the force amplitude is 0.1, the resonance peak is 13.8 and the starting frequency is 0.8. When the force amplitude is varied to 0.5, the resonance peak is 26.9 and the starting frequency is 1.3. As the force amplitude increased to 1, the resonance peak is 33.2 and the starting frequency is 1.6. It can be seen that the resonance peak and the starting frequency of vibration isolation gradually increase with the increase of the excitation force amplitude F. The effective frequency range of vibration isolation is reduced.

  Fig. 10

  

  Force transmissibility curve when parameter F is varied

• 2. When the system parameters $F = 1$ and $\gamma = 4$, the force transmissibility given by Eq. (30) for different values $\xi$ is as shown in Fig. 11. When the damping ratio $\xi = 0.05$, the curve bents towards the right trend obviously, and the jump phenomenon occurs. At this time, the expected vibration isolation effect occurs. When the damping ratio $\xi$ is varied to 0.2, the force transmissibility near the resonant peak decreases significantly, and the effective frequency range of vibration isolation is widened, but the vibration isolation performance in the high-frequency region becomes worse. As the damping ratio $\xi$ increased to 0.4, the jumping phenomenon disappears, and the low-frequency vibration isolation performance is excellent, but the high-frequency vibration isolation is further deteriorated. Therefore, with the increase of the damping parameters, the jump range of the nonlinear electromagnetic vibration isolation system is gradually narrowed.

  Fig. 11

  

  Force transmissibility curve when parameter $\xi$ is varied

• 3. When the system parameters $F = 1$ and $\xi = 0.1$, the force transmissibility given by Eq. (30) for several values $\gamma$ is as shown in Fig. 12. When the parameter $\gamma$ is 0.1, the resonance peak is 33.6 and the starting frequency is 0.5. When the force amplitude is changed to 1, the resonance peak is 44.7 and the starting frequency is 0.9. As the force amplitude increased to 4, the resonance peak is 55.1 and the starting frequency is 1.6. It can be seen that with the increase of the system parameter $\gamma$, the degree of right bending increases gradually, and the resonant peak and the starting frequency of the vibration isolation gradually increase.

  Fig. 12

  

  Force transmissibility curve when parameter $\gamma$ is varied

The force transmissibility of a linear vibration system given by Eq. (31) is also plotted in Figs. 10, 11 and 12. It can be seen that the novel electromagnetic nonlinear vibration system outperforms the linear system. First, the jump-down frequency of all the electromagnetic nonlinear vibration system is smaller than the natural frequency of the linear vibration system. Second, the starting frequency of the electromagnetic nonlinear vibration system is smaller than that of linear vibration system. Third, the maximum amplitudes of force transmissibility of all the electromagnetic nonlinear vibration system are less than that of linear vibration system. According to the analysis above, it is possible to obtain a good low-frequency vibration isolation performance by designing the appropriate system parameters.

Conclusions

In this paper, a new structure of vibration isolator using an electromagnetic spring consisted of a permanent magnet and electromagnet is proposed. The vibration isolator can be used as a passive isolator or a semi-active isolator. If the current is zero, the isolator works in a passive pattern. If the current is not zero, the magnitude of the negative stiffness varies with the current. The approximate expression of electromagnetic force is obtained by the experiment. Through the static analysis, the system will achieve quasi-zero-stiffness characteristics at the equilibrium position when the system parameters meet certain conditions. The dynamic characteristics of vibration isolation system are analyzed by the averaging method. The influence of system parameters on amplitude–frequency characteristics is obtained. Through the force transmissibility, the study shows the nonlinear electromagnetic isolator with suitable system parameters outperforms the linear system, and has the advantages of widening the vibration isolation range and improving the low-frequency vibration isolation effect.