On constrained minimization, variational inequality and split feasibility problem via new iteration scheme in Banach spaces

Abstract

The motive of this paper is to propose a new iterative algorithm for evaluating a solution of constrained minimization problem, variational inequality and split feasibility problem and common fixed point of two generalized $\alpha$-nonexpansive mappings. We obtain few convergence results in the setting of uniformly convex Banach space. We also present some numerical examples for supporting our main results and to demonstrate the convergence behaviour of the obtained process.

1 Introduction

One of the fast growing topic of nonlinear functional analysis is fixed point theory as its ground of application varies from game theory, engineering and natural sciences. The nature of many practical problems suggests an iterative approach to the solution so that in the last few years many iterative processes have been obtained in different domains to approximate the fixed points of numerous classes of mappings having applications in convex minimization, differential inclusions, fractals, discontinuous differential equations, solutions of ordinary and partial differential equation, optimal control, computing homology of maps, variational inequality, split feasibility problem, digital imaging and economics [1,2,3,4,5]. Ocejo [6] applied Banach fixed point theorem in Finance, Matta et al. [7], Ege and Karaca [8], Dolhare and Nalawade [9] did application in digital imaging, Yambangwai et al. [10] applied fixed point iteration procedure for de-blurring of image, Kitisak et al. [11] applied hybrid sub gradient method to signal recovery problem. Recently, Garodia and Uddin [12, 13] obtained two fixed point iterations and utilized them to solve delay differential equation and split feasibility problem. Also, owing to the fact that approximating the common fixed points and minimization problems are inter-related, several researchers have obtained various results for the same (cf. [14,15,16,17]).

Banach Contraction Principle is one of the prime result of fixed point theory. The early findings in fixed point theory revolve around generalization of Banach Contraction Principle. The whole mathematics community had to wait for the first fixed point theorem for nonexpansive mappings for 43 years. Let ${\tilde{G}}$ be a nonempty convex closed subset of a uniformly convex Banach space ${\tilde{J}}.$ Then, a mapping ${\tilde{P}}: {\tilde{G}}\rightarrow {\tilde{G}}$ is termed as nonexpansive if $\Vert {\tilde{P}}{\tilde{a}} - {\tilde{P}}{\tilde{v}}\Vert \le \Vert {\tilde{a}} - {\tilde{v}}\Vert$ for all ${\tilde{a}}, {\tilde{v}} \in {\tilde{G}}.$ If ${\tilde{P}}{\tilde{a}} = {\tilde{a}},$ where ${\tilde{a}} \in {\tilde{G}}$ then ‘${\tilde{a}}$’ is called the fixed point of ${\tilde{P}}.$ We will denote the set of fixed points of ${\tilde{P}}$ by ${\tilde{F}}({\tilde{P}}).$ ${\tilde{P}}$ is called quasi-nonexpansive if ${\tilde{F}}({\tilde{P}})\ne \emptyset$ and $\Vert {\tilde{P}}{\tilde{a}} - {\tilde{q}}\Vert \le \Vert {\tilde{a}} - {\tilde{q}}\Vert$ for all ${\tilde{a}} \in {\tilde{G}}$ and ${\tilde{q}} \in {\tilde{F}}({\tilde{P}}).$ It is worth mentioning that every nonexpansive mapping with a fixed point is quasi-nonexpansive mapping. In 1965, Browder [18], Göhde [19] and Kirk [20] gave three basic existence results in respect of nonexpansive mappings.

Following this, many mathematicians have introduced various generalizations and extensions of nonexpansive mappings. In 2008, Suzuki [21] obtained a new generalization of nonexpansive mappings and called the defining condition as Condition (C) which is also referred as Suzuki generalized nonexpansive mappings. A mapping ${\tilde{P}}: {\tilde{G}}\rightarrow {\tilde{G}}$ defined on a nonempty subset ${\tilde{G}}$ of a Banach space ${\tilde{J}}$ is said to satisfy the Condition (C) if

$$\begin{aligned} \frac{1}{2} \Vert {\tilde{a}} - {\tilde{P}}{\tilde{a}}\Vert \le \Vert {\tilde{a}} - {\tilde{v}}\Vert \Rightarrow \Vert {\tilde{P}}{\tilde{a}} - {\tilde{P}}{\tilde{v}}\Vert \le \Vert {\tilde{a}} - {\tilde{v}}\Vert \end{aligned}$$

for all ${\tilde{a}}$, ${\tilde{v}} \in {\tilde{G}}.$ Suzuki proved that the mappings satisfying the Condition (C) is weaker than nonexpansive and also obtained few results related to the existence of fixed points for such mappings.

Later, in 2011, Aoyama and Kohsaka [22] introduced another generalization of nonexpansive mappings, namely, $\alpha$-nonexpansive mappings and obtained few convergence results. A mapping ${\tilde{P}}:{\tilde{G}}\rightarrow {\tilde{G}}$ is said to be $\alpha$-nonexpansive if there exists an $\alpha \in [0, 1)$ such that for all ${\tilde{a}}, {\tilde{v}} \in {\tilde{G}},$

$$\begin{aligned} \Vert {\tilde{P}}{\tilde{a}} - {\tilde{P}}{\tilde{v}}\Vert ^2 \le \alpha \Vert {\tilde{P}}{\tilde{a}} - {\tilde{v}}\Vert ^2 + \alpha \Vert {\tilde{a}} - {\tilde{P}}{\tilde{v}}\Vert ^2 +(1 - 2\alpha )\Vert {\tilde{a}} - {\tilde{v}}\Vert ^2. \end{aligned}$$

Now, every nonexpansive mapping is 0-nonexpansive mapping and every $\alpha$-nonexpansive mapping with a fixed point is quasi-nonexpansive. It is worth mentioning that nonexpansive mappings are always continuous but mappings satisfying Condition (C) or $\alpha$-nonexpansive mappings need not be continuous in general.

In 2017, Pant and Shukla [23] introduced the class of generalized $\alpha$-nonexpansive mappings. A mapping ${\tilde{P}}:{\tilde{G}}\rightarrow {\tilde{G}}$ is said to be generalized $\alpha$-nonexpansive if there exists an $\alpha \in [0, 1)$ such that

$$\begin{aligned} \frac{1}{2} \Vert {\tilde{a}} - {\tilde{P}}{\tilde{a}}\Vert \le \Vert {\tilde{a}} - {\tilde{v}}\Vert \Rightarrow \Vert {\tilde{P}}{\tilde{a}} - {\tilde{P}}{\tilde{v}}\Vert \le \alpha \Vert {\tilde{P}}{\tilde{a}} - {\tilde{v}}\Vert + \alpha \Vert {\tilde{P}}{\tilde{v}} - {\tilde{a}}\Vert + (1 - 2\alpha )\Vert {\tilde{a}} - {\tilde{v}}\Vert \end{aligned}$$

for all ${\tilde{a}}$, ${\tilde{v}} \in {\tilde{G}}.$ They established few existence and convergence theorems for the newly introduced class of mappings. Clearly, every mapping satisfying the Condition (C) is a generalized $\alpha$-nonexpansive mapping.

Motivated by the recent development, we propose a new iteration process to approximate common fixed points of two generalized $\alpha$-nonexpansive mappings. Let ${\tilde{P}}, {\tilde{S}} : {\tilde{G}} \rightarrow {\tilde{G}}$ be two generalized $\alpha$-nonexpansive mappings, then we define our process as follows:

$$\begin{aligned} {{\left\{ \begin{array}{ll} {\tilde{u}}_1 \in {\tilde{G}} \\ {\tilde{w}}_k = (1 - \eta _k){\tilde{u}}_k + \eta _k{\tilde{P}}{\tilde{u}}_k \\ {\tilde{v}}_k = (1 - \theta _k){\tilde{S}}{\tilde{u}}_k + \theta _k{\tilde{w}}_k \\ {\tilde{u}}_{k+1} =(1 - \rho _k){\tilde{S}}{\tilde{w}}_k + \rho _k{\tilde{P}}{\tilde{v}}_k, k \in {\mathbb {N}} \end{array}\right. }} \end{aligned}$$

(1.1)

where $\{\eta _k\}$, $\{\theta _k\}$ and $\{\rho _k\}$ are sequences in (0, 1).

The main aim of this paper is to obtain an iteration method for approximating common fixed points of two generalized $\alpha$-nonexpansive mappings and to obtain some weak and strong convergence results in Banach space. We also present non trivial numerical examples to illustrate the convergence behaviour and advantages of the proposed method. In the last section, we discuss about the solution of constrained minimization problem, variational inequality and split feasibility problem using our newly introduced iterative algorithm.

2 Preliminaries

In this section, we collect some basic definitions and needed results.

Definition 2.1

A Banach space ${\tilde{J}}$ is called as uniformly convex if for each $\epsilon \in (0, 2]$ and for ${\tilde{u}}, {\tilde{v}} \in {\tilde{J}}$ with $\Vert {\tilde{u}}\Vert \le 1$, $\Vert {\tilde{v}}\Vert \le 1$ and $\Vert {\tilde{u}} - {\tilde{v}}\Vert > \epsilon$ there is a $\delta > 0$ , such that

$$\begin{aligned} \Big \Vert \frac{{\tilde{u}} + {\tilde{v}}}{2} \Big \Vert < 1 - \delta . \end{aligned}$$

Definition 2.2

A Banach space ${\tilde{J}}$ is called to satisfy the Opial’s condition if for any sequence $\{{\tilde{u}}_k\}$ in ${\tilde{J}}$ with ${\tilde{u}}_k \rightharpoonup {\tilde{u}}$ where ${\tilde{u}} \in {\tilde{J}}$ implies that

$$\begin{aligned} \limsup _{k\rightarrow \infty } \Vert {\tilde{u}}_k - {\tilde{u}}\Vert < \limsup _{k\rightarrow \infty } \Vert {\tilde{u}}_k - {\tilde{v}}\Vert \end{aligned}$$

for all ${\tilde{v}} \in {\tilde{J}}$ with ${\tilde{v}} \ne {\tilde{u}}.$

A mapping ${\tilde{P}} : {\tilde{G}} \rightarrow {\tilde{G}}$ is demiclosed at ${\tilde{v}} \in {\tilde{J}}$ if for each sequence $\{{\tilde{u}}_k\}$ in ${\tilde{G}}$ and each ${\tilde{u}} \in {\tilde{J}}$, ${\tilde{u}}_k \rightharpoonup {\tilde{u}}$ and ${\tilde{P}}{\tilde{u}}_k \rightarrow {\tilde{v}}$ imply that ${\tilde{u}} \in {\tilde{G}}$ and ${\tilde{P}}{\tilde{u}} = {\tilde{v}}.$

Let ${\tilde{G}}$ be a nonempty convex closed subset of a Banach ${\tilde{J}}$, and let $\{{\tilde{u}}_k\}$ be a bounded sequence in ${\tilde{J}}$. For ${\tilde{u}} \in {\tilde{J}}$ we write:

$$\begin{aligned} r({\tilde{u}},\{{\tilde{u}}_k\})=\limsup \limits _{k\rightarrow \infty }\Vert {\tilde{u}} - {\tilde{u}}_{n}\Vert . \end{aligned}$$

The asymptotic radius of $\{{\tilde{u}}_k\}$ relative to ${\tilde{G}}$ is given by

$$\begin{aligned} r({\tilde{G}}, \{{\tilde{u}}_k\})=\inf \{r({\tilde{u}}, \{{\tilde{u}}_k\}):{\tilde{u}}~\in {\tilde{G}}\}, \end{aligned}$$

and the asymptotic center $A({\tilde{G}}, \{{\tilde{u}}_k\})$ of $\{{\tilde{u}}_k\}$ is defined as:

$$\begin{aligned} A({\tilde{G}}, \{{\tilde{u}}_k\})=\{{\tilde{u}} \in {\tilde{G}}: r({\tilde{u}}, \{{\tilde{u}}_k\})=r({\tilde{G}}, \{{\tilde{u}}_k\})\}. \end{aligned}$$

It is well known that, $A({\tilde{G}}, \{{\tilde{u}}_k\})$ consists of exactly one unique point when ${\tilde{J}}$ is uniformly convex.

Now, we list an important lemma which was given by Schu [24].

Lemma 2.3

Let ${\tilde{J}}$ be a uniformly convex Banach space and $\{{\tilde{t}}_k\}$ be any sequence such that $0< p \le {\tilde{t}}_k \le q < 1$ for some $p, q \in {\mathbb {R}}$ and for all $k \ge 1.$ Let $\{{\tilde{u}}_k\}$ and $\{{\tilde{v}}_k\}$ be any two sequences of ${\tilde{J}}$ such that $\limsup \limits _{k\rightarrow \infty }\Vert {\tilde{u}}_k\Vert \le r$, $\limsup \limits _{k\rightarrow \infty }\Vert {\tilde{v}}_k\Vert \le r$ and $\limsup \limits _{k\rightarrow \infty }\Vert {\tilde{t}}_k{\tilde{u}}_k + (1-{\tilde{t}}_k){\tilde{v}}_k\Vert = r$ for some $r \ge 0.$ Then, $\lim \limits _{k\rightarrow \infty }\Vert {\tilde{u}}_k - {\tilde{v}}_k\Vert = 0.$

Now, we recall some important results involving generalized $\alpha$-nonexpansive mappings.

Lemma 2.4

[23] Let ${\tilde{G}}$ be a nonempty subset of a Banach space ${\tilde{J}}$ and ${\tilde{P}}: {\tilde{G}}\rightarrow {\tilde{G}}$ a generalized $\alpha$-nonexpansive mapping. Then,

• (i) ${\tilde{F}}({\tilde{P}})$ is closed. Further, if ${\tilde{J}}$ is strictly convex and ${\tilde{G}}$ is convex, then ${\tilde{F}}({\tilde{P}})$ is convex.

• (ii) If ${\tilde{F}}({\tilde{P}}) \ne \emptyset$, then ${\tilde{P}}$ is quasi-nonexpansive.

• (iii)
  $$\begin{aligned} \Vert {\tilde{u}} - {\tilde{P}}{\tilde{v}}\Vert \le \frac{3+\alpha }{1 - \alpha }\Vert {\tilde{u}} - {\tilde{P}}{\tilde{u}}\Vert + \Vert {\tilde{u}} - {\tilde{v}}\Vert \end{aligned}$$

  for all ${\tilde{u}}$, ${\tilde{v}} \in {\tilde{G}}.$

Lemma 2.5

[23] Let ${\tilde{P}}$ be a generalized $\alpha$-nonexpansive mapping defined on a nonempty closed subset ${\tilde{G}}$ of a Banach space ${\tilde{J}}$ with the Opial property. If a sequence $\{{\tilde{u}}_k\}$ converges weakly to ${\tilde{w}}$ and $\lim \limits _{k\rightarrow \infty }\Vert {\tilde{P}}{\tilde{u}}_k - {\tilde{u}}_k\Vert = 0,$ then ${\tilde{P}}{\tilde{w}} = {\tilde{w}}$. That is, $I - {\tilde{P}}$ is demiclosed at zero.

3 Convergence Results

First, we prove few lemmas which will be useful in obtaining convergence results.

Lemma 3.1

Let ${\tilde{P}}$ and ${\tilde{S}}$ be two generalized $\alpha$-nonexpansive mappings which are defined on a nonempty convex closed subset ${\tilde{G}}$ of a Banach space ${\tilde{J}}$ with ${\tilde{F}}({\tilde{P}}) \cap {\tilde{F}}({\tilde{S}}) \ne \emptyset .$ Let $\{{\tilde{u}}_k\}$ be the iterative sequence defined by the iteration process (1.1). Then, $\lim \limits _{k\rightarrow \infty } \Vert {\tilde{u}}_k - {\tilde{q}}\Vert$ exists for all ${\tilde{q}} \in {\tilde{F}}({\tilde{P}}) \cap {\tilde{F}}({\tilde{S}}).$

Proof

Let ${\tilde{q}} \in {\tilde{F}}({\tilde{P}}) \cap {\tilde{F}}({\tilde{S}}).$ By Lemma 2.4(ii), ${\tilde{P}}$ and ${\tilde{S}}$ are quasi-nonexpansive mappings, so we have

$$\begin{aligned} \begin{array}{lll} \Vert {\tilde{w}}_k - {\tilde{q}}\Vert &{}=&{} \Vert (1 - \eta _k){\tilde{u}}_k + \eta _k{\tilde{P}}{\tilde{u}}_k - {\tilde{q}}\Vert \\ &{}\le &{} (1 - \eta _k)\Vert {\tilde{u}}_k - {\tilde{q}} \Vert + \eta _k\Vert {\tilde{P}}{\tilde{u}}_k - {\tilde{q}}\Vert \\ &{}\le &{} (1 - \eta _k)\Vert {\tilde{u}}_k - {\tilde{q}} \Vert + \eta _k \Vert {\tilde{u}}_k - {\tilde{q}}\Vert \\ &{}=&{} \Vert {\tilde{u}}_k - {\tilde{q}}\Vert \end{array} \end{aligned}$$

(3.1)

and

$$\begin{aligned} \begin{array}{lll} \Vert {\tilde{v}}_k - {\tilde{q}}\Vert &{}=&{} \Vert (1 - \theta _k)S{\tilde{u}}_k + \theta _k{\tilde{w}}_k - {\tilde{q}}\Vert \\ &{}\le &{} (1 - \theta _k)\Vert {\tilde{S}}{\tilde{u}}_k - {\tilde{q}} \Vert + \theta _k\Vert {\tilde{w}}_k - {\tilde{q}}\Vert \\ &{}\le &{} (1 - \theta _k)\Vert {\tilde{u}}_k - {\tilde{q}} \Vert + \theta _k \Vert {\tilde{u}}_k - {\tilde{q}}\Vert \\ &{}=&{} \Vert {\tilde{u}}_k - {\tilde{q}}\Vert . \end{array} \end{aligned}$$

(3.2)

Using (3.1) and (3.2), we obtain

$$\begin{aligned} \begin{array}{lll} \Vert {\tilde{u}}_{k+1} - {\tilde{q}}\Vert &{}=&{} \Vert (1 - \rho _k){\tilde{S}}{\tilde{w}}_k + \rho _k{\tilde{P}}{\tilde{v}}_k - {\tilde{q}}\Vert \\ &{}\le &{} (1 - \rho _k)\Vert {\tilde{S}}{\tilde{w}}_k - {\tilde{q}} \Vert + \rho _k\Vert {\tilde{P}}{\tilde{v}}_k - {\tilde{q}}\Vert \\ &{}\le &{} (1 - \rho _k)\Vert {\tilde{w}}_k - {\tilde{q}} \Vert + \rho _k \Vert {\tilde{v}}_k - {\tilde{q}}\Vert \\ &{}\le &{} (1 - \rho _k)\Vert {\tilde{u}}_k - {\tilde{q}}\Vert + \rho _k \Vert {\tilde{u}}_k - {\tilde{q}}\Vert \\ &{}=&{} \Vert {\tilde{u}}_k - {\tilde{q}}\Vert \end{array} \end{aligned}$$

(3.3)

Thus, $\{\Vert {\tilde{u}}_k - {\tilde{q}}\Vert \}$ is non-increasing and bounded for all ${\tilde{q}} \in {\tilde{F}}({\tilde{P}}) \cap {\tilde{F}}({\tilde{S}})$ which gives that $\lim \limits _{k\rightarrow \infty } \Vert {\tilde{u}}_k - {\tilde{q}}\Vert$ exists for all ${\tilde{q}} \in {\tilde{F}}({\tilde{P}}) \cap {\tilde{F}}({\tilde{S}}).$ $\square$

Lemma 3.2

Let ${\tilde{J}},$ ${\tilde{G}},$ ${\tilde{P}},$ ${\tilde{S}}$ and $\{{\tilde{u}}_k\}$ be as in Lemma 3.1. Then, ${\tilde{F}}({\tilde{P}}) \cap {\tilde{F}}({\tilde{S}}) \ne \emptyset$ if and only if $\{{\tilde{u}}_k\}$ is bounded and $\lim \limits _{k\rightarrow \infty } \Vert {\tilde{P}}{\tilde{u}}_k - {\tilde{u}}_k\Vert = 0 = \lim \limits _{k\rightarrow \infty } \Vert {\tilde{S}}{\tilde{u}}_k - {\tilde{u}}_k\Vert .$

Proof

Suppose ${\tilde{F}}({\tilde{P}}) \cap {\tilde{F}}({\tilde{S}}) \ne \emptyset$ and let ${\tilde{q}} \in {\tilde{F}}({\tilde{P}}) \cap {\tilde{F}}({\tilde{S}}).$ Then, by Lemma 3.1, $\lim \limits _{k\rightarrow \infty }\Vert {\tilde{u}}_k - {\tilde{q}}\Vert$ exists. Let

$$\begin{aligned} \lim \limits _{k\rightarrow \infty } \Vert {\tilde{u}}_k - {\tilde{q}}\Vert = r. \end{aligned}$$

(3.4)

From inequalities (3.1) and (3.2), we have

$$\begin{aligned} \limsup \limits _{k\rightarrow \infty } \Vert {\tilde{v}}_k - {\tilde{q}}\Vert \le r \end{aligned}$$

(3.5)

and

$$\begin{aligned} \limsup \limits _{k\rightarrow \infty } \Vert {\tilde{w}}_k - {\tilde{q}}\Vert \le r. \end{aligned}$$

(3.6)

Now, from (3.1) and (3.3), we have

$$\begin{aligned} \begin{array}{lll} \Vert {\tilde{u}}_{k+1} - {\tilde{q}}\Vert &{}\le &{} (1 - \rho _k)\Vert {\tilde{w}}_k - {\tilde{q}} \Vert + \rho _k \Vert {\tilde{v}}_k - {\tilde{q}}\Vert \\ &{}\le &{} (1 - \rho _k)\Vert {\tilde{u}}_k - {\tilde{q}} \Vert + \rho _k \Vert {\tilde{v}}_k -{\tilde{q}}\Vert \end{array} \end{aligned}$$

which gives

$$\begin{aligned} \Vert {\tilde{u}}_{k+1} - {\tilde{q}}\Vert \le \Vert {\tilde{u}}_k - {\tilde{q}} \Vert - \rho _k\Vert {\tilde{u}}_k - {\tilde{q}} \Vert + \rho _k \Vert {\tilde{v}}_k - {\tilde{q}}\Vert . \end{aligned}$$

Now, since $\{\rho _k\}$ is a sequence in (0, 1),  we obtain

$$\begin{aligned} \Vert {\tilde{u}}_{k+1} - {\tilde{q}} \Vert - \Vert {\tilde{u}}_k - {\tilde{q}} \Vert \le {\rho _k} (\Vert {\tilde{v}}_k - {\tilde{q}} \Vert - \Vert {\tilde{u}}_k - {\tilde{q}} \Vert ) \le \Vert {\tilde{v}}_k - {\tilde{q}} \Vert - \Vert {\tilde{u}}_k - {\tilde{q}} \Vert . \end{aligned}$$

So, we get $\Vert {\tilde{u}}_{k+1} - {\tilde{q}} \Vert \le \Vert {\tilde{v}}_k - {\tilde{q}} \Vert$ and from (3.4), we get

$$\begin{aligned} r \le \liminf \limits _{k\rightarrow \infty } \Vert {\tilde{v}}_k - {\tilde{q}} \Vert . \end{aligned}$$

(3.7)

Hence, from (3.5) and (3.7), we obtain

$$\begin{aligned} \lim \limits _{k\rightarrow \infty } \Vert {\tilde{v}}_k - {\tilde{q}}\Vert = r. \end{aligned}$$

(3.8)

Again, from (3.3), we have

$$\begin{aligned} \Vert {\tilde{u}}_{k+1} - {\tilde{q}}\Vert \le (1 - \rho _k)\Vert {\tilde{w}}_k - {\tilde{q}} \Vert + \rho _k \Vert {\tilde{v}}_k - {\tilde{q}}\Vert . \end{aligned}$$

Since $\{\rho _k\}$ is a sequence in (0, 1),  let $\rho '_k = 1 - \rho _k$ where $\rho '_k \in (0, 1),$ we get

$$\begin{aligned} \Vert {\tilde{u}}_{k+1} - {\tilde{q}}\Vert \le (1 - \rho '_k)\Vert {\tilde{v}}_k - {\tilde{q}} \Vert + \rho '_k \Vert {\tilde{w}}_k - {\tilde{q}}\Vert , \end{aligned}$$

which gives

$$\begin{aligned} \Vert {\tilde{u}}_{k+1} - {\tilde{q}} \Vert - \Vert {\tilde{v}}_k - {\tilde{q}} \Vert \le {\rho '_k} (\Vert {\tilde{w}}_k - {\tilde{q}} \Vert - \Vert {\tilde{v}}_k - {\tilde{q}} \Vert ). \end{aligned}$$

So, we obtain

$$\begin{aligned} \Vert {\tilde{u}}_{k+1} - {\tilde{q}}\Vert - \Vert {\tilde{v}}_k - {\tilde{q}} \Vert \le \Vert {\tilde{w}}_k - {\tilde{q}} \Vert - \Vert {\tilde{v}}_k - {\tilde{q}} \Vert , \end{aligned}$$

which gives

$$\begin{aligned} \Vert {\tilde{u}}_{k+1} - {\tilde{q}} \Vert \le \Vert {\tilde{w}}_k - {\tilde{q}} \Vert \end{aligned}$$

and from (3.4), we have

$$\begin{aligned} r \le \liminf \limits _{k\rightarrow \infty } \Vert {\tilde{w}}_k - {\tilde{q}} \Vert . \end{aligned}$$

(3.9)

Hence, from (3.6) and (3.9), we obtain

$$\begin{aligned} \lim \limits _{k\rightarrow \infty } \Vert {\tilde{w}}_k - {\tilde{q}}\Vert = r. \end{aligned}$$

(3.10)

On using the fact that ${\tilde{P}}$ and ${\tilde{S}}$ are quasi nonexpansive mappings, we have

$$\begin{aligned} \limsup \limits _{k\rightarrow \infty }\Vert {\tilde{P}}{\tilde{u}}_k - {\tilde{q}}\Vert \le \limsup \limits _{k\rightarrow \infty } \Vert {\tilde{u}}_k - {\tilde{q}}\Vert = r \end{aligned}$$

(3.11)

and

$$\begin{aligned} \lim \limits _{k\rightarrow \infty } \Vert {\tilde{S}}{\tilde{u}}_k - {\tilde{q}}\Vert \le \limsup \limits _{k\rightarrow \infty } \Vert {\tilde{u}}_k - {\tilde{q}}\Vert = r. \end{aligned}$$

(3.12)

Now, on using (3.4), (3.10), (3.11) and Lemma 2.3, we get

$$\begin{aligned} \lim \limits _{k\rightarrow \infty } \Vert {\tilde{P}}{\tilde{u}}_k - {\tilde{u}}_k\Vert = 0. \end{aligned}$$

(3.13)

Again, on using (3.4), (3.8), (3.12) and Lemma 2.3, we get

$$\begin{aligned} \lim \limits _{k\rightarrow \infty } \Vert S{\tilde{u}}_k - {\tilde{w}}_k\Vert = 0. \end{aligned}$$

(3.14)

Consider

$$\begin{aligned} \begin{array}{lll} \Vert {\tilde{w}}_k - {\tilde{u}}_k\Vert &{}=&{}\Vert (1 - \eta _k){\tilde{u}}_k + \eta _k {\tilde{P}}{\tilde{u}}_k - {\tilde{u}}_k\Vert \\ &{}\le &{} \eta _k \Vert {\tilde{P}}{\tilde{u}}_k - {\tilde{u}}_k\Vert \end{array} \end{aligned}$$

which on using (3.13) yields

$$\begin{aligned} \lim \limits _{k\rightarrow \infty } \Vert {\tilde{w}}_k - {\tilde{u}}_k\Vert = 0. \end{aligned}$$

(3.15)

Finally, we have

$$\begin{aligned} \Vert {\tilde{S}}{\tilde{u}}_k - {\tilde{u}}_k \Vert \le \Vert {\tilde{S}}{\tilde{u}}_k - {\tilde{w}}_k \Vert + \Vert {\tilde{w}}_k - {\tilde{u}}_k \Vert , \end{aligned}$$

so from (3.14) and (3.15), we get

$$\begin{aligned} \lim \limits _{k\rightarrow \infty } \Vert {\tilde{S}}{\tilde{u}}_k - {\tilde{u}}_k\Vert = 0. \end{aligned}$$

Conversely, suppose that $\{{\tilde{u}}_k\}$ is bounded and $\lim \limits _{k\rightarrow \infty }\Vert {\tilde{P}}{\tilde{u}}_k - {\tilde{u}}_k\Vert = \lim \limits _{k\rightarrow \infty }\Vert {\tilde{S}}{\tilde{u}}_k - {\tilde{u}}_k\Vert = 0.$ Let $q \in A({\tilde{G}},\{{\tilde{u}}_k\}),$ we have

$$\begin{aligned} \begin{array}{lll} r({\tilde{P}}q, \{{\tilde{u}}_k\}) &{}=&{} \limsup \limits _{k\rightarrow \infty }\Vert {\tilde{u}}_k - {\tilde{P}}q\Vert \\ &{}\le &{} (\frac{3 + \alpha }{1 - \alpha })\limsup \limits _{k\rightarrow \infty }\Vert {\tilde{P}}{\tilde{u}}_k - {\tilde{u}}_k\Vert + \limsup \limits _{k\rightarrow \infty } \Vert {\tilde{u}}_k - q\Vert \\ &{}=&{} \limsup \limits _{k\rightarrow \infty }\Vert {\tilde{u}}_k - q\Vert \\ &{}=&{} r(q, \{{\tilde{u}}_k\}). \end{array} \end{aligned}$$

This implies that ${\tilde{P}}q \in A({\tilde{G}}, \{{\tilde{u}}_k\}).$ Since ${\tilde{J}}$ is uniformly convex, $A({\tilde{G}}, \{{\tilde{u}}_k\})$ is singleton, therefore we get ${\tilde{P}}q = q.$

Similarly, we can obtain that ${\tilde{S}}q = q,$ which gives $q \in {\tilde{F}}({\tilde{P}}) \cap {\tilde{F}}({\tilde{S}}).$ So, ${\tilde{F}}({\tilde{P}}) \cap {\tilde{F}}({\tilde{S}}) \ne \emptyset .$ This completes the proof. $\square$

Now, we prove the weak convergence result involving iteration scheme (1.1).

Theorem 3.3

Let ${\tilde{J}},$ ${\tilde{G}},$ ${\tilde{P}},$ and ${\tilde{S}}$ be as in Lemma 3.1, such that ${\tilde{J}}$ which satisfies the Opial’s condition, then $\{{\tilde{u}}_k\}$ describes as in (1.1) converges weakly to a common fixed point of ${\tilde{P}}$ and ${\tilde{S}}$.

Proof

Let ${\tilde{q}} \in {\tilde{F}}({\tilde{P}}) \cap {\tilde{F}}({\tilde{S}})$. Then, from Lemma 3.1$\lim \limits _{k\rightarrow \infty }\Vert {\tilde{u}}_k - {\tilde{q}}\Vert$ exists. Now, to prove that $\{{\tilde{u}}_k\}$ converges weakly to a common fixed point of ${\tilde{P}}$ and ${\tilde{S}}$, we will show that $\{{\tilde{u}}_k\}$ has a unique weak subsequential limit in ${\tilde{F}}({\tilde{P}}) \cap {\tilde{F}}({\tilde{S}}).$ So, let $\{{\tilde{u}}_{k_j}\}$ and $\{{\tilde{u}}_{k_m}\}$ be two subsequences of $\{{\tilde{u}}_k\}$ which converges weakly to w and y respectively. On using Lemma 3.2, we get $\lim \limits _{k\rightarrow \infty }\Vert {\tilde{P}}{\tilde{u}}_{k} - {\tilde{u}}_{k}\Vert = \lim \limits _{k\rightarrow \infty }\Vert {\tilde{S}}{\tilde{u}}_{k} - {\tilde{u}}_{k}\Vert = 0$ and from Lemma 2.5, we have $I - {\tilde{P}}$ and $I- {\tilde{S}}$ are demiclosed at zero. So ${\tilde{w}}, {\tilde{y}} \in {\tilde{F}}({\tilde{P}}) \cap {\tilde{F}}({\tilde{S}})$.

Next, we show the uniqueness. Since ${\tilde{w}}, {\tilde{y}} \in {\tilde{F}}({\tilde{P}}) \cap {\tilde{F}}({\tilde{S}})$, so $\lim \limits _{k\rightarrow \infty }\Vert {\tilde{u}}_k - {\tilde{w}}\Vert$ and $\lim \limits _{k\rightarrow \infty }\Vert {\tilde{u}}_k - {\tilde{y}}\Vert$ exists. Let ${\tilde{w}} \ne {\tilde{y}}$. Then, by using Opial’s condition, we obtain

$$\begin{aligned} \begin{array}{lll} \lim \limits _{k\rightarrow \infty }\Vert {\tilde{u}}_k - {\tilde{w}}\Vert &{}=&{} \lim \limits _{{k_{j}}\rightarrow \infty }\Vert {\tilde{u}}_{k_j} - {\tilde{w}}\Vert \\ &{}<&{} \lim \limits _{{k_{j}}\rightarrow \infty }\Vert {\tilde{u}}_{k_j} - {\tilde{y}}\Vert \\ &{}=&{} \lim \limits _{k\rightarrow \infty }\Vert {\tilde{u}}_k - {\tilde{y}}\Vert \\ &{}=&{} \lim \limits _{{k_{m}}\rightarrow \infty }\Vert {\tilde{u}}_{k_m} - {\tilde{y}}\Vert \\ &{}<&{} \lim \limits _{{k_{m}}\rightarrow \infty }\Vert {\tilde{u}}_{k_m} - {\tilde{w}}\Vert \\ &{}=&{} \lim \limits _{k\rightarrow \infty }\Vert {\tilde{u}}_k - {\tilde{w}}\Vert \end{array} \end{aligned}$$

which is a contradiction, so ${\tilde{w}} = {\tilde{y}}.$ Thus, $\{{\tilde{u}}_k\}$ converges weakly to a common fixed point of ${\tilde{P}}$ and ${\tilde{S}}$. $\square$

Next, we establish and prove some strong convergence results.

Theorem 3.4

Under the conditions of Lemma 3.1, the sequence $\{{\tilde{u}}_{k}\}$ has a strong limit in ${\tilde{F}}({\tilde{P}}) \cap {\tilde{F}}({\tilde{S}})$ if and only if $\liminf \limits _{k\rightarrow \infty }d({\tilde{u}}_{k},{\tilde{F}}({\tilde{P}}) \cap {\tilde{F}}({\tilde{S}}))=0.$

Proof

Let $\lim \limits _{k\rightarrow \infty }{\tilde{u}}_{k} = {\tilde{q}},$ where ${\tilde{q}} \in {\tilde{F}}({\tilde{P}}) \cap {\tilde{F}}({\tilde{S}}),$ then it is trivial that $\liminf \limits _{k \rightarrow \infty }d({\tilde{u}}_{k}, {\tilde{F}}({\tilde{P}}) \cap {\tilde{F}}({\tilde{S}}))=0.$

For the converse part, let $\liminf \limits _{k\rightarrow \infty }d({\tilde{u}}_{k}, {\tilde{F}}({\tilde{P}}) \cap {\tilde{F}}({\tilde{S}}))=0.$ From Lemma 3.1, we have $\lim \limits _{k\rightarrow \infty }\Vert {\tilde{u}}_{k}- {\tilde{q}} \Vert$ exists for all ${\tilde{q}} \in {\tilde{F}}({\tilde{P}}) \cap {\tilde{F}}({\tilde{S}})$, which gives

$$\begin{aligned} \Vert {\tilde{u}}_{k+1} - {\tilde{q}} \Vert \le \Vert {\tilde{u}}_{k} - {\tilde{q}} \Vert ~\text{ for } \text{ any }~{\tilde{q}}\in {\tilde{F}}({\tilde{P}}) \cap {\tilde{F}}({\tilde{S}}), \end{aligned}$$

which yields

$$\begin{aligned} d({\tilde{u}}_{k+1}, {\tilde{F}}({\tilde{P}}) \cap {\tilde{F}}({\tilde{S}})) \le d({\tilde{u}}_{k},{\tilde{F}}({\tilde{P}}) \cap {\tilde{F}}({\tilde{S}})). \end{aligned}$$

(3.16)

Thus, $\{d({\tilde{u}}_{k},{\tilde{F}}({\tilde{P}}) \cap {\tilde{F}}({\tilde{S}})\}$ is a bounded below and a non-increasing sequence so $\lim \limits _{k\rightarrow \infty }d({\tilde{u}}_{k},{\tilde{F}}({\tilde{P}}) \cap {\tilde{F}}({\tilde{S}}))$ exists. As, $\liminf \limits _{k \rightarrow \infty }d({\tilde{u}}_{k},{\tilde{F}}({\tilde{P}}) \cap {\tilde{F}}({\tilde{S}}))=0$ so, $\lim \limits _{k\rightarrow \infty }d({\tilde{u}}_{k},{\tilde{F}}({\tilde{P}}) \cap {\tilde{F}}({\tilde{S}}))=0.$

Now, we can find a subsequence $\{{\tilde{u}}_{k_j}\}$ of $\{{\tilde{u}}_k\}$ and a sequence $\{m_j\}$ in ${\tilde{F}}({\tilde{P}}) \cap {\tilde{F}}({\tilde{S}})$ such that $\Vert {\tilde{u}}_{k_j} - m_j\Vert \le \frac{1}{2^{j}}$ for all $j \in \mathbb {N.}$ From Lemma 3.1, we have

$$\begin{aligned} \Vert {\tilde{u}}_{k_{j+1}} - m_j\Vert \le \Vert {\tilde{u}}_{k_j} - m_j\Vert \le \frac{1}{2^{j}}. \end{aligned}$$

Using triangle inequality, we get

$$\begin{aligned} \begin{array}{lll} \Vert m_{j+1} - m_j\Vert &{}\le &{} \Vert m_{j+1} - {\tilde{u}}_{k_{j+1}}\Vert + \Vert {\tilde{u}}_{k_{j+1}} - m_j\Vert \\ &{}\le &{} \frac{1}{2^{j+1}} + \frac{1}{2^{j}}\\ &{}\le &{} \frac{1}{2^{j-1}}\\ &{}\rightarrow &{} 0~\text{ as }~j\rightarrow \infty . \end{array} \end{aligned}$$

So, $\{m_j\}$ is a cauchy sequence in ${\tilde{F}}({\tilde{P}}) \cap {\tilde{F}}({\tilde{S}}).$ From Lemma 2.4, ${\tilde{F}}({\tilde{P}}) \cap {\tilde{F}}({\tilde{S}})$ is closed, so $\{m_j\}$ converges to some $m \in {\tilde{F}}({\tilde{P}}) \cap {\tilde{F}}({\tilde{S}}).$

Again, owing to triangle inequality, we have

$$\begin{aligned} \Vert {\tilde{u}}_{k_j} - m\Vert \le \Vert {\tilde{u}}_{k_j} - m_j\Vert + \Vert m_j - m\Vert . \end{aligned}$$

Letting $j \rightarrow \infty$, we have $\{{\tilde{u}}_{k_j}\}$ converges strongly to $m \in {\tilde{F}}({\tilde{P}}) \cap {\tilde{F}}({\tilde{S}}).$

Since $\lim \limits _{k \rightarrow \infty }\Vert {\tilde{u}}_k - m\Vert$ exists by Lemma 3.1, therefore $\{{\tilde{u}}_k\}$ converges strongly to $m \in {\tilde{F}}({\tilde{P}}) \cap {\tilde{F}}({\tilde{S}}).$

Two mappings ${\tilde{P}}, {\tilde{S}}:{\tilde{G}}\rightarrow {\tilde{G}}$ are said to satisfy the Condition (A) ([25]) if there exists a nondecreasing function $g:[0,\infty ) \rightarrow [0,\infty )$ with $g(0)=0$ and $g(c)>0$ for all $c \in (0,\infty )$ such that

$$\begin{aligned} \Vert {\tilde{u}} - {\tilde{P}}{\tilde{u}}\Vert \ge g(d({\tilde{u}}, {\tilde{F}}({\tilde{P}}) \cap {\tilde{F}}({\tilde{S}}))) \end{aligned}$$

or

$$\begin{aligned} \Vert {\tilde{u}} - {\tilde{S}}{\tilde{u}}\Vert \ge g(d({\tilde{u}}, {\tilde{F}}({\tilde{P}}) \cap {\tilde{F}}({\tilde{S}}))) \end{aligned}$$

for all ${\tilde{u}} \in {\tilde{G}}.$ $\square$

Now, we present a strong convergence result using Condition (A).

Theorem 3.5

Under the hypothesis of Lemma 3.1, if ${\tilde{P}}$ and ${\tilde{S}}$ satisfies Condition (A), then $\{{\tilde{u}}_{k}\}$ converges strongly to a point of ${\tilde{F}}({\tilde{P}}) \cap {\tilde{F}}({\tilde{S}}).$

Proof

From (3.16), $\lim \limits _{k\rightarrow \infty } d({\tilde{u}}_k, {\tilde{F}}({\tilde{P}}) \cap {\tilde{F}}({\tilde{S}}))$ exists.

Also, by Lemma 3.2 we have $\lim \limits _{k\rightarrow \infty } \Vert {\tilde{u}}_k - {\tilde{P}}{\tilde{u}}_k\Vert = \lim \limits _{k\rightarrow \infty } \Vert {\tilde{u}}_k - {\tilde{S}}{\tilde{u}}_k\Vert =0.$

Then, the following can be concluded from condition (A)

$$\begin{aligned} \lim \limits _{k\rightarrow \infty } g(d({\tilde{u}}_k, {\tilde{F}}({\tilde{P}}) \cap {\tilde{F}}({\tilde{S}})))\le \lim \limits _{k\rightarrow \infty } \Vert {\tilde{u}}_k - {\tilde{P}}{\tilde{u}}_k\Vert =0 \end{aligned}$$

or

$$\begin{aligned} \lim \limits _{k\rightarrow \infty } g(d({\tilde{u}}_k, {\tilde{F}}({\tilde{P}}) \cap {\tilde{F}}({\tilde{S}})))\le \lim \limits _{k\rightarrow \infty } \Vert {\tilde{u}}_k - {\tilde{S}}{\tilde{u}}_k\Vert =0 \end{aligned}$$

so that $\lim \limits _{k\rightarrow \infty } g(d({\tilde{u}}_k, {\tilde{F}}({\tilde{P}}) \cap {\tilde{F}}({\tilde{S}})))=0.$

Since g is a non decreasing function satisfying $g(0)=0$ and $g(c) > 0$ for all $c \in (0, \infty )$, therefore $\lim \limits _{k\rightarrow \infty } d({\tilde{u}}_k, {\tilde{F}}({\tilde{P}}) \cap {\tilde{F}}({\tilde{S}}))=0.$

From Theorem 3.4., the sequence $\{{\tilde{u}}_k\}$ converges strongly to a point of ${\tilde{F}}({\tilde{P}}) \cap {\tilde{F}}({\tilde{S}}).$ $\square$

4 Numerical Example

In this section, we will construct an example of a generalized $\alpha$-nonexpansive mapping which is neither a Suzuki generalized nonexpansive mapping nor a nonexpansive mapping.

Example 4.1

Let ${\tilde{J}} = {\mathbb {R}}$ with the usual norm and ${\tilde{G}} = [0, \infty ).$ Let ${\tilde{P}}:{\tilde{G}} \rightarrow {\tilde{G}}$ be a mapping defined as

$$\begin{aligned} {\tilde{P}}({\tilde{u}})={ {\left\{ \begin{array}{ll} 0 {\tilde{u}} \in [0,\frac{3}{2}) \\ \frac{6{\tilde{u}}}{13} {\tilde{u}} \in [\frac{3}{2}, \infty ).\\ \end{array}\right. } } \end{aligned}$$

for all ${\tilde{u}} \in {\tilde{G}}$.

Proof

Clearly ${\tilde{u}} = 0$ is the fixed point of ${\tilde{P}}.$ Then, (i) Since ${\tilde{P}}$ is not continuous at ${\tilde{u}} = \frac{3}{2},$ so ${\tilde{P}}$ is not a nonexpansive map.

(ii) Let ${\tilde{u}} =1$ and ${\tilde{v}} = \frac{3}{2},$ then

$$\begin{aligned} \frac{1}{2} \Vert {\tilde{u}} - {\tilde{P}}{\tilde{u}}\Vert = \frac{1}{2} \le \frac{1}{2} = \Vert {\tilde{u}} - {\tilde{v}}\Vert . \end{aligned}$$

But

$$\begin{aligned} \Vert {\tilde{P}}{\tilde{u}} - {\tilde{P}}{\tilde{v}}\Vert = \frac{6{\tilde{v}}}{13} = \frac{18}{26} > \frac{1}{2} = \Vert {\tilde{u}} - {\tilde{v}}\Vert . \end{aligned}$$

So, ${\tilde{P}}$ is not a Suzuki generalized nonexpansive mapping.

(iii) Now, we prove that ${\tilde{P}}$ is a generalized $\alpha$-nonexpansive mapping. For this, let $\alpha = \frac{1}{3}$ and consider the following cases:

Case (A). When ${\tilde{u}} \in [\frac{3}{2}, \infty )$ and ${\tilde{v}} \in [0, \frac{3}{2})$ then,

$$\begin{aligned} \Vert {\tilde{P}}{\tilde{u}} - {\tilde{P}}{\tilde{v}}\Vert = |{\tilde{P}}{\tilde{u}} - {\tilde{P}}{\tilde{v}}| = \frac{6{\tilde{u}}}{13}. \end{aligned}$$

Now,

$$\begin{aligned} \begin{array}{lll} \alpha \Vert {\tilde{P}}{\tilde{u}} - {\tilde{v}}\Vert + \alpha \Vert {\tilde{P}}{\tilde{v}} - {\tilde{u}}\Vert +(1 - 2\alpha )\Vert {\tilde{u}} - {\tilde{v}}\Vert &{}=&{} \frac{1}{3}|{\tilde{P}}{\tilde{u}} - {\tilde{v}}| + \frac{1}{3}|{\tilde{P}}{\tilde{v}} - {\tilde{u}}| +\frac{1}{3}|{\tilde{u}} - {\tilde{v}}|\\ &{}=&{} \frac{1}{3}|\frac{6{\tilde{u}}}{13} - {\tilde{v}}| + \frac{1}{3}|{\tilde{u}}| +\frac{1}{3}|{\tilde{u}} - {\tilde{v}}|\\ &{}\ge &{} \frac{1}{3}|\frac{6{\tilde{u}}}{13} + {\tilde{v}}| +\frac{1}{3}|{\tilde{u}} - {\tilde{v}}|\\ &{}\ge &{} \frac{19{\tilde{u}}}{39}\\ &{}>&{} \frac{6{\tilde{u}}}{13}\\ &{}=&{} \Vert {\tilde{P}}{\tilde{u}} - {\tilde{P}}{\tilde{v}}\Vert . \end{array} \end{aligned}$$

Case (B). When ${\tilde{u}}, {\tilde{v}} \in [\frac{3}{2}, \infty )$ then,

$$\begin{aligned} \Vert {\tilde{P}}{\tilde{u}} - {\tilde{P}}{\tilde{v}}\Vert = \frac{6}{13}\Vert {\tilde{u}} - {\tilde{v}}\Vert = \frac{6}{13}|{\tilde{u}} - {\tilde{v}}|. \end{aligned}$$

Now,

$$\begin{aligned} \begin{array}{lll} \alpha \Vert {\tilde{P}}{\tilde{u}} - {\tilde{v}}\Vert + \alpha \Vert {\tilde{P}}{\tilde{v}} - {\tilde{u}}\Vert +(1 - 2\alpha )\Vert {\tilde{u}} - {\tilde{v}}\Vert &{}=&{} \frac{1}{3}|{\tilde{P}}{\tilde{u}} - {\tilde{v}}| + \frac{1}{3}|{\tilde{P}}{\tilde{v}} - {\tilde{u}}| +\frac{1}{3}|{\tilde{u}} - {\tilde{v}}|\\ &{}=&{} \frac{1}{3}|\frac{6{\tilde{u}}}{13} - {\tilde{v}}| + \frac{1}{3}|{\tilde{u}} - \frac{6{\tilde{v}}}{13}| +\frac{1}{3}|{\tilde{u}} - {\tilde{v}}|\\ &{}\ge &{} \frac{1}{3}|\frac{19{\tilde{u}}}{13} -\frac{19{\tilde{v}}}{13}| +\frac{1}{3}|{\tilde{u}} - {\tilde{v}}|\\ &{}=&{} \frac{19}{39}|{\tilde{u}} - {\tilde{v}}| +\frac{1}{3}|{\tilde{u}} - {\tilde{v}}|\\ &{}>&{} \frac{6}{13}|{\tilde{u}} - {\tilde{v}}|\\ &{}=&{} \Vert {\tilde{P}}{\tilde{u}} - {\tilde{P}}{\tilde{v}}\Vert . \end{array} \end{aligned}$$

Case (C). When ${\tilde{u}}, {\tilde{v}} \in [0, \frac{3}{2})$ then,

$$\begin{aligned} \Vert {\tilde{P}}{\tilde{u}} - {\tilde{P}}{\tilde{v}}\Vert = 0. \end{aligned}$$

So,

$$\begin{aligned} \begin{array}{lll} \alpha \Vert {\tilde{P}}{\tilde{u}} - {\tilde{v}}\Vert + \alpha \Vert {\tilde{P}}{\tilde{v}} - {\tilde{u}}\Vert +(1 - 2\alpha )\Vert {\tilde{u}} - {\tilde{v}}\Vert &{}=&{} \frac{1}{3}|{\tilde{P}}{\tilde{u}} - {\tilde{v}}| + \frac{1}{3}|{\tilde{P}}{\tilde{v}} - {\tilde{u}}| +\frac{1}{3}|{\tilde{u}} - {\tilde{v}}|\\ &{}\ge &{} \Vert {\tilde{P}}{\tilde{u}} - {\tilde{P}}{\tilde{v}}\Vert . \end{array} \end{aligned}$$

Therefore, ${\tilde{P}}$ is a generalized $\alpha$-nonexpansive mapping with $\alpha = \frac{1}{3}.$

Similarly, we can define ${\tilde{S}}:{\tilde{G}} \rightarrow {\tilde{G}}$ as

$$\begin{aligned} {\tilde{S}}({\tilde{u}})={ {\left\{ \begin{array}{ll} 0 {\tilde{u}} \in [0,\frac{3}{2}) \\ \frac{7{\tilde{u}}}{15}{\tilde{u}} \in [\frac{3}{2}, \infty ).\\ \end{array}\right. } } \end{aligned}$$

for all ${\tilde{u}} \in {\tilde{G}}$. It can be easily verified that ${\tilde{S}}$ is a generalized $\alpha$-nonexpansive mapping with $\alpha = \frac{1}{3}$ and 0 is the common fixed point of ${\tilde{S}}$ and ${\tilde{P}}.$

Now, we will examine the influence of parameters $\eta _k,$ $\theta _k,$ $\rho _k$ and initial value. For this, we will consider the three cases.

Case (I). In this case, we will show the convergence of our iteration scheme for three different set of parameters with same initial value. We take the following set of parameters:

1.:

$\eta _k = \frac{k}{k+1},$ $\theta _k = \frac{k}{k+5},$ $\rho _k = \frac{1}{\sqrt{2k+1}}$ for all $k \in {\mathbb {N}}$ and ${\tilde{u}}_1 = 5000$

2.:

$\eta _k = \frac{2k}{5k+2},$ $\theta _k = \frac{1}{k+5},$ $\rho _k = \frac{k}{k+9}$ for all $k \in {\mathbb {N}}$ and ${\tilde{u}}_1 = 5000$

3.:

$\eta _k = \frac{1}{\sqrt{k+5}},$ $\theta _k = \frac{1}{3k+7},$ $\rho _k = \sqrt{\frac{k+1}{5k+1}}$ for all $k \in {\mathbb {N}}$ and ${\tilde{u}}_1 = 5000$

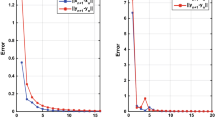
We get the following Table 1 and Graph 1 for the initial value 5000. $\square$

Table 1 Values of proposed iteration with respect to the same initial value and different sets of parameters $\eta _k , \theta _k , \rho _k$

Fig. 1

Graph corresponding to Table 1

Case (II). In this case, we will show the convergence for three different initial values with same set of parameters. Set $\eta _k = \frac{k}{k+1},$ $\theta _k = \frac{2k}{5k+2}$ and $\rho _k = \frac{1}{\sqrt{2k+1}}$ for all $k \in {\mathbb {N}}.$ We get the following Table 2 and Graph 2.

Table 2 Values of proposed iteration with respect to different initial values and the same set of parameters $\eta _k , \theta _k , \rho _k$

Fig. 2

Graph corresponding to Table 2

Case (III). In this case, we will consider three different set of parameters with different initial values. Consider the following different set of parameters:

1.:

$\eta _k = \frac{k}{k+1},$ $\theta _k = \frac{k}{k+5},$ $\rho _k = \frac{1}{\sqrt{2k+1}}$ for all $k \in {\mathbb {N}}$ and ${\tilde{u}}_1 = 1000$

2.:

$\eta _k = \frac{2k}{5k+2},$ $\theta _k = \frac{1}{k+5},$ $\rho _k = \frac{k}{k+9}$ for all $k \in {\mathbb {N}}$ and ${\tilde{u}}_1 = 5000$

3.:

$\eta _k = \frac{1}{\sqrt{k+5}},$ $\theta _k = \frac{1}{3k+7},$ $\rho _k = \sqrt{\frac{k+1}{5k+1}}$ for all $k \in {\mathbb {N}}$ and ${\tilde{u}}_1 = 9000$

We get the following Table 3 and Graph 3.

Table 3 Values of proposed iteration with respect to different initial values and different sets of parameters $\eta _k , \theta _k , \rho _k$

Fig. 3

Graph corresponding to Table 3

From the above three cases, it is clear that our iteration process (1.1) not only converges to the common fixed point of ${\tilde{P}}$ and ${\tilde{S}}$ but it also shows that iteration process is stable with respect to the different initial values and parameters $\eta _n,$ $\theta _n$ and $\rho _n.$

5 Applications

Application to constrained optimization and variational inequality problem: Now, we will use ${\tilde{J}}$ to denote a real Hilbert space and ${\tilde{G}}$ for a nonempty closed convex subset of ${\tilde{J}}.$ Let ${\tilde{S}}:{\tilde{G}}\rightarrow {\tilde{G}}$ a nonlinear operator. Then, ${\tilde{S}}$ is called to be:

• (i) Monotone if $\langle {\tilde{S}}{\tilde{u}}-{\tilde{S}}{\tilde{v}} , {\tilde{u}} - {\tilde{v}}\rangle \ge 0$ for all ${\tilde{u}}, {\tilde{v}}\in {\tilde{G}}$,

• (ii) ${\tilde{\lambda }}$- strongly monotone if there exist a constant ${\tilde{\lambda }}>0$ such that $\langle {\tilde{S}}{\tilde{u}} - {\tilde{S}}{\tilde{v}}, {\tilde{u}} - {\tilde{v}}\rangle \ge {\tilde{\lambda }} \Vert {\tilde{u}} - {\tilde{v}}\Vert ^{2}$ for all ${\tilde{u}} , {\tilde{v}}\in {\tilde{G}}$,

• (iii) ${\tilde{\xi }}$- inverse strongly monotone (${\tilde{\xi }}$-ism) if there exist a constant ${\tilde{\xi }} >0$ such that $\langle {\tilde{S}}{\tilde{u}} - {\tilde{S}}{\tilde{v}}, {\tilde{u}} - {\tilde{v}}\rangle \ge {\tilde{\xi }} \Vert {\tilde{S}}{\tilde{u}} - {\tilde{S}}{\tilde{v}}\Vert ^{2}$ for all ${\tilde{u}},{\tilde{v}}\in {\tilde{G}},$

• (iv) ${\tilde{L}}$-Lipschitzian if there exists a constant ${\tilde{L}}>0$ such that $\Vert S{\tilde{u}} - {\tilde{S}}{\tilde{v}} \Vert \le {\tilde{L}}\Vert {\tilde{u}} - {\tilde{v}} \Vert ,$ for all ${\tilde{u}}, {\tilde{v}}\in {\tilde{G}}.$

A point ${\tilde{z}}\in {\tilde{G}}$ with $\langle {\tilde{S}}{\tilde{z}}, {\tilde{z}} - {\tilde{u}}\rangle \ge 0$ for all ${\tilde{u}}\in {\tilde{G}}$ is termed as a solution of variational inequality problem denoted by $VI({\tilde{G}},{\tilde{S}}).$ $\Omega ({\tilde{G}},{\tilde{S}})$ is used to denote the solution set of $VI({\tilde{G}},{\tilde{S}}).$ It was Stampachhia [26, 27] who initiated the study of variational inequalities. Let $\mu >0$ is a constant and ${\tilde{P}}_{{\tilde{G}}}$ be the metric projection from ${\tilde{J}}$ onto ${\tilde{G}}$ then, the set of fixed points of ${\tilde{P}}_{{\tilde{G}}}(I-\mu {\tilde{S}})$ is same as the solution set of $VI({\tilde{G}},{\tilde{S}})$ i.e., ${\tilde{F}}({\tilde{P}}_{{\tilde{G}}}(I-\mu {\tilde{S}}))=\Omega ({\tilde{G}},{\tilde{S}}).$ Also, it is worth mentioning that if ${\tilde{S}}$ is ${\tilde{L}}$-Lipschitzian and ${\tilde{\lambda }}$ - strongly monotone, then the operator ${\tilde{P}}_{{\tilde{G}}}(I-\mu {\tilde{S}})$ is a contraction on ${\tilde{G}}$ when $0<\mu <2{\tilde{\lambda }} /{\tilde{L}}^{2}.$ Then, using the Banach contraction principle we can find a unique solution of $VI({\tilde{G}},{\tilde{S}})$ and the sequence generated by the Picard iteration process,

$$\begin{aligned} {\tilde{u}}_{k+1}={\tilde{P}}_{{\tilde{G}}}(I-\mu {\tilde{S}}){\tilde{u}}_{k},~~~~~~~k\in {\mathbb {N}} \end{aligned}$$

will converge strongly to that solution denoted by ${\tilde{u}}^{*}.$

If ${\tilde{S}} = {\tilde{P}},$ then the iterative process (1.1) gives the following iterative procedure:

$$\begin{aligned} {{\left\{ \begin{array}{ll} {\tilde{u}}_1 \in {\tilde{G}} \\ {\tilde{w}}_k = (1 - \eta _k){\tilde{u}}_k + \eta _n{\tilde{S}}{\tilde{u}}_k \\ {\tilde{v}}_k = (1 - \theta _k){\tilde{S}}{\tilde{u}}_k + \theta _k{\tilde{w}}_k \\ {\tilde{u}}_{k+1} =(1 - \rho _k){\tilde{S}}{\tilde{w}}_k + \rho _k{\tilde{S}}{\tilde{v}}_k, k\in {\mathbb {N}} \end{array}\right. }} \end{aligned}$$

(5.1)

where $\{\eta _k\}$, $\{\theta _k\}$ and $\{\rho _k\}$ are sequences in (0, 1).

Now, in view of Theorem 3.3, we obtain the following results:

Theorem 5.1

Let ${\tilde{P}}_{{\tilde{G}}} : {\tilde{J}} \rightarrow {\tilde{G}}$ be a metric projection defined on nonempty closed convex subset ${\tilde{G}}$ of ${\tilde{J}}$ and ${\tilde{S}}: {\tilde{G}} \rightarrow {\tilde{J}}$ a ${\tilde{\xi }}$- inverse strongly monotone mapping, where ${\tilde{\xi }} >0$ is a constant. Suppose $\Omega ({\tilde{G}}, {\tilde{S}})\ne \phi$ and $\mu \in (0,2 {\tilde{\xi }} )$. If $\{{\tilde{u}}_{k}\}$ is constructed from ${\tilde{u}}_{1}\in {\tilde{G}}$ as follows:

$$\begin{aligned} {{\left\{ \begin{array}{ll} \tilde{u}_1 \in \tilde{G} \\ \tilde{w}_k = (1 - \eta _k)\tilde{u}_k + \eta _k\tilde{P}_{\tilde{G}}(I-\mu \tilde{S})\tilde{u}_k \\ \tilde{v}_k = (1 - \theta _k)\tilde{P}_{\tilde{G}}(I-\mu \tilde{S})\tilde{u}_k + \theta _k\tilde{w}_k \\ \tilde{u}_{k+1} =(1 - \rho _k)\tilde{P}_{\tilde{G}}(I-\mu \tilde{S})\tilde{w}_k + \rho _k\tilde{P}_{\tilde{G}}(I-\mu \tilde{S})\tilde{w}_k,~~k\in \mathbb {N} \end{array}\right. }} \end{aligned}$$

where $\{\eta _k\}$, $\{\theta _k\}$ and $\{\rho _k\}$ are sequences in (0, 1) then, $\{{\tilde{u}}_{k}\}$ converges weakly to a solution of the variational inequality $VI({\tilde{G}}, {\tilde{S}}.)$

Proof

On combining the facts that ${\tilde{P}}_{{\tilde{G}}}(I-\mu {\tilde{S}})$ is nonexpansive mapping if $\mu \in (0,2\xi )$ and every nonexpansive map is a generalized 0-nonexpansive mapping, our result follows from Theorem 3.3 by taking ${\tilde{S}} = {\tilde{P}}_{{\tilde{G}}}(I-\mu {\tilde{S}})$ in (5.1).

Now, the iterative procedures developed to obtain extremum values of a convex differentiable function q(x) can also be used used for image and signal processing. Since every ${\tilde{L}}$-Lipschitzian operator is 2/${\tilde{L}}$-ism, we obtain the following result concerning minimizer of q. $\square$

Theorem 5.2

Let ${\tilde{D}}$ be an open set which contains a nonempty closed convex subset ${\tilde{G}}$ of a Hilbert space ${\tilde{J}}$ and q be a differentiable and convex defined on ${\tilde{D}}$. Suppose that $\nabla q$ is a ${\tilde{L}}$-Lipschitz continuous operator on ${\tilde{D}}$ with $\mu \in (0,2/{\tilde{L}})$ and minimizers of q relative to the set ${\tilde{G}}$ exist. Let $\{{\tilde{u}}_{k}\}$ be a sequence in ${\tilde{G}}$ constructed from ${\tilde{u}}_{1}\in {\tilde{G}}$ and defined by

$$\begin{aligned} {{\left\{ \begin{array}{ll} {\tilde{u}}_1 \in {\tilde{G}} \\ {\tilde{w}}_k = (1 - \eta _k){\tilde{u}}_k + \eta _k{\tilde{P}}_{{\tilde{G}}}(I-\mu \nabla q){\tilde{u}}_k \\ {\tilde{v}}_k = (1 - \theta _k){\tilde{P}}_{{\tilde{G}}}(I-\mu \nabla q){\tilde{u}}_k + \theta _n{\tilde{w}}_k \\ {\tilde{u}}_{k+1} =(1 - \rho _k){\tilde{P}}_{{\tilde{G}}}(I-\mu \nabla q){\tilde{w}}_k + \rho _k{\tilde{P}}_{{\tilde{G}}}(I-\mu \nabla q){\tilde{v}}_k, \quad k\in {\mathbb {N}} \end{array}\right. }} \end{aligned}$$

where $\{\eta _k\}$, $\{\theta _k\}$ and $\{\rho _k\}$ are sequences in (0, 1). Then, $\{{\tilde{u}}_{k}\}$ converges weakly to a minimizer of q.

Application to Split feasibility problem:

Let ${\tilde{G}}_1$ and ${\tilde{G}}_2$ be closed, convex and nonempty subsets of two real Hilbert spaces ${\tilde{J}}_1$ and ${\tilde{J}}_2$ respectively and let ${\tilde{A}}: {\tilde{J}}_1 \rightarrow {\tilde{J}}_2$ be a bounded and linear operator. Then, the split feasibility problem (abbreviate SFP) can be mathematically described as locating a point ${\tilde{u}} \in {{\tilde{G}}_1}$ such that

$$\begin{aligned} {\tilde{u}} \in {{\tilde{G}}_1}, {\tilde{A}}{\tilde{u}} \in {{\tilde{G}}_2}. \end{aligned}$$

(5.2)

Let

$$\begin{aligned} \Omega = \{{\tilde{u}} \in {{\tilde{G}}_1} : {\tilde{A}}{\tilde{u}} \in {{\tilde{G}}_2}\} = {{\tilde{G}}_1} \cap {\tilde{A}}^{-1} {{\tilde{G}}_2} \end{aligned}$$

(5.3)

be the solution set of SFP (5.2). Then, $\Omega$ is closed, convex and nonempty set. Also, we assume that $\Omega \ne \emptyset .$ Censor and Elfving [28] solved the class of inverse problems with the help of SFP. In 2002, Byrne [29] introduced the following famous algorithm for solving the SFP. In this, the iterative step ${\tilde{u}}_k$ is calculated as follows:

$$\begin{aligned} {\tilde{u}}_{k+1} = {\tilde{P}}_{{\tilde{G}}_1}[I- \gamma {\tilde{A}}^{*}(I - {\tilde{P}}_{{\tilde{G}}_2}){\tilde{A}}]{\tilde{u}}_k, ~~~~k \ge 0, \end{aligned}$$

(5.4)

where $0< \gamma < \frac{2}{{\Vert {\tilde{A}}\Vert }^{2}},$ ${\tilde{P}}_{{\tilde{G}}_1}$ and ${\tilde{P}}_{{\tilde{G}}_2}$ denote the projections onto sets ${{\tilde{G}}_1}$ and ${{\tilde{G}}_2}$, respectively and ${\tilde{A}}^{*} : {{\tilde{J}}_2}^{*} \rightarrow {{\tilde{J}}_1}^{*}$ is the adjoint of ${\tilde{A}}.$

Now, the following important Lemma was given by Feng et al. [30]

Lemma 5.3

Let operator ${\tilde{S}} = {\tilde{P}}_{{\tilde{G}}_1}[I- \gamma {\tilde{A}}^{*}(I - {\tilde{P}}_{{\tilde{G}}_2}){\tilde{A}}],$ with $0< \gamma < \frac{2}{{\Vert {\tilde{A}}\Vert }^{2}}$. Then, ${\tilde{S}}$ is a nonexpansive map.

Also, since we have assumed that solution set $\Omega \ne \emptyset$, it is easy to observe that any ${\tilde{u}}^{*} \in {{\tilde{G}}_1}$ is the solution of SFP if and only if it satisfies the following fixed point equation:

$$\begin{aligned} {\tilde{P}}_{{\tilde{G}}_1}[I- \gamma {\tilde{A}}^{*}(I - {\tilde{P}}_{{\tilde{G}}_2}){\tilde{A}}]{\tilde{u}} = {\tilde{u}}, ~~~~~~~ {\tilde{u}} \in {{\tilde{G}}_1}. \end{aligned}$$

So, the solution set $\Omega$ is equal to the fixed point set of ${\tilde{S}}$ , i.e, ${\tilde{F}}({\tilde{S}}) = \Omega = {{\tilde{G}}_1} \cap {\tilde{A}}^{-1}{{\tilde{G}}_2} \ne \emptyset .$ For details, one can refer [31, 32].

Now, we present our main results.

Theorem 5.4

Let $\{{\tilde{u}}_k\}$ be the sequence defined by iterative procedure (5.1) with ${\tilde{S}} = {\tilde{P}}_{{\tilde{G}}_1}[I- \gamma {\tilde{A}}^{*}(I - {\tilde{P}}_{{\tilde{G}}_2}){\tilde{A}}]$ then, $\{{\tilde{u}}_k\}$ converges weakly to the solution of SFP (5.2).

Proof

By Lemma 5.3, ${\tilde{S}}$ is a nonexpansive map and every nonexpansive mapping is a generalized 0-nonexpansive mapping, so we conclude our result from Theorem 3.3. $\square$

Theorem 5.5

Let $\{{\tilde{u}}_k\}$ be the sequence obtained by using (5.1) with ${\tilde{S}} = {\tilde{P}}_{{{\tilde{G}}_1}}[I- \gamma {\tilde{A}}^{*}(I - {\tilde{P}}_{{{\tilde{G}}_2}}){\tilde{A}}]$ then, $\{{\tilde{u}}_k\}$ converges to the solution of SFP (5.2) if and only if $\liminf \limits _{k\rightarrow \infty }d({\tilde{u}}_k, \Omega ) = 0$.

Proof

Proof follows from Theorem 3.4. $\square$