A modified Halpern algorithm for approximating a common solution of split equality convex minimization problem and fixed point problem in uniformly convex Banach spaces

Abstract

In this paper, we introduce a modified Halpern algorithm for approximating a common solution of split equality convex minimization problem and split-equality fixed-point problem for Bregman quasi-nonexpansive mappings in p-uniformly convex and uniformly smooth Banach spaces. We introduce a generalized step size such that the algorithm does not require a prior knowledge of the operator norms and prove a strong convergence theorem for the sequence generated by our algorithm. We give some applications and numerical examples to show the consistency and accuracy of our algorithm. Our results complement and extend many other recent results in this direction in literature.

1 Introduction

Let $E_1$ and $E_2$ be Banach spaces and let C and Q be nonempty closed convex subsets of $E_1$ and $E_2$, respectively. We denote the dual of $E_1$ and $E_2$ by $E_1^*$ and $E_2^*$, respectively. Let $A{:}\,E_1\rightarrow E_2$ ba a bounded linear operator. The split feasibility problem (SFP) can be formulated as:

$$\begin{aligned} \text {find} \quad x\in C \quad \text {such that}\quad Ax\in Q. \end{aligned}$$

(1.1)

The notion of SFP was first introduced by Censor and Elfving (1994) in the framework of Hilbert spaces for modeling inverse problems which arise from phase retrievals and medical image reconstruction. The SFP has attracted much attention due to its applications in modeling real-world problems such as inverse problem in signal processing, radiation therapy, data denoising and data compression (see Ansari and Rehan 2014; Bryne 2002; Censor et al. 2005, 2006; Mewomo and Ogbuisi 2018; Shehu and Mewomo 2016 for details). A very popular algorithm constructed to solve the SFP in real Hilbert spaces was the following CQ-algorithm proposed by Bryne (2002). Let $x_1\in C$ and compute

$$\begin{aligned} x_{n+1} = P_C(x_n -\mu A^*(I - P_Q)Ax_n), \quad n\ge 1, \end{aligned}$$

(1.2)

where $A^*$ is the adjoint of A, $P_C$ and $P_Q$ are the metric projections of C and Q, respectively, $\mu \in (0, \frac{2}{\lambda })$ with $\lambda$ being the spectral radius of the operator $A^*A$. The sequence generated by (1.2) was shown to converge weakly to a solution of the SFP (1.1).

Schöpfer et al. (2008) studied the problem (1.1) in p-uniformly convex real Banach spaces which are also uniformly smooth and proposed the following algorithm: for $x_1\in E_1$, set

$$\begin{aligned} x_{n+1}=\Pi _CJ^{E^*_1}\big [J^{E_1}(x_n)-\mu _nA^*J^{E_2}(Ax_n - P_{Q}(Ax_n))\big ], \quad n \ge 1, \end{aligned}$$

(1.3)

where $\Pi _C$ denotes the Bregman projection from $E_1$ onto C and $J^E$ is the duality mapping. The algorithm (1.3) generalizes the CQ-algorithm proposed by Bryne (2002). For several extensions of the CQ-algorithm and work on the SFP, please see Bryne (2004), Qu and Xiu (2005) and Yang (2004) and the references therein.

Moudafi and Thakur (2014) studied the proximal split minimization problem (PSMP) as generalization of SFP in real Hilbert spaces. Moudafi and Thakur (2014) considered finding a solution $x^*\in H_1$ of the problem

$$\begin{aligned} \min _{x\in H_1}\big \{f(x)+g_{\mu }(Ax)\big \}, \end{aligned}$$

(1.4)

where $f{:}\,H_1\rightarrow {\mathbb {R}}\cup \{+\infty \}$, $g{:}\,H_2\rightarrow {\mathbb {R}}\cup \{+\infty \}$ are two proper, convex, lower-semicontinuous functions and $g_\mu (x) =\min _{u\in H_2}\{g(u)+\frac{1}{2\mu }\Vert u-x\Vert ^2\}$ stands for the Moreau–Yosida approximate of the function g with respect to the parameter $\mu$.

By the differentiability of Yosida-approximate $g_\mu$, (1.4) can be formulated as: find $x^*\in H_1$ such that

$$\begin{aligned} 0\in \mu \partial f(x^*)+A^*(I - \mathrm{prox}_{\mu }g)(Ax^*), \end{aligned}$$

(1.5)

where $\mathrm{prox}_{\mu }g(x) = \arg \min \{g(u)+\frac{1}{2\mu }\Vert u -x\Vert ^2\}$ is the proximal mapping of g and $\partial f(x)$ is the subdifferential of f at x defined as

$$\begin{aligned} \partial f(x):=\{u\in H_1{:}\,f(y)\ge f(x)+\langle u, y-x\rangle \quad \forall y\in H_1\}. \end{aligned}$$

The inclusion (1.5) in turn yields the following equivalent fixed-point formulation

$$\begin{aligned} x^* = \mathrm{prox}_{\mu \lambda f}(x^* - \mu A^*(I - \mathrm{prox}_{\lambda }g)(Ax^*)). \end{aligned}$$

(1.6)

Thus, (1.6) suggests to consider the following split proximal algorithm.

$$\begin{aligned} x_{k+1} = \mathrm{prox}_{\mu _k\lambda f}(x_k - \mu _k A^*(I - \mathrm{prox}_{\lambda }g)Ax_k). \end{aligned}$$

Now, let $T{:}\,H \rightarrow H$ be a nonlinear operator, a point $x \in H$ is called a fixed point of T if $Tx = x$. The set of all fixed points of T is denoted by F(T). Let $H_1, H_2$ be real Hilbert spaces, $T_1{:}\,H_1 \rightarrow H_1$, $T_2{:}\,H_2 \rightarrow H_2$ be two nonlinear operators such that $F(T_1)$ and $F(T_2)$ are nonempty. The split common fixed point problem (SCFPP) is defined as:

$$\begin{aligned} \text {find} \quad x\in F(T_1) \quad \text {such that}\quad Ax\in F(T_2), \end{aligned}$$

(1.7)

where $A{:}\,H_1 \rightarrow H_2$ is a bounded linear operator. The SCFPP was first studied by Censor and Segal (2009) in the setting of Hilbert spaces for the case where $T_1$ and $T_2$ are nonexpansive mappings. They proposed the following algorithm and proved its weak convergence to a solution of (1.7) under some suitable conditions.

$$\begin{aligned} \left\{ \begin{array} {ll} x_0\in C,\\ x_{n+1} = T_1[x_n-\gamma A^*(I - T_2)Ax_n], \end{array} \right. \end{aligned}$$

where $\gamma \in (0, \frac{2}{\lambda })$ with $\lambda$ being the spectral radius of the operator $A^*A$. Moudafi (2011) studied the SCFPP in infinite-dimensional Hilbert spaces. Moudafi (2011) proposed the following algorithm (1.8) and obtained a weak convergence theorem for finding solution of (1.7) for quasi-nonexpansive mappings.

$$\begin{aligned} \left\{ \begin{array}{ll} x_0\in C,\\ y_n = x_n - \gamma A^*(I - T_1)Ax_n,\\ x_{n+1} = (1-\alpha _n)y_n+\alpha _nT_2y_n, \end{array} \right. \end{aligned}$$

(1.8)

where $\gamma \in (0, \frac{1}{\lambda \beta })$ for $\beta \in (0, 1)$ and $\lambda$ being the spectral radius of the operator $A^*A$.

Let $H_1$, $H_2$ and $H_3$ be real Hilbert spaces and let C, Q be nonempty, closed and convex subsets of $H_1$ and $H_2$, respectively. Let $A{:}\,H_1\rightarrow H_3$, $B{:}\,H_2\rightarrow H_3$ be bounded linear operators, the split equality fixed point problem (SEFPP) is defined as

$$\begin{aligned} \text {find}\quad x\in F(T_1)\quad \text {and} \quad y\in F(T_2)\quad \text {such that}\quad Ax = By, \end{aligned}$$

(1.9)

where $T_1{:}\,H_1\rightarrow H_1$ and $T_2{:}\,H_2\rightarrow H_2$ are nonlinear mappings on $H_1$ and $H_2$, respectively. The SEFPP allows asymmetric and partial relations between the variables x and y. It has applications in phase retrievals, decision sciences, medical image reconstruction and intensity-modulated radiation therapy. If in (1.9), $H_2 = H_3$ and $B =I$, the identity mapping, then SEFPP (1.9) reduces to the SCFPP (1.7). The SEFPP was introduced by Moudafi (2012) in the framework of Hilbert spaces for firmly nonexpansive operators. To solve this problem, Moudafi (2012) proposed the following alternating algorithm:

$$\begin{aligned} \left\{ \begin{array}{ll} x_{n+1} = U(x_n - \gamma _nA^*(Ax_n - By_n)),\\ y_{n+1} = T(y_n+\gamma _nB^*(Ax_{n+1} - By_n)), n\ge 1, \end{array} \right. \end{aligned}$$

(1.10)

where $\{\gamma _n\}$ is a positive non-decreasing sequence such that $\gamma _n\in \big (\epsilon , \min (\frac{1}{\lambda _A}, \frac{1}{\lambda _B})-\epsilon )$, $\lambda _A$, $\lambda _B$ stand for the spectral radii of $A^*A$ and $B^*B$, respectively, $I - T_1$ and $I - T_2$ are demiclosed at 0. It was established that the iterative scheme (1.10) converges weakly to a solution of (1.9) in Hilbert spaces.

Motivated by the work of Moudafi (2012), Moudafi and Al-Shemas (2013) studied the SEFPP (1.9) in the setting of Hilbert spaces and proposed the following simultaneous algorithm:

$$\begin{aligned} \left\{ \begin{array}{ll} x_{n+1} = U(x_n - \gamma _nA^*(Ax_n - By_n)),\\ y_{n+1} = T(y_n+\gamma _nB^*(Ax_{n} - By_n)),\quad n\ge 1, \end{array} \right. \end{aligned}$$

(1.11)

where $\{\gamma _n\}\subset (\epsilon , \frac{2}{\lambda _A+\lambda _B}-\epsilon )$. They proved that the iterative scheme (1.11) converges weakly to a solution of problem (1.9).

Ma et al. (2013) also proposed the following algorithm for solving the SEFPP (1.9) in Hilbert spaces:

$$\begin{aligned} \left\{ \begin{array}{ll} x_1\in H_1,\quad y_1\in H_2,\\ x_{n+1} = (1-\alpha _n)x_n + \alpha _nU(x_n - \gamma _nA^*(Ax_n - By_n)),\\ x_{n+1} = (1-\alpha _n)y_n+\alpha _nT(y_n+\gamma _nB^*(Ax_{n} - By_n)), n\ge 1, \end{array} \right. \end{aligned}$$

(1.12)

where $\{\gamma _n\}\subset (\epsilon , \frac{2}{\lambda _A+\lambda _B}-\epsilon )$, $\{\alpha _n\}\subset [ \alpha , 1]$ for some $\alpha > 0$ and $U{:}\,H_1\rightarrow H_1$ and $T{:}\,H_2\rightarrow H_2$ T are firmly quasi-nonexpansive mappings. They proved strong and weak convergence theorems for the iterative scheme under some mild conditions.

Note that algorithms (1.10)–(1.12) depend on a prior knowledge of the operator norms for their implementation. To overcome this difficulty, Zhao (2015) introduced a new algorithm with a way of selecting the stepsize such that its implementation does not require prior knowledge of the operator norms. In particular, Zhao (2015) proposed the following iterative method: choose initial guess $x_0\in H_1, y_0\in H_2$,

$$\begin{aligned} \left\{ \begin{array}{ll} u_{n} = x_n - \gamma _nA^*(Ax_n - By_n),\\ x_{n+1} =\alpha _nu_n+(1-\alpha _n)U(u_n),\\ v_{n} = y_n + \gamma _nB^*(Ax_n - By_n),\\ y_{n+1} =\beta _nv_n+(1-\beta _n)T(u_n), \end{array} \right. \end{aligned}$$

(1.13)

where $\alpha _k\in [0, 1], \beta _k\in [0, 1]$, and

$$\begin{aligned} \gamma _n\in \bigg (0, \frac{2\Vert Ax_n - By_n\Vert ^2}{\Vert A^*(A_n-By_n)\Vert ^2 +\Vert B^*(Ax_n-By_n)\Vert ^2}\bigg ), \end{aligned}$$

$n\in \Omega$ otherwise $\gamma _n = \gamma ~(\gamma ~ \text {being any nonnegative value})$, where the set of indexes $\Omega = \{n{:}\,Ax_n - By_n\ne 0\}$.

We note that while there are many literature on solving the SEFPP in Hilbert spaces there are only few literature on SEFPP in Banach spaces. Our aim in this paper is to study the SEFPP in the setting of other Banach spaces higher than the Hilbert spaces.

Let $E_1,$ $E_2$ and $E_3$ be p-uniformly convex and uniformly smooth Banach spaces and let $f{:}\,E_1\rightarrow {\mathbb {R}}\cup \{+\,\infty \}$ and $g{:}\,E_2\rightarrow {\mathbb {R}}\cup \{+\,\infty \}$ be proper, convex and lower semicontinuous functions. Let $T_1{:}\,E_1\rightarrow E_1$ and $T_2{:}\,E_2\rightarrow E_2$ be Bregman quasi-nonexpansive mappings. In this paper, we consider the following split equality convex minimization problem (SECMP) and fixed point problem:

$$\begin{aligned} \text {find}\quad x\in F(T_1)\cap \mathrm{Arg} \min (f),~~ y\in F(T_2)\cap \mathrm{Arg} \min (g) \quad \text {such that} \quad Ax = By, \nonumber \\ \end{aligned}$$

(1.14)

where $A{:}\,E_1\rightarrow E_3$ and $B{:}\,E_2\rightarrow E_3$ are bounded linear operators.

It is important to consider the problem of finding a common solution of SECMP and SEFPP due to its possible applications to mathematical models whose constraints can be expressed as SECMP and SEFPP. This happens, in particular, in the practical problems such as in signal processing, network resource allocation, image recovery, see for instance Iiduka (2012, 2015) and Maingé (2008b).

We denote the set of solutions of problem (1.14) by $\Omega$. We introduce a modified Halpern iterative algorithm with a generalized stepsize so that the implementation of our algorithm does not require prior knowledge of the operator norms. We prove a strong convergence result and give some applications of our result to other nonlinear problems. Finally, we present a numerical example to show the efficiency and accuracy of our algorithm. This result also extends the result of Mewomo et al. (2018) from Hilbert to Banach spaces settings.

2 Preliminaries

In this section, we give some preliminaries, definitions and results which will be needed in the sequel. We denote by ‘$x_n \rightharpoonup x$’ and ‘$x_n \rightarrow x$’, the weak and the strong convergence of $\{x_n\}$ to a point x, respectively.

Let E be a real Banach space with the norm $\Vert \cdot \Vert$ and $E^*$ be the dual with the norm $\Vert \cdot \Vert _*$. We denote the value of the functional $j\in E^*$ at $x\in E$ by $\langle x, j\rangle$. Let $1<q\le 2\le p$ with $\frac{1}{p}+\frac{1}{q} = 1$. The modulus of convexity of E is the function $\delta _E(\epsilon ){:}\,(0, 2]\rightarrow [0, 1]$ defined by

$$\begin{aligned} \delta _{E}(\epsilon ):= \inf \bigg \{1-\left\| \frac{x+y}{2}\right\| {:}\,\Vert x\Vert = \Vert y\Vert =1, \Vert x-y\Vert \ge \epsilon \bigg \}. \end{aligned}$$

E is said to be uniformly convex if $\delta _{E}(\epsilon )>0$ and p-uniformly convex if there exists a $C_p > 0$ such that $\delta _{E}(\epsilon )\ge C_p\epsilon ^p$, for any $\epsilon \in (0, 2]$. The $L_p$ spaces, $1<p<\infty$ are uniformly convex. A uniformly convex Banach space is strictly convex and reflexive. Also, the modulus of smoothness of E is the function $\rho _{E}{:}\,[0, \infty )\rightarrow [0, \infty )$ defined by

$$\begin{aligned} \rho _{E}(\tau ):=\sup \bigg \{\frac{\Vert x+\tau y\Vert +\Vert x-\tau y\Vert }{2} - 1{:}\,\Vert x\Vert =\Vert y\Vert =1\bigg \}. \end{aligned}$$

E is called uniformly smooth if $\lim _{\tau \rightarrow 0^+}\frac{\rho _{E}(\tau )}{\tau }=0$ and q-uniformly smooth if there exists $C_q>0$ such that $\rho _{E}(\tau )\le C_q\tau ^q$. Every uniformly smooth space Banach is smooth and reflexive.

A continuous strictly increasing function $\phi {:}\,{\mathbb {R}}^+\rightarrow {\mathbb {R}}^+$ such that $\phi (0)=0$ and $\lim _{t\rightarrow \infty }\phi (t) = \infty$ is called a gauge function. Given a gauge function $\phi$, the mapping $J^E_{\phi }{:}\,E\rightarrow 2^{E^*}$ defined by

$$\begin{aligned} J^{E}_{\phi }(x) = \{u^*\in E^*{:}\,\langle x, u^*\rangle = \Vert x\Vert \Vert u^*\Vert _*, \Vert u^*\Vert _* = \phi (\Vert x\Vert )\} \end{aligned}$$

is called the duality mapping with gauge function $\phi$. It is known (see Chidume 2009) that $J^E_{\phi }(x)$ is nonempty for any $x\in E$. In the particular case where $\phi (t) = t$, the duality map $J = J_{\phi }$ is called the normalized duality map. If $\phi (t) = t^{p-1}$ where $p>1$, the duality mapping $J^E_{\phi } = J^E_p$ is called the generalized duality mapping from E to $2^{E^*}$. Let $\phi$ be a gauge function and $f(t) = \int ^{t}_{0}\phi (s)\mathrm{d}s$, then f is a convex function on ${\mathbb {R}}^+$.

It is known that when E is uniformly smooth, then $J^E_p$ is norm to norm uniformly continuous on bounded subsets of E and E is smooth if and only if $J^E_p$ is single valued (see Chidume 2009).

If E is p-uniformly convex and uniformly smooth, then $E^*$ is q-uniformly smooth and uniformly convex. This then implies that the duality mapping $J^{E}_p$ is one-to-one, single valued and satisfies $J^{E}_p = (J^{E^*}_q)^{-1}$ (see, e.g. Chidume 2009; Cioranescu 1990).

Xu and Roach (1991) proved the following inequality for q-uniformly smooth Banach spaces.

Lemma 2.1

Let $x, y\in E$. If E is a q-uniformly smooth Banach space, then there exists a $C_q>0$ such that

$$\begin{aligned} \Vert x-y\Vert ^q\le \Vert x\Vert ^q - q\langle y, J^{E}_q(x)\rangle +C_q\Vert y\Vert ^q. \end{aligned}$$

Definition 2.2

(Bauschke et al. 2003; Bauschke and Combettes 2011) A function $f{:}\,E\rightarrow {\mathbb {R}}\cup \{+\infty \}$ is said to be

• (1) proper if its effective domain $D(f) = \{x\in E{:}\,f(x)<+\infty \}$ is nonempty,

• (2) convex if $f(\lambda x+(1-\lambda )y)\le \lambda f(x)+(1-\lambda )f(y)$ for every $\lambda \in (0, 1)$, $x, y \in D(f),$

• (3) lower semicontinuous at $x_0\in D(f)$ if $f(x_0)\le \lim _{x\rightarrow x_0}\inf f(x)$.

Let $x\in \mathrm{int}(\mathrm{dom}\,f)$, for any $y\in E$, the directional derivative of f at x denoted by $f^0(x,y)$ is defined by

$$\begin{aligned} f^0(x,y):=\lim _{t\rightarrow 0^+}\frac{f(x+ty)-f(x)}{t}. \end{aligned}$$

(2.1)

If the limit at $t\rightarrow 0^+$ in (2.1) exists for each y, then the function f is said to be directionally differentiable at x.

Let $f{:}\,E\rightarrow {\mathbb {R}}\cup \{+\infty \}$ be a proper, convex and lower semicontinuous function and $x\in \mathrm{int dom}(f)$. The subdifferential of f at x is the convex set defined by

$$\begin{aligned} \partial f(x) = \{x^*\in E^*{:}\,f(y)\ge \langle y -x, x^*\rangle + f(x) \quad \forall \quad y\in E\}, \end{aligned}$$

and the Fenchel conjugate of f is the function $f^*{:}\,E^*\rightarrow {\mathbb {R}}\cup \{+\infty \}$ defined by

$$\begin{aligned} f^*(y^*) = \sup \{\langle x, y^*\rangle -f(x){:}\,x\in E\}. \end{aligned}$$

Given a directionally differentiable function f, the bifunction $\Delta _f{:}\,\text {dom}\,f \times \text {int dom}\,f\rightarrow [0, +\,\infty )$ defined by

$$\begin{aligned} \Delta _f(y, x):= f(y)-f(x)-\langle \nabla f(x), y - x\rangle , \end{aligned}$$

(2.2)

where $\langle \nabla f(x), y \rangle = f^0(x,y)$ is called the Bregman distance with respect to f. Note that $\Delta _f(y, x)\ge 0$ (see Bauschke et al. 2003). In general, the Bregman distance is not a metric due to the fact that it is not symmetric. However, it possesses some distance-like properties. From (2.2), one can show that the following equality called three-point identity is satisfied:

$$\begin{aligned} \Delta _f(x, y)+\Delta _f(y, z)-\Delta _f(x, z) = \langle x - y, \nabla f(z) - \nabla f(y)\rangle \quad \forall x\in \mathrm{dom}(f), y, z\in \mathrm{int dom}(f). \end{aligned}$$

In addition, if $f(x) = \frac{1}{p}\Vert x\Vert ^p$, where $\frac{1}{p}+\frac{1}{q}=1$, then we have

$$\begin{aligned} \Delta _{f}(y, x) = \Delta _p(y, x)&= \frac{\Vert y\Vert ^p}{p}-\frac{\Vert x\Vert ^p}{p}-\langle y -x, J^E_p(x)\rangle \nonumber \\&= \frac{\Vert y\Vert ^p}{p}-\frac{\Vert x\Vert ^p}{p}-\langle y, J^E_p(x)\rangle + \langle x, J^E_p(x)\rangle \nonumber \\&= \frac{\Vert y\Vert ^p}{p}-\frac{\Vert x\Vert ^p}{p}-\langle y, J^E_p(x)\rangle +\Vert x\Vert ^p \nonumber \\&= \frac{\Vert y\Vert ^p}{p}-\langle y, J^E_p(x)\rangle +\frac{\Vert x\Vert ^p}{q}. \end{aligned}$$

(2.3)

The Bregman projection

$$\begin{aligned} \Pi _Cx := {\mathop {\mathrm{argmin}}\limits _{y\in C}}\Delta _p(x, y), \quad x\in E, \end{aligned}$$

is the unique minimizer of the Bregman distance (see Schöpfer 2007). It can be characterized by the variational inequality:

$$\begin{aligned} \langle J^E_p(x) - J^E_p(\Pi _Cx), z - \Pi _Cx\rangle \le 0, \quad \forall z\in C. \end{aligned}$$

We associate with $f(x) = \frac{1}{p}\Vert x\Vert ^p$, the function $V_p{:}\,E\times E^*\rightarrow [0, +\infty )$ defined by

$$\begin{aligned} V_p(x, {\bar{x}}) = \frac{1}{p}\Vert x\Vert ^p - \langle x, {\bar{x}} \rangle +\frac{1}{q}\Vert {\bar{x}}\Vert ^q, \quad x\in E, {\bar{x}}\in E^*. \end{aligned}$$

$V_p(x, {\bar{x}})\ge 0$ follows from Young’s inequality and the following properties are satisfied (see Kohsaka and Takahashi 2005; Phelps 1993):

$$\begin{aligned}&V_{p}(x, {\bar{x}}) = \Delta _p(x, J^{E^*}_q({\bar{x}})) \quad \forall x\in E, {\bar{x}}\in E^*, \end{aligned}$$

(2.4)

$$\begin{aligned}&V_{p}(x, {\bar{x}})+\langle J^{E^*}_q({\bar{x}})-x, {\bar{y}}\rangle \le V_p(x, {\bar{x}}+{\bar{y}}) \quad \forall x\in E, {\bar{x}}, {\bar{y}}\in E^*. \end{aligned}$$

(2.5)

Also, $V_p$ is convex in the second variable. Thus, for all $z\in E$

$$\begin{aligned} \Delta _p\left( z, J^{E^*}_q\left( \sum ^{N}_{i=1}t_iJ^{E}_px_i\right) \right) \le \sum ^{N}_{i}\Delta _p(z, x_i). \end{aligned}$$

A point $x^*\in C$ is called an asymptotic fixed points of T if C contains a sequence $\{x_n\}$ which converges weakly to $x^*$ such that $\lim _{n\rightarrow \infty }\Vert x_n - Tx_n\Vert =0$. The set of asymptotic fixed points of T will be denoted by ${\hat{F}}(T)$.

Definition 2.3

(Reich and Sabach 2010b, 2011) A mapping $T{:}\,C\rightarrow E$ is said to be

• (1) nonexpansive if $\Vert Tx - Ty\Vert \le \Vert x - y\Vert$ for each $x, y \in C$,

• (2) quasi-nonexpansive if $F(T)\ne \emptyset$ and $\Vert Tx - Ty^*\Vert \le \Vert x - y^*\Vert$ for each $x\in C$ and $y^*\in F(T)$,

• (3) Bregman nonexpansive if

  $$\begin{aligned} \Delta _p(Tx, Ty)\le \Delta _p(x, y)\quad \forall x, y\in C, \end{aligned}$$

• (4) Bregman quasi-nonexpansive if $F(T)\ne \emptyset$ and

  $$\begin{aligned} \Delta _p(Tx, y^*)\le \Delta _p(x, y^*)\quad \forall x \in C, y^*\in F(T), \end{aligned}$$

• (5) Bregman relative nonexpansive if $F(T)\ne \emptyset$, ${\hat{F}}(T)=F(T)$ and

  $$\begin{aligned} \Delta _p(Tx, y^*)\le \Delta _p(x, y^*)\quad \forall x \in C, y^*\in F(T), \end{aligned}$$

• (6) Bregman firmly nonexpansive if for all $x, y\in C,$

  $$\begin{aligned} \Delta _p(Tx, Ty)+\Delta _p(Ty, Tx)+\Delta _p(Tx, x)+\Delta _p(Ty, y)\le \Delta _p(Tx, y)+\Delta _p(Ty, x). \end{aligned}$$

From these definitions, it is evident that the class of Bregman quasi-nonexpansive contains the class of Bregman relative nonexpansive, the class of Bregman firmly nonexpansive and the class of Bregman nonexpansive mapping with $F(T)\ne \emptyset$.

Let E be a p-uniformly convex and uniformly smooth real Banach space and $f{:}\,E\rightarrow {\mathbb {R}}\cup \{+\,\infty \}$ be a proper, convex and lower semicontinuous function. The proximal mapping associated with f with respect to the Bregman distance is defined as

$$\begin{aligned} \mathrm{prox}_{\gamma f}(x):=\arg \min _{u\in E}\bigg \{f(u)+\frac{1}{\gamma }\Delta _p(u,x)\bigg \}. \end{aligned}$$

Bauschke et al. (2003) explore some important properties of the operator $\mathrm {prox}_{\gamma f}$. We note from Bauschke et al. (2003) that $\text {dom prox}_{\gamma f}\subset \text {int dom}\phi$ and $\text {ran prox}_{\gamma f}\subset \mathrm {dom}\phi \cap \mathrm {dom}\,f$, where $\phi (x) = \frac{1}{p}\Vert x\Vert ^p$ and it is convex and Gâteaux differentiable. Furthermore, if $\text {ran prox}_{\gamma f}\subset \text {int dom}\phi$, then $\mathrm{prox}_{\gamma f}$ is Bregman firmly nonexpansive and single-valued on its domain if $\text {int dom}\phi$ is strictly convex. The set of fixed points of $\mathrm{prox}_{\gamma f}$ is indeed the set of minimizers of f (see Bauschke et al. 2003 for more details). Throughout this paper, we shall assume that $\text {ran prox}_{\gamma f}\subset \text {int dom}\phi$.

The following result can be obtained from Jolaoso et al. (2017, Lemma 2.18).

Lemma 2.4

(Jolaoso et al. 2017) Let E be a p-uniformly convex Banach space which is uniformly smooth. Let $f{:}\,E \rightarrow {\mathbb {R}}\cup \{+\infty \}$ be a proper, convex and lower semicontinuous function and let $\mathrm{prox}_{\gamma f}{:}\,E \rightarrow E$ be the proximal operator associated with f for $\gamma >0$, then the following inequality holds: for all $x \in E$ and $z \in F(\mathrm{prox}_{\gamma f})$, we have

$$\begin{aligned} \Delta _p(z,\mathrm{prox}_{\gamma f}(x))+ \Delta _p(\mathrm{prox}_{\gamma f}(x),x) \le \Delta _p(z,x). \end{aligned}$$

The following results will be needed to establish our main theorem.

Lemma 2.5

(Naraghirad and Yao 2013) Let E be a smooth and uniformly convex real Banach space. Let $\{x_n\}$ and $\{y_n\}$ be two sequences in E. Then $\lim _{n\rightarrow \infty }\Delta _p(x_n, y_n) = 0$ if and only if $\lim _{n\rightarrow \infty }\Vert x_n - y_n\Vert = 0$.

Lemma 2.6

(Xu 2002) Let $\{a_n\}$ be a sequence of nonnegative real numbers satisfying the following relation:

$$\begin{aligned} a_{n+1}\le (1 - \alpha _n)a_n+a_n\delta _n, \quad n\ge 0, \end{aligned}$$

where $\{\alpha _n\}\subset (0, 1)$ and $\{\delta _n\}\subset {\mathbb {R}}$ such that $\sum ^{\infty }_{n=1}\alpha _n = \infty$, and $\limsup _{n\rightarrow \infty }\delta _n\le 0$. Then $\lim _{n\rightarrow \infty }a_n=0$.

Lemma 2.7

(Maingé 2008a) Let $\{a_n\}$ be sequence of real numbers such that there exists a subsequence $\{n_i\}$ of $\{n\}$ with $a_{n_i}< a_{n_{i}+1}$ for all $i\in {\mathbb {N}}$. Then, there exists an increasing sequence $\{m_k\}\subset {\mathbb {N}}$ such that $m_k\rightarrow \infty$ and the following properties are satisfied by all (sufficiently large) numbers $k\in {\mathbb {N}}$:

$$\begin{aligned} a_{m_k}\le a_{m_k+1}\quad \text {and}\quad a_k\le a_{m_k +1}. \end{aligned}$$

In fact, $m_k$ is the largest number n in the set $\{1, 2, \ldots k\}$ such that the condition $a_n\le a_{n+1}$ holds.

Lemma 2.8

(Xu and Roach 1991) Let $q\ge 1$ and $r>0$ be two fixed real numbers. Then, a Banach space E is uniformly convex if and only if there exists a continuous, strictly increasing and convex function $g{:}\,{\mathbb {R}}^+\rightarrow {\mathbb {R}}^+$, $g(0)=0$ such that for all $x, y\in B_r$ and $0\le \lambda \le 1$,

$$\begin{aligned} \Vert \lambda x+(1-\lambda )y\Vert ^q\le \lambda \Vert x\Vert ^q+(1-\lambda )\Vert y\Vert ^q - W_q(\lambda )g(\Vert x-y\Vert ), \end{aligned}$$

where $W_q(\lambda ):=\lambda ^q(1-\lambda )+\lambda (1-\lambda )^q$ and $B_r:=\{x\in E{:}\,\Vert x\Vert \le r\}.$

3 Main results

In this section, we present a modified Halpern algorithm for solving (1.14) where $T_1$ and $T_2$ are Bregman quasi-nonexpansive mappings.

Theorem 3.1

Let $E_1, E_2$ and $E_3$ be p-uniformly convex real Banach spaces which are also uniformly smooth. Let C and Q be nonempty closed, convex subsets of $E_1$ and $E_2$, respectively, $A{:}\,E_1\rightarrow E_3$ and $B{:}\,E_2\rightarrow E_3$ be bounded linear operators. Let $f{:}\,E_1\rightarrow {\mathbb {R}}\cup \{+\infty \}$ and $g{:}\,E_2\rightarrow {\mathbb {R}}\cup \{+\infty \}$ be proper, convex and lower semicontinuous functions, $T_1{:}\,E_1\rightarrow E_1$ and $T_2{:}\,E_2\rightarrow E_2$ be Bregman quasi-nonexpansive mappings such that $\Omega \ne \emptyset$. For fixed $u \in E_1$ and $v \in E_2$, choose an initial guess $(x_1,y_1) \in E_1 \times E_2$ and let $\{\alpha _n\} \subset [0,1]$. Assume that the nth iterate $(x_n,y_n) \subset E_1 \times E_2$ has been constructed; then we compute the $(n+1)th$ iterate $(x_{n+1},y_{n+1})$ via the iteration : 

$$\begin{aligned} {\left\{ \begin{array}{ll} u_n = \mathrm{prox}_{\gamma _n f}\left( J^{E^*_1}_q\left[ J^{E_1}_p(x_n)-\gamma _nA^*J^{E_3}_p(Ax_n - By_n)\right] \right) ,\\ x_{n+1} = J^{E^*_1}_q\Big (\alpha _nJ^{E_1}_p(u)+(1-\alpha _n)\left[ \beta _nJ^{E_1}_p(u_n)+(1-\beta _n)J^{E_1}_p(T_1u_n)\right] \Big ),\\ v_n = \mathrm{prox}_{\gamma _n g}\left( J^{E^*_2}_q\left[ J^{E_2}_p(y_n)+\gamma _nB^*J^{E_3}_p(Ax_n - By_n)\right] \right) ,\\ y_{n+1} = J^{E^*_2}_q\Big (\alpha _nJ^{E_2}_p(v)+(1-\alpha _n)\left[ \delta _nJ^{E_2}_p(v_n)+(1-\delta _n)J^{E_2}_p(T_2v_n)\right] \Big ), \end{array}\right. } \end{aligned}$$

(3.1)

for $n \ge 1$, $\{\beta _n\}, ~ \{\delta _n\} \subset (0,1)$, where $A^*$ is the adjoint operator of A. Further, we choose the stepsize $\gamma _n$ such that if $n \in \Gamma := \{n{:}\,Ax_n - B y_n \ne 0 \}$, then

$$\begin{aligned} \gamma ^{q-1}_n \in \left( 0, \frac{q\Vert Ax_n - By_n\Vert ^p}{C_q\Vert A^*J_p^{E_3}(Ax_n - By_n)\Vert ^q +D_q\Vert B^*J_p^{E_3}(Ax_n - By_n)\Vert ^q}\right) , \end{aligned}$$

(3.2)

where $C_q$ and $D_q$ are constants of smoothness of $E_1$ and $E_2$, respectively. Otherwise, $\gamma _{n} = \gamma$ $(\gamma$ being any nonnegative value). Then $\{x_n\}$ and $\{y_n\}$ are bounded.

Proof

Let $(x,y) \in \Omega$, using Lemma 2.1, (2.3) and the Bregman firmly nonexpansivity of prox operators, we have

$$\begin{aligned} \Delta _{p}(x, u_n)= & {} \Delta _p \left( x, \mathrm{prox}_{\gamma _n f}\left( J^{E^*_1}_q\left[ J^{E_1}_p(x_n)-\gamma _nA^*J^{E_3}_p(Ax_n - By_n)\right] \right) \right) \nonumber \\\le & {} \Delta _{p}\left( x, J^{E^*_1}_q\left[ J^{E_1}_p(x_n)-\gamma _nA^*J^{E_3}_p(Ax_n - By_n)\right] \right) \nonumber \\= & {} \frac{\Vert x\Vert ^p}{p} - \langle x, J_p^{E_1}x_n \rangle + \gamma _n \langle x, A^{*}J_p^{E_3}(Ax_n - By_n)\rangle \nonumber \\&+\,\frac{\left\| J_p^{E_1}x_n - \gamma _n A^{*}J_p^{E_3}(Ax_n- By_n)\right\| ^q}{q} \nonumber \\\le & {} \frac{\Vert x\Vert ^p}{p} - \langle x, J_p^{E_1}x_n \rangle + \gamma _n \langle x, A^*J_p^{E_3}(Ax_n - By_n)\rangle \nonumber \\&+\,\frac{\Vert J_p^{E_1}x_n\Vert ^q}{q} - \gamma _n\langle x_n, A^*J_p^{E_3}(Ax_n- By_n)\rangle \nonumber \\&+\,\frac{C_q}{q}{\gamma _n}^q\Vert A^{*}J_p^{E_3}(Ax_n - By_n)\Vert ^q \nonumber \\= & {} \frac{\Vert x\Vert ^p}{p} - \langle x, J_p^{E_1}x_n\rangle + \frac{\Vert x_n\Vert ^p}{q} -\gamma _n\langle x_n - x, A^{*}J_p^{E_3}(Ax_n- By_n)\rangle \nonumber \\&+\,\frac{C_q}{q}{\gamma _n}^q\Vert A^*J^{E_3}_p(Ax_n - By_n)\Vert ^{q}\nonumber \\= & {} \Delta _p(x, x_n) - \gamma _n\langle Ax_n - Ax, J_p^{E_3}(Ax_n- By_n)\rangle \nonumber \\&+\,\frac{C_q}{q}\gamma _n^q\Vert A^*J^{E_3}_p(Ax_n - By_n)\Vert ^{q}. \end{aligned}$$

(3.3)

Following similar to the argument as in (3.3), we have

$$\begin{aligned} \Delta _p\left( y, v_n\right)\le & {} \Delta _p(y, y_n) + \gamma _n\langle By_n - By, J_p^{E_3}(Ax_n- By_n)\rangle \nonumber \\&+ \frac{D_q}{q}\gamma _n^q\Vert B^*J^{E_3}_p(Ax_n - By_n)\Vert ^{q}.\nonumber \\ \end{aligned}$$

(3.4)

Adding (3.3) and (3.4) and noting that $Ax = By$, we obtain

$$\begin{aligned}&\Delta _p(x, u_n)+\Delta _p(y, u_n) \nonumber \\&\quad \le \Delta _p(x, x_n)+\Delta _p(y, y_n)-\gamma _n\langle Ax_n - By_n, J_p^{E_3}(Ax_n - By_n) \rangle \nonumber \\&\qquad +\,\frac{C_q}{q}\gamma _n^q\Vert A^*J_p^{E_3}(Ax_n - By_n)\Vert ^{q} + \frac{D_q}{q}\gamma _n^q\Vert B^*J_p^{E_3}(Ax_n - By_n)\Vert ^{q} \nonumber \\&\quad = \Delta _p(x, x_n)+\Delta _p(y, y_n) -\gamma _n \bigg \{\Vert Ax_n - Bx_n\Vert ^p \nonumber \\&\qquad -\,\frac{\gamma _n^{q-1}}{q}\Big (C_q\Vert A^*J_p^{E_3}(Ax_n - By_n)\Vert ^{q} + D_q\Vert B^*J_p^{E_3}(Ax_n - By_n)\Vert ^{q}\Big )\bigg \}. \end{aligned}$$

(3.5)

From the choice of $\gamma _n$ (3.2), we have that

$$\begin{aligned} \Delta _p(x, u_n)+\Delta _p(y, u_n)\le \Delta _p(x, x_n)+\Delta _p(y, y_n). \end{aligned}$$

(3.6)

Thus from (3.1) and (3.6), we get

$$\begin{aligned}&\Delta _p(x, x_{n+1})+\Delta _p(y, y_{n+1}) \\&\quad = \Delta _p \left( x, J_q^{E_1^*}\left( \alpha _n J_p^{E_1}u+(1-\alpha _n)\left[ \beta _n J_p^{E_1}u_n+(1-\beta _n)J_p^{E_1}(T_1u_n)\right] \right) \right) \\&\qquad +\,\Delta _p\left( y, J_q^{E_2^*}(\alpha _n J_p^{E_2}v+(1-\alpha _n)[\delta _n J_p^{E_2}v_n+(1-\delta _n)J_p^{E_2}(T_2v_n)])\right) \\&\quad \le \alpha _n\Delta _p(x, u)+(1-\alpha _n)\beta _n\Delta _p(x, u_n)+(1-\alpha _n)(1-\beta _n)\Delta _p(x, T_1u_n)\\&\qquad +\,\alpha _n\Delta _p(y, v)+(1-\alpha _n)\delta _n\Delta _p(y, v_n)+(1-\alpha _n)(1-\delta _n)\Delta _p(y, T_2v_n)\\&\quad \le \alpha _n\Delta _p(x, u)+(1-\alpha _n)\beta _n\Delta _p(x, u_n)+(1-\alpha _n)(1-\beta _n)\Delta _p(x, u_n)+\alpha _n\Delta _p(y, v)\\&\qquad +\,(1-\alpha _n)\delta _n\Delta _p(y, v_n)+(1-\alpha _n)(1-\delta _n)\Delta _p(y, v_n)\\&\quad = \alpha _n[\Delta _p(x, u)+\Delta _p(y,v)]+(1-\alpha _n)[\Delta _p(x, u_n)+\Delta _p(y, v_n)]\\&\quad \le \alpha _n[\Delta _p(x,u)+\Delta _p(y,v)]+(1-\alpha _n) [\Delta _p(x,x_n) +\Delta _p(y, y_n)\\&\quad \le \max \{(\Delta _p(x, u)+\Delta _p(y, v)), (\Delta _p(x, x_n)+\Delta _p(y, y_n))\}\\&\qquad \vdots \\&\quad \le \max \bigg \{(\Delta _p(x, u)+\Delta _p(y, v)), (\Delta _p(x, x_0)+\Delta _p(y, y_0))\bigg \}. \end{aligned}$$

Thus, the last inequality implies that $\{x_n\}$ and $\{y_n\}$ are bounded. Consequently, $\{u_n\}$, $\{v_n\}$, $\{T_1u_n\}$ and $\{T_2v_n\}$ are bounded. $\square$

Theorem 3.2

Let $E_1, E_2$ and $E_3$ be p-uniformly convex real Banach spaces which are also uniformly smooth. Let C and Q be nonempty closed, convex subsets of $E_1$ and $E_2$, respectively, $A{:}\,E_1\rightarrow E_3$ and $B{:}\,E_2\rightarrow E_3$ be bounded linear operators. Let $f{:}\,E_1\rightarrow {\mathbb {R}}\cup \{+\infty \}$ and $g{:}\,E_2\rightarrow {\mathbb {R}}\cup \{+\infty \}$ be proper, convex and lower semicontinuous functions, $T_1{:}\,E_1\rightarrow E_1$ and $T_2{:}\,E_2\rightarrow E_2$ be Bregman quasi-nonexpansive mappings such that $F(T_i) = {\hat{F}}(T_i)$, $i=1, 2$ and $\Omega \ne \emptyset$. For fixed $u \in E_1$ and $v \in E_2$, choose an initial guess $(x_1,y_1) \in E_1 \times E_2$ and let $\{\alpha _n\} \subset [0,1]$. Suppose $(\{x_n\},\{y_n\})$ is generated by algorithm (3.1) and the following conditions are satisfied:

• (i) $\lim _{n\rightarrow \infty }\alpha _n = 0,$ and $\sum _{n =0}^\infty \alpha _n = \infty$,

• (ii) $0< a \le \liminf _{n\rightarrow \infty }\beta _n \le \limsup _{n\rightarrow \infty }\beta _n <1,$

• (iii) $0< b \le \liminf _{n\rightarrow \infty }\delta _n \le \limsup _{n\rightarrow \infty }\delta _n <1.$

Then the sequence $\{(x_n,y_n)\}$ converges strongly to $(x^*,y^*) = (\Pi _\Omega u, \Pi _\Omega v).$

Proof

Let $(x,y)\in \Omega$. Then from (2.4) and (2.5), we have

$$\begin{aligned} \Delta _p(x, x_{n+1})= & {} \Delta _p\Big (x, J_q^{E_1^*}(\alpha _nJ_p^{E_1}u+(1-\alpha _n)[\beta _n J_p^{E_1}u_n+(1-\beta _n)J_p^{E_1}(T_1u_n)])\Big )\nonumber \\= & {} V_p\Big (x, \alpha _n J_p^{E_1}u+(1-\alpha _n)[\beta _n J_p^{E_1}u_n+(1-\beta _n)J_p^{E_1}T_1u_n]\Big ) \nonumber \\\le & {} V_p\Big (x, \alpha _n J_p^{E_1}u+(1-\alpha _n)[\beta _n J_p^{E_1}u_n+(1-\beta _n)J_p^{E_1}(T_1u_n)]\nonumber \\&-\,\alpha _n(J_p^{E_1}u -J_p^{E_1}x)\Big ) + \alpha _n\langle J_p^{E_1}u - J_p^{E_1}x, x_{n+1} - x\rangle \nonumber \\= & {} V_p\Big (x, \alpha _n J_p^{E_1}x + (1 - \alpha _n)\left[ \beta _n J_p^{E_1}u_n+(1-\beta _n)J_p^{E_1}T_1u_n\right] \Big )\nonumber \\&+\,\alpha _n\langle J_p^{E_1}u - J_p^{E_1}x, x_{n+1} - x\rangle \nonumber \\= & {} \Delta _p\Big (x, J_q^{E_1^*}\left( \alpha _n J_p^{E_1}x + (1-\alpha _n)\left[ \beta _n J_p^{E_1}u_n+(1 - \beta _n)J_p^{E_1}T_1u_n\right] \right) \Big ) \nonumber \\&+\,\alpha _n\langle J_p^{E_1}u - J_p^{E_1}x, x_{n+1} - x\rangle \nonumber \\\le & {} \alpha _n\Delta _p(x, x) + (1-\alpha _n)\beta _n\Delta _p(x, u_n)+(1-\alpha _n)(1-\beta _n)\Delta _p(x, T_1u_n) \nonumber \\&+\,\alpha _n\langle J_p^{E_1}u - J_p^{E_1}x, x_{n+1} - x\rangle \nonumber \\\le & {} (1 - \alpha _n)\beta _n\Delta _p(x, u_n)+(1-\alpha _n)(1-\beta _n)\Delta _p(x, u_n)\nonumber \\&+\,\alpha _n\langle J_p^{E_1}u-J_p^{E_1}x, x_{n+1} - x\rangle \nonumber \\= & {} (1-\alpha _n)\Delta _p(x, u_n)+\alpha _n\langle J_p^{E_1}u-J_p^{E_1}x, x_{n+1} - x\rangle . \end{aligned}$$

(3.7)

Similarly for $\Delta _p(y, y_{n+1})$, we obtain

$$\begin{aligned} \Delta _p(y, y_{n+1})\le (1-\alpha _n)\Delta _p(y, v_n)+\alpha _n\langle J_p^{E_2}v-J_p^{E_2}y, y_{n+1} - y\rangle . \end{aligned}$$

(3.8)

Thus, from (3.5), (3.7) and (3.8), we obtain that

$$\begin{aligned}&\Delta _p(x, x_{n+1})+\Delta _p(y, y_{n+1}) \nonumber \\&\quad \le (1-\alpha _n)\left( \Delta _p(x, u_n)+\Delta _p(y, v_n)\right) +\alpha _n (\langle J_p^{E_1}u-J_p^{E_1}x, x_{n+1} - x\rangle \nonumber \\&\qquad +\,\langle J_p^{E_2}v - J_p^{E_2}y, y_{n+1} - y \rangle ) \end{aligned}$$

(3.9)

$$\begin{aligned}&\quad \le (1-\alpha _n)(\Delta _p(x, x_{n})+\Delta _p(y, y_{n})) -\gamma _n(1-\alpha _n) \bigg \{\Vert Ax_n - Bx_n\Vert ^p\nonumber \\&\qquad -\,\frac{\gamma _n^{q-1}}{q}\Big (C_q\Vert A^*J_p^{E_3}(Ax_n - By_n)\Vert ^{q} + D_q\Vert B^*J_p^{E_3}(Ax_n - By_n)\Vert ^{q}\Big )\bigg \}\nonumber \\&\qquad +\,\alpha _n\langle J_p^{E_1}u - J_p^{E_1}x, x_{n+1}-x\rangle + \alpha _n\langle J_p^{E_2}v - J_p^{E_2}y, y_{n+1} - y\rangle . \end{aligned}$$

(3.10)

To this end, let $\Gamma _n = \Delta _p(x, x_n)+\Delta _p(y, y_n)$ and $\tau _n = \alpha _n\langle J_p^{E_1}u - J_p^{E_1}x, x_{n+1}-x\rangle + \alpha _n\langle J_p^{E_2}v - J_p^{E_2}y, y_{n+1} - y\rangle$. We consider the following cases:

Case 1 Suppose $\exists$ $n_0\in {\mathbf {N}}$ such that $\{\Gamma _n\}$ is monotonically non-increasing for all $n\ge n_0$. Since $\Gamma _n$ is bounded it implies that $\{\Gamma _n\}$ converges and

$$\begin{aligned} \Gamma _{n+1}-\Gamma _n \rightarrow 0, \quad \mathrm {as}\quad n\rightarrow \infty . \end{aligned}$$

Set

$$\begin{aligned} K_n = C_q\Vert A^*J_p^{E_3}(Ax_n - By_n)\Vert ^{q} + D_q\Vert B^*J_p^{E_3}(Ax_n - By_n)\Vert ^{q}, \end{aligned}$$

it follows from (3.10) that

$$\begin{aligned} \gamma _n(1-\alpha _n)\left( \Vert Ax_n - By_n\Vert ^p -\frac{\gamma _n^{q-1}}{q}K_n \right)&\quad \le (1-\alpha _n)\Gamma _n - \Gamma _{n+1}+\alpha _n\tau _n \rightarrow 0, \end{aligned}$$

(3.11)

as $n \rightarrow \infty$. By the choice of the stepsize (3.2), there exists a very small $\epsilon >0$ such that

$$\begin{aligned} 0 <\gamma _n^{q-1} \le \dfrac{q||Ax_n - By_n||^p}{K_n} - \epsilon , \end{aligned}$$

which means that

$$\begin{aligned} \gamma _n^{q-1}K_n \le q||Ax_n - By_n||^p - \epsilon K_n, \end{aligned}$$

and hence

$$\begin{aligned} \dfrac{\epsilon K_n}{q} \le ||Ax_n -By_n||^p - \dfrac{\gamma _n^{q-1}}{q}K_n \rightarrow 0, ~~\mathrm{as}~~n \rightarrow \infty . \end{aligned}$$

Hence

$$\begin{aligned} \lim _{n \rightarrow \infty } K_n = \lim _{n \rightarrow \infty } \Big (C_q\Vert A^*J_p^{E_3}(Ax_n - By_n)\Vert ^{q} + D_q\Vert B^*J_p^{E_3}(Ax_n - By_n)\Vert ^{q}\Big ) = 0. \end{aligned}$$

This implies that

$$\begin{aligned} \lim _{n \rightarrow \infty }\Vert A^*J_p^{E_3}(Ax_n - By_n)\Vert ^q = \lim _{n \rightarrow \infty }\Vert B^*J_p^{E_3}(Ax_n - By_n)\Vert ^q = 0. \end{aligned}$$

(3.12)

Also from (3.11), we have

$$\begin{aligned} \lim _{n \rightarrow \infty }||Ax_n - By_n||^p = 0. \end{aligned}$$

(3.13)

Let $w_n = J_q^{E_1^*}(\beta _nJ_p^{E_1}u_n +(1-\beta _n)J_p^{E_1}T_1u_n)$ and $z_n = J_q^{E_2^*}(\delta _nJ_p^{E_2}v_n +(1-\delta _n)J_p^{E_2}T_2v_n)$. Using Lemma 2.8, we have

$$\begin{aligned} \Delta _p(x,w_n)= & {} \Delta _p(x,J_q^{E_1^*}(\beta _n J_p^{E_1}u_n + (1-\beta _n)J_p^{E_1}T_1u_n)) \nonumber \\= & {} \frac{1}{p}\Vert x\Vert ^p - \beta _n\langle x, J_p^{E_1}u_n \rangle - (1 - \beta _n)\langle x, J_p^{E_1}T_1u_n\rangle \nonumber \\&+\,\frac{1}{q}\Vert \beta _nJ_p^{E_1}u_n +(1-\beta _n)J_p^{E_1}T_1u_n\Vert ^q \nonumber \\\le & {} \beta _n \frac{1}{p}\Vert x\Vert ^p + (1-\beta _n)\frac{1}{p}\Vert x\Vert ^p -\beta _n\langle x, J_p^{E_1}u_n \rangle - (1 - \beta _n)\langle x, J_p^{E_1}T_1u_n \rangle \nonumber \\&+\,\frac{1}{q}\beta _n\Vert u_n\Vert ^p +\frac{(1-\beta _n)}{q}\Vert T_1u_n\Vert ^p \nonumber \\&-\,\frac{W_q(\beta _n)}{q}g(\Vert J^{E_1}_pu_n - J^{E_1}_p(T_1u_n)\Vert ) \nonumber \\= & {} \beta _n\Delta _p(x,u_n)+(1-\beta _n)\Delta _p(x,T_1u_n) -\frac{W_q(\beta _n)}{q}g(\Vert J^{E_1}_pu_n - J^{E_1}_p(T_1u_n)\Vert ) \nonumber \\\le & {} \Delta _p(x,u_n) - \frac{W_q(\beta _n)}{q}g(\Vert J^{E_1}_pu_n - J^{E_1}_p(T_1u_n)\Vert ). \end{aligned}$$

(3.14)

Similarly, we have

$$\begin{aligned} \Delta _p(y, z_n)\le & {} \Delta _p(y,v_n) - \frac{W_q(\delta _n)}{q}g(\Vert J^{E_2}_pv_n - J^{E_2}_p(T_2v_n)\Vert ). \end{aligned}$$

(3.15)

By adding (3.14) and (3.15), we have

$$\begin{aligned} \Delta _p(x,w_n)+ \Delta _p(y, z_n)\le & {} \Delta _p(x,u_n) + \Delta _p(y,v_n)- \frac{W_q(\beta _n)}{q}g(\Vert J^{E_1}_pu_n - J^{E_1}_p(T_1u_n)\Vert ) \nonumber \\&-\,\frac{W_q(\delta _n)}{q}g(\Vert J^{E_2}_pv_n - J^{E_2}_p(T_2v_n)\Vert ) \nonumber \\\le & {} \Delta _p(x,x_n) + \Delta _p(y,y_n)- \frac{W_q(\beta _n)}{q}g(\Vert J^{E_1}_pu_n - J^{E_1}_p(T_1u_n)\Vert ) \nonumber \\&-\,\frac{W_q(\delta _n)}{q}g(\Vert J^{E_2}_pv_n - J^{E_2}_p(T_2v_n)\Vert ). \end{aligned}$$

(3.16)

Observe that

$$\begin{aligned} \Delta _p(x,x_{n+1}) + \Delta _p(y, y_{n+1})= & {} \Delta _p(x, J_q^{E_1^*}(\alpha _n J_p^{E_1}u + (1-\alpha _n)J_p^{E_1}w_n)) \\&+\,\Delta _p(y, J_q^{E_2^*}(\alpha _n J_p^{E_2}v + (1-\alpha _n)J_p^{E_2}z_n)) \\\le & {} \alpha _n \left( \Delta _p(x,u)+ \Delta _p(y,v)\right) \\&+\,(1-\alpha _n)\left( \Delta _p(x,w_n)+ \Delta _p(y,z_n)\right) , \end{aligned}$$

therefore, from (3.16), we get

$$\begin{aligned} \Delta _p(x,x_{n+1}) + \Delta _p(y, y_{n+1})\le & {} \alpha _n \left( \Delta _p(x,u)+ \Delta _p(y,v)\right) \\&+\,(1-\alpha _n)\Big ( \Delta _p(x,x_n) + \Delta _p(y,y_n) \\&-\,\frac{W_q(\beta _n)}{q}g(\Vert J^{E_1}_pu_n - J^{E_1}_p(T_1u_n)\Vert ) \\&-\,\frac{W_q(\delta _n)}{q}g(\Vert J^{E_2}_pv_n - J^{E_2}_p(T_2v_n)\Vert ) \Big ). \end{aligned}$$

This implies that

$$\begin{aligned}&(1-\alpha _n)\left( \frac{W_q(\beta _n)}{q}g(\Vert J^{E_1}_pu_n - J^{E_1}_p(T_1u_n)\Vert ) + \frac{W_q(\delta _n)}{q}g(\Vert J^{E_2}_pv_n - J^{E_2}_p(T_2v_n)\Vert ) \right) \nonumber \\&\quad \le \alpha _n \left( \Delta _p(x,u)+ \Delta _p(y,v)\right) + (1-\alpha _n)\left( \Delta _p(x,x_n) \right. \nonumber \\&\qquad \left. +\,\Delta _p(y,y_n) \right) - \left( \Delta _p(x,x_{n+1}) + \Delta _p(y, y_{n+1})\right) \nonumber \\&\quad = \Gamma _n - \Gamma _{n+1} + \alpha _n(\Delta _p(x,u)+ \Delta _p(y,v)) - \alpha _n \Gamma _n \rightarrow 0, ~~\mathrm{as}~~n \rightarrow \infty . \end{aligned}$$

(3.17)

Hence

$$\begin{aligned} \lim _{n \rightarrow \infty }\left( \frac{W_q(\beta _n)}{q}g(\Vert J^{E_1}_pu_n - J^{E_1}_p(T_1u_n)\Vert ) + \frac{W_q(\delta _n)}{q}g(\Vert J^{E_2}_pv_n - J^{E_2}_p(T_2v_n)\Vert ) \right) = 0.\nonumber \\ \end{aligned}$$

(3.18)

Thus, we obtain

$$\begin{aligned} \lim _{n\rightarrow \infty }g(\Vert J^{E_1}_pu_n - J^{E_1}_p(T_1u_n)\Vert ) = \lim _{n \rightarrow \infty }g(\Vert J^{E_2}_pv_n - J^{E_2}_p(T_2v_n)\Vert ) =0. \end{aligned}$$

By the continuity of g, we have

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert J^{E_1}_pu_n - J^{E_1}_p(T_1u_n)\Vert = \lim _{n \rightarrow \infty }\Vert J^{E_2}_pv_n - J^{E_2}_p(T_2v_n)\Vert =0. \end{aligned}$$

Also, since $J_q^{E_1}$ and $J_q^{E_2}$ are uniformly continuous on bounded subsets of $E_1$ and $E_2$, respectively, then

$$\begin{aligned} \lim _{n \rightarrow \infty }||T_1 u_n - u_n|| = \lim _{n \rightarrow \infty }||T_2 v_n - v_n|| = 0. \end{aligned}$$

(3.19)

Furthermore,

$$\begin{aligned} \Vert J_p^{E_1}w_n - J_p^{E_1}u_n\Vert = (1-\beta _n)\Vert J_p^{E_1}T_1u_n - J_p^{E_1}u_n\Vert \rightarrow 0, ~~\mathrm{as}~~n \rightarrow \infty , \end{aligned}$$

and

$$\begin{aligned} \Vert J_p^{E_2}z_n - J_p^{E_2}v_n\Vert = (1-\delta _n)\Vert J_p^{E_2}T_2v_n - J_p^{E_2}u_n\Vert \rightarrow 0, ~~\mathrm{as}~~n \rightarrow \infty . \end{aligned}$$

This implies that

$$\begin{aligned} \lim _{n \rightarrow \infty }||w_n - u_n|| = \lim _{n \rightarrow \infty } ||z_n - v_n|| = 0. \end{aligned}$$

(3.20)

Also

$$\begin{aligned} \Delta _p(x_{n+1}, w_n)&= \Delta _p(J_q^{E_1^*}(\alpha _nJ_p^{E_1}u+(1-\alpha _n)J_p^{E_1}w_n), w_n)\\&\le \alpha _n\Delta _p(u, w_n)+(1-\alpha _n)\Delta _p(w_n, w_n)\rightarrow 0 \quad \mathrm {as}\quad n\rightarrow \infty , \end{aligned}$$

therefore, by Lemma 2.5, we have

$$\begin{aligned} \lim _{n \rightarrow \infty }||x_{n+1}-w_n|| = 0. \end{aligned}$$

(3.21)

Similarly

$$\begin{aligned} \Delta _p(y_{n+1}, z_n)= & {} \Delta _p(J_q^{E_2^*}(\alpha _nJ_p^{E_2}v+(1-\alpha _n)J_p^{E_2}z_n), z_n)\\\le & {} \alpha _n\Delta _p(v, z_n)+(1-\alpha _n)\Delta _p(z_n, z_n)\rightarrow 0 \quad \mathrm {as}\quad n\rightarrow \infty , \end{aligned}$$

and

$$\begin{aligned} \lim _{n \rightarrow \infty }||y_{n+1} - z_n|| = 0. \end{aligned}$$

Now, let $s_n = J_q^{E_1^*}(J_p^{E_1}x_n-\gamma _nA^*J_p^{E_3}(Ax_n - By_n))$ and $t_n = J_q^{E_2^*}(J_p^{E_2}y_n + \gamma _n B^*J_p^{E_3}(Ax_n - By_n))$. Note that from (3.3) and (3.4), we have

$$\begin{aligned} \Delta _p(x,s_n) + \Delta _p(y,t_n)\le & {} \Delta _p(x,x_n) + \Delta _p(y,y_n). \end{aligned}$$

Using Lemma 2.4, we obtain

$$\begin{aligned} \Delta _p(x,u_n) + \Delta _p(y,v_n)= & {} \Delta _p(x,\mathrm{prox}_{\gamma _{n} f} s_n) + \Delta _p(y, \mathrm{prox}_{\gamma _{n} g} t_n) \\\le & {} \Delta _p(x,s_n) - \Delta _p( \mathrm{prox}_{\gamma _{n} f} s_n,s_n) + \Delta _p(y, t_n) - \Delta _p( \mathrm{prox}_{\gamma _{n} g} t_n,t_n). \end{aligned}$$

Hence from (3.10), we have

$$\begin{aligned}&\Delta _p( \mathrm{prox}_{\gamma _{n} f} s_n,s_n) + \Delta _p( \mathrm{prox}_{\gamma _{n} g} t_n,t_n) \\&\quad \le \Delta _p(x,s_n)+ \Delta _p(y, t_n) - (\Delta _p(x,u_n) + \Delta _p(y,v_n)) \\&\quad \le \Delta _p(x,x_n) + \Delta _p(y,y_n) - (\Delta _p(x,u_n) + \Delta _p(y,v_n)) \\&\quad \le \Delta _p(x,x_n) + \Delta _p(y,y_n) - (\Delta _p(x, x_{n+1})+\Delta _p(y, y_{n+1})) \\&\qquad +\,\alpha _n (\langle J_p^{E_1}u-J_p^{E_1}x, x_{n+1} - x\rangle + \langle J_p^{E_2}v - J_p^{E_2}y, y_{n+1} - y \rangle ) \\&\quad = \Gamma _n - \Gamma _{n+1} +\alpha _n (\langle J_p^{E_1}u-J_p^{E_1}x, x_{n+1} - x\rangle \\&\qquad +\,\langle J_p^{E_2}v - J_p^{E_2}y, y_{n+1} - y \rangle ) \rightarrow 0, ~~\mathrm{as}~~n \rightarrow \infty . \end{aligned}$$

Hence

$$\begin{aligned} \lim _{n \rightarrow \infty }\Delta _p( \mathrm{prox}_{\gamma _{n} f} s_n,s_n)= \lim _{n \rightarrow \infty }\Delta _p( \mathrm{prox}_{\gamma _{n} g} t_n,t_n) =0. \end{aligned}$$

Thus by Lemma 2.5, we get

$$\begin{aligned} \lim _{n \rightarrow \infty }||\mathrm{prox}_{\gamma _{n} f} s_n- s_n|| = \lim _{n \rightarrow \infty }||\mathrm{prox}_{\gamma _{n} g} t_n-t_n|| = 0. \end{aligned}$$

(3.22)

Since $E_1$ and $E_2$ are uniformly smooth, then $J_p^{E_1}$ and $J_p^{E_2}$ are uniformly continuous on bounded subsets of $E_1$ and $E_2$, respectively. Therefore

$$\begin{aligned} \lim _{n \rightarrow \infty }||J_p^{E_1}s_n - J_p^{E_1}u_n|| = \lim _{n \rightarrow \infty }||J_p^{E_2}t_n - J_p^{E_2}v_n|| = 0. \end{aligned}$$

It follows from the definition of $s_n$ that

$$\begin{aligned} 0\le & {} ||J_p^{E_1}s_n - J_p^{E_1}x_n|| \\\le & {} \gamma _n ||A^*||||J_p^{E_3}(Ax_n -By_n)|| \\= & {} \gamma _{n}||A^*||||Ax_n -By_n||^{p-1} \rightarrow 0,~~\mathrm{as}~~n \rightarrow \infty . \end{aligned}$$

Hence

$$\begin{aligned} \lim _{n \rightarrow \infty }||s_n -x_n|| = 0. \end{aligned}$$

Similarly, we can show that

$$\begin{aligned} \lim _{n\rightarrow 0} ||t_n -y_n|| = 0. \end{aligned}$$

(3.23)

It follows therefore from (3.22) that

$$\begin{aligned} \lim _{n \rightarrow \infty }||u_n - x_n|| \le \lim _{n \rightarrow \infty }\Big (||u_n -s_n||+||s_n - x_n||\Big ) = 0, \end{aligned}$$

(3.24)

and

$$\begin{aligned} \lim _{n\rightarrow \infty }||v_n - y_n|| \le \lim _{n \rightarrow \infty }\Big (||v_n - t_n||+||t_n - y_n||\Big )= 0. \end{aligned}$$

(3.25)

Hence, by combining (3.20), (3.21) and (3.24), we get

$$\begin{aligned} \lim _{n \rightarrow \infty }||x_{n+1} -x_n|| \le \lim _{n \rightarrow \infty }\Big (||x_{n+1} - w_n||+||w_n - u_n||+||u_n - x_n||\Big )= 0. \end{aligned}$$

(3.26)

Similarly, we obtain

$$\begin{aligned} \lim _{n \rightarrow \infty }||y_{n+1} -y_n|| \le \lim _{n \rightarrow \infty }\Big (||y_{n+1} - z_n||+||z_n - v_n||+||v_n - y_n||\Big )= 0. \end{aligned}$$

(3.27)

Since $E_1$, $E_2$ are uniformly convex and uniformly smooth and $\{(x_n, y_n)\}$ is bounded, there exists a subsequence $\{(x_{n_i}, y_{n_i})\}$ of $\{(x_n,y_n)\}$ such that $(x_{n_i}, y_{n_i})\,\rightharpoonup \,({\bar{x}}, {\bar{y}}) \in E_1 \times E_2$. Also from (3.24) and (3.25), we obtain that $\{(u_{n_i},v_{n_i})\}\,\rightharpoonup \,({\bar{x}},{\bar{y}})$. Since ${\hat{F}}(T_i) = F(T_i),$ for $i=1,2$, it follows from (3.19) that ${\bar{x}} \in F(T_1)$ and ${\bar{y}} \in F(T_2)$. Furthermore, we show that ${\bar{x}} \in \mathrm{Argmin}(f)$ and ${\bar{y}} \in \mathrm{Argmin}(g)$. Since $s_{n_i} - x_{n_i} \rightarrow 0$, as $i \rightarrow \infty$, it follows from (3.22) that ${\bar{x}} = \mathrm{prox}_{\gamma _{n_i}f}({\bar{x}})$, hence ${\bar{x}}$ is a fixed point of the proximal operator of f, or equivalently, $0 \in \partial f({\bar{x}})$. Thus, ${\bar{x}} \in \mathrm{Argmin}(f)$. Similarly, we obtain that ${\bar{y}} \in \mathrm{Argmin}(g)$.

Now, since $A{:}\,E_1 \rightarrow E_3$ and $B{:}\,E_2 \rightarrow E_3$ are bounded linear operators, we have $Ax_{n_i} \rightharpoonup A{\bar{x}}$ and $By_{n_i} \rightharpoonup B {\bar{y}}$. By the weak lower semicontinuity of the norm and (3.13), we have

$$\begin{aligned} ||A{\bar{x}} - B {\bar{y}}|| \le \liminf _{i\rightarrow \infty }||Ax_{n_i} - By_{n_i}||=0. \end{aligned}$$

Hence, $A{\bar{x}} = B{\bar{y}}$. This implies that $({\bar{x}},{\bar{y}}) \in \Omega$.

Next, we show that $\{(x_n,y_n)\}$ converges strongly to $(x^*,y^*) = (\Pi _\Omega u, \Pi _\Omega v).$ From (3.10), we have

$$\begin{aligned} \Delta _p(x, x_{n+1})+\Delta _p(y, y_{n+1})\le & {} (1-\alpha _n)(\Delta _p(x, x_{n})+\Delta _p(y, y_{n}))\nonumber \\&+\,\alpha _n(\langle J_p^{E_1}u - J_p^{E_1}x, x_{n+1}-x\rangle \nonumber \\&+\,\langle J_p^{E_2}v - J_p^{E_2}y, y_{n+1} - y\rangle ). \end{aligned}$$

(3.28)

Choose subsequences $\{x_{n_i}\}$ of $\{x_n\}$ and $\{y_{n_i}\}$ of $\{y_n\}$ such that

$$\begin{aligned} \limsup _{n\rightarrow \infty }\langle J_p^{E_1}u - J_p^{E_1}x^*, x_{n+1} -x^* \rangle = \lim _{i \rightarrow \infty }\langle J_p^{E_1}u - J_p^{E_1}x^*, x_{n_i+1} - x^* \rangle , \end{aligned}$$

and

$$\begin{aligned} \limsup _{n\rightarrow \infty }\langle J_p^{E_2}v - J_p^{E_2}y^*, y_{n+1} - y^* \rangle = \lim _{i \rightarrow \infty } \langle J_p^{E_2}v -J_p^{E_2}y^*, y_{n_i+1} - y^* \rangle . \end{aligned}$$

Since $(x_{n_i},y_{n_i}) \rightharpoonup ({\bar{x}},{\bar{y}})$ and from (3.26) and (3.27), we get

$$\begin{aligned} \limsup _{n\rightarrow \infty }\langle J_p^{E_1}u-J_p^{E_1}x^*,x_{n+1}-x^* \rangle= & {} \lim _{i\rightarrow \infty }\langle J_p^{E_1}u-J_p^{E_1}x^*,x_{{n_i}+1}-x^* \rangle \nonumber \\= & {} \langle J_p^{E_1}u-J_p^{E_1}x^*,{\bar{x}}-x^* \rangle \le 0, \end{aligned}$$

(3.29)

and

$$\begin{aligned} \limsup _{n\rightarrow \infty }\langle J_p^{E_2}(v)-J_p^{E_2}(y^*),y_{n+1}-y^* \rangle= & {} \lim _{i\rightarrow \infty }\langle J_p^{E_2}v-J_p^{E_2}y^*,y_{{n_i}+1}-y^* \rangle \nonumber \\= & {} \langle J_p^{E_2}v-J_p^{E_2}y^*,{\bar{y}}-y^* \rangle \le 0. \end{aligned}$$

(3.30)

Hence, from (3.28), (3.29), (3.30) and using Lemma 2.6, we get that

$$\begin{aligned} \lim _{n \rightarrow \infty }\big (\Delta _p(x_{n}, x^*)+\Delta _p(y_n, y^*)\big ) = 0. \end{aligned}$$

This therefore implies that $(x_n,y_n) \rightarrow (x^*,y^*) = (\Pi _\Omega u, \Pi _\Omega v).$

Case 2

Suppose $\Gamma _n$ is not eventually monotonically decreasing. Then by Lemma 2.7, there exists a nondecreasing sequence $\{m_k\}\subset {\mathbb {N}}$ such that $m_k\rightarrow \infty$ and

$$\begin{aligned} 0\le \Gamma _{m_k}\le \Gamma _{{m_k}+1} \quad \text {for all} \quad k\in {\mathbb {N}}. \end{aligned}$$

Following similar argument as in case 1, we obtain $\Vert x_{m_k} - u_{m_k}\Vert \rightarrow 0$, $\Vert y_{m_k} - v_{m_k}\Vert \rightarrow 0$, $\Vert T_1u_{m_k} - u_{m_k}\Vert \rightarrow 0$ and $\Vert T_2v_{m_k} - v_{m_k}\Vert \rightarrow 0$ as $k\rightarrow \infty$.

Also

$$\begin{aligned} \limsup _{k\rightarrow \infty }\langle J^{E_1}_pu - J^{E_1}_px^*, x_{{m_k}+1} - x^*\rangle \le 0. \end{aligned}$$

(3.31)

and

$$\begin{aligned} \limsup _{k\rightarrow \infty }\langle J^{E_2}_pv - J^{E_2}_py^*, y_{{m_k}+1} - y^*\rangle \le 0. \end{aligned}$$

(3.32)

From (3.10), we obtain

$$\begin{aligned} \Delta _p(x^*, x_{{m_k}+1})+\Delta _p(y^*, y_{{m_k}+1})&\le (1-\alpha _{m_k})(\Delta _p(x^*, x_{m_k})+\Delta _p(y^*, y_{m_k}))\nonumber \\&\quad +\,\alpha _{m_k}(\langle J_p^{E_1}u - J_p^{E_1}x^*, x_{{m_k}+1}-x^*\rangle \nonumber \\&\quad +\,\langle J_p^{E_2}v - J_p^{E_2}y, y_{{m_k}+1} - y^*\rangle ). \end{aligned}$$

(3.33)

Since $0\le \Gamma _{m_k}\le \Gamma _{{m_k}+1}$, then from (3.33), we have

$$\begin{aligned} 0\le & {} \Gamma _{{m_k}+1} - \Gamma _{m_k}\nonumber \\\le & {} (1-\alpha _{m_k})(\Delta _p(x^*, x_{m_k})+\Delta _p(y^*, y_{m_k})) \nonumber \\&+\,\alpha _{m_k}(\langle J_p^{E_1}u - J_p^{E_1}x^*, x_{{m_k}+1}-x^*\rangle + \langle J_p^{E_2}v - J_p^{E_2}y^*, y_{{m_k}+1} - y^*\rangle )\nonumber \\&-\,(\Delta _p(x^*, x_{m_k})+\Delta _p(y^*, y_{m_k})). \end{aligned}$$

(3.34)

Hence

$$\begin{aligned} \Delta _p(x^*, x_{m_k})+\Delta _p(y^*, y_{m_k})\le & {} \langle J_p^{E_1}u - J_p^{E_1}x^*, x_{{m_k}+1}-x^*\rangle \\&+ \langle J_p^{E_2}v - J_p^{E_2}y^*, y_{{m_k}+1} - y^*\rangle . \end{aligned}$$

Therefore from (3.31) and (3.32), we obtain

$$\begin{aligned} \lim _{k\rightarrow \infty }(\Delta _p(x^*, x_{m_k})+\Delta _p(y^*, y_{m_k})) = 0. \end{aligned}$$

This implies that

$$\begin{aligned} \lim _{n\rightarrow \infty }(\Delta _p(x^*, x_{n})+\Delta _p(y^*, y_{n})) = 0. \end{aligned}$$

Hence $\{(x_n, y_n)\}$ converges strongly to $(x^*, y^*) = (\Pi _\Omega u, \Pi _\Omega v).$ In both cases, we obtain that $(x_n,y_n) \rightarrow (x^*,y^*)$. This completes the proof. $\square$

We now give the following direct consequences of our main result.

• (i) Taking $T_1$ and $T_2$ to be Bregman firmly nonexpansive mappings on $E_1$ and $E_2$, respectively. Note that the class of Bregman firmly nonexpansive mappings satisfies the property ${\hat{F}}(T)= F(T)$ (see Lemma 15.6 in Reich and Sabach 2011, page 308). Then, we have the following results:

Corollary 3.3

Let $E_1, E_2$ and $E_3$ be p-uniformly convex real Banach spaces which are also uniformly smooth. Let C and Q be nonempty closed, convex subsets of $E_1$ and $E_2$, respectively, $A{:}\,E_1\rightarrow E_3$ and $B{:}\,E_2\rightarrow E_3$ be bounded linear operators. Let $f{:}\,E_1\rightarrow {\mathbb {R}}\cup \{+\infty \}$ and $g{:}\,E_2\rightarrow {\mathbb {R}}\cup \{+\infty \}$ be proper, convex and lower semicontinuous functions, $T_1{:}\,E_1\rightarrow E_1$ and $T_2{:}\,E_2\rightarrow E_2$ be Bregman firmly nonexpansive mappings such that $\Omega \ne \emptyset$. For fixed $u \in E_1$ and $v \in E_2$, choose an initial guess $(x_1,y_1) \in E_1 \times E_2$ and let $\{\alpha _n\} \subset [0,1]$. Suppose $(\{x_n\},\{y_n\})$ is generated by the following algorithm: for a fixed $(u,v) \in E_1 \times E_2$,

$$\begin{aligned} {\left\{ \begin{array}{ll}\ u_n = \mathrm{prox}_{\gamma _n f}\left( J^{E^*_1}_q\left[ J^{E_1}_p(x_n)-\gamma _nA^*J^{E_3}_p(Ax_n - By_n)\right] \right) ,\\ x_{n+1} = J^{E^*_1}_q\Big (\alpha _nJ^{E_1}_p(u)+(1-\alpha _n) \left[ \beta _nJ^{E_1}_p(u_n)+(1-\beta _n)J^{E_1}_p(T_1u_n)\right] \Big ),\\ v_n = \mathrm{prox}_{\gamma _n g}\left( J^{E^*_2}_q\left[ J^{E_2}_p(y_n)+\gamma _nB^*J^{E_3}_p(Ax_n - By_n)\right] \right) ,\\ y_{n+1} = J^{E^*_2}_q\Big (\alpha _nJ^{E_2}_p(v)+(1-\alpha _n) \left[ \delta _nJ^{E_2}_p(v_n)+(1-\delta _n)J^{E_2}_p(T_2v_n)\right] \Big ), \end{array}\right. } \end{aligned}$$

for $n \ge 1$, $\{\beta _n\}, ~ \{\delta _n\} \subset (0,1)$, where $A^*$ is the adjoint operator of A. Further, we choose the stepsize $\gamma _n$ such that if $n \in \Gamma := \{n {:}\,Ax_n - B y_n \ne 0 \}$, then

$$\begin{aligned} \gamma ^{q-1}_n \in \left( 0, \frac{q\Vert Ax_n - By_n\Vert ^p}{C_q\Vert A^*J_p^{E_3}(Ax_n - By_n)\Vert ^q +D_q\Vert B^*J_p^{E_3}(Ax_n - By_n)\Vert ^q}\right) . \end{aligned}$$

Otherwise, $\gamma _{n} = \gamma$ $(\gamma$ being any nonnegative value). Assume that the following conditions are satisfied:

• (i) $\lim _{n\rightarrow \infty }\alpha _n = 0,$ and $\sum _{n =0}^\infty \alpha _n = \infty$,

• (ii) $0< a \le \liminf _{n\rightarrow \infty }\beta _n \le \limsup _{n\rightarrow \infty }\beta _n <1,$

• (iii) $0< b \le \liminf _{n\rightarrow \infty }\delta _n \le \limsup _{n\rightarrow \infty }\delta _n <1.$

Then the sequence $\{(x_n,y_n)\}$ converges strongly to $(x^*,y^*) = (\Pi _\Omega u, \Pi _\Omega v).$

• (ii) Taking $f = i_C$ and $g= i_Q$, i.e., the indicator functions on C and Q, respectively. The the proximal operators $\mathrm{prox}_{\gamma f} = \Pi _C$ and $\mathrm{prox}_{\gamma g} =\Pi _Q$ (see Bauschke et al. 2003). Hence, we have the following result.

Corollary 3.4

Let $E_1, E_2$ and $E_3$ be p-uniformly convex real Banach spaces which are also uniformly smooth. Let C and Q be nonempty closed, convex subsets of $E_1$ and $E_2$, respectively, $A{:}\,E_1\rightarrow E_3$ and $B{:}\,E_2\rightarrow E_3$ be bounded linear operators. Let $T_1{:}\,E_1\rightarrow E_1$ and $T_2{:}\,E_2\rightarrow E_2$ be Bregman quasi-nonexpansive mappings such that $F(T_1) \ne \emptyset$ and $F(T_2) \ne \emptyset$. For fixed $u \in E_1$ and $v \in E_2$, choose an initial guess $(x_1,y_1) \in E_1 \times E_2$ and let $\{\alpha _n\} \subset [0,1]$. Suppose $(\{x_n\},\{y_n\})$ is generated by the following algorithm: for a fixed $(u,v) \in E_1 \times E_2$,

$$\begin{aligned} {\left\{ \begin{array}{ll}\ u_n = J^{E^*_1}_q\left( J^{E_1}_p(x_n)-\gamma _nA^*J^{E_3}_p(Ax_n - By_n)\right) ,\\ x_{n+1} = J^{E^*_1}_q\Big (\alpha _nJ^{E_1}_p(u)+(1-\alpha _n) \left[ \beta _nJ^{E_1}_p(u_n)+(1-\beta _n)J^{E_1}_p(T_1u_n)\right] \Big ),\\ v_n = J^{E^*_2}_q\left( J^{E_2}_p(y_n)+\gamma _nB^*J^{E_3}_p(Ax_n - By_n)\right) ,\\ y_{n+1} = J^{E^*_2}_q\Big (\alpha _nJ^{E_2}_p(v)+(1-\alpha _n) \left[ \delta _nJ^{E_2}_p(v_n)+(1-\delta _n)J^{E_2}_p(T_2v_n)\right] \Big ), \end{array}\right. } \end{aligned}$$

for $n \ge 1$, $\{\beta _n\}, ~ \{\delta _n\} \subset (0,1)$, where $A^*$ is the adjoint operator of A. Further, we choose the stepsize $\gamma _n$ such that if $n \in \Gamma := \{n {:}\,Ax_n - B y_n \ne 0 \}$, then

$$\begin{aligned} \gamma ^{q-1}_n \in \left( 0, \frac{q\Vert Ax_n - By_n\Vert ^p}{C_q\Vert A^*J_p^{E_3}(Ax_n - By_n)\Vert ^q +D_q\Vert B^*J_p^{E_3}(Ax_n - By_n)\Vert ^q}\right) . \end{aligned}$$

Otherwise, $\gamma _{n} = \gamma$ ($\gamma$ being any nonnegative value). Assume that the following conditions are satisfied:

• (i) $\lim _{n\rightarrow \infty }\alpha _n = 0,$ and $\sum _{n =0}^\infty \alpha _n = \infty$,

• (ii) $0< a \le \liminf _{n\rightarrow \infty }\beta _n \le \limsup _{n\rightarrow \infty }\beta _n <1,$

• (iii) $0< b \le \liminf _{n\rightarrow \infty }\delta _n \le \limsup _{n\rightarrow \infty }\delta _n <1.$

Then the sequence $\{(x_n,y_n)\}$ converges strongly to $(x^*,y^*) = (\Pi _{F(T_1)} u, \Pi _{F(T_2)} v).$

• (iii). Finally, if we let $E_1, E_2$ and $E_3$ to be real Hilbert spaces. Then we have the following corollary from our main result.

Corollary 3.5

Let $H_1, H_2$ and $H_3$ be real Hilbert spaces, C and Q be nonempty closed, convex subsets of $H_1$ and $H_2$, respectively, $A{:}\,H_1\rightarrow H_3$ and $B{:}\,H_2\rightarrow H_3$ be bounded linear operators. Let $f{:}\,H_1\rightarrow {\mathbb {R}}\cup \{+\infty \}$ and $g{:}\,H_2\rightarrow {\mathbb {R}}\cup \{+\infty \}$ be proper, convex and lower semicontinuous functions, $T_1{:}\,H_1\rightarrow H_1$ and $T_2{:}\,H_2\rightarrow H_2$ be quasi-nonexpansive mappings such that $\Omega \ne \emptyset$. For fixed $u \in H_1$ and $v \in H_2$, choose an initial guess $(x_1,y_1) \in H_1 \times H_2$ and let $\{\alpha _n\} \subset [0,1]$. For arbitrary $x_0, u\in H_1$ and $y_0, v\in H_2$ define an iterative algorithm by

$$\begin{aligned} \left\{ \begin{array}{ll} u_n = \mathrm{prox}_{\gamma _n f}(x_n-\gamma _nA^*(Ax_n - By_n))\\ x_{n+1} =\alpha _nu+(1-\alpha _n)[\beta _nu_n+(1-\beta _n)T_1u_n]\\ v_n = \mathrm{prox}_{\gamma _n g}(y_n+\gamma _nB^*(Ax_n - By_n))\\ y_{n+1} = \alpha _n v+(1-\alpha _n)[\delta _nv_n+(1-\delta _n)(T_2v_n)]\\ \end{array} \right. \end{aligned}$$

for $n \ge 1$, $\{\beta _n\}, ~ \{\delta _n\} \subset (0,1)$, where $A^*$ is the adjoint operator of A. Further, we choose the stepsize $\gamma _n$ such that if $n \in \Gamma := \{n {:}\,Ax_n - B y_n \ne 0 \}$, then

$$\begin{aligned} \gamma ^{q-1}_n \in \left( 0, \frac{2\Vert Ax_n - By_n\Vert ^2}{\Vert A^*(Ax_n - By_n)\Vert ^2 +\Vert B^*(Ax_n - By_n)\Vert ^2}\right) . \end{aligned}$$

Otherwise, $\gamma _{n} = \gamma$ ($\gamma$ being any nonnegative value). Assume that the following conditions are satisfied:

• (i) $\lim _{n\rightarrow \infty }\alpha _n = 0,$ and $\sum _{n =0}^\infty \alpha _n = \infty$,

• (ii) $0< a \le \liminf _{n\rightarrow \infty }\beta _n \le \limsup _{n\rightarrow \infty }\beta _n <1,$

• (iii) $0< b \le \liminf _{n\rightarrow \infty }\delta _n \le \limsup _{n\rightarrow \infty }\delta _n <1.$

Then (3.5) converges strongly to $(x^*, y^*)= (P_\Omega u, P_\Omega v).$

4 Applications

4.1 Split equality convex minimization and equilibrium problems

Let C be a nonempty, closed and convex subset of a real Banach space E and $G{:}\,C \times C \rightarrow {\mathbb {R}}$ be a nonlinear bifunction. The Equilibrium Problem (EP) introduced by Blum and Oettli (1994) as a form of generalization of variational inequality problem is given as

$$\begin{aligned} \text {find}~~x^* \in C \quad \text {such that}\quad G(x^*,x) \ge 0, \quad \forall x \in C. \end{aligned}$$

We shall denote the set of solutions of the EP with respect to the bifunction G by EP(G). Several algorithms have been introduced for finding the solution of EP in Banach spaces. For solving EP, it is customary to assume that the bifunction G satisfies the following conditions:

• (A1) $G(x, x)=0$, for all $x\in C$,

• (A2) G is monotone, i.e., $G(x, y)+G(y, x)\le 0$, for all $x, y\in C$,

• (A3) for all $x, y, z\in C$, $\limsup _{t\rightarrow 0^{+}}G(tz+(1-t)x, y)\le G(x, y)$,

• (A4) for each $x\in C$, $G(x,\cdot )$ is convex and lower semi-continuous.

The resolvent operator of the bifunction G with respect to the Bregman distance $\Delta _p$ is given as

$$\begin{aligned} \mathrm{Res}^p_G(x) = \left\{ u\in C{:}\,G(u,y)+\frac{1}{r}\langle y - u,J^E_p(u) - J^E_p(x)\rangle \ge 0 \quad \forall \quad y \in C\right\} . \end{aligned}$$

It was proved in Reich and Sabach (2010a) that $\mathrm{Res}^p_G$ satisfies the following properties:

• i. $\mathrm{Res}^p_G$ is single-valued;

• ii. $\mathrm{Res}^p_G$ is a Bregman firmly nonexpansive mapping;

• iii. $F(\mathrm{Res}^p_G) = \mathrm{EP}(G)$;

• iv. EP(G) is a closed and convex subset of C;

• v. for all $x\in E$ and $q\in F(\mathrm{Res}^p_G)$

  $$\begin{aligned} \Delta _p(q, \mathrm{Res}^p_G(x))+\Delta _p(\mathrm{Res}^p_G(x), x)\le \Delta _p(q, x). \end{aligned}$$

We now consider the following Split Equality Convex Minimization and Equilibrium Problems:

Let $E_1$, $E_2$ and $E_3$ be real Banach spaces, C and Q be nonempty, closed and convex subsets of $E_1$ and $E_2$, respectively. Let $G_1{:}\,C \times C \rightarrow {\mathbb {R}}$ and $G_2{:}\,Q \times Q \rightarrow {\mathbb {R}}$ be bifunctions, $f{:}\,E_1\rightarrow {\mathbb {R}}\cup \{+\infty \}$ and $g{:}\,E_2\rightarrow {\mathbb {R}}\cup \{+\infty \}$ be proper, lower-semicontinous convex functions, $A{:}\,E_1 \rightarrow E_3$ and $B{:}\,E_2 \rightarrow E_3$ be bounded linear operators.

$$\begin{aligned} \text {Find}~~ x \in { EP}(G_1)\cap \mathrm{Argmin}(f), ~~~ y \in EP(G_2)\cap \mathrm{Argmin}(g) \quad \text {such that}\quad Ax = By. \nonumber \\ \end{aligned}$$

(4.1)

We denote the solution set of the Problem (4.1) by $\Gamma .$ Finding the common solutions of convex minimization problem, equilibrium problem and fixed point problem (4.1) has been studied recently by many authors in the setting of real Hilbert spaces (see for instance Abass et al. 2018; Jolaoso et al. 2018; Ogbuisi and Mewomo 2017; Okeke and Mewomo 2017; Tian and Liu 2012; Yazdi 2019). However, there are very few results on the split equality convex minimization problem and split equality equilibrium problems in higher Banach spaces.

Setting $T_1 = \mathrm{Res}_{G_1}^p$ and $T_2 = \mathrm{Res}_{G_2}^p$ in our Theorem 3.2, we obtain the following result for approximating solution of Problem (4.1) in uniformly convex Banach spaces.

Theorem 4.1

Let $E_1, E_2$ and $E_3$ be p-uniformly convex real Banach spaces which are also uniformly smooth. Let C and Q be nonempty closed, convex subsets of $E_1$ and $E_2$, respectively, $A{:}\,E_1\rightarrow E_3$ and $B{:}\,E_2\rightarrow E_3$ be bounded linear operators. Let $f{:}\,E_1\rightarrow {\mathbb {R}}\cup \{+\infty \}$ and $g{:}\,E_2\rightarrow {\mathbb {R}}\cup \{+\infty \}$ be proper, lower-semicontinous convex functions, $G_1{:}\,C \times C \rightarrow {\mathbb {R}}$, and $G_2{:}\,Q \times Q \rightarrow {\mathbb {R}}$ be bifunctions satisfying condition (A1)–(A4) such that $\Gamma \ne \emptyset$. For fixed $u \in E_1$ and $v \in E_2$, choose an initial guess $(x_1,y_1) \in E_1 \times E_2$ and let $\{\alpha _n\} \subset [0,1]$. Assume that the $n\mathrm{th}$ iterate $(x_n,y_n) \subset E_1 \times E_2$ has been constructed; then we compute the $(n+1)\mathrm{th}$ iterate $(x_{n+1},y_{n+1})$ via the iteration:

$$\begin{aligned} {\left\{ \begin{array}{ll} u_n = \mathrm{prox}_{\gamma _n f}\left( J^{E^*_1}_q\left[ J^{E_1}_p(x_n)-\gamma _nA^*J^{E_3}_p(Ax_n - By_n)\right] \right) ,\\ x_{n+1} = J^{E^*_1}_q\Big (\alpha _nJ^{E_1}_p(u)+(1-\alpha _n) \left[ \beta _nJ^{E_1}_p(u_n)+(1-\beta _n)J^{E_1}_p(\mathrm{Res}_{G_1}^pu_n)\right] \Big ),\\ v_n = \mathrm{prox}_{\gamma _n g}\left( J^{E^*_2}_q\left[ J^{E_2}_p(y_n)+\gamma _nB^*J^{E_3}_p(Ax_n - By_n)\right] \right) ,\\ y_{n+1} = J^{E^*_2}_q\Big (\alpha _nJ^{E_2}_p(v)+(1-\alpha _n) \left[ \delta _nJ^{E_2}_p(v_n)+(1-\delta _n)J^{E_2}_p(\mathrm{Res}_{G_2}^pv_n) \right] \Big ), \end{array}\right. } \end{aligned}$$

(4.2)

for $n \ge 1$, $\{\beta _n\}, ~ \{\delta _n\} \subset (0,1)$, where $A^*$ is the adjoint operator of A. Further, we choose the stepsize $\gamma _n$ such that if $n \in \Gamma := \{n {:}\,Ax_n - B y_n \ne 0 \}$, then

$$\begin{aligned} \gamma ^{q-1}_n \in \left( 0, \frac{q\Vert Ax_n - By_n\Vert ^p}{C_q\Vert A^*J_p^{E_3}(Ax_n - By_n)\Vert ^q +D_q\Vert B^*J_p^{E_3}(Ax_n - By_n)\Vert ^q} \right) . \end{aligned}$$

Otherwise, $\gamma _{n} = \gamma$ ($\gamma$ being any nonnegative value). In addition, if the following conditions are satisfied:

• (i) $\lim _{n\rightarrow \infty }\alpha _n = 0,$ and $\sum _{n =0}^\infty \alpha _n = \infty$,

• (ii) $0< a \le \liminf _{n\rightarrow \infty }\beta _n \le \limsup _{n\rightarrow \infty }\beta _n <1,$

• (iii) $0< b \le \liminf _{n\rightarrow \infty }\delta _n \le \limsup _{n\rightarrow \infty }\delta _n <1.$

Then the sequence $\{(x_n,y_n)\}$ converges strongly to $(x^*,y^*) \in \Gamma .$

4.2 Zeros of maximal monotone operators

Let E be a Banach space with dual $E^*$. Let $A{:}\,E\rightarrow 2^{E^*}$ be a multivalued mapping. The graph of A denoted by gr(A) is defined by $gr(A)=\{(x, u)\in E\times E^*{:}\,u\in Ax\}$. A is called a non-trivial operator if $gr(A)\ne \emptyset$. A is called a monotone operator if $\forall$ $(x, u), (y, v)\in gr(A)$, $\langle x -y, u - v\rangle \ge 0.$

A is said to be a maximal monotone operator if the graph of A is not a proper subset of the graph of any other monotone operator. The Bregman resolvent operator associated with A is denoted by $\mathrm{Res}_{A}$ and defined by

$$\begin{aligned} \mathrm{Res}_A = (J_p + A)^{-1}\circ J_p{:}\,E\rightarrow 2^{E}. \end{aligned}$$

It is known that $\mathrm{Res}_A$ is single-valued and Bregman firmly nonexpansive. Also, $\forall$ $x\in E$, $\lambda \in (0, \infty )$, $x\in A^{-1}(0)$ if and only if $x\in F(\mathrm{Res}_{\lambda A})$ (see Bauschke et al. 2003). It is also known (see Reich and Sabach 2010a) that $D_p(z, \mathrm{Res}_Ax)+D_p(\mathrm{Res}_Ax, x)\le D_p(z, x)$.

Let $E_1, E_2$ and $E_3$ be p-uniformly convex real Banach spaces which are also uniformly smooth. Let $C_1$ and $C_2$ be nonempty closed and convex subsets of $E_1$ and $E_2$, respectively. Let $f{:}\,E_1\rightarrow {\mathbb {R}}\cup \{+\infty \}$ and $g{:}\,E_2\rightarrow {\mathbb {R}}\cup \{+\infty \}$ be proper, lower-semicontinous convex functions. Let $T_1{:}\,E_1\rightarrow 2^{E^*_1}$ and $T_2{:}\,E_2\rightarrow 2^{E_2^{*}}$ be maximal monotone operators and $A{:}\,E_1\rightarrow E_3$ and $B{:}\,E_2\rightarrow E_3$ be bounded linear operators. Consider the following problem:

$$\begin{aligned} \text {find}~~x\in T_1^{-1}(0)\cap \mathrm{Arg}\min f,~ y\in T_2^{-1}(0)\cap \mathrm{Arg}\min g ~~\text {such that}\quad Ax = By. \end{aligned}$$

(4.3)

Since $\mathrm{Res}_{\lambda A}$ is Bregman firmly nonexpansive and $F(\mathrm{Res}_{\lambda A}) = A^{-1}(0)$, then we have the following result for approximating solution of (4.3) in uniformly convex real Banach spaces.

Theorem 4.2

Let $E_1, E_2$ and $E_3$ be p-uniformly convex real Banach spaces which are also uniformly smooth. Let $C_1$ and $C_2$ be nonempty closed and convex subsets of $E_1$ and $E_2$, respectively. Let $f{:}\,E_1\rightarrow {\mathbb {R}}\cup \{+\infty \}$ and $g{:}\,E_2\rightarrow {\mathbb {R}}\cup \{+\infty \}$ be proper, lower-semicontinous convex functions. Let $T_1{:}\,E_1\rightarrow 2^{E^*_1}$ and $T_2{:}\,E_2\rightarrow 2^{E_2^{*}}$ be maximal monotone operators and $A{:}\,E_1\rightarrow E_3$ and $B{:}\,E_2\rightarrow E_3$ be bounded linear operators. Assume $\Omega = \big \{(x, y)\in T^{-1}_1(0)\times T^{-1}_2(0){:}\,x\in \mathrm{Arg} \min {f}, y\in \mathrm{Arg} \min {g}, Ax = By\big \} \ne \emptyset$. For fixed $u \in E_1$ and $v \in E_2$, choose an initial guess $(x_1,y_1) \in E_1 \times E_2$ and let $\{\alpha _n\} \subset [0,1]$. Assume that the $n\mathrm{th}$ iterate $(x_n,y_n) \subset E_1 \times E_2$ has been constructed; then we compute the $(n+1)\mathrm{th}$ iterate $(x_{n+1},y_{n+1})$ via the iteration:

$$\begin{aligned} {\left\{ \begin{array}{ll} u_n = \mathrm{prox}_{\gamma _nf}\left( J^{E^*_1}_q\left[ J^{E_1}_p(x_n) -\gamma _nA^*J^{E_3}_p(Ax_n - By_n)\right] \right) ,\\ x_{n+1} = J^{E^*_1}_q\Big (\alpha _nJ^{E_1}_p(u)+(1-\alpha _n) \left[ \beta _nJ^{E_1}_p(u_n)+(1-\beta _n)J^{E_1}_p(\mathrm{Res}_{T_1}u_n) \right] \Big ),\\ v_n = \mathrm{prox}_{\gamma _ng}\left( J^{E^*_2}_q\left[ J^{E_2}_p(y_n) +\gamma _nB^*J^{E_3}_p(Ax_n - By_n)\right] \right) ,\\ y_{n+1} = J^{E^*_2}_q\Big (\alpha _nJ^{E_2}_p(v)+(1-\alpha _n) \left[ \delta _nJ^{E_2}_p(v_n)+(1-\delta _n)J^{E_2}_p(\mathrm{Res}_{T_2}v_n) \right] \Big ), \end{array}\right. } \end{aligned}$$

(4.4)

for $n \ge 1$, $\{\beta _n\}, ~ \{\delta _n\} \subset (0,1)$, where $A^*$ and $B^*$ are the adjoint operators of A and B, respectively. Further, we choose the stepsize $\gamma _n$ such that if $n \in \Gamma := \{n{:}\,Ax_n - B y_n \ne 0 \}$, then

$$\begin{aligned} \gamma ^{q-1}_n \in \left( 0, \frac{q\Vert Ax_n - By_n\Vert ^p}{C_q\Vert A^*J_p^{E_3}(Ax_n - By_n)\Vert ^q +D_q\Vert B^*J_p^{E_3}(Ax_n - By_n)\Vert ^q} \right) . \end{aligned}$$

(4.5)

Otherwise, $\gamma _{n} = \gamma$ ($\gamma$ being any nonnegative value). In addition, if the following conditions are satisfied:

• (i) $\lim _{n\rightarrow \infty }\alpha _n = 0,$ and $\sum _{n =0}^\infty \alpha _n = \infty$,

• (ii) $0< a \le \liminf _{n\rightarrow \infty }\beta _n \le \limsup _{n\rightarrow \infty }\beta _n <1,$

• (iii) $0< b \le \liminf _{n\rightarrow \infty }\delta _n \le \limsup _{n\rightarrow \infty }\delta _n <1.$

Then the sequence $\{(x_n,y_n)\}$ converges strongly to $(x^*,y^*) \in (\Pi _{\Omega }u, \Pi _{\Omega }v)$.

5 Numerical example

In this section, we present two examples to show the behaviour of the iterative algorithm presented in this paper.

Example 5.1

Let $E_1 = E_2 = E_3 = {\mathbb {R}}^3$ and let A and B be $3 \times 3$ randomly generated matrices. Let $f(x) = ||x||_2$ for all $x \in {\mathbb {R}}^{3}$, the proximal operator with respect to f is defined as

$$\begin{aligned} \mathrm{prox}_f(x) = {\left\{ \begin{array}{ll} \left( 1 - \dfrac{1}{||x||_2}\right) ,&{}\quad \mathrm{if} ~~~||x||_2 \ge 1,\\ 0,&{}\quad \mathrm{if}~~||x||_2 < 1. \end{array}\right. } \end{aligned}$$

(5.1)

Also, define $g(x) = \max \Big \{1- |x|, 0\Big \}$ for $x \in {\mathbb {R}}^{3}$, then the proximal operator of g is given by

$$\begin{aligned} \mathrm{prox}_g(x) = {\left\{ \begin{array}{ll} x, &{}\quad \mathrm{if} ~~|x| <1,\\ \mathrm{sgn}(x), &{}\quad \mathrm{if}~~ 1 \le |x| \le 2,\\ \mathrm{sgn}(x-1), &{}\quad \mathrm{if} ~~ |x| >2. \end{array}\right. } \end{aligned}$$

Take $C = \{ x \in {\mathbb {R}}^{3}{:}\,\langle a,x \rangle \ge b \}$, where $a = (1,-\,5,4)$ and $b =1$. Then

$$\begin{aligned} \Pi _C(x) = P_C(x) = \dfrac{b - \langle a,x \rangle }{||a||_2^2}a + x. \end{aligned}$$

Also, let $Q = \{x \in {\mathbb {R}}^{3}{:}\,\langle c,x \rangle = d \},$ where $c = (1,2,3)$ and $d = 4$. Then, we have that

$$\begin{aligned} \Pi _Q(x) = P_Q(x) = \max \Big \{ 0, \dfrac{d - \langle c,x \rangle }{||c||^2}\Big \}c + x. \end{aligned}$$

Suppose $T_1 = P_C$ and $T_2 = P_Q$, let $u = \mathrm{rand}(3,1)$ and $v = 0.5*\mathrm{rand}(3,1)$. We let $\alpha _n = \frac{1}{n+1}$, $\beta _n = \frac{2n}{3(n+1)}$ and $\delta _n = \frac{3n+5}{7n+9}$. Then our algorithm (3.1) becomes

$$\begin{aligned} {\left\{ \begin{array}{ll} u_n = \mathrm{prox}_{\gamma _n f}\left( x_n-\gamma _nA^T(Ax_n - By_n)\right) ,\\ x_{n+1} = \frac{u}{n+1}+\frac{n}{n+1}\left[ \frac{2nu_n}{3(n+1)} +\frac{n+3}{3(n+1)}P_C(u_n)\right] ,\\ v_n = \mathrm{prox}_{\gamma _n g}\left( y_n+\gamma _nB^T(Ax_n - By_n)\right) ,\\ y_{n+1} = \frac{v}{n+1}+\frac{n}{n+1}\left[ \frac{(3n+5)}{7n+9}v_n +\frac{(4n+4)}{7n+9}P_Q(v_n)\right] , \end{array}\right. } \end{aligned}$$

(5.2)

for $n\ge 1$. If $Ax_n - By_n\ne 0$, then we choose $\gamma _n \in (0, \frac{2\Vert Ax_n - By_n\Vert ^2}{\Vert A^T(Ax_n - By_n)\Vert ^2 + \Vert B^T(Ax_n - By_n)\Vert ^2})$. Else, $\gamma _n = \gamma$ ($\gamma$ being any positive real number). We choose various values of the initial points $x_1$ and $y_1$ as follows:

• Case 1

  • (a) $x_1 = 1 * \mathrm{rand}(3,1)$, $y_1 = 2* \mathrm{rand}(3,1),$

  • (b) $x_1 = -5 * \mathrm{rand}(3,1),$ $y_1 = -10*\mathrm{rand}(3,1)$,

• Case 2

  • (a) $x_1 = -0.1*\mathrm{rand}(3,1)$, $y_1 = 0.2*\mathrm{rand}(3,1),$

  • (b) $x_1 = 0.5*\mathrm{rand}(3,1),$ $y_1 = -1*\mathrm{rand}(3,1).$

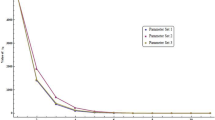
Using $\frac{\max \{||x_{n+1}-x_{n}||^2,||y_{n+1}-y_{n}||^2\}}{\max \{||x_2-x_1||^2,||y_2 - y_1||^2\}}<10^{-3}$ as the stopping criterion, we plot the graphs of $||x_{n+1} -x_{n}||^2$ and $||y_{n+1} -y_{n}||^2$ against the number of iterations in each cases. We note that the change in the initial values does not have any significant effect on the number of iterations nor the cpu time. The numerical results can be found in Figs. 1 and 2.

Fig. 1

Example 5.1, left: Case 1 (a), time: 0.0321 s; right: Case 1 (b), time: 0.0481 s

Fig. 2

Example 5.1, left: Case 2 (a), time: 0.0211 s; right: Case 2 (b), time: 0.0427 s

Example 5.2

In this second example, we consider the infinite-dimensional space and compare our algorithm (3.1) with algorithm (1.13) of Zhao (2015). Let $E_1=E_2=E_3= L^2([0,2\pi ])$ with norm $||x||^2 = \int _{0}^{2\pi }|x(t)|\mathrm{d}t$ and inner product $\langle x,y \rangle = \int _{0}^{2\pi }x(t)y(t)\mathrm{d}t,$ $x,y \in E.$ Suppose $C := \{x \in L^2([0,2\pi ]){:}\,\int _{0}^{2\pi }(t^2+1)x(t)\mathrm{d}t \le 1\}$ and $Q:= \{x \in L^2([0,2\pi ]){:}\,\int _{0}^{2\pi }|x(t)-\sin (t)|^2 \le 16\}$ are subsets of $E_1$ and $E_2$, respectively. Define $A{:}\,L^2([0,2\pi ]) \rightarrow L^2([0,2\pi ])$ by $A(x)(t) = \int _{0}^{2\pi }\exp ^{-st}x(t)\mathrm{d}t$ for all $x \in L^2([0,2\pi ])$ and $By(t) = \int _{0}^{2\pi }\frac{1}{10}(x(t))\mathrm{d}t.$ It is easy to verify that A and B are bounded linear operators.

Table 1 Comparison between algorithms (3.1) and (1.13) for example 5.2

Fig. 3

Example 5.2, left: Case 1 (a); right: Case 1 (b)

Now, let $f= i_C$ and $g=i_Q$, the indicator functions on C and Q, respectively, then $\mathrm{prox}_{\gamma f} =\Pi _C$ and $\mathrm{prox}_{\gamma g} = \Pi _Q$. Also, let $T_1x(t) = \int _{0}^{2\pi } x(t)\mathrm{d}t$ and $T_2y(t) = \int _{0}^{2\pi } \frac{1}{4}y(t)\mathrm{d}t$, choose $u= \cos (3t),$ $v = \exp ^{-2t}$, $\alpha _n = \frac{5}{10(n+1)}$, $\beta _n = \frac{5n}{8n+7}$ and $\delta _n = \frac{3n-2}{5n+5}.$ Then our algorithm (3.1) becomes:

$$\begin{aligned} {\left\{ \begin{array}{ll} u_n = \Pi _C\left( x_n-\gamma _nA^*(Ax_n - By_n)\right) ,\\ x_{n+1} = \frac{5\cos (3t)}{10(n+1)}+\frac{10n+5}{10(n+1)} \left[ \frac{5nu_n}{8n+7}+\frac{3n+7}{8n+7}T_1(u_n)\right] ,\\ v_n = \Pi _Q\left( y_n+\gamma _nB^*(Ax_n - By_n)\right) ,\\ y_{n+1} = \frac{5\exp ^{-2t}}{10(n+1)}+\frac{10n+5}{10(n+1)} \left[ \frac{3n-2}{5n+5}v_n+\frac{(2n+7)}{5n+5}T_2(v_n)\right] , \end{array}\right. } \end{aligned}$$

(5.3)

for $n\ge 1$. If $Ax_n - By_n\ne 0$, then we choose $\gamma _n \in (0, \frac{2\Vert Ax_n - By_n\Vert ^2}{\Vert A^*(Ax_n - By_n)\Vert ^2 + \Vert B^*(Ax_n - By_n)\Vert ^2})$. Else, $\gamma _n = \gamma$ ($\gamma$ being any positive real number). We choose various values of the initial points $x_1$ and $y_1$ as follows:

• Case 1

  • (a) $x_1 = 2t^3\exp ^{5t}$, $y_1 = t^3+2t-5,$

  • (b) $x_1 = 2t\sin (3\pi t),$ $y_1 = t^2\cos (2\pi t)$,

• Case 2

  • (a) $x_1 = 3\exp ^{-5t}$, $y_1 = 2t\sin (3t),$

  • (b) $x_1 = \exp ^{2t},$ $y_1 = \frac{3}{10}\exp ^{2t}.$

Using $\frac{||x_{n+1}-x_{n}||^2+||y_{n+1}-y_{n}||^2}{||x_2-x_1||^2+||y_2 - y_1||^2}<10^{-5}$ as the stopping criterion, we plot the graphs of $||x_{n+1} -x_{n}||^2+||y_{n+1} -y_{n}||^2$ against the number of iterations in each cases and also compare the performance of our algorithm (5.3) with algorithm (1.13). The numerical results are reported in Table 1 and Figs. 3 and 4.

Fig. 4

Example 5.2, left: Case 2 (a); right: Case 2 (b)