Improving GPU web simulations of spiking neural P systems

Abstract

The utilization of a parallel processor such as the graphics processing unit (GPU) is only natural for the simulation of spiking neural P systems (SN P systems) because of their inherent parallel nature. A recent work, created an SN P system simulator, GPUSnapse, that both utilizes GPU and runs on modern web browsers by exploiting the Web Graphics Library (WebGL) which creates shaders to generate textures that corresponds to SN P system simulation algorithms. Matrix representation operations were used in GPUSnapse. In GPUSnapse, when working with large matrices a common concern is sparse matrices. Sparse matrices are known to downgrade the performance of the simulation because of wasting memory and time due to performing redundant operations. In this work we extend GPUSnapse by: (a) using optimized sparse matrix operations to reduce the memory used in simulations and, (b) increase the number of neurons that can be handled by the simulator due to better memory usage. We also identify the limitations of GPUSnapse in terms of the size of each benchmark system that it can handle. We present two algorithms: deterministic and non-deterministic algorithms, which we use to compare the performance and memory requirements of the previous GPUSnapse and our present work. We also analyzed the performance between GPU and CPU implementations of all algorithms involved. Our results include up to 22$\times$ and 1.97$\times$ speedup using CPU and GPU, respectively, compared to the previous work. We also observed up to 30% reduction in memory usage with our work. Lastly, we identify some bottlenecks in our work and recommendations for improvements.

1 Introduction

Spiking neural P systems (in short, SN P systems) are a class of neural-like P systems which are parallel computing devices inspired by how neurons function and communicate [13]. The computing power (what problems can be solved) and efficiency (how much resources are required) of SN P systems and variants are active areas of investigation: on computing power see for instance [13, 21] with recent works such as [2, 16, 25]; on efficiency, see for instance [15, 23] with recent works in [3, 5, 32]. Works on practical applications using SN P systems and variants are also active especially in the last several years such as [27, 33] with recent surveys in [8, 14].

To better understand and investigate SN P systems, in [34] they were represented using vectors, matrices, and linear algebra operations. Ideas from [34] form the basis of our simulators, including the support for SN P systems with delays in [7]. Due to the parallel nature of SN P systems, the use of parallel computing devices such as graphics processing units or GPUs is a natural approach. With GPUs, large accelerations or speedups can be obtained when performing algebraic operations such as those used in the simulation of SN P systems using matrix representations.

However, GPUs have some caveats compared to CPUs. Best performance is achieved when GPU threads are executed in a synchronized manner and accessed data from memory are contiguous [19]. A problem arises for some large matrices with many zero elements. For instance, graphs with more nodes than edges have matrices with more zeroes than ones in their adjacency matrices. Such graphs are known to have sparse matrices which can degrade the performance of simulations: memory and time can be wasted on performing redundant or unnecessary operations, especially on zero elements [18].

In this work, we extend the work in [29] by using optimized sparse matrix vector operations introduced in [1, 18] to reduce memory requirements on GPUSnapse. In this way, we obtain a performance increase and we can simulate larger instances of SN P systems. We present two algorithms (deterministic and non-deterministic), each tested with a SN P system suitable to test sparse matrices: bitonic network SN P systems also used in [7] and non-uniform solutions to Subset Sum from [15].

The novelty of our GPUSnapse work in [29] and our present work compared to our previous works focusing on CUDA GPUs (see for instance [1, 6, 7] ) is a trade-off: our works with CUDA GPUs are mainly focused on accelerated performance or massive parallelism due to the use of both software and hardware by NVIDIA (company manufacturing CUDA GPUs); in comparison, GPUSnapse and our present work allow for some parallelism and acceleration even if a computer does not have a GPU, or has an NVIDIA GPU but is not CUDA (that is, the GPU is not general programmable).

Not all computers have GPUs manufactured by NVIDIA (especially since NVIDIA GPUs are powerful but can be quite expensive) and not all GPUs by NVIDIA support CUDA programming. Thus, our present work allows us to still simulate SN P systems using nonCUDA GPUs. Compared to our previous work in [29] and extended in [30], results from the present work include: up to 22$\times$ and 1.97$\times$ speedup using CPU and GPU, respectively; up to 30% reduction in memory usage, allowing us to simulate larger systems.

The paper is structured as follows: Sect. 2 provides the formal definition of SN P systems, the matrix representations (regular and optimized sparse) and some GPU terminologies that would be used in the discussion of the results of this work. Section 3 discusses the different simulators and how they compare to one another and the extension done in this work. It also contains more in-depth discussions about the techniques used in GPUSnapse and how WebGL was used for the simulation of the SN P Systems. Section 4 presents the technology, and simulation architecture and algorithms used in this work. Section 5 contains the tests done including the setups and the current working limitations of the work in terms of input sizes for both algorithms. This section also discusses the time and space analysis of the results from tests. Lastly, in Sect. 6 we state the conclusions of this work and future work recommendations.

2 Preliminaries

2.1 Spiking neural P systems

SN P Systems are formally defined in [13] as follows:

Definition 1

A spiking neural P system of degree $m\ge {1}$ is a construct of the form

$$\begin{aligned} \varPi = (O, \sigma _i, \ldots \sigma _m, \textrm{syn, in, out}) \end{aligned}$$

where:

• (1) $O = {a}$ is the singleton alphabet (a is called spike);

• (2) $\sigma _i, \ldots \sigma _m$ are neurons of the form $\sigma _i = (n_i, R_i), 1 \le i \le m$, where:

  • (a) $n_i \ge 0$ is the initial number of spikes contained in $\sigma _i$,

  • (b) $R_i$ is a finite set of rules of the forms: (i) $E/a^c \rightarrow a^p;d$, where E is a regular expression over a and $c \ge p \ge 1, d \ge 0$; (ii)$a^s \rightarrow \lambda$, for $s \ge 1$, with the restriction that for each rule $E/a^c \rightarrow a^p;d$ of type (1) from $R_i$, we have $a^s \notin L(E)$;

• (3) $\textrm{syn} \subseteq \{1,2, \ldots m\} \times \{1,2, \ldots m\}$ with $i \ne j$ for all $(i,j) \in \textrm{syn}$, $1 \le i, j \le m$;

• (4) $\textrm{in, out} \in \{1,2, \ldots m\}$ indicate the input and the output neurons, respectively.

Elaborating on the set of rules of 2b, 2(b)i are known as firing rules. If the number of spikes n present in a neuron satisfies $a^n \in L(E), n \ge c$, c spikes are consumed and $n-c$ spikes are left in the neuron while p spikes will be fired by the neuron to all connected neurons after a delay of d time units. While during the d times units of delay, the neuron is considered to be closed and cannot receive further spikes. All spikes sent to this neuron during this time period is considered to be lost. Consequently, during the delay period, this neuron cannot also apply new rules or fire spikes. In the case that multiple rules are satisfied by n, the rules are chosen non-deterministic manner however only one rule will be active at a given time. 2(b)(ii) are known as forgetting rules. If the number of spikes present in the neuron $n = s$ then n spikes are removed from the neuron hence the name forgetting rule.

In our work in the following sections, we only use systems without delays, that is d is always set to zero.

2.2 Matrix representation of SN P systems

SN P Systems have been represented as various discrete structures. A particularly relevant representation is through matrices as matrices are a well researched topic utilized across scientific and computing disciplines [28]. The matrix representation for a restricted SN P System with no delays from [34] are defined as follows:

Definition 2

(Configuration vectors) Let $\varPi$ be an SN P system with m neurons, the vector $C_0 = \langle n_1, n_2, \ldots n_m\rangle$ is called the initial configuration vector of $\varPi$, where $n_i$ is the amount of the initial spikes present in neuron $\sigma _i$, $i = 1, 2, \ldots m$ before a computation starts.

For the example in Fig. 1, we have the configuration vector $C_0 = \langle 2,1,1\rangle$.

Fig. 1

An SN P system $\varPi$ that generates the set $\mathbb {N} - \{1\}$

Definition 3

(Spiking vectors) Let $\varPi$ be an SN P system with m neurons and n rules, and $C_k = \langle n_1^{(k)},n_2^{(k)}, \ldots , n_m^{(k)} \rangle$ be the kth configuration vector of $\varPi$. Assume a total order $t: 1,\ldots ,n$ is given for all the n rules, so the rules can be referred as $r_1,\ldots ,r_n$. A spiking vector $s^{(k)}$ is defined as follows:

$$\begin{aligned} s^{(k)}= \langle r_1^{(k)},r_2^{(k)}, \ldots , r_n^{(k)}\rangle , \end{aligned}$$

where:

$$r_{i}^{{(k)}} = \left\{ {\begin{array}{*{20}c} 1 & {{\text{if the regular expression }}E_{i} {\text{ of rule }}r_{i} {\text{ is satisfied by the number of spikes }}n_{j}^{{(k)}} {\text{ (rule }}r_{i} {\text{ is in neuron }}\sigma _{j} {\text{) and rule }}r_{i} {\text{ is chosen and applied;}}} \\ 0 & {{\text{otherwise}}.} \\ \end{array} } \right.$$

For the example in Fig. 1, because the system is non-deterministic we have the spiking vectors $s_0 = \langle 1,0,1,1,0\rangle$ and $s_0 = \langle 0,1,1,1,0\rangle$.

Definition 4

(Spiking transition matrix) Let $\varPi$ be an SN P system with m neurons and n rules, and $t: 1,\ldots ,n$ be a total order given for all the n rules, A spiking transition matrix of the system $\varPi$, $M_\varPi$ is defined as follows:

$$\begin{aligned} M_\varPi =[a_{ij}]_{n \times m}, \end{aligned}$$

where:

$$a_{{ij}} = \left\{ {\begin{array}{*{20}l} { - c} \hfill & {{\text{if rule }}r_{i} {\text{ is in neuron }}\sigma _{j} {\text{ and it is applied consuming }}c{\text{ spikes;}}} \hfill \\ p \hfill & {{\text{if rule }}r_{i} {\text{ is in neuron }}\sigma _{s} (s \ne j{\text{ and }}(s,j) \in {\text{syn}}){\text{ and it is applied producing }}p{\text{ spikes;}}} \hfill \\ 0 \hfill & {{\text{if rule }}r_{i} {\text{ is in neuron }}\sigma _{s} (s \ne j{\text{ and }}(s,j) \notin {\text{syn}}).} \hfill \\ \end{array} } \right.$$

For the example in Fig. 1, we have the spiking transition matrix as follows:

$$\begin{aligned} M_{\varPi }=\begin{pmatrix} -1 &{} 1 &{} 1\\ -2 &{} 1 &{} 1\\ 1 &{} -1 &{} 1\\ 0 &{} 0 &{} -1\\ 0 &{} 0 &{} -2 \end{pmatrix} \end{aligned}$$

Definition 5

(Optimized sparse matrix representation) Let $\varPi$ be an SN P system with m neurons and n rules, and $t: 1,\ldots ,n$ be a total order given for all the n rules. An optimized sparse matrix representation of the system $\varPi$ redefines the spiking vector $s^{(k)}$ to contain only m positions, one per neuron, and states which rule is selected. The spiking vector $s^{(k)}$ is now defined as follows:

$$\begin{aligned} s^{(k)}= \langle m_1^{(k)},m_2^{(k)}, \ldots , m_m^{(k)}\rangle , \end{aligned}$$

where $m_i^{(k)} \in t$ is the selected rule for the neuron $\sigma _i$.

In addition to the spiking vector, the optimized sparse matrix representation also replaces the the spiking transition matrix with the synapse matrix Sy$_{\varPi }$. The synapse matrix Sy$_\varPi$ is defined as follows:

$$\begin{aligned} \textrm{Sy}_\varPi =[a_{ij}]_{m \times m}, \end{aligned}$$

where:

$$a_{{ij}} = \left\{ {\begin{array}{*{20}l} { - 1} \hfill & {{\text{if }}i = j{\text{ and thus neuron }}\sigma _{i} = \sigma _{j} ;} \hfill \\ 0 \hfill & {{\text{if neuron }}\sigma _{i} {\text{ is not connected to }}\sigma _{j} ;} \hfill \\ j \hfill & {{\text{if neuron }}\sigma _{i} {\text{ is connected to }}\sigma _{j} .} \hfill \\ \end{array} } \right.$$

2.3 More on the optimized sparse matrix representation

A typical matrix representation of an SN P system that is not fully connected leads to sparse matrices or matrices with more zeroes than nonzero values. Sparse matrices slow down computation because a majority of memory and computing time is dedicated to processing zeroes. Two approaches have been suggested by [20] for sparsity in matrices representing SN P systems. The first approach uses the ELL format and with the main idea to assign a thread to each rule one per column of the spiking vector $S_k$ and one per column of $M^{\varPi }_s$. The second optimized approach separates the synapses from the rule information. This is what we will be using and it is described as follows in [20]:

• Rule information. Using a CSR-like format, rules of the form $E/a^c \rightarrow a^p$ (also forgetting rules are included, assuming $p = 0$) can be represented by a double array storing the values c and p (also the regular expression, but this is required only to select a spiking vector, and hence is out of scope of this work). A pointer array is employed to relate, for each neuron, the subset of rules that it is associated with and this is called the neuron-rule map vector.

• Synapse matrix, $\textrm{Sy}_{\varPi }$. It has a column per neuron i, and a row for every neuron j such that $(i, j) \in \textrm{Syn}$ (there is a synapse). That is, every element of the matrix corresponds to a synapse or null, given that the number of rows equals to the maximum output degree in the neurons of the SN P system $\varPi$, and padding is required.

• Spiking vector is modified, containing only m positions, one per neuron, and stating which rule $0 \le r\le n$ is selected.

2.4 Graphics processing unit (GPU)

Graphics processing units (GPUs) are compute units designed to perform rendering of 3D or 3-dimensional visual effects on a 2D or 2-dimensional screen [24]. Graphics workloads are highly parallel, which in turn makes the GPUs also suitable for other general purpose parallel workloads [11]. In GPU programming models, we refer to the CPU and its memory as the host while the term device is used denote the GPU and its own memory [12]. Parallel programs ran on the GPU are referred to as kernels. The kernels are concurrently executed on threads which are the basic unit of a GPU that can run a single function [11].

3 Related works

Much work has been done in finding problems that can be solved using SN P system models. Recent examples are methods of fault diagnosis in power systems [31, 33] and visual cryptography [22]. However, we note that P systems are yet to be faithfully implemented in vivo, in vitro, or even in silico, thus developing simulators on electronic computers are necessary to validate P systems [4, 17]. Several simulators and representations developed for SN P Systems are discussed in the following sections to analyze how they compare to each other.

3.1 CuSNP

CuSNP is a project which involves both sequential (CPU) and parallel (GPU) simulators for SN P systems with delays [7]. For the sequential simulator, it used C++ implementation while for the parallel simulator, it utilized CUDA.

The matrix representation defined in [34] was modified to achieve an up to 50$\times$ speed up in a 512-input generalized sorting network over CPU only implementations. However, there are some downsides in using matrix representations in simulating SN P systems. Matrix representation of SN P systems with a low-connectivity-degree graph lead to sparse matrices, in other words, containing more zeros than nonzero values. Sparse matrices downgrades the performance of the simulators since it would waste memory and time [18]. Follow up research on CuSNP utilized sparse matrix representations from [18] to reduce the memory footprint of the simulator which allowed simulations of larger SN P systems than was previously supported [1].

3.2 WebSnapse

WebSnapse is a web-based SN P system simulator that aims to provide visualization of SN P systems for building and running computations [10]. It used the matrix representation extension discussed in [7] to account for SN P systems with delays.

Since the current configuration of WebSnapse is saved into local storage, the number of time steps that an SN P system simulation can run is limited by the amount of local storage available, which varies based on the web browser that the user is working on. This means that the number of rules, neurons, spikes and length of characters consumed by the rules will considerably impact the amount of data stored. Further work considered by the authors to improve the performance of the simulations would be the integration with a GPU simulator running on a web browser [29]. Additionally, a current work in progress of the extension of WebSnapse that have additional features and is more user-friendly, is being developed in parallel with this work (extension of GPUSnapse) and it was a great help in understanding the simulation of SN P Systems. Using it also helped to check the validity of our tests, further discussions of this can be found in Sect. 5.1.

3.3 GPUSnapse

Simulators like CuSNP use CUDA as a platform to make performant SN P system simulations but with the limitation of being restricted to only computers with CUDA capable GPUs while web based simulators such as WebSnapse are more accessible but only use CPUs which do not fully utilize the parallelized nature of SN P systems. GPUSnapse aims to create a web simulator that harnesses GPUs with the aim of providing better performance than current CPU based web simulators and making it more accessible than traditional native simulators by exploiting the WebGL framework which is designed to render graphics on the browser [29].

Two algorithms were used: the algorithm defined in [4] which simulate non-deterministic SN P systems without delays and a modified algorithm from [7] which simulate deterministic SN P systems with delays. In the first mentioned algorithm, the web based GPU simulator was able to achieve an up to 2$\times$ speedup compared to CPU based simulations while in the second algorithm, GPU simulations were slower than CPU simulations due to overhead on the browser and WebGL texture computations.

To utilize the WebGL framework in implementing the GPU algorithms, GPUSnapse used the GPU.js framework. GPU.js is a JavaScript library for General Purpose computing on GPUs (GPGPU) that can run in both websites and in Node.js. It serves as the bridge between code written in JavaScript to GPU specific code by transpiling JavaScript functions into shader language used by the GPU [26].

A kernel in GPU.js is a special function that runs on the GPU in parallel using WebGL. The key method in GPU.js is the gpu.createKernel() method that creates a kernel and takes in as arguments the kernel configuration such as output format and most importantly, the operations we will be running on the GPU. The kernel function acts as a loop and exposes this.thread.x and this.thread.y which we use to determine on which matrix element are we operating on.

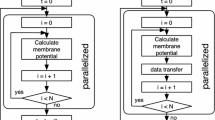
Using GPU.js, three kernels were implemented using the gpu.createKernel() method which all ran on the GPU. The kernel multSpikingTransition [30] takes in the Spiking Vector generated from the current configuration vector and the rules and performs a parallel matrix multiplication in the GPU to get the transition net gain vector. The kernel columnarAdd adds the current configuration and the transition net gain vector from multSpikingTransition to get the next configuration vector. To avoid wasting time on host to device data transfers, a combined kernel [30] was created that takes in the results of multSpikingTransition kernel directly to columnarAdd which keeps the computations entirely in the GPU to avoid the overhead present when transferring data from CPU host to GPU device and vice versa.

To better visualize the kernel functions, the kernel schema is presented in Fig. 2 [30]. The creation of the kernels start by the call to getConfigGPU(). All the kernel functions are inside it. We call on the compute function which uses the method, gpu.combineKernels(), to lessen the performance penalty of utilizing two kernels. Inside this compute function, the columnarAdd kernel is called and lastly, the multSpikingTransition kernel is called to be passed as a parameter to columnarAdd. For further details on the kernel usage, the source code of GPUSnapse can be viewed at https://github.com/Secretmapper/gpusnapse.

The laptop computers used in the experiments from [29, 30] are no longer available for this present work. Instead, the present work compares the implementation from [29, 30] to our present work using another set of computers.

Fig. 2

GPUSnapse kernel schema [30]

Fig. 3

Optimized sparse GPUSnapse architecture

4 Optimized sparse GPUSnapse

The following section discusses the development of the optimized GPUSnapse that uses sparse matrix representation. The source code can be accessed at https://github.com/accelthreat/sparse-optimized-gpusnapse. The optimized GPUSnapse still uses GPU.js as its way of utilizing the GPU for matrix computations for SN P systems on the web. GPU.js is a JavaScript library that uses WebGL to access the GPU for General Purpose computing [26]. This is done by transpiling regular JavaScript functions into shader language than can be ran by WebGL to produce a matrix result.

4.1 Architecture

Figure 3 shows the main architecture of the Optimized GPUSnapse and the boundaries between CPU and GPU. The function, getConfigGPU(), takes six inputs in optimized sparse representation: config, spikingVector (spikingMatrix for non-deterministic), ruleVector, synapseMatrix, neuronRuleMapVector, and ruleExpVector. By utilizing the kernel function detailed in algorithm 1 it produces the next configuration. This configuration goes out of the GPU back into the CPU to the function, generateSpikingVector(), (generateSpikingMatrix() for non-deterministic) to produce the next spiking vector (spiking matrix for non-deterministic). It is in these parts that we encountered problems in optimizing the algorithm to eliminate the device-host-device transfers which incurs a significant performance penalty: runtime is slower, but memory used is reduced (more details later). In the process of optimizing these parts, library issues were encountered concerning the generation of spiking vectors inside the GPU directly. At present we are not able to find a solution for such issues due to limited experience and documentation on GPU.js.

4.2 GPU algorithm

We present the two algorithms: deterministic and non-deterministic, both without support for delays, and both utilize optimized sparse matrix representation from [19].

Algorithm 2 shows the deterministic algorithm. Note the symbols: SN P System ${\varPi }$, initial configuration vector $C_0$, rule vector $Ru_{\varPi }$, rule expression vector rExpV (this is just the regular expressions for the rules), synapse matrix $Sy_{\varPi }$, neuron-rule map vector nmV, and spiking vector $S_k$ for the kth configuration vector. First, the algorithm starts with getting inputs from the generation of the benchmark SN P systems. For the deterministic algorithm in this work, the benchmark used is the bitonic network sorting SN P System. The function getFinalConfigOptimized is then called and this helps in the end-to-end computation of the configuration vectors. Inside, the spiking vectors are computed and passed on to the loop. The while loop would go on until the input maximum run, maxRun, is reached and the spiking vector computation is finished. Inside the loop, the function, getConfigGPUOptimized() (see Algorithm 1) is called and the spiking vectors and the last computed configuration vector is passed on as parameters (along with the original rule vector and synapse matrix) to compute for the next configuration. After the while loop, the last configuration vector is returned.

We discuss further the kernel functions in getConfigGPUOptimized(). It is divided into three sub-functions. The first one is getSubConfig which takes in as inputs spiking vector sV, rule vector rV, and synapse matrix sM. At line 5, it gets j, the index of rule that is activated from the spiking vector and in the following line prematurely terminates the function if j is not a valid rule index. At line 9, it extracts the tuple [c, p] from the rule vector which contains information on how much spikes are consumed and produced for the given neuron. From lines 10 to 16 is the main logic of the function. The function checks if $thread.x = thread.y$ which implies that the current neuron is the one consuming the spike, we return $-c$ to indicate this change. If $thread.x \ne thread.y$, the function checks using the synapse matrix if the neuron is connected. If the neuron is connected, then we return p to indicate that this neuron has received p spikes from the neuron that used this rule. If the above two cases are met, then the neuron the function is currently on is not the neuron that used this rule nor a connected neuron, therefore the current neuron is unaffected and we return 0.

The second function columnarAdd sums up a 2D matrix’s rows per column with a specified initial vector in parallel. This is used to combine the changes to each neuron made by different rules to produce the next configuration vector.

For the non-deterministic algorithm (see Algorithm 3), it has a similar structure as Algorithm 2 except that the CPU implementation uses a for loop to compute for each possible spiking vector for a given configuration. Compared to the GPU implementation, which is made to be parallel and computes and returns a spiking matrix $SM_k$ consisting of all the possible spiking vectors already. The vectors and techniques used for the generation of the spiking matrix and the configuration vectors are from [6], such as the 1D array, Q. This array holds all the configuration vectors computed for each spiking matrix, and that is why we have the marker indices, start and end, to mark the current batch of configuration vectors. For all the computed configuration vectors, the computation widens as it gets each of its corresponding spiking matrices. The loop goes on until the iterations reach 5, as the benchmark SN P systems, the non-uniform solution to subset sum, is sure to stop at 5 steps. After the while loop, we return the last batch of configuration vectors which are all the possible last configurations of the SN P system.

The function $getConfigGPUOptimized\_nd()$ is similar to Algorithm 1, except this time for the non-deterministic algorithm, the input $SM_k$ is 2D instead of $S_k$ which is 1D. Thus, the getSubConfig outputs a 3D matrix and the function columnarAdd accesses this 3D matrix. The overall output of the function is a 2D matrix of configuration vectors.

5 Experiments and results

To perform our experiments for testing we used two computer setups:

• Setup 1: CPU: Ryzen 5 2600, GPU: Geforce GTX 1070 (discrete).

• Setup 2: CPU: Intel(R) Core i5-1135G7, GPU: Intel Iris Xe graphics (integrated).

5.1 Test inputs

For testing the deterministic algorithm we used the bitonic sorting network system and its inputs from [7] as our benchmark. For each bitonic sorting network size from 2 to 64, the tests were ran 5 times to get the mean runtime. For non-deterministic algorithm, we used the non-uniform solution to subset sum from [15] as our benchmark. Although the uniform solution to subset sum works for the non-deterministic algorithm as well, we feel that the non-uniform solution was suitable as our benchmark since the non-uniform solution is better able to maximise the resources of the GPU for parallel computations. For each subset size from 3 to 9, we randomly chose values from 50 to 100 as our elements to our subset. We did this by running our python generator program, Subset_Generator.py, which generates a txt file for each subset size which we use as our input to our main program. Each input txt file were also ran 5 times to get the mean runtime. The runtimes were measured by getting the difference between two calls of performance.now() function. Both the test setups were ran on the unoptimized and optimized algorithms. The unoptimized algorithm is based from [29] while the optimized algorithm was previously discussed on Sect. 4.2.

The algorithms compute end-to-end configurations of the benchmark SN P Systems. It is also important to note that before we moved on to run and test bigger sizes, the validity of the resulting last configuration vector/s were checked first. The work from [9] which is an extension of WebSnapse version 1 in [10] (can be found here: https://nccruel.github.io/websnapse_extended/) greatly helped in understanding the basics of our chosen benchmark SN P systems. XML files of smaller systems were first created and outputs of the configurations were compared with the output of our extended GPUSnapse to check the configuration correctness of our program. We made a bitonic SN P system of size 2 and 4, and a non-uniform solution SN P system of subset size 3, for understanding the basics. All of these can be found in our github repository: https://github.com/accelthreat/sparse-optimized-gpusnapse

The tests currently works well within the sizes mentioned earlier for their respective algorithms. This is because of being limited by the supported maximum WebGL texture size of the browser that was used for the testing which is Google Chrome, 16,384 $\times$ 163,84. Future work recommendation for this is discussed in Sect. 6.

5.2 Estimating memory requirements

The memory was estimated using a function derived from the array and matrix sizes generated by our code. This is because measuring memory directly introduces a lot of variability because of the way chrome introduces metadata for array items. For an SN P system with m neurons and n rules:

Unoptimized deterministic algorithm: $Memory(m,n) = m + 3n + mn.$

Optimized deterministic (Algorithm 2): $Memory(m,n) = m^2 + 3m + 2n.$

Unoptimized non-deterministic algorithm: $Memory(m,n, subset size) = m + 2n + mn + (2^{subset size}n)$

Optimized non-deterministic (Algorithm 3): $Memory(m,n) = 2m + 2n + m^2 + (2^{subset size}m).$

Fig. 4

3D graph of deterministic algorithm memory Requirements

Fig. 5

3D graph of non-deterministic algorithm memory Requirements

The 3D graph of the memory equations are shown in Figs. 4 and 5. For the non-deterministic algorithm, the subset size used for graphing is 9 since this brings about the maximum difference in memory requirements between the unoptimized and optimized algorithms. As we can see, from both of the 3D graphs, the memory requirements for the optimized algorithm shows a proportional growth as the number of neurons and rules increase. Meanwhile, the unoptimized algorithm have high memory requirements despite having low number of neurons.

5.3 Results

First, we present the plot of the memory requirements of the unoptimized vs the optimized algorithm based on the values of our inputs for each input size (bitonic network size and subset size). The results are shown in Figs. 6 and 7. On both figures, unoptimized algorithm shows higher memory requirements than the optimized algorithm. Comparing the result in the deterministic algorithms to the non-deterministic, the former shows consistent growth for each bitonic network size while the latter have peaks and dips. This is because from the definition of the non-uniform solution to subset sum from [15], the number of neurons and rules depends on the values of the subset, and from the discussion in Sect. 5.1, it was mentioned that the values for each subset size were randomly chosen. Certain input sets of size 6 (that is, with 6 elements) may have elements with smaller values than other input sets of size 5. The chosen values for each subset can be seen in our repository in the file, readme_subsetsum_samples.txt.

Fig. 6

Estimated memory use of unoptimized versus optimized deterministic algorithm

Fig. 7

Estimated memory use of unoptimized versus optimized non-deterministic algorithm

Next, we present the results from the performance tests. Various tests were done to compare the performance of the algorithms (unoptimized vs optimized) between the two setups and the two processors (CPU vs GPU). We discuss first the deterministic algorithms.

Figures 8 and 9 show the runtimes of the unoptimized vs optimized algorithm using CPU on Setups 1 and 2, respectively.

Fig. 8

Running time of unoptimized CPU versus optimized CPU on setup 1 (deterministic)

Fig. 9

Running time of unoptimized CPU versus optimized CPU on setup 2 (deterministic)

As we can see, for both setups the unoptimized CPU shows a significant increase around bitonic network size 16 and ends with a large difference in runtime in bitonic network size 64. A similar trend can be seen in Figs. 10 and 11 for setups 1 and 2, respectively, where the unoptimized algorithm has significant higher runtimes than the optimized.

Fig. 10

Running time of unoptimized GPU versus optimized GPU on setup 1 (deterministic)

Fig. 11

Running time of unoptimized GPU versus optimized GPU on setup 2 (deterministic)

Both of the setups show a similar trend, except that setup 2 shows higher numbers for the GPU tests compared to setup 1 because the former uses an integrated graphics while the latter uses a discrete graphics card.

Lastly, we compare all the results that we have into one graph shown in Figs. 12 and 13 for the two setups. For both setups we see that the optimized algorithm shows better performance. Notice that the GPU performance for the optimized is slower than the CPU. This would be further discussed after the non-deterministic results are presented in the next paragraph.

Fig. 12

All running times on setup 1 (deterministic)

Fig. 13

All running times on setup 2 (deterministic)

For the non-deterministic results. Figures 14 and 15 show the runtimes of the unoptimized vs optimized algorithm using CPU on setups 1 and 2, respectively.

Fig. 14

Running time of unoptimized CPU versus optimized CPU on setup 1 (non-deterministic)

Fig. 15

Running time of unoptimized CPU versus optimized CPU on setup 2 (non-deterministic)

Table 1 Summary of results for setup 1

Table 2 Summary of results for setup 2

For both of the setups Tables 1 and 2, we can see that the optimized CPU performed better than the unoptimized. We especially see bigger differences in their performance as the subset size increase. Now for the GPUs, the results are shown in Figs. 16 and 17 for setups 1 and 2, respectively. For both of the setups, the same trend can be seen where the unoptimized GPU performs better than the optimized GPU. This is because for the unoptimized non-deterministic GPU implementation, it uses a single kernel unlike in the unoptimized deterministic GPU implementation. This is to take into account the 2D spiking matrix which consists of all the possible spiking vectors per configuration vector. Meanwhile, the optimized GPU uses two kernels and uses the combineKernels() method to lessen the cost of having multiple kernels. However, the cost is still significant and it shows in the results. To demonstrate this cost we ran a test that creates a single, empty kernel. We ran the program a total of 45 times and got its average. The creation of a single, empty kernel costs around 26 ms (milliseconds). Note that this does not mean that the creation of any kernel only takes 26 ms as this is an empty kernel and does not contain any computation.

Fig. 16

Running time of unoptimized GPU versus optimized GPU on setup 1 (non-deterministic)

Fig. 17

Running time of unoptimized GPU versus optimized GPU on setup 2 (non-deterministic)

Fig. 18

Measurement of host-to-device transfer by configuration steps

For the CPUs vs GPUs, from the results mentioned above, we see consistent trends that the CPUs perform better. This is because of the usage of multiple kernels and the host-to-device transfers that happens when we compute for the spiking vectors (for deterministic) and spiking matrices (for non-deterministic). We were not able to measure accurately the cost for host-to-device transfers: at present this is a limitation of GPU.js, that is, we know of no tool to accurately measure this using GPU.js, unlike in CUDA. However, we confirm these claims by performing tests for a single SN P system configuration only vs two configurations and see how much they differ in terms of runtimes.

The configurations mentioned here are the same configuration vectors defined in Definition 2. For more context, a configuration means getting the resulting number of spikes for each neuron after executing an applicable rule per neuron. For non-deterministic SN P systems, a configuration can have different results because it will vary per the choice of the rule to execute.

For this test, one algorithm and setup are enough just to see the difference. For each subset size, the program ran 5 times to get their average runtimes. We did this test for the optimized non-deterministic GPU implementation on setup 2. The results can be seen in Fig. 18. As we can see, the performance of the computation for a single configuration is consistently between 100–200 ms for all subset sizes. This single configuration computation does not have much host-to-device transfers as it only has to access the GPU to compute for the next configuration once, and return the result. The spiking matrix is also computed only once, thus, the consistency of the runtimes across the subset sizes. Meanwhile for the computation of two configuration vectors, we have to wait for the computation of the spiking matrix each time, and the data is transferred between host-to-device twice. Future work recommendation for this is mentioned in Sect. 6.

6 Final remarks

In this paper, we extended the GPUSnapse program to take advantage of optimized sparse matrix representation to reduce memory consumption and running time. We implemented 4 algorithms that simulate deterministic and non-deterministic SN P systems for both CPU and GPU using the optimized representation. From our tests we were able to observe an up to 1.97$\times$ speedup of GPU runtime and a 22$\times$ speedup of CPU runtime using the optimized representation for deterministic SN P systems. We also observed an up to 30% reduction in estimated memory usage for the optimized deterministic algorithms. For the non-deterministic algorithms, we were able to observe a 6.64$\times$ speedup of CPU runtime and an up to 24% reduction in estimated memory usage for the optimized algorithms. For the GPU implementation, the optimized algorithm shows promise already considering that it accesses and outputs a 3D matrix to compute for all the possible last configuration vectors. Its performance can be further improved by considering implementing it in a single kernel only. Note that, the performance of all the GPU implementations would benefit if all of them can be done in a single kernel. Since the algorithms presented in this work do not support delays, it may be extended to support delays for future work.

The simulation runtimes can still be improved in the future by minimizing device to host transfers, that is, reducing much overhead when processing the next configuration from a previous one. A better way of general purpose GPU programming in the web can be explored. Our current approach with GPU.js to exploit the graphics-focused WebGL introduces plenty of overhead which negatively impacts the runtime. In terms of limitations on texture sizes, this can be improved by exploring different implementations where the arrays would not reach the maximum supported texture size while accommodating bigger benchmark sizes. The work can also be improved by exploring better and newer technologies. WebGPU is one candidate to replace WebGL, as it is purposely built to help web developers to use for general computing. It was announced in 2021 that WebGPU was available for developers to test and give feedback. But as of February 2023, it is still in trial and not available to most web browsers.

We see our works in [29, 30] and in the present work as hybrids or bridges between our WebSnapse web-based and visual simulators in [9, 10], and our general purpose, accelerated/massively parallel CUDA simulators in [1, 6, 7]. That is, our present work runs in the web browser (like WebSnapse but unlike our performance or acceleration-focused CUDA simulators) and can perform some computations in the GPU (like our CUDA simulators and unlike WebSnapse). In this way our present work is a bridge or step towards combining (in the future) the benefits of web-based and visual simulators such as WebSnapse, and our performance/acceleration-focused CUDA simulators. Other limitations of our present work which we aim to work on: include other variants of SN P systems; more efficient representations and simulations to increase the sizes of the simulated systems. In [6] for instance, even with powerful CUDA GPUs we were only able to simulate subsets of size up to 7, since deterministic simulations for solving Subset Sum require massive amount of memory.