Keywords

1 Introduction

The brain has inspired many researchers due to its energy efficiency, accuracy and robustness. The field of neuromorphic computing aims to mimic the underlying neurological processes. Spiking Neural Networks (SNNs) are the most widely used neural network model in the neuromorphic research community [23].

Researchers from deep learning community are exploring bio-inspired Artificial Neural Networks (ANNs) [10]. ANNs are known for their ability to recognize patterns in images (e.g. [20]) or time-series data (e.g. [26]), and solve complex problems like navigating autonomous vehicles or –in combination with reinforcement learning– mastering the game of Go [29]. SNNs can be seen as the new, 3rd generation of ANNs [14] and can, in principle, be used for the same applications. One motivation to develop the “traditional” ANNs to a new generation is the surprising fact that ANNs are “easy to fool” [17], e.g. an adversarial image can be engineered in a way that, for example, a human can still easily recognize a stop-sign, however, the ANN will now identify the same sign as a speed-limit. SNNs may hold the promise of greater inherent robustness to such manipulations [9]. An additional motivation for the investigation of SNNs as per Roy et al. [28] is that the human brain accomplishes extremely complex tasks with a tiny energy budget when compared to traditional ANNs. Currently under investigation are memristor-based hardware [9], Intel Loihi [7], SpiNNaker [13], and IBM TrueNorth [8].

However, SNN computations are challenging in contrast to ANN computations, since they involve the timing information of spikes and internal neuron dynamics [23]. On the other hand, SNN training is an ongoing field of study [25, 32]. ANNs have already benefited massively from the utilization of Graphics Processing Units (GPUs) by using the Compute Unified Device Architecture (CUDA) programming framework. The most common modelling tools, PyTorch [27] and TensorFlow [1] readily provide a high-level CUDA interface for Deep Neural Networks (DNNs).

Another research field with interest in the efficient simulation of biologically plausible neural networks is computational neuroscience. The size and complexity of biological networks by far exceeds the one of current artificial neural networks [4]. It is recognized that the analysis of biological and ANN have developed largely independent in the past [32], though facing a set of similar challenges [4] and future synergies are expected [35]. To handle the additional requirements of SNNs simulation in the neuromorphic research community, several hardware and software frameworks have been developed, such as NEURON [6], NEST [11], NeMo [12], NCS6 [18], CARLsim [5], GeNN [33], Spike [2], BRIAN2 [30], PyNN [3] and NeuronGPU [15]. The frameworks differ in the level of detail with which they model neural functions. In terms of utilizing parallel hardware, BRIAN2 [30] supports multithreaded parallel computations, while NEURON [6] and NEST [11] support distributed simulations on computer clusters with NVIDIA GPUs using CUDA and Message Passing Interface (MPI).

At the core of simulators lie detailed algorithms which differ in their parallelization approach on NVIDIA GPUs. In such approaches, the number of parallel threads depends on either the number of neurons (Neuron (N)-algorithm), or synapses (Synapse (S)-algorithm) or action potentials (Action Potential (AP)-algorithm) [23]. The N-, S- and AP-algorithms have their own limitations when implemented on NVIDIA GPUs. The N-algorithm is compute-intensive, since the time-complexity of the N-algorithm is proportional to the number of synapses. The S-algorithm is resource-intensive with high GPU resource requirements, since the space-complexity is proportional to the number of neurons and synapses. Both N- and S- algorithms require Central Processing Unit (CPU) intervention which may result in the so-called CPU bottleneck. The AP-algorithm aims to overcome limitations of the N- and S-algorithms by using the Dynamic Parallelism (DP) [23]. However, the AP-algorithm is resource-intensive for a large number of spikes. There is only a limited amount of studies of the scaling of SNNs simulation time with the number of spikes [23].

All the above-mentioned challenges motivate an efficient use of CPU-GPU resources for improving the performance of SNN simulation. The objective of this paper is to optimize parallelization approaches for SNN simulation. We propose two novel algorithms for NVIDIA GPUs using CUDA. The overall contributions of our work are as follows:

  • We recognize that the scheduling and allocation of tasks on the GPU in existing SNN simulation algorithms limit the performance.

  • We propose two new parallelization algorithms [Single Kernel Launch (SKL) and Active Block (AB)] and evaluate them against the state-of-the-art (SOTA) approaches. For the evaluation, we use the same network (a pulse-coupled network of Izhikevich neurons) as in the SOTA work [23] across a wide range of modes, neuron and synapses values.

    • SKL-algorithm: The CPU bottleneck is completely avoided. Iterative kernel calling is shifted to the GPU, resulting in a single kernel call from the CPU.

    • AB-algorithm: An efficient GPU utilization based on available processing blocks for computations and communications has led to a significant speedup.

  • The average speedups obtained by the best of the proposed algorithms are factors of 0.83\(\times \), 1.36\(\times \) and 1.55\(\times \) in comparison to the SOTA algorithms with maximum speedups of 1.9\(\times \), 2.1\(\times \) and 2.1\(\times \) for firing modes 0, 1 and 2 respectively.

The rest of this paper is organized as follows. Section 2 provides background information on SNN simulation, the used neuronal model, and the grid-stride loop. Section 3 introduces the SOTA and the proposed algorithms for the SNN simulation on heterogeneous CPU-GPU platforms. Sections 4 and 5 explain the evaluation methodology and present the detailed experimental results and discussions. Finally, we conclude the paper in Sect. 6.

2 Background

In this section, we first discuss the general flow in an SNN simulation (Sect. 2.1). In particular, we use the popular Izhikevich neuron model, introduced in Sect. 2.2. The network dynamics and modes are discussed in Sect. 2.3. We conclude the section by giving the necessary background knowledge on the grid-stride loop in Sect. 2.4.

2.1 General Flow of SNN Simulation

SNN simulation involves the propagation of spikes through a network of neurons and synapses. An SNN simulation starts with input signals in the time domain (called spikes) applied to the neurons of the input layer. The state of each neuron is defined by its membrane potential value. The spike at the input layer causes an input current, which in turn results in a change of the neuron membrane potential. If the neuron membrane potential crosses a certain threshold, the neuron “fires” and the spike is propagated to the neurons of the subsequent layer in the next time stamp through synapses. Consequently, the membrane potential values of the neurons in the subsequent layer are updated and the spike is propagated again and so on. This process of spike propagation is recursive or iterative depending upon the implementation. In the recursive spike propagation model, only activated neurons take part in the computation, while in the iterative spike propagation model, the state of all neurons at all time steps is considered.

The implementation of the SNN simulation on the CUDA level involves the invocation of two main kernels. The first kernel is an update kernel, given by Pseudo-code 1, for updating the state variables of an individual neuron and the spike list if the potential crosses the threshold value.

figure a

The second kernel is propagating the spikes to postsynaptic neurons as given by Pseudo-code 2.

figure b

In each of the approaches presented in Sect. 3, these two kernels are executed in each iteration of the SNN simulation. Typically, the CPU invokes a parent kernel on the GPU and both kernels, corresponding to Pseudo-codes 1 and 2, are executed on the GPU. The resulting data is transferred back to the CPU and a new iteration starts.

2.2 Izhikevich Neuron Model

There are a number of neuron models that are currently being used in SNN simulations. These models range in complexity, biological plausibility, and computational efficiency. In this work we simulate a pulse-coupled Izhikevich neural network as it has been used to benchmark the SOTA AP algorithm by Kasap and Opstal [23], as well as the GeNN SNN simulator [34].

The Izhikevich neuron model [21] is a reduced-order model of the Hodgkin-Huxley model [19], which is obtained by means of bifurcation theory. The Izhikevich model sacrifices the biological plausibility of the Hodgkin-Huxley model, but retains its functionality. In this way the Izhikevich model is less complex and more efficient to simulate in comparison to Hodgkin-Huxley model [22]Footnote 1. Furthermore, it possesses the capacity to describe more complex neuronal behaviors (spiking patterns), which make it more attractive than Leaky-integrate-and-fire neuron models [21].

The Izhikevich model is a 2-dimensional system consisting of the states u and v, which are the membrane potential and its recovery variable, respectively. Their instantaneous rate of change obey the following set of ordinary differential equations:

$$\begin{aligned}&v^\prime = 0.04 v^2 + 5v+140-u+I \end{aligned}$$
(1)
$$\begin{aligned}&u^\prime = a(bv-u) \end{aligned}$$
(2)
$$\begin{aligned}&\text {if } v\ge 30\,\text {mV, then} {\left\{ \begin{array}{ll} &{} v \leftarrow c \\ &{} u \leftarrow u+d \end{array}\right. } \end{aligned}$$
(3)

where the prime \(\prime \) represents the derivative with respect to time, a, b, c and d are dimensionless parameters that are chosen to fine-tune the desired neuronal behavior (spiking, bursting, etc.), and I is the current. A spike is propagated if the neuron membrane potential crosses the threshold value of 30 mV given by Eq. (3)- if it accumulates the necessary amount of inputs. The value of v resets to resting value c and the value of u increases by recovery reset d when the neuron fires the spike. In our system the injected current I is modeled as

$$\begin{aligned} I_j (t_{n+1}) = g_{\text {e}xc, inh} \cdot q_j(t_n) + w_s \sum _{i}^{S} S_{ij} \delta _i(t_n) \end{aligned}$$
(4)

where \(S_{ij}\) is the connectivity matrix element from presynaptic neuron i to neuron j, and \(w_s\) is a fixed synaptic scaling factor that depends on the total number of synapses in the network. The \(\delta _i\) variable is equal to 1 if neuron i spikes at time \(t_{n}\), i.e. \(\delta _i(t_n)=1\) and \(\delta _i(t_n)=o\) otherwise.

Neurons are classified to be either excitatory or inhibitory, and their ratio is conventionally chosen as 4:1 in the network, inspired by the mammalian cortex [21, 23]. If a neuron is excitatory or inhibitory is defined by its connection strength: The connection strengths \(S_{ij}\) to an excitatory (or inhibitory) neuron are chosen randomly from a uniform distribution on \([0,\,0.5]\) (\([-1,\,0]\)) [23]. The input current \(I_{j}\) for neuron j from Eq. (4) consists of the sum of the stochastic input current \(q_j\) scaled by an excitatory or inhibitory conductance \(g_{\text {e}xc, inh}\) and the synaptic currents received from its active presynaptic neurons [23].

2.3 Network Dynamics and Modes

The network dynamics are determined by the values of the input conductance values \(g_{\text {e}xc, inh}\) in Eq. (4), resulting in different firing regimes or modes of the network as presented in Table 1. The definition is identical to the one used by Kasap and van Opstal in [23].

Table 1. Definition of the quiet, balanced and irregular firing modes based on the chosen excitatory or inhibitory conductance values \(g_{\text {e}xc, inh}\).
Full size table

The processing of the propagation of each spike through the network requires a certain amount of hardware resources. The balanced and irregular networks generate a large number of spikes, which makes their simulation computationally challenging compared to mode 0, i.e. quiet networks.

2.4 Grid-Stride Loop

GPUs, in general, support dynamic (or random) scheduling of the tasks based on the available hardware resources. This dynamic scheduling mode will assign a loop iteration to an available thread [16].

It allows a more balanced execution time across threads, but incurs a higher processing overhead as it requires the thread (or a block of threads) to wait after each task(s) to receive the next iteration(s) to execute. The default scheduling policy on the GPU, is generalized for the varying execution times for different workloads and does not favor tasks that have similar execution time [16].

Fig. 1.
figure 1

Illustrated are two processing methods for computational blocks of threads. In our example, the GPU can process four blocks in parallel at a time. In the random block processing (left hand side) the GPU-resource manager handles the workload allocation. In contrast, in the grid-stride loop (right hand side) the CPU organizes the workload, freeing resources on the GPU.

Full size image

An alternative scheduling, the grid-stride loop is illustrated in Fig. 1. The grid-stride loop [24] avoids inefficiencies in terms of idle time on the hardware by preallocating the loop iterations to each thread in the following way: The grid-stride loop uses a static schedule that assigns loop iterations to threads for execution [24]. In a 4-thread application with 8000 loops, static scheduling will assign loops 0 to 1999 to thread ID 0, loops 2000 to 3999 to thread ID 1, loops 4000 to 5999 to thread ID 2 and lastly loops 6000 to 7999 to thread ID 3 [16]. This scheduling policy favors tasks that have similar execution time which is suitable for the special case of spike propagation. Further, GPU resources are freed as in the grid-stride loop the block processing is CPU-orchestrated in the sense of a static pre-allocation.

Depending on the parallelized task static pre-allocation in the grid-stride loop demonstrates advantages over the random block processing, for example a speedup factor of 1.4x in [16].

3 SNN Simulation Algorithms

In this section, we discuss the SOTA (N-, S- and AP- [23]) algorithms and propose the AB- and SKL-algorithm. The implementation of the AB- and SKL-algorithm and comparison to the SOTA (AP, N, S) are made available as open access in the following GitHub repository: GPU4SNN.

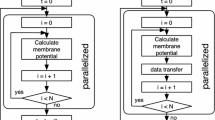
The number of neurons \(\mathcal {N}\) and synapses \(\mathcal {S}\) in the SNN determine the required processing blocks on the GPU. However, the algorithms differ in their scheduling and allocation tactics of the processing blocks, as well as their CPU-GPU communication pattern. Figure 2 shows a simplified overview and each algorithm is discussed in the following.

N-algorithm. In the N-algorithm, the spike kernel is implemented by invoking \(\mathcal {N}\) threads in parallel, as detailed in [23]. The heterogeneous implementation of the N-algorithm using CPU-GPU platforms is shown in Fig. 2. The algorithm implementation requires repeated GPU kernel calling from the CPU. Each iteration involves two kernel calls (Update Kernel and Propagate Spike Kernel) from the host CPU. The N-algorithm starts with \(\mathcal {N}\) parallel threads simultaneously. Each thread operates \(\mathcal {S}\) times repeatedly. Hence, the computational overhead for each thread is a factor of \(\mathcal {S}\) and therefore increases with the number of synapses. The potential problem with the N-algorithm is the underutilization of the GPU resources due to launching of only \(\mathcal {N}\) threads.

S -algorithm. In the N-algorithm, \(\mathcal {N}\) threads are invoked in parallel and each of them iterates \(\mathcal {S}\) times. In the S-algorithm [23], however, \(\mathcal {N}\times \mathcal {S}\) threads are invoked in parallel and each of them iterates one time. The \(\mathcal {N}\times \mathcal {S}\) threads might create a hardware resource constraint in terms of space on the GPU. Therefore, it is said to have an increased space-complexity. The N-algorithm, however, needs \(\mathcal {S}\) iterations, each of which due to its time-consumption might lead to an increased time-complexity.

Fig. 2.
figure 2

Simplified communication patterns between CPU and GPU for SNN simulation with the SOTA algorithms (left hand side) and proposed algorithms (right hand side). At the core of the proposed algorithms lies a grid-stride loop, which is shown schematically in Fig. 1.

Full size image

In all algorithms the same kernels as described in Sect. 2.4 are used. The kernel launch can be handled by the CPU or GPU. A counter tracks the iteration of the SNN simulation. Block processing can take place in a random or grid-stride loop fashion as described in Sect. 2.4. Particular CUDA methods are DP (dynamic parallelism) used by the AP-algorithm and kernel fusion used by the SKL-algorithm.

The \(\mathcal {N}\times \mathcal {S}\) threads in the S-algorithm are combined together to form blocks of threads. The GPU resource manager randomly allocates the blocks of threads as illustrated in Fig. 1. Due to this random allocation of tasks on the GPU, the hardware resources are likely to be used inefficiently.

AP -algorithm. The AP-algorithm exploits the DP using CUDA on an NVIDIA GPU [23]. As shown in Fig. 2, in the AP-algorithm, the CPU invokes one parent kernel on the GPU with \(\mathcal {N}\) threads. Given a spike from each of the \(\mathcal {N}\) neurons, the respective thread will launch a child kernel with \(\mathcal {S}\) threads of its own. Since launching of the child kernel depends on the presence of a spike, caused by the potential crossing of a threshold value, this algorithm is called the Action Potential algorithm. The space complexity of the AP-algorithm increases with the number of spikes.

AB -algorithm. The communication pattern of the AB-algorithm is similar to the N- or S-algorithm, as shown in Fig. 2. The main difference in the communication pattern of AB-algorithm between CPU and GPU in comparison to the N- and S-algorithm is as follows: In the AB-algorithm, the CPU is used to place the optimized workload on the GPU instead of immediately placing the total workload of the respective iteration, as was done in the case of the N- and S-algorithm. Therefore, hardware resources are used in a more balanced way. The time consuming random resource allocation and scheduling used in the N- and S-algorithm are thereby avoided to gain possible performance improvements.

SKL -algorithm. There are circumstances under which the AB-algorithm might not be the optimal choice, such as: i) If there is already a high workload present on the CPU, or ii) if the data transfers between CPU and GPU are costly. For these circumstances, we propose the SKL-algorithm. The SKL-algorithm is shown schematically in Fig. 2. The CPU launches one kernel only on the GPU. The initialization and computations of the grid-stride loop are handled by the GPU. Since all kernels are directly invoked on the GPU, the SKL-algorithm completely avoids a possible CPU bottleneck. However, it adds an extra step consisting of inter-block GPU synchronization after each stage, i.e. update and spike (kernel fusion).

In brief, each of the proposed algorithms first calculate the availability of the hardware resources in terms of the computational thread blocks. Later on, the proposed algorithms distribute the workload (i.e. loop iterations) of the simulation equally to each thread block using grid-stride loop on the GPU. The CPU is not only distributing the workload equally on the GPU by calling an application program interface using CUDA but also accumulating the total number of spikes obtained from the simulation for evaluating the accuracy of the simulation. The GPU simultaneously update the neurons mapped onto the threads and propagate the spikes while the accumulation of the spikes continues on the CPU. We named the proposed approaches the way they are implemented on the GPU (i.e. Active Block(AB) and Single Kernel Launch(SKL)) as opposed to the way described in terms of SNN terminologies i.e. Neuron(N), Synapses(S), and Active Potential(AP) [23].

4 Performance Evaluation

SNN simulators need to perform well on a wide range of possible neural networks: from relatively small ones with only a few number of neurons and synapses to extensively large ones. Additionally, the number of spikes may change in a quiet (0), balanced (1), or irregular (2) mode (defined in Table 1), and for how many time steps (or iterations) the simulation is performed. To ensure optimal performance under the above mentioned conditions, the scaling of the underlying parallelization algorithm needs to be favorable.

Here, the three SOTA parallelization algorithms (AP, N, S) are compared to the proposed ones (AB, SKL) in terms of their total simulation time under scaling of the number of neurons and synapses for 2000 iterations for modes 0, 1, and 2. We vary the number of neurons N by more than two orders of magnitude: in eight steps on a logarithmic scale from \(N=10^3, \ldots , 2.5 \cdot 10^5\). Similarly, we vary the number of synapses S in seven steps from \(S=2^7,\ldots , 2^{13}\) (128\(,\ldots ,\,\)8192).

We evaluate all scenarios by the total time each algorithm requires for the simulation. Figure 3 visualizes the winning algorithm with the shortest total simulation time for each neuron-synapses number pair. Overall, we see significant speedup factors of the proposed algorithms (AB, SKL) for larger spiking neural networks with a larger number of neurons in modes 1 and 2. The AP algorithm performs well in the low-spiking regime (mode 0).

Fig. 3.
figure 3

Shown is the winning algorithm with the smallest total simulation time t for firing modes 0, 1, and 2 when the total number of neurons (\(N=10^3 \ldots 2.5 \cdot 10^5\)) and synapses per neuron (\(S=2^7\ldots 2^{13}\)) are changed. The two names of the algorithms in each rectangle indicate the top two approaches with smallest simulation times, i.e. the winning algorithms, which can be SOTA and/or proposed algorithm(s). The number in the rectangle represents the speedup obtained by the best of the proposed algorithms over the best of the SOTA ones (i.e. \(t_\mathrm{best\ SOTA}/t_\mathrm{best\ prop.}\)). Therefore, factors \(>1\) show speedup obtained by the proposed algorithms over the SOTA ones. The average speedups obtained by the best of the proposed algorithms are factors of 0.83\(\times \), 1.36\(\times \) and 1.55\(\times \) in comparison to the SOTA algorithms with maximum speedups of 1.9\(\times \), 2.1\(\times \) and 2.1\(\times \) for firing modes 0, 1 and 2 respectively. Bold font highlights speedup factors above or equal to 1.5, i.e. the speedup is larger than 50% compared to the best current SOTA algorithm.

Full size image

In our case the total number of neurons N is equal to the number of pre-synaptic neurons, as well as the number of post-synaptic neurons. In region “(NA)”, no simulation is possible because the number of synapses per pre-synaptic neuron S is larger than the total number of post-synaptic neurons N.

Fig. 4.
figure 4

Shown are the total simulation times for each algorithm when the (left) number of neurons is scaled (\(S=2^{10}\), \(N=10^3 \ldots 2.5 \cdot 10^5\)), and (right) the number of synapses is scaled (\(N\approx 10^{4}\), \(S=2^7\ldots 2^{13}\)) in modes 0, 1, and 2 (from top to bottom) of Fig. 3.

Full size image

To discuss the scaling behavior of each algorithm in more detail, we perform following analysis: Fig. 4 shows the absolute values for the elapsed times of each algorithm for a horizontal cut (scaling with the number of neurons) and a vertical cut (scaling with the number of synapses) through Fig. 3. We evaluate the total number of spikes (“unsigned int”) obtained from each algorithm to evaluate the accuracy of the simulation. We use single precision (32-bit) float variables from CUDA for representing the state variables of neurons. We follow the same state variables (introduced in Sect. 2.2) and precision as mentioned in SOTA approaches [23]. We note the following scaling behaviors:

The N algorithm’s scaling behavior is compatible with our expectation: The GPU is likely to have enough (N) threads. Therefore, the N algorithm scales favorably with an increasing number of neurons (see left-hand side of Fig. 4). However, as each thread has to operate S times in the N algorithm, its time complexity increases with S (see right-hand side of Fig. 4).

The S algorithm shows a more favorable scaling with the number of synapses than the N algorithm. The S algorithm aims to launch \(N\times S\) threads in parallel. Each thread only operates one time. The GPU may not provide enough space (space complexity), and the random allocation will consume GPU resources.

The AP algorithm launches N threads. Given a spike of a neuron, the respective thread will launch a child kernel with S threads of its own. Therefore the space complexity is expected to increase with the number of spikes. Therefore the AP algorithm performs excellent under the conditions of low spike count. However, in the higher firing modes with higher spike count (left-hand side of Fig. 4) the launching of child kernels per spike can become costly and the total simulation time diverges.

The AB and SKL algorithm show a favorable scaling of the total simulation time under both, the number of neurons or synapses in Fig. 4. AB and SKL algorithm’s scaling with the number of synapses is comparable to the one of the S algorithm and therefore favorable. In contrast to the S algorithm, though, the two proposed algorithms show a more favorable scaling under an increasing neuron number. This favorable scaling explains why the proposed algorithms win in the higher neuron number region of Fig. 3. The difference between AB/SKL and the S algorithm is that for AB/SKL, the CPU orchestrates the workload on the GPU. The algorithm still aims to perform computations corresponding to \(N\times S\) threads. However, only maximum possible active threads are launched and the total workload is distributed among active threads. Hence, the GPU is free from the orchestration workload in AB/SKL.

5 Discussion

In this paper, we quantify the performance of the SOTA (S-, N-, AP-algorithm) and two proposed algorithms (AB-, SKL-algorithm) for SNN simulation on A100 NVIDIA GPU. The proposed algorithms show advantageous scaling under variation of the number of neurons and synapses (\(N=10^3, \ldots , 2.5 \cdot 10^5\), \(S=2^7,\ldots , 2^{13}\)).

Intuitively, we expect the SKL-algorithm to be the fastest among the other algorithms since all intermediate communications between host and device are completely avoided.

In comparison to the SKL-algorithm, the AB-algorithm does not need a counter on the GPU. The CPU controls the time steps and hence launches Update and Spike Propagation kernel iteratively on the GPU until the total number of time steps are evaluated for the simulation. In this way, the AB-algorithm distributes the tasks more efficiently on the hardware resources i.e. CPU and GPU, resulting in a significant speedup and maintaining the accuracy in terms of the total number of spikes.

Two possible drawbacks of the SKL-algorithm could be the following: First, since all intermediate communication is avoided, the SKL-algorithm cannot store the temporal variation of an SNN since the data is transferred in the last iteration. Especially in the context of neuroscience the time dynamics and evolution of membrane potentials and spikes in an SNN might be important. In such a case, the limitation of intermediate communication in the SKL-algorithm limits its applications. A possible future solution could be to modify the SKL-algorithm to provide flexibility to send the data after a certain number of iterations instead of the last iteration. Another solution is to always use the proposed AB-algorithm: In the N-S configurations where the SKL-algorithm is the winner in terms of total execution time, the runner-up in the vast majority of the cases is the proposed AB-algorithm (see Fig. 3). A second disadvantage may be memory limitation. The SKL-algorithm assumes the input data as well as intermediate results will be available in the GPU memory for all the iterations. If the device memory is not large enough then its better to utilize the AB-algorithm to pipeline computations and communications. If the device memory does not entirely fit the input data and/or neural network model, then the data and/or model will be evaluated in phases. This multi-phase mode will involve the CPU intervention to load the GPU memory when the evaluation of the previous phase of the data and/or model is finished. Such a mode requires iterative kernel launching, which can be implemented by the AB-algorithm but not by the SKL-algorithm.

6 Conclusion

In this paper, we propose and evaluate two novel GPU-based algorithms (SKL and AB) for SNN simulation with a grid-stride loop as their core element. Iterative invocations of a GPU kernel from the host CPU involve time consuming tasks and the corresponding complexity increases with an increase in the number of iterations. The SKL-algorithm avoids iterative kernel calling from the host CPU. In this way, the CPU bottleneck is completely avoided and iterative calling of a kernel is shifted to the GPU resulting in a single kernel call from the CPU.

An efficient heterogeneous CPU-GPU utilization using the AB-algorithm has also provided significant speedup while maintaining the SNN accuracy in terms of the total number of spikes. The average speedups obtained by the best of the proposed algorithms are factors of 0.83\(\times \), 1.36\(\times \) and 1.55\(\times \) in comparison to the SOTA algorithms with maximum speedups of 1.9\(\times \), 2.1\(\times \) and 2.1\(\times \) for firing modes 0, 1 and 2 respectively.