Solving subset sum by spiking neural P systems with astrocytes producing calcium

Abstract

We consider spiking neural P systems with astrocytes producing calcium that differs from the standard spiking neural P systems in several ways: we have a new type of resources called calcium unit alongside the standard spike, we have a new type of place called astrocyte alongside the standard neurons and we also have dedicated synapses for communicating calcium units alongside those used for communicating spikes. In order to illustrate how these systems work we give an example of a spiking neural P system with astrocytes producing calcium that generates all even numbers using only two neurons and one astrocyte and without using either forgetting rules or delay in the evolution rules. We prove that in this framework, we can provide semi-uniform and uniform constructions of spiking neural P system with astrocytes producing calcium working in a non-deterministic way that are able to solve the subset sum problem in a polynomial number of steps without using either forgetting rules or delay in the evolution rules.

1 Introduction

Membrane computing (Paun 2002) is a well-known branch of natural computing (Rozenberg et al. 2012) that aims to obtain formal models (membrane systems - also called P systems) inspired by the way the living cells function, are structured and communicate with other cells. The arrangement of the cells can form different patterns: trees (cell-like Paun 2000) or graphs (tissue-like Martín-Vide et al. 2003 or neural-like Ionescu et al. 2006). Inside each cell can be placed multisets of objects (inspired from the molecular species), and these multisets of objects can be rewritten using evolution rules (inspired from the chemical reactions).

Spiking neural P systems (Ionescu et al. 2006) are inspired by how the human brain works by spiking information, namely describing how spikes are transmitted from one neuron to another through specific connections called synapses (Gerstner and Kistler 2002). A spiking neural P system consists of a set of neurons placed in the nodes of a directed graph; the neurons send signals (spikes) along synapses (edges of the graph). The information stored inside the neurons is given by the number of spikes and their timings. Several variants of spiking neural P systems were proposed by considering additional features: spiking neural P systems with astrocytes (Paun 2007), spiking neural P systems with anti-spikes (Pan and Paun 2009) and spiking neural P systems with weights (Pan et al. 2012), spiking neural P systems with astrocytes producing calcium (Aman and Ciobanu 2020).

It was proven that spiking neural P systems and their variants: (i) have the same computational power as Turing machines (Leporati et al. 2009), (ii) can solve in a linear or polynomial-time NP-complete problems (Ishdorj and Leporati 2008; Leporati and Gutiérrez-Naranjo 2008; Leporati et al. 2009a; Pan et al. 2011; Song et al. 2014; iii) can be connected with automata (Aman and Ciobanu 2015, 2016; Cabarle et al. 2016); iv) can be used in applications (Wang et al. 2015; Zhang et al. 2014, 2017).

Regarding the application of spiking neural P systems to solve intractable problems, a frequent approach is to use families of spiking neural P systems such that each member of this family solves only a finite set of instances of a given size. The solutions of the intractable problems are specified either by the fact that the system halts and the output neuron emits a spike during the computation, or by the existence of output neurons signalling true or false.

The first step towards such a specification was taken already in Leporati et al. (2009a) for the case of non-deterministic (and non-confluent) SN P systems.

In this paper we study the efficiency of spiking neural P systems with astrocytes producing calcium. We show that these systems on which we impose additional restriction, namely we do not consider forgetting rules nor delay in the evolution rules, are powerful enough to provide polynomial-time solutions to the subset sum problem. We consider two ways of constructing the system: (i) semi-uniform: we construct a spiking neural P system with astrocytes producing calcium for each instance of the subset problem and embed the parameters into the constructed systems as number of spikes, graph of neurons and astrocytes, and evolution rules; (ii) uniform: we construct a spiking neural P system with astrocytes producing calcium for all instances of the same size of the subset problem and provide the parameters as resources provided to the input places. In both situations if the subset sum problem has a solution, the output neuron outputs a resource; otherwise, the output neuron does not output any resource.

The rest of the paper is structured as follows. In Sect. 2 we present the spiking neural P systems with astrocytes producing calcium, and in order to illustrate how these systems work we provide an example of a spiking neural P system with astrocytes producing calcium that generates all even numbers without using either forgetting rules or delay in the evolution rules. In Sect. 3, we provide semi-uniform and uniform constructions of spiking neural P system with astrocytes producing calcium working in a non-deterministic way that are able to provide solutions to the subset sum problem in a polynomial time without using either forgetting rules or delay in the evolution rules. Conclusion and references end the paper.

2 Spiking neural P systems with astrocytes producing calcium

Before presenting the spiking neural P systems with astrocytes producing calcium (Aman and Ciobanu 2020), we give several definitions and notations needed in what follows. The set of non-negative integers is denoted by $\mathbb {N}$. The free monoid obtained from a given finite alphabet $V = \{a_1, \ldots , a_n\}$ and the operation of concatenation operation is denoted by $V^*$; its elements are called strings, while $\lambda$ denotes the empty string. $V^+=V^* \backslash \{\lambda \}$ denotes the set of all non-empty strings over V. If $V = \{a\}$, then we use $a^*$ and $a^+$ to stand for $\{a\}^*$ and $\{a\}^+$, respectively.

A regular expression E over an alphabet V is recursively defined as: (i) $E\!=\!\lambda$ is a regular expression and if $a\in V$ then $E=a$ is also a regular expression; (ii) if the expressions $E_1$ and $E_2$ are regular, then also the expressions $E=(E_1)(E_2)$, $E=(E_1) \cup (E_2)$ and $E=(E_1)^+$ are regular. For each regular expression E we provide a language L(E) recursively defined as:

$L(E) = {\left\{ \begin{array}{ll} \{E\} &{}\text{ if } E=\lambda \text{ or } E=a; \\ L(E_1)L(E_2) &{} \text{ if } E=(E_1)(E_2);\\ L(E_1)\cup L(E_2) &{} \text{ if } E=(E_1)\cup (E_2);\\ L((E_1)^+) &{} \text{ if } E=(E_1)^+. \end{array}\right. }$

Some parentheses can be omitted when writing a regular expression, $(E_1)(E_2)$ denotes concatenation, and also $E^*=(E)^+\cup \{\lambda \}$. More details about formal languages can be found in Rozenberg and Salomaa (1997).

In Definition 1 we present the spiking neural P systems with astrocytes producing calcium introduced in Aman and Ciobanu (2020), and used in this paper to provide solutions to the subset sum problem in a polynomial time without using either forgetting rules or delay in the evolution rules.

Definition 1

A spiking neural P system with astrocytes producing calcium of degree $m+n\! \ge \! 1$ is a construct $\Pi = (O,\sigma _1, \ldots , \sigma _m,\tau _1,\ldots ,\tau _n, syn_a,syn_c, in, out)$, where:

• $O = \{a,c\}$ is an alphabet (a is called spike, and c is called calcium unit);

• $\sigma _1, \ldots , \sigma _m$ are neurons of the form $\sigma _i = (a_i , c_i, R_i )$, for $1 \le i \le m$, where: (a) $a_i,c_i \ge 0$ represent the initial number of spikes and calcium units contained in neuron $\sigma _i$; (b) $R_i$ represents a finite set containing rules of the form: (1) $E_aE_c/a^e c^{e'} \rightarrow a^p c^{p'}; d$, where $E_a$ and $E_c$ are regular expressions over a and c, respectively, and $e+e' \ge 1$, $p+p' \ge 1$, $d \ge 0$, with the restrictions $e \ge p$ and $e' \ge p'$; ${(1')}$ $a^e c^{e'} \rightarrow \lambda$, where $e,e' \ge 1$, with the restriction that $a^e c^{e'} \notin L(E_aE_c)$ for any rule of type (1) from $R_i$;

• $\tau , \ldots , \tau _n$ are astrocytes of the form $\tau _i = (c_i , A_i )$, for $1 \le i \le n$, where: (a) $c_i \ge 0$ represents the initial number of calcium units contained in astrocyte $\tau _i$; (b) $A_i$ represents a finite set containing rules of the form: (2) $E_c/c^e \rightarrow c^p;d$, where $E_c$ is a regular expression over c, and $e \ge 1$, $p \ge 0$, $d \ge 0$, with the restriction $e \ge p$; $(2')$ $c^e \rightarrow \lambda$, where $e \ge 1$, with the restriction that $c^{e} \notin L(E_c)$ for any rule of type (2) from $A_i$;

• $syn_a \subseteq \{(\sigma _i,\sigma _j)\mid 1\le i\ne j\le m\}$ indicates the synapses used to send spikes from neurons to neurons;

• $syn_c \subseteq \{(\tau _i,\tau _j)\mid 1\le i\ne j\le n\} \cup \{(\sigma _j,\tau _i)\mid 1\le i\le n, 1 \le j \le m\}\cup \{(\tau _i,\sigma _j)\mid 1\le i\le n, 1 \le j \le m\}$ indicates the synapses used to send calcium units from astrocytes to neurons and astrocytes, and from neurons to astrocytes;

• $in, out \in \{1, 2, \ldots ,m\}$ indicate the input and output neurons.

Note that unlike in spiking neural P systems (Ionescu et al. 2006) where only synapses from the set $syn_a$ are needed, in spiking neural P system with astrocytes producing calcium we use two types of synapses, defined by the relations $syn_a$ and $syn_c$, for communicating either spikes or calcium units; thus these synapses work as filters on the communicated resources. Also, the synapses from $syn_a$, those communicating spikes, can connect only neurons, while the synapses from $syn_c$, those communicating calcium units, can connect neurons to astrocytes and also can connect astrocytes to neurons and other astrocytes.

Next, we detail how the rules of the spiking neural P system with astrocytes producing calcium work.

A spiking rule of the form $E_aE_c/a^ec^{e'} \rightarrow a^p c^{p'}; d$ is applicable in neuron $\sigma _i$ containing k spikes and $k'$ calcium units if $k \ge e$, $k' \ge e'$ and $a^kc^{k'} \in L(E_aE_c)$. Applying the rule $E_aE_c/a^ec^{e'} \rightarrow a^p c^{p'}; d$ leads to the removal of e spikes and $e'$ calcium units from neuron $\sigma _i$, and the creation after d time units of p spikes and $p'$ calcium units to be sent on the synapses connected to the neuron $\sigma _i$. Note that if there are no synapses on which some of the created resources can be sent, then those resources are lost. If a rule has the form $a^ec^{e'}/a^ec^{e'} \rightarrow a^p c^{p'}; d$ is simply written as $a^ec^{e'} \rightarrow a^p c^{p'}; d$.

A forgetting rule of the form $a^e c^{e'} \rightarrow \lambda$ is applicable in neuron $\sigma _i$ containing only e spikes and $e'$ calcium units. Applying the rule $a^e c^{e'} \rightarrow \lambda$ leads to the removal of e spikes and $e'$ calcium units from neuron $\sigma _i$ without any delay.

A calcium rule of the form $E_c/c^e \rightarrow c^p;d$ is applicable in astrocyte $\tau _i$ containing k calcium units if $k \ge e$ and $c^k \in L(E_c)$. Applying the rule $E_c/c^e \rightarrow c^p;d$ leads to the removal of e calcium units from astrocyte $\tau _i$, and the creation after d time units of p calcium units to be sent on the synapses connected to astrocyte $\tau _i$. If a rule has the form $c^e/c^e \rightarrow c^p;d$ is simply written as $c^e \rightarrow c^p;d$.

A forgetting rule of the form $c^e \rightarrow \lambda$ is applicable in astrocyte $\tau _i$ containing only e calcium units. Applying the rule $c^e \rightarrow \lambda$ leads to the removal of e calcium units from astrocyte $\tau _i$ without any delay.

The evolution of the spiking neural P systems with astrocytes producing calcium implies the existence of a global clock. If the delay d appearing in the rules described above is 0, then the production of the spikes and/or calcium units is done instantaneously and these are sent using the existing synapses connected to the neuron or the astrocyte where the rule was executed. On the other hand, if the delay is greater than or equal to 1, a rule applied at step t leads to the closure of the neuron or the astrocyte for the steps t, $\ldots$, $t + d - 1$; this means that during these steps new spikes and/or calcium units cannot be sent nor received by the astrocyte or neuron where the applied rule resides. Due to the fact that a closed neuron or astrocyte cannot exchange resources, note that all spikes and/or calcium units being communicated towards closed neurons and astrocytes are lost. In the step $t+d$, after firing the created spikes and/or calcium units along the available synapses in $syn_a$ and $syn_c$, respectively, the neuron or astrocyte becomes open again and is available for receiving resources starting from the step $t+d+1$.

Using the application of rules as previously described, the number of resources (spikes and calcium units) of neuron $\sigma _i$ at time $t + 1$ can be deduced using its number of resources at time t:

$$\begin{aligned} a_i(t + 1) ={\left\{ \begin{array}{ll} a_i(t) - r_a + n_a &{} \mathrm{if~ a~ rule~{ r}~of~R_i~ is~ used};\\ a_i(t) + n_a &{} \mathrm{if~ no~ rule~of~R_i~ is~ used},\\ \end{array}\right. } \end{aligned}$$

$$\begin{aligned} c_i(t + 1) ={\left\{ \begin{array}{ll} c_i(t) - r_c + n_c &{} \mathrm{if~ a~ rule~{ r}~of~R_i~ is~ used};\\ c_i(t) + n_c &{} \mathrm{if~ no~ rule~of~R_i~ is~ used},\\ \end{array}\right. } \end{aligned}$$

where $r_a$ and $r_c$ are the number of spikes and calcium units consumed by the used rule r, while $n_a$ and $n_c$ are the number of spikes and calcium units received on the synapses from $syn_a$ and $syn_c$, respectively, connected to neuron $\sigma _i$. The number of calcium units of astrocyte $\tau _i$ at time $t + 1$ can be deduced using its number of calcium units at time t:

$$\begin{aligned} c_i(t + 1) ={\left\{ \begin{array}{ll} c_i(t) - r'_c + n'_c &{} \mathrm{if~ a~ rule~{ r'}~of~A_i~ is~ used};\\ c_i(t) + n'_c&{} \mathrm{if~ no~ rule~of~A_i~ is~ used},\\ \end{array}\right. } \end{aligned}$$

where $r'_c$ is the number of calcium units consumed by the used rule $r'$, while $n'_c$ is the number of calcium units received on the synapses from $syn_c$ connected to astrocyte $\tau _i$.

At every step of the computation if there exists an applicable rule in a neuron or in an astrocyte, then such a rule must be used. If more than one rule is applicable in a neuron or an astrocyte, then exactly one of the rule is selected in a non-deterministic manner and applied. This leads to sequential execution of rules inside each neuron and astrocyte, and parallel execution of rules in the neurons and astrocytes of the system.

For any computation there exists an output spike train that is a sequence of digits 0 and 1, in which 1 marks the steps at which the output neuron fires sending resources to the environment, while 0 marks the steps at which the output neuron does not send resources to the environment. Although there exist various ways of extracting the result of a computation in spiking neural P systems (Ionescu et al. 2006), in what follows we consider the standard one that counts the distance between the first two 1 digits appearing in the output spike train. We denote by $N_2(\Pi )$ the set of numbers computed in the standard mode by a spiking neural P system with astrocytes producing calcium $\Pi$, while we denote by $N_2SNP^k_{m,n}$ the family of all such sets computed by such a system, where m, n and k represent the maximum number of neurons, astrocytes or rules used in every neuron or astrocyte, respectively.

Example 1

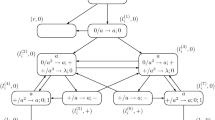
We illustrate how spiking neural P systems with astrocytes producing calcium work by constructing a system $\Pi$ that generates all even numbers without using either forgetting rules or delay in the evolution rules. The system in its initial state is depicted in Fig. 1.

Fig. 1

A spiking neural P system with astrocytes producing calcium generating all even numbers without using either forgetting rules or delay in the evolution rules. We use rectangles and ellipses to depict the neurons and astrocytes, respectively. We also use straight and snake like arrows to depict the synapses from $syn_a$ and $syn_c$, respectively. The straight arrow without a target leaving neuron $\sigma _1$ indicates that this is an output neuron that can send spikes into the environment

A spiking neural P system with seven neurons that generates all even natural numbers is given in Ionescu et al. (2006), while our system requires two neurons and one astrocyte for the same purpose. In the initial configuration, all neurons and astrocytes contain resources, namely a spike and a calcium unit are placed in the neuron $\sigma _1$, a spike is placed in the neuron $\sigma _2$, while two calcium units are placed in the astrocyte $\tau _1$. However in the first step of the computation only the neuron $\sigma _1$ (the output neuron) and the astrocyte $\tau _1$ have the necessary resources to fire; as the delay of the applied rules is 0, the resources (spikes and calcium units) are created and communicated to the connected neurons and astrocytes immediately.

This means that neuron $\sigma _1$ is able to apply the rule $ac \rightarrow a$ that sends a spike to the environment, thus marking the fact that we have to count till the second spike is sent to the environment to get the result of the computation. In parallel, the astrocyte $\tau _1$ can choose in a non-deterministic manner to execute any of its rules $c^2 \rightarrow c^2$ and $c^2 \rightarrow c$; assume that only rule $c^2 \rightarrow c^2$ is applied in the first $s\ge 0$ steps. This implies that astrocyte $\tau _1$ produces and sends instantly two calcium units to each of the neurons $\sigma _1$ and $\sigma _2$. In the next step, the astrocyte $\tau _1$ will contain no resources and thus will be unable to fire. On the other hand, the neurons $\sigma _1$ and $\sigma _2$ have enough spikes and calcium units to fire one of their rules. This means that two calcium units are sent from neuron $\sigma _1$ to the astrocyte $\tau _1$ by executing the rule $c^2 \rightarrow c^2$, while the neuron $\sigma _2$ removes the calcium units by executing the rule $ac^2 / c^c \rightarrow c$. Note that even if a calcium unit is produced by the rule $ac^2 / c^c \rightarrow c$ applied inside neuron $\sigma _2$, this calcium unit is discarded as there are no outgoing synapses from $syn_c$ connecting the neuron $\sigma _2$ with other neurons or astrocytes. Once the astrocyte $\tau _1$ has two calcium units is ready to fire again and to send calcium units to both neurons. After two computational steps we reached the same configuration of the system; these two steps form a loop that can be applied for an arbitrary number of times.

The neuron $\sigma _1$ can send again a spike into the environment only if the rule $ac \rightarrow a$ is applicable; this implies that the astrocyte $\tau _1$ needs to execute the rule $c^2 \rightarrow c$ at some point during the computation. Assume that the rule $c^2 \rightarrow c$ is applied at step t; notice that $t = 2\times s + 1$. This implies that immediately, the astrocyte $\tau _1$ sends a calcium unit to each of the neurons $\sigma _1$ and $\sigma _2$. At step $t+1$, only the neuron $\sigma _2$ can apply the rule $ac \rightarrow a$ sending a spike to neuron $\sigma _1$. Thus at step $t+2$ only the neuron $\sigma _1$ contains one spike and one calcium unit, and can apply the rule $ac \rightarrow a$ to output a second spike. As the second spike is fired into the environment at step $t + 2 = 2\times s + 1 + 2$, it means that $2\times s+2$ is the generated number, where $s \ge 0$. After the second spike is sent to the environment the computation halts as there are no more applicable rules in any neurons or in the astrocyte.

Thus $N_2(\Pi ) = \{ 2n \mid n \ge 1\}$ and $N_2(\Pi )\in N_2SNP^2_{2,1}$.

3 Solving the subset sum problem

Spiking neural P systems with astrocytes producing calcium can be used to solve a decision problem $I_X$, $\Theta _X$, where $I_X$ is a language over a finite alphabet (its elements are called instances) and $\Theta _X$ is a total Boolean function over $I_X$. We consider two ways of constructing the system that will solve the decision problem: (i) semi-uniform: we construct a spiking neural P system with astrocytes producing calcium for each instance of the subset sum problem and embed the parameters into the constructed systems as number of resources (spikes and calcium units), graph of neurons and astrocytes, and evolution rules; (ii) uniform: we construct a spiking neural P system with astrocytes producing calcium for all instances of the same size of the subset problem and provide the parameters as resources sent to the input places. In both situations if the subset sum problem has a solution, the output neuron sends a resource to the environment; otherwise, the output neuron does not output any resource to the environment. Usually the uniform solutions are preferred to the semi-uniform solutions as they relate only to the structure of a given decision problem.

The NP-complete subset sum problem (Garey and Johnson 1979) is as follows: given a finite (multi)set of positive integer numbers, $V = \{v_1, \ldots , v_n\}$ and a positive integer number S, determine whether or not there exists a non-empty (multi)set B, where $B \subseteq V$, such that $\sum _{b \in B} b = S$.

3.1 Semi-uniform solution to the subset sum problem

If we allow rules from a neuron or an astrocyte to be chosen in a non-deterministic manner, then the spiking neural P systems with astrocytes producing calcium can solve any given instance of the subset sum problem in a polynomial number of steps. Depending on how we encode the instance of the problem in spiking neural P systems with astrocytes producing calcium, there exist several possible solutions. We emphasize the fact that all these solutions occur without using either forgetting rules or delay in the evolution rules.

If we allow the instance of the problem to be encoded in the system in the rules and in the initial number of resources (spikes and calcium units), then the spiking neural P systems with astrocytes producing calcium depicted in Fig. 2 solves any given instance of the subset sum problem in two computational steps.

Fig. 2

A semi-uniform spiking neural P system with astrocytes producing calcium solving the subset sum problem without using either forgetting rules or delay in the evolution rules. The instance of the problem is encoded in the system in the rules and in number of the initial resources (spikes and calcium units)

The non-deterministic manner of applying the rules in the system of Fig. 2 results from using the rules $a^{v_i}c \rightarrow a^{v_i}$ and $a^{v_i}c\rightarrow c$, inside the neurons $\sigma _i$, for $1 \le i \le n$. If the rule $a^{v_i}c \rightarrow a^{v_i}$ is chosen in neuron $\sigma _i$, then neuron $\sigma _{out}$ receives immediately $v_i$ spikes meaning that the number $v_i$ was chosen to be included in the sum. On the other hand, if the rule $a^{v_i}c \rightarrow c$ is chosen in neuron $\sigma _i$, then the calcium unit is lost and neuron $\sigma _{out}$ does not receive any spikes meaning that the number $v_i$ was not chosen to be included in the sum. The output neuron $\sigma _{out}$ sends in step two of the computation a spike to the environment only if the number of spikes residing in it equals S. Note that the system consists of $n+1$ neurons, and initially contains $n+ \sum _i v_i$ spikes and calcium units. The construction represents an improvement with respect to the one presented in Leporati et al. (2009a, 2009) as we do not use forgetting rules nor delays in the evolution rules.

If we allow the instance of the problem to be encoded in the system in the rules and in the number of neurons and astrocytes, then the spiking neural P systems with astrocytes producing calcium depicted in Fig. 3 solves any given instance of the subset sum problem in three computational steps.

Fig. 3

A semi-uniform spiking neural P system with astrocytes producing calcium solving the subset sum problem without using either forgetting rules or delay in the evolution rules. The instance of the problem is encoded in the system in the rules and in the number of used places (neurons and astrocytes)

The non-deterministic manner of applying the rules results from using the rules $ac \rightarrow a$ and $ac\rightarrow c$ inside the neurons $\sigma _i$, for $1 \le i \le n$. If the rule $ac \rightarrow c$ is chosen in neuron $\sigma _i$, then each of the astrocytes $\tau _{i,1},\ldots ,\tau _{i,v_i}$ receive immediately a calcium unit meaning that the number $v_i$ was chosen to be included in the sum. On the other hand, if the rule $ac\rightarrow a$ is chosen in neuron $\sigma _i$, then the spike is lost and astrocytes $\tau _{i,1},\ldots ,\tau _{i,v_i}$ do not receive any calcium units meaning that the number $v_i$ was not chosen to be included in the sum. In the next step the neuron $\sigma _{out}$ receives immediately calcium units from all the astrocytes that had one calcium unit. The output neuron $\sigma _{out}$ sends in step three of the computation a calcium unit to the environment only if the number of calcium units residing in it equals S. Note that the system consists of $n+1$ neurons and $\sum _i v_i$ astrocytes, and initially contains $2 \times n$ resources (spikes and calcium units in equal amounts). The construction represents an improvement with respect to the one presented in Leporati et al. (2009a) as we do not use forgetting rules nor delays in the evolution rules, and also the number of used places (neurons and astrocytes) is smaller.

If we allow the instance of the problem to be encoded in the system in the initial number of resources (spikes and calcium units) and in the number of neurons and astrocytes, then the spiking neural P systems with astrocytes producing calcium depicted in Fig.  4 solves any given instance of the subset sum problem in a polynomial number of computational steps.

Fig. 4

A semi-uniform spiking neural P system with astrocytes producing calcium solving the subset sum problem without using either forgetting rules or delay in the evolution rules. The instance of the problem is encoded in the system in the initial number of resources (spikes and calcium units) and in the number of used places (neurons and astrocytes)

The non-deterministic manner of applying the rules results from using the rules $ac \rightarrow a$ and $ac\rightarrow c$ inside the neurons $\sigma '_i$, for $1 \le i \le n$. If the rule $ac \rightarrow c$ is chosen in neuron $\sigma '_i$, then each of the astrocytes $\tau _{i,1},\ldots ,\tau _{i,v_i}$ receive immediately a calcium unit meaning that the number $v_i$ was chosen to be included in the sum. On the other hand, if the rule $ac\rightarrow a$ is chosen in neuron $\sigma '_i$, then the spike is lost and astrocytes $\tau _{i,1},\ldots ,\tau _{i,v_i}$ do not receive any calcium units meaning that the number $v_i$ was not chosen to be included in the sum. In the next step the neurons $\sigma _3$ and $\sigma _4$ receive immediately calcium units from all the astrocytes that had one calcium unit; let us denote this value by $S_B$. In parallel in the first two steps in neuron $\sigma _3$ the rule $a^+c^+/ac \rightarrow c$ is applied twice reducing the multiset of $\sigma _3$ from $a^{S+3}c^3$ to $a^{S+1}c$ and the produced calcium units are lost as there are no synapses from $syn_c$ leaving from $\sigma _3$; also in neuron $\sigma _4$ the rule $a^+c^+/ac \rightarrow a$ is applied twice reducing the multiset of $\sigma _4$ from $a^{S+2}c^2$ to $a^{S}$ and the produced spikes are lost as there are no synapses from $syn_a$ leaving from $\sigma _4$. At the end of the first two steps, the neuron $\sigma _3$ contains the multiset $a^{S+1} c^{S_B+1}$, while the neuron $\sigma _4$ contains the multiset $a^S c^{S_B}$. Depending on the values of $S_B$ and S there exist three possible evolutions:

• $S_B <S$. In this case in the next $S_B$ steps in neuron $\sigma _3$ the rule $a^+c^+/ac \rightarrow c$ is applied reducing the multiset of $\sigma _3$ from $a^{S+1}c^{S_B+1}$ to $a^{S-S_B+1}c$ and the produced calcium units are lost as there are no synapses from $syn_c$ leaving from $\sigma _3$; also in neuron $\sigma _4$ the rule $a^+c^+/ac \rightarrow a$ is applied reducing the multiset of $\sigma _4$ from $a^{S}c^{S_B}$ to $a^{S-S_B}$ and the produced spikes are lost as there are no synapses from $syn_a$ leaving from $\sigma _4$.       In the next $S-S_B+1$ steps in neuron $\sigma _3$ the rule $a^+c^+/ac \rightarrow c$ is applied once and the produced calcium unit is lost as there are no synapses from $syn_c$ leaving from $\sigma _3$, while the rule $a^+c^0/a \rightarrow a$ is applied $S-S_B$ times sending $S-S_B$ spikes to neuron $\sigma _5$. Also in parallel in the next $S-S_B$ steps in neuron $\sigma _4$ the rule $a^+c^0/a \rightarrow a$ is applied and all $S-S_B$ spikes are lost as there are no synapses from $syn_a$ leaving from $\sigma _4$. Starting from step $S+4$ in neuron $\sigma _5$ the rule $a^+c/a \rightarrow a$ is applied for $S-S_B$ steps and the produced spikes are lost as there are no synapses from $syn_a$ leaving from $\sigma _5$. Thus no calcium unit is emitted into the environment and the computation stops after $2 \times S -S_B+3$ steps.

• $S_B \!=\! S$. In this case in the next $S-1$ steps in neuron $\sigma _3$ the rule $a^+\!c^+\!/ac \!\rightarrow \! c$ is applied reducing the multiset of $\sigma _3$ from $a^{S+1}c^{S_B+1}$ to $a^2c^2$ and the produced calcium units are lost as there are no synapses from $syn_c$ leaving from $\sigma _3$; also in neuron $\sigma _4$ the rule $a^+c^+/ac \rightarrow a$ is applied $S_B-1$ times reducing the multiset of $\sigma _4$ from $a^{S}c^{S_B}$ to ac and the produced spikes are lost as there are no synapses from $syn_a$ leaving from $\sigma _4$.       In the next step in neuron $\sigma _3$ the rule $a^+c^+/ac \rightarrow c$ is applied once reducing the multiset of $\sigma _3$ from $a^{2}c^{2}$ to ac and the produced calcium unit is lost as there are no synapses from $syn_c$ leaving from $\sigma _3$. In parallel in neuron $\sigma _4$ the rule $ac \rightarrow ac$ is applied sending a calcium unit to astrocyte $\tau _1$, while the spike is lost as there are no synapses from $syn_a$ leaving from $\sigma _4$. In the next step in neuron $\sigma _3$ the rule $ac \rightarrow ac$ sends a spike to neuron $\sigma _5$, while the calcium unit is lost as there are no synapses from $syn_c$ leaving from $\sigma _3$. In parallel the astrocyte $\tau _1$ applies the rule sending the calcium unit to the neuron $\sigma _5$. Thus after $S+3$ steps the neuron $\sigma _5$ contains a spike and a calcium unit being able to apply the rule $c^2 \rightarrow c^2$ sending two calcium units to astrocyte $\tau _2$, that will send in next step to both neurons $\sigma _6$ and $\sigma _7$ by applying the rule $c^2 \rightarrow c^2$. Next neuron $\sigma _7$ applies rule $ac^2 \rightarrow c$ removing all its resources as there are no synapses from $syn_c$ leaving from $\sigma _7$, while in parallel the neuron $\sigma _6$ applies the rule $ac^2 \rightarrow c$; thus a calcium unit is emitted into the environment and the computation stops after $S+6$ steps.

• $S_B >S$. In this case in the next S steps in neuron $\sigma _3$ the rule $a^+c^+/ac \rightarrow c$ is applied reducing the multiset of $\sigma _3$ from $a^{S+1}c^{S_B+1}$ to $ac^{S_B-S+1}$ and the produced calcium units are lost as there are no synapses from $syn_c$ leaving from $\sigma _3$; also in neuron $\sigma _4$ the rule $a^+c^+/ac \rightarrow a$ is applied reducing the multiset of $\sigma _4$ from $a^{S}c^{S_B}$ to $c^{S_B-S}$ and the produced spikes are lost as there are no synapses from $syn_a$ leaving from $\sigma _4$.       In the next $S_B-S+1$ steps in neuron $\sigma _3$ the rule $a^+c^+/ac \rightarrow c$ is applied once and afterwards the rule $a^0c^+/c \rightarrow c$ is applied $S_B-S$ times and the produced calcium units are lost as there are no synapses from $syn_c$ leaving from $\sigma _3$. Also in parallel in the next $S_B-S$ steps in neuron $\sigma _4$ the rule $a^0c^+/c \rightarrow c$ is applied sending $S_B-S$ calcium units to astrocyte $\tau _1$. Each calcium unit reaching astrocyte $\tau _1$ will be eliminated after four steps: (i) in astrocyte $\tau _1$ the rule $c \rightarrow c$ is applied sending the calcium unit to neuron $\sigma _5$; (ii) in neuron $\sigma _5$ the rule $c^+c/c \rightarrow c$ is applied sending the calcium unit to astrocyte $\tau _2$; (iii) in astrocyte $\tau _2$ the rule $c \rightarrow c$ is applied sending a calcium unit to both neurons $\sigma _6$ and $\sigma _7$; (iv) in neurons $\sigma _6$ and $\sigma _7$ the rule $ac \rightarrow a$ is applied removing the calcium unit. Thus no calcium unit is emitted into the environment and the computation stops after $S_B+8$ steps.

Note that the system consists of $n+5$ neurons and $2+\sum _i v_i$ astrocytes, initially contains $2 \times n+2 \times S+13$ resources (spikes and calcium units), and we do not use forgetting rules nor delays in the evolution rules.

3.2 Uniform solution to the subset sum problem

Constructing a spiking neural P system with astrocytes producing calcium which solves the subset sum problem in a uniform way implies that only the number n of variables is known by the system, while the values from V and the number S should be available only as resources in some input places (neurons and astrocytes) when the computation starts. We consider that the instance of the problem is provided to the system using $n+2$ input neurons; we introduce $v_i$, $1\le i \le n$, spikes in n input neurons, $2\times S+5$ spikes and $S+5$ calcium units in an input neuron and $2\times S+4$ spikes and $S+4$ calcium units in another input neuron.

The spiking neural P systems with astrocytes producing calcium depicted in Fig. 5 solves any given instance of the subset sum problem in a polynomial number of computational steps.

Fig. 5

An uniform spiking neural P system with astrocytes producing calcium solving the subset sum problem without using either forgetting rules or delay in the evolution rules. The instance of the problem is encoded in the system in the initial number of resources (spikes and calcium units)

The non-deterministic manner of applying the rules results from using the rules $ac \rightarrow a$ and $ac\rightarrow c$ inside the neurons $\sigma ''_i$, for $1 \le i \le n$. If the rule $ac\rightarrow a$ is chosen in neuron $\sigma ''_i$, then the spike is lost as there are no synapses from $syn_a$ leaving from neuron $\sigma ''_i$. On the other hand, if the rule $ac \rightarrow c$ is chosen in neuron $\sigma ''_i$, then the astrocyte $\tau ''_i$ receives immediately a calcium unit meaning that the number $v_i$ was chosen to be included in the sum. In the next step the astrocyte $\tau ''_i$ sends a calcium unit to both the neuron $\sigma '_i$ and the astrocyte $\tau '''_i$. This means that in the next $v_i$ steps the rule $c \rightarrow c$ from the astrocyte $\tau '''_1$ and the rule $a^+/ac \rightarrow c$ from the neuron $\sigma '_i$ are used to send the input placed inside the neuron $\sigma '_i$ towards the astrocyte $\tau '_i$. In the next $v_i$ steps the astrocyte $\tau '_i$ will use the rule $c \rightarrow c$ to send a calcium unit to the neurons $\sigma _3$ and $\sigma _4$. By assuming that for all $v_i \le S$, for $1 \le i \le n$, we expect that all input spikes from the neurons $\sigma ''_i$, for $1 \le i \le n$, will reach the neurons $\sigma _3$ and $\sigma _4$ in $S+4$ steps. In what follows we denote by $S_B$ the amount of calcium units that reached the neurons $\sigma _3$ and $\sigma _4$ in the first $S+4$ steps of the computation.

In parallel in the first $S+4$ steps in neuron $\sigma _3$ the rule $a^+c^+/ac \rightarrow c$ is applied reducing the multiset of $\sigma _3$ from $a^{2S+5}c^{S+5}$ to $a^{S+1}c$ and the produced calcium units are lost as there are no synapses from $syn_c$ leaving from $\sigma _3$; also in neuron $\sigma _4$ the rule $a^+c^+/ac \rightarrow a$ is applied reducing the multiset of $\sigma _4$ from $a^{2S+4}c^{S+4}$ to $a^{S}$ and the produced spikes are lost as there are no synapses from $syn_a$ leaving from $\sigma _4$. At the end of the first $S+4$ steps, the neuron $\sigma _3$ contains the multiset $a^{S+1} c^{S_B+1}$, while the neuron $\sigma _4$ contains the multiset $a^S c^{S_B}$. Depending on the values of $S_B$ and S there exist three possible evolutions:

• $S_B <S$. In this case in the next $S_B$ steps in neuron $\sigma _3$ the rule $a^+c^+/ac \rightarrow c$ is applied reducing the multiset of $\sigma _3$ from $a^{S+1}c^{S_B+1}$ to $a^{S-S_B+1}c$ and the produced calcium units are lost as there are no synapses from $syn_c$ leaving from $\sigma _3$; also in neuron $\sigma _4$ the rule $a^+c^+/ac \rightarrow a$ is applied reducing the multiset of $\sigma _4$ from $a^{S}c^{S_B}$ to $a^{S-S_B}$ and the produced spikes are lost as there are no synapses from $syn_a$ leaving from $\sigma _4$.       In the next $S-S_B+1$ steps in neuron $\sigma _3$ the rule $a^+c^+/ac \rightarrow c$ is applied once and the produced calcium unit is lost as there are no synapses from $syn_c$ leaving from $\sigma _3$, while the rule $a^+c^0/a \rightarrow a$ is applied $S-S_B$ times sending $S-S_B$ spikes to neuron $\sigma _5$. Also in parallel in the next $S-S_B$ steps in neuron $\sigma _4$ the rule $a^+c^0/a \rightarrow a$ is applied and all $S-S_B$ spikes are lost as there are no synapses from $syn_a$ leaving from $\sigma _4$. Starting from step $S+4$ in neuron $\sigma _5$ the rule $a^+c/a \rightarrow a$ is applied for $S-S_B$ steps and the produced spikes are lost as there are no synapses from $syn_a$ leaving from $\sigma _5$. Thus no calcium unit is emitted into the environment and the computation stops after $3 \times S -S_B+5$ steps.

• $S_B \!=\! S$. In this case in the next $S-1$ steps in neuron $\sigma _3$ the rule $a^+\!c^+\!/ac \!\rightarrow \! c$ is applied reducing the multiset of $\sigma _3$ from $a^{S+1}c^{S_B+1}$ to $a^2c^2$ and the produced calcium units are lost as there are no synapses from $syn_c$ leaving from $\sigma _3$; also in neuron $\sigma _4$ the rule $a^+c^+/ac \rightarrow a$ is applied $S_B-1$ times reducing the multiset of $\sigma _4$ from $a^{S}c^{S_B}$ to ac and the produced spikes are lost as there are no synapses from $syn_a$ leaving from $\sigma _4$.       In the next step in neuron $\sigma _3$ the rule $a^+c^+/ac \rightarrow c$ is applied once reducing the multiset of $\sigma _3$ from $a^{2}c^{2}$ to ac and the produced calcium unit is lost as there are no synapses from $syn_c$ leaving from $\sigma _3$. In parallel in neuron $\sigma _4$ the rule $ac \rightarrow ac$ is applied sending a calcium unit to astrocyte $\tau _1$, while the spike is lost as there are no synapses from $syn_a$ leaving from $\sigma _4$. In the next step in neuron $\sigma _3$ the rule $ac \rightarrow ac$ sends a spike to neuron $\sigma _5$, while the calcium unit is lost as there are no synapses from $syn_c$ leaving from $\sigma _3$. In parallel the astrocyte $\tau _1$ applies the rule sending the calcium to the neuron $\sigma _5$. Thus after $S+3$ steps the neuron $\sigma _5$ contains a spike and a calcium unit being able to apply the rule $c^2 \rightarrow c^2$ sending two calcium units to astrocyte $\tau _2$, that will send in next step to both neurons $\sigma _6$ and $\sigma _7$ by applying the rule $c^2 \rightarrow c^2$. Next neuron $\sigma _7$ applies rule $ac^2 \rightarrow c$ removing all its resources as there are no synapses from $syn_c$ leaving from $\sigma _7$, while in parallel the neuron $\sigma _6$ applies the rule $ac^2 \rightarrow c$; thus a calcium unit is emitted into the environment and the computation stops after $2\times S+8$ steps.

• $S_B >S$. In this case in the next S steps in neuron $\sigma _3$ the rule $a^+c^+/ac \rightarrow c$ is applied reducing the multiset of $\sigma _3$ from $a^{S+1}c^{S_B+1}$ to $ac^{S_B-S+1}$ and the produced calcium units are lost as there are no synapses from $syn_c$ leaving from $\sigma _3$; also in neuron $\sigma _4$ the rule $a^+c^+/ac \rightarrow a$ is applied reducing the multiset of $\sigma _4$ from $a^{S}c^{S_B}$ to $c^{S_B-S}$ and the produced spikes are lost as there are no synapses from $syn_a$ leaving from $\sigma _4$.       In the next $S_B-S+1$ steps in neuron $\sigma _3$ the rule $a^+c^+/ac \rightarrow c$ is applied once and afterwards the rule $a^0c^+/c \rightarrow c$ is applied $S_B-S$ times and the produced calcium units are lost as there are no synapses from $syn_c$ leaving from $\sigma _3$. Also in parallel in the next $S_B-S$ steps in neuron $\sigma _4$ the rule $a^0c^+/c \rightarrow c$ is applied sending $S_B-S$ calcium units to astrocyte $\tau _1$. Each calcium unit reaching astrocyte $\tau _1$ will be eliminated after four steps: (i) in astrocyte $\tau _1$ the rule $c \rightarrow c$ is applied sending the calcium unit to neuron $\sigma _5$; (ii) in neuron $\sigma _5$ the rule $c^+c/c \rightarrow c$ is applied sending the calcium unit to astrocyte $\tau _2$; (iii) in astrocyte $\tau _2$ the rule $c \rightarrow c$ is applied sending a calcium unit to both neurons $\sigma _6$ and $\sigma _7$; (iv) in neurons $\sigma _6$ and $\sigma _7$ the rule $ac \rightarrow a$ is applied removing the calcium unit. Thus no calcium unit is emitted into the environment and the computation stops after $S_B+S+10$ steps.

Note that the system consists of $2n+5$ neurons and $3n+2$ astrocytes, initially contains $2 \times n+2 \times S+13$ resources (spikes and calcium units), and the length of the computation depends on the values of S and $S_B$. The construction represents an improvement with respect to the one presented in Leporati et al. (2009a) as we do not use forgetting rules nor delays in the evolution rules, and also the number of used places (neurons and astrocytes) is smaller.

4 Conclusion

This paper represents a first step towards using spiking neural P systems with astrocytes producing calcium to solve, in a non-deterministic manner, computationally hard problems. We showed that non-deterministic spiking neural P systems with astrocytes producing calcium that do not consider forgetting rules nor delay in the evolution rules, are powerful enough to provide polynomial-time solutions to the subset sum problem. We provided four ways of constructing such a system: (i) semi-uniform: we constructed a spiking neural P system with astrocytes producing calcium for each instance of the subset problem and embedded the parameters into the constructed systems: in the rules and number of initial resources (Fig. 2), in the rules and in the number of used neurons and astrocytes (Fig. 3), and as number of resources (spikes and calcium units) and in the number of used neurons and astrocytes (Fig. 4) ; (ii) uniform: we constructed a spiking neural P system with astrocytes producing calcium for all instances of the same size of the subset problem and provided the parameters as number of spikes and calcium units (Fig. 5).

In all approaches if the subset sum problem has a solution, the output neuron outputs a resource to the environment; otherwise, the output neuron does not output any resource to the environment.