Abstract
This article presents the Haskell implementations of spiking neural P systems and of two variants subsequently introduced in the literature, namely the spiking neural P systems with inhibitory rules and spiking neural P systems with structural plasticity. These implementations are obtained using their operational semantics in which the involved configurations use continuations. For each variant, the formal syntax is presented, together with the semantics given accurately by the Haskell implementation.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Spiking neural P systems represent a class of distributed and parallel neural-like computing models inspired from the way in which neurons process information and communicate by means of spikes. Spiking neural P systems are a variant of neural-like P systems, incorporating the idea of spiking neurons into membrane computing [20]. Inspired by various biological phenomena and computing models, several variants of spiking neural P systems have been proposed, including spiking neural P systems with inhibitory rules [22, 33] and spiking neural P systems with structural plasticity [4], among others.
The idea of implementing (in silico) the evolution of various classes of P systems is old in the framework of membrane computing, some implementations (for the basic variants of P systems) being presented for the first time more than 20 years ago [2, 3, 5]. In this paper we present implementations for the general spiking neural P systems and for two variants, namely for spiking neural P systems with inhibitory rules and for spiking neural P systems with structural plasticity. The novel aspects of these implementations come from the fact that they are derived from an operational semantics in which the configurations use continuations. More exactly, for each implementation it is presented a formal syntax and an operational semantics designed with continuations, semantics translated then in the functional programming language Haskell (http://haskell.org/). We aim to develop a rigorous design and verification approach applicable to a wide class of spiking neural P systems.
Using a terminology specific to programming languages semantics, we study three languages named \({\mathcal {L}}_{snp}^{\alpha }\), \({\mathcal {L}}_{snp}^{ir}\) and \({\mathcal {L}}_{snp}^{sp}\). The language \({\mathcal {L}}_{snp}^{\alpha }\) is used to describe the structure and behaviour of spiking neural P systems as presented in the original paper [15]. The languages \({\mathcal {L}}_{snp}^{ir}\) and \({\mathcal {L}}_{snp}^{sp}\) are variants of \({\mathcal {L}}_{snp}^{\alpha }\), incorporating constructions specific to spiking neural P systems with inhibitory rules [22, 33] and with structural plasticity [4], respectively. We present semantic interpreters for these three languages, using Haskell as an implementation tool. These interpreters provide a sound simulation and verification support for the variants of spiking neural P systems under investigation.
The rest of the paper is organized as follows. Sections 2, 3 and 4 present the formal syntax and semantic interpreters for the languages \({\mathcal {L}}_{snp}^{\alpha }\), \({\mathcal {L}}_{snp}^{ir}\) and \({\mathcal {L}}_{snp}^{sp}\), respectively. Section 5 presents some concluding remarks.
This is a revised and distinct version of a paper [10] presented at the 23rd Conference on Membrane Computing (CMC’22). The differences between this version and the (unpublished) conference version come from several parts which are revised and improved, and a more concise way of presenting the whole approach.
2 Spiking neural P systems
This section introduces a language called \({\mathcal {L}}_{snp}^{\alpha }\), a language based on the \(\textsf{SNP}\) calculus [8] and the language presented in [7]. \({\mathcal {L}}_{snp}^{\alpha }\) is used to describe the structure and behaviour of spiking neural P systems [15]. The constructions of \({\mathcal {L}}_{snp}^{\alpha }\) are called ’statements’ and ’programs’, and we use the term ’execution’ to describe their behaviour. Following the monograph [11], in the sequel we use a terminology that is specific to programming languages.
Remark 1
For the formal aspects we use the same notation as in [7, 8]. We write \((a\in )A\) to introduce a set A with typical element a ranging over A. If A is a set, we denote by \(|A|\) the cardinal number of A, and by \({\mathcal {P}}_{fin}(A)\) the powerset of all finite subsets of A. For a countable set \((a\in )A\), we denote by \([A]\) the set of all finite multisets of elements of type A; \([A]\) is defined formally as in [7], and \(m\in [A]\) is given by enumerating its elements between square brackets ‘[’ and ‘]’ (in particular, we represent the empty multiset by \([\,]\)). A multiset can be seen as an unordered list, i.e., a collection in which repetition of elements is taken into account. For example, \([a_1,a_1,a_2]=[a_1,a_2,a_1]=[a_2,a_1,a_1]\) is the multiset where the element \(a_1\) occurs twice, and the element \(a_2\) occurs once. A multiset m can be presented using the multiplicities in the form \(m=[a_1^{i_1},\ldots ,a_n^{i_n}]\), where \(i_j\) is the multiplicity (the number of occurrences) of element \(a_j\) in the multiset m. For example, \([a_1,a_1,a_2]=[a_1^2,a_2^1]\). The operations used over multisets (namely multiset sum ’ \(\uplus \)’, submultiset ’\(\subseteq \)’, multiset difference ’ \(\setminus \)’ and multiset equality ’ \(=\)’) are formally defined in [7, 8]. Given a regular expression E, we denote by L(E) the language associated with E. For a multiset \(w\in [A]\) and E a regular expression over the same set A, we use the notation \(w\in {}L(E)\) to express that there is a permutation of multiset w that is an element of the language L(E). The reader may consult [25] for a comprehensive presentation of formal languages theory.
2.1 Syntax of \({\mathcal {L}}_{snp}^{\alpha }\)
The syntax of the language \({\mathcal {L}}_{snp}^{\alpha }\) is presented in Definition 2 by using BNF. Given a countable alphabet \((a\in )O\) of spikes (or objects) and a set \((N\in )Nn\) of neuron names, we define \((w\in )W=[O]\) as the set of all finite multisets over \(O\), and \((\xi \in )\Xi ={\mathcal {P}}_{fin}(Nn)\) as the set of all finite subsets of \(Nn\).
Definition 2
(Syntax of \({\mathcal {L}}_{snp}^{\alpha }\))
-
(a)
(Statements) \(s(\in S) \,\,{:}{:}=\,\,e \,\mid \,s\parallel {}s\) where \(e(\in ES) \,\,{:}{:}=\,\,a \,\mid \,\,{\textsf{snd}}\,\xi \,a\, \,\mid \,\,{\textsf{init}}\,\xi \,\)
-
(b)
(Rules) \(\,rs(\in Rs) \,\,{:}{:}=\,\,r_{\epsilon }\,\mid \,r,rs\) where \(r(\in Rule) \,\,{:}{:}=\,\,E/w\rightarrow s;\vartheta \,\mid \,w\rightarrow \lambda \) with E a regular expression over \(O\), and \(\vartheta \ge 0, \vartheta \in \mathbb {N}\)
-
(c)
(Neuron declarations) \(D(\in NDs) \,\,{:}{:}=\,\,d \,\mid \,d,D\) where \(d(\in ND) \,\,{:}{:}=\,\,\,\,\textsf{neuron}\,N\,\{\,rs\,\mid \,\xi \,\}\)
-
(d)
(Programs) \(\pi (\in {\mathcal {L}}_{snp}^{\alpha }) \,\,{:}{:}=\,\,D,s\)
A statement \(s\in S\) is either an elementary statement \(e\in ES\) or a parallel composition of two statements \(s_1\parallel {}s_2\). An elementary statement e is either a spike \(a\in O\), or a send statement \(\,{\textsf{snd}}\,\xi \,a\,\) (with \(\xi \in \Xi \) and \(a\in O\)), or an initialization statement \(\,{\textsf{init}}\,\xi \,\) (with \(\xi \in \Xi \)). A neuron declaration is a construct \(\,\,\textsf{neuron}\,N\,\{\,rs\,\mid \,\xi \,\}\), where \(N\in Nn\) is the name of the neuron, \(rs\in Rs\) is a list of rules, and \(\xi \in \Xi \) is a finite set of neuron names indicating the neurons that are adjacent (neighbouring) to neuron with name N. An empty set of neuron names is denoted by \(\{ \}\). An element \(D\in NDs\) is called a declaration. Note that a declaration \(D=\,\,\textsf{neuron}\,N_0\,\{\,rs_0\,\mid \,\xi _0\,\};\cdots ;\,\,\textsf{neuron}\,N_n\,\{\,rs_n\,\mid \,\xi _n\,\}\) is valid only if all neuron names \(N_0,\ldots ,N_n\) occurring in D are pairwise distinct, and \(N_i\notin \xi _i\) for \(i=0,\ldots ,n\). Also, the name of the first neuron in any valid declaration \(D\in NDs\) must be \(N_0\) (name \(N_0\) is reserved). An element \(rs\in Rs\) is a list of rules; a rule \(r\in Rule\) is either a firing rule (also called a spiking rule) \(E/w\rightarrow s;\vartheta \) or a forgetting rule \(w\rightarrow \lambda \). A firing rule is a construct \(E/w\rightarrow s;\vartheta \), where E is a regular expression over \(O\), \(w\in W\) is a multiset of spikes, \(s\in S\) is a statement and \(\vartheta \) is a natural number denoting a time interval. A forgetting rule is a construct \(w\rightarrow \lambda \), where \(w\in W\). The multiset \(w\in W\) occurring in the left-hand side of a firing or a forgetting rule must be nonempty: \(w\ne [\,]\). Also, for a list of rules \(rs\in Rs\) to be valid, the condition \(\lnot (w'\in {}L(E))\), where \(\lnot \) is the logical negation operator, must be satisfied for any pair of firing and forgetting rules \(E/w\rightarrow s;\vartheta \) and \(w'\rightarrow \lambda \). Usually, we omit the element \(r_{\epsilon }\) (denoting an empty list) occurring at the end of a non-empty list of rules \(rs=r_1,\ldots ,r_j,r_{\epsilon }\) (\(rs\in Rs\)), and write \(rs\) as \(rs=r_1,\ldots ,r_j\). Excepting minor differences in notation, the syntax of programs, declarations and rules is the same as in [7].
Let \((\varsigma \in )S_0\) be given by \(\varsigma \,\,{:}{:}=\,\,a \,\mid \,\varsigma \parallel \varsigma \), where \(a\in O\) is spike. Clearly, \(S_0\subseteq S\). A statement \(s\in S_0(\subseteq S)\) denotes a multiset of spikes that is executed in the context of a neuron and can be transmitted to the neighbouring neurons. For example, the \({\mathcal {L}}_{snp}^{\alpha }\) statement \((a_1\parallel {}a_1)\parallel (a_3\parallel (a_2\parallel {}a_3))\) denotes the multiset of spikes \([a_1,a_1,a_2,a_3,a_3]=[a_1^2,a_2,a_3^2]\). Let \(ms:S_0\rightarrow [O]\) be given by: \(ms(a)=[a]\) and \(ms(\varsigma _1\parallel \varsigma _2)=ms(\varsigma _1)\uplus {}ms(\varsigma _2)\), where \(\uplus \) is the multiset sum operation [1, 8]. The multiset of spikes denoted by a statement \(s\in S_0\,\, (\in S)\) is ms(s) (we recall that \(W=[O]\)). A statement may also contain send statements \(\,{\textsf{snd}}\,\xi \,a\,\) and initialization statements \(\,{\textsf{init}}\,\xi \,\). A statement \(\,{\textsf{snd}}\,\xi \,a\,\) specifies a spike transmission operation with target indication \(\xi \) [20]. A statement \(\,{\textsf{init}}\,\xi \,\) specifies an initialization operation. The language \({\mathcal {L}}_{snp}^{\alpha }\) incorporates the initialization mechanism described in [8]; this mechanism has no counterpart in the original model of spiking neural P systems [15].
As in the original model of spiking neural P systems [15], a neuron may be either open or closed. An open neuron accepts (can receive) spikes. A closed neuron does not accept (cannot receive) spikes. Any elementary statement is executed in the context of a neuron. When a spike a is executed in the context of a neuron \(\,\,\textsf{neuron}\,N\,\{\,rs_N\!\,\mid \,\!\xi _N\,\}\), the spike a is transmitted to all open neurons with names in the set \(\xi _N\). The set \(\xi _N\) contains the names of all neurons that are adjacent (neighbouring) with neuron N; they represent the default destination for the spikes that are executed in the context of neuron N.
As in SNP calculus [8], a neuron may be active or idle. Idle neurons cannot interact with other neurons, and cannot store spikes; only active neurons can send, receive and store spikes. Upon system start up, only a single neuron is active (namely the neuron with name \(N_0\)). All other neurons are idle and must be initialized using the initialization statements \(\,{\textsf{init}}\,\xi \,\) and send statements \(\,{\textsf{snd}}\,\xi \,a\,\). Once initialized, a neuron becomes active, and never returns to the idle state. Note that we use the notions of open neuron and closed neuron to refer only to neurons that are active (i.e., neurons that were initialized previously).
The statements \(\,{\textsf{init}}\,\xi \,\) and \(\,{\textsf{snd}}\,\xi \,a\,\) are the \({\mathcal {L}}_{snp}^{\alpha }\) counterparts for the initialization spike primitive and the selective spike primitive from the SNP calculus [8]. The effect of executing a statement \(\,{\textsf{init}}\,\xi \,\) in the context of a neuron \(\,\,\textsf{neuron}\,N\,\{\,rs_N\,\mid \,\xi _N\,\}\) is to initialize the neurons (which were not initialized previously) with names in the set \(\xi _N\cap \xi \) as open neurons containing each an empty multiset of spikes \([\,]\) (\(\xi _N\cap \xi \) is the set theoretic intersection of \(\xi _N\) and \(\xi \)). Note that the execution of a statement \(\,{\textsf{init}}\,\xi \,\) has no effect (is inoperative) whenever all the neurons with names in set \(\xi _N\cap \xi \) are active (were initialized previously). The effect of executing a statement \(\,{\textsf{snd}}\,\xi \,a\,\) in the context of a neuron \(\,\,\textsf{neuron}\,N\,\{\,rs_N\,\mid \,\xi _N\,\}\) depends on the status of the receiving neurons: each neuron that was not initialized previously (i.e., each idle neuron) with name in the set \(\xi _N\cap \xi \) is initialized as an open neuron containing the multiset of spikes \([a]\),Footnote 1 and each (active and) open neuron with name in the set \(\xi _N\cap \xi \) receives and adds the spike a to the multiset of spikes that it stores. In each step, all spikes are executed and transmitted concurrently (in a single time unit). Note that only the execution of an initialization statement \(\,{\textsf{init}}\,\xi \,\) or a send statements \(\,{\textsf{snd}}\,\xi \,a\,\) has initialization effects; the execution of a spike \(a\in O\) has no initialization effect. In each execution step, all initialization operations (associated with the execution of statements \(\,{\textsf{init}}\,\xi \,\) or \(\,{\textsf{snd}}\,\xi \,a\,\)) are performed before the transmission of spikes. Thus, all the spikes transmitted to open neurons (initialized in the present step or in any previous execution step) surely reach their destinations.
The execution of an \({\mathcal {L}}_{snp}^{\alpha }\) program \(\pi =(D,s)\) begins by executing the statement s in the context of neuron \(N_0\); the neuron with name \(N_0\) is automatically initialized as an open neuron containing an empty multiset of spikes \([\,]\) upon system start up.Footnote 2 All other neurons are idle in the initial state. In the original model of spiking neural P systems [15], the initial state is part of the system specification and there is no initialization mechanism. By contrast, the SNP calculus provides primitives which can be used for initialization purposes. The initialization mechanism of \({\mathcal {L}}_{snp}^{\alpha }\) is based on the SNP calculus [8]. The statement s can be used to initialize the whole system using initialization statements \(\,{\textsf{init}}\,\xi \,\) and send statements \(\,{\textsf{snd}}\,\xi \,a\,\). If the neuron with name \(N_0\) is connected directly with all other neurons in the system, then the initialization operation can be performed in a single computation step (one time unit) [8]. In all subsequent steps, the evaluation of an \({\mathcal {L}}_{snp}^{\alpha }\) statement s is caused by the execution of a firing rule \(E/w\rightarrow s;\vartheta \) with statement s occurring on the right-hand side. As in the original model of spiking neural P systems [15] and as in [8,9,10], the execution of an \({\mathcal {L}}_{snp}^{\alpha }\) program proceeds synchronously assuming a global clock to measure time, and each neuron is a nondeterministic sequential machine which executes at most one rule in each step.
A firing rule is a construct \(E/w\rightarrow s;\vartheta \) corresponding to the variant of extended rules with multiple types of spikes [16, 21]. The execution of a firing rule \(r=E/w\rightarrow s;\vartheta \) occurring in the list \(rs_N\) of a neuron \(\,\,\textsf{neuron}\,N\,\{\,rs_N\,\mid \,\xi _N\,\}\) currently open and storing a multiset of spikes \(w_N\) is triggered when the following conditions are satisfied: \(w_N\in {}L(E)\) and w is a submultiset of \(w_N\), \(w\subseteq {}w_N\) (see Remark 1, where notations \(w_N\in {}L(E)\) and \(w\subseteq {}w_N\) are explained). As in [8,9,10, 15], we say that the neuron fires (executes or applies) the rule r whenever the execution of a rule \(r=E/w\rightarrow s;\vartheta \) is triggered, and the effects of executing rule r are the following: the multiset of spikes w is consumed (only the multiset \(w_N\setminus {}w\) remains in neuron N), and the execution of statement s is triggered after \(\vartheta (\ge 0)\) time units. If \(\vartheta =0\), then the statement s is executed in the same computation step (the same time unit). If \(\vartheta >0\), then the statement s is temporarily suspended; it will be executed after exactly \(\vartheta \) time units. When the statement s is executed (after exactly \(\vartheta \) time units) we say that the neuron spikes, meaning that the spikes contained in statement s are executed in the context of neuron N and transmitted to the neighbouring neurons (as explained above). As in the original model [15], the neuron changes its status from open to closed whenever it fires; the neuron remains closed (i.e., it does not accept spikes) in the whole time interval between firing and spiking. After exactly \(\vartheta \) time units, the neuron executes statement s and it becomes open (meaning that it accepts spikes) again.
A forgetting rule is a construct \(w\rightarrow \lambda \), where \(w\in W\) is a multiset of spikes. A forgetting rule \(w\rightarrow \lambda \) can only be executed by a neuron containing exactly the multiset of spikes w; as the effect of executing a forgetting rule, all the spikes are removed from the neuron. This means that immediately after executing a forgetting rule, the neuron contains an empty multiset of spikes \([\,]\).
Example 3
We consider two \({\mathcal {L}}_{snp}^{\alpha }\) programs \(\pi ^{\alpha }_0\) and \(\pi ^{\alpha }_1\); \(\pi ^{\alpha }_0\) is a toy program to illustrate how we handle nondeterministic behaviour, and \(\pi ^{\alpha }_1\) is based on the spiking neural P system \(\Pi _1\) presented in [15, Section 5, Figure 2]. In the sequel, we write a firing rule \(E/[a^i]\rightarrow s;\vartheta \) with \(L(E)=\{a^i\}\) in its simpler form \([a^i]\rightarrow s;\vartheta \) (notation \([a^i]\) is explained in Remark 1). Also, the notation \(s^i\) is defined as follows: \(s^1=s\) and \(s^{i+1}=s\parallel {}s^i\), for \(s\in S\) and \(i\in \mathbb {N}\), \(i>0\).
-
(1)
The program \(\pi ^{\alpha }_0\in {\mathcal {L}}_{snp}^{\alpha }\) is given by \(\pi ^{\alpha }_0=(D^{\alpha }_0,s^{\alpha }_0)\), where statement \(s^{\alpha }_0\in S\) is \(s^{\alpha }_0=\,{\textsf{snd}}\,\{N_1\}\,a\,\parallel \,{\textsf{init}}\,\{N_2\}\,\), and declaration \(D^{\alpha }_0\in NDs\) is given by:
-
\(D^{\alpha }_0\,=\,\,\,\textsf{neuron}\,N_0\,\{\,r_{\epsilon }\,\mid \,\{N_1,N_2\}\,\},\)
-
\(\,\,\textsf{neuron}\,N_1\,\{\,[a]\rightarrow \,{\textsf{snd}}\,\{N_2\}\,a_1\,;0,[a]\rightarrow \,{\textsf{snd}}\,\{N_2\}\,a_2\,;0\,\mid \,\!\{N_0,N_2\}\!\,\},\)
-
\(\,\,\textsf{neuron}\,N_2\,\{\,[a_1]\rightarrow a_1^2;2,[a_2]\rightarrow a_2^2;2\,\mid \,\{N_0\}\,\}.\)
After the initialization step (in which the statement \(s^{\alpha }_0\) is executed) neuron \(N_1\) contains the multiset of spikes \([a]\), and neurons \(N_0\) and \(N_2\) are empty (containing each the multiset \([\,]\)). In this state, neuron \(N_1\) can select either of the spiking rules \([a]\rightarrow \,{\textsf{snd}}\,\{N_2\}\,a_1\,;0\) or \([a]\rightarrow \,{\textsf{snd}}\,\{N_2\}\,a_2\,;0\), and so it transmits to neuron \(N_2\) either the spike \(a_1\) or the spike \(a_2\) (in a nondeterministic manner). Although neuron \(N_1\) is connected by outgoing synapses to both neurons \(N_0\) and \(N_2\), it transmits spikes only to neuron \(N_2\) (using selective send operations \(\,{\textsf{snd}}\,\{N_2\}\,a_1\,\) or \(\,{\textsf{snd}}\,\{N_2\}\,a_2\,\)). In the next step neuron \(N_2\) fires. If neuron \(N_2\) received the spike \(a_1\), it will use the rule \([a_1]\rightarrow a_1^2;2\). If neuron \(N_2\) received the spike \(a_2\), it will use the rule \([a_2]\rightarrow a_2^2;2\) In each case, neuron \(N_2\) remains in the closed status for the next two steps. After exactly two steps, neuron \(N_2\) produces spikes which are transmitted to neuron \(N_0\) and the system reaches a halting configuration. The semantics of this simple nondeterministic program \(\pi ^{\alpha }_0\) can be described as a collection containing two alternative execution traces.
-
-
(2)
We also consider an example taken from the literature, namely the spiking neural P system \(\Pi _1\) presented in [15, Section 5, Figure 2], whose specification is given with respect to a natural number \(n>0\) which is a parameter of the model. The system \(\Pi _1\) consists of three neurons. In the initial state, the three neurons contain \(2^{n-1}\) spikes, 0 spikes and 1 spike, respectively. In [15], it is used the convention that the result of a computation performed by a spiking neural P system is the time interval (number of steps) elapsed between the first two spikes produced by the output neuron. Following this convention, the spiking neural P system \(\Pi _1\) computes the number \(3n+2\) (for further explanations, see [15]). Here we present an \({\mathcal {L}}_{snp}^{\alpha }\) program \(\pi ^{\alpha }_1\) which implements the spiking neural P system \(\Pi _1\). Let \(n\in \mathbb {N}, n>0\). The \({\mathcal {L}}_{snp}^{\alpha }\) program \(\pi ^{\alpha }_1\) is given by \((D^{\alpha }_1,s^{\alpha }_1)\), where the statement \(s^{\alpha }_1\) is given by \(s^{\alpha }_1 = (\,{\textsf{snd}}\,\{N_1\}\,a\,)^{2n-1}\parallel \,{\textsf{init}}\,\{N_2\}\,\parallel \,{\textsf{snd}}\,\{N_3\}\,a\,\), and declaration \(D^{\alpha }_1\) is given by
-
\(D^{\alpha }_1\,=\,\,\,\textsf{neuron}\,N_0\,\{\,r_{\epsilon }\,\mid \,\{N_1,N_2,N_3\}\,\},\)
-
\(\,\,\textsf{neuron}\,N_1\,\{\,a^+/[a]\rightarrow a;2\,\mid \,\{N_2\}\,\},\)
-
\(\,\,\textsf{neuron}\,N_2\,\{\,[a^n]\rightarrow a;1\,\mid \,\{N_3\}\,\},\)
-
\(\,\,\textsf{neuron}\,N_3\,\{\,[a]\rightarrow a;0\,\mid \,\{N_0\}\,\}\).
In the original model of spiking neural P systems [15], it is used the notion of an environment. Although the notion of an environment is not articulated in our paper, we use the neuron with the (reserved) name \(N_0\) to play the role of the environment (as in [8,9,10]). In this way, the neuron with name \(N_0\) receives the spikes produced by the output neuron. The three neurons \(N_1\), \(N_2\) and \(N_3\) implement the corresponding neurons from the spiking neural P system \(\Pi _1\) given in [15, Section 5, Figure 2], and \(N_3\) is the output neuron. The \({\mathcal {L}}_{snp}^{\alpha }\) program \(\pi ^{\alpha }_1\) implements faithfully the spiking neural P system \(\Pi _1\) presented in [15].
-
2.2 Semantic interpreter for \({\mathcal {L}}_{snp}^{\alpha }\) working with all possible traces
We present a semantic interpreter for \({\mathcal {L}}_{snp}^{\alpha }\) derived from an operational semantics [24]. The interpreter is implemented in Haskell, and can be found in the public repository [34] as file jmc23-snp0.hs. Essentially, the semantic interpreter is based on the operational semantics of \(\textsf{SNP}\) calculus presented in [8]; the differences are mentioned in Remark 4.
In general, formal semantics assign meanings taken from some mathematical domains of interpretation to syntactic language constructions. In this article, the syntax, the configurations of the operational semantics and the semantic domains are implemented using Haskell type declarations.
The Haskell types Obj and Nn implement the sets \(O\) and \(Nn\) of spikes (or objects) and neuron names, respectively. Also, the types W and Xi implement the sets \(W\) and \(\Xi \) of finite multisets over \(O\) and of finite sets of neuron names \(Nn\), respectively. We model sets and multisets as Haskell lists.

The abstract syntax of language \({\mathcal {L}}_{snp}^{\alpha }\) of Definition 1 can be implemented as:

The types S and ES implement the classes \(S\) of statements and \(ES\) of elementary statements, respectively.

The type Rule implements the class \(Rule\) of rules, using the type constructor RExp to represent regular expressions over spikes (or objects) of type Obj. A straightforward Haskell implementation of type RExp of regular expressions (with associated operators) is available at [34]. The same type RExp is employed in the implementation of each semantic interpreter presented in this paper. The type Rs implements the class \(Rs\) of lists of rules.

The types ND and NDs implement the class \(ND\) of neuron declarations and the class \(NDs\) of declarations, respectively. The type Prg implements the class \(Prg\) of programs presented in Definition 2.
All languages studied in this paper are concurrent and nondeterministic. Nondeterministic behaviour is implemented in two different ways for each of the three languages \({\mathcal {L}}_{snp}^{\alpha }\), \({\mathcal {L}}_{snp}^{ir}\) and \({\mathcal {L}}_{snp}^{sp}\) presented in this article. For each language, we provide both an implementation which produces all possible execution traces based on the concept of a linear time powerdomain [11], and an implementation where nondeterministic behaviour is simulated using a (pseudo) random number generator to choose an arbitrary execution trace.

In this and all subsequent sections, we implement nondeterministic behaviour using the type R. The implementation given in this subsection produces all possible execution traces; here, the type R is defined as a synonym for the type P which implements the concept of a linear time powerdomain [11] whose elements are collections of sequences of observables. We use the elements of types Omega, Q and P to implement observables, sequences of observables (modelling execution traces), and collections of sequences of observables (modelling collections of execution traces), respectively. An observable of type Omega is a list (implementing a set) of elements of type OS.
An element of type OS describes the current observable state of a neuron (an element of type OS is actually obtained based on information extracted from an element of type NS which describes the complete state of a neuron). An element of type OS is a construct of the form (OSO nn w) or (OSC nn w), where nn is a neuron name and w is a multiset of spikes currently stored by the neuron with name nn. The constructs (OSO nn w) and (OSC nn w) describe the current observable state of an open neuron and of a closed neuron, respectively.
A sequence of observables of type Q is implemented as a list of observables (Epsilon is the empty list of observables). A collection of sequences of observables of type P is a list (implementing a set) of sequences of observables. As in the original model [15], time is measured by considering a global clock. As in [8], time information is implicit in our implementation, being given by the number of steps in each sequence of observables of type Q.

To manipulate elements of type R, we use the operator fprefr and the n-ary operator bignedr handling observable prefixing and nondeterministic choice operations, respectively. The value re is used for computation termination.
In this subsection, R is a type synonym for P and the operators fprefr and bignedr behave the same as functions fpref and bigned, respectively. The mapping fpref prefixes an observable to each element in a collection of sequences of observables. The mapping bigned implements nondeterministic choice based on the standard set union operator union. To simplify the presentation, in the Haskell code we omit the Eq instance declarations needed in the definition of polymorphic functions such as the set union operator union. For nondeterministic programs, the implementation presented in this subsection produces all possible execution traces.
All the semantic interpreters presented in this article are designed with continuations for concurrency [6, 30]. As in [8], we employ two different classes of continuations: synchronous continuations and asynchronous continuations.Footnote 3

The type Conf implements the class of configurations that are used in the transition relation for the operational semantics of \({\mathcal {L}}_{snp}^{\alpha }\). The types F and K implement the classes of synchronous continuations and asynchronous continuations, respectively. We also use the term continuation to refer to any pair (f,k) of type Cont, where f is a synchronous continuation of type F and k is an asynchronous continuation of type K. A configuration of type Conf is either a construct (Kres k) or a construct of the form (Cres h (f,k) u), where f::F is a synchronous continuation, k::K is an asynchronous continuation, h and u are elements of types H and U, respectively.
A synchronous continuation of type F is either the empty synchronous continuation Fe or a construct (F h) with h a value of type H. An element of type H is either a construct (H (s,xi)) with s a statement of type S and xi a set of neuron names of type Xi, or a construct of the form (Hpar h1 h2) which is used to represent a parallel composition of the values h1 and h2 of type H. A construct of the form (H (s,xi)) is used to execute statement s in a context where the neuron names in the set xi represent the destination for the spikes contained in the statement s.
An asynchronous continuation of type K is a set of pairs of the form (nn,ns), where nn is a neuron name of type Nn and ns is a value of type NS. A value of type NS describes the (current) state of a neuron which can be open or closed. The state of an open neuron is described by a construct of the form (NSopen w), where w is the multiset of spikes that is currently stored in the neuron. The state of a closed neuron is described by a construct of the form (NSclosed w vartheta wr (s,xi)), where w is the multiset of spikes (of type W) that is currently stored in the neuron, vartheta is a (positive) integer number (of type Int) representing a time intervalFootnote 4, wr represents the multiset of spikes that remain in the neuron when the neuron moves to the open status, and (s,xi) is a computation that is activated when the neuron moves to the open status.

The mapping (sOmega nds k) extracts from the asynchronous continuation k the information that is produced as an observable element of type Omega (which is a synonym for the type [OS]). To obtain a readable output, the mapping (sOmega nds k) yields the list of elements of type OS describing the current observable state of all neurons in the order in which neurons occur in the declaration nds::NDs.
An element of type A is called an action. Values of type U are lists of elements of type A, implementing multisets of actions. Actions of the form (At a xi), (AtI a xiInit) and (AtInit xiInit) correspond to elementary statements of the form (Aspike a), (Snd xi1 a) and (Init xi), respectively. The elements of type Xi are sets (implemented as lists) of neuron names. We also use the type XiInit; its elements are constructs (XiInit xi), where xi:Xi and the data constructor XiInit carries an initialization indication. The correspondence between elementary statements and actions is computed by the following mapping act:

The mapping (act e xi) receives as arguments an elementary statement e::ES and a set of neuron names xi:Xi representing the set of neurons adjacent to the neuron which executes the elementary statement e. An action (At a xi) describes the execution of an elementary spike (Aspike a) with destination given by the set of neuron names xi. The definition of mapping act indicates that send statements (Snd xi1 a) and initialization statements (Init xi1)Footnote 5 have an initialization effect upon the neurons with names in the set (xi1 ‘intersect‘ xi), as explained in Sect. 2.1 (the expression (xi1 ‘intersect‘ xi) computes the set theoretic intersection between the sets xi1 and xi). We recall that immediately after initialization, a neuron is open (i.e., it accepts spikes). When executed in the context of a particular neuron whose neighbours are the neurons that have names in a given set xi, a send statement (Snd xi1 a) also transmits the spike a to all open neurons with names in the set (xi1 ‘intersect‘ xi).
The behaviour of \({\mathcal {L}}_{snp}^{\alpha }\) programs is specified based on a transition relation designed in the style of operational semantics [24]. The transition relation connects each \({\mathcal {L}}_{snp}^{\alpha }\) configuration of type Conf to a set of pairs of type [(Omega,K)], where type Omega implements the set of observables and type K implements the class of asynchronous continuations (the transition relation is designed with continuations for concurrency [6, 30]). We recall that a construct of the form (Kres k) is a configuration, where k::K is an asynchronous continuation. The class of asynchronous continuations is a subset of the class of configurations. For any \({\mathcal {L}}_{snp}^{\alpha }\) program (nds,s) with nds a declaration and s a statement, the definition of the transition relation also depends on the declaration nds::NDs.

The transition relation for \({\mathcal {L}}_{snp}^{\alpha }\) is implemented as a function tr of type  . Essentially, the function (tr t nds) yields the successor set (see [11]) for configuration t. When using synchronous continuations to capture the synchronized functioning that is specific to spiking neural P systems, the synchronization involves the components h::H, f::F and u::U for a configuration of the form (Cres h (f,k) u).
. Essentially, the function (tr t nds) yields the successor set (see [11]) for configuration t. When using synchronous continuations to capture the synchronized functioning that is specific to spiking neural P systems, the synchronization involves the components h::H, f::F and u::U for a configuration of the form (Cres h (f,k) u).
The definition of the transition relation tr consists of five equations. The first one describes the configuration (Cres (H (ES e, xi)) (Fe,k) u), where e::ES is an elementary statement executed in the context of a neuron whose neighbours are the neurons with names in the set xi:Xi, with respect to the empty synchronous continuation Fe, an asynchronous continuation k::K and a multiset of actions u::U. The implementations of the auxiliary mappings summs, initk and sndk are available in the public repository [34] in the file jmc23-snp0.hs; the function summs implements the multiset sum operation, while the mappings initk and sndk implement initialization and spike transmission operations, respectively. In the first equation of function tr, u2::U is the multiset obtained by adding the action (act e xi) to the multiset u, k1::K is the asynchronous continuation obtained by executing the initialization actions contained in the multiset u2 on the asynchronous continuation k, and k2::K is the asynchronous continuation obtained by executing the spike transmission actions contained in the multiset u2 on the asynchronous continuation k1. The mapping (sOmega nds k2) extracts from the asynchronous continuation k2 the information that is produced as an observable element obs. Thus, the first equation of function tr implements the transition from configuration (Cres (H (ES e, xi)) (Fe,k) u) to configuration k2 with observable obs; in this case, function tr yields a singleton set given by the list [(obs,k2)].
The second equation of function tr describes the execution of an elementary statement e::ES with respect to a nonempty synchronous continuation (F h), an asynchronous continuation k::K and a multiset of actions u::U. According to this equation, configurations (Cres (H (ES e, xi)) (F h,k) u) and (Cres h (Fe,k) ([(act e xi)] ‘summs‘ u)) behave the same.
The third equation and the fourth equation of function tr handle the parallel execution of the statements and of the synchronous continuations, respectively. The operator parf models parallel composition over the class of synchronous continuations.

The fifth equation evaluates a configuration (Kres k) using the scheduler function sfun, where k::K is an asynchronous continuation. The type of the scheduler function sfun is  . The scheduler function applies the rules contained in declaration in a nondeterministic sequential manner, as indicated in [15]. Hence, the scheduler function (sfun nds k) receives as arguments a declaration nds::NDs and an asynchronous continuation k::K, and yields a list of type [(H,K)]. It yields the empty list [] when the system reaches a halting configuration; otherwise, it yields a nonempty list. The implementation of the scheduler function sfun is available at [34] in file jmc23-snp0.hs.
. The scheduler function applies the rules contained in declaration in a nondeterministic sequential manner, as indicated in [15]. Hence, the scheduler function (sfun nds k) receives as arguments a declaration nds::NDs and an asynchronous continuation k::K, and yields a list of type [(H,K)]. It yields the empty list [] when the system reaches a halting configuration; otherwise, it yields a nonempty list. The implementation of the scheduler function sfun is available at [34] in file jmc23-snp0.hs.
Remark 4
The design of the semantic interpreter presented in this subsection is essentially based on the operational semantics of \(\textsf{SNP}\) calculus [8]. However, there are certain differences. In [8], the nondeterministic behaviour is modelled using a linear time powerdomain. In this article, we provide two alternative implementations for nondeterminism: in this subsection we use the type P to implement a linear time powerdomain, and in Sect. 2.3 the nondeterministic behaviour is simulated using a (pseudo)random number generator. Excepting the interpretation of nondeterminism, the other differences are minor.
As in [8], we define the operational semantics function osem for the language \({\mathcal {L}}_{snp}^{\alpha }\) as the fixed point of a higher-order function. Since Haskell features lazy evaluation, one can define the fixed point combinator as follows:

We define the operational semantics function  (mapping a configuration of type Conf to a final value of type R) as the fixed point of the higher-order function psiD defined by:
(mapping a configuration of type Conf to a final value of type R) as the fixed point of the higher-order function psiD defined by:

The predicate (hlt nds t) yields \(\textsf{true}\) when the system reaches a halting configuration (in which no rule can be applied, although the neurons are open). The implementation for  is available at [34].
is available at [34].

The initial asynchronous continuation k0::K occurring in the definition of function opsem contains a single active neuron named (Nn “n0”); this name (Nn “n0”) implements the (reserved) neuron name \(N_0\).
We present the main components of the semantic interpreters and illustrate how nondeterministic behaviour is handled. First, we present an implementation of the \({\mathcal {L}}_{snp}^{\alpha }\) program \(\pi ^{\alpha }_0\) described in Example 3(1). The Haskell implementation of \({\mathcal {L}}_{snp}^{\alpha }\) program \(\pi ^{\alpha }_0\) is stored in variable pi0a::Prg of the file jmc23-snp0.hs. Running the \({\mathcal {L}}_{snp}^{\alpha }\) program \(\pi ^{\alpha }_0\) with (opsem pi0a), we get:

The yield of the semantic interpreter is a value of type R (which in this subsection is a synonym for type P). The type P implements a linear time powerdomain. A value of type P is a list (implementing a set) of sequences of observables, representing execution traces (hence the order in which execution traces are displayed is not important). In this example there are two alternative execution traces. For each execution trace, the observables are displayed in chronological order. We recall that an observable of type Omega is a set (implemented as a list) of elements of type OS. For instance, [[(“n0”,[]),(“n1”,[“a”]),(“n2”,[])] is the first observable occurring in each execution trace. Each observable shows the name, the content and the open/closed status for all active neurons. The observable state of an open neuron is displayed between round brackets ‘(’ and ‘)’; the observable state of a closed neuron is displayed between angle brackets ‘ ’ and ‘
’ and ‘ ’. For example, in each of the two execution traces displayed above, neuron with name (Nn “n2”) is closed for two time units (in steps 3 and 4).
’. For example, in each of the two execution traces displayed above, neuron with name (Nn “n2”) is closed for two time units (in steps 3 and 4).
We also provide an implementation of the \({\mathcal {L}}_{snp}^{\alpha }\) program \(\pi ^{\alpha }_1\) presented in Example 3(2). The source code is contained in the file jmc23-snp0.hs (available at [34]), where the Haskell implementation for the \({\mathcal {L}}_{snp}^{\alpha }\) program \(\pi ^{\alpha }_1\) is stored in the variable pi1a::Prg (the variable pi1a::Prg implements the program \(\pi ^{\alpha }_1\) for \(n=2\)). Running this program with (opsem pi1a), the reader can observe that the program \(\pi ^{\alpha }_1\) is deterministic (it produces a single execution trace), the output neuron \(N_1\) spikes twice (in steps 2 and 10), and the spikes are received by the neuron with name \(N_0\) (\(N_0\) plays the role of the environment). The number computed by the \({\mathcal {L}}_{snp}^{\alpha }\) program \(\pi ^{\alpha }_1\) is \(10-2\)=8 and 8=\(3n+2\) (because n=2), which coincides with the result predicted in [15].

2.3 Interpreter for \({\mathcal {L}}_{snp}^{\alpha }\) based on random choice
The semantic interpreter presented in Sect. 2.2 implements an operational semantics for the language \({\mathcal {L}}_{snp}^{\alpha }\) modelling nondeterministic behaviour based on the type P, which implements a linear time powerdomain [11]. Since the length of execution traces may be infinite, a direct implementation based on a powerdomain is in general intractable, and can be used for executing only toy \({\mathcal {L}}_{snp}^{\alpha }\) programs. In this subsection, we consider an alternative implementation option in which nondeterministic behaviour is simulated using a (pseudo) random number generator. For any given \({\mathcal {L}}_{snp}^{\alpha }\) program, the implementation presented now generates incrementally a single execution trace (randomly selected). Since Haskell features lazy evaluation, this new implementation can be used to execute non-terminating \({\mathcal {L}}_{snp}^{\alpha }\) programs. In random trace semantics, our interpreter can be used to test nondeterministic and non-terminating programs.
Starting from the implementation given in Sect. 2.2 and using the features provided by the Haskell library System.Random, we obtain the semantic interpreter presented in this subsection with some simple modifications. We use the type Rand of random number generators given by System.Random.StdGen. We also use function System.Random.next to extract a value from the random number generator. For nondeterministic \({\mathcal {L}}_{snp}^{\alpha }\) programs, the implementation presented now can produce different outputs at each different execution. To obtain this new version of our semantic interpreter, it is enough to redefine the type R and the associated operators as follows:

No other modifications are required in the Haskell code (all other type and function definitions remain as in previous Sect. 2.2). However, to test this new version of our semantic interpreter, it is convenient to define the function tstRnd given below, which receives as argument a program of type Prg and can produce different random traces at different executions.

This new version of our semantic interpreter is available online at [34] in the file jmc23-snp0-rnd.hs, where program \({\pi }^{\alpha }_0\) is stored in variable pi0a : : Prg. Among the programs presented in Example 3, only \(\pi ^{\alpha }_0\) is nondeterministic. Since the program \(\pi ^{\alpha }_0\) is nondeterministic, by running this program \(\pi ^{\alpha }_0\) in random trace semantics we can obtain different outputs for different executions. However, since in this simple example there are only two possible different execution traces, two out of the three experiments presented here (the first one and the third one) happen to produce same output:



3 Spiking neural P systems with inhibitory rules
In this section we study a language named \({\mathcal {L}}_{snp}^{ir}\). This language \({\mathcal {L}}_{snp}^{ir}\) extends the language \({\mathcal {L}}_{snp}^{\alpha }\) with constructions specific to spiking neural P systems with inhibitory rules [22, 33]. Following [33], we consider spiking and inhibitory rules with time delays. Since the main ingredients were introduced in Sect. 2, in this section and in Sect. 4 we adopt a more concise style.
The syntax of language \({\mathcal {L}}_{snp}^{ir}\) is presented in Definition 5. The sets \((a\in )O\), \((N\in )Nn\), \((w\in )W\) and \((\xi \in )\Xi \) and the syntactic classes of statements \((s\in )S\) and elementary statements \((e\in )ES\) are as in Sect. 2. On the other hand, the class of rules \((r\in )Rule\) is different. However, the classes of lists of rules \((rs\in )Rs\), neuron declarations \((d\in )ND\), declarations \((D\in )NDs\) and programs \((\pi \in ){\mathcal {L}}_{snp}^{ir}\) are defined as in Sect. 2. The language \({\mathcal {L}}_{snp}^{ir}\) supports the same initialization mechanism like the language \({\mathcal {L}}_{snp}^{\alpha }\) (based on the statements \(\,{\textsf{snd}}\,\xi \,a\,\) and \(\,{\textsf{init}}\,\xi \,\) explained in Sect. 2.1).
Definition 5
(Syntax of \({\mathcal {L}}_{snp}^{ir}\))
-
(a)
(Statements) \(s(\in S) \,\,{:}{:}=\,\,e \,\mid \,s\parallel {}s\) where \(e(\in ES) \,\,{:}{:}=\,\,a \,\mid \,\,{\textsf{snd}}\,\xi \,a\, \,\mid \,\,{\textsf{init}}\,\xi \, \)
-
(b)
(Rules) \(\,rs(\in Rs) \,\,{:}{:}=\,\,r_{\epsilon }\,\mid \,r,rs\) with \(r(\in Rule) \,\,{:}{:}=\,\,E/w\rightarrow s;\vartheta \,\mid \,(E,\iota )/w\rightarrow s;\vartheta \,\mid \,E/w\rightarrow \lambda \) \(\iota (\in Iota) \,\,{:}{:}=\,\,(\overline{E},N) \,\mid \,\iota ,\iota \) where E and \(\overline{E}\) are regular expressions over \(O\), and \(\vartheta \ge 0, \vartheta \in \mathbb {N}\).
-
(c)
(Neuron declarations) \(D(\in NDs) \,\,{:}{:}=\,\,d \,\mid \,d,D\) where \(d(\in ND) \,\,{:}{:}=\,\,\,\,\textsf{neuron}\,N\,\{\,rs\,\mid \,\xi \,\}\)
-
(d)
(Programs) \(\pi (\in {\mathcal {L}}_{snp}^{ir}) \,\,{:}{:}=\,\,D,s\)
Spiking rules of the form \(E/w\rightarrow s;\vartheta \) remain as in Sect. 2. \(E/w\rightarrow \lambda \) is a particular kind of spiking rule, where no statement and no time delay indication occur in the right-hand side. Such a rule can be applied by a neuron N in case the neuron currently contains the multiset \(w_N\) of spikes, \(w_N\in {}L(E)\) (notation presented in Remark 1), and \(w\subseteq {}w_N\). In this case, the multiset w is consumed immediately (without any delay), and only the multiset \(w_N\setminus {}w\) remains in the neuron. In the particular case when \(L(E)=\{a^i\}\) and \(w=[a^i]\), we write such a rule in the simpler form \([a^i]\rightarrow \lambda \); such a rule \([a^i]\rightarrow \lambda \) behaves like a simple forgetting rule presented in Sect. 2.
Specific to the language \({\mathcal {L}}_{snp}^{ir}\) are the inhibitory rules. These inhibitory rules have the form \((E,\iota )/w\rightarrow s;\vartheta \), where E is a regular expression over \(O\), \(w\in W\) is a multiset, \(s\in S\) is an \({\mathcal {L}}_{snp}^{ir}\) statement and \(\vartheta \in \mathbb {N}\) is a natural number indicating a time delay interval. If \(E\) is a regular expression over \(O\), then \(\overline{E}\) is an indication that \(E\) is used as an inhibitory regular expression [22]. The component \(\iota \in Iota\) of an inhibitory rule \((E,\iota )/w\rightarrow s;\vartheta \) is a list of pairs \((\overline{E}_j,N_j)\), where \(\overline{E}_j\) is an (inhibitory) regular expression and \(N_j\) is a neuron name. Considering a neuron with name N that currently stores the multiset of spikes \(w_N\) and that contains in its list of rules an inhibitory rule \(r=(E,(\overline{E}_1,N_1),\ldots ,(\overline{E}_m,N_m))/w\rightarrow s;\vartheta \), \(r\in Rule\), the neurons with names \(N_1,\ldots ,N_m\) are inhibitory neurons.Footnote 6 Assuming that neurons \(N_1,\ldots ,N_m\) currently contain the multisets of spikes \(w_1,\ldots ,w_m\), the firing condition for the inhibitory rule r in neuron N isFootnote 7
If the firing condition of the rule \(r=(E,(\overline{E}_1,N_1),\ldots ,(\overline{E}_m,N_m))/w\rightarrow s;\vartheta \) is satisfied and \(\vartheta =0\), then the neuron with name N fires, the multiset w is consumed, and the execution of statement s is triggered (the neuron produces spikes) immediately. If \(\vartheta >0\), then the statement s is suspended for the next \(\vartheta \) time units, and the execution of statement s is triggered after exactly \(\vartheta \) time units. In each case, the spikes produced by the execution of statement s are transmitted to the neighbouring neurons. Moreover, rules are selected and applied in nondeterministic manner by each neuron, with all neurons working concurrently, as in any spiking neural P systems [15, 22].
Example 6
We consider two \({\mathcal {L}}_{snp}^{ir}\) programs \(\pi ^{ir}_1\) and \(\pi ^{ir}_2\) based on [22, 33], respectively. In each case, the result computed by the system is considered to be the spike train (the sequence of zeros and ones) obtained by observing the behaviour of the output neuron, writing 1 when the output neuron spikes, and 0 otherwise.
-
(1)
The program \(\pi ^{ir}_1\in {\mathcal {L}}_{snp}^{ir}\) is \(\pi ^{ir}_1=(D^{ir}_1,s^{ir}_1)\), where the statement \(s^{ir}_1\) is given by \(s^{ir}_1 =(\,{\textsf{snd}}\,\{N_1\}\,a\,)^2\parallel (\,{\textsf{snd}}\,\{N_2\}\,a\,)^2\parallel \,{\textsf{init}}\,\{N_3\}\,\), and the declaration \(D^{ir}_1\in NDs\) is given by
-
\(D^{ir}_1\,=\,\,\,\textsf{neuron}\,N_0\,\{\,r_{\epsilon }\,\mid \,\{N_1,N_2,N_3\}\,\},\)
-
\(\,\,\textsf{neuron}\,N_1\,\{\,a^+/[a]\rightarrow a;0\,\mid \,\{N_3\}\,\},\)
-
\(\,\,\textsf{neuron}\,N_2\,\{\,[a]\rightarrow \lambda ,(a^+,(\overline{aa^+},N_1))/[a]\rightarrow a;0\,\mid \,\{N_3\}\,\},\)
-
\(\,\,\textsf{neuron}\,N_3\,\{\,a^+/[a]\rightarrow a;0\,\mid \,\{N_0\}\,\}\).
The \({\mathcal {L}}_{snp}^{ir}\) program \(\pi ^{ir}_1\) implements the spiking neural P system with inhibitory rules presented in [22, Section 2.2, Figure 2]. This illustrative example consists of three neurons \(\sigma _1,\sigma _2\) and \(\sigma _3\) implemented in our program \(\pi ^{ir}_1\) by the neurons \(N_1, N_2\) and \(N_3\), respectively. The statement \(s^{ir}_1\) produces the initial configuration in which the neuron \(N_1\) contains 2 spikes, neuron \(N_2\) contains 2 spikes and neurons \(N_3\) is empty (\(N_3\) is the output neuron). In our implementation, neuron \(N_0\) (which is automatically initialized upon system start up as an open and empty neuron) plays the role of the environment, receiving the spikes produced by the output neuron \(N_3\) (more explanations are given in Example 3). The example presented in [22] can generate two different spike trains, namely: 0111 and 01111. Our \({\mathcal {L}}_{snp}^{ir}\) program \(\pi ^{ir}_1\) captures accurately this behaviour; the behaviour is illustrated by the experiments presented in Sect. 3.1.
-
-
(2)
The program \(\pi ^{ir}_2\in {\mathcal {L}}_{snp}^{ir}\) is \(\pi ^{ir}_2=(D^{ir}_2,s^{ir}_2)\), where the statement \(s^{ir}_2\) is given by \(s^{ir}_2 =(\,{\textsf{snd}}\,\{N_1\}\,a\,)^2\parallel (\,{\textsf{snd}}\,\{N_2\}\,a\,)^2\parallel (\,{\textsf{snd}}\,\{N_3\}\,a\,)^3\parallel \,{\textsf{init}}\,\{N_{out}\}\,\), and the declaration \(D^{ir}_2\in NDs\) is given by
-
\(D^{ir}_2\,=\,\,\,\textsf{neuron}\,N_0\,\{\,r_{\epsilon }\,\mid \,\{N_1,N_2,N_3,N_{out}\}\,\},\)
-
\(\,\,\textsf{neuron}\,N_1\,\{\,[a^2]\rightarrow a^2;0,[a^2]\rightarrow a^2;1,[a]\rightarrow \lambda \,\mid \,\!\{N_2,N_3,N_{out}\}\,\},\)
-
\(\,\,\textsf{neuron}\,N_2\,\{\,(a^2,(\overline{(a^2)^+},N_3))/[a^2]\rightarrow a^2;0, (a^2,(\overline{a^3},N_3))/[a^2]\rightarrow a;0\,\mid \,\{N_1,N_{out}\}\,\},\)
-
\(\,\,\textsf{neuron}\,N_3\,\{\,[a^4]\rightarrow \lambda ,a^3/[a^2]\rightarrow \lambda ,[a^2]\rightarrow \lambda \,\mid \,\{\}\,\},\)
-
\(\,\,\textsf{neuron}\,N_{out}\,\{\,[a^4]\rightarrow \lambda ,[a^2]\rightarrow a;0,[a]\rightarrow a;0\,\mid \,\!\{N_3,N_0\}\,\}.\)
The \({\mathcal {L}}_{snp}^{ir}\) program \(\pi ^{ir}_2\) implements the spiking neural P system with inhibitory rules presented in [33, Section 3.2, Figure 3]. This illustrative example consist of four neurons \(\sigma _1,\sigma _2, \sigma _3\) and \(\sigma _{out}\) implemented in our program \(\pi ^{ir}_2\) by neurons \(N_1, N_2, N_3\) and \(N_{out}\), respectively. The statement \(s^{ir}_2\) produces the initial configuration in which the neuron \(N_1\) contains 2 spikes, neuron \(N_2\) contains 2 spikes, neurons \(N_3\) contains 3 spikes and neuron \(N_{out}\) is empty (\(N_{out}\) is the output neuron). Neuron \(N_0\) plays the role of the environment, receiving the spikes produced by \(N_{out}\). The example presented in [33] generates the language \(L(0^+1110)\); at each execution, in a nondeterministic manner, it can produce a spike train described by the regular expression \(0^+1110\). Our \({\mathcal {L}}_{snp}^{ir}\) program \(\pi ^{ir}_2\) captures accurately this behaviour; the behaviour is illustrated by the experiments presented in Sect. 3.2. It is worth noting that program \(\pi ^{ir}_2\) can be executed using only our interpreter based on random choice.
-
3.1 Interpreter for \({\mathcal {L}}_{snp}^{ir}\) working with all possible traces
An interpreter for the language \({\mathcal {L}}_{snp}^{ir}\) (similar to the one presented in Sect. 2) is available online in the public repository [34] as file jmc23-snp-ird.hs. The interpreters presented in Sect. 2.2 and in this subsection are similar; both work in all possible traces semantics, where type R is a synonym with the type P. Only the definitions that are specific to language \({\mathcal {L}}_{snp}^{ir}\) are discussed below.

The type Rule implements the class \(Rule\) of rules given in Definition 5. Specific to language \({\mathcal {L}}_{snp}^{ir}\) are the inhibitory rules of the form \((E,\iota )/w\rightarrow s;\vartheta \); they are implemented using the construction (Rin re rens w s vartheta), where re is a regular expression of type (RExp Obj), rens is a list of pairs of type [(RExp Obj,Nn)] (which implements the syntactic class \(Iota\) of Definition 5), w::W is a multiset of spikes, s::S is a statement and vartheta::Int is a positive integer number representing a time interval.
The definitions of the scheduler function sfun and predicate hlt (which verifies whether the system reached a halting configuration) depend on the rules that are specific to spiking neural P systems with inhibitory rules. Hence, the implementations of the scheduler function sfun and of the predicate hlt are also specific to the interpreter for the language \({\mathcal {L}}_{snp}^{ir}\). The complete implementation of the semantic interpreter for \({\mathcal {L}}_{snp}^{ir}\) is available at [34] in the file jmc23-snp-ird.hs, where the Haskell implementations of \({\mathcal {L}}_{snp}^{ir}\) programs \(\pi ^{ir}_1\) and \(\pi ^{ir}_2\) (presented in Example 6) are stored in the variables pi1ir and pi2ir, respectively. Only the program \(\pi ^{ir}_1\) can be verified using our semantic interpreter in all possible traces semantics.
Running the program \(\pi ^{ir}_1\) with (opsem pi1ir) generates the output below:

As explained in Example 6(1), the program \(\pi ^{ir}_1\) implements the example presented in [22]. In this experiment, our interpreter produces as output a value of type P (i.e., a set of execution traces) comprising two execution traces. We recall that in our implementation the spikes produced by the output neuron are received by the neuron with name \(N_0\) (implemented by (Nn “n0”)) which models the environment. In this example, neuron \(N_3\) is the output neuron (implemented by (Nn “n3”)). In the first step of the both execution traces, the output neuron \(N_3\) does not produce spikes (and \(N_0\) does not receive spikes); after that, the output neuron spikes in each of the following steps. Thus, the first execution produces the spike train 0111, and the second execution produces the spike train 01111; both confirm the result predicted in [22].
3.2 Interpreter for \({\mathcal {L}}_{snp}^{ir}\) based on random choice
Starting from the interpreter presented in Sect. 3.1, we obtain an interpreter working in random trace semantics using the implementation of type R presented in Sect. 2.3. No other modification is needed. The semantic interpreter for the language \({\mathcal {L}}_{snp}^{ir}\) working in random trace semantics can simulate the behaviour of the example of spiking neural P system with inhibitory rules presented in [33, Section 3.2, Figure 3]. At each execution, it can produce in a nondeterministic manner a spike train described by the regular expression \(0^+1110\) (as explained in Example 6(2)). Since there is an infinite number of possible alternative execution traces, this example can be verified only using our interpreter based on random choice.
The illustrative example of spiking neural P system with inhibitory rules presented in [33] is implemented by the \({\mathcal {L}}_{snp}^{ir}\) program \(\pi ^{ir}_2\) (introduced in Example 6(2)). The semantic interpreter for the language \({\mathcal {L}}_{snp}^{ir}\) working in random trace semantics is available at [34] in the file jmc23-snp-ird-rnd.hs, where the Haskell implementation of the program \(\pi ^{ir}_2\) is stored in the variable pi2ir. The following experiments show three executions of the program \(\pi ^{ir}_2\) using random trace semantics. In the experiments presented below, the output neuron \(N_{out}\) (implemented by (Nn “out”)) spikes in steps \(m, m+1\) and \(m+2\), where \(m=8\), \(m=2\) and \(m=5\), respectively. The spikes emitted by \(N_{out}\) are received by the neuron \(N_0\) (implemented by (Nn “n0”)); in step \(m+3\), no spike is emitted by the output neuron and execution terminates. Thus, the program \(\pi ^{ir}_2\) always produces a spike train described by the regular expression \(0^+1110\), confirming the result predicted in [33].



4 Spiking neural P systems with structural plasticity
This section introduces a language named \({\mathcal {L}}_{snp}^{sp}\). The language \({\mathcal {L}}_{snp}^{sp}\) is a variant of the language \({\mathcal {L}}_{snp}^{\alpha }\) (presented in Sect. 2), incorporating constructions specific to spiking neural P systems with structural plasticity [4]. The syntax of language \({\mathcal {L}}_{snp}^{sp}\) is presented in Definition 7. The sets \((a\in )O\), \((N\in )Nn\), \((w\in )W\) and \((\xi \in )\Xi \) and the classes of statements \((s\in )S\) and elementary statements \((e\in )ES\) are as in Sect. 2. Only the class of rules \((r\in )Rule\) is different. However, the lists of rules \((rs\in )Rs\), neuron declarations \((d\in )ND\), declarations \((D\in )NDs\) and programs \((\pi \in ){\mathcal {L}}_{snp}^{ir}\) are defined as in Sect. 2.
Definition 7
(Syntax of \({\mathcal {L}}_{snp}^{sp}\))
-
(a)
(Statements) \(s(\in S) \,\,{:}{:}=\,\,e \,\mid \,s\parallel {}s\) where \(e(\in ES) \,\,{:}{:}=\,\,a \,\mid \,\,{\textsf{snd}}\,\xi \,a\, \,\mid \,\,{\textsf{init}}\,\xi \, \)
-
(b)
(Rules) \(\,rs(\in Rs) \,\,{:}{:}=\,\,r_{\epsilon }\,\mid \,r,rs\) where \(r(\in Rule) \,\,{:}{:}=\,\,E/w\rightarrow s \,\mid \,\rho \) \(\rho (\in PR) \,\,{:}{:}=\,\,E/w\rightarrow (\alpha \mu )\xi s \,\mid \,E/w\rightarrow (-\mu )\) with E a regular expression over \(O\), \(\alpha \in \{+,\pm ,{\mp }\}\), and \(\mu \ge 1, \mu \in \mathbb {N}\)
-
(c)
(Neuron declarations) \(D(\in NDs) \,\,{:}{:}=\,\,d \,\mid \,d,D\) where \(d(\in ND) \,\,{:}{:}=\,\,\,\,\textsf{neuron}\,N\,\{\,rs\,\mid \,\xi \,\}\)
-
(d)
(Programs) \(\pi (\in {\mathcal {L}}_{snp}^{sp}) \,\,{:}{:}=\,\,D,s\)
The language \({\mathcal {L}}_{snp}^{sp}\) supports the same initialization mechanism like the language \({\mathcal {L}}_{snp}^{\alpha }\) in Sect. 2. We recall that the neuron with name \(N_0\) is automatically initialized upon system start up, and all other neurons must be initialized explicitly by using statements \(\,{\textsf{snd}}\,\xi \,a\,\) and \(\,{\textsf{init}}\,\xi \,\) (Sect. 2.1). Before initialization, a neuron is idle; immediately after initialization, each neuron becomes active. An active neuron can be open or closed, but it never moves to an idle state. The connections between active neurons are given by the declarations of neurons. Let \(N_i\) be a neuron given by a declaration \(\,\,\textsf{neuron}\,N_i\,\{\,rs_i\,\mid \,\xi _i\,\}\); the set \(\xi _i\) contains the names of all neurons that are adjacent with neuron \(N_i\) and represent the destination for the spikes that are emitted by neuron \(N_i\). Once the neuron becomes active, there is an outgoing synapse between neuron \(N_i\) and each neuron with name \(N_j\in \xi _i\) that is also active. We write \(N_i\mapsto N_j\) to express that there is a synapse connecting neuron \(N_i\) to neuron \(N_j\). Let \(pres(N_i)=\{ N_j \,\mid \,N_i\mapsto N_j\}\) be the set of neuron names having the neuron with name \(N_i\) as their presynaptic neuron [4].
As in [4], the rules in language \({\mathcal {L}}_{snp}^{sp}\) are without delays; moreover, we do not use forgetting rules. A rule of the form \(E/w\rightarrow s\) is a spiking rule. When executed by a neuron currently containing the multiset \(w_N\) of spikes, a spiking rule \(E/w\rightarrow s\) fires if \(w\subseteq {}w_N\) (i.e., w is a submultiset of \(w_N\)) and \(w_N\in {}L(E)\). Unlike in previous sections, when such a rule is applied, the execution of statement s is always triggered (and the neuron produces spikes) immediately, without delay.
Rules \(\rho \in PR\) of the form \(\rho =E/w\rightarrow (\alpha \mu )\xi s\) and \(\rho =E/w\rightarrow (-\mu )\) are called plasticity rules; they are specific to the language \({\mathcal {L}}_{snp}^{sp}\) which is based on the model of spiking neural P systems with structural plasticity presented in [4]. There is a single syntactic construction in [4] for plasticity rules, with \(\alpha \in \{+,-,\pm ,{\mp }\}\). When a neuron with name N executing a plasticity rule with \(\alpha \in \{+,\pm ,{\mp }\}\) is attached to a neuron with name \(N_j\) using a synapse (during synapse creation), it also transmits one spike to neuron with name \(N_j\). On the other hand, if the neuron executes a plasticity rule with \(\alpha \)=−, then no spike is transmitted between neurons. In this article, the spikes emitted by a neuron are specified by means of statements \(s\in S\); we use two different syntactic constructions for plasticity rules: \(E/w\rightarrow (\alpha \mu )\xi s\) (when \(\alpha \in \{+,\pm ,{\mp }\}\)) and \(E/w\rightarrow (-\mu )\). A plasticity rule can be applied by a neuron with name N which currently contains \(w_N\) spikes whenever \(w\subseteq {}w_N\) and \(w_N\in {}L(E)\). If the plasticity rule is applied, then the multiset of spikes w is consumed, i.e., only the multiset \(w_N{\setminus }{}w\) remains in the neuron. In addition, a plasticity rule \(\rho \in PR\) can create or delete synapses.
No synapse is created or deleted when a rule of the form \(\rho =E/w\rightarrow (\alpha \mu )\xi s\) with \(\alpha =+\) and \((\xi \setminus pres(N))=\emptyset \) is applied,Footnote 8 or when a rule \(\rho \) of the form \(\rho =E/w\rightarrow (-\mu )\) with \(pres(N)=\emptyset \) is applied.
If a plasticity rule \(\rho \) of the form \(\rho =E/w\rightarrow (\alpha \mu )\xi s\) with \(\alpha =+\) is applied, then there are two possibilities: if \(|\xi \setminus pres(N)|\le \mu \), then it is created a synapse to each neuron with name \(N_j\in (\xi \setminus pres(N))\); if \(|\xi \setminus pres(N)|>\mu \), then it is selected nondeterministically a subset of \((\xi \setminus pres(N))\) containing \(\mu \) neurons, and a synapse is created to each selected neuron.
If a plasticity rule \(\rho \) of the form \(\rho =E/w\rightarrow (-\mu )\) is applied, then we have two alternatives: if \(|pres(N)|\le \mu \), then all synapses in \(pres(N)\) are erased; if \(|pres(N)|>\mu \), then it is selected in a nondeterministic manner a subset of \(pres(N)\) containing \(\mu \) neurons, and all synapses to the selected neurons are removed.
If a plasticity rule \(\rho \) of the form \(\rho =E/w\rightarrow (\alpha \mu )\xi s\) with \(\alpha \in \{\pm ,{\mp }\}\) is applied, then some synapses are created (respectively deleted) at the current time t and then they are deleted (respectively created) at time \(t+1\). Neurons are always open (i.e., they can receive spikes), including in the two steps t and \(t+1\) during the application of a plasticity rule \(\rho =E/w\rightarrow (\alpha \mu )\xi s\) with \(\alpha \in \{\pm ,{\mp }\}\). Only at time \(t+2\) the neuron can apply another rule.
A neuron emits no spikes when it applies a plasticity rule \(\rho \) of the form \(\rho =E/w\rightarrow (-\mu )\). On the other hand, when a neuron N applies a plasticity rule \(\rho \) of the form \(\rho =E/w\rightarrow (\alpha \mu )\xi s\) (with \(\alpha \in \{+,\pm ,{\mp }\}\)), it executes the statement s, meaning that the spikes contained in statement s are executed in the context of neuron N and are transmitted to the neighbouring neurons (as explained in Sect. 2.1).
In the particular case when \(L(E)=\{a^i\}\) and \(w=[a^i]\), we write a plasticity rule \(E/w\rightarrow (\alpha \mu )\xi s\) in the simpler form \(w\rightarrow (\alpha \mu )\xi s\). Also, in the particular case when \(L(E)=\{a^i\}\) and \(w=[a^i]\), we write a plasticity rule \(E/w\rightarrow (-\mu )\) in the simpler form \(w\rightarrow (-\mu )\). As standard for spiking neural P systems, the rules are selected and applied in nondeterministic manner by each neuron, and all neurons work concurrently and synchronously (according to a global clock).
Example 8
We consider two \({\mathcal {L}}_{snp}^{sp}\) programs \(\pi ^{sp}_1\) and \(\pi ^{sp}_2\) based on an example from [4], and a simpler \({\mathcal {L}}_{snp}^{sp}\) program \(\pi ^{sp}_0\).
-
(1)
The program \(\pi ^{sp}_1\) is given by \(\pi ^{sp}_1=(D^{sp}_1,s^{sp}_1)\), where the statement \(s^{sp}_1\) is
$$\begin{aligned} {\ \ s^{sp}_1 =(\,{\textsf{snd}}\,\{N_1\}\,a\,)^2\parallel (\,{\textsf{snd}}\,\{N_3\}\,a\,)\parallel \,{\textsf{init}}\,\{N_2,N_{A_1},N_{A_2}\}\,,} \end{aligned}$$and the declaration \(D^{sp}_1\in NDs\) is given by
-
\(D^{sp}_1\,=\,\,\,\textsf{neuron}\,N_0\,\{\,r_{\epsilon }\,\mid \,\{N_1,N_2,N_3,N_{A_1},N_{A_2}\}\,\},\)
-
\(\,\,\textsf{neuron}\,N_1\,\{\,a^2/[a]\rightarrow (+1)\{N_2,N_3\}a,[a]\rightarrow (-1)\,\mid \,\{\}\,\},\)
-
\(\,\,\textsf{neuron}\,N_2\,\{\,[a]\rightarrow a\,\mid \,\{N_{A_1},N_{A_2}\}\,\},\)
-
\(\,\,\textsf{neuron}\,N_3\,\{\,[a]\rightarrow a\,\mid \,\{N_0\}\,\},\)
-
\(\,\,\textsf{neuron}\,N_{A_1}\,\{\,[a]\rightarrow a\,\mid \,\{N_1\}\,\},\)
-
\(\,\,\textsf{neuron}\,N_{A_2}\,\{\,[a]\rightarrow a\,\mid \,\{N_1\}\,\}.\)
The \({\mathcal {L}}_{snp}^{sp}\) programs \(\pi ^{sp}_1\) implements the spiking neural P system with structural plasticity \(\Pi _{ex}\) given in [4, Section 4, Figure 1]. This system \(\Pi _{ex}\) comprises five neurons \(\sigma _1, \sigma _2, \sigma _3, \sigma _{A_1}\) and \(\sigma _{A_2}\), implemented in our program \(\pi ^{sp}_1\) by the neurons \(N_1, N_2, N_3, N_{A_1}\) and \(N_{A_2}\), respectively. The statement \(s^{sp}_1\) produces the initial configuration in which neuron \(N_1\) contains 2 spikes, neuron \(N_3\) contains 1 spike and neurons \(N_2\), \(N_{A_1}\) and \(N_{A_2}\) are empty (each containing 0 spikes). \(N_3\) is the output neuron. Neuron \(N_0\) (which is automatically initialized upon system start up) plays the role of the environment, receiving the spikes produced by the output neuron \(N_3\) (as in Example 3). Following the convention that the result is given by the difference between the first two time instances when the output neuron spikes [4, 15], the system \(\Pi _{ex}\) presented in [4] generates in a nondeterministic manner the sequence \(1,4,7,10,\ldots \) (namely, all numbers \(3m+1\) for \(m\ge 0\)). Our \({\mathcal {L}}_{snp}^{sp}\) program \(\pi ^{sp}_1\) captures accurately this behaviour, fact illustrated by the experiments presented in Sect. 4.2.
-
-
(2)
The program \(\pi ^{sp}_2\in {\mathcal {L}}_{snp}^{sp}\) is almost identical to \(\pi ^{sp}_1\); the single difference is that the two plasticity rules in neuron \(N_1\) are replaced by a single plasticity rule \([a^2]\rightarrow (\pm 1)\{N_2,N_3\}a\). More precisely, \(\pi ^{sp}_2\) is given by \((D^{sp}_2,s^{sp}_2)\), where \(s^{sp}_2=s^{sp}_1\) and the declaration \(D^{sp}_2\in NDs\) is given by
-
\(D^{sp}_2\,= \,\,\textsf{neuron}\,N_0\,\{\,r_{\epsilon }\,\mid \,\{N_1,N_2,N_3,N_{A_1},N_{A_2}\}\,\},\)
-
\(\,\,\textsf{neuron}\,N_1\,\{\,[a^2]\rightarrow (\pm 1)\{N_2,N_3\}a\,\mid \,\{\}\,\},\)
-
\(\,\,\textsf{neuron}\,N_2\,\{\,[a]\rightarrow a\,\mid \,\{N_{A_1},N_{A_2}\}\,\},\)
-
\(\,\,\textsf{neuron}\,N_3\,\{\,[a]\rightarrow a\,\mid \,\{N_0\}\,\},\)
-
\(\,\,\textsf{neuron}\,N_{A_1}\,\{\,[a]\rightarrow a\,\mid \,\{N_1\}\,\},\)
-
\(\,\,\textsf{neuron}\,N_{A_2}\,\{\,[a]\rightarrow a\,\mid \,\{N_1\}\,\}.\)
The \({\mathcal {L}}_{snp}^{sp}\) program \(\pi ^{sp}_2\) implements a variant of the spiking neural P system with structural plasticity \(\Pi _{ex}\) given in [4, Section 4, Figure 1], where the two plasticity rules with \(\alpha =+\) and \(\alpha =-\) are replaced by a single plasticity rule with \(\alpha =\pm \). The experiments performed in random trace semantics show that the two programs \(\pi ^{sp}_1\) and \(\pi ^{sp}_2\) behave the same. When executed in random trace semantics, the program \(\pi ^{sp}_2\) generates in a nondeterministic manner the numbers in the sequence \(1,4,7,10,\ldots \) (the same as \(\pi ^{sp}_1\)).
-
-
(3)
The two \({\mathcal {L}}_{snp}^{sp}\) programs \(\pi ^{sp}_1\) and \(\pi ^{sp}_2\) are designed to generate the numbers \(3m+1\) for \(m\ge 0\). They can only be executed by our interpreter in random trace semantics. Now we present a simple \({\mathcal {L}}_{snp}^{sp}\) program \(\pi ^{sp}_0\) that we verify using our semantic interpreter in all possible traces semantics. The program \(\pi ^{sp}_0\) is given by \((D^{sp}_0,s^{sp}_0)\), where the statement \(s^{sp}_0\) is given by
$$\begin{aligned} {s^{sp}_0 =(\,{\textsf{snd}}\,\{N_1\}\,a\,)\parallel \,{\textsf{init}}\,\{N_2,N_3\}\,,} \end{aligned}$$and the declaration \(D^{sp}_0\in NDs\) are given by
-
\(D^{sp}_0=\,\,\textsf{neuron}\,N_0\,\{\,r_{\epsilon }\,\mid \,\{N_1,N_2,N_3\}\,\},\)
-
\(\,\,\textsf{neuron}\,N_1\,\{\,[a]\rightarrow (\pm 1)\{N_2,N_3\}a\,\mid \,\{\}\,\},\)
-
\(\,\,\textsf{neuron}\,N_2\,\{\,[a]\rightarrow a\,\mid \,\{N_0\}\,\},\)
-
\(\,\,\textsf{neuron}\,N_3\,\{\,[a]\rightarrow a\,\mid \,\{N_0\}\,\}\)
By executing statement \(s^{sp}_0\), the program \(\pi ^{sp}_0\) produces the initial configuration in which neuron \(N_1\) contains 1 spike and neurons \(N_2\) and \(N_3\) are empty (containing 0 spikes). After the initialization step, neuron \(N_1\) contains 1 spike, and so it can apply its plasticity rule \([a]\rightarrow (\pm 1)\{N_2,N_3\}a\). Since \(\alpha =\pm \) and
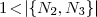 , neuron \(N_1\) creates nondeterministically one synapse (either \(N_1\mapsto N_2\) or \(N_1\mapsto N_3\)), and transmits one spike to either neuron \(N_2\) or \(N_3\). In the next step, the newly created synapse is removed and the receiving neuron (either \(N_2\) or \(N_3\)) applies its firing rule (\([a]\rightarrow a\)), transmitting one spike to neuron \(N_0\). The behaviour of the program \(\pi ^{sp}_0\) is illustrated by an experiment presented in Sect. 4.1.
, neuron \(N_1\) creates nondeterministically one synapse (either \(N_1\mapsto N_2\) or \(N_1\mapsto N_3\)), and transmits one spike to either neuron \(N_2\) or \(N_3\). In the next step, the newly created synapse is removed and the receiving neuron (either \(N_2\) or \(N_3\)) applies its firing rule (\([a]\rightarrow a\)), transmitting one spike to neuron \(N_0\). The behaviour of the program \(\pi ^{sp}_0\) is illustrated by an experiment presented in Sect. 4.1. -
4.1 Interpreter for \({\mathcal {L}}_{snp}^{sp}\) working with all possible traces
A semantic interpreter for the language \({\mathcal {L}}_{snp}^{sp}\) (similar to the semantic interpreters presented in previous sections) is available online at [34] as file jmc23-snp-sp.hs. The interpreter contained in file jmc23-snp-sp.hs works in all possible traces semantics, where type R is a synonym for type P. Since the interpreter is similar to the previous ones, we present only what is different.

The type Rule implements the class \(Rule\) of rules given in Definition 7, and the type Alpha implements the set \(\{+,\pm ,{\mp }\}\).
Specific to the language \({\mathcal {L}}_{snp}^{sp}\) is that a value of type OS (given by data OS = OS Nn Xi W) describes the current observable state of a neuron. Also, the rules of the language \({\mathcal {L}}_{snp}^{sp}\) are without delays, and the connections between neurons can be modified dynamically. A value of type OS is a construct (OS nn xi w), where nn::Nn is a neuron name, w::W is the multiset of spikes currently contained in the neuron, and xi::Xi is a set of neuron names describing the current connections (neighbours) of the neuron with name nn.

The structure of an asynchronous continuation is specific to the language \({\mathcal {L}}_{snp}^{sp}\), where the connections between neurons can be changed dynamically. In this language, an asynchronous continuation of type K is a list of tuples (nn,xi,w,ns), where nn::Nn is a neuron name, xi::Xi is a set of neuron names describing the current connections (i.e., the current neighbours) of the neuron with name nn, w::W is the multiset of spikes currently contained in the neuron, and ns:NS is the current state of the neuron. A value of type NS describes the (current) state of a neuron. We recall that a neuron applying a plasticity rule with \(\alpha \in \{\pm ,{\mp }\}\) at time t, cannot apply another rule at times t and \(t+1\). The constructs (NSplus mu xi s) and (NSminus mu) (where mu::Int, xi::Xi and s::S) are used in our implementation to model the temporary state of a neuron which executes a plasticity rule with \(\alpha \in \{\pm ,{\mp }\}\).
The definitions of the scheduler function sfun and predicate hlt (verifying whether the system reached a halting configuration) depend on the rules that are specific to spiking neural P systems with plasticity rules. Thus, the implementation of the scheduler function sfun and the implementation of the predicate hlt are also specific to the semantic interpreter for the language \({\mathcal {L}}_{snp}^{sp}\).
The complete implementation of the semantic interpreter for the language \({\mathcal {L}}_{snp}^{sp}\) is available online in the public repository [34] as file jmc23-snp-sp.hs. The Haskell implementations of programs \(\pi ^{sp}_1\), \(\pi ^{sp}_2\) and \(\pi ^{sp}_0\) (of Example 8) are stored in the variables pi1sp, pi2sp and pi0sp, respectively. Among these programs, only the program \(\pi ^{sp}_0\) can be verified using all possible traces semantics (the programs \(\pi ^{sp}_1\) and \(\pi ^{sp}_2\) can generate an infinite number of different execution traces, and so they can be executed only in random trace semantics). The \({\mathcal {L}}_{snp}^{sp}\) program \(\pi ^{sp}_0\) behaves as explained in Example 8(3).
Running the program \(\pi ^{sp}_0\) with (opsem pi0sp), we get the following output:

The output produced by our interpreter shows for each neuron both the content of the neuron and its current connections (synapses). For readability, in the experiments presented here is displayed only the list of connections (the names of the neighbouring neurons) for the neurons whose connections change at runtime. In this example, only the connections of neuron \(N_1\) (implemented by the construct (Nn "n1")) change during the execution of the program; for other neurons (whose connections do not change), we replace the list of connections by the character ’_’.
4.2 Interpreter for \({\mathcal {L}}_{snp}^{sp}\) based on random choice
We present an interpreter for the language \({\mathcal {L}}_{snp}^{sp}\) working in random trace semantics, interpreter available at [34] in the file jmc23-snp-sp-rnd.hs. This interpreter can be obtained from the interpreter presented in Sect. 4.1 using the implementation of the type R presented in Sect. 2.3. Using this interpreter, we can simulate the behaviour of the spiking neural P system with structural plasticity \(\Pi _{ex}\) presented in [4] by the programs \(\pi ^{sp}_1\) and \(\pi ^{sp}_2\) presented in Example 8. At each execution, these programs can produce in a nondeterministic manner a number in the sequence \(1,4,7,10,\ldots \) (i.e., a number \(3m+1\) for \(m\ge 0\)). Since there is an infinite number of possible alternative execution traces, this example can only be verified using our semantic interpreter in random trace semantics. The following experiments show three executions of the program \(\pi ^{sp}_1\) in random trace semantics. The reader can observe that the output neuron \(N_3\) (implemented by (Nn “n3”)) always fires (and produces spikes received by neuron \(N_0\), implemented by (Nn “n0”)) in steps 1 and m, with \(m=2,5,8,11,\ldots \). Following the convention that the number computed by the system is given by the number of steps between the first two consecutive spikes produced by the output neuron, the numbers computed by the program \(\pi ^{sp}_1\) are \(1,4,7,10,\ldots \) (i.e., (\(m-1\)) for \(m=2,5,8,11,\ldots \)).
The experiments confirm the result predicted in [4].



For readability, in the experiments presented here is displayed only the list of connections (the names of the neighbouring neurons) for the neuron \(N_1\) (implemented by (Nn “n1”)) whose connections change at runtime. For other neurons (whose connections do not change), we replace the list of connections by the character ’_’.
According to the experiments performed using our interpreter based on random choice, it is verified that both the programs \(\pi ^{sp}_1\) and \(\pi ^{sp}_2\) compute numbers in the sequence \(1,4,7,10,\ldots \). Even the programs \(\pi ^{sp}_2\) and \(\pi ^{sp}_1\) are similar, they are not identical: the program \(\pi ^{sp}_2\) is obtained from program \(\pi ^{sp}_1\) by replacing the two plasticity rules using \(\alpha =+\) and \(\alpha =-\) with a single plasticity rule using \(\alpha =\pm \).
5 Conclusion
There exist several software tools related to P systems [32]. Among them, the general framework P-Lingua allows to define a unified standard for different classes of P systems: cell-like P systems [14], tissue-like P systems [18] and spiking neural P systems [17]. Recently, P-Lingua was redesigned to provide improved generic support for membrane computing [23]. The development of formal frameworks [31] and software simulators [12] for spiking neural P systems represent recent research.
In this paper we presented implementations of the spiking neural P systems, spiking neural P systems with inhibitory rules and spiking neural P systems with structural plasticity. These implementations were derived from their operational semantics. For each implementation it was presented a formal syntax and an operational semantics; these semantics were translated then in the functional programming language Haskell. Being based on a rigorous approach, these implementations can be used for the verification of various properties for spiking neural P systems and their variants.
As related work, we mention [9] in which is presented a semantic interpreter of a language similar to \({\mathcal {L}}_{snp}^{\alpha }\). However, the semantic interpreter presented in [9] is designed following the discipline of denotational semantics [26], in contrast with the current approach in which we presented semantic interpreters for the languages \({\mathcal {L}}_{snp}^{\alpha }\), \({\mathcal {L}}_{snp}^{ir}\) and \({\mathcal {L}}_{snp}^{sp}\) derived from operational semantics. Spiking neural P systems are currently employed to solve problems in large and real-life applications [13]; the development of semantic interpreters providing simulation and verification support for such complex applications will be considered in our future research. In future work we also intend to develop semantic interpreters for various other types of spiking neural P systems, including those with rules on synapses [27], delay on synapses [29], communication on request [19] and learning functions [28].
The ingredients used in this work (namely operational semantics and Haskell) are quite general. We are confident that they can be used to develop prototype implementations for a wide class of spiking neural P systems.
Notes
\([a]\) is the multiset containing only (one occurrence of) the spike a.
The neuron name \(N_0\) is reserved (as name of the first neuron in any valid \(D\in NDs\)).
In [8], both an operational semantics and a denotational semantics for \(\textsf{SNP}\) calculus are presented; it is used the term resumption as an operational counterpart of the term continuation; in this article we use (only) the term continuation.
vartheta decreases by 1 with each clock tick, and becomes 0 when the neuron moves to the open status.
The constructs (Snd xi1 a) and (Init xi1) implement elementary statements of the form \(\,{\textsf{snd}}\,\xi _1\,a\,\) and \(\,{\textsf{init}}\,\xi _1\,\) given in Definition 2.
A spiking neural P system with inhibitory rules can be represented as a graph with inhibitory arcs [22]. For each \(j=1,\ldots ,m\), there is an arc between neurons \(N_j\) and N corresponding to an inhibitory synapse.
\(\lnot \) is the logical negation operator; the notations were presented in Remark 1.
\(\xi {\setminus }pres(N)\) is the set theoretic difference between sets \(\xi \) and \(pres(N)\); we use the same symbol \(\setminus \) to represent the multiset difference operator, because it is always clear from the context whether the arguments of this operator \(\setminus \) are sets or multisets.
References
Alexandru, A., & Ciobanu, G. (2015). Mathematics of multisets in the Fraenkel–Mostowski framework. Bulletin Mathematique de la Societe des Sciences Mathematiques de Roumanie, 58(106), 3–18.
Arroyo, F., Luengo, C., Baranda, A. V., & de Mingo, L. (2002). A software simulation of transition P systems in Haskell. Lecture Notes in Computer Science, 2597, 19–32.
Bonchiş, C., Ciobanu, G., Izbaşa, C., & Petcu, D. (2005). A web-based P systems simulator and its parallelization. Lecture Notes in Computer Science, 3699, 58–69.
Cabarle, F. G., Adorna, H. N., Perez-Jimenez, M. J., & Song, T. (2015). Spiking neural P systems with structural plasticity. Neural Computing and Applications, 26(8), 1905–1917.
Ciobanu, G., & Paraschiv, D. (2002). A P system software simulator. Fundamenta Informaticae, 49, 61–66.
Ciobanu, G., & Todoran, E. N. (2014). Continuation semantics for asynchronous concurrency. Fundamenta Informaticae, 131(3–4), 373–388.
Ciobanu, G., & Todoran, E. N. (2019). A semantic investigation of spiking neural P systems. Lecture Notes in Computer Science, 11399, 108–130.
Ciobanu, G., & Todoran, E. N. (2022). A process calculus for spiking neural P systems. Information Sciences, 604, 298–319.
Ciobanu, G., & Todoran, E. N. (2023). Spiking neural P systems and their semantics in Haskell. Natural Computing, 22(1), 41–54
Ciobanu, G., & Todoran, E. N. (2022). Variants of spiking neural P systems and their operational semantics in Haskell. In 23rd Int’l Conference on Membrane Computing, CMC
de Bakker, J. W., & de Vink, E. P. (1996). Control flow semantics. MIT Press.
Dupaya, A. G., Galano, A. C., Cabarle, F. G., de la Cruz, R. T., Ballesteros, K. J., & Lazo, P. P. (2022). A web-based visual simulator for spiking neural P systems. Journal of Membrane Computing, 4(1), 21–40.
Fan, S., Paul, P., Wu, T., Rong, H., & Zhang, G. (2020). On applications of spiking neural P systems. Applied Sciences, 10, 7011.
García-Quismondo, M., Gutiérrez-Escudero, R., Martínez-del-Amor, M. A., Orejuela-Pinedo, E., & Pérez-Hurtado, I. (2009). P-Lingua 2.0: A software framework for cell-like P systems. International Journal of Computers Communication & Control, 4, 234–243.
Ionescu, M., Păun, G., & Yokomori, T. (2006). Spiking neural P systems. Fundamenta Informaticae, 71, 279–308.
Ionescu, M., Păun, G., Pérez-Jiménez, M. J., & Rodriguez-Patón, A. (2011). Spiking neural P systems with several types of spikes. International Journal of Computers & Control, 6, 647–655.
Macías-Ramos, L. F., Pérez-Hurtado, I., García-Quismondo, M., Valencia-Cabrera, L., Pérez-Jiménez, M. J., & Riscos-Núñez, A. (2012). A P-Lingua based simulator for spiking neural P systems. Lecture Notes in Computer Science, 7184, 257–281.
Martínez-del-Amor, M. A., Pérez-Hurtado, I., Pérez-Jiménez, M. J., & Riscos-Núñez, A. (2010). A P-Lingua based simulator for tissue P systems. Journal of Logic and Algebraic Programming, 79, 374–382.
Pan, L., Păun, Gh., Zhang, G., & Neri, F. (2017). Spiking neural P systems with communication on request. International Journal of Neural Systems, 27(8), 1750042.
Păun, Gh. (2002). Membrane computing. An introduction. Springer.
Păun, G., Rozenberg, G., & Salomaa, A. (Eds.). (2010). Handbook of membrane computing. Oxford University Press.
Peng, H., Li, B., Wang, J., Song, X., Wang, T., Valencia-Cabrera, L., Perez-Hurtado, I., Riscos-Nunez, A., & Perez-Jimenez, M. J. (2020). Spiking neural P systems with inhibitory rules. Knowledge-Based Systems, 188, 105064.
Pérez-Hurtado, I., Orellana-Martín, D., Martínez-del-Amor, M. A., Valencia-Cabrera, L., & Riscos-Núñez, A. (2022). A new P-Lingua toolkit for agile development in membrane computing. Information Sciences, 587, 1–22.
Plotkin, G. (2004). A structural approach to operational semantics. Journal of Logic and Algebraic Programming, 60–61, 17–139.
Rozenberg, G., & Salomaa, A. (Eds.). (1998). Handbook of formal languages (Vol. 3). Springer.
Schmidt, D. A. (1986). Denotational semantics: A methodology for language development. Allyn & Bacon.
Song, T., Pan, L., & Păun, Gh. (2014). Spiking neural P systems with rules on synapses. Theoretical Computer Science, 529, 82–95.
Song, T., Pan, L., Wu, T., Zheng, P., Wong, M. L. D., & Rodríguez-Patón, A. (2019). Spiking neural P systems with learning functions. IEEE Transactions on Nanobioscience, 18(2), 176–190.
Song, X., Valencia-Cabrera, L., Peng, H., Wang, J., & Pérez-Jiménez, M. J. (2021). Spiking neural P systems with delay on synapses. International Journal of Neural Systems, 31(1), 2050042.
Todoran, E. N. (2000). Metric semantics for synchronous and asynchronous communication: A continuation-based approach. Electronic Notes in Theoretical Computer Science, 28, 101–127.
Verlan, S., Freund, R., Alhazov, A., Ivanov, S., & Pan, L. (2020). A formal framework for spiking neural P systems. Journal of Membrane Computing, 2(4), 355–368.
Zhang, G., Pérez-Jiménez, M. J., Riscos-Núñez, A., Verlan, S., Konur, S., Hinze, T., & Gheorghe, M. (2021). Membrane computing models: Implementations. Springer.
Zhou, N., Peng, H., Wang, J., Yang, Q., & Luo, X. (2022). Computational completeness of spiking neural P systems with inhibitory rules for generating string languages. Theoretical Computer Science, 920, 64–75.
(2023). Haskell implementation of the operational semantics presented in this paper http://ftp.utcluj.ro/pub/users/gc/eneia/jmc2023
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Ciobanu, G., Todoran, E.N. Variants of spiking neural P systems and their operational semantics in Haskell. J Membr Comput 5, 81–99 (2023). https://doi.org/10.1007/s41965-023-00122-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s41965-023-00122-z



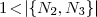 , neuron
, neuron