A formal framework for spiking neural P systems

Abstract

Spiking neural P systems are a class of distributed parallel computing models, inspired by the way in which neurons process information and communicate with each other by means of spikes. In 2007, Freund and Verlan developed a formal framework for P systems to capture most of the essential features of P systems and to define their functioning in a formal way. In this work, we present an extension of the formal framework related to spiking neural P systems by considering the applicability of each rule to be controlled by specific conditions on the current contents of the cells. The main objective of this extension is to also capture spiking neural P systems in the formal framework. Another goal of our extension is to incorporate the notions of input and output. Finally, we also show that in the case of spiking neural P systems, the rules have a rather simple form and in that way spiking neural P systems correspond to vector addition systems where the application of rules is controlled by semi-linear sets.

1 Introduction

Based on the biological background of neurons sending electrical impulses along axons to other neurons, spiking neural P systems were introduced in [17]. In spiking neural P systems, the contents of a cell—a neuron—consists of a number of so-called spikes. The rules assigned to a cell allow for sending information to other neurons in the form of spikes corresponding to electrical impulses, which are summed up in the target cells. The application of the rules depends on the current contents of the neuron and in the general case is described by a filter language (e.g., a regular set).

As inspired from biology, the cell sending out spikes may be closed for a specific time period corresponding to the refractory period of a neuron. During this refractory period, the neuron is closed for new input and cannot get excited—fire—for spiking. As already shown in [14], considering such a delay usually is not needed to obtain the desired results, hence, we will not consider this feature in the following.

Since their introduction, many variants of spiking neural P systems have been considered. As a first example, we cite spiking neural P systems with extended rules [6], which allow the rules to produce more than one spike in each step. Another example are extended spiking neural P systems, which allow the rules to send different numbers of spikes along the axons to different neurons depending on the rule applied in a cell [2].

Cell-like spiking neural P systems reflect the feature of a hierarchical arrangement of neurons in cell-like P systems [36]. Spiking neural P systems with structural plasticity incorporate the idea of self-organization and self-adaptivity from artificial neural networks [3, 4]. Spiking neural P systems with communication on request are inspired by the request-response patterns in parallel cooperating grammar systems [20, 34]. Spiking neural P systems with polarizations are inspired by polarized cell membranes of a neuron [35]. Coupled neural P systems follow Eckhorn’s neuron model [24].

In the basic model of spiking neural P systems, at each step, for each cell with applicable rules, one of the rules nondeterministically is chosen to be applied, while all neurons work simultaneously in the sense that each cell in which a rule can be applied must apply one of the rules applicable in the neuron. This condition for the standard derivation mode of spiking neural P systems—sequential application of rules in each cell, but maximal parallelism on the level of the whole system—may be alleviated by considering asynchronous [5] (any subset of the cells applies a rule) or sequential [13] (only one cell applies a rule) spiking neural P systems.

With regard to the complexity of communication, the systems in [6] allow more than one spike to be sent along an axon, whereas in [2] the number of spikes sent along different axons even depends on the applied rule.

A first overview on results for spiking neural P systems can be found in Chapter 13 of the Handbook of Membrane Computing [26]. A rather extensive bibliography on spiking neural P systems was published in the first volume of the Bulletin of the International Membrane Computing Society 2016, see [22]. A recent survey can be found in [27].

The richness of variants of spiking neural P systems calls for the introduction of a unifying framework, capturing the various possible features on a common formal basis. Such formal groundwork typically ensures that the semantics is consistent across different definitions, and thereby allows for comparing different extensions and ingredients. In [11], a formal framework for P systems was already developed bringing a formal basis for comparing different variants and discussing numerous extensions for P systems, see [7, 9, 10, 12, 30]. Here, we continue this line of research by extending the formal framework to capture several basic features of spiking neural P systems, but also allowing for many other new variants and extensions.

The paper is organized as follows. Section 2 recalls notions from formal language theory. Section 3 introduces the extensions we propose to the formal framework. It contains all necessary definitions (sometimes recalling those from [11]). Section 4 simplifies the notations and the definitions for the case of spiking neural P systems, i.e., using a single letter alphabet. Section 5 shows how different extensions of the model of spiking neural P systems can be expressed in the new framework.

We remark that a preliminary version of this paper was presented in 2019 at the Conference of Membrane Computing (CMC 2019) in Curtea de Argeş [31].

2 Preliminaries

The set of natural numbers, i.e., the set of non-negative integers, is denoted by ${\mathbb {N}}$. Moreover, ${\mathbb {N}}_{\infty }:={\mathbb {N}}\cup \{\infty \}$. The finite set of natural numbers $\{ 1, \ldots ,n\}$ will also be written as [1..n]. We will use the standard notation $2^{[1..n]}$ to denote the set of subsets of numbers from 1 to n.

The set of all finite multisets over the set V is denoted by $V^{\circ }$ and the set of vectors of finite multisets over V of dimension n by $V^{\circ n}$. The set of finite languages over the alphabet T is denoted by $\mathrm{FIN}(T)$, the set of regular languages over the alphabet T by $\mathrm{REG}(T)$. The families of finite and regular languages over arbitrary alphabets are denoted by $\mathrm{FIN}$ and $\mathrm{REG}$, respectively. In general, we use the notation ${\mathscr {F}}(T)$ to specify a family of languages of a specific type over the alphabet T and ${\mathscr {F}}$ to specify the family of languages of that specific type. The corresponding families of multiset languages are denoted by ${{\mathscr {F}}(T)}^{\circ }$ and ${{\mathscr {F}}}^{\circ }$, respectively.

We remark that regular expressions are a way to specify regular languages. The regular expressions over an alphabet T are denoted by $\mathrm{REGEX}(T)$. For any $E\in \mathrm{REGEX}(T)$, $L(E) \subseteq T^*$ denotes the regular language over T corresponding to the regular expression E, whereas ${L}^{\circ }(E)\subseteq {T}^{\circ }$ denotes the corresponding regular multiset language. We remark that if $|T|=1$, then ${L}^{\circ }(E)$ can be identified with L(E).

3 The definition of the formal framework

We extend the definitions from [11] in order to be able to handle control conditions, as for example the regular conditions used in the standard definition of many variants of spiking neural P systems. We also remark that our definition will only include spiking neural P systems without delays. While it may not be too difficult to integrate the notion of delay in the definition, it makes all corresponding notations much more complex. Not considering delays is not very restrictive, as it was shown in [14] that for any spiking neural P system with delays there exists an equivalent spiking neural P system without delays. We would like to notice that the corresponding proofs are not constructive, so in practice it might be extremely difficult to transform a system with delays into a system without delays. Another remark concerns the use of forgetting rules. They are special in the spiking framework, as normally any spiking rule should produce at least one spike, whereas forgetting rules just consume the finite number of spikes present in the underlying neuron. In our framework, there is no such restriction, so forgetting rules just correspond to rules with empty right-hand side.

3.1 Basic structure

We start with a new definition of an interaction rule.

Definition 1

Let V be an alphabet and $n>0$. An interaction rule of dimension n is defined as

$$\begin{aligned} \left( X\rightarrow Y;K\right) \end{aligned}$$

where $X=\left( X_{1},\ldots ,X_{n}\right)$, $Y=\left( Y_{1},\ldots ,Y_{n}\right)$, $X_{i},Y_{i}\in {V}^{\circ }$, $1\le i\le n$, are n-vectors of multisets over V, and $K\subseteq {{V}^{\circ }}^n$, i.e., K consists of n-vectors with components from ${V}^{\circ }$.

Remark 1

In spiking neural P systems, the control condition K usually is the Cartesian product of independent regular sets $K_{i}\subseteq {V}^{\circ }$, where each $K_{i}$ is given by a regular expression $E_i \in \mathrm{REGEX}(V)$ such that ${L}^{\circ }(E_i)=K_{i}$, $1\le i\le n$.

Moreover, in that case, the rule $\left( X\rightarrow Y;K\right)$ can be written as

$$\begin{aligned} i: \left( X_i\rightarrow Y;K_i\right) \end{aligned}$$

because each rule is assigned to a specific neuron i, i.e., we are only interested in the contents of neuron i and whether this contents fulfills the control condition to be in ${L}^{\circ }(E_i)$ or not.

Since in most of the cases the corresponding vectors are sparse, we will also use the notation

$$\begin{aligned} ( 1, X_{1}) \ldots (n, X_{n}) \rightarrow ( 1, Y_{1}) \ldots (n, Y_{n}) ;(1, K_{1}) \ldots (n, K_{n}) \end{aligned}$$

for a rule $\left( X\rightarrow Y;K\right)$. For any $1\le i\le n$, whenever possible, we will omit $(i,K_{i})$, if $K_i={{\mathbb {N}}}$, and we will also not indicate $(i,X_{i})$ or $(i,Y_{i})$ when such a multiset is empty.

Remark 2

To keep computability, in spiking neural P systems, the control condition K usually is assumed to be a recursive set; compare this with the concepts of control sets elaborated in [8] as part of a general framework for regulated rewriting.

Next, we adapt the definition of a network of cells from [11] in order to incorporate specific concepts for control languages as well as for input and output:

Definition 2

An ${\mathscr {F}}$-controlled network of cells of degree $n\ge 1$ is a construct:

$$\begin{aligned} \varPi =\left( n,V,w,c_{\mathrm{in}},c_{\mathrm{out}},R\right) \end{aligned}$$

where

• 1. n is the number of cells;

• 2. V is a finite alphabet;

• 3. $w=\left( w_{1},\ldots ,w_{n}\right)$, where $w_{i}\in {V}^{\circ }$, for $1\le i\le n$, is the finite multiset initially assigned to cell i;

• 4. $c_{\mathrm{in}}\subseteq \{1,\ldots ,n\}$ is the set of input cells;

• 5. $c_{\mathrm{out}}\subseteq \{1,\ldots ,n\}$ is the set of output cells;

• 6. R is a finite set of interaction rules of the form given in Definition 1;

• 7. ${\mathscr {F}}$ is a family of control languages containing at least all the sets K appearing in the rules in R.

In most variants of P systems, the notion of environment is used, which can be seen as an unlimited storage of objects of some type. At the same time, the case of spiking neural P systems is a notorious example of a variant of P systems that does not use this concept. Since our aim is to consider an extension of the formal framework introduced in [11] we give the corresponding definitions in order to complete the picture.

Definition 3

An ${\mathscr {F}}$-controlled network of cells of degree $n\ge 1$ with environment is a construct:

$$\begin{aligned} \varPi _{{\textsf {Inf}}} =( \varPi ,{{{\textsf {Inf}}}}) \end{aligned}$$

where

• 1. $\varPi$ is an ${\mathscr {F}}$-controlled network of cells of degree n,

• 2. ${\textsf {Inf}}=\left( {\textsf {Inf}}_{1},\ldots ,{\textsf {Inf}}_{n}\right)$, ${\textsf {Inf}}_{i}\subseteq V$, for $1\le i\le n$, is the set of symbols occurring infinitely often in cell i (in most of the cases, only one cell, called the environment, will contain symbols occurring with infinite multiplicity);

We now adapt the definition of a configuration from [11]:

Definition 4

Consider an ${\mathscr {F}}$-controlled network of cells $\varPi =\left( n,V,w,c_{\mathrm{in}},c_{\mathrm{out}},R\right)$. Then a configuration C of $\varPi$ is an n-tuple $\left( u_{1},\ldots ,u_{n}\right)$ of finite multisets over V with $u_{i}\in {V}^{\circ }$, $1\le i\le n$.

When using the environment, as in [11], the definition is slightly different:

Definition 5

Consider an ${\mathscr {F}}$-controlled network of cells with environment:

$$\begin{aligned} \varPi _{{\textsf {Inf}}} =\left( (n,V,w,c_{\mathrm{in}},c_{\mathrm{out}},R), {\textsf {Inf}}\right) . \end{aligned}$$

A full configuration C of $\varPi _{{\textsf {Inf}}}$ is an n-tuple $\left( u_{1},\ldots ,u_{n}\right)$ of (possibly) infinite multisets over V with $u_{i}\in {V}^{\circ }\cup V^{ \{\infty \} }$, $1\le i\le n$.

We will also consider the configuration $\varPi _{{\textsf {fin}}} = \left( u_{1}',\ldots ,u_{n}'\right)$ as the finite part of the full configuration of $\varPi _{{\textsf {Inf}}}$, i.e., satisfying $u_{i}=u_{i}'\cup {{\textsf {Inf}}_{i}}^{\infty }$ and $u_{i}'\cap {{\textsf {Inf}}_{i}}=\emptyset$, $1\le i\le n$.

3.2 Rule application and derivation modes

The next definition defines the applicability of a rule, again adapting the corresponding definition from [11] by replacing permitting and forbidding conditions by control languages.

Definition 6

We say that an interaction rule $r=\left( X\rightarrow Y;K\right)$ is eligible for the configuration C with $C=(u_{1},\ldots {},u_{n})$ if and only if for all i, $1\le i\le n$, we have

• $X_{i}\subseteq u_{i}$ ($X_{i}$ is a submultiset of $u_{i}$) and

• $u_{i}\in K_{i}$ ($u_{i}$ belongs to the control language $K_{i}$).

When using environment, the eligibility condition should be completed by an additional item: $u_{i}\cap \left( V-\mathrm{Inf}_{i}\right) \ne \emptyset$, for at least one i, $1\le i\le n$. This explicitly forbids to apply a rule that uses infinite symbols only in its left-hand side, thus allowing for properly defining the applicability condition for unbounded derivation modes. However, the classical spiking derivation mode is bounded, disallowing parallelism inside a neuron (as discussed later), hence, in such a particular case this additional requirement is not needed, and even rules with empty left-hand side make sense.

The application of a group of rules and the definition of the derivation modes can be taken over from [11] as well; some important details are recalled below.

Definition 7

Let $\varPi$ be an ${\mathscr {F}}$-controlled network of cells and C be a configuration over $\varPi$. Let $R'$ be a multiset of rules from $Eligible(\varPi ,C)$, i.e., a multiset of eligible rules. Moreover, let

$$\begin{aligned} X=\sum _{(X_r\rightarrow Y_r;K_r)\in R'}X_r. \end{aligned}$$

If $X\subseteq C$, we say that the multiset of rules $R'$ is applicable to C.

Hence, in order for a multiset of rules to be applicable, each rule should be eligible, and moreover, there should be enough objects in the configuration to cover the sum of all left-hand sides of the rules in $R'$.

The set of all multisets of rules applicable to C is denoted by $Appl\left( \varPi ,C\right)$. It is clear that in general the cardinality of this set may be greater than one, i.e., usually for a configuration C there are several different multisets of rules that can be applied to C. In particular, for a multiset of rules $R'$ any submultiset $R''\subseteq R'$ also belongs to $Appl(\varPi ,C)$.

Example 1

Let $V=\{a,b,c\}$ and $n=3$. Consider rule $r:(X\rightarrow Y; K)$, where $X=(a,b,\emptyset )$, $Y=(\emptyset ,\emptyset ,c)$ and $K=(K_1, K_2, K_3)$, where $K_1=L^\circ ((a^2)^*)$, $K_2=L^\circ (b(b^2)^*)$ and $K_3=\overline{L^\circ (c^+)}$. Then r is applicable only in configurations having an even number of a’s in cell 1, an odd number of b’s in cell 2 and having no symbols c in cell 3.

The notion of a derivation mode allows for specifying which types of multisets of rules we are interested in for the computation.

Definition 8

A derivation mode $\delta$ is a restriction of the set of multisets of applicable rules. For an ${\mathscr {F}}$-controlled network of cells and C being a configuration over $\varPi$, in general

$$\begin{aligned} \mathrm{Appl}\left( \varPi ,C,\delta \right) \subseteq \mathrm{Appl}(\varPi ,C) \end{aligned}$$

denotes the set of multisets of rules in $\varPi$ applicable to the configuration C according to the derivation mode $\delta$.

The derivation mode acts like a filter allowing for keeping only multisets with specific properties. The simplest way to define a derivation mode is using a set restriction.

In that sense, the simplest mode is the sequential derivation mode (seq) which allows the application of a single rule only:

$$\begin{aligned} \mathrm{Appl}(\varPi ,C,\mathrm{seq}) = \{R\in \mathrm{Appl}(\varPi ,C)\mid |R| = 1\}. \end{aligned}$$

On the other hand, a derivation mode used in many variants of P systems is the maximally parallel derivation mode max, according to [11] defined as follows:

$$\begin{aligned} \mathrm{Appl}(\varPi ,C,\mathrm{max})= & {} \{R\in \mathrm{Appl}(\varPi ,C)\mid \not \exists R'\in \mathrm{Appl}(\varPi ,C) \\&\quad {{\text {such that }}} R'\supset R\}. \end{aligned}$$

The traditional derivation mode used in spiking P systems can be interpreted as using a special derivation mode called $\mathrm{min}_1$ in [11].

We start with the rules being grouped in partitions; in spiking neural P systems each partition normally corresponds to the union of rules from one neuron. In the derivation mode $min_1$, from each partition a single rule is taken, whereas as many rules as possible from different partitions have to be chosen. In fact this means that on the level of the cells we apply rules in a sequential way, whereas seen from the level of the system the partitions have to be used in a maximal way. This is already emphasized in the first paper on spiking neural P systems [17].

Now let us suppose that the set of rules R contains n partitions (neurons) denoted by $R_i$, $1\le i\le n$. Then the derivation mode $min_1$ is defined as follows:

$$\begin{aligned}&\mathrm{Appl}(\varPi ,C,\mathrm{min}_1) \\&\quad = \{ R\in \mathrm{Appl}(\varPi ,C) \mid |R\cap R_i|\le 1 {{\text { for all }}} 1\le i\le n {{\text { and }}}\\&\qquad \not \exists R'\in \mathrm{Appl}(\varPi ,C) {{\text { such that }}} R'\supset R {\text { and }}\\&\qquad |R'\cap R_i|\le 1 \text { for all } 1\le i\le n\}. \end{aligned}$$

We remark that if one considers a different partitioning, where each rule belongs to a different partition (hence there is one rule per partition), then the corresponding $\mathrm{min}_1$ derivation mode is called set-maximal (or also flat) derivation mode [21, 32].

Definition 9

In the following, an ${\mathscr {F}}$-controlled network of cells of degree n working over the alphabet V in the derivation mode $\delta$ is written as

$$\begin{aligned} \varPi '=\left( \varPi ,\delta \right) =\left( n,V,w,c_{\mathrm{in}},c_{\mathrm{out}},R,\delta \right) \end{aligned}$$

with $\varPi =\left( n,V,w,c_{\mathrm{in}},c_{\mathrm{out}},R\right)$ being as in Definition 2.

The class of all ${\mathscr {F}}$-controlled networks of cells of degree n working over the alphabet V in the derivation mode $\delta$ is denoted by

$$\begin{aligned} {{\mathsf {N}}{\mathsf {C}}}{(}n,V,{\mathscr {F}},\delta ). \end{aligned}$$

3.3 Computation and input/output

In [11], the computation of a network of cells is performed as a sequence of applications of applicable multisets of rules, starting from some initial configuration, until a halting condition is met, for example, the standard total halting, when no rule is applicable anymore. In the case of spiking neural P systems and the generalized model of ${\mathscr {F}}$-controlled networks of cells as considered in this paper, also a transducer-like strategy is used to transform an input into an output. Since the definitions from [11] cannot handle this aspect, we now present a different notion of computation.

First, we adapt the definition from [11] for the result of the application of a multiset of rules.

Definition 10

Consider a network of cells

$$\begin{aligned} \varPi '=\left( \varPi ,\delta \right) =\left( n,V,w,c_{\mathrm{in}},c_{\mathrm{out}},R,\delta \right) \end{aligned}$$

from ${{\mathsf {N}}{\mathsf {C}}}{(}n,V,{\mathscr {F}},\delta )$ as well as a configuration C over $\varPi '$ and a multiset of rules $R^{\prime }\in \mathrm{Appl}\left( \varPi ,C,\delta \right)$. We define the configuration being the result of applying $R^{\prime }$ to C as

$$\begin{aligned}&\mathrm{Apply}\left( \varPi ',C,R^{\prime }\right) \\&\quad =\left( C - \sum _{(X_r\rightarrow Y_r;K_r)\in R'}X_r + \sum _{(X_r\rightarrow Y_r;K_r)\in R'}Y_r \right) \end{aligned}$$

Now, we have to elaborate on the notion of a computation in $\varPi '$. In an informal way, it starts with the initial configuration, and in each step $t\ge 0$ it may use the contents of the input cells, which is “fed” by a (recursive) function ${\mathsf{Input}}$, and in each step it (possibly) also produces a result using a recursive function ${\mathsf{Output}}$. For traditional variants of P systems the input function is either empty except at the beginning of a computation (no input is fed into the system during the computation) or very restricted with only a bounded number of symbols fed into the input cells during a sequence of computation steps. The output function will monitor the applicability of rules and then will yield a result when no rule is applicable anymore (corresponding to the condition of total halting).

Definition 11

For a given system $\varPi ' \in {{\mathsf {N}}{\mathsf {C}}}{(}n,V,{\mathscr {F}},\delta )$, $\varPi '=\left( \varPi ,\delta \right)$, $\varPi =\left( n,V,w,c_{\mathrm{in}},c_{\mathrm{out}},R\right)$, an input function for $\varPi '$ is a function ${\mathsf{Input}}(\varPi '):{\mathbb {N}}\rightarrow {{V}^{\circ }}^n$ fulfilling the condition that for all $i\notin c_{\mathrm{in}}$ the component i of the resulting input vector in ${{V}^{\circ }}^n$ has to be the empty multiset, which means that at any time only the input cells can receive an input.

Definition 12

Let $\varPi ' \in {{\mathsf {N}}{\mathsf {C}}}{(}n,V,{\mathscr {F}},\delta )$, $\varPi '=\left( \varPi ,\delta \right)$, $\varPi =\left( n,V,w,c_{\mathrm{in}},c_{\mathrm{out}},R\right)$. Then a computation of $\varPi '$ using an input function ${\mathsf{Input}}(\varPi ')$ is performed as follows:

$$\begin{aligned} C_0&= w + {\mathsf{Input}}(\varPi ')(0)\\ C_{j+1}&= {\mathsf{Input}}(\varPi ')(j+1)+\mathrm{Apply}(\varPi ',C_j,R'),\\&\quad R'\in \mathrm{Appl}(\varPi ,C_j,\delta ) \end{aligned}$$

We remark that due to the definition of the input function ${\mathsf{Input}}(\varPi ')$, the defined computation may be considered as infinite, even if $\mathrm{Appl} (\varPi ,C_j,\delta )$ is empty for some $j\ge 0$. However, in most cases we consider only a finite portion of the computation, basically until no more rules are applicable, in which case the (infinite) remainder of the input sequence is not relevant anymore. Moreover, as already mentioned above, in most cases the input function is assumed to only yield non-empty vectors for a finite number of time steps.

Example 2

The standard variant of the computation used in P systems starts from an initial configuration and iterates the choice and the application of some multiset of rules. In this case, the input function is defined as follows:

For all $t\ge 0$, ${\mathsf{Input}}(\varPi ')(t)= \emptyset _n$, where $\emptyset _n$ denotes the n-vector containing only the empty multiset in every component. We should call this case empty input.

Example 3

In some variants of P systems (e.g., some variants of P automata) as well as in standard variants of spiking neural P systems, the computation starts from an initial configuration and an initial input, and then just iterates the choice and the application of some multiset of rules in each computation step until no rule can be applied anymore. In this case, the input function ${\mathsf{Input}}(\varPi ')$ is defined as follows:

• ${\mathsf{Input}}(\varPi ')(0)$ is the initial input added to the initial vector w, and

• ${\mathsf{Input}}(\varPi ')(t)= \emptyset _n$ for all $t > 0$.

This variant may be called a P system with initial input.

Example 4

A spike train input is an input function ${\mathsf{Input}}(\varPi ')$ satisfying the following property:

$$\begin{aligned} \exists t_1,t_2\ge 0,\ t_1<t_2:\ {\left\{ \begin{array}{ll} {\mathsf{Input}}(\varPi ')(t)\ne \emptyset _n &{} t\in \{t_1,t_2\}\\ {\mathsf{Input}}(\varPi ')(t) = \emptyset _n &{} t\not \in \{t_1,t_2\} \end{array}\right. } \end{aligned}$$

We also say that the value of the input is $t_2-t_1$.

We remark that, according to the definitions given above, also the input cells keep the non-consumed multisets from the previous steps. It is possible to use a different strategy by emptying the input cells in $c_{\mathrm{in}}$ in every step:

For that purpose, we first define an additional function $\pi : {{V}^{\circ }}^{n} \times 2^{[1..n]} \rightarrow {{V}^{\circ }}^{n}$ such that $\pi (X,c)$ empties all components of $X=(X_1,\ldots ,X_n)$ that are not indicated in c (it is similar to a projection, where instead of deleting components their value is set to $\emptyset$); formally:

$$\begin{aligned} \forall 1\le i\le n,\ \pi (X,c)_i = {\left\{ \begin{array}{ll} X_i,&{}\text {if } i\in c\\ \emptyset , &{}\text {otherwise} \end{array}\right. } \end{aligned}$$

We will also use the notation $\pi (X,\lnot c)$ in order to define the application of $\pi$ to the complement of c with respect to [1..n].

Now, we can define a computation with a transient input.

Definition 13

Let $\varPi ' \in {{\mathsf {N}}{\mathsf {C}}}{(}n,V,{\mathscr {F}},\delta )$, $\varPi '=\left( \varPi ,\delta \right)$, $\varPi =\left( n,V,w,c_{\mathrm{in}},c_{\mathrm{out}},R\right)$. Then a computation with transient input of $\varPi '$ is a computation performed as follows using a transient input function ${\mathsf{Input}}(\varPi ')$, $j\ge 0$:

$$\begin{aligned} C_0&= w + {\mathsf{Input}}(\varPi ')(0)\\ C_{j+1}&= {\mathsf{Input}}(\varPi ')(j+1)+ \pi (\mathrm{Apply}(\varPi ',C_j,R'),\lnot c_{\mathrm{in}}),\\&\quad R'\in \mathrm{Appl}(\varPi ,C_j,\delta ) \end{aligned}$$

A system with a transient input is useful for some applications, e.g., for image processing or deep learning, as it becomes simpler to feed the data into the system.

The result of the computation, or the output, is defined as the result of the corresponding output function over the time series of the values of output cells. The output function has a memory and can decide on a value based on the whole history of the computation, which means that the output is a time series, too. Moreover, the output function may need (nearly) the entire description of the system, i.e., the number of cells n, the alphabet V, the set of output cells $c_{\mathrm{out}}$, as well as the derivation mode $\delta$ in order to correctly compute the result(s) of a given computation. Such a complex description is necessary to accommodate generating, accepting and transducer-like output strategies. For concrete cases, the definition of the output may be much simpler.

Definition 14

Consider $\varPi ' \in {{\mathsf {N}}{\mathsf {C}}}{(}n,V,{\mathscr {F}},\delta )$, with $\varPi '=\left( \varPi ,\delta \right)$, $\varPi =\left( n,V,w,c_{\mathrm{in}},c_{\mathrm{out}},R\right)$.

Moreover, let $C=C_0,\ldots ,C_k,\ldots$ be a computation of $\varPi '$ on the sequence of inputs given by an input function ${\mathsf{Input}}(\varPi ')$. Then, let us denote by C(t) the finite sequence of configurations $C_0,\ldots ,C_t$, i.e., $C(t)=C_0,\ldots ,C_t$.

An output function for $\varPi '$ for a computation C is a function ${\mathsf{Output}}(\varPi ',C):{\mathbb {N}}\rightarrow S$ where S is the set containing all possible outputs for computations of $\varPi '$. Such a function yields a possible result in every time step, i.e., ${\mathsf{Output}}(\varPi ',C)(t)$, which in fact, for any $t\ge 0$, can also be considered as the result of the finite computation C(t). We may write this fact as

$$\begin{aligned} R(t)={\mathsf{Output}}(\varPi ',C(t))(t) \end{aligned}$$

There may be many variants how to obtain the result of an (infinite) computation C of $\varPi '$; for example, we may restrict ourselves to finite computations by using an additional condition for transforming an infinite computation to a single result, e.g., we use the result of the output function at the moment at which the computation halts.

Another solution is to use the following convention: we expect the output function to produce only a finite number of non-empty results, i.e., for any computation C there exists a $t_C\ge 0$ such that R(t) is empty for all $t>t_C$. Then the total result obtained by the computation C is just the union of the corresponding values obtained from the first $t_C$ computation steps.

Example 5

A traditional output concept for P systems yields the result in the output cell(s) when a halting configuration is reached (total halting). This can be described using the following output function:

$$\begin{aligned} {\mathsf{Output}}(\varPi ',C(t))(t)= {\left\{ \begin{array}{ll} \pi (C_t,c_{\mathrm{out}}) &{} \text {if } \mathrm{Appl}(\varPi ,C_t,\delta )=\emptyset \\ \emptyset &{} \mathrm{otherwise} \end{array}\right. } \end{aligned}$$

$\pi (C_t,c_{\mathrm{out}})$ still is a vector of dimension n, with only possibly non-empty components i for $i\in c_{\mathrm{out}}$. If instead of $\pi$ we use the projection $\pi _{c_{\mathrm{out}}}: {{V}^{\circ }}^n \rightarrow {{V}^{\circ }}^{|c_{\mathrm{out}}|}$, which projects an n-vector v of multisets over V to a vector of dimension $|c_{\mathrm{out}}|$ only containing the components of v from $c_{\mathrm{out}}$, then all the results are vectors of multisets over V of dimension $|c_{\mathrm{out}}|$. In the simplest case, when $c_{\mathrm{out}}$ designates a single output cell, then the result is just the multiset which is contained in this cell at the end of a halting computation.

Remark 3

In the simplified definition of the output function as described in the example elaborated above, in every computation step we only need to check for a halting condition, and if the halting condition is satisfied then we just collect the results, in most of the cases given by the contents of the output cell(s).

Example 6

One of the traditional output strategies in spiking neural P systems is to count the time difference between two consecutive spikes of the output neuron (using rules that produce spikes). This can be mimicked by using the output function which for each time step $t\ge 0$ checks if in the output cell there is a non-empty contents at time $t_1$ for the first time and a non-empty contents at time $t_2$ for the second time, which means that the output cell is empty for all other time steps $t<t_2, t\ne t_1$. In this case, the result of the computation is the value $t_2-t_1$.

Example 7

Another common output strategy is the decision output, used in acceptor variants of P systems. It is based on checking deterministic computations on a specific input for total halting, but yields only a Boolean value from $\{ {{\mathsf{true}}},{{\mathsf{false}}}\}$, i.e., when at some step there are no more applicable rules, the function yields ${{\mathsf{true}}}$ (in which case we call the computation to be accepting), otherwise it yields ${{\mathsf{false}}}$ (in which case we call the computation to be rejecting). We remark that with such a definition we even need not get a partial recursive function.

4 Spiking neural P systems

In the case of spiking neural P systems the definitions given in the preceding section can be simplified using the observation that the alphabet of the system contains a single object a, also called a spike. In this case, the contents of each cell just corresponds to a natural number, and the whole configuration is an n-vector of natural numbers, i.e., in the following, for any $M\subseteq {{\mathbb {N}}}$ we will not distinguish between a set of multisets over $\{ a \}$ $\{ a^m \mid m\in M\}$ and its corresponding set of natural numbers M.

Moreover, the control sets are regular, which over a one letter alphabet means that they correspond to semi-linear sets of numbers. Hence, in total, a generalized version of traditional spiking neural P systems of degree n thus can be seen as the family of ${REG}^{\circ }(\{ a\})$-controlled networks of cells of degree n working over the alphabet $\{ a\}$, under the derivation mode $\mathrm{min}_{1}(\mathrm{cells})$, where $\mathrm{min}_{1}(\mathrm{cells})$ denotes the derivation mode $\mathrm{min}_{1}$ with the partitions being exactly the rules in each neuron. According to the definitions elaborated in the previous section, spiking neural P systems of degree n are networks of cells in the family ${{\mathsf {N}}{\mathsf {C}}}{(}n,\{ a\},{REG}^{\circ }(\{ a\}),\mathrm{min}_{1}(\mathrm{cells}))$.

Following the restrictions for rules in traditional spiking neural P systems, the rules assigned to a neuron i are of the form

$$\begin{aligned} \left( (\emptyset , \ldots ,X_i,\ldots ,\emptyset ) \rightarrow Y; \left( \{ a\}^*, \ldots ,K_i, \ldots , \{ a\}^*\right) \right) \end{aligned}$$

(1)

where $X_i\in \{ a\}^*$, $Y\in {\{ a\}^*}^n$, $Y_i=\emptyset$ (which indicates that self-loops are not allowed, i.e., the neuron which spikes cannot receive spikes itself), and $K_i\subseteq \{ a\}^*$. Such a specific rule then can be written in a different way with vectors of integer numbers:

$$\begin{aligned} \left( {{\mathbb {N}}}, \ldots ,M_i, \ldots {{\mathbb {N}}}\right) /\left( y_1, \ldots ,-x_i, \ldots , y_n\right) , \end{aligned}$$

(2)

where $X_i=a^{x_i}$, $Y_j=a^{y_j}$, $1\le j\le n$, ($Y_i=\emptyset$ corresponds to $y_i=0$) and $K_i=\{ a^m \mid m\in M_i\}$. We observe that by definition, the only negative value will be $-x_i$, whereas in order to make the rule eligible for an application in a multiset of rules, it is required that $x_i$ does not exceed the number $u_i$ in neuron i and $u_i\in M_i$.

We emphasize that only this very special kind of rules is allowed in the systems of ${{\mathsf {N}}{\mathsf {C}}}{(}n,\{ a\},{REG}^{\circ }(\{ a\}),\mathrm{min}_{1}(\mathrm{cells}))$.

Moreover, there is an even more restricted variant reflecting the most restricted standard definition of spiking neural P systems in the literature, where only one spike can be sent along the axons to other neurons, i.e., in rules of the form in Eq. 2, $y_j\in \{ 0,1 \}$ for all $1\le j\le n$, $j\ne i$. The family of such systems with all these restrictions on the rules is denoted by ${{\mathsf {N}}{\mathsf {C}}}{(}n,\{ a\},{REG}^{\circ }(\{ a\}),\mathrm{min}_{1}(\mathrm{cells}_1))$.

For a rule as defined in Eq. 2, we will also use the following notation:

$$\begin{aligned} i:M_i/Z, \mathrm{where \ } M_i\in {\mathsf{SL}}, \ Z\in {{\mathbb {Z}}}^n \end{aligned}$$

(3)

with ${\mathsf{SL}}$ denoting the semi-linear sets (of natural numbers), possibly also taking into account all the restrictions as discussed above. This notation only keeps the i-th component of the control vector, thereby coming even closer to how spiking rules are traditionally written as

$$\begin{aligned} i:E_i / a^{x_i} \rightarrow a \end{aligned}$$

(4)

where a regular expression $E_i$ for $M_i$ is used, i.e., $L^\circ (E_i)=K_i$, and the connection structure (the synapses) between the neurons has to be specified in the definition of the spiking neural P system; this structure is assumed to be fixed.

In terms of the Eq. (1) such rule is written as

$$\begin{aligned} \left( \emptyset , \ldots ,X_i,\ldots ,\emptyset \rightarrow Y; \left( \{ a\}^*, \ldots ,K_i, \ldots , \{ a\}^*\right) \right) \end{aligned}$$

where the regular set $K_i$ is defined by $L^\circ (E_i)=K_i$ and the components j for which $Y_j$ may be a are given by the connection structure of the system.

The following example shows how the original definition for a rule in a spiking neural P system can be translated into our framework:

Example 8

Consider the standard spiking neural P system $\varPi '$ having a total of four cells, with cell 1 connected to cells 2 and 3, $\varPi ' \in {{\mathsf {N}}{\mathsf {C}}}{(}n,\{ a\},{REG}^{\circ }(\{ a\}), \mathrm{min}_{1}(\mathrm{cells}_1))$.

The spiking rule $(a^2+a^3)^*/a^2\rightarrow a$ in cell 1, with the regular expression $(a^2+a^3)^*$ corresponding to the regular control set $L^{\circ }((a^2+a^3)^*)$ now can be written as follows using notation (2):

$$\begin{aligned}&(M_1,{{\mathbb {N}}},{{\mathbb {N}}}, {{\mathbb {N}}})/(-2,1,1,0), \\&\quad \text {where }M_1=\{2n+3k\mid n,k\ge 0, n+k>0\}. \end{aligned}$$

Using notation (3), we would write $1:M_1/(-2,1,1,0)$.

Since the rule applicability is controlled by semi-linear sets, it is easily possible to decide which (multisets of) rules might compete for being executed. This is highlighted by the following normal form.

Definition 15

A spiking neural P system in ${{\mathsf {N}}{\mathsf {C}}}{(}n,\{ a\},{REG}^{\circ }(\{ a\}),\mathrm{min}_{1}(\mathrm{cells}_1))$ is said to be in a normal form if the following conditions hold:

• for any rule i : M/Z, with $Z(i)=k$ assigned to neuron i, and any $x\in M$, $x_i\ge |k|$,

• for any two rules $i:M_1/Z_1$ and $i:M_2/Z_2$ in the same neuron i, either $M_1=M_2$ or $M_1\cap M_2=\emptyset$.

The next theorem shows that we can effectively construct an equivalent system in normal form for any spiking neural P system in ${{\mathsf {N}}{\mathsf {C}}}{(}n,\{ a\},{REG}^{\circ }(\{ a\}),\mathrm{min}_{1}(\mathrm{cells}_1))$.

Theorem 1

For any spiking neural P system $\varPi$ in ${{\mathsf {N}}{\mathsf {C}}}{(}n,\{ a\},{REG}^{\circ }(\{ a\}),\mathrm{min}_{1}(\mathrm{cells}_1))$ , we can effectively construct an equivalent system $\varPi '$ from ${{\mathsf {N}}{\mathsf {C}}}{(}n,\{ a\},{REG}^{\circ }(\{ a\}),\mathrm{min}_{1}(\mathrm{cells}_1))$ in normal form such that all computations in $\varPi$ can be simulated by computations in $\varPi '$ in real time and vice versa, i.e. there is a bijective mapping $\phi$ between any reachable configurations of $\varPi$ and $\varPi '$ such that $C\Longrightarrow C_1$ implies $\phi (C)\Longrightarrow \phi (C_1)$ and conversely.

Proof

The first condition is easy to be satisfied as the set M is semi-linear and therefore the set $\{x\in M\mid x_i\ge |k|\}$ is semi-linear, too; moreover, the applicability condition anyway requires the cell to contain at least k spikes.

For the second condition it is enough to observe that the sets $A=M_1\cap M_2$, $B=M_1{\setminus } M_2$, and $C=M_2{\setminus } M_1$ are semi-linear. Then the two rules from the condition can be replaced by $A/Z_1$ and $A/Z_2$ as well as $B/Z_1$, and $C/Z_2$. $\square$

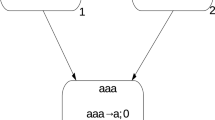
Example 9

Consider the spiking neural P system depicted on Fig. 1. It has an input neuron labeled by 1 and no output neurons. The system uses a spike train input and a Boolean output function based on the halting condition (it outputs ${{\mathsf{true}}}$ if the system halts, see Example 7). Hence, the system works as an acceptor (using the decision output strategy) in the following way: with the first spike arriving in the input cell in the first step, the system starts spiking in a cycle of three steps with different configurations. It halts and outputs ${{\mathsf{true}}}$ if the difference between the times at which the two spikes of the input spike train arrived was a multiple of 3, and thus forced the system to halt. Otherwise the system does not reach a halting configuration, and thus we consider, as it is commonly done in the literature, that the corresponding output is ${{\mathsf{false}}}$.

Fig. 1

A spiking neural P system recognizing numbers divisible by 3

The rules of the system can be written as follows using notation (2), with labels x.y for the rules in neuron x:

$$\begin{aligned} 1.1:&(\{1\},{{\mathbb {N}}},{{\mathbb {N}}},{{\mathbb {N}}})/(-1,1,0,1)\\ 2.1:&({{\mathbb {N}}},\{1\},{{\mathbb {N}}},{{\mathbb {N}}})/(0,-1,1,0) \quad 2.2: ({{\mathbb {N}}},\{3\},{{\mathbb {N}}},{{\mathbb {N}}})/(0,-3,0,0) \\ 3.1:&({{\mathbb {N}}},{{\mathbb {N}}},\{1\},{{\mathbb {N}}})/(0,0,-1,1) \quad 3.2: ({{\mathbb {N}}},{{\mathbb {N}}},\{3\},{{\mathbb {N}}})/(0,0,-3,0) \\ 4.1:&({{\mathbb {N}}},{{\mathbb {N}}},{{\mathbb {N}}},\{1\})/(1,0,0,-1) \quad 4.2: ({{\mathbb {N}}},{{\mathbb {N}}},{{\mathbb {N}}},\{2\})/(1,0,0,-2) \end{aligned}$$

Using notation (3), these rules can be written in an even simpler way:

$$\begin{aligned} 1.1:&\{1\}/(-1,1,0,1)\\ 2.1:&\{1\}/(0,-1,1,0) \quad 2.2: \{3\}/(0,-3,0,0) \\ 3.1:&\{1\}/(0,0,-1,1) \quad 3.2: \{3\}/(0,0,-3,0) \\ 4.1:&\{1\}/(1,0,0,-1) \quad 4.2: \{2\}/(1,0,0,-2) \end{aligned}$$

We observe that the system recognizes input sequences with an initial part of the form $0^*1(000)^{k}1$, $k\ge 1$, i.e., the time between the two input spikes represents a number divisible by 3.

As long as the input is 0, the 4-vector describing the configuration is (0, 0, 2, 0). With the first spike arriving in neuron 1, we get the following sequence of configurations using the spiking rules in the four neurons, assuming 3k time steps, $k\ge 1$, until the second spike arrives in neuron 1:

• (1, 0, 2, 0)

• (0, 1, 2, 1)

• (0, 1, 3, 0)

• (0, 0, 1, 0)

Then the system loops in neurons 2, 3, and 4 as follows:

• (0, 0, 0, 1)

• (0, 1, 0, 0)

• (0, 0, 1, 0)

Finally, when the second spike arrives in neuron 1 at the right time, we end up with the following sequence, which finally yields a halting configuration:

• (1, 0, 0, 1)

• (0, 2, 0, 1)

• (0, 3, 0, 0)

• (0, 0, 0, 0)

The interested reader may verify that in all other cases where the time between the two spikes arriving in the input neuron 1 is not divisible by 3 yields a non-halting computation.

In the more general setting of this paper, rules need not be assigned to single cells (neurons). Hence, we can use a more general form of spiking rules for systems in the families ${{\mathsf {N}}{\mathsf {C}}}{(}n,\{ a\},{REG}^{\circ }(\{ a\}),\delta )$:

$$\begin{aligned} M/Z, {{\text { where }}} M\in {{{\mathsf{SL}}}}^n, \ Z\in {{\mathbb {Z}}}^n \end{aligned}$$

(5)

Remark 4

We also remark that systems in ${{\mathsf {N}}{\mathsf {C}}}{(}n,\{ a\},{REG}^{\circ }(\{ a\}),\mathrm{seq})$ could be interpreted as vector addition systems with regular control: given a configuration, i.e., a vector of natural numbers v, applying the rule M/Z can be interpreted as adding Z to v provided the regular condition M is fulfilled and the result $v+Z$ is an n-vector of natural numbers.

In this more general setting, loops are allowed, arbitrary numbers of spikes may be sent to different neurons, and these numbers may even differ depending on the chosen rule(s). Such extended spiking neural P systems have already been considered in [2].

Based on Theorem 1, it is possible to obtain an interesting insight on the functioning of the basic variant of spiking neural P systems. We recall that a spiking P system evolves in the derivation mode $\mathrm{min}_1$ with the partitions defined cell-wise, i.e. from each neuron (cell) at most one rule is selected, and rules from several neurons (cells) can be executed in parallel. Since the application of each rule is governed by a regular control set K and since the complement of K is also regular, it is possible to construct complementary regular sets for every rule. Then it is possible to write a series of rules each of them corresponding to the action of any combination of the initial rules, using the corresponding regular control sets. More precisely, for any combination of individual rules from each neuron, it is possible to construct a single general rule that will check whether the chosen rules are applicable. Moreover, if in the normal form there are no identical control sets for any two rules in a cell, then the resulting system is deterministic as it is possible for each rule to extend the regular control set with the complement of all other regular sets in order to verify that no other rule is applicable.

In sum, our general framework for spiking neural P systems has allowed us to show that, using more general rules, spiking neural P systems in fact can be seen as working in the sequential derivation mode, without any parallelism, as exhibited above.

As a conclusion we obtain the following theorem and the related corollary expressing the result of the theorem in terms of families of networks of cells with regular control.

Theorem 2

For any spiking neural P system $\varPi$ in ${{\mathsf {N}}{\mathsf {C}}}{(}n,\{ a\},{REG}^{\circ }(\{ a\}),\mathrm{min}_{1}(\mathrm{cells}_1))$ we can effectively construct an equivalent spiking neural P system $\varPi '$ in ${{\mathsf {N}}{\mathsf {C}}}{(}n,\{ a\},{REG}^{\circ }(\{ a\}),\mathrm{seq})$ such that any computation in $\varPi$ can be simulated in real time by a computation in $\varPi '$ and vice versa.

Corollary 1

For any $n\ge 1$,

$$\begin{aligned}&{{\mathsf {N}}{\mathsf {C}}}{(}n,\{ a\},{REG}^{\circ }(\{ a\}),\mathrm{min}_{1}(\mathrm{cells}_1))\subseteq {{\mathsf {N}}{\mathsf {C}}}{(}n,\{ a\},\\&\quad {REG}^{\circ }(\{ a\}),\mathrm{seq}). \end{aligned}$$

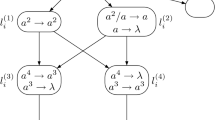
Example 10

Consider the following system $\varPi$ from ${{\mathsf {N}}{\mathsf {C}}}{(}n,\{ a\},{REG}^{\circ }(\{ a\}),\mathrm{min}_{1}(\mathrm{cells}_1))$ as shown in Fig. 2 using the standard notation of rules in the neurons (where $\lambda$ is used to denote forgetting rules):

Fig. 2

Spiking neural P system $\varPi$ from Example 10

These are the rules of $\varPi$:

$$\begin{aligned} \begin{array}{ll} 1.1: a^2/a\rightarrow a &{}\quad 1.2: a\rightarrow \lambda \\ 2.1: a\rightarrow a &{}\quad 2.2: a^3\rightarrow \lambda \end{array} \end{aligned}$$

Consider the sets $S_1=\{1\}$, $S_{2}=\{2\}$, $S_{3}=\{3\}$ as well as their complements denoted by a bar, e.g. ${\bar{S}}_1={{\mathbb {N}}}{\setminus } \{1\}$. In the general notation according to Eq. 5, these rules can be written in the following form:

$$\begin{aligned}&1.1: (S_{2},{{\mathbb {N}}})/(-1,1) \quad 1.2: (S_1,{{\mathbb {N}}})/(-1,0)\\&2.1: ({{\mathbb {N}}},S_1)/(1,-1) \quad 2.2: ({{\mathbb {N}}},S_3)(0,-3) \end{aligned}$$

Since it is possible to have at most two rules run in parallel in $\varPi$, this gives the following combinations of rules to be considered in an equivalent system $\varPi '$ to be constructed with $\varPi '$ in ${{\mathsf {N}}{\mathsf {C}}}{(}n,\{ a\},{REG}^{\circ }(\{ a\}),seq)$:

• only one of the rules is applicable

• rules 1.1 and 2.1 or 2.2 are applicable

• rules 1.2 and 2.1 or 2.2 are applicable

This yields the following rules for $\varPi '$:

$$\begin{aligned} \begin{array}{ll} A_{1.1} : (S_2,{\bar{S}}_1\cup {\bar{S}}_3)/(-1,1) &{}\quad A_{1.2} : (S_1,{\bar{S}}_1\cup {\bar{S}}_3)/(-1,0) \\ A_{2.1} : ({\bar{S}}_1\cup {\bar{S}}_2,S_1)/(1,-1) &{}\quad A_{2.2} : ({\bar{S}}_1\cup {\bar{S}}_2,S_3)/(0,-3) \\ B_{1.1+2.1}: (S_2,S_1)(0,0) &{}\quad B_{1.1+2.2}: (S_2,S_3)(-1,-2)\\ B_{1.2+2.1}: (S_1,S_1)(0,-1) &{}\quad B_{1.2+2.2}: (S_1,S_3)(-1,-3) \end{array} \end{aligned}$$

The obtained system $\varPi '$ is sequential but has the same behavior as the initial system $\varPi$ which was working in the derivation mode $\mathrm{min}_1$.

5 Extensions

In this section we briefly discuss several extensions of the basic model as well as further variants to be investigated more deeply in the future.

5.1 Extended rules

Generalizing the rules as in (5) is a natural way to extend spiking neural P systems. One of the first variants typically considered are spiking neural P systems with extended rules (for short, SNPe systems, [6]), having rules of the form $i:E/a^m\rightarrow a^n$. When applied, each of the connected cells will receive $a^n$ spikes in the next step, in contrast to the basic rule $i:E/a^m\rightarrow a$ which only allows for sending one spike along each axon. It is easy to see that this can be simulated using general rules as exhibited in the following. For the examples, we suppose that there are two other cells connected to the cell where the rules are applied. Moreover, in the description of these examples we do not distinguish between the regular expression E and the corresponding semi-linear set:

$$\begin{aligned} (E,{{\mathbb {N}}},{{\mathbb {N}}})/(-m,n,n), \quad \text {see Fig.}~3\text {a}. \end{aligned}$$

The second basic type of extended rules considers weights attached to synapses (axons), namely spiking neural P systems with weighted synapses [23]. Then each cell will receive the number of spikes corresponding to the indicated weight. Using general rules this variant can be simulated as follows:

$$\begin{aligned} (E,{{\mathbb {N}}},{{\mathbb {N}}})/(-m,n,k), \quad \text {see Fig.}~3 \text {b}. \end{aligned}$$

Using the general rules in extended spiking neural P systems (for short, ESNP systems) as introduced in [2], each rule may send different numbers of spikes along the axons to other cells, and these different amounts of spikes may even depend on the applied rule. A simpler concept of this kind is considered in [25] as spiking neural P systems with multiple channels. An example for this third type of extended rules is depicted in Fig. 3c.

Fig. 3

Different extended spiking rules: (a) extended (sending $a^n$ over all synapses); (b) weights on synapses (sending $a^k$ over the synapse with weight k); (c) generalized rules in the formal framework (allow for choosing different amounts of spikes to be sent over specified synapses, may even depend on the applied rule)

5.2 Non-natural numbers of spikes

It is obvious that the vectors of natural numbers used to represent rules and the configurations can be replaced by integer, real, or complex vectors. This allows for using quite powerful transformations. In this case, the control sets are no longer sets of natural numbers (for example, semi-linear sets of natural numbers), but have to be sets over the underlying scalars (integer, real, or complex). Moreover, we may also use predicates over the corresponding domains.

There exist already several models where the number of spikes is not a natural number. The best known one is the model using anti-spikes, for example see one recent paper [29]. Anti-spikes correspond to “negative” spikes that annihilate if they are in the same neuron with normal spikes. Such a model can be directly simulated using general rules working with integer vectors. In fact, if the annihilation rule has priority over all other rules, a neuron may contain either only spikes or only anti-spikes, which corresponds to having positive or negative integers.

Another model [33] uses a variant of extended rules with real weights on synapses. This can be simulated using real vectors, however the corresponding control sets have to be replaced by sets of real numbers or real-number predicates. In [33], equality predicates on real numbers are used, allowing for classifying the value of the cell below or above some fixed real threshold. More precisely, neurons (cells) contain real values and rules are of the form $T/d\rightarrow 1$, where T and d are real numbers. The rule is applied if the value in the neuron (cell) is exactly T, and with the application of the rule the new value of the neuron (cell) then becomes $T-d$. The unit “spike” is multiplied by real weights present on synapses, and then added to the corresponding cells. If some cell has the value below T, then only values of zero are transmitted. This behavior can be obtained by using the following rules written in our framework (we suppose that cell 1 is connected to cells 2 and 3 using synapses with weights $w_1$ and $w_2$):

$$\begin{aligned} (\{T\},{\mathbb {R}},{\mathbb {R}})/(-d,w_1,w_2) \qquad ({\mathbb {R}}_{<T},{\mathbb {R}},{\mathbb {R}})/(0,0,0) \end{aligned}$$

where ${\mathbb {R}}_{<T}=\{x\in {\mathbb {R}}\mid x<T\}$. The second rule allows the computation to progress even while the value in the cell is below T.

5.3 Astrocytes

In spiking neural P systems with astrocytes two networks interleave—a normal spiking neural P system and a second network of cells interacting with the axons of the first one. An astrocyte senses several axons. Depending on the signals (numbers of spikes) sent through these astrocyte-axon connections, the number of spikes allowed to pass through each of the axons is determined.

For example, the astrocyte may define an upper bound k on the total number of spikes allowed to go through an axon. In this case, if more than k spikes attempt to pass, they are discarded and nothing reaches the target cells. One can also consider different semantics, in which the astrocyte could determine the lower bound on the number of allowed spikes, or even more generally, implement a function giving the numbers of allowed spikes based on the number of spikes scheduled for the given axon.

In the case in which only one rule application per neuron is allowed at any step, astrocytes can be directly modelled using general rules. The simulation is based on the fact that it is possible to precompute in advance the number of spikes that can be generated by any combination of rules, since the number of rules in any given neuron is finite.

For example, consider two axons leaving from neuron 1 and an astrocyte sensing these two axons going to neurons 2 and 3. The application of a rule

$$\begin{aligned} (E_1, {{\mathbb {N}}}, {{\mathbb {N}}})/(-m,p,q) \end{aligned}$$

without the astrocyte controlling the axons would describe the application of a spiking rule in neuron 1 consuming m spikes, with $m\in E_1$, and sending p spikes to cell 2 and q spikes to cell 3. Using a simple astrocyte with lower bound k, i.e., only allowing the spikes to pass along the axons if their sum is at least k, this can be expressed by the rules

$$\begin{aligned} \begin{array}{ll} (E_1, {{\mathbb {N}}}, {{\mathbb {N}}})/(-m,p,q) &{}\quad \text {if } \ p+q\ge k, \text { and}\\ (E_1, {{\mathbb {N}}}, {{\mathbb {N}}})/(-m,0,0) &{}\quad \text {otherwise.} \end{array} \end{aligned}$$

5.4 Families of control languages

Already with the definition of the families of networks of cell ${{\mathsf {N}}{\mathsf {C}}}{(}n,V,{\mathscr {F}},\delta )$ it has become clear that we may consider various different families ${\mathscr {F}}$ of control languages, not only regular ones. For controlling the application of rules, other classes of formal languages can be used, for example, even subregular classes. In many variants of spiking neural P systems considered so far, ${\mathscr {F}}=\mathrm{FIN}(\{a\})\cup \{\{a^*\}\}$ is sufficient, for example, see [14]. With ${\mathscr {F}}=\mathrm{FIN}(\{a\})$, usually only semi-linear sets can be obtained.

On the other hand, more complicated types of control languages may be considered, too. To give a weird example (e.g., see [8]), let L be any recursive language over the alphabet V, i.e., $L\in {REC}^{\circ }(V)$, and construct a simple system in ${{\mathsf {N}}{\mathsf {C}}}{(}n,V,{REC}^{\circ }(V),\mathrm{seq})$ as follows:

Example 11

Let $L\in {REC}^{\circ }(V)$. Then consider the system

$$\begin{aligned} \varPi =\left( 2,V,w=(\emptyset , \emptyset ),c_{\mathrm{in}}=\{1\},c_{\mathrm{out}}=\{2\}, R,seq \right) \end{aligned}$$

in ${{\mathsf {N}}{\mathsf {C}}}{(}n,V,{REC}^{\circ }(V),seq)$ with initial input, i.e., at time 0 a multiset from ${V}^{\circ }$ is provided. There are only two rules in R ($a\in V$):

$$\begin{aligned} (L,\emptyset )/(0,1) \;\;\; \text { and } \;\;\; ({V}^{\circ }{\setminus } L,\emptyset )/(0,2) \end{aligned}$$

The output function checks the contents of the output cell after one computation step, after which the system must halt in any case. Just one symbol a in cell 2 indicates that the input multiset has been recognized as a member of L, whereas two symbols a indicate that the input multiset has been recognized not being a member of L. Looking at $\varPi$ as a recognizer system, one symbol a in cell 2 indicates acceptance, whereas two symbols a indicate rejection.

We remark that the construction for $\varPi$ also works for any other family of languages ${\mathscr {F}}$ over V, thus yielding a system in ${{\mathsf {N}}{\mathsf {C}}}{(}n,V,{\mathscr {F}},seq)$.

5.5 Derivation modes

For systems in ${{\mathsf {N}}{\mathsf {C}}}{(}n,V,{\mathscr {F}},\delta )$, also varying the derivation mode $\delta$ needs further investigation. For example, spiking neural P systems working in the maximally parallel mode $\delta = max$ seem to be a promising target.

Interesting models related to ${{\mathsf {N}}{\mathsf {C}}}{(}n,V,{\mathscr {F}},\delta )$ are spiking neural P systems with white hole rules [1] and spiking neural P systems with exhaustive use of rules [15, 18], but there are several technical details to be considered carefully, hence a thorough discussion of such models must be postponed for future research.

6 Conclusion

The generalization of spiking neural P systems proposed in this paper allows us to describe many spiking-based models in a uniform way. In the same way as the formal framework for static P systems [11], this approach may open new directions for future research, including the comparison between different spiking models and the introduction of new features. As possible examples we would like to mention systems working with real numbers as well as systems with a probabilistic evolution.

Another conclusion that can be drawn from using our formalization is that spiking neural P systems in fact can be seen as working in the sequential derivation mode, without any parallelism, as shown in Theorem 2.

It seems worthwhile to continue the development of the formal framework for spiking neural P systems with different degrees of parallelism, for example the kind of local parallelism reflected by the exhaustive use of rules, as proposed in [15, 18], where in each neuron, an applicable rule must be used as many times as possible. The so-called “white hole rules” were introduced in [1]; they allow for using the whole contents of a neuron and then sending it to other neurons.

Most of the results presented in this paper were obtained for the case $V=\{a\}$. It is a challenging task for future research to consider the case with $|V|>1$ in more detail. Some initial research on spiking neural P systems with several types of spikes was done in [16, 28], where arbitrary alphabets of symbols are used. Another possibility is to consider control conditions over ${\mathbb {Z}}$ or ${\mathbb {R}}$, extending the ideas from [9]. Spiking neural P systems with anti-spikes [19] are an example for the first condition, where two types of symbols (i.e., spikes and anti-spikes) are considered with $V=\{a, {\bar{a}}\}$ corresponding to a positive and a negative value of the spike a used in control conditions and rules.

We believe that the formal framework for spiking neural P systems offers a general, uniform, and straightforward perspective on these families of devices. This theoretical tool should be able to efficiently guide further exploration of these models of computing.