Notes on spiking neural P systems and finite automata

Abstract

Spiking neural P systems (in short, SN P systems) are membrane computing models inspired by the pulse coding of information in biological neurons. SN P systems with standard rules have neurons that emit at most one spike (the pulse) each step, and have either an input or output neuron connected to the environment. A variant known as SN P modules generalize SN P systems by using extended rules (more than one spike can be emitted each step) and a set of input and output neurons. In this work we continue relating SN P modules and finite automata. In particular, we amend and improve previous constructions for the simulatons of deterministic finite automata and state transducers. Our improvements reduce the number of neurons from three down to one, so our results are optimal. We also simulate finite automata with output, and we use these simulations to generate automatic sequences.

1 Introduction

Spiking neural P systems (in short, SN P systems) introduced in Ionescu et al. (2006), incorporated into membrane computing the idea of pulse coding of information in computations using spiking neurons [see for example Maass 2002; Maass and Bishop 1999 and references therein for more information]. In pulse coding from neuroscience, pulses known as spikes are not distinct, so information is instead encoded in their multiplicity or the time they are emitted.

On the computing side, SN P systems have neurons processing only one object (the spike symbol a), and neurons are placed on nodes of a directed graph. Arcs between neurons are called synapses. SN P systems are known to be universal in both generative (an output is given, but not an input) and accepting (an input is given, but not an output) modes. SN P systems can also solve hard problems in feasible (polynomial to constant) time. Another active line of investigation on the computability and complexity of SN P systems is taking mathematical and biological inspirations in order to create new variants, e.g. asynchronous operation, weighted synapses, rules on synapses, structural plasticity. We do not go into details, and we refer to Cabarle et al. (2015), Ionescu et al. (2006), Leporati et al. (2007), Pan et al. (2011), Păun and Pérez-Jiménez (2009), Song and Pan (2015), Song et al. (2015), Zeng et al. (2014), Zeng et al. (2013) and Zhang et al. (2015) and references therein.

SN P systems with standard rules (as introduced in their seminal paper) have neurons that can emit at most one pulse (the spike) each step, and either an input or output neuron connected to the environment, but not both. In Păun et al. (2007), SN P systems were equipped with both an input and output neuron, and were known as SN P transducers. Furthermore, extended rules were introduced in Chen et al. (2008) and Păun and Păun (2007), so that a neuron can produce more than one spike each step. The introduced SN P modules in Ibarra et al. (2010) can then be seen as generalizations of SN P transducers: more than one spike can enter or leave the system, and more than one neuron can function as input or output neuron.

In this work we continue investigations on SN P modules. In particular we amend the problem introduced in the construction of Ibarra et al. (2010), where SN P modules were used to simulate deterministic finite automata and state transducers. Our constructions also reduce the neurons for such SN P modules: from three neurons down to one. Our reduction relies on more involved superscripts, similar to some of the constructions in Neary (2010).

We also provide constructions for SN P modules simulating DFA with output. Establishing simulations between DFA with output and SN P modules, we are then able to generate automatic sequences. Such class of sequences contain, for example, a well known and useful automatic sequence known as the Thue-Morse sequence. The Thue-Morse sequence, among others, play important roles in many areas of mathematics (e.g. number theory) and computer science (e.g. automata theory). Aside from DFA with output, another way to generate automatic sequences is by iterating morphisms. We invite the interested reader to Allouche and Shallit (2003) for further theories and applications related to automatic sequences.

This paper is organized as follows: Sect. 2 provides our preliminaries. In Sect. 3 the main results are presented. Lastly, some final remarks are drawn and then provided in Sect. 4.

2 Preliminaries

It is assumed that the readers are familiar with the basics of membrane computing (a good introduction is Păun (2002) with recent results and information in the P systems webpage in http://ppage.psystems.eu/ and a recent handbook in Păun et al. (2010) ) and formal language theory (available in many monographs). We only briefly mention notions and notations which will be useful throughout the paper.

2.1 Language theory and string notations

We denote the set of natural numbers as ${\mathbb {N}} = \{0,1,2, \ldots \}$. Let V be an alphabet, $V^*$ is the set of all finite strings over V with respect to concatenation and the identity element $\lambda$ (the empty string). The set of all non-empty strings over V is denoted as $V^+$ so $V^+ = V^* - \{\lambda \}$. We call V a singleton if $V = \{a\}$ and simply write $a^*$ and $a^+$ instead of $\{a\}^*$ and $\{a\}^+$. If a is a symbol in V, then $a^0 = \lambda$, A regular expression over an alphabet V is constructed starting from $\lambda$ and the symbols of V using the operations union, concatenation, and $+$. Specifically, (i) $\lambda$ and each $a \in V$ are regular expressions, (ii) if $E_1$ and $E_2$ are regular expressions over V then $(E_1 \cup E_2)$, $E_1E_2$, and $E_1^+$ are regular expressions over V, and (iii) nothing else is a regular expression over V. The length of a string $w \in V^*$ is denoted by |w|. Unnecessary parentheses are omitted when writing regular expressions, and $E^+ \cup \{\lambda \}$ is written as $E^*$. We write the language associated with a regular expression E as L(E). If V has k symbols, then $[w]_k =n$ is the base-k representation of $n \in {\mathbb {N}}$.

2.2 Deterministic finite automata

Definition 1

A deterministic finite automaton (in short, a DFA) D, is a 5-tuple $D = (Q, \Sigma , q_1, \delta , F)$, where:

• $Q = \{q_1, \ldots , q_n \}$ is a finite set of states,

• $\Sigma = \{b_1, \ldots , b_m \}$ is the input alphabet,

• $\delta :$ $Q \times \Sigma \rightarrow Q$ is the transition function,

• $q_1 \in Q$ is the initial state,

• $F \subseteq Q$ is a set of final states.

Definition 2

A deterministic finite state transducer (in short, a DFST) with accepting states T, is a 6-tuple $T = (Q, \Sigma , \varDelta , q_1, \delta ', F)$, where Q, $\Sigma$, $q_1$, and F are as above, and $\varDelta = \{c_1, \ldots , c_t \}$ is the output alphabet, while $\delta ': Q \times \Sigma \rightarrow Q \times \varDelta$ is the transition function.

Definition 3

A deterministic finite automaton with output (in short, a DFAO) M, is a 6-tuple $M = (Q, \Sigma , \delta , q_1, \varDelta , \tau )$, where $Q, \delta , \Sigma , q_1$, and $\varDelta$ are as above, and $\tau : Q \rightarrow \varDelta$ is the output function.

A given DFAO M defines a function from $\Sigma ^*$ to $\varDelta$, denoted as $f_M(w) = \tau (\delta (q_1,w))$ for $w \in \Sigma ^*$. If $\Sigma = \{1, ..., k\}$, denoted as $\Sigma _k$, then M is a k-DFAO.

Definition 4

A sequence ${\mathbf {a}} = (a_n)_{n\ge 0}$, is k-automatic if there exists a k-DFAO, M, such that given $w \in \Sigma ^*_k$, $a_n = f_M(w)= \tau (\delta (q_1, w))$, where $[w]_k = n$.

Example 1

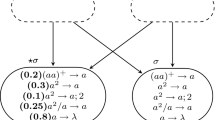
(Thue-Morse sequence) The Thue-Morse sequence $\mathbf {t} = (t_n)_{n \ge 0}$ counts the number of 1’s (mod 2) in the base-2 representation of n. The 2-DFAO for t is given in Fig. 1. In order to generate t, the 2-DFAO is in state $q_1$ with output 0, if the input bits seen so far sum to 0 (mod 2). In state $q_2$ with output 1, the 2-DFAO has so far seen input bits that sum to 1 (mod 2). For example, we have $t_0 = 0$, $t_1 = t_2 = 1$, and $t_3 = 0$.

Fig. 1

2-DFAO generating the Thue-Morse sequence

2.3 Spiking neural P systems

Definition 5

A spiking neural P system (in short, an SN P system) of degree $m \ge 1$, is a tuple of the form ${\Pi } = (\{a\}, \sigma _1, \ldots , \sigma _m, syn, in, out )$

where:

• $\{a\}$ is the singleton alphabet (a is called spike);

• $\sigma _1, \ldots , \sigma _m$ are neurons of the form $\sigma _i = (n_i, R_i), 1 \le i \le m,$ where:

  • $n_i \ge 0$ is the initial number of spikes inside $\sigma _i$;

  • $R_i$ is a finite set of rules of the general form: $E/a^c \rightarrow a^p$, where E is a regular expression over $\{a\}$, $c \ge 1$, with $p \ge 0$, and $c \ge p$;

• $syn \subseteq \{1,\ldots ,m\} \times \{1, \ldots , m\}$, with $(i,i) \notin syn$ for $1 \le i \le m$ (synapses);

• $in, out \in \{1, \ldots , m\}$ indicate the input and output neurons, respectively.

A rule $E/a^c \rightarrow a^p;d$ in neuron $\sigma _i$ (we also say neuron i or simply $\sigma _i$ if there is no confusion) is called a spiking rule if $p \ge 1$. If $p =0$, the rule is written simply as $a^c \rightarrow \lambda$, known as a forgetting rule. If a spiking rule has $L(E) = \{a^c\},$ we simply write it as $a^c \rightarrow a^p$.

The rules are applied as follows: If $\sigma _i$ contains k spikes, $a^k \in L(E)$ and $k \ge c$, then the rule $E/a^c \rightarrow a^p \in R_i$ with $p \ge 1,$ is enabled and can be applied. Rule application means consuming c spikes, so only $k-c$ spikes remain in $\sigma _i$. The neuron produces p spikes (also referred to as spiking) to every $\sigma _j$ where $(i,j) \in syn$. Applying a forgetting rule means producing no spikes.

SN P systems operate under a global clock, i.e. they are synchronous. At every step, every neuron that can apply a rule must do so. It is possible that at least two rules $E_1/a^{c_1} \rightarrow a^{p_1}$ and $E_2/a^{c_2} \rightarrow a^{p_2}$, with $L(E_1) \cap L(E_2) \ne \emptyset$, can be applied at the same step. The system nondeterministically chooses exactly one rule to apply. The system is globally parallel (each neuron can apply a rule) but is locally sequential (a neuron can apply at most one rule).

A configuration or state of the system at time t can be described by $C_t = \langle r_1, \ldots , r_m \rangle$ for $1 \le i \le m$, where neuron i contains $r_i \ge 0$ spikes. The initial configuration of the system is therefore $C_0 = \langle n_1, \ldots , n_m \rangle$. Rule application provides us a transition from one configuration to another. A computation is any (finite or infinite) sequence of configurations such that: (a) the first term is the initial configuration $C_0$; (b) for each $n \ge 2$, the nth configuration of the sequence is obtained from the previous configuration in one transition step; and (c) if the sequence is finite (called halting computation) then the last term is a halting configuration, i.e. a configuration where all neurons are open and no rule can be applied.

If $\sigma _{out}$ produces i spikes in a step, we associate the symbol $b_i$ to that step. In particular, the system (using rules in its output neuron) generates strings over $\Sigma = \{ p_1, \ldots , p_m \},$ for every rule $r_\ell = E_\ell /a^{j_\ell } \rightarrow a^{p_\ell }, 1 \le \ell \le m,$ in $\sigma _{out}$. From Chen et al. (2008) we can have two cases: associating $b_0$ (when no spikes are produced) with a symbol, or as $\lambda$. In this work and as in Ibarra et al. (2010), we only consider the latter.

Definition 6

A spiking neural P module (in short, an SN P module) of degree $m \ge 1$, is a tuple of the form ${\Pi } = (\{a\},$ $\sigma _1,$ $\ldots ,$ $\sigma _m,$ $syn, N_{in}, N_{out})$ where $\{a\}, \sigma _1, \ldots , \sigma _m, syn$ are as above and $N_{in}, N_{out} \subseteq \{1,2,\ldots ,m\}$ indicate the sets of input and output neurons, respectively.

SN P transducers in Păun et al. (2007) operated on strings over a binary alphabet as well considering $b_0$ as a symbol. SN P modules in Ibarra et al. (2010) are a special type of SN P systems with extended rules and they generalize SN P transducers. SN P modules behave in the usual way as SN P systems, except that spiking and forgetting rules now both contain no delays. In contrast to SN P systems, SN P modules have the following distinguishing feature: at each step, each input neuron $\sigma _i, i \in N_{in},$ takes as input multiple copies of a from the environment; Each output neuron $\sigma _o, o \in N_{out},$ produces p spikes to the enviroment, if a rule $E/a^c \rightarrow a^p$ is applied in $\sigma _o$; Note that $N_{in} \cap N_{out}$ is not necessarily empty.

3 Main results

In this section we amend and improve constructions given in Ibarra et al. (2010) to simulate DFA and DFST using SN P modules. Then, k-DFAO are also simulated with SN P modules. Lastly, SN P modules are related to k-automatic sequences.

3.1 DFA and DFST simulations

We briefly recall the constructions from Theorems 8 and 9 of Ibarra et al. (2010) for SN P modules simulating DFAs and DFSTs. The constructions for both DFAs and DFSTs have a similar structure, which is shown in Fig. 2. Let $D = (Q, \Sigma , \delta , q_1, F)$ be a DFA, where $\Sigma = \{b_1, \ldots , b_m\}$, $Q = \{q_1, \ldots , q_n\}$. The construction for Theorem 8 of Ibarra et al. (2010) for an SN P Module ${\Pi }_D$ simulating D is as follows:

$${\Pi }_D = (\{a\}, \sigma _1, \sigma _2, \sigma _3, syn, \{3\}, \{3\} ),$$

where

• $\sigma _1 = \sigma _2 = (n,\{a^n \rightarrow a^n\}),$

• $\sigma _3 = (n, \{ a^{2n+i+k}/a^{2n+i+k-j} \rightarrow a^j \mid \delta (q_i, b_k) = q_j \}),$

• $syn = \{ (1,2), (2,1), (1,3) \}.$

The structure for ${\Pi }_D$ is shown in Fig. 2. Note that $n,m \in {\mathbb {N}},$ are fixed numbers, and each state $q_i \in Q$ is represented as $a^i$ spikes in $\sigma _3$, for $1 \le i \le n$. For each symbol $b_k \in \Sigma$, the representation is $a^{n+k}$. The operation of ${\Pi }_D$ is as follows: $\sigma _1$ and $\sigma _2$ interchange $a^n$ spikes at every step, while $\sigma _1$ also sends $a^n$ spikes to $\sigma _3$.

Suppose that D is in state $q_i$ and will receive input $b_k$, so that $\sigma _3$ of ${\Pi }_D$ has $a^i$ spikes and will receive $a^{n+k}$ spikes. In the next step, $\sigma _3$ will collect $a^n$ spikes from $\sigma _1$, $a^{n+k}$ spikes from the enviroment, so that the total spikes in $\sigma _3$ is $a^{2n+i+k}$. A rule in $\sigma _3$ with $L(E) = \{a^{2n+i+k}\}$ is applied, and the rule consumes ${2n+i+k-j}$ spikes, therefore leaving only $a^j$ spikes. A single state transition $\delta (q_i,b_k) = q_j$ is therefore simulated.

With a 1-step delay, ${\Pi }_D$ receives a given input $w = b_{i_1},\ldots , b_{i_r}$ in $\Sigma ^*$ and produces a sequence of states $z = q_{i_1}, \ldots , q_{i_r}$ (represented by $a^{i_1},\ldots ,a^{i_r}$) such that $\delta (q_{i_\ell }, b_{i_\ell }) = q_{i_{\ell + 1}},$ for each $\ell = 1,\ldots ,r$ where $q_{i_1} = q_1$. Then, w is accepted by D (i.e. $\delta (q_1,w) \in F$) iff $z = {\Pi }_D(w)$ ends with a state in F (i.e. $q_{i_r} \in F$). Let the language accepted by ${\Pi }_D$ be defined as:

$$L({\Pi }_D) = \{ w \in \Sigma ^* \mid {\Pi }_D(w) \in Q^*F \}.$$

Then, the following is Theorem 8 from Ibarra et al. (2010)

Theorem 1

(Ibarra et al. 2010) Any regular language L can be expressed as $L = L({\Pi }_D)$ for some SN P module ${\Pi }_D$.

Fig. 2

Structure of SN P modules from Ibarra et al. (2010) simulating DFAs and DFSTs

The simulation of DFSTs requires a slight modification of the DFA construction. Let $T=(Q,\Sigma ,\varDelta , \delta ',q_1,F)$ be a DFST, where $\Sigma = \{b_1, \ldots , b_k\}, \varDelta = \{c_1, \ldots ,c_t\}, Q = \{q_1, \ldots , q_n\}$. We construct the following SN P module simulating T:

$${\Pi }_T = (\{a\},\sigma _1, \sigma _2, \sigma _3, syn, \{3\}, \{3\}),$$

where:

• $\sigma _1 = \sigma _2 = (n, \{a^n \rightarrow a^n\}),$

• $\sigma _3 = (n, \{ a^{2n+i+k+t}/a^{2n+i+k+t-j} \rightarrow a^{n+s} \mid \delta '(q_i,b_k) = (q_j,c_s) \}),$

• $syn = \{ (1,2),(2,1), (1,3) \}.$

The structure for ${\Pi }_T$ is shown in Fig. 2. Note that $n,m,t \in {\mathbb {N}}$ are fixed numbers. For $1 \le i \le n, 1 \le k \le m, 1 \le s \le t$: each state $q_i \in Q$, each input symbol $b_k \in \Sigma$, and each output symbol $c_s \in \varDelta$, is represented by $a^i$, $a^{n+t+k}$, and $a^{n+s}$, respectively.

The operation of ${\Pi }_T$ given an input $w \in \Sigma ^*$ is in parallel to the operation of ${\Pi }_D$; the difference is that the former produces a $c_s \in \varDelta$, while the latter produces a $q_i \in Q$. From the construction of ${\Pi }_T$ and the claim in Theorem 1, the following is Theorem 9 from Ibarra et al. (2010):

Theorem 2

(Ibarra et al. 2010) Any finite transducer T can be simulated by some SN P module ${\Pi }_T$.

The previous constructions from Ibarra et al. (2010) on simulating DFAs and DFSTs have however, the following technical problem:

Suppose we are to simulate DFA D with at least two transitions, (1) $\delta (q_i, b_k) = q_j,$ and (2) $\delta (q_{i'}, b_{k'}) = q_{j'}$. Let $j \ne j', i= k',$ and $k = i'$. The SN P module ${\Pi }_D$ simulating D then has at least two rules in $\sigma _3$: $r_1 = a^{2n+i+k}/a^{2n+i+k-j} \rightarrow a^j,$ (simulating (1)) and $r_2 = a^{2n+i'+k'}/ a^{2n+i'+k' -j'} \rightarrow a^{j'}$ (simulating (2)).

Observe that $2n+i+k = 2n+i' +k',$ so that in $\sigma _3$, the regular expression for $r_1$ is exactly the regular expression for $r_2$. We therefore have a nondeterministic rule selection in $\sigma _3$. However, D being a DFA, transitions to two different states $q_j$ and $q_{j'}$ should be deterministic. Therefore, ${\Pi }_D$ is a nondeterministic SN P module that can, at certain steps, incorrectly simulate the DFA D. This nondeterminism also occurs in the DFST simulation.

Next, we amend the problem and modify the constructions for simulating DFAs and DFSTs in SN P modules. Given a DFA D, we construct an SN P module ${\Pi }'_D$ simulating D as follows:

$${\Pi }'_D = ( \{a\}, \sigma _1, syn, \{1\}, \{1\} ),$$

where

• $\sigma _1 = (1, \{ a^{ k(n+1) +i }/ a^{ k(n+1) +i -j} \rightarrow a^j \mid \delta (q_i,b_k) = q_j \} ),$

• $syn = \emptyset .$

We have ${\Pi }_D$ containing only 1 neuron, which is both the input and output neuron. Again, $n,m \in {\mathbb {N}}$ are fixed numbers. Each state $q_i$ is again represented as $a^i$ spikes, for $1 \le i \le n$. Each symbol $b_k \in \Sigma$ is now represented as $a^{k(n+1)}$ spikes. The operation of ${\Pi }'_D$ is as follows: neuron 1 starts with $a^1$ spike, representing $q_1$ in D. Suppose that D is in some state $q_i$, receives input $b_k$, and transitions to $q_j$ in the next step. We then have ${\Pi }'_D$ combining $a^{k(n+1)}$ spikes from the enviroment with $a^i$ spikes, so that a rule with regular expression $a^{k(n+1)+i}$ is applied, producing $a^j$ spikes to the enviroment. After applying such rule, $a^j$ spikes remain in $\sigma _1,$ and a single transition of D is simulated.

Note that the construction for ${\Pi }'_D$ does not involve nondeterminism, and hence the previous technical problem: Let D have at least two transitions, (1) $\delta (q_i,b_k) = q_j,$ and (2) $\delta (q_{i'}, b_{k'}) = q_{j'}$. We again let $j \ne j', i = k',$ and $k = i'$. Note that being a DFA, we have $i \ne k$. Observe that $k(n+1) +i \ne k'(n+1) +i'.$ Therefore, ${\Pi }'_D$ is deterministic, and has two rules $r_1$ and $r_2$ correctly simulating (1) and (2), respectively. We now have the following result.

Theorem 3

Any regular language L can be expressed as $L = L({\Pi }'_D)$ for some 1-neuron SN P module ${\Pi }'_D$

For a given DFST T, we construct an SN P module ${\Pi }'_T$ simulating T as follows:

$${\Pi }'_T = (\{a\}, \sigma _1, syn, \{1\}, \{1\} ),$$

where

• $\sigma _1 = (1, \{ a^{k(n+1)+i+t}/a^{k(n+1)+i+t-j} \rightarrow a^{n+s}\mid \delta '(q_i,b_k) = (q_j,c_s) \}),$

• $syn = \emptyset$.

We also have ${\Pi }'_T$ as a 1-neuron SN P module similar to ${\Pi }'_D$. Again, $n,m,t \in {\mathbb {N}}$ are fixed numbers, and for each $1 \le i \le n, 1 \le k \le m,$ and $1 \le s \le t$: each state $q_i \in Q$, each input symbol $b_k \in \Sigma$, and each output symbol $c_s \in \varDelta$, is represented as $a^i, a^{k(n+1)+t},$ and $a^{n+s}$ spikes, respectively. The functioning of ${\Pi }'_T$ is in parallel to ${\Pi }'_D$. Unlike ${\Pi }_T$, ${\Pi }'_T$ is deterministic and correctly simulates T. We now have the next result.

Theorem 4

Any finite transducer T can be simulated by some 1-neuron SN P module ${\Pi }'_T$.

3.2 k-DFAO simulation and generating automatic sequences

Next, we modify the construction from Theorem 4 specifically for k-DFAOs by: (a) adding a second neuron $\sigma _2$ to handle the spikes from $\sigma _1$ until end of input is reached, and (b) using $\sigma _2$ to output a symbol once the end of input is reached. Also note that in k-DFAOs we have $t \le n$, since each state must have exactly one output symbol associated with it. Observing k-DFAOs from Definition 3 and DFSTs from Definition 2, we find a subtle but interesting distinction as follows:

The output of the state after reading the last symbol in the input is the requirement from a k-DFAO, i.e. for every w over some $\Sigma _k$, the k-DFAO produces only one $c \in \varDelta$ (recall the output function $\tau$); In contrast, the output of DFSTs is a sequence of $Q\times \varDelta$ (states and symbols), since $\delta (q_i,b_k) = (q_j,c_s)$. Therefore, if we use the construction in Theorem 4 for DFST in order to simulate k-DFAOs, we must ignore the first $|w|-1$ symbols in the output of the system in order to obtain the single symbol we require.

For a given k-DFAO $M= (Q, \Sigma , \varDelta , \delta , q_1, \tau )$, we have $1 \le i,j \le n$, $1 \le s \le t$, and $1 \le k \le m$. Construction of an SN P module ${\Pi }_M$ simulating M, is as follows:

$${\Pi }= ( \{a\}, \sigma _{1}, \sigma _{2}, syn, \{1\}, \{2\} ),$$

where

• $\sigma _1 = (1,R_1), \sigma _2 = (0,R_2),$

• $R_1 = \{ a^{k(n+1)+i+t}/a^{k(n+1)+i+t-j} \rightarrow a^{n+s}\mid \delta (q_i,b_k) = q_j, \tau (q_j) =c_s \}$

  $\cup \{ a^{m(n+1)+n+t+i} \rightarrow a^{m(n+1)+n+t+i}\mid 1 \le i \le n \},$

• $R_2 = \{a^{n+s} \rightarrow \lambda | \tau (q_i) = c_s \} \cup \{ a^{ m(n+1)+n+t+i } \rightarrow a^{ n+s } \mid \tau (q_i) = c_s \},$

• $syn = \{(1,2)\}.$

We have ${\Pi }_M$ as a 2-neuron SN P module, and $n,m,t \in {\mathbb {N}}$ are fixed numbers. Each state $q_i \in Q$, each input symbol $b_k \in \Sigma ,$ and each output symbol $c_s \in \varDelta$, is represented as $a^i$, $a^{k(n+1)+t}$, and $a^{n+s}$ spikes, respectively. In this case however, we add an end-of-input symbol $ (represented as $a^{m(n+1)+n+t}$ spikes) to the input string, i.e. if $w \in \Sigma ^*$, the input for ${\Pi }_M$ is w$.

For any $b_k \in \Sigma$, $\sigma _1$ of ${\Pi }_M$ functions in parallel to $\sigma _1$ of ${\Pi }'_D$ and ${\Pi }'_T$, i.e. every transition $\delta (q_i,b_k) = q_j$ is correctly simulated by $\sigma _1$. The difference however lies during the step when $ enters $\sigma _1$, indicating the end of the input. Suppose during this step $\sigma _1$ has $a^i$ spikes, then those spikes are combined with the $a^{m(n+1)+n+t}$ spikes from the enviroment. Then, one of the n rules in $\sigma _1$ with regular expression $a^{m(n+1)+n+t+i}$ is applied, sending $a^{m(n+1)+n+t+i}$ spikes to $\sigma _2$.

The first function of $\sigma _2$ is to erase, using forgetting rules, all $a^{n+s}$ spikes it receives from $\sigma _1$. Once $\sigma _2$ receives $a^{m(n+1)+n+t+i}$ spikes from $\sigma _1$, this means that the end of the input has been reached. The second function of $\sigma _2$ is to produce $a^{n+s}$ spikes exactly once, by using one rule of the form $a^{m(n+1)+n+t+i} \rightarrow a^{n+s} .$ The output function $\tau ( \delta (q_1, w\$) )$ is therefore correctly simulated. We can then have the following result.

Theorem 5

Any k-DFAO M can be simulated by some 2-neuron SN P module ${\Pi }_M$.

Next, we establish the relationship of SN P modules and automatic sequences.

Theorem 6

Let a sequence ${\mathbf {a}} = (a_n)_{n\ge 0}$ be k-automatic, then it can be generated by some 2-neuron SN P module $\Pi$.

k-automatic sequences have several interesting robustness properties. One property is the capability to produce the same output sequence given that the input string is read in reverse, i.e. for some finite string $w = a_1a_2 \ldots a_n$, we have $w^R = a_{n}a_{n-1}\ldots a_2a_1$. It is known [e.g. Allouche and Shallit (2003)] that if $(a_n)_{n \ge 0}$ is a k-automatic sequence, then there exists a k-DFAO M such that $a_n = \tau ( \delta (q_0, w^R))$ for all $n \ge 0$, and all $w \in \Sigma ^*_k,$ where $[w]_k = n$. Since the construction of Theorem 5 simulates both $\delta$ and $\tau$, we can include robustness properties as the following result shows.

Theorem 7

Let ${\mathbf {a}} =(a_n)_{n \ge 0}$ be a k-automatic sequence. Then, there is some 2-neuron SN P module $\Pi$ where ${\Pi }(w^R\$) = a_n, w \in \Sigma ^*_k, [w]_k = n,$ and $n \ge 0$.

4 Final remarks

We have shown that a single neuron in an SN P module is enough to simulate a DFA or DFST, and this is the optimal result in terms of the number of neurons per module (improving and amending some constructions in Ibarra et al. (2010)). In this simulating SN P module with one neuron, a rule simulates a transition in the simulated finite automata, i.e. given a simulated DFA or DFST with m number of transitions, the simulating SN P module with neuron i has $|R_i| = m$. The SN P module simulating a k-DFAO contains two neurons: the general idea is that the first neuron simulates $\delta$ while the second neuron simulates $\tau$ of the simulated k-DFAO. We were then able to generate automatic sequences using SN P modules, as well as transfer some robustness properties of k-DFAOs to the simulating module.

In Chen et al. (2008), strict inclusions for the types of languages characterized by SN P systems with extended rules having one, two, and three neurons were given. Then in Păun et al. (2007), it was shown that there is no SN P transducer that can compute nonerasing and nonlength preserving morphisms: for all $a \in \Sigma$, the former is a morphism h such that $h(a) \ne \lambda$, while the latter is a morphism h where $|h(a)| \ge 2$. It is known [e.g. in Allouche and Shallit (2003)] that the Thue-Morse morphism is given by $\mu (0) = 01$ and $\mu (1) = 10$. It is interesting to further investigate SN P modules with respect to other classes of sequences, morphisms, and finite transition systems. Another technical note is that in Păun et al. (2007) a time step without a spike entering or leaving the system was considered as a symbol of the alphabet, while in Ibarra et al. (2010) (and in this work) it was considered as $\lambda$.

We also leave as an open problem a more systematic analysis of input/output encoding size and system complexity: in the constructions for Theorems 3–4, SN P modules consist of only one neuron for each module, compared to three neurons in the constructions of Ibarra et al. (2010). However, the encoding used in our results is more involved, i.e. with multiplication and addition of indices (instead of simply addition of indices in Ibarra et al. (2010)). On the practical side, SN P modules might also be used for computing functions, as well as other tasks involving (streams of) input-output transformations. Practical applications might include image modification or recognition, sequence analyses, online algorithms, et al. For example, perhaps improving or extending the work done in Díaz-Pernil et al. (2013).

Some preliminary work on SN P modules and morphisms was given in Cabarle et al. (2012). From finite sequences, it is interesting to extend SN P modules to infinite sequences. In Freund and Oswald (2008), extended SN P systems¹ were used as acceptors of $\omega$-languages. SN P modules could also be a way to “go beyond Turing” by way of interactive computations, as in interactive components or transducers given in Goldin et al. (2006). While the syntax of SN P modules may prove sufficient for these “interactive tasks”, or at least requiring only minor modifications, a (major) change in the semantics is probably necessary.