1 Introduction

Being a rich source of inspiration for informatics, brain has provided plenty of ideas to propose high performance computing models, as well as to design efficient algorithm. In the brain, it is a common phenomenon that neurons cooperate by exchanging spikes via synapses. Taking inspiration from this phenomenon, various neural-like computing models have been proposed. In the framework of membrane computing, a kind of distributed and parallel neural-like computing model was proposed in 2006 [1], which is called spiking neural P systems (SN P systems, for short).

Inspired from biological phenomena such as synapse weight, neuron division, astrocytes, inhibitory synapses, et al., many variants of SN P systems [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22] have been proposed. The theoretical and practical usefulness of these variants were also investigated: regarding computing power the relationship between these variants and well-known models of computation, e.g. finite automata, register machines, grammars, computing numbers or strings was investigated in [23,24,25,26,27,28,29,30,31,32,33,34,35]; computing efficiency of these variants in solving hard problems was investigated in [36, 37].

Moreover, practical applications and software for simulations have been developed for SN P systems and their variants: for designing logic gates and logic circuits [38], for designing databases [39], for representing knowledge [40], for diagnosing fault [41,42,43], and for approximately solving combinatorial optimization problems [44].

Briefly, SN P systems have neurons that process spikes, and these neurons are placed on nodes of a directed graph, whose edges are called synapses. This construction is abstracted from indistinct signal and synapses in biological neurons. In SN P systems, spikes are processed by applying firing rules or forgetting rules. Firing rules are of the form \(E/a^c\rightarrow a^p;d\), where E is a regular expression over \(\{a\}\), and c, p, d are natural numbers, \(c\ge p\ge 1\), \(d\ge 0\). Applying a firing rule \(E/a^c\rightarrow a^p;d\) means consuming c spikes in the neuron and producing p spikes after a delay of d steps. The produced p spikes are sent to all neurons in connection with the neuron where the rule was applied by an outgoing synapses. Forgetting rules are of the form \(E/a^c \rightarrow \lambda\), where E is also a regular expression over \(\{a\}\), and c is a natural number. Applying a forgetting rule \(E/a^c \rightarrow \lambda\) means removing c spikes from the neuron and generating no spike.

At some step during the evolution of SN P systems, several spiking rules may be enabled in some neuron, and one of the applicable rules is chosen nondeterministically. In this case, the way of applying rules plays a crucial role. In the earlier version of SN P systems, the spiking rules were usually applied sequentially [9, 23, 25, 26, 36, 37]. At the level of a neuron, the sequential way of applying rules means the chosen rule was used only once, so it was a kind of local sequential. Inspired from the biological fact that an enabled chemical reaction consumes as many related substances as possible, exhaustive way of using rules was proposed [4] later. The exhaustive use of rules means the chosen rule was applied as many times as possible. So at the level of a neuron, the exhaustive use of rules was a kind of local parallelism [33, 34].

Recently, the sequential use of rules combines with the exhaustive use of rules to form generalized use of rules [46]. This new way of applying rules is similar to the minimal parallelism mode in P systems [45]. Specifically, under exhaustive mode of applying rules, the chosen rule can be used at most m times, while generalized use of rules means the chosen rule can be applied for l times, where \(1\le l\le m\).

It was proved in [46] that as number computing devices SN P systems with generalized use of rules (SNGR P systems, for short) are Turing universal. When each neuron contained at most 7 rules, and for each time each firing rule consumes at most 9 spikes and each forgetting rule removes at most 7 spikes, computational completeness is achieved in SNGR P systems. Also in [46], it was mentioned that the parameters in this completeness result may be optimized without losing the universality.

In this work, the related parameters in the completeness result of SNGR P systems are improved. Specifically, a universal SNGR P system is proposed, with each neuron containing at most 5 rules, and for each time each spiking rule consuming at most 6 spikes, and each forgetting rule removing at most 4 spikes. This universality result provides an answer to the open problem mentioned in [46], and makes it possible to construct universal SNGR P systems with less resources (neurons and spikes involved in the evolution of system).

This work is organized as follows. The computing models investigated in this work, i.e. SNGR P systems, are simply reviewed in Sect. 2, . In Sect. 3, the computational completeness of SNGR P systems is investigated. Conclusions and remarks are given in Sect. 4.

2 Spiking neural P systems with generalized use of rules

In this section, SNGR P systems is simply reviewed. For more details, readers can look up in [46].

Formally, an SNGR P system of degree \(m\ge 1\), is a construct of the form

$$\varPi = (O,\sigma _{1} ,\sigma _{2} , \ldots ,\sigma _{m} ,syn,out),$$

where:

  1. 1.

    \(O=\{a\}\) is a singleton alphabet (a is called spike);

  2. 2.

    \(\sigma _1, \sigma _2, \ldots , \sigma _m\) are neurons with the form of

    $$\begin{aligned} \sigma _i=(n_i, R_i), 1\le i\le m, \end{aligned}$$

    where:

    1. (1)

      \(n_i\ge 0\) is the number of spikes initially placed in neuron \(\sigma _i\);

    2. (2)

      \(R_i\) is a finite set of rules and two forms of rule are as follows:

      • Firing rule: \(E_1/a^{c_1} \rightarrow a^p;d\), where \(E_1\) is a a regular expression over \(\{a\}\), and \(c_1\ge p\ge 1\), \(d\ge 0\) (called as delay).

      • Forgetting rule: \(E_2/a^{c_2} \rightarrow \lambda\), where \(E_2\) is a a regular expression over \(\{a\}\), and \(c_2\ge 1\).

      For each firing rule \(E_1/a^{c_1} \rightarrow a^p;d\) from \(R_i\), it is worthy noting the restriction that \(L(E_1)\cap L(E_2)=\emptyset\);

  3. 3.

    \({syn} \subseteq \{ 1,2, \ldots ,m\} \times \{ 1,2, \ldots ,m\}\) is the set of synapses between neurons. Self-loop synapse is not allowed in the system, so \((i,i) \notin {\text{syn}}\) for \(1\le i\le m\);

  4. 4.

    \({out} \in \{ 1,2, \ldots ,m\}\) indicates the output neuron, which can emit spikes to environment.

In a firing rule \(E/a^c \rightarrow a^p;d\), if \(d=0\), then the delay can be omitted, and the rule can be written as \(E/a^c \rightarrow a^p\); if \(E=a^c\) and \(d=0\), then the rule is simply written as \(a^c\rightarrow a^p\). Similarly, if a forgetting rule \(E/a^c \rightarrow \lambda\) has \(E=a^c\), then it is simply written as \(a^c\rightarrow \lambda\). The feature of delay is not used in the following sections, so the firing rules are always of the form \(E/a^c \rightarrow a^p\).

In a neuron \(\sigma _i\) with \(k_1\) spikes and a firing rule \(E/a^{c_1}\rightarrow a^p\), if \(a^{k_1}\in L(E)\) and \(k_1\ge c_1\), then this firing rule can be applied. Or in a neuron \(\sigma _i\) with \(k_2\) spikes and a forgetting rule \(E/a^{c_2} \rightarrow \lambda\), if \(a^{k_2}\in L(E)\) and \(k_2\ge c_2\), then this forgetting rule can be applied. This is how firing rule and forgetting rule can be applied in SN P systems. However, the essential that should be considered in SNGR P system is the way the rules are applied. The application of rules in SNGR P systems are explained in detail as follows.

As suggested in the Introduction section, applying the firing rule \(E/a^{c_1}\rightarrow a^p\) in a generalized manner means the following. Assume that \(k_1=s_1c_1+r_1\), where \(s_1\ge 1\) and \(0\le r_1<c_1\), thus \(n_1c_1\) spikes can be consumed, where \(n_1\in \{1,2,\ldots , s_1\}\) and \(n_1\) is chosen nondeterministically from the set. If \(n_1c_1\) spikes, \(1\le n_1\le s_1\), are consumed by the rule, then after the application of rule, \(n_1p\) spikes are produced, and \(k_1-n_1c_1\) spikes remain in neuron \(\sigma _i\). The produced \(n_1p\) spikes are sent to all neighbouring neurons \(\sigma _j\) with \((i,j) \in {syn}\). If neuron \(\sigma _i\) is output neuron, the produced \(n_1p\) spikes will be sent to the environment. If there is no synapse leaving from neuron \(\sigma _i\), the produced \(n_1p\) spikes will simply be lost.

Similarly, applying the forgetting rule \(E/a^{c_2} \rightarrow \lambda\) in a generalized manner means the following. After dividing \(k_2\) by \(c_2\), we can get \(k_2=s_2c_2+r_2\), with \(s_2\ge 1\) and \(0\le r_2<c_2\). Given this assumption of \(k_2=s_2c_2+r_2\), \(n_2c_2\) spikes can be removed, where \(n_2\in \{1,2,\ldots , s_2\}\) and \(n_2\) is chosen nondeterministically from the set. If \(n_2c_2\) spikes, \(1\le n_2\le s_2\), are removed by the rule, then after the application of rule, \(k_2-n_2c_2\) spikes remain in neuron \(\sigma _i\).

In each time unit, in each neuron, if there is a rule can be used, no matter it is a firing rule or a forgetting rule, the rule must be applied. At some time, in a neuron, there may be several rules can be applied. In this case, only one of the rules is nondeterministically chosen to be applied. In SNGR P systems, the chosen rule will be used in a generalized way as mentioned above.

The configuration of system is defined as the numbers of spikes present in each neuron. Thus, the initial configuration of system is \(\langle n_1, n_2, \ldots , n_m\rangle\). Applying the rules in a generalized way as described above, transitions among configurations can be defined. A computation is defined as any sequence of transitions starting from the initial configuration. When there is no rule can be used in any neuron of the system, the computation halts, and this configuration is usually called the halting configuration.

The result of a computation can be defined in several ways. In this work, SNGR P systems are considered as number generating devices, and the computation result is defined as the total number of spikes that are sent from the output neuron to environment during the computation. This means only a halting computation can lead to a result, or else the computation is considered as invalid and it gives no result. In this way, the set of all numbers that are computed by an SNGR P system \(\varPi\) is denoted by \(N^{{{\text{gen}}}} (\varPi )\), where subscript gen indicates that the rules are used in a generalized mode. Furthermore, the family of all sets \(N^{{{\text{gen}}}} (\varPi )\) computed as above is denoted by \({Spik}P_{m}^{{{gen}}} ({rule}_{k} ,{cons}_{r} ,{forg}_{q} )\). The parameters m, k, r, q put restrictions on the system as follows: the SNGR P system contains at most \(m\ge 1\) neurons; in each neuron of the system, there are at most \(k\ge 1\) rules; regarding to the rules in the system, all spiking rules \(E/a^{c_1} \rightarrow a^p\) have \(c_1\le r\), and all forgetting rules \(E/a^{c_2} \rightarrow \lambda\) have \(c_2\le q\). These parameters can be replaced with * when they are not bounded.

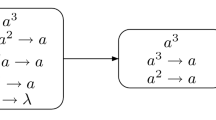
In order to understand the SNGR P systems easily, they are represented graphically in the next sections: an oval with initial spikes and rules inside represents a neuron; communication between neurons is represented by incoming and outgoing arrows of neurons; for output neuron, there is an outgoing arrow pointing to environment, which suggests that the output neuron can send spikes to the environment.

3 The improved result of universality for SNGR P systems

In this section, an improved universal SNGR P system is present, with each neuron containing at most 5 rules, and for each time during computation, each spiking rule consuming at most 4 spikes, and each forgetting rule removing at most 4 spikes. This universality result will be proved by characterizing NRE by means of register machine.

A register machine is a construct \(M = (m,H,l_{0} ,l_{{\text{h}}} ,I)\). In this construction, m is the number of registers; H is the set of labels of instructions; \(l_0\) is the start label, which is the label of an ADD instruction; \(l_{{\text{h}}}\) is the halt label, which is assigned to HALT instruction; I is the set of instructions. Label of instruction can precisely identify instruction, for each label from H labels only one instruction from I. As follows, there are three forms of labeled instructions:

  • ADD instruction \(l_{i} :({ADD}(r),l_{j})\),

  • SUB instruction \(l_{i} :({SUB}(r),l_{j} ,l_{k} )\) (if register r is non-empty, then subtract 1 from it and go to the instruction with label \(l_j\), otherwise go to the instruction with label \(l_k\)),

  • HALT instruction \(l_{{\text{h}}} :{HALT}\).

These instructions have different function. By applying an ADD instruction \(l_{i} :({ADD}(r),l_{j} )\), 1 is added to register r and the machine switches to instruction with label \(l_j\). When applying an SUB instruction \(l_{i} :({SUB}(r),l_{j} ,l_{k} )\), there are two branches to go: if register r is non-empty, then 1 is subtracted from this register, and the machine goes to instruction with label \(l_j\); if register r is empty, then the machine goes to instruction with label \(l_k\). When getting to the HALT instruction \(l_{{\text{h}}} :{HALT}\), the machine stops working.

A set of number N (M) can be generated by a register machine M as follows. Initial state of the machine is all registers being empty, which means they store number 0. At initial state the machine applies the instruction with label \(l_0\). According to the labels of instructions and the contents of registers, the machine continues to apply instructions. It is possible that the machine can finally reache HALT instruction. At this moment, the number n present in register 1 is said to be generated by machine M. N (M) denotes the set of all numbers generated by M. It is known that with only three registers, register machine can generates all recursively enumerable sets of numbers [47]. Hence, register machines can characterize NRE, i.e., \(N(M) = {NRE}\). when comparing the power of two number generating devices, it is a convention that number 0 is ignored. Without loss of generality, this convention is followed here.

The characterization of NRE by means of register machine will be used in the proof below. Moreover, an additional attention should be paid to the number of rules in each neuron, and the number of spikes consumed or removed in each rule.

Theorem 1

\({Spik}^{{{gen}}} P_{*} ({rule}_{5} ,{cons}_{6} ,{forg}_{4} ) = {NRE}.\)

Proof

The inclusion \({Spik}^{{gen}} P_{*} ({rule}_{5} ,{cons}_{6} ,{forg}_{4} ) \subseteq {NRE}\) can be proved directly in view of Turing–Church thesis. In order to prove the inclusion \({NRE}\subseteq {Spik}^{{gen}} P_{*} ({rule}_{5} ,{cons}_{6} ,{forg}_{4} )\), thus complete the proof of the theorem, an SNGR P system is constructed to simulate the universal register machine.

Let \(M = (m,H,l_{0} ,l_{{\text{h}}} ,I)\) be a universal register machine. Without lose of generality, the result of a computation is assumed to be the number stored in register 1 and the register 1 is assumed to be never decremented during the computation.

In what follows, an SNGR P system \(\varPi\) is constructed to simulate the register machine M.

In this SNGR P system \(\varPi\), a neuron \(\sigma _r\) is considered for each register r of M, and spikes in the neuron corresponds to contents of the register. Specifically, neuron \(\sigma _r\) containing 2n spikes corresponds to the fact that register r holds the number \(n\ge 0\). Therefore, if the contents of a register r is increased by 1, then the number of spikes in neuron \(\sigma _r\) is correspondingly increased by 2; if the contents of a non-empty register is decreased by 1, then the number of spikes in neuron \(\sigma _r\) is correspondingly decreasing by 2; when checking whether the register is empty, it correspondingly only need to check whether \(\sigma _r\) has no spike inside.

Also in \(\varPi\), a neuron \(\sigma _l\) is considered for each label l of an instruction in M. Initially, all these neurons are empty, but neuron \(\sigma _{l_0}\), which is associated with the start label of M, is an exception. Neuron \(\sigma _{l_0}\) contains 3 spikes at initial state, which means that this neuron is “activated” at beginning of the computation.

Furthermore, in a way which is described below, neurons associated with the registers and the labels of M will be added in system \(\varPi\). When receiving 3 spikes during the computation, neuron \(\sigma _l\) will be active, which initiates the simulation of some instruction \(l_{i} :({OP}(r),l_{j} ,l_{k} )\) of M (OP is ADD or SUB). Full simulation of instruction \(l_{i} :({OP}(r),l_{j} ,l_{k} )\) of M includes: neuron \(\sigma _{l_i}\) gets activated, register r is operated according to the request of OP, at last 3 spikes are introduced in neuron \(\sigma _{l_j}\) or \(\sigma _{l_k}\). In this way, one of the neurons \(\sigma _{l_j}\) and \(\sigma _{l_k}\) becomes activated. Simulation of the computation in M is completed when neuron \(\sigma _{{l_{{\text{h}}} }}\), which is associated with the halting label of M, becomes activated.

It is worthy noting that we do not know whether neurons \(\sigma _{l_j}\) and \(\sigma _{l_k}\) correspond to a label of ADD, SUB, or halting instruction. Thus, rules in neurons \(\sigma _{l_j}\) and \(\sigma _{l_k}\) are written as the form of \(a^3\rightarrow a^{\delta (l_q)}\) (\(q=j\) or \(q=k\)), where the function \(\delta\) on H is defined as follows:

$$\delta (l) = \left\{ {\begin{array}{*{20}l} {2,} \hfill & {{\text{if}}\,l\,{\text{is}}\,{\text{the}}\,{\text{label}}\,{\text{of}}\,{\text{an}}\,{ADD}\,{\text{instruction}},} \hfill \\ {3,} \hfill & {{\text{otherwise}}.} \hfill \\ \end{array} } \right.$$

The work of system \(\varPi\), which includes simulating all instructions of register machine M and outputting the computation result, is described as follows.

Module ADD : simulating an ADD instruction \(l_{i} :({ADD}(r),l_{j} ,l_{k} )\)

Fig. 1
figure 1

Module ADD for simulating \(l_{i} :({ADD}(r),l_{j} ,l_{k} )\)

Full size image

The ADD module is shown in Fig. 1, and how it works is described as follows.

Given the assumption that at some step t, register r holds number n, and the system starts to simulate an ADD instruction \(l_{i} :({ADD}(r),l_{j} ,l_{k} )\) of M. At this step, there are 3 spikes in neuron \(\sigma _{l_i}\), and no spike in the other neurons, except for neurons which are associated with registers. With 3 spikes in neuron \(\sigma _{l_i}\), rule \(a^3\rightarrow a^2\) in neuron \(\sigma _{l_i}\) is applicable, and the ADD module is initiated.

At step t, the rule \(a^3\rightarrow a^2\) in \(\sigma _{l_i}\) is enabled and is used for only once. After application of the rule, 2 spikes are sent to each of neurons \(\sigma _{l_i^{(1)}}\), \(\sigma _{l_i^{(2)}}\) and \(\sigma _r\). At step \(t+1\), the 2 spikes are received by neuron \(\sigma _r\), which means the content in register r is incremented by one. Also at step \(t+1\), both neurons \(\sigma _{l_i^{(1)}}\) and \(\sigma _{l_i^{(2)}}\) receives the 2 spikes and becomes activated. In neuron \(\sigma _{l_i^{(1)}}\), rule \(a^2\rightarrow a^2\) is enabled and can be applied for only once, and 2 spikes are sent to each of neurons \(\sigma _{l_i^{(3)}}\) and \(\sigma _{l_i^{(4)}}\). In neuron \(\sigma _{l_i^{(2)}}\), rule \(a^2/a\rightarrow a\) is enabled and can be applied for once or twice nondeterministically, sending one spike or two spikes to each of neurons \(\sigma _{l_i^{(3)}}\) and \(\sigma _{l_i^{(4)}}\), respectively. Consequently, if rule \(a^2/a\rightarrow a\) is applied for once, both neurons \(\sigma _{l_i^{(3)}}\) and \(\sigma _{l_i^{(4)}}\) receives 3 spikes; if the rule is applied for twice, both neurons receive 4 spikes.

If both neurons \(\sigma _{l_i^{(3)}}\) and \(\sigma _{l_i^{(4)}}\) accumulates 3 spikes, the 3 spikes will be removed from neuron \(\sigma _{l_i^{(3)}}\) by applying forgetting rule \(a^3\rightarrow \lambda\), while the 3 spikes in neuron \(\sigma _{l_i^{(4)}}\) enables rule \(a^3\rightarrow a^3\). This rule makes neuron \(\sigma _{l_i^{(4)}}\) firing, and after its application, 3 spikes will be sent to neuron \(\sigma _{l_k}\). After receiving 3 spikes, neuron \(\sigma _{l_k}\) becomes active, which means the system switches to simulate instruction \(l_k\) of machine M.

If both neurons \(\sigma _{l_i^{(3)}}\) and \(\sigma _{l_i^{(4)}}\) accumulates 4 spikes, the 4 spikes will be removed from neuron \(\sigma _{l_i^{(4)}}\) by applying forgetting rule \(a^4\rightarrow \lambda\), while the 4 spikes in neuron \(\sigma _{l_i^{(3)}}\) enables rule \(a^4\rightarrow a^3\). This rule makes the neuron firing, and after its application, 3 spikes will be sent to neuron \(\sigma _{l_j}\). After receiving 3 spikes, neuron \(\sigma _{l_j}\) becomes active, which means the system switches to simulate instruction \(l_j\) of machine M.

To summarize, in some Module ADD, if neuron \(\sigma _{l_i}\) gets fired, 2 spikes will be added to neuron \(\sigma _r\), and neuron \(\sigma _{l_j}\) or \(\sigma _{l_k}\) will get fired nondeterministically. Therefore, ADD instruction \(l_{i} :({ADD}(r),l_{j} ,l_{k} )\) is correctly simulated by Module ADD.

Module SUB : simulating a SUB instruction \(l_{i} :({SUB}(r),l_{j} ,l_{k} ).\)

Fig. 2
figure 2

Module SUB for simulating \(l_{i} :({SUB}(r),l_{j} ,l_{k} )\)

Full size image

The SUB module is shown in Fig. 2, and how it works is described as follows.

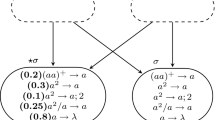
Given the assumption that at some step t, register r holds the number n, and the system starts to simulate an SUB instruction \(l_{i} :({SUB}(r),l_{j} ,l_{k} )\) of M. At this step, there are 3 spikes in neuron \(\sigma _{l_i}\), and no spike in the other neurons, except for neurons which are associated with registers. With 3 spikes in neuron \(\sigma _{l_i}\), rule \(a^3\rightarrow a^3\) in the neuron is applicable, and the SUB module is initiated.

At step t, the rule \(a^3\rightarrow a^3\) in \(\sigma _{l_i}\) is enabled and is used for only once. After application of the rule, 3 spikes are sent to both of neurons \(\sigma _r\) and \(\sigma _{l_i^{(1)}}\). In neuron \(\sigma _{l_i^{(1)}}\), rule \(a^3\rightarrow a\) is applicable at step \(t+1\), which makes 1 spike sent to both neurons \(\sigma _{l_i^{(2)}}\) and \(\sigma _r\) at the same time. Also at step \(t+1\), neuron \(\sigma _r\) receives 3 spikes from neuron \(\sigma _{l_i}\), and the rules in it can be applied. The situation in neuron \(\sigma _r\) is complicate, and there are three cases need to be considered.

In case 1, there is no spike in neuron \(\sigma _r\) at step t, which corresponds to the fact that register r holds number 0. Thus, there are 3 spikes in neuron \(\sigma _r\) at step \(t+1\), and the rule \(a^3\rightarrow a\) is enabled, which makes 1 spike sent to neuron \(\sigma _{l_i^{(2)}}\). Consequently, at step \(t+2\) neuron \(\sigma _{l_i^{(2)}}\) will accumulate 2 spikes (one spike is sent by neurons \(\sigma _{l_i^{(1)}}\), and the other one by neuron \(\sigma _r\)), and the rule \(a^2\rightarrow a\) is enabled. By applying this rule, 1 spike will be sent to each of neurons \(\sigma _{l_i^{(s)}}\), \(3\le s\le 7\). The spike in both neurons \(\sigma _{l_i^{(3)}}\) and \(\sigma _{l_i^{(4)}}\) will be removed by rule \(a\rightarrow \lambda\) at the next step. The spike in neuron \(\sigma _{l_i^{(5)}}\), \(\sigma _{l_i^{(6)}}\) and \(\sigma _{l_i^{(7)}}\) enables rule \(a\rightarrow a\), and each application of the rule makes 1 spike sent to neuron \(\sigma _{l_k}\). At step \(t+4\), neuron \(\sigma _{l_k}\) will accumulate 3 spikes. It is worthy noting that at step \(t+2\) neuron \(\sigma _{l_i^{(1)}}\) sends 1 spike to neuron \(\sigma _r\). This spike will be consumed in two steps: by applying firing rule \(a\rightarrow a\), this spike is sent to neuron \(\sigma _{l_i^{(2)}}\) and then gets removed by forgetting rule \(a\rightarrow \lambda\).

At the beginning of this simulation, there is no spike in neuron \(\sigma _r\). Finally, neuron \(\sigma _{l_k}\) becomes active, and the number of spikes stored in neuron \(\sigma _r\) remains 0. Therefore, SUB instruction \(l_i\) is simulated correctly.

In case 2, there are 2 spikes in neuron \(\sigma _r\) at step t, which corresponds to the fact that register r holds number 1. Thus, there are 5 spikes in neuron \(\sigma _r\) at step \(t+1\), and the rule \(a^5\rightarrow a^4\) is enabled, which makes 4 spikes sent to neuron \(\sigma _{l_i^{(2)}}\) and no spike left in \(\sigma _r\). Consequently, at step \(t+2\) neuron \(\sigma _{l_i^{(2)}}\) will accumulate 5 spikes (one spike is sent by neurons \(\sigma _{l_i^{(1)}}\), and the other 4 by neuron \(\sigma _r\)), and the rule \(a^5\rightarrow a^3\) is enabled. By applying this rule, 3 spikes will be sent to each of neurons \(\sigma _{l_i^{(s)}}\), \(3\le s\le 7\). By forgetting rule \(a^3\rightarrow \lambda\), the 3 spikes in each of neurons \(\sigma _{l_i^{(3)}}\), \(\sigma _{l_i^{(5)}}\), \(\sigma _{l_i^{(6)}}\) and \(\sigma _{l_i^{(7)}}\) will be removed at the next step. The 3 spikes in neuron \(\sigma _{l_i^{(4)}}\) enables rule \(a^3\rightarrow a^3\), and its application makes 3 spikes sent to neuron \(\sigma _{l_j}\). At step \(t+4\), neuron \(\sigma _{l_j}\) will accumulate 3 spikes. Similarly, at step \(t+2\) neuron \(\sigma _{l_i^{(1)}}\) send 1 spike to neuron \(\sigma _r\). By applying rule \(a\rightarrow a\) in neuron \(\sigma _r\) and then rule \(a\rightarrow \lambda\) in neuron \(\sigma _{l_i^{(2)}}\), this spike will finally be removed.

At the begining of this simulation, there are 2 spikes in neuron \(\sigma _r\). Finally, neuron \(\sigma _{l_j}\) becomes active, and the number of spikes stored in neuron \(\sigma _r\) becomes 0. Therefore, SUB instruction \(l_i\) is simulated correctly.

In case 3, there are 2n (\(n\ge 2\)) spikes in neuron \(\sigma _r\) at step t. Accordingly, register r holds a number that is greater than 1. Thus, there are \(2n+3\) (\(n\ge 2\)) spikes in neuron \(\sigma _r\) at step \(t+1\), and rule \(a^5(a^2)^+/a^6\rightarrow a^4\) is enabled. Under a generalized mode of applying rules, rule \(a^5(a^2)^+/a^6\rightarrow a^4\) can be applied for several times, nondeterministically chosen.

As follows, a simple example, i.e. register r holds number 5, is used to show how SUB instruction \(l_i\) simulates in this case.

For register r holds number 5, neuron \(\sigma _r\) contains 10 spikes at the begining of this simulation. So at step \(t+1\), neuron \(\sigma _r\) contains 13 spikes, and rule \(a^5(a^2)^+/a^6\rightarrow a^4\) can be applied for once or twice, nondeterministically chosen.

If rule \(a^5(a^2)^+/a^6\rightarrow a^4\) in neuron \(\sigma _r\) is used for once, then 4 spikes are sent to neuron \(\sigma _{l_i^{(2)}}\), and 7 spikes remain in neuron \(\sigma _r\). Consequently, at step \(t+2\) neuron \(\sigma _r\) will accumulate 8 spikes (the other one spike is sent by neurons \(\sigma _{l_i^{(1)}}\)), and no rule in this neuron can be used again. For neuron \(\sigma _{l_i^{(2)}}\), 5 spikes are accumulated at step \(t+2\) (one spike is sent by neurons \(\sigma _{l_i^{(1)}}\), and the other 4 by neuron \(\sigma _r\)), and the rule \(a^5\rightarrow a^3\) is enabled. By applying this rule, 3 spikes will be sent to each of neurons \(\sigma _{l_i^{(s)}}\), \(3\le s\le 7\). By forgetting rule \(a^3\rightarrow \lambda\), the 3 spikes in each of neurons \(\sigma _{l_i^{(3)}}\), \(\sigma _{l_i^{(5)}}\), \(\sigma _{l_i^{(6)}}\) and \(\sigma _{l_i^{(7)}}\) will be removed at the next step. The three spikes in neuron \(\sigma _{l_i^{(4)}}\) enables rule \(a^3\rightarrow a^3\), and its application makes 3 spikes sent to neuron \(\sigma _{l_j}\). In this way, neuron \(\sigma _{l_j}\) becomes active, and the number of spikes remaining in neuron \(\sigma _r\) becomes 8, which means the number held by register r becomes 4.

If rule \(a^5(a^2)^+/a^6\rightarrow a^4\) in neuron \(\sigma _r\) is used for twice, then 8 spikes are sent to neuron \(\sigma _{l_i^{(2)}}\), and 1 spike remains in neuron \(\sigma _r\). At the next step, neuron \(\sigma _r\) will accumulates 2 spikes (the other spike is sent by neuron \(\sigma _{l_i^{(1)}}\)), and no rule can be used again in this neuron. For neuron \(\sigma _{l_i^{(2)}}\), it accumulates 9 spikes in total at step \(t+2\) (8 spikes are sent by neuron \(\sigma _r\) and one by neuron \(\sigma _{l_i^{(1)}}\)), enabling rule \(a^5(a^4)^+/a^4\rightarrow a^4\). Under a generalized mode, this rule can be used for once or twice:

  • At step \(t+2\), if rule \(a^5(a^4)^+/a^4\rightarrow a^4\) is used for once, then 4 spikes are sent to each of neurons \(\sigma _{l_i^{(s)}}\), \(3\le s\le 7\), and 5 spikes remain in neuron \(\sigma _{l_i^{(2)}}\). At step \(t+3\), rule \(a^5\rightarrow a^3\) in neuron \(\sigma _{l_i^{(2)}}\) is used, consuming all of the 5 spikes and sending 3 spikes to each of neurons \(\sigma _{l_i^{(s)}}\), \(3\le s\le 7\). In this way, each of neurons \(\sigma _{l_i^{(4)}}\), \(\sigma _{l_i^{(5)}}\), \(\sigma _{l_i^{(6)}}\) and \(\sigma _{l_i^{(7)}}\) accumulates 7 spikes at step \(t+4\), and no rule in these neurons can be used again. Neuron \(\sigma _{l_i^{(3)}}\) receives 4 spikes and 3 spikes from \(\sigma _{l_i^{(2)}}\) at step \(t+3\) and \(t+4\), respectively. The 4 spikes enable rule \((a^4)^+/a^4\rightarrow a^4\), sending 4 spikes to neuron \(\sigma _{l_i^{(9)}}\), while by applying rule \(a^3\rightarrow \lambda\) the 3 spikes are removed. In this case, neuron \(\sigma _{l_i^{(8)}}\) accumulates 4 spikes, enabling rule \((a^4)^+/a^4\rightarrow a^4\). Rule \((a^4)^+/a^4\rightarrow a^4\) in neurons \(\sigma _{l_i^{(8)}}\) and \(\sigma _{l_i^{(9)}}\) will be used forever. This makes the computation cannot halt and give a result, so it should be ignored.

  • At step \(t+2\), if rule \(a^5(a^4)^+/a^4\rightarrow a^4\) is used for twice, then 8 spikes are sent to each of neurons \(\sigma _{l_i^{(s)}}\), \(3\le s\le 7\), and 1 spikes remains in neuron \(\sigma _{l_i^{(4)}}\). In this case, rule \((a^4)^+/a^4\rightarrow a^4\) in neurons \(\sigma _{l_i^{(8)}}\) and \(\sigma _{l_i^{(9)}}\) will be used repeatedly. Thus the computation also enters an endless loop and it also should be ignored.

So in case 3, there are two possible simulations when the system using rules generally: in one case, neuron \(\sigma _{l_i}\) becomes active, and the number of spikes in neuron \(\sigma _r\) is decremented by 2; in the other case, computation does not halt and it gives no result. No matter what, SUB instruction \(l_i\) is correctly simulated in case 3.

To summarize, SUB instruction is simulated correctly in all these 3 cases:

starting from neuron \(\sigma _{l_i}\), system \(\varPi\) will end in \(\sigma _{l_j}\) if register r holds a number that is greater than 0, or it will end in \(\sigma _{l_k}\) if register r holds number 0. It is worthy noting the non-halting simulation is ignored for it gives no result.

ModuleFIN: Outputting the result of computation

The FIN module is shown in Fig. 3, and how a computation output its result is described as follows.

Fig. 3
figure 3

Module FIN for outputting the result

Full size image

Assuming that at the moment register 1 holding number n, \(n\ge 0\), machine M reaches its halting instruction \(l_{{h}}\), thus the computation of M halts. Correspondingly, in system \(\varPi\), neuron \(\sigma _{{l_{{h}} }}\) receives three spikes, and neuron \(\sigma _1\) contains 2n spikes. With three spikes inside, rule \(a^3\rightarrow a^3\) in neuron \(\sigma _{{l_{{h}} }}\) is applicable. By this application, 3 spikes are sent to neuron \(\sigma _{{l_{{\text{h}}}^\prime }}\), and makes rule \(a^3\rightarrow a\) in neuron \(\sigma _{{l_{{\text{h}}}^\prime }}\) enabled. With three spikes inside, rule \(a^3\rightarrow a\) in neuron \(\sigma _{{l_{{h}}^\prime }}\) is applicable, and this application makes 1 spike sent to neuron \(\sigma _1\). This 1 spike makes rule \(a(a^2)^+/a^2\rightarrow a\) in neuron \(\sigma _1\) enabled. Under a generalized mode, rule \(a(a^2)^+/a^2\rightarrow a\) can be applied for several times at step \(t+2\), nondeterministically chosen. No matter how many times the rule being applied at step \(t+2\), it will be applied repeatedly until there is only one spike remaining in neuron \(\sigma _1\). It is easy to figure out that for each time rule \(a(a^2)^+/a^2\rightarrow a\) is applied, 2 spikes are consumed and 1 spike is sent to environment. Besides, by forgetting rule \(a\rightarrow \lambda\) in neuron \(\sigma _1\), the remaining 1 spike will finally be removed. Therefore, during the computation the number of spikes sent from system to environment is n, which is exact the number held by register 1 when the computation of M halts.

We should stress that when instructions sharing register happens, an instruction of M is still correctly simulated. As shown in Figs. 2 and 3, during the simulation of SUB instruction \(l_{i} :({SUB}(r),l_{j} ,l_{k} )\), neuron \(\sigma _r\) will send 4k, \(k\ge 1\) spikes (or 1 spike) to each neuron with a synapse linked from neuron \(\sigma _r\). If there exist another SUB instruction \(l_{{i^{\prime}}}\) acting on the same register r, then neuron \(\sigma _r\) will send 4k, \(k\ge 1\) spikes (or 1 spike) to both neurons \(\sigma _{l_i^{(6)}}\) and \(\sigma _{{{l_i^{\prime}}}^{{(6)}} }\). Since the neuron \(\sigma _{{l_i^{\prime}}^{{(6)}} }\) do not receive the other spike from neuron \(\sigma _{l_i^{(1)}}\), the 4k spikes (or 1 spike) in neuron \(\sigma _{{l_{{i^{\prime}}}^{{(6)}} }}\) received from neuron \(\sigma _r\) will be removed by using rule \((a^4)^+/a^4\rightarrow \lambda\) or rule \(a\rightarrow \lambda\).

Based on these explanations as above, it is clear that the register machine M is correctly simulated by SNGR P system \(\varPi\). Therefore, \(N^{{{gen}}} (\varPi ) = N(M)\), which completes the proof. \(\square\)

4 Remarks and conclusion

In this work, an improved universal SNGR P system is present. In proof of the universality result, each neuron of the constructed system contains at most 5 rules, and for each time each firing rule consumes at most 6 spikes, and each forgetting rule removes at most 4 spikes. Compared with the construction in [46], these related parameters are optimized without losing the universality. It is worth noting that the constructed system in our proof works in generating mode. The related parameters may be further optimized when system works in accepting mode or works for function computing. This task is left as an open problem to the readers.