1 Introduction

Dynamic evaluation of the deep rock materials, subject to various types of loading from vehicles, earthquakes, underground excavation and construction, drilling, blasting and detonation, or hydraulic fracturing, is of high interest in geomechanics and geoengineering projects. Subsequently, rock materials experienced different ranges of strain rates and confining pressure. Therefore, accurately determining the triaxial failure strength of rock under different loading strain rates is a significant issue in geomechanics applications.

To evaluate major principal stress at failure, \(\sigma_1\), of rock, several laboratory research studies and modified empirical formula have been presented in the past (e.g., Handin et al. 1967; Sangha and Dhir 1975; Zhao 2000; Si et al. 2019; Liu et al. 2019, 2020; Xie et al. 2020). Donath and Fruth (1971) performed triaxial compression tests on lithographic limestone, marble, siltstone, and very fine-grained sandstone at five different strain rates ranging from \(10^{ - 7}\) to \(10^{ - 3} { }\;{\text{s}}^{ - 1}\). Their findings showed that there is no considerable effect on the siltstone or sandstone strength under the mentioned strain rates range and under confining pressures of 1000 and 2000 bars. Blanton (1981) conducted compression tests on Charcoal Granodiorite (confining pressure up to 450 MPa), Berea Sandstone, and Indiana Limestone (confining pressure up to 250 MPa) at strain rates ranging from \(10^{ - 2}\) to 10 \({\text{s}}^{ - 1}\). He stated that the actual failure stresses of the rocks are relatively independent of strain rate. Masuda et al. (1987) indicated that the compressive strength of granite increases linearly as the logarithm of the strain rate increases from \(10^{ - 8}\) to \(10^{ - 4} \;{\text{s}}^{ - 1}\) and that the strain rate dependency on the strength is increased ed at high confining pressures. Li et al. (1999) performed dynamic triaxial compression tests on the Bukit Timah granite under six confining pressures up to 170 MPa and four strain rates (\(10^{ - 4}\), \(10^{ - 3}\), \(10^{ - 1}\), and \(10^0 \;{\text{s}}^{ - 1}\)). They found that the deviator strength generally increases with the confining pressure and strain rate. Hokka et al. (2016) carried out dynamic triaxial compression tests on the Kuru Gray granite under eleven confining pressures up to 225 MPa and at strain rates of \(10^{ - 6}\) and 600 \({\text{s}}^{ - 1}\). Their study showed that the strength of Kuru granite increases with strain rate and confining pressure. They evaluated the effect of confining pressure and strain rate sensitivity on rock strength. Hoek–Brown and power-law models’ parameters are also calibrated based on their experimental data. Gong et al. (2019) conducted dynamic triaxial compression tests on the sandstone at five confining pressures (5, 7.5, 10, 12.5, and 15 MPa) and various strain rates from approximately 40–160 \({\text{s}}^{ - 1}\). They stated that the dynamic triaxial compressive strengths would linearly increase with the logarithm of the strain rate. Moreover, the dynamic triaxial compressive strength would linearly increase with the confining pressure under the same strain rate.

As illustrated above, a considerable amount of triaxial experimental data on rock samples has been recorded under various strain rates in the previous laboratory experiments. These valuable data provide the feasibility for developing a predictive model for the estimation of dynamic rock behavior, i.e., major principal stress at failure, \(\sigma_1\), of rocks. Despite extensive practical applications of \(\sigma_1\), a review of the available studies shows a lack of a generalized model for this key parameter. Moreover, the advent of technology with the increasing use of data mining and artificial intelligence techniques has led to the proposal and use of data-driven approaches. These techniques extract unknown structure relationships among parameters in databases. However, in the past, despite the vast literature on this domain, no effort was made to implement and develop data-oriented machine learning (ML) methods for estimating the strength of the rock under different confining pressure and strain rate.

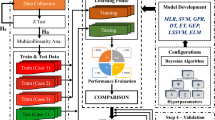
The present study aims to construct ensemble ML-derived triaxial strength criteria for predicting the major principal stress at failure, \(\sigma_1\) of seven rocks in terms of confining pressure (up to 450 MPa) and strain rate (from \(10^{ - 8}\) to 600 \({\text{s}}^{ - 1}\)) based on a considerable database of triaxial laboratory tests performed in previous studies. This study provides the first quantification of this potential. In this regard, Gaussian process (GP) with two kernels (Radial basis kernel function (RBF) and Pearson VII kernel function (PUK)), random forest (RF), decision table (DT), and K-nearest neighbor (KNN) algorithms were constructed. Then, individual ML methods are considered as the base model in the ensemble methods. Finally, results from the developed strength models were compared against the original experimental values and the potentiality of proposed computational ML models for the effective prediction of dynamic strength of rocks was evaluated and demonstrated. A reliable model is evidently easier to use in typical geomechanical projects than the expensive, time-consuming, and complicated field-based evaluation or laboratory techniques. Moreover, a sensitivity analysis was also performed and discussed to evaluate the effects of the input parameters on the rock dynamic strength modeling process. To the best of our knowledge, this study is the first to use and compare different individual and meta ensemble ML paradigms for this purpose.

This paper is organized as follows: First, the theoretical basis of the ML methods is presented in Sect. 2. Second, the performance evaluation indicators are presented in Sect. 3. Third, the statistical properties of the considered dataset are analyzed in Sect. 4. The compiled datasets from the literature will be considered to test the ML models. The use and results of the ML methods on the experimental triaxial rock dynamic strength dataset are presented in Sect. 5. A sensitivity analysis is detailed in Sect. 6. Discussions on the results, algorithms, importance of each feature are presented in Sect. 7. The concluding remarks are listed in Sect. 8.

2 Surrogate models

2.1 Gaussian process (GP)

A Gaussian process (GP) model is a nonparametric probabilistic model that directly expresses a prior probability distribution over a latent function (Rasmussen and Williams 2006; Fathipour-Azar 2021, 2022a, b, d). GP is a collection of random variables \(\left\{ {f\left( x \right):x \in X} \right\}\) characterized by its mean and covariance functions in the following form:

$$\left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {f(x_1 )} \\ {f(x_2 )} \\ \vdots \\ \end{array} } \\ {f(x_n )} \\ \end{array} } \right]\ N\left( {\left[ {\begin{array}{*{20}c} {m(x_1 )} \\ {m(x_2 )} \\ {\begin{array}{*{20}c} \vdots \\ {m(x_n )} \\ \end{array} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {k(x_1 ,x_1 )} \\ {k(x_2 ,x_1 )} \\ \end{array} } & {\begin{array}{*{20}c} {k(x_1 ,x_2 )} \\ {k(x_2 ,x_2 )} \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} \cdots \\ \cdots \\ \end{array} } & {\begin{array}{*{20}c} {k(x_1 ,x_n )} \\ {k(x_2 ,x_n )} \\ \end{array} } \\ \end{array} } \\ {\begin{array}{*{20}c} {\begin{array}{*{20}c} \vdots \\ {k(x_n ,x_1 )} \\ \end{array} } & {\begin{array}{*{20}c} \vdots \\ {k(x_n ,x_2 )} \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} \ddots \\ \cdots \\ \end{array} } & {\begin{array}{*{20}c} \vdots \\ {k(x_n ,x_n )} \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]} \right).$$
(1)

The preceding expression can be restated as follows:

$$f(x)\ GP\left( {m\left( x \right),{ }k(x,x^{\prime} )} \right),$$
(2)

where GP presents the GP model, \(m\left( x \right){ }\) is mean function of GP, \(k(x,x^{\prime} )\) is kernel function of GP, \(x\) and \(x^{\prime}\) indicate an arbitrary random variable.

Given a training set \(D = \left\{ {\left. {(x_i ,y_i )} \right|i = 1,{ }2, \ldots ,n} \right\}\) of data samples with unknown distribution, where \(x_i \in R^d\) and \(y_i \in R\). The assumption of GP regression method is that the relationship between input and output variables is calculated as follows:

$$y_i = f\left( {x_i } \right) + \varepsilon_i ,$$
(3)

where \(\varepsilon_i\) are additive noise variables (Gaussian noise); therefore, \(\varepsilon \ N\left( {0,\sigma_n^2 } \right)\). \(\varepsilon\) has zero mean and variance \(\sigma_n^2\). Consequently, the GP is stated as follows:

$$f\left( x \right)\ GP\left( {m\left( x \right),k\left( {x,x^{\prime} } \right) + \sigma_n^2 I} \right),$$
(4)

where \(I\) is the identity matrix. Generally, mean value of zero is preprocessed for the dataset. Consider \(u = \left\{ {\left. {(x_i^u ,y_i^u )} \right|i = 1, \ldots ,n} \right\}\) be a set of testing data samples drawn form the same unknown distribution as D. Considering the assumption that the training and the test data samples have a multivariate Gaussian distribution, the predictive distribution is presented as follows:

$$p\left( {\left. {\overline{y}^u } \right|\overline{y},{ }X,X^u } \right)\ N\left( {m^u ,\sigma^u } \right),$$
(5)

where \(m^u\) is the predictive mean value representing the most appropriate outputs for the inputs and \(\sigma^u\) indicates the predictive variance. The posterior mean and variance are expressed as follows:

$$\begin{aligned} & m^u = K\left( {X^u ,X} \right) \cdot \left[ {K\left( {X,X} \right) + \sigma_n^2 \cdot I} \right]^{ - 1} \cdot \overline{y}, \\ & \sigma^u = K\left( {X^u ,X^u } \right) - K\left( {X^u ,X} \right) \cdot \left[ {K\left( {X,X} \right) + \sigma_n^2 \cdot I} \right]^{ - 1} \cdot K\left( {X,X^u } \right). \\ \end{aligned}$$
(6)

\(K\left( {X^u ,X} \right) \in R^{n \times n}\) is described as \(K\left( {X^u ,X} \right)_{ij} = k\left( {x_i^u ,x_j } \right),{ }i,{ }j = 1,{ }2, \ldots ,n\). The same is for the \(K\left( {X,X} \right)\), \(K\left( {X^u ,X^u } \right)\), and \(K(X,X^u )\) cases. In addition:

$$\begin{aligned} & \overline{y} = \left[ {y_1 ,y_2 , \ldots ,y_n } \right]^{\text{T}} , \\ & \overline{y}^u = \left[ {y_1^u ,y_2^u , \ldots ,y_n^u } \right]^{\text{T}} , \\ & X = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {x_{11} } & {x_{12} } \\ {x_{21} } & {x_{22} } \\ \end{array} } & {\begin{array}{*{20}c} \cdots & {x_{1m} } \\ \cdots & {x_{2m} } \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots & \vdots \\ {x_{n1} } & {x_{n2} } \\ \end{array} } & {\begin{array}{*{20}c} \ddots & \vdots \\ \cdots & {x_{nm} } \\ \end{array} } \\ \end{array} } \right],{ }\;X \in R^{n \times m} . \\ \end{aligned}$$
(7)

\(X^u\) is described similarly. Therefore, any new value as the mean of a posterior predictive distribution can be estimated. In this study, two covariance functions (kernels), namely radial basis function kernel (RBF, Eq. 8) and Pearson VII function-based kernel (PUK, Eq. 9) were used:

$$k\left( {x,{ }x_i } \right) = e^{ - \gamma x - x_i^2 } ,$$
(8)
$$k\left( {x,{ }x_i { }} \right) = \left( {{1 / {\left[ {1 + \left( {2\sqrt {x - x_i }^2 \sqrt {{2^{\left( {1/\omega } \right)} - 1}} /l} \right)^2 } \right]^\omega }}} \right),$$
(9)

where \(\gamma\), \(l\), \(\omega\), and d are kernel constant parameters and have to be optimized for curve-fitting purposes. \(x - x_i\) is the Euclidean distance between \(x\) and \(x_i\). Besides, the data standardization was calculated through the following equation:

$$z_i = \frac{x_i - \mu }{\sigma },$$
(10)

where \(x_i\), \(\mu\), and \(\sigma\) are original data, mean, and standard deviation of the data, respectively.

2.2 Random forest (RF)

Random forest is an ensemble learning technique that creates a number of trees that correspond to random bootstrapped training samples. On the bootstrapping method, RF generates training samples using random binary decision trees. Moreover, a random selection of the training information is used to build the model from the initial database; however, the data that are not used are described out of a bag (OOB). In the RF methodology, two variables should be adjusted: the number of trees (k trees) and the number of features in the random subset at each node (m features). The average of the outputs of individual regression tree regressors constitutes the final output of RF (Breiman 2001). The structure of the RF algorithm is demonstrated in Fig. 1. The RF procedures for regression can be summarized as follows:

  • Step 1: The k tree bootstrap samples \(X_k\) (\(k =\) bootstrap iteration) are picked at random from the original dataset with replacement, each comprising about two-thirds of the elements. The OOB data for that bootstrap sample refer to the samples that were not included in \(X_k\).

  • Step 2: An unpruned regression tree is built with each bootstrap sample \(X_k\). Rather than picking the best split among all predictors, as in classic regression trees, the m predictor variables are picked at random and the best split among them is selected at each node.

  • Step 3: The OOB data is estimated by averaging the k tree estimations, as described below. The OOB components are used to calculate an error rate, which is referred to as the OOB estimate of the error rate (\(ERR_{OOB}\)):

    • Step 3.1: The OOB elements are estimated by the tree constructed using the bootstrap samples \(X_k\) at each bootstrap iteration.

    • Step 3.2: All trees in which the \(i\)th sample is OOB are examined for the \(i\)th sample (\(y_i\)) of the training dataset \(X\). In one-third of the k tree iterations, each sample of \(X\) is OOB on average. An aggregated prediction \(g_{OOB}\) is created based on the random trees. The error rate is calculated using the following formula:

      $$ERR_{OOB} = (1/k tree)\mathop \sum \limits_{k = 1}^{k\; tree} \left[ {y_i - g_{OOB} \left( {X_k } \right)} \right]^2 .$$
      (11)

    \(ERR_{OOB}\) is employed to avoid overfitting and to find the best k tree and m features values by minimizing \(ERR_{OOB}\). As a result, we first determined the optimal k tree and m features values to minimize \(ERR_{OOB}\), and then continued to create the RF model (Breiman 2001).

Fig. 1
figure 1

Structure of RF algorithm

Full size image

2.3 Decision table (DT)

A decision table (DT) is a model of a scheme-specific learning algorithm that displays complicated logics (Witten et al. 2011). This method uses a best-first search method to identify a suitable subset of features for inclusion in the table. DT creates a decision rule using a simple decision table majority classifier (Kohavi 1995) and sorts the rules and classes in several rows and columns. In general, a DT consists of four parts namely condition stubs, condition entries, action stubs, and action entries that each of which is located in a quarter of the table (upper left quarter, upper right quarter, lower left quarter, and lower right quarter). Finally, DT attempts to find an excellent match in the table for a given new instance.

2.4 K-nearest neighbors (KNN)

\(K\)-nearest neighbors (KNN) is a nonparametric algorithm that stores all training data samples and predicts the output value of test data samples based on a similarity measure (Aha et al. 1991). In this study, the brute force search algorithm is used to find the nearest neighbors and Euclidean distance is used to measure the distance between the data instances. The Euclidean distance \(d_i\) between \(x\) and each sample is sorted. If \(d_i\) is ranked in the \(i\)th place, the corresponding sample is referred to as the \(i\)th nearest neighbor with output \(y_i\). Ultimately, the prediction output \(\hat{y}\) would be the mean of the outputs of its \(K{ }\) nearest neighbors, described by the following equation:

$$\hat{y} = \frac{1}{k}\mathop \sum \limits_{i = 1}^k y_i .$$
(12)

2.5 Ensemble learning

Ensemble methods as expert systems are meta-algorithms that combine multiple ML approaches into one predictive model. Stacking, also known as stacked generalization, is an ensemble ML approach that uses a meta model to combine several heterogeneous base artificial intelligence and ML models. The base model is trained on the training data through k-fold cross-validation, and the meta model is trained on the base models' predictions of each fold. On the other hand, voting entails creating a number of submodels and incorporating each of them in a voting procedure to determine what should be the prediction's outcome. The concept of stacking model is illustrated in Fig. 2.

Fig. 2
figure 2

Schematic representation of the stacking model

Full size image

3 Performance evaluation criteria

The outputs of each ML and ensemble models are major principal stress. Then, these predictions are compared against the observations. In the present research, the following model performance evaluation metrics (Eqs. 11–14) were applied which are: correlation coefficient (R), root means square error (RMSE), mean absolute error (MAE), and Nash–Sutcliffe Efficiency (NSE).

$$R = \frac{{\sum_{i = 1}^n \left( {\sigma_{1,measured} - \overline{\sigma }_{1,measured} } \right).\left( {\sigma_{1,predicted} - \overline{\sigma }_{1,predicted} } \right)}}{{\sqrt {{\sum_{i = 1}^n \left( {\sigma_{1,measured} - \overline{\sigma }_{1,measured} } \right)^2 \sum_{i = 1}^n \left( {\sigma_{1,predicted} - \overline{\sigma }_{1,predicted} } \right)^2 }} }},$$
(13)
$$RMSE = \sqrt {{\frac{1}{n}\mathop \sum \limits_{i = 1}^n (\sigma_{1, measured} - \sigma_{1, predicted} )^2 }} ,$$
(14)
$$MAE = \frac{1}{n}\mathop \sum \limits_{i = 1}^n \left| {\sigma_{1, measured} - \sigma_{1, predicted} } \right|,$$
(15)
$$NSE = 1 - \frac{{\sum_{i = 1}^n \left( {\sigma_{1, measured} - \sigma_{1, predicted} } \right)^2 }}{{\sum_{i = 1}^n \left( {\sigma_{1,measured} - \overline{\sigma }_{1,measured} } \right)^2 }},$$
(16)

where \(\sigma_{1,{ }measured}\), \(\overline{\sigma }_{1,measured}\), \(\sigma_{1,{ }predicted}\), and \(\overline{\sigma }_{1,predicted}\) denote the measured, mean of measured, predicted, and mean of predicted values of major principal stress, \(\sigma_1\), respectively, and \(n\) is the total number of observations. The correlation coefficient (R) index describes the weight of the relationship between measurements and predictions \(\sigma_1\) values. RMSE shows the residual value between the predictions and the measurements \(\sigma_1\) values. MAE shows the closeness of the prediction to the measurement \(\sigma_1\) values. NSE is for assessing the capability of proposed methods. R = 1, RMSE = 0, MAE = 0, and NSE = 1 represents a perfect prediction.

4 Statistical analysis of the used dataset

In this study, the dataset comprised the triaxial compression test results under different confining pressure and strain rates on seven rocks including Charcoal Granodiorite, Berea Sandstone, and Indiana Limestone (Blanton 1981), Granite (Masuda et al. 1987), Bukit Timah granite (Li et al. 1999), Kuru granite (Hokka et al. 2016), and Sandstone (Gong et al. 2019). The total database contained 267 datasets. Figure 3 presents the scatterplot matrix of the variables with the histogram in diagonal and correlation coefficient in the upper part. In Fig. 4, the histogram, density, and violin plot (combination of box plot and density) describe the distribution pattern of data. 213 sets of data were randomly allocated for training and the remaining 54 data sets (20% of all data) were used to test the developed models. The statistical parameters of the training and testing databases are presented in Table 1. After training the proposed ML models, the testing data were fed into the developed models to predict the target parameter. The evolved models were evaluated and compared as stated in Sect. 3 using statistical indicators, including R, MAE, RMSE, and NSE in the training and testing periods. The results are presented in the next section.

Fig. 3
figure 3

Scatterplot matrix of the variables with histogram in diagonal and correlation coefficient

Full size image
Fig. 4
figure 4

Histogram, density, and violin plot of the dataset

Full size image
Table 1 Statistics analysis of the training and testing datasets
Full size table

5 Results

The objective of this research is to propose and investigate the ability and performance of two ensemble learning models namely stacking and voting with five developed ML algorithms, namely the GP, RF, DT, and KNN models, to predict major principal stress, \(\sigma_1\). Trial-and-error and grid search methods were performed with different initial values of parameters for each model to achieve the optimal models’ architectures and thereafter performance of developed ML-based strength models was evaluated and compared in accordance with error indices and real data. The developed model was constituted by three input parameters (i.e., rock type, confining pressure, and strain rate) and one output (i.e., major principal stress).

An ensemble of GP, RF, DT, and KNN algorithms using stacking and voting methods is constructed. These ML models are base models and linear regression is considered as the meta model to combine results of these base ML models for the stacking methods, and the average of probabilities is used as a combination rule of voting methods. 10-fold cross-validation is used in the ensemble stacking ML method.

Figure 5 presents the values of R, MAE, RMSE, and NSE of the developed ML-based models for training and testing datasets. Based on the statistical measured presented in Fig. 5, RF and KNN, in particular, had the best performance in terms of R, MAE, RMSE, and NSE values in the training and testing dataset. GP-RBF and GP-PUK are in the next place. According to Fig. 5, PUK and RBF functions performed approximately the same in terms of accuracy and error. DT showed poor performance among evolved models with R, MAE, RMSE, and NSE values equal to 0.984, 52.025 MPa, 72.069 MPa, and 0.968 for the training stage and 0.982, 64.831 MPa, 81.099 MPa, and 0.962 for the testing stage. Ensemble stacking and voting learning methods demonstrated high performances in terms of R, MAE, RMSE, and NSE values similarly to RF and KNN models.

Fig. 5
figure 5

Radar plot of the models’ performances in predicting major principal stress, \(\sigma_1\) (MPa) using the developed models for training (solid blue) and testing (dashed orange) datasets (color figure online)

Full size image

The accuracy of the developed models is examined and compared by plotting the predicted versus measured values of the \(\sigma_1\) for the testing sets as shown in Fig. 6. The comparisons show that there is good agreement between the results of RF, KNN, stacking, voting, then GP-RBF and GP-PUK, and finally the DT models and measured stress values. The developed models’ results lie around a 45° straight line implying a good fit. From the plots presented in Figs. 5 and 6, it could be concluded that the evolved individual and ensemble ML-based models demonstrate good performance and capability and therefore can predict the \(\sigma_1\) of rock with appropriate accuracy for the testing dataset.

Fig. 6
figure 6figure 6

Plots of the observed and predicted major principal stress, \(\sigma_1\) (MPa) using the models developed for the testing dataset

Full size image

Figure 7 presents cumulative distribution functions (CDFs) of the observed and predicted major principal stress, \(\sigma_1\) (MPa) using the models developed for (a) training and (b) testing datasets, respectively. In Fig. 7, the CDFs of estimated \(\sigma_1\) from RF, KNN, stacking, and voting are close to that of measured \(\sigma_1\). This agreement suggests that the information contained in the estimated \(\sigma_1\) using these developed models is consistent with that obtained from the measured \(\sigma_1\). Although the CDFs of the estimated \(\sigma_1\) obtained from GP-RBF, GP-PUK, and DT models are also close to that of measured \(\sigma_1\) and follows the pattern and trend of the CDF of measured \(\sigma_1\), small errors and deviations could be seen between these models and measured \(\sigma_1\), particularly for DT model. This further confirms the statistical results of the estimated \(\sigma_1\) (Figs. 5, 6), indicating that RF, KNN, stacking, and voting provide better estimates than other models.

Fig. 7
figure 7

Cumulative distribution function of the observed and predicted major principal stress, \(\sigma_1\) (MPa) using the models developed for a training and b testing datasets

Full size image

Overall error prediction distribution of developed models in the training and testing phases is shown in the violin plot in Fig. 8. The negative and positive prediction error values indicate the developed models’ over-and under-estimation behavior, respectively. In this figure, the prediction error of RF, KNN, stacking, and voting models is lower than that of the DT model. A similar prediction error could be seen for GP-RBF and GP-PUK in the training and testing phases.

Fig. 8
figure 8

Violin plot for error prediction using the developed models in a training and b testing datasets

Full size image

Finally, Taylor diagrams are presented in Fig. 9 for training and testing datasets. Taylor diagram (Taylor 2001) is a concise description of statistical analysis that demonstrates how well the constructed models reproduce the measured \(\sigma_1\) values. It is a mathematical visualization approach that is meant to display the correctness of various models in terms of the correlation coefficient, the root-mean-square-difference, and the ratio of the two variables’ standard deviations. The distance between each algorithm and the measured point represents how accurately each model matches the measured \(\sigma_1\) values. The stacking and ensemble voting, as well as RF and KNN models, predicted all output parameters more accurately in the training (Fig. 9a) and testing (Fig. 9b) phases and, therefore, lies nearest the measured point.

Fig. 9
figure 9

Taylor diagram representing model performance

Full size image

6 Sensitivity analysis

A parametric study is a useful tool for determining the importance and effectiveness of the relevant input variables on the objective (output) variable. The cosine amplitude method (CAM) (Yang and Zhang 1997) was employed in this study to identify the most sensitive factors influencing the major principal stress, \(\sigma_1\). The degree of sensitivity of each input factor (rock type, confining pressure, and strain rate) was assigned by establishing the strength of the relationship \((R_{ij} )\) between the \(\sigma_1\) and the input factors under consideration. A higher CAM value indicates a greater impact on the \(\sigma_1\).

Consider n data samples are gathered from a common data array \(X\); then the datasets employed to construct a data array \(X\) are defined as follows:

$$X = \left\{ {x_1 ,x_2 ,x_3 , \ldots ,x_m } \right\}.$$
(17)

Each of the elements \(x_i\) in the data array \(X\) is a vector of length \(m\), that is

$$x_i = \left\{ {x_{i1} ,x_{i2} ,x_{i3} , \ldots ,x_{im} } \right\}.$$
(18)

Therefore, each of the data pairs can be thought of as a point in an \(m\)-dimensional space, wherein each point requires \(m\) coordinates for a complete description. The strength of the relationship between the data pairs \(x_i\) and \(x_j\) is estimated and demonstrated using the following equation:

$$R_{ij} = \frac{{\sum_{k = 1}^m x_{ik} x_{jk} }}{{\sqrt {{\sum_{k = 1}^m x_{ik}^2 \sum_{k = 1}^m x_{jk}^2 }} }}, \quad 0 \le R_{ij} \le 1,$$
(19)

where \(i,j = 1,2, \ldots ,n.\)

According to Eq. (19), the parametric study results, that is, the influence of the input variables on the \(\sigma_1\) are illustrated in Fig. 10. As can be seen from the figure, the confining pressure is the most influential variable; however, strain rate has the lowest influence on the target variable.

Fig. 10
figure 10

The parametric study results for major principal stress, \(\sigma_1\)

Full size image

7 Discussion

Triaxial dynamic strength is of interest in various fields of engineering and science. Estimating triaxial rock dynamic strength is an important task and has gained utmost research relevance in recent times due to its complexities and persistent applications in geomechanics and geoengineering. However, conducting experiments to determine rock dynamic strength is time-consuming and requires costly laboratory equipment. Thus, the prediction of dynamic strength using soft computing techniques is an effective solution for quick estimation and avoids costly numerically, laboratory, or on-field experiments (Fathipour Azar and Torabi 2014; Fathipour-Azar et al. 2017, 2020; Fathipour-Azar 2021, 2022a, b, c, d, e, f, g, 2023a, b, c). In this study, various individual and ensemble ML techniques including GP, RF, DT, KNN, stacking, and voting models were introduced to assess major principal stress subject to confining pressure and loading strain rate. This research is the first to quantify this potential.

Results demonstrate that the developed individual and ensemble surrogate models possess significant capability in mimicking the unknown, nonlinear, and complex relationships between triaxial dynamic strength and its influential variables (Figs. 4, 5, 6, 7, 8). In this paper, generalized efficiency and performance of the proposed developed models are demonstrated by considering various input variables, including different rock types, confining pressure up to 450 MPa, and strain rates ranging from \(10^{ - 8}\) to 600 \({\text{s}}^{ - 1}\) (Table 1, Figs. 3, 4). Future investigations could benefit from including additional geological factors to create a more comprehensive predictive model for rock strength.

The potential application of a wide range of data-oriented ML algorithms is explored. In general, GP is a probabilistic-based regression approach; RF and DT are decision tree and table-based approaches; KNN as a lazy learner is based on the nearest search algorithm. Therefore, while combining the advantages of different approaches using meta ensemble learning techniques is valuable, individual algorithms like RF have also demonstrated high performance in terms of accuracy and low error (Fig. 5), agreement between observed and predicted values (Fig. 6), and CDFs (Fig. 7). The Taylor diagrams further validate the accuracy of these models in both training and testing phases (Fig. 9). The utilization of different algorithms can strengthen the statement of the analysis. The ensemble learning methods, including stacking and voting, contribute to the overall success of the predictive models. Although stacking may be viewed as a generalization of voting, the capacity to explore the solution space with multiple models in the same issue is a benefit of ensemble learning methods. The strength of these ML algorithms lies in their simplicity, ease of implementation, and they are inexpensive to build and run-in comparison to theoretical, numerical, and experimental models. The proposed models in this study can be practically used to estimate rock dynamic strength in geomechanics and geoengineering applications.

A parametric study using CAM indicates that confining pressure is the most influential variable, while and strain rate is the least influential variable on the major principal stress variable. Moreover, all evolved ML models show approximately the same importance for each feature (Fig. 10). In fact, the parametric analysis results are derived from the inferences drawn from the input–output relations in the measured dataset. Therefore, they can be convincing and practical.

8 Conclusions

The prediction of rock failure strength under various confining pressures and strain rate is a significant issue in geomechanics engineering. In the present research, a triaxial experimental database with confining pressure up to 450 MPa and under different loading strain rates ranging from \(10^{ - 8}\) to 600 \({\text{s}}^{ - 1}\) was used. The aim of this research is to introduce ensemble ML methods to predict the major principal stress depending on confining pressure and loading strain rate. The developed models namely GPs, RF, DT, KNN, stacking, and voting methods are compared with the measured principal stress values. The findings of this study demonstrate the good performance and capability of the proposed individual and ensemble ML-derived dynamic strength models. Therefore, the used ML techniques can be considered as a reliable surrogate technique to model triaxial rock strength and they would be more economical than other available approaches. Finally, the comparisons show that there is a better agreement between the results of the RF, KNN, stacking, and voting models and principal stress values than the GP-TBF, GP-PUK, and DT models. Furthermore, PUK and RBF functions performed approximately the same in terms of accuracy and error. At the end of modeling process, sensitivity analysis was conducted and revealed that confining pressure is the most influential variable, while strain rate is the least influential variable on the major principal stress variable, \(\sigma_1\) in this study.