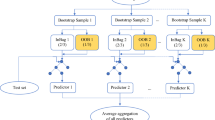
Abstract
The accurate evaluation of polyaxial rock strength is important in the mining, geomechanics, and geoengineering fields. In this research, hybrid meta models based on the boosting additive regression (AR) combined with three machine learning (ML) methods are developed for polyaxial rock strength predicting. The ML algorithms used include Gaussian process regression (GP), random tree (RT), and M5P methods. Polyaxial tests for 14 different rocks from published literature are used for assessing these data-oriented based strength criteria. The input variables are minor principal stress and intermediate principal stress data. The modeling is evaluated by coefficient of determination (\({R}^{2}\)), root mean square error (RMSE), and mean absolute error (MAE) statistical metrics. Results indicated that the hybrid AR-RT model performed superior prediction results (\({R}^{2}\) = 1, RMSE = 0 MPa, and MAE = 0 MPa) in the training phase and (\({R}^{2}\) = 0.987, RMSE = 29.771 MPa, and MAE = 22.517 MPa) in the testing phase. The findings of this study indicate that boosting-based additive regression algorithm enhanced developed hybrid models’ performances. Moreover, AR-RT and RT demonstrate promising results and are feasible for modeling polyaxial rock strength prediction. The RT and M5P models visualize variables and their thresholds in a simple and interpretable way. Also, sensitivity analysis indicates that input intermediate principal stress is the most effective parameter on the output polyaxial rock strength. Finally, successful implementation of the probabilistic and interpretable tree-based regressions can capture uncertainty of the model and be an alternative to complicated conventional strength criteria.
Highlights
-
Study proposes hybrid approach for estimating polyaxial failure strength using probabilistic- and three-based boosting additive regression.
-
Hybrid AR-RT model performs better than other models for predicting polyaxial rock failure strength.
-
Major principal strength is estimated based on rock type, minor and intermediate principal stresses, using 14 different rocks including igneous, metamorphic, and sedimentary rocks.
-
Sensitivity analysis indicates that σ3 and rock type significantly impact polyaxial rock strength prediction, while σ2 has a minor impact.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
The estimation of polyaxial rock strength is of great importance in the mining, geomechanics, and geoengineering areas due to its increasing application in great depth projects such as wellbore stability and storage caverns or in order to make excavation or hydrofracturing. Furthermore, as engineering depth increases, the true triaxial stress condition (\({\sigma }_{1}\) > \({\sigma }_{2}\) > \({\sigma }_{3}\)) becomes more general. Moreover, there is a growing body of experimental evidence (Mogi 1967, 1971a, b; 2007; Takahashi and Koide 1989; Chang and Haimson 2000; Haimson and Rudnicki 2010; Sriapai et al. 2013; Feng et al. 2016; 2019; Ma and Haimson 2016) to illustrate that the intermediate principal stress (\({\sigma }_{2}\)) is a significant contributor to their compressive strength, deformability, failure types, and fault angle of rocks. However, different rock types exhibit varying degrees of \({\sigma }_{2}\) dependency.
A number of theoretical and empirical failure criteria have been proposed to model geomaterial strength in the last century, among which Mohr–Coulomb, Hoek and Brown, Lade–Duncan, Wiebols and Cook, Mogi, and Drucker–Prager criteria are widely adopted and well-known failure criteria. Cohesion, friction angle, hardness parameter (\(m\) of Hoek–Brown criterion), and uniaxial strength are basic constants to define these criteria. These well-known expressions have been developed and modified or unified by this time. In addition to smoothness and convexity problems, in the process of developing failure criteria, determining strength parameters that best-fit the whole sets of experimental data is a challenge to achieve the precise form of a failure equation (Lee et al. 2012). In general, the generalized theoretical and mathematical modeling of realistic nonlinear rock behaviour under different multiaxial stresses is a difficult task, which also needs further constants, constrains, and assumptions. Despite the existence of several strength criteria, developing a universal strength criterion capable of describing the behavior of different materials subject to anisotropic stress conditions is of great interest (Li et al. 2021; Fathipour-Azar 2022b). Comparisons of some of these failure criteria were made by Colmenares and Zoback (2002), Zhang (2008), Benz and Schwab (2008), You (2009), Rafiai (2011), Priest (2010, 2012), Zhang et al. (2010), Lee et al. (2012), Jiang and Xie (2012), Sriapai et al. (2013), Liolios and Exadaktylos (2013), Rukhaiyar and Samadhiya (2017b), Bahrami et al. (2017), Jiang (2018), Ma et al. (2020), and Feng et al. (2020). It has been revealed that the performance of a failure criterion to polyaxial strength data is affected by both the type of failure criterion and the varying \({\sigma }_{2}\)-dependence of the rock (Ma et al. 2020). Because of the considerable differences between hard and soft rocks, different failure criteria may be used (e.g., soft rocks (Wang and Liu 2021) and hard rocks (Feng et al. 2020)). Strength models have been built under circumstances such as for specific rock type and stresses (Sheorey 1997; Yu et al. 2002; Rafiai and Jafari 2011; Rafiai et al. 2013; Moshrefi et al. 2018; Gao 2018; Fathipour-Azar 2022b), while data-oriented machine learning (ML) methods are flexible. ML as a statistical modeling technique identifies hidden and unknown implicit patterns and relation between independent and dependent parameters of a given experimental database without any explicit description. Generalization (applicability to different rocks and stress conditions) and accuracy are key factors for rock failure criteria assessment.
In the field of rock mechanics, several studies have investigated the effectiveness of using ML techniques to predict the failure strength of intact rocks under polyaxial and triaxial stress conditions. Some of these studies include Rafiai and Jafari (2011), Rafiai et al. (2013), Kaunda (2014), Zhu et al. (2015), Rukhaiyar and Samadhiya (2017a), Moshrefi et al. (2018), and Fathipour-Azar (2022b).
Rafiai and Jafari (2011) and Rafiai et al. (2013) developed artificial neural network (ANN)-based failure criteria for different rocks under triaxial and polyaxial conditions. These criteria were compared with traditional failure criteria proposed by Bieniawski and Yudhbir, Hoek and Brown, modified Weibols and Cook, and Rafiai, and showed better efficiency. Similarly, Kaunda (2014) used ANN to study the effect of intermediate principal stress on the strength of intact rock for five different rock types.
Zhu et al. (2015) used least squares support vector machines (LSSVM) to establish a criterion for rock failure and compared it with Mohr–Coulomb and Hoek–Brown criteria. Rukhaiyar and Samadhiya (2017a) used ANN to predict the polyaxial strength of intact sandstone rock types and found it to be more accurate than five conventional polyaxial criteria namely modified Wiebols and Cook, Mogi-Coulomb, modified Lade, 3D version of Hoek–Brown, and modified Mohr–Coulomb criteria for testing dataset.
Moshrefi et al. (2018) compared ANN, SVM, and multiple regression models to predict the triaxial and polyaxial strength of shale rock types. They found that ANN predicted strength with minimum root mean squared error compared to Drucker-Prager and Mogi-Coulomb failure criteria. Fathipour-Azar (2022b) proposed an interpretable multivariate adaptive regression splines-based polyaxial rock failure strength with \({R}^{2}\) = 0.98 and used multiple linear regression, SVM, random forest, extreme gradient boosting, and K-nearest neighbors methods to predict major principal stress (\({\sigma }_{1}\)) at the failure of intact rock material under the polyaxial stress condition. In general, using ML techniques displayed superior performance accuracy and generalization ability in predicting the failure strength of different intact rocks subject to polyaxial conditions compared with conventional failure criteria in the form of such as Drucker–Prager, modified Weibols and Cook, and Mogi-Coulomb criteria.
To our knowledge, there is not an effort in the literature consisting of probabilistic and interpretable tree based-ML methods, namely the Gaussian process regression model (GP), random tree (RT), and M5P algorithms, to predict failure strength (major principal stress at failure) in polyaxial empirical and computational failure models for rocks. One of the advantages of using the GP model is its probabilistic nature, which allows the model to define the space of functions that relate inputs to outputs by specifying the mean and covariance functions of the process. By doing so, the GP provides a more informative and flexible representation of the underlying data distribution than deterministic models, and allows for uncertainty quantification in both the predictions and the model parameters. Tree-based models provides a more transparent way to predict rock failure strength for different rock types. The advantage of tree-based approach lies in its interpretability, which enables the investigation of how the algorithm uses the selected inputs and help in understanding the contribution of each input variable to the output, which can be valuable in rock engineering applications.
This study explores this gap in the current literature by implementing not only with GP, RT, and M5P algorithms but also by using a hybrid approach based on boosting additive regression and these three ML methods as an alternative way to the commonly used black box models (e.g., ANN) or conventional models to predict failure strength (major principal stress) from rock type, minor principal stress, and intermediate principal stress data. The advantage of using a hybrid approach based on boosting additive regression and these three ML methods is that it can combine the strengths of different models and improve the accuracy of the predictions. Boosting additive regression can enhance the performance of the GP and tree-based models by combining them in an ensemble method that focuses on the strengths of each model. The hybrid approach can also reduce overfitting and increase the generalization of the model, allowing it to be applied to a wider range of rock types. The proposed approaches also offer the advantage of generalization as it can be applied to a wide range of rock types, unlike the conventional approaches that are often designed for each specific rock type separately. The validation and comparison of developed failure models were performed using coefficient of determination (\({R}^{2}\)), root mean square error (RMSE), and mean absolute error (MAE) statistical metrics. Moreover, a sensitivity analysis was also performed and discussed to evaluate the effects of the input parameters on the polyaxial rock strength modelling process.
2 Data Mining Algorithms
Data mining is an approach that employs data-oriented techniques to find unknown and complex patterns and relationships within the data. In this study, ML techniques, namely Gaussian process regression model (GP), random tree (RT), M5P, and additive regression (AR) models are implemented to predict major principal stress of rock at failure. The performances of different models were assessed based on calculating the error indices of the RMSE and MAE. RMSE is used to measure the differences between predicted values by the models and the actual values. MAE is a quantity used to measure how close predictions are to the actual values. \({R}^{2}\) is also used to evaluate the correlation between the actual and predicted values. The three statistical RMSE, MAE, and \({R}^{2}\) formulas that are utilized to compare the performances of developed models are as follows:
where \({t}_{k}\) and \({y}_{k}\) are target and output of developed models for the kth output, respectively. \(\overline{t }\) is the average of targets of models and \(N\) is the total number of events considered. The models that minimized the two error measures beside the optimum of \({R}^{2}\) is selected as the best ones.
2.1 Gaussian Process Regression Model
Gaussian process (GP) regression is a nonparametric Bayesian method to regression issues (Rasmussen and Williams 2006; Wang 2020). Because of the kernel functions, GP regression is very efficient in modeling nonlinear data.
Consider a training dataset of \(D = \left\{ {x_{i} ,y_{i} } \right\}_{i = 1}^{n}\), where \(X\in {R}^{D*n}\) represents the input data (design matrix) and \(y\in {R}^{n}\) is the corresponding output vector. In this study, rock type, minor principal stress, and intermediate principal stress are input variables for predicting failure strength (major principal stress). The GP regression output is major principal stress. Therefore, \(x = \left[ {{\text{rock type}},{ }\sigma_{3} ,\sigma_{2} } \right]\) and \(y=[{\sigma }_{1}]\). In GP regression, it is assumed that the output can be expressed as follows (Rasmussen and Williams 2006; Ebden 2015):
where \(\varepsilon \sim N(0,{\sigma }_{n}^{2})\in R\) is the equal noise variance for all \({x}_{i}\) samples.
The GP method considers n observations in \(y=\left\{{y}_{1},\cdots ,{y}_{n}\right\}\) vector as a single point instance of a multivariate Gaussian distribution. This Gaussian distribution can also be assumed to have the mean of zeros. The covariance function defines the relationship of one observation to another.
A covariance function \(k(x, x\mathrm{^{\prime}})\) describes a relationship between observations and is often defined by "exponential squares" in GP method to approximate function, which is as follows:
where \({\sigma }_{f}^{2}\) denotes the maximum allowable covariance. It is worth noting that \(k\left(x, {x}^{\mathrm{^{\prime}}}\right)\) equals to the maximum allowable covariance only when \(x\) and \({x}^{\mathrm{^{\prime}}}\) are so close to each other; thus, \(f\left(x\right)\) is approximately equal to \(f\left({x}^{\mathrm{^{\prime}}}\right)\). Besides, \(l\) indicates the kernel function's length. Furthermore, \(\delta \left(x, {x}^{\mathrm{^{\prime}}}\right)\) is the Kronecker delta function, which has the following definition:
In terms of the training dataset, final aim of the learning process is to predict the output value of \(y*\) for a new input pattern. To accomplish this, three covariance matrices should be developed as follows:
The data sample can be represented as a sample of a multivariate Gaussian distribution based on the Gaussian distribution assumptions, as follows:
where \(T\) is matrix transpose. Since \(\left.{y}_{*}\right|y\) is developed from a multivariate Gaussian distribution with the mean of \({K}_{*}{K}^{-1}y\) and the variance of \({K}_{**}-{K}_{*}{K}^{-1}{K}_{*}^{T}\), the estimated mean and variance of the predicted output \({y}_{*}\) are stated as follows:
Following the determination of kernel function hyperparameters, Bayesian inference can find model parameters such as \(x\) and \({\sigma }_{n}\). Following training, the GP model can be used to predict unknown values based on known input values.
It is important to select a suitable covariance or kernel function since it has a direct impact on predictive efficiency. In the study, two different (Gaussian or Radial basis kernel and Pearson VII kernel function (PUK)) widely used and well-understood kernel functions were selected for GP model development and to provide a good baseline for comparison. These two kernels have been shown to perform well in a variety of applications (Fathipour-Azar 2021a, b; 2022a, b, c, d, e).
where \(\gamma\), \(\sigma\), and \(\omega\) are kernels parameters (also known as hyper-parameters). In this study, the data are normalized before fitting a GP using the following equation:
where \({d}_{\mathrm{norm}}\) is the normalized data, \({d}_{i}\) represents the experimental value of value for \(i\)th data point, and \({d}_{\mathrm{max}}\) and \({d}_{\mathrm{min}}\) show the maximum and minimum values of the data, respectively.
2.2 Random Tree (RT) Model
A decision tree constructs classification or regression models in the framework of a tree structure. RT uses a bagging idea to splits a random data set into sub-spaces for constructing a decision tree. Therefore, RT is generally built by a stochastic process and assigning the best among the sub-spaces of randomly selected attributes at that node. Since the features are chosen at random, all trees in the group have an equal chance of being sampled (Witten and Frank 2005).
2.3 M5P Model
The M5P tree is a reconstruction of Quinlan's M5 algorithm (Quinlan 1992). This technique is based on a binary decision tree that assigns a series of linear regression functions at the leaf (terminal) node, which helps in estimating continuous numerical parameters. This model uses two steps to fit the model tree. In the first step, the data are split into subsets and form a decision tree. The splitting of decision tree is based on treating the standard deviation of class values reaching a node. It measures the error at the nodes and evaluates the expected reduction in error as a result of testing each parameter at the node. The Standard Deviation Reduction (SDR) is calculated as follows:
where \(N\) is a set of examples that reach the node. \({N}_{i}\) is ith outcome of subset of examples of potential set, and \(sd\) is the standard deviation. Due to the splitting process, the standard deviation of child node will be less than that of the parent node (Quinlan 1992). After evaluating all possible splits, M5P tree chooses the one that maximises the error reductions. This process of splitting the data may overgrow the tree which may cause over fitting. To overcome this overfitting, the next step, the overgrown tree is pruned and then the pruned sub-trees are replaced with linear regression functions.
2.4 Additive Regression (AR)
In order to improve the performance of the above mentioned (i.e., GP, RT, and M5P) basic regression base approaches, additive regression (AR) as an implementation of gradient boosting ensemble learning technique is used (Friedman 2002). In this algorithm, each iteration applies a new base model to the residuals from the previous one. The predictions of each base model are added together to make a final estimation.
3 Dataset for Models
Polyaxial tests dataset for fourteen different rocks including Aghajari sandstone; Jahrom Dolomite; Soltanieh Granite; Pabdeh Shale; Asmari Limestone; Karaj Trachyte; Karaj Andesite; Naqade Amphibolite; Jolfa Marble; Hormoz Salt; Mahalat Granodiorite; Shourijeh Siltstone; Shahr-e babak Hornfels; Chaldoran Metapelite rocks’ results were taken from published literature (Bahrami et al. 2017) are used for assessing data-oriented strength criteria. Scatter plot of variables with correlation and diagonal frequency histograms is presented in Fig. 1. Scatter plots below and on the left of the diagonal (lower triangle) show the relationships failure strength (major principal stress), minor principal stress, intermediate principal stress, and rock type. Values above and on the right of the diagonal (upper triangle) show the coefficient of determination between variables. The diagonal graphs show the frequency histograms and density plots of the corresponding variable. A total of 480 samples were used for the predictive modeling, out of which, 80% were randomly selected for the training of models and the remainder 20% for testing developed models in estimating major principal stress based on minor and intermediate principal stresses. The statistical parameters of the training and testing datasets are presented in Table 1.
4 Results
In the present study, data-oriented surrogate models are first developed and compared to predict polyaxial rock strength. To improve the performance of these basic regression base approaches, AR as an implementation of boosting approach is used.
Grid search optimization is applied to tune hyperparameters of ML models. Grid search trains a ML model with each combination of possible values of hyperparameters and assesses its performance using a predefined measure. For the GP regression based on the RBF kernel, the optimum values for \(\varepsilon\) and \(\gamma\) are determined 0.001 and 3 respectively. The optimal hyper-parameters of the GP model based on the PUK kernel are \(\varepsilon =0.001\), \(\omega =0.1\), and \(\sigma =4\), which provide better performance values. In case of the RT model, 3 randomly chosen attribute is determined as optimal parameter. For the M5P model, minimum 8 instances at a leaf node are used.
The calculated performance indices (\({R}^{2}\), RMSE, MAE) for developed data-oriented models in the training and testing phases are shown in Fig. 2. Comparison of results presents that the AR-RT outperforms other developed models for the training and testing periods, indicating improved performance in terms of the highest \({R}^{2}\) (1) and the lowest RMSE (0 MPa) and MAE (0 MPa) in the training phase and the highest \({R}^{2}\) (0.987) and the lowest RMSE (29.771 MPa) and MAE (22.517 MPa) in the training phase. According to the statistical indices presented in Fig. 2, using AR based on boosting enhanced the model’s performance. This improvement is more noticeable in AR-M5P model compared to M5P model in the training and testing phases.
The M5P model tree-based polyaxial rock strength regression tree structure is shown in Fig. 3. As can be observed, 21 linear models (LMs) or rules have been constructed based on conditional statements. In this diagram, boxes signify terminal leaf nodes with labels within, whilst ellipses indicate other nodes with a symbol inside alluding to the split feature. The splitting rules are indicated on the corresponding paths. For each leaf of the tree, more information is presented in brackets. For instance, LM 1 contains 26 instances, with a 4.206% error in that leaf. It is obvious that the accumulation of number of instances in each leaf equals 384, the number of the training dataset. The LMs for all situations obtained by the M5P model are given in Table 2.
Tree visualization of constructed M5P regression tree for the polyaxial rock strength prediction. The terminal leaf nodes are represented by boxes with labels within, while the other nodes are represented by ellipses with symbols inside that correspond to the feature where the split occurs. On the respective pathways, the dividing rules are listed
Figure 4 presents the variation in predicted values of major principal stress using different surrogate modeling techniques in comparison with experimental values of major principal stress.
Although according to Fig. 2, AR-RT, AR-GP-PUK, GP-PUK, and RT models demonstrated high performances in terms of high accuracy and low error, Figs. 2 and 4 show that the AR-RT, RT, and the AR-M5P strength models are closer to the experimental value than other models in the testing phase in comparison to other evolved models.
Figure 5 presents cumulative distribution functions (CDFs) of the observed and predicted major principal stress, \({\sigma }_{1}\) (MPa) using the models developed for training and testing datasets, respectively. In Fig. 5, the CDFs of estimated \({\sigma }_{1}\) from AR-RT, AR-GP-PUK, GP-PUK, and RT models are the same as of measured \({\sigma }_{1}\). This agreement suggests that the information contained in the estimated \({\sigma }_{1}\) using these developed models is consistent with that obtained from the measured \({\sigma }_{1}\). Although the CDFs of the estimated \({\sigma }_{1}\) obtained from other developed models are also close to that of measured \({\sigma }_{1}\) and follows the pattern and trend of the CDF of measured \({\sigma }_{1}\), small errors and deviations could be seen between these models and measured \({\sigma }_{1}\). This further confirms the statistical results of the estimated \({\sigma }_{1}\) (Figs. 2 and 4), indicating that RT, hybrid AR-RT, and hybrid AR-M5P models provide better estimates than other models.
The cumulative distribution function (CDF) versus relative error was provided in Fig. 6 for all the developed ML-based failure criteria. According to Fig. 6a, AR-RT, AR-GP-PUK, and GP-PUK-based failure criteria have 100% probability that error in prediction will be 0 in the training data, respectively. These results are in consistency with Fig. 5a. In the testing phase (Fig. 5b), the probability will be more than 70% of predicting error within 10% for AR-RT, RT, AR-M5P, and AR-GP-PUK-based failure criterion. Therefore, AR-RT based failure criterion demonstrates a higher degree of confidence and accordingly is effective for strength prediction.
Overall error prediction distribution of developed models in training and testing phase is shown in the violin plot in Fig. 7. The negative and positive prediction error values indicate the developed models’ over- and under-estimation behavior, respectively. In this figure, the prediction error of AR-RT is lower than the rest models in the training and testing phases. Approximately similar prediction errors could be seen for RT in the training and testing phases. According to this figure, AR-GP-PUK has 0 error in training phase; however, the noticeable error is seen in the testing phase.
A Taylor diagram (Taylor 2001) is a graphical representation of comparing various model outcomes to measured data. The standard deviation, RMSE, and R between different models and measurements are depicted in this diagram. This diagram is plotted for major principal stress in Fig. 8. The location of each model in the diagram indicates how closely the predicted pattern matches with measurements. According to these figures, due to the distance of developed models points to the measured point, developed AR-RT model is generally promising method in estimating shear strength properties.
The efficacy of the proposed data-oriented models was also compared with each other and against several well-known failure criteria over the literature including the Mohr–Coulomb (MC); Hoek–Brown (HB); Modified Lade (ML); Drucker-Prager (DP); Linear Mogi 1971a, b; Modified Wiebols and Cook (MWC); 3D Hoek–Brown (3D HB); Bieniawski-Yudhbir (BY); Hoek–Brown-Matsuoka-Nakai (HBMN); Modified Mohr–Coulomb (MMC) in uniaxial compressive strength (UCS) prediction of fourteen rocks as depicted in Fig. 9. Data-oriented based strength models are generally robust modeling techniques that also predict UCS in consistency with those of well-established criteria from best fit to experimental data. As a result, ML approaches are able to capture the nonlinearity of the polyaxial strength response of rock.
Comparison of developed data-oriented models and some well-known criteria. Note: Mohr–Coulomb (MC); Hoek–Brown (HB); Modified Lade (ML); Drucker-Prager (DP); Linear Mogi 1971a, b; Modified Wiebols and Cook (MWC); 3D Hoek–Brown (3D HB); Bieniawski-Yudhbir (BY); Hoek–Brown-Matsuoka-Nakai (HBMN); Modified Mohr–Coulomb (MMC)
5 Sensitivity Analysis
Sensitivity analysis was performed to identify the most effective input parameter for predicting polyaxial rock strength using the established models. By eliminating one input parameter in each case and determining its effect on polyaxial rock strength using \({R}^{2}\) and RMSE performance metrics. Figure 10 shows that the prediction of polyaxial rock strength is mainly influenced by \({\sigma }_{3}\) and rock type, with \({\sigma }_{2}\) having the least significant impact on the strength.
6 Discussion
The accurate determination of rock strength subject to various loading conditions and given circumstances is pivotal for a wide range of geoengineering applications (Zhang et al. 2010; Haimson and Bobet 2012; Lee et al. 2012; Burghardt 2018; Wang and Liu 2021; Bao and Burghardt 2022), and various empirical, mathematical, and theoretical strength criteria have been proposed for strength prediction in geoengineering practice. However, finding the most appropriate criterion for a given situation remains challenging (Ulusay and Hudson 2012), and failure models based on experimental results of one specific type of geomaterial are not applicable to other types of geomaterials. In geoengineering practice, all failure criteria need to be modified by trial and error (Wang and Liu 2021). In addition, defining the real behavior of geomaterials under different stress circumstances is difficult due to the complexity of the materials. Conventional failure models require assumptions, and the number of material parameters that need to be determined increases as the complexity of models increases, which restricts their practical application in engineering (Gao 2018).
ML-based failure models have emerged as a promising approach to address these challenges. ML-based models can process large amounts of data and learn complex model functions from input and output training experimental datasets without any assumption and physical background. This allows abstract information or theoretically unknown behaviour to be represented. Moreover, the ML models can be improved by retraining them with new data, and the established models and learned information can be stored (Fathipour-Azar and Torabi 2014; Fathipour-Azar et al. 2017, 2020; Gao 2018; Zhang et al. 2020; Fathipour-Azar 2021a, b; 2022a, b, c, d, e, f; 2023a, b).
In this study, the efficiency of probabilistic (i.e., GP) and tree-based (i.e., RT and M5P) ML algorithms is demonstrated first in predicting failure strength of rock under polyaxial conditions. The GP is a nonparametric kernel-based Bayesian method that computes posterior predictive distributions for new test inputs and allows the quantification of uncertainty in model estimations. While Bayesian analysis is a general framework for statistical inference that combines prior knowledge with new data to estimate parameters and quantify uncertainties (e.g., Burghardt 2018; Bao and Burghardt 2022), GP is a specific method for modeling functions as Gaussian processes. Nonlinear regression can also be performed using regression trees. The RT and M5P algorithms use regression trees to partition the space into smaller parts and apply simple models to each of them. While the M5P regression tree has a lower predictive performance than that of the other ML algorithms in this study (Fig. 2), RT and M5P models provide an intuitive visualization and explicit description of how inputs affect the output, which is beneficial in engineering practices (Fig. 3 and Table 2).
Finally, boosting-based AR is used to enhance efficiency of the GP, RT, and M5P algorithms in terms of high accuracy and low error. According to the findings of this study, the prediction strength and performance of individual algorithms could be enhanced by hybrid algorithms for this dataset (Figs. 2, 4, 5, 6, 7 and 8). This is due to the adaptability and structural compatibility of AR with different models. This improvement is more noticeable in M5P model results with the results of hybrid AR-M5P model. The study shows that the accuracy and performance of the ML models are dependent on the type of algorithm used, and hybrid models that combine multiple algorithms can improve the predictive accuracy.
Comparison with well-known failure criteria over the literature showed that the developed ML-based strength models were able to predict UCS in consistency with those of well-established criteria from best fit to experimental data. This highlights the effectiveness of data-oriented modeling techniques in capturing the nonlinearity of the polyaxial strength response of rock.
The sensitivity analysis revealed that predicting polyaxial rock strength is primarily influenced by \({\sigma }_{3}\) and rock type, followed by \({\sigma }_{2}\) with a less significant impact. This indicates that the microstructure and properties of the rock are important factors in determining its strength under polyaxial loading conditions.
Properties of rock vary with rock type. In this context, a wide variety of data using 14 rocks from different types of rocks including igneous, metamorphic, and sedimentary rocks are employed as database of simulations, to demonstrate the efficiency of the ML algorithms. \({\sigma }_{3}\) and \({\sigma }_{2}\) ranges from 5 to 140 MPa and 5 to 360 MPa, respectively (Table 1 and Fig. 1). The findings of this study contribute to the field of rock mechanics by providing insights into the factors that influence polyaxial rock strength and demonstrating the effectiveness and potential of these individual or hybrid ML-based techniques in improving the accuracy and reliability of rock strength predictions, which can have important applications in the design and construction of rock engineering structures. The integration of various regression models through boosting can enhance the accuracy and robustness of predictions while preventing overfitting. Additionally, Bayesian analysis can be applied to a wider range of problems beyond function modeling (e.g., Burghardt 2018; Bao and Burghardt 2022). These methods can aid in making informed-site decisions in a variety of subsurface engineering applications.
Further research is needed to investigate the generalization of the developed models to other rock types and testing conditions and to evaluate their effectiveness in practical applications. Moreover, a larger dataset with more explanatory data variables could be analyzed to improve the model’s precision and reliability in future research.
7 Conclusion
Data-oriented models for predicting polyaxial rock strength can be valuable methods in actual projects. In this study, hybrid additive regression combined with three ML algorithms is utilized to estimate polyaxial rock strength and capture nonlinear patterns. The ML algorithms employed include Gaussian process regression (GP) with two kernels, random tree (RT), and M5P methods. Three parameters (rock type, minor, intermediate, and major principal stress) are used from the 480 polyaxial rock experiments from published research to construct the data-oriented surrogate models. The AR-RT performed superior to the other individual and hybrid models in the training and testing datasets. The efficiency of the hybrid models to individual developed models is demonstrated in terms of high accuracy and low error. The hybrid AR-RT model with \({R}^{2}\) = 1, RMSE = 0 MPa, and MAE = 0 MPa in training period and \({R}^{2}\) = 0.987, RMSE = 29.771 MPa, and MAE = 22.517 MPa in testing period could be regarded to be excellent polyaxial rock strength surrogate model. The results of the sensitivity analysis indicate that \({\sigma }_{3}\) and rock type are the most important parameters for measuring the polyaxial strength failure of the rock.
Data availabilty
Enquiries about data availability should be directed to the authors. The datasets used during the current study are available at https://doi.org/10.1016/j.petrol.2017.09.065.
References
Bahrami B, Mohsenpour S, Miri MA, Mirhaseli R (2017) Quantitative comparison of fifteen rock failure criteria constrained by polyaxial test data. J Petrol Sci Eng 159:564–580. https://doi.org/10.1016/j.petrol.2017.09.065
Bao T, Burghardt J (2022) A Bayesian approach for in-situ stress prediction and uncertainty quantification for subsurface engineering. Rock Mech Rock Eng 55(8):4531–4548. https://doi.org/10.1007/s00603-022-02857-0
Benz T, Schwab R (2008) A quantitative comparison of six rock failure criteria. Int J Rock Mech Min Sci 45(7):1176–1186. https://doi.org/10.1016/j.ijrmms.2008.01.007
Burghardt J (2018) Geomechanical risk assessment for subsurface fluid disposal operations. Rock Mech Rock Eng 51(7):2265–2288. https://doi.org/10.1007/s00603-018-1409-1
Chang C, Haimson B (2000) True triaxial strength and deformability of the German continental deep drilling program (KTB) deep hole amphibolite. J Geophys Res 105(B8):18999–19013
Colmenares LB, Zoback MD (2002) A statistical evaluation of intact rock failure criteria constrained by polyaxial test data for five different rocks. Int J Rock Mech Min Sci 39(6):695–729. https://doi.org/10.1016/S1365-1609(02)00048-5
Ebden M (2015). Gaussian processes: a quick introduction. arXiv preprint arXiv:1505.02965.
Fathipour-Azar H (2021a) Machine learning assisted distinct element models calibration: ANFIS, SVM, GPR, and MARS approaches. Acta Geotech. https://doi.org/10.1007/s11440-021-01303-9
Fathipour-Azar H (2021b) Data-driven estimation of joint roughness coefficient (JRC). J Rock Mech Geotech Eng 13(6):1428–1437. https://doi.org/10.1016/j.jrmge.2021.09.003
Fathipour-Azar H (2022a) New interpretable shear strength criterion for rock joints. Acta Geotech 17:1327–1341. https://doi.org/10.1007/s11440-021-01442-z
Fathipour-Azar H (2022b) Polyaxial rock failure criteria: Insights from explainable and interpretable data driven models. Rock Mech Rock Eng 55:2071–2089. https://doi.org/10.1007/s00603-021-02758-8
Fathipour-Azar H (2022c) Hybrid machine learning-based triaxial jointed rock mass strength. Environ Earth Sci 81:118. https://doi.org/10.1007/s12665-022-10253-8
Fathipour-Azar H (2022d) Stacking ensemble machine learning-based shear strength model for rock discontinuity. Geotech Geol Eng 40:3091–3106. https://doi.org/10.1007/s10706-022-02081-1
Fathipour-Azar H (2022e) Data-oriented prediction of rocks’ Mohr-Coulomb parameters. Arch Appl Mech 92(8):2483–2494. https://doi.org/10.1007/s00419-022-02190-6
Fathipour-Azar H (2022f) Multi-level machine learning-driven tunnel squeezing prediction: review and new insights. Arch Comput Methods Eng 29:5493–5509. https://doi.org/10.1007/s11831-022-09774-z
Fathipour-Azar H (2023a) Mean cutting force prediction of conical picks using ensemble learning paradigm. Rock Mech Rock Eng 56:221–236. https://doi.org/10.1007/s00603-022-03095-0
Fathipour-Azar H (2023b) Shear strength criterion for rock discontinuities: a comparative study of regression approaches. Rock Mech Rock Eng. https://doi.org/10.1007/s00603-023-03302-6
Fathipour-Azar H and Torabi SR (2014). Estimating fracture toughness of rock (KIC) using artificial neural networks (ANNS) and linear multivariable regression (LMR) models. 5th Iranian Rock Mechanics Conference.
Fathipour-Azar H, Saksala T, Jalali SME (2017) Artificial neural networks models for rate of penetration prediction in rock drilling. J Struct Mech 50(3):252–255
Fathipour-Azar H, Wang J, Jalali SME, Torabi SR (2020) Numerical modeling of geomaterial fracture using a cohesive crack model in grain-based DEM. Comput Part Mech 7:645–654. https://doi.org/10.1007/s40571-019-00295-4
Feng XT, Zhang X, Kong R, Wang G (2016) A novel Mogi type true triaxial testing apparatus and its use to obtain complete stress–strain curves of hard rocks. Rock Mech Rock Eng 49(5):1649–1662. https://doi.org/10.1007/s00603-015-0875-y
Feng XT, Kong R, Zhang X, Yang C (2019) Experimental study of failure differences in hard rock under true triaxial compression. Rock Mech Rock Eng 52(7):2109–2122. https://doi.org/10.1007/s00603-018-1700-1
Feng XT, Kong R, Yang C, Zhang X, Wang Z, Han Q, Wang G (2020) A three-dimensional failure criterion for hard rocks under true triaxial compression. Rock Mech Rock Eng 53(1):103–111. https://doi.org/10.1007/s00603-019-01903-8
Friedman JH (2002) Stochastic gradient boosting. Comput Stat Data Anal 38(4):367–378
Gao W (2018) A comprehensive review on identification of the geomaterial constitutive model using the computational intelligence method. Adv Eng Inform 38:420–440. https://doi.org/10.1016/j.aei.2018.08.021
Haimson B, Bobet A (2012) Introduction to suggested methods for failure criteria. Rock Mech Rock Eng 45(6):973–974. https://doi.org/10.1007/s00603-012-0274-6
Haimson B, Rudnicki JW (2010) The effect of the intermediate principal stress on fault formation and fault angle in siltstone. J Struct Geol 32(11):1701–1711. https://doi.org/10.1016/j.jsg.2009.08.017
Jiang H (2018) Simple three-dimensional Mohr-Coulomb criteria for intact rocks. Int J Rock Mech Min Sci 105:145–159. https://doi.org/10.1016/j.ijrmms.2018.01.036
Jiang H, Xie YL (2012) A new three-dimensional Hoek-Brown strength criterion. Acta Mech Sin 28(2):393–406. https://doi.org/10.1007/s10409-012-0054-2
Kaunda R (2014) New artificial neural networks for true triaxial stress state analysis and demonstration of intermediate principal stress effects on intact rock strength. J Rock Mech Geotech Eng 6(4):338–347. https://doi.org/10.1016/j.jrmge.2014.04.008
Lee YK, Pietruszczak S, Choi BH (2012) Failure criteria for rocks based on smooth approximations to Mohr-Coulomb and Hoek-Brown failure functions. Int J Rock Mech Min Sci 56:146–160. https://doi.org/10.1016/j.ijrmms.2012.07.032
Li H, Guo T, Nan Y, Han B (2021) A simplified three-dimensional extension of Hoek-Brown strength criterion. J Rock Mech Geotech Eng. https://doi.org/10.1016/j.jrmge.2020.10.004
Liolios P, Exadaktylos G (2013) Comparison of a hyperbolic failure criterion with established failure criteria for cohesive-frictional materials. Int J Rock Mech Min Sci 63:12–26. https://doi.org/10.1016/j.ijrmms.2013.06.005
Ma X, Haimson BC (2016) Failure characteristics of two porous sandstones subjected to true triaxial stresses. J Geophys Res 121(9):6477–6498. https://doi.org/10.1002/2016JB012979
Ma L, Li Z, Wang M, Wu J, Li G (2020) Applicability of a new modified explicit three-dimensional Hoek-Brown failure criterion to eight rocks. Int J Rock Mech Mining Sci 133:104311. https://doi.org/10.1016/j.ijrmms.2020.104311
Mogi K (1967) Effect of the intermediate principal stress on rock failure. J Geophys Res 72(20):5117–5131. https://doi.org/10.1029/JZ072i020p05117
Mogi K (1971a) Effect of the triaxial stress system on the failure of dolomite and limestone. Tectonophysics 11(2):111–127. https://doi.org/10.1016/0040-1951(71)90059-X
Mogi K (1971b) Fracture and flow of rocks under high triaxial compression. J Geophys Res 76(5):1255–1269. https://doi.org/10.1029/JB076i005p01255
Mogi K (2007) Experimental rock mechanics. Tailor and Francis, United Kingdom
Moshrefi S, Shahriar K, Ramezanzadeh A, Goshtasbi K (2018) Prediction of ultimate strength of shale using artificial neural network. J Min Env 9(1):91–105. https://doi.org/10.22044/JME.2017.5790.1390
Priest SD (2010) Comparisons between selected three-dimensional yield criteria applied to rock. Rock Mech Rock Eng 43(4):379–389. https://doi.org/10.1007/s00603-009-0064-y
Priest S (2012) Three-dimensional failure criteria based on the Hoek-Brown criterion. Rock Mech Rock Eng 45(6):989–993. https://doi.org/10.1007/s00603-012-0277-3
Quinlan JR (1992). Learning with continuous classes. In: Proceedings of Australian joint conference on artificial intelligence. World Scientific Press, Vol. 92, pp. 343–348.
Rafiai H (2011) New empirical polyaxial criterion for rock strength. Int J Rock Mech Min Sci 48(6):922–931. https://doi.org/10.1016/j.ijrmms.2011.06.014
Rafiai H, Jafari A (2011) Artificial neural networks as a basis for new generation of rock failure criteria. Int J Min Sci Technol 48(7):1153–1159. https://doi.org/10.1016/j.ijrmms.2011.06.001
Rafiai H, Jafari A, Mahmoudi A (2013) Application of ANN-based failure criteria to rocks under polyaxial stress conditions. Int J Min Sci Technol 59:42–49. https://doi.org/10.1016/j.ijrmms.2012.12.003
Rasmussen CE, Williams C (2006) Gaussian processes for machine learning. MIT Press, Cambridge
Rukhaiyar S, Samadhiya NK (2017a) A polyaxial strength model for intact sandstone based on artificial neural network. Int J Rock Mech Mining Sci 95:26–47. https://doi.org/10.1016/j.ijrmms.2017.03.012
Rukhaiyar S, Samadhiya NK (2017b) Strength behaviour of sandstone subjected to polyaxial state of stress. Int J Min Sci Technol 27(6):889–897. https://doi.org/10.1016/j.ijmst.2017.06.022
Sheorey PR (1997) Empirical rock failure criteria. Balkema, Rotterdam
Sriapai T, Walsri C, Fuenkajorn K (2013) True-triaxial compressive strength of Maha Sarakham salt. Int J Rock Mech Min Sci 61:256–265. https://doi.org/10.1016/j.ijrmms.2013.03.010
Takahashi M, Koide H (1989) Effect of the intermediate principal stress on strength and deformation behavior of sedimentary rocks at the depth shallower than 2000 m. In: Maury V, Fourmaintraux D (eds) Rock at great depth. Balkema A.A, pp 19–26
Taylor KE (2001) Summarizing multiple aspects of model performance in a single diagram. J Geophys Res 106(D7):7183–7192. https://doi.org/10.1029/2000JD900719
Ulusay R, Hudson JA (2012) Suggested methods for rock failure criteria: general introduction. Rock Mech Rock Eng. https://doi.org/10.1007/978-3-319-07713-0_17
Wang J (2020). An intuitive tutorial to Gaussian processes regression. arXiv preprint arXiv:2009.10862.
Wang Z, Liu Q (2021) Failure criterion for soft rocks considering intermediate principal stress. Int J Min Sci Technol 31(4):565–575. https://doi.org/10.1016/j.ijmst.2021.05.005
Witten IH, Frank E (2005) Practical machine learning tools and techniques. Morgan Kaufmann
You M (2009) True-triaxial strength criteria for rock. Int J Rock Mech Min Sci 46(1):115–127. https://doi.org/10.1016/j.ijrmms.2008.05.008
Yu MH, Zan YW, Zhao J, Yoshimine M (2002) A unified strength criterion for rock material. Int J Rock Mech Min Sci 39(8):975–989. https://doi.org/10.1016/S1365-1609(02)00097-7
Zhang L (2008) A generalized three-dimensional Hoek-Brown strength criterion. Rock Mech Rock Eng 41(6):893–915. https://doi.org/10.1007/s00603-008-0169-8
Zhang L, Cao P, Radha KC (2010) Evaluation of rock strength criteria for wellbore stability analysis. Int J Rock Mech Min Sci 47(8):1304–1316. https://doi.org/10.1016/j.ijrmms.2010.09.001
Zhang W, Zhang R, Wu C, Goh ATC, Lacasse S, Liu Z, Liu H (2020) State-of-the-art review of soft computing applications in underground excavations. Geosci Front 11(4):1095–1106. https://doi.org/10.1016/j.gsf.2019.12.003
Zhu C, Zhao H, Ru Z (2015) LSSVM-based rock failure criterion and its application in numerical simulation. Math Probl Eng. https://doi.org/10.1155/2015/246068
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
None.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Fathipour-Azar, H. Hybrid Data-Driven Polyaxial Rock Strength Meta Model. Rock Mech Rock Eng 56, 5993–6007 (2023). https://doi.org/10.1007/s00603-023-03383-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00603-023-03383-3