1 Introduction

Rock mass behavior and, therefore, stability of the slope and underground cavities are strongly affected by the shear strength of rock joints in the rock mass. It is not straightforward to precisely predict the shear strength of the rock joints due to a variety of complex variables. Various methods, such as empirical (Patton 1966; Jaeger 1971; Barton 1973; Barton and Choubey 1977; Maksimovic 1996; Kulatilake et al. 1995; Zhao 1997; Grasselli 2001; Tatone 2009; Xia et al. 2014; Yang et al. 2016; Tang et al. 2016; Tian et al. 2018), semi-theoretical (Ladanyi and Archambault 1969; Seidel and Haberfield 1995; Johansson and Stille 2014), and theoretical (Lanaro and Stephansson 2003), have been applied to describe shear strength of rock discontinuities over the years. In the literature, there has been a comparative investigation of shear strength models of rock discontinuities (e.g., Singh and Basu 2018; Tian et al. 2018; Li et al. 2020).

Conventional regression methods can be improved to better capture and represent the multi-variable, nonlinear, complex, and constitutive responses of systems such as the shear behavior of rock discontinuities with the processing capability of current computers. Data-driven-based methods are widely used in geoengineering (Fathipour-Azar and Torabi 2014; Fathipour-Azar et al. 2017, 2020; Zhang et al. 2020a, b, c; Fathipour-Azar 2021a, b, 2022a, b, c, d, e, f, 2023). Based on the literature reviews, the previously published machine learning methods for predicting shear strength of rock discontinuity are summarized, as shown in Table 1.

Table 1 A summary of previously published machine learning methods to predict shear strength of rock discontinuity
Full size table

The shear strength of a joint varies depending on parameters such as rock type, joint material, normal stress level, and morphology characteristics (e.g., Tang et al. 2016; Wang and Li 2018; Xia et al. 2019). Although some current machine-learning-based surrogate models and criteria are well suited for the shear behavior of rock joints, there is a still need for a simple adoptable model that takes into consideration all the influential factors that affect the nonlinear complicated nature of joint strength. Moreover, there is a need to use black-box visualization tools to explain and interpret black-box models developed by these techniques. However, Fathipour-Azar (2022a) proposed an effective shear strength criterion (\({R}^{2}\) = 0.98) to use in rock mechanics application with fewer input variables using interpretable multivariate adaptive regression splines (MARS) method.

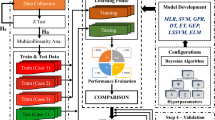
The purpose of this study is to construct shear strength criteria for rock discontinuities based on data-driven models using the simple linear regression (SLR), multiple linear regression (MLR), least median squared regression (LMSR), isotonic regression (IR), pace regression (PR), k-nearest neighbors (kNN), and extreme gradient boosting (XGBoost) learning models. The universal applicability of the developed models is validated with the result of measured shear strength data of rock discontinuities in the earlier studies, previous machine-learning-based models, and several well-known shear strength criteria. To do this, \({R}^{2}\) (coefficient of determination), root mean square error (RMSE), and mean absolute error (MAE) are used to calculate the validity of the predictive models, and sensitivity analysis is carried out on the established XGBoost model to analyze the relationship between shear strength and influencing factors. This study can be used for the comparative analysis of the use of different surrogate-based methodologies for estimating shear strength of rock discontinuities.

2 Data-Driven Modeling Methodologies

Data-driven surrogate-based methodologies that have been used to construct the failure criteria and predict the shear strength of rock discontinuities are briefly outlined in this section.

2.1 Simple Linear Regression (SLR)

Linear regression is a method of mathematically modeling the relationship between a response variable (also called the outcome or dependent variable) and one or more input variables (also called the predictor, explanatory, or independent variable). A linear regression model with a satisfactory fit may be used to predict future values of the output variable. Simple linear regression (SLR) selects the variable feature that results in the lowest squared error. For a single explanatory variable, the SLR can be written as:

$$y={\beta }_{0}+{\beta }_{1}x+\varepsilon$$
(1)

where \({\beta }_{0}\) and \({\beta }_{1}\) are the regression parameters to be estimated and \(\varepsilon\) is the error term.

2.2 Multiple Linear Regression (MLR)

Multiple linear regression (MLR) is the approach used when there are more than one estimator variable. In this study, MLR with ridge regularization is performed based on standard least squares linear regression. To solve ill-posed problems and control the potential over-fitting issues in the MLR, a regularized version of the MLR, namely, the ridge regression is used (Witten and Frank 2005). In the linear regression model, the least square method is used to determine \({\beta }_{0}\) and \({\beta }_{1}\) predictions such that the sum of squared distance from the real \({y}_{i}\) response \(\widehat{y}={b}_{0}+{b}_{1}{x}_{i}\) approaches the lowest of all feasible regression coefficients.

$$\left({\beta }_{0},{\beta }_{1}\right)=\mathrm{arg} \underset{\left({b}_{0},{b}_{1}\right)}{\mathrm{min}}\sum_{i=1}^{n}{\left[{y}_{i}-\left({b}_{0}+{b}_{1}{x}_{i}\right)\right]}^{2}$$
(2)

2.3 Least Median Squared Regression (LMSR)

Least median squared regression (LMSR) predicts using MLR. Least squared regression functions are created from random subsamples of the data. The final model is the least squared regression with the lowest median squared error (Rousseeuw 1984), that is:

$$\left({\beta }_{0},{\beta }_{1}\right)=arg \underset{\left({b}_{0},{b}_{1}\right)}{\mathrm{min}}median{\left[{y}_{i}-\left({b}_{0}+{b}_{1}{x}_{i}\right)\right]}^{2}, i=\mathrm{1,2}, ..,n$$
(3)

2.4 Isotonic Regression (IR)

Isotonic regression (IR) is a nonparametric method for fitting a freestyle line to a sequential of perceptions under following conditions: the given freestyle line model needs to be consistent with the monotonicity and as close to the observed values as possible (Salanti 2003; Leeuw et al. 2010). It selects the attribute with the lowest squared error and bases its isotonic regression model on this decision. The IR optimization formula is as follows:

$${\widehat{y}}^{IR}=arg \underset{y}{\mathrm{min}}\sum_{i=1}^{n}{{w}_{i}\left[{y}_{i}-{\widehat{y}}_{i}\right]}^{2}$$
(4)

where \({w}_{i}\) is chosen weights.

2.5 Pace Regression

Projection adjustment by contribution estimation (pace) regression (PR) improves on classical MLR by assessing the influence of each variable and using clustering analysis to improve the statistical basis for determining their contribution to the overall regression. When the number of coefficients approaches infinity, PR is provably optimum under regularity conditions. PR is an approach to fitting linear models in high-dimensional spaces. It consists of a set of estimators that are either overall or conditionally optimum (Wang 2000; Wang and Witten 2002).

2.6 k-Nearest Neighbors (kNN) Model

k-nearest neighbors (kNN) is a nonparametric, instance-based, lazy learner algorithm (Aha et al. 1991). The target of test data sample is predicted by searching the entire training set for the \(k\) most similar samples (neighbors) and averaging the values of k-nearest neighbors as an output variable. In this study, the brute force search algorithm is used to find the nearest neighbors and Chebyshev distance is used to measure the distance. If D is a dataset consisting of \({\left({x}_{i}\right)}_{i\in \left[1,n\right]}\) training instances (where \(n=\left|D\right|\)) with a set of features \(F\) and the value of an unknown instance \(p\) is to be predicted, the Chebyshev distance between \(p\) and \({x}_{i}\) is (Cunningham and Delany 2021):

$$d\left(p,{x}_{i}\right)=\underset{f\in F}{\mathrm{max}}\left|{p}_{f}-{x}_{if}\right|$$
(5)

2.7 Extreme Gradient Boosting (XGBoost) Model

Extreme gradient boosting (XGBoost) model is an advanced ensemble tree boosting algorithm (Chen and Guestrin 2016). It is an improvement on Friedman's gradient boosting method (Friedman 2001). XGBoost functions by building a base model for the pre-existing model, which consists of training an initial tree, constructing a second tree combined with the initial tree, and repeating the second step until the stopping condition(i.e., required number of trees) is met (Zhang et al. 2020c). When \(t\) trees are created, the newly generated tree is utilized to fit the residual of the last prediction. The sum of each tree's predictions yields the model's ultimate prediction. The general function for approximating the system response at step \(t\) is as:

$${\widehat{y}}_{i}^{(t)}=\sum_{k=1}^{t}{f}_{k}\left({x}_{i}\right)={\widehat{y}}_{i}^{(t-1)}+{f}_{t}({x}_{i})$$
(6)

where \({f}_{t}({x}_{i})\) is the learner at step \(t\), \({\widehat{y}}_{i}^{(t)}\) and \({\widehat{y}}_{i}^{(t-1)}\) are the estimations at step \(t\) and \(t\) − 1, and \({x}_{i}\) is the input variable.

To optimize and prevent over-fitting issues, the objective function of XGBoost can be minimized as follows:

$${Obj}^{(t)}=\sum_{k=1}^{n}l({y}_{i},{\widehat{y}}_{i}^{(t)})+\Omega ({f}_{t})$$
(7)

where \(l\) is a convex function (i.e., loss function) that is used to find the difference between exact and computed values, \({y}_{i}\) is a measured value, \(n\) is the number of observations used, and \(\Omega\) is the penalty factor (regularization term), and defined as:

$$\Omega \left(f\right)=\gamma T+\frac{1}{2}\lambda {\Vert \omega \Vert }^{2}$$
(8)

where \(\omega\) is the vector of scores in the leaves, \(\lambda\) is the regularization parameter, and \(\gamma\) is the minimum loss needed to further partition the leaf node.

Using a greedy algorithm, the XGBoost technique examines all feature points adopting the objective function value as the evaluation function. The split objective function value is compared with the gain of a single leaf node's objective function within a preset threshold that restricts tree growth, and the split is executed only when the gain exceeds the threshold. As a consequence, the best features and splitting points for constructing the tree structure can be found (Zhang et al. 2020a).

3 Database

To predict peak shear strength of discontinuities, the results of direct shear tests from published literature (Grasselli 2001; Tatone 2009; Xia et al. 2014; Yang et al. 2015, 2016) are used for training and testing the proposed SLR, MLR, LMSR, IR, PR, kNN, and XGBoost techniques. A total of 83 tests were conducted on 6 different material types of discontinuities (granite, sandstone, limestone, marble, serpentinite, mortar).

Based on the literature review conducted on the parameters considered by previous machine-learning-based models and common criteria to predict shear strength of rock discontinuity, eight main influencing input parameters are employed in the analyses: sampling interval \((l)\), maximum contact area ratio \({(A}_{0})\), distribution parameter \((C)\), maximum apparent dip angle \(({\theta }_{max}^{*})\), basic friction angle \(({\varphi }_{b})\), tensile strength (\({\sigma }_{t}\)), uniaxial compressive strength \({(\sigma }_{c})\), and normal stress \(({\sigma }_{n})\). The dataset consisting of 83 instances has been divided into 2 phases: 80% training dataset (66 experimental datasets) and 20% testing dataset (17 experimental datasets), by random sampling. Therefore, the training dataset is used for model construction and testing dataset is used for evaluating the prediction performance of the developed models for testing purposes.

Figure 1 presents a plot matrix for the variables considered, the lower triangle of the matrix shows scatter plots of each pair of variables, while the upper triangle shows the correlations of the variables. Different color represents each group of material type in the lower triangle of the matrix. It is seen that the \({\tau }_{p}\) is highly correlated to the \({\sigma }_{n}\).

Fig. 1
figure 1

A plot matrix with histograms of the variables in the diagonal and correlation coefficients

Full size image

In this study, various statistical analysis is computed to justify the attainment of the adopted SLR, MLR, LMSR, IR, PR, kNN, and XGBoost models. Three most frequently used metrics for model assessment in regression problems are \({R}^{2}\) (coefficient of determination), root mean square error (RMSE), and mean absolute error (MAE). The following four equations express the mathematical indicators:

$$R^{2} = 1 - \frac{{\mathop \sum \limits_{i = 1}^{n} \left( {y_{i} - y_{i}^{^{\prime}} } \right)^{2} }}{{\mathop \sum \nolimits_{i = 1}^{n} \left( {y_{i} - \overline{y}} \right)^{2} }}$$
(9)
$${\text{RMSE}} = \sqrt {{\text{MSE}}} = \sqrt {\frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left( {y_{i} - y_{i}^{^{\prime}} } \right)^{2} }$$
(10)
$${\text{MAE}} = \frac{1}{n}\sum\limits_{i = 1}^{n} {\left| {y_{i} - y_{i}^{i} } \right|}$$
(11)

where \(y_{i}\) and \(y_{i}^{^{\prime}}\) are measured and predicted values, respectively, \(\overline{y}\) is the mean of the measured values, and \(n\) is the total number of data. The predictive technique will be excellent if \({R}^{2}=1\), RMSE = 0, and MAE = 0.

4 Results and Discussion

4.1 Comparison Analysis of Models

Different surrogate models are constructed based on seven data-driven modeling techniques, viz., SLR, MLR, LMSR, IR, PR, kNN, and XGBoost, and used to predict the shear strength of rock discontinuity. A tuning phase was performed utilizing the grid search and tenfold cross-validation methods to determine suitable values for the parameters that characterize considered models. Ridge parameter of \(1\times {10}^{-8}\) is used in MLR model. The optimal number of closest instances in the training dataset for predicting the value of the test instance for the kNN model is 1. For the XGBoost model, tree (XGBtree) is considered as base learners and boosters. Accordingly, boosting iterations = 972, maximum depth of tree = 1, minimum loss reduction = 0, subsample ratio of columns = 0.7, minimum sum of instance weight (node size) = 1, subsample percentage = 0.71, and booster learning rate (shrinkage) = 0.1 are found optimal parameters for the model.

Regression equations obtained from the application of the statistical algorithms using tenfold cross-validation on train dataset are given as below:

$$\mathrm{SLR}: {\tau }_{p}=1.5{\sigma }_{n}+0.33$$
(12)
$$\mathrm{MLR}:{\tau }_{p}=2.87*l+2.362*{A}_{0}-0.163*C+0.033*{\uptheta }_{\mathrm{max}}^{*}+0.041*{\varphi }_{b}+1.428*{\sigma }_{n}+0.004*{\sigma }_{c}+0.081*{\sigma }_{t}-4.618$$
(13)
$$\mathrm{LMSR}: {\tau }_{p}=0.803*l-1.515*{A}_{0}-0.125*C+0.011*{\theta }_{\mathrm{max}}^{*}+0.041*{\varphi }_{b}+1.584*{\sigma }_{n}+0.007*{\sigma }_{c}-0.002*{\sigma }_{t}-0.965$$
(14)
$${\mathrm{PR}:\tau }_{p}=2.168*l+2.441*{A}_{0}-0.159*C+0.027*{\uptheta }_{\mathrm{max}}^{*}+0.048*{\varphi }_{b}+1.424*{\sigma }_{n}+0.004*{\sigma }_{c}-0.076*{\sigma }_{t}-4.392$$
(15)

To verify the reliability and accuracy of the models established, statistical indices, i.e., RMSE, \({R}^{2}\), and MAE are used. Table 2 presents the results of all data-driven criteria performances during the training and testing stages. It is seen from Table 2 that the XGBoost model demonstrates the highest prediction accuracy and generalization capability by achieving the highest \({R}^{2}\) and lowest RMSE and MAE compared with SLR, MLR, LMSR, IR, PR, and kNN models in both the training and testing phases.

Table 2 Shear strength prediction performance of the developed surrogate models
Full size table

As shown in Fig. 2, the measured data are plotted against predicted data to provide a better insight into the prediction success of the criteria. It can be seen that the data predicted by the XGBoost-based criterion match the measured experimental data perfectly on the regression line for the training and testing dataset.

Fig. 2
figure 2

Cross plot between measured and predicted data of rock discontinuity shear strength using developed models

Full size image

The performance of established models is compared to those achieved with the shear strength criteria and other machine learning techniques used to address estimating problems. Shear strength criteria are given in Table 3 and machine learning paradigms considered to perform this comparison are MARS, Gaussian process (GP), alternating model tree (AMT), Cubist, radial basis function (RBF) networks, and elastic net (EN) (Fathipour-Azar 2022a). Figure 3 shows the comparison results of the criteria, previous machine-learning-based models, and developed data-driven surrogate models employed in this study for the same train and test dataset in the training and testing phases. Generally, Fig. 3 demonstrates that surrogate models established in this study performed satisfactory and comparable to those criteria and previous machine-learning-based models. A good correlation between measured and predicted data is seen for proposed data-driven models, particularly the XGBoost model with a lower error. However, the kNN-based model performs poorly.

Table 3 Review of used shear strength criteria
Full size table
Fig. 3
figure 3

Shear strength prediction performance of the developed models and criteria for train and test data

Full size image

Generally, a predefined functional representation of the model is not required for data-driven surrogate-based methodologies. Such data-driven intelligence modeling gains information from training data and then more effectively represents a complex and nonlinear constitutive behavior of rock discontinuities. Moreover, these developed surrogate models are computationally inexpensive. Statistical learning methods enable us to express the relationship between the input and response variables as a mathematical equation. SLR, MLR, LMSR, IR, PR techniques fall into this group. The regression equation is determined by minimizing the sum or median of squared residuals. kNN is an instance-based lazy learner. It stores the training data in the memory and uses it when predicting a new test instance. XGBoost is an ensemble machine learning algorithm. It creates a weak prediction model at each stage, which is then weighted and incorporated to the overall model, reducing variance and bias and so improving model performance. Therefore, the results of this study demonstrated that proposed techniques can assist scholars in comprehensively considering influential shear behavior parameters and make fast and accurate shear failure evaluation of rock discontinuities without the need for a computationally complex mathematical equation or expensive and specialized laboratory facilities.

A Taylor diagram (Taylor 2001) is a graphical representation of comparing various model outcomes to measured data. The standard deviation, RMSE, and R between different models and measurements are depicted in this diagram. This diagram is plotted for shear strength in Fig. 4. The location of each model in the diagram indicates how closely the predicted pattern matches with measurements. According to this figure, the distance between developed models points to the measured point indicates that while the developed XGBoost-based model is close to the measurement, and therefore a promising technique in estimating shear strength, the kNN-based model is far from the measurement.

Fig. 4
figure 4

Taylor diagram for presenting the predictive effect of models

Full size image

4.2 Sensitivity Analysis

The feature importance score is a strategy for determining the relevance of features and the interpretability of models. Figure 8 depicts the relative importance of the features for the XGBoost model illustrating the influence of features on shear strength of rock discontinuities, \({\tau }_{p}\). A trained XGBoost model can automatically compute feature importance based on the interface feature important criteria, such as gain, cover, and frequency criteria. The sum of the importance of each feature equals 1. Gain denotes each feature’s contribution of each tree to the model performance improvement. Cover indicates the relative number of observations related to a feature. Frequency is the percentage defining the relative number of times a feature decides on a split in the trees. A higher value of these indices, compared with another, implies that such a feature is more important for making an estimation. Figure 5 presents the eight feature predictors’ average of feature relative importance (%) under tenfold cross-validation. The figure shows that the \({\sigma }_{n}\), \({A}_{0}\), C, and \({\theta }_{max}^{*}\) affect the shear strength more than other variables.

Fig. 5
figure 5

Relative influence of the variables using XGBoost model

Full size image

Figure 6 depicts one-way partial dependence plots (PDPs) (Friedman 2001) for the eight predictor features. PDPs demonstrate how variation of one or more variables throughout their marginal distributions affects the average predicted value (Goldstein et al. 2015). Each plot in Fig. 6 represents the influence of each variable while the other variables are held constant. Although positive associations with shear strength are seen for \({\sigma }_{n}\), \({\sigma }_{t}\), \({\theta }_{max}^{*}\), and \(l\) features, a negative correlation can be seen for \(C\). In general, the shear strength increases with all features except for \(C\). The strength of the association varies for all features. A wider variation range for the average estimated shear strength value could be seen for the \({\sigma }_{n}\) (0.839–11.590) compared with other features in the range 2.607–3.642. The sharp changes in shear strength occur particularly for \({\sigma }_{c}\), \({\varphi }_{b}\), and \({A}_{0}\). However, it can be seen that specific ranges of each feature affect the estimated shear strength value. Out of these specific ranges, these features are less important variables and variation of the average estimated shear strength is insignificant.

Fig. 6
figure 6

Partial dependence plots for the features of the XGBoost model

Full size image

The H-statistic (Friedman and Popescu 2008) is used to determine how much variation in the shear strength value is attributable to feature interaction. Figure 7 depicts the interaction strength for each of the features with any other features for predicting the shear strength. Overall, each variable explains less than 4.5e-5% of the variance, implying that the interaction effects between the features are quite weak.

Fig. 7
figure 7

The interaction strength for each feature with all other features for the XGBoost model

Full size image

Finally, local interpretable model-agnostic explanations (LIME) (Ribeiro et al. 2016) is used to investigate and explain the relevance of each feature in the testing data set for each shear strength estimation by approximating it locally with an interpretable model. The results are shown in Fig. 8 as a heat map, with the rock joint profile numbers on the \(x\) axis and the categorized features on the \(y\) axis. Feature weights are represented by colors. The color of each cell reflects the importance of the features in determining the associated shear strength value. A feature with a positive (blue) weight supports the shear strength, whereas a feature with a negative (red) weight contradicts the shear strength. In addition, the LIME algorithm considers optimally four knobs for each feature (except for \(l\) with three knobs) that the model fits the local region. Therefore, similar to PDPs plots in Fig. 6, the influential range of each eight features could be understood that supports shear strength. In general, it can be seen that \({\sigma }_{n}\) feature is highly relevant to the estimated shear strength value. This result is consistent with feature importance obtained with the gain, cover, and frequency approaches for the training phase. This figure is useful for understanding how machine learning techniques, in this case the XGBoost model, estimate shear strength.

Fig. 8
figure 8

Feature importance as heat map visualization of all case-feature combinations for testing dataset in the XGBoost model

Full size image

5 Conclusion

Shear strength estimation of rock discontinuities is crucial in geoengineering analysis and applications. The present study proposed a new approach to predict the \({\tau }_{p}\) from the \(l\), \({A}_{0}\), \(C\), \({\theta }_{max}^{*}\), \({\varphi }_{b}\), \({\sigma }_{t}\), \({\sigma }_{c}\), and \({\sigma }_{n}\) data. Using a compiled dataset from the direct shear tests, SLR, MLR, LMSR, IR, PR, kNN, and XGBoost models are introduced to establish the relationship between the \({\tau }_{p}\) and various indicators. According to statistical indices, the XGBoost model outperforms all other techniques in predicting shear strength values of rock discontinuity, with the highest \({R}^{2}\) and lowest error values, indicating that the model has a superior generalization performance for provided dataset. Based on the trained XGBoost model, feature importance rank is provided using gain, cover, and frequency indices. PDPs are used to demonstrate the effect of features on the average predicted value in the training phase. The H-statistic is utilized to evaluate how much of the shear strength value's variation is explained by feature interaction. Moreover, the LIME algorithm is employed to indicate the effect of the variables on the shear strength using the testing dataset. The shear strength models were then compared to some criteria and previous machine-learning-based surrogate models, which demonstrates the effectiveness of established data-driven models by achieving comparable performance in evaluating the shear strength of rock discontinuities. It is worth highlighting that the predictive accuracy of the proposed MLR and PR-based formula (\({R}^{2}\) = 0.98 and 0.96 for the training and test dataset, respectively) is better or comparable to that of conventional criteria.

Further studies based on more datasets are required to improve the accuracy of the developed models. The promising results of this paper certainly give hope that with sufficient amounts of experimental data, the underlying strength model describing datasets can be much more efficiently identified.