Interval-valued q-rung orthopair fuzzy interactive Dubois–Prade operator and its application in group decision-making

Abstract

The Dubois–Prade operator can transform its parameter into different values when processing data, which can make it more flexible. Interval-valued q-rung orthopair fuzzy sets (IVq-ROFSs) give decision-makers more degrees of freedom. Combining the flexibility of the Dubois–Prade operators and the degrees of freedom of IVq-ROFSs, this paper proposes the interval-valued q-rung orthopair fuzzy Dubois–Prade (IVq-ROFDP) operations and the interval-valued q-rung orthopair Dubois–Prade ordered weighted average (IVq-ROFDPOWA) operator under IVq-ROFSs. Built upon this, considering the interaction between the membership degree and nonmembership degree, the interval-valued q-rung orthopair fuzzy interactive Dubois–Prade (IVq-ROFIDP) operations and the interval-valued q-rung orthopair fuzzy interactive Dubois–Prade ordered weighted average (IVq-ROFIDPOWA) operator are further proposed, and their properties are studied. Finally, a new group decision-making method based on the IVq-ROFIDPOWA operator is proposed to solve the multiattribute group decision-making (MAGDM) problem. The results of two case implementations and the sensitivity analysis show that the proposed operator and group decision-making method are feasible and effective. Furthermore, the comparative analysis shows that the group decision-making method proposed in this paper can better reflect the differences between alternatives.

1 Introduction

The fuzzy sets theory proposed by Zadeh (1965) is widely used in group decision-making problems concerning uncertain and complex systems (Chen and Niou 2011; Dong et al. 2021) and some other fields (Chen and Phuong 2017; Chen and Wang 2009). To further improve the degrees of freedom possessed by decision-makers, Atanassov proposed intuitionistic fuzzy sets (Atanassov 1986), whose membership degree ($\mu$) and nonmembership degree ($\nu$) satisfy the inequality $\mu +\nu \le 1$, and interval-valued intuitionistic fuzzy sets (Atanassov and Gargov 1989), which are used to solve group decision-making problems with multiple attributes and multiple objectives (Chen and Chiou 2014; Liu et al. 2019; Zeng et al. 2020). Yager proposed Pythagorean fuzzy sets (Yager 2013, 2014) and q-rung orthopair fuzzy sets (Yager 2017), whose ranges of membership degree ($\mu$) and nonmembership degree ($\nu$) are extended to ${\mu }^{q}+{\nu }^{q}\le 1\left(q\ge 1\right)$, greatly expanding the degrees of freedom possessed by decision-makers. For uncertain fuzzy problems, researchers further proposed and extended interval-valued q-rung orthopair fuzzy sets (IVq-ROFSs) (Joshi et al. 2018; Peng and Yong 2016), which have been widely used in group decision-making problems (Gao et al. 2020; Liu et al. 2018; Rawat and Komal 2022; Wang et al. 2019a). In addition, researchers have explored the application of many other kinds of fuzzy sets, such as Fermatean fuzzy sets (Ganie 2022), T-spherical fuzzy sets (Saad and Rafiq 2022), and probabilistic generalized orthopair fuzzy sets (Feng et al. 2022).

However, during the group decision-making process, it is necessary to aggregate the decision values of different decision-makers and the different attribute values of the scheme. For this reason, researchers have proposed many aggregation operators (AOs), such as the power average (PA) operator (Yager 2001), the Dombi Bonferroni mean operator (DBWA) (Liu et al. 2017), the Heronian mean operator (Beliakov et al. 2007), the weighted fairly aggregation operator (Saha et al. 2020), and the probabilistic weighted average operator (Merigo 2012). Among these aggregation operators, many of them are based on the t-norm operation and the t-conorm operation (Gupta and Qi 1991), such as the max–min operator (Boukezzoula et al. 2007), the Yager operator (Yager 1994), the Hamacher operator (Hamacher 1975; Wang et al. 2021), and the Einstein operator (Khaista et al. 2018). The Dubois–Prade operator (Dubois and Prade 1980) is a t-norm operator with the parameter proposed by Dubois and Prade, which is actually an ordinal sum of t-norm operations. At the same time, it can also be regarded as a combination of operators that can transform different parameters when processing data, thereby making it more flexible and convenient with improved processing efficiency.

Many research results have also been presented regarding aggregate operators and decision-making methods under interval-valued q-rung orthopair fuzzy sets. Combining the interval-valued q-rung orthopair fuzzy set with the averaging operator, Ju et al. (2019) proposed a series of interval-valued q-rung orthopair fuzzy set averaging operators. Gao et al. (2019) proposed the interval-valued q-rung orthopair fuzzy Archimedes–Moorhead mean operator. Wang et al. (2019a) proposed a series of interval-valued q-rung orthopair fuzzy Hamy mean operators and applied them to group decision-making problems. Yang et al. (2021) proposed the continuous interval-valued q-rung orthopair fuzzy ordered weighted average operator, and defined new score and accuracy functions. Combining the type-2 language set with interval-valued q-rung orthopair fuzzy sets, Wang et al. (2019b) defined the interval-valued q-rung orthopair type-2 language set and provided a new method for solving multiattribute decision-making problems. Garg (2021) combined the possibility measure with interval-valued q-rung orthopair fuzzy sets, defined a possibility measure for interval-valued q-rung orthopair fuzzy sets, and then proposed a new multiattribute group decision-making method. By combining the traditional VIKOR model with interval-valued q-rung orthopair fuzzy sets, Gao et al. (2020) proposed an interval-valued q-rung orthopair fuzzy VIKOR model. Combining the maximum deviation method with q-rung orthopair fuzzy sets and interval-valued q-rung orthopair fuzzy sets, Wang et al. (2019c) proposed two new multiattribute decision-making models. In addition, Farid and Riaz (2021) found in their study that the Einstein operator has no interaction between the membership degree and nonmembership degree when processing data, and if either the membership degree or the nonmembership degree is zero throughout the aggregation process, the other grades of these degrees have no effect on the corresponding averaging or geometric AO, which reduces the efficiency of the operator.

ESG rating is a method for measuring the social responsibility of companies and institutions by scoring them based on three aspects: the environment (E), society (S) and corporate governance (G). However, the ESG rating results of different rating companies are different due to the lack of an industry consensus. It is necessary to have a method for aggregating these data so that subsequent evaluations will be more rational; this problem can be seen as a MAGDM problem. Upon investigating and analyzing the literature, no scholars have studied the Dubois–Prade operator in the interval-valued q-rung orthopair fuzzy environment and its applications in MAGDM problems. The main contributions of the paper are as follows.

• (1) The Dubois–Prade operations and the IVq-ROFDPOWA operator are proposed for the interval-valued q-rung orthopair fuzzy environment. We find that the interaction between the membership degree and nonmembership degree is not considered in the IVq-ROFDP operations and the IVq-ROFDPOWA operator.

• (2) Inspired by Farid and Riaz (2021), this paper further proposes the IVq-ROFIDP operations and the IVq-ROFIDPOWA operator, which can address the issue that the membership and nonmembership degrees in the IVq-ROFDP operations are not affected by each other, and studies their idempotency, permutation invariance, monotonicity and boundedness.

• (3) A group decision-making method based on the IVq-ROFIDPOWA operator is proposed. The provided implementation of ESG ratings and an evaluation of students’ concentration demonstrate the feasibility and effectiveness of the proposed operator and group decision-making method. Moreover, by comparing the proposed operator with some other operators, the group decision-making method developed by this paper can better reflect the differences between alternatives.

The remainder of this paper is arranged as follows. Section 2 introduces the preliminaries. Section 3 presents the IVq-ROFDPOWA operator and its shortcomings. Section 4 develops the IVq-ROFIDP operations and the IVq-ROFIDPOWA operator, as well as the proposed group decision-making method. Section 5 implements two group decision-making cases and analyzes the proposed operator and group decision-making method. Section 6 is the conclusion which summarizes our work and future research.

2 Preliminaries

2.1 Interval-valued q-rung orthopair fuzzy sets

Definition 2.1

(Joshi et al. 2018) Suppose that $X$ is the domain of discourse; then, an interval-valued q-rung orthopair fuzzy set (IVq-ROFS) $A$ in $X$ is defined as:

$$A=\left\{\left.\left\langle x,{\mu }_{a}\left(x\right),{\nu }_{a}\left(x\right)\right\rangle \right|x\epsilon X\right\},$$

(1)

where the membership function and nonmembership function are the mappings of interval values, which satisfy ${\mu }_{a}\left(x\right)=\left[{\mu }_{a}^{-}\left(x\right),{\mu }_{a}^{+}\left(x\right)\right]\subseteq \left[\mathrm{0,1}\right]$ and ${\nu }_{a}\left(x\right)=\left[{\nu }_{a}^{-}\left(x\right),{\nu }_{a}^{+}\left(x\right)\right]\subseteq \left[\mathrm{0,1}\right]$, respectively, with $0\le {\left({\mu }_{a}^{+}\left(x\right)\right)}^{q}+{\left({\nu }_{a}^{+}\left(x\right)\right)}^{q}\le 1,\left(q\ge 1\right)$. The hesitation of $A$ is shown as follows:

$${\pi }_{A}\left(x\right)=\left[{\pi }_{A}^{-}\left(x\right),{\pi }_{A}^{+}\left(x\right)\right]=\left[\sqrt[q]{1-{\left({\mu }_{a}^{+}\left(x\right)\right)}^{q}-{\left({\nu }_{a}^{+}\left(x\right)\right)}^{q}},\sqrt[q]{1-{\left({\mu }_{a}^{-}\left(x\right)\right)}^{q}-{\left({\nu }_{a}^{-}\left(x\right)\right)}^{q}}\right].$$

(2)

Definition 2.2

(Wang et al. 2019a) Let $a=\left\langle \left[{\mu }^{-},{\mu }^{+}\right],\left[{\nu }^{-},{\nu }^{+}\right]\right\rangle$, ${a}_{1}=\left\langle \left[{\mu }_{{a}_{1}}^{-},{\mu }_{{a}_{1}}^{+}\right],\left[{\nu }_{{a}_{1}}^{-},{\nu }_{{a}_{1}}^{+}\right]\right\rangle$ and ${a}_{2}=\left\langle \left[{\mu }_{{a}_{2}}^{-},{\mu }_{{a}_{2}}^{+}\right],\left[{\nu }_{{a}_{2}}^{-},{\nu }_{{a}_{2}}^{+}\right]\right\rangle$ be three interval-valued q-rung orthopair fuzzy numbers (IVq-ROFNs) with $q\ge 1$; then, the basic operations for IVq-ROFNs can be defined as:

$${a_1} \oplus {a_2} =\left\langle \begin{array}{*{20}{c}} {\left[ {\sqrt[q]{{{{\left( {\mu _{{a_1}}^ - } \right)}^q} + {{\left( {\mu _{{a_2}}^ - } \right)}^q} - {{\left( {\mu _{{a_1}}^ - } \right)}^q}{{\left( {\mu _{{a_2}}^ - } \right)}^q}}},\sqrt[q]{{{{\left( {\mu _{{a_1}}^ + } \right)}^q} + {{\left( {\mu _{{a_2}}^ + } \right)}^q} - {{\left( {\mu _{{a_1}}^ + } \right)}^q}{{\left( {\mu _{{a_2}}^ + } \right)}^q}}}} \right],}\\ {\left[ {\nu _{{a_1}}^ - \nu _{{a_2}}^ - ,\nu _{{a_1}}^ + \nu _{{a_2}}^ + } \right]} \end{array}\right\rangle$$

(3)

$${a_1} \otimes {a_2} =\left\langle \begin{array}{*{20}{c}} {\left[ {\mu _{{a_1}}^ - \mu _{{a_2}}^ - ,\mu _{{a_1}}^ + \mu _{{a_2}}^ + } \right],}\\ {\left[ {\sqrt[q]{{{{\left( {\nu _{{a_1}}^ - } \right)}^q} + {{\left( {\nu _{{a_2}}^ - } \right)}^q} - {{\left( {\nu _{{a_1}}^ - } \right)}^q}{{\left( {\nu _{{a_2}}^ - } \right)}^q}}},\sqrt[q]{{{{\left( {\nu _{{a_1}}^ + } \right)}^q} + {{\left( {\nu _{{a_2}}^ + } \right)}^q} - {{\left( {\nu _{{a_1}}^ + } \right)}^q}{{\left( {\nu _{{a_2}}^ + } \right)}^q}}}} \right]} \end{array}\right\rangle$$

(4)

$$\lambda a=\left\langle \left[\sqrt[q]{1-{\left(1-{\left({\mu }^{-}\right)}^{q}\right)}^{\lambda }},\sqrt[q]{1-{\left(1-{\left({\mu }^{+}\right)}^{q}\right)}^{\lambda }}\right],\left[{\left({\nu }^{-}\right)}^{\lambda },{\left({\nu }^{+}\right)}^{\lambda }\right]\right\rangle ,$$

(5)

$${a}^{\lambda }=\left\langle \left[{\left({\mu }^{-}\right)}^{\lambda },{\left({\mu }^{+}\right)}^{\lambda }\right],\left[\sqrt[q]{1-{\left(1-{\left({\nu }^{-}\right)}^{q}\right)}^{\lambda }},\sqrt[q]{1-{\left(1-{\left({\nu }^{+}\right)}^{q}\right)}^{\lambda }}\right]\right\rangle .$$

(6)

Definition 2.3

(Peng and Yong 2016) For each IVq-ROFN $a=\left\langle \left[{\mu }^{-},{\mu }^{+}\right],\left[{\nu }^{-},{\nu }^{+}\right]\right\rangle$, the score function is defined as:

$$S\left(a\right)=\frac{1}{2}\left[{\left({\mu }^{-}\right)}^{q}+{\left({\mu }^{+}\right)}^{q}-{\left({\nu }^{-}\right)}^{q}-{\left({\nu }^{+}\right)}^{q}\right],\left(q\ge 1\right).$$

(7)

Definition 2.4

(Peng and Yong 2016) For each IVq-ROFN $a=\left\langle \left[{\mu }^{-},{\mu }^{+}\right],\left[{\nu }^{-},{\nu }^{+}\right]\right\rangle$, the accuracy function is defined as:

$$H\left(a\right)=\frac{1}{2}\left[{\left({\mu }^{-}\right)}^{q}+{\left({\mu }^{+}\right)}^{q}+{\left({\nu }^{-}\right)}^{q}+{\left({\nu }^{+}\right)}^{q}\right],\left(q\ge 1\right).$$

(8)

Definition 2.5

(Peng and Yong 2016) Let ${a}_{1}=\left\langle \left[{\mu }_{{a}_{1}}^{-},{\mu }_{{a}_{1}}^{+}\right],\left[{\nu }_{{a}_{1}}^{-},{\nu }_{{a}_{1}}^{+}\right]\right\rangle$ and ${a}_{2}=\left\langle \left[{\mu }_{{a}_{2}}^{-},{\mu }_{{a}_{2}}^{+}\right],\left[{\nu }_{{a}_{2}}^{-},{\nu }_{{a}_{2}}^{+}\right]\right\rangle$ be two IVq-ROFNs; then, the rule for comparing their sizes are defined as follows:

(1) If $S({a}_{1})>S({a}_{2})$, then ${a}_{1}>{a}_{2}$;

(2) If $S({a}_{1})<S({a}_{2})$, then ${a}_{1}<{a}_{2}$;

(3) If $S\left({a}_{1}\right)=S({a}_{2})$, then further calculate their accuracies and compare them, ①if $H({a}_{1})>H({a}_{2})$, then ${a}_{1}>{a}_{2}$; ②if $H({a}_{1})<H({a}_{2})$, then ${a}_{1}<{a}_{2}$; ③if $H\left({a}_{1}\right)=H({a}_{2})$, then ${a}_{1}={a}_{2}$.

2.2 Dubois–Prade operator

Definition 2.6

(Dubois and Prade 1980) For any two real numbers $a,b\epsilon \left[\mathrm{0,1}\right]$, the Dubois–Prade operator is a t-norm operation, and it is defined as follows:

$${T}_{DP}\left(a,b\right)=\frac{ab}{\mathrm{max}\left(a,b,p\right)},\left(p\epsilon \left[\mathrm{0,1}\right]\right).$$

(9)

Its corresponding t-conorm operation is shown as follows:

$${T}_{DP}^{*}\left(a,b\right)=1-\frac{\left(1-a\right)\left(1-b\right)}{\mathrm{max}\left(1-a,1-b,p\right)},\left(p\epsilon \left[\mathrm{0,1}\right]\right).$$

(10)

In Formulas (9) and (10), $p$ is a variable parameter. When $p$ changes, the Dubois–Prade operator also changes. When $p=1$, the operator is transformed into the product operator, and when $p=0$, the operator is transformed into the minimum operator.

3 Interval-valued q-rung orthopair fuzzy Dubois–Prade operator

In this section, the interval-valued q-rung orthopair fuzzy Dubois–Prade (IVq-ROFDP) operations and the interval-valued q-rung orthopair fuzzy Dubois–Prade ordered weighted aggregation (IVq-ROFDPOWA) operator are interpreted.

3.1 IVq-ROFDP operations

Based on the t-norm and t-conorm operations of Dubois–Prade operator in Formulas (9) and (10), respectively, the IVq-ROFDP operations are defined.

Definition 3.1

Let $a=\left\langle \left[{\mu }^{-},{\mu }^{+}\right],\left[{\nu }^{-},{\nu }^{+}\right]\right\rangle$, ${a}_{1}=\left\langle \left[{\mu }_{{a}_{1}}^{-},{\mu }_{{a}_{1}}^{+}\right],\left[{\nu }_{{a}_{1}}^{-},{\nu }_{{a}_{1}}^{+}\right]\right\rangle$ and ${a}_{2}=\left\langle \left[{\mu }_{{a}_{2}}^{-},{\mu }_{{a}_{2}}^{+}\right],\left[{\nu }_{{a}_{2}}^{-},{\nu }_{{a}_{2}}^{+}\right]\right\rangle$ be three IVq-ROFNs with $q\ge 1$; then, the IVq-ROFDP operations can be defined as:

$$\begin{aligned} &{a}_{1}{\oplus }_{DP}{a}_{2}\\ &\quad=\left\langle\!\begin{array}{*{20}{c}} {\left[\!\sqrt[q]{1\!-\!\frac{\left(1\!-\!{{\mu }_{{a}_{1}}^{-}}^{q}\right)\left(1\!-\!{{\mu }_{{a}_{2}}^{-}}^{q}\right)}{max\left\{1\!-\!{{\mu }_{{a}_{1}}^{-}}^{q},1\!-\!{{\mu }_{{a}_{2}}^{-}}^{q},p\right\}}},\sqrt[q]{1\!-\!\frac{\left(1\!-\!{{\mu }_{{a}_{1}}^{+}}^{q}\right)\left(1\!-\!{{\mu }_{{a}_{2}}^{+}}^{q}\right)}{max\left\{1\!-\!{{\mu }_{{a}_{1}}^{+}}^{q},1\!-\!{{\mu }_{{a}_{2}}^{+}}^{q},p\!\right\}}}\!\right],}\\{\left[\sqrt[q]{\frac{{{\nu }_{{a}_{1}}^{-}}^{q}{{\nu }_{{a}_{2}}^{-}}^{q}}{max\left\{{{\nu }_{{a}_{1}}^{-}}^{q},{{\nu }_{{a}_{2}}^{-}}^{q},p\right\}}},\sqrt[q]{\frac{{{\nu }_{{a}_{1}}^{+}}^{q}{{\nu }_{{a}_{2}}^{+}}^{q}}{max\left\{{{\nu }_{{a}_{1}}^{+}}^{q},{{\nu }_{{a}_{2}}^{+}}^{q},p\right\}}}\right]} \end{array}\right\rangle,\end{aligned}$$

(11)

$$\begin{aligned}&{a}_{1}{\otimes }_{DP}{a}_{2}\\ &\quad=\left\langle \!\begin{array}{*{20}{c}}{\left[\sqrt[q]{\frac{{{\mu }_{{a}_{1}}^{-}}^{q}{{\mu }_{{a}_{2}}^{-}}^{q}}{max\left\{{{\mu }_{{a}_{1}}^{-}}^{q},{{\mu }_{{a}_{2}}^{-}}^{q},p\right\}}},\sqrt[q]{\frac{{{\mu }_{{a}_{1}}^{+}}^{q}{{\mu }_{{a}_{2}}^{+}}^{q}}{max\left\{{{\mu }_{{a}_{1}}^{+}}^{q},{{\mu }_{{a}_{2}}^{+}}^{q},p\right\}}}\right],}\\{\left[\!\sqrt[q]{1\!-\!\frac{\left(1\!-\!{{\nu }_{{a}_{1}}^{-}}^{q}\right)\left(1\!-\!{{\nu }_{{a}_{2}}^{-}}^{q}\right)}{max\left\{\!1\!-\!{{\nu }_{{a}_{1}}^{-}}^{q},1\!-\!{{\nu }_{{a}_{2}}^{-}}^{q},p\!\right\}}},\sqrt[q]{1\!-\!\frac{\left(1\!-\!{{\nu }_{{a}_{1}}^{+}}^{q}\!\right)\!\left(1\!-\!{{\nu }_{{a}_{2}}^{+}}^{q}\right)}{max\left\{\!1\!-\!{{\nu }_{{a}_{1}}^{+}}^{q},1\!-\!{{\nu }_{{a}_{2}}^{+}}^{q},p\!\right\}}}\!\right]}\end{array}\!\right\rangle , \end{aligned}$$

(12)

$$\lambda a=\left\langle \begin{array}{*{20}{c}}{\left[\sqrt[q]{1-\frac{{\left(1-{{\mu }^{-}}^{q}\right)}^{\lambda }}{{\left(max\left\{1-{{\mu }^{-}}^{q},p\right\}\right)}^{\left(\lambda -1\right)}}},\sqrt[q]{1-\frac{{\left(1-{{\mu }^{+}}^{q}\right)}^{\lambda }}{{\left(max\left\{1-{{\mu }^{+}}^{q},p\right\}\right)}^{\left(\lambda -1\right)}}}\right],}\\{\left[\sqrt[q]{\frac{{\left({{\nu }^{-}}^{q}\right)}^{\lambda }}{{\left(max\left\{{{\nu }^{-}}^{q},p\right\}\right)}^{\left(\lambda -1\right)}}},\sqrt[q]{\frac{{\left({{\nu }^{+}}^{q}\right)}^{\lambda }}{{\left(max\left\{{{\nu }^{+}}^{q},p\right\}\right)}^{\left(\lambda -1\right)}}}\right]} \end{array}\right\rangle ,$$

(13)

$${a}^{\lambda }=\left\langle \begin{array}{*{20}{c}}{\left[\sqrt[q]{\frac{{\left({{\mu }^{-}}^{q}\right)}^{\lambda }}{{\left(max\left\{{{\mu }^{-}}^{q},p\right\}\right)}^{\left(\lambda -1\right)}}},\sqrt[q]{\frac{{\left({{\mu }^{+}}^{q}\right)}^{\lambda }}{{\left(max\left\{{{\mu }^{+}}^{q},p\right\}\right)}^{\left(\lambda -1\right)}}}\right],}\\{ \left[\sqrt[q]{1-\frac{{\left(1-{{\nu }^{-}}^{q}\right)}^{\lambda }}{{\left(max\left\{1-{{\nu }^{-}}^{q},p\right\}\right)}^{\left(\lambda -1\right)}}},\sqrt[q]{1-\frac{{\left(1-{{\nu }^{+}}^{q}\right)}^{\lambda }}{{\left(max\left\{1-{{\nu }^{+}}^{q},p\right\}\right)}^{\left(\lambda -1\right)}}}\right]} \end{array}\right\rangle .$$

(14)

It can be verified that the IVq-ROFDP addition and product operations defined in this section satisfy the rules of t-conorms and t-norms. Additionally, the multiplication and power operations satisfy the rules of t-conorms and t-norms.

3.2 IVq-ROFDPOWA operator

Definition 3.2

Let ${a}_{i}=\left\langle \left[{\mu }_{{a}_{i}}^{-},{\mu }_{{a}_{i}}^{+}\right],\left[{\nu }_{{a}_{i}}^{-},{\nu }_{{a}_{i}}^{+}\right]\right\rangle \left(i=\mathrm{1,2},3,\cdots ,n\right)$ be a group of IVq-ROFNs and $\omega ={\left({\omega }_{1},{\omega }_{2},{\omega }_{3},\cdots ,{\omega }_{n}\right)}^{T}$ be the corresponding weight vector that satisfies ${\sum }_{i=1}^{n}{\omega }_{i}=1,{\omega }_{i}\ge 0\left(i=\mathrm{1,2},3,\cdots ,n\right)$. The IVq-ROFDPOWA operator, shown as Formula (15), is a mapping from ${\mathrm{IVq}-\mathrm{ROFNs}}^{n}$ to an $\mathrm{IVq}-\mathrm{ROFN}$.

$$\begin{aligned}&IVq-ROFDPOWA\left({a}_{1},{a}_{2},{a}_{3},\cdots ,{a}_{n}\right)\\&=\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} n\\ {{ \oplus _{DP}}} \end{array}}\\ {i = 1} \end{array}{\omega _i}{a_{\sigma \left( i \right)}}\\&=\left\langle \begin{array}{*{20}{c}}{\left[\!\sqrt[q]{1\!-\frac{{\prod }_{i=1}^{n}\frac{{\left(1\!-\!{{\mu }_{{a}_{\sigma \left(i\right)}}^{-}}^{q}\right)}^{{\omega }_{i}}}{{\left(\!max\left\{\!1\!-\!{{\mu }_{{a}_{\sigma \left(i\right)}}^{-}}^{q},p\right\}\right)}^{\left({\omega }_{i}-1\right)}}}{{\prod }_{i=1}^{n-1}max\left\{1\!-\!{{\mu }_{{a}_{\alpha \left(i\right)}}^{-}}^{q},p\right\}}},\sqrt[q]{1\!-\!\frac{{\prod }_{i=1}^{n}\frac{{\left(1-{{\mu }_{{a}_{\sigma \left(i\right)}}^{+}}^{q}\right)}^{{\omega }_{i}}}{{\left(max\left\{1-{{\mu }_{{a}_{\sigma \left(i\right)}}^{+}}^{q},p\right\}\right)}^{\left({\omega }_{i}-1\right)}}}{{\prod }_{i=1}^{n-1}max\!\left\{\!1\!-\!{{\mu }_{{a}_{\beta \left(i\right)}}^{+}}^{q},p\!\right\}}}\right],}\\{\left[\sqrt[q]{\frac{{\prod }_{i=1}^{n}\frac{{\left({{\nu }_{{a}_{\sigma \left(i\right)}}^{-}}^{q}\right)}^{{\omega }_{i}}}{{\left(max\left\{{{\nu }_{{a}_{\sigma \left(i\right)}}^{-}}^{q},p\right\}\right)}^{\left({\omega }_{i}-1\right)}}}{{\prod }_{i=1}^{n-1}max\left\{{{\nu }_{{a}_{\gamma \left(i\right)}}^{-}}^{q},p\right\}}},\sqrt[q]{\frac{{\prod }_{i=1}^{n}\frac{{\left({{\nu }_{{a}_{\sigma \left(i\right)}}^{+}}^{q}\right)}^{{\omega }_{i}}}{{\left(max\left\{{{\nu }_{{a}_{\sigma \left(i\right)}}^{+}}^{q},p\right\}\right)}^{\left({\omega }_{i}-1\right)}}}{{\prod }_{i=1}^{n-1}max\left\{{{\nu }_{{a}_{\delta \left(i\right)}}^{+}}^{q},p\right\}}}\right]} \end{array}\right\rangle .\end{aligned}$$

(15)

In Formula (15), $\left(\sigma \left(1\right),\sigma \left(2\right),\cdots ,\sigma \left(n\right)\right)$, $\left(\alpha \left(1\right),\alpha \left(2\right),\cdots ,\alpha \left(n\right)\right)$, $\left(\beta \left(1\right),\beta \left(2\right),\cdots ,\beta \left(n\right)\right)$, $\left(\gamma \left(1\right),\gamma \left(2\right),\cdots ,\gamma \left(n\right)\right)$, and $\left(\delta \left(1\right),\delta \left(2\right),\cdots ,\delta \left(n\right)\right)$ are replacements of $\left(\mathrm{1,2},\cdots ,n\right)$ that satisfy ${a}_{\sigma \left(i\right)}\ge {a}_{\sigma \left(i+1\right)}$, $1-{{\mu }_{{a}_{\alpha \left(i\right)}}^{-}}^{q}\ge 1-{{\mu }_{{a}_{\alpha \left(i+1\right)}}^{-}}^{q}$, $1-{{\mu }_{{a}_{\beta \left(i\right)}}^{+}}^{q}\ge 1-{{\mu }_{{a}_{\beta \left(i+1\right)}}^{+}}^{q}$, ${{\nu }_{{a}_{\gamma \left(i\right)}}^{-}}^{q}\ge {{\nu }_{{a}_{\gamma \left(i+1\right)}}^{-}}^{q}$, and ${{\nu }_{{a}_{\delta \left(i\right)}}^{+}}^{q}\ge {{\nu }_{{a}_{\delta \left(i+1\right)}}^{+}}^{q}\left(i=\mathrm{1,2},3,\cdots ,n-1\right)$, respectively.

While testing and applying the IVq-ROFDP operations and the IVq-ROFDPOWA operator, we find that the aggregation results may not be very satisfactory, especially when extreme data such as 0s are present in the IVq-ROFNs. The main reason for this situation is that the interaction between the membership degree and the nonmembership degree is not represented. It can be seen from Formulas (11) to (14) that during the process of the IVq-ROFDP operations, the membership degree and nonmembership degree are independent, so neither of them is not affected by the change of the other. Furthermore, in Formula (15), the nonmembership degree in the result of the IVq-ROFDPOWA operator remains $\left[\mathrm{0,0}\right]$, when there is at least one IVq-ROFN whose nonmembership is $\left[\mathrm{0,0}\right]$, regardless of how the other IVq-ROFNs and the weight vector change. Example 1 demonstrates the issue.

Example 1

Suppose that ${a}_{1}=\left\langle \left[\mathrm{0.65,0.75}\right],\left[\mathrm{0,0}\right]\right\rangle$, ${a}_{2}=\left\langle \left[\mathrm{0.55,0.8}\right],\left[\mathrm{0.1,0.2}\right]\right\rangle$ and ${a}_{3}=\left\langle \left[\mathrm{0.85,0.95}\right],\left[\mathrm{0.05,0.2}\right]\right\rangle$ are three IVq-ROFNs, and the weight vector is $\omega =\left(\mathrm{0.3,0.4,0.3}\right)$. Using the IVq-ROFDPOWA operator with $q=3$ and $p=0.5$, the aggregation result is $IVq-ROFDPOWA\left({a}_{1},{a}_{2},{a}_{3}\right)=\left\langle \left[\mathrm{0.8130,0.8704}\right],\left[\mathrm{0,0}\right]\right\rangle$. If we modify the values of these IVq-ROFNs, and change them to ${a}_{1}^{^{\prime}}=\left\langle \left[\mathrm{0.15,0.3}\right],\left[\mathrm{0,0}\right]\right\rangle$, ${a}_{2}^{^{\prime}}=\left\langle \left[\mathrm{0.4,0.5}\right],\left[\mathrm{0.1,0.2}\right]\right\rangle$, ${a}_{3}^{^{\prime}}=\left\langle \left[\mathrm{0.25,0.35}\right],\left[0.\mathrm{05,0.2}\right]\right\rangle$, then, using the IVq-ROFDPOWA operator, the aggregation result will become $IVq-ROFDPOWA\left({a}_{1}^{^{\prime}},{a}_{2}^{^{\prime}},{a}_{3}^{^{\prime}}\right)=\left\langle \left[\mathrm{0.4,0.5}\right],\left[\mathrm{0,0}\right]\right\rangle$.

In this case, it can be seen that the membership degree and the nonmembership degree are not affected by each other’s changes.

4 Group decision-making method based on interactive Dubois–Prade operator

To address the issue of IVq-ROFDP, this section proposes the IVq-ROFIDP operations and the IVq-ROFIDPOWA operator. A group decision-making method based on the IVq-ROFIDPOWA operator is also interpreted.

4.1 IVq-ROFIDP operations

Definition 4.1

Let $a=\left\langle \left[{\mu }^{-},{\mu }^{+}\right],\left[{\nu }^{-},{\nu }^{+}\right]\right\rangle$, ${a}_{1}=\left\langle \left[{\mu }_{{a}_{1}}^{-},{\mu }_{{a}_{1}}^{+}\right],\left[{\nu }_{{a}_{1}}^{-},{\nu }_{{a}_{1}}^{+}\right]\right\rangle$ and ${a}_{2}=\left\langle \left[{\mu }_{{a}_{2}}^{-},{\mu }_{{a}_{2}}^{+}\right],\left[{\nu }_{{a}_{2}}^{-},{\nu }_{{a}_{2}}^{+}\right]\right\rangle$ be three IVq-ROFNs with $q\ge 1$; then, the IVq-ROFIDP operations can be defined as:

$$\begin{aligned} &{a}_{1}{\oplus }_{IDP}{a}_{2}\\ &\quad=\left\langle \begin{array}{*{20}{c}} {\left[\sqrt[q]{1-\frac{\left(1-{{\mu }_{{a}_{1}}^{-}}^{q}\right)\left(1-{{\mu }_{{a}_{2}}^{-}}^{q}\right)}{max\left\{1-{{\mu }_{{a}_{1}}^{-}}^{q},1-{{\mu }_{{a}_{2}}^{-}}^{q},p\right\}}},\sqrt[q]{1-\frac{\left(1-{{\mu }_{{a}_{1}}^{+}}^{q}\right)\left(1-{{\mu }_{{a}_{2}}^{+}}^{q}\right)}{max\left\{1-{{\mu }_{{a}_{1}}^{+}}^{q},1-{{\mu }_{{a}_{2}}^{+}}^{q},p\right\}}}\right],}\\ {\left[ \begin{array}{*{20}{c}} {\sqrt[q]{\frac{\left(1-{{\mu }_{{a}_{1}}^{-}}^{q}\right)\left(1-{{\mu }_{{a}_{2}}^{-}}^{q}\right)-\left(1-{{\mu }_{{a}_{1}}^{-}}^{q}-{{\nu }_{{a}_{1}}^{-}}^{q}\right)\left(1-{{\mu }_{{a}_{2}}^{-}}^{q}-{{\nu }_{{a}_{2}}^{-}}^{q}\right)}{max\left\{1-{{\mu }_{{a}_{1}}^{-}}^{q},1-{{\mu }_{{a}_{2}}^{-}}^{q},p\right\}}},}\\ {\sqrt[q]{\frac{\left(1-{{\mu }_{{a}_{1}}^{+}}^{q}\right)\left(1-{{\mu }_{{a}_{2}}^{+}}^{q}\right)-\left(1-{{\mu }_{{a}_{1}}^{+}}^{q}-{{\nu }_{{a}_{1}}^{+}}^{q}\right)\left(1-{{\mu }_{{a}_{2}}^{+}}^{q}-{{\nu }_{{a}_{2}}^{+}}^{q}\right)}{max\left\{1-{{\mu }_{{a}_{1}}^{+}}^{q},1-{{\mu }_{{a}_{2}}^{+}}^{q},p\right\}}}} \end{array}\right]} \end{array} \right\rangle ,\end{aligned}$$

(16)

$$\begin{aligned} &{a}_{1}{\otimes }_{IDP}{a}_{2}\\ &\quad=\left\langle \begin{array}{*{20}{c}} {\left[\begin{array}{*{20}{c}}{\sqrt[q]{\frac{\left(1-{{\nu }_{{a}_{1}}^{-}}^{q}\right)\left(1-{{\nu }_{{a}_{2}}^{-}}^{q}\right)-\left(1-{{\mu }_{{a}_{1}}^{-}}^{q}-{{\nu }_{{a}_{1}}^{-}}^{q}\right)\left(1-{{\mu }_{{a}_{2}}^{-}}^{q}-{{\nu }_{{a}_{2}}^{-}}^{q}\right)}{max\left\{1-{{\nu }_{{a}_{1}}^{-}}^{q},1-{{\nu }_{{a}_{2}}^{-}}^{q},p\right\}}},}\\ {\sqrt[q]{\frac{\left(1-{{\nu }_{{a}_{1}}^{+}}^{q}\right)\left(1-{{\nu }_{{a}_{2}}^{+}}^{q}\right)-\left(1-{{\mu }_{{a}_{1}}^{+}}^{q}-{{\nu }_{{a}_{1}}^{+}}^{q}\right)\left(1-{{\mu }_{{a}_{2}}^{+}}^{q}-{{\nu }_{{a}_{2}}^{+}}^{q}\right)}{max\left\{1-{{\nu }_{{a}_{1}}^{+}}^{q},1-{{\nu }_{{a}_{2}}^{+}}^{q},p\right\}}}} \end{array}\right],}\\ {\left[\sqrt[q]{1-\frac{\left(1-{{\nu }_{{a}_{1}}^{-}}^{q}\right)\left(1-{{\nu }_{{a}_{2}}^{-}}^{q}\right)}{max\left\{1-{{\nu }_{{a}_{1}}^{-}}^{q},1-{{\nu }_{{a}_{2}}^{-}}^{q},p\right\}}},\sqrt[q]{1-\frac{\left(1-{{\nu }_{{a}_{1}}^{+}}^{q}\right)\left(1-{{\nu }_{{a}_{2}}^{+}}^{q}\right)}{max\left\{1-{{\nu }_{{a}_{1}}^{+}}^{q},1-{{\nu }_{{a}_{2}}^{+}}^{q},p\right\}}}\right]} \end{array}\right\rangle ,\end{aligned}$$

(17)

$$\lambda a=\left\langle \begin{array}{*{20}{c}} {\left[\sqrt[q]{1-\frac{{\left(1-{{\mu }^{-}}^{q}\right)}^{\lambda }}{{\left(max\left\{1-{{\mu }^{-}}^{q},p\right\}\right)}^{\left(\lambda -1\right)}}},\sqrt[q]{1-\frac{{\left(1-{{\mu }^{+}}^{q}\right)}^{\lambda }}{{\left(max\left\{1-{{\mu }^{+}}^{q},p\right\}\right)}^{\left(\lambda -1\right)}}}\right],}\\ {\left[\sqrt[q]{\frac{{\left(1-{{\mu }^{-}}^{q}\right)}^{\lambda }-{\left(1-{{\mu }^{-}}^{q}-{{\nu }^{-}}^{q}\right)}^{\lambda }}{{\left(max\left\{1-{{\mu }^{-}}^{q},p\right\}\right)}^{\left(\lambda -1\right)}}},\sqrt[q]{\frac{{\left(1-{{\mu }^{+}}^{q}\right)}^{\lambda }-{\left(1-{{\mu }^{+}}^{q}-{{\nu }^{+}}^{q}\right)}^{\lambda }}{{\left(max\left\{1-{{\mu }^{+}}^{q},p\right\}\right)}^{\left(\lambda -1\right)}}}\right]} \end{array} \right\rangle ,$$

(18)

$${a}^{\lambda }=\left\langle \begin{array}{*{20}{c}} {\left[\sqrt[q]{\frac{{\left(1-{{\nu }^{-}}^{q}\right)}^{\lambda }-{\left(1-{{\mu }^{-}}^{q}-{{\nu }^{-}}^{q}\right)}^{\lambda }}{{\left(max\left\{1-{{\nu }^{-}}^{q},p\right\}\right)}^{\left(\lambda -1\right)}}},\sqrt[q]{\frac{{\left(1-{{\nu }^{+}}^{q}\right)}^{\lambda }-{\left(1-{{\mu }^{+}}^{q}-{{\nu }^{+}}^{q}\right)}^{\lambda }}{{\left(max\left\{1-{{\nu }^{+}}^{q},p\right\}\right)}^{\left(\lambda -1\right)}}}\right],}\\ { \left[\sqrt[q]{1-\frac{{\left(1-{{\nu }^{-}}^{q}\right)}^{\lambda }}{{\left(max\left\{1-{{\nu }^{-}}^{q},p\right\}\right)}^{\left(\lambda -1\right)}}},\sqrt[q]{1-\frac{{\left(1-{{\nu }^{+}}^{q}\right)}^{\lambda }}{{\left(max\left\{1-{{\nu }^{+}}^{q},p\right\}\right)}^{\left(\lambda -1\right)}}}\right]}\end{array} \right\rangle .$$

(19)

It can be verified that the results of the IVq-ROFIDP operations are still IVq-ROFNs.

Theorem 4.1

Let $a=\left\langle \left[{\mu }^{-},{\mu }^{+}\right],\left[{\nu }^{-},{\nu }^{+}\right]\right\rangle$, ${a}_{1}=\left\langle \left[{\mu }_{{a}_{1}}^{-},{\mu }_{{a}_{1}}^{+}\right],\left[{\nu }_{{a}_{1}}^{-},{\nu }_{{a}_{1}}^{+}\right]\right\rangle$ and ${a}_{2}=\left\langle \left[{\mu }_{{a}_{2}}^{-},{\mu }_{{a}_{2}}^{+}\right],\left[{\nu }_{{a}_{2}}^{-},{\nu }_{{a}_{2}}^{+}\right]\right\rangle$ be three IVq-ROFNs with $q\ge 1$; then, the IVq-ROFIDP operations satisfy the following six properties when $\lambda ,{\lambda }_{1},{\lambda }_{2}>0$.

$${\text{Commutative Law of Addition}}:\quad a_{1} \oplus_{IDP} a_{2} = a_{2} \oplus_{IDP} a_{1} ,$$

(20)

$${\text{Commutative Law of Multiplication:}}\quad a_{1} \otimes_{IDP} a_{2} = a_{2} \otimes_{IDP} a_{1} ,$$

(21)

$${\text{Distributive Law of Multiplication:}}\quad \lambda \left( {a_{1} \oplus_{IDP} a_{2} } \right) = \left( {\lambda a_{1} } \right) \oplus_{IDP} \left( {\lambda a_{2} } \right),$$

(22)

$${\text{Distributive Law of Power:}}\quad \left( {a_{1} \otimes_{IDP} a_{2} } \right)^{\lambda } = \left( {a_{1}^{\lambda } } \right) \otimes_{IDP} \left( {a_{2}^{\lambda } } \right),$$

(23)

$${\text{Associative Law of Multiplication:}}\quad (\lambda_{1} a) \oplus_{IDP} (\lambda_{2} a) = (\lambda_{1} + \lambda_{2} )a,$$

(24)

$${\text{Associative Law of Power:}}\quad \left( {a^{{\lambda_{1} }} } \right) \otimes_{IDP} \left( {a^{{\lambda_{2} }} } \right) = a^{{\left( {\lambda_{1} + \lambda_{2} } \right)}} .$$

(25)

The proof of Theorem 4.1 can be verified by applying the IVq-ROFIDP operations. This paper only presents the proof of Formula (22).

Proof

From Formulas (16) and (18), we have that

$$\begin{aligned}&\left(\lambda {a}_{1}\right){\oplus }_{IDP}\left(\lambda {a}_{2}\right)\\& =\left\langle \begin{array}{*{20}{c}} {\left[\sqrt[q]{1-\frac{{\left(1-{{\mu }_{{a}_{1}}^{-}}^{q}\right)}^{\lambda }}{{\left(max\left\{1-{{\mu }_{{a}_{1}}^{-}}^{q},p\right\}\right)}^{\left(\lambda -1\right)}}},\sqrt[q]{1-\frac{{\left(1-{{\mu }_{{a}_{1}}^{+}}^{q}\right)}^{\lambda }}{{\left(max\left\{1-{{\mu }_{{a}_{1}}^{+}}^{q},p\right\}\right)}^{\left(\lambda -1\right)}}}\right],}\\{\left[\sqrt[q]{\frac{{\left(1-{{\mu }_{{a}_{1}}^{-}}^{q}\right)}^{\lambda }-{\left(1-{{\mu }_{{a}_{1}}^{-}}^{q}-{{\nu }_{{a}_{1}}^{-}}^{q}\right)}^{\lambda }}{{\left(max\left\{1-{{\mu }_{{a}_{1}}^{-}}^{q},p\right\}\right)}^{\left(\lambda -1\right)}}},\sqrt[q]{\frac{{\left(1-{{\mu }_{{a}_{1}}^{+}}^{q}\right)}^{\lambda }-{\left(1-{{\mu }_{{a}_{1}}^{+}}^{q}-{{\nu }_{{a}_{1}}^{+}}^{q}\right)}^{\lambda }}{{\left(max\left\{1-{{\mu }_{{a}_{1}}^{+}}^{q},p\right\}\right)}^{\left(\lambda -1\right)}}}\right]} \end{array}\right\rangle\\& {\oplus }_{IDP}\left\langle \begin{array}{*{20}{c}}{\left[\sqrt[q]{1-\frac{{\left(1-{{\mu }_{{a}_{2}}^{-}}^{q}\right)}^{\lambda }}{{\left(max\left\{1-{{\mu }_{{a}_{2}}^{-}}^{q},p\right\}\right)}^{\left(\lambda -1\right)}}},\sqrt[q]{1-\frac{{\left(1-{{\mu }_{{a}_{2}}^{+}}^{q}\right)}^{\lambda }}{{\left(max\left\{1-{{\mu }_{{a}_{2}}^{+}}^{q},p\right\}\right)}^{\left(\lambda -1\right)}}}\right],}\\{\left[\sqrt[q]{\frac{{\left(1-{{\mu }_{{a}_{2}}^{-}}^{q}\right)}^{\lambda }-{\left(1-{{\mu }_{{a}_{2}}^{-}}^{q}-{{\nu }_{{a}_{2}}^{-}}^{q}\right)}^{\lambda }}{{\left(max\left\{1-{{\mu }_{{a}_{2}}^{-}}^{q},p\right\}\right)}^{\left(\lambda -1\right)}}},\sqrt[q]{\frac{{\left(1-{{\mu }_{{a}_{2}}^{+}}^{q}\right)}^{\lambda }-{\left(1-{{\mu }_{{a}_{2}}^{+}}^{q}-{{\nu }_{{a}_{2}}^{+}}^{q}\right)}^{\lambda }}{{\left(max\left\{1-{{\mu }_{{a}_{2}}^{+}}^{q},p\right\}\right)}^{\left(\lambda -1\right)}}}\right]} \end{array}\right\rangle \end{aligned}$$

$$\begin{aligned} &=\left\langle \begin{array}{*{20}{c}} {\left[\begin{array}{*{20}{c}}{\sqrt[q]{1-\frac{\left(\frac{{\left(1-{{\mu }_{{a}_{1}}^{-}}^{q}\right)}^{\lambda }}{{\left(max\left\{1-{{\mu }_{{a}_{1}}^{-}}^{q},p\right\}\right)}^{\left(\lambda -1\right)}}\right)\left(\frac{{\left(1-{{\mu }_{{a}_{2}}^{-}}^{q}\right)}^{\lambda }}{{\left(max\left\{1-{{\mu }_{{a}_{2}}^{-}}^{q},p\right\}\right)}^{\left(\lambda -1\right)}}\right)}{max\left\{\left(\frac{{\left(1-{{\mu }_{{a}_{1}}^{-}}^{q}\right)}^{\lambda }}{{\left(max\left\{1-{{\mu }_{{a}_{1}}^{-}}^{q},p\right\}\right)}^{\left(\lambda -1\right)}}\right),\left(\frac{{\left(1-{{\mu }_{{a}_{2}}^{-}}^{q}\right)}^{\lambda }}{{\left(max\left\{1-{{\mu }_{{a}_{2}}^{-}}^{q},p\right\}\right)}^{\left(\lambda -1\right)}}\right),p\right\}}},}\\ {\sqrt[q]{1-\frac{\left(\frac{{\left(1-{{\mu }_{{a}_{1}}^{+}}^{q}\right)}^{\lambda }}{{\left(max\left\{1-{{\mu }_{{a}_{1}}^{+}}^{q},p\right\}\right)}^{\left(\lambda -1\right)}}\right)\left(\frac{{\left(1-{{\mu }_{{a}_{2}}^{+}}^{q}\right)}^{\lambda }}{{\left(max\left\{1-{{\mu }_{{a}_{2}}^{+}}^{q},p\right\}\right)}^{\left(\lambda -1\right)}}\right)}{max\left\{\left(\frac{{\left(1-{{\mu }_{{a}_{1}}^{+}}^{q}\right)}^{\lambda }}{{\left(max\left\{1-{{\mu }_{{a}_{1}}^{+}}^{q},p\right\}\right)}^{\left(\lambda -1\right)}}\right),\left(\frac{{\left(1-{{\mu }_{{a}_{2}}^{+}}^{q}\right)}^{\lambda }}{{\left(max\left\{1-{{\mu }_{{a}_{2}}^{+}}^{q},p\right\}\right)}^{\left(\lambda -1\right)}}\right),p\right\}}}}\end{array}\right],}\\ {\left[\begin{array}{*{20}{c}}{\sqrt[q]{\frac{\left(\frac{{\left(1-{{\mu }_{{a}_{1}}^{-}}^{q}\right)}^{\lambda }}{{\left(max\left\{1-{{\mu }_{{a}_{1}}^{-}}^{q},p\right\}\right)}^{\left(\lambda -1\right)}}\right)\left(\frac{{\left(1-{{\mu }_{{a}_{2}}^{-}}^{q}\right)}^{\lambda }}{{\left(max\left\{1-{{\mu }_{{a}_{2}}^{-}}^{q},p\right\}\right)}^{\left(\lambda -1\right)}}\right)-\left(\frac{{\left(1-{{\mu }_{{a}_{1}}^{-}}^{q}-{{\nu }_{{a}_{1}}^{-}}^{q}\right)}^{\lambda }}{{\left(max\left\{1-{{\mu }_{{a}_{1}}^{-}}^{q},p\right\}\right)}^{\left(\lambda -1\right)}}\right)\left(\frac{{\left(1-{{\mu }_{{a}_{2}}^{-}}^{q}-{{\nu }_{{a}_{2}}^{-}}^{q}\right)}^{\lambda }}{{\left(max\left\{1-{{\mu }_{{a}_{2}}^{-}}^{q},p\right\}\right)}^{\left(\lambda -1\right)}}\right)}{max\left\{\left(\frac{{\left(1-{{\mu }_{{a}_{1}}^{-}}^{q}\right)}^{\lambda }}{{\left(max\left\{1-{{\mu }_{{a}_{1}}^{-}}^{q},p\right\}\right)}^{\left(\lambda -1\right)}}\right),\left(\frac{{\left(1-{{\mu }_{{a}_{2}}^{-}}^{q}\right)}^{\lambda }}{{\left(max\left\{1-{{\mu }_{{a}_{2}}^{-}}^{q},p\right\}\right)}^{\left(\lambda -1\right)}}\right),p\right\}}},}\\ {\sqrt[q]{\frac{\left(\frac{{\left(1-{{\mu }_{{a}_{1}}^{+}}^{q}\right)}^{\lambda }}{{\left(max\left\{1-{{\mu }_{{a}_{1}}^{+}}^{q},p\right\}\right)}^{\left(\lambda -1\right)}}\right)\left(\frac{{\left(1-{{\mu }_{{a}_{2}}^{+}}^{q}\right)}^{\lambda }}{{\left(max\left\{1-{{\mu }_{{a}_{2}}^{+}}^{q},p\right\}\right)}^{\left(\lambda -1\right)}}\right)-\left(\frac{{\left(1-{{\mu }_{{a}_{1}}^{+}}^{q}-{{\nu }_{{a}_{1}}^{+}}^{q}\right)}^{\lambda }}{{\left(max\left\{1-{{\mu }_{{a}_{1}}^{+}}^{q},p\right\}\right)}^{\left(\lambda -1\right)}}\right)\left(\frac{{\left(1-{{\mu }_{{a}_{2}}^{+}}^{q}-{{\nu }_{{a}_{2}}^{+}}^{q}\right)}^{\lambda }}{{\left(max\left\{1-{{\mu }_{{a}_{2}}^{+}}^{q},p\right\}\right)}^{\left(\lambda -1\right)}}\right)}{max\left\{\left(\frac{{\left(1-{{\mu }_{{a}_{1}}^{+}}^{q}\right)}^{\lambda }}{{\left(max\left\{1-{{\mu }_{{a}_{1}}^{+}}^{q},p\right\}\right)}^{\left(\lambda -1\right)}}\right),\left(\frac{{\left(1-{{\mu }_{{a}_{2}}^{+}}^{q}\right)}^{\lambda }}{{\left(max\left\{1-{{\mu }_{{a}_{2}}^{+}}^{q},p\right\}\right)}^{\left(\lambda -1\right)}}\right),p\right\}}}}\end{array}\right]}\end{array}\right\rangle \\&=\left\langle \begin{array}{*{20}{c}} {\left[\sqrt[q]{1-\frac{{\left(\left(1-{{\mu }_{{a}_{1}}^{-}}^{q}\right)\left(1-{{\mu }_{{a}_{2}}^{-}}^{q}\right)\right)}^{\lambda }}{{\left(max\left\{1-{{\mu }_{{a}_{1}}^{-}}^{q},1-{{\mu }_{{a}_{2}}^{-}}^{q},p\right\}\right)}^{\left(\lambda -1\right)}}},\sqrt[q]{1-\frac{{\left(\left(1-{{\mu }_{{a}_{1}}^{+}}^{q}\right)\left(1-{{\mu }_{{a}_{2}}^{+}}^{q}\right)\right)}^{\lambda }}{{\left(max\left\{1-{{\mu }_{{a}_{1}}^{+}}^{q},1-{{\mu }_{{a}_{2}}^{+}}^{q},p\right\}\right)}^{\left(\lambda -1\right)}}}\right],}\\ {\left[\begin{array}{*{20}{c}}{\sqrt[q]{\frac{{\left(\left(1-{{\mu }_{{a}_{1}}^{-}}^{q}\right)\left(1-{{\mu }_{{a}_{2}}^{-}}^{q}\right)\right)}^{\lambda }-{\left(\left(1-{{\mu }_{{a}_{1}}^{-}}^{q}-{{\nu }_{{a}_{1}}^{-}}^{q}\right)\left(1-{{\mu }_{{a}_{2}}^{-}}^{q}-{{\nu }_{{a}_{2}}^{-}}^{q}\right)\right)}^{\lambda }}{{\left(max\left\{1-{{\mu }_{{a}_{1}}^{-}}^{q},1-{{\mu }_{{a}_{2}}^{-}}^{q},p\right\}\right)}^{\left(\lambda -1\right)}}},}\\ {\sqrt[q]{\frac{{\left(\left(1-{{\mu }_{{a}_{1}}^{+}}^{q}\right)\left(1-{{\mu }_{{a}_{2}}^{+}}^{q}\right)\right)}^{\lambda }-{\left(\left(1-{{\mu }_{{a}_{1}}^{+}}^{q}-{{\nu }_{{a}_{1}}^{+}}^{q}\right)\left(1-{{\mu }_{{a}_{2}}^{+}}^{q}-{{\nu }_{{a}_{2}}^{+}}^{q}\right)\right)}^{\lambda }}{{\left(max\left\{1-{{\mu }_{{a}_{1}}^{+}}^{q},1-{{\mu }_{{a}_{2}}^{+}}^{q},p\right\}\right)}^{\left(\lambda -1\right)}}}}\end{array}\right]}\end{array}\right\rangle \\&=\lambda \left\langle \begin{array}{*{20}{c}}{\left[\sqrt[q]{1-\frac{\left(1-{{\mu }_{{a}_{1}}^{-}}^{q}\right)\left(1-{{\mu }_{{a}_{2}}^{-}}^{q}\right)}{max\left\{1-{{\mu }_{{a}_{1}}^{-}}^{q},1-{{\mu }_{{a}_{2}}^{-}}^{q},p\right\}}},\sqrt[q]{1-\frac{\left(1-{{\mu }_{{a}_{1}}^{+}}^{q}\right)\left(1-{{\mu }_{{a}_{2}}^{+}}^{q}\right)}{max\left\{1-{{\mu }_{{a}_{1}}^{+}}^{q},1-{{\mu }_{{a}_{2}}^{+}}^{q},p\right\}}}\right],}\\ {\left[\begin{array}{*{20}{c}}{\sqrt[q]{\frac{\left(1-{{\mu }_{{a}_{1}}^{-}}^{q}\right)\left(1-{{\mu }_{{a}_{2}}^{-}}^{q}\right)-\left(1-{{\mu }_{{a}_{1}}^{-}}^{q}-{{\nu }_{{a}_{1}}^{-}}^{q}\right)\left(1-{{\mu }_{{a}_{2}}^{-}}^{q}-{{\nu }_{{a}_{2}}^{-}}^{q}\right)}{max\left\{1-{{\mu }_{{a}_{1}}^{-}}^{q},1-{{\mu }_{{a}_{2}}^{-}}^{q},p\right\}}},}\\ {\sqrt[q]{\frac{\left(1-{{\mu }_{{a}_{1}}^{+}}^{q}\right)\left(1-{{\mu }_{{a}_{2}}^{+}}^{q}\right)-\left(1-{{\mu }_{{a}_{1}}^{+}}^{q}-{{\nu }_{{a}_{1}}^{+}}^{q}\right)\left(1-{{\mu }_{{a}_{2}}^{+}}^{q}-{{\nu }_{{a}_{2}}^{+}}^{q}\right)}{max\left\{1-{{\mu }_{{a}_{1}}^{+}}^{q},1-{{\mu }_{{a}_{2}}^{+}}^{q},p\right\}}}}\end{array}\right]}\end{array}\right\rangle\\&= \lambda \left({a}_{1}{\oplus }_{IDP}{a}_{2}\right).\end{aligned}$$

4.2 IVq-ROFIDPOWA operator

Definition 4.2

Let ${a}_{i}=\left\langle \left[{\mu }_{{a}_{i}}^{-},{\mu }_{{a}_{i}}^{+}\right],\left[{\nu }_{{a}_{i}}^{-},{\nu }_{{a}_{i}}^{+}\right]\right\rangle (i=\mathrm{1,2},3,\break\cdots ,n)$ be a group of IVq-ROFNs and $\omega ={\left({\omega }_{1},{\omega }_{2},{\omega }_{3},\cdots ,{\omega }_{n}\right)}^{T}$ be the corresponding weight vector that satisfies ${\sum }_{i=1}^{n}{\omega }_{i}=1,{\omega }_{i}\ge 0\left(i=\mathrm{1,2},3,\cdots ,n\right)$. The IVq-ROFIDPOWA operator, shown as Formula (26), is a mapping from ${\mathrm{IVq}-\mathrm{ROFNs}}^{n}$ to an $\mathrm{IVq}-\mathrm{ROFN}$.

$$IVq-ROFIDPOWA\left({a}_{1},{a}_{2},{a}_{3},\cdots ,{a}_{n}\right)=\begin{array}{*{20}{c}}{n}\\ {{\oplus }_{IDP}}\\ {i=1}\end{array}{\omega }_{i}{a}_{\sigma \left(i\right).}$$

(26)

In Formula (26), $\left(\sigma \left(1\right),\sigma \left(2\right),\sigma \left(3\right),\cdots ,\sigma \left(n\right)\right)$ is a replacement of $\left(\mathrm{1,2},3,\cdots ,n\right)$ that satisfies ${a}_{\sigma \left(i\right)}\ge {a}_{\sigma \left(i+1\right)}\left(i=\mathrm{1,2},3,\cdots ,n\right)$.

Theorem 4.2

Let ${a}_{i}=\left\langle \left[{\mu }_{{a}_{i}}^{-},{\mu }_{{a}_{i}}^{+}\right],\left[{\nu }_{{a}_{i}}^{-},{\nu }_{{a}_{i}}^{+}\right]\right\rangle (i=\mathrm{1,2},3,\break\cdots ,n)$ be a group of IVq-ROFNs; then, the result of the IVq-ROFIDPOWA operator remains an IVq-ROFN and is shown as follows:

$$\begin{aligned}&IVq-ROFIDPOWA\left({a}_{1},{a}_{2},{a}_{3},\cdots ,{a}_{n}\right)\\&=\left\langle \begin{array}{*{20}{c}}{\left[\sqrt[q]{1-\frac{{\prod }_{i=1}^{n}\frac{{\left(1-{{\mu }_{{a}_{\sigma \left(i\right)}}^{-}}^{q}\right)}^{{\omega }_{i}}}{{\left(max\left\{1-{{\mu }_{{a}_{\sigma \left(i\right)}}^{-}}^{q},p\right\}\right)}^{\left({\omega }_{i}-1\right)}}}{{\prod }_{i=1}^{n-1}max\left\{1-{{\mu }_{{a}_{\alpha \left(i\right)}}^{-}}^{q},p\right\}}},\sqrt[q]{1-\frac{{\prod }_{i=1}^{n}\frac{{\left(1-{{\mu }_{{a}_{\sigma \left(i\right)}}^{+}}^{q}\right)}^{{\omega }_{i}}}{{\left(max\left\{1-{{\mu }_{{a}_{\sigma \left(i\right)}}^{+}}^{q},p\right\}\right)}^{\left({\omega }_{i}-1\right)}}}{{\prod }_{i=1}^{n-1}max\left\{1-{{\mu }_{{a}_{\beta \left(i\right)}}^{+}}^{q},p\right\}}}\right],}\\ {\left[\sqrt[q]{\frac{\frac{{\prod }_{i=1}^{n}{\left(1-{{\mu }_{{a}_{\sigma \left(i\right)}}^{-}}^{q}\right)}^{{\omega }_{i}}-{\prod }_{i=1}^{n}{\left(1-{{\mu }_{{a}_{\sigma \left(i\right)}}^{-}}^{q}-{{\nu }_{{a}_{\sigma \left(i\right)}}^{-}}^{q}\right)}^{{\omega }_{i}}}{{\prod }_{i=1}^{n}{\left(max\left\{1-{{\mu }_{{a}_{\sigma \left(i\right)}}^{-}}^{q},p\right\}\right)}^{\left({\omega }_{i}-1\right)}}}{{\prod }_{i=1}^{n-1}max\left\{1-{{\mu }_{{a}_{\alpha \left(i\right)}}^{-}}^{q},p\right\}}},\sqrt[q]{\frac{\frac{{\prod }_{i=1}^{n}{\left(1-{{\mu }_{{a}_{\sigma \left(i\right)}}^{+}}^{q}\right)}^{{\omega }_{i}}-{\prod }_{i=1}^{n}{\left(1-{{\mu }_{{a}_{\sigma \left(i\right)}}^{+}}^{q}-{{\nu }_{{a}_{\sigma \left(i\right)}}^{+}}^{q}\right)}^{{\omega }_{i}}}{{\prod }_{i=1}^{n}{\left(max\left\{1-{{\mu }_{{a}_{\sigma \left(i\right)}}^{+}}^{q},p\right\}\right)}^{\left({\omega }_{i}-1\right)}}}{{\prod }_{i=1}^{n-1}max\left\{1-{{\mu }_{{a}_{\beta \left(i\right)}}^{+}}^{q},p\right\}}}\right]}\end{array}\right\rangle ,\end{aligned}$$

(27)

where $\left(\sigma \left(1\right),\sigma \left(2\right),\sigma \left(3\right),\cdots ,\sigma \left(n\right)\right)$, $\left(\alpha \left(1\right),\alpha \left(2\right),\break\alpha \left(3\right),\cdots ,\alpha \left(n\right)\right)$ and $\left(\beta \left(1\right),\beta \left(2\right),\beta \left(3\right),\cdots ,\beta \left(n\right)\right)$ are three replacements of $\left(\mathrm{1,2},3,\cdots ,n\right)$ that satisfy ${a}_{\sigma \left(i\right)}\ge {a}_{\sigma \left(i+1\right)}$, $1-{{\mu }_{{a}_{\alpha \left(i\right)}}^{-}}^{q}\ge 1-{{\mu }_{{a}_{\alpha \left(i+1\right)}}^{-}}^{q}$, and $1-{{\mu }_{{a}_{\beta \left(i\right)}}^{+}}^{q}\ge 1-{{\mu }_{{a}_{\beta \left(i+1\right)}}^{+}}^{q}\left(i=\mathrm{1,2},3,\cdots ,n-1\right)$, respectively.

Proof

Theorem 4.2 can be proven by mathematical induction.

Assume that ${a}_{i}\ge {a}_{i+1}\left(i=\mathrm{1,2},3,\cdots ,n-1\right)$; i.e., $\left(\sigma \left(1\right),\sigma \left(2\right),\sigma \left(3\right),\cdots ,\sigma \left(n\right)\right)=\left(\mathrm{1,2},3,\cdots ,n\right)$.

① For $n=2$, we have

$${\omega }_{1}{a}_{1}=\left\langle \begin{array}{*{20}{c}}{\left[\sqrt[q]{1-\frac{{\left(1-{{\mu }_{{a}_{1}}^{-}}^{q}\right)}^{{\omega }_{1}}}{{\left(max\left\{1-{{\mu }_{{a}_{1}}^{-}}^{q},p\right\}\right)}^{\left({\omega }_{1}-1\right)}}},\sqrt[q]{1-\frac{{\left(1-{{\mu }_{{a}_{1}}^{+}}^{q}\right)}^{{\omega }_{1}}}{{\left(max\left\{1-{{\mu }_{{a}_{1}}^{+}}^{q},p\right\}\right)}^{\left({\omega }_{1}-1\right)}}}\right],}\\ {\left[\sqrt[q]{\frac{{\left(1-{{\mu }_{{a}_{1}}^{-}}^{q}\right)}^{{\omega }_{1}}-{\left(1-{{\mu }_{{a}_{1}}^{-}}^{q}-{{\nu }_{{a}_{1}}^{-}}^{q}\right)}^{{\omega }_{1}}}{{\left(max\left\{1-{{\mu }_{{a}_{1}}^{-}}^{q},p\right\}\right)}^{\left({\omega }_{1}-1\right)}}},\sqrt[q]{\frac{{\left(1-{{\mu }_{{a}_{1}}^{+}}^{q}\right)}^{{\omega }_{1}}-{\left(1-{{\mu }_{{a}_{1}}^{+}}^{q}-{{\nu }_{{a}_{1}}^{+}}^{q}\right)}^{{\omega }_{1}}}{{\left(max\left\{1-{{\mu }_{{a}_{1}}^{+}}^{q},p\right\}\right)}^{\left({\omega }_{1}-1\right)}}}\right]}\end{array}\right\rangle$$

and

$${\omega }_{2}{a}_{2}=\left\langle \begin{array}{*{20}{c}}{\left[\sqrt[q]{1-\frac{{\left(1-{{\mu }_{{a}_{2}}^{-}}^{q}\right)}^{{\omega }_{2}}}{{\left(max\left\{1-{{\mu }_{{a}_{2}}^{-}}^{q},p\right\}\right)}^{\left({\omega }_{2}-1\right)}}},\sqrt[q]{1-\frac{{\left(1-{{\mu }_{{a}_{2}}^{+}}^{q}\right)}^{{\omega }_{2}}}{{\left(max\left\{1-{{\mu }_{{a}_{2}}^{+}}^{q},p\right\}\right)}^{\left({\omega }_{2}-1\right)}}}\right],}\\ {\left[\sqrt[q]{\frac{{\left(1-{{\mu }_{{a}_{2}}^{-}}^{q}\right)}^{{\omega }_{2}}-{\left(1-{{\mu }_{{a}_{2}}^{-}}^{q}-{{\nu }_{{a}_{2}}^{-}}^{q}\right)}^{{\omega }_{2}}}{{\left(max\left\{1-{{\mu }_{{a}_{2}}^{-}}^{q},p\right\}\right)}^{\left({\omega }_{2}-1\right)}}},\sqrt[q]{\frac{{\left(1-{{\mu }_{{a}_{2}}^{+}}^{q}\right)}^{{\omega }_{2}}-{\left(1-{{\mu }_{{a}_{2}}^{+}}^{q}-{{\nu }_{{a}_{2}}^{+}}^{q}\right)}^{{\omega }_{2}}}{{\left(max\left\{1-{{\mu }_{{a}_{2}}^{+}}^{q},p\right\}\right)}^{\left({\omega }_{2}-1\right)}}}\right]}\end{array}\right\rangle .$$

Then, we can obtain

$$\begin{aligned}&IVq-ROFIDPOWA\left({a}_{1},{a}_{2}\right)= \begin{array}{*{20}{c}} {2}\\ {{\oplus }_{IDP}}\\ {i=1}\end{array}{\omega }_{i}{a}_{i}\\&=\left\langle \begin{array}{*{20}{c}} {\left[\begin{array}{*{20}{c}} {\sqrt[q]{1-\frac{\left(\frac{{\left(1-{{\mu }_{{a}_{1}}^{-}}^{q}\right)}^{{\omega }_{1}}}{{\left(max\left\{1-{{\mu }_{{a}_{1}}^{-}}^{q},p\right\}\right)}^{\left({\omega }_{1}-1\right)}}\right)\left(\frac{{\left(1-{{\mu }_{{a}_{2}}^{-}}^{q}\right)}^{{\omega }_{2}}}{{\left(max\left\{1-{{\mu }_{{a}_{2}}^{-}}^{q},p\right\}\right)}^{\left({\omega }_{2}-1\right)}}\right)}{max\left\{\frac{{\left(1-{{\mu }_{{a}_{1}}^{-}}^{q}\right)}^{{\omega }_{1}}}{{\left(max\left\{1-{{\mu }_{{a}_{1}}^{-}}^{q},p\right\}\right)}^{\left({\omega }_{1}-1\right)}},\frac{{\left(1-{{\mu }_{{a}_{2}}^{-}}^{q}\right)}^{{\omega }_{2}}}{{\left(max\left\{1-{{\mu }_{{a}_{2}}^{-}}^{q},p\right\}\right)}^{\left({\omega }_{2}-1\right)}},p\right\}}},}\\ {\sqrt[q]{1-\frac{\left(\frac{{\left(1-{{\mu }_{{a}_{1}}^{+}}^{q}\right)}^{{\omega }_{1}}}{{\left(max\left\{1-{{\mu }_{{a}_{1}}^{+}}^{q},p\right\}\right)}^{\left({\omega }_{1}-1\right)}}\right)\left(\frac{{\left(1-{{\mu }_{{a}_{2}}^{+}}^{q}\right)}^{{\omega }_{2}}}{{\left(max\left\{1-{{\mu }_{{a}_{2}}^{+}}^{q},p\right\}\right)}^{\left({\omega }_{2}-1\right)}}\right)}{max\left\{\frac{{\left(1-{{\mu }_{{a}_{1}}^{+}}^{q}\right)}^{{\omega }_{1}}}{{\left(max\left\{1-{{\mu }_{{a}_{1}}^{+}}^{q},p\right\}\right)}^{\left({\omega }_{1}-1\right)}},\frac{{\left(1-{{\mu }_{{a}_{2}}^{+}}^{q}\right)}^{{\omega }_{2}}}{{\left(max\left\{1-{{\mu }_{{a}_{2}}^{+}}^{q},p\right\}\right)}^{\left({\omega }_{2}-1\right)}},p\right\}}}}\end{array}\right],}\\ {\left[\begin{array}{*{20}{c}}{\sqrt[q]{\frac{\left(\frac{{\left(1-{{\mu }_{{a}_{1}}^{-}}^{q}\right)}^{{\omega }_{1}}}{{\left(max\left\{1-{{\mu }_{{a}_{1}}^{-}}^{q},p\right\}\right)}^{\left({\omega }_{1}-1\right)}}\right)\left(\frac{{\left(1-{{\mu }_{{a}_{2}}^{-}}^{q}\right)}^{{\omega }_{2}}}{{\left(max\left\{1-{{\mu }_{{a}_{2}}^{-}}^{q},p\right\}\right)}^{\left({\omega }_{2}-1\right)}}\right)-\left(\frac{{\left(1-{{\mu }_{{a}_{1}}^{-}}^{q}-{{\nu }_{{a}_{1}}^{-}}^{q}\right)}^{{\omega }_{1}}}{{\left(max\left\{1-{{\mu }_{{a}_{1}}^{-}}^{q},p\right\}\right)}^{\left({\omega }_{1}-1\right)}}\right)\left(\frac{{\left(1-{{\mu }_{{a}_{2}}^{-}}^{q}-{{\nu }_{{a}_{2}}^{-}}^{q}\right)}^{{\omega }_{2}}}{{\left(max\left\{1-{{\mu }_{{a}_{2}}^{-}}^{q},p\right\}\right)}^{\left({\omega }_{2}-1\right)}}\right)}{max\left\{\frac{{\left(1-{{\mu }_{{a}_{1}}^{-}}^{q}\right)}^{{\omega }_{1}}}{{\left(max\left\{1-{{\mu }_{{a}_{1}}^{-}}^{q},p\right\}\right)}^{\left({\omega }_{1}-1\right)}},\frac{{\left(1-{{\mu }_{{a}_{2}}^{-}}^{q}\right)}^{{\omega }_{2}}}{{\left(max\left\{1-{{\mu }_{{a}_{2}}^{-}}^{q},p\right\}\right)}^{\left({\omega }_{2}-1\right)}},p\right\}}},}\\ {\sqrt[q]{\frac{\left(\frac{{\left(1-{{\mu }_{{a}_{1}}^{+}}^{q}\right)}^{{\omega }_{1}}}{{\left(max\left\{1-{{\mu }_{{a}_{1}}^{+}}^{q},p\right\}\right)}^{\left({\omega }_{1}-1\right)}}\right)\left(\frac{{\left(1-{{\mu }_{{a}_{2}}^{+}}^{q}\right)}^{{\omega }_{2}}}{{\left(max\left\{1-{{\mu }_{{a}_{2}}^{+}}^{q},p\right\}\right)}^{\left({\omega }_{2}-1\right)}}\right)-\left(\frac{{\left(1-{{\mu }_{{a}_{1}}^{+}}^{q}-{{\nu }_{{a}_{1}}^{+}}^{q}\right)}^{{\omega }_{1}}}{{\left(max\left\{1-{{\mu }_{{a}_{1}}^{-}}^{q},p\right\}\right)}^{\left({\omega }_{1}-1\right)}}\right)\left(\frac{{\left(1-{{\mu }_{{a}_{2}}^{+}}^{q}-{{\nu }_{{a}_{2}}^{+}}^{q}\right)}^{{\omega }_{2}}}{{\left(max\left\{1-{{\mu }_{{a}_{2}}^{-}}^{q},p\right\}\right)}^{\left({\omega }_{2}-1\right)}}\right)}{max\left\{\frac{{\left(1-{{\mu }_{{a}_{1}}^{+}}^{q}\right)}^{{\omega }_{1}}}{{\left(max\left\{1-{{\mu }_{{a}_{1}}^{+}}^{q},p\right\}\right)}^{\left({\omega }_{1}-1\right)}},\frac{{\left(1-{{\mu }_{{a}_{2}}^{+}}^{q}\right)}^{{\omega }_{2}}}{{\left(max\left\{1-{{\mu }_{{a}_{2}}^{+}}^{q},p\right\}\right)}^{\left({\omega }_{2}-1\right)}},p\right\}}}}\end{array}\right]} \end{array}\right\rangle\\&=\left\langle \begin{array}{*{20}{c}} {\left[\sqrt[q]{1-\frac{{\prod }_{i=1}^{2}\frac{{\left(1-{{\mu }_{{a}_{i}}^{-}}^{q}\right)}^{{\omega }_{i}}}{{\left(max\left\{1-{{\mu }_{{a}_{i}}^{-}}^{q},p\right\}\right)}^{\left({\omega }_{i}-1\right)}}}{max\left\{1-{{\mu }_{{a}_{\alpha \left(i\right)}}^{-}}^{q},p\right\}}},\sqrt[q]{1-\frac{{\prod }_{i=1}^{2}\frac{{\left(1-{{\mu }_{{a}_{i}}^{+}}^{q}\right)}^{{\omega }_{i}}}{{\left(max\left\{1-{{\mu }_{{a}_{i}}^{+}}^{q},p\right\}\right)}^{\left({\omega }_{i}-1\right)}}}{max\left\{1-{{\mu }_{{a}_{\beta \left(i\right)}}^{+}}^{q},p\right\}}}\right],}\\ {\left[\sqrt[q]{\frac{\frac{{\prod }_{i=1}^{2}{\left(1-{{\mu }_{{a}_{i}}^{-}}^{q}\right)}^{{\omega }_{i}}-{\prod }_{i=1}^{2}{\left(1-{{\mu }_{{a}_{i}}^{-}}^{q}-{{\nu }_{{a}_{i}}^{-}}^{q}\right)}^{{\omega }_{i}}}{{\prod }_{i=1}^{2}{\left(max\left\{1-{{\mu }_{{a}_{i}}^{-}}^{q},p\right\}\right)}^{\left({\omega }_{i}-1\right)}}}{max\left\{1-{{\mu }_{{a}_{\alpha \left(i\right)}}^{-}}^{q},p\right\}}},\sqrt[q]{\frac{\frac{{\prod }_{i=1}^{2}{\left(1-{{\mu }_{{a}_{i}}^{+}}^{q}\right)}^{{\omega }_{i}}-{\prod }_{i=1}^{2}{\left(1-{{\mu }_{{a}_{i}}^{+}}^{q}-{{\nu }_{{a}_{i}}^{+}}^{q}\right)}^{{\omega }_{i}}}{{\prod }_{i=1}^{2}{\left(max\left\{1-{{\mu }_{{a}_{i}}^{+}}^{q},p\right\}\right)}^{\left({\omega }_{i}-1\right)}}}{max\left\{1-{{\mu }_{{a}_{\beta \left(i\right)}}^{+}}^{q},p\right\}}}\right]}\end{array} \right\rangle.\end{aligned}$$

This shows that Formula (27) holds for n = 2.

② Assuming that Formula (27) holds for $n=k$, we can obtain

$$\begin{aligned}&IVq-ROFIDPOWA\left({a}_{1},{a}_{2},{a}_{3},\cdots ,{a}_{k}\right)\\&=\left\langle \begin{array}{*{20}{c}} {\left[\sqrt[q]{1-\frac{{\prod }_{i=1}^{k}\frac{{\left(1-{{\mu }_{{a}_{i}}^{-}}^{q}\right)}^{{\omega }_{i}}}{{\left(max\left\{1-{{\mu }_{{a}_{i}}^{-}}^{q},p\right\}\right)}^{\left({\omega }_{i}-1\right)}}}{{\prod }_{i=1}^{k-1}max\left\{1-{{\mu }_{{a}_{\alpha \left(i\right)}}^{-}}^{q},p\right\}}},\sqrt[q]{1-\frac{{\prod }_{i=1}^{k}\frac{{\left(1-{{\mu }_{{a}_{i}}^{+}}^{q}\right)}^{{\omega }_{i}}}{{\left(max\left\{1-{{\mu }_{{a}_{i}}^{+}}^{q},p\right\}\right)}^{\left({\omega }_{i}-1\right)}}}{{\prod }_{i=1}^{k-1}max\left\{1-{{\mu }_{{a}_{\beta \left(i\right)}}^{+}}^{q},p\right\}}}\right],}\\ {\left[\sqrt[q]{\frac{\frac{{\prod }_{i=1}^{k}{\left(1-{{\mu }_{{a}_{i}}^{-}}^{q}\right)}^{{\omega }_{i}}-{\prod }_{i=1}^{k}{\left(1-{{\mu }_{{a}_{i}}^{-}}^{q}-{{\nu }_{{a}_{i}}^{-}}^{q}\right)}^{{\omega }_{i}}}{{\prod }_{i=1}^{k}{\left(max\left\{1-{{\mu }_{{a}_{i}}^{-}}^{q},p\right\}\right)}^{\left({\omega }_{i}-1\right)}}}{{\prod }_{i=1}^{k-1}max\left\{1-{{\mu }_{{a}_{\alpha \left(i\right)}}^{-}}^{q},p\right\}}},\sqrt[q]{\frac{\frac{{\prod }_{i=1}^{k}{\left(1-{{\mu }_{{a}_{i}}^{+}}^{q}\right)}^{{\omega }_{i}}-{\prod }_{i=1}^{k}{\left(1-{{\mu }_{{a}_{i}}^{+}}^{q}-{{\nu }_{{a}_{i}}^{+}}^{q}\right)}^{{\omega }_{i}}}{{\prod }_{i=1}^{k}{\left(max\left\{1-{{\mu }_{{a}_{i}}^{+}}^{q},p\right\}\right)}^{\left({\omega }_{i}-1\right)}}}{{\prod }_{i=1}^{k-1}max\left\{1-{{\mu }_{{a}_{\beta \left(i\right)}}^{+}}^{q},p\right\}}}\right]}\end{array} \right\rangle\end{aligned}$$

③ When $n=k+1$, we have

$$\begin{aligned}&IVq-ROFIDPOWA\left({a}_{1},{a}_{2},{a}_{3},\cdots ,{a}_{k},{a}_{k+1}\right)\\&=IVq-ROFIDPOWA\left({a}_{1},{a}_{2},{a}_{3},\cdots ,{a}_{k}\right){\oplus }_{IDP}{\omega }_{k+1}{a}_{k+1}\\&=\left\langle \begin{array}{*{20}{c}} {\left[\sqrt[q]{1-\frac{{\prod }_{i=1}^{k}\frac{{\left(1-{{\mu }_{{a}_{i}}^{-}}^{q}\right)}^{{\omega }_{i}}}{{\left(max\left\{1-{{\mu }_{{a}_{i}}^{-}}^{q},p\right\}\right)}^{\left({\omega }_{i}-1\right)}}}{{\prod }_{i=1}^{k-1}max\left\{1-{{\mu }_{{a}_{\alpha \left(i\right)}}^{-}}^{q},p\right\}}},\sqrt[q]{1-\frac{{\prod }_{i=1}^{k}\frac{{\left(1-{{\mu }_{{a}_{i}}^{+}}^{q}\right)}^{{\omega }_{i}}}{{\left(max\left\{1-{{\mu }_{{a}_{i}}^{+}}^{q},p\right\}\right)}^{\left({\omega }_{i}-1\right)}}}{{\prod }_{i=1}^{k-1}max\left\{1-{{\mu }_{{a}_{\beta \left(i\right)}}^{+}}^{q},p\right\}}}\right],}\\ {\left[\sqrt[q]{\frac{\frac{{\prod }_{i=1}^{k}{\left(1-{{\mu }_{{a}_{i}}^{-}}^{q}\right)}^{{\omega }_{i}}-{\prod }_{i=1}^{k}{\left(1-{{\mu }_{{a}_{i}}^{-}}^{q}-{{\nu }_{{a}_{i}}^{-}}^{q}\right)}^{{\omega }_{i}}}{{\prod }_{i=1}^{k}{\left(max\left\{1-{{\mu }_{{a}_{i}}^{-}}^{q},p\right\}\right)}^{\left({\omega }_{i}-1\right)}}}{{\prod }_{i=1}^{k-1}max\left\{1-{{\mu }_{{a}_{\alpha \left(i\right)}}^{-}}^{q},p\right\}}},\sqrt[q]{\frac{\frac{{\prod }_{i=1}^{k}{\left(1-{{\mu }_{{a}_{i}}^{+}}^{q}\right)}^{{\omega }_{i}}-{\prod }_{i=1}^{k}{\left(1-{{\mu }_{{a}_{i}}^{+}}^{q}-{{\nu }_{{a}_{i}}^{+}}^{q}\right)}^{{\omega }_{i}}}{{\prod }_{i=1}^{k}{\left(max\left\{1-{{\mu }_{{a}_{i}}^{+}}^{q},p\right\}\right)}^{\left({\omega }_{i}-1\right)}}}{{\prod }_{i=1}^{k-1}max\left\{1-{{\mu }_{{a}_{\beta \left(i\right)}}^{+}}^{q},p\right\}}}\right]}\end{array}\right\rangle {\oplus }_{IDP}\\ &\left\langle \frac{\left[\sqrt[q]{1-\frac{{\left(1-{{\mu }_{{a}_{k+1}}^{-}}^{q}\right)}^{{\omega }_{k+1}}}{{\left(max\left\{1-{{\mu }_{{a}_{k+1}}^{-}}^{q},p\right\}\right)}^{\left({\omega }_{k+1}-1\right)}}},\sqrt[q]{1-\frac{{\left(1-{{\mu }_{{a}_{k+1}}^{+}}^{q}\right)}^{{\omega }_{k+1}}}{{\left(max\left\{1-{{\mu }_{{a}_{k+1}}^{+}}^{q},p\right\}\right)}^{\left({\omega }_{k+1}-1\right)}}}\right],}{\left[\sqrt[q]{\frac{{\left(1-{{\mu }_{{a}_{k+1}}^{-}}^{q}\right)}^{{\omega }_{k+1}}-{\left(1-{{\mu }_{{a}_{k+1}}^{-}}^{q}-{{\nu }_{{a}_{k+1}}^{-}}^{q}\right)}^{{\omega }_{k+1}}}{{\left(max\left\{1-{{\mu }_{{a}_{k+1}}^{-}}^{q},p\right\}\right)}^{\left({\omega }_{k+1}-1\right)}}},\sqrt[q]{\frac{{\left(1-{{\mu }_{{a}_{k+1}}^{+}}^{q}\right)}^{{\omega }_{k+1}}-{\left(1-{{\mu }_{{a}_{k+1}}^{+}}^{q}-{{\nu }_{{a}_{k+1}}^{+}}^{q}\right)}^{{\omega }_{k+1}}}{{\left(max\left\{1-{{\mu }_{{a}_{k+1}}^{+}}^{q},p\right\}\right)}^{\left({\omega }_{k+1}-1\right)}}}\right]}\right\rangle \\ \end{aligned}$$

$$\begin{aligned} &=\left\langle \frac{\left[\frac{\sqrt[q]{1-\frac{\left(\frac{{\prod }_{i=1}^{k}\frac{{\left(1-{{\mu }_{{a}_{i}}^{-}}^{q}\right)}^{{\omega }_{i}}}{{\left(max\left\{1-{{\mu }_{{a}_{i}}^{-}}^{q},p\right\}\right)}^{\left({\omega }_{i}-1\right)}}}{{\prod }_{i=1}^{k-1}max\left\{1-{{\mu }_{{a}_{\alpha \left(i\right)}}^{-}}^{q},p\right\}}\right)\left(\frac{{\left(1-{{\mu }_{{a}_{k+1}}^{-}}^{q}\right)}^{{\omega }_{k+1}}}{{\left(max\left\{1-{{\mu }_{{a}_{k+1}}^{-}}^{q},p\right\}\right)}^{\left({\omega }_{1}-1\right)}}\right)}{max\left\{\frac{{\prod }_{i=1}^{k}\frac{{\left(1-{{\mu }_{{a}_{i}}^{-}}^{q}\right)}^{{\omega }_{i}}}{{\left(max\left\{1-{{\mu }_{{a}_{i}}^{-}}^{q},p\right\}\right)}^{\left({\omega }_{i}-1\right)}}}{{\prod }_{i=1}^{k-1}max\left\{1-{{\mu }_{{a}_{\alpha \left(i\right)}}^{-}}^{q},p\right\}},\frac{{\left(1-{{\mu }_{{a}_{k+1}}^{-}}^{q}\right)}^{{\omega }_{k+1}}}{{\left(max\left\{1-{{\mu }_{{a}_{k+1}}^{-}}^{q},p\right\}\right)}^{\left({\omega }_{k+1}-1\right)}},p\right\}}},}{\sqrt[q]{1-\frac{\left(\frac{{\prod }_{i=1}^{k}\frac{{\left(1-{{\mu }_{{a}_{i}}^{+}}^{q}\right)}^{{\omega }_{i}}}{{\left(max\left\{1-{{\mu }_{{a}_{i}}^{+}}^{q},p\right\}\right)}^{\left({\omega }_{i}-1\right)}}}{{\prod }_{i=1}^{k-1}max\left\{1-{{\mu }_{{a}_{\beta \left(i\right)}}^{+}}^{q},p\right\}}\right)\left(\frac{{\left(1-{{\mu }_{{a}_{k+1}}^{+}}^{q}\right)}^{{\omega }_{k+1}}}{{\left(max\left\{1-{{\mu }_{{a}_{k+1}}^{+}}^{q},p\right\}\right)}^{\left({\omega }_{k+1}-1\right)}}\right)}{max\left\{\frac{{\prod }_{i=1}^{k}\frac{{\left(1-{{\mu }_{{a}_{i}}^{+}}^{q}\right)}^{{\omega }_{i}}}{{\left(max\left\{1-{{\mu }_{{a}_{i}}^{+}}^{q},p\right\}\right)}^{\left({\omega }_{i}-1\right)}}}{{\prod }_{i=1}^{k-1}max\left\{1-{{\mu }_{{a}_{\beta \left(i\right)}}^{+}}^{q},p\right\}},\frac{{\left(1-{{\mu }_{{a}_{k+1}}^{+}}^{q}\right)}^{{\omega }_{k+1}}}{{\left(max\left\{1-{{\mu }_{{a}_{k+1}}^{+}}^{q},p\right\}\right)}^{\left({\omega }_{k+1}-1\right)}},p\right\}}}}\right],}{\left[ \begin{array}{*{20}{c}}{\sqrt[q]{\frac{\left(\frac{{\prod }_{i=1}^{k}\frac{{\left(1-{{\mu }_{{a}_{i}}^{-}}^{q}\right)}^{{\omega }_{i}}}{{\left(max\left\{1-{{\mu }_{{a}_{i}}^{-}}^{q},p\right\}\right)}^{\left({\omega }_{i}-1\right)}}}{{\prod }_{i=1}^{k-1}max\left\{1-{{\mu }_{{a}_{\alpha \left(i\right)}}^{-}}^{q},p\right\}}\right)\left(\frac{{\left(1-{{\mu }_{{a}_{k+1}}^{-}}^{q}\right)}^{{\omega }_{k+1}}}{{\left(max\left\{1-{{\mu }_{{a}_{k+1}}^{-}}^{q},p\right\}\right)}^{\left({\omega }_{k+1}-1\right)}}\right)-\left(\frac{\frac{{\prod }_{i=1}^{k}{\left(1-{{\mu }_{{a}_{i}}^{-}}^{q}-{{\nu }_{{a}_{i}}^{-}}^{q}\right)}^{{\omega }_{i}}}{{\prod }_{i=1}^{k}{\left(max\left\{1-{{\mu }_{{a}_{i}}^{-}}^{q},p\right\}\right)}^{\left({\omega }_{i}-1\right)}}}{{\prod }_{i=1}^{k-1}max\left\{1-{{\mu }_{{a}_{\alpha \left(i\right)}}^{-}}^{q},p\right\}}\right)\left(\frac{{\left(1-{{\mu }_{{a}_{k+1}}^{-}}^{q}-{{\nu }_{{a}_{k+1}}^{-}}^{q}\right)}^{{\omega }_{k+1}}}{{\left(max\left\{1-{{\mu }_{{a}_{k+1}}^{-}}^{q},p\right\}\right)}^{\left({\omega }_{k+1}-1\right)}}\right)}{max\left\{\frac{{\prod }_{i=1}^{k}\frac{{\left(1-{{\mu }_{{a}_{i}}^{-}}^{q}\right)}^{{\omega }_{i}}}{{\left(max\left\{1-{{\mu }_{{a}_{i}}^{-}}^{q},p\right\}\right)}^{\left({\omega }_{i}-1\right)}}}{{\prod }_{i=1}^{k-1}max\left\{1-{{\mu }_{{a}_{\alpha \left(i\right)}}^{-}}^{q},p\right\}},\frac{{\left(1-{{\mu }_{{a}_{k+1}}^{-}}^{q}\right)}^{{\omega }_{k+1}}}{{\left(max\left\{1-{{\mu }_{{a}_{k+1}}^{-}}^{q},p\right\}\right)}^{\left({\omega }_{k+1}-1\right)}},p\right\}}},}\\ {\sqrt[q]{\frac{\left(\frac{{\prod }_{i=1}^{k}\frac{{\left(1-{{\mu }_{{a}_{i}}^{+}}^{q}\right)}^{{\omega }_{i}}}{{\left(max\left\{1-{{\mu }_{{a}_{i}}^{+}}^{q},p\right\}\right)}^{\left({\omega }_{i}-1\right)}}}{{\prod }_{i=1}^{k-1}max\left\{1-{{\mu }_{{a}_{\beta \left(i\right)}}^{+}}^{q},p\right\}}\right)\left(\frac{{\left(1-{{\mu }_{{a}_{k+1}}^{+}}^{q}\right)}^{{\omega }_{k+1}}}{{\left(max\left\{1-{{\mu }_{{a}_{k+1}}^{+}}^{q},p\right\}\right)}^{\left({\omega }_{{k+1}^{-1}}\right)}}\right)-\left(\frac{\frac{{\prod }_{i=1}^{k}{\left(1-{{\mu }_{{a}_{i}}^{+}}^{q}-{{\nu }_{{a}_{i}}^{+}}^{q}\right)}^{{\omega }_{i}}}{{\prod }_{i=1}^{k}{\left(max\left\{1-{{\mu }_{{a}_{i}}^{+}}^{q},p\right\}\right)}^{\left({\omega }_{i}-1\right)}}}{{\prod }_{i=1}^{k-1}max\left\{1-{{\mu }_{{a}_{\beta \left(i\right)}}^{+}}^{q},p\right\}}\right)\left(\frac{{\left(1-{{\mu }_{{a}_{k+1}}^{+}}^{q}-{{\nu }_{{a}_{k+1}}^{+}}^{q}\right)}^{{\omega }_{k+1}}}{{\left(max\left\{1-{{\mu }_{{a}_{k+1}}^{+}}^{q},p\right\}\right)}^{\left({\omega }_{k+1}-1\right)}}\right)}{max\left\{\frac{{\prod }_{i=1}^{k}\frac{{\left(1-{{\mu }_{{a}_{i}}^{+}}^{q}\right)}^{{\omega }_{i}}}{{\left(max\left\{1-{{\mu }_{{a}_{i}}^{+}}^{q},p\right\}\right)}^{\left({\omega }_{i}-1\right)}}}{{\prod }_{i=1}^{k-1}max\left\{1-{{\mu }_{{a}_{\beta \left(i\right)}}^{+}}^{q},p\right\}},\frac{{\left(1-{{\mu }_{{a}_{k+1}}^{+}}^{q}\right)}^{{\omega }_{k+1}}}{{\left(max\left\{1-{{\mu }_{{a}_{k+1}}^{+}}^{q},p\right\}\right)}^{\left({\omega }_{k+1}-1\right)}},p\right\}}}}\end{array}\right]}\right\rangle\\ &=\left\langle \frac{\left[\sqrt[q]{1-\frac{{\prod }_{i=1}^{k+1}\frac{{\left(1-{{\mu }_{{a}_{i}}^{-}}^{q}\right)}^{{\omega }_{i}}}{{\left(max\left\{1-{{\mu }_{{a}_{i}}^{-}}^{q},p\right\}\right)}^{\left({\omega }_{i}-1\right)}}}{{\prod }_{i=1}^{k}max\left\{1-{{\mu }_{{a}_{\alpha \left(i\right)}}^{-}}^{q},p\right\}}},\sqrt[q]{1-\frac{{\prod }_{i=1}^{k+1}\frac{{\left(1-{{\mu }_{{a}_{i}}^{+}}^{q}\right)}^{{\omega }_{i}}}{{\left(max\left\{1-{{\mu }_{{a}_{i}}^{+}}^{q},p\right\}\right)}^{\left({\omega }_{i}-1\right)}}}{{\prod }_{i=1}^{k}max\left\{1-{{\mu }_{{a}_{\beta \left(i\right)}}^{+}}^{q},p\right\}}}\right],}{\left[\sqrt[q]{\frac{\frac{{\prod }_{i=1}^{k+1}{\left(1-{{\mu }_{{a}_{i}}^{-}}^{q}\right)}^{{\omega }_{i}}-{\prod }_{i=1}^{k+1}{\left(1-{{\mu }_{{a}_{i}}^{-}}^{q}-{{\nu }_{{a}_{i}}^{-}}^{q}\right)}^{{\omega }_{i}}}{{\prod }_{i=1}^{k+1}{\left(max\left\{1-{{\mu }_{{a}_{i}}^{-}}^{q},p\right\}\right)}^{\left({\omega }_{i}-1\right)}}}{{\prod }_{i=1}^{k}max\left\{1-{{\mu }_{{a}_{\alpha \left(i\right)}}^{-}}^{q},p\right\}}},\sqrt[q]{\frac{\frac{{\prod }_{i=1}^{k+1}{\left(1-{{\mu }_{{a}_{i}}^{+}}^{q}\right)}^{{\omega }_{i}}-{\prod }_{i=1}^{k+1}{\left(1-{{\mu }_{{a}_{i}}^{+}}^{q}-{{\nu }_{{a}_{i}}^{+}}^{q}\right)}^{{\omega }_{i}}}{{\prod }_{i=1}^{k+1}{\left(max\left\{1-{{\mu }_{{a}_{i}}^{+}}^{q},p\right\}\right)}^{\left({\omega }_{i}-1\right)}}}{{\prod }_{i=1}^{k}max\left\{1-{{\mu }_{{a}_{\beta \left(i\right)}}^{+}}^{q},p\right\}}}\right]}\right\rangle\end{aligned}$$

That is, Formula (27) holds for $n=k+1$.

Thus, by the principle of mathematical induction, Theorem 4.2 is true.

It can be proven that the IVq-ROFIDPOWA operator satisfies idempotency, permutation invariance, monotonicity, and boundedness, and these properties are given in detail below. Because it is easy to prove these properties, using the IVq-ROFIDP operations given by Formula (18)–Formula (21), the proofs are omitted in this paper.

Theorem 4.3

(Idempotency) Let ${a}_{i}=\left\langle \left[{\mu }_{{a}_{i}}^{-},{\mu }_{{a}_{i}}^{+}\right],\left[{\nu }_{{a}_{i}}^{-},{\nu }_{{a}_{i}}^{+}\right]\right\rangle \left(i=\mathrm{1,2},3,\cdots ,n\right)$ be a group of IVq-ROFNs; then, the IVq-ROFIDPOWA operator satisfies idempotency, i.e., Formula (28) holds when $a={a}_{1}={a}_{2}=\cdots ={a}_{n}$.

$$IVq-ROFIDPOWA\left({a}_{1},{a}_{2},{a}_{3},\cdots ,{a}_{n}\right)=a.$$

(28)

Theorem 4.4

(Permutation Invariance) Let ${a}_{i}=\left\langle \left[{\mu }_{{a}_{i}}^{-},{\mu }_{{a}_{i}}^{+}\right],\left[{\nu }_{{a}_{i}}^{-},{\nu }_{{a}_{i}}^{+}\right]\right\rangle \left(i=\mathrm{1,2},3,\cdots ,n\right)$ be a group of IVq-ROFNs; then, the IVq-ROFIDPOWA operator satisfies permutation invariance, i.e., Formula (29) holds when $\left({a}_{1}^{^{\prime}},{a}_{2}^{^{\prime}},{a}_{3}^{^{\prime}},\cdots ,{a}_{n}^{^{\prime}}\right)$ is an arbitrary replacement of $\left({a}_{1},{a}_{2},{a}_{3},\cdots ,{a}_{n}\right)$.

$$IVq-ROFIDPOWA\left({a}_{1}^{{\prime}},{a}_{2}^{{\prime}},{a}_{3}^{{\prime}},\cdots ,{a}_{n}^{{\prime}}\right)=IVq-ROFIDPOWA\left({a}_{1},{a}_{2},{a}_{3},\cdots ,{a}_{n}\right).$$

(29)

Theorem 4.5

(Monotonicity) Let ${a}_{i}=\left\langle \left[{\mu }_{{a}_{i}}^{-},{\mu }_{{a}_{i}}^{+}\right],\left[{\nu }_{{a}_{i}}^{-},{\nu }_{{a}_{i}}^{+}\right]\right\rangle \left(i=\mathrm{1,2},3,\cdots ,n\right)$ and ${b}_{i}=\left\langle \left[{\mu }_{{b}_{i}}^{-},{\mu }_{{b}_{i}}^{+}\right],\left[{\nu }_{{b}_{i}}^{-},{\nu }_{{b}_{i}}^{+}\right]\right\rangle \left(i=\mathrm{1,2},3,\cdots ,n\right)$ be two groups of IVq-ROFNs; then, the IVq-ROFIDPOWA operator satisfies monotonicity, i.e., Formula (30) holds if ${\mu }_{{a}_{i}}^{-}\le {\mu }_{{b}_{i}}^{-}$, ${\mu }_{{a}_{i}}^{+}\le {\mu }_{{b}_{i}}^{+}$, ${\nu }_{{a}_{i}}^{-}\ge {\nu }_{{b}_{i}}^{-}$, ${\nu }_{{a}_{i}}^{+}\ge {\nu }_{{b}_{i}}^{+}(i=\mathrm{1,2},3,\cdots ,n)$.

$$IVq-ROFIDPOWA\left({a}_{1},{a}_{2},{a}_{3},\cdots ,{a}_{n}\right)\le IVq-ROFIDPOWA\left({b}_{1},{b}_{2},{b}_{3},\cdots ,{b}_{n}\right).$$

(30)

It is worth noting that the monotonicity property given here must satisfy the size comparison between the IVq-ROFNs. When the data do not satisfy this relationship, monotonicity does not necessarily hold.

Theorem 4.6

(Boundedness) Let ${a}_{i}=\left\langle \left[{\mu }_{{a}_{i}}^{-},{\mu }_{{a}_{i}}^{+}\right],\left[{\nu }_{{a}_{i}}^{-},{\nu }_{{a}_{i}}^{+}\right]\right\rangle \left(i=\mathrm{1,2},3,\cdots ,n\right)$ be a group of IVq-ROFNs; then, the IVq-ROFIDPOWA operator satisfies boundedness, i.e., Formula (31) holds when ${a}_{min}=\left\langle \left[\underset{i}{\mathrm{min}}\left\{{\mu }_{{a}_{i}}^{-}\right\},\underset{i}{\mathrm{min}}\left\{{\mu }_{{a}_{i}}^{+}\right\}\right],\left[\underset{i}{\mathrm{min}}\left\{{\nu }_{{a}_{i}}^{-}\right\},\underset{i}{\mathrm{min}}\left\{{\nu }_{{a}_{i}}^{+}\right\}\right]\right\rangle$ and ${a}_{max}=\left\langle \left[\underset{i}{\mathrm{max}}\left\{{\mu }_{{a}_{i}}^{-}\right\},\underset{i}{\mathrm{max}}\left\{{\mu }_{{a}_{i}}^{+}\right\}\right],\left[\underset{i}{\mathrm{max}}\left\{{\nu }_{{a}_{i}}^{-}\right\},\underset{i}{\mathrm{max}}\left\{{\nu }_{{a}_{i}}^{+}\right\}\right]\right\rangle$.

$${a}_{min}\le IVq-ROFIDPOWA\left({a}_{1},{a}_{2},{a}_{3},\cdots ,{a}_{n}\right)\le {a}_{max}.$$

(31)

4.3 Group decision-making method based on the IVq-ROFIDPOWA operator

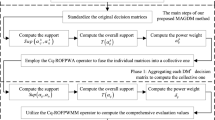
This section proposes the group decision-making method based on the IVq-ROFIDPOWA operator. For a MAGDM problem, let $X=\left\{{x}_{1},{x}_{2},{x}_{3},\cdots ,{x}_{m}\right\}$ be the alternative set, $C=\left\{{c}_{1},{c}_{2},{c}_{3},\cdots ,{c}_{n}\right\}$ be the attribute set whose attribute weights are $\omega =\left({\omega }_{1},{\omega }_{2},{\omega }_{3},\cdots ,{\omega }_{n}\right)$ and satisfy ${\sum }_{j=1}^{n}{\omega }_{j}=1,{\omega }_{j}\epsilon \left[\mathrm{0,1}\right]\left(j=\mathrm{1,2},3,\cdots ,n\right)$, and $D=\left\{{d}_{1},{d}_{2},{d}_{3},\cdots ,{d}_{t}\right\}$ be the expert set whose expert weights are $w=\left({w}_{1},{w}_{2},{w}_{3},\cdots ,{w}_{t}\right)$ and satisfy ${\sum }_{k=1}^{t}{w}_{k}=1,{w}_{k}\epsilon \left[\mathrm{0,1}\right]\left(k=\mathrm{1,2},3,\cdots ,t\right)$. The decision matrix of the $k$-th expert is ${A}^{\left(k\right)}={\left({a}_{ij}^{\left(k\right)}\right)}_{m\times n}$, in which the element ${a}_{ij}^{\left(k\right)}$ represents the decision value of the $k$-th expert regarding attribute $j$ of alternative $i$ and is an IVq-ROFN that satisfies ${\left({\mu }_{{a}_{ij}^{\left(k\right)}}^{+}\right)}^{q}+{\left({\nu }_{{a}_{ij}^{\left(k\right)}}^{+}\right)}^{q}\le 1,q\ge 1$. It should be noted that the value of $q$ is adapted to the actual situation. In addition, in practical applications, different attributes have different meanings and must be normalized. This paper adopts Formulas (32) and (33) for normalization, where Formula (33) is the complement operation for IVq-ROFNs. Assuming that ${\Omega }_{1}$ represents the benefit type and that ${\Omega }_{2}$ represents the cost type, both formulas are given as follows.

$${r}_{ij}^{\left(k\right)}=\left\{\begin{array}{c}{a}_{ij}^{\left(k\right)},{a}_{ij}^{\left(k\right)}\epsilon {\Omega }_{1}\\ {\left({a}_{ij}^{\left(k\right)}\right)}^{c},{a}_{ij}^{\left(k\right)}\epsilon {\Omega }_{2}\end{array}\right.,i=\mathrm{1,2},3,\cdots ,m,j=\mathrm{1,2},3,\cdots ,n.$$

(32)

$${\left({a}_{ij}^{\left(k\right)}\right)}^{c}=\left\langle \left[{\nu }_{{a}_{ij}^{\left(k\right)}}^{-},{\nu }_{{a}_{ij}^{\left(k\right)}}^{+}\right],\left[{\mu }_{{a}_{ij}^{\left(k\right)}}^{-},{\mu }_{{a}_{ij}^{\left(k\right)}}^{+}\right]\right\rangle .$$

(33)

The specific steps of the group decision-making processing method are as follows.

Step 1: The selection of $q$. According to the decision matrices given by experts, a suitable $q$ should be chosen, so that all elements in ${A}^{\left(k\right)}\left(k=\mathrm{1,2},3,\cdots ,t\right)$ satisfy the definition of an IVq-ROFS, that is, ${\left({\mu }_{{a}_{ij}^{\left(k\right)}}^{+}\right)}^{q}+{\left({\nu }_{{a}_{ij}^{\left(k\right)}}^{+}\right)}^{q}\le 1\left(q\ge 1\right)$. Usually, the value of $q$ that satisfies the requirement can be found by the traversal method.

Step 2: Normalization. In practical applications, if both benefit-type attributes and cost-type attributes are involved, the decision matrix ${A}^{\left(k\right)}$ is transformed into the normal evaluation matrix ${R}^{\left(k\right)}$ using Formulas (32) and (33).

Step 3: The selection of $p$. Utilizing the IVq-ROFIDPOWA operator to preprocess the normal evaluation matrix ${R}^{\left(k\right)}$ with different parameters $p$, the appropriate range of $p$ can be obtained by comparing the results produced with different values to better reflect the differences between the alternatives. It should be noted that because the different values of $p$ do not affect the ranking of the alternatives, this step is not necessary if the final result only requires the ranks of the alternatives and not their scores for further analysis or processing.

Step 4: The aggregation of ${R}^{\left(k\right)}$. The standard evaluation matrix ${R}^{\left(k\right)}$ is aggregated by using the IVq-ROFIDPOWA operator combined with the given expert weight $w$, and then the aggregated matrix $R={\left({r}_{ij}\right)}_{m\times n}$ is obtained. The aggregation process is shown in Formula (34).

$${r}_{ij}= IVq-ROFIDPOWA\left({r}_{ij}^{\left(1\right)},{r}_{ij}^{\left(2\right)},{r}_{ij}^{\left(3\right)},\cdots ,{r}_{ij}^{\left(t\right)}\right).$$

(34)

Step 5: The aggregation of $R$. Similar to step 4, the aggregated matrix $R$ is aggregated using the IVq-ROFIDPOWA operator combined with the given attribute weight $\omega$, and then the attribute values ${r}_{i}$ of the $i$-th alternative are obtained. The aggregation process is shown in Formula (35).

$${r}_{i}= IVq-ROFIDPOWA\left({r}_{i1},{r}_{i2},{r}_{i3},\cdots ,{r}_{in}\right).$$

(35)

Step 6: Calculating the exact values of scores. According to the score function and the accuracy function, which are defined in Formulas (7) and (8), respectively, the score and accuracy of ${r}_{i}$ can be obtained, and then the ${r}_{i}$ are ranked according to definition 2.5.

Step 7: Determination of the best alternative. Based on the ranking results of the ${r}_{i}$ in step 6, the ranking results of the alternatives ${x}_{i}$ are obtained, and then the alternative with the largest score is selected as the optimal alternative.

In addition, during the actual group decision-making process, the decision matrices may be difficult to obtain because of the experts’ lack of understanding of fuzzy theory. To make it easier for experts to make reasonable evaluations, grades can be used to obtain the decision matrices. Inspired by Ilbahar et al. (2018) and Yucesan and Kahraman (2019), the evaluation grades include 10 grades: certainly low important (CLI), very low important (VLI), lower important (LI), below average important (BAI), average important (AI), above average important (AAI), high important (HI), very high important (VHI), certainly high important (CHI) and exactly equal (EE). Then, these grades can be transformed into interval-valued q-rung orthopair fuzzy numbers accordingly, as shown in Table 1.

Table 1 Interval-valued q-rung orthopair fuzzy number transformations

5 Group decision-making cases analysis

5.1 Case 1

5.1.1 Case

ESG ratings (Duuren et al. 2016) are used to score companies and institutions based on three aspects, the environment (E), society (S) and corporate governance (G), to measure the social responsibility of companies and institutions. ESG ratings, as the basis for performing value judgments to guide investors' investment decisions, have attracted increasing attention from international investors, and domestic investors have also begun to pay attention to ESG information disclosures and ratings. However, due to the differences among the ESG data collected by different rating companies, especially their data processing methods, the ESG rating results of different rating companies are also very different, and the lack of an industry consensus has seriously affected the use of ESG ratings by investors. Therefore, the operator and group decision-making method proposed in this paper are used to aggregate the ESG rating data of the Ping An Bank, the China Merchants Bank, the Shanghai Pudong Development Bank, the Industrial Bank, the CITIC Bank and the Minsheng Bank from 2020 by selecting Bloomberg, Shangdao Ronglu and Huaxun to obtain their comprehensive ESG ratings.

In this case, the three evaluation attributes are recorded as $e$ (environment), $s$ (society) and $g$ (corporate governance), and the attribute weights are $\omega =(\frac{1}{3},\frac{1}{3},\frac{1}{3})$. The weights of the three evaluation institutions are $w=(\frac{1}{3},\frac{1}{3},\frac{1}{3})$. At the same time, the evaluated institutions are recorded as ${x}_{1}$, ${x}_{2}$, ${x}_{3}$, ${x}_{4}$, ${x}_{5}$, and ${x}_{6}$ in order. Due to the different ESG evaluation systems and scoring standards of different institutions, to ensure the rationality of the aggregation and evaluation processes, the original scoring matrices given by the three institutions are converted into grade evaluation matrices. Tables 2, 3, 4 shows the grades given by the three institutions.

Table 2 Bloomberg’s grade evaluation matrix

Table 3 Shangdao Ronglu’s grade evaluation matrix

Table 4 Huaxun’s grade evaluation matrix

(1) The grade matrices are converted into the normal evaluation matrices ${R}^{(1)}$, ${R}^{(2)}$, and ${R}^{(3)}$ under the interval-valued q-rung orthopair fuzzy sets according to Table 1. The conversion results are shown in Tables 5, 6, 7.

Table 5 Bloomberg’s standard evaluation matrix ${R}^{(1)}$

Table 6 Shangdao Ronglu’s standard evaluation matrix ${R}^{(2)}$

Table 7 Bloomberg’s standard evaluation matrix ${R}^{(3)}$

(2) According to the observations, when $q=3$, the elements in ${R}^{(1)}$, ${R}^{(2)}$, and ${R}^{(3)}$ satisfy the conditions defined by the IVq-ROFS.

(3) Utilizing the IVq-ROFIDPOWA operator to preprocess the standard evaluation matrix ${R}^{\left(k\right)}$ with different parameters $p$, it is found that the data aggregation effect is better when the parameter $p\epsilon \left[\mathrm{0.7,0.9}\right]$ for the IVq-ROFIDPOWA operator.

(4) The normal evaluation matrix ${R}^{\left(k\right)}$ is aggregated using the IVq-ROFIDPOWA operator with the parameter $p$ found in step (2) and the expert weights $w=(\frac{1}{3},\frac{1}{3},\frac{1}{3})$. When the parameter $p=0.8$, the result of the aggregation matrix ${R}^{\left(k\right)}$ is shown in Table 8.

Table 8 The aggregation matrix $R$

(5) The aggregation matrix $R$ is aggregated using the IVq-ROFIDPOWA operator with the parameter $p$ found in step (2) and the attribute weights $\omega =(\frac{1}{3},\frac{1}{3},\frac{1}{3})$. When using the parameter $p=0.8$, the results of the attribute values ${r}_{i}$ for the $i$-th alternative are shown as follows.

$${r}_{1}=\langle \left[\mathrm{0.6951,0.7638}\right],[\mathrm{0.5173,0.5673}]\rangle ,$$

$${r}_{2}=\langle \left[\mathrm{0.8104,0.8891}\right],[\mathrm{0.2277,0.2718}]\rangle ,$$

$${r}_{3}=\langle \left[\mathrm{0.6624,0.7025}\right],[\mathrm{0.6153,0.6815}]\rangle ,$$

$${r}_{4}=\langle \left[\mathrm{0.6682,0.7295}\right],[\mathrm{0.5908,0.6409}]\rangle ,$$

$${r}_{5}=\langle \left[\mathrm{0.7818,0.8555}\right],[\mathrm{0.4455,0.4636}]\rangle ,$$

$${r}_{6}=\langle \left[\mathrm{0.6624,0.7118}\right],[\mathrm{0.6678,0.7182}]\rangle .$$

(6) The score function in Formula (7) is used to calculate the scores of r as follows: $S\left({r}_{1}\right)=0.2302, S\left({r}_{2}\right)=0.6016, S\left({r}_{3}\right)=0.0439, S\left({r}_{4}\right)=0.1086, S\left({r}_{5}\right)=0.4580, S\left({r}_{6}\right)=-0.0085$. The ranking of the scores of different institutions is $S\left({r}_{2}\right)>S\left({r}_{5}\right)>S\left({r}_{1}\right)>S\left({r}_{4}\right)>S\left({r}_{3}\right)>S\left({r}_{6}\right).$

(7) According to the ranking of the scores in (6), the ranking of the institutions is: ${x}_{2}>{x}_{5}>{x}_{1}>{x}_{4}>{x}_{3}>{x}_{6}$.

According to step (7), the organization with the best sense of social responsibility is ${x}_{2}$. This institution is the China Merchants Bank, and the results are consistent with its actual performance, thereby validating the feasibility of the proposed group decision-making method.

5.1.2 Sensitivity analysis of the IVq-ROFIDPOWA operator

To verify the feasibility and effectiveness of the group decision-making method, this section changes the parameters $p$ and $q$ of the IVq-ROFIDPOWA operator, and analyzes the impacts of the changes in $p$ and $q$ on the decision results.

(1) The effect of $p$ changes on the decision results. When $q=3$, $p$ changes within its domain of $\left[\mathrm{0,1}\right]$, and the scores of each alternative are shown in Fig. 1.

Fig. 1

The trends of the scores when the parameter $p$ changes

It can be seen from Fig. 1 that when the other conditions remain unchanged, the change in the parameter $p$ of the IVq-ROFIDPOWA operator within its domain does not affect the evaluation results of each alternative.

(2) The effect of $q$ changes on the decision results. When $p=0.8$, $q$ changes within the interval $\left[\mathrm{3,15}\right]$, and the scores of each alternative are shown in Fig. 2.

Fig. 2

The trends of the scores when $q$ changes

It can be seen from Fig. 2 that when the other conditions remain unchanged, the change in the parameter $q$ of the IVq-ROFIDPOWA operator does not affect the evaluation results of each alternative. In general, when the parameters $p$ and $q$ of the IVq-ROFIDPOWA operator are changed, the evaluation results of each alternative remain unchanged, which effectively verifies the feasibility and effectiveness of this decision-making method.

5.1.3 Comparative analysis

In this section, the DBWA operator (Liu et al.2017), the PA operator (Yager 2001), the Hamacher operator (Hamacher 1975; Wang et al. 2021) and the IVq-ROFIDPOWA operator are used for comparative analysis. When $y=2$ in the DBWA operator, $\varphi =3$ in the Hamacher operator, and $p=0.8$ in the IVq-ROFIDPOWA operator, while $q$ changes within the range $\left[\mathrm{3,15}\right]$, and the scores and rankings of each ESG rating are obtained, as shown in Fig. 3.

Fig. 3

Comparative analysis among different operators

It can be seen from Fig. 3 that the IVq-ROFIDPOWA operator proposed in this paper has the same ranking results as the DBWA operator, the PA operator and the Hamacher operator. With the change in $q$, the ranking results of each alternative remain unchanged. Moreover, compared with the other three operators, the IVq-ROFIDPOWA operator has more obvious score differences between the alternatives, so it is more conducive to making decisions. This further verifies the feasibility and effectiveness of the group decision-making method proposed in this paper.

5.2 Case 2

5.2.1 Case

To evaluate the concentration level of a student in class, 3 classmates are invited to evaluate the concentration of this student, and their expert weights are $w=[\mathrm{0.33,0.34,0.33}]$. The evaluation values, which are represented as the IVq-ROFNs, have five attributes, ${c}_{1}$ (eye movement), ${c}_{2}$ (facial expression), ${c}_{3}$ (body posture), ${c}_{4}$ (degree of interaction), and ${c}_{5}$ (concentration tune), and the attribute weights are $\omega =[\mathrm{0.2,0.2,0.2,0.2,0.2}]$. Because data normalization does not require complex calculations and the amount of data is small, the normal evaluation matrices are directly given in this paper, as shown in Tables 9, 10, 11.

Table 9 The normal evaluation matrix ${R}^{(1)}$ given by classmate 1

Table 10 The normal evaluation matrix ${R}^{(2)}$ given by classmate 2

Table 11 The normal evaluation matrix ${R}^{(3)}$ given by classmate 3

(1) According to the observations, when $q=2$, the elements in ${R}^{(1)}$, ${R}^{(2)}$, and ${R}^{(3)}$ satisfy the condition defined by the IVq-ROFS.

(2) Using the IVq-ROFIDPOWA operator to preprocess the normal evaluation matrices ${R}^{\left(k\right)}$ produced with different parameters $p$, it is found that the data aggregation effect is better when the parameter $p\epsilon \left[\mathrm{0.9,1}\right]$ in the IVq-ROFIDPOWA operator.

(3) The normal evaluation matrix ${R}^{\left(k\right)}$ is aggregated using the IVq-ROFIDPOWA operator with the parameter $p$ found in step (2) and the expert weights $w=\left(\mathrm{0.33,0.34,0.33}\right)$. When the parameter $p=0.95$, the result of the aggregation matrix $R$ is as shown in Table 12.

Table 12 The aggregation matrix $R$

(4) The aggregation matrix $R$ is aggregated using the IVq-ROFIDPOWA operator with the parameter $p$ found in step (2) and the attribute weights $\omega =\left(\mathrm{0.2,0.2,0.2,0.2,0.2}\right)$. When using the parameter $p=0.95$, the results of the attribute values ${r}_{i}$ for the $i$-th alternative are shown as follows.

$${r}_{1}=\langle \left[\mathrm{0.3784,0.4662}\right],\left[\mathrm{0.5573,0.6785}\right]\rangle ,$$

$${r}_{2}=\langle \left[\mathrm{0.5052,0.6194}\right],\left[\mathrm{0.4102,0.5069}\right]\rangle ,$$

$${r}_{3}=\langle \left[\mathrm{0.6640,0.7898}\right],\left[\mathrm{0.2532,0.3494}\right]\rangle ,$$

$${r}_{4}=\langle \left[\mathrm{0.5462,0}.6635\right],\left[\mathrm{0.3792,0.4673}\right]\rangle ,$$

$${r}_{5}=\langle \left[\mathrm{0.2840,0.3737}\right],\left[\mathrm{0.6593,0.7842}\right]\rangle .$$

(5) The score function is used to calculate the scores of ${r}_{i}$ as $S\left({r}_{1}\right)=-0.2052,S\left({r}_{2}\right)=0.1069,S\left({r}_{3}\right)=0.4392,S\left({r}_{4}\right)=0.1883,S\left({r}_{5}\right)=-0.4171$. The ranking of the scores of the different alternatives is $S\left({r}_{3}\right)>S\left({r}_{4}\right)>S\left({r}_{2}\right)>S\left({r}_{1}\right)>S\left({r}_{5}\right)$.

(6) According to the score ranking results in step (5), the alternative ranking is ${x}_{3}>{x}_{4}>{x}_{2}>{x}_{1}>{x}_{5}$.

According to step (6), the optimal alternative is ${x}_{2}$. This alternative is “average-focused” and consistent with the student's performance in the class, thereby validating the feasibility of the proposed group decision-making method.

5.2.2 Sensitivity analysis of the IVq-ROFIDPOWA Operator

To verify the feasibility and effectiveness of the group decision method, this section changes the parameters $p$ and $q$ of the IVq-ROFIDPOWA operator, and analyzes the impacts of the changes in $p$ and $q$ on the decision results.

(1) The effect of $p$ changes on the decision results. When $q=2$, $p$ changes within its domain of $\left[\mathrm{0,1}\right]$, and the scores of each alternative are shown in Fig. 4.

Fig. 4

The trends of the scores when the parameter $p$ changes

It can be seen from Fig. 4 that when the other conditions remain unchanged, the change in the parameter $p$ of the IVq-ROFIDPOWA operator within its domain does not affect the evaluation results of each alternative.

(2) The effect of $q$ changes on the decision results. When $p=0.95$, $q$ changes within the interval $\left[\mathrm{2,15}\right]$, and the scores of each alternative are shown in Fig. 5.

Fig. 5

The trends of the scores when $q$ changes

It can be seen from Fig. 5 that when the other conditions remain unchanged, the change in the parameter $q$ of the IVq-ROFIDPOWA operator does not affect the evaluation results of each alternative. In general, when the parameters $p$ and $q$ of the IVq-ROFIDPOWA operator are changed, the evaluation results of each alternative remain unchanged, which effectively verifies the feasibility and effectiveness of this decision-making method.

5.2.3 Comparative analysis

In this section, the DBWA operator (Liu et al.2017), the PA operator (Yager 2001), the Hamacher operator (Hamacher 1975; Wang et al. 2021) and the IVq-ROFIDPOWA operator are used for comparative analysis. When $y=2$ in the DBWA operator, $\varphi =3$ in the Hamacher operator, and $p=0.95$ in the IVq-ROFIDPOWA operator, while $q$ changes within the range $\left[\mathrm{2,15}\right]$, and the scores and rankings of each alternative rating are obtained, as shown in Fig. 6.

Fig. 6

Comparative analysis among different operators

It can be seen from Fig. 6 that the IVq-ROFIDPOWA operator proposed in this paper has the same ranking as the DBWA operator, the PA operator and the Hamacher operator. With the change in $q$, the ranking results of each alternative remain unchanged. Moreover, compared with the other three operators, the IVq-ROFIDPOWA operator has more obvious score differences between the alternatives, so it is more conducive to making decisions. This further verifies the feasibility and effectiveness of the group decision-making method proposed in this paper.

6 Conclusion

Based on the t-norm and t-conorm operations of the Dubois and Prade operator, this paper defines the IVq-ROFDP operations and introduces the IVq-ROFDPOWA operator. At the same time, we find that the interactions between the membership and nonmembership degrees in the IVq-ROFDP operations and the IVq-ROFDPOWA operator are not considered. To address this issue concerning the IVq-ROFDP operations, the IVq-ROFIDP operations and the IVq-ROFIDPOWA operator are proposed, and we study the IVq-ROFIDPOWA operator’s idempotency, permutation invariance, monotonicity and boundedness. Then, this paper proposes a group decision-making method based on the IVq-ROFIDPOWA operator. Finally, this paper verifies the proposed group decision-making method with two cases. The decision-making results are consistent with those of practical applications and the results of existing operators, thus confirming the feasibility and effectiveness of the improved operator with interactivity and the group decision-making method proposed in this paper. The further comparative analysis shows that the group decision-making method proposed in this paper can better reflect the differences between alternatives.

The proposed group decision-making method can be used to select the optimal alternative using the IVq-ROFIDPOWA operator when the attribute weights and expert weights are known in advance. The unknown attribute weights and expert weights of group decision-making methods are the main focus of our research. Moreover, the fusion of big data using aggregation operators will also be the focus of our future research.