Multiple attribute decision making based on q-rung orthopair fuzzy Hamacher Muirhead mean operators

Abstract

The q-rung orthopair fuzzy set (q-ROFS) is a generalized orthopair fuzzy set which quantifies vague information comprehensively. The objective of this paper was to develop some novel Muirhead mean (MM) operators for any orthopair fuzzy numbers using Hamacher t-norm and t-conorm inspired arithmetic operations. The benefit of using Hamacher t-norm and t-conorm based arithmetic operations with MM operator is that their combination can consider not only the interrelationship among the multiple attributes but also provides flexibility in aggregation process due to additional parameters involved. Also, MM has prominent characteristics of being generalization of some well-known aggregation operators such as arithmetic mean (AM), geometric mean (GM), Bonferroni mean (BM), and Maclaurin symmetric mean (MSM). So, this paper develops MM operators based on Hamacher operations under q-rung orthopair fuzzy environment, i.e., q-rung orthopair fuzzy Hamacher Muirhead mean (q-ROFHMM) and q-rung orthopair fuzzy Hamacher weighted Muirhead mean (q-ROFHWMM) operators with some of their desirable properties. Paper also provide some special cases of these operators. Further, a multiple attribute decision making (MADM) method based on the proposed q-ROFHWMM operator has been developed. Finally, by utilizing this developed approach, a real-world MADM problem related to the selection of enterprise resource planning (ERP) system is discussed to illustrate the effectiveness of proposed operators

1 Introduction

Multiple attribute decision making (MADM) is an inevitable process to select an optimal alternative from a set of feasible alternatives based on multiple attributes (Chen and Tan 1994; Li 2005). This process is conducted with the help of experts and decision makers (DMs). Information extraction and its fusion by considering the interrelationship between multiple attributes are the major challenges for the experts and DMs to analyze any real-life decision-making problem. In most real-life decision problems, it is difficult to extract the associated information precisely, and thus the issue is related to imprecision in data, vagueness, or ambiguity. To cope up with such problems, the fuzzy set theory was introduced by Zadeh (1965). Informally, the fuzzy set can be defined as a class of objects having no sharp boundaries. However, the fuzzy set has limitations because it counts only the sense of satisfaction called membership of an element in the set. To address these limitations differently, several extensions are available in the literature including interval-valued fuzzy set, type-2 fuzzy set, intuitionistic fuzzy set (IFS), fuzzy soft set, neutrosophic fuzzy set, complex fuzzy set, hesitant fuzzy set, Pythagorean fuzzy set (PFS), q-rung orthopair fuzzy set (q-ROFS), temporal intuitionistic fuzzy set, etc. (Bustince et al. 2015; Yager 2017; Alcantud et al. 2020). Specifically, IFS, PFS, and q-ROFS are preferably used to deal with two-dimensional (membership and non-membership) decision-making problems. More specifically, Atanassov (1986) introduced the notion of dissatisfaction and extended the definition of fuzzy sets to IFS in which both membership ($\mu$) and non-membership ($\nu$) degrees of every element are considered with conditions $0\le \mu ,\nu \le 1;~0\le \mu +\nu \le 1$. Over the decades, a substantial amount of work has been done by several researchers to investigate intuitionistic fuzzy MADM problems by utilizing different aggregation operators (Xu and Yager 2006; Xu 2007; Tan and Chen 2010; Xu and Yager 2011), and information measures (Szmidt and Kacprzyk 2000; Chen 2007; Guo and Song 2014; Chen and Chang 2015), etc. Further, it is noticed that for some real-life MADM problems, IFS is ill-suited because the assessment values are not satisfying the condition $0\le \mu +\nu \le 1$. To handle such real-life MADM problems, an extended decision space is required. Yager (2013) noticed this shortcoming of IFS and proposed the concept of PFS by making use of the conditions $0\le \mu ,\nu \le 1;~0\le \mu ^2+\nu ^2\le 1$. Zhang and Xu (2014) defined the score function and two fundamental operations namely additional and multiplication for PFS, while Peng and Yang (2015) defined the accuracy function along with subtraction and division operations for PFS. Using the definition of PFS and related concepts, several aggregation operators have been developed including average mean, geometric mean, Choquet integral (CI), BM, and MSM (Zhang 2016; Peng and Yang 2016; Liang et al. 2018; Wei et al. 2018; Garg 2016). It is observed that for some real-life decision-making problems, PFS does not effectively provide the required decision space due to its strict condition $0\le \mu ^2+\nu ^2\le 1$.

For providing more flexibility to expand the decision space as per the need of the problem and the requirement of the DM, Yager (2017) introduced the concept of q-ROFS with conditions $0\le \mu ,\nu \le 1;~0\le \mu ^q+\nu ^q\le 1;~q\ge 1$. Utilizing q-ROFS and considering the interrelationship between multiple attributes, several aggregation operators have been developed for MADM problems owning their features and constraints. Some of the popular aggregation operators that have been developed under q-ROFS are: weighted average and weighted geometric (Liu et al. 2018), point weighted averaging, and point weighted geometric operators (Xing et al. 2019), Bonferroni mean (Liu and Liu 2018), Heronian mean (Wei et al. 2018), Maclaurin symmetric mean (Wei et al. 2019), Hamy and dual Hamy mean (Wang et al. 2019a), Muirhead mean (Wang et al. 2019b), weighted continuous interval-valued q-ROFS ordered weighted averaging (Yang et al. 2021), etc. It is noticeable that the above-reviewed aggregation operators rely either on the algebraic or Einstein norms and conorms based arithmetic operations to analyze any MADM problem. However, it is a fact that Hamacher norm and conorm (Hamacher 1978) based arithmetic operations are a generalized version of algebraic and Einstein norms and conorms based arithmetic operations. It also provides flexibility in the aggregation process due to the presence of a parameter $\gamma$. Many researchers utilized these characteristics of Hamacher norm and conorm based arithmetic operations and analyzed many MADM problems under different fuzzy environments including IFS, PFS, and complex intuitionistic fuzzy set, proportional interval type-2 hesitant fuzzy set (Huang 2014; Wu and Wei 2017; Akram et al. 2021; Chen et al. 2019). Recently, Darko and Liang (2020) used Hamacher norm and conorm-based arithmetic operations for q-ROFS and developed some novel aggregation operators including weighted average and MSM to solve a MADM problem.

Motivated by the above-reviewed literature, the objective of the paper includes the development of some novel aggregation operators for real-life MADM problems which can handle the need of the extended decision space in two dimensions, provide flexibility in the aggregation process and consider interrelationship between multiple attributes. To fulfill the requirements of the objective, this paper adopts q-ROFS to handle the requirement of extended decision space in two dimensions formed by membership and non-membership degrees, applies Hamacher norm- and conorm-based arithmetic operations to provide flexibility in the aggregation process, while Muirhead mean (MM) aggregation operator is utilized to consider all the possible interrelationships between multiple attributes in a given MADM problem. To the best of our knowledge, no study has been found which fuses the notion of Hamacher t-norm and t-conorm, and MM operator in any orthopair fuzzy environments (IFS, PFS, or q-ROFS), and this will be the main contribution of the paper.

The benefit of using the Muirhead (1902) aggregation operator is that it considers all the possible interrelationships between multiple attributes with the help of a parameter vector P. By taking different values of parameter vector P, various popular averaging means like AM, GM, BM, and MSM can be deducted. Based on these benefits, the MM operator is used by many researchers for handling MADM problems in different fuzzy environments, such as IFS, PFS, hesitant fuzzy linguistic set, q-ROFS, 2-tuple linguistic neutrosophic numbers set, etc. (Liu and Li 2017; Zhu and Li 2018; Liu and Liu 2018; Wang et al. 2019, 2019b). The paper develops two novel aggregation operators including q-rung orthopair fuzzy Hamacher Muirhead mean (q-ROFHMM), and q-rung orthopair fuzzy Hamacher weighted Muirhead mean (q-ROFHWMM) along with their desirable properties and some special cases. The advantage of the proposed aggregation operators are as follows:

• 1. The parameter q of the generalized orthopair fuzzy set can help the DM to extend their assessment decision space as per the need of the problem.

• 2. The integration between Hamacher t-norm and t-conorm based operations with MM operator captures the interrelationship among the multiple attributes and also provides flexibility in decision making due to the use of additional parameters $\gamma$ and P.

• 3. The proposed aggregation operators are more general in nature and provide a range of aggregation operators by substituting some specific values to the parameters $q,\gamma$ and P.

The rest of the paper is systematized as follows: Sect. 2 briefly discusses some prerequisite knowledge of q-ROFS, Hamacher operations, and MM operator. Section 3 proposes the q-ROFHMM, q-ROFHWMM operators and discusses some of their desirable properties along with some special cases. In Sect. 4, a MADM method based on the q-ROFHWMM operator has been developed and a practical MADM problem has been examined by using the developed approach. The section also conducts sensitivity and comparative analyses. Finally, in Sect. 5, some concluding remarks are given.

2 Preliminaries

In this section, some fundamental concepts of q-ROFS, Hamacher operations, and Muirhead mean operators are reviewed.

2.1 q-rung orthopair fuzzy set

The concept of q-ROFS was introduced by Yager (2017) as a generalization of IFS and PFS.

Definition 1

(Yager 2017) Let X be a universal set, then a q-ROFS A on X is defined as follows:

$$\begin{aligned} A = \{\langle x,(\mu _A(x),\nu _A(x))\rangle | ~x\in X\} \end{aligned}$$

(1)

where $\mu _A(x) \in [0,1]$ and $\nu _A(x) \in [0,1]$ is the membership and non-membership function, respectively, which satisfy the condition $0\le (\mu _A(x))^q + (\nu _A(x))^q \le 1,~q\ge 1$. When $q=1$ and $q=2$ it becomes IFS and PFS, respectively.

The degree of indeterminacy of x in A is defined as $\pi _A(x) = \big ((\mu _A(x))^q+(\nu _A(x))^q-(\mu _A(x))^q(\nu _A(x))^q\big )^{1/q}$. For convenience, a q-rung orthopair fuzzy number (q-ROFN), i.e., $(\mu _A(x),\nu _A(x))$ can be written as $(\mu _A,\nu _A)$.

Definition 2

(Liu et al. 2018) For any three q-ROFNs, $a= (\mu , \nu )$, $a_1= (\mu _1,\nu _1)$, and $a_2= (\mu _2,\nu _2)$, the basic operations can be defined as follows:

• 1. ${\bar{a}}=(\nu ,\mu )$,

• 2. $a_1 \oplus a_2 =\left( (\mu _1^q + \mu _2^q - \mu _1^q\mu _2^q)^{1/q}, \nu _1\nu _2\right)$,

• 3. $a_1 \otimes a_2 = \left( \mu _1\mu _2, (\nu _1^q + \nu _2^q - \nu _1^q\nu _2^q)^{1/q}\right)$,

• 4. $\lambda a = \left( (1-(1-\mu ^q)^\lambda )^{1/q}, \nu ^\lambda \right)$,

• 5. $a^\lambda = \left( \mu ^\lambda ,(1-(1-\nu ^q)^\lambda )^{1/q}\right)$.

Furthermore, for comparing any two q-ROFNs, score and accuracy functions are defined as follows:

Definition 3

(Liu et al. 2018) Let $A = (\mu _A, \nu _A)$ be any q-ROFN, then a score function S(A) is defined as follows:

$$\begin{aligned} S(A) = \mu _A^q - \nu _A^q \end{aligned}$$

(2)

where $S(A)\in [-1,1]$, greater score value S(A) ensures larger q-ROFN A. But in some cases score function itself is unable to distinguish two q-ROFNs. So to resolve such problems, the accuracy function is defined as follows:

$$\begin{aligned} H(A) = \mu _A^q + \nu _A^q \end{aligned}$$

(3)

where $H(A)\in [0,1]$, higher the accuracy value H(A) bigger the q-ROFN A. Now, based on the definitions of score and accuracy functions, a comparison method is formulated as follows.

Definition 4

Suppose $A = (\mu _A, \nu _A)$ and $B = (\mu _B, \nu _B)$ be two q-ROFNs and S(A), S(B) are their score values, while H(A), H(B) are their accuracy values. Then

• (1) $S(A) > S(B)$ $\Rightarrow$ $A > B$.

• (2) If $S(A) = S(B)$, then $H(A) > H(B)$ $\Rightarrow$ $A > B$; $H(A) = H(B)$ $\Rightarrow$ $A = B$.

2.2 Hamacher operations

In fuzzy set theory, t-norm and t-conorm are used for fuzzy intersection and fuzzy union, respectively. There are several t-norms and t-conorms are available in literature including algebraic, Einstein, Hamacher, Frank, Dombi, etc. Hamacher t-norm(T) and t-conorm($T^{*}$) are general in nature because they generate algebraic and Einstein t-norms and t-conorms by setting certain fixed values to its parameter $\gamma$ (Hamacher 1978). In particular, Hamacher product($\otimes$) and Hamacher sum($\oplus$) are defined as follows:

$$\begin{aligned}&T(a,b)= a\otimes b= \frac{ab}{\gamma +(1-\gamma )(a+b-ab)} ,\\&\quad ~ T^*(a,b)= a\oplus b=\frac{a+b-ab-(1-\gamma )ab}{1-(1-\gamma )(ab)};~\gamma > 0. \end{aligned}$$

As a special case, when $\gamma = 1$ then Hamacher t-norm and t-conorm will reduce to the algebraic t-norm and t-conorm as follow:

$$\begin{aligned} T(a,b)=a\otimes b=ab ,~~ T^*(a,b)=a\oplus b=a+b-ab. \end{aligned}$$

Similarly, when $\gamma = 2$, then Hamacher t-norm and t-conorm will reduce to the Einstein t-norm and t-conorm as follows:

$$\begin{aligned} T(a,b)= & {} a\otimes b =\frac{ab}{1+(1-a)(1-b)},\\ T^*(a,b)= & {} a \oplus b=\frac{a+b}{1+ab}. \end{aligned}$$

2.3 Hamacher operations for q-ROFNs

Let $a= (\mu , \nu )$, $a_1= (\mu _1,\nu _1)$ and $a_2= (\mu _2,\nu _2)$ be three q-ROFNs and $\gamma > 0$, then some basic Hamacher operations for q-ROFNs are defined as follows (Liu and Liu 2018):

$$\begin{aligned}&a_1\oplus a_2 = \left( \left( \frac{(\mu _1)^q+(\mu _2)^q-(\mu _1)^q(\mu _2)^q-(1-\gamma )(\mu _1)^q(\mu _2)^q}{1-(1-\gamma )(\mu _1)^q(\mu _2)^q}\right) ^{1/q},\right. \\&\quad \left. \frac{\nu _1\nu _2}{\left( \gamma +(1-\gamma )\left( (\nu _1)^q+(\nu _2)^q-(\nu _1)^q(\nu _2)^q\right) \right) ^{1/q}}\right) , \\&a_1\otimes a_2 = \left( \frac{\mu _1\mu _2}{\left( \gamma +(1-\gamma )\left( (\mu _1)^q+(\mu _2)^q-(\mu _1)^q(\mu _2)^q\right) \right) ^{1/q}},\right. \\&\left. \left( \frac{(\nu _1)^q+(\nu _2)^q-(\nu _1)^q(\nu _2)^q-(1-\gamma )(\nu _1)^q(\nu _2)^q}{1-(1-\gamma )(\nu _1)^q(\nu _2)^q}\right) ^{1/q}\right) , \\&\lambda a = \left( \left( \frac{(1+(\gamma -1)\mu ^q)^\lambda -(1-\mu ^q)^\lambda }{(1+(\gamma -1)\mu ^q)^\lambda +(\gamma -1)(1-\mu ^q)^\lambda }\right) ^{1/q},\right. \\&\quad \left. \frac{(\gamma )^{1/q}\nu ^\lambda }{\left( (1+(\gamma -1)(1-\nu ^q))^\lambda +(\gamma -1)(\nu ^q)^\lambda \right) ^{1/q}}\right) , \\&a^\lambda = \left( \frac{(\gamma )^{1/q}\mu ^\lambda }{\left( (1+(\gamma -1)(1-\mu ^q))^\lambda +(\gamma -1)(\mu ^q)^\lambda \right) ^{1/q}},\right. \\&\quad \left. \left( \frac{(1+(\gamma -1)\nu ^q)^\lambda -(1-\nu ^q)^\lambda }{(1+(\gamma -1)\nu ^q)^\lambda +(\gamma -1)(1-\nu ^q)^\lambda }\right) ^{1/q}\right) . \end{aligned}$$

when $\gamma = 1$ and $\gamma = 2$, then Hamacher operations will reduce to the algebraic operations and Einstein operations, respectively.

2.4 MM operator

In 1902, Muirhead proposed the concept of Muirhead mean for crisp numbers, which can deal with the association among multiple arguments and provides the interrelationship among all aggregated arguments.

Definition 5

Let $a_i(i=1,2,...,n)$ be a collection of crisp numbers and $P =(p_1,p_2,...,p_n)\in \Re ^n$ be a vector of parameters. Then, the MM is defined as follows (Muirhead 1902):

$$\begin{aligned} MM ^P (a_1, a_2,..., a_n) = \left( \frac{1}{n!}\sum _{\vartheta (j)\in S_n}\prod _{j=1}^n a_{\vartheta (j)}^{p_j}\right) ^{\frac{1}{\sum _{j=1}^n p_j}} \end{aligned}$$

(4)

where $\vartheta (j)(j = 1, 2,..., n)$ is any permutation of $(1,2,...,n)$, and $S_n$ is the collection of all permutations of (1, 2, ..., n). There are several special cases of the MM operator with respect to different values of parameter vector P.

• 1. If $P=(p,p,...,p)$, i.e., all $p_i$ are equal to p, then MM is converted into the geometric mean (GM).

  $$\begin{aligned} MM ^P(a_1,a_2,...,a_n)=\left( \prod _{i=1}^{n}a_i\right) ^\frac{1}{n}. \end{aligned}$$

• 2. If $P=(1,0,0...,0)$, then MM is converted into the arithmetic mean (AM).

  $$\begin{aligned} MM ^{(1,0,0,...,0)}(a_1,a_2,...,a_n)=\frac{1}{n}{\sum _{i=1}^{n} a_i}. \end{aligned}$$

• 3. If $P=(p_1,p_2,0,0,...,0)$, then MM is converted into the $BM ^{p_1,p_2}$ operator.

  $$\begin{aligned}&MM ^{(p_1,p_2,0,0,...,0)}(a_1,a_2,...,a_n)\\&\quad =\left( \frac{1}{n(n-1)}\sum _{\begin{array}{c} i,j=1\\ i\ne j \end{array}}^n a_i^{p_1}a_j^{p_2} \right) ^{\frac{1}{p_1+p_2}}. \end{aligned}$$

• 4. If $P=(\overbrace{1,1,...,1}^k,\overbrace{0,0,...,0}^{n-k})$, then MM is converted into the $MSM ^k$ operator.

  $$\begin{aligned}&MM ^{(\overbrace{1,1,...,1}^k,\overbrace{0,0,...,0}^{n-k})}(a_1,a_2,...,a_n)\\&\quad = \left( \frac{\sum _{1\le i_1< ... < i_k\le n}\prod _{j=1}^k a_{i_j}}{C_n^k}\right) ^{\frac{1}{k}}. \end{aligned}$$

3 q-Rung orthopair fuzzy Hamacher Muirhead mean operators

In this section, utilizing Hamacher operations and MM operator, a family of q-rung orthopair fuzzy Hamacher Muirhead mean operators are proposed. Further, some desirable properties and special cases for these aggregation operators are being discussed.

3.1 q-ROFHMM operator

Definition 6

Suppose $\{a_1,a_2,...,a_n\}$ be a collection of q-ROFNs and $P = (p_1, p_2, ..., p_n) \in \Re ^n$ is a n-dimensional parameter vector s.t. $\sum _{j=1}^np_j>0$, then the q-rung orthopair fuzzy Hamacher Muirhead mean (q-ROFHMM) operator is defined as

$$\begin{aligned}&q-ROFHMM ^P (a_1, a_2, ..., a_n) \nonumber \\&\quad = \left( \frac{1}{n!}\bigoplus _{\vartheta (j)\in S_n}\bigotimes _{j=1}^n a_{\vartheta (j)}^{p_j}\right) ^{\frac{1}{\sum _{j=1}^np_j}} \end{aligned}$$

(5)

where $\vartheta (j)(j=1,2, ..., n)$ is an any permutation of (1, 2, ..., n), and $S_n$ be the set of all permutations of (1, 2, ..., n).

Theorem 1

Let $\{a_1,a_2,...,a_n\}$ be a set of q-ROFNs, then the aggregated result by applying q-ROFHMM operator is also a q-ROFN and is equal to

$$\begin{aligned}&q-ROFHMM ^P(a_1,a_2,...,a_n)\nonumber \\&\quad =\begin{pmatrix}\left( \frac{\gamma \left( \left( \displaystyle \prod _{\vartheta \in S_n}(\phi _1+(\gamma ^2-1)\varphi _1)\right) ^\frac{1}{n!}-\left( \displaystyle \prod _{\vartheta \in S_n}(\phi _1-\varphi _1)\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}}{\left( \left( \displaystyle \prod _{\vartheta \in S_n}(\phi _1+(\gamma ^2-1)\varphi _1)\right) ^\frac{1}{n!}+(\gamma ^2-1)\left( \displaystyle \prod _{\vartheta \in S_n}(\phi _1-\varphi _1)\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}+(\gamma -1)\left( \left( \displaystyle \prod _{\vartheta \in S_n}(\phi _1+(\gamma ^2-1)\varphi _1)\right) ^\frac{1}{n!}-\left( \displaystyle \prod _{\vartheta \in S_n}(\phi _1-\varphi _1)\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}}\right) ^{1/q}, \\ \quad \times \left( \frac{\left( \left( \displaystyle \prod _{\vartheta \in S_n}(\psi _1+(\gamma ^2-1)\chi _1)\right) ^\frac{1}{n!}+(\gamma ^2-1)\left( \displaystyle \prod _{\vartheta \in S_n}(\psi _1-\chi _1)\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}-\left( \left( \displaystyle \prod _{\vartheta \in S_n}(\psi _1+(\gamma ^2-1)\chi _1)\right) ^\frac{1}{n!}-\left( \displaystyle \prod _{\vartheta \in S_n}(\psi _1-\chi _1)\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}}{\left( \left( \displaystyle \prod _{\vartheta \in S_n}(\psi _1+(\gamma ^2-1)\chi _1)\right) ^\frac{1}{n!}+(\gamma ^2-1)\left( \displaystyle \prod _{\vartheta \in S_n}(\psi _1-\chi _1)\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}+(\gamma -1)\left( \left( \displaystyle \prod _{\vartheta \in S_n}(\psi _1+(\gamma ^2-1)\chi _1)\right) ^\frac{1}{n!}-\left( \displaystyle \prod _{\vartheta \in S_n}(\psi _1-\chi _1)\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}}\right) ^{1/q}\end{pmatrix}\nonumber \\ \end{aligned}$$

(6)

where

$$\begin{aligned} \phi _1= & {} \prod _{j=1}^n\big (1+(\gamma -1)(1-\mu _{\vartheta (j)}^q)\big )^{p_j},\\ \varphi _1= & {} \prod _{j=1}^n(\mu _{\vartheta (j)}^q)^{p_j},\\ \psi _1= & {} \prod _{j=1}^n(1+(\gamma -1)\nu _{\vartheta (j)}^q)^{p_j},\\ \chi _1= & {} \prod _{j=1}^n(1-\nu _{\vartheta (j)}^q)^{p_j}. \end{aligned}$$

Proof

In order to show equation(6), first we will apply Hamacher operations of q-ROFNs (Sect. 2.3) and get,

$$\begin{aligned}&a_{\vartheta (j)}^{p_j} = \left( \frac{\gamma ^{1/q}\mu _{\vartheta (j)}^{p_j}}{\left( (1+(\gamma -1)(1-\mu _{\vartheta (j)}^q))^{p_j}+(\gamma -1)(\mu _{\vartheta (j)}^q)^{p_j}\right) ^{1/q}},\right. \\&\left. \left( \frac{(1+(\gamma -1)\nu _{\vartheta (j)}^q)^{p_j}-(1-\nu _{\vartheta (j)}^q)^{p_j}}{(1+(\gamma -1)\nu _{\vartheta (j)}^q)^{p_j}+(\gamma -1)(1-\nu _{\vartheta (j)}^q)^{p_j}} \right) ^{1/q}\right) \end{aligned}$$

and,

$$\begin{aligned}&\displaystyle \bigotimes _{j=1}^{n}a_{\vartheta (j)}^{p_j}\\&\quad =\left( \frac{\gamma ^{1/q}\displaystyle \prod _{j=1}^{n}\mu _{\vartheta (j)}^{p_j}}{\left( \displaystyle \prod _{j=1}^{n}(1+(\gamma -1)(1-\mu _{\vartheta (j)}^q))^{p_j}+ (\gamma -1)\displaystyle \prod _{j=1}^{n}(\mu _{\vartheta (j)}^q)^{p_j}\right) ^{1/q}},\right. \\&\qquad \left. \left( \frac{\displaystyle \prod _{j=1}^{n}(1+(\gamma -1)\nu _{\vartheta (j)}^q)^{p_j}- \displaystyle \prod _{j=1}^{n}(1-\nu _{\vartheta (j)}^q)^{p_j}}{\displaystyle \prod _{j=1}^{n}(1+(\gamma -1)\nu _{\vartheta (j)}^q)^{p_j} +(\gamma -1)\displaystyle \prod _{j=1}^{n}(1-\nu _{\vartheta (j)}^q)^{p_j}}\right) ^{1/q}\right) \end{aligned}$$

On adding it for every permutation, we get

$$\begin{aligned}&\displaystyle \bigoplus _{\vartheta (j)\in S_n}\displaystyle \bigotimes _{j=1}^n a_{\vartheta (j)}^{p_j}\\&\quad = \left( \left( \frac{\displaystyle \prod _{\vartheta \in S_n}(\phi _1+(\gamma ^2-1)\varphi _1)-\displaystyle \prod _{\vartheta \in S_n}(\phi _1-\varphi _1)}{\displaystyle \prod _{\vartheta \in S_n}(\phi _1+(\gamma ^2-1)\varphi _1)+(\gamma -1)\displaystyle \prod _{\vartheta \in S_n}(\phi _1-\varphi _1)}\right) ^{1/q},\right. \\&\qquad \left. \left( \frac{\gamma \displaystyle \prod _{\vartheta \in S_n}(\psi _1-\chi _1)}{\displaystyle \prod _{\vartheta \in S_n}(\psi _1+(\gamma ^2-1)\chi _1)+(\gamma -1)\displaystyle \prod _{\vartheta \in S_n}(\psi _1-\chi _1)}\right) ^{1/q}\right) \end{aligned}$$

Thus,

$$\begin{aligned}&\displaystyle \frac{1}{n!}\left( \displaystyle \bigoplus _{\vartheta (j)\in S_n}\displaystyle \bigotimes _{j=1}^n a_{\vartheta (j)}^{p_j}\right) \\&= \left( \left( \frac{\left( \displaystyle \prod _{\vartheta \in S_n}(\phi _1+(\gamma ^2-1)\varphi _1)\right) ^\frac{1}{n!}-\left( \displaystyle \prod _{\vartheta \in S_n}(\phi _1-\varphi _1)\right) ^\frac{1}{n!}}{\left( \displaystyle \prod _{\vartheta \in S_n}(\phi _1+(\gamma ^2-1)\varphi _1)\right) ^\frac{1}{n!}+(\gamma -1)\left( \displaystyle \prod _{\vartheta \in S_n}(\phi _1-\varphi _1)\right) ^\frac{1}{n!}}\right) ^{1/q},\right. \\&\quad \times \left. \left( \frac{\gamma \left( \displaystyle \prod _{\vartheta \in S_n}(\psi _1-\chi _1)\right) ^\frac{1}{n!}}{\left( \displaystyle \prod _{\vartheta \in S_n}(\psi _1+(\gamma ^2-1)\chi _1)\right) ^\frac{1}{n!}+(\gamma -1)\left( \displaystyle \prod _{\vartheta \in S_n}(\psi _1-\chi _1)\right) ^\frac{1}{n!}}\right) ^{1/q}\right) \end{aligned}$$

Finally, raising its whole power by $\frac{1}{\sum _{j=1}^np_j}$, we have

$$\begin{aligned}&q-ROFHMM ^P(a_1,a_2,...,a_n)=\left( \displaystyle \frac{1}{n!}\displaystyle \bigoplus _{\vartheta (j)\in S_n}\displaystyle \bigotimes _{j=1}^na_{\vartheta (j)}^{p_j}\right) ^{\frac{1}{\sum _{j=1}^np_j}}\nonumber \\&\quad =\begin{pmatrix}\left( \frac{\gamma \left( \left( \displaystyle \prod _{\vartheta \in S_n}(\phi _1+(\gamma ^2-1)\varphi _1)\right) ^\frac{1}{n!}-\left( \displaystyle \prod _{\vartheta \in S_n}(\phi _1-\varphi _1)\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}}{\left( \left( \displaystyle \prod _{\vartheta \in S_n}(\phi _1+(\gamma ^2-1)\varphi _1)\right) ^\frac{1}{n!}+(\gamma ^2-1)\left( \displaystyle \prod _{\vartheta \in S_n}(\phi _1-\varphi _1)\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}+(\gamma -1)\left( \left( \displaystyle \prod _{\vartheta \in S_n}(\phi _1+(\gamma ^2-1)\varphi _1)\right) ^\frac{1}{n!}-\left( \displaystyle \prod _{\vartheta \in S_n}(\phi _1-\varphi _1)\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}}\right) ^{1/q},\\ ~\left( \frac{\left( \left( \displaystyle \prod _{\vartheta \in S_n}(\psi _1+(\gamma ^2-1)\chi _1)\right) ^\frac{1}{n!}+(\gamma ^2-1)\left( \displaystyle \prod _{\vartheta \in S_n}(\psi _1-\chi _1)\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}-\left( \left( \displaystyle \prod _{\vartheta \in S_n}(\psi _1+(\gamma ^2-1)\chi _1)\right) ^\frac{1}{n!}-\left( \displaystyle \prod _{\vartheta \in S_n}(\psi _1-\chi _1)\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}}{\left( \left( \displaystyle \prod _{\vartheta \in S_n}(\psi _1+(\gamma ^2-1)\chi _1)\right) ^\frac{1}{n!}+(\gamma ^2-1)\left( \displaystyle \prod _{\vartheta \in S_n}(\psi _1-\chi _1)\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}+(\gamma -1)\left( \left( \displaystyle \prod _{\vartheta \in S_n}(\psi _1+(\gamma ^2-1)\chi _1)\right) ^\frac{1}{n!}-\left( \displaystyle \prod _{\vartheta \in S_n}(\psi _1-\chi _1)\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}}\right) ^{1/q}\end{pmatrix}\nonumber \\&\quad =(\mu ^*,\nu ^*). \end{aligned}$$

(7)

Now, to show that equation (7) is a q-ROFN, we have to prove the following conditions:

(a) $0\le \mu ^*\le 1$, and $0\le \nu ^*\le 1$

(b) $0\le (\mu ^*)^q+(\nu ^*)^q\le 1$

where $\mu ^*$ and $\nu ^*$ are the membership and non-membership degrees of equation (7), respectively.

Proof (a) For any $\gamma > 0$, $q \ge 1$ and $P \in \Re ^n$ s.t. $\sum _{j=1}^np_j>0$, we have $\phi _1,~\varphi _1,~\psi _1,~\chi _1\ge 0$ with $\phi _1\ge \varphi _1$, $\psi _1\ge \chi _1$ and the q-ROFN $(\mu ^*, \nu ^*)$ can be written as $\left( \left( 1-\frac{A^*-B^*}{A^*-B^*+\gamma B^*}\right) ^{1/q}, \left( \frac{C^*-D^*}{C^*-D^*+\gamma D^*}\right) ^{1/q}\right)$. where,

$$\begin{aligned} A^*= & {} \left( \left( \prod _{\vartheta \in S_n}(\phi _1+(\gamma ^2-1)\varphi _1)\right) ^\frac{1}{n!} +(\gamma ^2-1)\left( \prod _{\vartheta \in S_n}(\phi _1-\varphi _1)\right) ^\frac{1}{n!}\right) ^\frac{1}{\sum _{j=1}^np_j},\\ B^*= & {} \left( \left( \prod _{\vartheta \in S_n}(\phi _1+(\gamma ^2-1)\varphi _1)\right) ^\frac{1}{n!} -\left( \prod _{\vartheta \in S_n}(\phi _1-\varphi _1)\right) ^\frac{1}{n!}\right) ^\frac{1}{\sum _{j=1}^np_j},\\ C^*= & {} \left( \left( \prod _{\vartheta \in S_n}(\psi _1+(\gamma ^2-1)\chi _1)\right) ^\frac{1}{n!} +(\gamma ^2-1)\left( \prod _{\vartheta \in S_n}(\psi _1-\chi _1)\right) ^\frac{1}{n!}\right) ^\frac{1}{\sum _{j=1}^np_j},\\ D^*= & {} \left( \left( \prod _{\vartheta \in S_n}(\psi _1+(\gamma ^2-1)\chi _1)\right) ^\frac{1}{n!} -\left( \prod _{\vartheta \in S_n}(\psi _1-\chi _1)\right) ^\frac{1}{n!}\right) ^\frac{1}{\sum _{j=1}^np_j}. \end{aligned}$$

Since $A^*,~B^*,~C^*,~D^*\ge 0$ s.t. $A^*\ge B^*$ and $C^*\ge D^*$, Therefore it is easy to show that $\mu ^*$ and $\nu ^*$ satisfy the condition (a).

Proof (b) Condition (a) implies that $0\le (\mu ^*)^q+(\nu ^*)^q$. Now show that $(\mu ^*)^q+(\nu ^*)^q\le 1$.

As we have $\mu _{\vartheta (j)}^q+\nu _{\vartheta (j)}^q\le 1$, So by utilizing $\mu _{\vartheta (j)}^q\le 1-\nu _{\vartheta (j)}^q$ and equation (7) for $\mu ^*$ and $\nu ^*$, we can easily obtain

$$\begin{aligned} (\mu ^*)^q+(\nu ^*)^q\le 1. \end{aligned}$$

Remark

On putting the value of $q=1$ and $q=2$ in Eq.(7), we will get intuitionistic fuzzy Hamacher Muirhead mean (IFHMM) operator and pythagorean fuzzy Hamacher Muirhead mean (PFHMM) operator, respectively.

In the following, proof of some fundamental properties of q-ROFHMM operator are given.

Property 1

(Idempotency) Let $\{a_1,a_2,...,a_n\}$ be a set of q-ROFNs, if all $a_i=(\mu _i,\nu _i)(i=1,2,...,n)$ are equal, i.e., $a_i= a =(\mu ,\nu )$, the

$$\begin{aligned} q-ROFHMM ^P(a_1,a_2,...,a_n)=a. \end{aligned}$$

Proof

Since $a_i= a =(\mu ,\nu )$ for all i, then Theorem 1 yields

$$\begin{aligned} \phi _1= & {} \prod _{j=1}^n\big (1+(\gamma -1)(1-\mu _{\vartheta (j)}^q)\big )^{p_j}=\big (1+(\gamma -1)(1-\mu ^q)\big )^{\sum _{j=1}^np_j}=\phi ,\\ \varphi _1= & {} \prod _{j=1}^n(\mu _{\vartheta (j)}^q)^{p_j}=(\mu ^q)^{\sum _{j=1}^np_j}=\varphi ,\\ \psi _1= & {} \prod _{j=1}^n(1+(\gamma -1)\nu _{\vartheta (j)}^q)^{p_j}=\big (1+(\gamma -1)\nu ^q\big )^{\sum _{j=1}^np_j}=\psi ,\\ \chi _1= & {} \prod _{j=1}^n(1-\nu _{\vartheta (j)}^q)^{p_j}=(1-\nu ^q)^{\sum _{j=1}^np_j}=\chi . \end{aligned}$$

and

$$\begin{aligned}&q-ROFHMM ^P(a_1, a_2, ..., a_n) =\\&\begin{pmatrix}\left( \frac{\gamma \left( \left( \displaystyle \prod _{\vartheta \in S_n}(\phi +(\gamma ^2-1)\varphi )\right) ^\frac{1}{n!}-\left( \displaystyle \prod _{\vartheta \in S_n}(\phi -\varphi )\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}}{\left( \left( \displaystyle \prod _{\vartheta \in S_n}(\phi +(\gamma ^2-1)\varphi )\right) ^\frac{1}{n!}+(\gamma ^2-1)\left( \displaystyle \prod _{\vartheta \in S_n}(\phi -\varphi )\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}+(\gamma -1)\left( \left( \displaystyle \prod _{\vartheta \in S_n}(\phi +(\gamma ^2-1)\varphi )\right) ^\frac{1}{n!}-\left( \displaystyle \prod _{\vartheta \in S_n}(\phi -\varphi )\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}}\right) ^{1/q}, \\ \left( \frac{\left( \left( \displaystyle \prod _{\vartheta \in S_n}(\psi +(\gamma ^2-1)\chi )\right) ^\frac{1}{n!}+(\gamma ^2-1)\left( \displaystyle \prod _{\vartheta \in S_n}(\psi -\chi )\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j} -\left( \left( \displaystyle \prod _{\vartheta \in S_n}(\psi +(\gamma ^2-1)\chi )\right) ^\frac{1}{n!}-\left( \displaystyle \prod _{\vartheta \in S_n}(\psi -\chi )\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}}{\left( \left( \displaystyle \prod _{\vartheta \in S_n}(\psi +(\gamma ^2-1)\chi )\right) ^\frac{1}{n!}+(\gamma ^2-1)\left( \displaystyle \prod _{\vartheta \in S_n}(\psi -\chi )\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}+(\gamma -1)\left( \left( \displaystyle \prod _{\vartheta \in S_n}(\psi +(\gamma ^2-1)\chi )\right) ^\frac{1}{n!}-\left( \displaystyle \prod _{\vartheta \in S_n}(\psi -\chi )\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}}\right) ^{1/q}\end{pmatrix} \\&\quad =\begin{pmatrix}\left( \frac{\gamma \left( \left( (\phi +(\gamma ^2-1)\varphi )^{n!}\right) ^\frac{1}{n!}-\left( (\phi -\varphi )^{n!}\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}}{\left( \left( (\phi +(\gamma ^2-1)\varphi )^{n!}\right) ^\frac{1}{n!}+(\gamma ^2-1)\left( (\phi -\varphi )^{n!}\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}+(\gamma -1)\left( \left( (\phi +(\gamma ^2-1)\varphi )^{n!}\right) ^\frac{1}{n!}-\left( (\phi -\varphi )^{n!}\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}}\right) ^{1/q}, \\ \left( \frac{\left( \left( (\psi +(\gamma ^2-1)\chi )^{n!}\right) ^\frac{1}{n!}+(\gamma ^2-1)\left( (\psi -\chi )^{n!}\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}-\left( \left( (\psi +(\gamma ^2-1)\chi )^{n!}\right) ^\frac{1}{n!}-\left( (\psi -\chi )^{n!}\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}}{\left( \left( (\psi +(\gamma ^2-1)\chi )^{n!}\right) ^\frac{1}{n!}+(\gamma ^2-1)\left( (\psi -\chi )^{n!}\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}+(\gamma -1)\left( \left( (\psi +(\gamma ^2-1)\chi )^{n!}\right) ^\frac{1}{n!}-\left( (\psi -\chi )^{n!}\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}}\right) ^{1/q}\end{pmatrix} \\&=\left( \left( \frac{\gamma \left( \gamma ^2\varphi \right) ^\frac{1}{\sum _{j=1}^np_j}}{\left( \gamma ^2\phi \right) ^\frac{1}{\sum _{j=1}^np_j}+(\gamma -1)\left( \gamma ^2\varphi \right) ^\frac{1}{\sum _{j=1}^np_j}}\right) ^{1/q}, \left( \frac{\left( \gamma ^2\psi \right) ^\frac{1}{\sum _{j=1}^np_j}-\left( \gamma ^2\chi \right) ^\frac{1}{\sum _{j=1}^np_j}}{\left( \gamma ^2\psi \right) ^\frac{1}{\sum _{j=1}^np_j}+(\gamma -1)\left( \gamma ^2\chi \right) ^\frac{1}{\sum _{j=1}^np_j}}\right) ^{1/q}\right) \\&=\left( \left( \frac{\gamma \left( \mu ^q\right) }{\left( 1+(\gamma -1)(1-\mu ^q)\right) +(\gamma -1)\left( \mu ^q\right) }\right) ^{1/q}, \left( \frac{\left( 1+(\gamma -1)\nu ^q\right) -\left( 1-\nu ^q\right) }{\left( 1+(\gamma -1)\nu ^q\right) +(\gamma -1)\left( 1-\nu ^q\right) }\right) ^{1/q}\right) =(\mu ,\nu )=a. \end{aligned}$$

Property 2

(Monotonicity) If $a_i = (\mu _i,\nu _i)$ and $a_i' = (\mu _i',\nu _i')$ $(i = 1,2,...,n)$ are two sets of q-ROFNs such that, $\mu _i\le \mu _i'$ and $\nu _i\ge \nu _i'$ for all i, then

$$\begin{aligned} q-ROFHMM ^P(a_1,a_2,...,a_n)\le q-ROFHMM ^P(a_1',a_2',...,a_n'). \end{aligned}$$

Proof

In order to prove this property first we modified the equation (6) as follow:

$$\begin{aligned} \begin{pmatrix} q-ROFHMM ^P(a_1,a_2, ...,a_n)= \left( 1-\begin{pmatrix}\frac{1}{1+\begin{pmatrix}\frac{\gamma }{\left( 1+\begin{pmatrix}\frac{\gamma ^2}{\left( \displaystyle \prod _{\vartheta \in S_n}\left( 1+\begin{pmatrix}\frac{\gamma ^2}{\displaystyle \prod _{j=1}^n\left( \frac{\gamma }{\mu _{\vartheta (j)}^q}-(\gamma -1)\right) ^{p_j}-1}\end{pmatrix}\right) \right) ^{\frac{1}{n!}}-1}\end{pmatrix}\right) ^{\frac{1}{\sum _{j=1}^np_j}}-1}\end{pmatrix}}\end{pmatrix}\right) ^{1/q}, \\ \begin{pmatrix}\frac{1}{1+\begin{pmatrix}\frac{\gamma }{\left( 1+\begin{pmatrix}\frac{\gamma ^2}{\left( \displaystyle \prod _{\vartheta \in S_n}\left( 1+\begin{pmatrix}\frac{\gamma ^2}{\displaystyle \prod _{j=1}^n\left( 1+\begin{pmatrix}\frac{\gamma }{\begin{pmatrix}\frac{1}{\nu _{\vartheta (j)}^q}-1\end{pmatrix}}\end{pmatrix}\right) ^{p_j}-1}\end{pmatrix}\right) \right) ^{\frac{1}{n!}}-1}\end{pmatrix}\right) ^{\frac{1}{\sum _{j=1}^np_j}}-1}\end{pmatrix}}\end{pmatrix}^{1/q} \end{pmatrix} \end{aligned}$$

Since, $\mu _i\le \mu _i'$ for all i then, $\mu _{\vartheta (j)}^q\le (\mu _{\vartheta (j)}')^q$

$$\begin{aligned}&\Rightarrow \displaystyle \prod _{j=1}^n\left( \frac{\gamma }{\mu _{\vartheta (j)}^q}-(\gamma -1)\right) ^{p_j}-1 \ge \displaystyle \prod _{j=1}^n\left( \frac{\gamma }{(\mu _{\vartheta (j)}')^q}-(\gamma -1)\right) ^{p_j}-1 \\&\Rightarrow \displaystyle \left( \displaystyle \prod _{\vartheta \in S_n}\left( 1+\begin{pmatrix}\frac{\gamma ^2}{\displaystyle \prod _{j=1}^n\left( \frac{\gamma }{\mu _{\vartheta (j)}^q}-(\gamma -1)\right) ^{p_j} -1}\end{pmatrix}\right) \right) ^{\frac{1}{n!}} -1 ~\le ~ \left( \displaystyle \prod _{\vartheta \in S_n}\left( 1+\begin{pmatrix}\frac{\gamma ^2}{\displaystyle \prod _{j=1}^n\left( \frac{\gamma }{(\mu _{\vartheta (j)}')^q}-(\gamma -1)\right) ^{p_j}-1}\end{pmatrix}\right) \right) ^{\frac{1}{n!}}-1\\&\Rightarrow \left( 1+\begin{pmatrix}\frac{\gamma ^2}{\left( \displaystyle \prod _{\vartheta \in S_n}\left( 1+\begin{pmatrix}\frac{\gamma ^2}{\displaystyle \prod _{j=1}^n\left( \frac{\gamma }{\mu _{\vartheta (j)}^q}-(\gamma -1)\right) ^{p_j}-1}\end{pmatrix}\right) \right) ^{\frac{1}{n!}}-1}\end{pmatrix} \right) ^{\frac{1}{\sum _{j=1}^np_j}}\\&\quad -1 \ge \left( 1+\begin{pmatrix}\frac{\gamma ^2}{\left( \displaystyle \prod _{\vartheta \in S_n}\left( 1+\begin{pmatrix}\frac{\gamma ^2}{\displaystyle \prod _{j=1}^n\left( \frac{\gamma }{(\mu _{\vartheta (j)}')^q}-(\gamma -1)\right) ^{p_j}-1}\end{pmatrix}\right) \right) ^{\frac{1}{n!}}-1}\end{pmatrix} \right) ^{\frac{1}{\sum _{j=1}^np_j}}-1 \\&\Rightarrow \frac{\gamma }{\left( 1+\begin{pmatrix}\frac{\gamma ^2}{\left( \displaystyle \prod _{\vartheta \in S_n}\left( 1+\begin{pmatrix}\frac{\gamma ^2}{\displaystyle \prod _{j=1}^n\left( \frac{\gamma }{\mu _{\vartheta (j)}^q}-(\gamma -1)\right) ^{p_j}-1}\end{pmatrix}\right) \right) ^{\frac{1}{n!}}-1}\end{pmatrix} \right) ^{\frac{1}{\sum _{j=1}^np_j}}-1}\\&\quad \le \frac{\gamma }{\left( 1+\begin{pmatrix}\frac{\gamma ^2}{\left( \displaystyle \prod _{\vartheta \in S_n}\left( 1+\begin{pmatrix}\frac{\gamma ^2}{\displaystyle \prod _{j=1}^n\left( \frac{\gamma }{(\mu _{\vartheta (j)}')^q}-(\gamma -1)\right) ^{p_j}-1}\end{pmatrix}\right) \right) ^{\frac{1}{n!}}-1}\end{pmatrix} \right) ^{\frac{1}{\sum _{j=1}^np_j}}-1} \end{aligned}$$

$$\begin{aligned}&\Rightarrow \frac{1}{1+\begin{pmatrix}\frac{\gamma }{\left( 1+\begin{pmatrix}\frac{\gamma ^2}{\left( \displaystyle \prod _{\vartheta \in S_n}\left( 1+\begin{pmatrix}\frac{\gamma ^2}{\displaystyle \prod _{j=1}^n\left( \frac{\gamma }{\mu _{\vartheta (j)}^q}-(\gamma -1)\right) ^{p_j}-1}\end{pmatrix}\right) \right) ^{\frac{1}{n!}}-1}\end{pmatrix} \right) ^{\frac{1}{\sum _{j=1}^np_j}}-1}\end{pmatrix}}\\&\quad \ge \frac{1}{1+\begin{pmatrix}\frac{\gamma }{\left( 1+\begin{pmatrix}\frac{\gamma ^2}{\left( \displaystyle \prod _{\vartheta \in S_n}\left( 1+\begin{pmatrix}\frac{\gamma ^2}{\displaystyle \prod _{j=1}^n\left( \frac{\gamma }{(\mu _{\vartheta (j)}')^q}-(\gamma -1)\right) ^{p_j}-1}\end{pmatrix}\right) \right) ^{\frac{1}{n!}}-1}\end{pmatrix} \right) ^{\frac{1}{\sum _{j=1}^np_j}}-1}\end{pmatrix}} \\&\Rightarrow \left( 1-\begin{pmatrix}\frac{1}{1+\begin{pmatrix}\frac{\gamma }{\left( 1+\begin{pmatrix}\frac{\gamma ^2}{\left( \displaystyle \prod _{\vartheta \in S_n}\left( 1+\begin{pmatrix}\frac{\gamma ^2}{\displaystyle \prod _{j=1}^n\left( \frac{\gamma }{\mu _{\vartheta (j)}^q}-(\gamma -1)\right) ^{p_j}-1}\end{pmatrix}\right) \right) ^{\frac{1}{n!}}-1}\end{pmatrix} \right) ^{\frac{1}{\sum _{j=1}^np_j}}-1}\end{pmatrix}}\end{pmatrix}\right) ^{1/q}\\&\quad \le \left( 1-\begin{pmatrix}\frac{1}{1+\begin{pmatrix}\frac{\gamma }{\left( 1+\begin{pmatrix}\frac{\gamma ^2}{\left( \displaystyle \prod _{\vartheta \in S_n}\left( 1+\begin{pmatrix}\frac{\gamma ^2}{\displaystyle \prod _{j=1}^n\left( \frac{\gamma }{(\mu _{\vartheta (j)}')^q}-(\gamma -1)\right) ^{p_j}-1}\end{pmatrix}\right) \right) ^{\frac{1}{n!}}-1}\end{pmatrix} \right) ^{\frac{1}{\sum _{j=1}^np_j}}-1}\end{pmatrix}}\end{pmatrix}\right) ^{1/q} \end{aligned}$$

that is, $\mu ^* \le (\mu ')^*$. Similarly, we also get $\nu ^*\ge (\nu ')^*$. Hence,

$$\begin{aligned} \left( \mu ^*,\nu ^*\right) \le \left( (\mu ')^*,(\nu ')^*\right) \end{aligned}$$

that is,

$$\begin{aligned}&q-ROFHMM ^P(a_1,a_2,...,a_n)\\&\le q-ROFHMM ^P(a_1',a_2',...,a_n'). \end{aligned}$$

Property 3

(Boundedness) Let $\{a_1,a_2,...,a_n\}$ be a set of q-ROFNs. If

$a^-{=}\left( \displaystyle \min _{i=1}^n(\mu _i),\displaystyle \max _{i=1}^n(\nu _i)\right)$and $a^+{=}\left( \displaystyle \max _{i=1}^n(\mu _i),\displaystyle \min _{i=1}^n(\nu _i)\right)$, then

$$\begin{aligned} a^-\le q-ROFHMM ^P(a_1,a_2, ...,a_n)\le a^+. \end{aligned}$$

Proof

On the basis of Property 1 and 2, we have

$a^- = q-ROFHMM ^P(a^-,a^-, ...,a^-) \le q-ROFHMM ^P(a_1,a_2,...,a_n)$ and

$q-ROFHMM ^P(a_1,a_2,...,a_n) \le q-ROFHMM ^P(a^+,a^+, ...,a^+)=a^+$

$$\begin{aligned} \Rightarrow ~~~ a^-\le q-ROFHMM ^P(a_1,a_2, ...,a_n)\le a^+. \end{aligned}$$

Property 4

(Commutativity) If $a_i'$ is an any permutation of $a_i$ $(i=1,2, ...,n)$, then

$$\begin{aligned}&q-ROFHMM ^P(a_1,a_2, ...,a_n)\\&\quad = q-ROFHMM ^P(a_1',a_2', ...,a_n'). \end{aligned}$$

Proof

Since we have $a_i'$ is any permutation of $a_i(i=1,2, ...,n)$ then by definition (6), we have

$$\begin{aligned} q-ROFHMM ^P (a_1, a_2, ..., a_n)= & {} \left( \frac{1}{n!}\bigoplus _{\vartheta (j)\in S_n}\bigotimes _{j=1}^n a_{\vartheta (j)}^{p_j}\right) ^{\frac{1}{\sum _{j=1}^np_j}}\\= & {} \left( \frac{1}{n!}\bigoplus _{\vartheta (j)\in S_n}\bigotimes _{j=1}^na_{\vartheta (j)}'^{p_j}\right) ^{\frac{1}{\sum _{j=1}^np_j}}\\= & {} q-ROFHMM ^P(a_1',a_2', ...,a_n'). \end{aligned}$$

Now, to show the generality of purposed operator, some special cases of q-ROFHMM operator with respect to the parameter $\gamma$ and parameter vector P are discussed as follows:

• 1. If $\gamma =1$, then q-ROFHMM operator is converted into the q-rung orthopair fuzzy Muirhead mean (q-ROFMM) operator:

  $$\begin{aligned}&q-ROFMM ^P(a_1,a_2,...,a_n) =\\&\left( \left( \left( 1-\left( \displaystyle \prod _{\vartheta \in S_n}\left( 1-\displaystyle \prod _{j=1}^n(\mu _{\vartheta (j)}^q)^{p_j}\right) \right) ^\frac{1}{n!}\right) ^\frac{1}{\sum _{j=1}^np_j}\right) ^{1/q},\right. \\&\left. \left( 1-\left( 1-\left( \displaystyle \prod _{\vartheta \in S_n}\left( 1-\displaystyle \prod _{j=1}^n(1-\nu _{\vartheta (j)}^q)^{p_j}\right) \right) ^\frac{1}{n!}\right) ^\frac{1}{\sum _{j=1}^np_j}\right) ^{1/q}\right) . \end{aligned}$$

  This form of the operator can be applied for those MADM problems in which the interrelationship among any number of attributes with all its possible permutations needs to consider, also the flexibility in decision space is essentially required.

• 2. If $\gamma =2$, then q-ROFHMM operator is converted into the q-rung orthopair fuzzy Einstein Muirhead mean (q-ROFEMM) operator:

  $$\begin{aligned}&q-ROFEMM ^P(a_1,a_2,...,a_n) \\&\quad =\begin{pmatrix}\left( \frac{2\left( \left( \displaystyle \prod _{\vartheta \in S_n}(\alpha _1+3\beta _1)\right) ^\frac{1}{n!}-\left( \displaystyle \prod _{\vartheta \in S_n}(\alpha _1-\beta _1)\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}}{\left( \left( \displaystyle \prod _{\vartheta \in S_n}(\alpha _1+3\beta _1)\right) ^\frac{1}{n!}+3\left( \displaystyle \prod _{\vartheta \in S_n}(\alpha _1-\beta _1)\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}+\left( \left( \displaystyle \prod _{\vartheta \in S_n}(\alpha _1+3\beta _1)\right) ^\frac{1}{n!}-\left( \displaystyle \prod _{\vartheta \in S_n}(\alpha _1-\beta _1)\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}}\right) ^{1/q}, \\ \left( \frac{\left( \left( \displaystyle \prod _{\vartheta \in S_n}(\gamma _1+3\delta _1)\right) ^\frac{1}{n!}+3\left( \displaystyle \prod _{\vartheta \in S_n}(\gamma _1-\delta _1)\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}-\left( \left( \displaystyle \prod _{\vartheta \in S_n}(\gamma _1+3\delta _1)\right) ^\frac{1}{n!}-\left( \displaystyle \prod _{\vartheta \in S_n}(\gamma _1-\delta _1)\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}}{\left( \left( \displaystyle \prod _{\vartheta \in S_n}(\gamma _1+3\delta _1)\right) ^\frac{1}{n!}+3\left( \displaystyle \prod _{\vartheta \in S_n}(\gamma _1-\delta _1)\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}+\left( \left( \displaystyle \prod _{\vartheta \in S_n}(\gamma _1+3\delta _1)\right) ^\frac{1}{n!}-\left( \displaystyle \prod _{\vartheta \in S_n}(\gamma _1-\delta _1)\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}}\right) ^{1/q} \end{pmatrix} \end{aligned}$$

  where

  $$\begin{aligned} \alpha _1= & {} \prod _{j=1}^n(2-\mu _{\vartheta (j)}^q)^{p_j},\quad \beta _1 = \prod _{j=1}^n(\mu _{\vartheta (j)}^q)^{p_j},\\ \gamma _1= & {} \prod _{j=1}^n(1+\nu _{\vartheta (j)}^q)^{p_j},\quad \delta _1 = \prod _{j=1}^n(1-\nu _{\vartheta (j)}^q)^{p_j}. \end{aligned}$$

  This operator is a good alternative for getting smooth approximations (due to the Einstein operations). The operator also considers multiple attributes’ interrelationships for all possible permutations.

• 3. If $P=(p,p,...,p)$, i.e., all $p_i$ are equal to p, then q-ROFHMM operator is converted into the q-rung orthopair fuzzy Hamacher geometric averaging (q-ROFHG) operator :

  $$\begin{aligned}&q-ROFHMM ^{(p,p,...,p)}(a_1,a_2,...,a_n) = \left( \displaystyle \bigotimes _{i=1}^na_i\right) ^\frac{1}{n}\\&=\left( \frac{\gamma ^{1/q}\displaystyle \prod _{i=1}^n(\mu _i)^{\frac{1}{n}}}{\left( \displaystyle \prod _{i=1}^n(1+(\gamma -1)(1-\mu _i^q))^{\frac{1}{n}}+(\gamma -1)\displaystyle \prod _{i=1}^n(\mu _i^q)^{\frac{1}{n}}\right) ^{1/q}},\right. \\&\left. \left( \frac{\displaystyle \prod _{i=1}^n\left( 1+(\gamma -1)\nu _i^q\right) ^{\frac{1}{n}}-\displaystyle \prod _{i=1}^n(1-\nu _i^q)^{\frac{1}{n}}}{\displaystyle \prod _{i=1}^n\left( 1+(\gamma -1)\nu _i^q\right) ^{\frac{1}{n}}+(\gamma -1)\displaystyle \prod _{i=1}^n(1-\nu _i^q)^{\frac{1}{n}}}\right) ^{1/q}\right) . \end{aligned}$$

  This operator can be utilized for those MADM problems in which no attributes are not correlated with each other, and flexibility in decision space and aggregation process are required. Note: By taking $\gamma =2$, the q-ROFHG operator will reduce to q-rung orthopair fuzzy Einstein geometric averaging (q-ROFEG) operator.

• 4. If $P=(1, 0,0, ..., 0)$, then q-ROFHMM operator is converted into the q-rung orthopair fuzzy Hamacher arithmetic averaging (q-ROFHA) operator:

  $$\begin{aligned}&q-ROF HMM ^{(1,0,0,...,0)}(a_1,a_2,...,a_n)=\frac{1}{n}\displaystyle \bigoplus _{i=1}^na_i\\&=\left( \left( \frac{\displaystyle \prod _{i=1}^n\left( 1+(\gamma -1)\mu _i^q\right) ^{\frac{1}{n}}-\displaystyle \prod _{i=1}^n(1-\mu _i^q)^{\frac{1}{n}}}{\displaystyle \prod _{i=1}^n\left( 1+(\gamma -1)\mu _i^q\right) ^{\frac{1}{n}}+(\gamma -1)\displaystyle \prod _{i=1}^n(1-\mu _i^q)^{\frac{1}{n}}}\right) ^{1/q},\right. \\&\left. \frac{\gamma ^{1/q}\displaystyle \prod _{i=1}^n(\nu _i)^{\frac{1}{n}}}{\left( \displaystyle \prod _{i=1}^n(1+(\gamma -1)(1-\nu _i^q))^{\frac{1}{n}}+(\gamma -1)\displaystyle \prod _{i=1}^n(\nu _i^q)^{\frac{1}{n}}\right) ^{1/q}}\right) . \end{aligned}$$

  This form of the operator can be used in situations where the attributes are not interrelated with each other, whereas flexibility in both the decision space and aggregation process is needed. Note: By taking $\gamma =2$, the q-ROFHA operator will reduce to the q-rung orthopair fuzzy Einstein arithmetic averaging (q-ROFEA) operator.

• 5. If $P=(p_1, p_2, 0, 0, ..., 0)$, then q-ROFHMM operator is converted into the q-rung orthopair fuzzy Hamacher Bonferroni mean (q-ROFHBM) operator :

  $$\begin{aligned}&q-ROFH MM ^{(p_1,p_2,0,0,...,0)}(a_1,a_2,...,a_n)=\left( \frac{1}{n(n-1)}\displaystyle \bigoplus _{\begin{array}{c} i,j=1\\ i\ne j \end{array}}^n a_i^{p_1}\otimes a_j^{p_2}\right) ^{\frac{1}{p_1+p_2}}\\&=\begin{pmatrix}\left( \frac{\gamma \left( \displaystyle \prod _{\begin{array}{c} i,j=1\\ i\ne j \end{array}}^n\left( \rho _i\rho _j+(\gamma ^2-1)\sigma _i\sigma _j\right) ^\frac{1}{n(n-1)}-\displaystyle \prod _{\begin{array}{c} i,j=1\\ i\ne j \end{array}}^n\left( \rho _i\rho _j-\sigma _i\sigma _j\right) ^\frac{1}{n(n-1)}\right) ^\frac{1}{2}}{\left( \displaystyle \prod _{\begin{array}{c} i,j=1\\ i\ne j \end{array}}^n\left( \rho _i\rho _j+(\gamma ^2-1)\sigma _i\sigma _j\right) ^\frac{1}{n(n-1)}+(\gamma ^2-1)\displaystyle \prod _{\begin{array}{c} i,j=1\\ i\ne j \end{array}}^n\left( \rho _i\rho _j-\sigma _i\sigma _j\right) ^\frac{1}{n(n-1)}\right) ^\frac{1}{2}+(\gamma -1)\left( \displaystyle \prod _{\begin{array}{c} i,j=1\\ i\ne j \end{array}}^n\left( \rho _i\rho _j+(\gamma ^2-1)\sigma _i\sigma _j\right) ^\frac{1}{n(n-1)}-\displaystyle \prod _{\begin{array}{c} i,j=1\\ i\ne j \end{array}}^n\left( \rho _i\rho _j-\sigma _i\sigma _j\right) ^\frac{1}{n(n-1)}\right) ^\frac{1}{2}}\right) ^{1/q}, \\ \left( \frac{\left( \displaystyle \prod _{\begin{array}{c} i,j=1\\ i\ne j \end{array}}^n\left( \tau _i\tau _j+(\gamma ^2-1)\omega _i\omega _j\right) ^\frac{1}{n(n-1)}+(\gamma ^2-1)\displaystyle \prod _{\begin{array}{c} i,j=1\\ i\ne j \end{array}}^n\left( \tau _i\tau _j-\omega _i\omega _j\right) ^\frac{1}{n(n-1)}\right) ^\frac{1}{2}-\left( \displaystyle \prod _{\begin{array}{c} i,j=1\\ i\ne j \end{array}}^n\left( \tau _i\tau _j+(\gamma ^2-1)\omega _i\omega _j\right) ^\frac{1}{n(n-1)}-\displaystyle \prod _{\begin{array}{c} i,j=1\\ i\ne j \end{array}}^n\left( \tau _i\tau _j-\omega _i\omega _j\right) ^\frac{1}{n(n-1)}\right) ^\frac{1}{2}}{\left( \displaystyle \prod _{\begin{array}{c} i,j=1\\ i\ne j \end{array}}^n\left( \tau _i\tau _j+(\gamma ^2-1)\omega _i\omega _j\right) ^\frac{1}{n(n-1)}+(\gamma ^2-1)\displaystyle \prod _{\begin{array}{c} i,j=1\\ i\ne j \end{array}}^n\left( \tau _i\tau _j-\omega _i\omega _j\right) ^\frac{1}{n(n-1)}\right) ^\frac{1}{2}+(\gamma -1)\left( \displaystyle \prod _{\begin{array}{c} i,j=1\\ i\ne j \end{array}}^n\left( \tau _i\tau _j+(\gamma ^2-1)\omega _i\omega _j\right) ^\frac{1}{n(n-1)}-\displaystyle \prod _{\begin{array}{c} i,j=1\\ i\ne j \end{array}}^n\left( \tau _i\tau _j-\omega _i\omega _j\right) ^\frac{1}{n(n-1)}\right) ^\frac{1}{2}}\right) ^{1/q} \end{pmatrix} \end{aligned}$$

  where

  $$\begin{aligned} \rho _i= & {} \left( 1+(\gamma -1)(1-\mu _i^q)\right) ^{p_1},\\ \sigma _i= & {} \left( \mu _i^q\right) ^{p_1},\\ \tau _i= & {} \left( 1+(\gamma -1)\nu _i^q\right) ^{p_1},\\ \omega _i= & {} \left( 1-\nu _i^q\right) ^{p_1},\\ \rho _j= & {} \left( 1+(\gamma -1)(1-\mu _j^q)\right) ^{p_2},\\ \sigma _j= & {} \left( \mu _j^q\right) ^{p_2},\\ \tau _j= & {} \left( 1+(\gamma -1)\nu _j^q\right) ^{p_2},\\ \omega _j= & {} \left( 1-\nu _j^q\right) ^{p_2}. \end{aligned}$$

  This operator reflects the correlation between any two attributes of a MADM problem and provides a flexible decision making and aggregation process. Note: By taking $\gamma =2$, the q-ROFHBM operator will reduce to the q-rung orthopair fuzzy Einstein Bonferroni mean (q-ROFEG) operator.

• 6. If $P=(\overbrace{1, 1, ..., 1}^k,\overbrace{0, 0, ..., 0}^{n-k})$, then q-ROFHMM operator is converted into the q-rung orthopair fuzzy Hamacher Maclaurin symmetric mean (q-ROFHMSM) operator:

  $$\begin{aligned}&q-ROFHMM ^{(\overbrace{1, 1, ..., 1}^k,\overbrace{0, 0, ..., 0}^{n-k})}(a_1,a_2,...,a_n) = \left( \frac{\bigoplus _{1\le i_1< ...< i_k\le n}\bigotimes _{j=1}^k a_{i_j}}{C_n^k}\right) ^{\frac{1}{k}} \\&=\begin{pmatrix}\left( \frac{\gamma \left( \displaystyle \prod _{1\le i_1< ...< i_k\le n}\left( \rho +(\gamma ^2-1)\sigma \right) ^\frac{1}{C_n^k}-\displaystyle \prod _{1\le i_1< ...< i_k\le n}^n\left( \rho -\sigma \right) ^\frac{1}{C_n^k}\right) ^\frac{1}{k}}{\left( \displaystyle \prod _{1\le i_1< ...< i_k\le n}\left( \rho +(\gamma ^2-1)\sigma \right) ^\frac{1}{C_n^k}+(\gamma ^2-1)\displaystyle \prod _{1\le i_1< ...< i_k\le n}\left( \rho -\sigma \right) ^\frac{1}{C_n^k}\right) ^\frac{1}{k}+(\gamma -1)\left( \displaystyle \prod _{1\le i_1< ...< i_k\le n}\left( \rho +(\gamma ^2-1)\sigma \right) ^\frac{1}{C_n^k}-\displaystyle \prod _{1\le i_1< ...< i_k\le n}\left( \rho -\sigma \right) ^\frac{1}{C_n^k}\right) ^\frac{1}{k}}\right) ^{1/q}, \\ \left( \frac{\left( \displaystyle \prod _{1\le i_1< ...< i_k\le n}\left( \tau +(\gamma ^2-1)\omega \right) ^\frac{1}{C_n^k}+(\gamma ^2-1)\displaystyle \prod _{1\le i_1< ...< i_k\le n}\left( \tau -\omega \right) ^\frac{1}{C_n^k}\right) ^\frac{1}{k}-\left( \displaystyle \prod _{1\le i_1< ...< i_k\le n}\left( \tau +(\gamma ^2-1)\omega \right) ^\frac{1}{C_n^k}-\displaystyle \prod _{1\le i_1< ...< i_k\le n}\left( \tau -\omega \right) ^\frac{1}{C_n^k}\right) ^\frac{1}{k}}{\left( \displaystyle \prod _{1\le i_1< ...< i_k\le n}\left( \tau +(\gamma ^2-1)\omega \right) ^\frac{1}{C_n^k}+(\gamma ^2-1)\displaystyle \prod _{1\le i_1< ...< i_k\le n}\left( \tau -\omega \right) ^\frac{1}{C_n^k}\right) ^\frac{1}{k}+(\gamma -1)\left( \displaystyle \prod _{1\le i_1< ...< i_k\le n}\left( \tau +(\gamma ^2-1)\omega \right) ^\frac{1}{C_n^k}-\displaystyle \prod _{1\le i_1< ... < i_k\le n}\left( \tau -\omega \right) ^\frac{1}{C_n^k}\right) ^\frac{1}{k}}\right) ^{1/q} \end{pmatrix} \end{aligned}$$

  where

  $$\begin{aligned} \rho= & {} \prod _{j=1}^k\big (1+(\gamma -1)(1-\mu _{i_j}^q)\big ),\quad \sigma = \prod _{j=1}^k\mu _{i_j}^q,\\ \tau= & {} \prod _{j=1}^k\big (1+(\gamma -1)\nu _{i_j}^q\big ),\quad \omega =\prod _{j=1}^k\big (1-\nu _{i_j}^q\big ). \end{aligned}$$

  This operator can be applied for those MADM problems in which the interrelationship among multiple attributes for all combinations is possible and when the flexibility in the decision making is essentially required. Note: By taking $\gamma =2$, q-ROFHMSM operator will reduce to the q-rung orthopair fuzzy Einstein Maclaurin symmetric mean (q-ROFEMSM) operator.

3.2 q-ROFHWMM operator

Since the purposed q-ROFHMM operator does not count the importance of attributes for aggregating the information, therefore this subsection introduces the q-ROFHWMM operator which considers the corresponding importance of attributes in terms of weights to aggregate the q-ROFNs.

Definition 7

Suppose $\{a_1,a_2,...,a_n\}$ be a collection of q-ROFNs, $P=(p_1, p_2, ..., p_n) \in \Re ^n$ is a n-dimensional parameter vector s.t. $\sum _{j=1}^np_j>0$ and $w_i\in [0,1]$ be the weight vector of $a_i$ $(i=1,2, ...,n)$ s.t. $\sum _{i=1}^nw_i=1$, then the q-rung orthopair fuzzy Hamacher weighted Muirhead mean (q-ROFHWMM) operator is defined as

$$\begin{aligned}&q-ROFHWMM ^P (a_1, a_2, ..., a_n)\nonumber \\&= \left( \frac{1}{n!}\bigoplus _{\vartheta (j)\in S_n}\bigotimes _{j=1}^n (nw_{\vartheta (j)}a_{\vartheta (j)})^{p_j}\right) ^{\frac{1}{\sum _{j=1}^n p_j}} \end{aligned}$$

(8)

where $\vartheta (j) (j = 1, 2, ..., n)$ is an any permutation of (1, 2, ..., n), and $S_n$ be the set of all permutations of (1, 2, ..., n).

Theorem 2

Let $\{a_1,a_2,...,a_n\}$ be a set of q-ROFNs, then the aggregated result by applying q-ROFHWMM operator is also a q-ROFN and is equal to

$$\begin{aligned}&q-ROFHWMM ^P (a_1, a_2, ..., a_n) \nonumber \\&\qquad =\begin{pmatrix}\left( \frac{\gamma \left( \left( \displaystyle \prod _{\vartheta \in S_n}(\phi _1'+(\gamma ^2-1)\varphi _1')\right) ^\frac{1}{n!}-\left( \displaystyle \prod _{\vartheta \in S_n}(\phi _1'-\varphi _1')\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}}{\left( \left( \displaystyle \prod _{\vartheta \in S_n}(\phi _1'+(\gamma ^2-1)\varphi _1')\right) ^\frac{1}{n!}+(\gamma ^2-1)\left( \displaystyle \prod _{\vartheta \in S_n}(\phi _1'-\varphi _1')\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}+(\gamma -1)\left( \left( \displaystyle \prod _{\vartheta \in S_n}(\phi _1'+(\gamma ^2-1)\varphi _1')\right) ^\frac{1}{n!}-\left( \displaystyle \prod _{\vartheta \in S_n}(\phi _1'-\varphi _1')\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}}\right) ^{1/q}, \\ \left( \frac{\left( \left( \displaystyle \prod _{\vartheta \in S_n}(\psi _1'+(\gamma ^2-1)\chi _1')\right) ^\frac{1}{n!}+(\gamma ^2-1)\left( \displaystyle \prod _{\vartheta \in S_n}(\psi _1'-\chi _1')\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}-\left( \left( \displaystyle \prod _{\vartheta \in S_n}(\psi _1'+(\gamma ^2-1)\chi _1')\right) ^\frac{1}{n!}-\left( \displaystyle \prod _{\vartheta \in S_n}(\psi _1'-\chi _1')\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}}{\left( \left( \displaystyle \prod _{\vartheta \in S_n}(\psi _1'+(\gamma ^2-1)\chi _1')\right) ^\frac{1}{n!}+(\gamma ^2-1)\left( \displaystyle \prod _{\vartheta \in S_n}(\psi _1'-\chi _1')\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}+(\gamma -1)\left( \left( \displaystyle \prod _{\vartheta \in S_n}(\psi _1'+(\gamma ^2-1)\chi _1')\right) ^\frac{1}{n!}-\left( \displaystyle \prod _{\vartheta \in S_n}(\psi _1'-\chi _1')\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}}\right) ^{1/q}\end{pmatrix} \end{aligned}$$

(9)

where

$$\begin{aligned} \phi _1'= & {} \prod _{j=1}^n\Big (\left( 1+(\gamma -1)\mu _{\vartheta (j)}^q\right) ^{nw_{\vartheta (j)}}+(\gamma ^2-1)\left( 1-\mu _{\vartheta (j)}^q\right) ^{nw_{\vartheta (j)}}\Big )^{p_j},\\ \varphi _1'= & {} \prod _{j=1}^n\Big (\Big (1+(\gamma -1)\mu _{\vartheta (j)}^q\Big )^{nw_{\vartheta (j)}}-\Big (1-\mu _{\vartheta (j)}^q\Big )^{nw_{\vartheta (j)}}\Big )^{p_j},\\ \psi _1'= & {} \prod _{j=1}^n\Big (\left( 1+(\gamma -1)(1-\nu _{\vartheta (j)}^q)\right) ^{nw_{\vartheta (j)}}+(\gamma ^2-1)\left( \nu _{\vartheta (j)}^q\right) ^{nw_{\vartheta (j)}}\Big )^{p_j},\\ \chi _1'= & {} \prod _{j=1}^n\Big (\left( 1+(\gamma -1)(1-\nu _{\vartheta (j)}^q)\right) ^{nw_{\vartheta (j)}}-\left( \nu _{v(j)}^q\right) ^{nw_{\vartheta (j)}}\Big )^{p_j}. \end{aligned}$$

Proof

Based on the Hamacher operations discussed in section 2.3, we have

$$\begin{aligned}&nw_{\vartheta (j)}a_{\vartheta (j)}\\&=\left( \left( \frac{\left( 1+(\gamma -1)\mu _{\vartheta (j)}^q\right) ^{nw_{\vartheta (j)}}-\left( 1-\mu _{\vartheta (j)}^q\right) ^{nw_{\vartheta (j)}}}{\left( 1+(\gamma -1)\mu _{\vartheta (j)}^q\right) ^{nw_{\vartheta (j)}}+(\gamma -1)\left( 1-\mu _{\vartheta (j)}^q\right) ^{nw_{\vartheta (j)}}}\right) ^{1/q},\right. \\&\quad \left. \frac{\gamma ^{1/q}\nu _{\vartheta (j)}^{nw_{\vartheta (j)}}}{\left( \left( 1+(\gamma -1)(1-\nu _{\vartheta (j)}^q)\right) ^{nw_{\vartheta (j)}}+(\gamma -1)\left( \nu _{\vartheta (j)}^q\right) ^{nw_{\vartheta (j)}}\right) ^{1/q}}\right) \end{aligned}$$

Therefore, according to the proof of Theorem 1, the required results can be proved easily.

Monotonicity and Boundedness are the essential properties of an aggregation operator. For the q-ROFHWMM operator, monotonicity and boundedness are discussed below. Since it is easy to prove them therefore, their proofs are omitted here.

Property 5

(Monotonicity) If $a_i = (\mu _i,\nu _i)$ and $a_i' = (\mu _i',\nu _i')$ $(i = 1,2,...,n)$ are two sets of q-ROFNs such that, $\mu _i\le \mu _i'$ and $\nu _i\ge \nu _i'$ for all i, then

$$\begin{aligned}&q-ROFHWMM ^P(a_1,a_2, ...,a_n)\\&\le q-ROFHWMM^P(a_1',a_2', ...,a_n'). \end{aligned}$$

Property 6

(Boundedness) Let $\{a_1,a_2,...,a_n\}$ be a set of q-ROFNs. If

$$\begin{aligned}&a^-=\left( \displaystyle \min _{i=1}^n(\mu _i),\displaystyle \max _{i=1}^n(\nu _i)\right) ~~and \\&a^+=\left( \displaystyle \max _{i=1}^n(\mu _i),\displaystyle \min _{i=1}^n(\nu _i)\right) \end{aligned}$$

then,

$$\begin{aligned}&a^-\le q-ROFHWMM ^P(a_1,a_2, ...,a_n)\\&\le q-ROFHWMM ^P(a_1',a_2', ...,a_n')\le a^+. \end{aligned}$$

Corollary The q-ROFHMM operator is a special case of the q-ROFHWMM operator.

Proof

Let $w = (1/n, 1/n, ..., 1/n)^T$, then

$$\begin{aligned}&\phi _1'=\prod _{j=1}^n\left( \left( 1+(\gamma -1)\mu _{\vartheta (j)}^q\right) ^{nw_{\vartheta (j)}}\right. \\&\left. +(\gamma ^2-1)\left( 1-\mu _{\vartheta (j)}^q\right) ^{nw_{\vartheta (j)}} \right) ^{p_j}\\&\quad =\prod _{j=1}^n\gamma ^{p_j}\left( 1+(\gamma -1)(1-\mu _{\vartheta (j)}^q)\right) ^{p_j}=\phi ',\\&\varphi _1'=\prod _{j=1}^n\left( \left( 1+(\gamma -1)\mu _{\vartheta (j)}^q\right) ^{nw_{\vartheta (j)}} -\left( 1-\mu _{\vartheta (j)}^q\right) ^{nw_{\vartheta (j)}}\right) ^{p_j}\\&\quad =\prod _{j=1}^n\gamma ^{p_j}(\mu _{\vartheta (j)}^q)^{p_j}= \varphi ',\\&\psi _1'=\prod _{j=1}^n\left( \left( 1+(\gamma -1)(1-\nu _{\vartheta (j)}^q)\right) ^{nw_{\vartheta (j)}}\right. \\&\quad \left. +(\gamma ^2-1)\left( \nu _{\vartheta (j)}^q\right) ^{nw_{\vartheta (j)}} \right) ^{p_j}\\&\quad =\prod _{j=1}^n\gamma ^{p_j}\left( 1+(\gamma -1)\nu _{\vartheta (j)}^q\right) ^{p_j} =\psi ',\\&\chi _1'=\prod _{j=1}^n\left( \left( 1+(\gamma -1)(1-\nu _{\vartheta (j)}^q)\right) ^{nw_{\vartheta (j)}}-\left( \nu _{v(j)}^q\right) ^{nw_{\vartheta (j)}}\right) ^{p_j}\\&\quad = \prod _{j=1}^n\gamma ^{p_j}(1-\nu _{\vartheta (j)}^q)^{p_j}=\chi '. \end{aligned}$$

and

$$\begin{aligned}&q-ROFHWMM ^P(a_1, a_2, ..., a_n) =\\&\begin{pmatrix}\left( \frac{\gamma \left( \left( \displaystyle \prod _{\vartheta \in S_n}(\phi '+(\gamma ^2-1)\varphi ')\right) ^\frac{1}{n!}-\left( \displaystyle \prod _{\vartheta \in S_n}(\phi '-\varphi ')\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}}{\left( \left( \displaystyle \prod _{\vartheta \in S_n}(\phi '+(\gamma ^2-1)\varphi ')\right) ^\frac{1}{n!}+(\gamma ^2-1)\left( \displaystyle \prod _{\vartheta \in S_n}(\phi '-\varphi ')\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}+(\gamma -1)\left( \left( \displaystyle \prod _{\vartheta \in S_n}(\phi '+(\gamma ^2-1)\varphi ')\right) ^\frac{1}{n!}-\left( \displaystyle \prod _{\vartheta \in S_n}(\phi '-\varphi ')\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}}\right) ^{1/q}, \\ \left( \frac{\left( \left( \displaystyle \prod _{\vartheta \in S_n}(\psi '+(\gamma ^2-1)\chi ')\right) ^\frac{1}{n!}+(\gamma ^2-1)\left( \displaystyle \prod _{\vartheta \in S_n}(\psi '-\chi ')\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}-\left( \left( \displaystyle \prod _{\vartheta \in S_n}(\psi '+(\gamma ^2-1)\chi ')\right) ^\frac{1}{n!}-\left( \displaystyle \prod _{\vartheta \in S_n}(\psi '-\chi ')\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}}{\left( \left( \displaystyle \prod _{\vartheta \in S_n}(\psi '+(\gamma ^2-1)\chi ')\right) ^\frac{1}{n!}+(\gamma ^2-1)\left( \displaystyle \prod _{\vartheta \in S_n}(\psi '-\chi ')\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}+(\gamma -1)\left( \left( \displaystyle \prod _{\vartheta \in S_n}(\psi '+(\gamma ^2-1)\chi ')\right) ^\frac{1}{n!}-\left( \displaystyle \prod _{\vartheta \in S_n}(\psi '-\chi ')\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}}\right) ^{1/q} \end{pmatrix} \end{aligned}$$

$$\begin{aligned}&=\begin{pmatrix}\left( \frac{\gamma \left( \left( \displaystyle \prod _{\vartheta \in S_n}(\phi _1+(\gamma ^2-1)\varphi _1)\right) ^\frac{1}{n!}-\left( \displaystyle \prod _{\vartheta \in S_n}(\phi _1-\varphi _1)\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}}{\left( \left( \displaystyle \prod _{\vartheta \in S_n}(\phi _1+(\gamma ^2-1)\varphi _1)\right) ^\frac{1}{n!}+(\gamma ^2-1)\left( \displaystyle \prod _{\vartheta \in S_n}(\phi _1-\varphi _1)\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}+(\gamma -1)\left( \left( \displaystyle \prod _{\vartheta \in S_n}(\phi _1+(\gamma ^2-1)\varphi _1)\right) ^\frac{1}{n!}-\left( \displaystyle \prod _{\vartheta \in S_n}(\phi _1-\varphi _1)\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}}\right) ^{1/q}, \\ \left( \frac{\left( \left( \displaystyle \prod _{\vartheta \in S_n}(\psi _1+(\gamma ^2-1)\chi _1)\right) ^\frac{1}{n!}+(\gamma ^2-1)\left( \displaystyle \prod _{\vartheta \in S_n}(\psi _1-\chi _1)\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}-\left( \left( \displaystyle \prod _{\vartheta \in S_n}(\psi _1+(\gamma ^2-1)\chi _1)\right) ^\frac{1}{n!}-\left( \displaystyle \prod _{\vartheta \in S_n}(\psi _1-\chi _1)\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}}{\left( \left( \displaystyle \prod _{\vartheta \in S_n}(\psi _1+(\gamma ^2-1)\chi _1)\right) ^\frac{1}{n!}+(\gamma ^2-1)\left( \displaystyle \prod _{\vartheta \in S_n}(\psi _1-\chi _1)\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}+(\gamma -1)\left( \left( \displaystyle \prod _{\vartheta \in S_n}(\psi _1+(\gamma ^2-1)\chi _1)\right) ^\frac{1}{n!}-\left( \displaystyle \prod _{\vartheta \in S_n}(\psi _1-\chi _1)\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}}\right) ^{1/q}\end{pmatrix}\\&\quad =q-ROFHMM ^P(a_1, a_2, ..., a_n). \end{aligned}$$

Now, special cases with respect to parameter $\gamma$ are discussed here for q-ROFHWMM operator.

• 1. If $\gamma = 1$, then q-ROFHWMM operator is converted into the q-rung orthopair fuzzy weighted Muirhead mean (q-ROFWMM) operator:

  $$\begin{aligned}&q-ROFWMM ^P(a_1, a_2, ..., a_n) \\&\quad =\left( \left( \left( 1-\left( \displaystyle \prod _{v\in S_n}\left( 1-\displaystyle \prod _{j=1}^n\left( 1-(1-\mu _{v(j)}^q)^{nw_{v(j)}}\right) ^{p_j}\right) \right) ^\frac{1}{n!}\right) ^\frac{1}{\sum _{j=1}^np_j}\right) ^{1/q},\right. \\&\qquad \left. \left( 1-\left( 1-\left( \displaystyle \prod _{v\in S_n}\left( 1-\displaystyle \prod _{j=1}^n\left( 1-(\nu _{v(j)}^q)^{nw_{v(j)}}\right) ^{p_j}\right) \right) ^\frac{1}{n!}\right) ^\frac{1}{\sum _{j=1}^np_j}\right) ^{1/q}\right) . \end{aligned}$$

• 2. If $\gamma = 2$, then q-ROFHWMM operator is converted into the q-rung orthopair fuzzy Einstein weighted Muirhead mean (q-ROFEWMM) operator:

  $$\begin{aligned}&q-ROFEWMM ^P(a_1, a_2, ..., a_n) \\&\quad = \begin{pmatrix}\left( \frac{2\left( \left( \displaystyle \prod _{v\in S_n}(\alpha _1'+3\beta _1')\right) ^\frac{1}{n!}-\left( \displaystyle \prod _{v\in S_n}(\alpha _1'-\beta _1')\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}}{\left( \left( \displaystyle \prod _{v\in S_n}(\alpha _1'+3\beta _1')\right) ^\frac{1}{n!}+3\left( \displaystyle \prod _{v\in S_n}(\alpha _1'-\beta _1')\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}+\left( \left( \displaystyle \prod _{v\in S_n}(\alpha _1'+3\beta _1')\right) ^\frac{1}{n!}-\left( \displaystyle \prod _{v\in S_n}(\alpha _1'-\beta _1')\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}}\right) ^{1/q}, \\ \left( \frac{\left( \left( \displaystyle \prod _{v\in S_n}(\gamma _1'+3\delta _1')\right) ^\frac{1}{n!}+3\left( \displaystyle \prod _{v\in S_n}(\gamma _1'-\delta _1')\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}-\left( \left( \displaystyle \prod _{v\in S_n}(\gamma _1'+3\delta _1')\right) ^\frac{1}{n!}-\left( \displaystyle \prod _{v\in S_n}(\gamma _1'-\delta _1')\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}}{\left( \left( \displaystyle \prod _{v\in S_n}(\gamma _1'+3\delta _1')\right) ^\frac{1}{n!}+3\left( \displaystyle \prod _{v\in S_n}(\gamma _1'-\delta _1')\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}+\left( \left( \displaystyle \prod _{v\in S_n}(\gamma _1'+3\delta _1')\right) ^\frac{1}{n!}-\left( \displaystyle \prod _{v\in S_n}(\gamma _1'-\delta _1')\right) ^\frac{1}{n!}\right) ^\frac{1}{\displaystyle \sum _{j=1}^np_j}}\right) ^{1/q} \end{pmatrix} \end{aligned}$$

  where

  $$\begin{aligned} \alpha _1'= & {} \prod _{j=1}^n\left( \left( 1+\mu _{v(j)}^q\right) ^{nw_{v(j)}}+3\left( 1-\mu _{v(j)}^q\right) ^{nw_{v(j)}}\right) ^{p_j},\\ \beta _1'= & {} \prod _{j=1}^n\left( \left( 1+\mu _{v(j)}^q\right) ^{nw_{v(j)}}-\left( 1-\mu _{v(j)}^q\right) ^{nw_{v(j)}}\right) ^{p_j},\\ \gamma _1'= & {} \prod _{j=1}^n\left( \left( 2-\nu _{v(j)}^q\right) ^{nw_{v(j)}}+3\left( \nu _{v(j)}^q\right) ^{nw_{v(j)}}\right) ^{p_j},\\ \delta _1'= & {} \prod _{j=1}^n\left( \left( 2-\nu _{v(j)}^q\right) ^{nw_{v(j)}}-\left( \nu _{v(j)}^q\right) ^{nw_{v(j)}}\right) ^{p_j}. \end{aligned}$$

4 Application of developed aggregation operator on MADM

4.1 MADM method based on the proposed q-ROFHWMM operator

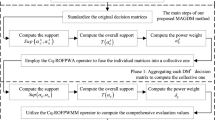
In this section, we are going to develop a MADM method for q-rung orthopair fuzzy numbers by utilizing the proposed q-ROFHWMM operator. Let $A=\{A_1,A_2,...,A_m\}$ be a discrete set of available alternatives, each alternative is being evaluated based on all n-attributes $\{G_1,G_2,...,G_n\}$ having weight vector $w=\{w_1, w_2, ...,w_n\}$ that is, every attribute is associated with some weight $w_j\in [0,1]~(j=1,2,...,n)$ and $\sum _{j=1}^nw_j=1$. Let $R =(r_{ij})_{m\times n}$ be the q-rung orthopair fuzzy numbers decision matrix, where $r_{ij}=(\mu _{ij},\nu _{ij})$ represent the evaluated information of an alternative $A_i$ corresponding to the attribute $G_j$. The detailed approach of our MADM method which is based on the proposed aggregation operator with q-rung orthopair fuzzy information is given hereafter.

Step 1. Normalize the decision matrix

The attributes involved in the decision matrix can be classified into two types namely cost type and benefit type. In order to consider both types of attributes at the same time, we need to normalize the decision matrix by using following formula.

$$\begin{aligned} r_{ij}=(\mu _{ij},\nu _{ij})= {\left\{ \begin{array}{ll} r_{ij}, &{} for~benefit~attributes ~A_j\\ {\bar{r}}_{ij}, &{} for~cost~attributes ~A_j \end{array}\right. } \end{aligned}$$

If all the attributes are of benefit type, then there is no need to normalize the decision matrix.

Step 2. Comprehensive value evaluation

Utilizing the proposed q-ROFHWMM operator, obtain a comprehensive value $r_i$ for each alternative $A_i$ by considering the all n-attributes in the decision matrix. The corresponding values of these n-attributes are $r_{ij}(j=1,2,...,n)$.

$$\begin{aligned} r_i= q-ROFHWMM(r_{i1},r_{i2},...,r_{in}) \end{aligned}$$

Step 3. Calculation of score and accuracy values

Calculate the score value $S(r_{i})$ and accuracy value $H(r_{i})$ for each comprehensive value $r_i(i=1,2, ...,m)$. The formula for $S(r_{i})$ and $H(r_{i})$ are given in Eqs. (2) and (3) respectively. If all the score values $S(r_{i})(i=1,2, ...,m)$ are different, then there is no need to calculate accuracy values $H(r_{i})(i=1,2, ...,m)$.

Table 1 q-Rung orthopair fuzzy decision matrix R

Table 2 Comprehensive values, score values, and ranking results of alternatives

Table 3 Ranking results for different values of q

Table 4 Ranking results for different values of $\gamma$

Table 5 Ranking results by assigning different values to P

Step 4. Ranking of alternatives

Now rank the alternatives on the basis of their score value $S(r_{i})(i=1,2, ...,m)$ and accuracy value $H(r_{i})(i=1,2, ...,m)$ based on the methodology discussed in definition 4, finally choose the most suitable alternative.

Fig. 1

Score function values for alternative $A_1$

Fig. 2

Score function values for alternative $A_2$

Fig. 3

Score function values for alternative $A_3$

Fig. 4

Score function values for alternative $A_4$

Fig. 5

Score function values for alternative $A_5$

4.2 An illustrative example

In this section, to investigate the applicability of the proposed aggregation operator based MADM approach, a practical MADM problem is being analyzed. The selected MADM problem is related to the implementation of an ERP system in an organization, that is adopted from Wei et al. (2018). The available information regarding vendors and systems is configured and based on experts’ suggestions, the project team chooses five potential ERP systems $A_i(i= 1,2,3,4,5)$ as alternatives and four attributes $G_j(j= 1,2,3,4)$ to evaluate these five alternatives. Here $G_1$ represents function and technology, $G_2$ means strategic fitness, $G_3$ shows vendor’s ability, and $G_4$ reflects vendor’s reputation. The importance of these four attributes are provided as a weight vector $w= (0.2, 0.1, 0.3, 0.4)$. Considering the five alternatives $A_i(i= 1,2,3,4,5)$ and four attributes $G_j(j= 1,2,3,4)$, the associated information of these alternative is presented in the form of a q-ROFNs decision matrix $R=(r_{ij})_{5\times 4}$ as shown in Table 1.

To select the most desirable ERP system, we shall utilize the developed approach as discussed in Sect. 4.1, which includes the following steps:

Step 1. Normalize the decision matrix

As all the attributes are of benefit types, so there is no need to normalize the decision matrix R. Hence, the decision matrix R as given in Table 1 is considered for the further analysis.

Step 2. Comprehensive value evaluation

By using the given decision data of matrix R and taking parameters’ values as $q=3$, $\gamma = 1$, and $P=(1,1,1,1)$, the proposed q-ROFHWMM operator is applied which provides the comprehensive value $r_i(i= 1,2,3,4,5)$ for each ERP system $A_i(i= 1,2,3,4,5)$, respectively. The aggregated results are provided in column 2 of Table 2.

Step 3. Calculation of score and accuracy values

Now, calculate the score value $S(r_{i})(i= 1,2,3,4,5)$ for each $r_i$ as discussed in step 3 of Sect. 4.1. The calculated score values are given in column 3 of Table 2. Since the score value for each alternative is distinct, therefore the corresponding accuracy values of any $r_i$ is not computed.

Step 4. Ranking of alternatives

Finally, rank the alternatives $A_i(i= 1,2,3,4,5)$ on the basis of their score values $S(r_{i})$ by utilizing the methodology as discussed in step 4 of Sect. 4.2. The ranking results are provided in column 4 of Table 2. It is clear from Table 2 that ERP system $A_2$ is the best choice among the five potential ERP systems. Selection of the best alternative depends upon the values of parameters $q,~\gamma ,~P$. Similarly different aggregation operators may provide different ranking results as per their aggregation characteristics. It is essential to investigate the efficiency of the method on the basis of sensitivity of parameters’ values selection and aggregation operator applied. So in the following Sects. 4.3 and 4.4, sensitivity and comparative analyses have been conducted.

4.3 Sensitivity analysis

To demonstrate the efficiency of the developed MADM approach based on q-ROFHWMM operator, a sensitivity analysis has been conducted in multiple phases by varying parameters’ values q, $\gamma$, and taking different values of parameter vector P. The effects of these variations on the result are analyzed and discussed hereafter.

Table 6 Quantitative comparison based on the score values and ranking results of different aggregation operators

In the first phase, parameter q is varied by taking integer values in the range 2 to 10. Herein, $q=1$ is not considered because data is not IFS. At the same time, values of the other two parameters are fixed as $\gamma =1$ and $P=(1,1,1,1)$. The computed results are summarized in Table 3. The results reveal that as the parameter q varies, the scores and ranking order of all the alternatives change accordingly. However, the best($A_2$) and worst($A_5$) alternatives are always same for all the considered variations of parameter q. This infer that the parameter q is not only provide the expanded decision space but also influence the final decision. In the second phase, the parameter $\gamma$ varies in the range [1, 10] by taking integer values, however parameters $q=3$ and $P=(1,1,1,1)$ are fixed. The computed results are given in Table 4. From Table 4, the results show that as the parameter $\gamma$ varies, the scores and ranking order of different alternatives change accordingly. In this case, the best alternative is still same as $A_2$ for all the considered variations of parameter $\gamma$ while the worst alternative changes. This infer that the parameter $\gamma$ provides flexibility in aggregation process and also affect the final decision. In third phase, the effect of interrelationship among multiple attributes are examined by taking different values of parameter vector P with fixed values of parameters $q=3$ and $\gamma =1$. The computed results are shown in Table 5 and infer that the interrelationship between multiple attributes somehow influences the final decision. Since, the proposed aggregation operators consider interrelationship between multiple attributes, hence results are more realistic. In this case, the best alternative is again $A_2$ for all the considered variations of parameter vector P while the worst alternative changes.

Fig. 6

Radar graph of score values for different MADM methods

In the above discussion, the effect on the final decision is analyzed by taking variation in the value of an individual parameter q, $\gamma$, or P, and fixing the values of rest of the other parameters at the same time. To provide the depth in the analysis, the combined effect of variation in the values of these parameters on the final decision is carried out. Herein, the parameters q and $\gamma$ can take any value in the closed intervals [2, 10], and [1, 10] respectively, while parameter vector P has been fixed as (1, 1, 1, 1), i.e., interrelationship between all the attributes has been considered. The score of each alternative has been computed for these values of parameters, and results in the form of surface plots are shown in Figs. 1–5 for all the five alternatives, respectively. From these figures, it can be observed that the Figs. 2, 3 and 4 have some flat areas while other two Figs. 1 and 5, are not showing such type of areas. This infers that the variational tendency of scores of alternatives $A_1$ and $A_5$ is rapidly changing with change in parameter values while the scores of alternatives $A_2, A_3$ and $A_4$ are not showing such tendency. Thus, based on the score values associated with these figures, we can say that the alternatives $A_2$, $A_3$, and $A_4$ are more stable than $A_1$ and A5. But, the overall score value of alternative $A_2$ is relatively high in comparison to other alternatives, due to the flat area of its score function around the score value 0.02. These graphical results also concluded that alternative $A_2$ is the best choice of an ERP system among all other possible alternatives under consideration. Hence, we can conclude that combination of q and $\gamma$ has a positive effect on decision making and provide a range of solutions to the decision maker.

Table 7 Qualitative comparison between different aggregation methods based on their Characteristic

4.4 Comparative analysis

To investigate the effectiveness of the proposed aggregation operators, this section provides a quantitative and qualitative comparison between some existing aggregation operators such as q-ROFWA, q-ROFWG, q-ROFWBM,q-ROFGWHM,q-ROFWGHM, q-ROFWMSM, and the proposed aggregation operator q-ROFHWMM under same working environment.

To apply these aggregation operators under same q-ROFS working environment, the value of parameter q is taken as 3. The classical q-ROFWA operator proposed by Liu et al. (2018) does not consider any interrelationship between attributes, while their q-ROFWG operator considers interrelationship between all the attributes at the same time. However, both these operators do not have any additional parameter. The other existing aggregation operators such as q-ROFWBM, q-ROFGWHM, q-ROFWGHM, and q-ROFWMSM have different types of interrelationships between attributes, and there are some additional parameters involved in these operators as per their basic definitions(Liu and Liu 2018; Wei et al. 2018, 2019). The q-ROFWBM operator considers interrelationship between any two attributes, and the selected values of its additional parameters are $s=1,~t=1$. For applying q-ROFGWHM and q-ROFWGHM aggregation operators, the selected values of their additional parameters are $\phi =1,~\varphi =1$, and they consider interrelationship between any two attributes(Wei et al. 2018. The q-ROFWMSM operator proposed by Wei et al. (2019) considers interrelationship between multiple attributes, and its granularity parameter is taken as $k=2$, so that it can capture interrelationship between any two attributes for creating same interactional environment. To keep the same working and interactional environment, the values of the additional parameters in the proposed q-ROFHWMM operators are taken as $\gamma =1,~~P=(1,1,0,0)$. After creating same working and interactional environment, a quantitative comparative analysis for these aggregation operators is conducted and results are summarized in Table 6. From the table, it is observed that the best alternative obtained from all the operators under investigation are almost same, except the best alternative obtained from q-ROFWG and q-ROFWGHM operators which is due to the structural difference of these operators. The score values for all the five alternatives computed by all these aggregation operators are also plotted as a radar graph shown in Fig. 6. The figure reflects that the alternatives $A_2$ (red color) is unanimously the best and acceptable alternative.

To further show the superiority of the proposed aggregating operator over other considered existing operators, a qualitative comparison has been provided in Table 7. In this comparison, the aggregation operators are compared on the basis of their characteristics, such as capability to quantify uncertainty in extended space, the power of considering interrelationships between different attributes, flexibility to consider different degrees of granularity between attributes. The findings suggested that the proposed q-ROFHWMM operator is superior to the other existing operators considered in this study.

5 Conclusions

The paper provides some novel MM aggregation operators based on Hamacher t-norm and t-conorm inspired arithmetic operations under q-rung orthopair fuzzy environment. Namely, this article introduced q-ROFHMM and q-ROFHWMM aggregation operators. The advantage of employing Hamacher t-norm and t-conorm inspired operations in these aggregation operators is that, they provide flexibility in the aggregation process due to the parameter ($\gamma$) involved. While the use of MM aggregation operator provides the flexibility in capturing the interaction between any number of attributes with every possible permutation. Some desirable properties and special cases of these novel aggregation operators have been investigated. To show the effectiveness of the proposed q-ROFHWMM aggregation operator, a MADM problem to select an efficient ERP system for an organization has been analyzed. Sensitivity and comparative analyses with some well-known existing aggregation operators have also been done to elaborate the applicability of the developed MADM approach. Results suggested that the proposed MADM approach based on q-ROFHWMM operator is more flexible and general in nature, which can be used to solve a variety of real-life MADM problems. The limitation of the method is its complexity in computation. The future research work will be conducted in the following directions to enhance the capabilities of the method and reduce its limitations:

• (a) The proposed aggregation operators can be extended further for other fuzzy environments like Hesitant fuzzy sets, Complex fuzzy sets, Neutrosophic fuzzy sets, Temporal intuitionistic fuzzy sets and Interval type-2 fuzzy sets, etc., and for continuous fuzzy information too.

• (b) The proposed aggregation operators can be investigated with heterogeneous relationship between attributes to rectify the limitations of the method.

• (c) The method may be further extended by determining a reasonable value of attitude parameter ($\gamma$) through an optimization model.