Multi-attribute decision making using q-rung orthopair fuzzy weighted fairly aggregation operators

Abstract

In this study, in view of expressing the uncertain information more elegantly, we shall enlighten the q-rung orthopair fuzzy sets (q-ROFSs) and the q-rung orthopair fuzzy numbers (q-ROFNs) which are considered to be superior of the intuitionistic fuzzy sets and the Pythagorean fuzzy sets, respectively. Here our aim is towards the development of some new operational laws and their corresponding weighted aggregation operators under the q-rung orthopair fuzzy environment. In this regard, at the very beginning, we define some new neutral or fair operational laws that include the concept of proportional distribution to achieve a neutral or fair treatment to the membership and non-membership functions of q-ROFN. Subsequently, with these operations, we develop q-rung orthopair fuzzy weighted fairly aggregation operator (qROFWFA) and q-rung orthopair fuzzy ordered weighted fairly aggregation operator (qROFOWFA) which can neutrally or fairly serve the membership and non-membership degrees. We observe the noteworthy features of these proposed aggregation operators. Furthermore, we exercise also an MADM (multi-attribute decision-making) approach with multiple decision makers and partial weight information in the framework of q-rung orthopair fuzzy sets. At the end of this study, we provide an illustrative example to highlight the feasibility and a practical look of the approach proposed herein.

1 Introduction

In our daily life, we frequently come across problems occur mostly various fields in engineering, social, medical and natural sciences, computer software development, public policy, and business analysis, etc. and hence we proceed in quest of having right solution with the help of traditional mathematical methods but because of various uncertainties presented sometimes in these applied problems, it becomes highly essential to look for some new proper mathematical tools to execute the inherent inexact information lying in those problems and to achieve of its the best feasible solutions. Fuzzy set theory is one such extremely useful tool that helps us to get so. In 1965, Lotfi A. Zadeh (1965) first published the famous research paper on fuzzy sets that originated due to mainly the inclusion of vague human assessments in computing problems. In other words, the fuzzy set theory can deal with the fact evolving from computational perception and cognition that is meaning the uncertainty, vagueness, partially trueness, impreciseness, sharpless boundaries, etc. The theory of fuzzy set is founded on the concept of relative graded membership which deals with the partial belongings of an element in a set to process inexact information. Later on, fuzzy sets have been generalized to intuitionistic fuzzy sets (IFSs) through adopting a non-membership function by Atanassov (1986) in order to get over problems that possess incomplete information.

We know that the concept of intuitionistic fuzzy set (IFS) is one of the pioneering contributions and useful approaches in the complex fuzzy environment which has been discussed in various perspectives by the researchers. Firstly, it is noticed that the fundamental research mainly deals with the algorithms of intuitionistic fuzzy numbers (IFNs) (De et al. (2000a, 2000b), Deschrijver et al. 2004, He et al. 2014) including the study of similarity and distance function on IFNs (Szmidt and Kacprzyk 2000; Chen 2007; Chen and Chang 2015; Milosevic et al. 2017) and comparison method of IFNs (Chen 2014; Zhang et al. 2015), etc. Secondly, at the advent of information aggregation operators, many achievements could have been possible in various fields or research and with few examples, it can be explained in brief. Weighted arithmetic (WA) operators based on IFNs were first proposed by Xu (2007). In next, Xu and Yager (2006, 2011) introduced both the weighted geometric (WG) operators and the extended Bonferroni mean (BM) operators based on IFNs. Simultaneously, Qin and Liu (2014) developed the weighted Maclaurin symmetric mean operator based on IFNs. Furthermore, Liu and Liu (2017) provided partitioned BM operator for intuitionistic uncertain linguistic variables etc. Thirdly, we observe that in the some useful approaches like TOPSIS method for IFNs (Wang et al. 2016; Shen et al. 2018), triangular intuitionistic fuzzy-TODIM method (Li et al. 2015; Qin et al. 2017), intuitionistic fuzzy PROMETHE II method (Montajabiha 2016) etc. have been illustrated in details during the discussion of extended MADM method. However, the applicability of IFS is limited on account of the constraint to be followed which is the sum of membership degree µ and non-membership degree ν cannot exceed one that is µ + ν ≤ 1. But, later on, we note that based on the preference given by decision makers/experts for complex decision-making problems, the above condition does not hold good. For instance, if an expert favors membership degree 0.8 and non-membership degree 0.6 during the implementation of IFS, then clearly their sum becomes 1.4 which exceeds 1. Thus the IFSs fail to describe properly this situation. To overcome this kind of situation, Yager (2013a, 2013b) proposed the nonstandard fuzzy set called Pythagorean fuzzy sets (PFSs) with membership degree µ and non-membership degree ν obeying the condition µ² + ν² ≤ 1.

The above study makes it clear that the PFSs adapt more uncertainties than the IFSs and consequently, we see its wide possible applications compared to IFSs. In recent days, almost all researchers honor PFSs.

As for example, Yager and Abbasov (2013) were able to establish the relationship between the Pythagorean numbers and the complex numbers. Some subtraction and division operations for PFSs were developed by Peng and Yang (2015). Zhang and Xu (2014) first defined Pythagorean fuzzy numbers (PFNs) and fitted this approach for order preference with TOPSIS method that aimed to have a similar ideal solution and successfully dealt PFN in MADM. Zeng et al (2016) propounded a heterogeneous method for Pythagorean fuzzy MAGDM problems. We refer here that Yager (2013a, 2013b) developed the Pythagorean fuzzy weighted averaging (PFWA) operator and Pythagorean fuzzy weighted geometric (PFWG) operator and exploited these to cope with MADM problems. Furthermore, Ma and Xu (2016) contributed to defining the symmetric Pythagorean fuzzy weighted geometric/averaging operators. Next, Garg (2016a, 2018a) developed some generalized Pythagorean fuzzy Einstein weighted and ordered weighted averaging operators and these were studied how to apply into Pythagorean fuzzy MADM problems. Also, Zhang (2016a, b) provided a new PFWA operator and Pythagorean fuzzy ordered weighted averaging (PFOWA) operator that amounting PFSs. Garg (2016b) defined the correlation coefficients between the PFSs. Zhang (2016a, b) showed how to reach the interval-valued PFSs (IPFSs) from PFS. Garg (2016c) determined the averaging and geometric aggregation operators (AOs) under the interval-valued PF environment. Notably, a Pythagorean fuzzy Choquet integral operator in MAGDM was developed by Peng and Yang (2016). It was discussed by Garg (2017) about the incorporation of the confidence level of the DMs during the decision-making process and suggested how to solve MADM problems with that of confidence levels based Pythagorean fuzzy weighted average and geometric operators. Some Pythagorean fuzzy Maclaurin symmetric mean operators in MADM have been extensively studied by Wei and Lu (2018). Moreover, Pythagorean fuzzy Maclaurin symmetric mean operators for hesitant PFSs were proposed by Garg (2019a). On the other hand, both new exponential and logarithm operational laws for PFSs were proposed by Garg (2018b, 2019b). Fairly recently, Nguyen et al. (2019) introduced the exponential similarity measures for PFSs and clearly explained of their probable applications into the decision-making process and also to the pattern recognition.

We note that PFSs can be made possible to implement subject to the condition that sum of the square of membership grade plus the square of non-membership grade must lie in the interval [0,1] and if not i.e. the sum goes beyond the interval [0,1], it requires to define information expression in an alternate way to overcome this underlying difficulty easily. Yager (2017) first re-defined q-rung orthopair fuzzy sets (q- ROFSs) through extending PFSs’ domain. The fact that, the q-ROFSs obeying the condition which is the sum of the qth power of the membership grade and the qth power of the non-membership grade must attain the value in the range [0,1], i.e., 0 ≤ µ^q + ν^q≤ 1, and in that case the pairs of values < µ, ν > are called q-rung orthopair fuzzy numbers (q-ROFNs). Point to be noted that the q-ROFNs are converted into the IFNs when q = 1 and on the other hand, the q-ROFNs are transformed into the PFNs for q = 2, which indicate that the q-ROFNs are nothing but a generalized forms of IFNs and PFNs. q-ROFNs can maximize the accuracy and integrity of fuzzy information as because q-ROFNs allowing the membership grade and non-membership grade to move within the range [0,1] and more importantly, the value of the parameter q may vary that also facilitates the scope of dynamical information expression. Since the last few years, the information aggregation had been a topic of discussion after realizing its importance and close connectivity with the problems of MAGDM under the q-rung orthopair fuzzy environment. q-rung orthopair fuzzy weighted averaging operator (q-ROFWA) and q-rung orthopair fuzzy weighted averaging operator (q-ROFWG) and their application into MADM problems were first reported by Liu and Wang (2018). q-rung orthopair fuzzy-weighted averaging (q-IROFWA) aggregation operator and improved q-rung orthopair fuzzy-weighted power averaging (q-IROFWPA) aggregation operator along with their few properties were extensively studied in Xu et al. (2019). Standing upon the concepts of possibility and certainty, Yager and Alajlan (2017) suggested approximate reasoning with q‐ROFSs. During this time, it was also explored by Liu et al. (2018a, b) several new q‐rung orthopair fuzzy aggregation operators based on Bonferroni mean and power Maclaurin symmetric mean for accumulating the expert’s driven decision‐making information. Furthermore, the exploration of various q‐rung orthopair fuzzy Heronian mean operators in multi-criteria decision making (MCDM) has been illustrated in Wei et al (2018). Keeping in mind of the possible appearance of a new score function during characterization of q‐ROFS, Peng et al. (2018) included exponential operation and aggregation operator and obtained satisfactory results using them into the selection of the teaching management system. Du (2018) developed Minkowski‐type distance measures, including Hamming, Euclidean, and Chebyshev distances for q‐ROFSs and discussed their applications to MCDM problems. Two new approaches had been demonstrated by Ali (2018) to be well acquainted with q‐ROFSs. MCDM method that invokes heterogeneous relationships among attributes and unknown attribute weight information in the framework of q‐ROFS was exclusively chalked out by Liu et al. (2018a, b). It was precisely administered by Yager et al. (2018) the concrete coordination among possibility, certainty, plausibility and belief in q‐ROFS environment. Joshi et al (2018) delineated in detail the generalized interval valued q‐ROFSs from q‐ROFS sand their corresponding properties. Soon after, both the axiomatic definitions of q-rung orthopair fuzzy information measures and corresponding formulae of information measure as well their transformation relationships have been explained thoroughly by Peng and Liu (2019). Mi et al. (2019) solved a multi-criteria decision-making problem using a score based q-ROFS VIKOR method. Liu and Wang (2018) were able to extend the Bonferroni mean (BM) operator in the q-ROFNs environment and alongside proposed both the q-rung orthopair fuzzy Archimedean BM (q-ROFABM) operator and the q-rung orthopair fuzzy weighted Archimedean BM (q-ROFWABM) operator and studied their worthy properties. Liu and Liu (2018) put forth a new concept called the linguistic q‐rung orthopair fuzzy number (Lq‐ROFN) where the membership and non-membership of q‐ROFNs are represented as linguistic variables and subsequently they developed Lq‐ROFN based few aggregation operators. Darko and Liang (2019) developed some q-rung orthopair fuzzy Hamacher aggregation operators and have shown how to solve a mobile payment platform selection problem based on Distance from Average Solution (EDAS) method. Sirbiladze (2019) extensively studied the maximum (minimum) associated probabilities q‐rung orthopair fuzzy weighted averaging (APs‐q‐ROFWA) and the maximum (minimum) associated probabilities q‐rung orthopair fuzzy weighted geometric (APs‐q‐ROFWG) aggregation operators and applied them into the evaluation of candidate sites’ selection ranking index at the facility location selection problem. Yang and Peng (2019) developed q-rung orthopair fuzzy Bonferroni mean Dombi aggregation operators and applied them for new campus site selection. Xing et al. (2019a, b) suggested a new class of weighted aggregation operators to aggregate q-rung ortho pair fuzzy information which takes part in the redistribution of membership and non-membership in q-ROFNs according to various principles. Shu et al. (2019) proposed q-rung orthopair fuzzy definite integrals (q-ROFDIs) and derived the limit of a q-ROFN sequence Qin et al. (2019a, b.) introduced Archimedean Muirhead aggregation operators of q-rung orthopair fuzzy numbers and also have shown its possible application in solving multi-criteria group decision-making problem. Based on interaction operational rules and Dual Hamy mean operator (DHM), Xing et al. (2019a, b) presented q-rung orthopair fuzzy interaction DHM operator and its weighted form which have shown to be exploited to solve a novel multi-attribute group decision-making approach Qin et al. (2019a, b.) developed the Archimedean power partitioned Muirhead mean operator of qROFNs and its weighted form and even proposed a MCGDM method based on the weighted operator. Jana et al. (2019) used Dombi operations to construct a few q‐rung orthopair fuzzy Dombi aggregation operators. Zhong et al. (2019) developed q-rung orthopair fuzzy Dombi power partitioned Heronian mean operator and its weighted form to reduce the negative effect of unearthly attribute values of the aggregation results of these operators that contributed to serve various real-life decision-making problems. Liu and Liu (2019a, b) propounded the linguistic q‐rung orthopair fuzzy Power aggregation (PA) operator and linguistic q‐rung orthopair fuzzy weighted Power aggregation. Further, for better comprehensibility in terms of advantages of the Muirhead mean (MM) operator and PA operator they suggested the linguistic q‐rung orthopair fuzzy power MM (PMM) operator and linguistic q‐rung orthopair fuzzy weighted PMM operator. Considering the probable advantages of q-ROFSs, Liu et al. (2019a, b) articulated a vulnerable extended fuzzy group TOPSIS method which is not standing on aggregation technology but is indispensable because of its capacity to reduce practically the distortion of decision information and consequently improve the accuracy of evaluation results. Liu et al. (2019a, b) put forward a new idea, coined as complex q-rung orthopair linguistic sets (Cq-ROLSs) to nicely serve the complex uncertain information in real decision-making problems. Besides, in the subsequent stage they laid a remarkable contribution in developing the complex q-rung orthopair linguistic Heronian mean (Cq-ROLHM) operator and complex q-rung orthopair linguistic weighted Heronian mean (Cq-ROLWHM) operator. Garg and Chen (2020) solved MADM problem by developing neutrality aggregation operators of q‐ROFSs. Qin et al. (2020) developed a multi-criteria decision-making (MCDM) method based on weighted Archimedean power partitioned Bonferroni aggregation operators of generalized orthopair membership grades characterizing the heterogeneous interrelationships of criteria to reduce the negative influence of biased criterion values and even to perceive the risk attitudes of decision-makers. Yang et al. (2020) proposed an online shopping support model applying deep‐learning–based opinion mining and q‐rung orthopair fuzzy interaction weighted Heronian mean (q‐ROFIWHM) operators. Joshi and Gegov (2020) deployed the familiarity degree of the experts with the evaluated objects for initial assessments under q‐rung orthopair fuzzy environment and proposed some aggregation operators to merge these two types of information. Maclaurin symmetric mean operator helped to Liu and Wang (2020) to introduce q-rung orthopair fuzzy generalized Maclaurin symmetric mean operator (q-ROFGMSM) and q-rung orthopair fuzzy geometric Maclaurin symmetric mean operator (q-ROFGGMSM) which may access the grades of membership and non-membership in the interval [0,1] respectively and confess multiple attributes. Some more applications of qROFSs can be found in the work of Liu and Wang (2019), Darko and Liang (2020), Garg (2020), Yang and Pang (2020) and Sirbiladze (2020).

We note that although the existing aggregation operators (Liu and Wang 2018, 2020; Liu et al. 2018a, b; Liu and Liu 2018; Wei et al. 2018; Xu et al. 2019) intervene to solve the MADM problems under q-rung orthopair fuzzy environment, however, it is hardly found among them the unbiased nature while dealing with membership and non-membership degrees. For example, the usual consolidated values achieved through aggregation operators which already exist in the literature (Joshi et al. 2018; Liu and Wang 2018, 2020; Liu et al. 2018a, b; Liu and Liu 2018; Wei et al. 2018; Xu et al. 2019) cannot be segregated for the case when a comparative work to both the membership and non-membership degrees is governed by a decision-maker. It indicates that partiality occurs in the final judgment indeed. Hence, we require to provide some new fairly or neutral operations for q-ROFNs to be ensured at the fair treatment for the membership as well as non-membership information. In this situation, to have the true satisfaction in performing the activity to evaluate the membership as well as non-membership degrees, by utilizing the idea of proportional distribution rules of both membership and non-membership functions we build up two neutral or fairly operations. In what follows at this point of view, there is a wide scope to exercise the fairly aggregation operators because the problematic information in more productive manners is signified by the q-ROFSs than the IFSs and PFSs. Below we alluded in summary form, the aims in this study followed by the above discussion:

(1) To employ the interaction coefficient to construct some new neutral or fairly operations for equitable treatment of the membership and non-membership function.

(2) To introduce the weighted aggregation operators such as q-rung orthopair fuzzy weighted fairly aggregation operator (qROFWFA) and q-rung orthopair fuzzy ordered weighted fairly aggregation operator (qROFOWFA) as well as to familiar with their properties.

(3) To develop a decision making method by making use of the aforementioned weighted aggregation operators to tackle multi-attribute decision-making problems with q-rung orthopair fuzzy information.

The arrangement of this article is as follows:

Section 2 is solely devoted to the review of some preliminaries. In Sect. 3, we define a few neutral or fairly operations under the q-rung orthopair fuzzy environment and elucidate their properties. Section 4 introduces us with the formulation of the q-rung orthopair fuzzy weighted fairly aggregation operator (qROFWFA) to aggregate q-rung orthopair fuzzy information. In Sect. 5, we discuss how to develop the q-rung orthopair fuzzy ordered weighted fairly aggregation operator (qROFOWFA) to amalgamate q-rung orthopair fuzzy ordered information. Section 6 is focused on vindicating a multi-attribute decision-making.

(MADM) approach comprising the qROFWFA and qROFOWFA operators and score of q-ROFNs. In this proposed method, the rating values of alternatives on the attribute are expressed in terms of q-ROFNs and the ranking process for the alternatives is made based on the values of the score of q-ROFNs to select the best/most desirable one. Hereto, we illustrate a practical example related to supplier selection followed by the proposed method. Section 7 deals with the subject of comparative study. The last section (Sect. 8) is the conclusion part.

2 Preliminaries

Here we emphasize on some relevant expressions, operational laws, score and accuracy values and ranking rules of the q-ROFNs.

Definition 2.1

(Yager 2017) Suppose U is the domain of discourse. Then a q-ROFS $\alpha$ in U is indicated by.

$$ \alpha = \{ < x,\mu_{\alpha } (x),\nu_{\alpha } (x) > :x \in U\} , $$

where $\mu_{\alpha } (x)$ and $\gamma_{\alpha } (x)$ represent the membership grade and non-membership grades respectively of $x \in U$ in the q-ROFS $\alpha$ and $0 \le \mu_{\alpha } (x),\nu_{\alpha } (x) \le 1$ with $0 \le (\mu_{\alpha } (x))^{q} + (\nu_{\alpha } (x))^{q} \le 1,$

($q \ge 1$).

According to Yager (Yager 2017), the hesitancy grade of $x \in U$ in the q-ROFS $\Delta$ is defined as:

$\delta_{\alpha } (x) = \left( {1 - (\mu_{\alpha } (x))^{q} - (\nu_{\alpha } (x))^{q} } \right)^{\frac{1}{q}}$. One can easily verify that $0 \le \delta_{\alpha } (x) \le 1$.

Yager (Yager 2017) termed the pair $< \mu_{\alpha } (x),\nu_{\alpha } (x) >$ a q-ROFN. For sake of simplicity, throughout the paper we shall use the notation $\alpha = < \mu_{\alpha } ,\nu_{\alpha } >$ to denote a q-ROFN.

Definition 2.2

(Liu and Wang 2018) Suppose $\alpha = < \mu_{\alpha } ,\nu_{\alpha } >$ be a q-ROFN. Then the score value of $\alpha$ is described as:

$$ S(\alpha ) = \mu_{\alpha }^{q} - \nu_{\alpha }^{q} . $$

Clearly, $0 \le S(\alpha ) \le 1$. It is pertinent to mention that the score values can’t be successfully applied to differentiate many q-ROFNs in some particular cases. For example, if $\alpha_{1} = < 0.6138,0.2534 >$ and $\alpha_{2} = < 0.7147,0.4453 >$, then $S(\alpha_{1} ) = 0.3125 = S(\alpha_{2} )$ (taking q = 2). Therefore, we should not rely solely on the score values to compare the q-ROFNs. To deal with such an issue, Liu and Wang (Liu and Wang 2018) proposed the concept of accuracy value of a q-ROFN.

Definition 2.3

(Liu and Wang 2018) Suppose $\alpha = < \mu_{\alpha } ,\nu_{\alpha } >$ be a q-ROFN. Then the accuracy value of $\alpha$ is described as:

$$ A(\alpha ) = \mu_{\alpha }^{q} + \nu_{\alpha }^{q} . $$

Clearly, $- 1 \le A(\alpha ) \le 1$.

Based on the score value and accuracy value, a comparison method of q-ROFNs is described below:

Definition 2.4

(Liu and Wang 2018) Suppose $\alpha_{1} = < \mu_{{\alpha_{1} }} ,\nu_{{\alpha_{1} }} >$ and $\alpha_{2} = < \mu_{{\alpha_{2} }} ,\nu_{{\alpha_{2} }} >$ be two q-ROFNs. Then.

• (1) If $S(\alpha_{1} ) > S(\alpha_{2} )$, then $\alpha_{1} \succ \alpha_{2}$.

• (2) If $S(\alpha_{1} ) = S(\alpha_{2} )$, then.

• (i) if $A(\alpha_{1} ) > A(\alpha_{2} )$, then $\alpha_{1} \succ \alpha_{2}$.

• (ii) if $A(\alpha_{1} ) = A(\alpha_{2} )$, then $\alpha_{1} = \alpha_{2}$.

Definition 2.5

(Liu and Wang 2018) Suppose $\alpha_{1} = < \mu_{{\alpha_{1} }} ,\nu_{{\alpha_{1} }} >$ and $\alpha_{2} = < \mu_{{\alpha_{2} }} ,\nu_{{\alpha_{2} }} >$ be two q-ROFNs and $\lambda > 0$. Then.

• i. $\alpha_{1} \oplus \alpha_{2} = \left\langle {\left( {1 - \left( {1 - \mu_{{\alpha_{1} }}^{q} } \right)\left( {1 - \mu_{{\alpha_{2} }}^{q} } \right)} \right)^{\frac{1}{q}} ,\nu_{{\alpha_{1} }} \nu_{{\alpha_{2} }} } \right\rangle$

• ii. $\alpha_{1} \otimes \alpha_{2} = \left\langle {\mu_{{\alpha_{1} }} \mu_{{\alpha_{2} }} ,\left( {1 - \left( {1 - \nu_{{\alpha_{1} }}^{q} } \right)\left( {1 - \nu_{{\alpha_{2} }}^{q} } \right)} \right)^{\frac{1}{q}} } \right\rangle$

• iii. $\lambda \alpha_{1} = \left\langle {\left( {1 - \left( {1 - \mu_{{\alpha_{1} }}^{q} } \right)^{\lambda } } \right)^{\frac{1}{q}} ,\nu_{{\alpha_{1} }}^{\lambda } } \right\rangle$

• iv. $\alpha_{1}^{\lambda } = \left\langle {\mu_{{\alpha_{1} }}^{\lambda } ,\left( {1 - \left( {1 - \nu_{{\alpha_{1} }}^{q} } \right)^{\lambda } } \right)^{\frac{1}{q}} } \right\rangle$

Theorem 2.6:

(Liu and Wang 2018) Suppose $\alpha_{1} = < \mu_{{\alpha_{1} }} ,\nu_{{\alpha_{1} }} >$ and $\alpha_{2} = < \mu_{{\alpha_{2} }} ,\nu_{{\alpha_{2} }} >$ be two q-ROFNs and $\lambda ,\lambda_{1} ,\lambda_{2} > 0$ be three real numbers. Then we have,

$$ {\text{(i)}}\,\alpha_{1} \oplus \alpha_{2} = \alpha_{2} \oplus \alpha_{1} $$

$$ {\text{(ii)}}\,\alpha_{1} \otimes \alpha_{2} =_{2} \otimes \alpha_{1} $$

$$ {\text{(iii)}}\,\lambda (\alpha_{1} \oplus \alpha_{2} ) = (\lambda \alpha_{1} ) \oplus (\lambda \alpha_{2} ) $$

$$ {\text{(iv)}}\,(\alpha_{1} \otimes \alpha_{2} )^{\lambda } = \alpha_{1}^{\lambda } \otimes \alpha_{2}^{\lambda } $$

$(v)\,(\lambda_{1} + \lambda_{2} )\alpha_{1} = (\lambda_{1} \alpha_{1} ) \oplus (\lambda_{2} \alpha_{2} )$

$$ {\text{(vi)}}\,\alpha_{1}^{{\lambda_{1} + \lambda_{2} }} = \alpha_{1}^{{\lambda_{1} }} \otimes \alpha_{2}^{{\lambda_{2} }} $$

If $\mu_{{\alpha_{1} }} = \nu_{{\alpha_{1} }}$ and $\mu_{{\alpha_{2} }} = \nu_{{\alpha_{2} }}$ then from definition 2.5 we attain, $\mu_{{\alpha_{1} \oplus \alpha_{2} }} \ne \nu_{{\alpha_{1} \oplus \alpha_{2} }} ,\mu_{{\alpha_{1} \otimes \alpha_{2} }} \ne \nu_{{\alpha_{1} \otimes \alpha_{2} }} ,$$\mu_{{\lambda \alpha_{1} }} \ne \nu_{{\lambda \alpha_{1} }} ,\mu_{{\alpha_{1}^{\lambda } }} \ne \nu_{{\alpha_{1}^{\lambda } }}$. Thus none of the operations $\alpha_{1} \oplus \alpha_{2} ,\alpha_{1} \otimes \alpha_{2} ,\lambda \alpha_{1} ,\alpha_{1}^{\lambda }$ found to be neutral or fair indeed. So, at the very beginning our attention must be towards develop some fairly operations between q-ROFNs.

3 Fairly operations on q-ROFNs:

In this section, we develop some fairly or neutral operations between q-ROFNs and study their basic properties.

Definition 3.1

Suppose $\alpha_{1} = < \mu_{{\alpha_{1} }} ,\nu_{{\alpha_{1} }} >$ and $\alpha_{2} = < \mu_{{\alpha_{2} }} ,\nu_{{\alpha_{2} }} >$ be two q-ROFNs and $\lambda > 0$. Then we define.

$$ \begin{gathered} {\text{(i)}}\,\,\alpha_{1} \tilde{ \otimes }\alpha_{2} = \left\langle {\left( {\left( {\frac{{\mu_{{\alpha_{1} }}^{q} \mu_{{\alpha_{2} }}^{q} }}{{\mu_{{\alpha_{1} }}^{q} \mu_{{\alpha_{2} }}^{q} + \nu_{{\alpha_{1} }}^{q} \nu_{{\alpha_{2} }}^{q} }}} \right) \times \left( {1 - \left( {1 - \mu_{{\alpha_{1} }}^{q} - \nu_{{\alpha_{1} }}^{q} } \right)\left( {1 - \mu_{{\alpha_{2} }}^{q} - \nu_{{\alpha_{2} }}^{q} } \right)} \right)} \right)^{\frac{1}{q}} ,} \right. \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left. {\left( {\left( {\frac{{\nu_{{\alpha_{1} }}^{q} \nu_{{\alpha_{2} }}^{q} }}{{\mu_{{\alpha_{1} }}^{q} \mu_{{\alpha_{2} }}^{q} + \nu_{{\alpha_{1} }}^{q} \nu_{{\alpha_{2} }}^{q} }}} \right) \times \left( {1 - \left( {1 - \mu_{{\alpha_{1} }}^{q} - \nu_{{\alpha_{1} }}^{q} } \right)\left( {1 - \mu_{{\alpha_{2} }}^{q} - \nu_{{\alpha_{2} }}^{q} } \right)} \right)} \right)^{\frac{1}{q}} } \right\rangle \hfill \\ {\text{(ii)}}\,\lambda * \alpha_{1} = \left\langle {\left( {\left( {\frac{{\mu_{{\alpha_{1} }}^{q\lambda } }}{{\mu_{{\alpha_{1} }}^{q\lambda } + \nu_{{\alpha_{1} }}^{q\lambda } }}} \right) \times \left( {1 - \left( {1 - \mu_{{\alpha_{1} }}^{q} - \nu_{{\alpha_{1} }}^{q} } \right)^{\lambda } } \right)} \right)^{\frac{1}{q}} ,} \right.\left. {\left( {\left( {\frac{{\nu_{{\alpha_{1} }}^{q\lambda } }}{{\mu_{{\alpha_{1} }}^{q\lambda } + \nu_{{\alpha_{1} }}^{q\lambda } }}} \right) \times \left( {1 - \left( {1 - \mu_{{\alpha_{1} }}^{q} - \nu_{{\alpha_{1} }}^{q} } \right)^{\lambda } } \right)} \right)^{\frac{1}{q}} } \right\rangle \hfill \\ \end{gathered} $$

It can be easily verified that each of $\alpha_{1} \tilde{ \otimes }\alpha_{2} ,\lambda * \alpha_{1}$ is a q-ROFN.

Proposition 3.2

Suppose $\alpha_{1} = < \mu_{{\alpha_{1} }} ,\nu_{{\alpha_{1} }} >$ and $\alpha_{2} = < \mu_{{\alpha_{2} }} ,\nu_{{\alpha_{2} }} >$ be two q-ROFNs. If $\mu_{{\alpha_{1} }} = \nu_{{\alpha_{1} }}$ and $\mu_{{\alpha_{2} }} = \nu_{{\alpha_{2} }}$, then we have.

$$ \begin{gathered} {\text{(i)}}\,\mu_{{\alpha_{1} \tilde{ \otimes }\alpha_{2} }} = \nu_{{\alpha_{1} \tilde{ \otimes }\alpha_{2} }} \hfill \\ {\text{(ii)}}\,\mu_{{\lambda * \alpha_{1} }} = \nu_{{\lambda * \alpha_{1} }} \hfill \\ \end{gathered} $$

Proof

Suppose $\mu_{{\alpha_{1} }} = \nu_{{\alpha_{1} }}$ and $\mu_{{\alpha_{2} }} = \nu_{{\alpha_{2} }}$. Then we have,

$$ {\text{(i)}}\,\,\frac{{\mu_{{\alpha_{1} \tilde{ \otimes }\alpha_{2} }} }}{{\nu_{{\alpha_{1} \tilde{ \otimes }\alpha_{2} }} }} = \frac{{\left( {\left( {\frac{{\mu_{{\alpha_{1} }}^{q} \mu_{{\alpha_{2} }}^{q} }}{{\mu_{{\alpha_{1} }}^{q} \mu_{{\alpha_{2} }}^{q} + \nu_{{\alpha_{1} }}^{q} \nu_{{\alpha_{2} }}^{q} }}} \right) \times \left( {1 - \left( {1 - \mu_{{\alpha_{1} }}^{q} - \nu_{{\alpha_{1} }}^{q} } \right)\left( {1 - \mu_{{\alpha_{2} }}^{q} - \nu_{{\alpha_{2} }}^{q} } \right)} \right)} \right)^{\frac{1}{q}} }}{{\left( {\left( {\frac{{\nu_{{\alpha_{1} }}^{q} \nu_{{\alpha_{2} }}^{q} }}{{\mu_{{\alpha_{1} }}^{q} \mu_{{\alpha_{2} }}^{q} + \nu_{{\alpha_{1} }}^{q} \nu_{{\alpha_{2} }}^{q} }}} \right) \times \left( {1 - \left( {1 - \mu_{{\alpha_{1} }}^{q} - \nu_{{\alpha_{1} }}^{q} } \right)\left( {1 - \mu_{{\alpha_{2} }}^{q} - \nu_{{\alpha_{2} }}^{q} } \right)} \right)} \right)^{\frac{1}{q}} }} = \left( {\frac{{\mu_{{\alpha_{1} }}^{q} \mu_{{\alpha_{2} }}^{q} }}{{\nu_{{\alpha_{1} }}^{q} \nu_{{\alpha_{2} }}^{q} }}} \right)^{\frac{1}{q}} = 1. $$

Consequently, $\mu_{{\alpha_{1} \tilde{ \otimes }\alpha_{2} }} = \nu_{{\alpha_{1} \tilde{ \otimes }\alpha_{2} }}$ if $\mu_{{\alpha_{1} }} = \nu_{{\alpha_{1} }}$ and $\mu_{{\alpha_{2} }} = \nu_{{\alpha_{2} }}$.

$$ {\text{(ii)}}\,\frac{{\mu_{{\lambda * \alpha_{1} }} }}{{\nu_{{\lambda * \alpha_{1} }} }} = \frac{{\left( {\left( {\frac{{\mu_{{\alpha_{1} }}^{q\lambda } }}{{\mu_{{\alpha_{1} }}^{q\lambda } + \nu_{{\alpha_{1} }}^{q\lambda } }}} \right) \times \left( {1 - \left( {1 - \mu_{{\alpha_{1} }}^{q} - \nu_{{\alpha_{1} }}^{q} } \right)^{\lambda } } \right)} \right)^{\frac{1}{q}} }}{{\left( {\left( {\frac{{\nu_{{\alpha_{1} }}^{q\lambda } }}{{\mu_{{\alpha_{1} }}^{q\lambda } + \nu_{{\alpha_{1} }}^{q\lambda } }}} \right) \times \left( {1 - \left( {1 - \mu_{{\alpha_{1} }}^{q} - \nu_{{\alpha_{1} }}^{q} } \right)^{\lambda } } \right)} \right)^{\frac{1}{q}} }} = \frac{{\left( {\mu_{{\alpha_{1} }}^{q\lambda } } \right)^{\frac{1}{q}} }}{{\left( {\nu_{{\alpha_{1} }}^{q\lambda } } \right)^{\frac{1}{q}} }} = 1. $$

Consequently, $\mu_{{\lambda * \alpha_{1} }} = \nu_{{\lambda * \alpha_{1} }}$ if $\mu_{{\alpha_{1} }} = \nu_{{\alpha_{1} }}$ and $\mu_{{\alpha_{2} }} = \nu_{{\alpha_{2} }}$.

The above proposition shows that the operations $\alpha_{1} \tilde{ \otimes }\alpha_{2} ,\lambda * \alpha_{1}$ show the neutral or fairly nature to the decision makers when the membership and non-membership degrees are equal initially. This is why we call the operations $\tilde{ \otimes }, *$ fairly operations.

Theorem 3.3

Suppose $\alpha_{1} = < \mu_{{\alpha_{1} }} ,\nu_{{\alpha_{1} }} >$ and $\alpha_{2} = < \mu_{{\alpha_{2} }} ,\nu_{{\alpha_{2} }} >$ be two q-ROFNs and $\lambda ,\lambda_{1} ,\lambda_{2} > 0$ be three real numbers. Then we have,

$$ \begin{gathered} {\text{(i)}}\,\alpha_{1} \tilde{ \otimes }\alpha_{2} = \alpha_{2} \tilde{ \otimes }\alpha_{1} \hfill \\ {\text{(ii)}}\,\lambda * (\alpha_{1} \tilde{ \otimes }\alpha_{2} ) = (\lambda * \alpha_{1} )\tilde{ \otimes }(\lambda * \alpha_{2} ) \hfill \\ ({\text{ii}}i)\,(\lambda_{1} + \lambda_{2} ) * \alpha_{1} = (\lambda_{1} * \alpha_{1} )\tilde{ \otimes }(\lambda_{2} * \alpha_{2} ) \hfill \\ \end{gathered} $$

Proof

• (1) Straight forward.

• (2) We have, $\lambda * (\alpha_{1} \tilde{ \otimes }\alpha_{2} )$

$$ = \left\langle {\left( {\frac{{\left( {\frac{{\mu_{{\alpha_{1} }}^{q} \mu_{{\alpha_{2} }}^{q} }}{{\mu_{{\alpha_{1} }}^{q} \mu_{{\alpha_{2} }}^{q} + \nu_{{\alpha_{1} }}^{q} \nu_{{\alpha_{2} }}^{q} }}} \right)^{{\frac{\lambda }{q} \times q}} }}{{\left( {\frac{{\mu_{{\alpha_{1} }}^{q} \mu_{{\alpha_{2} }}^{q} }}{{\mu_{{\alpha_{1} }}^{q} \mu_{{\alpha_{2} }}^{q} + \nu_{{\alpha_{1} }}^{q} \nu_{{\alpha_{2} }}^{q} }}} \right)^{{\frac{\lambda }{q} \times q}} + \left( {\frac{{\nu_{{\alpha_{1} }}^{q} \nu_{{\alpha_{2} }}^{q} }}{{\mu_{{\alpha_{1} }}^{q} \mu_{{\alpha_{2} }}^{q} + \nu_{{\alpha_{1} }}^{q} \nu_{{\alpha_{2} }}^{q} }}} \right)^{{\frac{\lambda }{q} \times q}} }}\left( {1 - \left( {1 - \left( {1 - \left( {1 - \mu_{{\alpha_{1} }}^{q} - \nu_{{\alpha_{1} }}^{q} } \right)\left( {1 - \mu_{{\alpha_{2} }}^{q} - \nu_{{\alpha_{2} }}^{q} } \right)} \right)} \right)^{\lambda } } \right)} \right)^{\frac{1}{q}} ,} \right. $$

$$ \,\,\,\,\,\,\,\left. {\,\left( {\frac{{\left( {\frac{{\nu_{{\alpha_{1} }}^{q} \nu_{{\alpha_{2} }}^{q} }}{{\mu_{{\alpha_{1} }}^{q} \mu_{{\alpha_{2} }}^{q} + \nu_{{\alpha_{1} }}^{q} \nu_{{\alpha_{2} }}^{q} }}} \right)^{{\frac{\lambda }{q} \times q}} }}{{\left( {\frac{{\mu_{{\alpha_{1} }}^{q} \mu_{{\alpha_{2} }}^{q} }}{{\mu_{{\alpha_{1} }}^{q} \mu_{{\alpha_{2} }}^{q} + \nu_{{\alpha_{1} }}^{q} \nu_{{\alpha_{2} }}^{q} }}} \right)^{{\frac{\lambda }{q} \times q}} + \left( {\frac{{\nu_{{\alpha_{1} }}^{q} \nu_{{\alpha_{2} }}^{q} }}{{\mu_{{\alpha_{1} }}^{q} \mu_{{\alpha_{2} }}^{q} + \nu_{{\alpha_{1} }}^{q} \nu_{{\alpha_{2} }}^{q} }}} \right)^{{\frac{\lambda }{q} \times q}} }}\left( {1 - \left( {1 - \left( {1 - \left( {1 - \mu_{{\alpha_{1} }}^{q} - \nu_{{\alpha_{1} }}^{q} } \right)\left( {1 - \mu_{{\alpha_{2} }}^{q} - \nu_{{\alpha_{2} }}^{q} } \right)} \right)} \right)^{\lambda } } \right)} \right)^{\frac{1}{q}} \,} \right\rangle \,\,\,\, $$

$$ \begin{gathered} = \left\langle {\left( {\frac{{\mu_{{\alpha_{1} }}^{\lambda q} \mu_{{\alpha_{2} }}^{\lambda q} }}{{\mu_{{\alpha_{1} }}^{\lambda q} \mu_{{\alpha_{2} }}^{\lambda q} + \nu_{{\alpha_{1} }}^{\lambda q} \nu_{{\alpha_{2} }}^{\lambda q} }}\left( {1 - \left( {1 - \mu_{{\alpha_{1} }}^{q} - \nu_{{\alpha_{1} }}^{q} } \right)^{\lambda } \left( {1 - \mu_{{\alpha_{2} }}^{q} - \nu_{{\alpha_{2} }}^{q} } \right)^{\lambda } } \right)} \right)^{\frac{1}{q}} ,} \right. \hfill \\ \,\,\,\left. {\left( {\frac{{\nu_{{\alpha_{1} }}^{\lambda q} \nu_{{\alpha_{2} }}^{\lambda q} }}{{\mu_{{\alpha_{1} }}^{\lambda q} \mu_{{\alpha_{2} }}^{\lambda q} + \nu_{{\alpha_{1} }}^{\lambda q} \nu_{{\alpha_{2} }}^{\lambda q} }}\left( {1 - \left( {1 - \mu_{{\alpha_{1} }}^{q} - \nu_{{\alpha_{1} }}^{q} } \right)^{\lambda } \left( {1 - \mu_{{\alpha_{2} }}^{q} - \nu_{{\alpha_{2} }}^{q} } \right)^{\lambda } } \right)} \right)^{\frac{1}{q}} \,} \right\rangle \,\,\,\,\,\,\,\, \hfill \\ \end{gathered} $$

On the other hand, $(\lambda * \alpha_{1} )\tilde{ \otimes }(\lambda * \alpha_{2} )$

$$ \begin{gathered} = \left\langle {\left( {\left( {\frac{{\mu_{{\alpha_{1} }}^{q\lambda } }}{{\mu_{{\alpha_{1} }}^{q\lambda } + \nu_{{\alpha_{1} }}^{q\lambda } }}} \right) \times \left( {1 - \left( {1 - \mu_{{\alpha_{1} }}^{q} - \nu_{{\alpha_{1} }}^{q} } \right)^{\lambda } } \right)} \right)^{\frac{1}{q}} ,} \right.\left. {\left( {\left( {\frac{{\nu_{{\alpha_{1} }}^{q\lambda } }}{{\mu_{{\alpha_{1} }}^{q\lambda } + \nu_{{\alpha_{1} }}^{q\lambda } }}} \right) \times \left( {1 - \left( {1 - \mu_{{\alpha_{1} }}^{q} - \nu_{{\alpha_{1} }}^{q} } \right)^{\lambda } } \right)} \right)^{\frac{1}{q}} } \right\rangle \hfill \\ \,\,\,\,\tilde{ \otimes }\left\langle {\left( {\left( {\frac{{\mu_{{\alpha_{2} }}^{q\lambda } }}{{\mu_{{\alpha_{2} }}^{q\lambda } + \nu_{{\alpha_{2} }}^{q\lambda } }}} \right) \times \left( {1 - \left( {1 - \mu_{{\alpha_{2} }}^{q} - \nu_{{\alpha_{2} }}^{q} } \right)^{\lambda } } \right)} \right)^{\frac{1}{q}} ,} \right.\left. {\left( {\left( {\frac{{\nu_{{\alpha_{2} }}^{q\lambda } }}{{\mu_{{\alpha_{2} }}^{q\lambda } + \nu_{{\alpha_{2} }}^{q\lambda } }}} \right) \times \left( {1 - \left( {1 - \mu_{{\alpha_{2} }}^{q} - \nu_{{\alpha_{2} }}^{q} } \right)^{\lambda } } \right)} \right)^{\frac{1}{q}} } \right\rangle \hfill \\ \end{gathered} $$

$$ \begin{gathered} = \left\langle {\left( {\frac{{\frac{{\mu_{{\alpha_{1} }}^{q\lambda } }}{{\mu_{{\alpha_{1} }}^{q\lambda } + \nu_{{\alpha_{1} }}^{q\lambda } }} \times \frac{{\mu_{{\alpha_{2} }}^{q\lambda } }}{{\mu_{{\alpha_{2} }}^{q\lambda } + \nu_{{\alpha_{2} }}^{q\lambda } }}}}{{\frac{{\mu_{{\alpha_{1} }}^{q\lambda } }}{{\mu_{{\alpha_{1} }}^{q\lambda } + \nu_{{\alpha_{1} }}^{q\lambda } }} \times \frac{{\mu_{{\alpha_{2} }}^{q\lambda } }}{{\mu_{{\alpha_{2} }}^{q\lambda } + \nu_{{\alpha_{2} }}^{q\lambda } }} + \frac{{\nu_{{\alpha_{1} }}^{q\lambda } }}{{\mu_{{\alpha_{1} }}^{q\lambda } + \nu_{{\alpha_{1} }}^{q\lambda } }} \times \frac{{\nu_{{\alpha_{2} }}^{q\lambda } }}{{\mu_{{\alpha_{2} }}^{q\lambda } + \nu_{{\alpha_{2} }}^{q\lambda } }}}}} \right.} \right. \times \hfill \\ \left. {\,\,\,\,\,\,\,\,\,\left( {1 - \left( {1 - \left( {1 - \left( {1 - \mu_{{\alpha_{1} }}^{q} - \nu_{{\alpha_{1} }}^{q} } \right)^{\lambda } } \right)} \right) \times \left( {1 - \left( {1 - \left( {1 - \mu_{{\alpha_{2} }}^{q} - \nu_{{\alpha_{2} }}^{q} } \right)^{\lambda } } \right)} \right)} \right)} \right)^{\frac{1}{q}} , \hfill \\ \,\,\,\,\,\,\,\,\,\left( {\frac{{\frac{{\nu_{{\alpha_{1} }}^{q\lambda } }}{{\mu_{{\alpha_{1} }}^{q\lambda } + \nu_{{\alpha_{1} }}^{q\lambda } }} \times \frac{{\nu_{{\alpha_{2} }}^{q\lambda } }}{{\mu_{{\alpha_{2} }}^{q\lambda } + \nu_{{\alpha_{2} }}^{q\lambda } }}}}{{\frac{{\mu_{{\alpha_{1} }}^{q\lambda } }}{{\mu_{{\alpha_{1} }}^{q\lambda } + \nu_{{\alpha_{1} }}^{q\lambda } }} \times \frac{{\mu_{{\alpha_{2} }}^{q\lambda } }}{{\mu_{{\alpha_{2} }}^{q\lambda } + \nu_{{\alpha_{2} }}^{q\lambda } }} + \frac{{\nu_{{\alpha_{1} }}^{q\lambda } }}{{\mu_{{\alpha_{1} }}^{q\lambda } + \nu_{{\alpha_{1} }}^{q\lambda } }} \times \frac{{\nu_{{\alpha_{2} }}^{q\lambda } }}{{\mu_{{\alpha_{2} }}^{q\lambda } + \nu_{{\alpha_{2} }}^{q\lambda } }}}}} \right. \times \hfill \\ \,\,\,\,\left. {\left. {\,\,\,\,\left( {1 - \left( {1 - \left( {1 - \left( {1 - \mu_{{\alpha_{1} }}^{q} - \nu_{{\alpha_{1} }}^{q} } \right)^{\lambda } } \right)} \right) \times \left( {1 - \left( {1 - \left( {1 - \mu_{{\alpha_{2} }}^{q} - \nu_{{\alpha_{2} }}^{q} } \right)^{\lambda } } \right)} \right)} \right)} \right)^{\frac{1}{q}} } \right\rangle \hfill \\ = \left\langle {\left( {\frac{{\mu_{{\alpha_{1} }}^{\lambda q} \mu_{{\alpha_{2} }}^{\lambda q} }}{{\mu_{{\alpha_{1} }}^{\lambda q} \mu_{{\alpha_{2} }}^{\lambda q} + \nu_{{\alpha_{1} }}^{\lambda q} \nu_{{\alpha_{2} }}^{\lambda q} }}\left( {1 - \left( {1 - \mu_{{\alpha_{1} }}^{q} - \nu_{{\alpha_{1} }}^{q} } \right)^{\lambda } \left( {1 - \mu_{{\alpha_{2} }}^{q} - \nu_{{\alpha_{2} }}^{q} } \right)^{\lambda } } \right)} \right)^{\frac{1}{q}} ,} \right. \hfill \\ \end{gathered} $$

$$ \,\,\,\,\,\,\left. {\left( {\frac{{\nu_{{\alpha_{1} }}^{\lambda q} \nu_{{\alpha_{2} }}^{\lambda q} }}{{\mu_{{\alpha_{1} }}^{\lambda q} \mu_{{\alpha_{2} }}^{\lambda q} + \nu_{{\alpha_{1} }}^{\lambda q} \nu_{{\alpha_{2} }}^{\lambda q} }}\left( {1 - \left( {1 - \mu_{{\alpha_{1} }}^{q} - \nu_{{\alpha_{1} }}^{q} } \right)^{\lambda } \left( {1 - \mu_{{\alpha_{2} }}^{q} - \nu_{{\alpha_{2} }}^{q} } \right)^{\lambda } } \right)} \right)^{\frac{1}{q}} \,} \right\rangle \, $$

Hence, $\lambda * (\alpha_{1} \tilde{ \otimes }\alpha_{2} ) = (\lambda * \alpha_{1} )\tilde{ \otimes }(\lambda * \alpha_{2} )$.

• (3) We have, $(\lambda_{1} + \lambda_{2} ) * \alpha_{1}$

$$ = \left\langle {\left( {\left( {\frac{{\mu_{{\alpha_{1} }}^{{q(\lambda_{1} + \lambda_{2} )}} }}{{\mu_{{\alpha_{1} }}^{{q(\lambda_{1} + \lambda_{2} )}} + \nu_{{\alpha_{1} }}^{{q(\lambda_{1} + \lambda_{2} )}} }}} \right) \times \left( {1 - \left( {1 - \mu_{{\alpha_{1} }}^{q} - \nu_{{\alpha_{1} }}^{q} } \right)^{{\lambda_{1} + \lambda_{2} }} } \right)} \right)^{\frac{1}{q}} ,} \right.\left. {\,\left( {\left( {\frac{{\nu_{{\alpha_{1} }}^{{q(\lambda_{1} + \lambda_{2} )}} }}{{\mu_{{\alpha_{1} }}^{{q(\lambda_{1} + \lambda_{2} )}} + \nu_{{\alpha_{1} }}^{{q(\lambda_{1} + \lambda_{2} )}} }}} \right) \times \left( {1 - \left( {1 - \mu_{{\alpha_{1} }}^{q} - \nu_{{\alpha_{1} }}^{q} } \right)^{{\lambda_{1} + \lambda_{2} }} } \right)} \right)^{\frac{1}{q}} } \right\rangle $$

On the other hand, $(\lambda_{1} * \alpha_{1} )\tilde{ \otimes }(\lambda_{2} * \alpha_{2} )$

$$ \begin{gathered} = \left\langle {\left( {\frac{{\mu_{{\alpha_{1} }}^{{q\lambda_{1} }} }}{{\mu_{{\alpha_{1} }}^{{q\lambda_{1} }} + \nu_{{\alpha_{1} }}^{{q\lambda_{1} }} }} \times \left( {1 - \left( {1 - \mu_{{\alpha_{1} }}^{q} - \nu_{{\alpha_{1} }}^{q} } \right)^{{\lambda_{1} }} } \right)} \right)^{\frac{1}{q}} ,} \right.\left. {\left( {\frac{{\nu_{{\alpha_{1} }}^{{q\lambda_{1} }} }}{{\mu_{{\alpha_{1} }}^{{q\lambda_{1} }} + \nu_{{\alpha_{1} }}^{{q\lambda_{1} }} }} \times \left( {1 - \left( {1 - \mu_{{\alpha_{1} }}^{q} - \nu_{{\alpha_{1} }}^{q} } \right)^{{\lambda_{1} }} } \right)} \right)^{\frac{1}{q}} } \right\rangle \hfill \\ \,\,\,\,\tilde{ \otimes }\left\langle {\left( {\frac{{\mu_{{\alpha_{1} }}^{{q\lambda_{2} }} }}{{\mu_{{\alpha_{1} }}^{{q\lambda_{2} }} + \nu_{{\alpha_{1} }}^{{q\lambda_{2} }} }} \times \left( {1 - \left( {1 - \mu_{{\alpha_{1} }}^{q} - \nu_{{\alpha_{1} }}^{q} } \right)^{{\lambda_{2} }} } \right)} \right)^{\frac{1}{q}} ,} \right.\left. {\left( {\frac{{\nu_{{\alpha_{1} }}^{{q\lambda_{2} }} }}{{\mu_{{\alpha_{1} }}^{{q\lambda_{2} }} + \nu_{{\alpha_{1} }}^{{q\lambda_{2} }} }} \times \left( {1 - \left( {1 - \mu_{{\alpha_{1} }}^{q} - \nu_{{\alpha_{1} }}^{q} } \right)^{{\lambda_{2} }} } \right)} \right)^{\frac{1}{q}} } \right\rangle \hfill \\ = \left\langle {\left( {\frac{{\frac{{\mu_{{\alpha_{1} }}^{{q\lambda_{1} }} }}{{\mu_{{\alpha_{1} }}^{{q\lambda_{1} }} + \nu_{{\alpha_{1} }}^{{q\lambda_{1} }} }} \times \frac{{\mu_{{\alpha_{1} }}^{{q\lambda_{2} }} }}{{\mu_{{\alpha_{1} }}^{{q\lambda_{2} }} + \nu_{{\alpha_{1} }}^{{q\lambda_{2} }} }}}}{{\frac{{\mu_{{\alpha_{1} }}^{{q\lambda_{1} }} }}{{\mu_{{\alpha_{1} }}^{{q\lambda_{1} }} + \nu_{{\alpha_{1} }}^{{q\lambda_{1} }} }} \times \frac{{\mu_{{\alpha_{1} }}^{{q\lambda_{2} }} }}{{\mu_{{\alpha_{1} }}^{{q\lambda_{2} }} + \nu_{{\alpha_{1} }}^{{q\lambda_{2} }} }} + \frac{{\nu_{{\alpha_{1} }}^{{q\lambda_{1} }} }}{{\mu_{{\alpha_{1} }}^{{q\lambda_{1} }} + \nu_{{\alpha_{1} }}^{{q\lambda_{1} }} }} \times \frac{{\nu_{{\alpha_{1} }}^{{q\lambda_{2} }} }}{{\mu_{{\alpha_{1} }}^{{q\lambda_{2} }} + \nu_{{\alpha_{1} }}^{{q\lambda_{2} }} }}}}} \right.} \right. \times \hfill \\ \,\,\,\,\left. {\left( {1 - \left( {1 - \left( {1 - \left( {1 - \mu_{{\alpha_{1} }}^{q} - \nu_{{\alpha_{1} }}^{q} } \right)^{{\lambda_{1} }} } \right)} \right) \times \left( {1 - \left( {1 - \left( {1 - \mu_{{\alpha_{1} }}^{q} - \nu_{{\alpha_{1} }}^{q} } \right)^{{\lambda_{2} }} } \right)} \right)} \right)} \right)^{\frac{1}{q}} , \hfill \\ \,\,\,\,\,\left( {\frac{{\frac{{\nu_{{\alpha_{1} }}^{{q\lambda_{1} }} }}{{\mu_{{\alpha_{1} }}^{{q\lambda_{1} }} + \nu_{{\alpha_{1} }}^{{q\lambda_{1} }} }} \times \frac{{\nu_{{\alpha_{1} }}^{{q\lambda_{2} }} }}{{\mu_{{\alpha_{1} }}^{{q\lambda_{2} }} + \nu_{{\alpha_{1} }}^{{q\lambda_{2} }} }}}}{{\frac{{\mu_{{\alpha_{1} }}^{{q\lambda_{1} }} }}{{\mu_{{\alpha_{1} }}^{{q\lambda_{1} }} + \nu_{{\alpha_{1} }}^{{q\lambda_{1} }} }} \times \frac{{\mu_{{\alpha_{1} }}^{{q\lambda_{2} }} }}{{\mu_{{\alpha_{1} }}^{{q\lambda_{2} }} + \nu_{{\alpha_{1} }}^{{q\lambda_{2} }} }} + \frac{{\nu_{{\alpha_{1} }}^{{q\lambda_{1} }} }}{{\mu_{{\alpha_{1} }}^{{q\lambda_{1} }} + \nu_{{\alpha_{1} }}^{{q\lambda_{1} }} }} \times \frac{{\nu_{{\alpha_{1} }}^{{q\lambda_{2} }} }}{{\mu_{{\alpha_{1} }}^{{q\lambda_{2} }} + \nu_{{\alpha_{1} }}^{{q\lambda_{2} }} }}}}} \right. \times \hfill \\ \,\,\,\,\,\left. {\left. {\left( {1 - \left( {1 - \left( {1 - \left( {1 - \mu_{{\alpha_{1} }}^{q} - \nu_{{\alpha_{1} }}^{q} } \right)^{{\lambda_{1} }} } \right)} \right) \times \left( {1 - \left( {1 - \left( {1 - \mu_{{\alpha_{1} }}^{q} - \nu_{{\alpha_{1} }}^{q} } \right)^{{\lambda_{2} }} } \right)} \right)} \right)} \right)^{\frac{1}{q}} } \right\rangle \hfill \\ \end{gathered} $$

$$ = \left\langle {\left( {\left( {\frac{{\mu_{{\alpha_{1} }}^{{q(\lambda_{1} + \lambda_{2} )}} }}{{\mu_{{\alpha_{1} }}^{{q(\lambda_{1} + \lambda_{2} )}} + \nu_{{\alpha_{1} }}^{{q(\lambda_{1} + \lambda_{2} )}} }}} \right) \times \left( {1 - \left( {1 - \mu_{{\alpha_{1} }}^{q} - \nu_{{\alpha_{1} }}^{q} } \right)^{{\lambda_{1} + \lambda_{2} }} } \right)} \right)^{\frac{1}{q}} ,} \right.\left. {\,\left( {\left( {\frac{{\nu_{{\alpha_{1} }}^{{q(\lambda_{1} + \lambda_{2} )}} }}{{\mu_{{\alpha_{1} }}^{{q(\lambda_{1} + \lambda_{2} )}} + \nu_{{\alpha_{1} }}^{{q(\lambda_{1} + \lambda_{2} )}} }}} \right) \times \left( {1 - \left( {1 - \mu_{{\alpha_{1} }}^{q} - \nu_{{\alpha_{1} }}^{q} } \right)^{{\lambda_{1} + \lambda_{2} }} } \right)} \right)^{\frac{1}{q}} } \right\rangle $$

Hence, $(\lambda_{1} + \lambda_{2} ) * \alpha_{1} = (\lambda_{1} * \alpha_{1} )\tilde{ \otimes }(\lambda_{2} * \alpha_{2} )$.

4 Weighted fairly aggregation operators

This section is devoted to the study of weighted fairly aggregation operators and their properties.

Definition 4.1

Let $\Omega$ be the collection of q-ROFNs $\alpha_{i} = < \mu_{i} ,\nu_{i} > \,\,(i = 1,2,3,........,n)$. Then we denote the weighted fairly q-rung orthopair fuzzy aggregation operator by $qROFWFA(\alpha_{1} ,\alpha_{2} ,\alpha_{3} ,........,\alpha_{n} )$ and defined as follows:

$$ qROFWFA(\alpha_{1} ,\alpha_{2} ,\alpha_{3} ,........,\alpha_{n} ) = (w_{1} * \alpha_{1} )\tilde{ \otimes }(w_{2} * \alpha_{2} )\tilde{ \otimes }(w_{3} * \alpha_{3} )\tilde{ \otimes }........\tilde{ \otimes }(w_{n} * \alpha_{n} ) $$

where $w_{i}$ is the weight of $\alpha_{i} \,\,(i = 1,2,3,........,n)$ with $w_{i} > 0$ and $\sum\limits_{i = 1}^{n} {w_{i} } = 1$.

Theorem 4.2

Let $\Omega$ be the collection of q-ROFNs $\alpha_{i} = < \mu_{i} ,\nu_{i} > \,\,(i = 1,2,3,........,n)$. Then the aggregated value $qROFWFA(\alpha_{1} ,\alpha_{2} ,\alpha_{3} ,........,\alpha_{n} )$ is also a q-ROFN and is given by:

$$ \begin{gathered} qROFWFA(\alpha_{1} ,\alpha_{2} ,\alpha_{3} ,........,\alpha_{n} ) \hfill \\ = \left\langle {\left( {\frac{{\prod\limits_{i = 1}^{n} {(\mu_{i}^{q} )^{{w_{i} }} } }}{{\prod\limits_{i = 1}^{n} {(\mu_{i}^{q} )^{{w_{i} }} } + \prod\limits_{i = 1}^{n} {(\nu_{i}^{q} )^{{w_{i} }} } }} \times \left( {1 - \prod\limits_{i = 1}^{n} {\left( {1 - \mu_{i}^{q} - \nu_{i}^{q} } \right)^{{w_{i} }} } } \right)} \right)^{\frac{1}{q}} ,} \right.\left. {\left( {\frac{{\prod\limits_{i = 1}^{n} {(\nu_{i}^{q} )^{{w_{i} }} } }}{{\prod\limits_{i = 1}^{n} {(\mu_{i}^{q} )^{{w_{i} }} } + \prod\limits_{i = 1}^{n} {(\nu_{i}^{q} )^{{w_{i} }} } }} \times \left( {1 - \prod\limits_{i = 1}^{n} {\left( {1 - \mu_{i}^{q} - \nu_{i}^{q} } \right)^{{w_{i} }} } } \right)} \right)^{\frac{1}{q}} } \right\rangle \hfill \\ \end{gathered} $$

where $w_{i}$ is the weight of $\alpha_{i} \,\,(i = 1,2,3,........,n)$ with $w_{i} > 0$ and $\sum\limits_{i = 1}^{n} {w_{i} } = 1$.

Proof

The first result holds immediately from definition 4.1. Now to show the rest part, we use the method of mathematical induction on n which are summarized as follows:

Step-1: For n = 1, we have $\alpha_{1} = < \mu_{1} ,\gamma_{1} >$ and $w_{1} = 1$. Then we have,

$$ qROFWFA(\alpha_{1} ) = w_{1} * \alpha_{1} = \left\langle {\left( {\frac{{(\mu_{1}^{q} )^{{w_{1} }} }}{{(\mu_{1}^{q} )^{{w_{1} }} + (\nu_{1}^{q} )^{{w_{1} }} }} \times \left( {1 - \left( {1 - \mu_{1}^{q} - \nu_{1}^{q} } \right)^{{w_{1} }} } \right)} \right)^{\frac{1}{q}} ,} \right.\left. {\left( {\frac{{(\nu_{1}^{q} )^{{w_{1} }} }}{{(\mu_{1}^{q} )^{{w_{1} }} + (\nu_{1}^{q} )^{{w_{1} }} }} \times \left( {1 - \left( {1 - \mu_{1}^{q} - \nu_{1}^{q} } \right)^{{w_{1} }} } \right)} \right)^{\frac{1}{q}} } \right\rangle $$

Thus the result is true for n = 1.

Step-2: Let us assume that the result is true for n = k. Then we have,

$$ \begin{gathered} qROFWFA(\alpha_{1} ,\alpha_{2} ,\alpha_{3} ,........,\alpha_{k} ) \hfill \\ = \left\langle {\left( {\frac{{\prod\limits_{i = 1}^{k} {(\mu_{i}^{q} )^{{w_{i} }} } }}{{\prod\limits_{i = 1}^{k} {(\mu_{i}^{q} )^{{w_{i} }} } + \prod\limits_{i = 1}^{k} {(\nu_{i}^{q} )^{{w_{i} }} } }} \times \left( {1 - \prod\limits_{i = 1}^{k} {\left( {1 - \mu_{i}^{q} - \nu_{i}^{q} } \right)^{{w_{i} }} } } \right)} \right)^{\frac{1}{q}} ,} \right.\left. {\left( {\frac{{\prod\limits_{i = 1}^{k} {(\nu_{i}^{q} )^{{w_{i} }} } }}{{\prod\limits_{i = 1}^{k} {(\mu_{i}^{q} )^{{w_{i} }} } + \prod\limits_{i = 1}^{k} {(\nu_{i}^{q} )^{{w_{i} }} } }} \times \left( {1 - \prod\limits_{i = 1}^{k} {\left( {1 - \mu_{i}^{q} - \nu_{i}^{q} } \right)^{{w_{i} }} } } \right)} \right)^{\frac{1}{q}} } \right\rangle \hfill \\ \end{gathered} $$

Step-3: For n = k + 1,

$$ \begin{gathered} qROFWFA(\alpha_{1} ,\alpha_{2} ,\alpha_{3} ,........,\alpha_{k + 1} ) \hfill \\ = qROFWFA(\alpha_{1} ,\alpha_{2} ,\alpha_{3} ,........,\alpha_{k} )\tilde{ \otimes }(w_{k + 1} * \alpha_{k + 1} ) \hfill \\ = \left\langle {\left( {\frac{{\prod\limits_{i = 1}^{k} {(\mu_{i}^{q} )^{{w_{i} }} } }}{{\prod\limits_{i = 1}^{k} {(\mu_{i}^{q} )^{{w_{i} }} } + \prod\limits_{i = 1}^{k} {(\nu_{i}^{q} )^{{w_{i} }} } }} \times \left( {1 - \prod\limits_{i = 1}^{k} {\left( {1 - \mu_{i}^{q} - \nu_{i}^{q} } \right)^{{w_{i} }} } } \right)} \right)^{\frac{1}{q}} ,} \right.\left. {\left( {\frac{{\prod\limits_{i = 1}^{k} {(\nu_{i}^{q} )^{{w_{i} }} } }}{{\prod\limits_{i = 1}^{k} {(\mu_{i}^{q} )^{{w_{i} }} } + \prod\limits_{i = 1}^{k} {(\nu_{i}^{q} )^{{w_{i} }} } }} \times \left( {1 - \prod\limits_{i = 1}^{k} {\left( {1 - \mu_{i}^{q} - \nu_{i}^{q} } \right)^{{w_{i} }} } } \right)} \right)^{\frac{1}{q}} } \right\rangle \hfill \\ \end{gathered} $$

$$ \begin{gathered} \,\,\,\,\,\tilde{ \otimes }\left\langle {\left( {\frac{{(\mu_{k + 1}^{q} )^{{w_{k + 1} }} }}{{(\mu_{k + 1}^{q} )^{{w_{k + 1} }} + (\nu_{k + 1}^{q} )^{{w_{k + 1} }} }} \times \left( {1 - \left( {1 - \mu_{k + 1}^{q} - \nu_{k + 1}^{q} } \right)^{{w_{k + 1} }} } \right)} \right)^{\frac{1}{q}} ,} \right.\left. {\left( {\frac{{(\nu_{k + 1}^{q} )^{{w_{k + 1} }} }}{{(\mu_{k + 1}^{q} )^{{w_{k + 1} }} + (\nu_{k + 1}^{q} )^{{w_{k + 1} }} }} \times \left( {1 - \left( {1 - \mu_{k + 1}^{q} - \nu_{k + 1}^{q} } \right)^{{w_{k + 1} }} } \right)} \right)^{\frac{1}{q}} } \right\rangle \hfill \\ = \left\langle {\left( {\frac{{\frac{{\prod\limits_{i = 1}^{k} {(\mu_{i}^{q} )^{{w_{i} }} } }}{{\prod\limits_{i = 1}^{k} {(\mu_{i}^{q} )^{{w_{i} }} } + \prod\limits_{i = 1}^{k} {(\nu_{i}^{q} )^{{w_{i} }} } }} \times \frac{{(\mu_{k + 1}^{q} )^{{w_{k + 1} }} }}{{(\mu_{k + 1}^{q} )^{{w_{k + 1} }} + (\nu_{k + 1}^{q} )^{{w_{k + 1} }} }}}}{{\frac{{\prod\limits_{i = 1}^{k} {(\mu_{i}^{q} )^{{w_{i} }} } }}{{\prod\limits_{i = 1}^{k} {(\mu_{i}^{q} )^{{w_{i} }} } + \prod\limits_{i = 1}^{k} {(\nu_{i}^{q} )^{{w_{i} }} } }} \times \frac{{(\mu_{k + 1}^{q} )^{{w_{k + 1} }} }}{{(\mu_{k + 1}^{q} )^{{w_{k + 1} }} + (\nu_{k + 1}^{q} )^{{w_{k + 1} }} }} + \frac{{\prod\limits_{i = 1}^{k} {(\nu_{i}^{q} )^{{w_{i} }} } }}{{\prod\limits_{i = 1}^{k} {(\mu_{i}^{q} )^{{w_{i} }} } + \prod\limits_{i = 1}^{k} {(\nu_{i}^{q} )^{{w_{i} }} } }} \times \frac{{(\nu_{k + 1}^{q} )^{{w_{k + 1} }} }}{{(\mu_{k + 1}^{q} )^{{w_{k + 1} }} + (\nu_{k + 1}^{q} )^{{w_{k + 1} }} }}}}} \right.} \right. \hfill \\ \,\,\,\,\, \times \left. {\left( {1 - \left( {1 - \left( {1 - \prod\limits_{i = 1}^{k} {\left( {1 - \mu_{i}^{q} - \nu_{i}^{q} } \right)^{{w_{i} }} } } \right)} \right)\left( {1 - \left( {1 - \left( {1 - \mu_{k + 1}^{q} - \nu_{k + 1}^{q} } \right)^{{w_{k + 1} }} } \right)} \right)} \right)} \right)^{\frac{1}{q}} , \hfill \\ \,\,\,\,\,\left( {\frac{{\frac{{\prod\limits_{i = 1}^{k} {(\nu_{i}^{q} )^{{w_{i} }} } }}{{\prod\limits_{i = 1}^{k} {(\mu_{i}^{q} )^{{w_{i} }} } + \prod\limits_{i = 1}^{k} {(\nu_{i}^{q} )^{{w_{i} }} } }} \times \frac{{(\nu_{k + 1}^{q} )^{{w_{k + 1} }} }}{{(\mu_{k + 1}^{q} )^{{w_{k + 1} }} + (\nu_{k + 1}^{q} )^{{w_{k + 1} }} }}}}{{\frac{{\prod\limits_{i = 1}^{k} {(\mu_{i}^{q} )^{{w_{i} }} } }}{{\prod\limits_{i = 1}^{k} {(\mu_{i}^{q} )^{{w_{i} }} } + \prod\limits_{i = 1}^{k} {(\nu_{i}^{q} )^{{w_{i} }} } }} \times \frac{{(\mu_{k + 1}^{q} )^{{w_{k + 1} }} }}{{(\mu_{k + 1}^{q} )^{{w_{k + 1} }} + (\nu_{k + 1}^{q} )^{{w_{k + 1} }} }} + \frac{{\prod\limits_{i = 1}^{k} {(\nu_{i}^{q} )^{{w_{i} }} } }}{{\prod\limits_{i = 1}^{k} {(\mu_{i}^{q} )^{{w_{i} }} } + \prod\limits_{i = 1}^{k} {(\nu_{i}^{q} )^{{w_{i} }} } }} \times \frac{{(\nu_{k + 1}^{q} )^{{w_{k + 1} }} }}{{(\mu_{k + 1}^{q} )^{{w_{k + 1} }} + (\nu_{k + 1}^{q} )^{{w_{k + 1} }} }}}}} \right. \hfill \\ \,\,\,\,\left. { \times \left. {\left( {1 - \left( {1 - \left( {1 - \prod\limits_{i = 1}^{k} {\left( {1 - \mu_{i}^{q} - \nu_{i}^{q} } \right)^{{w_{i} }} } } \right)} \right)\left( {1 - \left( {1 - \left( {1 - \mu_{k + 1}^{q} - \nu_{k + 1}^{q} } \right)^{{w_{k + 1} }} } \right)} \right)} \right)} \right)^{\frac{1}{q}} } \right\rangle \hfill \\ = = \left\langle {\left( {\frac{{\prod\limits_{i = 1}^{k} {(\mu_{i}^{q} )^{{w_{i} }} } \times (\mu_{k + 1}^{q} )^{{w_{k + 1} }} }}{{\prod\limits_{i = 1}^{k} {(\mu_{i}^{q} )^{{w_{i} }} } \times (\mu_{k + 1}^{q} )^{{w_{k + 1} }} + \prod\limits_{i = 1}^{k} {(\nu_{i}^{q} )^{{w_{i} }} } \times (\nu_{k + 1}^{q} )^{{w_{k + 1} }} }} \times \left. {\left( {1 - \prod\limits_{i = 1}^{k} {\left( {1 - \mu_{i}^{q} - \nu_{i}^{q} } \right)^{{w_{i} }} \times \left( {1 - \mu_{k + 1}^{q} - \nu_{k + 1}^{q} } \right)^{{w_{k + 1} }} } } \right)} \right)^{\frac{1}{q}} } \right.} \right., \hfill \\ \,\,\,\,\,\,\,\,\left. {\left( {\frac{{\prod\limits_{i = 1}^{k} {(\nu_{i}^{q} )^{{w_{i} }} } \times (\nu_{k + 1}^{q} )^{{w_{k + 1} }} }}{{\prod\limits_{i = 1}^{k} {(\mu_{i}^{q} )^{{w_{i} }} } \times (\mu_{k + 1}^{q} )^{{w_{k + 1} }} + \prod\limits_{i = 1}^{k} {(\nu_{i}^{q} )^{{w_{i} }} } \times (\nu_{k + 1}^{q} )^{{w_{k + 1} }} }} \times \left. {\left( {1 - \prod\limits_{i = 1}^{k} {\left( {1 - \mu_{i}^{q} - \nu_{i}^{q} } \right)^{{w_{i} }} \times \left( {1 - \mu_{k + 1}^{q} - \nu_{k + 1}^{q} } \right)^{{w_{k + 1} }} } } \right)} \right)^{\frac{1}{q}} } \right.} \right\rangle \hfill \\ \end{gathered} $$

$$ = \left\langle {\left( {\frac{{\prod\limits_{i = 1}^{k + 1} {(\mu_{i}^{q} )^{{w_{i} }} } }}{{\prod\limits_{i = 1}^{k + 1} {(\mu_{i}^{q} )^{{w_{i} }} } + \prod\limits_{i = 1}^{k + 1} {(\nu_{i}^{q} )^{{w_{i} }} } }} \times \left. {\left( {1 - \prod\limits_{i = 1}^{k + 1} {\left( {1 - \mu_{i}^{q} - \nu_{i}^{q} } \right)^{{w_{i} }} } } \right)} \right)^{\frac{1}{q}} } \right.} \right.,\left. {\left( {\frac{{\prod\limits_{i = 1}^{k + 1} {(\nu_{i}^{q} )^{{w_{i} }} } }}{{\prod\limits_{i = 1}^{k + 1} {(\mu_{i}^{q} )^{{w_{i} }} } + \prod\limits_{i = 1}^{k + 1} {(\nu_{i}^{q} )^{{w_{i} }} } }} \times \left. {\left( {1 - \prod\limits_{i = 1}^{k + 1} {\left( {1 - \mu_{i}^{q} - \nu_{i}^{q} } \right)^{{w_{i} }} } } \right)} \right)^{\frac{1}{q}} } \right.} \right\rangle $$

Thus the result holds good for n = k + 1 also. Therefore, by the principle of Induction on ‘n’, the result is true for all n.

The proposed aggregation operator satisfies few certain properties which are presented in the form of the following theorems.

Theorem 4.3

(Idempotency) Let $\alpha_{0} = < \mu_{0} ,\nu_{0} >$ be a q-ROFN and $\alpha_{i} = < \mu_{i} ,\nu_{i} > \,\,(i = 1,2,3,........,n)$ be a collection of q-ROFNs such that $\alpha_{i} = \alpha_{0}$ for all i. Then, $qROFWFA(\alpha_{1} ,\alpha_{2} ,\alpha_{3} ,........,\alpha_{n} ) = \alpha_{0}$.

Proof

Since $\alpha_{i} = \alpha_{0}$, we have $\mu_{i} = \mu_{0}$ and $\nu_{i} = \nu_{0}$ for all i.

So $qROFWFA(\alpha_{1} ,\alpha_{2} ,\alpha_{3} ,........,\alpha_{n} )$

$$ \begin{gathered} = \left\langle {\left( {\frac{{\prod\limits_{i = 1}^{n} {(\mu_{i}^{q} )^{{w_{i} }} } }}{{\prod\limits_{i = 1}^{n} {(\mu_{i}^{q} )^{{w_{i} }} } + \prod\limits_{i = 1}^{n} {(\nu_{i}^{q} )^{{w_{i} }} } }} \times \left( {1 - \prod\limits_{i = 1}^{n} {\left( {1 - \mu_{i}^{q} - \nu_{i}^{q} } \right)^{{w_{i} }} } } \right)} \right)^{\frac{1}{q}} ,} \right.\left. {\left( {\frac{{\prod\limits_{i = 1}^{n} {(\nu_{i}^{q} )^{{w_{i} }} } }}{{\prod\limits_{i = 1}^{n} {(\mu_{i}^{q} )^{{w_{i} }} } + \prod\limits_{i = 1}^{n} {(\nu_{i}^{q} )^{{w_{i} }} } }} \times \left( {1 - \prod\limits_{i = 1}^{n} {\left( {1 - \mu_{i}^{q} - \nu_{i}^{q} } \right)^{{w_{i} }} } } \right)} \right)^{\frac{1}{q}} } \right\rangle \hfill \\ = \left\langle {\left( {\frac{{\prod\limits_{i = 1}^{n} {(\mu_{0}^{q} )^{{w_{i} }} } }}{{\prod\limits_{i = 1}^{n} {(\mu_{0}^{q} )^{{w_{i} }} } + \prod\limits_{i = 1}^{n} {(\nu_{0}^{q} )^{{w_{i} }} } }} \times \left( {1 - \prod\limits_{i = 1}^{n} {\left( {1 - \mu_{0}^{q} - \nu_{0}^{q} } \right)^{{w_{i} }} } } \right)} \right)^{\frac{1}{q}} ,} \right.\left. {\left( {\frac{{\prod\limits_{i = 1}^{n} {(\nu_{0}^{q} )^{{w_{i} }} } }}{{\prod\limits_{i = 1}^{n} {(\mu_{0}^{q} )^{{w_{i} }} } + \prod\limits_{i = 1}^{n} {(\nu_{0}^{q} )^{{w_{i} }} } }} \times \left( {1 - \prod\limits_{i = 1}^{n} {\left( {1 - \mu_{0}^{q} - \nu_{0}^{q} } \right)^{{w_{i} }} } } \right)} \right)^{\frac{1}{q}} } \right\rangle \hfill \\ = \left\langle {\left( {\frac{{(\mu_{0}^{q} )^{{\sum\limits_{i = 1}^{n} {w_{i} } }} }}{{(\mu_{0}^{q} )^{{\sum\limits_{i = 1}^{n} {w_{i} } }} + (\nu_{0}^{q} )^{{\sum\limits_{i = 1}^{n} {w_{i} } }} }} \times \left( {1 - \left( {1 - \mu_{0}^{q} - \nu_{0}^{q} } \right)^{{\sum\limits_{i = 1}^{n} {w_{i} } }} } \right)} \right)^{\frac{1}{q}} ,} \right.\left. {\left( {\frac{{(\nu_{0}^{q} )^{{\sum\limits_{i = 1}^{n} {w_{i} } }} }}{{(\mu_{0}^{q} )^{{\sum\limits_{i = 1}^{n} {w_{i} } }} + (\nu_{0}^{q} )^{{\sum\limits_{i = 1}^{n} {w_{i} } }} }} \times \left( {1 - \left( {1 - \mu_{0}^{q} - \nu_{0}^{q} } \right)^{{\sum\limits_{i = 1}^{n} {w_{i} } }} } \right)} \right)^{\frac{1}{q}} } \right\rangle \hfill \\ \end{gathered} $$

$$ \begin{gathered} = \left\langle {\left( {\frac{{(\mu_{0}^{q} )}}{{(\mu_{0}^{q} ) + (\nu_{0}^{q} )}} \times \left( {1 - \left( {1 - \mu_{0}^{q} - \nu_{0}^{q} } \right)} \right)} \right)^{\frac{1}{q}} ,} \right.\left. {\left( {\frac{{(\nu_{0}^{q} )}}{{(\mu_{0}^{q} ) + (\nu_{0}^{q} )}} \times \left( {1 - \left( {1 - \mu_{0}^{q} - \nu_{0}^{q} } \right)} \right)} \right)^{\frac{1}{q}} } \right\rangle \hfill \\ = < \mu_{0} ,\nu_{0} > = \alpha_{0} . \hfill \\ \end{gathered} $$

Theorem 4.4

(Boundedness) Let $\alpha_{i} = < \mu_{i} ,\nu_{i} > \,\,(i = 1,2,3,........,n)$ be a collection of q-ROFNs. Then for $qROFWFA(\alpha_{1} ,\alpha_{2} ,\alpha_{3} ,........,\alpha_{n} ) = < \mu_{k} ,\nu_{k} >$ we have,

• a. $\mathop {\min }\limits_{i} \left\{ {\mu_{i}^{q} + \nu_{i}^{q} } \right\} \le \mu_{k}^{q} + \nu_{k}^{q} \le \mathop {\max }\limits_{i} \left\{ {\mu_{i}^{q} + \nu_{i}^{q} } \right\}$

• b. $\frac{{\mathop {\min }\limits_{i} \left\{ {\mu_{i}^{q} + \nu_{i}^{q} } \right\} \times \mathop {\min }\limits_{i} \left\{ {\mu_{i}^{q} } \right\}}}{{\mathop {\max }\limits_{i} \left\{ {\nu_{i}^{q} } \right\} + \mathop {\min }\limits_{i} \left\{ {\mu_{i}^{q} } \right\}}} \le \mu_{k}^{q} \le \mathop {\min }\limits_{i} \left\{ {\frac{{\mathop {\max }\limits_{i} \left\{ {\mu_{i}^{q} + \nu_{i}^{q} } \right\} \times \mathop {\max }\limits_{i} \left\{ {\mu_{i}^{q} } \right\}}}{{\mathop {\min }\limits_{i} \left\{ {\nu_{i}^{q} } \right\} + \mathop {\max }\limits_{i} \left\{ {\mu_{i}^{q} } \right\}}},1} \right\}$

• c. $\frac{{\mathop {\min }\limits_{i} \left\{ {\mu_{i}^{q} + \nu_{i}^{q} } \right\} \times \mathop {\min }\limits_{i} \left\{ {\nu_{i}^{q} } \right\}}}{{\mathop {\max }\limits_{i} \left\{ {\mu_{i}^{q} } \right\} + \mathop {\min }\limits_{i} \left\{ {\nu_{i}^{q} } \right\}}} \le \nu_{k}^{q} \le \mathop {\min }\limits_{i} \left\{ {\frac{{\mathop {\max }\limits_{i} \left\{ {\mu_{i}^{q} + \gamma_{i}^{q} } \right\} \times \mathop {\max }\limits_{i} \left\{ {\nu_{i}^{q} } \right\}}}{{\mathop {\max }\limits_{i} \left\{ {\nu_{i}^{q} } \right\} + \mathop {\min }\limits_{i} \left\{ {\mu_{i}^{q} } \right\}}},1} \right\}.$

Proof

(a) $\mathop {\min }\limits_{i} \left\{ {\mu_{i}^{q} + \nu_{i}^{q} } \right\}$.

$$ \begin{gathered} = 1 - \left( {1 - \mathop {\min }\limits_{i} \left\{ {\mu_{i}^{q} + \nu_{i}^{q} } \right\}} \right) = 1 - \left( {1 - \mathop {\min }\limits_{i} \left\{ {\mu_{i}^{q} + \nu_{i}^{q} } \right\}} \right)^{{\sum\limits_{i = 1}^{n} {w_{i} } }} \hfill \\ = 1 - \prod\limits_{i = 1}^{n} {\left( {1 - \mathop {\min }\limits_{i} \left\{ {\mu_{i}^{q} + \nu_{i}^{q} } \right\}} \right)}^{{w_{i} }} \le 1 - \prod\limits_{i = 1}^{n} {\left( {1 - \mu_{i}^{q} - \nu_{i}^{q} } \right)}^{{w_{i} }} \le 1 - \prod\limits_{i = 1}^{n} {\left( {1 - \mathop {\max }\limits_{i} \left\{ {\mu_{i}^{q} + \nu_{i}^{q} } \right\}} \right)} \hfill \\ \end{gathered} $$

$$ = 1 - \left( {1 - \mathop {\max }\limits_{i} \left\{ {\mu_{i}^{q} + \nu_{i}^{q} } \right\}} \right)^{{\sum\limits_{i = 1}^{n} {w_{i} } }} = \mathop {\max }\limits_{i} \left\{ {\mu_{i}^{q} + \nu_{i}^{q} } \right\} $$

(1)

Now by theorem 4.3, we get

$$ \begin{gathered} \mu_{k} = \left( {\frac{{\prod\limits_{i = 1}^{n} {(\mu_{i}^{q} )^{{w_{i} }} } }}{{\prod\limits_{i = 1}^{n} {(\mu_{i}^{q} )^{{w_{i} }} } + \prod\limits_{i = 1}^{n} {(\nu_{i}^{q} )^{{w_{i} }} } }} \times \left( {1 - \prod\limits_{i = 1}^{n} {\left( {1 - \mu_{i}^{q} - \nu_{i}^{q} } \right)^{{w_{i} }} } } \right)} \right)^{\frac{1}{q}} , \hfill \\ \vartheta_{k} = \left( {\frac{{\prod\limits_{i = 1}^{n} {(\nu_{i}^{q} )^{{w_{i} }} } }}{{\prod\limits_{i = 1}^{n} {(\mu_{i}^{q} )^{{w_{i} }} } + \prod\limits_{i = 1}^{n} {(\nu_{i}^{q} )^{{w_{i} }} } }} \times \left( {1 - \prod\limits_{i = 1}^{n} {\left( {1 - \mu_{i}^{q} - \nu_{i}^{q} } \right)^{{w_{i} }} } } \right)} \right)^{\frac{1}{q}} . \hfill \\ \end{gathered} $$

Therefore, $\mu_{k}^{q} + \nu_{k}^{q} = 1 - \prod\limits_{i = 1}^{n} {\left( {1 - \mu_{i}^{q} - \nu_{i}^{q} } \right)^{{w_{i} }} } .$

Consequently, $\mathop {\min }\limits_{i} \left\{ {\mu_{i}^{q} + \nu_{i}^{q} } \right\} \le \mu_{k}^{q} + \nu_{k}^{q} \le \mathop {\max }\limits_{i} \left\{ {\mu_{i}^{q} + \nu_{i}^{q} } \right\}$.

(b) Since $\mathop {\min }\limits_{i} \left\{ {\mu_{i} } \right\} \le \mu_{i} \le \mathop {\max }\limits_{i} \left\{ {\mu_{i} } \right\}$ and $\mathop {\min }\limits_{i} \left\{ {\nu_{i} } \right\} \le \nu_{i} \le \mathop {\max }\limits_{i} \left\{ {\nu_{i} } \right\}$, we have

$$ \begin{gathered} \frac{{\mathop {\min }\limits_{i} \left\{ {\nu_{i}^{q} } \right\}}}{{\mathop {\max }\limits_{i} \left\{ {\mu_{i}^{q} } \right\}}} \le \frac{{\nu_{i}^{q} }}{{\mu_{i}^{q} }} \le \frac{{\mathop {\max }\limits_{i} \left\{ {\nu_{i}^{q} } \right\}}}{{\mathop {\min }\limits_{i} \left\{ {\mu_{i}^{q} } \right\}}} \hfill \\ \Rightarrow \frac{{\mathop {\min }\limits_{i} \left\{ {\nu_{i}^{q} } \right\}}}{{\mathop {\max }\limits_{i} \left\{ {\mu_{i}^{q} } \right\}}} \le \prod\limits_{i = 1}^{n} {\left( {\frac{{\nu_{i}^{q} }}{{\mu_{i}^{q} }}} \right)^{{w_{i} }} } \le \frac{{\mathop {\max }\limits_{i} \left\{ {\nu_{i}^{q} } \right\}}}{{\mathop {\min }\limits_{i} \left\{ {\mu_{i}^{q} } \right\}}} \hfill \\ \Rightarrow \frac{{\mathop {\min }\limits_{i} \left\{ {\nu_{i}^{q} } \right\} + \mathop {\max }\limits_{i} \left\{ {\mu_{i}^{q} } \right\}}}{{\mathop {\max }\limits_{i} \left\{ {\mu_{i}^{q} } \right\}}} \le \frac{{\prod\limits_{i = 1}^{n} {\left( {\nu_{i}^{q} } \right)^{{w_{i} }} } + \prod\limits_{i = 1}^{n} {\left( {\mu_{i}^{q} } \right)^{{w_{i} }} } }}{{\prod\limits_{i = 1}^{n} {\left( {\mu_{i}^{q} } \right)^{{w_{i} }} } }} \le \frac{{\mathop {\max }\limits_{i} \left\{ {\nu_{i}^{q} } \right\} + \mathop {\min }\limits_{i} \left\{ {\mu_{i}^{q} } \right\}}}{{\mathop {\min }\limits_{i} \left\{ {\mu_{i}^{q} } \right\}}} \hfill \\ \Rightarrow \frac{{\mathop {\min }\limits_{i} \left\{ {\mu_{i}^{q} } \right\}}}{{\mathop {\max }\limits_{i} \left\{ {\nu_{i}^{q} } \right\} + \mathop {\min }\limits_{i} \left\{ {\mu_{i}^{q} } \right\}}} \le \frac{{\prod\limits_{i = 1}^{n} {\left( {\mu_{i}^{q} } \right)^{{w_{i} }} } }}{{\prod\limits_{i = 1}^{n} {\left( {\nu_{i}^{q} } \right)^{{w_{i} }} } + \prod\limits_{i = 1}^{n} {\left( {\mu_{i}^{q} } \right)^{{w_{i} }} } }} \le \frac{{\mathop {\max }\limits_{i} \left\{ {\mu_{i}^{q} } \right\}}}{{\mathop {\min }\limits_{i} \left\{ {\nu_{i}^{q} } \right\} + \mathop {\max }\limits_{i} \left\{ {\mu_{i}^{q} } \right\}}} \hfill \\ \end{gathered} $$

(2)

Also from (1) we have

$$ \mathop {\min }\limits_{i} \left\{ {\mu_{i}^{q} + \nu_{i}^{q} } \right\} \le 1 - \prod\limits_{i = 1}^{n} {\left( {1 - \mu_{i}^{q} - \nu_{i}^{q} } \right)^{{w_{i} }} \le \mathop {\max }\limits_{i} \left\{ {\mu_{i}^{q} + \nu_{i}^{q} } \right\}} $$

(3)

Combining (2) and (3) we get,

$$ \frac{{\mathop {\min }\limits_{i} \left\{ {\mu_{i}^{q} + \nu_{i}^{q} } \right\} \times \mathop {\min }\limits_{i} \left\{ {\mu_{i}^{q} } \right\}}}{{\mathop {\max }\limits_{i} \left\{ {\nu_{i}^{q} } \right\} + \mathop {\min }\limits_{i} \left\{ {\mu_{i}^{q} } \right\}}} \le \mu_{k}^{q} \le \frac{{\mathop {\max }\limits_{i} \left\{ {\mu_{i}^{q} + \nu_{i}^{q} } \right\} \times \mathop {\max }\limits_{i} \left\{ {\mu_{i}^{q} } \right\}}}{{\mathop {\min }\limits_{i} \left\{ {\nu_{i}^{q} } \right\} + \mathop {\max }\limits_{i} \left\{ {\mu_{i}^{q} } \right\}}} $$

Further by definition of q-ROFN and theorem, we get $\mu_{k}^{q} \le 1$. Thus we have,

$\frac{{\mathop {\min }\limits_{i} \left\{ {\mu_{i}^{q} + \nu_{i}^{q} } \right\} \times \mathop {\min }\limits_{i} \left\{ {\mu_{i}^{q} } \right\}}}{{\mathop {\max }\limits_{i} \left\{ {\nu_{i}^{q} } \right\} + \mathop {\min }\limits_{i} \left\{ {\mu_{i}^{q} } \right\}}} \le \mu_{k}^{q} \le \mathop {\min }\limits_{i} \left\{ {\frac{{\mathop {\max }\limits_{i} \left\{ {\mu_{i}^{q} + \nu_{i}^{q} } \right\} \times \mathop {\max }\limits_{i} \left\{ {\mu_{i}^{q} } \right\}}}{{\mathop {\min }\limits_{i} \left\{ {\nu_{i}^{q} } \right\} + \mathop {\max }\limits_{i} \left\{ {\mu_{i}^{q} } \right\}}},1} \right\}$.

Theorem 4.5

(Monotonicity) Let $\alpha_{i} = < \mu_{i} ,\nu_{i} > \,\,{\text{and}}\,\,\alpha^{\prime}_{i} = < \mu^{\prime}_{i} ,\nu^{\prime}_{i} > \,(i = 1,2,3,........,n)$ be two collection of q-ROFNs. Also let $qROFWFA(\alpha_{1} ,\alpha_{2} ,\alpha_{3} ,........,\alpha_{n} ) = \alpha = < \mu ,\nu >$ and $qROFWFA(\alpha^{\prime}_{1} ,\alpha^{\prime}_{2} ,\alpha^{\prime}_{3} ,........,\alpha^{\prime}_{n} ) =$ $\alpha^{\prime} = < \mu^{\prime},\nu^{\prime} >$ we have,

• a. $\mu^{q} + \nu^{q} \le \mu^{\prime q} + \nu^{\prime q} \,\,{\text{if}}\,\,\mu_{i}^{q} + \nu_{i}^{q} \le \mu_{i}^{\prime q} + \nu{i}^{\prime q}$

• b. $\mu^{q} \le\mu^{\prime q} \,\,{\text{and}}\,\,\nu_{{}}^{q} \ge \nu^{\prime q} \,\,{\text{if}}\,\,\mu_{i}^{q} \le \mu_{i}^{\prime q} \,\,{\text{and}}\,\,\mu_{i}^{q} + \nu_{i}^{q} = \mu_{i}^{\prime q} + \nu{i}^{\prime q}$

• c. $qROFWFA(\alpha_{1} ,\alpha_{2} ,\alpha_{3} ,........,\alpha_{n} ) \prec qROFWFA(\alpha^{\prime}_{1} ,\alpha^{\prime}_{2} ,\alpha^{\prime}_{3} ,........,\alpha^{\prime}_{n} )$ if $\mu_{i}^{q} + \nu_{i}^{q} = \mu_{i}^{\prime q} + \nu{i}^{\prime q}$ and $\mu_{i} \le \mu^{\prime}_{i}$.

Proof

Applying theorem 4.2 to the collections $\alpha_{i} = < \mu_{i} ,\nu_{i} > \,\,{\text{and}}\,\,\alpha^{\prime}_{i} = < \mu^{\prime}_{i} ,\nu^{\prime}_{i} > \,(i = 1,2,3,........,n)$, we get:

$$ \begin{gathered} \mu^{q} = \frac{{\prod\limits_{i = 1}^{n} {(\mu_{i}^{q} )^{{w_{i} }} } }}{{\prod\limits_{i = 1}^{n} {(\mu_{i}^{q} )^{{w_{i} }} } + \prod\limits_{i = 1}^{n} {(\nu_{i}^{q} )^{{w_{i} }} } }} \times \left( {1 - \prod\limits_{i = 1}^{n} {\left( {1 - \mu_{i}^{q} - \nu_{i}^{q} } \right)^{{w_{i} }} } } \right),\nu^{q} = \frac{{\prod\limits_{i = 1}^{n} {(\nu_{i}^{q} )^{{w_{i} }} } }}{{\prod\limits_{i = 1}^{n} {(\mu_{i}^{q} )^{{w_{i} }} } + \prod\limits_{i = 1}^{n} {(\nu_{i}^{q} )^{{w_{i} }} } }} \times \left( {1 - \prod\limits_{i = 1}^{n} {\left( {1 - \mu_{i}^{q} - \nu_{i}^{q} } \right)^{{w_{i} }} } } \right), \hfill \\ \mu^{\prime q} = \frac{{\prod\limits_{i = 1}^{n} {(\mu_{i}^{\prime q} )^{{w_{i} }} } }}{{\prod\limits_{i = 1}^{n} {(\mu_{i}^{\prime q} )^{{w_{i} }} } + \prod\limits_{i = 1}^{n} {(\nu_{i}^{\prime q} )^{{w_{i} }} } }} \times \left( {1 - \prod\limits_{i = 1}^{n} {\left( {1 - \mu_{i}^{\prime q} - \nu_{i}^{\prime q} } \right)^{{w_{i} }} } } \right),\,\nu^{\prime q} = \frac{{\prod\limits_{i = 1}^{n} {(\nu_{i}^{\prime q} )^{{w_{i} }} } }}{{\prod\limits_{i = 1}^{n} {(\mu_{i}^{\prime q} )^{{w_{i} }} } + \prod\limits_{i = 1}^{n} {(\nu_{i}^{\prime q} )^{{w_{i} }} } }} \times \left( {1 - \prod\limits_{i = 1}^{n} {\left( {1 - \mu_{i}^{\prime q} - \nu_{i}^{\prime q} } \right)^{{w_{i} }} } } \right). \hfill \\ \end{gathered} $$

Based on these, we have.

(a) if $\mu_{i}^{q} + \nu_{i}^{q} \le \mu_{i}^{\prime q} + \nu{i}^{\prime q}$, then we have

$$ \mu^{q} +\nu^{q} \le 1 - \prod\limits_{i = 1}^{n} {\left( {1 - \mu_{i}^{q} - \nu_{i}^{q} } \right)^{{w_{i} }} } \le 1 - \prod\limits_{i = 1}^{n} {\left( {1 - \mu_{i}^{\prime q} - \nu{i}^{\prime q} } \right)^{{w_{i} }} } \le\mu^{\prime q} + \nu^{\prime q} . $$

(b) If $\mu_{i}^{q} \le \mu_{i}^{\prime q} \,\,{\text{and}}\,\,\mu_{i}^{q} + \nu_{i}^{q} = \mu_{i}^{\prime q} + \nu{i}^{\prime q}$ then clearly $\nu_{i}^{q} \ge \nu{i}^{\prime q}$. Thus $\frac{{\nu_{i}^{q} }}{{\mu_{i}^{q} }} \ge \frac{{\nu{i}^{\prime q} }}{{\mu_{i}^{\prime q} }}$ which gives.

$\prod\limits_{i = 1}^{n} {\left( {\frac{{\nu_{i}^{q} }}{{\mu_{i}^{q} }}} \right)}^{{w_{i} }} \ge \prod\limits_{i = 1}^{n} {\left( {\frac{{\nu{i}^{\prime q} }}{{\mu_{i}^{\prime q} }}} \right)}^{{w_{i} }}$.

Therefore, $\frac{1}{{1 + \prod\limits_{i = 1}^{n} {\left( {\frac{{\nu_{i}^{q} }}{{\mu_{i}^{q} }}} \right)}^{{w_{i} }} }} \le \frac{1}{{1 + \prod\limits_{i = 1}^{n} {\left( {\frac{{\nu{i}^{\prime q} }}{{\mu_{i}^{\prime q} }}} \right)}^{{w_{i} }} }}$ which gives $\frac{{\prod\limits_{i = 1}^{n} {\left( {\mu_{i}^{q} } \right)}^{{w_{i} }} }}{{1 + \prod\limits_{i = 1}^{n} {\left( {\frac{{\nu_{i}^{q} }}{{\mu_{i}^{q} }}} \right)}^{{w_{i} }} }} \le \frac{{\prod\limits_{i = 1}^{n} {\left( {\mu_{i}^{\prime q} } \right)}^{{w_{i} }} }}{{1 + \prod\limits_{i = 1}^{n} {\left( {\frac{{\nu{i}^{\prime q} }}{{\mu_{i}^{\prime q} }}} \right)}^{{w_{i} }} }}$. Then,

$\mu^{q}$$= \frac{{\prod\limits_{i = 1}^{n} {(\mu_{i}^{q} )^{{w_{i} }} } }}{{\prod\limits_{i = 1}^{n} {(\mu_{i}^{q} )^{{w_{i} }} } + \prod\limits_{i = 1}^{n} {(\nu_{i}^{q} )^{{w_{i} }} } }} \times \left( {1 - \prod\limits_{i = 1}^{n} {\left( {1 - \mu_{i}^{q} - \nu_{i}^{q} } \right)^{{w_{i} }} } } \right) \le \frac{{\prod\limits_{i = 1}^{n} {(\mu_{i}^{\prime q} )^{{w_{i} }} } }}{{\prod\limits_{i = 1}^{n} {(\mu_{i}^{\prime q} )^{{w_{i} }} } + \prod\limits_{i = 1}^{n} {(\nu{i}^{\prime q} )^{{w_{i} }} } }} \times \left( {1 - \prod\limits_{i = 1}^{n} {\left( {1 - \mu_{i}^{\prime q} - \nu{i}^{\prime q} } \right)^{{w_{i} }} } } \right) = \mu^{\prime q}$.

Similarly we can obtain, $\,\nu_{{}}^{q} \ge \nu^{\prime q} \,$.

(c) Follows from part (b) and definition 2.4.

5 Ordered weighted fairly aggregation operator

In this section, motivated from ordered weighted aggregation operator, we present q-rung orthopair fuzzy ordered weighted fairly aggregation operator and study its properties.

Definition 5.1

Let $\Omega$ be the collection of q-ROFNs $\alpha_{i} = < \mu_{i} ,\nu_{i} > \,\,(i = 1,2,3,........,n)$. Then we denote the q-rung orthopair fuzzy ordered weighted fairly aggregation operator by $qROFOWFA(\alpha_{1} ,\alpha_{2} ,\alpha_{3} ,........,\alpha_{n} )$ and defined as follows:

$$ qROFOWFA(\alpha_{1} ,\alpha_{2} ,\alpha_{3} ,........,\alpha_{n} ) = \mathop {\tilde{ \otimes }}\limits_{i = 1}^{n} (w_{i} * \alpha_{\sigma (i)} ) $$

where $\sigma :\{ 1,2,3,.......,n\} \to \{ 1,2,3,.......,n\}$ is a permutation map such that $\alpha_{\sigma (i - 1)} \ge \alpha_{\sigma (i)}$ for $i = 1,2,3,.......,n$ and $w_{i}$ is the weight of $\alpha_{i} \,\,(i = 1,2,3,........,n)$ with $w_{i} > 0$ and $\sum\limits_{i = 1}^{n} {w_{i} } = 1$.

Theorem 5.2

Let $\Omega$ be the collection of q-ROFNs $\alpha_{i} = < \mu_{i} ,\nu_{i} > \,\,(i = 1,2,3,........,n)$. Then the aggregated value $qROFOWFA(\alpha_{1} ,\alpha_{2} ,\alpha_{3} ,........,\alpha_{n} )$ is also a q-ROFN and is given by:$\begin{gathered} qROFOWFA(\alpha_{1} ,\alpha_{2} ,\alpha_{3} ,........,\alpha_{n} ) \hfill \\ = \left\langle {\left( {\frac{{\prod\limits_{i = 1}^{n} {(\mu_{\sigma (i)}^{q} )^{{w_{i} }} } }}{{\prod\limits_{i = 1}^{n} {(\mu_{\sigma (i)}^{q} )^{{w_{i} }} } + \prod\limits_{i = 1}^{n} {(\nu_{\sigma (i)}^{q} )^{{w_{i} }} } }}\left( {1 - \prod\limits_{i = 1}^{n} {\left( {1 - \mu_{\sigma (i)}^{q} - \nu_{\sigma (i)}^{q} } \right)^{{w_{i} }} } } \right)} \right)^{\frac{1}{q}} ,} \right.\left. {\left( {\frac{{\prod\limits_{i = 1}^{n} {(\nu_{\sigma (i)}^{q} )^{{w_{i} }} } }}{{\prod\limits_{i = 1}^{n} {(\mu_{\sigma (i)}^{q} )^{{w_{i} }} } + \prod\limits_{i = 1}^{n} {(\nu_{\sigma (i)}^{q} )^{{w_{i} }} } }}\left( {1 - \prod\limits_{i = 1}^{n} {\left( {1 - \mu_{\sigma (i)}^{q} - \nu_{\sigma (i)}^{q} } \right)^{{w_{i} }} } } \right)} \right)^{\frac{1}{q}} } \right\rangle \hfill \\ \end{gathered}$where $w_{i}$ is the weight of $\alpha_{i} \,\,(i = 1,2,3,........,n)$ with $w_{i} > 0$ and $\sum\limits_{i = 1}^{n} {w_{i} } = 1$.

Proof

Similar to the proof of theorem 4.2.

The proposed aggregation operator satisfies few certain properties which are presented in the form of the following theorems.

Theorem 5.3

(Idempotency) Let $\alpha_{0} = < \mu_{0} ,\nu_{0} >$ be a q-ROFN and $\alpha_{i} = < \mu_{i} ,\nu_{i} > \,\,(i = 1,2,3,........,n)$ be a collection of q-ROFNs such that $\alpha_{i} = \alpha_{0}$ for all i. Then $qROFOWFA(\alpha_{1} ,\alpha_{2} ,\alpha_{3} ,........,\alpha_{n} ) = \alpha_{0}$.

Proof

Proof is similar to the theorem 4.3.

Theorem 5.4

(Boundedness) Let $\alpha_{i} = < \mu_{i} ,\nu_{i} > \,\,(i = 1,2,3,........,n)$ be a collection of q-ROFNs. Then for $qROFOWFA(\alpha_{1} ,\alpha_{2} ,\alpha_{3} ,........,\alpha_{n} ) = < \mu_{k} ,\nu_{k} >$ we have,

• a. $\mathop {\min }\limits_{i} \left\{ {\mu_{\sigma (i)}^{q} + \nu_{\sigma (i)}^{q} } \right\} \le \mu_{k}^{q} + \nu_{k}^{q} \le \mathop {\max }\limits_{i} \left\{ {\mu_{\sigma (i)}^{q} + \nu_{\sigma (i)}^{q} } \right\}$

• b. $\frac{{\mathop {\min }\limits_{i} \left\{ {\mu_{\sigma (i)}^{q} + \nu_{\sigma (i)}^{q} } \right\} \times \mathop {\min }\limits_{i} \left\{ {\mu_{\sigma (i)}^{q} } \right\}}}{{\mathop {\max }\limits_{i} \left\{ {\nu_{\sigma (i)}^{q} } \right\} + \mathop {\min }\limits_{i} \left\{ {\mu_{\sigma (i)}^{q} } \right\}}} \le \mu_{k}^{q} \le \mathop {\min }\limits_{i} \left\{ {\frac{{\mathop {\max }\limits_{i} \left\{ {\mu_{\sigma (i)}^{q} + \nu_{\sigma (i)}^{q} } \right\} \times \mathop {\max }\limits_{i} \left\{ {\mu_{\sigma (i)}^{q} } \right\}}}{{\mathop {\min }\limits_{i} \left\{ {\nu_{\sigma (i)}^{q} } \right\} + \mathop {\max }\limits_{i} \left\{ {\mu_{\sigma (i)}^{q} } \right\}}},1} \right\}$

• c. $\frac{{\mathop {\min }\limits_{i} \left\{ {\mu_{\sigma (i)}^{q} + \nu_{\sigma (i)}^{q} } \right\} \times \mathop {\min }\limits_{i} \left\{ {\nu_{\sigma (i)}^{q} } \right\}}}{{\mathop {\max }\limits_{i} \left\{ {\mu_{\sigma (i)}^{q} } \right\} + \mathop {\min }\limits_{i} \left\{ {\nu_{\sigma (i)}^{q} } \right\}}} \le \nu_{k}^{q} \le \mathop {\min }\limits_{i} \left\{ {\frac{{\mathop {\max }\limits_{i} \left\{ {\mu_{\sigma (i)}^{q} + \nu_{\sigma (i)}^{q} } \right\} \times \mathop {\max }\limits_{i} \left\{ {\nu_{\sigma (i)}^{q} } \right\}}}{{\mathop {\max }\limits_{i} \left\{ {\nu_{\sigma (i)}^{q} } \right\} + \mathop {\min }\limits_{i} \left\{ {\mu_{\sigma (i)}^{q} } \right\}}},1} \right\}.$

Proof

Similar to the proof of theorem 4.4.

Theorem 5.5

(Monotonicity) Let $\alpha_{i} = < \mu_{i} ,\nu_{i} > \,\,{\text{and}}\,\,\alpha^{\prime}_{i} = < \mu^{\prime}_{i} ,\nu^{\prime}_{i} > \,(i = 1,2,3,........,n)$ be two collection of q-ROFNs. Also let $qROFOWFA(\alpha_{1} ,\alpha_{2} ,\alpha_{3} ,........,\alpha_{n} ) = \alpha = < \mu ,\nu >$ and $qROFOWFA(\alpha^{\prime}_{1} ,\alpha^{\prime}_{2} ,\alpha^{\prime}_{3} ,........,\alpha^{\prime}_{n} ) =$ $\alpha^{\prime} = < \mu^{\prime},\nu^{\prime} >$ we have,

• a. $\mu^{q} +\nu^{q} \le\mu^{\prime q} + \nu^{\prime q} \,\,{\text{if}}\,\,\mu_{\sigma (i)}^{q} + \nu_{\sigma (i)}^{q} \le \mu_{\sigma (i)}^{\prime q} + \nu_{\sigma (i)}^{\prime q}$

• b. $\mu^{q} \le\mu^{\prime q} \,\,{\text{and}}\,\,\nu_{{}}^{q} \ge \nu^{\prime q} \,\,{\text{if}}\,\,\mu_{\sigma (i)}^{q} \le \mu_{\sigma (i)}^{\prime q} \,\,{\text{and}}\,\,\mu_{\sigma (i)}^{q} + \nu_{\sigma (i)}^{q} = \mu_{\sigma (i)}^{\prime q} + \nu_{\sigma (i)}^{\prime q}$

• c. $qROFWFA(\alpha_{1} ,\alpha_{2} ,\alpha_{3} ,........,\alpha_{n} ) \prec qROFWFA(\alpha^{\prime}_{1} ,\alpha^{\prime}_{2} ,\alpha^{\prime}_{3} ,........,\alpha^{\prime}_{n} )$ if $\mu_{\sigma (i)}^{q} + \nu_{\sigma (i)}^{q} = \mu_{\sigma (i)}^{\prime q} + \nu_{\sigma (i)}^{\prime q}$ and $\mu_{\sigma (i)} \le \mu^{\prime}_{\sigma (i)}$.

Proof

Similar to the proof of theorem 4.5.

6 Multi attribute decision making

We envisage a multi-attribute decision making problem comprising m different alternatives A₁, A₂, …., A_m in which these alternatives are assessed under the set of n distinct attributes C₁, C₂, ……, C_n. It is required to propose in this case a set of $l$ experts $D_{1} ,D_{2} ,....,D_{l}$ whose weights are respectively $w_{1} ,w_{2} ,....,w_{l}$ such that $w_{k} \ge 0\,(k = 1,2,...,l)$ and $\sum\limits_{k = 1}^{l} {w_{k} } = 1$ for the estimation of the given alternatives.

We recall that the given alternative $A_{i} \,(i = 1,2,...,m)$ can be obtained from expert $D_{k} \,(k = 1,2,...,l)$ endowed by the attribute $C_{j} \,(j = 1,2,...,n)$ in the form of q-rung ortho-pair fuzzy environment and hence the assessed result is expressed in the form of q-ROFNs $\alpha_{ij}^{(k)} = \left\langle {\mu_{ij}^{(k)} ,\nu_{ij}^{(k)} } \right\rangle$ subject to $0 \le \mu_{ij}^{(k)} ,\nu_{ij}^{(k)} \le 1$ and $0 \le \left( {\mu_{ij}^{(k)} } \right)^{q} + \left( {\nu_{ij}^{(k)} } \right)^{q} \le 1$ where $i = 1,2,...,m;\,j = 1,2,...,n$ and $k = 1,2,...,l$. Furthermore, let us consider that $\lambda_{t} \,(t = 1,2,...,n)$ would be the weight for the attribute $C_{j}$ obeying the conditions $\lambda_{t} \, > 0\,(t = 1,2,...,n)$ and $\sum\limits_{t = 1}^{n} {\lambda_{t} } = 1$. Thus, in view of investigation of the most desirable alternative (s), the proposed operator is used to develop a multi-attribute decision making pertaining to the q-RFOFs information with the steps incurred as follows:

Step-1: Determine the weights of decision makers judging importance of the decision makers which are considered as philological terms expressed in q-ROFNs.

Let $\tilde{D}_{k} = \left\langle {\mu_{k} ,\nu_{k} } \right\rangle$ be a q-ROFN for rating of k-th decision maker. Then the weight $w_{k}$ of k-th decision maker $D_{k}$ can be obtained as:

$$ \begin{gathered} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,w_{k} = \frac{{\tilde{D}_{k}^{q} }}{{\sum\limits_{k = 1}^{l} {\tilde{D}_{k}^{q} } }},\,\,\,\,k = 1,2,3,.....,l \hfill \\ {\text{where}}\,\,\tilde{D}_{k}^{q} = \mu_{k} + \left( {1 - \mu_{k}^{q} - \nu_{k}^{q} } \right)^{\frac{1}{q}} \left( {\frac{{\nu_{k} }}{{\mu_{k} + \nu_{k} }}} \right)\,\,\,\,\,\,\,(k = 1,2,.....,l). \hfill \\ \end{gathered} $$

Clearly $\sum\limits_{k = 1}^{l} {w_{k} = 1}$.

Step-2: Arrange the rating values of each experts is the form of decision matrices $\tilde{D}_{k} = \left( {\alpha_{ij}^{(k)} } \right)_{m \times n} = \left( {\left\langle {\mu_{ij}^{(k)} ,\nu_{ij}^{(k)} } \right\rangle } \right)_{m \times n} \,\,\,\,(k = 1,2,.....,l)$.

Thus, $\tilde{D}_{k} = \begin{array}{*{20}c} {} & {\begin{array}{*{20}c} {C_{1} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,} & {C_{2} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,} & {C_{3} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,} & {\begin{array}{*{20}c} {.....} & {\,\,\,\,\,\,\,\,\,\,C_{n} } \\ \end{array} } \\ \end{array} } \\ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {A_{1} } \\ {A_{2} } \\ \end{array} } \\ {A_{3} } \\ \vdots \\ {A_{m} } \\ \end{array} } & {\left( {\begin{array}{*{20}c} {\left\langle {\mu_{11}^{(k)} ,\nu_{11}^{(k)} } \right\rangle } & {\left\langle {\mu_{12}^{(k)} ,\nu_{12}^{(k)} } \right\rangle } & {\left\langle {\mu_{13}^{(k)} ,\nu_{13}^{(k)} } \right\rangle } & {\begin{array}{*{20}c} \cdots & {\left\langle {\mu_{1n}^{(k)} ,\nu_{1n}^{(k)} } \right\rangle } \\ \end{array} } \\ {\left\langle {\mu_{21}^{(k)} ,\nu_{21}^{(k)} } \right\rangle } & {\left\langle {\mu_{22}^{(k)} ,\nu_{22}^{(k)} } \right\rangle } & {\left\langle {\mu_{23}^{(k)} ,\nu_{23}^{(k)} } \right\rangle } & {\begin{array}{*{20}c} \cdots & {\left\langle {\mu_{2n}^{(k)} ,\nu_{2n}^{(k)} } \right\rangle } \\ \end{array} } \\ {\left\langle {\mu_{31}^{(k)} ,\nu_{31}^{(k)} } \right\rangle } & {\left\langle {\mu_{32}^{(k)} ,\nu_{32}^{(k)} } \right\rangle } & {\left\langle {\mu_{33}^{(k)} ,\nu_{33}^{(k)} } \right\rangle } & {\begin{array}{*{20}c} \cdots & {\left\langle {\mu_{3n}^{(k)} ,\nu_{3n}^{(k)} } \right\rangle } \\ \end{array} } \\ {\begin{array}{*{20}c} \cdots \\ {\left\langle {\mu_{m1}^{(k)} ,\nu_{m1}^{(k)} } \right\rangle } \\ \end{array} } & {\begin{array}{*{20}c} \cdots \\ {\left\langle {\mu_{m2}^{(k)} ,\nu_{m2}^{(k)} } \right\rangle } \\ \end{array} } & {\begin{array}{*{20}c} \cdots \\ {\left\langle {\mu_{m3}^{(k)} ,\nu_{m3}^{(k)} } \right\rangle } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} \cdots \\ \cdots \\ \end{array} } & {\begin{array}{*{20}c} \cdots \\ {\left\langle {\mu_{mn}^{(k)} ,\nu_{mn}^{(k)} } \right\rangle } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right)} \\ \end{array}$.

Step-3: Construct aggregated q-rung orthopair fuzzy decision matrix. Note that in a group decision making process, all the individual opinions need to sum up and form a group opinion to build the aggregated q-rung orthopair fuzzy decision matrix. To execute so, the proposed operator will contribute as follows:

Let $\tilde{R} = \left( {\tilde{R}_{ij} } \right)_{m \times n}$ be the aggregated q-rung orthopair fuzzy decision matrix, where

$$ \tilde{R}_{ij} = qROFWFA\,\left( {\alpha_{ij}^{(1)} ,\alpha_{ij}^{(2)} ,.....,\alpha_{ij}^{(l)} } \right)\,\,\,or\,\,\,\tilde{R}_{ij} = qROFOWFA\,\left( {\alpha_{ij}^{(1)} ,\alpha_{ij}^{(2)} ,.....,\alpha_{ij}^{(l)} } \right) $$

For sake of simplicity we write $\tilde{R}_{ij} = \left\langle {\mu_{ij} ,\nu_{ij} } \right\rangle$.

Step-4: Normalize the q-ROFNs $\tilde{R}_{ij}$, if required, by converting all the cost type attribute into the benefit type attribute by using the following formula:

$$ \tilde{R}_{ij}^{N} = \left\{ \begin{gathered} \left\langle {\nu_{ij} ,\mu_{ij} } \right\rangle {,}\,\,{\text{if}}\,\,C_{j} \,{\text{is}}\,\,{\text{a}}\,{\text{cost}}\,{\text{type}}\,\,{\text{attribute}} \hfill \\ \left\langle {\mu_{ij} ,\nu_{ij} } \right\rangle {,}\,\,{\text{if}}\,\,C_{j} \,{\text{is}}\,\,{\text{a}}\,{\text{benefit}}\,{\text{type}}\,\,{\text{attribute}} \hfill \\ \end{gathered} \right. $$

The normalized decision matrix is: $\tilde{R}_{N} = \left( {\tilde{R}_{ij}^{N} } \right)_{m \times n} = \left( {\left\langle {\tilde{\mu }_{ij} ,\tilde{\nu }_{ij} } \right\rangle } \right)_{m \times n}$.

Step-5: By using the score value $S\left( {\tilde{R}_{ij}^{N} } \right)$ of q-ROFNs $\tilde{R}_{ij}^{N} (i = 1,2,...,m;j = 1,2,...,n)$, we formulate the score matrix $\tilde{S} = \left( {S\left( {\tilde{R}_{ij}^{N} } \right)} \right)_{m \times n}$.

Thus

$$ \tilde{S} = \left( {S\left( {\tilde{R}_{ij}^{N} } \right)} \right)_{m \times n} = \begin{array}{*{20}c} {} & {\begin{array}{*{20}c} {C_{1} } & {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,C_{2} } & {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,C_{3} } & {\begin{array}{*{20}c} {\,\,\,\,\,....\,\,\,\,\,\,\,\,\,} & {C_{n} } \\ \end{array} } \\ \end{array} } \\ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {A_{1} } \\ {A_{2} } \\ \end{array} } \\ {A_{3} } \\ \vdots \\ {A_{m} } \\ \end{array} } & {\left( {\begin{array}{*{20}c} {S\left( {\tilde{R}_{11}^{N} } \right)} & {S\left( {\tilde{R}_{12}^{N} } \right)} & {S\left( {\tilde{R}_{13}^{N} } \right)} & {\begin{array}{*{20}c} \cdots & {S\left( {\tilde{R}_{1n}^{N} } \right)} \\ \end{array} } \\ {S\left( {\tilde{R}_{21}^{N} } \right)} & {S\left( {\tilde{R}_{22}^{N} } \right)} & {S\left( {\tilde{R}_{23}^{N} } \right)} & {\begin{array}{*{20}c} \cdots & {S\left( {\tilde{R}_{2n}^{N} } \right)} \\ \end{array} } \\ {S\left( {\tilde{R}_{31}^{N} } \right)} & {S\left( {\tilde{R}_{32}^{N} } \right)} & {S\left( {\tilde{R}_{33}^{N} } \right)} & {\begin{array}{*{20}c} \cdots & {S\left( {\tilde{R}_{34}^{N} } \right)} \\ \end{array} } \\ {\begin{array}{*{20}c} \cdots \\ {S\left( {\tilde{R}_{m1}^{N} } \right)} \\ \end{array} } & {\begin{array}{*{20}c} \cdots \\ {S\left( {\tilde{R}_{m2}^{N} } \right)} \\ \end{array} } & {\begin{array}{*{20}c} \cdots \\ {S\left( {\tilde{R}_{m3}^{N} } \right)} \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} \cdots \\ \cdots \\ \end{array} } & {\begin{array}{*{20}c} \cdots \\ {S\left( {\tilde{R}_{mn}^{N} } \right)} \\ \end{array} } \\ \end{array} } \\ \end{array} } \right)} \\ \end{array} $$

where $S\left( {\tilde{R}_{ij}^{N} } \right) = \left\{ \begin{gathered} \nu_{ij}^{q} - \mu_{ij}^{q} {,}\,\,{\text{if}}\,\,C_{j} \,{\text{is}}\,\,{\text{a}}\,{\text{cost}}\,{\text{type}}\,\,{\text{attribute}} \hfill \\ \mu_{ij}^{q} - \nu_{ij}^{q} {,}\,\,{\text{if}}\,\,C_{j} \,{\text{is}}\,\,{\text{a}}\,{\text{benefit}}\,{\text{type}}\,\,{\text{attribute}} \hfill \\ \end{gathered} \right.$

Step 6: A weighted sum of the scores of each alternative $A_{i} \,(i = 1,\,2,\,...,m)$ on the basis of this score matrix $\tilde{S}$ is given by

$$ \Omega \left( {A_{i} } \right) = \sum\limits_{j = 1}^{n} {\lambda_{j} \tilde{S}\left( {\tilde{R}_{ij}^{N} } \right)} ,\,\,\,\,\,\,\,\,\,\,\,\,i = 1,2,.....,m. $$

where $\lambda_{1} ,\lambda_{2} ,...,\lambda_{n}$ are normalized weights of the criteria $C_{1} ,C_{2} ,......,C_{n}$ respectively.

Assume the weights $\lambda_{i} \,(i = 1,\,2,\,...,m)$ are unknown and denote a subset of the weights by $\psi$. We compute these unknown weights with the help of the following mathematical model:

$$ \begin{gathered} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,Max\,f = \sum\limits_{i = 1}^{m} {\Omega \left( {A_{i} } \right)} \, \hfill \\ {\text{Subject}}\,{\text{to:}}\,\,\,\sum\limits_{j = 1}^{n} {\lambda_{j} = } 1 \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\lambda_{j} \ge 0\,\,(j = 1,\,2,\,...,n) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\lambda_{j} \in \Psi \,\,(j = 1,\,2,\,...,n) \hfill \\ \end{gathered} $$

After solving this model, we get the weight vector $\lambda = \left( {\lambda_{1} ,\lambda_{2} ,...,\lambda_{n} } \right)^{T} .$

Step 7: Construct the aggregated weighted q-rung orthopair fuzzy decision matrix $\tilde{R}_{N}^{W}$ using the normalized aggregated decision matrix and the attribute weight vector $\lambda = \left( {\lambda_{1} ,\lambda_{2} ,...,\lambda_{n} } \right)^{T}$ utilizing, the qROFWFA operator or qROFOWFA operator as described below:

$$ \tilde{R}_{N}^{W} = qROFWFA\left( {\tilde{R}_{i1}^{N} ,\tilde{R}_{i2}^{N} ,...,\tilde{R}_{in}^{N} } \right)\, = \left( {\Gamma_{i} } \right)_{m \times 1} = \left( {\left\langle {\tilde{\xi }_{i} ,\tilde{\vartheta }_{i} } \right\rangle } \right)_{m \times 1} \,\,{\text{(say)}} $$

where

$$ \begin{gathered} \Gamma_{i} = \left\langle {\left( {\frac{{\prod\limits_{j = 1}^{n} {\left( {\tilde{\mu }_{ij}^{q} } \right)^{{\lambda_{j} }} } }}{{\prod\limits_{j = 1}^{n} {\left( {\tilde{\mu }_{ij}^{q} } \right)^{{\lambda_{j} }} } + \prod\limits_{j = 1}^{n} {\left( {\tilde{\nu }_{ij}^{q} } \right)^{{\lambda_{j} }} } }} \times \left( {1 - \prod\limits_{k = 1}^{l} {\left( {1 - \tilde{\mu }_{ij}^{q} - \tilde{\nu }_{ij}^{q} } \right)^{{\lambda_{j} }} } } \right)} \right)^{\frac{1}{q}} } \right.,\left. {\left( {\frac{{\prod\limits_{j = 1}^{n} {\left( {\tilde{\nu }_{ij}^{q} } \right)^{{\lambda_{j} }} } }}{{\prod\limits_{j = 1}^{n} {\left( {\tilde{\mu }_{ij}^{q} } \right)^{{\lambda_{j} }} } + \prod\limits_{j = 1}^{n} {\left( {\tilde{\nu }_{ij}^{q} } \right)^{{\lambda_{j} }} } }} \times \left( {1 - \prod\limits_{k = 1}^{l} {\left( {1 - \tilde{\mu }_{ij}^{q} - \tilde{\nu }_{ij}^{q} } \right)^{{\lambda_{j} }} } } \right)} \right)^{\frac{1}{q}} } \right\rangle \, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(\,i = 1,2,.....,m) \hfill \\ \end{gathered} $$

or $\tilde{R}_{N}^{W} = qROFOWFA\left( {\tilde{R}_{i1}^{N} ,\tilde{R}_{i2}^{N} ,...,\tilde{R}_{in}^{N} } \right) = \left( {\hat{\Gamma }_{i} } \right)_{m \times 1} = \left( {\left\langle {\hat{\xi }_{i} ,\hat{\vartheta }_{i} } \right\rangle } \right)_{m \times 1} \,\,{\text{(say)}}$.where

$$ \begin{gathered} \hat{\Gamma }_{i} = \left\langle {\left( {\frac{{\prod\limits_{j = 1}^{n} {\left( {\tilde{\mu }_{i\sigma (j)}^{q} } \right)^{{\lambda_{j} }} } }}{{\prod\limits_{j = 1}^{n} {\left( {\tilde{\mu }_{i\sigma (j)}^{q} } \right)^{{\lambda_{j} }} } + \prod\limits_{j = 1}^{n} {\left( {\tilde{\nu }_{i\sigma (j)}^{q} } \right)^{{\lambda_{j} }} } }} \times \left( {1 - \prod\limits_{j = 1}^{n} {\left( {1 - \tilde{\mu }_{i\sigma (j)}^{q} - \tilde{\nu }_{i\sigma (j)}^{q} } \right)^{{\lambda_{j} }} } } \right)} \right)^{\frac{1}{q}} } \right., \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\left. {\left( {\frac{{\prod\limits_{j = 1}^{n} {\left( {\tilde{\nu }_{i\sigma (j)}^{q} } \right)^{{\lambda_{j} }} } }}{{\prod\limits_{j = 1}^{n} {\left( {\tilde{\mu }_{i\sigma (j)}^{q} } \right)^{{\lambda_{j} }} } + \prod\limits_{j = 1}^{n} {\left( {\tilde{\nu }_{i\sigma (j)}^{q} } \right)^{{\lambda_{j} }} } }} \times \left( {1 - \prod\limits_{j = 1}^{n} {\left( {1 - \tilde{\mu }_{i\sigma (j)}^{q} - \tilde{\nu }_{i\sigma (j)}^{q} } \right)^{{\lambda_{j} }} } } \right)} \right)^{\frac{1}{q}} } \right\rangle \,\,\,\,\,\,\,\,\,\,\,\,(\,i = 1,2,.....,m) \hfill \\ \end{gathered} $$

Step-8: Compute the score value of overall weighted aggregated value $\Gamma_{i} = \,\left\langle {\tilde{\xi }_{i} ,\tilde{\vartheta }_{i} } \right\rangle \,(i = 1,2,...,m)$ by using the formula:

$$ S\left( {\Gamma_{i} } \right) = \,\tilde{\xi }_{i}^{q} - \tilde{\vartheta }_{i}^{q} \,\,\,\,\,\,(i = 1,2,...,m). $$

If there is no difference between two score values $S\left( {\Gamma_{q} } \right)$ and $S\left( {\Gamma_{s} } \right)$, then we need to calculate the accuracy value of the alternatives as $A\left( {\Gamma_{i} } \right) = \,\tilde{\xi }_{i}^{q} + \tilde{\vartheta }_{i}^{q} \,\,\,\,\,\,(i = 1,2,...,m)$.

Step-9: Rank all the alternatives $A_{i} \,(i = 1,2,...,m)$ according to the definition 2.5 and hence select the most desirable alternative(s).

7 An illustrative example

We consider a multi attribute decision making problem (adapted from Boran et al., 2009) given below.

“An automotive company is desired to select the most appropriate supplier for one of the key elements in its manufacturing process. After pre evaluation, five suppliers A₁, A₂, A₃, A₄, A₅ have remained as alternatives for further evaluation. In order to evaluate alternative suppliers, a committee composed of three decision makers D₁, D₂, D₃ has been formed.

Four criteria are considered as:

C₁: Product quality.

C₂: Relationship closeness.

C₃: Delivery performance.

C₄: Price”.

Among them only C₄ is the cost type attribute.

Take q = 2.

Step-1: Determine the weights of the decision makers.

Linguistic terms and the corresponding q-ROFN used for the ratings of the decision makers are given in Table 1.

Table 1 aaa

The importance of the decision makers are given in Table 2.

Table 2 bbb

Then the weights of the decision makers are calculated as below:

$$ \begin{gathered} \tilde{D}_{1}^{2} = 0.90 + \left( {1 - 0.90^{2} - 0.10^{2} } \right)^{\frac{1}{2}} \left( {\frac{0.10}{{0.90 + 0.10}}} \right) = 0.942426, \hfill \\ \tilde{D}_{2}^{2} = 0.50 + \left( {1 - 0.50^{2} - 0.45^{2} } \right)^{\frac{1}{2}} \left( {\frac{0.45}{{0.50 + 0.45}}} \right) = 0.850494, \hfill \\ \tilde{D}_{3}^{2} = 0.75 + \left( {1 - 0.75^{2} - 0.20^{2} } \right)^{\frac{1}{2}} \left( {\frac{0.20}{{0.75 + 0.20}}} \right) = 0.882731. \hfill \\ \therefore \,\,w_{1} = \frac{{\tilde{D}_{1}^{2} }}{{\tilde{D}_{1}^{2} + \tilde{D}_{2}^{2} + \tilde{D}_{3}^{2} }} = 0.352,\,\,w_{2} = \frac{{\tilde{D}_{1}^{2} }}{{\tilde{D}_{1}^{2} + \tilde{D}_{2}^{2} + \tilde{D}_{3}^{2} }} = 0.318,\,\,w_{3} = \frac{{\tilde{D}_{1}^{2} }}{{\tilde{D}_{1}^{2} + \tilde{D}_{2}^{2} + \tilde{D}_{3}^{2} }} = 0.330. \hfill \\ \end{gathered} $$

Step-2: We express the rating values of each experts is the form of decision matrices $\tilde{D}_{k} = \left( {\alpha_{ij}^{(k)} } \right)_{5 \times 4} = \left( {\left\langle {\mu_{ij}^{(k)} ,\nu_{ij}^{(k)} } \right\rangle } \right)_{5 \times 4} \,\,\,\,(k = 1,2,3)$

$$ \begin{gathered} \tilde{D}_{1} :\,\,\begin{array}{*{20}c} {} & {\begin{array}{*{20}c} {C_{1} \,\,\,\,\,\,\,\,\,\,\,\,\,} & {\,\,\,\,\,\,\,\,\,\,\,\,\,C_{2} \,\,\,\,\,\,} & {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,C_{3} } & {\begin{array}{*{20}c} {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,} & {C_{4} } \\ \end{array} } \\ \end{array} } \\ {\,\,\,\,\begin{array}{*{20}c} {\begin{array}{*{20}c} {A_{1} } \\ {A_{2} } \\ \end{array} } \\ {A_{3} } \\ {A_{4} } \\ {A_{5} } \\ \end{array} } & {\left( {\begin{array}{*{20}c} { < 0.70,0.20 > } & { < 0.60,0.30 > } & { < 0.80,0.10 > } & { < 0.70,0.20 > } \\ { < 0.60,0.30 > } & { < 0.50,0.40 > } & { < 0.70,0.20 > } & { < 0.60,0.30 > } \\ { < 0.90,0.10 > } & { < 0.80,0.10 > } & { < 0.80,0.10 > } & { < 0.80,0.10 > } \\ { < 0.60,0.30 > } & { < 0.50,0.40 > } & { < 0.80,0.10 > } & { < 0.70,0.20 > } \\ { < 0.50,0.40 > } & { < 0.40,0.50 > } & { < 0.70,0.20 > } & { < 0.50,0.40 > } \\ \end{array} } \right)} \\ \end{array} \hfill \\ \hfill \\ \tilde{D}_{2} :\,\,\begin{array}{*{20}c} {} & {\begin{array}{*{20}c} {C_{1} \,\,\,\,\,\,\,\,\,\,\,\,\,} & {\,\,\,\,\,\,\,\,\,\,\,\,\,C_{2} \,\,\,\,\,\,} & {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,C_{3} } & {\begin{array}{*{20}c} {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,} & {C_{4} } \\ \end{array} } \\ \end{array} } \\ {\,\,\,\,\begin{array}{*{20}c} {\begin{array}{*{20}c} {A_{1} } \\ {A_{2} } \\ \end{array} } \\ {A_{3} } \\ {A_{4} } \\ {A_{5} } \\ \end{array} } & {\left( {\begin{array}{*{20}c} { < 0.80,0.10 > } & { < 0.70,0.20 > } & { < 0.70,0.20 > } & { < 0.70,0.20 > } \\ { < 0.70,0.20 > } & { < 0.60,0.30 > } & { < 0.60,0.30 > } & { < 0.50,0.40 > } \\ { < 0.80,0.10 > } & { < 0.70,0.20 > } & { < 0.80,0.10 > } & { < 0.80,0.10 > } \\ { < 0.70,0.20 > } & { < 0.50,0.40 > } & { < 0.70,0.20 > } & { < 0.60,0.30 > } \\ { < 0.60,0.30 > } & { < 0.50,0.40 > } & { < 0.70,0.20 > } & { < 0.60,0.30 > } \\ \end{array} } \right)} \\ \end{array} \hfill \\ \end{gathered} $$

$$ \tilde{D}_{3} :\,\,\begin{array}{*{20}c} {} & {\begin{array}{*{20}c} {C_{1} \,\,\,\,\,\,\,\,\,\,\,\,\,} & {\,\,\,\,\,\,\,\,\,\,\,\,\,C_{2} \,\,\,\,\,\,} & {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,C_{3} } & {\begin{array}{*{20}c} {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,} & {C_{4} } \\ \end{array} } \\ \end{array} } \\ {\,\,\,\,\begin{array}{*{20}c} {\begin{array}{*{20}c} {A_{1} } \\ {A_{2} } \\ \end{array} } \\ {A_{3} } \\ {A_{4} } \\ {A_{5} } \\ \end{array} } & {\left( {\begin{array}{*{20}c} { < 0.70,0.20 > } & { < 0.60,0.30 > } & { < 0.80,0.10 > } & { < 0.70,0.20 > } \\ { < 0.50,0.40 > } & { < 0.70,0.20 > } & { < 0.60,0.30 > } & { < 0.60,0.30 > } \\ { < 0.80,0.10 > } & { < 0.80,0.10 > } & { < 0.70,0.20 > } & { < 0.70,0.20 > } \\ { < 0.70,0.20 > } & { < 0.60,0.30 > } & { < 0.70,0.20 > } & { < 0.60,0.30 > } \\ { < 0.60,0.30 > } & { < 0.50,0.40 > } & { < 0.60,0.30 > } & { < 0.50,0.40 > } \\ \end{array} } \right)} \\ \end{array} $$

Step-3: We construct aggregated q-rung orthopair fuzzy decision matrix $\tilde{R} = \left( {\tilde{R}_{ij} } \right)_{5 \times 4}$ as given below:

$\begin{gathered} \tilde{R}_{ij} = \left\langle {\mu_{ij} ,\nu_{ij} } \right\rangle = qROFFWA\,\left( {\alpha_{ij}^{(1)} ,\alpha_{ij}^{(2)} ,\alpha_{ij}^{(3)} } \right) = \left( {w_{1} * \alpha_{ij}^{(1)} } \right)\tilde{ \otimes }\left( {w_{2} * \alpha_{ij}^{(2)} } \right)\tilde{ \otimes }\left( {w_{3} * \alpha_{ij}^{(3)} } \right)^{{w_{l} }} \hfill \\ \begin{array}{*{20}c} {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,C_{1} \,\,} & {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,C_{2} } \\ \end{array} \hfill \\ \,\,\,\,\,\, = \begin{array}{*{20}c} {A_{1} } \\ {A_{2} } \\ {A_{3} } \\ {A_{4} } \\ {A_{5} } \\ \end{array} \left( {\begin{array}{*{20}c} { < 0.738732383,0.162274438 > } & { < 0.636988955,0.266572783 > } \\ { < 0.612367693,0.299264891 > } & { < 0.612059157,0.300200272 > } \\ { < 0.84427015,0.101247838 > } & { < 0.774434038,0.125910928 > } \\ { < 0.670015488,0.233112838 > } & { < 0.536878247,0.367795321 > } \\ { < 0.568865319,0.335605984 > } & { < 0.467461971,0.437583484 > } \\ \end{array} } \right. \hfill \\ \begin{array}{*{20}c} {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,C_{3} \,\,} & {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,C_{4} } \\ \end{array} \hfill \\ \,\,\,\,\,\,\,\,\,\,\begin{array}{*{20}c} {A_{1} } \\ {A_{2} } \\ {A_{3} } \\ {A_{4} } \\ {A_{5} } \\ \end{array} \left. {\begin{array}{*{20}c} { < 0.774434038,0.125910928 > } & { < 0.7,0.2 > } \\ { < 0.640633872,0.263045277 > } & { < 0.572068682,0.332145468 > } \\ { < 0.773377174,0.126992655 > } & { < 0.773377174,0.126992655 > } \\ { < 0.74241761,0.158563965 > } & { < 0.640633872,0.263045277 > } \\ { < 0.672039077,0.230955888 > } & { < 0.535600736,0.368995439 > } \\ \end{array} } \right) \hfill \\ \end{gathered}$.

Step-4: By converting all the cost type attributes into the benefit type attributes, we get the following normalized decision matrix as given below:

$$ \begin{gathered} \tilde{R}_{N} = \left( {\tilde{R}_{ij}^{N} } \right)_{5 \times 4} = \left( {\left\langle {\tilde{\mu }_{ij} ,\tilde{\nu }_{ij} } \right\rangle } \right)_{5 \times 4} \hfill \\ \begin{array}{*{20}c} {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,C_{1} \,\,} & {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,C_{2} } \\ \end{array} \hfill \\ \,\,\,\,\,\, = \begin{array}{*{20}c} {A_{1} } \\ {A_{2} } \\ {A_{3} } \\ {A_{4} } \\ {A_{5} } \\ \end{array} \left( {\begin{array}{*{20}c} { < 0.738732383,0.162274438 > } & { < 0.636988955,0.266572783 > } \\ { < 0.612367693,0.299264891 > } & { < 0.612059157,0.300200272 > } \\ { < 0.84427015,0.101247838 > } & { < 0.774434038,0.125910928 > } \\ { < 0.670015488,0.233112838 > } & { < 0.536878247,0.367795321 > } \\ { < 0.568865319,0.335605984 > } & { < 0.467461971,0.437583484 > } \\ \end{array} } \right. \hfill \\ \begin{array}{*{20}c} {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,C_{3} \,\,} & {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,C_{4} } \\ \end{array} \hfill \\ \,\,\,\,\,\,\,\,\,\,\begin{array}{*{20}c} {A_{1} } \\ {A_{2} } \\ {A_{3} } \\ {A_{4} } \\ {A_{5} } \\ \end{array} \left. {\begin{array}{*{20}c} { < 0.774434038,0.125910928 > } & { < 0.2,0.7 > } \\ { < 0.640633872,0.263045277 > } & { < 0.332145468,0.572068682 > } \\ { < 0.773377174,0.126992655 > } & { < 0.126992655,0.773377174 > } \\ { < 0.74241761,0.158563965 > } & { < 0.263045277,0.640633872 > } \\ { < 0.672039077,0.230955888 > } & { < 0.368995439,0.535600736 > } \\ \end{array} } \right) \hfill \\ \end{gathered} $$

Step-5: By using the score value $S\left( {\tilde{R}_{ij}^{N} } \right)$ of q-ROFNs $\tilde{R}_{ij}^{N} (i = 1,2,...,5;j = 1,2,...,4)$, we formulate the score matrix $\tilde{S} = \left( {S\left( {\tilde{R}_{ij}^{N} } \right)} \right)_{5 \times 4}$ described below:

$$ \tilde{S} = \left( {S\left( {\tilde{R}_{ij}^{N} } \right)} \right)_{5 \times 4} = \begin{array}{*{20}c} {} & {\begin{array}{*{20}c} {C_{1} \,\,\,\,\,\,\,\,\,\,\,\,\,} & {\,\,\,\,\,\,\,\,\,\,\,\,\,C_{2} \,\,\,\,\,\,} & {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,C_{3} } & {\begin{array}{*{20}c} {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,} & {C_{4} } \\ \end{array} } \\ \end{array} } \\ {\,\,\,\,\begin{array}{*{20}c} {\begin{array}{*{20}c} {A_{1} } \\ {A_{2} } \\ \end{array} } \\ {A_{3} } \\ {A_{4} } \\ {A_{5} } \\ \end{array} } & {\left( {\begin{array}{*{20}c} {0.51939254} & {0.334693879} & {0.583894518} & { - 0.45} \\ {0.285434716} & {0.284496208} & {0.341218941} & { - 0.21694} \\ {0.702540962} & {0.583894518} & {0.581985118} & { - 0.58199} \\ {0.39457916} & {0.152964853} & {0.526041377} & { - 0.34122} \\ {0.210976374} & {0.027041389} & {0.398295899} & { - 0.15071} \\ \end{array} } \right)} \\ \end{array} $$

Step 6: Assume that the partial weight information about the attribute weights as given by the decision makers is:

$$ \Psi = \{ 0.15 \le \lambda_{1} \le 0.20,\,0.25 \le \lambda_{2} \le 0.35,0.20 \le \lambda_{3} \le 0.50,0.10 \le \lambda_{4} \le 0.20,\lambda_{1} + \lambda_{3} \le 2\lambda_{2} ,\lambda_{1} + 2\lambda_{4} \le \lambda_{3} \} . $$

Based on these information, an optimization model can be formulated as below:

$$ \begin{gathered} \max \,f = 0.51939254\lambda_{1} + 0.285434716\lambda_{1} + 0.702540962\lambda_{1} + 0.39457916\lambda_{1} + 0.210976374\lambda_{1} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + 0.334693879\lambda_{2} + 0.284496208\lambda_{2} + 0.583894518\lambda_{2} + 0.152964853\lambda_{2} + 0.027041389\lambda_{2} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + 0.583894518\lambda_{3} + 0.341218941\lambda_{3} + 0.581985118\lambda_{3} + 0.526041377\lambda_{3} + 0.398295899\lambda_{3} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - 0.45\lambda_{4} - 0.21694\lambda_{4} - 0.58199\lambda_{4} - 0.34122\lambda_{4} - 0.15071\lambda_{4} \hfill \\ {\text{Such}}\,\,{\text{that}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,0.15 \le \lambda_{1} \le 0.20,\,\,\,\,0.25 \le \lambda_{2} \le 0.35,\,\,\,\,\,0.20 \le \lambda_{3} \le 0.50, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,0.10 \le \lambda_{4} \le 0.20,\,\,\,\,\lambda_{1} + \lambda_{3} \le 2\lambda_{2} ,\,\,\,\,\,\,\lambda_{1} + 2\lambda_{4} \le \lambda_{3} , \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\lambda_{1} + \lambda_{2} + \lambda_{3} + \lambda_{4} = 1, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\lambda_{1} ,\lambda_{2} ,\lambda_{3} ,\lambda_{4} \ge 0 \hfill \\ \end{gathered} $$

Solving this LPP we get, $\lambda_{1} = 0.15,\lambda_{2} = 0.30,\lambda_{3} = 0.45,\lambda_{4} = 0.10\,\,\,{\text{and}}\,\,\max \,f = 1.6519.$

Step 7: We construct the aggregated weighted q-rung orthopair fuzzy decision matrix $\tilde{R}_{N}^{W}$ as described below:

$$ \begin{gathered} \tilde{R}_{N}^{W} = qROFFWA\left( {\tilde{R}_{i1}^{N} ,\tilde{R}_{i2}^{N} ,...,\tilde{R}_{i4}^{N} } \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\, = \left( {\lambda_{1} * \tilde{R}_{i1}^{N} } \right)\tilde{ \otimes }\left( {\lambda_{2} * \tilde{R}_{i2}^{N} } \right)\tilde{ \otimes }\left( {\lambda_{3} * \tilde{R}_{i3}^{N} } \right)\tilde{ \otimes }\left( {\lambda_{4} * \tilde{R}_{i4}^{N} } \right) \hfill \\ \,\,\,\,\,\,\,\,\,\, = \left( {\Gamma_{i} } \right)_{5 \times 1} = \left( {\left\langle {\tilde{\xi }_{i} ,\tilde{\vartheta }_{i} } \right\rangle } \right)_{5 \times 1} \,\, = \left[ {\begin{array}{*{20}c} { < 0.717170861,0.220183416 > } \\ { < 0.609201812,0.312575025 > } \\ { < 0.776552876,0.174066789 > } \\ { < 0.662120518,0.27531927 > } \\ { < 0.586164393,0.340784165 > } \\ \end{array} } \right] \hfill \\ \end{gathered} $$

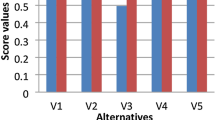
Step-8: The score values of the alternatives are computed as:

$$ \begin{gathered} S\left( {A_{1} } \right) = 0.465853307,S\left( {A_{2} } \right) = 0.273423701,S\left( {A_{3} } \right) = 0.572735122,S\left( {A_{4} } \right) = 0.36260288, \hfill \\ S\left( {A_{5} } \right) = 0.227454849. \hfill \\ \end{gathered} $$

Step-9: Based on the score values, the ranking of the alternatives is given by:

$$ A_{3} \succ A_{1} \succ A_{4} \succ A_{2} \succ A_{5} $$

Thus we conclude that $A_{3}$ is the most appropriate supplier which is exactly the same obtained Boran et al. (2009).

Besides this analysis, even we bring to pass an experiment taking the different aggregation operators to assemble the expert’s preferences along with the criterion. For instance, we followed the above mentioned steps and their results are briefed in Table 3 in case of a person when wants to bring to bear upon qROFOWFA operator in place of qROFWFA operator to aggregate the expert preferences. In fact, the influences of the aggregation operators on the ranking order of the alternatives are observed in that table followed by step 3 and step 7 successively keeping in mind that a different operator has been used at those steps. More importantly, for the selection of the best alternative based on the desired goal, one can opt the appropriate aggregation operator.

Table 3 Ranking order of alternatives (for q = 2)

8 Comparative study

In pursuance of performance comparison of the eloquent method developed by us discussed above with some existing MADM methods under q-rung orthopair fuzzy environment, we have conducted an analysis with some of the existing aggregation operators namely q-rung orthopair fuzzy weighted averaging operator (qROFWA) (Liu and Wang 2017), q-rung orthopair fuzzy weighted geometric operator (qROFWG) (Liu and Wang 2017), q-rung orthopair fuzzy power weighted Maclaurin Symmetric Mean operator (qROFPWMSM) (Liu et al. 2018a, b) (taking k = 2), q-rung orthopair fuzzy weighted geometric Bonferroni mean operator (qROFWGBM) (Liu and Liu 2018) (taking s = t = 2), q-rung orthopair fuzzy weighted generalized Maclaurin Symmetric Mean operator (qROFWGMSM) and q-rung orthopair fuzzy weighted generalized geometric Maclaurin Symmetric Mean operator (qROFWGGMSM) (Liu and Wang 2020) (taking λ₁ = 1 and λ₂ = 2), q-rung orthopair fuzzy generalized weighted geometric Heronian Mean operator (qROFGWGHM) (taking $\phi = 2,\varphi = 2$) (Wei et al. 2018), Improved q-rung orthopair fuzzy weighted averaging aggregation operator (IqROFWA) and Improved q-rung orthopair fuzzy weighted power averaging aggregation operator (IqROFWPA) (Xu et al. 2019). We use the same operator in step-3 and step-7 when we apply the methodology upon the data considered herein. Table 4 highlights in summary form about the final score values and the ranking order of the given alternatives. If we concentrate on the results presented at this table then we will be able to understand that the best alternative obtained from the proposed technique coincides with all other the existing approaches and as results, this advanced approach may be well versed due to the stability of the proposed operators. Moreover, this table states that although the ranking order becomes the same and the optimal alternative is $A_{3}$ for all the approaches but, in particular, the computational steps of these approaches are different.

Table 4 Comparative analysis with the existing operators

However, while exploring proposition 3.2, it leads to the fact that the existing operators (Liu and Wang 2017, Liu et al. 2018a, b; Xu et al. 2019; Liu and Wang 2020; Wei et al. 2018; Liu and Liu 2018) are not neutral with respect to the membership and non-membership information and hence these operators are not fair to consolidate the preferences. On the other hand, the fair or neutral behavior of the proposed operators is observed while dealing with those with the membership as well as non-membership degree of the q-rung orthogonal fuzzy information. Henceforth, without loss of generality, we ensure the elegancy and effectiveness of the proposed method and the aggregation operators.

Further analysis as a part of comparative study is given below:

• (1) It is observed that in the existing works of (Liu and Wang 2017, Liu et al. 2018a, b; Xu et al. 2019; Liu and Wang 2020; Wei et al. 2018; Liu and Liu 2018), the weights of respective decision-makers have not been taken into consideration subject to decision importance of the decision-makers. This underlying issue affects adversely to the decision results in any multi-attribute group decision-making process. To illustrate this fact in-depth, let us consider a multi-attribute decision-making problem where three experts D₁, D₂ and D₃ are engaged to assess the five candidates A₁, A₂, A₃, A₄ and A₅ for the post of Assistant Professors in Mathematics in one National Institute of Technology in India under four attributes, namely- C₁ (quality research works), C₂ (teaching experience), C₃ (knowledge in mathematics) and C₄ (teaching skills). Assume that D₁ is a member of MHRD (Ministry of Human Resource and Development), D₂ is the Director of the NIT and D₃ is the H.O.D of Mathematics of that NIT. As D₁ is holding a higher post comparing to D₂ and D₃, and D₂ is holding a higher post comparing to D₃, we can’t give equal weights to D₁, D₂ and D₃ during the selection of best candidate. The existing approaches (Liu and Wang 2017, Liu et al. 2018a, b; Xu et al. 2019; Liu and Wang 2020; Wei et al. 2018; Liu and Liu 2018) cannot appropriately deal with this situation. In such cases, based on the decision maker’s importance, our proposed approach can compute their corresponding weights. This makes the decision-making process more realistic naturally.

• (2) Garg and Chen (2020), carried out their research work upon decision-makers where the weights have been chosen arbitrarily and without any valid justification. So this will genuinely create an issue while dealing with risk-preference type decision-making problems. But in our developed method, the preference has been given to decision-makers based on the real decision needs. Thus, the weight assigning technique is more acceptable and practical that has been reflected in our proposed method.

• (3) In real-life decision-making problems, it is quite obvious that all the attributes do not pay attention equally during the process. For instance, in some certain problems, it is imparted the preference to reliability than the cost a well as the manufacturing time of the product. Thus, the importance is to be given very carefully towards the choice of the proper weight to the attributes. In the existing approaches (Liu and Wang 2017, Liu et al. 2018a, b; Xu et al. 2019; Liu and Wang 2020; Wei et al. 2018; Liu and Liu 2018), on account of the choosing of attribute weights arbitrarily by the authors, the ranking order of alternatives gets affected. But in our developed approach, we have employed an optimization model based on partial weight information of attributes to meet the attribute weights. Thus, our proposed method for computing the attributes weight is more effective and accurate in particular.

9 Conclusion

To sum up, we proposed in this study some new operational laws for the q-ROFNs which maintain the neutrality or fairness while dealing with the membership and non-membership functions of the corresponding q-ROFSs. The existing studies talk about the fact that at the time of evaluation of the objects when a decision maker offers an equal degree of the acceptance and rejection, then their corresponding aggregation values (Liu and Wang 2017, Liu et al. 2018a, b; Xu et al. 2019; Liu and Wang 2020; Wei et al. 2018; Liu and Liu 2018) are unequal. In such a scenario, giving importance to preciseness and relevance during decision making that depends upon decision-makers attitude, we suggested some new fairly or neutrality operations by using q-ROFS and proportional distribution rules of membership and non-membership functions. We discussed in detail the properties of the proposed operators. Similarly, getting inspired by the present contribution, further, we provided some weighted fairly aggregation operators and ordered weighted fairly aggregation operators for the q-rung orthopair fuzzy information. The main advantage of the proposed operators is not only to accomplish the interaction between the pairs of different q-ROFNs but also help to examine the attitude characteristics of the decision-makers to permit a categorical deal with the membership degrees of the q-ROFSs. The proposed approach is examined on a multi-attribute group decision-making related problem. Finally, we did a comparative analysis of the proposed approach and get ensured about its best performance.