1 Introduction

Atanassov (1986, 1989, 1994) integrated the notion of hesitancy degree in the definition of fuzzy set by adding a new component which describes the degree of nonmembership in a given fuzzy set and called such a set an intuitionistic fuzzy set. While the definition of the fuzzy set provides the degree of membership of an element in a given set and its nonmembership degree is understood as one minus its membership degree, the definition of an intuitionistic fuzzy set provides a more-or-less independent degree of membership and degree of nonmembership of an element in a given set. The only requirement in latter is that the sum of the two degrees is not greater than one. As a result, an intuitionistic fuzzy set exhibits characteristics of affirmation and negation, as well as hesitation. For instance, in any confronting situation in decision making, besides support or positive response and objection or negative response, there could also be an abstention which indicates hesitation and indeterminacy in response to the situation. Intuitionistic fuzzy set, very naturally, a model such cases in decision-making problems. These sets are widely applied in real-life decision-making problems, one may refer to Xu et al. (2008) for clustering, medical diagnosis De et al. (2001), multi-criteria decision making (Li 2010a, b; Liu and Wang 2007; Wang et al. 2009), pattern recognition (Li and Chuntian 2002; Vlachos and Sergiadis 2007), transportation problem (Atanassov 1999), for other applications (Szmidt and Kacprzyk 1996), to name a few.

There had been some controversies (see Dubois et al. 2005 and Grzegorzewski and Mrówka 2005) surrounding the nomenclature of Atanassov’s intuitionistic fuzzy set because similar nomenclature had also been used for intuitionistic logic, and the two concepts differ in their mathematical structure and treatment. It makes sense to avoid using the same terminology for two different concepts. Hence, as suggested in Dubois et al. (2005) and Grzegorzewski and Mrówka (2005), Atanassov intuitionistic fuzzy set is called Atanassov’s I-fuzzy set or simply I-fuzzy set. Henceforth, in this paper, we shall be using I-fuzzy set only.

In the earlier study on fuzzy linear programming, two approaches have contributed significantly. These are due to Zimmermann (1978) and, Tanaka and Asai (1984). While Zimmermann’s approach is applied to linear programming with fuzzy goals (also called flexible linear programming problems), the approach of Tanaka and Asai (1984) is useful for solving linear programming with fuzzy parameters (also called fuzzy number linear programming problems).

The work on linear programming with fuzzy parameters followed a somewhat different direction. This has been mainly because there is no unique method of comparing fuzzy numbers. Therefore, depending on the choice of order, we have the similar solution concept for the given fuzzy linear programming problem. Most of the early work in this direction is based on the ranking function approach of Yager (1981). This leads to several variants of the original work of Yager (1981), e.g., Bector et al. (2004b), Li (2005) and Li and Nan (2009). Different from these ranking function approaches, Clemente et al. (2011) have recently defined fuzzy ordering via a finite set of \(\alpha\)-cuts (say r). This approach results in solving an appropriate multi-objective linear programming problem for the given fuzzy linear programming problem.

Compared to the ordering methodologies discussed above, the conceptual framework of Tanaka and Asai (1984) for comparing fuzzy numbers is different and seems to be very natural. Moreover, Tanaka and Asai introduced a fundamental notion of ‘almost positive triangular fuzzy number (TFN)’ and used the same to transform a fuzzy number linear programming problem to an appropriate crisp optimization problem.

1.1 Motivation behind the proposed work

In recent years, attempts have been made to extend the results of the crisp game theory to the fuzzy games. The motivating force behind these extensions is the advancement in the duality theory for fuzzy linear programming. The earliest study of a two person zero-sum matrix game with fuzzy pay-offs is due to Campos (1989). Also, Bector and Chandra (2005) and Bector et al. (2004a) interpreted the model of Campos (1989) in context of the fuzzy linear programming duality and showed that solving a two person zero-sum matrix game with fuzzy goals and, or, fuzzy pay-offs are equivalent to solving an appropriate pair of primal-dual fuzzy linear programming problems. On the lines of Bector and Chandra (2005), Bector et al. (2004a, b) and Aggarwal et al. (2012) studied duality for I-fuzzy linear programming problems and discussed its application in I-fuzzy matrix games. Based on fuzzy ‘max’ order, Maeda (2003) defines three types of min-max equilibrium strategies and utilizes its properties to design a solution procedure for the fuzzy matrix games. Li (1999) presents a multi-objective linear programming model to solve fuzzy matrix games when entries in the pay-offs matrix are fuzzy triangular numbers. Further Li (2012) develops a method for solving matrix games with triangular fuzzy numbers which assure triangular fuzzy values for such games. Using the fuzzy relational approach, Vijay et al. (2007) extended the duality results of Inuiguchi et al. (2003) and Ramík (2005, 2006) to study a generalized model of fuzzy matrix games with fuzzy goals or fuzzy pay-offs. Xu et al. (2017) introduce the possibility and the necessity measures for matrix game with fuzzy pay-offs and define a \((\alpha , \beta )\)-PN equilibrium strategy for two players playing the game. Recently, Ammar and Brikaa (2018) studied matrix game under rough fuzzy sets and Khan and Mehra (2019) studied the same in possibility and the necessity measures scenario.

In recent work, Aggarwal et al. (2017) presented a new approach for solving I-fuzzy linear programming problem with I-fuzzy parameters via Tanaka and Asai (1984) approach.

The primary advantage of our approach is that it neither requires any preassigned tolerance levels (as in Zimmermann’s approach) nor pre-chosen ranking function (as in Bector and Chandra 2005). Our approach is based on the definition of ‘almost positive’ fuzzy number, which is only membership function based and is very natural the way we understand a positive real number. Since no tolerance level is needed and no ranking function is required, so in this way, our approach is more universal. Also, our approach also provides a precise degree of belief and disbelief in achieving goals set by each player.

The rest of the paper unfolds as follows. Section 2 revisits the basic definitions and preliminaries on I-fuzzy numbers. Section 3 demonstrates the proposed solution approach. Section 4 displays numerical examples from marketing strategy and voting share problem. Section 5 presents a comparative study with the existing models in the literature. Section 6 concludes some observations and an outlook on future research.

2 Preliminaries

This section presents basic definitions regarding I-fuzzy set and I-fuzzy numbers. Further, it presents an important concept of ‘almost positive symmetric triangular I-fuzzy number’ introduced by Aggarwal et al. (2017).

Definition 1

(I-fuzzy set)  (Atanassov 1986, 1994) An I-fuzzy set \(\tilde{a}\) in X is described by

$$\begin{aligned} \tilde{a} =\{\langle x,\mu _{\tilde{a}}(x),\nu _{\tilde{a}}(x)\rangle \mid x\in X, ~~ \mu _{\tilde{a}}(x)+\nu _{\tilde{a}}(x)\leq 1\}, \end{aligned}$$

where \(\mu _{\tilde{a}}: X\rightarrow [0,1]\) and \(\nu _{\tilde{a}}: X \rightarrow [0,1]\) define, respectively, the membership function and the non-membership function.

If \(\mu _{\tilde{a}}(x)+\nu _{\tilde{a}}(x)=1,\) for all \(x\in X\), then \(\tilde{a}\) degenerates to the standard fuzzy set.

We now take \(X=\mathbb {R}\), the real Euclidean space, and recall an I-fuzzy number.

Definition 2

(I-fuzzy number)  (Li 1999; Nehi 2010) An I-fuzzy number \(\tilde{a}\) is an I-fuzzy set over \(\mathbb {R}\) whose membership function \(\mu _{\tilde{a}}: \mathbb {R} \rightarrow [0,1]\) and non-membership function \(\nu _{\tilde{a}}: \mathbb {R} \rightarrow [0,1]\) satisfy the following conditions:

  1. (i)

    there are real numbers c and d such that \(\mu _{\tilde{a}}(c)=1\) and \(\nu _{\tilde{a}}(d)=1\);

  2. (ii)

    \(\mu _{\tilde{a}}\) is quasi-concave and \(\nu _{\tilde{a}}\) is quasi-convex on \(\mathbb {R}\);

  3. (iii)

    \(\mu _{\tilde{a}}\) is upper semi-continuous and \(\nu _{\tilde{a}}\) is lower semi-continuous;

  4. (iv)

    the support sets \(\{x\in \mathbb {R}\,|\, \mu _{\tilde{a}}(x)>0 \}\) and \(\{x\in \mathbb {R}\,|\, \nu _{\tilde{a}}(x)<1 \}\) are bounded.

We denote the set of I-fuzzy numbers by \(IFN(\mathbb {R})\). From above definition, we get at once that for any I-fuzzy number \(\tilde{a}\) there exist eight numbers \(a_1,a_2,a_3,a_4, c_1, c_2, c_3, c_4\in \mathbb {R}\) such that \(c_1\leqq a_1\leqq c_2 \leqq a_2 \leqq a_3 \leqq c_3 \leqq a_4 \leqq c_4\) and four functions \(f_1,f_2,f_3,f_4 :\mathbb {R}\rightarrow [0,1],\) called the sides of a I-fuzzy number, where \(f_1\) and \(f_4\) are non-decreasing and \(f_2\) and \(f_3\) are non-increasing functions. The membership function \(\mu _{\tilde{a}}\) of an I-fuzzy number \(\tilde{a}\) can be specified as

$$\begin{aligned} \mu _{\tilde{a}}(x)=\left\{ \begin{array}{ll} 0, &{}\quad x<a_1, \\ f_1(x), &{}\quad a_1\leq x<a_2, \\ 1, &{}\quad a_2\leq x \leq a_3, \\ f_2(x), &{}\quad a_3< x \leq a_4, \\ 0, &{}\quad x>a_4, \end{array} \right. \end{aligned}$$

while the non-membership function \(\nu _{\tilde{a}}\) has the following form:

$$\begin{aligned} \nu _{\tilde{a}}(x)=\left\{ \begin{array}{ll} 1, &{}\quad x<c_1, \\ f_3(x), &{}\quad c_1\leq x< c_2, \\ 0, &{}\quad c_2\leq x \leq c_3, \\ f_4(x), &{}\quad c_3< x \leq c_4,\\ 1, &{}\quad x>c_4. \end{array} \right. \end{aligned}$$

It is worth noting that each I-fuzzy number \(\tilde{a}\) is the conjunction of two fuzzy numbers, the membership function of one is \(\mu _{\tilde{a}}\) and that of the other is \(1-\nu _{\tilde{a}}\).

In particular, if the non-decreasing functions \(f_1\) and \(f_4\) and non-increasing functions \(f_2\) and \(f_3\) are linear and \(a_2 = c_2, \; a_3=c_3\), then the given I-fuzzy number is a trapezoidal I-fuzzy number. The membership function and non-membership function for the trapezoidal I-fuzzy number are as follows:

$$\begin{aligned} \mu _{\tilde{a}}(x)=\left\{ \begin{array}{ll} 0, &{}\quad x<a_1, \\ \frac{x-a_1}{a_2 - a_1}, &{}\quad a_1\leq x< a_2, \\ 1, &{}\quad a_2\leq x \leq a_3, \\ \frac{a_4 - x}{a_4-a_3}, &{}\quad a_3< x \leq a_4, \\ 0, &{}\quad x>a_4, \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} \nu _{\tilde{a}}(x)=\left\{ \begin{array}{ll} 1, &{}\quad x<c_1, \\ \frac{x-c_2}{c_1 - c_2}, &{}\quad c_1\leq x<c_2, \\ 0, &{}\quad c_2\leq x \leq c_3, \\ \frac{x-c_3}{c_4-c_3}, &{}\quad c_3< x \leq c_4,\\ 1, &{}\quad x>c_4. \end{array} \right. \end{aligned}$$

We can represent a trapezoidal I-fuzzy number (TrIFN) by

$$\begin{aligned} \tilde{a}=\langle [a_1, a_2, a_3, a_4], [c_1, c_2, c_3, c_4]\rangle \end{aligned}$$

with \(a_2=c_2, ~a_3=c_3\). Now if, \(a_2 = a_3=c_2=c_3=a\;(\texttt {say})\) then the a above given trapezoidal I-fuzzy number is the triangular I-fuzzy number. Similarly, a triangular I-fuzzy number (TIFN) is represented by \(\tilde{a}=\langle [a_1, a_2, a_3],[c_1, c_2, c_3]\rangle\)  with \(a_2=c_2\). Again if \((a_2-a_1) = (a_3-a_2)=p \;(\text {say})\) and \((c_2-c_1)= (c_3-c_2)=q \;(\text {say})\), then the given (TIFN) will be a symmetric triangular I-fuzzy number. We note that a symmetric triangular I-fuzzy number \(\tilde{a}\) may be denoted by \(\tilde{a}=\langle [a-p, a, a+p],[a-q, a, a+q]\rangle\).

Definition 3

(I-fuzzy arithmetic)  (Li 1999; Nehi 2010) Let \(\tilde{a}=\langle [a_1, a_2, a_3],[c_1, c_2, c_3]\rangle\) and \(\tilde{b}= \langle [b_1, b_2, b_3],[d_1, d_2, d_3]\rangle\) be two triangular I-fuzzy number and k be a real number. Then, the standard addition \(\tilde{a} + \tilde{b}\) and subtraction \(\tilde{a} -\tilde{b}\) are, respectively, the I-fuzzy numbers defined as

$$\begin{aligned} \begin{array}{lll} \tilde{a}+\tilde{b} &{}=&{}\langle [a_1+b_1, a_2 +b_2,a_3+b_3], \\ &{}&{}[c_1+d_1, c_2+d_2, c_3+d_3]\rangle ,\\ \text {and} &{}&{}\\ \tilde{a} - \tilde{b} &{}=&{}\langle [a_1 -b_3, a_2 -b_2,a_3-b_1],\\ &{}&{} [c_1 -d_3, c_2-d_2, c_3-d_1]\rangle . \end{array} \end{aligned}$$

Further, multiplication with any real number k, \(k\tilde{a}\), is an another I-fuzzy number defined as

$$\begin{aligned} \begin{array}{lll} k\tilde{a}&{}=&{}\langle [ka_1, ka_2, ka_3], [kc_1, kc_2, k c_3]\rangle ,\quad \text {if}\quad k >0,\\ k\tilde{a}&{}=&{} \langle [ka_3,ka_2,ka_1], [kc_3,kc_2,kc_1]\rangle , \quad \text {if} \quad k <0. \end{array} \end{aligned}$$

Let ‘\(\gtrsim ^{IF}\)’ and ‘\(\lesssim ^{IF}\)’ be the I-fuzzy versions of the symbols ‘\(\ge\)’ and ‘\(\le\)’, respectively, and interpretation of ‘greater than or equal to’ and ‘less than or equal to’ in I-fuzzy sense.

Definition 4

(Almost positive symmetric triangular I-fuzzy number) (Aggarwal et al. 2017) Let \(\tilde{a}=\langle [a-p,a,a+p][a-q,a,a+q]\rangle\) be a symmetric triangular I-fuzzy number. Let \(0 \le h_1 \le 1\) and \(0 \le h_2 \le 1\). Then, \(\tilde{a}\) is said to be ‘almost positive I-fuzzy number’, denoted by \(\tilde{a}\gtrsim ^{IF}_{h_1,h_2}0\), if \(a>0\) and

  1. 1.

    \(\mu _{\tilde{a}}(0) \le (1-h_1)\), and

  2. 2.

    \(\nu _{\tilde{a}}(0) \ge h_2\),

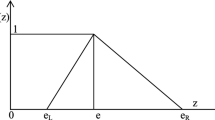
where \(h_1\) and \((1-h_2)\), respectively, are interpreted as the ‘degree of belief’ and ‘degree of disbelief’ in making the statement ’\(\tilde{a}\) almost positive’. Figure 1 depicts the meaning of \(\tilde{a}\gtrsim ^{IF}_{h_1,h_2}0\).

Fig. 1
figure 1

Almost positive symmetric triangular I-fuzzy number

Full size image

Definition 5

(Belief Score)  (Aggarwal et al. 2017) Let \(\tilde{a}\) be almost positive with degree of belief \(h_1\) and degree of disbelief \((1-h_2)\). Then, the difference \(h_1-(1-h_2)\), i.e., \((h_1+h_2-1)\) is called the belief score of the I-fuzzy statement \(\tilde{a}\gtrsim ^{IF}_{h_1,h_2}0\).

Remark 1

As \(\tilde{a}\) is a I-fuzzy number, \(\mu _{\tilde{a}}(0)+\nu _{\tilde{a}}(0) \le 1\). This gives \(h_1 \ge h_2\).

Remark 2

Also, for a meaningful decision, we expect that the degree of belief is greater than or equal to the degree of disbelief. Thus, \(h_1 \ge (1-h_2)\), i.e., \(h_1+h_2 \ge 1\), which means that the belief score is always expected to be non-negative.

Remark 3

An I-fuzzy number \(\tilde{a}\) is ‘more than or equal to’ another I-fuzzy number \(\tilde{b}\), denoted by \(\tilde{a}\gtrsim ^{IF}_{h_1,h_2}\tilde{b}\) if the triangular I-fuzzy number \((\tilde{a}-\tilde{b})\) is almost positive, i.e., \((\tilde{a}-\tilde{b})\gtrsim ^{IF}_{h_1,h_2}0\).

Remark 4

An I-fuzzy number \(\tilde{a}\) is ‘less than or equal to’ another I-fuzzy number \(\tilde{b}\), denoted by \(\tilde{a}\lesssim ^{IF}_{h_1,h_2}\tilde{b}\) if the triangular I-fuzzy number \((\tilde{b}-\tilde{a})\) is almost positive, i.e., \((\tilde{b}-\tilde{a})\gtrsim ^{IF}_{h_1,h_2}0\).

3 I-fuzzy matrix games with I-fuzzy goals and I-fuzzy pay-offs: proposed approach

We begin this section by describing a crisp game. For this, we shall need some notations.

Let \(\mathbb {R}^n\) be the n-dimensional Euclidean space and \(\mathbb {R}^n_+\) be its non-negative orthant. \(A \in \mathbb {R}^{m \times n}\) be \(m \times n\) matrix and \(e^T=(1,\ldots ,1)\) be a vector of ones whose dimension is specified as per the specific context, and \(S^m=\{x \in \mathbb {R}^{m}_+\;|\; e^Tx=1\}\) and \(S^n=\{y \in \mathbb {R}^{n}_+\;|\; e^Ty=1\}.\)

Mathematically, the two person zero-sum matrix game is represented by the triplet \(G=(S^m, S^n, A),\) where \(S^m\) and \(S^n\) are the strategy spaces for player I and player II, respectively, and A is the pay-off matrix. Also, it is a convention to assume that player I is a maximizing player and player II is a minimizing player. Therefore, for \(x \in S^m\), \(y \in S^n\), the scalar \(x^TAy\) is the expected pay-offs to player I, and since the game is zero-sum, the pay-offs to player II is \(-x^{T}Ay\).

Herein, we introduce the I-fuzzy matrix game with I-fuzzy goals and I-fuzzy pay-offs. Let \(\widetilde{A}\) be the pay-offs matrix with entries as symmetric triangular I-fuzzy numbers. Since the entries in the pay-offs matrix are symmetric triangular I-fuzzy numbers, it is natural to assume that the pay-offs of both players be symmetric triangular I-fuzzy number. Suppose player I and player II prescribe their aspiration levels as symmetric triangular I-fuzzy numbers \(\widetilde{U}_0\) and \(\widetilde{V}_0\), respectively. Let \(0 \le h_1 \le 1\) and \(0 \le h_2 \le 1\). Let \(h_1\) and \(1-h_2\) be the degree of belief and degree of disbelief of player I, that his/her expected pay-offs are more than or equal to the aspiration level \(\tilde{U_0}\). Similarly, let \(h'_1\) and \(1-h'_2\) be the degree of belief and degree of disbelief of player II, that his/her expected pay-offs value is less than or equal to the aspiration level \(\tilde{V_0}\). Then, a generalized model for a matrix game with I-fuzzy goals and I-fuzzy pay-offs is

$$\begin{aligned} {\text {(IFG)}}=(S^{m}, S^{n},\widetilde{A} , {\widetilde{U}_0}, {\gtrsim }^{IF}_{h_1,h_2}\;,\;\widetilde{V}_0,\;{\lesssim }^{IF}_{h'_1,h'_2}). \end{aligned}$$

Here, \(\widetilde{U}_0 = \langle [u_0-p_{00}, u_0, u_0 +p_{00} ],[u_0-q_{00},u_0, u_0 +q_{00}]\rangle\), \(\widetilde{V}_0 = \langle [v_0-r_{00}, v_0, v_0 +r_{00} ],[v_0-t_{00},v_0, v_0 +t_{00}]\rangle\) and \(\widetilde{A}=[\tilde{a}_{ij}]\) are an \(m \times n\) matrix with \(\tilde{a}_{ij}, \; i=1,2,\ldots ,m, \; j=1,2,\ldots ,n\) as symmetric triangular I-fuzzy numbers. Thus, \(\tilde{a}_{ij}=\langle [a_{ij}-p_{ij}, a_{ij}, a_{ij} +p_{ij}],[a_{ij}-q_{ij}, a_{ij}, a_{ij} +q_{ij}] \rangle \; i=1,2,\ldots ,m, \; j=1,2,\ldots ,n\). Now the solution of the I-fuzzy matrix game (IFG) can be defined as follows:

Definition 6

(Solution of Game) An element \((\overline{x},\overline{y}) \in S^m \times S^n\) is called the solution of the I-fuzzy matrix game (IFG) if

$$\begin{aligned}&{\overline{x}}^T\widetilde{A}y \; \;{\gtrsim }^{IF}_{h_1,h_2}\; \widetilde{U}_0,\; \; \forall\; y \in S^n, \\&x^T\widetilde{A}{\overline{y}} \;\;{\lesssim }^{IF}_{h'_1,h'_2}\; \widetilde{V}_0, \; \; \forall\; x\in S^m. \end{aligned}$$

As \(S^m\) and \(S^n\) are convex polytopes, it is sufficient to consider only the extreme points of \(S^m\) and \(S^n\). Therefore, solving the game (IFG) is equivalent to solve the following two I-fuzzy linear programming problems, (IFP-I) and (IFP-II) for player I and player II, respectively

$$\begin{aligned} \begin{array}{ll} {\text {(IFP-I)}}&{} \text{ Find } x \in S^m\;\, \text{ such } \text{ that, }\\ &{}x^T{\widetilde{A}_j}\;\; {\gtrsim }^{IF}_{h_1, h_2}\;\;\widetilde{U}_0, \;\; j=1,2,\ldots ,n, \end{array} \end{aligned}$$

nd

$$\begin{aligned} \begin{array}{ll} {\text {(IFP-II)}}&{} \text{ Find } y \in S^{n}\;\, \text{ such } \text{ that, } \\ &{} {\widetilde{A}_i}y\;\; {\lesssim }^{IF}_{h'_1, h'_2}\;\;\widetilde{V}_0, \;\; i=1,2,\ldots ,m. \end{array} \end{aligned}$$

Without loss of generality, the above system of I-fuzzy inequalities in (IFP-I) and (IFP-II) is equivalent to (EIFP-I) and (EIFP-II), respectively, and is as follows:

(EIFP-I)

Find \(x \in \mathbb {R}^m\) such that,

$$\begin{aligned}&\widetilde{X}_j = -\widetilde{U}_0 x_0+ \sum \nolimits _{i=1}^{m}\tilde{a}_{ij}x_i\;{\gtrsim }^{IF}_{h_1, h_2},\;\; j=1,2,\ldots ,n,\\&\sum\nolimits _{i=1}^{m}x_i=\;1,\;\; x_0=1,\\&x_i \ge 0, \;\; i=1,2,\ldots ,m, \end{aligned}$$

and

(EIFP-II)

Find \(y \in \mathbb {R}^n\) such that

$$\begin{aligned}&\widetilde{Y}_i =\widetilde{V}_0 y_0- \sum \nolimits _{j=1}^{n}\tilde{a}_{ij}y_j {\gtrsim }^{IF}_{h'_1,h'_2} 0,\;\; i=1,2,\ldots ,m,\\&\sum \nolimits _{j=1}^{n}y_j =\;1,\;\; y_0=1\\&y_j \ge 0, \;\; j=1,2,\ldots ,n. \end{aligned}$$

Here, it may be noted that the  inequalities \(\widetilde{X}_j\;\;{\gtrsim }^{IF}_{h_1,h_2}\;\; 0\), \(j=1,2,\ldots ,n\) and \(\tilde{Y}_i\;\;{\gtrsim }^{IF}_{h'_1, h'_2}\;\; 0\), \(i=1,2,\ldots ,m\) are to be understood in the sense of ‘almost positive’ in I-fuzzy environment (Definition 4).

The membership and non-membership functions for \(\widetilde{X_j},\) \(j=1,2,\ldots ,n\), where \(X_j=-u_{0}x_0+ \sum\nolimits _{i=1}^{m}a_{ij}x_i, \; j=1,2,\ldots ,n\), are

$$\begin{aligned} {\mu _{\widetilde{X}_j}}(X)= {\left\{ \begin{array}{ll} 1+\frac{X-X_j}{\sum\nolimits _{i=0}^{m}p_{ij}x_i}; &{}\quad X_j- \sum _{i=0}^{m}p_{ij}x_i\le X \le X_j,\\ 1; &{}\quad X = X_j,\\ 1-\frac{X-X_j}{\sum \nolimits_{i=0}^{m}p_{ij}x_i}; &{}\quad X_j \le X \le X_j+ \sum\nolimits _{i=0}^{m}p_{ij}x_i,\\ 0; &{}\quad {\text {otherwise}}. \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} {\nu _{\widetilde{X}_j}}(X)= {\left\{ \begin{array}{ll} \frac{-X+X_j}{\sum \nolimits_{i=0}^m q_{ij}x_i} ; &{}\quad X_j-\sum\nolimits _{i=0}^m q_{ij}x_i \le X \le X_j, \\ 0; &{}\quad X=X_j,\\ \frac{X-Xj}{\sum \nolimits_{i=0}^m q_{ij}x_i} ; &{}\quad X_j \le X \le X_j+\sum\nolimits _{i=0}^m q_{ij}x_i,\\ 1; &{} \quad {\text {otherwise}}. \end{array}\right. } \end{aligned}$$

respectively, where \(p_{0j}=p_{00}\) and \(q_{0j}=q_{00}, \; j=1,2,\ldots ,n.\)

Similarly, the membership and non-membership functions for \(\widetilde{Y}_i, \; i=1,2,\ldots ,m,\) where \(\widetilde{Y}_i =\tilde{V}_0 y_0- \sum_{j=1}^{n}\tilde{a}_{ij}y_j\) \(i=1,2,\ldots ,m,\) are

$$\begin{aligned} {\mu _{\widetilde{Y}_i}}(Y)= {\left\{ \begin{array}{ll} 1+\frac{Y-Y_i}{\sum\nolimits _{j=0}^{n}p_{ij}y_j}; &{}Y_i-\sum \nolimits_{j=0}^{n}p_{ij}y_j \le Y \le Y_i,\\ 1; &{}Y = Y_i,\\ 1-\frac{Y-Y_i}{\sum \nolimits_{j=0}^{n}p_{ij}y_j}; &{}Y_i \le Y \le Y_i+ \sum\nolimits _{j=0}^{n}p_{ij}y_j,\\ 0; &{} {\text {otherwise}}. \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} {\nu _{\widetilde{Y}_i}}(Y)= {\left\{ \begin{array}{ll} \frac{-Y+Y_i}{\sum \nolimits_{j=0}^n q_{ij}y_j} ; &{}Y_i-\sum \nolimits_{j=0}^n q_{ij}y_j \le Y \le Y_i,\\ 0; &{}Y=Y_i,\\ \frac{Y-Yi}{\sum \nolimits _{j=0}^n q_{ij}y_j} ; &{} Y_i \le Y \le Y_i+\sum\nolimits _{j=0}^n q_{ij}y_j,\\ 1; &{} {\text {otherwise}}. \end{array}\right. } \end{aligned}$$

respectively, and \(p_{i0}=r_{00}\) and \(q_{i0}=t_{00}, \; i=1,2,\ldots ,m\) and \(Y_i=v_0 y_0-{\sum \nolimits_{j=1}^n a_{ij}y_j}, \; i=1,2,\ldots ,m\).

Since with any I-fuzzy inequality, there is a degree of belief and also degree of disbelief associated with it. Thus, the two players would like to choose the solution for which the belief score is maximum. Therefore, to solve the two problems (EIFP-I) and (EIFP-II), it is equivalent to solve the following problems for player I and player II, respectively

(EPP-I)

$$\begin{aligned}&\max \qquad \quad (h_1+h_2-1)\\&\text{ subject } \text{ to, } \\&\mu _{\widetilde{X}_j}(0) \le 1-h_1, \;\;j=1,2,\ldots ,n, \\&\nu _{\widetilde{X}_j}(0) \ge h_2, \;\;\;\;\;\;\;\;j=1,2,\ldots ,n, \\&\sum _{i=1}^{m}x_i=\;1,\\& h_1+h_2\ge 1, \\&h_1\ge h_2, \\& x_0 =1, \; x_i \ge 0,\;\;\;\; i=1,2,\ldots ,m. \end{aligned}$$

and

(EPP-II)

$$\begin{aligned}&\max \quad \quad \quad (h'_1+h'_2-1)\\&\text{ subject } \text{ to, } \\&\mu _{\widetilde{Y}_j}(0) \le (1-h'_1), \;\; i=1,2,\ldots ,m, \\&\nu _{\widetilde{Y}_i}(0) \ge h'_2, \;\;\;\;\;\;\;\;\;\;\;i=1,2,\ldots ,m, \\& \sum _{j=1}^{n}y_j =\;1,\\&h'_1+h'_2 \ge 1, \\&h'_1\ge h'_2, \\&y_0 =1, \; y_j \ge 0, \;\;\;\;\;\;j=1,2,\ldots ,n. \end{aligned}$$

Substituting the values of \(\mu _{\widetilde{X}_j}(0)\) and \(\nu _{\widetilde{X}_j}(0)\), \(j=1,2,\ldots ,n\) in (EPP-I) and (EPP-II) respectively, we get the following non-linear programming optimization problem:

(EPP-I)

$$\begin{aligned}&\max \quad (h_1+h_2-1)\\&\text{ subject } \text{ to, }\\&-u_{0}x_0+\sum \nolimits_{i=1}^{m}a_{ij}x_i \le (1-h_1)\sum \nolimits _{i=0}^{m}p_{ij}x_i,\;\; j=1,2,\ldots ,n, \\&-u_{0}x_0+\sum \nolimits_{i=1}^{m}a_{ij}x_i \ge h_2\left( \sum \nolimits _{i=0}^{m}q_{ij}x_i\right) ,\;\;\;\; j=1,2,\ldots ,n, \\&\sum\nolimits _{i=1}^{m} x_i =\;1,\\&h_1+h_2 \ge 1, \\&h_1\ge h_2, \\&x_0 =1,\;x_i \ge 0, \quad \qquad i=1,2,\ldots ,m,\\&p_{0j} =p_{00} \text{ and } q_{0j}=q_{00}, \quad \qquad j=1,2,\ldots ,n. \end{aligned}$$

and problem for player II is

(EPP-II)

$$\begin{aligned}&\max \quad (h'_1+h'_2-1)\\&\text{ subject } \text{ to, } \\&v_{0}y_0-\sum\nolimits _{j=1}^{n}a_{ij}y_j \le (1-h'_1)\sum \nolimits _{j=0}^{n}p_{ij}y_j, \;\;j=1,2,\ldots ,n, \\&v_{0}y_0-\sum \nolimits_{j=1}^{n}a_{ij}y_j \ge h'_2\left( \sum \nolimits _{j=0}^{n}q_{ij}y_j\right) , \;\;\;\;i=1,2,\ldots ,m, \\&\sum\nolimits _{j=1}^{n}y_j =1,\\&h'_1+h'_2 \ge 1, \\&h'_1\ge h'_2, \\&y_0 =1, \; y_j \ge 0, j=1,2,\ldots ,n,\\&p_{i0} =r_{00} \text{ and } q_{i0}=t_{00}, \;\;\;\;\;\; \;i=1,2,\ldots ,m. \end{aligned}$$

Let \((x^*,h_{1}^*, h_{2}^*)\) and \((y^*,h^{'*}_{1}, h^{'*}_{2})\) be the optimal solutions of (EPP-I) and (EPP-II) of player I and player II, respectively. Then, we say that \(x^*\) is called the solution of I-fuzzy matrix games problem (EIFP-I) with degree of belief \(h_{1}^*\) and degree of disbelief \((1-h_{2}^*)\) and the quantity (\(h_1^*+h_2^*-1\)) is called the belief score of the player I. This elucidates that player I achieves its aspired level of goals with degree of belief \(h_1^*\) and degree of disbelief (\(1-h_2^*\)) when he employs strategy set \(x^*\). Analogous explanations follows for player II.

Remark 5

At origin, the value of membership function and non-membership function takes the value \(1-h_1\) and \(h_2\), respectively. As this I-fuzzy scenario subsumes to fuzzy environment, the sum of membership and non-membership function should be equal to 1. Hence, \(1-h_1+h_2=1\); therefore, \(h_1=h_2\). Now, for \(h_1=h_2=h\), the I-fuzzy game problem (EPP-I) reduces to the player I’s problem in fuzzy environment (EFPP-I), i.e.,

(EFPP-I)

$$\begin{aligned}&\max \quad (2h-1)\\&\text{ subject } \text{ to, } \\&\mu _{\widetilde{X}_j}(0) \le 1-h,\;\; j=1,2,\ldots ,n, \\&\sum \nolimits_{i=1}^{m}x_i = 1,\\&h \ge \frac{1}{2}, \\&x_i \ge 0, \; i=1,2,\ldots ,m. \end{aligned}$$

Similarly, for player II, when \(h_1'=h_2'=h'\), the I-fuzzy problem reduces to (EFPP-II) in fuzzy environment, i.e., (EFPP-II)

$$\begin{aligned}&\max \quad \;(2h'-1)\\&\text{ subject } \text{ to, } \\&\mu _{\widetilde{Y}_i}(0) \le 1-h', \;\; i=1,2,\ldots ,m, \\& \sum\nolimits _{j=1}^{n}y_j =\;1,\\&h' \ge \frac{1}{2}, \\&y_j \ge 0, \; j=1,2,\ldots ,n. \end{aligned}$$

Remark 6

It is to be noted that the problems (EFPP-I) and (EFPP-II) cannot be compared to any of the approaches discussed by Bector and Chandra (2005). All these approaches are based on defuzzification number, while the approach defined in this paper to solve the matrix game is independent of any transformation or ranking function.

4 Numerical illustrations

To demonstrate the applicability and validity of the proposed work, we present two real-world problems. First of all, we consider the famous example of Campos (1989) which has also been examined by Bector and Chandra (2005) under fuzzy environment.

Example 1

Suppose that there are two companies P1 and P2 aiming to enhance the market share of a product in a targeted market under the circumstance that the amount of demand of the product in the targeted market is fixed. In other words, the market share of one company increases while the one of another company decreases.

The two companies are considering two strategies to increase the market share: \(\delta _1\) strategy (advertisement) and \(\delta _2\) (reduce the price). The above problem may be regarded as a matrix game. Namely, the companies P1 and P2 be regarded as a player I and player II, respectively. They may use strategies \(\delta _1\) and \(\delta _2\). Due to a lack of information or the imprecision of the available information, the managers of the two companies usually are not able to exactly forecast the sales amount of the companies. They can estimate the sales amount with a certain confidence degree, but it is possible that they are not so sure about it. Thus, there may be hesitation about the estimation of the sales amount. To handle the uncertain situation, symmetric triangular I-fuzzy numbers are used to express the sales amount of the product. The pay-offs matrix \(\tilde{A}\) for P1 is given as follows:

$$\begin{aligned}\widetilde{A}= \begin{bmatrix} \widetilde{180}&\widetilde{156} \\ \widetilde{90}&\widetilde{180} \end{bmatrix} \end{aligned}$$

where \(\widetilde{180}=\langle[175,180,185],[170,180,190]\rangle,\) in the matrix \(\widetilde{A}\) is a symmetric triangular I-fuzzy number, which is a special case of triangular I-fuzzy number which indicates that the sales amount of the company is about 180 when the companies P1 and P2 use the strategy \(\delta _1\) (advertisement) simultaneously. The aspiration level is also described by symmetric triangular I-fuzzy number and is defined as \(\widetilde{U_0}=\widetilde{152}\) and \(\widetilde{V_0}=\widetilde{172}\) for player I and player II, respectively. Let

$$\begin{aligned} \widetilde{180}= & {} \langle [175,180,185],[170,180,190]\rangle , \\ \widetilde{156}= & {} \langle [150,156,162],[148,156,164]\rangle , \\ \widetilde{90}= & {} \langle [80,90,100],[75,90,105]\rangle , \\ \widetilde{152}= & {} \langle [147,152,157],[144,152,160]\rangle , \\ \text{ and }\;\; \;\widetilde{172}= & {} <[162,172,182],[157,172,187]\rangle . \end{aligned}$$

Solution by the proposed method

To solve the game IFG, we need to solve the following problem for player I:

$$\begin{aligned} \begin{array}{ll} {\text {(IFP-I)}} &{}\text{ Find } x \in \mathbb {R}^2 \; \text{ such } \text{ that, } \\ &{}\widetilde{180}x_1+\widetilde{90}x_2 \;{\gtrsim }^{IF}_{h_1,h_2}\;\;\widetilde{152}, \\ &{}\widetilde{156}x_1+\widetilde{180}x_2\; {\gtrsim }^{IF}_{h_1,h_2}\;\widetilde{152},\\ &{} \sum \nolimits _{i=1}^2 x_i=1,\\ &{} x_1, \;x_2 \ge 0. \end{array} \end{aligned}$$

The above inequalities can be written as

$$\begin{aligned} \begin{array}{ll} {\text {(EIFP-I)}}&{}\text{ Find } x \in \mathbb {R}^2 \; \text{ such } \text{ that, } \\ &{}\widetilde{X_1}=-\widetilde{152}x_0+\widetilde{180}x_1+\widetilde{90}x_2 \;{\gtrsim }^{IF}_{h_1, h_2} \;0, \\ &{}\widetilde{X_2}=-\widetilde{152}x_0+\widetilde{156}x_1+\widetilde{180}x_2 \;{\gtrsim }^{IF}_{h_1, h_2} 0,\\ &{} \sum \nolimits _{i=1}^2 x_i=1,\\ &{} x_0=1, \;x_1, \;x_2 \ge 0. \end{array} \end{aligned}$$

Thus, \(\widetilde{X_1}=-\widetilde{152}x_0+ \widetilde{180}x_1+ \widetilde{90}x_2\), \(\widetilde{X_2}=-\widetilde{152}x _0+\widetilde{156}x_1+\widetilde{180}x_2\) and hence the membership and non-membership functions for each I-fuzzy inequality are as follows:

$$\begin{aligned} \begin{array}{l} {\mu _{\widetilde{X}_1}}(X)=\\ {\left\{ \begin{array}{ll} 1+ \frac{X-X_1}{5+5x_1+10x_2};&{}\quad X_1-(5+5x_1+10x_2) \le X \le X_1,\\ 1;&{}\quad X = X_1,\\ 1- \frac{X-X_1}{5+5x_1+10x_2};&{}\quad X_1 \le X \le X_1+ 5+5x_1+10x_2,\\ 0; &{}\quad {\text {otherwise}}. \end{array}\right. } \end{array} \end{aligned}$$

and

$$\begin{aligned}&\begin{array}{l} {\nu _{\widetilde{X}_1}}(X)=\\ {\left\{ \begin{array}{ll} \frac{-X+X_1}{5+5x_1+10x_2}; &{}X_1-(5+5x_1+10x_2) \le X \le X_1,\\ 0; &{}X = X_1,\\ \frac{X-X_1}{5+5x_1+10x_2}; &{}X_1 \le X \le X_1+ 5+5x_1+10x_2,\\ 1; &{} {\text {otherwise}}. \end{array}\right. } \end{array}\\&\begin{array}{l} {\mu _{\widetilde{X}_2}}(X)=\\ {\left\{ \begin{array}{ll} 1+\frac{X-X_2}{5+6x_1+5x_2}; &{}X_2-(5+5x_1+10x_2) \le X \le X_2,\\ 1; &{}X = X_2,\\ 1- \frac{X-X_2}{5+6x_1+5x_2}; &{}X_2 \le X \le X_2+ 5+6x_1+5x_2,\\ 0; &{} {\text {otherwise}} \end{array}\right. } \end{array} \\&\begin{array}{l} {\nu _{\widetilde{X}_2}}(X)=\\ {\left\{ \begin{array}{ll} \frac{-X+X_2}{8+8x_1+10x_2}; &{}X_2-(8+8x_1+10x_2)\le X \le X_2,\\ 0; &{}X = X_2,\\ \frac{X-X_2}{8+8x_1+10x_2}; &{}X_2 \le X \le X_2+ 8+8x_1+10x_2,\\ 1; &{} {\text {otherwise}} \end{array}\right. } \end{array} \end{aligned}$$

The equivalent problem for player I is

(EPP-I)

$$\begin{aligned}&\max \quad (h_1+h_2-1)\\&\text{ subject } \text{ to, } \\&-152-5h_1+(180-5h_1)x_1+(90-10h_1)x_2 \ge 0,\\&-152-5h_1+(156-6h_1)x_1+(180-5h_1)x_2 \ge 0,\\&-152-5h_2+(180-10h_2)x_1+(90-15h_2)x_2 \ge 0,\\&-152-5h_2+(156-8h_2)x_1+(180-10h_2)x_2 \ge 0,\\&\sum \nolimits_{i=1}^{2}x_i =\;1,\\&h_1+h_2\ge 1, \\&h_1\ge h_2, \\&x_1 \ge 0,\; x_2 \ge 0. \end{aligned}$$

Thus, the optimal solution for player I is (\(x_1^*= 0.8107452\), \(x_2^*= 0.1892548\), \(h_1^*= 0.7901506\), \(h_2^*=0.5788483\)). Hence, the degree of belief and degree of disbelief in making the statement that the system of non-linear inequalities almost positive are 0.7901506 and 0.4211517, respectively. On the similar lines, the problem for player II is as follows (IFP-II):

Find \(y \in \mathbb {R}^2\) such that,

$$\begin{aligned} \begin{array}{ll} &{}\widetilde{180}y_1+\widetilde{156}y_2 \;\;{\lesssim }^{IF}_{h'_1, h'_2}\; \;\widetilde{172}, \\ &{}\widetilde{90}y_1+\widetilde{180}y_2 \;\;{\lesssim }^{IF}_{h'_1, h'_2}\;\;\;\widetilde{172}.\\ &{} \sum \limits _{j=0}^2 y_j=1,\\ &{}y_1, \;y_2 \ge 0. \end{array} \end{aligned}$$

The equivalent problem is  

(EIFP-II)

Find \(y \in \mathbb {R}^2\)  such that

$$\begin{aligned} \begin{array}{ll} &{}\widetilde{Y_1}=\widetilde{172}y_0-\widetilde{180}y_1-\widetilde{156}y_2 {\lesssim }^{IF}_{h'_1,h'_2} \;\;0, \\ &{}\widetilde{Y_2}=\widetilde{172}y_0-\widetilde{90}y_1-\widetilde{180}y_2 \; \; {\lesssim }^{IF}_{h'_1,h'_2}\; \;0,\\ &{} \sum \nolimits _{j=1}^2 y_j=1,\\ &{} y_0=1, \;y_1, \;y_2 \ge 0. \end{array} \end{aligned}$$

Now, \(Y_1=172x_0-180x_1-156x_2\), \(Y_2=172x _0-90x_1-180x_2\). Hence, the membership and non-membership functions, for each I-fuzzy inequality, are as follows:

$$\begin{aligned} & \mu _{{\widetilde{Y}_{1} }} (Y) \\ & \quad = \left\{ {\begin{array}{*{20}l} {1 +\frac{{Y - Y_{1} }}{{10 + 5y_{1} + 6y_{2} }};\quad } \hfill & {Y_{1} - (10 + 5y_{1} + 6y_{2} ) \le Y \le Y_{1} ,} \hfill \\ {1;} \hfill & {Y = Y_{1} ,} \hfill \\ {1 -\frac{{Y - Y_{1} }}{{10 + 5y_{1} + 6y_{2} }};} \hfill & {Y_{1} \le Y \le Y_{1} + 10 + 5y_{1} + 6y_{2} ,} \hfill \\ {0;} \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right. \\ \end{aligned}$$

and

$$\begin{aligned} & \nu _{{\widetilde{Y}_{1} }} (Y) \\ & \quad = \left\{ {\begin{array}{*{20}l} {\frac{{ - Y + Y_{1} }}{{15 + 10y_{1} + 8y_{2} }};\quad } \hfill & {Y_{1} - (15 + 10y_{1} + 8y_{2} ) \le Y \le Y_{1} ,} \hfill \\ {0;} \hfill & {Y = Y_{1} ,} \hfill \\ {\frac{{Y - Y_{1} }}{{15 + 10y_{1} + 8y_{2} }};} \hfill & {Y_{1} \le Y \le Y_{1} + 15 + 10y_{1} + 8y_{2} ,} \hfill \\ {1;} \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right. \\ & \mu _{{\widetilde{Y}_{2} }} (Y) \\ & \quad = \left\{ {\begin{array}{*{20}l} {1 + \frac{{Y - Y_{2} }}{{10 + 10y_{1} + 5y_{2} }};} \hfill & {Y_{1} - (10 + 10y_{1} + 5y_{2} ) \le Y \le Y_{2} ,} \hfill \\ {1;} \hfill & {Y = Y_{2} ,} \hfill \\ {1 -\frac{{Y - Y_{2} }}{{10 + 10y_{1} + 5y_{2} }};} \hfill & {Y_{2} \le Y \le Y_{2} + 10 + 10y_{1} + 5y_{2} ,} \hfill \\ {0;} \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right. \\ \end{aligned}$$

and

$$\begin{aligned} &\nu _{{\widetilde{Y}_{2} }} (Y) \\ &\quad = \left\{ {\begin{array}{*{20}l} { \frac{{ - Y + Y_{2} }}{{15 + 15y_{1} + 10y_{2} }};\quad } \hfill & {Y_{2} - (15 + 15y_{1} + 10y_{2} ) \le Y \le Y_{2} ,} \hfill \\ {0;} \hfill & {Y = Y_{2} ,} \hfill \\ { \frac{{Y - Y_{2} }}{{15 + 15y_{1} + 10y_{2} }};} \hfill & {Y_{2} \le Y \le Y_{2} + 15 + 15y_{1} + 10y_{2} ,} \hfill \\ {1;} \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right. \hfill \\ \end{aligned}$$

Thus, problem of player II becomes

(EPP-II)

$$\begin{aligned}&\max (h'_1+h'_2-1)\\&\text{ subject } \text{ to, } \\&-172+10h'_1+(180+5h'_1)y_1+(156+10h'_1)y_2 \le 0, \\&-172+10h'_1+(90+10h'_1)y_1+(180+15h'_1)y_2 \le 0, \\&172-15h'_2-(180+10h'_2)y_1-(156+8h'_2)y_2 \ge 0, \\&172-15h'_2-(90+15h'_2)y_1-(180+10h'_2)y_2 \ge 0, \\&\sum \nolimits_{j=1}^{2}y_j=\;1,\\&h_1+h_2\ge 1, \\&h_1\ge h_2, \\&y_1 \ge 0,\; y_2 \ge 0. \end{aligned}$$

The optimal solution of player II is (\(y_1^*=0.2211824, \; y_2^*= 0.7788176, \; h_1^{'*}=0.6775934 , \; h_2^{'*}= 0.4560812\)). Here, the degree of belief and degree of disbelief in making a statement that the system is almost positive are 0.6775934 and 0.54391880, respectively.

Next, we present another important real-world problem of voting, which one also was discussed by Bandyopadhyay et al. (2013). It is suitably modified to explain the proposed technique.

Example 2

Suppose that there is an election where two major political parties A and B take part, and a total number of voters in that region is constant. It means that the increase in the percentage of voters for one political party results in the same for the other political party. Suppose A has two strategies as

  1. 1.

    A1: Giving importance in the door to door campaigning and carrying their ideology and issues to people.

  2. 2.

    A2: Co-operating with other small political parties to reduce secured votes of the opposition.

At the same time, B takes two strategies:

  1. 1.

    B1: Campaigning by celebrities and big rallies.

  2. 2.

    B2: Making lots of promises to people.

Now the chief voting agents cannot say exactly about the voting percentage, but they have a certain confidence level. Still, there is some hesitancy in that confidence level due to the bad weather forecast. In such a win–win situation, we may consider the pay-offs as symmetric triangular I-fuzzy number and the matrix is given as

$$\begin{aligned} \widetilde{A}= \begin{bmatrix} \widetilde{6}&\widetilde{7} \\ \widetilde{7}&\widetilde{5} \end{bmatrix} \end{aligned}$$

Let

$$\begin{aligned} &\widetilde{6}= \langle [5.7,6,6.3],[5.5,6,6.5]\rangle , \\ &\widetilde{7}= \langle [6.8,7,7.2],[6.4,7,7.6]\rangle , \\ \text{ and }&\widetilde{5} = \langle [4.8,5,5.2],[4.5,5,5.5]\rangle . \end{aligned}$$

Now \(\widetilde{6}= \langle [5.7,6,6.3],[5.5,6,6.5]\rangle\), in the pay-offs matrix \(\widetilde{A}\) indicates that when party A plays the strategy A1 and party B plays strategy B1, then the resulting expected votes in favor of party A are approximately 6 lakhs. Let the aspiration levels for party A and party B be \(\widetilde{U}_0=\widetilde{5} =\langle [4,5,6],[3,5,7]\rangle\) and \(\widetilde{V}_0=\widetilde{8}=\langle [6.7,8,9.3),[6.5,8,9.5]\rangle\), respectively. This indicates that approximately 5 lakhs votes are the minimum requirement for party A to win elections; similarly maximum requirement of votes for party B to win the elections will be 8 lakhs. According to present scheme, we need to solve the following crisp non-linear programming problem for party A:

(EPP-I)

$$\begin{aligned}&\max \quad \quad (h_1+h_2-1)\\&\text{ subject } \text{ to, } \\&6x_1+7x_2-5-h_1-0.6x_1h_1-0.2x_2h_1 \ge 0, \\&7x_1+5x_2-5-h_1-0.2h_1x_1-0.2x_2h_1 \ge 0, \\&6x_1+7x_2-5-2h_2-0.5x_1h_2-0.6x_2h_2 \ge 0, \\&7x_1+5x_2-5-2h_2-0.6x_1h_2-0.5x_2h_2 \ge 0, \\&\sum _{i=1}^{2}x_i=\;1,\\&h_1+h_2 \ge 1, \\&h_1\ge h_2, \\&0\le h_1\le 1, \\&0 \le h_2\le 1, \\&x_1 \ge 0,\; x_2 \ge 0. \end{aligned}$$

Thus, the optimal solution for party A is (\(x_1^*= 0.5894542, x_2^*= 0.4105458 , \; h_1^*=0.9824236, \; h_2^*= 0.4607009\)). Hence, the degree of belief and degree of disbelief in making a statement that the system of non-linear inequalities is almost positive are 0.9824236 and 0.5392991, respectively.

On the similar lines, the problem for party B is as follows:

(EPP-II)

$$\begin{aligned}&\max \quad \quad (h'_1+h'_2-1)\\&\text{ subject } \text{ to, } \\&-8+6y_1+7y_2+1.3h'_1+0.6y_1h'_1+0.2y_2 h'_1 \le 0, \\&-8+7y_1+5y_2+1.3h'_1+0.2y_1h'_1+0.2y_2h'_1 \le 0, \\&8-1.5h'_2-6y_1-0.5y_1h'_2-7y_2-0.6y_2h'_2 \ge 0, \\&8-1.5h'_2-7y_1-0.6y_1h'_2-5y_2-0.5y_2h'_2 \ge 0, \\&\sum _{j=1}^{2}y_j=\;1,\\&h'_1+h'_2 \ge 1, \\&h'_1 \ge h'_2, \\&0 \le h'_1\le 1, \\&0 \le h'_2 \le 1, \\& y_1 \ge 0,\; y_2 \ge 0 \end{aligned}$$

The optimal solution of party B is (\(y_1^*=0.6580763, \; y_2^*= 0.3419237, \; h_1^{'*}=0.9403628, \; h_2^{'*}=0.8151033\)). Here, the degree of belief and degree of disbelief in making a statement that the system is almost positive are 0.9403628 and 0.1848967, respectively.

5 A comparative study with the existing models in the literature

First of all it is to be noted that similar to fuzzy linear programming problems, fuzziness in matrix games can also appear in so many ways, but two cases of fuzziness seem to be very natural. These being the one in which players have fuzzy goals and the other in which the elements of the pay off matrix are given by fuzzy parameters or both.

Here, we explain why our proposed model is not comparable with some other relevant work reported in the literature.

The methods given in Aggarwal et al. (2012), Aggarwal et al. (2014), Vijay et al. (2007), Khan et al. (2017) and Nan et al. (2014) are to solve either fuzzy matrix games with fuzzy goals or fuzzy matrix games with fuzzy pay-offs. To solve these two matrix games, we have Zimmermann’s approach for matrix game with fuzzy goals and defuzzification or Yager’s ranking function approach for matrix game with fuzzy pay-offs in the literature. The Zimmermann (1978) approach requires pre-chosen tolerance levels while ranking function approach requires an appropriate choice of such function. Since our approach does not match with either of these two approaches, so no such comparison is possible. Also, different tolerance levels/ different ranking functions will, in general, give different solutions, so it does not seem to be possible to compare our method with that of the existing methods.

6 Conclusion

In this paper, we study a two person zero-sum matrix game with I-fuzzy goals and I-fuzzy pay-offs. An essential concept of ‘almost positive I-fuzzy number’ introduced by Aggarwal et al. (2017) is employed here to study such a game. Here, the comparison of two I-fuzzy numbers are only membership function based and is very natural the way we understand a positive real number. So without using any ranking function here, we can get precise degree of belief and degree of disbelief in achieving the goal set by the decision maker.

The multi-objective I-fuzzy matrix games and I-fuzzy bi-matrix games are other potential problems to study in the near future. An interesting area where this model can be explored is the group matrix game (studied by Figueroa-García et al. 2019), where the two groups of players play a game using the individual knowledge of every player to define the pay-offs.

As Ammar and Brikaa (2018) studied matrix game under rough fuzzy sets. It will be interesting if we study the ‘almost positive fuzzy number’ in rough fuzzy set environment.

Our proposed approach has the limitation of being applied in that situations where the pay-offs matrix contains symmetric triangular fuzzy numbers only. It will be exciting and challenging, if the proposed approach can work for non-symmetric fuzzy and, or I-fuzzy number in the pay-offs matrix.