Solving LP Models for Multi-objective Matrix Games with I-Fuzzy Goals

Abstract

The principal objective of this work is to obtain the optimal strategies for a multi-objective two-person zero-sum matrix game with intuitionistic fuzzy goals (MOMGIFG). In this problem, the fuzziness in aspiration levels of both players are characterized by intuitionistic fuzzy sets. The developed linear models are solved in maxmin–minmax way using linear membership function (mf) and non-membership function (nmf). A numerical example is incorporated to demonstrate the proposed solution procedure.

1 Introduction

Multi-objective game theory optimizes those multi-objective problems that involve two or more than two decision makers. In fact, real game problems cannot be characterized precisely because of fuzzy information about their elements. Various studies about the zero-sum matrix game models with two players have been done so far, e.g., [6,7,8, 10, 16] and references therein, where fuzziness in payoffs and goals are characterized by fuzzy sets. But, a situation in which an element feels a hesitation to belong or not belong to a subset of universe cannot be represented by fuzzy sets. Intuitionistic fuzzy sets (I-fuzzy sets) [4] can give a suitable description of such kind vague information. Firstly, Atanassov [5] used I-fuzzy set in game models. Thereafter, many researchers studied single- and multi-objective two-person zero-sum matrix game in I-fuzzy environment [1, 2, 11,12,13, 17, 18] and references therein.

The focus of this paper is introducing a solution approach for MOMGIFG. The notion for the proposed technique is inspired from max–min principle of classical game theory.

The outline of this research work is as follows: Sect. 2 introduces some preliminaries which are relevant to this work such as I-fuzzy set, maxmin–minmax solution and decision-making principle in I-fuzzy environment. In Sect. 3, a single-objective game model in matrix form with I-fuzzy goals is reviewed under some assumptions. A solution procedure for MOMGIFG with a set of assumptions is proposed in Sect. 4. In Sect. 5, an example is given to demonstrate the effectiveness of present work.

2 Preliminaries

Present section concerns some necessary definitions and one principle which are used throughout this paper.

Definition 1

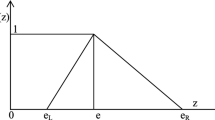
(I-fuzzy Set) An I-fuzzy set $\widetilde{T}$ on space S is defined by two functions, $\mu _+$ and $\mu _-$, such that $\mu _+(s)\in [0,1]$ represents the grade of membership of s in $\widetilde{T}$ and $\mu _-(s)\in [0,1]$ represents the grade of non-membership of s in $\widetilde{T}$ with condition $0\le \mu _+(s)+\mu _-(s)\le 1$. The expression $\mu ^h(s)=1-\mu _+(s)-\mu _-(s)$ is called degree of hesitancy of s in $\widetilde{T}$. An I-fuzzy set $\widetilde{T}$ is denoted by

$$ \widetilde{T} = \left\{ {\left\langle {s,\,} \right. } \right. \mu _+ (s),\,\left. {\mu _- (s)} \right\rangle \,|\left. {s \in S} \right\} .$$

In this paper, the goals for each player are viewed as I-fuzzy sets. The meaning of the value of $\mu _+(s)$ for an I-fuzzy goal is the grade of satisfaction of I-fuzzy goal for an expected payoff, whereas the value of $\mu _-(s)$ represents the degree of dissatisfaction of I-fuzzy goal. Recently, some I-fuzzy and fuzzy programming in term of goal programming have been found in [9, 14, 15].

A MOMGIFG is described by multi-payoff matrices $M^1, M^2, \ldots , M^r$. In this problem, Player I and II are denoted by $P_1$ and $P_2$, respectively. Suppose that I-fuzzy goal for kth payoff for $P_1$ and $P_2$ is denoted by $\tilde{g}_{P_1}^k$ and $\tilde{g}_{P_2}^k$, respectively. It is supposed that the r objectives of $P_1$ are also the objectives for $P_2$.

Definition 2

The maxmin–minmax value w. r. t. the grade of satisfaction of an aggregated I-fuzzy goal to $P_1$ is

$$\begin{aligned} \mathop {\mathrm{{max}}}\limits _{p\,\, \in \,\,U^m } \mathop {\min }\limits _{q\,\, \in \,\,U^n } \mathop {\mathrm{{min}}}\limits _k \,\,\,\,\,\{ \mu _{\tilde{g}_{P_1}^k+} (p^T M^k q)\} \end{aligned}$$

(1)

$$\begin{aligned} \mathop {\mathrm{{min}}}\limits _{p\,\, \in \,\,U^m } \mathop {\max }\limits _{q\,\, \in \,\,U^n } \mathop {\mathrm{{max}}}\limits _k \,\,\,\,\,\{ \mu _{\tilde{g}_{P_1}^k -} (p^T M^k q)\} \end{aligned}$$

(2)

where $U^m/U^n$ is mixed strategy space to $P_1$/$P_2$. Such a strategy $p^*$ is known as the maxmin–minmax solution of matrix game with aggregated I-fuzzy goal for $P_1$.

Similarly, the maxmin–minmax value w. r. t. the grade of satisfaction of an aggregated I-fuzzy goal to $P_2$ is

$$\begin{aligned} \mathop {\mathrm{{max}}}\limits _{q\,\, \in \,\,U^n } \mathop {\min }\limits _{p\,\, \in \,\,U^m } \mathop {\mathrm{{min}}\,\,\,}\limits _k \{ \mu _{\tilde{g}_{P_2}^k+} (p^T M^k q)\} \end{aligned}$$

(3)

$$\begin{aligned} \mathop {\mathrm{{min}}}\limits _{q\,\, \in \,\,U^n } \mathop {\max }\limits _{p\,\, \in \,\,U^m } \mathop {\mathrm{{max}}\,\,\,}\limits _k \{ \mu _{\tilde{g}_{P_2}^k -} (p^T M^k q)\}. \end{aligned}$$

(4)

Such a strategy $q^*$ is known as the maxmin–minmax solution of matrix game with aggregated I-fuzzy goal for $P_2$.

Definition 3

(Angelov’s Decision-Making Principle) Suppose that there are m goals $A_1, A_2,\ldots ,A_m$ and n constraints $B_1, B_2,\ldots ,B_n$ in a domain of alternatives $\Omega$. All these goals $(A_i's)$ and constraints $(B_j's)$ are I-fuzzy sets on $\Omega$. Angelov [3] proposed that an I-fuzzy decision which is evaluated by a suitable aggregation of the I-fuzzy sets $A_i (i=1,2,\ldots ,m)$ and $B_j (j=1,2,\ldots ,n)$. He used fuzzy intersection and fuzzy union as aggregation operators. Therefore, an I-fuzzy decision D which is an I-fuzzy set, defined by $\mu _{D+} :\,\Omega \rightarrow \,\,[0,\,1]$ given by $\mu _{D+} (\omega ) = \mathop {\mathrm{{min }}}\limits _{i,j} \left( {\mu _{{A_i}+ } (\omega ),\;\mu _{{B_j}+} (\omega )} \right)$ and $\mu _{D-} :\Omega \rightarrow [0,1]$ given by $\mu _{D-} (\omega ) = \mathop {\mathrm{{max }}}\limits _{i,j} \left( {\mu _{{A_i}- } (\omega ),\;\mu _{{B_j}-} (\omega )} \right)$.

The optimal decision can be obtained as $\mathop {\mathrm{{max }}}\limits _\omega \mu _{D+} (\omega )$ and $\mathop {\mathrm{{min }}}\limits _\omega \mu _{D-} (\omega )$.

According to this principle, the crisp version of above I-fuzzy optimization problem in linear programming (LP) form can be formulated as follows:

            $\begin{array}{l} \mathrm{{max}}\, ~~ (\alpha _+-\alpha _-)\\ \mathrm{{s.t.},} \end{array}$

$$\begin{aligned} \nonumber \mu _{{A_i}+ } (\omega )\ge & {} \alpha _+,\\\nonumber \mu _{{A_i}-} (\omega )\le & {} \alpha _- ,\,\,(i = 1,2, \ldots ,m),\\\nonumber \mu _{{B_j }+} (\omega )\ge & {} \alpha _+ ,\\ \nonumber \mu _{{B_j}-} (\omega )\le & {} \alpha _- ,\,\,(j = 1,2, \ldots ,n),\\\nonumber \alpha _+ + \alpha _-\le & {} 1,\\ \alpha _+ \ge \alpha _- ,\,\alpha _-\ge & {} 0,\,\omega \ge 0. \end{aligned}$$

(5)

Here, the optimal solution of model (5) is denoted by $(\omega ^*,{\alpha _+}^*, {\alpha _-}^*)$.

3 Single-Objective Matrix Game with I-Fuzzy Goal (SOMGIFG)

Present section demonstrates in what way a SOMGIFG can be solved through a pair of linear programming problem (LPP).

Let $M=[m_{ij}]_{m\times n}$ denote a payoff matrix of real constants for $P_1$. Since game is zero-sum, so $-M=[-m_{ij}]_{m\times n}$ is payoff matrix for $P_2$. Here, $U^m/U^n$ represents a set of mixed strategies for $P_1/P_2$. The sets $U^m$ and $U^n$ are defined as:

$$ U^m= \{ p=(p_1,p_2,\ldots ,p_m)^T|\displaystyle \sum _{i = 1 \;\textit{ to }\; m} p_i=1, p_i\ge 0\},$$

and

$$ U^n= \{ q=(q_1,q_2,\ldots ,q_n)^T|\displaystyle \sum _{j = 1 \;\textit{ to }\; n} q_j=1, q_j\ge 0\}.$$

In this work, the goals of $P_1$ and $P_2$ are characterized by I-fuzzy sets. Suppose that $\bar{v}_a$ is the aspiration level for $P_1$ with tolerance error $p_a$ and $\bar{v}_r$ is the rejection level for $P_1$ with tolerance error $p_r$. For $P_2$, let $\underline{v}_a$ be aspiration level with tolerance error $q_a$ and $\underline{v}_r$ be rejection level with tolerance error $q_r$.

To solve two-person zero-sum SOMGIFG, the following conditions are assumed as:  

$(H_1)$ :

The I-fuzzy goals of both players $P_1$ and $P_2$ are represented by linear mf and nmf;

$(H_2)$ :

For $P_1$, ${\bar{v}}_r { - p}_r \le {\bar{v}}_a { - p}_a$ & ${\bar{v}}_r \le {\bar{v}}_a;$

$(H_3)$ :

For $P_2$, $\underline{v}_a+ q_a \le \underline{v}_r + q_r$ & $\underline{v}_a \le \underline{v}_r.$

  Using $(H_1)$–$(H_2)$, the solution for optimization problem of $P_1$ will be produced as:

Theorem 1

[11] The maxmin–minmax solution for $P_1$ is equivalent to the solution of a LPP which is described as

            $\begin{array}{l} \mathrm{{max}}\, ~~ (\lambda _+-\lambda _-)\\ \mathrm{{s.t.},} \end{array}$

$$\begin{aligned} \nonumber \sum \limits _{i = 1 \;\textit{ to }\; m} {m_{ij} } p_i + p_a - {\bar{v}}_a \,\ge & {} \,p_a \lambda _+ ,\\ \nonumber \sum \limits _{i = 1\;\textit{ to }\; m} {m_{ij} } p_i - {\bar{v}}_r \,\ge & {} \, - p_r \lambda _- \,,\,\,\,\,\,(j = 1,2, \ldots ,\,n),\\\nonumber \sum \limits _{i = 1 \;\textit{ to }\; m} {p_i } \,\, = \,\,1, 0\le & {} \lambda _+ ,\lambda _- \,\, \le \,\,1,\\ \lambda _+ + \lambda _-\le & {} 1,\lambda _+\ge \lambda _-, p\ge 0. \end{aligned}$$

(6)

Theorem 2

[11] The maxmin–minmax solution for $P_2$ with assumptions $(H_1)$ and $(H_3)$ is equivalent to the solution of a LPP which is described as:

            $\begin{array}{l} \mathrm{{max}}\, ~~ (\eta _+-\eta _-)\\ \mathrm{{s.t.},} \end{array}$

$$\begin{aligned} \nonumber \sum \limits _{j = 1 \;\textit{ to }\; n} {m_{ij} } q_j - \underline{v}_a - q_a \,\le & {} - \,q_a \eta _+,\nonumber \\ \sum \limits _{j = 1 \;\textit{ to }\; n} {m_{ij} } q_j - \underline{v}_r \,\le & {} - \,q_r \eta _- \,,\,\,\,\,\,(i = 1,2, \ldots ,\,m), \nonumber \\ \sum \limits _{j = 1 \;\textit{ to }\; n} {q_j } \,\, = \,\,1, 0\le & {} \eta _+ ,\eta _- \,\, \le \,\,1, \nonumber \\ \eta _+ + \eta _- \,\,\le & {} \,\,1, \eta _+ \ge \eta _-, q\ge 0. \end{aligned}$$

(7)

4 Solution Procedure to MOMGIFG

In a multi-objective matrix game, each player has more than one objective and each objective is represented by a payoff matrix. Suppose that both players ($P_1$ and $P_2$) have same r objectives.

For this matrix game problem, following conditions are assumed as:  

$(H_4)$ :

The payoff values in each payoff matrix are real numbers;

$(H_5)$ :

The fuzziness in aspiration level of each objective is represented by an I-fuzzy set; and

$(H_6)$ :

mf and nmf for each I-fuzzy goal are linear.

  Now, a methodology is proposed to obtain the models in LP form for strategic problem to $P_1$ and $P_2$, respectively, as follows:

Optimization problem for $P_1$

Suppose that mf and nmf of the I-fuzzy goal for kth objective of $P_1$ are denoted by $\mu _{\tilde{g}_{P_1}^k +} (p^T M^k q)$ and $\mu _{\tilde{g}_{P_1}^k -} (p^T M^k q)$, respectively. Using $(H_4)$–$(H_6)$, $\mu _{\tilde{g}_{P_1}^k +} (p^T M^k q)$ can be represented as

$$\begin{aligned} \mu _{\tilde{g}^k _{P_1} +} (p^T M^k q)\,\, = \,\,\left\{ \begin{array}{l} 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,,\,\,\,p^T M^k q< {\bar{v}}^k _a { - p}_a^k \mathrm{{,}} \\ 1 - \frac{{{\bar{v}}^k _a - p^T M^k q}}{{p_a^k }}\,\,\,\,\,,\,\,{\bar{v}}^k _a { - p}_a^k \, \le \mathrm{{ }}p^T M^k q < {\bar{v}}^k _a \mathrm{{,}} \\ \mathrm{{1}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,,\,\,\,{\bar{v}}^k _a \le p^T M^k q, \\ \end{array} \right. \end{aligned}$$

(8)

and nmf $\mu _{\tilde{g}_{P_1}^k -} (p^T M^k q)$ is

$$\begin{aligned} \mu _{\tilde{g}^k _{P_1}-} (p^T M^k q)\,\, = \,\,\left\{ \begin{array}{l} 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,,\,\,\,p^T M^k q< {\bar{v}}^k _r { - p}_r^k \mathrm{{,}} \\ 1 - \frac{{p^T M^k q - ({\bar{v}}^k _r - p_r^k )}}{{p_r^k }}\,\,\,\,\,,\,\,{\bar{v}}^k _r { - p}_r^k \, \le \mathrm{{ }} p^T M^k q < {\bar{v}}^k _r \mathrm{{,}} \\ 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,,\,\,\,{\bar{v}}^k _r \le p^T M^k q, \\ \end{array} \right. \end{aligned}$$

(9)

with conditions ${\bar{v}}_r^k { - p}_r^k \le {\bar{v}}_a^k { - p}_a^k$ and ${\bar{v}}_r^k \le {\bar{v}}_a^k.$

Using [3], mf and nmf for aggregated I-fuzzy goal to $P_1$ can be formed in respective order as:

$$\begin{aligned} \mathop {\mathrm{{min}}\,\,\,}\limits _k \{ \mu _{\tilde{g}_{P_1}^k +} (p^T M^k q)\} \end{aligned}$$

(10)

and,

$$\begin{aligned} \mathop {\mathrm{{max}}\,\,\,}\limits _k \{ \mu _{\tilde{g}_{P_1}^k -} (p^T M^k q)\} \end{aligned}$$

(11)

Assuming that  

$(H_7)$ :

The calculating mf in (10) and nmf in (11) are linear.

 

The maxmin–minmax value in terms of degree of acceptance of an aggregated I-fuzzy goal to $P_1$ is

$$ \mathop {\mathrm{{max}}}\limits _{p\,\, \in \,\,U^m } \mathop {\min }\limits _{q\,\, \in \,\,U^n } \mathop {\mathrm{{min}}}\limits _k \,\,\,\,\,\{ \mu _{\tilde{g}_{P_1}^k +} (p^T M^k q)\}, $$

$$ \mathop {\mathrm{{min}}}\limits _{p\,\, \in \,\,U^m } \mathop {\max }\limits _{q\,\, \in \,\,U^n } \mathop {\mathrm{{max}}}\limits _k \,\,\,\,\,\{ \mu _{\tilde{g}_{P_1}^k -} (p^T M^k q)\}. $$

Theorem 3

The maxmin–minmax solution for $P_1$ with assumption $(H_7)$ is equivalent to the following LP model

            $\begin{array}{l} \mathrm{{max}}\, ~~ (\lambda _+-\lambda _-)\\ \mathrm{{s.t.},} \end{array}$

$$\begin{aligned} \sum \limits _{i = 1\;\textit{ to }\;m} {m_{ij}^k } p_i + p_a^k - {\bar{v}}^k _a \,\ge & {} \,p_a^k \lambda _+, \nonumber \\ \nonumber \sum \limits _{i = 1\;\textit{ to }\;m} {m_{ij}^k } p_i - {\bar{v}}^k _r \,\ge & {} \, - p_r^k \lambda _- \,,\,\,\,\,\,(j = 1,2, \ldots ,\,n), \\ \nonumber \sum \limits _{i = 1\;\textit{ to }\;m} {p_i } \,\,= & {} \,\,1, 0 \le \lambda _+ ,\lambda _- \,\, \le \,\,1,\\ \lambda _+ + \lambda _- \,\,\le & {} \,\,1,\lambda _+\ge \lambda _-, p\ge 0, \end{aligned}$$

(12)

where $k=1,2,\ldots ,r.$

Proof

The maxmin–minmax problem for $P_1$ is

$$ \mathop {\mathrm{{max}}}\limits _{p\,\, \in \,\,U^m } \mathop {\min }\limits _{q\,\, \in \,\,U^n } \mathop {\mathrm{{min}}}\limits _k \,\,\,\,\,\{ \mu _{\tilde{g}_{P_1}^k +} (p^T M^k q)\}, $$

$$ \mathop {\mathrm{{min}}}\limits _{p\,\, \in \,\,U^m } \mathop {\max }\limits _{q\,\, \in \,\,U^n } \mathop {\mathrm{{max}}}\limits _k \,\,\,\,\,\{ \mu _{\tilde{g}_{P_1}^k -} (p^T M^k q)\}. $$

For mf

$$\begin{aligned}&\mathop {\mathrm{{max}}}\limits _{p\,\, \in \,\,U^m } \mathop {\min }\limits _{q\,\, \in \,\,U^n } \mathop {\mathrm{{min}}}\limits _k \,\,\,\,\,\left( {1 - \frac{{{\bar{v}}^k _a - p^T M^k q}}{{p_a^k }}\,\,} \right) \\&= \frac{1}{{p_a^k }}\mathop {\mathrm{{max}}}\limits _{p\,\, \in \,\,U^m } \mathop {\min }\limits _{q\,\, \in \,\,U^n } \mathop {\mathrm{{min}}}\limits _k \,\,\,\,\,\left( {\sum \limits _{i\, = \,1\;\textit{ to }\;m} {\sum \limits _{j\, = \,1\;\textit{ to }\;n} {m_{ij}^k p_i q_j \, + \,c^k } } } \right) \\&= \frac{1}{{p_a^k }}\mathop {\mathrm{{max}}}\limits _{p\,\, \in \,\,U^m } \mathop {\mathrm{{min}}}\limits _k \mathop {\min }\limits _{q\,\, \in \,\,U^n } \,\,\,\,\sum \limits _{j\, = \,1\;\textit{ to }\;n} {\left( {\sum \limits _{i\, = \,1\;\textit{ to }\;m} {m_{ij}^k p_i \, + \,c^k } } \right) } \,q_j\\&= \frac{1}{{p_a^k }}\mathop {\mathrm{{max}}}\limits _{p\,\, \in \,\,U^m } \mathop {\mathrm{{min}}}\limits _k \mathop {\min }\limits _{j \in \,\,J} \,\,\,\,\left( {\sum \limits _{i\, = \,1\;\textit{ to }\;m} {m_{ij}^k p_i \, + \,c^k } } \right) . \end{aligned}$$

Let $\mathop {\mathrm{{min}}}\limits _{j\, \in \,J} \,\,\,\,\left( {\sum \limits _{i\, = \,1\;\textit{ to }\;m} {m_{ij}^k p_i \, + \,c^k } } \right) \, = \,\lambda _{k+}$ and further let $\mathop {\min }\limits _k \,\,\lambda _{k+} \,\, = \,\,\lambda _+$. In similar way, for nmf, letting $\mathop {\max }\limits _k \,\,\lambda _{k-} \,\, = \,\,\lambda _-$. The maxmin–minmax problem for $P_1$ reduces to LP model (12).

Optimization problem for $P_2$

Let mf and nmf of an I-fuzzy goal for $k^{th}$ objective of $P_2$ be denoted by $\mu _{\tilde{g}_{P_2}^k +} (p^T M^k q)$ and $\mu _{\tilde{g}_{P_2}^k -} (p^T M^k q)$, respectively. Using $(H_4)$–$(H_6)$, $\mu _{\tilde{g}_{P_2}^k +} (p^T M^k q)$ can be represented as

$$\begin{aligned} \mu _{\tilde{g}^k _{P_2} +} (p^T M^k q)\,\, = \,\,\left\{ \begin{array}{l} 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,,\,\,\,p^T M^k q< {\underline{v}}^k _a \mathrm{{,}} \\ 1 - \frac{{p^T M^k q}-{\underline{v}}^k _a}{{q_a^k }}\,\,\,\,\,,\,\, {\underline{v}}^k _a \, \le \mathrm{{ }}p^T M^k q < {\underline{v}}^k _a+{ q}_a^k \mathrm{{,}} \\ \mathrm{{0}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,,\,\,\,{\underline{v}}^k _a +{ q}_a^k \le p^T M^k q, \\ \end{array} \right. \end{aligned}$$

(13)

and $\mu _{\tilde{g}_{P_2}^k -} (p^T M^k q)$ is

$$\begin{aligned} \mu _{\tilde{g}^k _{P_2}-} (p^T M^k q)\,\, = \,\,\left\{ \begin{array}{l} 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,,\,\,\,p^T M^k q< {\underline{v}}^k _r \mathrm{{,}} \\ \frac{p^T M^k q - {\underline{v}}^k _r }{q_r^k }\,\,\,\,\,,\,\,{\underline{v}}^k _r \, \le \mathrm{{ }} p^T M^k q < {\underline{v}}^k _r+ q_r^k \mathrm{{,}} \\ 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,,\,\,\,{\underline{v}}^k _r + q_r^k \le p^T M^k q, \\ \end{array} \right. \end{aligned}$$

(14)

with conditions $\underline{v}^k_a +q_a^k\le \underline{v}^k_r +q_r^k$ and $\underline{v}^k_a \le \underline{v}^k_r$ for $k=1,2,\ldots ,r$.

Using [3], mf and nmf for aggregated I-fuzzy goal can be calculated in respective order as

$$\begin{aligned} \mathop {\mathrm{{min}}\,\,\,}\limits _k \{ \mu _{\tilde{g}_{P_2}^k +} (p^T M^k q)\} \end{aligned}$$

(15)

and,

$$\begin{aligned} \mathop {\mathrm{{max}}\,\,\,}\limits _k \{ \mu _{\tilde{g}_{P_2}^k -} (p^T M^k q)\} \end{aligned}$$

(16)

In similar to problem of $P_1$, assuming that  

$(H_8)$ :

The calculating mf in (15) and nmf in (16) are linear.

  The maxmin–minmax value in terms of the degree of acceptance of an aggregated I-fuzzy goal to $P_2$ is

$$ \mathop {\mathrm{{max}}}\limits _{p\,\, \in \,\,U^m } \mathop {\min }\limits _{q\,\, \in \,\,U^n } \mathop {\mathrm{{min}}}\limits _k \,\,\,\,\,\{ \mu _{\tilde{g}_{P_2}^k +} (p^T M^k q)\}, $$

$$ \mathop {\mathrm{{min}}}\limits _{p\,\, \in \,\,U^m } \mathop {\max }\limits _{q\,\, \in \,\,U^n } \mathop {\mathrm{{max}}}\limits _k \,\,\,\,\,\{ \mu _{\tilde{g}_{P_2}^k -} (p^T M^k q)\}. $$

Theorem 4

The maxmin–minmax solution for $P_2$ with assumption $(H_8)$ is equivalent to the following LP model

            $\begin{array}{l} \mathrm{{max}}\, ~~ (\eta _+-\eta _-)\\ \mathrm{{s.t.},} \end{array}$

$$\begin{aligned} \nonumber \sum \limits _{j = 1\;\textit{ to }\;n} {m_{ij}^k } q_j - {\underline{v}}^k _a - q_a^k \,\le & {} - \,q_a^k \eta _+, \\ \nonumber \sum \limits _{j = 1\;\textit{ to }\;n} {m_{ij}^k } q_j - {\underline{v}}^k _r \,\le & {} \, -q_r^k \eta _- \,,\,\,\,\,\,(i = 1,2, \ldots ,\,m), \\ \nonumber \sum \limits _{j = 1\;\textit{ to }\;n} {q_j } \,\,= & {} \,\,1, 0 \le \eta _+ ,\eta _- \,\, \le \,\,1,\\ \eta _+ + \eta _- \,\,\le & {} \,\,1,\eta _+ \ge \eta _-, q\ge 0, \end{aligned}$$

(17)

where $k=1,2,\ldots ,r.$

Proof

Proof is similar to Theorem 3.

5 Example

This section consists of an example of MOMGIFG which shows the validity of the proposed work.

The payoff matrices $M^1,M^2$ are separately indicated as:

$$ M^1 = \left( \begin{array}{l} \,\,\,4\,\,\,\,\,\,2\,\,\,\,\,\, - 1 \\ - 2\,\,\,\,\,\,0\,\,\,\,\,\,\,\,\,\,1 \\ \end{array} \right) , M^2 = \left( \begin{array}{l} 10\,\,\,\,\,\,24\,\,\,\,\,\,\,9 \\ 7\,\,\,\,\,\,\,\,15\,\,\,\,\,\,11 \\ \end{array} \right) $$

Here, we assume that

${{\bar{v}}}_a^1 \,\, = \,\,3,\,\,p_a^1 = 4,\,{{\bar{v}}}_r^1 = 2,\,\,p_r^1 = 6$ and ${{\bar{v}}}_a^2 \,\, = \,\,10,\,\,p_a^2 = 5,\,{{\bar{v}}}_r^2 = 7,\,\,p_r^2 = 4$.

Now, model (12) becomes,

            $\begin{array}{l} \mathrm{{max}}\, ~~ (\lambda _+-\lambda _-)\\ \mathrm{{s.t.},} \end{array}$

$$\begin{aligned} \nonumber 4p_1-2p_2+1\ge 4\lambda _+&,&2p_1+1\ge 4\lambda _+,\\\nonumber -p_1+p_2\ge 4\lambda _+&,&10p_1+7p_2-5\ge 5\lambda _+,\\\nonumber 24p_1+15p_2-5\ge 5\lambda _+&,&9p_1+11p_2-5\ge 5\lambda _+,\\\nonumber 4p_1-2p_2-2\ge -6\lambda _-&,&2p_1-2\ge -6\lambda _-,\\\nonumber -p_1+p_2-2\ge -6\lambda _-&,&10p_1+7p_2-7\ge -4\lambda _-,\\\nonumber 24p_1+15p_2-7\ge -4\lambda _-&,&9p_1+11p_2-7\ge -4\lambda _-,\\\nonumber p_1+p_2=1&,&\lambda _+ + \lambda _- \,\, \le \,\,1,\\ p_1,p_2\ge 0&,&\lambda _+\ge \lambda _-, \lambda _-\ge 0. \end{aligned}$$

(18)

The optimal solution for $P_1$ is obtained as;

$\left( {p^* \,\, = \,\,\left( {0.3750,\,0.6250} \right) ^T ,\,{\lambda _+} ^* = 0.3125,\,\,{\lambda _-} ^* = 0.2917} \right) .$

For $P_2$, we take ${\underline{v}}_a^1 \,\, = \,\, - 2,\,\,q_a^1 = 5,\,{\underline{v}}_r^1 = 0,\,\,q_r^1 = 4$ and ${\underline{v}}_a^2 \,\, = \,\,7,\,\,q_a^2 = 4,\,{\underline{v}}_r^2 = 10,\,\,q_r^2 = 5$.

Model (17) is reduced as follows,

            $\begin{array}{l} \mathrm{{max}}\, ~~ (\eta _+-\eta _-)\\ \mathrm{{s.t.},} \end{array}$

$$\begin{aligned} \nonumber 4q_1+2q_2-q_3-3\le -5\eta _+&,&-2q_1+q_3-3\le -5\eta _+,\\\nonumber 10q_1+24q_2+9q_3-11\le -4\eta _+&,&7q_1+15q_2+11q_3-11\le -4\eta _+,\\\nonumber 4q_1+2q_2-q_3\le -4\eta _-&,&-2q_1+q_3\le -4\eta _-,\\\nonumber 10q_1+24q_2+9q_3-10\le -5\eta _-&,&7q_1+15q_2+11q_3-10\le -5\eta _-,\\\nonumber q_1+q_2+q_3=1&,&\eta _+ + \eta _- \,\, \le \,\,1,\\ q_1,q_2,q_3\ge 0&,&\eta _+\ge \eta _-, \eta _-\ge 0. \end{aligned}$$

(19)

The optimal solution for $P_2$ is obtained as;

$\left( {q^* \,\, = \,\,\left( {0.25,\,0,\,0.75} \right) ^T ,\,{\eta _+} ^* = 0.25,\,\,{\eta _-} ^* = 0.0625} \right)$.

These results are calculated by TORA software.

6 Conclusions

A solution procedure is introduced for MOMGIFG in this paper. This work shows that the strategic problems for both players are equivalent to two LPP. An example is given to show the existence of this theory. The author intends to study a case in which assumption $(H_4)$ is violated, i.e., entries of payoff matrices having fuzziness in future.