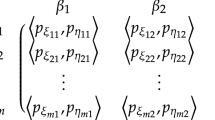Mehar approach for solving matrix games with triangular dual hesitant fuzzy payoffs

Abstract

The dual hesitant fuzzy set (DHFS) is an effective mathematical approach to deal with the data which are imprecise, uncertain or incomplete information. DHFS is an extension of hesitant fuzzy sets (HFS) which encompass fuzzy sets (FS), intuitionistic fuzzy sets (IFS), HFS, and fuzzy multisets as a special case. DHFS consist of two parts, that is, the membership and non-membership degrees which are represented by two sets of possible values. Therefore, in accordance with the practical demand these sets are more flexible and provide much more information about the situation. The aim of this paper is to develop an effective methodology for solving matrix games with payoffs of triangular dual hesitant fuzzy numbers (TDHFNs). The flaws of the existing approach to solve matrix games with TDHFNs payoffs are pointed out. Moreover, to resolve these flaws, novel, general and corrected approach called Mehar approach is proposed to obtain the optimal strategies for TDHFNs matrix games. In this methodology, the concepts and ranking order relations of TDHFNs are defined. A pair of bi-objective linear programming models for matrix games with payoffs of TDHFNs is derived from two auxiliary dual hesitant fuzzy programming models based on the ranking order relations of TDHFNs defined in this paper. An effective methodology based on the weighted average method is developed to determine optimal strategies for two players. In this approach, it is verified that any matrix game with TDHFNs payoffs always has a TDHFNs equilibrium value. Finally, a numerical experiment is incorporated to illustrate the applicability and feasibility of the proposed Mehar approach in TDHFNs matrix game. The obtained results are compared with the results obtained by the previous approaches for solving TDHFNs matrix game.

1 Introduction

Game theory mainly concerns in competitive and skillful interaction between the decisions makers. Therefore, how to make decisions in competitive environment is as usual and important one. In the real world, game theory is mainly used in military, finance, economic, strategic welfares, cartel behaviour, management problems, auctions or social problems, political voting systems, development research and races (Owen 1982). In reality, due to the lack of information and ambiguity of players, the decision may be imprecise. To handle such an environment, researchers use the notion of FS and its various extensions.

Initially, the FS was introduced by Zadeh (1965), where every element of a set was defined along with their membership values. FS theory proved to be a useful tool to handle the uncertainty in real life problems. In 1980, (Dubois and Prade 1980) applied the concept of FS in game theory. Jana and Roy (2018b) presented the solution of matrix games with payoffs of generalised trapezoidal fuzzy numbers. KumarRoy and Mula (2013) studied bi-matrix game with bi-fuzzy parameters. Roy and Maiti (2020) discussed Stackelberg game with type-2 fuzzy variables. Campos (1989) developed fuzzy linear programming models to solve fuzzy matrix games. Nan et al. (2010) applied lexicographic method for matrix games with pay-offs of triangular fuzzy numbers. Li and Hong (2012) discussed constrained matrix games with payoffs of triangular fuzzy numbers. Aggarwal and Khan (2016) presented multi-objective fuzzy matrix games via multi-objective linear programming approach.

However, the FS uses only the membership degree, which measures the degree of belongingness, and the degree of non-belongingness is easily calculated as the complement of the belongingness to 1. However, after introducing the IFS and intuitionistic fuzzy number (IFN) by Atanassov (1999), the mode of description of a FS experienced a little change with great significance. In IFS, the elements of the set are described along with its degree of membership and non-membership, where the sum of the membership and non-membership value must be less than or equal to 1; if it is less than 1 then the remaining part is left as the hesitation degree. Li and Nan (2009) proposed a nonlinear programming algorithm for matrix games in which payoffs are expressed by IFNs. Nan et al. (2010) developed a lexicographic approach to matrix games with payoffs of triangular IFNs. Seikh et al. (2013) discussed matrix games in intuitionistic fuzzy (IF) environment. Bandyopadhyay et al. 2013) studied matrix games with IF payoffs through a score function. Aggarwal et al. (2012) applied linear programming approach with IFSs to matrix games with IF goals. Li et al. (2012) presented bi-objective programming technique for solving matrix games with payoffs of triangular IFNs. Nayak and Pal (2011) implemented IF optimization algorithm for optimal solution of multi-objective bi-matrix game. Nan et al. (2014a; b) described an algorithm for matrix games with payoffs of triangular IFN. Seikh et al. (2015) discussed matrix games with IF payoffs. Nan et al. (2009) proposed a linear programming algorithm for solving matrix games with IF payoffs. Nan et al. (2014a; b) investigated IF programming problems for matrix games with trapezoidal IF payoffs. Verma and Kumar (2014) proposed a methodology for solving matrix games with triangular IF payoffs. Xing and Qiu (2019) applied accuracy function technique for solving triangular IF matrix game. Brikaa et al. (2020) applied resolving indeterminacy method to solve multi-criteria matrix games with IF goals.

Nevertheless, it can be seen that the degree of membership and non-membership values are not enough in some problems to assign an element correctly. Considering the decision-makers hesitancy, Torra (2010) extended the concept of FS to HFS, where the belongingness of an element is assigned by a set of possible membership values which must be lying on [0, 1]. Based on the extensive research of IFS and HFS, Zhu et al. (2012) have combined the idea of IFS theory with HFS theory and introduced the concept of DHFS. Similar to the IFS theory, DHFS also have membership degree function and non-membership degree function. However, these two functions are expressed by several determined numbers rather a single number and make the descriptions of the fuzziness of the real world more accurately than the other extended FS theory. Due to its importance, many scholars have applied the DHFS theory in various disciplines. For example, Hao et al. (2017) studied probabilistic DHFS and its application in risk evaluation. Ren et al. (2017) proposed dual hesitant fuzzy VIKOR method for multi-criteria group decision making based on fuzzy measure and new comparison method. Garg and Kaur (2020) discussed quantifying gesture information in brain hemorrhage patients using probabilistic DHFS with unknown probability information. Singh (2014) introduced new method for solving dual hesitant fuzzy assignment problems with restrictions based on similarity measure. Narayanamoorthy et al. (2019) studied application of normal wiggly DHFS to site selection for hydrogen underground storage. Maity et al. (2019) presented new approach for solving dual-hesitant fuzzy transportation problem with restrictions. Yu et al. (2016) introduced dual hesitant fuzzy group decision making method and its application to supplier selection.

In the recent decades, many researchers have discussed matrix games under uncertainty; for example, Figueroa-García et al. (2019) studied group matrix games involving interval-valued fuzzy numbers. Turksen (1986) introduced interval valued fuzzy sets based on normal forms. Chen et al. (1997) discussed bidirectional approximate reasoning based on interval-valued fuzzy sets. Chen and Hsiao (2000) presented bidirectional approximate reasoning for rule-based systems using interval-valued fuzzy sets. Chen (1997) introduced interval-valued fuzzy hypergraph and fuzzy partition. Akram et al. (2021c) studied fully Pythagorean fuzzy linear programming problems with equality constraints. Akram et al. (2021b) presented methods for solving-Type Pythagorean fuzzy linear programming problems with mixed constraints. Akram et al. (2021d) investigated LR-type fully Pythagorean fuzzy linear programming problems with equality constraints. (Akram et al. 2021a) presented geometric–arithmetic energy and atom bond connectivity energy of dual hesitant q-rung orthopair fuzzy graphs. Jana and Roy (2018a) introduced DHF matrix games based on similarity measure. Singh et al. (2020) discussed matrix games with 2-tuple linguistic information. Zhou and Xiao (2019) constructed new matrix game with payoffs of generalized Dempster Shafer structures. Seikh et al. (2020) solved matrix games with hesitant fuzzy pay-offs. Han and Deng (2019) described novel matrix game with payoffs of Maxitive Belief structure. Khalifa (2019) proposed an approach for solving two-person zero-sum matrix games in neutrosophic environment. Bhaumik et al. (2020) considered hesitant interval-valued intuitionistic fuzzy-linguistic term set approach in Prisoners’ dilemma matrix game. Ammar and Brikaa (2019a, b) solved bi-matrix games in tourism planning management under rough interval approach. Brikaa et al. (2019) developed fuzzy multi-objective programming algorithm for solving fuzzy rough constrained matrix games. Bhaumik et al. (2021) introduced multi-objective linguistic neutrosophic matrix game and its applications to tourism management. Khan and Mehra (2020) proposed novel equilibrium solution concept for IF bi-matrix games considering proportion mix of possibility and necessity expectations. Ammar and Brikaa (2019a, b) studied the solution of constraint matrix games under rough interval approach. Naqvi et al. (2021) solved IF two person zero-sum matrix games using Tanaka and Asai approach. Bhaumik and Roy (2021) constructed intuitionistic interval-valued hesitant fuzzy matrix games with a new aggregation operator for solving management problem. Brikaa et al. (2021) proposed rough set approach to non-cooperative continuous differential games. Xue et al. (2021) solved matrix games based on Ambika method with hesitant fuzzy information and its application in the counter-terrorism issue. Roy and Jana (2021) studied the multi-objective linear production planning games in triangular hesitant fuzzy sets. Seikh and Karmakar (2021) introduced credibility equilibrium strategy for matrix games with payoffs of triangular dense fuzzy lock sets. Seikh et al. (2021) proposed novel defuzzification approach of Type-2 fuzzy variable to solving matrix games with application to plastic ban problem. Xia (2019) developed methods for solving matrix games with cross-evaluated payoffs. Mi et al. (2021) studied two-person and zero-sum matrix game with probabilistic linguistic information. Gaber et al. (2021) introduced optimal solutions for constrained bi-matrix games with payoffs represented by single-valued trapezoidal neutrosophic numbers.

However, in matrix games due to lack of information in data and lack of attention of a decision-maker, always exist some hesitancy. Therefore, neither FS nor IFS are sufficient to describe pay-off values. This motivates us to imply the concept of DHFS in matrix games. The elements of the pay-off matrix are represented by TDHFNs, introduced by Yang and Song (2020) and Zhu et al. (2012).

In this article, we propose a novel mathematical programming approach, called the Mehar approach, for solving matrix games with TDHFNs payoffs. This approach improves (Yang and Song 2020) algorithm by being based on properties and assumptions that are valid in general so that the novel mathematical programming algorithm yields a generally valid solution. Pair of dual hesitant fuzzy optimization problems is established for each player, which are transformed into bi-objective linear programming problems based on the ranking order relations of TDHFNs. Using the weighted average technique, two simpler auxiliary linear programming problems are formulated to find the minimax and maximin dual hesitant fuzzy strategies for two players and the game value of the TDHFNs matrix game.

This paper is organized as follows. Section 2 briefly reviews some basic concepts, such as DHFS and TDHFNs. Section 3 formulates matrix games with TDHFNs payoffs. The flaws of the existing method (Yang and Song 2020) are discussed in Sect. 4. Section 5 develops Mehar approach to solve TDHFNs matrix games. Section 6 presents a numerical example to illustrate the proposed approach, and finally, a short conclusion is drawn in Sect. 7.

2 Preliminaries

In this section, the basic definitions and concepts related to TDHFNs (Yang and Song 2020; Zhu et al. 2012) will be presented for further convenience.

Definition 1

(Ishibuchi and Tanaka 1990) Let ${c}^{\mathrm{I}}=\left[{c}^{\mathrm{L}},{c}^{\mathrm{U}}\right]$ and ${d}^{\mathrm{I}}=\left[{d}^{\mathrm{L}},{d}^{\mathrm{U}}\right]$ be two intervals. Then, ${c}^{\mathrm{I}}\ge {d}^{\mathrm{I}}$ iff ${c}^{\mathrm{L}}\ge {d}^{\mathrm{L}}$ and ${c}^{\mathrm{U}}\ge {d}^{\mathrm{U}}$. Similarly, ${c}^{\mathrm{I}}\le {d}^{\mathrm{I}}$ iff ${c}^{\mathrm{L}}\le {d}^{\mathrm{L}}$ and ${c}^{\mathrm{U}}\le {d}^{\mathrm{U}}$.

Definition 2

(Ishibuchi and Tanaka 1990) Let ${c}^{\mathrm{I}}=\left[{c}^{\mathrm{L}},{c}^{\mathrm{U}}\right]$ be an interval. Then, the maximization model with interval objective function is represented as $\mathrm{max}\left\{\left.{c}^{\mathrm{I}}\right|{c}^{\mathrm{I}}\in {\Upsilon }_{1}\right\}$ which is equivalent to the bi-objective programming model: $\mathrm{max}\left\{\left.\left({c}^{\mathrm{L}},\frac{{c}^{\mathrm{L}}+{c}^{\mathrm{U}}}{2}\right)\right|{c}^{\mathrm{I}}\in {\Upsilon }_{1}\right\}$, where ${\Upsilon }_{1}$ is the set of constraint conditions.

Definition 3

(Ishibuchi and Tanaka 1990) Let ${c}^{\mathrm{I}}=\left[{c}^{\mathrm{L}},{c}^{\mathrm{U}}\right]$ be an interval. Then, the minimization model with interval objective function is represented as $\mathrm{min}\left\{\left.{c}^{\mathrm{I}}\right|{c}^{\mathrm{I}}\in {\Upsilon }_{2}\right\}$ which is equivalent to the bi-objective programming model: $\mathrm{min}\left\{\left.\left({c}^{\mathrm{U}},\frac{{c}^{\mathrm{L}}+{c}^{\mathrm{U}}}{2}\right)\right|{c}^{\mathrm{I}}\in {\Upsilon }_{2}\right\}$, where ${\Upsilon }_{2}$ is the set of constraint conditions.

Suppose a DHFS described as $F=\left\{\left.\left\langle y, {g}_{\mathrm{F}}\left(y\right)\right\rangle \right|y\in Y\right\}$, where $g_{{\text{F}}} \left( y \right) = \left\langle {\left( {\underline{{b_{t} }} ,b_{t} ,\overline{{b_{t} }} } \right);\delta _{{\widetilde{{b_{t} }}}} ,\gamma _{{\widetilde{{b_{t} }}}} } \right\rangle \;\left( {t = 1,2, \ldots ,m} \right)$ is a TDHFN describing the possible non-membership and membership degree of $y\in Y\mathrm{ to }F$, respectively.

The possible non-membership functions are given as follows:

$$\gamma_{{\widetilde{{b_{t} }}}} = \left\{ {\begin{array}{*{20}l} {\frac{{b_{t} - y + v_{{\widetilde{{b_{t} }}}} \left( {y - \underline{{b_{t} }} } \right)}}{{b_{t} - \underline{{b_{t} }} }}, \quad \underline{{b_{t} }} \le y \le b_{t} } \\ {\frac{{y - b_{t} + v_{{\widetilde{{b_{t} }}}} \left( {\overline{{b_{t} }} - y} \right)}}{{\overline{{b_{t} }} - b_{t} }}, \quad b_{t} < y \le \overline{{b_{t} }} } \\ {1, \quad \quad \quad \quad \quad y < \underline{{b_{t} }} \;{\text{or}}\; y > \overline{{b_{t} }} .} \\ \end{array} } \right.$$

(1)

The possible membership functions are given as follows:

$$\delta_{{\widetilde{{b_{t} }}}} = \left\{ {\begin{array}{*{20}l} {\frac{{y - \underline{{b_{t} }} }}{{b_{t} - \underline{{b_{t} }} }}\omega_{{\widetilde{{b_{t} }}}} , \quad \underline{{b_{t} }} \le y \le b_{t} , } \\ {\frac{{\overline{{b_{t} }} - y}}{{\overline{{b_{t} }} - b_{t} }}\omega_{{\widetilde{{b_{t} }}}} , \quad b_{t} < y \le \overline{{b_{t} }} ,} \\ {0, \quad \quad \quad \; y < \underline{{b_{t} }} \;{\text{or}}\; y > \overline{{b_{t} }} ,} \\ \end{array} } \right.$$

(2)

where ${v}_{\widetilde{{b}_{t}}}$ and ${\omega }_{\widetilde{{b}_{t}}}$ describe the minimum possible non-membership degree and maximum possible membership degree of $y\in Y\mathrm{ to }F$, respectively. Which satisfy the conditions ${0\le v}_{\widetilde{{b}_{t}}}\le 1, { 0\le \omega }_{\widetilde{{b}_{t}}}\le 1, \mathrm{and} { 0\le {v}_{\widetilde{{b}_{t}}}+\omega }_{\widetilde{{b}_{t}}}\le 1.$

Definition 4

$\tilde{b} = \left\langle {\left( {\underline{{b_{t} ,}} b_{t} ,\overline{{b_{t} }} } \right);\omega_{{\widetilde{{b_{t} }}}} ,v_{{\widetilde{{b_{t} }}}} } \right\rangle$ is called a positive TDHFN if ${\underline{{b}_{t}}}\ge 0, \overline{{b}_{t}}>0 \left(t=1,2,\ldots, m\right)$, which given by $\tilde{{b}}\tilde{>}0$. Likewise, $\tilde{b} = \left\langle {\left( {\underline{{b_{t} ,}} b_{t} ,\overline{{b_{t} }} } \right);\omega_{{\widetilde{{b_{t} }}}} ,v_{{\widetilde{{b_{t} }}}} } \right\rangle$ is called a negative TDHFN if ${\underline{{b}_{t}}}<0, \overline{{b}_{t}}\le 0 \left(t=1,2,\ldots, m\right)$, which given by $\tilde{b}\tilde{ < }0$. Let $\tilde{ > } \;{\text{and}}\; \tilde{ < }$ denote “dual hesitant fuzzy greater than” and “dual hesitant fuzzy less than”, respectively.

Definition 5

A $\mathrm{\alpha }$-cut set of a TDHFN $\tilde{b} = \left\langle {\left( {\underline{{b_{t} ,}} b_{t} ,\overline{{b_{t} }} } \right);\omega_{{\widetilde{{b_{t} }}}} ,v_{{\widetilde{{b_{t} }}}} } \right\rangle$ is given as ${\tilde{b }}_{\alpha }=\left\{\left.y\right|{\delta }_{\widetilde{{b}_{t}}}(y)\ge \alpha \right\}$, where $0\le \alpha \le \mathrm{min}\left\{{\omega }_{\widetilde{{b}_{t}}}\right\}$.

Definition 6

A $\beta$-cut set of a TDHFN $\tilde{b }=\left\langle \left({\underline{{b}_{t}}},{b}_{t},\overline{{b}_{t}}\right);{\omega }_{\widetilde{{b}_{t}}},{v}_{\widetilde{{b}_{t}}}\right\rangle$ is given as ${\tilde{b }}_{\beta }=\left\{\left.y\right|{\gamma }_{\widetilde{{b}_{t}}}(y)\le \beta \right\}$, where $\mathrm{max}\left\{{v}_{\widetilde{{b}_{t}}}\right\}\le \beta \le 1$.

Definition 7

A $\left(\alpha ,\beta \right)$-cut set of a TDHFN $\tilde{b }=\left\langle \left({\underline{{b}_{t}}},{b}_{t},\overline{{b}_{t}}\right);{\omega }_{\widetilde{{b}_{t}}},{v}_{\widetilde{{b}_{t}}}\right\rangle$ is given as ${\tilde{b }}_{\left(\alpha ,\beta \right)}=\left\{\left.y\right|{\delta }_{\widetilde{{b}_{t}}}\left(y\right)\ge \alpha ,{\upgamma }_{\widetilde{{b}_{t}}}(y)\le \beta \right\}$, where $0\le \alpha \le \mathrm{min}\left\{{\omega }_{\widetilde{{b}_{t}}}\right\}$, $\mathrm{max}\left\{{v}_{\widetilde{{b}_{t}}}\right\}\le \beta \le 1$ and $0\le \alpha +\beta \le 1$.

Theorem 1

Let $\tilde{b }=\left\langle \left({\underline{{b}_{t}}},{b}_{t},\overline{{b}_{t}}\right);{\omega }_{\widetilde{{b}_{t}}},{v}_{\widetilde{{b}_{t}}}\right\rangle$ be any TDHFN, ${\tilde{b }}_{\left(\alpha ,\beta \right)}$ can be obtained as ${\tilde{b }}_{\left(\alpha ,\beta \right)}={\tilde{b }}_{\alpha }\cap {\tilde{b }}_{\beta }$.

Definition 8

If $\tilde{b}_{\alpha } \le \tilde{c}_{\alpha }$ and $\tilde{b}_{\beta } \le \tilde{c}_{\beta }$, then $\tilde{b} \le \tilde{c}$, which is called $\tilde{b}$ is less than $\tilde{c}$.

Likewise to the ranking order of intuitionistic fuzzy number, let ${\widetilde{b }}_{i}=\left\langle \left({\underline{{b}_{i}}},{b}_{i},\overline{{b}_{i}}\right);{\omega }_{\widetilde{{b}_{i}}},{v}_{\widetilde{{b}_{i}}}\right\rangle$ and ${\widetilde{b }}_{j}=\left\langle \left({\underline{{b}_{j}}},{b}_{j},\overline{{b}_{j}}\right);{\omega }_{\widetilde{{b}_{j}}},{v}_{\widetilde{{b}_{j}}}\right\rangle$, if ${\widetilde{b }}_{i\alpha }\le {\widetilde{b }}_{j\alpha }$ and ${\widetilde{b }}_{i\beta }\le {\widetilde{b }}_{j\beta }$ then ${\widetilde{b }}_{i}\le {\widetilde{b }}_{j}(0\le i,j\le m)$.

Definition 9

Let $\tilde{b }=\left\langle \left({\underline{{b}_{t}}},{b}_{t},\overline{{b}_{t}}\right);{\omega }_{\widetilde{{b}_{t}}},{v}_{\widetilde{{b}_{t}}}\right\rangle \left(t=1,2,\dots ,{m}_{1}\right)$ and $\tilde{c }=\left\langle \left({\underline{{c}_{t}}},{c}_{t},\overline{{c}_{t}}\right);{\omega }_{\widetilde{{c}_{t}}},{v}_{\widetilde{{c}_{t}}}\right\rangle \left(t=1,2,\dots ,{m}_{2}\right)$ be two TDHFNs. If ${m}_{1}={m}_{2}$, then they are called two normalized TDHFNs.

Definition 10

Let $\tilde{b }=\left\langle \left({\underline{{b}_{t}}},{b}_{t},\overline{{b}_{t}}\right);{\omega }_{\widetilde{{b}_{t}}},{v}_{\widetilde{{b}_{t}}}\right\rangle$ and $\tilde{c }=\left\langle \left({\underline{{c}_{t}}},{c}_{t},\overline{{c}_{t}}\right);{\omega }_{\widetilde{{c}_{t}}},{v}_{\widetilde{{c}_{t}}}\right\rangle \left(t=1,2,\ldots, m\right)$ be two normalized TDHFNs and $\rho$ be a real number. The arithmetic operations of TDHFNs are defined as follows:

$$\tilde{b }+\tilde{c }=\left\langle \left({\underline{{b}_{t}}}+{\underline{{c}_{t}}},{b}_{t}+{c}_{t},\overline{{b}_{t}}+\overline{{c}_{t}}\right);\mathrm{min}\left\{{\omega }_{\widetilde{{b}_{t}}},{\omega }_{\widetilde{{c}_{t}}}\right\},\mathrm{max}\left\{{v}_{\widetilde{{b}_{t}}},{v}_{\widetilde{{c}_{t}}}\right\}\right\rangle .$$

(3)

$$\tilde{b }\tilde{c }=\left\{\begin{array}{l}\left({\underline{{b}_{t}}} \underset{\_}{{c}_{t}}, {b}_{t} {c}_{t},\overline{{b}_{t}} \overline{{c}_{t}}\right);\mathrm{min}\left\{{\omega }_{\widetilde{{b}_{t}}},{\omega }_{\widetilde{{c}_{t}}}\right\},\mathrm{max}\left\{{v}_{\widetilde{{b}_{t}}},{v}_{\widetilde{{c}_{t}}}\right\}, \tilde{b }{>}_{d}0, \tilde{c }{>}_{d}0, \\ \left({\underline{{b}_{t}}} \overline{{c}_{t}}, {b}_{t} {c}_{t},\overline{{b}_{t}} \underset{\_}{{c}_{t}}\right);\mathrm{min}\left\{{\omega }_{\widetilde{{b}_{t}}},{\omega }_{\widetilde{{c}_{t}}}\right\},\mathrm{max}\left\{{v}_{\widetilde{{b}_{t}}},{v}_{\widetilde{{c}_{t}}}\right\}, \tilde{b }{>}_{d}0, \tilde{c }{<}_{d}0,\\ \left(\overline{{b}_{t}} \overline{{c}_{t}},{b}_{t} {c}_{t},{\underline{{b}_{t}}} \underset{\_}{{c}_{t}}\right);\mathrm{min}\left\{{\omega }_{\widetilde{{b}_{t}}},{\omega }_{\widetilde{{c}_{t}}}\right\},\mathrm{max}\left\{{v}_{\widetilde{{b}_{t}}},{v}_{\widetilde{{c}_{t}}}\right\}, \tilde{b }{<}_{d}0, \tilde{c }{<}_{d}0.\end{array}\right.$$

(4)

$$\tilde{b }=\left\{\begin{array}{l}\left\langle \left(\rho {\underline{{b}_{t}}},{\rho b}_{t},\rho \overline{{b}_{t}}\right);{\omega }_{\widetilde{{b}_{t}}},{v}_{\widetilde{{b}_{t}}}\right\rangle ,\rho >0, \\ \left\langle \left(\rho \overline{{b}_{t}}, {\rho b}_{t},\rho {\underline{{b}_{t}}}\right);{\omega }_{\widetilde{{b}_{t}}},{v}_{\widetilde{{b}_{t}}}\right\rangle ,\rho <0.\end{array}\right.$$

(5)

$${\tilde{b }}^{-1}=\left\langle \left(1/{\underline{{b}_{t}}},{1/b}_{t},1/\overline{{b}_{t}}\right);{\omega }_{\widetilde{{b}_{t}}},{v}_{\widetilde{{b}_{t}}}\right\rangle .$$

(6)

3 Matrix games with triangular dual hesitant fuzzy payoffs

In real-world problems, the payoffs may not be known precisely by the decision makers. Then some sorts of uncertainty arise about the payoffs. Therefore, DHFS theory is applied to accommodate such types of matrix game problems. Let’s suppose that the matrix game with TDHFNs payoffs (Yang and Song 2020). The pure strategies sets for both players I and II are represented by ${T}_{1}=\left\{{\xi }_{1},{\xi }_{2},\dots .,{\xi }_{r}\right\}$ and ${T}_{2}=\left\{{\eta }_{1},{\eta }_{2},\dots ,{\eta }_{{s}} \right\}$, respectively. The vectors $\mathbf{y}={\left({y}_{1},{y}_{2},\dots ,{y}_{r} \right)}^{T}$ and $\mathbf{z}={\left({z}_{1},{z}_{2},\dots ,{z}_{s} \right)}^{T}$ are probabilities in which players I and II choose their pure strategies ${\xi }_{i}\in {T}_{1}$ and ${\eta }_{j}\in {T}_{2}$, respectively. Sets of all mixed strategies for players I and II are defined by Y and Z, where $Y=\left\{\left.\mathbf{y}=\left({y}_{1},{y}_{2},\dots ,{y}_{r} \right)\right|\sum_{i=1}^{r}{y}_{i}=1, {y}_{i}\ge 0\right\}$ and $Z=\left\{\left.\mathbf{z}=\left({z}_{1},{z}_{2},\dots ,{z}_{s} \right)\right|\sum_{j=1}^{s}{z}_{j}=1, {z}_{j}\ge 0\right\}$, respectively. Without loss of generality, suppose that the payoff matrix of player I is given as $\tilde{B }={\left({\widetilde{b }}_{ij}\right)}_{r\times s}$, where ${\widetilde{b }}_{ij}=\left\langle \left({\underline{b}}_{ijt}{,b}_{ijt},{\overline{b}}_{ijt}\right);{\omega }_{{\widetilde{b }}_{ijt}},{v}_{{\widetilde{b }}_{ijt}}\right\rangle$ $\left(i=1,2,\dots ,r; j=1,2,\ldots ,s; \quad t=1,2,\ldots, m\right)$ are TDHFNs. Then, the TDHFNs matrix game is described as the triplet $\left(Y,Z,\tilde{B }\right)$. From Definition 10, the player I’s dual hesitant fuzzy expectation payoff can be obtained as follows:

$$\tilde{E }\left(\tilde{B }\right)={\mathbf{y}}^{T}\tilde{ B} \mathbf{z}=\sum_{i=1}^{r}\sum_{j=1}^{s}{\widetilde{b }}_{ij} {y}_{i}{z}_{j}=\left\langle \left(\sum_{i=1}^{r}\sum_{j=1}^{s}{\underline{b}}_{ijt} {y}_{i}{z}_{j},\sum_{i=1}^{r}\sum_{j=1}^{s}{b}_{ijt} {y}_{i}{z}_{j},\sum_{i=1}^{r}\sum_{j=1}^{s}{\overline{b}}_{ijt} {y}_{i}{z}_{j}\right);\mathrm{min}\left\{{\omega }_{{\widetilde{b }}_{ijt}}\right\},\mathrm{max}\left\{{v}_{{\widetilde{b }}_{ijt}}\right\}\right\rangle$$

(7)

which is TDHFNs.

Since the matrix game $\tilde{B }$ with triangular dual hesitant fuzzy payoffs is zero-sum, from Definition 10, the player II’s dual hesitant fuzzy expectation payoff can be obtained as follows:

$$\tilde{E }\left(\tilde{-B}\right)={\mathbf{y}}^{T}\left(-\tilde{B }\right) \mathbf{z}=\sum_{i=1}^{r}\sum_{j=1}^{s}{-\widetilde{b }}_{ij} {y}_{i}{z}_{j}=\left\langle \left(\sum_{i=1}^{r}\sum_{j=1}^{s}{-\overline{b}}_{ijt} {y}_{i}{z}_{j},\sum_{i=1}^{r}\sum_{j=1}^{s}{-b}_{ijt} {y}_{i}{z}_{j},\sum_{i=1}^{r}\sum_{j=1}^{s}{-\underline{b}}_{ijt} {y}_{i}{z}_{j}\right);\mathrm{min}\left\{{\omega }_{{\widetilde{b }}_{ijt}}\right\},\mathrm{max}\left\{{v}_{{\widetilde{b }}_{ijt}}\right\}\right\rangle ,$$

(8)

which is TDHFNs.

Definition 11

(Yang and Song 2020): Let $\tilde{u }=\left\langle \left({\underline{u}}_{t},{u}_{t},{\overline{u}}_{t}\right);{\omega }_{{\widetilde{u }}_{t}},{v}_{{\widetilde{u }}_{t}}\right\rangle$ and $\tilde{v }=\left\langle \left({\underline{v}}_{t},{v}_{t},{\overline{v}}_{t}\right);{\omega }_{{\widetilde{v }}_{t}},{v}_{{\widetilde{v }}_{t}}\right\rangle$ be TDHFNs. Suppose that there exist $\left({\mathbf{y}}^{*},{\mathbf{z}}^{*},{\tilde{u }}^{*},{\tilde{v }}^{*}\right)$, where ${\mathbf{y}}^{*}\in Y$, ${\mathbf{z}}^{*}\in Z$, satisfying the following two conditions.

• (a) ${\mathbf{y}}^{*T} \tilde{B} \mathbf{z}\tilde{\ge }{\tilde{u}}^{*}$ and ${\mathbf{y}}^{*T} \tilde{B} \mathbf{z}\tilde{\le }{\tilde{v}}^{*}$,

• (b) There do not exist any $\tilde{u}\ne {\tilde{u}}^{*}$ and $\tilde{v}\ne {\tilde{v}}^{*}$ such that $\tilde{u }\tilde{\ge }{\tilde{u }}^{*}$ and $\tilde{v }\tilde{\le }{\tilde{v }}^{*}$,then, $\left({\mathbf{y}}^{*},{\mathbf{z}}^{*},{\tilde{u }}^{*},{\tilde{v }}^{*}\right)$ is the solution of matrix game $\tilde{B }$ with TDHFNs payoffs. ${\mathbf{z}}^{*}\in Z$ is player II’s optimal strategy and ${\mathbf{y}}^{*}\in Y$ is player I's optimal strategy. ${\tilde{v}}^{*}$ is player II's loss-ceiling and ${\tilde{u}}^{*}$ is player I’s gain-floor. Finally, ${\mathbf{y}}^{*T} \tilde{B} \mathbf{z}$ is the game value of the TDHFNs matrix games.

From Definition 11, the player I's optimal strategy ${\mathbf{y}}^{*}\in Y$ and player II's optimal strategy ${\mathbf{z}}^{*}\in Z$ can be obtained by solving the following pair of dual hesitant fuzzy mathematical programming problems:

$$\begin{array}{l}\mathrm{max}\left\{\tilde{u }\right\}\\ {\text{s.t.}} \left\{\begin{array}{l}\sum_{i=1}^{r}{\widetilde{b }}_{ij}{ \widetilde{y }}_{i}{ \widetilde{z }}_{j}\tilde{\ge }\tilde{u }, \quad j=1,2,\dots ,s;\\ \begin{array}{l}\sum_{i=1}^{r}{\widetilde{y }}_{{i}}\cong \tilde{1 }; \\ {\widetilde{y }}_{i}\tilde{\ge }\tilde{0 }, \quad i=1,2,\dots r.\end{array}\end{array}\right.\end{array}$$

(9)

and

$$\begin{array}{l}\mathrm{min}\left\{\tilde{v }\right\}\\ \mathrm{s.t}.\left\{\begin{array}{l}\sum_{j=1}^{s}{\widetilde{b }}_{ij}{ \widetilde{y }}_{i}{ \widetilde{z }}_{j}\tilde{\le }\tilde{v }, i=1,2,\dots r;\\ \begin{array}{l}\sum_{j=1}^{s}{ \widetilde{z }}_{j}\cong \tilde{1 }; \\ { \widetilde{z }}_{j}\tilde{\ge }\tilde{0 }, \quad j=1,2,\dots s.\end{array}\end{array}\right.\end{array}$$

(10)

respectively, where $\tilde{u }$ and $\tilde{v }$ are TDHFNs. It makes sense to use only the extreme points of Y and Z in the constraints of Eqs. (9) and (10), since “$\tilde{\ge }$” and “$\tilde{\le }$” preserve the ranking order relations when TDHFNs are multiplied by positive numbers. Then, Eqs. (9) and (10) are reduced to the following dual hesitant fuzzy mathematical programming problems:

$$\begin{array}{l}\mathrm{max}\left\{\tilde{u }\right\}\\ {\text{s.t.}}\left\{\begin{array}{l}\sum_{i=1}^{r}{\widetilde{b }}_{ij}{ \widetilde{y }}_{i}\tilde{\ge }\tilde{u }, \quad j=1,2,\dots s;\\ \begin{array}{l}\sum_{i=1}^{r}{\widetilde{y }}_{i}\cong \tilde{1 }; \\ {\widetilde{y }}_{i}\tilde{\ge }\tilde{0 }, i=1,2,\dots r.\end{array}\end{array}\right.\end{array}$$

(11)

and

$$\begin{array}{*{20}l} {\min \left\{ {\tilde{v}} \right\}} \\ {{\text{s}}{\text{.t}}{.}\left\{ {\begin{array}{*{20}l} {\mathop \sum \limits_{j = 1}^{s} \widetilde{b}_{ij} \widetilde{z}_{j} \tilde{ \le }\tilde{v}, \quad i = 1,2, \ldots r;} \\ {\begin{array}{*{20}l} {\mathop \sum \limits_{j = 1}^{s} \widetilde{z}_{j} \cong \tilde{1}; } \\ { \widetilde{z}_{j} \tilde{ \ge }\tilde{0},\quad \quad j = 1,2, \ldots s.} \\ \end{array} } \\ \end{array} } \right.} \\ \end{array} ,{\text{ respectively}}.$$

(12)

4 Flaws of the existing method

Yang and Song (2020) proposed an approach for solving matrix games with TDHFNs payoffs. In this section, flaws in the existing Yang’s approach are pointed out.

1. In the existing approach (Yang and Song 2020), the authors have converted (Eqs. (5) and (6), PP. 5) into (Eqs. (7) and (14), PP. 5 and 7), respectively, using the mathematical properties ${\left(\sum_{i=1}^{r}{\widetilde{b }}_{i}\right)}_{\alpha }=\sum_{i=1}^{r}{\left({\widetilde{b }}_{i}\right)}_{\alpha }$ and ${\left(\sum_{i=1}^{r}{\widetilde{b }}_{i}\right)}_{\beta }=\sum_{i=1}^{r}{\left({\widetilde{b }}_{i}\right)}_{\beta }.$

However, it is clear that ${\left(\sum_{i=1}^{r}{\widetilde{b }}_{i}\right)}_{\alpha }\ne \sum_{i=1}^{r}{\left({\widetilde{b }}_{i}\right)}_{\alpha }$ in general as follows:

$${\left(\sum_{i=1}^{r}{\widetilde{b }}_{it}\right)}_{\alpha }={\left(\sum_{i=1}^{r}\left\langle \left({\underline{b}}_{it},{b}_{it},{\overline{b}}_{it}\right);{\omega }_{{\widetilde{b }}_{it}},{v}_{{\widetilde{b }}_{it}}\right\rangle \right)}_{\alpha }={\left(\left\langle \left(\sum_{i=1}^{r}{\underline{b}}_{\mathrm{i}t},\sum_{i=1}^{r}{b}_{it},\sum_{i=1}^{r}{\overline{b}}_{it}\right);\mathrm{min}\left\{{\omega }_{{\widetilde{b }}_{it}}\right\},\mathrm{max}\left\{{v}_{{\widetilde{b }}_{it}}\right\}\right\rangle \right)}_{\alpha }=\left[\frac{\left(\mathrm{min}\left\{{\omega }_{{\widetilde{b }}_{it}}\right\}-\alpha \right)\sum_{\mathrm{i}=1}^{\mathrm{r}}{\underline{b}}_{\mathrm{it}}+\alpha \sum_{i=1}^{r}{b}_{it}}{\mathrm{min}\left\{{\omega }_{{\widetilde{b }}_{it}}\right\}},\frac{\left(\mathrm{min}\left\{{\omega }_{{\widetilde{b }}_{it}}\right\}-\alpha \right)\sum_{i=1}^{r}{\overline{b}}_{it}+\alpha \sum_{i=1}^{r}{b}_{it}}{\mathrm{min}\left\{{\omega }_{{\widetilde{b }}_{it}}\right\}}\right],$$

and

$$\sum_{i=1}^{r}{\left({\widetilde{b }}_{i}\right)}_{\alpha }=\sum_{i=1}^{r}{\left(\left\langle \left({\underline{b}}_{it},{b}_{it},{\overline{b}}_{it}\right);{\omega }_{{\widetilde{b }}_{it}},{v}_{{\widetilde{b }}_{it}}\right\rangle \right)}_{\alpha }=\sum_{i=1}^{r}\left[\frac{\left({\omega }_{{\widetilde{b }}_{it}}-\alpha \right){\underline{b}}_{it}+\alpha {b}_{it}}{{\omega }_{{\widetilde{b }}_{it}}},\frac{\left({\omega }_{{\widetilde{b }}_{it}}-\alpha \right){\overline{b}}_{it}+\alpha {b}_{it}}{{\omega }_{{\widetilde{b }}_{it}}}\right]=\left[\sum_{i=1}^{r}\left(\frac{\left({\omega }_{{\widetilde{b }}_{it}}-\alpha \right){\underline{b}}_{it}+\alpha {b}_{it}}{{\omega }_{{\widetilde{b }}_{it}}}\right),\sum_{i=1}^{r}\left(\frac{\left({\omega }_{{\widetilde{b }}_{it}}-\alpha \right){\overline{b}}_{it}+\alpha {b}_{it}}{{\omega }_{{\widetilde{b }}_{it}}}\right)\right].$$

2. In the interval $\left[c,d\right]$, the inequality $c\le d$ should be always hold. However, in Yang’s approach (Eqs. (13) and (14), PP. 7) are solved without the restrictions ${u}_{t\alpha }^{\mathrm{L}}\le {u}_{t\alpha }^{\mathrm{R}}, {u}_{t\beta }^{\mathrm{L}}\le {u}_{t\beta }^{\mathrm{R}},{v}_{t\alpha }^{\mathrm{L}}\le {v}_{t\alpha }^{\mathrm{R}}\, \text{ and } \,{v}_{t\beta }^{\mathrm{L}}\le {v}_{t\beta }^{\mathrm{R}}$. Therefore, for the obtained values of ${u}_{t\alpha }^{\mathrm{L}}, {u}_{t\alpha }^{\mathrm{R}}, {u}_{t\beta }^{\mathrm{L}}, {u}_{t\beta }^{\mathrm{R}},{v}_{t\alpha }^{\mathrm{L}}, {v}_{t\alpha }^{\mathrm{R}}, {v}_{t\beta }^{\mathrm{L}}\, \text{ and } \,{v}_{t\beta }^{\mathrm{R}}$ the inequalities ${u}_{t\alpha }^{\mathrm{L}}\le {u}_{t\alpha }^{\mathrm{R}},{u}_{t\beta }^{\mathrm{L}}\le {u}_{t\beta }^{\mathrm{R}},{v}_{t\alpha }^{\mathrm{L}}\le {v}_{t\alpha }^{\mathrm{R}}\, \text{ and } \,{v}_{t\beta }^{\mathrm{L}}\le {v}_{t\beta }^{\mathrm{R}}$ may or may not be satisfied, in general.

5 Mehar method for solving triangular dual hesitant fuzzy matrix game

In this section, inspired by Verma et al. (2015) which overcomes some drawbacks of intuitionistic fuzzy matrix games, the Mehar approach is applied for solving TDHFNs matrix games. In the following, we will focus on discussing the solution approach and procedure of Eqs. (11) and (12).

5.1 Optimization models for Player I

Since ${\widetilde{b }}_{ij}$ are known, then by assuming ${\widetilde{b }}_{ij}=\left\langle \left({\underline{b}}_{ijt},{b}_{ijt},{\overline{b}}_{ijt}\right);{\omega }_{{\widetilde{{b}}}_{ijt}},{v}_{{\widetilde{{b}}}_{ijt}}\right\rangle$, $\tilde{u }=\left\langle \left({\underline{u}}_{t},{u}_{t},{\overline{u}}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle$, ${\widetilde{y }}_{i}=\left\langle \left({\underline{y}}_{it},{y}_{it},{\overline{y}}_{it}\right);{\omega }_{t},{v}_{t}\right\rangle$, $\tilde{1 }=\left\langle \left({1}_{t},{1}_{t},{1}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle$ and $\tilde{0 }=\left\langle \left({0}_{t},{0}_{t},{0}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle$, where ${\omega }_{t}=\mathrm{min}\left\{{\omega }_{{\widetilde{b }}_{ijt}}\right\}$ and ${v}_{t}=\mathrm{max}\left\{{v}_{{\widetilde{b }}_{ijt}}\right\}$, then Eq. (11) can be converted into

$$\begin{array}{l}\mathrm{max}\left\{\left\langle \left({\underline{u}}_{t},{u}_{t},{\overline{u}}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle \right\}\\ {\text{s.t.}}\left\{\begin{array}{l}\sum_{i=1}^{\mathrm{r}}\left(\left\langle \left({\underline{b}}_{ijt},{b}_{ijt},{\overline{b}}_{ijt}\right);{\omega }_{{\widetilde{b }}_{ijt}},{v}_{{\widetilde{b }}_{ijt}}\right\rangle \right)\left(\left\langle \left({\underline{y}}_{it},{y}_{it},{\overline{y}}_{it}\right);{\omega }_{t},{v}_{t}\right\rangle \right)\tilde{\ge }\left\langle \left({\underline{u}}_{t},{u}_{t},{\overline{u}}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle ,\quad j=1,2,\ldots ,s,\quad t=1,2,\ldots, m;\\ \begin{array}{l}\sum_{i=1}^{r}\left\langle \left({\underline{y}}_{it},{y}_{it},{\overline{y}}_{it}\right);{\omega }_{t},{v}_{t}\right\rangle \cong \left\langle \left({1}_{t},{1}_{t},{1}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle, \quad t=1,2,\dots ,m; \\ \left\langle \left({\underline{y}}_{it},{y}_{it},{\overline{y}}_{it}\right);{\omega }_{t},{v}_{t}\right\rangle \tilde{\ge }\left\langle \left({0}_{t},{0}_{\mathrm{t}},{0}_{\mathrm{t}}\right);{\omega }_{t},{v}_{t}\right\rangle , i=1,2,\dots ,r, \quad t=1,2,\ldots, m.\end{array}\end{array}\right.\end{array}$$

(13)

According to Definition 10, Eq. (13) can be rewritten as follows:

$$\begin{array}{l}\mathrm{max}\left\{\left\langle \left({\underline{u}}_{t},{u}_{t},{\overline{u}}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle \right\}\\ {\text{s.t.}}\left\{\begin{array}{l}\sum_{i=1}^{r}\left\langle \left({\underline{q}}_{ijt},{q}_{ijt},{\overline{q}}_{ijt}\right);{\omega }_{t},{v}_{t}\right\rangle \tilde{\ge }\left\langle \left({\underline{u}}_{t},{u}_{t},{\overline{u}}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle ,\quad j=1,2,\ldots ,s,\quad t=1,2,\ldots, m;\\ \begin{array}{l}\sum_{i=1}^{r}\left\langle \left({\underline{y}}_{it},{y}_{it},{\overline{y}}_{it}\right);{\omega }_{t},{v}_{t}\right\rangle \cong \left\langle \left({1}_{\mathrm{t}},{1}_{\mathrm{t}},{1}_{\mathrm{t}}\right);{\omega }_{t},{v}_{t}\right\rangle , \quad t=1,2,\ldots, m; \\ \left\langle \left({\underline{y}}_{it},{y}_{it},{\overline{y}}_{it}\right);{\omega }_{t},{v}_{t}\right\rangle \tilde{\ge }\left\langle \left({0}_{\mathrm{t}},{0}_{\mathrm{t}},{0}_{\mathrm{t}}\right);{\omega }_{t},{v}_{t}\right\rangle , i=1,2,\dots ,r,t=1,2,\ldots, m,\end{array}\end{array}\right.\end{array}$$

(14)

$$\mathrm{where}\, \left\langle \left({\underline{q}}_{ijt},{q}_{ijt},{\overline{q}}_{ijt}\right);{\omega }_{t},{v}_{t}\right\rangle =\left\{\begin{array}{l}\left\langle \left({\underline{b}}_{ijt} {\underline{y}}_{it},{b}_{ijt}{ y}_{it},{\overline{b}}_{ijt} {\overline{y}}_{it}\right);{\omega }_{t},{v}_{t}\right\rangle ,{\widetilde{b }}_{ij}{ \tilde{>}0, \tilde{y }}_{i}\tilde{>}0, \\ \left\langle \left({\underline{b}}_{ijt}{\overline{ y}}_{it},{b}_{ijt}{ y}_{it},{\overline{b}}_{ijt }{\underline{y}}_{it}\right);{\omega }_{t},{v}_{t}\right\rangle , {\widetilde{{b}}}_{{ij}}{ \tilde{>}0, \tilde{\mathrm{y}}}_{\mathrm{i}}\tilde{<}0,\\ \left\langle \left({\overline{b}}_{ijt} {\overline{y}}_{it},{b}_{ijt}{ y}_{it},{\underline{b}}_{ijt} {\underline{y}}_{it}\right);{\omega }_{t},{v}_{t}\right\rangle ,{\tilde{b }}_{ij}{ \tilde{<}0, \widetilde{y }}_{i}\tilde{<}0.\end{array}\right.$$

Since $\sum_{i=1}^{r}\left(\left\langle \left({\underline{b}}_{ijt},{b}_{ijt},{\overline{b}}_{ijt}\right);{\omega }_{t},{v}_{t}\right\rangle \right)=\left\langle \left(\sum_{i=1}^{r}{\underline{b}}_{ijt},\sum_{i=1}^{r}{b}_{ijt},\sum_{i=1}^{r}{\overline{b}}_{ijt}\right);{\omega }_{t},{v}_{t}\right\rangle$, then Eq. (14) can be transformed into

$$\begin{array}{l}\mathrm{max}\left\{\left\langle \left({\underline{u}}_{t},{u}_{t},{\overline{u}}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle \right\}\\ {\text{s.t.}}\left\{\begin{array}{l}\left\langle \left(\sum_{i=1}^{r}{\underline{q}}_{ijt},\sum_{i=1}^{r}{q}_{ijt},\sum_{i=1}^{r}{\overline{q}}_{ijt}\right);{\omega }_{t},{v}_{t}\right\rangle \tilde{\ge }\left\langle \left({\underline{u}}_{t},{u}_{t},{\overline{u}}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle j=1,2,\ldots ,s,\quad t=1,2,\ldots, m;\\ \begin{array}{l}\left\langle \left(\sum_{i=1}^{r}{\underline{y}}_{it},\sum_{i=1}^{r}{y}_{it},\sum_{i=1}^{r}{\overline{y}}_{it}\right);{\omega }_{t},{v}_{t}\right\rangle \cong \left\langle \left({1}_{t},{1}_{t},{1}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle , \quad t=1,2,\ldots, m; \\ \left\langle \left({\underline{y}}_{it},{y}_{it},{\overline{y}}_{it}\right);{\omega }_{t},{v}_{t}\right\rangle \tilde{\ge }\left\langle \left({0}_{t},{0}_{t},{0}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle , i=1,2,\dots ,r,t=1,2,\ldots, m.\end{array}\end{array}\right.\end{array}$$

(15)

Using Definition 8, Eq. (15) is converted into the interval-valued bi-objective programming model as follows:

$$\begin{array}{l}\mathrm{max}\left\{{\left(\left\langle \left({\underline{u}}_{t},{u}_{t},{\overline{u}}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\alpha },{\left(\left\langle \left({\underline{u}}_{t},{u}_{t},{\overline{u}}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\beta }\right\}\\ {\text{s.t.}}\left\{\begin{array}{l}\begin{array}{l}{\left(\left\langle \left(\sum_{i=1}^{r}{\underline{q}}_{ijt},\sum_{i=1}^{r}{q}_{ijt},\sum_{i=1}^{r}{\overline{q}}_{ijt}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\alpha }\ge {\left(\left\langle \left({\underline{u}}_{t},{u}_{t},{\overline{u}}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\alpha } j=1,2,\ldots ,s,\quad t=1,2,\ldots, m;\\ {\left(\left\langle \left(\sum_{i=1}^{r}{\underline{q}}_{ijt},\sum_{i=1}^{r}{q}_{ijt},\sum_{i=1}^{r}{\overline{q}}_{ijt}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\beta }\ge {\left(\left\langle \left({\underline{u}}_{t},{u}_{t},{\overline{u}}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\beta } j=1,2,\ldots ,s,\quad t=1,2,\ldots, m;\end{array}\\ \begin{array}{l}\begin{array}{l}{\left(\left\langle \left(\sum_{i=1}^{r}{\underline{y}}_{it},\sum_{i=1}^{r}{y}_{it},\sum_{i=1}^{r}{\overline{y}}_{it}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\alpha }= {\left(\left\langle \left({1}_{t},{1}_{t},{1}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\alpha }, \quad t=1,2,\ldots, m; \\ {\left(\left\langle \left(\sum_{i=1}^{r}{\underline{y}}_{\mathrm{it}},\sum_{i=1}^{r}{y}_{it},\sum_{i=1}^{r}{\overline{y}}_{it}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\beta }= {\left(\left\langle \left({1}_{t},{1}_{t},{1}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\beta }, \quad t=1,2,\ldots, m; \end{array} \\ \begin{array}{l}{\left(\left\langle \left({\underline{y}}_{it},{y}_{it},{\overline{y}}_{it}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\alpha }\ge {\left(\left\langle \left({0}_{t},{0}_{t},{0}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\alpha }, i=1,2,\dots ,r,t=1,2,\ldots, m; \\ {\left(\left\langle \left({\underline{y}}_{it},{y}_{it},{\overline{y}}_{it}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\beta }\ge {\left(\left\langle \left({0}_{t},{0}_{t},{0}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\beta }, i=1,2,\dots ,r,t=1,2,\ldots, m. \end{array}\end{array}\end{array}\right.\end{array}$$

(16)

Let ${\left(\left\langle \left({\underline{u}}_{t},{u}_{t},{\overline{u}}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\alpha }=\left[{{u}^{\mathrm{L}}}_{t\alpha },{{u}^{\mathrm{U}}}_{t\alpha }\right]$, ${\left(\left\langle \left({\underline{u}}_{t},{u}_{t},{\overline{u}}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\beta }=\left[{{u}^{\mathrm{L}}}_{t\beta },{{u}^{\mathrm{U}}}_{t\beta }\right]$, ${\left(\left\langle \left(\sum_{i=1}^{r}{\underline{q}}_{ijt},\sum_{i=1}^{r}{q}_{ijt},\sum_{i=1}^{r}{\overline{q}}_{ijt}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\alpha }=\left[{{\left({Q}_{ijt}\right)}^{\mathrm{L}}}_{\alpha },{{\left({Q}_{ijt}\right)}^{\mathrm{U}}}_{\alpha }\right]$, ${\left(\left\langle \left(\sum_{i=1}^{r}{\underline{q}}_{ijt},\sum_{i=1}^{r}{q}_{ijt},\sum_{i=1}^{r}{\overline{q}}_{ijt}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\beta }=\left[{{\left({Q}_{ijt}\right)}^{\mathrm{L}}}_{\beta },{{\left({Q}_{ijt}\right)}^{\mathrm{U}}}_{\beta }\right]$, ${\left(\left\langle \left(\sum_{i=1}^{r}{\underline{y}}_{it},\sum_{i=1}^{r}{y}_{it},\sum_{i=1}^{r}{\overline{\mathrm{y}}}_{\mathrm{it}}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\alpha }=\left[{{\left({\mathbb{Y}}_{it}\right)}^{\mathrm{L}}}_{\alpha },{{\left({\mathbb{Y}}_{it}\right)}^{\mathrm{U}}}_{\alpha }\right]$, ${\left(\left\langle \left(\sum_{i=1}^{r}{\underline{y}}_{it},\sum_{i=1}^{r}{y}_{it},\sum_{i=1}^{r}{\overline{y}}_{it}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\beta }=\left[{{\left({\mathbb{Y}}_{it}\right)}^{\mathrm{L}}}_{\beta },{{\left({\mathbb{Y}}_{it}\right)}^{\mathrm{U}}}_{\beta }\right]$, ${\left(\left\langle \left({\underline{y}}_{it},{y}_{it},{\overline{y}}_{it}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\alpha }=\left[{{\left({y}_{it}\right)}^{\mathrm{L}}}_{\alpha },{{\left({y}_{it}\right)}^{\mathrm{U}}}_{\alpha }\right]$, ${\left(\left\langle \left({\underline{y}}_{it},{y}_{it},{\overline{y}}_{it}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\beta }=\left[{{\left({y}_{it}\right)}^{\mathrm{L}}}_{\beta },{{\left({y}_{it}\right)}^{\mathrm{U}}}_{\beta }\right]$, ${\left(\left\langle \left({1}_{t},{1}_{t},{1}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\alpha }=\left[{{\left({1}_{t}\right)}^{\mathrm{L}}}_{\alpha },{{\left({1}_{t}\right)}^{\mathrm{U}}}_{\alpha }\right]$, ${\left(\left\langle \left({1}_{t},{1}_{t},{1}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\beta }=\left[{{\left({1}_{t}\right)}^{\mathrm{L}}}_{\beta },{{\left({1}_{t}\right)}^{\mathrm{U}}}_{\beta }\right]$, ${\left(\left\langle \left({0}_{t},{0}_{t},{0}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\alpha }=\left[{{\left({0}_{t}\right)}^{\mathrm{L}}}_{\alpha },{{\left({0}_{t}\right)}^{\mathrm{U}}}_{\alpha }\right]$ and ${\left(\left\langle \left({0}_{t},{0}_{t},{0}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\beta }=\left[{{\left({0}_{t}\right)}^{\mathrm{L}}}_{\beta },{{\left({0}_{t}\right)}^{\mathrm{U}}}_{\beta }\right]$.

According to Definition 1, Eq. (16) can be rewritten as follows:

$$\begin{array}{l}\mathrm{max}\left\{\left[{{u}^{\mathrm{L}}}_{t\alpha },{{u}^{\mathrm{U}}}_{t\alpha }\right],\left[{{u}^{\mathrm{L}}}_{t\beta },{{u}^{\mathrm{U}}}_{t\beta }\right]\right\}\\ {\text{s.t.}}\left\{\begin{array}{l}\begin{array}{l}{{\left({Q}_{ijt}\right)}^{\mathrm{L}}}_{\alpha }\ge {{u}^{\mathrm{L}}}_{t\alpha }, {{\left({Q}_{ijt}\right)}^{\mathrm{U}}}_{\alpha }\ge {{u}^{\mathrm{U}}}_{t\alpha },\quad j=1,2,\ldots ,s,\quad t=1,2,\ldots, m;\\ {{\left({Q}_{ijt}\right)}^{\mathrm{L}}}_{\beta }\ge {{u}^{\mathrm{L}}}_{t\beta }, {{\left({\mathrm{Q}}_{\mathrm{ijt}}\right)}^{\mathrm{U}}}_{\beta }\ge {{u}^{\mathrm{U}}}_{t\beta }, \quad j=1,2,\dots s, \quad t=1,2,\ldots, m;\end{array}\\ \begin{array}{l}\begin{array}{l}{{\left({\mathbb{Y}}_{it}\right)}^{\mathrm{L}}}_{\alpha }={{\left({1}_{t}\right)}^{\mathrm{L}}}_{\alpha }, {{\left({\mathbb{Y}}_{it}\right)}^{\mathrm{U}}}_{\mathrm{\alpha }}={{\left({1}_{t}\right)}^{\mathrm{U}}}_{\alpha }, \quad t=1,2,\ldots, m; \\ {{\left({\mathbb{Y}}_{it}\right)}^{\mathrm{L}}}_{\beta }={{\left({1}_{t}\right)}^{\mathrm{L}}}_{\beta }, {{\left({\mathbb{Y}}_{it}\right)}^{\mathrm{U}}}_{\beta }={{\left({1}_{t}\right)}^{\mathrm{U}}}_{\beta }, \quad t=1,2,\ldots, m; \end{array} \\ \begin{array}{l}{{\left({y}_{it}\right)}^{\mathrm{L}}}_{\alpha }\ge {{\left({0}_{t}\right)}^{\mathrm{L}}}_{\mathrm{\alpha }},{{\left({y}_{it}\right)}^{\mathrm{U}}}_{{\alpha }}\ge {{\left({0}_{t}\right)}^{\mathrm{U}}}_{\alpha }, i=1,2,\dots ,r,t=1,2,\ldots, m; \\ {{\left({y}_{it}\right)}^{\mathrm{L}}}_{\beta }\ge {{\left({0}_{\mathrm{t}}\right)}^{\mathrm{L}}}_{\beta },{{\left({y}_{it}\right)}^{\mathrm{U}}}_{\beta }\ge {{\left({0}_{t}\right)}^{\mathrm{U}}}_{\beta }, \quad i=1,2,\dots ,r,t=1,2,\ldots, m. \end{array}\end{array}\end{array}\right.\end{array}$$

(17)

According to Definition 2, Eq. (17) can be converted into the bi-objective programming problem as follows:

$$\begin{array}{l}\mathrm{max}\left\{\frac{\sum_{t=1}^{m}\left({{u}^{\mathrm{L}}}_{t\alpha }+{{u}^{\mathrm{L}}}_{t\beta }\right)}{2\mathrm{m}},\frac{\sum_{t=1}^{m}\left({{u}^{\mathrm{L}}}_{t\alpha }+{{u}^{\mathrm{L}}}_{t\beta }+{{u}^{\mathrm{U}}}_{t\alpha }+{{u}^{\mathrm{U}}}_{t\beta }\right)}{4\mathrm{m}}\right\}\\ {\text{s.t.}}\left\{\begin{array}{l}\begin{array}{l}{{\left({Q}_{ijt}\right)}^{\mathrm{L}}}_{\alpha }\ge {{u}^{\mathrm{L}}}_{t\alpha }, {{\left({Q}_{ijt}\right)}^{\mathrm{U}}}_{\alpha }\ge {{u}^{\mathrm{U}}}_{t\alpha },\quad j=1,2,\ldots ,s,\quad t=1,2,\ldots, m;\\ {{\left({Q}_{ijt}\right)}^{\mathrm{L}}}_{\beta }\ge {{u}^{\mathrm{L}}}_{t\beta }, {{\left({Q}_{ijt}\right)}^{\mathrm{U}}}_{\beta }\ge {{u}^{\mathrm{U}}}_{t\beta }, \quad j=1,2,\dots s, \quad t=1,2,\ldots, m;\end{array}\\ \begin{array}{l}\begin{array}{l}{{\left({\mathbb{Y}}_{\mathrm{it}}\right)}^{\mathrm{L}}}_{\alpha }={{\left({1}_{t}\right)}^{\mathrm{L}}}_{\alpha }, {{\left({\mathbb{Y}}_{it}\right)}^{\mathrm{U}}}_{\alpha }={{\left({1}_{t}\right)}^{\mathrm{U}}}_{\alpha }, \quad t=1,2,\ldots, m; \\ {{\left({\mathbb{Y}}_{it}\right)}^{\mathrm{L}}}_{\beta }={{\left({1}_{t}\right)}^{\mathrm{L}}}_{\beta }, {{\left({\mathbb{Y}}_{it}\right)}^{\mathrm{U}}}_{\beta }={{\left({1}_{t}\right)}^{\mathrm{U}}}_{\beta }, \quad t=1,2,\ldots, m; \end{array} \\ \begin{array}{l}{{\left({y}_{it}\right)}^{\mathrm{L}}}_{\alpha }\ge {{\left({0}_{t}\right)}^{\mathrm{L}}}_{\alpha },{{\left({y}_{it}\right)}^{\mathrm{U}}}_{\alpha }\ge {{\left({0}_{t}\right)}^{\mathrm{U}}}_{\alpha }, i=1,2,\dots ,r,t=1,2,\ldots, m; \\ {{\left({y}_{it}\right)}^{\mathrm{L}}}_{\beta }\ge {{\left({0}_{t}\right)}^{\mathrm{L}}}_{\beta },{{\left({\mathrm{y}}_{\mathrm{it}}\right)}^{\mathrm{U}}}_{\beta }\ge {{\left({0}_{t}\right)}^{\mathrm{U}}}_{\beta }, i=1,2,\dots ,r,t=1,2,\ldots, m. \end{array}\end{array}\end{array}\right.\end{array}$$

(18)

There exist many approaches for solving the bi-objective programming problem. However, in this article we focus on a weighted average method (Chankong and Haimes 1983; Hwang and Yoon 1981; Li 2003) to solve Eq. (18) in the sense of Pareto optimality. Therefore, Eq. (18) can be converted into linear programming problem as follows:

$$\begin{array}{l}\mathrm{max}\left\{\lambda \left(\frac{\sum_{t=1}^{m}\left({{u}^{L}}_{t\alpha }+{{u}^{L}}_{t\beta }\right)}{2m}\right)+(1-\lambda )\left(\frac{\sum_{t=1}^{m}\left({{u}^{L}}_{t\alpha }+{{u}^{L}}_{t\beta }+{{u}^{U}}_{t\alpha }+{{u}^{U}}_{t\beta }\right)}{4m}\right)\right\}\\ {\text{s.t.}}\left\{\begin{array}{l}\begin{array}{l}{{\left({Q}_{ijt}\right)}^{\mathrm{L}}}_{\alpha }\ge {{u}^{\mathrm{L}}}_{t\alpha }, {{\left({Q}_{ijt}\right)}^{\mathrm{U}}}_{\alpha }\ge {{u}^{\mathrm{U}}}_{t\alpha },\quad j=1,2,\ldots ,s,\quad t=1,2,\ldots, m;\\ {{\left({Q}_{ijt}\right)}^{\mathrm{L}}}_{\beta }\ge {{u}^{\mathrm{L}}}_{t\beta }, {{\left({Q}_{ijt}\right)}^{U}}_{\beta }\ge {{u}^{\mathrm{U}}}_{t\beta },\quad j=1,2,\ldots ,s,\quad t=1,2,\ldots, m;\end{array}\\ \begin{array}{l}\begin{array}{l}{{\left({Y}_{it}\right)}^{\mathrm{L}}}_{\alpha }={{\left({1}_{t}\right)}^{L}}_{\alpha }, {{\left({Y}_{it}\right)}^{U}}_{\alpha }={{\left({1}_{t}\right)}^{\mathrm{U}}}_{\alpha }, \quad t=1,2,\ldots, m; \\ {{\left({Y}_{it}\right)}^{\mathrm{L}}}_{\beta }={{\left({1}_{t}\right)}^{\mathrm{L}}}_{\beta }, {{\left({Y}_{it}\right)}^{U}}_{\beta }={{\left({1}_{t}\right)}^{\mathrm{U}}}_{\beta }, \quad t=1,2,\ldots, m; \end{array} \\ \begin{array}{l}{{\left({y}_{it}\right)}^{\mathrm{L}}}_{\alpha }\ge {{\left({0}_{t}\right)}^{\mathrm{L}}}_{\alpha },{{\left({y}_{it}\right)}^{U}}_{\alpha }\ge {{\left({0}_{t}\right)}^{\mathrm{U}}}_{\alpha }, i=1,2,\dots ,r,t=1,2,\ldots, m; \\ {{\left({y}_{it}\right)}^{\mathrm{L}}}_{\beta }\ge {{\left({0}_{t}\right)}^{\mathrm{L}}}_{\beta },{{\left({y}_{it}\right)}^{U}}_{\beta }\ge {{\left({0}_{t}\right)}^{\mathrm{U}}}_{\beta }, i=1,2,\dots ,r,t=1,2,\ldots, m, \end{array}\end{array}\end{array}\right.\end{array}$$

(19)

where $\lambda \in \left[\mathrm{0,1}\right]$ is the weight determined by both players. According to Definitions 4, 5 and 6, Eq. (19) can be constructed as follows:

$$\begin{array}{l}\mathrm{max}\left\{\begin{array}{l}\lambda \left(\frac{\sum_{t=1}^{m}\left(\frac{\left({\omega }_{t}-\alpha \right) {\underline{u}}_{t}+\alpha {u}_{t}}{{\omega }_{t}}+\frac{\left(1-\beta \right) {u}_{t}+\left(\beta -{v}_{t}\right) {\underline{u}}_{t}}{1-{v}_{t}}\right)}{2m}\right)+\\ (1-\lambda )\left(\frac{\sum_{t=1}^{m}\left(\frac{\left({\omega }_{t}-\alpha \right) {\underline{u}}_{t}+\alpha {u}_{t}}{{\omega }_{t}}+\frac{\left(1-\beta \right) {u}_{t}+\left(\beta -{v}_{t}\right) {\underline{u}}_{t}}{1-{v}_{t}}+\frac{\left({\omega }_{t}-\alpha \right){ \overline{u}}_{t}+\alpha { u}_{t}}{{\omega }_{t}}+\frac{\left(1-\beta \right) {u}_{t}+\left(\beta -{v}_{t}\right) { \overline{u}}_{t}}{1-{v}_{t}}\right)}{4m}\right)\end{array}\right\}\\ {\text{s.t.}}\left\{\begin{array}{l}\begin{array}{l}\begin{array}{l}\frac{\left({\omega }_{t}-\alpha \right)\sum_{i=1}^{r}{\underline{q}}_{ijt}+\alpha \sum_{i=1}^{r}{q}_{ijt}}{{\omega }_{t}}\ge \frac{\left({\omega }_{t}-\alpha \right) {\underline{u}}_{t}+\alpha {u}_{t}}{{\omega }_{t}},\quad j=1,2,\ldots ,s,\quad t=1,2,\ldots, m;\\ \frac{\left({\omega }_{t}-\alpha \right)\sum_{i=1}^{r}{\overline{q}}_{ijt}+\alpha \sum_{i=1}^{r}{q}_{ijt}}{{\omega }_{t}}\ge \frac{\left({\omega }_{t}-\alpha \right){ \overline{u}}_{t}+\alpha { u}_{t}}{{\omega }_{t}},\quad j=1,2,\ldots ,s,\quad t=1,2,\ldots, m;\end{array}\\ \begin{array}{l}\frac{\left(1-\beta \right)\sum_{i=1}^{r}{q}_{ijt}+\left(\beta -{v}_{t}\right)\sum_{i=1}^{r}{\underline{q}}_{ijt}}{1-{v}_{t}}\ge \frac{\left(1-\beta \right) {u}_{t}+\left(\beta -{v}_{t}\right) {\underline{u}}_{t}}{1-{v}_{t}},\quad j=1,2,\ldots ,s,\quad t=1,2,\ldots, m;\\ \frac{\left(1-\beta \right)\sum_{i=1}^{r}{q}_{ijt}+\left(\beta -{v}_{t}\right)\sum_{i=1}^{r}{\overline{q}}_{ijt}}{1-{v}_{t}}\ge \frac{\left(1-\beta \right) {u}_{t}+\left(\beta -{v}_{t}\right) { \overline{u}}_{t}}{1-{v}_{t}},\quad j=1,2,\ldots ,s,\quad t=1,2,\ldots, m;\end{array}\end{array}\\ \begin{array}{l}\begin{array}{l}\begin{array}{l}\begin{array}{l}\frac{\left({\omega }_{t}-\alpha \right)\sum_{i=1}^{r}{\underline{y}}_{it}+\alpha \sum_{i=1}^{r}{y}_{it}}{{\omega }_{t}}=\frac{\left({\omega }_{t}-\alpha \right)+\alpha }{{\omega }_{t}}, \quad t=1,2,\ldots, m;\\ \frac{\left({\omega }_{t}-\alpha \right)\sum_{i=1}^{r}{\overline{y}}_{it}+\alpha \sum_{i=1}^{r}{y}_{it}}{{\omega }_{t}}=\frac{\left({\omega }_{t}-\alpha \right)+\alpha }{{\omega }_{t}}, \quad t=1,2,\ldots, m;\end{array} \\ \frac{\left(1-\beta \right)\sum_{i=1}^{r}{y}_{it}+\left(\beta -{v}_{t}\right)\sum_{i=1}^{r}{\underline{y}}_{it}}{1-{v}_{t}}=\frac{\left(1-\beta \right)+\left(\beta -{v}_{t}\right)}{1-{v}_{t}}, \quad t=1,2,\ldots, m; \end{array}\\ \frac{\left(1-\beta \right)\sum_{i=1}^{r}{y}_{it}+\left(\beta -{v}_{t}\right)\sum_{i=1}^{r}{\overline{y}}_{it}}{1-{v}_{t}}=\frac{\left(1-\beta \right)+\left(\beta -{v}_{t}\right)}{1-{v}_{t}}, \quad t=1,2,\ldots, m;\end{array} \\ \begin{array}{l}\begin{array}{l}\frac{\left({\omega }_{t}-\alpha \right){ \underline{y}}_{it}+\alpha {y}_{it}}{{\omega }_{t}}\ge 0, i=1,2,\dots ,r,t=1,2,\ldots, m;\\ \frac{\left({\omega }_{t}-\alpha \right) {\overline{y}}_{it}+\alpha {y}_{it}}{{\omega }_{t}}\ge 0, i=1,2,\dots ,r,t=1,2,\ldots, m;\end{array} \\ \begin{array}{l}\frac{\left(1-\beta \right){y}_{it}+\left(\beta -{v}_{t}\right){ \underline{y}}_{it}}{1-{v}_{t}}\ge 0, i=1,2,\dots ,r,t=1,2,\ldots, m; \\ \frac{\left(1-\beta \right){y}_{it}+\left(\beta -{v}_{t}\right) {\overline{y}}_{it}}{1-{v}_{t}}\ge 0, i=1,2,\dots ,r,t=1,2,\ldots, m;\\ \begin{array}{l}\frac{\left({\omega }_{t}-\alpha \right) {\overline{y}}_{it}+\alpha {y}_{it}}{{\omega }_{t}}\ge \frac{\left({\omega }_{t}-\alpha \right){ \underline{y}}_{it}+\alpha {y}_{it}}{{\omega }_{t}}, \quad t=1,2,\ldots, m;\\ \frac{\left(1-\beta \right){y}_{it}+\left(\beta -{v}_{t}\right) {\overline{y}}_{it}}{1-{v}_{t}}\ge \frac{\left(1-\beta \right){y}_{it}+\left(\beta -{v}_{t}\right){ \underline{y}}_{it}}{1-{v}_{t}}, \quad t=1,2,\ldots, m;\\ \begin{array}{l}{{u}^{\mathrm{U}}}_{t\alpha }\ge {{u}^{\mathrm{L}}}_{t\alpha }, \quad t=1,2,\ldots, m;\\ {{u}^{\mathrm{U}}}_{t\beta }\ge {{u}^{\mathrm{L}}}_{t\beta }, \quad t=1,2,\ldots, m.\end{array}\end{array}\end{array} \end{array}\end{array}\end{array}\right.\end{array}$$

(20)

Using the Simplex technique for linear programming by taking $\alpha =0\, \text{ and } \,\beta =1$, the optimal solutions of Eq. (20) is obtained. The Eq. (20) can be used to find the lower and upper limits of player I’s TDHFN optimal strategies ${\underline{y}}_{it}^{*}={e}_{it},{\overline{y}}_{it}^{*}={f}_{it}$ and the corresponding lower and upper limits of the TDHFN gain-floor ${\underline{u}}_{t}^{*}={c}_{t},{\overline{u}}_{t}^{*}={d}_{t}.$

$$\begin{array}{l}\mathrm{max}\left\{\begin{array}{l}\lambda \left(\frac{\sum_{t=1}^{m}\left(\frac{\left({\omega }_{t}-\alpha \right) {\underline{u}}_{t}+\alpha {u}_{t}}{{\omega }_{t}}+\frac{\left(1-\beta \right) {u}_{t}+\left(\beta -{v}_{t}\right) {\underline{u}}_{t}}{1-{v}_{t}}\right)}{2m}\right)+\\ (1-\lambda )\left(\frac{\sum_{t=1}^{m}\left(\frac{\left({\omega }_{t}-\alpha \right) {\underline{u}}_{t}+\alpha {u}_{t}}{{\omega }_{t}}+\frac{\left(1-\beta \right) {u}_{t}+\left(\beta -{v}_{t}\right) {\underline{u}}_{t}}{1-{v}_{t}}+\frac{\left({\omega }_{t}-\alpha \right){ \overline{u}}_{t}+\alpha { u}_{t}}{{\omega }_{t}}+\frac{\left(1-\beta \right) {u}_{t}+\left(\beta -{v}_{t}\right) { \overline{u}}_{t}}{1-{v}_{t}}\right)}{4m}\right)\end{array}\right\}\\ {\text{s.t.}}\left\{\begin{array}{l}\mathrm{Constraints \, of \,Eq}.\,\, \left(20\right); \\ \begin{array}{l} \\ \begin{array}{l}{y}_{it}\ge {e}_{it}, i=1,2,\dots r, \quad t=1,2,\ldots, m;\\ \begin{array}{l}{y}_{it}\le {f}_{it}, i=1,2,\dots r, \quad t=1,2,\ldots, m;\\ {u}_{t}\ge {c}_{t}, \quad t=1,2,\ldots, m;\\ {u}_{t}\le {d}_{t}, \quad t=1,2,\ldots, m.\end{array}\end{array}\end{array}\end{array}\right.\end{array}$$

(21)

Using the Simplex technique for linear programming by taking $\alpha ={\omega }_{t} \mathrm{and} \beta ={v}_{t}$, the optimal solutions of Eq. (21) is obtained. The Eq. (21) can be used to find the mean of player I's TDHFN optimal strategies ${y}_{it}^{*}$ and the corresponding mean of the TDHFN gain-floor ${u}_{t}^{*}$. Therefore, the TDHFN optimal solutions of Eq. (11) is $\left\{{\tilde{u }}^{*}=\left\langle \left({\underline{u}}_{t}^{*},{u}_{t}^{*},{\overline{u}}_{t}^{*}\right);{\omega }_{t},{v}_{t}\right\rangle , {{\widetilde{y }}_{i}}^{*}=\left\langle \left({\underline{y}}_{it}^{*},{y}_{it}^{*},{\overline{y}}_{it}^{*}\right);{\omega }_{t},{v}_{t}\right\rangle ;i=1,2,\ldots ,r, \quad t=1,2,\ldots, m \right\}.$

5.2 Optimization models for Player II

In the same analysis to that of player I, since ${\widetilde{{b}}}_{{ij}}$ are known, then by assuming ${\widetilde{b }}_{ij}=\left\langle \left({\underline{b}}_{ijt},{b}_{ijt},{\overline{b}}_{ijt}\right);{\omega }_{{\widetilde{b }}_{ijt}},{v}_{{\widetilde{b }}_{ijt}}\right\rangle$, $\tilde{v }=\left\langle \left({\underline{v}}_{t},{v}_{t},{\overline{v}}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle$, ${\widetilde{z }}_{j}=\left\langle \left({\underline{z}}_{jt},{z}_{jt},{\overline{z}}_{jt}\right);{\omega }_{t},{v}_{t}\right\rangle$, $\tilde{1 }=\left\langle \left({1}_{t},{1}_{t},{1}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle$ and $\tilde{0 }=\left\langle \left({0}_{t},{0}_{t},{0}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle$, where ${\omega }_{t}=\mathrm{min}\left\{{\omega }_{{\widetilde{b }}_{ijt}}\right\}$ and ${v}_{t}=\mathrm{max}\left\{{v}_{{\widetilde{b }}_{ijt}}\right\}$, then Eq. (12) can be converted into

$$\begin{array}{l}\mathrm{min}\left\{\left\langle \left({\underline{v}}_{t},{v}_{t},{\overline{v}}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle \right\}\\ {\text{s.t.}}\left\{\begin{array}{l}\sum_{j=1}^{s}\left(\left\langle \left({\underline{b}}_{ijt},{b}_{ijt},{\overline{b}}_{ijt}\right);{\omega }_{{\widetilde{b }}_{ijt}},{v}_{{\widetilde{b }}_{ijt}}\right\rangle \right)\left(\left\langle \left({\underline{z}}_{jt},{z}_{jt},{\overline{z}}_{jt}\right);{\omega }_{t},{v}_{t}\right\rangle \right)\tilde{\le }\left\langle \left({\underline{v}}_{t},{v}_{t},{\overline{v}}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle , \quad i=1,2,\ldots ,r, \quad t=1,2,\ldots, m;\\ \begin{array}{l}\sum_{j=1}^{s}\left\langle \left({\underline{z}}_{jt},{z}_{jt},{\overline{z}}_{jt}\right);{\omega }_{t},{v}_{t}\right\rangle \cong \left\langle \left({1}_{t},{1}_{t},{1}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle , \quad t=1,2,\ldots, m; \\ \left\langle \left({\underline{z}}_{jt},{z}_{jt},{\overline{z}}_{jt}\right);{\omega }_{t},{v}_{t}\right\rangle \tilde{\ge }\left\langle \left({0}_{t},{0}_{t},{0}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle , \quad j=1,2,\dots s,t=1,2,\ldots, m.\end{array}\end{array}\right.\end{array}$$

(22)

According to Definition 10, Eq. (22) can be rewritten as follows:

$$\begin{array}{l}\mathrm{min}\left\{ \left\langle \left({\underline{v}}_{t},{v}_{t},{\overline{v}}_{t}\right);{\omega }_{t},{v}_{t} \right\rangle \right\}\\ \mathrm{s.t}.\left\{\begin{array}{l}\sum_{j=1}^{s}\left\langle \left({\underline{p}}_{ijt},{p}_{ijt},{\overline{p}}_{ijt}\right);{\omega }_{t},{v}_{t}\right\rangle \tilde{\le }\left\langle \left({\underline{v}}_{t},{v}_{t},{\overline{v}}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle , \quad i=1,2,\ldots ,r, \quad t=1,2,\ldots, m;\\ \begin{array}{l}\sum_{j=1}^{s}\left\langle \left({\underline{z}}_{jt},{z}_{jt},{\overline{z}}_{jt}\right);{\omega }_{t},{v}_{t}\right\rangle \cong \left\langle \left({1}_{t},{1}_{t},{1}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle , \quad t=1,2,\ldots, m; \\ \left\langle \left({\underline{z}}_{jt},{z}_{jt},{\overline{z}}_{jt}\right);{\omega }_{t},{v}_{t}\right\rangle \tilde{\ge }\left\langle \left({0}_{t},{0}_{t},{0}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle , \qquad \quad j=1,2,\ldots ,s,\quad t=1,2,\ldots, m,\end{array}\end{array}\right.\end{array}$$

(23)

$$\mathrm{where} \left\langle \left({\underline{p}}_{ijt},{p}_{ijt},{\overline{p}}_{ijt}\right);{\omega }_{t},{v}_{t}\right\rangle =\left\{\begin{array}{l}\left\langle \left({\underline{b}}_{ijt} {\underline{z}}_{jt},{b}_{ijt}{ z}_{jt},{\overline{b}}_{ijt} {\overline{z}}_{jt}\right);{\omega }_{t},{v}_{t}\right\rangle ,{\widetilde{b }}_{ij}{ \tilde{>}0, \tilde{z }}_{j}\tilde{>}0, \\ \left\langle \left({\underline{b}}_{ijt}{\overline{ z}}_{jt},{b}_{ijt}{ z}_{jt},{\overline{b}}_{ijt }{\underline{z}}_{jt}\right);{\omega }_{t},{v}_{t}\right\rangle , {\widetilde{b }}_{ij}{ \tilde{>}0, \widetilde{z }}_{j}\tilde{<}0,\\ \left\langle \left({\overline{b}}_{ijt} {\overline{z}}_{jt},{b}_{ijt}{ z}_{jt},{\underline{b}}_{ijt} {\underline{z}}_{jt}\right);{\omega }_{t},{v}_{t}\right\rangle ,{\widetilde{b }}_{ij}{ \tilde{<}0, \widetilde{z }}_{j}\tilde{<}0.\end{array}\right.$$

Using Definition 8, Eq. (23) is converted into the interval-valued bi-objective programming model as follows:

$$\begin{array}{l}\mathrm{min}\left\{{\left(\left\langle \left({\underline{v}}_{t},{v}_{t},{\overline{v}}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\alpha },{\left(\left\langle \left({\underline{v}}_{t},{v}_{t},{\overline{v}}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\beta }\right\}\\ {\text{s.t.}}\left\{\begin{array}{l}\begin{array}{l}{\left(\left\langle \left(\sum_{j=1}^{s}{\underline{p}}_{ijt},\sum_{j=1}^{s}{p}_{ijt},\sum_{j=1}^{s}{\overline{p}}_{ijt}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\alpha }\le {\left(\left\langle \left({\underline{v}}_{t},{v}_{t},{\overline{v}}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\alpha } i=1,2,\ldots ,r, \quad t=1,2,\ldots, m;\\ {\left(\left\langle \left(\sum_{j=1}^{s}{\underline{p}}_{ijt},\sum_{j=1}^{s}{p}_{ijt},\sum_{j=1}^{s}{\overline{p}}_{ijt}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\beta }\le {\left(\left\langle \left({\underline{v}}_{t},{v}_{t},{\overline{v}}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\beta } i=1,2,\ldots ,r, \quad t=1,2,\ldots, m;\end{array}\\ \begin{array}{l}\begin{array}{l}{\left(\left\langle \left(\sum_{j=1}^{s}{\underline{z}}_{jt},\sum_{j=1}^{s}{z}_{jt},\sum_{j=1}^{s}{\overline{z}}_{jt}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\alpha }= {\left(\left\langle \left({1}_{t},{1}_{t},{1}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\alpha }, \quad t=1,2,\ldots, m; \\ {\left(\left\langle \left(\sum_{j=1}^{s}{\underline{z}}_{jt},\sum_{j=1}^{s}{z}_{jt},\sum_{j=1}^{s}{\overline{z}}_{jt}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\beta }= {\left(\left\langle \left({1}_{t},{1}_{t},{1}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\beta }, \quad t=1,2,\ldots, m; \end{array} \\ \begin{array}{l}{\left(\left\langle \left({\underline{z}}_{jt},{z}_{jt},{\overline{z}}_{jt}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\alpha }\ge {\left(\left\langle \left({0}_{t},{0}_{t},{0}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\alpha },\quad j=1,2,\ldots ,s,\quad t=1,2,\ldots, m; \\ {\left(\left\langle \left({\underline{z}}_{jt},{z}_{jt},{\overline{z}}_{jt}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\beta }\ge {\left(\left\langle \left({0}_{t},{0}_{t},{0}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\beta },\quad j=1,2,\ldots ,s,\quad t=1,2,\ldots, m. \end{array}\end{array}\end{array}\right.\end{array}$$

(24)

Let ${\left(\left\langle \left({\underline{v}}_{t},{v}_{t},{\overline{v}}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\alpha }=\left[{{v}^{L}}_{t\alpha },{{v}^{U}}_{t\alpha }\right]$, ${\left(\left\langle \left({\underline{v}}_{t},{v}_{t},{\overline{v}}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\beta }=\left[{{v}^{L}}_{t\beta },{{v}^{U}}_{t\beta }\right]$, ${\left(\left\langle \left(\sum_{j=1}^{s}{\underline{p}}_{ijt},\sum_{j=1}^{s}{p}_{ijt},\sum_{j=1}^{s}{\overline{p}}_{ijt}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\alpha }=\left[{{\left({P}_{ijt}\right)}^{L}}_{\alpha },{{\left({P}_{ijt}\right)}^{U}}_{\alpha }\right]$, ${\left(\left\langle \left(\sum_{j=1}^{s}{\underline{p}}_{ijt},\sum_{j=1}^{s}{p}_{ijt},\sum_{j=1}^{s}{\overline{p}}_{ijt}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\beta }=\left[{{\left({P}_{ijt}\right)}^{L}}_{\beta },{{\left({P}_{ijt}\right)}^{U}}_{\beta }\right]$, ${\left(\left\langle \left(\sum_{j=1}^{s}{\underline{z}}_{jt},\sum_{j=1}^{s}{z}_{jt},\sum_{j=1}^{s}{\overline{z}}_{jt}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\alpha }=\left[{{\left({Z}_{jt}\right)}^{L}}_{\alpha },{{\left({Z}_{jt}\right)}^{U}}_{\alpha }\right]$, ${\left(\left\langle \left(\sum_{j=1}^{s}{\underline{z}}_{jt},\sum_{j=1}^{s}{z}_{jt},\sum_{j=1}^{s}{\overline{z}}_{jt}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\beta }=\left[{{\left({Z}_{jt}\right)}^{L}}_{\beta },{{\left({Z}_{jt}\right)}^{U}}_{\beta }\right]$, ${\left(\left\langle \left({\underline{z}}_{jt},{z}_{jt},{\overline{z}}_{jt}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\alpha }=\left[{{\left({z}_{jt}\right)}^{L}}_{\alpha },{{\left({z}_{jt}\right)}^{U}}_{\alpha }\right]$, ${\left(\left\langle \left({\underline{z}}_{jt},{z}_{jt},{\overline{z}}_{jt}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\beta }=\left[{{\left({z}_{jt}\right)}^{L}}_{\beta },{{\left({z}_{jt}\right)}^{U}}_{\beta }\right]$, ${\left(\left\langle \left({1}_{t},{1}_{t},{1}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\alpha }=\left[{{\left({1}_{t}\right)}^{L}}_{\alpha },{{\left({1}_{t}\right)}^{U}}_{\alpha }\right]$, ${\left(\left\langle \left({1}_{t},{1}_{t},{1}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\beta }=\left[{{\left({1}_{t}\right)}^{L}}_{\beta },{{\left({1}_{t}\right)}^{U}}_{\beta }\right]$, ${\left(\left\langle \left({0}_{t},{0}_{t},{0}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\alpha }=\left[{{\left({0}_{t}\right)}^{L}}_{\alpha },{{\left({0}_{t}\right)}^{U}}_{\alpha }\right]$ and ${\left(\left\langle \left({0}_{t},{0}_{t},{0}_{t}\right);{\omega }_{t},{v}_{t}\right\rangle \right)}_{\beta }=\left[{{\left({0}_{t}\right)}^{L}}_{\beta },{{\left({0}_{t}\right)}^{U}}_{\beta }\right]$.

According to Definition 1, Eq. (24) can be rewritten as follows:

$$\begin{array}{l}\mathrm{min}\left\{\left[{{v}^{\mathrm{L}}}_{t\alpha },{{v}^{\mathrm{U}}}_{t\alpha }\right],\left[{{v}^{\mathrm{L}}}_{t\beta },{{v}^{\mathrm{U}}}_{t\beta }\right]\right\}\\ {\text{s.t.}}\left\{\begin{array}{l}\begin{array}{l}{{\left({P}_{ijt}\right)}^{\mathrm{L}}}_{\alpha }\le {{v}^{\mathrm{L}}}_{t\alpha }, {{\left({P}_{ijt}\right)}^{\mathrm{U}}}_{\alpha }\le {{v}^{\mathrm{U}}}_{t\alpha }, \quad i=1,2,\ldots ,r, \quad t=1,2,\ldots, m;\\ {{\left({P}_{ijt}\right)}^{\mathrm{L}}}_{\beta }\le {{v}^{\mathrm{L}}}_{t\beta }, {{\left({P}_{ijt}\right)}^{\mathrm{U}}}_{\beta }\le {{v}^{\mathrm{U}}}_{t\beta }, \quad i=1,2,\ldots ,r, \quad t=1,2,\ldots, m;\end{array}\\ \begin{array}{l}\begin{array}{l}{{\left({Z}_{jt}\right)}^{\mathrm{L}}}_{\alpha }={{\left({1}_{t}\right)}^{\mathrm{L}}}_{\alpha }, {{\left({Z}_{jt}\right)}^{\mathrm{U}}}_{\alpha }={{\left({1}_{t}\right)}^{\mathrm{U}}}_{\alpha }, \quad t=1,2,\ldots, m; \\ {{\left({Z}_{jt}\right)}^{\mathrm{L}}}_{\beta }={{\left({1}_{t}\right)}^{\mathrm{L}}}_{\beta }, {{\left({Z}_{jt}\right)}^{\mathrm{U}}}_{\beta }={{\left({1}_{t}\right)}^{\mathrm{U}}}_{\beta }, \quad t=1,2,\ldots, m; \end{array} \\ \begin{array}{l}{{\left({z}_{jt}\right)}^{\mathrm{L}}}_{\alpha }\ge {{\left({0}_{t}\right)}^{\mathrm{L}}}_{\alpha },{{\left({z}_{jt}\right)}^{\mathrm{U}}}_{\alpha }\ge {{\left({0}_{t}\right)}^{\mathrm{U}}}_{\alpha },\quad j=1,2,\ldots ,s,\quad t=1,2,\ldots, m; \\ {{\left({z}_{jt}\right)}^{\mathrm{L}}}_{\beta }\ge {{\left({0}_{t}\right)}^{\mathrm{L}}}_{\beta },{{\left({z}_{jt}\right)}^{\mathrm{U}}}_{\beta }\ge {{\left({0}_{t}\right)}^{\mathrm{U}}}_{\beta },\quad j=1,2,\ldots ,s,\quad t=1,2,\ldots, m. \end{array}\end{array}\end{array}\right.\end{array}$$

(25)

According to Definition 2, Eq. (25) can be converted into the bi-objective programming problem as follows:

$$\begin{array}{l}\mathrm{min}\left\{\frac{\sum_{t=1}^{m}\left({{v}^{\mathrm{L}}}_{t\alpha }+{{v}^{\mathrm{L}}}_{t\beta }\right)}{2m},\frac{\sum_{t=1}^{m}\left({{v}^{\mathrm{L}}}_{t\alpha }+{{v}^{\mathrm{L}}}_{t\beta }+{{v}^{\mathrm{U}}}_{t\alpha }+{{v}^{\mathrm{U}}}_{t\beta }\right)}{4m}\right\}\\ {\text{s.t.}}\left\{\begin{array}{l}\begin{array}{l}{{\left({P}_{ijt}\right)}^{\mathrm{L}}}_{\alpha }\le {{v}^{\mathrm{L}}}_{t\alpha }, {{\left({P}_{ijt}\right)}^{\mathrm{s}}}_{\alpha }\le {{v}^{\mathrm{U}}}_{t\alpha }, \quad i=1,2,\ldots ,r, \quad t=1,2,\ldots, m;\\ {{\left({P}_{ijt}\right)}^{\mathrm{L}}}_{\beta }\le {{v}^{\mathrm{L}}}_{t\beta }, {{\left({P}_{ijt}\right)}^{\mathrm{U}}}_{\beta }\le {{v}^{\mathrm{U}}}_{t\beta }, \quad i=1,2,\ldots ,r, \quad t=1,2,\ldots, m;\end{array}\\ \begin{array}{l}\begin{array}{l}{{\left({Z}_{jt}\right)}^{\mathrm{L}}}_{\alpha }={{\left({1}_{t}\right)}^{\mathrm{L}}}_{\alpha }, {{\left({Z}_{jt}\right)}^{\mathrm{U}}}_{\alpha }={{\left({1}_{t}\right)}^{\mathrm{U}}}_{\alpha }, \quad t=1,2,\ldots, m; \\ {{\left({Z}_{jt}\right)}^{\mathrm{L}}}_{\beta }={{\left({1}_{t}\right)}^{\mathrm{L}}}_{\beta }, {{\left({Z}_{jt}\right)}^{\mathrm{U}}}_{\beta }={{\left({1}_{t}\right)}^{\mathrm{U}}}_{\beta }, \quad t=1,2,\ldots, m; \end{array} \\ \begin{array}{l}{{\left({z}_{jt}\right)}^{\mathrm{L}}}_{\alpha }\ge {{\left({0}_{t}\right)}^{\mathrm{L}}}_{\alpha },{{\left({z}_{jt}\right)}^{\mathrm{U}}}_{\alpha }\ge {{\left({0}_{t}\right)}^{\mathrm{U}}}_{\alpha },\quad j=1,2,\ldots ,s,\quad t=1,2,\ldots, m; \\ {{\left({z}_{jt}\right)}^{\mathrm{L}}}_{\beta }\ge {{\left({0}_{t}\right)}^{\mathrm{L}}}_{\beta },{{\left({z}_{jt}\right)}^{\mathrm{U}}}_{\beta }\ge {{\left({0}_{t}\right)}^{\mathrm{U}}}_{\beta },\quad j=1,2,\ldots ,s,\quad t=1,2,\ldots, m, \end{array}\end{array}\end{array}\right.\end{array}$$

(26)

which is easily formulated as follows:

$$\begin{array}{l}\mathrm{min}\left\{\lambda \left(\frac{\sum_{t=1}^{m}\left({{v}^{L}}_{t\alpha }+{{v}^{L}}_{t\beta }\right)}{2m}\right)+(1-\lambda )\left(\frac{\sum_{t=1}^{m}\left({{v}^{L}}_{t\alpha }+{{v}^{L}}_{t\beta }+{{v}^{U}}_{t\alpha }+{{v}^{U}}_{t\beta }\right)}{4m}\right)\right\}\\ {\text{s.t.}}\left\{\begin{array}{l}\begin{array}{l}{{\left({P}_{ijt}\right)}^{\mathrm{L}}}_{\alpha }\le {{v}^{\mathrm{L}}}_{t\alpha }, {{\left({P}_{ijt}\right)}^{\mathrm{U}}}_{\alpha }\le {{v}^{\mathrm{U}}}_{t\alpha }, \quad i=1,2,\ldots ,r, \quad t=1,2,\ldots, m;\\ {{\left({P}_{ijt}\right)}^{\mathrm{L}}}_{\beta }\le {{v}^{\mathrm{L}}}_{t\beta }, {{\left({P}_{ijt}\right)}^{\mathrm{U}}}_{\beta }\le {{v}^{\mathrm{U}}}_{t\beta }, \quad i=1,2,\ldots ,r, \quad t=1,2,\ldots, m;\end{array}\\ \begin{array}{l}\begin{array}{l}{{\left({Z}_{jt}\right)}^{L}}_{\alpha }={{\left({1}_{t}\right)}^{\mathrm{L}}}_{\alpha }, {{\left({Z}_{jt}\right)}^{U}}_{\alpha }={{\left({1}_{t}\right)}^{\mathrm{U}}}_{\alpha }, \quad t=1,2,\ldots, m; \\ {{\left({Z}_{jt}\right)}^{\mathrm{L}}}_{\beta }={{\left({1}_{t}\right)}^{\mathrm{L}}}_{\beta }, {{\left({Z}_{jt}\right)}^{\mathrm{U}}}_{\beta }={{\left({1}_{t}\right)}^{\mathrm{U}}}_{\beta }, \quad t=1,2,\ldots, m; \end{array} \\ \begin{array}{l}{{\left({z}_{jt}\right)}^{L}}_{\alpha }\ge {{\left({0}_{t}\right)}^{\mathrm{L}}}_{\alpha },{{\left({z}_{jt}\right)}^{\mathrm{U}}}_{\alpha }\ge {{\left({0}_{t}\right)}^{\mathrm{U}}}_{\alpha },\quad j=1,2,\ldots ,s,\quad t=1,2,\ldots, m; \\ {{\left({z}_{jt}\right)}^{\mathrm{L}}}_{\beta }\ge {{\left({0}_{t}\right)}^{\mathrm{L}}}_{\beta },{{\left({z}_{jt}\right)}^{\mathrm{U}}}_{\beta }\ge {{\left({0}_{t}\right)}^{\mathrm{U}}}_{\beta },\quad j=1,2,\ldots ,s,\quad t=1,2,\ldots, m \end{array}\end{array}\end{array}\right.\end{array}$$

(27)

where $\lambda \in \left[\mathrm{0,1}\right]$ is the weight determined by the two players. According to Definitions 4, 5 and 6, Eq. (27) can be constructed as follows:

$$\begin{array}{l}\mathrm{min}\left\{\begin{array}{l}\lambda \left(\frac{\sum_{t=1}^{m}\left(\frac{\left({\omega }_{t}-\alpha \right) {\underline{v}}_{t}+\alpha {v}_{t}}{{\omega }_{t}}+\frac{\left(1-\beta \right) {v}_{t}+\left(\beta -{v}_{t}\right) {\underline{v}}_{t}}{1-{v}_{t}}\right)}{2m}\right)+\\ (1-\lambda )\left(\frac{\sum_{t=1}^{m}\left(\frac{\left({\omega }_{t}-\alpha \right) {\underline{v}}_{t}+\alpha {v}_{t}}{{\omega }_{t}}+\frac{\left(1-\beta \right) {v}_{t}+\left(\beta -{v}_{t}\right) {\underline{v}}_{t}}{1-{v}_{t}}+\frac{\left({\omega }_{t}-\alpha \right){ \overline{v}}_{t}+\alpha { v}_{t}}{{\omega }_{t}}+\frac{\left(1-\beta \right) {v}_{t}+\left(\beta -{v}_{t}\right) { \overline{v}}_{t}}{1-{v}_{t}}\right)}{4m}\right)\end{array}\right\}\\ s.t.\left\{\begin{array}{l}\begin{array}{l}\begin{array}{l}\frac{\left({\omega }_{t}-\alpha \right)\sum_{j=1}^{s}{\underline{p}}_{ijt}+\alpha \sum_{j=1}^{s}{p}_{ijt}}{{\omega }_{t}}\le \frac{\left({\omega }_{t}-\alpha \right) {\underline{v}}_{t}+\alpha {v}_{t}}{{\omega }_{t}}, \quad i=1,2,\ldots ,r, \quad t=1,2,\ldots, m;\\ \frac{\left({\omega }_{t}-\alpha \right)\sum_{j=1}^{s}{\overline{p}}_{ijt}+\alpha \sum_{j=1}^{s}{p}_{ijt}}{{\omega }_{t}}\le \frac{\left({\omega }_{t}-\alpha \right){ \overline{v}}_{t}+\alpha { v}_{t}}{{\omega }_{t}}, \quad i=1,2,\ldots ,r, \quad t=1,2,\ldots, m;\end{array}\\ \begin{array}{l}\frac{\left(1-\beta \right)\sum_{j=1}^{s}{p}_{ijt}+\left(\beta -{v}_{t}\right)\sum_{j=1}^{s}{\underline{p}}_{ijt}}{1-{v}_{t}}\le \frac{\left(1-\beta \right) {v}_{t}+\left(\beta -{v}_{t}\right) {\underline{v}}_{t}}{1-{v}_{t}}, \quad i=1,2,\ldots ,r, \quad t=1,2,\ldots, m;\\ \frac{\left(1-\beta \right)\sum_{j=1}^{s}{p}_{ijt}+\left(\beta -{v}_{t}\right)\sum_{j=1}^{s}{\overline{p}}_{ijt}}{1-{v}_{t}}\le \frac{\left(1-\beta \right) {v}_{t}+\left(\beta -{v}_{t}\right) { \overline{v}}_{t}}{1-{v}_{t}}, \quad i=1,2,\ldots ,r, \quad t=1,2,\ldots, m;\end{array}\end{array}\\ \begin{array}{l}\begin{array}{l}\begin{array}{l}\begin{array}{l}\frac{\left({\omega }_{t}-\alpha \right)\sum_{j=1}^{s}{ \underline{z}}_{jt}+\alpha \sum_{j=1}^{s} {z}_{jt}}{{\omega }_{t}}=\frac{\left({\omega }_{t}-\alpha \right)+\alpha }{{\omega }_{t}}, \quad t=1,2,\ldots, m;\\ \frac{\left({\omega }_{t}-\alpha \right)\sum_{j=1}^{s}{\overline{z}}_{jt}+\alpha \sum_{j=1}^{s} {z}_{jt}}{{\omega }_{t}}=\frac{\left({\omega }_{t}-\alpha \right)+\alpha }{{\omega }_{t}}, \quad t=1,2,\ldots, m;\end{array} \\ \frac{\left(1-\beta \right)\sum_{j=1}^{s} {z}_{jt}+\left(\beta -{v}_{t}\right)\sum_{j=1}^{s}{ \underline{z}}_{jt}}{1-{v}_{t}}=\frac{\left(1-\beta \right)+\left(\beta -{v}_{t}\right)}{1-{v}_{t}}, \quad t=1,2,\ldots, m; \end{array}\\ \frac{\left(1-\beta \right)\sum_{j=1}^{s} {z}_{jt}+\left(\beta -{v}_{t}\right)\sum_{j=1}^{s}{\overline{z}}_{jt}}{1-{v}_{t}}=\frac{\left(1-\beta \right)+\left(\beta -{v}_{t}\right)}{1-{v}_{t}}, \quad t=1,2,\ldots, m;\end{array} \\ \begin{array}{l}\begin{array}{l}\frac{\left({\omega }_{t}-\alpha \right){ \underline{z}}_{jt}+\alpha {z}_{jt}}{{\omega }_{t}}\ge 0,\quad j=1,2,\ldots ,s,\quad t=1,2,\ldots, m;\\ \frac{\left({\omega }_{t}-\alpha \right) {\overline{z}}_{jt}+\alpha {z}_{jt}}{{\omega }_{t}}\ge 0,\quad j=1,2,\ldots ,s,\quad t=1,2,\ldots, m;\end{array} \\ \begin{array}{l}\frac{\left(1-\beta \right) {z}_{jt}+\left(\beta -{v}_{t}\right){ \underline{z}}_{jt}}{1-{v}_{t}}\ge 0,\quad j=1,2,\ldots ,s,\quad t=1,2,\ldots, m; \\ \frac{\left(1-\beta \right) {z}_{jt}+\left(\beta -{v}_{t}\right) {\overline{z}}_{jt}}{1-{v}_{t}}\ge 0,\quad j=1,2,\ldots ,s,\quad t=1,2,\ldots, m;\\ \begin{array}{l}\frac{\left({\omega }_{t}-\alpha \right) {\overline{z}}_{jt}+\alpha {z}_{jt}}{{\omega }_{t}}\ge \frac{\left({\omega }_{t}-\alpha \right){ \underline{z}}_{jt}+\alpha {z}_{jt}}{{\omega }_{t}}, \quad t=1,2,\ldots, m;\\ \frac{\left(1-\beta \right) {z}_{jt}+\left(\beta -{v}_{t}\right) {\overline{z}}_{jt}}{1-{v}_{t}}\ge \frac{\left(1-\beta \right) {z}_{jt}+\left(\beta -{v}_{t}\right){ \underline{z}}_{jt}}{1-{v}_{t}}, \quad t=1,2,\ldots, m;\\ \begin{array}{l}{{v}^{U}}_{t\alpha }\ge {{v}^{L}}_{t\alpha }, \quad t=1,2,\ldots, m;\\ {{v}^{U}}_{t\beta }\ge {{v}^{L}}_{t\beta }, \quad t=1,2,\ldots, m.\end{array}\end{array}\end{array} \end{array}\end{array}\end{array}\right.\end{array}$$

(28)

Using the Simplex technique for linear programming by taking $\alpha =0\, \text{ and } \,\beta =1$, the optimal solutions of Eq. (28) is obtained. The Eq. (28) can be used to find the lower and upper limits of player II's TDHFN optimal strategies ${\underline{z}}_{jt}^{*}={a}_{jt},{\overline{z}}_{jt}^{*}={g}_{jt}$ and the corresponding lower and upper limits of the TDHFN loss-ceiling ${\underline{v}}_{t}^{*}={k}_{t},{\overline{v}}_{t}^{*}={l}_{t}$:

$$\begin{array}{l}\mathrm{min}\left\{\begin{array}{l}\lambda \left(\frac{\sum_{t=1}^{m}\left(\frac{\left({\omega }_{t}-\alpha \right) {\underline{v}}_{t}+\alpha {v}_{t}}{{\omega }_{t}}+\frac{\left(1-\beta \right) {v}_{t}+\left(\beta -{v}_{t}\right) {\underline{v}}_{t}}{1-{v}_{t}}\right)}{2m}\right)+\\ (1-\lambda )\left(\frac{\sum_{t=1}^{m}\left(\frac{\left({\omega }_{t}-\alpha \right) {\underline{v}}_{t}+\alpha {v}_{t}}{{\omega }_{t}}+\frac{\left(1-\beta \right) {v}_{t}+\left(\beta -{v}_{t}\right) {\underline{v}}_{t}}{1-{v}_{t}}+\frac{\left({\omega }_{t}-\alpha \right){ \overline{v}}_{t}+\alpha { v}_{t}}{{\omega }_{t}}+\frac{\left(1-\beta \right) {v}_{t}+\left(\beta -{v}_{t}\right) { \overline{v}}_{t}}{1-{v}_{t}}\right)}{4m}\right)\end{array}\right\}\\ {\text{s.t.}}\left\{\begin{array}{l}\mathrm{Constraints \, of\, Eq}. \, \left(28\right); \\ \begin{array}{l} \\ \begin{array}{l}{z}_{jt}\ge {a}_{jt}, \quad j=1,2,\dots s, \quad t=1,2,\ldots, m;\\ \begin{array}{l}{z}_{jt}\le {g}_{jt}, , \quad j=1,2,\dots s, \quad t=1,2,\ldots, m;\\ {v}_{t}\ge {k}_{t}, \quad t=1,2,\ldots, m;\\ {v}_{t}\le {l}_{t}, \quad t=1,2,\ldots, m.\end{array}\end{array}\end{array}\end{array}\right.\end{array}$$

(29)

Using the Simplex technique for linear programming by taking $\alpha ={\omega }_{t}\, \text{ and } \,\beta ={v}_{t}$, the optimal solutions of Eq. (29) is obtained. The Eq. (29) can be used to find the mean of player II's TDHFN optimal strategies ${z}_{jt}^{*}$ and the corresponding mean of the TDHFN loss-ceiling ${v}_{t}^{*}$. Therefore, the TDHFN optimal solutions of Eq. (12) is $\left\{{\tilde{v }}^{*}=\left\langle \left({\underline{v}}_{t}^{*},{v}_{t}^{*},{\overline{v}}_{t}^{*}\right);{\omega }_{t},{v}_{t}\right\rangle , {{\widetilde{z }}_{j}}^{*}=\left\langle \left({\underline{z}}_{jt}^{*},{z}_{jt}^{*},{\overline{z}}_{jt}^{*}\right);{\omega }_{t},{v}_{t}\right\rangle ;j=1,2,\ldots ,s,\quad t=1,2,\ldots, m \right\}.$

6 The numerical example

This Section provides a numerical example adapted from Yang and Song (2020) to illustrate the solution procedure of a matrix game with payoffs of TDHFNs.

6.1 Application problem

“Suppose a monopoly company which plans to produce products with ${E}_{1}$ and ${E}_{2}$, where ${E}_{1}$ and ${E}_{2}$ are mutually replaceable products. In the current highly competitive business environment, it is very important for the enterprise to capture the customer effectively. There are two types of customer group, ${B}_{1}$ and ${B}_{2}$, in the market. As the demand for the product is basically fixed, an increase in the sales volume of one will inevitably lead to a decrease in the sales volume of the other. The company and the customer group can be regarded as two players, and the price selection for the company and the customer group can be viewed as a matrix strategy”. The payoff matrix of the company is expressed as follows:

$$\tilde{B }=\left(\begin{array}{ll}\left\{\left\langle \left(\mathrm{160,165,170}\right);\mathrm{0.8,0.1}\right\rangle ,\left\langle \left(\mathrm{160,170,180}\right);\mathrm{0.9,0.1}\right\rangle \right\}& \left\{\left\langle \left(\mathrm{145,148,150}\right);\mathrm{0.7,0.2}\right\rangle ,\left\langle \left(\mathrm{145,150,155}\right);\mathrm{0.8,0.1}\right\rangle \right\}\\ \left\{\left\langle \left(\mathrm{85,90,95}\right);\mathrm{0.6,0.2}\right\rangle ,\left\langle \left(\mathrm{90,95,100}\right);\mathrm{0.7,0.1}\right\rangle \right\}& \left\{\left\langle \left(\mathrm{155,160,165}\right);\mathrm{0.6,0.2}\right\rangle ,\left\langle \left(\mathrm{160,165,170}\right);\mathrm{0.7,0.1}\right\rangle \right\}\end{array}\right),$$

where $\left\langle \left(\mathrm{160,165,170}\right);\mathrm{0.8,0.1}\right\rangle$ means that the most possible price of ${E}_{1}$ is 165, the lowest possible price is 160, the highest possible price is 170, the maximum satisfaction of ${B}_{1}$ is 0.8, and the minimum dissatisfaction is 0.1. The other values can be interpreted similarly.

6.2 The solution procedure

According to Eq. (20), we can obtain the linear programming problem as follows:

$$\begin{array}{l}\mathrm{max}\left\{\begin{array}{l}\frac{1}{2}\left(\frac{\left(\frac{\left(0.6-\alpha \right){ \underline{u}}_{1}+\alpha {u}_{1}}{0.6}\right)+\left(\frac{\left(0.6-\alpha \right){ \underline{u}}_{2}+\alpha {u}_{2}}{0.6}\right)+\left(\frac{\left(1-\beta \right){ u}_{1}+(\beta -0.2){ \underline{u}}_{1}}{1-0.2}\right)+\left(\frac{\left(1-\beta \right){ u}_{2}+(\beta -0.2){ \underline{u}}_{2}}{1-0.2}\right)}{4}\right)\\ +\frac{1}{2}\left(\begin{array}{l}\frac{\left(\frac{\left(0.6-\alpha \right){ \underline{u}}_{1}+\alpha {u}_{1}}{0.6}\right)+\left(\frac{\left(0.6-\alpha \right){ \underline{u}}_{2}+\alpha {u}_{2}}{0.6}\right)+\left(\frac{\left(1-\beta \right){ u}_{1}+\left(\beta -0.2\right){ \underline{u}}_{1}}{1-0.2}\right)+\left(\frac{\left(1-\beta \right){ u}_{2}+\left(\beta -0.2\right){ \underline{u}}_{2}}{1-0.2}\right)}{8}\\ +\frac{\left(\frac{\left(0.6-\alpha \right){ \overline{u}}_{1}+\alpha {u}_{1}}{0.6}\right)+\left(\frac{\left(0.6-\alpha \right){ \overline{u}}_{2}+\alpha {u}_{2}}{0.6}\right)+\left(\frac{\left(1-\beta \right){ u}_{1}+(\beta -0.2){ \overline{u}}_{1}}{1-0.2}\right)+\left(\frac{\left(1-\beta \right){ u}_{2}+(\beta -0.2){ \overline{u}}_{2}}{1-0.2}\right)}{8}\end{array}\right)\end{array}\right\}\\ {\text{s.t.}}\left\{\begin{array}{l}\begin{array}{l}\begin{array}{l}\frac{\left(0.6-\alpha \right)\left(160 {\underline{y}}_{11}+85 {\underline{y}}_{21}\right)+\alpha \left(165 {y}_{11}+90 {y}_{21}\right)}{0.6}\ge \frac{\left(0.6-\alpha \right) {\underline{u}}_{1}+\alpha {u}_{1}}{0.6}, \frac{\left(0.6-\alpha \right)\left(160 {\underline{y}}_{12}+90 {\underline{y}}_{22}\right)+\alpha \left(170 {y}_{12}+95 {y}_{22}\right)}{0.6}\ge \frac{\left(0.6-\alpha \right) {\underline{u}}_{2}+\alpha {u}_{2}}{0.6}, \\ \frac{\left(0.6-\alpha \right)\left(170{ \overline{y}}_{11}+95 { \overline{y}}_{21}\right)+\alpha \left(165 {y}_{11}+90 {y}_{21}\right)}{0.6}\ge \frac{\left(0.6-\alpha \right) {\overline{u}}_{1}+\alpha {u}_{1}}{0.6}, \frac{\left(0.6-\alpha \right)\left(180{ \overline{y}}_{12}+100 { \overline{y}}_{22}\right)+\alpha \left(170 {y}_{12}+95 {y}_{22}\right)}{0.6}\ge \frac{\left(0.6-\alpha \right) {\overline{u}}_{2}+\alpha {u}_{2}}{0.6},\end{array}\\ \begin{array}{l}\frac{\left(\beta -0.2\right)\left(160 {\underline{y}}_{11}+85 {\underline{y}}_{21}\right)+(1-\beta ) \left(165 {y}_{11}+90 {y}_{21}\right)}{1-0.2}\ge \frac{\left(\beta -0.2\right) {\underline{u}}_{1}+(1-\beta ) {u}_{1}}{1-0.2}, \frac{\left(\beta -0.2\right)\left(160 {\underline{y}}_{12}+90 {\underline{y}}_{22}\right)+(1-\beta ) \left(170 {y}_{12}+95 {y}_{22}\right)}{1-0.2}\ge \frac{\left(\beta -0.2\right) {\underline{u}}_{2}+(1-\beta ) {u}_{2}}{1-0.2}, \\ \frac{\left(\beta -0.2\right)\left(170{ \overline{y}}_{11}+95 { \overline{y}}_{21}\right)+(1-\beta ) \left(165 {y}_{11}+90 {y}_{21}\right)}{1-0.2}\ge \frac{\left(\beta -0.2\right) {\overline{u}}_{1}+(1-\beta ) {u}_{1}}{1-0.2}, \frac{\left(\beta -0.2\right)\left(180{ \overline{y}}_{12}+100 { \overline{y}}_{22}\right)+(1-\beta ) \left(170 {y}_{12}+95 {y}_{22}\right)}{1-0.2}\ge \frac{\left(\beta -0.2\right) {\overline{u}}_{2}+(1-\beta ) {u}_{2}}{1-0.2},\end{array}\end{array}\\ \begin{array}{l}\begin{array}{l}\begin{array}{l}\frac{\left(0.6-\alpha \right)\left(145 {\underline{y}}_{11}+155 {\underline{y}}_{21}\right)+\alpha \left(148 {y}_{11}+160 {y}_{21}\right)}{0.6}\ge \frac{\left(0.6-\alpha \right) {\underline{u}}_{1}+\alpha {u}_{1}}{0.6}, \frac{\left(0.6-\alpha \right)\left(145 {\underline{y}}_{12}+160 {\underline{y}}_{22}\right)+\alpha \left(150 {y}_{12}+165 {y}_{22}\right)}{0.6}\ge \frac{\left(0.6-\alpha \right) {\underline{u}}_{2}+\alpha {u}_{2}}{0.6}, \\ \frac{\left(0.6-\alpha \right)\left(150{ \overline{y}}_{11}+165 { \overline{y}}_{21}\right)+\alpha \left(148 {y}_{11}+160 {y}_{21}\right)}{0.6}\ge \frac{\left(0.6-\alpha \right) {\overline{u}}_{1}+\alpha {u}_{1}}{0.6}, \frac{\left(0.6-\alpha \right)\left(155{ \overline{y}}_{12}+170 { \overline{y}}_{22}\right)+\alpha \left(150 {y}_{12}+165 {y}_{22}\right)}{0.6}\ge \frac{\left(0.6-\alpha \right) {\overline{u}}_{2}+\alpha {u}_{2}}{0.6},\end{array}\\ \begin{array}{l}\frac{\left(\beta -0.2\right)\left(145 {\underline{y}}_{11}+155 {\underline{y}}_{21}\right)+(1-\beta ) \left(148 {y}_{11}+160 {y}_{21}\right)}{1-0.2}\ge \frac{\left(\beta -0.2\right) {\underline{u}}_{1}+(1-\beta ) {u}_{1}}{1-0.2}, \frac{\left(\beta -0.2\right)\left(145 {\underline{y}}_{12}+160 {\underline{y}}_{22}\right)+(1-\beta ) \left(150 {y}_{12}+165 {y}_{22}\right)}{1-0.2}\ge \frac{\left(\beta -0.2\right) {\underline{u}}_{2}+(1-\beta ) {u}_{2}}{1-0.2}, \\ \frac{\left(\beta -0.2\right)\left(150{ \overline{y}}_{11}+165 { \overline{y}}_{21}\right)+(1-\beta ) \left(148 {y}_{11}+160 {y}_{21}\right)}{1-0.2}\ge \frac{\left(\beta -0.2\right) {\overline{u}}_{1}+(1-\beta ) {u}_{1}}{1-0.2}, \frac{\left(\beta -0.2\right)\left(155{ \overline{y}}_{12}+170 { \overline{y}}_{22}\right)+(1-\beta ) \left(150 {y}_{12}+165 {y}_{22}\right)}{1-0.2}\ge \frac{\left(\beta -0.2\right) {\overline{u}}_{2}+(1-\beta ) {u}_{2}}{1-0.2},\end{array}\end{array} \\ \begin{array}{l}\begin{array}{l}\begin{array}{l}\frac{\left(0.6-\alpha \right)\left( {\underline{y}}_{11}+ {\underline{y}}_{21}\right)+\alpha \left( {y}_{11}+ {y}_{21}\right)}{0.6}=\frac{\left(0.6-\alpha \right)+\alpha }{0.6}, \frac{\left(0.6-\alpha \right)\left( {\underline{y}}_{12}+ {\underline{y}}_{22}\right)+\alpha \left( {y}_{12}+ {y}_{22}\right)}{0.6}=\frac{\left(0.6-\alpha \right) +\alpha }{0.6}, \\ \frac{\left(0.6-\alpha \right)\left({ \overline{y}}_{11}+ { \overline{y}}_{21}\right)+\alpha \left( {y}_{11}+ {y}_{21}\right)}{0.6}=\frac{\left(0.6-\alpha \right) +\alpha }{0.6}, \frac{\left(0.6-\alpha \right)\left({ \overline{y}}_{12}+ { \overline{y}}_{22}\right)+\alpha \left( {y}_{12}+ {y}_{22}\right)}{0.6}=\frac{\left(0.6-\alpha \right)+\alpha }{0.6},\end{array}\\ \begin{array}{l}\frac{\left(\beta -0.2\right)\left( {\underline{y}}_{11}+ {\underline{y}}_{21}\right)+(1-\beta ) \left( {y}_{11}+ {y}_{21}\right)}{1-0.2}=\frac{\left(\beta -0.2\right)+(1-\beta )}{1-0.2}, \frac{\left(\beta -0.2\right)\left( {\underline{y}}_{12}+ {\underline{y}}_{22}\right)+(1-\beta ) \left( {y}_{12}+ {y}_{22}\right)}{1-0.2}=\frac{\left(\beta -0.2\right)+(1-\beta )}{1-0.2}, \\ \frac{\left(\beta -0.2\right)\left({ \overline{y}}_{11}+ { \overline{y}}_{21}\right)+(1-\beta ) \left( {y}_{11}+ {y}_{21}\right)}{1-0.2}=\frac{\left(\beta -0.2\right)+(1-\beta )}{1-0.2}, \frac{\left(\beta -0.2\right)\left({ \overline{y}}_{12}+ { \overline{y}}_{22}\right)+(1-\beta ) \left( {y}_{12}+ {y}_{22}\right)}{1-0.2}=\frac{\left(\beta -0.2\right)+(1-\beta )}{1-0.2},\end{array}\end{array}\\ \begin{array}{l}\begin{array}{l}\begin{array}{l}\begin{array}{l}\begin{array}{l}\frac{\left(0.6-\alpha \right) {\underline{y}}_{11}+\alpha {y}_{11}}{0.6}\ge 0, \frac{\left(0.6-\alpha \right) {\underline{y}}_{12}+\alpha {y}_{12}}{0.6}\ge 0, \frac{\left(0.6-\alpha \right) { \overline{y}}_{11}+\alpha {y}_{11}}{0.6}\ge 0, \frac{\left(0.6-\alpha \right) { \overline{y}}_{12}+\alpha {y}_{12}}{0.6}\ge 0,\\ \frac{\left(\beta -0.2\right) {\underline{y}}_{11}+(1-\beta ) {y}_{11}}{1-0.2}\ge 0, \frac{\left(\beta -0.2\right) {\underline{y}}_{12}+(1-\beta ) {y}_{12}}{1-0.2}\ge 0, \frac{\left(\beta -0.2\right) { \overline{y}}_{11}+(1-\beta ) {y}_{11}}{1-0.2}\ge 0, \frac{\left(\beta -0.2\right) { \overline{y}}_{12}+(1-\beta ) {y}_{12}}{1-0.2}\ge 0,\\ \frac{\left(0.6-\alpha \right) {\underline{y}}_{21}+\alpha {y}_{21}}{0.6}\ge 0, \frac{\left(0.6-\alpha \right) {\underline{y}}_{22}+\alpha {y}_{22}}{0.6}\ge 0, \frac{\left(0.6-\alpha \right) { \overline{y}}_{21}+\alpha {y}_{21}}{0.6}\ge 0, \frac{\left(0.6-\alpha \right) { \overline{y}}_{22}+\alpha {y}_{22}}{0.6}\ge 0,\end{array}\\ \frac{\left(\beta -0.2\right) {\underline{y}}_{21}+ {(1-\beta ) y}_{21}}{1-0.2}\ge 0, \frac{\left(\beta -0.2\right) {\underline{y}}_{22}+(1-\beta ) {y}_{22}}{1-0.2}\ge 0, \frac{\left(\beta -0.2\right) { \overline{y}}_{21}+{(1-\beta ) y}_{21}}{1-0.2}\ge 0, \frac{\left(\beta -0.2\right) { \overline{y}}_{22}+(1-\beta ) {y}_{22}}{1-0.2}\ge 0,\end{array}\\ \frac{\left(0.6-\alpha \right) { \overline{u}}_{1}+\alpha {u}_{1}}{0.6}\ge \frac{\left(0.6-\alpha \right) {\underline{u}}_{1}+\alpha {u}_{1}}{0.6}, \frac{\left(0.6-\alpha \right) { \overline{u}}_{2}+\alpha {u}_{2}}{0.6}\ge \frac{\left(0.6-\alpha \right) {\underline{u}}_{2}+\alpha {u}_{2}}{0.6} ,\\ \frac{\left(\beta -0.2\right) { \overline{u}}_{1}+ {\left(1-\beta \right) u}_{1}}{0.6}\ge \frac{\left(\beta -0.2\right) {\underline{u}}_{1}+(1-\beta ) {u}_{1}}{0.6}, \frac{\left(\beta -0.2\right) { \overline{u}}_{2}+(1-\beta ) {u}_{2}}{0.6}\ge \frac{\left(\beta -0.2\right) {\underline{u}}_{2}+(1-\beta ) {u}_{2}}{0.6} ,\end{array}\\ \frac{\left(0.6-\alpha \right) { \overline{y}}_{11}+\alpha {y}_{11}}{0.6}\ge \frac{\left(0.6-\alpha \right) {\underline{y}}_{11}+\alpha {y}_{11}}{0.6}, \frac{\left(0.6-\alpha \right) { \overline{y}}_{12}+\alpha {y}_{12}}{0.6}\ge \frac{\left(0.6-\alpha \right) {\underline{y}}_{12}+\alpha {y}_{12}}{0.6},\\ \frac{\left(\beta -0.2\right) { \overline{y}}_{11}+(1-\beta ) {y}_{11}}{0.6}\ge \frac{\left(\beta -0.2\right) {\underline{y}}_{11}+(1-\beta ) {y}_{11}}{0.6}, \frac{\left(\beta -0.2\right) { \overline{y}}_{12}+(1-\beta ) {y}_{12}}{0.6}\ge \frac{\left(\beta -0.2\right) {\underline{y}}_{12}+(1-\beta ) {y}_{12}}{0.6},\end{array}\end{array}\\ \begin{array}{l}\frac{\left(0.6-\alpha \right) { \overline{y}}_{21}+\alpha {y}_{21}}{0.6}\ge \frac{\left(0.6-\alpha \right) {\underline{y}}_{21}+\alpha {y}_{21}}{0.6}, \frac{\left(0.6-\alpha \right) { \overline{y}}_{22}+\alpha {y}_{22}}{0.6}\ge \frac{\left(0.6-\alpha \right) {\underline{y}}_{22}+\alpha {y}_{22}}{0.6},\\ \begin{array}{l}\frac{\left(\beta -0.2\right) { \overline{y}}_{21}+ {(1-\beta )y}_{21}}{0.6}\ge \frac{\left(\beta -0.2\right) {\underline{y}}_{21}+\left(1-\beta \right){y}_{21}}{0.6}, \frac{\left(\beta -0.2\right) { \overline{y}}_{22}+\left(1-\beta \right){y}_{22}}{0.6}\ge \frac{\left(\beta -0.2\right) {\underline{y}}_{22}+\left(1-\beta \right) {y}_{22}}{0.6}.\end{array}\end{array}\end{array}\end{array}\end{array}\right.\end{array}$$

(30)

Solving Eq. (30) using the Simplex technique by taking $\alpha =0\, \text{ and } \,\beta =1$, the optimal solutions can be obtained as ${\underline{u}}_{1}=146.7647,{\overline{u}}_{1}=152.6471,{\underline{u}}_{2}=147.6471,{\overline{u}}_{2}=157.6471,$ ${\underline{y}}_{11}=0.8235294,{\overline{y}}_{11}=0.8235294,{\underline{y}}_{12}=0.8235294,{\overline{y}}_{12}=0.8235294,{\underline{y}}_{21}=0.1764706$, ${\overline{y}}_{21}=0.1764706,{\underline{y}}_{22}=0.1764706 \; {\text{and}} \; {\overline{y}}_{22}=0.1764706.$

According to Eq. (21), we can obtain the linear programming problem as follows:

$$\begin{array}{l}\mathrm{max}\left\{\begin{array}{l}\frac{1}{2}\left(\frac{\left(\frac{\left(0.6-\alpha \right){ \underline{u}}_{1}+\alpha {u}_{1}}{0.6}\right)+\left(\frac{\left(0.6-\alpha \right){ \underline{u}}_{2}+\alpha {u}_{2}}{0.6}\right)+\left(\frac{\left(1-\beta \right){ u}_{1}+(\beta -0.2){ \underline{u}}_{1}}{1-0.2}\right)+\left(\frac{\left(1-\beta \right){ u}_{2}+(\beta -0.2){ \underline{u}}_{2}}{1-0.2}\right)}{4}\right)\\ +\frac{1}{2}\left(\begin{array}{l}\frac{\left(\frac{\left(0.6-\alpha \right){ \underline{u}}_{1}+\alpha {u}_{1}}{0.6}\right)+\left(\frac{\left(0.6-\alpha \right){ \underline{u}}_{2}+\alpha {u}_{2}}{0.6}\right)+\left(\frac{\left(1-\beta \right){ u}_{1}+\left(\beta -0.2\right){ \underline{u}}_{1}}{1-0.2}\right)+\left(\frac{\left(1-\beta \right){ u}_{2}+\left(\beta -0.2\right){ \underline{u}}_{2}}{1-0.2}\right)}{8}\\ +\frac{\left(\frac{\left(0.6-\alpha \right){ \overline{u}}_{1}+\alpha {u}_{1}}{0.6}\right)+\left(\frac{\left(0.6-\alpha \right){ \overline{u}}_{2}+\alpha {u}_{2}}{0.6}\right)+\left(\frac{\left(1-\beta \right){ u}_{1}+(\beta -0.2){ \overline{u}}_{1}}{1-0.2}\right)+\left(\frac{\left(1-\beta \right){ u}_{2}+(\beta -0.2){ \overline{u}}_{2}}{1-0.2}\right)}{8}\end{array}\right)\end{array}\right\}\\ {\text{s.t.}}\left\{\begin{array}{l}\mathrm{Constraints \, of \,Eq}.\, \left(30\right), \\ \begin{array}{l} \\ \begin{array}{l}\begin{array}{l}\begin{array}{l}\begin{array}{l}{y}_{11}\ge 0.8235294,\\ {y}_{11}\le 0.8235294,\end{array}\\ {y}_{12}\ge 0.8235294,\\ {y}_{12}\le 0.8235294,\end{array}\\ \begin{array}{l}\begin{array}{l}\begin{array}{l}{y}_{21}\ge 0.1764706,\\ {y}_{21}\le 0.1764706,\end{array}\\ {y}_{22}\ge 0.1764706,\\ {y}_{22}\le 0.1764706,\end{array}\\ {u}_{1}\ge 146.7647,\\ {u}_{1}\le 152.6471,\end{array}\\ \begin{array}{l}{u}_{2}\ge 147.6471,\\ {u}_{2}\le 157.6471.\end{array}\end{array} \end{array}\end{array}\end{array}\right.\end{array}$$

(31)

Solving Eq. (31) using the Simplex technique by taking $\alpha =0.6\, \text{ and } \,\beta =0.2$, the optimal solutions can be obtained as ${u}_{1}=150.1176,{u}_{2}=152.6471, {y}_{11}=0.8235294$, ${y}_{12}=0.8235294,{y}_{21}=0.1764706 \mathrm{and}{ y}_{22}= 0.1764706.$ Therefore, the dual hesitant fuzzy maximin strategy and dual hesitant fuzzy gain-floor for player I are ${\tilde{y }}_{1}^{*}=\left\{\left\langle \left(0.8235294,0.8235294,0.8235294\right);\mathrm{0.6,0.2}\right\rangle ,\left\langle \left(0.8235294,0.8235294,0.8235294\right);\mathrm{0.6,0.2}\right\rangle \right\}$, ${\tilde{y }}_{2}^{*}=\left\{\left\langle \left(0.1764706,0.1764706,0.1764706\right);\mathrm{0.6,0.2}\right\rangle ,\left\langle \left(0.1764706,0.1764706,0.17647064\right);\mathrm{0.6,0.2}\right\rangle \right\}$ and ${\tilde{u }}^{*}=\left\{\left\langle \left(146.7647,150.1176,152.6471\right);\mathrm{0.6,0.2}\right\rangle ,\left\langle \left(147.6471,152.6471,157.6471\right);\mathrm{0.6,0.2}\right\rangle \right\}$, respectively.

According to Eq. (28), we can obtain the linear programming problem as follows:

$$\begin{array}{l}\mathrm{min}\left\{\begin{array}{l}\frac{1}{2}\left(\frac{\left(\frac{\left(0.6-\alpha \right){ \underline{v}}_{1}+\alpha {v}_{1}}{0.6}\right)+\left(\frac{\left(0.6-\alpha \right){ \underline{v}}_{2}+\alpha {v}_{2}}{0.6}\right)+\left(\frac{\left(1-\beta \right){ v}_{1}+(\beta -0.2){ \underline{v}}_{1}}{1-0.2}\right)+\left(\frac{\left(1-\beta \right){ v}_{2}+(\beta -0.2){ \underline{v}}_{2}}{1-0.2}\right)}{4}\right)\\ +\frac{1}{2}\left(\begin{array}{l}\frac{\left(\frac{\left(0.6-\alpha \right){ \underline{v}}_{1}+\alpha {v}_{1}}{0.6}\right)+\left(\frac{\left(0.6-\alpha \right){ \underline{v}}_{2}+\alpha {v}_{2}}{0.6}\right)+\left(\frac{\left(1-\beta \right){ v}_{1}+(\beta -0.2){ \underline{v}}_{1}}{1-0.2}\right)+\left(\frac{\left(1-\beta \right){ v}_{2}+(\beta -0.2){ \underline{v}}_{2}}{1-0.2}\right)}{8}\\ +\frac{\left(\frac{\left(0.6-\alpha \right){ \overline{v}}_{1}+\alpha {v}_{1}}{0.6}\right)+\left(\frac{\left(0.6-\alpha \right){ \overline{v}}_{2}+\alpha {v}_{2}}{0.6}\right)+\left(\frac{\left(1-\beta \right){ v}_{1}+(\beta -0.2){ \overline{v}}_{1}}{1-0.2}\right)+\left(\frac{\left(1-\beta \right){ v}_{2}+(\beta -0.2){ \overline{v}}_{2}}{1-0.2}\right)}{8}\end{array}\right)\end{array}\right\}\\ {\text{s.t.}}\left\{\begin{array}{l}\begin{array}{l}\begin{array}{l}\frac{\left(0.6-\alpha \right)\left(160 {\underline{z}}_{11}+145 {\underline{z}}_{21}\right)+\alpha \left(165 {z}_{11}+148 {z}_{21}\right)}{0.6}\le \frac{\left(0.6-\alpha \right) {\underline{v}}_{1}+\alpha {v}_{1}}{0.6}, \frac{\left(0.6-\alpha \right)\left(160 {\underline{z}}_{12}+145 {\underline{z}}_{22}\right)+\alpha \left(170 {z}_{12}+150 {z}_{22}\right)}{0.6}\le \frac{\left(0.6-\alpha \right) {\underline{v}}_{2}+\alpha {v}_{2}}{0.6}, \\ \frac{\left(0.6-\alpha \right)\left(170{ \overline{z}}_{11}+150 { \overline{z}}_{21}\right)+\alpha \left(165 {z}_{11}+148 {z}_{21}\right)}{0.6}\le \frac{\left(0.6-\alpha \right) {\overline{v}}_{1}+\alpha {v}_{1}}{0.6}, \frac{\left(0.6-\alpha \right)\left(180{ \overline{z}}_{12}+155 { \overline{z}}_{22}\right)+\alpha \left(170 {z}_{12}+150 {z}_{22}\right)}{0.6}\le \frac{\left(0.6-\alpha \right) {\overline{v}}_{2}+\alpha {v}_{2}}{0.6},\end{array}\\ \begin{array}{l}\frac{\left(\beta -0.2\right)\left(160 {\underline{z}}_{11}+145 {\underline{z}}_{21}\right)+(1-\beta ) \left(165 {z}_{11}+148 {z}_{21}\right)}{1-0.2}\le \frac{\left(\beta -0.2\right) {\underline{v}}_{1}+(1-\beta ) {v}_{1}}{1-0.2}, \frac{\left(\beta -0.2\right)\left(160 {\underline{z}}_{12}+145 {\underline{z}}_{22}\right)+(1-\beta ) \left(170 {z}_{12}+150 {z}_{22}\right)}{1-0.2}\le \frac{\left(\beta -0.2\right) {\underline{v}}_{2}+(1-\beta ) {v}_{2}}{1-0.2}, \\ \frac{\left(\beta -0.2\right)\left(170{ \overline{z}}_{11}+150 { \overline{z}}_{21}\right)+(1-\beta ) \left(165 {z}_{11}+148 {z}_{21}\right)}{1-0.2}\le \frac{\left(\beta -0.2\right) {\overline{v}}_{1}+(1-\beta ) {v}_{1}}{1-0.2}, \frac{\left(\beta -0.2\right)\left(180{ \overline{z}}_{12}+155 { \overline{z}}_{22}\right)+(1-\beta ) \left(170 {z}_{12}+150 {z}_{22}\right)}{1-0.2}\le \frac{\left(\beta -0.2\right) {\overline{v}}_{2}+(1-\beta ) {v}_{2}}{1-0.2},\end{array}\end{array}\\ \begin{array}{l}\begin{array}{l}\begin{array}{l}\frac{\left(0.6-\alpha \right)\left(85 {\underline{z}}_{11}+155 {\underline{z}}_{21}\right)+\alpha \left(90 {z}_{11}+160 {z}_{21}\right)}{0.6}\le \frac{\left(0.6-\alpha \right) {\underline{v}}_{1}+\alpha {v}_{1}}{0.6}, \frac{\left(0.6-\alpha \right)\left(90 {\underline{z}}_{12}+160 {\underline{z}}_{22}\right)+\alpha \left(95 {z}_{12}+165 {z}_{22}\right)}{0.6}\le \frac{\left(0.6-\alpha \right) {\underline{v}}_{2}+\alpha {v}_{2}}{0.6}, \\ \frac{\left(0.6-\alpha \right)\left(95{ \overline{z}}_{11}+165 { \overline{z}}_{21}\right)+\alpha \left(90 {z}_{11}+160 {z}_{21}\right)}{0.6}\le \frac{\left(0.6-\alpha \right) {\overline{v}}_{1}+\alpha {v}_{1}}{0.6}, \frac{\left(0.6-\alpha \right)\left(100{ \overline{z}}_{12}+170 { \overline{z}}_{22}\right)+\alpha \left(95 {z}_{12}+165 {z}_{22}\right)}{0.6}\le \frac{\left(0.6-\alpha \right) {\overline{v}}_{2}+\alpha {v}_{2}}{0.6},\end{array}\\ \begin{array}{l}\frac{\left(\beta -0.2\right)\left(85 {\underline{z}}_{11}+155 {\underline{z}}_{21}\right)+(1-\beta ) \left(90 {z}_{11}+160 {z}_{21}\right)}{1-0.2}\le \frac{\left(\beta -0.2\right) {\underline{v}}_{1}+(1-\beta ) {v}_{1}}{1-0.2}, \frac{\left(\beta -0.2\right)\left(90 {\underline{z}}_{12}+160 {\underline{z}}_{22}\right)+(1-\beta ) \left(95 {z}_{12}+165 {z}_{22}\right)}{1-0.2}\le \frac{\left(\beta -0.2\right) {\underline{v}}_{2}+(1-\beta ) {v}_{2}}{1-0.2}, \\ \frac{\left(\beta -0.2\right)\left(95{ \overline{z}}_{11}+165 { \overline{z}}_{21}\right)+(1-\beta ) \left(90 {z}_{11}+160 {z}_{21}\right)}{1-0.2}\le \frac{\left(\beta -0.2\right) {\overline{v}}_{1}+(1-\beta ) {v}_{1}}{1-0.2}, \frac{\left(\beta -0.2\right)\left(100{ \overline{z}}_{12}+170 { \overline{z}}_{22}\right)+(1-\beta ) \left(95 {z}_{12}+165 {z}_{22}\right)}{1-0.2}\le \frac{\left(\beta -0.2\right) {\overline{v}}_{2}+(1-\beta ) {v}_{2}}{1-0.2},\end{array}\end{array} \\ \begin{array}{l}\begin{array}{l}\begin{array}{l}\frac{\left(0.6-\alpha \right)\left( {\underline{z}}_{11}+ {\underline{z}}_{21}\right)+\alpha \left( {z}_{11}+ {z}_{21}\right)}{0.6}=\frac{\left(0.6-\alpha \right)+\alpha }{0.6}, \frac{\left(0.6-\alpha \right)\left( {\underline{z}}_{12}+ {\underline{z}}_{22}\right)+\alpha \left( {z}_{12}+ {z}_{22}\right)}{0.6}=\frac{\left(0.6-\alpha \right) +\alpha }{0.6}, \\ \frac{\left(0.6-\alpha \right)\left({ \overline{z}}_{11}+ { \overline{z}}_{21}\right)+\alpha \left( {z}_{11}+ {z}_{21}\right)}{0.6}=\frac{\left(0.6-\alpha \right) +\alpha }{0.6}, \frac{\left(0.6-\alpha \right)\left({ \overline{z}}_{12}+ { \overline{z}}_{22}\right)+\alpha \left( {z}_{12}+ {z}_{22}\right)}{0.6}=\frac{\left(0.6-\alpha \right)+\alpha }{0.6},\end{array}\\ \begin{array}{l}\frac{\left(\beta -0.2\right)\left( {\underline{z}}_{11}+ {\underline{z}}_{21}\right)+(1-\beta ) \left( {z}_{11}+ {z}_{21}\right)}{1-0.2}=\frac{\left(\beta -0.2\right)+(1-\beta )}{1-0.2}, \frac{\left(\beta -0.2\right)\left( {\underline{z}}_{12}+ {\underline{z}}_{22}\right)+(1-\beta ) \left( {z}_{12}+ {z}_{22}\right)}{1-0.2}=\frac{\left(\beta -0.2\right)+(1-\beta )}{1-0.2}, \\ \frac{\left(\beta -0.2\right)\left({ \overline{z}}_{11}+ { \overline{z}}_{21}\right)+(1-\beta ) \left( {z}_{11}+ {z}_{21}\right)}{1-0.2}=\frac{\left(\beta -0.2\right)+(1-\beta )}{1-0.2}, \frac{\left(\beta -0.2\right)\left({ \overline{z}}_{12}+ { \overline{z}}_{22}\right)+(1-\beta ) \left( {z}_{12}+ {z}_{22}\right)}{1-0.2}=\frac{\left(\beta -0.2\right)+(1-\beta )}{1-0.2},\end{array}\end{array}\\ \begin{array}{l}\begin{array}{l}\begin{array}{l}\begin{array}{l}\begin{array}{l}\frac{\left(0.6-\alpha \right) {\underline{z}}_{11}+\alpha {z}_{11}}{0.6}\ge 0, \frac{\left(0.6-\alpha \right) {\underline{z}}_{12}+\alpha {z}_{12}}{0.6}\ge 0, \frac{\left(0.6-\alpha \right) { \overline{z}}_{11}+\alpha {z}_{11}}{0.6}\ge 0, \frac{\left(0.6-\alpha \right) { \overline{z}}_{12}+\alpha {z}_{12}}{0.6}\ge 0,\\ \frac{\left(\beta -0.2\right) {\underline{z}}_{11}+(1-\beta ) {z}_{11}}{1-0.2}\ge 0, \frac{\left(\beta -0.2\right) {\underline{z}}_{12}+(1-\beta ) {z}_{12}}{1-0.2}\ge 0, \frac{\left(\beta -0.2\right) { \overline{z}}_{11}+(1-\beta ) {z}_{11}}{1-0.2}\ge 0, \frac{\left(\beta -0.2\right) { \overline{z}}_{12}+(1-\beta ) {z}_{12}}{1-0.2}\ge 0,\\ \frac{\left(0.6-\alpha \right) {\underline{z}}_{21}+\alpha {z}_{21}}{0.6}\ge 0, \frac{\left(0.6-\alpha \right) {\underline{z}}_{22}+\alpha {z}_{22}}{0.6}\ge 0, \frac{\left(0.6-\alpha \right) { \overline{z}}_{21}+\alpha {z}_{21}}{0.6}\ge 0, \frac{\left(0.6-\alpha \right) { \overline{z}}_{22}+\alpha {z}_{22}}{0.6}\ge 0,\end{array}\\ \frac{\left(\beta -0.2\right) {\underline{z}}_{21}+ {(1-\beta ) z}_{21}}{1-0.2}\ge 0, \frac{\left(\beta -0.2\right) {\underline{z}}_{22}+(1-\beta ) {z}_{22}}{1-0.2}\ge 0, \frac{\left(\beta -0.2\right) { \overline{z}}_{21}+{(1-\beta ) z}_{21}}{1-0.2}\ge 0, \frac{\left(\beta -0.2\right) { \overline{z}}_{22}+(1-\beta ) {z}_{22}}{1-0.2}\ge 0,\end{array}\\ \frac{\left(0.6-\alpha \right) { \overline{v}}_{1}+\alpha {v}_{1}}{0.6}\ge \frac{\left(0.6-\alpha \right) {\underline{v}}_{1}+\alpha {v}_{1}}{0.6}, \frac{\left(0.6-\alpha \right) { \overline{v}}_{2}+\alpha {v}_{2}}{0.6}\ge \frac{\left(0.6-\alpha \right) {\underline{v}}_{2}+\alpha {v}_{2}}{0.6} ,\\ \frac{\left(\beta -0.2\right) { \overline{v}}_{1}+ {\left(1-\beta \right) v}_{1}}{0.6}\ge \frac{\left(\beta -0.2\right) {\underline{v}}_{1}+(1-\beta ) {v}_{1}}{0.6}, \frac{\left(\beta -0.2\right) { \overline{v}}_{2}+(1-\beta ) {v}_{2}}{0.6}\ge \frac{\left(\beta -0.2\right) {\underline{v}}_{2}+(1-\beta ) {v}_{2}}{0.6} ,\end{array}\\ \frac{\left(0.6-\alpha \right) { \overline{z}}_{11}+\alpha {z}_{11}}{0.6}\ge \frac{\left(0.6-\alpha \right) {\underline{z}}_{11}+\alpha {z}_{11}}{0.6}, \frac{\left(0.6-\alpha \right) { \overline{z}}_{12}+\alpha {z}_{12}}{0.6}\ge \frac{\left(0.6-\alpha \right) {\underline{z}}_{12}+\alpha {z}_{12}}{0.6},\\ \frac{\left(\beta -0.2\right) { \overline{z}}_{11}+(1-\beta ) {z}_{11}}{0.6}\ge \frac{\left(\beta -0.2\right) {\underline{z}}_{11}+(1-\beta ) {z}_{11}}{0.6}, \frac{\left(\beta -0.2\right) { \overline{z}}_{12}+(1-\beta ) {z}_{12}}{0.6}\ge \frac{\left(\beta -0.2\right) {\underline{z}}_{12}+(1-\beta ) {z}_{12}}{0.6},\end{array}\end{array}\\ \begin{array}{l}\frac{\left(0.6-\alpha \right) { \overline{z}}_{21}+\alpha {z}_{21}}{0.6}\ge \frac{\left(0.6-\alpha \right) {\underline{z}}_{21}+\alpha {z}_{21}}{0.6}, \frac{\left(0.6-\alpha \right) { \overline{z}}_{22}+\alpha {z}_{22}}{0.6}\ge \frac{\left(0.6-\alpha \right) {\underline{z}}_{22}+\alpha {z}_{22}}{0.6},\\ \begin{array}{l}\frac{\left(\beta -0.2\right) { \overline{z}}_{21}+ {(1-\beta )z}_{21}}{0.6}\ge \frac{\left(\beta -0.2\right) {\underline{z}}_{21}+\left(1-\beta \right){z}_{21}}{0.6}, \frac{\left(\beta -0.2\right) { \overline{z}}_{22}+\left(1-\beta \right){z}_{22}}{0.6}\ge \frac{\left(\beta -0.2\right) {\underline{z}}_{22}+\left(1-\beta \right){z}_{22}}{0.6}.\end{array}\end{array}\end{array}\end{array}\end{array}\right.\end{array}$$

(32)

Solving Eq. (32) using the Simplex technique by taking $\alpha =0\, \text{ and } \,\beta =1$, the optimal solutions can be obtained as ${\underline{v}}_{1}=147.5,{\overline{v}}_{1}=153.3333,{\underline{v}}_{2}=147.6471,{\overline{v}}_{2}=159.4118,$ ${\underline{z}}_{11}=0.1666667,{\overline{z}}_{11}=0.1666667, {\underline{z}}_{12}=0.1764706, {\overline{z}}_{12}=0.1764706,{\underline{z}}_{21}=0.8333333$, ${\overline{z}}_{21}=0.8333333,{\underline{z}}_{22}=0.8235294$ and ${\overline{z}}_{22}=0.8235294.$

According to Eq. (29), we can obtain the linear programming problem as follows:

$$\begin{array}{l}\mathrm{min}\left\{\begin{array}{l}\frac{1}{2}\left(\frac{\left(\frac{\left(0.6-\alpha \right){ \underline{v}}_{1}+\alpha {v}_{1}}{0.6}\right)+\left(\frac{\left(0.6-\alpha \right){ \underline{v}}_{2}+\alpha {v}_{2}}{0.6}\right)+\left(\frac{\left(1-\beta \right){ v}_{1}+(\beta -0.2){ \underline{v}}_{1}}{1-0.2}\right)+\left(\frac{\left(1-\beta \right){ v}_{2}+(\beta -0.2){ \underline{v}}_{2}}{1-0.2}\right)}{4}\right)\\ +\frac{1}{2}\left(\begin{array}{l}\frac{\left(\frac{\left(0.6-\alpha \right){ \underline{v}}_{1}+\alpha {v}_{1}}{0.6}\right)+\left(\frac{\left(0.6-\alpha \right){ \underline{v}}_{2}+\alpha {v}_{2}}{0.6}\right)+\left(\frac{\left(1-\beta \right){ v}_{1}+(\beta -0.2){ \underline{v}}_{1}}{1-0.2}\right)+\left(\frac{\left(1-\beta \right){ v}_{2}+(\beta -0.2){ \underline{v}}_{2}}{1-0.2}\right)}{8}\\ +\frac{\left(\frac{\left(0.6-\alpha \right){ \overline{v}}_{1}+\alpha {v}_{1}}{0.6}\right)+\left(\frac{\left(0.6-\alpha \right){ \overline{v}}_{2}+\alpha {v}_{2}}{0.6}\right)+\left(\frac{\left(1-\beta \right){ v}_{1}+(\beta -0.2){ \overline{v}}_{1}}{1-0.2}\right)+\left(\frac{\left(1-\beta \right){ v}_{2}+(\beta -0.2){ \overline{v}}_{2}}{1-0.2}\right)}{8}\end{array}\right)\end{array}\right\}\\ {\text{s.t.}}\left\{\begin{array}{l}\mathrm{Constraints \, of \,Eq}.\, \left(32\right), \\ \begin{array}{l} \\ \begin{array}{l}\begin{array}{l}\begin{array}{l}\begin{array}{l}{z}_{11}\ge 0.1666667,\\ {z}_{11}\le 0.1666667,\end{array}\\ {z}_{12}\ge 0.1764706,\\ {z}_{12}\le 0.1764706,\end{array}\\ \begin{array}{l}\begin{array}{l}\begin{array}{l}{z}_{21}\ge 0.8333333,\\ {z}_{21}\le 0.8333333,\end{array}\\ {z}_{22}\ge 0.8235294,\\ {z}_{22}\le 0.8235294,\end{array}\\ {v}_{1}\ge 147.5,\\ {v}_{1}\le 153.3333,\end{array}\\ \begin{array}{l}{v}_{2}\ge 147.6471,\\ {v}_{2}\le 159.4118.\end{array}\end{array} \end{array}\end{array}\end{array}\right.\end{array}$$

(33)

Solving Eq. (33) using the Simplex technique by taking $\alpha =0.6\, \text{ and } \, \beta =0.2$, the optimal solutions can be obtained as ${v}_{1}=150.8333,{v}_{2}=153.5294, {z}_{11}=0.1666667$, ${z}_{12}=0.1764706,{z}_{21}=0.8333333 \mathrm{and}{ z}_{22}= 0.8235294.$ Therefore, the dual hesitant fuzzy minimax strategy and dual hesitant fuzzy loss-ceiling for player I are ${\tilde{z }}_{1}^{*}=\left\{\left\langle \left(0.1666667,0.1666667,0.1666667\right);\mathrm{0.6,0.2}\right\rangle ,\left\langle \left(0.1764706,0.1764706,0.1764706\right);\mathrm{0.6,0.2}\right\rangle \right\}$, ${\tilde{z }}_{2}^{*}=\left\{\left\langle \left(0.8333333, 0.8333333, 0.8333333\right);\mathrm{0.6,0.2}\right\rangle ,\left\langle \left(0.8235294,0.8235294,0.8235294\right);\mathrm{0.6,0.2}\right\rangle \right\}$ and ${\tilde{v }}^{*}=\left\{\left\langle \left(147.5, 150.8333,153.3333\right);\mathrm{0.6,0.2}\right\rangle ,\left\langle \left(147.6471,153.5294,159.4118\right);\mathrm{0.6,0.2}\right\rangle \right\}$, respectively. The value of the triangular dual hesitant matrix game is $E\left({\mathbf{y}}^{*}, {\mathbf{z}}^{*}\right)={\mathbf{y}}^{*}\tilde{B }{\mathbf{z}}^{*}=\left\{\left\langle \left(146.747035, 150.3921545, 153.333331\right);\mathrm{0.6,0.2}\right\rangle ,\left\langle \left(147.6470565, 153.333331, 159.0196055\right);\mathrm{0.6,0.2}\right\rangle \right\}$ which is an TDHFN.

6.3 Discussion

In the incomplete information game, players may encounter with some assessment information that cannot be expressed as accurate as real numbers when estimating the uncertain subjects or utility functions. Since DHFS have great flexibility and superiority in seizing and expressing various uncertainties under complex environments, it is convenient and effective to describe the payoffs of matrix games with dual hesitant fuzzy information. Due to decision makers growing requirements of expressing their judgments in a human friendly and neatly manner, it is urgent to extend the fuzzy or intuitionistic fuzzy matrix games into dual hesitant fuzzy environment. The DHFS is an effective tool to satisfy the increasing requirement of more complicated and higher uncertain matrix game problems.

Furthermore, due to the fact that TDHFNs are of universality (in reality, real numbers, fuzzy numbers and IF numbers), it is easy to see that the derived parameterized linear programming models for matrix games with payoffs of TDHFNs are an extension of the linear programming models for matrix games (Owen 1982) and/or fuzzy matrix games (Campos 1989).

It is obvious from Tables 1 and 2 of Yang and Song (2020) approach that the values of ${\mathbf{y}}^{*\mathrm{T}}$ and ${\mathbf{z}}^{*\mathrm{T}}$ vary with the change of $\mathrm{\alpha and \beta }$ which indicates that ${\mathbf{y}}^{*\mathrm{T}}$ and ${\mathbf{z}}^{*\mathrm{T}}$ should rather be meant, in our context, as TDHFNs. However, Yang et al. has assumed that ${\mathbf{y}}^{*\mathrm{T}}$ and ${\mathbf{z}}^{*\mathrm{T}}$ are real numbers which is certainly the simplest assumption but it does not allow capturing the very essence of the ${\mathbf{y}}^{*\mathrm{T}}$ and ${\mathbf{z}}^{*\mathrm{T}}$. Hence, the mathematical formulation of such matrix games in which the payoffs are represented by TDHFNs, is not valid in general.

Table 1 Yang and Song (2020) for Player I

Table 2 Yang and Song (2020) for Player II

7 Conclusion

The matrix game with uncertain information is an important research topic of game theory and has been applied to many domains. However, there exists little research about the uncertain matrix games under the TDHFNs environment. In this paper, we formulate matrix games with payoffs of TDHFNs and propose corresponding parameterized linear programming Mehar method. The highlights include:

• The arithmetic operations and ranking order relation of TDHFNs are proposed.

• We develop a matrix game model with TDHFNs as uncertain payoff elements and define some important concepts, such as the solution of a TDHFNs matrix game and optimal mixed strategies of players.

• A pair of parameterized linear programming models is derived from the TDHFN mathematical programming models to obtain the optimal mixed strategies for players.

• Proposing an effective algorithm based on the rank order relations of the TDHFNs and (Verma et al. 2015) Mehar algorithm.

• Conducting a numerical simulation to evaluate the applicability and effectiveness of the proposed approach.

• The numerical results show that the TDHFNs represents information more flexible and abundant than the FS when it is applied to study uncertainty in the game theory.

To conclude, the algorithm proposed in this article is applicable to general decision‐making problems with TDHFNs environments. As a potential future research direction, we will investigate the application of the proposed algorithm to solve n‐person matrix games, Stackelberg matrix games, nonzero‐sum matrix games, constrained bi‐matrix matrix games, and non‐cooperative matrix games with TDHFNs environments. Moreover, the adoption of the proposed algorithm and models for solving competitive decision‐making problems can apply in other fields, such as supply chain management and advertising.