1 Introduction

This paper studies the stability of linear systems with asymmetric constraints on the control. A main problem which is always inherent to all dynamical systems is the presence of actuators saturations. The class of systems with saturations has obtained great interest during the last decades. Even for linear systems, this problem has been an active area of research for many years. Two main approaches have been developed in the literature:

– The first is the so-called positive invariance approach. It is based on the design of controllers which work inside a region of linear behavior where saturations do not occur (see [1–3, 9, 10, 12] and the references therein). The stabilizing gain regulator \(F\) obtained with this approach is a solution to the non-linear algebraic equation \(FA + FBF = HF\), where matrix \(H\) satisfies the main condition of positive invariance. One can cite the work of [4, 7] where the resolution of this equation is presented as a technique of partial eigenstructure assignment. This resolution was also associated to the constrained regulator problem.

The Positive Invariance approach was selected, for the first time, in [20, 21] to deal with the problem of linear systems with input saturation and asymmetric constraints on the control increment or rate. It gives simple methods to calculate constant state feedback controllers, in both the continuous and the discrete-time cases, and with asymmetric constraints and disturbances. The gain controller is calculated by solving a linear program problem. This technique does not use LMIs formulation. Note that this approach is based on constraint avoidance: preventing the saturation, the closed-loop system, therefore, stays in a region of linear behavior.

– The second approach allows saturations to take effect while guaranteeing asymptotic stability (see [17–19] and the references therein). This approach leads to a bounded region of stability which, although can be obtained easily by the resolution of a set of LMIs, is ellipsoidal and symmetric.

The main challenge in these two approaches is to obtain a large enough domain of initial states which ensures asymptotic stability for the system despite the presence of saturations [5, 15, 17, 23].

It is well known that only works using constraints of symmetric nature as in [8, 14, 17–19] can be expressed under LMI form. To the best of the authors knowledge, no work on asymmetrical constraints using LMIs exist in the literature. However, the asymmetric character of the actuator constraints is very important in practical situations since these constraints are inherently asymmetric. Many attempts were developed to emphasis LMIs and problems with asymmetric saturations but without great success as in [6, 7].

In this paper, we address the regulator problem for linear continuous systems with asymmetric saturations on the control in terms of an LMI problem. The main contribution of this work is to overcome the drawback encountered by the based LMI approach developed by [17–19] which is limited only to symmetric constraints very far from the practical reality of actuators. Hence, this work presents for the first time the solution, expressed under LMIs form, dealing with the problem of non-symmetrical saturations. These results extends those of the same authors developing unsaturating controllers working inside a region of linear behavior [11].

The remainder of the paper is organized as follows: The problem studied hereafter is stated in Sect. \(3\). Section \(4\) presents the main results of this paper, which consist in new LMIs allowing a direct solution of the regulator problem for continuous-time linear systems with asymmetrical saturations on the control. Examples illustrating this new technique are also presented in this section. Finally some conclusions are given.

2 Problem Formulation

The saturated studied system is given by

$$\begin{aligned} \dot{x}&= A x(t) + B Sat(u(t)), \\ x_0&= x(0),\nonumber \end{aligned}$$
(1)

where \(x(t)\) \(\in \mathbb {R}^n\) is the state vector and \(u\) \(\in \mathbb {R}^m\) is the control.

The expression of each component of the vector \(Sat(u)\) can be described by the following relation:

$$\begin{aligned} Sat(u)_i = \left\{ \begin{array}{lll} \; \alpha _i &{} \text {if} &{} \,\,\,u_{i} \ge \alpha _i \\ \; u_{i} &{} \text {if} &{} -\beta _i \le u_{i} \le \alpha _i \\ -\beta _i &{} \text {if} &{} \,\,\,u_{i} \le -\beta _i \end{array} \right. \nonumber \\ \text {for}\; \; i \; =\; 1, \ldots ,m \end{aligned}$$
(2)

To stabilize the unsymmetrically saturated system a state feedback control of type,

$$\begin{aligned} u(t)&= LK x(t) + K_o \end{aligned}$$
(3)

is used.

The gain \(K\) has to stabilize the system, while the gains \(K_o, L\) play the role of symmetrizing the asymmetrical set \(\pounds (K)\) induced in the state space by the constraints and given as follows:

$$\begin{aligned} \pounds (K)=\left\{ x \in \mathfrak {R}^n| - \Gamma \zeta \le L K x+ K_o \le \Lambda \zeta \right\} , \end{aligned}$$
(4)

where the diagonal matrices \(\Lambda \) and \(\Gamma \) are given by

$$\begin{aligned} \Lambda&= \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} \alpha _1 &{} 0 &{} \dots &{} 0\\ * &{} \alpha _2 &{} \dots &{} 0\\ * &{} * &{} \dots &{} 0\\ * &{} * &{} * &{} \alpha _m\\ \end{array}\right] , \end{aligned}$$
(5)
$$\begin{aligned} \Gamma&= \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} \beta _1 &{} 0 &{} \dots &{} 0\\ * &{} \beta _2 &{} \dots &{} 0\\ * &{} * &{} \dots &{} 0\\ * &{} * &{} * &{} \beta _m\\ \end{array}\right] \end{aligned}$$
(6)

The problem studied thereafter is to stabilize by state feedback control (3) the saturated system (1)–(2). It is a classical problem where the novelty is to handle unsymmetrical saturations on the control in the frame work of LMIs.

The objective of this work is to design the gains \(K, \;\;L, \;\; K_o\) for the unsymmetrical saturated controller.

3 Preliminary Results

In this section, the cornerstone of developments allowing to transform the asymmetrical problem to a symmetrical one is presented. Further, the main lemma of the work [23] is recalled. This last enables to write a saturated system in closed-loop, as a convex combination of \(2^m\) linear systems:

Lemma 3.1

[23] For all \(z\in \mathfrak {R}^m\) and \(\nu \in \mathfrak {R}^{\bar{m}}, \bar{m}= m2^{m-1}\) such that \(| \nu _i| \le 1, i=1, \dots , \bar{m}.\):

$$\begin{aligned} sat(z) \in co\{D_s z \, +\, \hat{D}^-_s \nu \}, \quad s \in [1,N], \end{aligned}$$
(7)

where \(D_s\) are diagonal matrices with each element of the diagonal either \(1\) or \(0\), \(D_s+D^-_s=\mathbb {I}_m\), \(N=2^m\), and \(\hat{D}^-_s \in \mathfrak {R}^{m \times \bar{m}}\) is defined by

$$\begin{aligned} \hat{D}^-_s= e_{f_m(s)} \otimes D^-_s, \quad s \in [1,N] \end{aligned}$$
(8)

and \(e_{f_m(s)} \in \mathfrak {R}^{1 \times 2^{m-1}}\) is the row vector with zeros except \(1\) in the position \(f_m(s)\) which is defined by

$$\begin{aligned} f_m(s)= \left\{ \begin{array}{ccc} f_m(s-1)+1, &{} D_s+D_j \ne \mathbb {I}_m, &{} \forall j \in [1, s] \\ f_m(j), &{} D_s+D_j = \mathbb {I}_m, &{}\exists j \in [1, s] \end{array} \right. \end{aligned}$$
(9)

The Lemma 3.1 allows to rewrite the saturated control using an auxiliary control \(\nu \) which satisfies \(|\nu _i|\le 1\). Hence, there exist scalars \(\delta _s \ge 0 \; (s=1,\ldots , N)\) with \(\sum _{s=1}^{N}\delta _s=1\), such that

$$\begin{aligned} sat(z(t))\,\,=\,\,\sum _{s=1}^{N}\delta _s(t)(D_s z(t) + \hat{D}_s^- \nu (t)). \end{aligned}$$
(10)

The obtained closed-loop system becomes linear.

On the other hand, for each component of the control \(u_i\), one can make the following change of variables:

$$\begin{aligned} w_i=u_i - \frac{\alpha _i - \beta _i}{2}\!. \end{aligned}$$
(11)

With this change, one can then rewrite the saturation of the control as

$$\begin{aligned} Sat(u_i)=sat_s(w_i) + \frac{\alpha _i - \beta _i}{2}, \end{aligned}$$
(12)

with \(sat_s(w_i)\) is considered as the symmetrical non normalized saturation defined by

$$\begin{aligned} sat_s(w_i)=\left\{ \begin{array}{lll} \frac{\alpha _i+\beta _i}{2}&{}\text {if}&{} \; w_{i} \ge \frac{\alpha _i+\beta _i}{2}\\ \; w_{i}&{} \text {if} &{}-\frac{\alpha _i+\beta _i}{2} \le w_{i} \le \frac{\alpha _i +\beta _i}{2}, \quad i = 1, \ldots ,m. \\ -\frac{\alpha _i+\beta _i}{2}&{}\text {if} &{} \; w_{i} \le -\frac{\alpha _i+\beta _i}{2} \end{array} \right. \end{aligned}$$
(13)

A second change of variable is used:

$$\begin{aligned} z_i = w_i \frac{2}{\alpha _i + \beta _i}, \end{aligned}$$
(14)

and let \(sat(z_i)\) stands for the normalized symmetric saturation as

$$\begin{aligned} sat(z_i)&= \left\{ \begin{array}{lll} \; 1 &{}\text {if}&{} \; z_{i} \ge 1\\ \; z_{i}&{} \text {if} &{}-1 \le z_{i} \le 1, \quad i =1, \ldots ,m \\ -1 &{}\text {if} &{} \; z_{i} \le -1 \end{array} \right. \end{aligned}$$
(15)

With the change of variables (11) and (14), one can rewrite \(u_i\) as follows:

$$\begin{aligned} u_i=\frac{\alpha _i + \beta _i}{2} z_i + \frac{\alpha _i - \beta _i}{2}. \end{aligned}$$
(16)

or in matrix notation, the expression (16) can be written as

$$\begin{aligned} u=\frac{\Lambda + \Gamma }{2} z + \frac{\Lambda - \Gamma }{2} \zeta . \end{aligned}$$
(17)

With relation (16), we prove in lemma below that the expression of \(Sat(u_i)\) given by (2) is equivalent to \(sat(z_i)\) given by (15):

Lemma 3.2

The non-symmetrical saturation \(Sat(u)\) is linked to the normalized symmetric saturation by the following relation:

$$\begin{aligned} Sat(u)&= \left( \frac{\Lambda +\Gamma }{2}\right) sat(z) + \left( \frac{\Lambda - \Gamma }{2}\right) \zeta \!. \end{aligned}$$
(18)

Proof

The proof is obvious and is omitted. \(\square \)

By introducing (18) in the state Eq. (1), the term \(B Sat(u)\) can be developed as follows:

$$\begin{aligned} B Sat(u)&= B\left( \frac{\Lambda +\Gamma }{2}\right) sat(z) + B\left( \frac{\Lambda - \Gamma }{2}\right) \zeta \nonumber \\&= \tilde{B}sat(z)+ E w, \end{aligned}$$
(19)

where matrices \(E\) and \(\tilde{B}\) are given by

$$\begin{aligned} \tilde{B}=B\left( \frac{\Lambda +\Gamma }{2}\right) , \; \; E=\sqrt{n} B\left( \frac{\Lambda - \Gamma }{2}\right) , \; w =\frac{ \zeta }{\sqrt{n}}. \end{aligned}$$
(20)

With these notations, we can rewrite the state equation of the system as follows:

$$\begin{aligned} \dot{x}(t) = A x(t) + \tilde{B} sat(z(t)) + Ew. \end{aligned}$$
(21)

Note that \(w^Tw = 1\). In order to use available results on saturated systems, the obtained system (21), which is affine since \(w\) is known and constant, can be seen as a saturated one with a bounded disturbance.

Let us use a state feedback control of the form:

$$\begin{aligned} z(t)=K x(t). \end{aligned}$$
(22)

The link between control expression (3) and the one given by (17) is given by the following lemma.

Lemma 3.3

The feedback control (3) with \( L=\frac{\Lambda +\Gamma }{2}\) and \(K_o=\frac{\Lambda - \Gamma }{2} \zeta \) symmetrizes the asymmetrical set \(\pounds (K)\) given by (4).

Proof

The proof is obvious and is omitted. \(\square \)

Define the following sets:

$$\begin{aligned} \pounds _s(K)=\left\{ x \in \mathfrak {R}^n|\; \; |Kx|_i \le 1, \quad i=1, \ldots , m\right\} \end{aligned}$$
(23)
$$\begin{aligned} \varepsilon _s(P,\rho )=\left\{ x \in \mathfrak {R}^n| \;\;x^TP x \le \rho \right\} . \end{aligned}$$
(24)

Henceforth, for the stabilization problem, the system (21) is considered. Further, the gain feedback we are looking for will be designed to stabilize this system that is system (21).

Note that stabilizing this system (symmetrical saturated system) one has to design a control using (10) with \(z=Kx\) and \(\nu = Hx, H \in \mathfrak {R}^{\bar{m} \times n}\) the auxiliary control with \(|H_i x| \le 1\), \(H_i\) the \(i\)th row of matrix \(H\).

The matrices \(K\) and \(H\) are to be designed.

The system equation with saturation in closed loop, using Lemma 3.1, is then written as follows:

$$\begin{aligned} \dot{x}(t) = A x(t) + \tilde{B} \sum _{s=1}^{N}\delta _s(t)(D_s K + \hat{D}_s^- H) x(t) + Ew, \end{aligned}$$
(25)

or in the equivalent form

$$\begin{aligned} \dot{x}(t) = \sum _{s=1}^{N}\delta _s(t)A_{s} x(t) +Ew=A_c x(t) +Ew, \end{aligned}$$
(26)

where the matrix in closed-loop \(A_{c}\) is given by

$$\begin{aligned} A_{c}&= \sum _{s=1}^{N}\delta _s(t)A_{s}\nonumber \\ A_{s}&= A + \tilde{B}(D_s K + \hat{D}_s^- H). \end{aligned}$$
(27)

Notice that the set \(\pounds (H)\) is defined by the same expression (4) of \(\pounds (K)\). While \(\pounds (H)\) is defined by

$$\begin{aligned} \pounds _s(H)=\left\{ x \in \mathfrak {R}^n|\; \; |Hx|_i \le 1, \quad i=1, \ldots , \bar{m}\right\} . \end{aligned}$$
(28)

4 Main Results

The following theorem gives sufficient conditions for the system (25) to be strictly invariant in the sense of the following definition.

Definition 1

[16] A set in \(\mathbb {R}^n\) is said to be invariant if all the trajectories starting from it will remain in it regardless of \(w\). An ellipsoid \(\varepsilon _s(P,\rho )\) is said to be strictly invariant if \(\dot{V}= 2x^TP( B sat(Fx) + Ew) < 0\) for all \(w\) such that \(w^Tw \le 1\) and all \(x \in \partial \varepsilon _s(P,\rho )\), the boundary of \(\varepsilon _s(P,\rho )\), where \(V(x) = x^TPx\).

Theorem 4.1

If there exist matrices \(H \in \mathbb {R}^{\bar{m} \times n}\), \(K\in \mathbb {R}^{m \times n}\), a symmetric positive definite matrix \(P\in \mathbb {R}^{n \times n}\) and positive scalars \(\rho , \eta \), such that

$$\begin{aligned} A_{s}^T P + P A_{s} + \frac{1}{\eta }PEE^TP + \frac{\eta }{\rho }P < 0, \quad s \; = \; 1, \dots , N, \end{aligned}$$
(29)

and

$$\begin{aligned} \varepsilon _s(P,\rho ) \subset \pounds (H), \end{aligned}$$
(30)

where the matrix \(A_{s}\) is given by (27), then the set \(\varepsilon _s(P,\rho )\) is a strictly invariant set for system (26).

Proof

The proof follows the same reasoning as the one of [16] where the classical convex writing of the saturation is replaced by the one given by Lemma 3.1. \(\square \)

Similar result can be found in [22] where state constraints are also considered.

With the equivalent writing of the unsymmetrically saturated system in closed loop under symmetrical form developed above, we are able to derive sufficient conditions of stabilizability using LMIs. The previous result gives sufficient conditions for stabilizability for the closed-loop system. Below we reformulate these conditions in the form of LMIs that allows to deduce the controller gain.

Corollary 4.1

For positive scalars \(\rho , \eta \) if there exist matrices \(Z \in \mathfrak {R}^{\bar{m} \times n}\), \(Y \in \mathfrak {R}^{m \times n} \) and \(X=X^T \in \mathfrak {R}^{n \times n}, X >0\) such that the following LMIs are satisfied:

$$\begin{aligned}&[A X + B (\mathcal {D}_s Y + \hat{\mathcal {D}}_s^- Z)] + [A X + B (\mathcal {D}_s Y + \hat{\mathcal {D}}_s^- Z)]^T \nonumber \\&\quad \,+ \frac{\eta }{\rho } X + \frac{1}{\eta }EE^T < 0, \quad s \; = \; 1, \dots , N, \end{aligned}$$
(31)
$$\begin{aligned}&\quad \left[ \begin{array}{ll} \mu &{}\;\; Z_{i}\\ * &{}\;\; X\\ \end{array}\right] > 0, \quad i \; =\; 1, \ldots , \bar{m}, \end{aligned}$$
(32)

with matrix \(\mathcal {D}_s\) stands for a diagonal matrix with component either \(\frac{\Lambda _s+\beta _s}{2}\) or \(0\), \(\mathcal {D}_s+\mathcal {D}_s^{-}=\frac{\Lambda +\Gamma }{2}\) and \(\hat{\mathcal {D}}_s^-\) is defined by

$$\begin{aligned} \hat{\mathcal {D}}^-_s= e_{f_m(s)} \otimes \mathcal {D}^-_s, \quad s \in [1,N], \end{aligned}$$
(33)

then the set \(\varepsilon _s(P,\rho )\) is a strictly invariant set for system (26), with \(\mu = 1/\rho \), \(Z_{i}\) is the ith row of matrix \(Z\). The controller gains are given by

$$\begin{aligned} K = Y X^{-1} \; \text {and} \; H = Z X^{-1}, \; \text {with}\; P=X^{-1}. \end{aligned}$$
(34)

Proof

The sufficient condition of invariance of the set \(\varepsilon _s(P,\rho )\) with respect to the saturated system is given by (29)

$$\begin{aligned} A_{s}^T P + P A_{s} +\frac{\eta }{\rho }P + \frac{1}{\eta } PEE^TP < 0, \quad s \; = \; 1, \ldots , N. \end{aligned}$$
(35)

Multiplying the left and right of inequality (35) by \(X=P^{-1}\) leads to LMIs (31) while replacing \(\tilde{B}D\) by \(B \mathcal {D}\) and using the change of variables \(Y=K X\), \(Z=H X\). These conditions are equivalent to the sufficient conditions of strict invariance (29), for the closed-loop system, for any initial state within the set \(\varepsilon _s(P, \rho )\).

Furthermore, the inclusion (30) is equivalent to \(\rho H_i P^{-1}H_i^T\le 1,\) \(i=1,\ldots , \bar{m}\) [13]. Develop equivalently as follows:

\(\rho (H X)_iX^{-1}(HX)_i^T\le 1,\) \(i=1,\ldots , \bar{m}\), which is equivalent to \(\rho Z_iX^{-1}Z_i^T\le 1,\) \(i=1,\dots , \bar{m}\).

Using the Schur complement, we obtain the LMIs (32). \(\square \)

Instead of using Lemma 3.1, one can use the convex writing of saturation given in [17, 19],

$$\begin{aligned} sat(z) \in co\{D_s z \, +\, D^-_s \nu \}, \quad s \in [1,N] \end{aligned}$$
(36)

the closed-loop system becomes

$$\begin{aligned} \dot{x}(t) = \sum _{s=1}^{N}\delta _s(t)A_{s} x(t) +Ew=A_c x(t) +Ew, \end{aligned}$$
(37)

where the matrix in closed-loop \(A_{c}\) is given by

$$\begin{aligned} A_{c}&= \sum _{s=1}^{N}\delta _s(t)A_{s}\nonumber \\ A_{s}&= A + \tilde{B}(D_s K + D_s^- H). \end{aligned}$$
(38)

In this case, Corollary 4.1 can be announced as follows:

Corollary 4.2

For positive scalars \(\rho , \eta \) if there exist matrices \(Z \in \mathfrak {R}^{m \times n}\), \(Y \in \mathfrak {R}^{m \times n} \) and \(X=X^T \in \mathfrak {R}^{n \times n}, X >0\) such that the following LMIs are satisfied:

$$\begin{aligned}&[A X + B (\mathcal {D}_s Y + \mathcal {D}_s^- Z)] + [A X + B (\mathcal {D}_s Y + \mathcal {D}_s^- Z)]^T \nonumber \\&\quad \,+ \frac{\eta }{\rho } X + \frac{1}{\eta }EE^T< 0, \quad s \; = \; 1, \dots , N,\\ \nonumber \end{aligned}$$
(39)
$$\begin{aligned} \quad&\left[ \begin{array}{l@{\quad }l} \mu &{}\;\; Z_{i}\\ * &{}\;\; X\\ \end{array}\right] > 0, \quad i \; =\; 1, \dots , m, \end{aligned}$$
(40)

then the set \(\varepsilon _s(P,\rho )\) is a strictly invariant set for system (26), with \(\mu = 1/\rho \), \(Z_{i}\) is the ith row of matrix \(Z\). The controller gains that stabilizes the system are as follows:

$$\begin{aligned} K = Y X^{-1} \; \text {and} \; H = Z X^{-1}, \; \text {with}\; P=X^{-1}. \end{aligned}$$
(41)

Comment 4.1

  • It is worth noting that the convex expression (36) is more conservative than expression (7) for \(m > 1\), according to [23]. In order to compare results obtained upon both expressions, Corollary 4.1 and Corollary 4.2 are presented and tested in the example below.

  • These LMIs are established by the symmetric control \(z\). However, by replacing matrix \(\tilde{B}\) and \(E\) by their expressions with \(\Lambda _i \) and \(\Gamma _i \), one take account of the asymmetry of the saturation on the control. Consequently, the derived LMIs (31)–(32) deal in reality with unsymmetrical saturations. This result is obtained for the first time reducing considerably the conservatism of the results of [23].

In the following example, we illustrate the obtained results.

Example

Consider the system governed by (1) with the following matrices:

$$\begin{aligned} A&= \left[ \begin{array}{c@{\quad }c} -1 &{} 0.7 \\ 1 &{} 1\\ \end{array}\right] ;\quad B= \left[ \begin{array}{c@{\quad }c} 1 &{} 0.2\\ -0.3 &{} 0.5\\ \end{array}\right] . \end{aligned}$$
(42)

For this example, we have \(n=2\),  \(m=2\) and the control bounds are \(\alpha _1=5\), \(\beta _1 =10\), \(\alpha _2 =10\) and \(\beta _2 =5\).

It follows:

$$\begin{aligned} \tilde{B}= \left[ \begin{array}{l@{\quad }l} 7.5 &{} 1.5\\ -2.25 &{} 3.75 \\ \end{array}\right] , \;\\ E= \left[ \begin{array}{c@{\quad }c} -3.5355 &{} -0.7071\\ -1.0607 &{} 1.7678 \\ \end{array}\right] . \end{aligned}$$

We solve LMIs (31) and (32). The obtained solutions in this case for \(\rho =1\) and \(\eta =1\) are:

$$\begin{aligned} X&= \left[ \begin{array}{r@{\quad }r} 401.3375 &{}\;\; -161.6653\\ -161.6653 &{}\;\; 67.4476\\ \end{array}\right] ;\\ Y&= \left[ \begin{array}{r@{\quad }r} 22.9276 &{}\;\; -20.2454\\ -11.8235&{}\;\; -35.2446\\ \end{array}\right] ;\\ Z&= \left[ \begin{array}{r@{\quad }r} 5.2535 &{}\;\; -3.0268\\ -5.6885 &{}\;\; 0.9464\\ 0.0496 &{}\;\; -0.0218\\ -0.3650 &{}\;\; 0.1467\\ \end{array}\right] ; \end{aligned}$$

and thus gains \(K\) and \(H\) for the closed-loop system, with a non-symmetrical saturated control, are

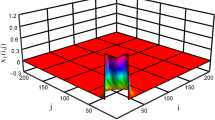
$$\begin{aligned} K&= \left[ \begin{array}{c@{\quad }c} -1.8494 &{}\;\; -4.7330\\ -6.9574 &{}\;\; -17.1987\\ \end{array}\right] ;\\ H&= \left[ \begin{array}{c@{\quad }c} -0.1446 &{}\;\; -0.3915\\ -0.2471 &{}\;\; -0.5782\\ -0.0002 &{}\;\; -0.0008\\ -0.0010 &{}\;\; -0.0001\\ \end{array}\right] . \end{aligned}$$

Figure 1 represents the inclusion of the ellipsoid set \(\varepsilon _s(P,\rho )\) inside the polyhedral set of saturation \(\pounds (H)\). Figure 2 shows some trajectories of the state vector \(x\) with different initial states \(x_0\). If \(x_0 \in \varepsilon (P,\rho )\), then the trajectory converges surely to the equilibrium point given by \(x_e=-(A+\tilde{B}K)^{-1}Ew\) which is closed to the origin due to the presence of the pseudo permanent perturbation \(w\).

In order to compare between Corollary 4.1 and Corollary 4.2, system (42) is slightly modified as follows:

$$\begin{aligned} A&= \left[ \begin{array}{c@{\quad }c} a &{}\;\; 0.7 \\ 1 &{}\;\; 1 \\ \end{array}\right] ;\quad B= \left[ \begin{array}{c@{\quad }c} b &{}\;\; 0.2\\ -0.3 &{}\;\; 0.5 \\ \end{array}\right] . \end{aligned}$$

The feasibility of LMIs (39)–(40) and (31)–(32) is tested for \(a, b\) varying from \(-1\) to \(2\) by a step of \(0.1\). The result of comparison is plotted in Fig. 3 showing the less conservatism of Corollary 4.1 based on the approach of [23].

Fig. 1
figure 1

Inclusion \(\varepsilon _s(P,\rho ) \subset \pounds (H)\) with the equilibrium point \(x_e\)

Full size image
Fig. 2
figure 2

Trajectories of the state vector \(x\) converging to the equilibrium point \(x_e\)

Full size image
Fig. 3
figure 3

Feasibility of LMIs (39)–(40) indicated with \(x\) and (31)–(32) with \(o\)

Full size image

5 Conclusion

In this paper, the regulator problem for linear continuous-time systems with asymmetric saturations on the control is developed in terms of an LMI problem. The main contribution of this work is to allow to the results of [18, 23] that make possible to consider only symmetric constraints, easily written under LMIs, to be also extended to systems with asymmetric saturations formulated under LMIs form for the first time. These results extend those of the same authors developing unsaturating controllers working inside a region of linear behavior [11]. Two numerical examples are studied to illustrate the proposed methodology and to show that the less conservative result is the one based on the approach of [23].