1 Introduction

Since the last two decades, fluid flow incorporating nanometer-sized particles, so-called nanofluids, over various surfaces has attracted much attention among researchers due to their improved heat transfer and mass rates in many manufacturing and high tech processes (Guo 2020). These novel fluids also offer generous support in biomedical sciences such as nanodrug delivery, cancer therapeutics, MRI, and the classification of cancerous tissues (Sheikholeslami and Ganji 2017). In addition, the macroscopic heat flow of the nanofluid induced by the gradual change in density resulting from the collective swimming of mobile microbes is known as bioconvection flow. The stability of nanofluid suspension can be improved by combining microorganisms with nanometer-sized particles and preventing the particles from clumping in the base fluid (Pal and Mondal 2018). Thus, bioconvective flow in nanofluids has gained a lot of interest among investigators, researchers, scientist, and engineers owing to its applications in many fields of biotechnology and science. The benefits of embedding nanometer-sized particles in the suspension of mobile microscopic organisms are generally obtained in microscale mixing, microvolumes, and stable suspensions of nanofluids. Initially, Wager (1911) and Platt (1961) gave detailed observations of bioconvection. Ahmed and Mahdy (2016) investigated free bioconvective nanofluid in the presence of gyrotactic microorganisms via a vertically implanted surface with a permeable medium. Khan (2018) reported numerical results of a second grade fluid having both nanoparticles and gyrotactic microorganisms using a passively controlled nanofluid model. Shaw et al. (2018) performed mathematical analyses of bioconvection nanofluid flow in a porous sphere surrounded by a permeable medium containing gyrotactic microbacteria while taking a magnetic field and viscous dissipation into account. Chamkha et al. (2019) used a mathematical model to study mixed bioconvection flow, considering both nanoparticles and gyrotactic microorganisms over a straight-up segment surrounded with permeable media. Ahmad et al. (2020) studied fluid flow with particles of nanosize and gyrotactic microorganisms over a permeable medium beyond a nonlinearly contracting or expanding surface. They found that the porous medium marginally disturbed the mass of motile microorganisms. Mondal and Pal (2022) worked on bio-nanoconvective fluid flow over a stretching surface surrounded by a permeable medium containing microorganisms. The numerical results showed a deceleration in the velocity of nanofluid as compared to the speed of nanofluid without gyrotactic microorganisms. Naganthran et al. (2021) investigated the flow of micropolar fluids and heat transfer caused by a vertically stretched porous plate in bioconvection. Sarkar et al. (2016) discussed bioconvective nanofluid flow involving gyrotactic microorganisms moving past an expanding surface implanted in an absorbent medium.

In many practical applications, there are cases where species are transported extensively through evaporation, like the procedure of drying paper (Nellis et al. 2005). So, in this type of application, movement of mass or species is important and gives a “blowing effect,” which derives from Stefan’s problem of species transmission. The spread of the species results in a mass movement of the fluid and provides additional movement of the fluid (Nellis et al. 2005; Lienhard and John 2005). Thus, the blowing effect was implemented by researchers for different flow patterns. Fang and Jing (2014) considered Stefan blowing effects to study momentum, heat, and mass transfer past an expanding plate analytically. They discovered that the blowing effect caused significant changes in momentum, energy, and mass transfer equations. Uddin et al. (2016a) scrutinized the influences of multiple slip and Stefan blowing on bioconvective flow over a moving surface incorporating nanoparticle and microorganism concentrations. In another paper, Uddin et al. (2016b) reported free convective mass transportation along a revolving cone in permeable media. Sultan et al. (2019) have solved a mathematical model that considers blowing effects on Poiseuille nanofluid flow through a medium that is not clear with second-order slip. A mathematical exploration of free convective mass transportation has been performed by Beg et al. (2020) along a revolving cone in permeable media.

The investigation of flow, heat, and mass transfer taking into account the slippery effect is a fundamental problem; still, a significant amount of consideration has been paid to slip flow considering different aspects. Ibrahim (2017) examined the impact of MHD and second-order slip on the boundary layer flow of micropolar fluid over an expanding sheet. They have elucidated the numerical profiles of velocity, temperature, microrotation, and friction factor, as well as the Nusselt number, using the bvp4c solver in MATLAB. Amirsom et al. (2019) studied the effects of second-order slip, viscous dissipation, and variable transport properties on the convective flow of the bio-nanofluid convection through the stretching sheet. Recently, Abdelmalek et al. (2021, 2020) have also incorporated the influence of second-order slip flow in their studies and claimed that the presence of slip factors significantly controls the heat, mass transfer, and motile microorganism density profiles. Some recent studies focused on bio-nanoconvective flow with gyrotactic microorganisms in different situations. Siddiqa et al. (2016) reported numerical results of bio-nanofluid convection of gyrotactic microorganisms from an upright, curvy cone. Mahdy (2016) examined free convection of flow with nanoparticles and gyrotactic microorganisms past a vertical cone placed in porous media. The bioconvection flow induced by a truncated cone considering nanoparticles and gyrotactic microorganisms was investigated by Khan et al. (2019). The problem was simulated by RKF7 using the shooting method. Saleem et al. (2019) described the bioconvection flow of magneto-nanoparticles configured by a rotating vertical cone with a concentration of microorganisms. The recent study by Rao et al. (2021) dealt with bio-nanofluid convection flow due to an isothermal cone containing gyrotactic microorganisms on a porous surface with reactive chemical species.

The finite element method (FEM) is an efficient numerical method that is used to solve nonlinear ordinary and partial differential equations that arise in fluid flow, heat transfer, mass transfer problems, and other branches of science and engineering. In the recent past, it has been widely used to solve nanofluid flow models. Rana and Bhargava (2012a) (nanofluid flow over a nonlinear expanding sheet), Rana and Bhargava (2012b) (numerical solution for viscoelastic nanofluid), and (Rana et al. 2012) (combined convective flow past an inclined plate with porous media) successfully applied the finite element method to solve nanofluid flow and heat transfer phenomena. Turk and Tezer-Sezgin (2017) used the finite element technique to solve the free convection of a micropolar nanofluid under the influence of magnetohydrodynamics. Ali et al. (2019) reported a finite element simulation of the influence of multiple slip on unsteady MHD bioconvective micropolar nanofluid flow induced by a sheet with a thermal and solutal boundary. Recently, Shashikumar et al. (2020) inspected the influence of radiation on micropolar nanofluid flow past an inclined microchannel, and (Rana et al. 2020, 2021) studied the problem of MHD with various heating along an exponential stretching surface and a chemically reactive bioconvective flow model over a circular cylinder using the finite element method, and the solution was further validated with other numerical techniques.

The present investigation is focused on the bioconvection micropolar nanofluid flow in a Darcy porous medium along a cone with the Stefan blowing (Rana and Gupta 2022), second-order velocity, and thermal slip effect involving both nanoparticles and gyrotactic microorganisms. The impact of various controlling parameters on the skin friction factor, heat transfer rates, mass transfer rates, and motile microorganism transfer rates is explored. An efficient FE numerical algorithm is validated with the FDM MATLAB built-in solver before employing it to solve the micropolar-based Buongiorno model in porous media with gyrotactic microorganisms.

2 Nano-bioconvective Micropolar Slip Flow Model

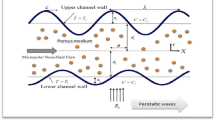
Free convective steady-state flow of bio-nanofluid past an upright cone is governed by the balance laws (mass, momentum, angular momentum, energy, nanoparticle volume fraction, and density of motile microorganism). Stefan blowing is incorporated at the wall of the cone. The coordinate’s system and flow model are displayed in Fig. 1.

Fig. 1
figure 1

Coordinate’s system and flow model

Full size image

The buoyancy forces are produced due to differences of temperature, volume fraction, and microorganism density number. The non-isothermal, non-isosolutal cone surface is considered. The \(\overline{x}\)-axis is along the cone slant surface, the \(\overline{y}\)-axis perpendicular to this. A is the semi-vertex angle of the cone. The equations which govern the flow regime are (Hering and Grosh 1962; Rana and Gupta 2022).

Mass

$$\frac{{\partial \left( {\overline{r}\overline{u} } \right)}}{{\partial \overline{x}}} + \frac{{\partial \left( {\overline{r}\overline{v} } \right)}}{{\partial \overline{y}}} = 0,$$
(1)

Momentum

$$\begin{aligned} \left( {\overline{u}\frac{{\partial \overline{u}}}{{\partial \overline{x}}} + \overline{v}\frac{{\partial \overline{u}}}{{\partial \overline{y}}}} \right) = & \left( {\frac{\mu + k}{{\rho_{{{f}}} }}} \right)\frac{{\partial^{2} \overline{u}}}{{\partial \overline{y}^{2} }} + \frac{k}{{\rho_{{{f}}} }}\frac{{\partial \overline{N}}}{{\partial \overline{y}}} - \frac{\nu }{{k_{{\text{p}}} \left( {\overline{x}} \right)}}\overline{u} \\ & + \frac{\cos A}{{\rho_{{{f}}} }}\left[ {\left( {1 - C_{\infty } } \right)\rho_{{{{f}}\infty }} g\beta \left( {T - T_{\infty } } \right)} \right. \\ & + g\left( {\rho_{{{p}}} - \rho_{f\infty } } \right)\left( {C - C_{\infty } } \right) \\ & \left. { + g\gamma\left( {\rho_{{{p}}} - \rho_{{{{f}}\infty }} } \right)\left( {n - n_{\infty } } \right)} \right] \\ \end{aligned}$$
(2)

Angular momentum (Micropolar)

$$\overline{u}\frac{{\partial \overline{N}}}{{\partial \overline{x}}} + \overline{v}\frac{{\partial \overline{N}}}{{\partial \overline{y}}} = - \frac{k}{{\rho_{f} j}}\left( {2\overline{N} + \frac{{\partial \overline{u}}}{{\partial \overline{y}}}} \right) + \frac{{\gamma_{s} }}{{\rho_{f} j}}\frac{{\partial^{2} \overline{N}}}{{\partial \overline{y}^{2} }},$$
(3)

Energy

$$\overline{u}\frac{\partial T}{{\partial \overline{x}}} + \overline{v}\frac{\partial T}{{\partial \overline{y}}} = \alpha \left( {\frac{{\partial^{2} T}}{{\partial \overline{y}^{2} }}} \right) + \frac{\tau }{{(\overline x/L)^{{\text{m}}} }}\left[ {D_{{\text{B}}} \left( {\frac{\partial C}{{\partial \overline{y}}}\frac{\partial T}{{\partial \overline{y}}}} \right) + \frac{{D_{T} }}{{T_{\infty } }}\left\{ {\left( {\frac{\partial T}{{\partial \overline{y}}}} \right)^{2} } \right\}} \right],$$
(4)

Nanoparticle volume fraction

$$\overline{u}\frac{\partial C}{{\partial \overline{x}}} + \overline{v}\frac{\partial C}{{\partial \overline{y}}} = D_{{\text{B}}} \frac{{\partial^{2} C}}{{\partial \overline{y}^{2} }} + \frac{{D_{{\text{T}}} }}{{T_{\infty } }}\left( {\frac{{\partial^{2} T}}{{\partial \overline{y}^{2} }}} \right),$$
(5)

Microorganism species number density

$$\overline{u}\frac{\partial n}{{\partial \overline{x}}} + \overline{v}\frac{\partial n}{{\partial \overline{y}}} + \frac{1}{{(\overline x/L)^{{\text{m}}} }}\frac{\partial }{{\partial \overline{y}}}\left( {n\tilde{v}} \right) = D_{{\text{n}}} \frac{{\partial^{2} n}}{{\partial \overline{y}^{2} }}.$$
(6)

Note that the momentum equation (Eq. 2) is coupled with other equations so as to establish a free convective flow. The relevant wall and far field boundary conditions are:

$$\begin{aligned} & \overline{u} = N_{1} \left( {\frac{{\overline{x}}}{L}} \right)\nu \frac{{\partial \overline{u}}}{{\partial \overline{y}}} + N_{2} \left( {\frac{{\overline{x}}}{L}} \right)\nu \frac{{\partial^{2} \overline{u}}}{{\partial \overline{y}^{2} }}, \\ & \overline{v} = - \frac{{D_{{\text{B}}} }}{{\left( {\frac{{\overline{x}}}{L}} \right)^{{\text{m}}} \left( {1 - C_{w} } \right)}}\left( {\frac{\partial C}{{\partial \overline{y}}}} \right),\,\overline{N} = - l\frac{{\partial \overline{u}}}{{\partial \overline{y}}} \\ & T = T_{\infty } + \left( {T_{{\text{w}}} - T_{\infty } } \right)\left( {\frac{{\overline{x}}}{L}} \right)^{{\text{m}}} + D_{1} \left( {\frac{{\overline{x}}}{L}} \right)\frac{\partial T}{{\partial \overline{y}}} + D_{2} \left( {\frac{{\overline{x}}}{L}} \right)\frac{{\partial^{2} T}}{{\partial \overline{y}^{2} }}, \\ & C = C_{\infty } + \left( {C_{{\text{w}}} - C_{\infty } } \right)\left( {\frac{{\overline{x}}}{L}} \right)^{{\text{m}}} + E_{1} \left( {\frac{{\overline{x}}}{L}} \right)\frac{\partial C}{{\partial \overline{y}}}, \\ & n = n_{\infty } + \left( {n_{{\text{w}}} - n_{\infty } } \right)\left( {\frac{{\overline{x}}}{L}} \right)^{{\text{m}}} + F_{1} \left( {\frac{{\overline{x}}}{L}} \right)\frac{\partial n}{{\partial \overline{y}}} \,{\text{at}}\quad \overline{y} = 0, \\ & \overline{u} = 0,\quad T = T_{\infty } ,C = C_{\infty } ,n = n_{\infty } , \overline{N} = 0\,{\text{as}}\quad \overline{y} \to \infty . \\ \end{aligned}$$
(7)

Equation (7) represents physically relevant behavior at the wall as well as in the potential flow regime. The velocity component \(\overline{u}\) has gradient conditions (second-order velocity slips), while velocity component \(\overline{v}\) is coupled with the nanoparticle volume fraction (Stefan blowing). The manufacturing of slip flow surfaces is of countless interest in a number of uses and in a range of technologies, from lubrication to microfluidics. The quantities having dimension are: \(T\): temperature, C: nanoparticle volume fraction, n: number of motile microorganisms, \(\rho\): fluid density, \(\nu\): kinematic coefficient of viscosity, \(k\): micropolar vortex viscosity (for viscous fluid \(k=0\)), \(\alpha\): thermal diffusivity, \({\left(\rho c\right)}_{\mathrm{f}}\): fluid heat capacity, \({\left(\rho c\right)}_{\mathrm{p}}\): effective nanoparticles heat capacity, \({ D}_{\mathrm{B}}\): Brownian diffusion coefficient, \({D}_{\mathrm{T}}\): thermophoretic diffusion coefficient, \({D}_{\mathrm{n}}\): microorganism diffusion coefficient, \({T}_{\mathrm{w}}\): surface temperature, \({T}_{\infty }\): ambient temperature, \({ C}_{\mathrm{w}}\): surface nanoparticle volume fraction, \({C}_{\infty }\): ambient nanoparticle volume fraction, \({N}_{1}\left(\overline{x}\right),{N}_{2}\left(\overline{x}\right)\) a: first- and second-order velocity slip factors, \({D}_{1}\left(\overline{x}\right),{D}_{2}(\overline{x})\): first- and second-order thermal slip factors, \({E}_{1}(\overline{x}),{F}_{1}(\overline{x})\): mass and microorganism slip factors, \(\widetilde{v}\left(=\frac{\widetilde{b}{W}_{\mathrm{c}}}{\Delta C}\frac{\partial C}{\partial \overline{z}}\right)\): mean swimming velocity associated with microorganisms, \(\widetilde{b}\): chemotaxis constant, \({W}_{c}\): maximum cell swimming speed, \(\overline{u}\) and \(\overline{v}\): components of velocity along and normal to the cone, \(\overline{N}\): angular velocity, \({c}_{\mathrm{p}}\): specific heat capacity, \(\nu\): kinematic viscosity, \(\beta\): thermal volumetric expansion coefficient, \(\mu\): dynamic viscosity, \(g\): gravitational acceleration, \(j\): microinertia density, \({\gamma }_{s}\): micropolar spin gradient viscosity.

The dimension-free parameters are: m is a power law exponent. \(l\) is the non-dimensional particle concentration difference which specifies the degree of rotation of microelements close the channel walls and diverges in the range of \(0<l<1.\) Here, \(l=0\) implies flow has substantial particle concentration, around the wall the microelements are so packed and incapable of spinning or rotating, while \(l=0.5\) means flow has reduced particle concentration; antisymmetric portion of the stress tensor is about to vanish, and \(l=1\) represents the turbulent flow. An analytical solution is not possible, and to get a solution, and we now nondimensionalize the governing equations using the variables given below:

$$\begin{aligned} & x = \frac{{\overline{x}}}{L},y = \frac{{\overline{y}}}{{L{\text{Gr}}^{ - 1/4} }},r = \frac{{\overline{r}}}{L},u = \frac{{\overline{u}}}{{U_{{{r}}} }},v = \frac{{\overline{v}}}{{U_{{{r}}} {\text{Gr}}^{ - 1/4} }}, \\ & U_{r} = \left[ {\left( {1 - C_{\infty } } \right)g\beta L\cos A\left( {T_{{\text{w}}} - T_{\infty } } \right)} \right]^{1/2} , \\ & \theta = \frac{{T - T_{\infty } }}{{\left( {T_{{\text{w}}} - T_{\infty } } \right)x^{{\text{m}}} }},\phi = \frac{{C - C_{\infty } }}{{\left( {C_{{\text{w}}} - C_{\infty } } \right)x^{{\text{m}}} }}, \\ & \chi = \frac{{n - n_{\infty } }}{{\left( {n_{{\text{w}}} - n_{\infty } } \right)x^{{\text{m}}} }},N = \frac{{\overline{N}L}}{{U_{{{r}}} {\text{Gr}}^{1/4} }}, \\ & k_{p} \left( {\overline{x}} \right) = \left( {k_{p} } \right)_{0} x^{2 - 2m} ,N_{1} \left( x \right) = \left( {N_{1} } \right)_{0} x^{{\frac{1 - m}{4}}} , \\ & N_{2} \left( x \right) = \left( {N_{2} } \right)_{0} x^{{\frac{1 - m}{2}}} , D_{1} \left( x \right) = \left( {D_{1} } \right)_{0} x^{{\frac{1 - m}{4}}} , D_{2} \left( x \right) = \left( {D_{2} } \right)_{0} x^{{\frac{1 - m}{2}}} , \\ & E_{1} \left( x \right) = \left( {E_{1} } \right)_{0} x^{{\frac{1 - m}{4}}} ,F_{1} \left( x \right) = \left( {F_{1} } \right)_{0} x^{{\frac{1 - m}{4}}}. \\ \end{aligned}$$
(9)

The governing equations are transformed to the following dimensionless form

$$\frac{{\partial \left( {ru} \right)}}{\partial x} + \frac{{\partial \left( {rv} \right)}}{\partial y} = 0,$$
(10)
$$\begin{aligned} u\frac{\partial u}{{\partial x}} + v\frac{\partial u}{{\partial y}} & = \left( {1 + \Delta } \right)\frac{{\partial^{2} u}}{{\partial y^{2} }} + \Delta \frac{\partial N}{{\partial y}} + x^{{\text{m}}} \left( {\theta + {\text{Nr}}\phi + {\text{Rb}}\chi } \right) \\ &\quad - \frac{1}{Da}x^{{2{\text{m}} - 2}} u, \end{aligned}$$
(11)
$$u\frac{\partial N}{{\partial x}} + v\frac{\partial N}{{\partial y}} = - I\left( {2N\frac{\partial u}{{\partial y}}} \right) + \lambda \frac{{\partial^{2} N}}{{\partial y^{2} }},$$
(12)
$$u\frac{\partial \theta }{{\partial x}} + v\frac{\partial \theta }{{\partial y}} + \frac{{{\text{mu}}\theta }}{x} = \frac{1}{\Pr }\frac{{\partial^{2} \theta }}{{\partial y^{2} }} + \frac{{{\text{Nb}}}}{\Pr }\frac{\partial \theta }{{\partial y}}\frac{\partial \phi }{{\partial y}} + \frac{{{\text{Nt}}}}{\Pr }\left( {\frac{\partial \theta }{{\partial y}}} \right)^{2}$$
(13)
$$u\frac{\partial \phi }{{\partial x}} + v\frac{\partial \phi }{{\partial y}} + \frac{{{\text{mu}}\phi }}{x} = \frac{1}{{{\text{Le}}\,{\text{Pr}}}}\frac{{\partial^{2} \phi }}{{\partial y^{2} }} + \frac{Nt}{{{\text{Nb}}\,{\text{Le}}\,{\text{Pr}}}}\left( {\frac{{\partial^{2} \theta }}{{\partial y^{2} }}} \right)$$
(14)
$$u\frac{\partial \chi }{{\partial x}} + v\frac{\partial \chi }{{\partial y}} + \frac{{{\text{mu}}\chi }}{x} + \frac{{{\text{Pe}}}}{{{\text{Lb}}}}\left[ {\frac{\partial \chi }{{\partial y}}\frac{\partial \phi }{{\partial y}} + \chi \frac{{\partial^{2} \phi }}{{\partial y^{2} }}} \right] = \frac{1}{{{\text{Lb}}}}\frac{{\partial^{2} \chi }}{{\partial y^{2} }}.$$
(15)

The boundary conditions are also changed to:

$$\begin{aligned} & v = - \frac{s}{{{\text{Le}}\,\Pr }}\frac{\partial \phi }{{\partial y}}, \\ & u = \frac{{\left( {N_{1} } \right)_{0} x^{{\frac{1 - m}{4}}} \nu }}{L}{\text{Gr}}^{\frac{1}{4}} \frac{\partial u}{{\partial y}} + \frac{{\left( {N_{2} } \right)_{0} x^{{\frac{1 - m}{2}}} \nu }}{{L^{2} }}{\text{Gr}}^{\frac{1}{2}} \frac{{\partial^{2} u}}{{\partial y^{2} }}, \\ & \chi = 1 + \frac{{\left( {F_{1} } \right)_{0} x^{{\frac{1 - m}{4}}} Gr^{\frac{1}{4}} }}{L}\frac{\partial \chi }{{\partial y}}, \\ & \theta = 1 + \frac{{\left( {D_{1} } \right)_{0} x^{{\frac{1 - m}{4}}} {\text{Gr}}^{1/4} }}{L}\frac{\partial T}{{\partial y}} + \frac{{\left( {D_{2} } \right)_{0} x^{{\frac{1 - m}{2}}} {\text{Gr}}^{1/2} }}{{L^{2} }}\frac{{\partial^{2} T}}{{\partial y^{2} }}, \\ & \phi = 1 + \frac{{\left( {E_{1} } \right)_{0} x^{{\frac{1 - m}{4}}} {\text{Gr}}^{1/4} }}{L}\frac{\partial \phi }{{\partial y}}, \\ & N = - l\frac{\partial u}{{\partial y}}\quad {\text{at}}\quad y = 0 \\ \end{aligned}$$
(16)
$$u = \theta = \phi = \chi = N = 0\,{\text{as}}\quad y \to \infty .$$
(17)

To reduce the number of variables, we define a stream function,\(\psi\):

$$ru = \frac{\partial \psi }{{\partial y}},\,rv = - \frac{\partial \psi }{{\partial x}}.$$
(18)

To transform the PDEs to SODEs, we re-scaled \(r=x \mathrm{sin} A\) and hence using the invariant transformation below (developed by Lie symmetry analysis):

$$\begin{aligned} & \psi = x^{{\frac{m + 3}{4}}} rf\left( \eta \right),\eta = yx^{{\frac{m - 1}{4}}} ,\theta = \theta \left( \eta \right), \\ & \phi = \phi \left( \eta \right),\chi = \chi \left( \eta \right),N = x^{{\frac{3m + 1}{4}}} h\left( \eta \right). \\ \end{aligned}$$
(19)

Using these relations into Eqns. (10)–(17), we have:

$$\left( {1 + \Delta } \right)f^{\prime \prime \prime } + \frac{m + 7}{4}ff^{\prime \prime } - \frac{m + 1}{2}f^{\prime 2} + \left( {\theta + {\text{Nr}}\phi + {\text{Rb}}\chi } \right) + \Delta h^{\prime } - \frac{1}{{{\text{Da}}}}f^{\prime } = 0,$$
(20)
$$\lambda h^{\prime \prime } - I\left( {2h + f^{\prime \prime } } \right) + \frac{m + 7}{4}fh^{\prime } - \frac{3m + 1}{4}f^{\prime } h = 0,$$
(21)
$$\theta^{\prime \prime } + \Pr \left( {\frac{m + 7}{4}f\theta^{\prime } - mf^{\prime } \theta } \right) + {\text{Nb}}\theta^{\prime } \phi^{\prime } + {\text{Nt}}\theta^{\prime 2} = 0,$$
(22)
$$\phi^{\prime \prime } + \frac{{{\text{Nt}}}}{{{\text{Nb}}}}\theta^{\prime \prime } + {\text{Le}}\,\Pr \left( {\frac{m + 7}{4}f\phi^{\prime } - mf^{\prime } \phi } \right) = 0$$
(23)
$$\chi^{\prime \prime } - {\text{Pe}}\left( {\chi \phi^{\prime \prime } + \chi^{\prime } \phi^{\prime } } \right) + {\text{Lb}}\left( {\frac{m + 7}{4}f\chi^{\prime } - mf^{\prime } \chi } \right) = 0$$
(24)

BCs are now become

$$\begin{aligned} & f\left( 0 \right) = \frac{4s}{{Le\Pr (m + 7)}}\phi^{\prime } \left( 0 \right), \\ & f^{\prime } \left( 0 \right) = \delta_{u1} f^{\prime \prime } \left( 0 \right) + \delta_{u2} f^{\prime \prime \prime } \left( 0 \right), \\ & \theta \left( 0 \right) = 1 + \delta_{T1} \theta^{\prime } \left( 0 \right) + \delta_{T2} \theta^{\prime \prime } \left( 0 \right), \\ & \phi \left( 0 \right) = 1 + \delta_{C} \phi^{\prime } \left( 0 \right), \\ & \chi \left( 0 \right) = 1 + \delta_{n} \chi^{\prime } \left( 0 \right), \\ & h\left( 0 \right) = - lf^{\prime \prime } \left( 0 \right), \\ & f^{\prime } \left( \infty \right) = h\left( \infty \right) = \theta \left( \infty \right) = \phi \left( \infty \right) = \chi \left( \infty \right) = h\left( \infty \right) = 0, \\ \end{aligned}$$
(25)

The dimension-free parameters are f: stream function, m: constant, \(Re\): Reynolds number, \(\theta\): temperature, \(\phi\): nanoparticles volume fraction, \(\chi\): density of motile microorganism, \(h\): angular velocity, \(\mathrm{Nr}\): buoyancy ratio parameter, \(\mathrm{Rb}\): bioconvection Rayleigh number, \(\mathrm{Pe}\): bioconvection Péclet number, \(\mathrm{Pr}\) : Prandtl number, \(\mathrm{Nb}\): Brownian motion, \(\mathrm{Nt}\): thermophoresis, \(\mathrm{Le}\): Lewis number, \(\mathrm{Lb}\): bioconvection Lewis number, \({\delta }_{\mathrm{u}1},{\delta }_{\mathrm{u}2}\): first- and second-order velocity slips, \({\delta }_{\mathrm{T}1},{\delta }_{\mathrm{T}2}\): first- and second-order thermal slips, \({\delta }_{\mathrm{C}}\): mass slip, \({\delta }_{\mathrm{n}}\): microorganism slip, \(\Delta\): micropolar, \(I\): vortex viscosity, \(\lambda\): microrotational density, \(s\): blowing parameter, Da: Darcy number. These parameters are defined as follows:

$$\begin{aligned} & {\text{Nr}} = \frac{{\left( {\rho_{{\text{p}}} - \rho_{\infty } } \right)}}{{\left( {1 - C_{\infty } } \right)\rho_{f\infty } \beta }}\frac{{C_{{\text{w}}} - C_{\infty } }}{{T_{{\text{w}}} - T_{\infty } }},{\text{Rb}} = \frac{{\gamma\left( {\rho_{{\text{m}}} - \rho_{f\infty } } \right)}}{{\left( {1 - C_{\infty } } \right) \beta \rho_{f\infty }}}\frac{{n_{{\text{w}}} - n_{\infty } }}{{T_{{\text{w}}} - T_{\infty } }}, \\ & {\text{Pe}} = \frac{{\tilde{b}Wc}}{{D_{{\text{B}}} }},{\text{Gr}} = \left( {\frac{{U_{{{r}}} L}}{\nu }} \right)^{2} ,\Pr = \frac{\nu }{\alpha },{\text{Nb}} = \frac{{\tau D_{{\text{B}}} \Delta C}}{\alpha },{\text{Nt}} = \frac{{\tau D_{{\text{T}}} \Delta T}}{{\alpha T_{\infty } }}, \\ & {\text{Le}} = \frac{\alpha }{{D_{{\text{B}}} }},{\text{Lb}} = \frac{\nu }{{D_{{\text{n}}} }},\delta_{{{\text{u1}}}} = \frac{{\left( {N_{1} } \right)_{0} }}{L}\nu \,{\text{Gr}}^{1/4} ,\delta_{{{\text{u2}}}} = \frac{{\left( {N_{2} } \right)_{0} }}{{L^{2} }}\nu \,{\text{Gr}}^{1/2} , \\ & \delta_{{{\text{T1}}}} = \frac{{\left( {D_{1} } \right)_{0} }}{L}{\text{Gr}}^{1/4} ,\delta_{{{\text{T2}}}} = \frac{{\left( {D_{2} } \right)_{0} }}{{L^{2} }}{\text{Gr}}^{1/2} ,\delta_{{\text{C}}} = \frac{{\left( {E_{1} } \right)_{0} }}{L}{\text{G}}r^{1/4} , \\ & \delta_{{\text{n}}} = \frac{{\left( {F_{1} } \right)_{0} }}{L}{\text{Gr}}^{1/4} ,\Delta = \frac{k}{\mu },\lambda = \frac{{\gamma_{{\text{S}}} }}{\mu j},I = \frac{Lk}{{\rho_f jU_{r} }},s = \frac{\Delta C}{{1 - C_{{\text{w}}} }},{\text{Da}} = \frac{\nu L}{{U_{{{r}}} \left( {k_{{\text{p}}} } \right)_{0} }}. \\ \end{aligned}$$

where s \(>0\) signifies mass travels out from the disk to the free stream, while \(s<0\) indicates mass transports in the disk from the free stream.

3 Professional Design Quantities

The professional quantities are: the friction at the surface (\(C_{{{\text{f}}_{{{\overline{\text{x}}}}} }}\)), wall heat transfer rates \(({\text{Nu}}_{{{\overline{\text{x}}}}} )\), wall mass transfer rates (\({\text{Sh}}_{{{\overline{\text{x}}}}}\)), and wall density number motile microorganism transfer rates (\({\text{Nn}}_{{{\overline{\text{x}}}}} )\). Their mathematical definitions are, respectively, as:

$$\begin{aligned} & C_{{{\text{f}}_{{{\overline{\text{x}}}}} }} = \frac{{\tau_{{\text{w}}} }}{{\rho U_{{\text{r}}}^{2} }},\quad {\text{Nu}}_{{{\overline{\text{x}}}}} = \frac{{\overline{x}}}{k}\frac{{q_{{\text{w}}} }}{{\left( {T_{{\text{w}}} - T_{\infty } } \right)}}, \\ & {\text{Sh}}_{{{\overline{\text{x}}}}} = \frac{{\overline{x}}}{{D_{{\text{B}}} }}\frac{{J_{{\text{w}}} }}{{\left( {C_{{\text{w}}} - C_{\infty } } \right)}},\quad {\text{Nn}}_{{{\overline{\text{x}}}}} = \frac{{\overline{x}}}{{D_{{\text{n}}} }}\frac{{P_{{\text{w}}} }}{{\left( {n_{{\text{w}}} - n_{\infty } } \right)}} \\ \end{aligned}$$
(26)

where \({\tau }_{w}\) denotes the shearing stress at the surface of the cone, while \({q}_{\mathrm{w}},{J}_{\mathrm{w}},{P}_{\mathrm{w}}\) symbolize surface heat, mass, and motile microorganism flux, respectively, and demarcated as follows:

$$\begin{aligned} & \tau_{{\text{w}}} = \left( {\mu + k} \right)\left[ {\frac{{\partial \overline{u}}}{{\partial \overline{y}}} + k\overline{N}} \right]_{{\overline{y} = 0}} = \frac{{\mu U_{{\text{r}}} }}{{L\,{\text{Gr}}^{{ - \frac{1}{4}}} }}x^{{\frac{3m + 1}{4}}} \left[ {1 + \Delta \left( {1 - l} \right)} \right]f^{\prime\prime}\left( 0 \right), \\ & q_{{\text{w}}} = - k\left[ {\frac{\partial T}{{\partial \overline{y}}}} \right]_{{\overline{y} = 0}} = \frac{{ - kx\left( {T_{{\text{w}}} - T_{\infty } } \right)}}{{{\text{Gr}}^{{ - \frac{1}{4}}} }}x^{{\frac{m - 1}{4}}} \theta^{\prime}\left( 0 \right), \\ & J_{{\text{w}}} = - D_{B} \left[ {\frac{\partial C}{{\partial \overline{y}}}} \right]_{{\overline{y} = 0}} = \frac{{ - D_{{\text{B}}} x\left( {C_{w} - C_{\infty } } \right)}}{{{\text{Gr}}^{{ - \frac{1}{4}}} }}x^{{\frac{m - 1}{4}}} \phi^{\prime}\left( 0 \right), \\ & P_{{\text{w}}} = - D_{n} \left[ {\frac{\partial n}{{\partial \overline{y}}}} \right]_{{\overline{y} = 0}} = \frac{{ - D_{{\text{n}}} x\left( {n_{{\text{w}}} - n_{\infty } } \right)}}{{{\text{Gr}}^{{ - \frac{1}{4}}} }}x^{{\frac{m - 1}{4}}} \chi^{\prime}\left( 0 \right). \\ \end{aligned}$$
(27)

Applying Eq. (27) in Eq. (26), we get

$$\begin{aligned} & C_{{{\text{f}}_{{{\overline{\text{x}}}}} }} \,{\text{Gr}}^{\frac{1}{4}} x^{{ - \frac{3m + 1}{4}}} = \left[ {1 + \Delta \left( {1 - l} \right)} \right]f^{\prime\prime}\left( 0 \right), \\ & {\text{Nu}}_{{{\overline{\text{x}}}}} \,{\text{Gr}}^{{ - \frac{1}{4}}} x^{{ - \frac{m + 3}{4}}} = - \theta^{\prime}\left( 0 \right), \\ & {\text{Sh}}_{{{\overline{\text{x}}}}} \,{\text{Gr}}^{{ - \frac{1}{4}}} x^{{ - \frac{m + 3}{4}}} = - \phi^{\prime} \left( 0 \right), \\ & {\text{Nn}}_{{{\overline{\text{x}}}}} \,{\text{Gr}}^{{ - \frac{1}{4}}} x^{{ - \frac{m + 3}{4}}} = - \chi^{\prime}\left( 0 \right). \\ \end{aligned}$$
(28)

4 Finite Element Method Computations

After the application of variational formulation on governing Eqs. (20)-(24), using linear element \({\Omega }_{e}=({\eta }_{e},{\eta }_{e+1})\) leads to the finite element method (FEM) given below:

$$\left[ {\begin{array}{*{20}l} {H^{11} } \hfill & {\quad H^{12} } \hfill & {\quad H^{13} } \hfill & {\quad H^{14} } \hfill & {\quad H^{15} } \hfill & {\quad H^{16} } \hfill \\ {H^{21} } \hfill & {\quad H^{22} } \hfill & {\quad H^{23} } \hfill & {\quad H^{24} } \hfill & {\quad H^{25} } \hfill & {\quad H^{26} } \hfill \\ {H^{31} } \hfill & {\quad H^{32} } \hfill & {\quad H^{33} } \hfill & {\quad H^{34} } \hfill & {\quad H^{35} } \hfill & {\quad H^{36} } \hfill \\ {H^{41} } \hfill & {\quad H^{42} } \hfill & {\quad H^{43} } \hfill & {\quad H^{44} } \hfill & {\quad H^{45} } \hfill & {\quad H^{46} } \hfill \\ {H^{51} } \hfill & {\quad H^{52} } \hfill & {\quad H^{53} } \hfill & {\quad H^{54} } \hfill & {\quad H^{55} } \hfill & {\quad H^{56} } \hfill \\ {H^{61} } \hfill & {\quad H^{62} } \hfill & {\quad H^{63} } \hfill & {\quad H^{64} } \hfill & {\quad H^{65} } \hfill & {\quad H^{66} } \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {\left\{ f \right\}} \hfill \\ {\left\{ {f^{\prime} = g} \right\}} \hfill \\ {\left\{ h \right\}} \hfill \\ {\left\{ {h^{\prime} = l} \right\}} \hfill \\ {\left\{ \theta \right\}} \hfill \\ {\left\{ \phi \right\}} \hfill \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\left\{ c \right\}^{1} } \\ {\left\{ c \right\}^{2} } \\ {\left\{ c \right\}^{3} } \\ {\left\{ c \right\}^{4} } \\ {\left\{ c \right\}^{5} } \\ {\left\{ c \right\}^{6} } \\ \end{array} } \right]$$

where \([{\mathrm{H}}^{mn}]\text{and }[{\{c\}}^{m}](m,n=1,..,6)\) are defined as:

$$\begin{aligned} H_{ij}^{11} & = \int_{{\eta_{e} }}^{{\eta_{e + 1} }} {S_{i} \frac{{dS_{j} }}{d\eta }d\eta } ,H_{ij}^{12} = - \int_{{\eta_{e} }}^{{\eta_{e + 1} }} {S_{i} S_{j} d\eta } ,H_{ij}^{13} = H_{ij}^{14} = H_{ij}^{15} = H_{ij}^{16} = 0, \\ H_{ij}^{21} & = 0,H_{ij}^{22} = - \left( {1 + {\Delta }} \right)\int_{{\eta_{e} }}^{{\eta_{e + 1} }} {\frac{{\partial S_{i} }}{\partial \eta }\frac{{\partial S_{j} }}{\partial \eta }d\eta } + \frac{m + 7}{4}\int_{{\eta_{e} }}^{{\eta_{e + 1} }} {S_{i} \overline{f}\frac{{\partial S_{j} }}{\partial \eta }d\eta } \\ & \quad - \frac{m + 1}{2}\int_{{\eta_{e} }}^{{\eta_{e + 1} }} {S_{i} \overline{g}S_{j} d\eta } - \frac{1}{Da}\int_{{\eta_{e} }}^{{\eta_{e + 1} }} {S_{i} S_{j} d\eta ,H_{ij}^{23} } = {\Delta }\int_{{\eta_{e} }}^{{\eta_{e + 1} }} {S_{i} \frac{{dS_{j} }}{d\eta }d\eta } ,{ }H_{ij}^{24} \\ & = \int_{{\eta_{e} }}^{{\eta_{e + 1} }} {S_{i} S_{j} d\eta } ,H_{ij}^{25} = Nr\int_{{\eta_{e} }}^{{\eta_{e + 1} }} {S_{i} S_{j} d\eta } , H_{ij}^{26} = {\text{Rb}}\int_{{\eta_{e} }}^{{\eta_{e + 1} }} {S_{i} S_{j} d\eta } , \\ H_{ij}^{31} & = 0, H_{ij}^{32} = - I\int_{{\eta_{e} }}^{{\eta_{e + 1} }} {S_{i} \frac{{\partial S_{j} }}{\partial \eta }d\eta } ,H_{ij}^{33} \\ & = - \lambda \int_{{\eta_{e} }}^{{\eta_{e + 1} }} {\frac{{\partial S_{i} }}{\partial \eta }\frac{{\partial S_{j} }}{\partial \eta }d\eta } - 2I\int_{{\eta_{e} }}^{{\eta_{e + 1} }} {S_{i} S_{j} d\eta } + \frac{m + 7}{4}\int_{{\eta_{e} }}^{{\eta_{e + 1} }} {S_{i} \overline{f}\frac{{\partial S_{j} }}{\partial \eta }d\eta } \\ & \quad - \frac{3m + 1}{4}\int_{{\eta_{e} }}^{{\eta_{e + 1} }} {S_{i} \overline{h}S_{j} d\eta } ,H_{ij}^{34} = H_{ij}^{35} = H_{ij}^{36} = 0, \\ H_{ij}^{41} & = 0,H_{ij}^{42} = 0,H_{ij}^{43} = 0,H_{ij}^{44} \\ & = - \int_{{\eta_{e} }}^{{\eta_{e + 1} }} {\frac{{\partial S_{i} }}{\partial \eta }\frac{{\partial S_{j} }}{\partial \eta }d\eta } + {\text{Pr}}\left( {\frac{m + 7}{4}} \right)\int_{{\eta_{e} }}^{{\eta_{e + 1} }} {S_{i} \overline{f}\frac{{\partial S_{j} }}{\partial \eta }d\eta } \\ & \quad - m{\text{Pr}}\int_{{\eta_{e} }}^{{\eta_{e + 1} }} {S_{i} \overline{g}S_{j} d\eta } + {\text{Nt}}\int_{{\eta_{e} }}^{{\eta_{e + 1} }} {\frac{{\partial S_{i} }}{\partial \eta }\overline{\theta }\frac{{\partial S_{j} }}{\partial \eta }} ,H_{ij}^{45} \\ & = {\text{Nb}}\int_{{\eta_{e} }}^{{\eta_{e + 1} }} {\frac{{\partial S_{i} }}{\partial \eta }\overline{\theta }\frac{{\partial S_{j} }}{\partial \eta }} ,H_{ij}^{46} = 0, \\ H_{ij}^{51} & = H_{ij}^{52} = H_{ij}^{53} = H_{ij}^{56} = 0,H_{ij}^{54} = - \frac{{{\text{Nt}}}}{{{\text{Nb}}}}\int_{{\eta_{e} }}^{{\eta_{e + 1} }} {\frac{{\partial S_{i} }}{\partial \eta }\frac{{\partial S_{j} }}{\partial \eta }d\eta } , \\ H_{ij}^{55} & = - \int_{{\eta_{e} }}^{{\eta_{e + 1} }} {\frac{{\partial S_{i} }}{\partial \eta }\frac{{\partial S_{j} }}{\partial \eta }d\eta } + {\text{Pr}}\,{\text{Le}}\left( {\frac{m + 7}{4}} \right)\int_{{\eta_{e} }}^{{\eta_{e + 1} }} {S_{i} \overline{f}\frac{{\partial S_{j} }}{\partial \eta }d\eta } - m{\text{Pr}}\,{\text{Le}}\int_{{\eta_{e} }}^{{\eta_{e + 1} }} {S_{i} \overline{g}S_{j} d\eta } , \\ H_{ij}^{61} & = H_{ij}^{62} = H_{ij}^{63} = H_{ij}^{64} = 0,H_{ij}^{65} = - {\text{Pe}}\int_{{\eta_{e} }}^{{\eta_{e + 1} }} {\frac{{\partial S_{i} }}{\partial \eta } \frac{{\partial \overline{\chi }}}{\partial \eta }\frac{{\partial S_{j} }}{\partial \eta }d\eta } , \\ H_{ij}^{66} & = - \int_{{\eta_{e} }}^{{\eta_{e + 1} }} {\frac{{\partial S_{i} }}{\partial \eta }\frac{{\partial S_{j} }}{\partial \eta }d\eta } + {\text{Lb}}\left( {\frac{m + 7}{4}} \right)\int_{{\eta_{e} }}^{{\eta_{e + 1} }} {S_{i} \overline{f}\frac{{\partial S_{j} }}{\partial \eta }d\eta } - m\,{\text{Lb}}\int_{{\eta_{e} }}^{{\eta_{e + 1} }} {S_{i} \overline{g}S_{j} d\eta } , \\ \end{aligned}$$
$$\begin{aligned} c_{i}^{1} & = 0,c_{i}^{2} = - \left( {1 + \Delta } \right)\left( {S_{i} \frac{dg}{{d\eta }}} \right)_{{\eta_{e} }}^{{\eta_{e + 1} }} ,c_{i}^{3} = - \lambda \left( {S_{i} \frac{dh}{{d\eta }}} \right)_{{\eta_{e} }}^{{\eta_{e + 1} }} , \\ c_{i}^{4} & = - \left( {S_{i} \frac{d\theta }{{d\eta }}} \right)_{{\eta_{e} }}^{{\eta_{e + 1} }} ,c_{i}^{5} = - \left( {S_{i} \left( {\frac{d\phi }{{d\eta }} + \frac{{{\text{Nt}}}}{{{\text{Nb}}}}\frac{d\theta }{{d\eta }}} \right)} \right)_{{\eta_{e} }}^{{\eta_{e + 1} }} , \\ c_{i}^{6} & = - \left( {S_{i} \left( {\frac{d\chi }{{d\eta }} + \chi {\text{Pe}}\frac{d\phi }{{d\eta }}} \right)} \right)_{{\eta_{e} }}^{{\eta_{e + 1} }} . \\ \end{aligned}$$

where \(\overline{\Theta }={\sum }_{i=1}^{2}\overline{{\Theta }_{i}}{S}_{i}\) and \(\Theta\) is dependent variable and \({S}_{i}\) is linear shape function. Gaussian quadrature is used to evaluate the integrations. The linearization process has been implemented to solve the nonlinear problem, and the Gauss elimination method has been applied after imposing boundary conditions. The mesh-independent test is conducted in Table 1, and the mesh size (he = \({\eta }_{e+1}-{\eta }_{e}\)) of 0.005 with optimal boundary layer length (\({\eta }_{\infty }=\) 10) is considered to ensure six decimal computational accuracy. For second-order momentum, thermal boundary condition has been implemented by removing the third-order derivative, \(f^{\prime\prime\prime}\left( 0 \right)\), and second-order derivative, \(\theta^{\prime\prime}\left( 0 \right),\) using Eqs. (20) and (22) as

$$\begin{aligned} f^{\prime}\left( 0 \right) & = \delta_{{{\text{u1}}}} f^{\prime\prime}\left( 0 \right) + \delta_{u2} f^{\prime\prime\prime}\left( 0 \right) \\ & = \delta_{{{\text{u1}}}} f^{\prime\prime}\left( 0 \right) - \frac{{\delta_{u2} }}{1 + \Delta }\left[ {\frac{m + 7}{4}f\left( 0 \right)f^{\prime \prime } \left( 0 \right) - \frac{m + 1}{2}f^{\prime}\left( 0 \right)^{2} } \right. \\ & \quad \left. { + \left( {\theta \left( 0 \right) + {\text{Nr}}\phi \left( 0 \right) + {\text{Rb}}\chi (0} \right) + \Delta h^{\prime}\left( 0 \right) - \frac{1}{{{\text{Da}}}}f^{\prime}\left( 0 \right)} \right] \\ \end{aligned}$$
(29)
Table 1 Mesh independency test
Full size table

After rearranging the terms of Eq. (29), we have

$$\begin{aligned} & \left[ {1 + \frac{{\delta_{u2} }}{{{\text{Da}}\left( {1 + \Delta } \right)}} - \frac{{\delta_{u2} \left( {m + 1} \right)f^{\prime}\left( 0 \right)}}{{2{\text{Da}}\left( {1 + \Delta } \right)}}} \right]f^{\prime}\left( 0 \right) \\ & \quad + \left[ {\delta_{u1} + \frac{{\delta_{u2} }}{1 + \Delta }\frac{m + 7}{4}f\left( 0 \right)} \right] f^{\prime \prime } \left( 0 \right) \\ & \quad - \left[ {\left( {\theta \left( 0 \right) + {\text{Nr}}\phi \left( 0 \right) + {\text{Rb}}\chi (0} \right) + \Delta h^{\prime}\left( 0 \right)} \right] = 0, \\ \end{aligned}$$

Similarly, thermal boundary conditions at the initial point may be written as

$$\left[ {1 - \delta_{T2} \Pr mf^{\prime}\left( 0 \right)} \right]\theta \left( 0 \right) + \theta^{\prime}\left( 0 \right)\left[ { - \delta_{T1} + \frac{{\Pr \delta_{T2} \left( {m + 7} \right)}}{4}f\left( 0 \right) + {\text{Nb}}\,\delta_{T2} \phi^{\prime}\left( 0 \right) + {\text{Nt}}\,\delta_{T2} \theta^{\prime}\left( 0 \right)} \right] = 1$$

The accuracy of the employed method (finite element method algorithm) is established by direct comparisons. We have compared the results obtained by FEM with those of a MATLAB built-in FDM code (bvp5c solver). The results obtained from the FEM are promising with those obtained from FDM, as shown in Table 2.

Table 2 Validation of some \(- \theta^{\prime}\left( 0 \right)\) values from finite element method (FEM) simulation with MATLAB bvp5c solver
Full size table

5 Interpretation of Results

To validate our simulated results, we have compared our results for the limiting case, with the earlier published results (Table 3). An excellent correlation is found, and hence, the correctness of the other results is justifiably high. Results are computed for important range of parameters i.e. power law parameter (\(0\le m\le 2\)), Stefan blowing parameter (\(-1\le s\le 1\)), micropolar parameter (\(0\le \Delta \le 2\)), Darcy number (\(0.1\le \mathrm{Da}\le 10\)), velocity slip parameter (\(0\le {\delta }_{\mathrm{u}1}\le 1\)), thermal slip parameter (\(0\le {\delta }_{\mathrm{T}1}\le 1)\), and microrotational density (\(0.1\le \lambda \le 0.5\)) keeping other parameters fixed as \(\mathrm{Pr}=6.8, \mathrm{Le}=\mathrm{Lb}=\mathrm{Pe}=\mathrm{Rb}=\mathrm{Nr}=1,\)\(\mathrm{Nb}=\mathrm{Nt}=0.01, {\delta }_{\mathrm{c}}={\delta }_{\mathrm{n}}=0.1.\) Table 4 provides the influence of governing parameters on the friction factor, heat transfer, mass transfer, and microorganism transfer rates. It is noticed that all quantities decrease as the suction parameter changes from negative to positive, as well as with the first-order velocity slip parameter. All physical quantities are reduced as the cone surface temperature changes from isothermal to linear, then to quadratically. As the microrotation parameter and the mass slip parameter rise, all physical quantities decrease. The first-order thermal slip parameter decreases the friction factor, heat transfer, and mass transfer while increasing the rates at which microorganisms are transferred. The microorganism slip parameter decreases the friction factor, heat transfer, and microbial transfer while increasing mass transfer rates.

Table 3 Comparison of limiting case with the published literature
Full size table
Table 4 Variations in friction, heat transfer, mass transfer, microorganisms transfer rates with some important controlling parameters
Full size table

Graphs in Fig. 2 display the effect of power law (m) and blowing (s) parameters on the dimensionless velocity, temperature, nanoparticles volume fraction, and density of motile microorganism. Before describing the comprehensive principal transport physics, it is imperative to remember that \(s<0\) means the evaporation process, \(s>0\) means the condensation process, and \(s=0\) means the no Stefan blowing phenomenon. As the magnitude of the evaporation process declines, the velocity field increases; however, the condensation process helps to improve the velocity field. It is also observed that all other physical quantities increase with an increase in the blowing parameter for both isothermal and non-isothermal conditions, i.e., the linearly and quadratically varying wall cone surface temperature and volume fraction.

Fig. 2
figure 2

Effect of power law (m = 0, 1, 2) and blowing parameters (s = −1, 0, 1) on (a) velocity, (b) temperature, (c) volume fraction, and (d) microorganism profiles

Full size image

Effects of micropolar and Darcy number on the dimensionless velocity, temperature, volume fraction, and density of motile microorganisms are illustrated in the graphs of Fig. 3. All of the quantities rise with the increase in the micropolar parameter. It is found that velocity increase with the increase in the Darcy parameter both regular (\(\Delta = 0\)) fluid and micropolar fluid opposite phenomena is noticed for temperature, volume fraction, and density of motile microorganisms. For the velocity profile, the behavior is reversed near the \(\eta \sim 1\) with micropolar parameter. It can be attributed to the fact that the microrotation slows down the velocity near the wall, and this impact declines as one moves away from the wall.

Fig. 3
figure 3

Effect of micropolar (\(\Delta =0, 1, 2)\) and Darcy number (Da = 0.1, 1, 10) on (a) velocity, (b) temperature, (c) volume fraction, and (d) microorganism profiles

Full size image

The impact of first- and second-order velocity slip parameters for various controlling profiles is shown in Fig. 4. Slip velocity parameter controls the velocity of the nanofluid relative to the surface of the cone, reflects the interaction between the nanoliquid and the isothermal or non-isothermal wall, and influences the heat and mass transfer characteristics. It can be noted that the velocity increases both in the presence and absence of first-order slip, whereas it decreases with second-order slip both in the presence and absence of the first-order slip parameter. In addition, there are crossover points in the velocity profiles. It is also found from Fig. 4 that temperature decreases with first-order slip for both the presence and absence of second-order slip, whereas temperature increases with second-order slip for both the presence and absence of the first-order slip parameter. No crossover points are found for other profiles.

Fig. 4
figure 4

Effect of first-order and second-order velocity parameters on (a) velocity, (b) temperature, (c) volume fraction, and (d) microorganism profiles

Full size image

The influence of the first-order thermal slip parameter and microrotational density parameters on the velocity, temperature, and nanoparticle volume fraction is illustrated in the graphs of Fig. 5. For a small value of the microrotational density parameter, it is discovered that all four quantities increase as the first-order slip parameter increases. In addition, the velocity got a sudden boost above the wall velocity near the wall for higher microrotational density. It is also found from Fig. 5 that temperature, volume fraction, and density of microorganisms increase with microrotational density both in the presence and absence of the first-order thermal slip parameter. An opposite response to the parameters has been reported for the velocity function.

Fig. 5
figure 5

Effect of microrotational density and first-order thermal slip parameters on (a) velocity, (b) temperature, (c) volume fraction, and (d) microorganism profiles

Full size image

Effects of the first-order thermal slip parameter and microrotational density parameters on friction, heat, mass, and microorganism transfer are illustrated in the graphs of Fig. 6. Figure 6 shows that friction increases for both regular and micropolar fluids. Heat, mass, and microorganism transfer decrease with the micropolar parameter for both isothermal and non-isothermal cones. Furthermore, the fluctuation in all physical quantities has been discovered to be more prominent for smaller Darcy numbers, but the effect becomes invariant for large Darcy numbers, Da > 10.

Fig. 6
figure 6

Effect of micropolar parameter and Darcy number on the (a) friction factor \((\left[ {1 + \Delta \left( {1 - l} \right)} \right]f^{\prime\prime}\left( 0 \right)\)), the (b) heat transfer rates \(( - \theta^{\prime}\left( 0 \right)\)), the (c) mass transfer rates \(( - \phi^{\prime}\left( 0 \right)\)), and (d) microorganisms transfer rates \(( - \chi^{\prime}\left( 0 \right)\))

Full size image

The influences of various slip parameters are discussed in Fig. 7 on the engineering quantities. It is revealed from the figure that friction factor decreases with first-order thermal slip parameter in the absence of second-order slip reverse trends which is noticed in the presence of the second-order slip. A heat transfer rate is decreased with the increase in the first-order thermal slip parameter. Mass and microorganism transfer rates increased with the increase in the first-order thermal slip parameter both in the presence and absence of second-order slips. Figure 8 displays the streamline fluctuation, which can be seen through colormap for different values of non-isothermal parameters (m = 1 and 2) in the case of Newtonian and micropolar fluids as base fluid. By considering the micropolar rheological fluid having microstructure and random orientation diminishes the flow regime and regulate the heat transfer more efficiently, which coincides with the finding of Rana et al. (2020). With the increment in non-isothermal parameters, the boost in velocity can be noticed easily due to the nonlinear increment in temperature and particle profiles over the conical surface. The maximum value of stream function is achieved as we move away from the surface with the boundary layer. There is a decrement of nearly 20% in maximum stream function value if the micropolar parameter \(\Delta\) changes from 0 to 1.

Fig. 7
figure 7

Effect of first- and second-order slip parameters on the (a) friction factor \((\left[ {1 + \Delta \left( {1 - l} \right)} \right]f^{\prime\prime}\left( 0 \right)\)), the (b) heat transfer rates \(( - \theta ^{\prime}\left( 0 \right)\)), the (c) mass transfer rates \(( - \phi^{\prime}\left( 0 \right)\)), and (d) microorganisms transfer rates \(( - \chi^{\prime}\left( 0 \right)\))

Full size image
Fig. 8
figure 8

Variation in streamlines for different values of m for Newtonian (Δ=0) and micropolar nanofluid (Δ=1)

Full size image

6 Conclusions

A theoretical and computational model based on both the second-order velocity and thermal slips is presented. The model is converted to similarity ordinary differential equations (SODEs) prior to conduct simulation with the finite element method (FEM). Moreover, the accuracy of the employed finite element technique is validated with the finite-difference built-in program in MATLAB. The influence of emerging parameters on the flow characteristics, heat transfer, nanoparticles migration, and microorganism transfers has been illustrated using tables and graphs. Some of the key points are listed below:

  1. (1)

    The friction factor increases, while heat, mass, and microorganism transfer decrease with the micropolar parameter for both isothermal and non-isothermal conical surfaces.

  2. (2)

    The friction factor decreases with the first-order thermal slip parameter in the absence of second-order slip, whereas reverse trends are noticed in the presence of second-order slip.

  3. (3)

    As the first-order thermal slip parameter is increased, the heat transfer rate decreases. Mass and microorganism transfer rates increased with the increase in the first-order thermal slip parameter, both in the presence and absence of second-order slips.

  4. (4)

    A quadratically varied non-isothermal surface has significantly higher transfer rates than a linearly varied non-isothermal or isothermal surface.

  5. (5)

    The variation of all the physical quantities is noticed for small Darcy numbers, whereas these physical quantities become independent of Darcy number for Da > 10.

  6. (6)

    When considering micropolar basefluid for non-isothermal variation, the intensity of flow streamlines decreases.

The current work can be extended for other Newtonian and non-Newtonian nanofluid models under different physical and experimental conditions (Haider and Muhammad 2022a, 2022b; Haider and Ahmad 2022; Nadeem et al. 2022a, b; Haider et al. 2023).