Bioconvection in Second Grade Nanofluid Flow Containing Nanoparticles and Gyrotactic Microorganisms

Abstract

The bioconvection in steady second grade nanofluid thin film flow containing nanoparticles and gyrotactic microorganisms is considered using passively controlled nanofluid model boundary conditions. A real-life system evolves under the flow and various taxis. The study is initially proposed in the context of gyrotactic system, which is used as a key element for the description of complex bioconvection patterns and dynamics in such systems. The governing partial differential equations are transformed into a system of ordinary ones through the similarity variables and solved analytically via homotopy analysis method (HAM). The solution is expressed through graphs and illustrated which show the influences of all the parameters.

1 Introduction

Bioconvection has many applications in biological systems and biotechnology. It is defined as the pattern formation in suspensions of microorganisms, such as bacteria and algae, due to up-swimming of the microorganisms. These microorganisms include gravitaxis, gyroitaxis, or oxytaxis organisms. Convective heat transfer in the presence of nanofluids and gyrotactic microorganisms is the major area of research. According to this viewpoint regarding convection, Turkyilmazoglu [1] analyzed the magnetohydrodynamic mixed convection flow and heat of a micropolar fluid past a heated or cooled stretching permeable surface in the presence of heat generation and absorption effects. He found that a magneto-convection parameter controls the magnetic and convection effects. Different features of the bioconvection have been analyzed by many researchers. Mabood et al. [2] presented the analytical modeling of free convection of non-Newtonian nanofluids flow in porous media with gyrotactic microorganisms using OHAM. Das et al. [3] discussed the laminar MHD natural convection of nanofluid bioconvection in presence of gyrotactic microorganisms and chemical reaction in porous medium. Ahmed and Mahdy [4] analyzed the laminar MHD natural convection of nanofluid containing nanoparticles and gyrotactic microorganisms over a vertical wavy surface saturated non-Darcian porous medium. Sk et al. [5] explored the multiple slip effects on bioconvection of nanofluid flow containing microorganisms and nanoparticles. Xu and Pop [6] discussed the mixed convection flow of a nanofluid over a stretching surface with uniform free stream in the presence of both nanoparticles and gyrotactic microorganisms. Very recently Khan et al. [7] reported the comparison of non-Newtonian Casson and Williamson nanofluids flow containing nanoparticles and gyrotactic microorganisms using actively controlled nanofluid model boundary conditions. Their results show that the bioconvective system under consideration is dependent on gyrotactic microorganisms concentration, and both the nanofluids have almost the same behaviors for the effects of all the pertinent parameters except the effect of Schmidt number on the microorganism density function where the effect is opposite. Raees et al. [8] presented the study of gravity-driven nano-biconvection Newtonian thin liquid film containing nanoparticles and gyrotactic microorganisms using both actively and passively controlled nanofluid model boundary conditions. In terms of nanofluids, bioconvection is highly valuable. Nanotecnology has been widely used in many industrial applications. Nanofluids were introduced by Choi [9] and are defined as colloidal solutions of nanosized solid particles in base liquids. The particles are different from conventional particles (millimeter or microscale) in that they keep suspended in the base fluid and no sedimentation occurs. Nanofluids show anomalously high thermal conductivity and significant change in properties, such as viscosity and specific heat in comparison to the base fluid, features which have attracted many researchers to stimulate nanofluid flows with an emphasis on their performance in engineering applications. Buongiorno and Hu [10] reported the nanofluid heat transfer enhancement for nuclear reactor application. Huminic and Huminic [11] showed the applications of nanofluids in heat exchangers.

The study of non-Newtonian fluids has attracted the attention of engineers and scientists in recent times due to its important applications in many engineering process. The analysis of such flows is very important in both theory and practice. From a theoretical point of view, flows of this type are fundamental in fluid mechanics and convective heat transfer. From a practical point of view, these flows have applications in convection cooling processes where a coolant is impinged on a continuously moving plate. Heat and mass transfer of non-Newtonian fluids are also very important in many engineering applications, such as oil recovery, food processing, paper making, and slurry transporting. Similarly, dusty fluid flow has applications in petroleum and chemical engineering, metallurgy, dust entertainment in a cloud during a nuclear explosion, nuclear reactor cooling, powder technology, and paint spraying. Owing to such significance, Turkyilmazoglu [12] investigated the fluid flow dispensed with dust particles and heat transfer over stretching and shrinking bodies from a mathematical point of view rather than a numerical analysis published in the open literature. He proved that the two-phase flow and heat can be represented through a simple but ingeniously smart formula from which knowledge can be gained for the momentum and thermal layer behaviors in both phases, and hence exact information on the shear stress and Nusselt number of practical interest can be achieved. Nowadays, researchers have keen interest in investigating non-Newtonian fluid flows. Khan et al. [13] investigated thermophoresis and thermal radiation with heat and mass transfer in a magnetohydrodynamic thin film second grade fluid of variable properties past a stretching sheet. By using HAM for the solution, they showed the significant role of the fluid variable properties like thermal conductivity and viscosity under the variation of thin film. Abel et al. [14] examined the influences of viscous dissipation and non-uniform heat source/sink on the boundary layer flow and heat transfer characteristics of a non-Newtonian second grade fluid through a porous medium. Khan et al. [15] analyzed the steady boundary layer flow and heat transfer of a non-Newtonian second grade fluid through a porous medium past a stretching sheet showing that velocity and temperature decrease by increasing the magnitude of different parameters. Ahmad et al. [16] carried out the mathematical analysis of heat transfer effects on the axisymmetric flow of a second grade fluid over a radially stretching sheet employing homotopy analysis method for the solution. Khan et al. [17] discussed the magnetohydrodynamic nanoliquid thin film sprayed on a stretching cylinder with heat transfer using HAM, showing that pressure and spray rate enhance with increasing the film size. Sahoo [18] analyzed the numerical solution of the laminar flow and heat transfer of an incompressible third grade electrically conducting fluid impinging normal to a plane in the presence of a uniform magnetic field. Khan et al. [19] presented Brownian motion and thermophoresis effects on MHD mixed convective thin film second grade nanofluid flow with Hall effect and heat transfer past a stretching sheet by proving that the two dimensional flow converts into three dimensions due to the strong applied magnetic field.

Homotopy analysis method (HAM) [20] is followed in the present study to solve the transformed equations. In this method, homotopy with an embedding parameter is constructed. So, the nonlinear problem is converted into an infinite number of linear problems without using perturbation methods. Turkyilmazoglu [21] used the homotopy technique for the solution of an Airy equation with suitable boundary conditions to show the decaying/growing Airy solutions where the homotopy is handled in such a way that an appropriate auxiliary linear operator with constant coefficients is employed, generating pure analytic and uniform valid solutions. Optimum values for the convergence control parameter of the resulted homotopy series can be calculated from the square residual error idea, and the error can be analytically evaluated via absolute error formula. The proposed homotopy analysis method gives exact formulae for the displacement function that presents a close agreement with the problems solved numerically. Employing this approach, Turkyilmazoglu [22] considered the nonlinear problem of Duffing equation by a homotopy analysis method treatment, not using any small parameter like the perturbation methods, generating explicit analytic formulae for the quantities of physical interest for any given parameters. Moreover, the approximate analytic solutions achieved via HAM have been proven to be uniformly convergent for the chosen damping and stiffness parameters and are not only restricted to these parameters. The current study specifies physical parameters in (10–14) prevailing the flow resulting from the non-dimensionalization of (2–7). If (10–15) are to be solved through numerical methods, then all values of these parameters must be pre-entered. The range of physical parameters must be specified because the generated solution may be meaningless, since the desired accuracy of the solution may not be hit or the worst, is the unconsciously use of divergent solutions. To solve this issue, Turkyilmazoglu [23] proposed a technique to combine the Adomian decomposition method (ADM) with the squared residual error to investigate the correct range of physical parameters that exist in different flow models. He concluded that with the proposed mathematical approach, the correct range of physical parameters satisfying a certain degree of accuracy can be extracted and upon the selection of physical parameters from this range; the ADM series solutions are safely convergent, thereby no further need to justify the results with other numerical methods.

The Taylor series method is one of the classical methods and is equally important to find the approximate solutions. It has a close relationship with other computing methods like the homotopy perturbation method (HPM), because under certain constraints, by particular choice of auxiliary linear operator and initial approximation, the homotopy perturbation method simply collapses onto the Taylor series expansion. Turkyilmazoglu [24] proved that under certain special conditions, the traditional homotopy perturbation method becomes the well-known Taylor series expansion.

The purpose of the present study is to discuss the bioconvection in gravity-driven non-Newtonian second grade nanoliquid thin film flow containing both nanoparticles and gyrotactic microorganisms along a convectively heated vertical solid surface. Employing appropriate transformations the basic governing equations of the problem are obtained in dimensionless form, which have been solved using a powerful analytic tool HAM. The influences of all the pertinent parameters on velocity, temperature, concentration, and microorganism concentration fields have been shown graphically and illustrated.

2 Methods

2.1 Basic Equations

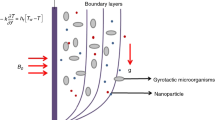
A motion of a two-dimensional, time-independent, laminar, and an incompressible second grade thin nanoliquid film falling downwards due to gravity along a vertical solid surface is considered as shown in Fig. 1. The uniform incoming second grade thin film nanofluid flow on the left side of the plate has constant temperature T _f and on the right side of the plate has another constant temperature T _∞ at x = 0.

Fig. 1

Geometry of the physical model and coordinates system

Convection through the plate plays an important role in cooling or heating the thin film. To avoid the bioconvection instability, it is assumed that the nanofluid is dilute. Also, the assumption is taken for the stability of the nanoparticles suspended in the base fluid so that the nanoparticles do not agglomerate in the fluid. The passive control of nanoparticles volume fraction at the boundary (on the solid wall) is taken. It is assumed that the microorganisms have constant distributions on the wall. It is most important to note that the base fluid is water so that the microorganisms can survive. The assumption is also maintained that the existence of nanoparticles have few effects on the motion of the microorganisms.

Under the use of abovementioned assumptions, the equations for the conservations of total mass, momentum, thermal energy, nanoparticles, and microorganisms are written in the following as in [7, 8]

$$ \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0, $$

(1)

$$\begin{array}{@{}rcl@{}} \rho_{f} \left( u \frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y}\right) &=& \rho_{f}U\frac{dU}{dx} + \mu_{f}\frac{\partial^{2}u}{\partial y^{2}}\\ && +{\kern2pt}\alpha_{1}\;\left[\frac{\partial}{\partial x} \left( u\frac{\partial^{2}u}{\partial y^{2}}\right) - \frac{\partial u}{\partial y} \frac{\partial^{2}u}{\partial x\partial y} + v \frac{\partial^{3}u}{\partial y^{3}}\right]\\ && + \left[(1 - C) \rho_{f_{\infty}} g\beta (T - T_{\infty})\right]\\ && - \left[ (\rho_{p} - \rho_{f_{\infty}}) g(C - C_{\infty})\right]\\ && + \left[g(N - N_{\infty}) \gamma_{av}{\Delta}\rho \right], \end{array} $$

(2)

$$ u \frac{\partial T}{\partial x} + v \frac{\partial T}{\partial y} = \lambda \frac{\partial^{2}T}{\partial y^{2}} + \tau \left[ D_{B} \left( \frac{\partial C}{\partial y} \frac{\partial T}{\partial y}\right) + \left( \frac{D_{T}}{T_{\infty}} \right) \left( \frac{\partial T}{\partial y} \right)^{2} \right], $$

(3)

$$ u \frac{\partial C}{\partial x} + v\frac{\partial C}{\partial y} = \frac{D_{B}\partial^{2}C}{\partial y^{2}} + \frac{D_{T}}{T_{\infty}} \frac{\partial^{2}T}{\partial y^{2}}, $$

(4)

$$ u \frac{\partial N}{\partial x} + v \frac{\partial N}{\partial y} + \frac{\partial (N\overset{\thicksim}{v})}{\partial y} = D_{n}\frac{\partial^{2}N}{\partial y^{2}}, $$

(5)

where

$$ \frac{\text{dp}}{\text{dx}} = \rho_{f}U\frac{\text{dU}}{\text{dx}}, \quad U = (2\text{ax})^{\frac{1}{2}}, $$

(6)

U is the free-stream velocity, a is constant, and when the flow is due to gravity, then a = g, u, and v being the velocity components in the x- and y-directions. α₁ is the normal stress moduli, $\overset {\thicksim }{v}= \left (\frac {\text {bW}_{c}}{{\Delta } C} \right ) \frac {\partial C}{\partial y}$ is the average swimming velocity vector of the oxytactic microorganisms in which b is the chemotaxis constant and W _c is the maximum cell swimming speed. The subscripts p, f, and f _∞ denote respectively the solid particles: the nanofluid and the base fluid at far field. ${\Delta }\rho = \rho _{\text {cell}} - \rho _{f_{\infty }}$ is the density difference between a cell and base fluid density at far field, μ _f is the dynamic viscosity, γ_av is the average volume of microorganisms and ρ _f is the density of the nanoliquid. β is the coefficient of volumetric volume expansion of a second grade nanofluid, g is the acceleration due to gravity, C is the nanopartical volume fraction, N is the number density of motile microorganisms, C _∞ is the ambient nanofluid volume fraction, $\lambda = \frac {k}{\rho _{f}}$ is the thermal diffusivity of the nanofluid in which k is the thermal conductivity, $\tau = \frac {(\rho c)_{p}}{(\rho c)_{f}}$ is the ratio of nanoparticle heat capacity and the base fluid heat capacity, D _B is the Brownian diffusion coefficient, D _n is the diffusivity of microorganisms, T _∞ is the ambient temperature, D _T is the thermophoretic diffusion coefficient, and T is the temperature inside the boundary layer.

The boundary conditions for the passively controlled nanofluid model (second grade) are

$$\begin{array}{@{}rcl@{}} && u = 0, \quad v = 0, \quad - k \frac{\partial T}{\partial y} = h_{f} (T_{f} - T),\\ && D_{B} \frac{\text{dC}}{\text{dy}} + \frac{D_{T}}{T_{\infty}} \frac{\text{dT}}{\text{dy}} = 0, \quad N = N_{w} \quad \text{at} \quad y = 0, \end{array} $$

(7)

$$\begin{array}{@{}rcl@{}} && u \rightarrow U(x), \quad \frac{\partial u}{\partial x} \rightarrow 0, \quad T \rightarrow T_{\infty}, \quad C \rightarrow C_{\infty},\\ && N \rightarrow N_{\infty} \quad \text{as} \quad y \rightarrow \infty, \end{array} $$

(8)

where h _f (x) denotes the heat transfer coefficient due to T _f ,N _w is the wall concentration of microorganisms, and N _∞ is the ambient concentration of microorganisms. Note that, in order to satisfy the boundary conditions at infinity, it is necessary to set N _∞ = 0.

Introducing the transformations for non-dimensional variables f, 𝜃,ϕ,Ω, and similarity variable ζ as

$$\begin{array}{@{}rcl@{}} && \psi(x, y) = \left( \frac{4U\nu_{f}x}{3}\right)^{\frac{1}{2}} f(\zeta), \quad \theta(\zeta) = \frac{T-T_{\infty}}{T_{f}-T_{\infty}},\\ && \phi = \frac{C-C_{\infty}}{C_{w}-C_{\infty}}, \quad {\Omega} = \frac{N-N_{\infty}}{N_{w}-N_{\infty}}, \quad \zeta = \left[ \frac{3U}{4\nu_{f}x}\right]^{\frac{1}{2}} y,\\ \end{array} $$

(9)

where ψ is the stream function such that $u=\frac {\partial \psi }{\partial y}$ and $v=-\frac {\partial \psi }{\partial x}$, x and y are the Cartesian coordinates along surface and normal to it. $\nu _{f}=\frac {\mu _{f}}{\rho _{f}}$ is the kinematic viscosity of the second grade nanoliquid film. Equation (9) automatically satisfies mass conservation (1). With the help of (9), (2–5, 7–8) yield the following six equations (10–15)

$$\begin{array}{@{}rcl@{}} && f^{\prime\prime\prime} + \frac{2}{3} (1 - f^{\prime 2}) + ff^{\prime\prime} + \gamma_{1}(2 f^{\prime} f^{\prime\prime\prime} - f^{\prime\prime 2} - ff^{\text{iv}})\\ &&\quad\,\,\, +\, \mathit{\text{Gr}} \theta - \mathit{\text{Nr}} \phi + \mathit{\text{Rb}}{\Omega} = 0, \end{array} $$

(10)

$$ \theta^{\prime\prime} + \mathit{\text{Prf}}\theta^{\prime} + \mathit{\text{Nt}}(\theta^{\prime})^{2} + \mathit{\text{Nb}} \theta^{\prime}\phi^{\prime} = 0, $$

(11)

$$ \phi^{\prime\prime} + \mathit{\text{Lef}}\phi^{\prime} + \frac{\text{Nt}}{\text{Nb}}\theta^{\prime\prime} = 0, $$

(12)

$$ {\Omega}^{\prime\prime} + \mathit{\text{Scf}}{\Omega}^{\prime} - \mathit{\text{Pe}} (\phi^{\prime}{\Omega}^{\prime} + \phi^{\prime\prime}{\Omega}) = 0, $$

(13)

$$\begin{array}{@{}rcl@{}} && f = f^{\prime} = 0, \quad \theta^{\prime} = -\gamma_{2}(1 - \theta), \quad N_{b} \phi^{\prime} + N_{t} \theta^{\prime} = 0,\\ && {\Omega} = 1 \quad at \quad \zeta = 0, \end{array} $$

(14)

$$ f^{\prime} = 1, \quad f^{\prime\prime} = 0, \quad \theta =\phi = {\Omega} = 0 \quad \text{at} \quad \zeta = \infty, $$

(15)

where prime (^′) represents the derivative with respect to $\zeta , \gamma _{1}=\frac {4\alpha _{1}}{3a\mu _{f}}$ is the dimensionless second grade nanofluid parameter, $\mathit {\text {Gr}} = \frac {2(1 - C_{\infty })\rho _{f_{\infty }}g\beta (T_{f}-T_{\infty })}{3a\rho _{f}}$ is the buoyancy parameter naming Grashof number, $\mathit {\text {Nr}}=\frac {2(\rho _{p} - \rho _{f}) C_{\infty } g}{3a\rho _{f}}$ is the buoyancy ratio parameter, $\mathit {\text {Rb}}=\frac {2(N_{w}-N_{\infty }) g\gamma _{av}{\Delta }\rho }{3a\rho _{f}}$ is the bioconvection Rayleigh number, $\mathit {\text {Pr}}=\frac {\nu _{f}}{\lambda }$ is the Prandtl number, $\mathit {\text {Nt}}=\frac {\tau D_{T}(T_{f} - T_{\infty })}{\lambda T_{\infty }}$ is the thermophoresis parameter, $\mathit {\text {Nb}}=\frac {\tau D_{B}C_{\infty }}{\lambda }$ is the Brownian motion parameter, $\mathit {\text {Le}}=\frac {\nu _{f}}{D_{B}}$ is the Lewis number, $\mathit {\text {Sc}}=\frac {\nu _{f}}{D_{n}}$ is the Schmidt number, $\mathit {\text {Pe}}=\frac {\text {bW}_{c}}{D_{n}}$ is the bioconvection Peclet number, $\gamma _{2}=\frac {1}{k(\frac {4\mu _{f}}{3})^{\frac {1}{2}}}$ is the reduced heat transfer parameter. For γ₁ = 0, the present study corresponds to viscous fluid case.

3 Solution of the Problem by Homotopy Analysis Method

Choosing the appropriate initial approximations to satisfy the boundary conditions and auxiliary linear operators for velocity, temperature, concentration, and motile microorganism concentration in the following form

$$\begin{array}{@{}rcl@{}} && f_{0} (\zeta) = \zeta - \left[ \exp (- \zeta) - \exp(- 2 \zeta) \right],\\ && \theta_{0}(\zeta) = \exp(- \zeta) - \frac{\exp(- 2\zeta)}{2 + \gamma_{2}},\\ && \phi_{0}(\zeta) = - \frac{\text{Nt}\gamma_{2}}{\text{Nb}(2 + \gamma_{2})} \exp(- \zeta),\\ && {\Omega}_{0}(\zeta) = \exp(- \zeta), \end{array} $$

(16)

$$ {L}_{f} = f^{\prime\prime\prime} - f^{\prime}, \quad {L}_{\theta} = \theta^{\prime\prime} - \theta, \quad {L}_{\phi} = \phi^{\prime\prime} - \phi, \quad {L}_{{\Omega}} = {\Omega}^{\prime\prime} - {\Omega} $$

(17)

The following properties are satisfied with the above linear operators

$$\begin{array}{@{}rcl@{}} && {L}_{f}\left[C_{1} + C_{2}\exp(\zeta) + C_{3} \exp(-\zeta)\right] = 0,\\ && {L}_{\theta} \left[ C_{4} \exp(\zeta) + C_{5}\exp(-\zeta) \right] = 0,\\ && {L}_{\phi}\left[C_{6} \exp(\zeta) + C_{7} \exp(- \zeta) \right] = 0,\\ && {L}_{{\Omega}} \left[ C_{8} \exp(\zeta) + C_{9}\exp(- \zeta) \right] = 0, \end{array} $$

(18)

where C _i (i = 1 − 9) are the arbitrary constants.

3.1 Zeroth-Order Deformation Problems

Introducing the nonlinear operator ℵ as

$$\begin{array}{@{}rcl@{}} && \aleph_{f}[f(\zeta, p), \theta(\zeta, p), \phi(\zeta, p), {\Omega}(\zeta, p)] = \frac{\partial^{3}f(\zeta, p)}{\partial \zeta^{3}} \\&&\quad+ \frac{2}{3} \left[ 1 - \left( \frac{\partial f(\zeta, p)}{\partial \zeta}\right)^{2}\right] + f(\zeta, p) \frac{\partial^{2}f(\zeta, p)}{\partial \zeta^{2}}\\ && \quad+\,\, \gamma_{1}\;\left[ {}2 \frac{\partial f(\zeta, p)}{\partial \zeta} \frac{\partial^{3}f(\zeta, p)}{\partial \zeta^{3}}{}-{}\left( \frac{\partial^{2}f(\zeta, p)}{\partial \zeta^{2}}\right)^{2} {}-{} f(\zeta, p) \frac{\partial^{4}f(\zeta, p)}{\partial \zeta^{4}}{}\right] \\&&\quad+\,\, \mathit{\text{Gr}} \theta (\zeta, p) - \mathit{\text{Nr}} \phi(\zeta, p) + \mathit{\text{Rb}} {\Omega}(\zeta, p), \end{array} $$

(19)

$$\begin{array}{@{}rcl@{}} && \aleph_{\theta} [f(\zeta, p), \theta(\zeta, p), \phi(\zeta, p)] = \frac{\partial^{2} \theta(\zeta, p)}{\partial \zeta^{2}}\\ && \quad+\,\, \mathit{\text{Prf}}(\zeta, p) \frac{\partial \theta(\zeta, p)}{\partial \zeta} + \mathit{\text{Nt}}\left( \frac{\partial \theta(\zeta, p)}{\partial \zeta}\right)^{2}\\ && \quad+\,\, \mathit{\text{Nb}}\frac{\partial \theta(\zeta, p)}{\partial \zeta}\frac{\partial \phi(\zeta, p)}{\partial \zeta}, \end{array} $$

(20)

$$\begin{array}{@{}rcl@{}} && \aleph_{\phi}[f(\zeta, p), \theta(\zeta, p), \phi(\zeta, p)] = \frac{\partial^{2} \phi(\zeta, p)}{\partial \zeta^{2}}\\ && \quad+\, \mathit{\text{Lef}}(\zeta, p)\frac{\partial \phi(\zeta, p)}{\partial \zeta} + \frac{\text{Nt}}{\text{Nb}} \frac{\partial^{2} \theta(\zeta, p)}{\partial \zeta^{2}}, \end{array} $$

(21)

$$\begin{array}{@{}rcl@{}} &&\aleph_{{\Omega}}[f(\zeta, p), \phi(\zeta, p), {\Omega}(\zeta, p)] = \frac{\partial^{2} {\Omega}(\zeta, p)}{\partial \zeta^{2}} \\&&\quad+\, \mathit{\text{Scf}}(\zeta, p)\frac{\partial {\Omega}(\zeta, p)}{\partial \zeta} \\&&\quad-\, \mathit{\text{Pe}} \left[ \frac{\partial \phi(\zeta, p)}{\partial \zeta}\frac{\partial {\Omega}(\zeta, p)}{\partial \zeta} \,+\, \frac{\partial^{2} \phi(\zeta, p)}{\partial \zeta^{2}}{\Omega}(\zeta, p) \right], \end{array} $$

(22)

where p is an embedding parameter such that p ∈ [0,1].

The zeroth-order deformation equations are constructed as

$$\begin{array}{@{}rcl@{}} &&(1 - p) l{L}_{f} [f(\zeta, p) - f_{0}(\zeta)] \\&&\quad= p \hslash \aleph_{f} [f(\zeta, p), \theta(\zeta, p), \phi(\zeta, p), {\Omega}(\zeta, p)], \end{array} $$

(23)

$$\begin{array}{@{}rcl@{}} (1 - p) {L}_{\theta} [\theta(\zeta, p) - \theta_{0}(\zeta)] = p \hslash \aleph_{\theta} [f(\zeta, p), \theta(\zeta, p), \phi(\zeta, p)], \end{array} $$

(24)

$$ (1 - p) {L}_{\phi} [\phi(\zeta, p) - \phi_{0}(\zeta)] = p \hslash \aleph_{\phi} [f(\zeta, p), \theta(\zeta, p), \phi(\zeta, p)], $$

(25)

$$ (1 - p) {L}_{{\Omega}} [{\Omega}(\zeta, p) - {\Omega}_{0}(\zeta)] = p \hslash \aleph_{{\Omega}} [f(\zeta, p), \phi(\zeta, p), {\Omega}(\zeta, p)], $$

(26)

where $\hslash$ represents the auxiliary non-zero parameter. Equation (23) has the boundary conditions

$$ f (0, p) = 0, \quad f^{\prime} (0, p) = 0, \quad f^{\prime\prime} (\infty, p) = 0, \quad f^{\prime} (\infty, p) = 1. $$

(27)

Equation (24) has the boundary conditions

$$ \theta^{\prime} (0, p) = -\gamma_{2}(1 - \theta (0, p)), \quad \theta (\infty, p) = 0. $$

(28)

Equation (25) has the boundary conditions

$$ N_{b} \phi^{\prime} (0, p) + N_{t} \theta^{\prime} (0, p) = 0, \quad \phi(\infty, p) = 0. $$

(29)

Similarly, (26) has the boundary conditions

$$ {\Omega} (0, p) = 1, \quad {\Omega}(\infty, p) = 0. $$

(30)

Considering the role of p when it assumes the values 0 and 1,

$$ p = 0 \Rightarrow f (\zeta, 0) = f_{0}(\zeta) \quad \text{and} \quad p = 1 \Rightarrow f(\zeta, 1) = f(\zeta), $$

(31)

$$ p = 0 \Rightarrow \theta (\zeta, 0) = \theta_{0}(\zeta) \quad \text{and} \quad p = 1 \Rightarrow \theta(\zeta, 1) = \theta(\zeta), $$

(32)

$$ p = 0 \Rightarrow \phi (\zeta, 0) = \phi_{0}(\zeta) \quad \text{and} \quad p = 1 \Rightarrow \phi(\zeta, 1) = \phi(\zeta), $$

(33)

Similarly,

$$ p = 0 \Rightarrow {\Omega} (\zeta, 0) = {\Omega}_{0}(\zeta) \quad \text{and} \quad p = 1 \Rightarrow {\Omega}(\zeta, 1) = {\Omega}(\zeta). $$

(34)

f(ζ,p) becomes f₀(ζ) to f(ζ) when p assumes the values from 0 to 1. 𝜃(ζ,p) becomes 𝜃₀(ζ) to 𝜃(ζ) when p has the values from 0 to 1. Similarly, ϕ(ζ,p) becomes ϕ₀(ζ) to ϕ(ζ) when p assumes the values from 0 to 1. Exactly in the same manner for p = 0,Ω(ζ,0) = Ω₀(ζ) and for p = 1,Ω(ζ,1) = Ω(ζ). Using the Taylor series expansion and (23–26), these become

$$\begin{array}{@{}rcl@{}} && f(\zeta, p) = f_{0} (\zeta) + \sum\limits_{m = 1}^{\infty} f_{m} (\zeta) p^{m},\\ && f_{m} (\zeta) = \frac{1}{m!} \frac{\partial^{m} f(\zeta, p)}{\partial p^{m}} \mid_{p = 0}, \end{array} $$

(35)

$$\begin{array}{@{}rcl@{}} && \theta(\zeta, p) = \theta_{0}(\zeta) + \sum\limits_{m = 1}^{\infty} \theta_{m}(\zeta)p^{m},\\ && \theta_{m}(\zeta) = \frac{1}{m!} \frac{\partial^{m} \theta(\zeta, \textit{p})}{\partial p^{m}}\mid_{p = 0}, \end{array} $$

(36)

$$\begin{array}{@{}rcl@{}} && \phi(\zeta, p) = \phi_{0}(\zeta) + \sum\limits_{m = 1}^{\infty} \phi_{m}(\zeta) p^{m},\\ && \phi_{m}(\zeta) = \frac{1}{m!} \frac{\partial^{m} \phi(\zeta, p)}{\partial p^{m}} \mid_{p = 0}, \end{array} $$

(37)

$$\begin{array}{@{}rcl@{}} && {\Omega}(\zeta, p) = {\Omega}_{0}(\zeta) + \sum\limits_{m = 1}^{\infty} {\Omega}_{m}(\zeta) p^{m},\\ && {\Omega}_{m}(\zeta) = \frac{1}{m!} \frac{\partial^{m} {\Omega}(\zeta, p)}{\partial p^{m}} \mid_{p = 0}. \end{array} $$

(38)

The convergence of the series is sharply relying on $\hslash$. Suppose $\hslash$ is taken in such a manner that the series in (35–38) converge at p = 1, then (35–38) result in

$$ f(\zeta) = f_{0} (\zeta) + \sum\limits_{m = 1}^{\infty} f_{m} (\zeta), $$

(39)

$$ \theta(\zeta) = \theta_{0}(\zeta) + \sum\limits_{m = 1}^{\infty}\theta_{m}(\zeta), $$

(40)

$$ \phi(\zeta) = \phi_{0}(\zeta) + \sum\limits_{m = 1}^{\infty}\phi_{m}(\zeta), $$

(41)

$$ {\Omega}(\zeta) = {\Omega}_{0}(\zeta) + \sum\limits_{m = 1}^{\infty}{\Omega}_{m}(\zeta). $$

(42)

3.2 M-th Order Deformation Problems

By taking m times derivative with respect to p of (23) and (27), then dividing by m! and substituting p = 0, yield the following simplifications

$$ {L}_{f} [f_{m} (\zeta) - \chi_{m} f_{m-1} (\zeta)] = \hslash \mathfrak{R}^{f}_{m}(\zeta), $$

(43)

$$ f_{m}(0) = f^{\prime}_{m}(0) = f^{\prime}_{m}(\infty) = f^{\prime\prime}_{m}(\infty) = 0, $$

(44)

$$\begin{array}{@{}rcl@{}} \mathfrak{R}_{m}^{f}(\zeta) &&= {f}_{m-1}^{\prime\prime\prime} + \frac{2}{3} \sum\limits_{k = o}^{m - 1} \left[ 1 - {f}_{m-1-k}^{\prime} {f}_{k}^{\prime} \right] + \sum\limits_{k = o}^{m - 1} \left[ f_{m - 1 - k} {f}_{k}^{\prime\prime} \right]\\ && \quad+\, \gamma_{1} \sum\limits_{k = 0}^{m - 1} \left[ 2 {f}_{m-1-k}^{\prime} {f}_{k}^{\prime\prime\prime} - {f}_{m - 1 - k}^{\prime\prime} {f}_{k}^{\prime\prime} - f_{m - 1 - k} {f}_{k}^{iv} \right] \\&&\quad+\, \mathit{\text{Gr}}\theta_{m-1} - \mathit{\text{Nr}}\phi_{m-1} + \mathit{\text{Rb}}{\Omega}_{m-1}. \end{array} $$

(45)

By taking m times derivative with respect to p of (24) and (28), then dividing by m! and substituting p = 0, yield the following simplifications

$$ {L}_{\theta} [\theta_{m}(\zeta) - \chi_{m}\theta_{m-1}(\zeta)] = \hslash \mathfrak{R}^{\theta}_{m}(\zeta), $$

(46)

$$ {\theta}_{m}^{\prime}(0) = \theta_{m}(\infty) = 0, $$

(47)

$$\begin{array}{@{}rcl@{}} \mathfrak{R}_{m}^{\theta}(\zeta) &=& {\theta}_{m-1}^{\prime\prime} + \mathit{\text{Pr}} \sum\limits_{k = o}^{m - 1} f_{m - 1 - k} {\theta}_{k}^{\prime} + \mathit{\text{Nt}} \sum\limits_{k = o}^{m - 1} {\theta}_{m - 1 - k}^{\prime} {\theta}_{k}^{\prime}\\ && +\,\, \mathit{\text{Nb}} \sum\limits_{k = o}^{m - 1} {\theta}_{m - 1 - k}^{\prime} {\phi}_{k}^{\prime}. \end{array} $$

(48)

By taking m times derivative with respect to p of (25) and (29), then dividing by m! and substituting p = 0, result in the below simplifications

$$ {L}_{\phi} [\phi_{m}(\zeta) - \chi_{m}\phi_{m-1}(\zeta)] = \hslash {\mathfrak{R}}_{m}^{\phi}(\zeta), $$

(49)

$$ N_{b} {\phi}_{m}^{\prime} (0) + N_{t} {\theta}_{m}^{\prime} (0) = \phi_{m}(\infty) = 0, $$

(50)

$$ {\mathfrak{R}}_{m}^{\phi}(\zeta) = {\phi}_{m-1}^{\prime\prime} + \mathit{Le} \sum\limits_{k = o}^{m - 1} f_{m - 1 - k} {\phi}_{k}^{\prime} + \frac{\text{Nt}}{\text{Nb}} {\theta}_{m-1}^{\prime\prime}. $$

(51)

Similarly, by taking m times derivative with respect to p of (26) and (30), then diving by m! and substituting p = 0, develop the below simplifications

$$ {L}_{{\Omega}} [{\Omega}_{m}(\zeta) - \chi_{m}{\Omega}_{m-1}(\zeta)] = \hslash {\mathfrak{R}}_{m}^{{\Omega}}(\zeta), $$

(52)

$$ {\Omega}_{m}(0) = {{\Omega}}_{m}^{\prime} (\infty) = 0, $$

(53)

$$\begin{array}{@{}rcl@{}} {\mathfrak{R}}_{m}^{{\Omega}} (\zeta) &=& {{\Omega}}_{m-1}^{\prime\prime} + \mathit{\text{Sc}} \sum\limits_{k = o}^{m - 1} f_{m - 1 - k} {{\Omega}}_{k}^{\prime}\\ && -\,\, \mathit{Pe} \sum\limits_{k = o}^{m - 1} \left[ {\phi}_{m-1-k}^{\prime} {{\Omega}}_{k}^{\prime} + {\phi}_{m-1-k}^{\prime\prime} {\Omega}_{k} \right], \end{array} $$

(54)

$$ \chi_{m} = \left\{\begin{array}{ll} 0, & m \leqslant 1 \\ 1, & m > 1. \end{array}\right. $$

(55)

If ${f}_{m}^{*} (\zeta ), {\theta }_{m}^{*}(\zeta ), {\phi }_{m}^{*}(\zeta )$, and ${{\Omega }}_{m}^{*}(\zeta )$ are the particular solutions, then the general solutions of (43), (46), (49), and (52) are

$$ f_{m}(\zeta) = {f}_{m}^{*} (\zeta) + C_{1} + C_{2} \exp(\zeta) + C_{3} \exp(- \zeta), $$

(56)

$$ \theta_{m}(\zeta) = {\theta}_{m}^{*} (\zeta) + C_{4} \exp(\zeta) + C_{5} \exp(- \zeta), $$

(57)

$$ \phi_{m}(\zeta) = {\phi}_{m}^{*} (\zeta) + C_{6} \exp(\zeta) + C_{7} \exp(- \zeta), $$

(58)

$$ {\Omega}_{m}(\zeta) = {{\Omega}}_{m}^{*} (\zeta) + C_{8} \exp(\zeta) + C_{9} \exp(- \zeta). $$

(59)

4 Results and Discussion

The nonlinear differential (10–13) accompanying boundary conditions in (14–15) have been solved with the help of symbolic computation software MATHEMATICA employing HAM program. It is necessary for the analysis to discuss the effect of all the emerging parameters on the non-dimensional velocity profile, non-dimensional temperature profile, non-dimensional concentration profile and non-dimensional motile gyrotactic microorganisms profile f(ζ),𝜃(ζ),ϕ(ζ), and Ω(ζ) respectively. The effects of embedded parameters on the velocity f(ζ), temperature 𝜃(ζ), concentration ϕ(ζ), and motile gyrotactic microorganisms Ω(ζ) fields have been depicted in Figs. 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26 and 27, 28, 29, 30, 31, 32, 33 respectively. The schematic diagram of the problem is demonstrated in Fig. 1. Liao [20] introduced $\hslash$ curves for the convergence of the series solutions of the problems. Therefore, the admissible $\hslash$-curves for f(ζ),𝜃(ζ),ϕ(ζ) and Ω(ζ) are drawn in the ranges $-~1.3~\leq ~\hslash ~ \leq ~0.2, -~1.4~\leq ~\hslash ~\leq ~0.5, -~1.3~\leq ~\hslash ~\leq ~0.0$ and $-~1.9~\leq ~\hslash ~\leq ~0.0$ in Figs. 2, 3, 4, and 5 respectively.

Fig. 2

$\hslash$ curve of f(ζ)

Fig. 3

$\hslash$ curve of 𝜃(ζ)

Fig. 4

$\hslash$ curve of ϕ(ζ)

Fig. 5

$\hslash$ curve of Ω(ζ)

4.1 Velocity Profile

The non-Newtonian nanofluids are thick to flow and their speed is low compared to that of Newtonian nanofluids. Figure 6 presents the elevation of velocity f(ζ) profile as a function of second grade nanofluid parameter γ₁. It predicts the linear dependency between f(ζ) and γ₁. The reason is that the velocity of the second grade nanofluid enhances due to gravity. The same behavior is seen in Fig. 7, where the non-dimensional velocity f(ζ) increases for the larger values of reduced heat transfer parameter γ₂. In line with the experimental observations, Fig. 7 predicts that the higher the reduced heat transfer parameter γ₂ is, the higher the velocity will be. It is due to the orientation of the fluid farther apart from the vertical surface. Considering Fig. 8 which shows that the uniform flow can be fully captured against the buoyancy parameter Gr. To our knowledge, this constitutes the direction of flow due to gravitational force. Figure 9 reveals dynamical regimes: a fast flow regime. This diagram presents that the velocity f(ζ) increases with the rise of buoyancy ratio parameter Nr. Figure 10 measures pattern formation in suspension of gyrotactic microorganisms in terms of velocity as a function of the bioconvection Rayleigh number Rb. Note that velocity f(ζ) decreases with increasing the bioconvection Rayleigh number Rb. Figure 11 reports that the non-dimensional velocity f(ζ) is an increasing function of thermophoresis parameter Nt as the momentum boundary layer thickness amplifies. It is observed that Fig. 12 is composed of Lewis number Le and velocity f(ζ). Quite remarkably, the density of the interacting objects (nanoparticles and microorganisms) increase the velocity f(ζ) when the Lewis number Le increases. Figure 13 shows that with the rise of Schmidt number Sc the velocity f(ζ) increases. It is due to the fact that the Schmidt number Sc involves the effective physical property like viscosity. Figure 14 reveals that the velocity f(ζ) enhances with the amplification of Prandtl number Pr. The reason is that the suspension becomes dense due to nanoparticles and gyrotactic microorganisms consequently, high values of Pr associate with the elevation of f(ζ).

Fig. 6

Behavior of velocity field for $\hslash = - 1.10, \gamma _{2} = 0.60, \mathit {\text {Gr}} = 0.50, \mathit {\text {Nr}} = 0.60, \mathit {\text {Rb}} = 0.70, \mathit {\text {Nb}} = 0.80, \mathit {\text {Nt}} = 0.90, \mathit {\text {Le}} = 0.60, \mathit {\text {Sc}} = 0.70, \mathit {\text {Pe}} = 1.00, \mathit {\text {Pr}} = 10.00$ and different values of γ₁

Fig. 7

Behavior of velocity field for $\hslash = - 5.00, \gamma _{1} = 0.50, \mathit {\text {Gr}} = 0.50, \mathit {\text {Nr}} = 0.60, \mathit {\text {Rb}} = 0.70, \mathit {\text {Nb}} = 0.80, \mathit {\text {Nt}} = 0.90, \mathit {\text {Le}} = 0.60, \mathit {\text {Sc}} = 0.70, \mathit {\text {Pe}} = 1.00, \mathit {\text {Pr}} = 10.00$ and different values of γ₂

Fig. 8

Behavior of velocity field for $\hslash = -~1.10, \gamma _{1} = 0.50, \gamma _{2} = 0.60, \mathit {\text {Nr}} = 0.60, \mathit {\text {Rb}} = 0.70, \mathit {\text {Nb}} = 0.80, \mathit {\text {Nt}} = 0.90, \mathit {\text {Le}} = 0.60, \mathit {\text {Sc}} = 0.70, \mathit {\text {Pe}} = 1.00, \mathit {\text {Pr}} = 10.00$ and different values of Gr

Fig. 9

Behavior of velocity field for $\hslash = -~3.00, \gamma _{1} = 0.50, \gamma _{2} = 0.60, \mathit {\text {Gr}} = 0.50, \mathit {\text {Rb}} = 0.70, \mathit {\text {Nb}} = 0.80, \mathit {\text {Nt}} = 0.90, \mathit {\text {Le}} = 0.60, \mathit {\text {Sc}} = 0.70, \mathit {\text {Pe}} = 1.00, \mathit {\text {Pr}} = 10.00$ and different values of Nr

Fig. 10

Behavior of velocity field for $\hslash = -~3.00, \gamma _{1} = 0.50, \gamma _{2} = 0.60, \mathit {\text {Gr}} = 0.50, \mathit {\text {Nr}} = 0.60, \mathit {\text {Nb}} = 0.80, \mathit {\text {Nt}} = 0.90, \mathit {\text {Le}} = 0.60, \mathit {\text {Sc}} = 0.70, \mathit {\text {Pe}} = 1.00, \mathit {\text {Pr}} = 10.00$ and different values of Rb

Fig. 11

Behavior of velocity field for $\hslash = -~5.00, \gamma _{1} = 0.50, \gamma _{2} = 0.60, \mathit {\text {Gr}} = 0.50, \mathit {\text {Rb}} = 0.70, \mathit {\text {Nb}} = 0.80, \mathit {\text {Nr}} = 0.60, \mathit {\text {Le}} = 0.60, \mathit {\text {Sc}} = 0.70, \mathit {\text {Pe}} = 1.00, \mathit {\text {Pr}} = 10.00$ and different values of Nt

Fig. 12

Behavior of velocity field for $\hslash = -~5.00, \gamma _{1} = 0.50, \gamma _{2} = 0.60, \mathit {\text {Gr}} = 0.50, \mathit {\text {Rb}} = 0.70, \mathit {\text {Nb}} = 0.80, \mathit {\text {Nt}} = 0.90, \mathit {\text {Nr}} = 0.60, \mathit {\text {Sc}} = 0.70, \mathit {\text {Pe}} = 1.00, \mathit {\text {Pr}} = 10.00$ and different values of Le

Fig. 13

Behavior of velocity field for $\hslash = -~3.00, \gamma _{1} = 0.50, \gamma _{2} = 0.60, \mathit {\text {Gr}} = 0.50, \mathit {\text {Rb}} = 0.70, \mathit {\text {Nb}} = 0.80, \mathit {\text {Nt}} = 0.90, \mathit {\text {Le}} = 0.60, \mathit {\text {Nr}} = 0.60, \mathit {\text {Pe}} = 1.00, \mathit {\text {Pr}} = 10.00$ and different values of Sc

Fig. 14

Behavior of velocity field for $\hslash = -~3.00, \gamma _{1} = 0.50, \gamma _{2} = 0.60, \mathit {\text {Gr}} = 0.50, \mathit {\text {Rb}} = 0.70, \mathit {\text {Nb}} = 0.80, \mathit {\text {Nt}} = 0.90, \mathit {\text {Le}} = 0.60, \mathit {\text {Sc}} = 0.70, \mathit {\text {Pe}} = 1.00, \mathit {\text {Nr}} = 0.60$ and different values of Pr

4.2 Temperature Profile

Temperature is affected by the nanofluid behaviors. Figure 15 exhibits the activity of second grade nanofluid parameter γ₁. It shows that the temperature 𝜃(ζ) increases with the non-Newtonian effect of the nanofluid. Figure 16 shows that the temperature 𝜃(ζ) upsurges with the rising behavior of reduced heat transfer parameter γ₂. In fact, the reduced heat transfer parameter γ₂ represents the thermal slip parameter; hence, the temperature increases spontaneously in the presence of convective conditions. Figure 17 demonstrates that the quantity of non-dimensional temperature 𝜃(ζ) enriches with the amplification in magnitude of buoyancy parameter Gr. Figure 18 reveals that the development in thermophoresis parameter Nt leads to an enhancement in the temperature. Physically, intriguing property of nanofluids like Brownian motion focuses on random motion of the particles which opens up the way for the elevation of non-dimensional temperature 𝜃(ζ). Figure 19 portrays the effect of Lewis number Le on the present system under consideration. This illustrates that temperature bears much significance rise with the greater values of Lewis number Le. The cooling of surrounding and system involve the influence of Prandtl number Pr. For such situation, Fig. 20 is helpful to show that the temperature 𝜃(ζ) diminishes with the increasing values of Pr.

Fig. 15

Behavior of temperature field for $\hslash = -~0.90, \gamma _{2} = 0.60, \mathit {\text {Gr}} = 0.50, \mathit {\text {Nr}} = 0.60, \mathit {\text {Rb}} = 0.70, \mathit {\text {Nb}} = 0.80, \mathit {\text {Nt}} = 0.90, \mathit {\text {Le}} = 0.60, \mathit {\text {Sc}} = 0.70, \mathit {\text {Pe}} = 1.00, \mathit {\text {Pr}} = 10.00$ and different values of γ₁

Fig. 16

Behavior of temperature field for $\hslash = - 0.90, \gamma _{1} = 0.50, \mathit {\text {Gr}} = 0.50, \mathit {\text {Nr}} = 0.60, \mathit {\text {Rb}} = 0.70, \mathit {\text {Nb}} = 0.80, \mathit {\text {Nt}} = 0.90, \mathit {\text {Le}} = 0.60, \mathit {\text {Sc}} = 0.70, \mathit {\text {Pe}} = 1.00, \mathit {\text {Pr}} = 10.00$ and different values of γ₂

Fig. 17

Behavior of temperature field for $\hslash = -~1.10, \gamma _{1} = 0.50, \gamma _{2} = 0.60, \mathit {\text {Nr}} = 0.60, \mathit {\text {Rb}} = 0.70, \mathit {\text {Nb}} = 0.80, \mathit {\text {Nt}} = 0.90, \mathit {\text {Le}} = 0.60, \mathit {\text {Sc}} = 0.70, \mathit {\text {Pe}} = 1.00, \mathit {\text {Pr}} = 10.00$ and different values of Gr

Fig. 18

Behavior of temperature field for $\hslash = -~0.90, \gamma _{1} = 0.50, \gamma _{2} = 0.60, \mathit {\text {Nr}} = 0.60, \mathit {\text {Rb}} = 0.70, \mathit {\text {Nb}} = 0.80, \mathit {\text {Gr}} = 0.50, \mathit {\text {Le}} = 0.60, \mathit {\text {Sc}} = 0.70, \mathit {\text {Pe}} = 1.00, \mathit {\text {Pr}} = 10.00$ and different values of Nt

Fig. 19

Behavior of temperature field for $\hslash = -~0.90, \gamma _{1} = 0.50, \gamma _{2} = 0.60, \mathit {\text {Nr}} = 0.60, \mathit {\text {Rb}} = 0.70, \mathit {\text {Nb}} = 0.80, \mathit {\text {Nt}} = 0.90, \mathit {\text {Gr}} = 0.50, \mathit {\text {Sc}} = 0.70, \mathit {\text {Pe}} = 1.00, \mathit {\text {Pr}} = 10.00$ and different values of Le

Fig. 20

Behavior of temperature field for $\hslash = -~0.70, \gamma _{1} = 0.50, \gamma _{2} = 0.60, \mathit {\text {Nr}} = 0.60, \mathit {\text {Rb}} = 0.70, \mathit {\text {Nb}} = 0.80, \mathit {\text {Nt}} = 0.90, \mathit {\text {Le}} = 0.60, \mathit {\text {Sc}} = 0.70, \mathit {\text {Pe}} = 1.00, \mathit {\text {Gr}} = 0.50$ and different values of Pr

4.3 Concentration Profile

In the present study of bioconvection, nanoparticle concentration has important results. The role of passively controlled nanofluid model boundary conditions N _b ϕ^′(0) + N _t 𝜃^′(0) = 0 in (14) is worth seeing. It is also evident from the initial guess $\phi _{0}(\zeta ) = - \frac {N_{t}\gamma _{2}}{N_{b}({2} +\gamma _{2})} \exp (- \zeta )$ in (16). Due to the influence of these conditions, all the concentration graphs are negative. Figure 21 highlights the essential consequences of the non-Newtonian second grade nanofluid parameter γ₁. It is identified that the concentration ϕ(ζ) profile decreases with the addition of non-Newtonian second grade nanofluid. It may be due to the remarkable effect of viscoelasticity of non-Newtonian second grade nanofluid. Figure 22 sheds light on the structuring capabilities of reduced heat parameter γ₂. It is observed that the concentration ϕ(ζ) profile decreases. Figure 23 presents the possible outcomes of concentration ϕ(ζ) and Brownian motion parameter Nb. It shows that the non-dimensional nanoparticle concentration ϕ(ζ) profile increases, since the system involves additional internal constraints due to many gyrotactic microswimmers. The effect of thermophoresis parameter Nt on the concentration ϕ(ζ) profile is elucidated in Fig. 24. Due to the interaction of concentration with the temperature, a whole set of microorganisms and nanoparticles posses the additional ability to improve the saturation for some increasing values of Nt but then ϕ(ζ) decreases as Nt increases. Figure 25 shows that the concentration field ϕ(ζ) shows an increasing function of the Lewis number Le. The flowing suspension remains fully homogeneous on the surface. Figure 26 is plotted to depict the effect of the Prandtl number Pr on the nanoparticle concentration ϕ(ζ). It is noted that the non-dimensional concentration ϕ(ζ) decreases for the greater values of Prandtl number Pr.

Fig. 21

Behavior of concentration field for $\hslash = -~3.00, \gamma _{2} = 0.60, \mathit {\text {Gr}} = 0.50, \mathit {\text {Nr}} = 0.60, \mathit {\text {Rb}} = 0.70, \mathit {\text {Nb}} = 0.80, \mathit {\text {Nt}} = 0.90, \mathit {\text {Le}} = 0.60, \mathit {\text {Sc}} = 0.70, \mathit {\text {Pe}} = 1.00, \mathit {\text {Pr}} = 10.00$ and different values of γ₁

Fig. 22

Behavior of concentration field for $\hslash = -~3.00, \gamma _{1} = 0.50, \mathit {\text {Gr}} = 0.50, \mathit {\text {Nr}} = 0.60, \mathit {\text {Rb}} = 0.70, \mathit {\text {Nb}} = 0.80, \mathit {\text {Nt}} = 0.90, \mathit {\text {Le}} = 0.60, \mathit {\text {Sc}} = 0.70, \mathit {\text {Pe}} = 1.00, \mathit {\text {Pr}} = 10.00$ and different values of γ₂

Fig. 23

Behavior of concentration field for $\hslash = -~3.00, \gamma _{1} = 0.50, \gamma _{2} = 0.60, \mathit {\text {Nr}} = 0.60, \mathit {\text {Rb}} = 0.70, \mathit {\text {Nt}} = 0.90, \mathit {\text {Le}} = 0.60, \mathit {\text {Sc}} = 0.70, \mathit {\text {Pe}} = 1.00, \mathit {\text {Pr}} = 10.00$ and different values of Nb

Fig. 24

Behavior of concentration field for $\hslash = -~0.90, \gamma _{1} = 0.50, \gamma _{2} = 0.60, \mathit {\text {Nr}} = 0.60, \mathit {\text {Rb}} = 0.70, \mathit {\text {Nb}} = 0.80, \mathit {\text {Nt}} = 0.90, \mathit {\text {Le}} = 0.60, \mathit {\text {Sc}} = 0.70, \mathit {\text {Pe}} = 1.00, \mathit {\text {Pr}} = 10.00$ and different values of Nt

Fig. 25

Behavior of concentration field for $\hslash = -~0.90, \gamma _{1} = 0.50, \gamma _{2} = 0.60, \mathit {\text {Nr}} = 0.60, \mathit {\text {Rb}} = 0.70, \mathit {\text {Nb}} = 0.80, \mathit {\text {Nt}} = 0.90, \mathit {\text {Sc}} = 0.70, \mathit {\text {Pe}} = 1.00, \mathit {\text {Pr}} = 10.00$ and different values of Le

Fig. 26

Behavior of concentration field for $\hslash = -~0.90, \gamma _{1} = 0.50, \gamma _{2} = 0.60, \mathit {\text {Nr}} = 0.60, \mathit {\text {Rb}} = 0.70, \mathit {\text {Nb}} = 0.80, \mathit {\text {Nt}} = 0.90, \mathit {\text {Le}} = 0.60, \mathit {\text {Sc}} = 0.70, \mathit {\text {Pe}} = 1.00$ and different values of Pr

4.4 Microorganism Concentration

The present biological system has high sensitivity for the microorganism concentration in terms of various parameters. It is worth seeing from Fig. 27 that the microorganism concentration Ω(ζ) leads to remarkably development with the interaction of second grade nanofluid. The reason is that with the emergence of clusters of the nanoparticles and second grade fluid bear much significance, e. g., from a fundamental statistical physics point of view, many relevant practical situations actually involve additional constraints like gravity, pressure etc. Hence, by increasing second grade nanofluid parameter γ₁, the microorganism concentration Ω(ζ) elevates. The possibility of gyrotactic microorganisms existence in terms of thermal slip is demonstrated by Fig. 28. When the reduced heat parameter γ₂ magnifies, the microorganism concentration Ω(ζ) profile also magnifies. Figure 29 reports that the microorganism concentration Ω(ζ) reduces when the Brownian motion parameter Nb rises. Since Brownian motion associates with random motion of particles in fluid so there exists collisions which offer resistance to the motion of gyrotactic microorganisms. Figure 30 provides the sketch for thermophoresis parameter Nt and the microorganism concentration Ω(ζ). Thermophoresis depends on temperature mainly so with the enhancement of thermophoresis the gyrotactic microorganisms synthesize; consequently, the microorganism concentration Ω(ζ) enhances. Figure 31 shows the behavior of the microorganism concentration field Ω(ζ) with the rising values of Lewis number Le. From this plot, it is realized that when the Lewis number Le amplifies then microorganism concentration Ω(ζ) profile increases. The reason is that Lewis number Le defines the ratio of viscosity of nanofluid to the Brownian diffusion coefficient. So, for the less values of Le, microorganism concentration Ω(ζ) increases. Figure 32 focuses the high values of Schmidt number Sc to estimate the microorganism concentration Ω(ζ). When the magnitude of Schmidt number Sc amplifies the microorganism concentration Ω(ζ) decreases. Schmidt number Sc is inversely related to the diffusivity of microorganisms so at the greater values of Schmidt number Sc, the microorganism concentration Ω(ζ) profile depreciates. Figure 33 shows the effect of bioconvection Peclet number Pe on the microorganism concentration Ω(ζ), which explains the major purpose of the present study about the gyrotactic microorganism concentration. It is seen that the microorganism concentration Ω(ζ) grows high with the rising values of Peclet number Pe. Equation (13), Ω^″ + ScfΩ^′−Pe(ϕ^′Ω^′ + ϕ^″Ω) = 0 demonstrates that there is a strong coupling of nanoparticle field ϕ to the microorganism field Ω, suggesting the lower sensitivity of temperature and velocity fields to bioconvection Peclet number Pe compared with the nanoparticle field.

Fig. 27

Behavior of microorganisms concentration field for $\hslash = -~3.00, \gamma _{2} = 0.60, \mathit {\text {Gr}} = 0.50, \mathit {\text {Nr}} = 0.60, \mathit {\text {Rb}} = 0.70, \mathit {\text {Nb}} = 0.80, \mathit {\text {Nt}} = 0.90, \mathit {\text {Le}} = 0.60, \mathit {\text {Sc}} = 0.70, \mathit {\text {Pe}} = 1.00, \mathit {\text {Pr}} = 10.00$ and different values of γ₁

Fig. 28

Behavior of microorganisms concentration field for $\hslash = -~3.00, \gamma _{1} = 0.50, \mathit {\text {Gr}} = 0.50, \mathit {\text {Nr}} = 0.60, \mathit {\text {Rb}} = 0.70, \mathit {\text {Nb}} = 0.80, \mathit {\text {Nt}} = 0.90, \mathit {\text {Le}} = 0.60, \mathit {\text {Sc}} = 0.70, \mathit {\text {Pe}} = 1.00, \mathit {\text {Pr}} = 10.00$ and different values of γ₂

Fig. 29

Behavior of microorganisms concentration field for $\hslash = -~3.00, \gamma _{1} = 0.50, \gamma _{2} = 0.60, \mathit {\text {Gr}} = 0.50, \mathit {\text {Nr}} = 0.60, \mathit {\text {Rb}} = 0.70, \mathit {\text {Nt}} = 0.90, \mathit {\text {Le}} = 0.60, \mathit {\text {Sc}} = 0.70, \mathit {\text {Pe}} = 1.00, \mathit {\text {Pr}} = 10.00$ and different values of Nb

Fig. 30

Behavior of microorganisms concentration field for $\hslash = -~3.00, \gamma _{1} = 0.50, \gamma _{2} = 0.60, \mathit {\text {Gr}} = 0.50, \mathit {\text {Nr}} = 0.60, \mathit {\text {Rb}} = 0.70, \mathit {\text {Nb}} = 0.80, \mathit {\text {Le}} = 0.60, \mathit {\text {Sc}} = 0.70, \mathit {\text {Pe}} = 1.00, \mathit {\text {Pr}} = 10.00$ and different values of Nt

Fig. 31

Behavior of microorganisms concentration field for $\hslash = -~3.00, \gamma _{1} = 0.50, \gamma _{2} = 0.60, \mathit {\text {Gr}} = 0.50, \mathit {\text {Nr}} = 0.60, \mathit {\text {Rb}} = 0.70, \mathit {\text {Nt}} = 0.90, \mathit {\text {Nb}} = 0.80, \mathit {\text {Sc}} = 0.70, \mathit {\text {Pe}} = 1.00, \mathit {\text {Pr}} = 10.00$ and different values of Le

Fig. 32

Behavior of microorganisms concentration field for $\hslash = -~3.00, \gamma _{1} = 0.50, \gamma _{2} = 0.60, \mathit {\text {Gr}} = 0.50, \mathit {\text {Nr}} = 0.60, \mathit {\text {Nb}} = 0.80, \mathit {\text {Nt}} = 0.90, \mathit {\text {Le}} = 0.60, \mathit {\text {Pe}} = 1.00, \mathit {\text {Pr}} = 10.00$ and different values of Sc

Fig. 33

Behavior of microorganisms concentration field for $\hslash = -~3.00, \gamma _{1} = 0.50, \gamma _{2} = 0.60, \mathit {\text {Gr}} = 0.50, \mathit {\text {Nr}} = 0.60, \mathit {\text {Rb}} = 0.70, \mathit {\text {Nt}} = 0.90, \mathit {\text {Sc}} = 0.70, \mathit {\text {Nb}} = 0.80, \mathit {\text {Pr}} = 10.00$ and different values of Pe

5 Conclusions

This article investigates the analytical solution of bioconvection in gravity-driven non-Newtonian second grade nanoliquid thin film flow containing both nanoparticles and gyrotactic microorganisms along a convectively heated vertical solid surface. The thin film considered in this work contains the mixture of copper nanoparticles and motile gyrotactic microorganisms. The solution of the problem has been obtained by using the analytical technique HAM (homotopy analysis method) for the velocity, temperature, concentration, and microorganism concentration fields. The solution has been shown through the diagrams in which the influences of all the parameters on velocity, temperature, concentration, and microorganism concentration fields have been described. The main findings of the study are summarized as following.

• (i) The velocity f(ζ) depreciates for the bioconvection Rayleigh number Rb, while it elevates for the second grade nanofluid parameter γ₁, reduced heat transfer parameter γ₂, buoyancy parameter Gr, buoyancy ratio parameter Nr, thermophoresis parameter Nt, Lewis number Le, Schmidt number Sc, and Prandtl number Pr.

• (ii) The temperature 𝜃(ζ) diminishes for the reduced heat transfer parameter γ₂ and Prandtl number Pr while it elevates for the second grade nanofluid parameter γ₁, buoyancy parameter Gr, thermophoresis parameter Nt and Lewis number Le.

• (iii) The concentration ϕ(ζ) diminishes for the second grade nanofluid parameter γ₁, reduced heat transfer parameter γ₂, thermophoresis parameter Nt and Prandtl number Pr, while it elevates for the Brownian motion parameter Nb and Lewis number Le.

• (iv) The microorganism concentration Ω(ζ) diminishes for the Brownian motion parameter Nb and Schmidt number Sc, while it elevates for the second grade nanofluid parameter γ₁, reduced heat parameter γ₂, thermophoresis parameter Nt, Lewis number Le and bioconvection Peclet number Pe.