MHD boundary layer flow and heat transfer of micropolar fluid past a stretching sheet with second order slip

Abstract

The intention of this article is to examine a second order slip flow and magnetic field on boundary layer flow of micropolar fluid past a stretching sheet. Employing appropriate similarly transformation and non-dimensional variables, the governing non-linear boundary-value problems were reduced into coupled higher order non-linear ordinary differential equation. Then, solution for velocity, microrotation and temperature has been obtained numerically. The equations were numerically solved using the function bvp4c from the matlab for different values of governing parameters. Numerical results have been discussed for non-dimensional velocity, temperature, microrotation, the skin friction coefficient and local Nusselt number. The results indicate that the skin friction coefficient $C_{\text {f}}$ increases as the values of slip parameter $\gamma$ increase. However, the local Nusselt number $-\theta '(0)$ decreases as both slip parameter $\gamma$ and $\delta$ increase. A comparison with previous studies available in the literature has been done and an excellent agreement is obtained.

1 Introduction

A large number of research papers are available in open literature which deal with the boundary layer flow of micropolar fluid past a stretching sheet due to the fact that the boundary layer flow and heat transfer of a micropolar fluid has a significant importance in engineering applications. For example, it is important in the design of chemical processing materials which are useful in polymeric liquids, foodstuffs and slurries. The pioneering work on the theory of micropolar fluid was done by Eringen [1, 2] about half a century ago. By using this theory, the mathematical model of many non-Newtonian fluids was developed for which the classical Navier–Stokes theory is inappropriate. Since then, the analysis of a micropolar fluid has got the attention of many researchers in the areas of fluid science and engineering owing to its vast applications in many modern industries. Following him, many scholars have published papers on micropolar fluid by considering different aspects under different situations. Particularly, the study of boundary layer flow of micropolar fluid past a stretching surface has received more attention than other geometrical surfaces. This is because the boundary layer flow of an incompressible micropolar over a stretching sheet has important applications in many industrial and engineering processes such as in polymer industries. Especially, the study of flow of micropolar fluids due to stretching sheet has paramount importance in many industrial and engineering applications such as liquid crystal, dilute solution of polymers and suspensions etc [3]. However, the analysis of micropolar over shrinking sheet is another aspect. Accordingly, Yacob and Ishak [4] numerically examined the boundary layer flow of a micropolar fluid past a shrinking sheet. Similarly Ishak [5] studied the effect of thermal radiation on the boundary layer flow of micropolar fluid past a stretching sheet. It was indicated that radiation reduces the heat transfer rate at the surface. Furthermore, Ishak et al. [6–8] examined MHD stagnation point flow of a micropolar fluid towards a stretching, vertical and wedge. The analysis of convection in a doubly stratified micropolar fluid was extensively studied by Sinivasacharia and RamReddy [9–11]. Their numerical result indicated that the values of microrotation changes in sign with in the boundary layer.

The study of slip flow is a classical problem, however, it is still an active research area. Many scholars have examined slip flow under different aspects. For instance, Anderson [12, 13] examined the effects of slip, viscous dissipation, joule heating on boundary layer flow of a stretching surface. Moreover, scholars in Refs. [14–18] extended the investigation to a non-Newtonian fluid and analyzed the effects of partial slip, viscous dissipation, joule heating and MHD past a stretching surface. Furthermore, Das [19] studied the partial slip flow on MHD stagnation point flow of micropolar fluid past a shrinking sheet. The results show that an increase in slip parameter decreases the microrotation profile graphs. Still further, Noghrehabadi et al. [20] extended the study of slip flow to a nanofluid and numerically examined the effect of partial slip boundary condition on the flow and heat transfer of nanofluid past stretching sheet with prescribed constant wall temperature. Furthermore, Wubshet and Shanker [21] extended velocity slip boundary condition to thermal and concentration slip flow to a nanofluid and numerically analyzed MHD boundary layer flow and heat transfer of a nanofluid past a permeable stretching sheet with velocity, thermal and solutal slip boundary conditions.

The aforementioned studies consider only the first order slip flow. However, second order slip flow occurs in many industrial areas, but researchers have not paid much attention on it. Therefore, this study has given a full consideration to examine the effect of second order slip flow. Accordingly, Fang et al. [22] and Fang and Aziz [23] discussed viscous flow of a Newtonian fluid over a shrinking sheet with second order slip flow model. Similarly, Mahantesh et al. [24] examined second order slip flow and heat transfer over a stretching sheet with non-linear Navier boundary condition. They showed that both the first and the second order slip parameter significantly affect the shear stress. Moreover, Rosca and Pop [25, 26] investigated the second order slip flow and heat transfer over a vertical permeable stretching/shrinking sheet. The result of their study indicated that flow and heat transfer characteristics are strongly influenced by mixed convection, mass transfer and slip flow model parameters. By considering magnetic field, Turkyilmazoglu [27] studied analytically heat and mass transfer of MHD second order slip flow over a stretching sheet. Their study shows that increasing the values of magnetic parameter and second order slip parameter considerably reduce the magnitude of shear stress at the wall. Sing and Chamkha [28] also analyzed the dual solution for viscous fluid flow and heat transfer with second-order slip at linearly shrinking isothermal sheet in a quiescent medium.

To the best of author knowledge, no studies has been reported which discusses the effect of second order slip boundary condition on MHD boundary layer flow and heat transfer of micropolar fluid over a stretching sheet. Therefore, this study is targeted to fill this knowledge gap.

This study examine the effect of first, second order slip flow and magnetic parameter on boundary layer flow towards stretching sheet in micropolar fluid. The governing boundary layer equations were transformed into a two-point boundary value problem using similarity variables and numerically solved using bvp4c from matlab. The effects of physical parameters on fluid velocity, temperature and microrotation were discussed and shown in graphs and tables as well.

2 Mathematical formulation

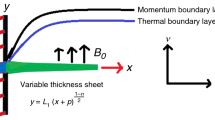
Consider a steady laminar boundary layer flow of a micropolar fluid past a stretching sheet with second order slip boundary condition with a constant temperature $T_{w}$. The uniform ambient temperature is given by $T_{\infty }$. It is assumed that the sheet is stretched with a velocity $u_{w}=ax$. Where a is a stretching constant. The flow is subjected to a constant transverse magnetic field of strength $B = B_{0}$ which is assumed to be applied in the positive y-direction, normal to the surface. Where $T_{w}$, $T_{\infty }$, and $B_{0}$ are temperature at the surface of the sheet, ambient temperature of the fluid and magnetic field strength respectively.

The coordinate frame selected in such away that x-axis is extending along the stretching sheet and y-axis is normal to it. The flow equations after boundary layer approximations can be defined as:

$$\begin{aligned}&\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0 \end{aligned}$$

(1)

$$\begin{aligned}&u ~ \frac{\partial u}{\partial x} + v ~ \frac{\partial u}{\partial y} = \frac{(\mu +\kappa )}{\rho } \left( \frac{\partial ^2 u}{\partial y^2}\right) + \frac{\kappa }{\rho }\frac{\partial N}{\partial y} -\frac{\sigma B^{2}_{0}}{\rho }u \end{aligned}$$

(2)

$$\begin{aligned}&u\frac{\partial N}{\partial x} + v ~ \frac{\partial N}{\partial y}= \frac{\Omega }{\rho j} \frac{\partial ^2 N}{\partial y^2}-\frac{\kappa }{\rho j}\bigg (2N + \frac{\partial u}{\partial y}\bigg )\end{aligned}$$

(3)

$$\begin{aligned}&u ~ \frac{\partial T}{\partial x} + v \frac{\partial T}{\partial y} = \frac{k}{\rho c_{p}} \left( \frac{\partial ^2 T}{\partial y^2}\right) \end{aligned}$$

(4)

The boundary conditions are:

$$\begin{aligned}&u = u_{w} + U_{\text {slip}}, \quad v = 0, \quad N =-n\frac{\partial u}{\partial y}, \quad T = T_{w}, \quad \text {at} \quad y = 0 \nonumber \\&u \rightarrow 0, \quad N \rightarrow 0, \quad T\rightarrow T_{\infty }, \quad \quad \text {as} \quad y\rightarrow \infty \end{aligned}$$

(5)

$U_{\text {slip}}$ is the slip velocity at the surface; Wu’s [29] slip velocity equation (valid for arbitrary Knudsen number, K $_n$) and used by researchers such as [17, 23, 24] is given by:

$$\begin{aligned}&U_{\text {slip}} = \frac{2}{3} \left( \frac{3-\alpha l^2}{\alpha }-\frac{3}{2}\frac{1-l^2}{K_{n}}\right) \lambda \frac{\partial u}{\partial y}-\frac{1}{4}\left[ l^4 +\frac{2}{K_{n}^2}(1-l^2)\right] \lambda ^2 \frac{\partial ^2 u}{\partial y^2}\nonumber \\&U_{\text {slip}} = A\frac{\partial u}{\partial y} + B\frac{\partial ^2 u}{\partial y^2} \end{aligned}$$

(6)

where A and B are constant, $K_{n}$ is Knudsen number, $l={\text {min}}\left[ \frac{1}{K_{n}},1\right]$, $\alpha$ is the momentum accommodation coefficient with $0 \le \alpha \le 1$, and $\lambda$ is the molecular mean free path. Based on the definition of l, it is noticed that for any given value of $K_{n}$, we have $0 \le l \le 1$. The molecular mean free path is always positive. Thus, it is known that $B < 0$, and hence the second term in the right hand side of Eq. (6) is a positive number. Moreover, $\gamma$ is the first order velocity slip parameter with $\gamma = A\sqrt{\frac{a}{\upsilon }}$, which is positive, $\delta$ is the second order velocity slip parameter with $\delta = \frac{Ba}{\upsilon }$ is negative. x and y represent coordinate axes along the continuous surface in the direction of motion and normal to it respectively. The velocity components along x and y-axis are u and v respectively. N is the microrotation or angular velocity whose direction of rotation is normal to the x–y plane, $\upsilon$ is the kinematics viscosity, $\kappa$ is the vortex viscosity, j is the micro-inertia density, $\Omega$ is the spin-gradient viscosity and given by $\Omega = (\mu + \frac{\kappa }{2})j=\mu (1+\frac{\beta }{2})j$, where $\beta =\frac{\kappa }{\mu }$, T is the temperature inside the boundary layer, $\rho$ is the fluid density, $T_\infty$ is ambient the temperature far away from the sheet and n is microrotation parameter which is a constant such that $0\le n \le 1$.

The similarity variable is defined by:

$$\begin{aligned} \eta = \sqrt{\frac{a}{\upsilon }}y \end{aligned}$$

(7)

The dimensionless variables $f, \theta , g$ are introduced as:

$$\begin{aligned}&f(\eta ) = \frac{\psi }{ \sqrt{a\upsilon } x}, \quad g(\eta ) = \frac{N}{ ax\sqrt{\frac{a}{\upsilon }}},\quad \theta (\eta ) = \frac{T - T_\infty }{T_{w}-T_\infty } \end{aligned}$$

(8)

The equation of continuity is satisfied if we choose a stream function $\psi (x,y)$ such that

$$\begin{aligned} u = \frac{\partial \psi }{\partial y},\quad \quad v = -\frac{\partial \psi }{\partial x} \end{aligned}$$

(9)

Using the above similarity transformation and dimensionless variables, the governing Eqs. (1)–(4) are reduced into the ordinary differential equation as follows:

$$\begin{aligned}&(1+\beta )f^{'''} + f f^{''}- f'^{2} +\beta g' - Mf' = 0 \end{aligned}$$

(10)

$$\begin{aligned}&\left(1+\frac{\beta }{2}\right) g''-\beta (2g + f'') + fg'-f'g = 0\end{aligned}$$

(11)

$$\begin{aligned}&\theta ^{''} + Pr f \theta ' = 0 \end{aligned}$$

(12)

With boundary conditions

$$\begin{aligned} f(0) = 0, f{'}(0) = 1 + \gamma f''(0) + \delta f'''(0), g(0)=-nf''(0), \theta (0) = 1,\quad \text {at}\quad \eta = 0,\nonumber \\ f{'}(\infty ) \rightarrow 0,\quad g(\infty ) \rightarrow 0, \quad \theta (\infty ) \rightarrow 0,\quad \text {as}\quad \eta \rightarrow \infty \end{aligned}$$

(13)

where the governing parameters are defined by:

$$Pr = \frac{\upsilon }{\Lambda }, \quad M = \frac{\sigma B_{0}^{2}}{\rho a},\quad \beta = \frac{\kappa }{\mu }. $$

where $f'$, $\theta$ and g are the dimensionless velocity, temperature and microrotation respectively. $\eta$ is the similarity variable, the prime denotes differentiation with respect to $\eta$. $\gamma$, $\delta$, Pr, M denotes first order slip parameter, second order slip parameter, Prandtl number and a magnetic parameter, respectively.

The engineering quantities of interest in this article are the skin friction coefficient $C_{\text {f}}$, and local Nusselt number $Nu_{x }$ are defined as:

$$\begin{aligned} C_{\text {f}}=\frac{\tau _w}{\rho u^2_w },\quad Nu_{x} = \frac{xq_w}{k(T_{w}-T_\infty )} \end{aligned}$$

(14)

where the wall shear stress $\tau _w$ and wall heat flux $q_w$ are given by:

$$\begin{aligned} \tau _w= \left[ (\mu +\kappa )\frac{\partial u}{\partial y} + \kappa N \right] _{y=0},\quad q_w = -k \left( \frac{\partial T }{\partial y} \right) _{y=0} \end{aligned}$$

(15)

By using the above equations, we get:

$$\begin{aligned} C_{\text {f}} \sqrt{Re_x} = -(1 + \beta (1-n))f''(0),\quad \frac{Nu_x}{\sqrt{Re_x}} = -\theta '(0) \end{aligned}$$

(16)

where $Re_x =\frac{ax^{2}}{\upsilon }$ and $Nu_{x}$ are local Reynolds and local Nusselt numbers, respectively.

3 Numerical solution

The coupled three ordinary differential equations Eqs. (10)–(12) which are subjected to the boundary conditions Eq. (13) are solved numerically using the function bvp4c from matlab for different values of physical parameters, viz. slip parameters $\gamma$ and $\delta$, Prandtl number Pr and magnetic parameter M.

4 Results and discussion

In this section, the effects of physical parameters on dimensionless velocity, temperature, microrotation, skin friction coefficient and local heat transfer rate have been discussed.

Fig. 1

Graph of f profile for different values of $\gamma$ when $n = 0.5$, $Pr=M=1$, $\delta =-1$, $\beta = 2$

Fig. 2

Graph of f profile for different values of $\delta$ when $n = 0.5$, $Pr = M =\gamma =1$, $\beta = 2$

Fig. 3

Graph of f profile for different values of $\beta$ when $n= 0.5$, $Pr=M=\gamma =1$, $\delta = -1$

Figures 1, 2 and 3 show the f profile graphs for different values of parameters such as first order slip parameter $\gamma$, second order slip parameter $\delta$ and material parameter $\beta$. The figures reveal that the boundary layer thickness increases with increasing values of $\gamma$ and $\delta$ while, it decreases with increasing values of $\beta$. These results are found to be in an excellent agreement with the results reported by Mahantesh et al. [24].

Fig. 4

Velocity profile for different values of $\gamma$ when $n= 0.5$, $Pr=M=1$, $\delta = -1$, $\beta =2$

Fig. 5

Velocity profile for different values of $\delta$ when $n= 0.5$, $Pr=M=\gamma =1$, $\beta = 2$

Fig. 6

Velocity graph for different values of $\beta$ when $n= 0.5$, $Pr=M=\gamma =1$, $\delta = -1$

The non-dimensional velocity profile graph $f'(\eta )$ for various values of the first order slip parameter $\gamma$, second order slip parameter $\delta$ and material parameter $\beta$ are depicted in Figs. 4, 5 and 6. These figures point out that $f'(\eta )$ is decreasing with increasing values of $\gamma$ and $\delta$, but the opposite effect is observed with $\beta$. Moreover, the velocity boundary thickness is decreasing as the values of $\gamma$ and $\delta$ are increasing in absolute value and also velocity at the surface decreases as the values of $\gamma$ and $\delta$ increase. Furthermore, as the values of material parameter $\beta$ increase, the surface velocity also increases.

Fig. 7

$f^{\prime\prime}$($\eta$) profile for different values of $\delta$ when $n= 0.5$, $Pr=M=\gamma =1$, $\beta = 2$

Fig. 8

$f^{\prime\prime}$($\eta$) profile for different values of $\gamma$ when $n= 0.5$, $Pr=M= 1$, $\delta =-1$, $\beta = 2$

Fig. 9

$f^{\prime\prime}$($\eta$) profile for different values of $\beta$ when $n= 0.5$, $Pr=M=\gamma = 1$, $\delta =-1$

Figures 7, 8 and 9 respectively show the effect of first order slip parameter $\gamma$, second order $\delta$ and material parameter $\beta$ on the skin friction profile $f''(\eta )$. These graphs are the increasing functions of all the three parameters in absolute value. Moreover, the boundary layer thickness of the coefficient of skin friction is an decreasing function of the first and second slip parameters, but it is increasing with the material parameter $\beta$.

Fig. 10

Temperature profile for different values of $\gamma$ when $n= 0.5$, $Pr=M=\beta = 1$, $\delta =-1$

Fig. 11

Temperature profile for different values of $\delta$ when $n= 0.5$, $Pr=M=\beta = \gamma = 1$

Fig. 12

Temperature profile for different values of $\beta$ when $n= 0.5$, $Pr=M=\gamma = 1$, $\delta =-1$

Fig. 13

Temperature graph for different values of n when $\beta = 2$, $Pr=M=\gamma = 1$, $\delta =-1$

Fig. 14

Temperature graph for different values of M when $\beta = 2$, $Pr=\gamma = 1$, $\delta =-1$, $n=0.5$

The effects of the slip parameters $\gamma$, $\delta$ and material parameter $\beta$, magnetic parameter M and n on temperature profile are given in Figs. 10, 11, 12, 13 and 14. From the figures, we can observe that the temperature of flow field is a decreasing function for both slip parameters. However, its thermal boundary thickness is increasing function for both slip parameters. Moreover, it is observed that the thermal boundary layer thickness is a decreasing function of material parameter $\beta$, but the thermal boundary layer thickness increases when the values of n and magnetic parameter M increase.

Fig. 15

Microrotation profile graph $g(\eta )$ for different values of $\gamma$ when $Pr=M=\beta = 1$, $\delta =-1$, $n=0.5$

Fig. 16

Microrotation profile graph $g(\eta )$ for different values of $\delta$ when $Pr=M=\beta =\gamma = 1$, $n=0.5$

Fig. 17

Microrotation profile graph $g(\eta )$ for different values of $\beta$ when $Pr=M=\gamma = 1$, $n=0.5$, $\delta =-1$

Fig. 18

Microrotation profile graph $g(\eta )$ for different values of M when $Pr=\gamma = 1$, $n=0.5$, $\delta =-1$

The microrotation (Angular velocity) profile graphs for physical parameters are given in Figs. 15, 16, 17 and 18. The graphs show that, as the values of both slip parameter $\gamma$ and $\delta$ increase, the microrotation boundary layer thickness decreases. Moreover, the angular velocity at the surface decreases as both the slip parameters increase. However, the angular velocity boundary layer thickness increases with material parameter $\beta$. Similarly, as the magnetic parameter M increases, the angular velocity boundary layer thickness decreases as shown in Fig. 18.

Table 1 Comparison of values of $f^{\prime\prime}\left( 0 \right)$ with slip factor $\gamma$ when $\mathrm {\mathrm{M}}=\delta =0$

In order to assess the accuracy of the method used, comparison with previously reported data available in the literature has been made. From Table 1, it can be seen that the numerical values of the skin friction coefficient $-f''(0)$ in this paper for different values of $\gamma$, when $M = \delta = 0$ are in an excellent agreement with the pervious results published in [14].

Table 2 Comparison of local Nusselt number $\theta ^{{\prime }}$ at $\beta =M=0.0,n=0.5,$ for different values of Pr with previously published result

To further confirm the accuracy of the numerical method used in the paper, comparison of local Nusselt number $-\theta '(0)$ for different values of Prandtl number Pr by ignoring the effects of M, $\lambda$ and $\delta$ parameters has been shown in Table 2, which is found to be in excellent agreement with [5]. These both results indicate that the numerical used in the study is appropriate and highly accurate.

Table 3 The computed values of skin friction coefficient $f^{\prime\prime}\left( 0 \right)$ and local Nusselt number $\theta ^{\prime }\left( 0 \right)$ when $Pr=1, n=0.5$ for different values of $\mathrm {\mathrm{M}}\beta \,$ and $\, \delta$

Furthermore, Table 3 shows the computed values of skin friction coefficient $-f''(0)$ and the local Nusselt number $-\theta '(0)$ for different values of the governing parameters such as M, $\beta$ and $\delta$. It is found that the heat transfer rate $-\theta '(0)$ is a decreasing function of the parameters $\beta$, $\gamma$ and $\delta$; however, the skin friction coefficient $-f''(0)$ is an increasing function of M, but a decreasing function of slip parameters $\gamma$ and $\delta$ and material parameter $\beta$.

5 Conclusions

In this paper, the effects of second order slip flow and magnetic field on boundary layer flow and heat transfer of micropolar fluid over a stretching sheet were discussed. The boundary layer equations governing the flow problem are reduced into a couple of high order non-linear ordinary differential equations using the similarity transformation. Then, the obtained differential equations are solved numerically using bvp4c from matlab software. The effects of various governing parameters, such as slip parameters $\gamma$ and $\delta$, magnetic parameter M, Prandtl number Pr, Material parameter $\beta$ on momentum, energy and microrotation equations are discussed using figures and tables.

From the study, it is found that the flow velocity and the skin friction coefficient are strongly influenced by slip and material parameters. It is also observed that the velocity boundary layer thickness decreases as the absolute values of slip parameters increase. However, the thermal boundary layer thickness increases as the absolute values of the two slip parameters increase. Furthermore, the skin friction coefficient $-f''(0)$ and the local Nusselt number $-\theta '(0)$ decrease as the absolute values of slip parameters increase.