1 Introduction

Superior properties of nanomaterials such as high mechanical strength, low density and good thermal and electrical properties make them suitable for various applications in microelectromechanical systems (MEMS) and nanoelectromechanical systems (NEMS). Since their discovery by Ge and Sattler (1994), carbon nanocones (CNCs) have attracted the attention of researchers from different disciplines. Due to the various applications of CNCs in nanomechanical systems, such as high resolution probes in atomic force microscopy (Mohammadi et al. 2010; Yeh et al. 2006) and also thermal rectifier (Yang et al. 2008), their mechanical analysis is of paramount importance.

Several experimental studies have been conducted to describe the mechanical behavior of nanostructures (Akita et al. 2006; Jeng et al. 2007; Endo et al. 2002; Terrones et al. 2001). However, as conducting such experiments is generally expensive and difficult to control at nanoscale, theoretical modeling is widely used in the area of nanomechanics. Different atomistic methods such as molecular dynamics (MD) (Hu et al. 2012; Firouz-Abadi et al. 2012; Liao 2014; Liao 2015) and molecular mechanics (MM) (Fakhrabadi et al. 2012; Ansari et al. 2014) have been employed to theoretically investigate the vibration and buckling of nanocones. The computational cost of atomistic simulations is also a restrictive parameter, especially for a nanostructure with a large number of atoms. Hence, the continuum mechanics can be regarded as a computationally efficient tool to study the mechanical behavior of nanomaterials.

The mechanical behavior of structures at the nanoscale is size-dependent (Sharma et al. 2003; Sun and Zhang 2003), and classical continuum mechanics cannot take the size effect into consideration. In this regard, the modified continuum theories are employed. Among size-dependent continuum theories, the nonlocal elasticity theory proposed by Eringen (1983, 2002), has been widely used to predict the mechanical behavior of graphene sheets (Peddieson et al. 2003; Arash and Wang 2011; Ebrahimi and Barati 2016) and carbon nanotubes (Wang et al. 2006; Pradhan and Reddy 2011; Hoseinzadeh and Khadem 2014). The major difference between classical and nonlocal theories is that in the classical theory one can determine the stress state at a given point by the strain state at the same point, whereas in the nonlocal theory, the stress state at a given point is a function of the strain state of all points in the body.

The nonlocal elasticity theory can properly predict the mechanical behavior of nanostructures (Gibson et al. 2007). Based on Eringen’s nonlocal theory and considering beam models, the vibration (Ebrahimi and Barati 2016; Dinçkal 2016; Yang et al. 2010) and buckling (Pradhan and Reddy 2011; Wu and Liou 2016; Wang et al. 2012) of carbon nanotubes has been studied by many researchers. Also, various studies have been carried out on the static (Ghorbanpour Arani et al. 2011, 2012; Gholami et al. 2017) and dynamic (Li and Kardomateas 2007; Hu et al. 2008; Asghari and Rafati 2010) behaviors of carbon nanotubes based on the nonlocal shell model. However, based on the nonlocal elasticity theory, a few studies have been performed on the vibration and buckling of CNCs. Based on the nonlocal elasticity theory and using the tapered rod model, Shu and Shau (2012) studied the axial vibration of CNCs. Using a nonlocal shell model and employing the Galerkin technique, Firouz-Abadi et al. (2011) investigated the free vibration of CNCs. Furthermore, Fotouhi et al. (2013) examined the free vibration of CNCs embedded in an elastic foundation based on a nonlocal continuum shell model. In that study, by considering Donnell’s linear strain–displacement relations for thin shells, the natural frequencies of simply supported CNCs were obtained. Based on an analytical approach, the nonlocal vibration of CNCs was analyzed by Ansari et al. (2014). They used the Galerkin method together with beam functions to study the effects of boundary conditions, semi-vertex angle and nonlocal parameter on the natural frequencies of CNCs. Firouz-Abadi et al. (2012) studied the mechanical buckling of CNCs under combined loading based on the nonlocal shell model. In that study, by considering the nonlinear von Kármán strain–displacement relations and using Hamilton’s principle, the governing equations were presented and the critical buckling load was calculated using the Galerkin method. The influences of different geometrical parameters and scale effects on the stability of nanocones were analyzed in their work. A survey of the literature indicates that no study has been performed on the thermal buckling of CNCs up to now. Consequently, in the present study, the thermal buckling of CNCs is studied based on the nonlocal elasticity theory. The CNC is considered as a conical shell structure. Employing Donnell’s strain–displacement relations for thin shells and considering the nonlocal effect, the governing equations are presented. To solve these equations, a semi-analytical approach is applied based on the GDQ method and trigonometric expansion. The effects of nonlocal parameter, boundary conditions and different geometrical parameters on the thermal instability of CNC are studied.

2 Governing Equations

The thermal buckling analysis of CNCs based on nonlocal shell theory is presented in this section. Based on the nonlocal elasticity theory proposed by Eringen (1983, 2002), the stress at a point is a function of strains at all points in the continuum. According to the nonlocal theory, the differential form of constitutive relation can be expressed as

$$ \left( {1 - \left( {e_{0} a} \right)^{2} \nabla^{2} } \right)\sigma = C\epsilon $$
(1)

where \( \sigma \) and \( \epsilon \) are the stress and strain vectors, respectively, and C is the material stiffness matrix. In addition, e0a stands for the characteristic length or nonlocal parameter which captures the size effect in small-scale structures and ∇2 introduces the Laplacian operator. Thus, for the linearly thermo-elastic material, the stress and strain relations can be defined according to Eq. (1) and based on Hooke’s law as

$$ \left\{ {\begin{array}{*{20}c} {\sigma_{x} } \\ {\sigma_{\theta } } \\ {\sigma_{x\theta } } \\ \end{array} } \right\} - \left( {e_{0} a} \right)^{2} \nabla^{2} \left\{ {\begin{array}{*{20}c} {\sigma_{x} } \\ {\sigma_{\theta } } \\ {\sigma_{x\theta } } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {Q_{11} } & {Q_{12} } & 0 \\ {Q_{12} } & {Q_{22} } & 0 \\ 0 & 0 & {Q_{66} } \\ \end{array} } \right]\left( {\left\{ {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{\theta } } \\ {\gamma_{x\theta } } \\ \end{array} } \right\} - \alpha \Delta T\left( z \right)\left\{ {\begin{array}{*{20}c} 1 \\ 1 \\ 0 \\ \end{array} } \right\}} \right) $$
(2)

where \( \Delta T\left( z \right) \) is the temperature difference through the thickness direction and the coefficients \( Q_{ij} \left( {i,j = 1,2,6} \right) \) are given as

$$ Q_{11} = Q_{22} = \frac{E}{{1 - \nu^{2} }}, \quad Q_{12} = \frac{E\nu }{{1 - \nu^{2} }}, \quad Q_{66} = \frac{E}{{2\left( {1 + \nu } \right)}}, $$
(3)

in which E and ν are Young’s modulus and Poisson’s ratio of the nanocone. In order to model the CNC, the following assumptions are considered:

  • The nanocone is considered as an elastic conical shell.

  • The governing equations are derived based on the thin shell model, and the nonlocal elasticity theory is used to capture the size-dependent behavior of CNC.

  • It is assumed that the material properties of CNC such as its Young’s modulus and Poisson’s ratio depend on the apex angle of the cone.

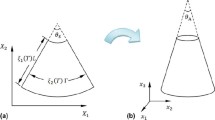
Figure 1 shows the schematic of conical shell with the small radius \( R_{1} \), large radius \( R_{2} \), thickness h, semi-apex angle β and length \( L \). Additionally, it should be pointed out that according to coordinate system shown in Fig. 1, the Laplacian operator can be expressed as \( \nabla^{2} = \frac{{\partial^{2} }}{{\partial x^{2} }} + \frac{\sin \left( \beta \right)}{R\left( x \right)}\frac{\partial }{\partial x} + \frac{1}{{R\left( x \right)^{2} }}\frac{{\partial^{2} }}{{\partial \theta^{2} }} \).

Fig. 1
figure 1

Geometry and coordinate system of nanocone

Full size image

Considering thin shell theory, the displacement field of CNC can be presented as

$$ \bar{u}\left( {x,\theta ,z} \right) = u\left( {x,\theta } \right) + z\frac{{\partial w\left( {x,\theta } \right)}}{\partial x},\;\bar{v}\left( {x,\theta ,z} \right) = v\left( {x,\theta } \right) + \frac{z}{R\left( x \right)}\frac{{\partial w\left( {x,\theta } \right)}}{\partial \theta },\;\bar{w}\left( {x,\theta ,z} \right) = w\left( {x,\theta } \right) $$
(4)

in which \( \bar{u}, \bar{v} \) and \( \bar{w} \) are the displacements of an arbitrary point of the CNC; and \( u, v \) and w represent the displacements of the mid-plane in the x, θ and z directions, respectively. Based on Kirchhoff–Love’s hypothesis, the strains at any point of the shell are Brush and Almroth (1975) and Eslami et al. (1996)

$$ \left\{ {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{\theta } } \\ {\gamma_{x\theta } } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\bar{\varepsilon }_{x} } \\ {\bar{\varepsilon }_{\theta } } \\ {\bar{\gamma }_{x\theta } } \\ \end{array} } \right\} + z\left\{ {\begin{array}{*{20}c} {\kappa_{x} } \\ {\kappa_{\theta } } \\ {\kappa_{x\theta } } \\ \end{array} } \right\} $$
(5)

where \( \bar{\varepsilon }_{x} \) and \( \bar{\varepsilon }_{\theta } \) are the mid-plane normal strains, \( \bar{\gamma }_{x\theta } \) is the mid-plane shear strain, κx and κθ are the mid-plane curvature changes, and κxθ is the mid-plane twist change. On the basis of classical shell theory and considering Donnell’s approach, the strain–displacement relations are defined as Brush and Almroth (1975).

$$ \left\{ {\begin{array}{*{20}c} {\bar{\varepsilon }_{x} } \\ {\bar{\varepsilon }_{\theta } } \\ {\bar{\gamma }_{x\theta } } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {u_{,x} } \\ {\frac{{v_{,\theta } }}{R\left( x \right)} + \frac{\cos \left( \beta \right)}{R\left( x \right)}w + \frac{\sin \left( \beta \right)}{R\left( x \right)}u} \\ {\frac{{u_{,\theta } }}{R\left( x \right)} + v_{,x} - \frac{\sin \left( \beta \right)}{R\left( x \right)}v} \\ \end{array} } \right\} + \frac{1}{2}\left\{ {\begin{array}{*{20}c} {w_{,x}^{2} } \\ {\frac{{w_{,\theta }^{2} }}{{R\left( x \right)^{2} }}} \\ {2\frac{{w_{,x} w_{,\theta } }}{R\left( x \right)}} \\ \end{array} } \right\} $$
(6)
$$ \left\{ {\begin{array}{*{20}c} {\kappa_{x} } \\ {\kappa_{\theta } } \\ {\kappa_{x\theta } } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} { - w_{,xx} } \\ { - \frac{{w_{,\theta \theta } }}{{R\left( x \right)^{2} }} - \frac{\sin \left( \beta \right)}{R\left( x \right)}w_{,x} } \\ { - 2\frac{{w_{,x\theta } }}{R\left( x \right)} + 2\frac{{{ \sin }\left( \beta \right)}}{{R\left( x \right)^{2} }}w_{,\theta } } \\ \end{array} } \right\} $$
(7)

In these equations, \( \left( {\blacksquare} \right)_{,x} \) and \( \left( {\blacksquare} \right)_{,\theta } \) denote the derivatives with respect to axial and circumferential directions, respectively.

Considering Eqs. (2)–(7), the nonlocal force and moment resultants can be obtained as

$$ \left\{ {\begin{array}{*{20}c} {N_{x} } \\ {N_{\theta } } \\ {N_{x\theta } } \\ \end{array} } \right\} - \left( {e_{0} a} \right)^{2} \nabla^{2} \left\{ {\begin{array}{*{20}c} {N_{x} } \\ {N_{\theta } } \\ {N_{x\theta } } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {A_{11} } & {A_{12} } & 0 \\ {A_{12} } & {A_{22} } & 0 \\ 0 & 0 & {A_{66} } \\ \end{array} } \right]\left( {\left\{ {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{\theta } } \\ {\gamma_{x\theta } } \\ \end{array} } \right\} - \left\{ {\begin{array}{*{20}c} {N^{T} } \\ {N^{T} } \\ 0 \\ \end{array} } \right\}} \right) $$
(8)
$$ \left\{ {\begin{array}{*{20}c} {M_{x} } \\ {M_{\theta } } \\ {M_{x\theta } } \\ \end{array} } \right\} - \left( {e_{0} a} \right)^{2} \nabla^{2} \left\{ {\begin{array}{*{20}c} {M_{x} } \\ {M_{\theta } } \\ {M_{x\theta } } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {D_{11} } & {D_{12} } & 0 \\ {D_{12} } & {D_{22} } & 0 \\ 0 & 0 & {D_{66} } \\ \end{array} } \right]\left( {\left\{ {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{\theta } } \\ {\gamma_{x\theta } } \\ \end{array} } \right\} - \left\{ {\begin{array}{*{20}c} {M^{T} } \\ {M^{T} } \\ 0 \\ \end{array} } \right\}} \right) $$
(9)

with

$$ (A_{ij} , D_{ij} ) = \mathop \int \limits_{ - h/2}^{h/2} Q_{ij} \left( {1,z^{2} } \right){\text{d}}z,\quad \left( {i,j = 1,2,6} \right) $$
(10)

and

$$ N^{T} = \mathop \int \limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} E\alpha \Delta T\left( z \right){\text{d}}z\quad M^{T} = \mathop \int \limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} E\alpha z\Delta T\left( z \right){\text{d}}z $$
(11)

where NT and MT stand for thermal force and moment resultants. The stability equations of carbon nanocones based on Dannell’s shell theory and using the adjacent equilibrium criterion can be written as Brush and Almroth (1975) and Akbari et al. (2015).

$$ \begin{aligned} & N_{x,x} + \frac{{N_{x\theta ,\theta } }}{R\left( x \right)} + \frac{\sin \left( \beta \right)}{R\left( x \right)}\left( {N_{x} - N_{\theta } } \right) = 0,\;\frac{{N_{\theta ,\theta } }}{R\left( x \right)} + N_{x\theta ,x} + \frac{2\sin \left( \beta \right)}{R\left( x \right)}N_{x\theta } = 0, \\ & M_{x,xx} + \frac{{2M_{x\theta ,x\theta } }}{R\left( x \right)} + \frac{{M_{\theta ,\theta \theta } }}{{R\left( x \right)^{2} }} - \frac{\cos \left( \beta \right)}{R\left( x \right)}N_{\theta } + \frac{{{ \sin }\left( \beta \right)}}{R\left( x \right)}\left( {2M_{x,x} - M_{\theta ,x} + \frac{{2M_{x\theta ,\theta } }}{R\left( x \right)}} \right) + \\ & \quad + \frac{1}{R\left( x \right)}\left( {R\left( x \right)N_{x}^{0} w_{,x} + N_{x\theta }^{0} w_{,\theta } } \right)_{,x} + \frac{1}{R\left( x \right)}\left( {N_{x\theta }^{0} w_{,x} + N_{\theta }^{0} \frac{{w_{,\theta } }}{R\left( x \right)}} \right)_{,\theta } = 0. \\ \end{aligned} $$
(12)

In addition, the clamped (C) and simply supported (S) boundary conditions can be given as

Clamped:

$$ u = v = w = w_{,x} = 0 $$
(13)

Simply supported:

$$ u = v = w = M_{x} = 0 $$
(14)

Moreover, N 0 x N 0 θ and N 0 xθ are prebuckling force resultants which according to the membrane solution of linear equilibrium equations can be obtained as Akbari et al. (2015) and Torabi et al. (2013).

$$ N_{x}^{0} = - \frac{{\left( {1 - \nu } \right)\sin \left( \beta \right)L}}{{R\left( x \right) { \ln }\left( {1 + \frac{{L{ \sin }\left( \beta \right)}}{{R_{1} }}} \right)}}N^{T} , $$
(15)

Substituting Eqs. (8) and (9) into Eq. (12) and considering the prebuckling force resultants defined in Eq. (15), one can write the nonlocal stability equations of CNCs in terms of displacement components as

$$ \begin{aligned} A_{{11}} \left( {u_{{,xx}} + \frac{{\sin \left( \beta \right)}}{{R\left( x \right)}}u_{{,x}} - \frac{{\sin ^{2} \left( \beta \right)}}{{R\left( x \right)}}u} \right) + \frac{{A_{{66}} }}{{R\left( x \right)^{2} }}u_{{,\theta \theta }} - \frac{{(A_{{11}} + A_{{66}} )\sin \left( \beta \right)}}{{R\left( x \right)^{2} }}v_{{,\theta }} \hfill \\ ~\quad + \frac{{(A_{{12}} + A_{{66}} )}}{{R\left( x \right)}}v_{{,x\theta }} - \frac{{{\text{A}}_{{11}} \cos \left( \beta \right)\sin \left( \beta \right)}}{{R\left( x \right)^{2} }}w + \frac{{{\text{A}}_{{12}} \cos \left( \beta \right)}}{{R\left( x \right)}}w_{{,x}} = 0, \hfill \\ \end{aligned} $$
(16)
$$ \begin{aligned} &\frac{{(A_{{11}} + A_{{66}} )\sin \left( \beta \right)}}{{R\left( x \right)^{2} }}u_{{,\theta }} + \frac{{(A_{{12}} + A_{{66}} )}}{{R\left( x \right)}}u_{{,x\theta }} + \frac{{A_{{11}} }}{{R\left( x \right)^{2} }}v_{{,\theta \theta }} + A_{{66}} \left( {v_{{,xx}} } \right. + \frac{{\sin \left( \beta \right)}}{{R\left( x \right)}}v_{{,x}} \hfill \\& \quad \left. { - \frac{{\sin ^{2} \left( \beta \right)}}{{{\text{R}}\left( {\text{x}} \right)}}v} \right) + \frac{{{\text{A}}_{{11}} \cos \left( \beta \right)}}{{R\left( x \right)^{2} }}w_{{,\theta }} = 0, \hfill \\ \end{aligned} $$
(17)
$$ \begin{aligned} & \frac{{{\text{A}}_{11} \cos \left( \beta \right)\sin \left( \beta \right)}}{{R\left( x \right)^{2} }}u + \frac{{{\text{A}}_{12} \cos \left( \beta \right)}}{R\left( x \right)}u_{,x} + \frac{{{\text{A}}_{11} \cos \left( \beta \right)}}{{R\left( x \right)^{2} }}v_{,\theta } + \frac{{A_{11} { \cos }^{2} \left( \beta \right)}}{{R\left( x \right)^{2} }}w + D_{11} w_{,xxxx} \\ & \quad + \frac{{2\left( {D_{12} + 2D_{66} } \right)\cos \left( \beta \right)}}{{R\left( x \right)^{2} }}w_{,xx\theta \theta } + \frac{{D_{11} }}{{R\left( x \right)^{4} }}w_{,\theta \theta \theta \theta } + \frac{{2D_{11} \sin \left( \beta \right)}}{R\left( x \right)}w_{,xxx} \\ & \quad - \frac{{2\left( {D_{12} + 2D_{66} } \right)\sin \left( \beta \right)}}{{R\left( x \right)^{3} }}w_{,x\theta \theta } - \frac{{D_{11} { \sin }^{2} \beta }}{{R\left( x \right)^{2} }}w_{,xx} + \frac{{2\left( {D_{12} + D_{11} + 2D_{66} } \right)\sin^{2} \left( \beta \right)}}{{R\left( x \right)^{4} }}w_{,\theta \theta } \\ & \quad + \frac{{D_{11} { \sin }^{3} \beta }}{{R\left( x \right)^{3} }}w_{,x} + \frac{{\left( {1 - \nu } \right)\sin \left( \beta \right)L N^{T} }}{{ { \ln }\left( {1 + \frac{{L{ \sin }\left( \beta \right)}}{{R_{1} }}} \right)}}\left[ {\frac{{w_{,xx} }}{R\left( x \right)} - \left( {e_{0} \alpha } \right)^{2} \left( {\frac{{w_{,xxxx} }}{R\left( x \right)} - \frac{\sin \left( \beta \right)}{{R\left( x \right)^{2} }}w_{,xxx} } \right.} \right. \\ & \quad \left. {\left. { - \frac{{\sin^{2} \left( \beta \right)}}{{R\left( x \right)^{3} }}w_{,xx} + \frac{1}{{R\left( x \right)^{3} }}w_{,xx\theta \theta } } \right)} \right] = 0. \\ \end{aligned} $$
(18)

3 Solution Procedure

The governing equations for thermal buckling of carbon nanocones are derived in previous section based on the nonlocal shell theory. Due to the circular shape of conical shell, the displacement components in circumferential direction (0 ≤ θ ≤ 2π) are periodic. Therefore, the partial differential Eqs. (16)–(18) can be converted into ordinary differential equations using the following separation of variables approach (Brush and Almroth 1975; Akbari et al. 2015)

$$ \left\{ {\begin{array}{*{20}c} {u\left( {x,\theta } \right)} \\ {v\left( {x,\theta } \right)} \\ {w\left( {x,\theta } \right)} \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {{ \sin }\left( {n\theta } \right)} & 0 & 0 \\ 0 & {{ \cos }\left( {n\theta } \right)} & 0 \\ 0 & 0 & {{ \sin }\left( {n\theta } \right)} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {U\left( x \right)} \\ {V\left( x \right)} \\ {W\left( x \right)} \\ \end{array} } \right\} $$
(19)

where in the above equation ns the wave number through the circumferential direction. Applying Eq. (19), the three coupled ordinary differential equations are obtained which are discretized by the use of the GDQ method. In this regard, a brief description of GDQ method is presented here.

3.1 GDQ Method

On the basis of the GDQ method (Shu 2000), the rth derivative of function f(x) is specified as a linear sum of the function, i.e.,

$$ \left. {\frac{{\partial^{r} f\left( x \right)}}{{\partial x^{r} }}} \right|_{{x = x_{i} }} = \mathop \sum \limits_{j = 1}^{{n_{1} }} \varsigma_{ij}^{r} f\left( {x_{j} } \right), \quad i = 1,2, \ldots ,n_{1} $$
(20)

in which ς r ij is the weighting coefficients and n1 is the number of grid points in x direction. A column vector \( {\mathbf{F}} \) can be given as

$$ {\mathbf{F}} = \left[ {F_{j} } \right] = \left[ {f\left( {x_{j} } \right)} \right] = \left[ {f\left( x \right),f\left( {x_{2} } \right), \ldots ,f\left( {x_{{n_{1} }} } \right)} \right]^{T} $$
(21)

where f(xj) is the nodal values of f(x) at x = xj. According to Eq. (20), a differential matrix operator can be written as

$$ \frac{{\partial^{r} }}{{\partial x^{r} }}\left( {\mathbf{F}} \right) = {\mathbf{D}}_{x}^{\left( r \right)} {\mathbf{F}} = \left[ {D_{x}^{\left( r \right)} } \right]_{i,j} \left\{ {F_{j} } \right\} $$
(22)

where

$$ {\mathbf{D}}_{x}^{\left( r \right)} = \left[ {D_{x}^{\left( r \right)} } \right]_{i,j} = \varsigma_{ij}^{r} , i,j = 1:n_{1} $$
(23)

In the above equation, ς r ij is presented by Shu (2000)

$$ \varsigma_{ij}^{r} = \left\{ {\begin{array}{*{20}l} {I_{ij} ,} \hfill & { r = 0 } \hfill \\ {\frac{{{\mathcal{L}}\left( {x_{i} } \right)}}{{\left( {x_{i} - x_{j} } \right){\mathcal{L}}\left( {x_{j} } \right)}}, } \hfill & {\left\{ {\begin{array}{*{20}l} {i \ne j\;{\text{and}}\;i,j = 1, \ldots ,n_{1} } \hfill \\ {r = 1} \hfill \\ \end{array} } \right.} \hfill \\ {n\left[ {\varsigma_{ij}^{1} \varsigma_{ii}^{r - 1} - \frac{{\varsigma_{ij}^{r - 1} }}{{x_{i} - x_{j} }}} \right], } \hfill & {\left\{ {\begin{array}{*{20}l} {i \ne j\;{\text{and}}\;i,j = 1, \ldots ,n_{1} } \hfill \\ {r = 2,3, \ldots ,n_{1} - 1} \hfill \\ \end{array} } \right.} \hfill \\ { - \sum\limits_{j = 1;j \ne i}^{{n_{1} }} {\varsigma_{ij}^{r} ,} } \hfill & {\left\{ {\begin{array}{*{20}l} {i = j\;{\text{and}}\;i,j = 1, \ldots ,n_{1} } \hfill \\ {r = 1,2, \ldots ,n_{1} - 1} \hfill \\ \end{array} } \right.} \hfill \\ \end{array} } \right. $$
(24)

where \( {\mathbf{I}} \) is a n1 × n1 identity matrix and \( {\mathcal{L}}\left( {x_{i} } \right) \) is given as

$$ {\mathcal{L}}\left( {x_{i} } \right) = \mathop \prod \limits_{j = 1;j \ne i}^{{n_{1} }} \left( {x_{i} - x_{j} } \right) $$
(25)

Previous studies (Tornabene et al. 2009) showed that the Chebyshev–Gauss–Lobatto grid point distribution has the most convergence and stability. Consequently, the grid points in axial direction can be generated as

$$ x_{i} = \frac{1}{2}\left( {1 - { \cos }\frac{i - 1}{{n_{1} - 1}}\pi } \right)L $$
(26)

Therefore, using the separation variables approach and GDQ method, the discretized form of governing equations of CNCs can be given as

$$ \left( {\left[ {\begin{array}{*{20}c} {K_{11} } & {K_{12} } & {K_{13} } \\ {K_{21} } & {K_{22} } & {K_{23} } \\ {K_{31} } & {K_{32} } & {K_{33} } \\ \end{array} } \right] + N^{\text{T}} \left[ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & {K_{g} } \\ \end{array} } \right]} \right)\left\{ {\begin{array}{*{20}c} U \\ V \\ W \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ \end{array} } \right\} $$
(27)

with

$$ \varvec{K}_{11} = A_{11} \left( {D_{x}^{2} + \sin \left( \beta \right)\bar{\varvec{R}}^{1} \varvec{D}_{x}^{1} - \sin^{2} \left( \beta \right)\bar{\varvec{R}}^{1} \varvec{D}_{x}^{0} } \right) - n^{2} A_{66} \bar{\varvec{R}}^{2} \varvec{D}_{x}^{0} $$
(28)
$$ \varvec{K}_{12} = n(A_{11} + A_{66} )\sin \left( \beta \right)\bar{\varvec{R}}^{2} \varvec{D}_{x}^{0} - n(A_{12} + A_{66} )\bar{\varvec{R}}^{1} \varvec{D}_{x}^{1} $$
(29)
$$ \varvec{K}_{13} = - {\text{A}}_{11} \cos \left( \beta \right)\sin \left( \beta \right)\bar{\varvec{R}}^{2} \varvec{D}_{x}^{0} + {\text{A}}_{12} \cos \left( \beta \right)\bar{\varvec{R}}^{1} \varvec{D}_{x}^{1} $$
(30)
$$ \varvec{K}_{21} = n(A_{11} + A_{66} )\sin \left( \beta \right)\bar{\varvec{R}}^{2} \varvec{D}_{x}^{0} + n(A_{12} + A_{66} )\bar{\varvec{R}}^{1} \varvec{D}_{x}^{1} $$
(31)
$$ \varvec{K}_{22} = - n^{2} A_{11} \bar{\varvec{R}}^{2} \varvec{D}_{x}^{0} + A_{66} \left( {\varvec{D}_{x}^{2} + \sin \left( \beta \right)\bar{\varvec{R}}^{1} \varvec{D}_{x}^{1} - \sin^{2} \left( \beta \right)\bar{\varvec{R}}^{1} \varvec{D}_{x}^{0} } \right) $$
(32)
$$ \varvec{K}_{23} = n{\text{A}}_{11} \cos \left( \beta \right)\bar{\varvec{R}}^{2} \varvec{D}_{x}^{0} $$
(33)
$$ \varvec{K}_{31} = {\text{A}}_{11} \cos \left( \beta \right)\sin \left( \beta \right)\bar{\varvec{R}}^{2} \varvec{D}_{x}^{0} + {\text{A}}_{12} \cos \left( \beta \right)\bar{\varvec{R}}^{1} \varvec{D}_{x}^{1} $$
(34)
$$ \varvec{K}_{32} = - n{\text{A}}_{11} \cos \left( \beta \right)\bar{\varvec{R}}^{2} \varvec{D}_{x}^{0} $$
(35)
$$ \begin{aligned} \varvec{K}_{33} & = D_{11} \varvec{D}_{x}^{4} + 2D_{11} \sin \left( \beta \right)\bar{\varvec{R}}^{1} \varvec{D}_{x}^{3} - \left( {2n^{2} \left( {D_{12} + 2D_{66} } \right)\cos \left( \beta \right) + D_{11} { \sin }^{2} \beta } \right)\bar{\varvec{R}}^{2} \varvec{D}_{x}^{2} \\ \qquad \left( {2n^{2} \left( {D_{12} + 2D_{66} } \right)\sin \left( \beta \right) + D_{11} { \sin }^{3} \beta } \right)\bar{\varvec{R}}^{3} \varvec{D}_{x}^{1} \\ \qquad \left. { + \left( { - 2n^{2} \left( {D_{12} + D_{11} + 2D_{66} } \right)\sin^{2} \left( \beta \right)\bar{\varvec{R}}^{4} } \right. + A_{11} { \cos }^{2} \left( \beta \right)\bar{\varvec{R}}^{2} + n^{4} D_{11} \bar{\varvec{R}}^{4} } \right)\varvec{D}_{x}^{0} \\ \end{aligned} $$
(36)
$$ \varvec{K}_{\varvec{g}} = \frac{{\left( {1 - \nu } \right)\sin \left( \beta \right)L}}{{ { \ln }\left( {1 + \frac{{L{ \sin }\left( \beta \right)}}{{R_{1} }}} \right)}}\left( {\bar{\varvec{R}}^{1} \varvec{D}_{x}^{2} } \right. - \left( {e_{0} \alpha } \right)^{2} \left( {\bar{\varvec{R}}^{1} \varvec{D}_{x}^{4} - \sin \left( \beta \right)\bar{\varvec{R}}^{2} \varvec{D}_{x}^{3} } \right.\left. { - \sin^{2} \left( \beta \right)\bar{\varvec{R}}^{3} \varvec{D}_{x}^{2} - n^{2} \bar{\varvec{R}}^{3} \varvec{D}_{x}^{2} } \right) $$
(37)

where

$$ \bar{\varvec{R}}^{i} = {\text{diag}}\left( {\left[ {\begin{array}{*{20}c} {\frac{1}{{\left( {R_{1} + \sin \left( \beta \right)x_{1} } \right)^{i} }}} \\ {\frac{1}{{\left( {R_{1} + \sin \left( \beta \right)x_{2} } \right)^{i} }}} \\ \vdots \\ {\frac{1}{{\left( {R_{1} + \sin \left( \beta \right)x_{{n_{1} }} } \right)^{i} }}} \\ \end{array} } \right]} \right),\quad \left( {i = 1,2,3,4} \right). $$
(38)

Substituting the boundary conditions into Eq. (27) and setting the determinant of coefficient matrix to zero, the critical thermal load can be obtained.

4 Results and Discussion

On the basis of nonlocal shell model, the buckling analysis of CNCs subjected to thermal loading was presented. The mechanical properties of CNCs such as Young’s modulus and Poisson’s ratio depend on the apex angle of the cone and can be given as follows (Hu et al. 2012; Firouz-Abadi et al. 2012; Wei et al. 2007): \( E = 0.89\cos^{4} \left( \beta \right) \left( {\text{TPa}} \right) \) and ν = 0.25 sin2(β). The wall thickness of the cone is considered to be \( h = 0.34\;{\text{nm}} \). In addition, the uniform temperature rise through the thickness direction of the nanocone is assumed as the thermal loading. The numerical results for thermal buckling of CNC is given based on non-dimensional thermal buckling load defined as

$$ n^{\text{T}} = \frac{{N^{\text{T}} R_{1}^{2} }}{{D_{11} }} $$
(39)

As mentioned before, the carbon nanocone is modeled as a continuum conical shell. In this regard, the accuracy of the present study is validated by the thermal buckling load of the conical shell given by Akbari et al. (2015). The critical buckling temperature difference of conical shell subjected to uniform temperature rise through the thickness direction is compared in Table 1 for different boundary conditions. For another comparison, the critical buckling temperature difference of conical shell is compared in Table 2 with the results reported by Sofiyev (2007) and Torabi et al. (2013). Sofiyev (2007) presented the stability equations based on modified Donnell’s shell theory, and the stress function together with the Galerkin method was employed to solve the problem. Also, Torabi et al. (2013) derived the stability equations based on the classical shell theory and Sander’s kinematic relations, and Galerkin method was used to find the critical buckling temperature. As it can be seen, the results are in good agreement with the reported data.

Table 1 Comparison of critical buckling temperature difference of conical shell (\( \frac{{R_{1} }}{h} = 300,\;\frac{L}{{R_{1} }} = 1, \;\beta = 15^\circ ,\;E = 322.27 \;{\text{GPa}}, \;\alpha = 7.47 \times 10^{ - 6} 1/^\circ {\text{C}}, \;\nu = 0.24 \))
Full size table
Table 2 Comparison of critical buckling temperature difference of conical shell (\( R_{2} = 0.25,\;L = 0.5077,\; \beta = 10^\circ ,\;E = 380\;{\text{GPa}},\;\alpha = 7.4 \times 10^{ - 6} 1/^\circ {\text{C}}, \;\nu = 0.3 \))
Full size table

Figure 2 shows the variations of non-dimensional thermal buckling load of CNC versus length-to-radius ratio for various nonlocal parameter values. Clamped–clamped (CC) and simply supported–simply supported (SS) boundary conditions are considered. As it can be seen, in the case of CC boundary condition and e0α = 1, the increase of length-to-radius ratio of the cone from L/R1 = 5 to L/R1 = 30 decreases the non-dimensional thermal buckling load for more than 58%. This amount is about 49% for SS boundary condition. The nonlocal parameter has an important effect on the thermal stability of the CNC, as the increase of nonlocal parameter considerably decreases the non-dimensional thermal buckling load. In addition, the results show that the buckling behavior of cones with the larger L/R1 ratio is less size-dependent.

Fig. 2
figure 2

Variation of non-dimensional thermal buckling load of CNC versus length-to-radius ratio for various nonlocal parameters and different boundary conditions (\( \frac{{R_{1} }}{h} = 25, \;2\beta = 38.9 \))

Full size image

Variations of non-dimensional thermal buckling load of CC and SS carbon nanocones versus the apex angle are demonstrated in Fig. 3 for various nonlocal parameters. Five apex angles of 19.2°, 38.9°, 60°, 86.6° and 112.9° are considered for CNC. It is observed that the cones with the smaller apex angles are more stable and buckle at higher thermal buckling loads. Moreover, the increase in apex angle of CNCs decreases the influence of nonlocal parameter and this effect is more evident in the case of CC carbon nanocones.

Fig. 3
figure 3

Variation of non-dimensional thermal buckling load of CNC versus apex angle for various nonlocal parameters and different boundary conditions (\( \frac{{R_{1} }}{h} = 25,\;\frac{L}{{R_{1} }} = 4 \))

Full size image

Figure 4 shows the variations of non-dimensional thermal buckling load of CC and SS CNCs versus the length-to-radius ratio for various radius-to-thickness ratios. It is found that increasing the R1/h ratio increases the non-dimensional thermal buckling load. In addition, one can see that in the case of the smaller radius-to-thickness ratios, the stability of the CNCs is less affected by the increase of L/R1 ratio.

Fig. 4
figure 4

Variation of non-dimensional thermal buckling load of CNC versus length-to-radius ratio for various radius-to-thickness ratios and different boundary conditions (\( e_{0} \alpha = 0.5\;{\text{nm}}, \;2\beta = 38.9 \))

Full size image

The changes of the non-dimensional thermal buckling load of CNCs are presented in Table 3 for different boundary conditions, nonlocal parameter values, radius-to-thickness ratios and length-to-radius ratios. In addition, the influences of boundary conditions on the non-dimensional thermal buckling load of CNCs are illustrated in Fig. 5. The results reveal that the edge conditions can play an important role on the buckling behavior of the short carbon nanocones, while in the case of the larger L/R1 ratios, the effects of boundary conditions are less significant. Furthermore, it can be seen that the increase of R1/h ratio decreases the size-dependent behavior of CNCs. Additionally, considering the stiffer boundary conditions at the edges of CNC makes the structure more stable and increases the non-dimensional thermal buckling load.

Table 3 Variations of non-dimensional thermal buckling load of CNCs (2β = 38.9)
Full size table
Fig. 5
figure 5

Variation of non-dimensional thermal buckling load of CNC versus length-to-radius ratio for various boundary conditions (\( e_{0} \alpha = 0.4\;{\text{nm}},\; 2\beta = 38.9,\;\frac{{R_{1} }}{h} = 20 \))

Full size image

5 Conclusion

Eringen’s nonlocal elasticity theory was incorporated into the thin shell theory to study the thermal buckling of CNCs. Considering Donnell’s strain–displacement relations for thin shells and taking the nonlocal effect into account, the governing equations were obtained. Employing the GDQ method in the axial direction and trigonometric expansion in circumferential direction, the stability equations were solved and the thermal buckling load was calculated. The accuracy of results was verified through comparison with those available in the literature. Moreover, the effects of various boundary conditions, apex angle and nonlocal parameter on the thermal instability of CNCs were examined.

The results indicated that the small-scale effect plays an important role in the thermal buckling of CNCs. The increase of nonlocal parameter significantly decreases the non-dimensional thermal buckling load of CNCs. Also, geometrical parameters such as length and apex angle have significant effects on the size-dependent thermal buckling load. The increase of length-to-radius ratio and apex angle makes the structure more flexible and reduces the non-dimensional thermal buckling load. Moreover, increasing the apex angle weakens the nonlocal effect on the buckling behavior of CNCs. Moreover, the effects of different boundary conditions on the thermal buckling of CNCs were examined, and the results revealed that the cones with CC and SS edge conditions have the highest and the lowest thermal buckling load. Also, the influences of boundary conditions on the thermal buckling load of short CNCs are more significant. Furthermore, the results showed that the increase in radius-to-thickness ratio decreases the size-dependency of non-dimensional thermal buckling load.