Application of Local Integrated Radial Basis Function Method for Solving System of Fredholm Integro-Differential Equations

Abstract

This paper thoroughly examines the Local Integrated Radial Basis Function (LIRBF) method’s performance in addressing linear systems and first- to higher-order Fredholm integro-differential problems. Utilizing a meshless approach with Gauss–Lobatto quadrature points for spatial discretization, we rigorously assess the method’s accuracy and efficiency across various numerical problems from the existing literature. Evaluation criteria, including maximum absolute errors and rates of convergence, validate the method’s effectiveness. To gauge the proposed LIRBF method’s efficacy, we benchmark it against well-established numerical techniques like Multi-Scale-Galerkin’s, Alpert Multiwavelets, Legendre multi-wavelets collocation, Legendre–Galerkin, Legendre polynomial approximation, and variational iteration methods. A comparative analysis based on criterion norms assesses the numerical results obtained by each method. The findings reveal that the proposed method demonstrates a significant reduction in sensitivity to the shape parameter compared to the RBF method. This observation establishes the robustness and stability of the proposed method, highlighting its ability to maintain accuracy and efficiency across diverse conditions. Results from numerical experiments and comparisons with other established techniques affirm the efficiency and accuracy of the LIRBF method in solving Fredholm integro-differential problems. The outcomes demonstrate promising performance, emphasizing the LIRBF method’s potential as a compelling alternative for addressing similar problems with high precision and computational efficiency.

1 Introduction

Fredholm integro-differential equations are a type of mathematical equation that combine both differential equations and integral equations. They were named after the Swedish mathematician Ivar Fredholm, who made significant contributions to the field of integral equations (Thieme 1977).

A Fredholm integro-differential equation involves an unknown function that appears both in the form of a differential equation and as an integral in the equation. These equations can be written in various forms, but generally, they can be expressed as Jalilian and Tahernezhad (2020):

$$\begin{aligned} L[u(x)]=f(x)+\lambda \int _a^b K(x, s, u(s)) d s, \end{aligned}$$

(1)

where u(x) is the unknown function, L is a linear differential operator, f(x) is a given function, K(x, s, u(s)) is the kernel function that depends on the unknown function and its value at s, $\lambda$ is a parameter and a and b define the interval of integration. These equations find applications in various scientific and engineering fields, such as physics, biology, economics, and engineering. They are used to model a wide range of phenomena involving time-dependent processes and interactions between different variables. To solve Fredholm integro-differential equations, one typically employs techniques from integral equations and differential equations, such as the method of successive approximations, numerical methods like finite difference or finite element methods, or other specialized methods developed for specific types of equations.

The search for efficient numerical methods to approximate solutions of integro-differential equations has been a subject of considerable research. Traditional analytical methods often face limitations in handling the complex nature of these equations, which involve both differential and integral operators. As a result, various numerical techniques have been developed to address these challenges and provide reliable approximations. One popular approach is the wavelet method (Behiry and Hashish 2003; ul Islam et al. 2013), which utilizes wavelet functions to discretize the equation and approximate the unknown function. Another method that has gained attention is the differential transform method (Behiry and Mohamed 2012), which involves transforming the integro-differential equation into a system of algebraic equations using differential operators. The Bernoulli matrix method (Bhrawy et al. 2012) offers an alternative approach by employing matrices constructed based on Bernoulli polynomials. The Chebyshev finite difference method (Dehghan and Saadatmandi 2008) combines the accuracy of Chebyshev polynomials with the finite difference scheme to approximate the solution of integro-differential equations. Hybrid methods, such as the one based on a combination of block pulse functions and normalized Bernstein polynomials (Behiry 2014), have been proposed to tackle integro-differential equations. Matrix methods utilizing Bell polynomials (Mirzaee 2017) provide effective tools for solving Fredholm-Volterra integral equations. The homotopy analysis method (Shidfar et al. 2010) offers a powerful technique for finding series solutions of high-order nonlinear Volterra and Fredholm integro-differential equations. Other methods, such as the exponential spline method (Jalilian and Tahernezhad 2020), multilevel augmentation method (Chen et al. 2019), multiscale Galerkin method (Chen et al. 2015), iterative method (Yulan et al. 2009), Sinc collocation method (Yeganeh et al. 2012), improved reproducing kernel method (Xue et al. 2018), Legendre polynomial method (Saadatmandi and Dehghan 2010), Walsh function method (Ordokhani 2010), and the parameterization method (Dzhumabaev 2016), form a part of the diverse array of numerical approaches. Each method offers its own unique advantages, making them suitable for different types of problems and providing valuable insights into the behavior of complex systems. In recent studies, several approaches have been proposed to solve integro-differential equations with diverse characteristics. Yalcin et al. (2020) introduced a matched Hermite-Taylor matrix method to address combined partial integro-differential equations involving nonlinearity and delay terms. Tchier et al. (2021) explored the pseudo-spectral method based on Chebyshev cardinal functions for the approximate solution of partial integro-differential equations. Another notable contribution comes from Parand and Nikarya (2014), who applied Bessel functions to solve differential and integro-differential equations of fractional order. Elahi et al. (2018) employed the Laguerre approach for solving systems of linear Fredholm integro-differential equations. Cabre et al. (2022) delved into the Bernstein technique for integro-differential equations, presenting a novel perspective in this area. Yuzbasi and Yildirim (2022) proposed a collocation method using PellLucas polynomials to solve parabolic-type partial integro-differential equations. In the realm of numerical techniques, Kajani and Vencheh (2004) focused on solving linear integro-differential equations with Legendre wavelets, showcasing the versatility of wavelet methods. Lotfi and Alipanah (2020) introduced the Legendre spectral element method for solving Volterra-integro differential equations, providing a valuable tool for researchers dealing with integral equations. Hashemi et al. (2016) introduced a geometric approach for solving the density-dependent diffusion Nagumo equation, providing insights into the behavior of this important equation. Building upon this work, Hashemi (2021) conducted a numerical study focusing on the one-dimensional coupled nonlinear sine-Gordon equations using a novel geometric meshless method, which demonstrated promising results in terms of computational efficiency and accuracy. Furthermore, Hashemi and Hajikhah (2021) proposed the Generalized Squared Remainder Minimization Method as a powerful technique for solving multi-term fractional differential equations, addressing a wide range of applications in mathematical modeling and control theory. Recently, Hashemi (2024) developed a variable coefficient third-degree generalized Abel equation method for solving the stochastic Schrodinger-Hirota model, contributing to the advancement of understanding complex systems described by stochastic differential equations. These diverse contributions underscore the richness of mathematical methods employed to address challenges in partial integro-differential equations across different domains.

Meshless methods have gained popularity in recent years as a numerical approach for solving functional equations. These methods utilize a scattered set of collocation points, without the need for explicit relationships between them. This characteristic sets meshless methods apart from mesh-dependent techniques like finite difference and finite element methods. By eliminating the reliance on structured grids, meshless methods offer flexibility and allow computations to be solely based on the distribution of collocation points. This advantage makes them a valuable tool in solving functional equations efficiently and effectively. Meshless methods have emerged as a versatile approach for approximating solutions to a wide range of linear and nonlinear functional equations, including Partial Differential Equations (PDEs), Ordinary Differential Equations (ODEs), Integral Equations (IEs), and Integro-Differential Equations (IDEs) such as the moving least squares (MLS) method (Mirzaei and Dehghan 2010; Assari et al. 2014b), discrete collocation method based on radial basis functions (RBFs) (Dastjerdi et al. 2013; Assari et al. 2013a, b; Wang and Wang 2016; Assari and Dehghan 2017; Esmaeilbeigi et al. 2017), local meshless formulations with modified Levin’s quadrature (Aziz 2015), spectral meshless radial point interpolation (SMRPI) method (Fatahi et al. 2016), local radial basis function method (Assari et al. 2019), meshless product integration (MPI) method (Assari et al. 2014c), meshless discrete Galerkin (MDG) method (Assari et al. 2014b), RBF and spectral collocation method (Mirzaee et al. 2021), Meshfree approach based on barycentric Lagrange interpolation (Liu et al. 2019) and Legendre polynomial approximation (Bildik et al. 2010).

In recent years, the versatility and effectiveness of mesh-free methods have garnered significant attention, leading to their widespread development and application (Chen et al. 2022; Hu et al. 2005; Khosravifard et al. 2011). In this paper, we present a novel numerical approach that employs the local integrated radial basis functions (IRBFs) method to address the problem of solving systems of linear one-dimensional Fredholm integro-differential equations. The proposed research extends the existing body of knowledge by exploring the applications of indirect/integrated radial basis function (IRBF) approaches introduced and developed in Ho and Le (2020); Ho et al. (2021); Mai-Duy et al. (2007); Mai-Duy and Tanner (2005); Mai-Duy and Tran-Cong (2006); Sarra (2006); Vu et al. (2022). The proposed method utilizes an interpolating extension of local IRBFs, which are constructed to approximate the unknown function u within the discrete collocation method. To approximate the integrals involved, the scheme employs the Gauss–Legendre (DGL) quadrature formula. As a result, solving the linear Fredholm integral equation is transformed into solving a system of linear algebraic equations.

The key novelties and advantages of the proposed method can be summarized as: The LIRBF method is a meshless collocation approach utilizing IRBFs to approximate unknown functions in the integro-differential equations, extending existing RBF collocation methods by integrating RBFs for constructing approximation functions. The LIRBF method demonstrates reduced sensitivity to the shape parameter compared to conventional RBF methods, offering increased robustness and stability across various problems and conditions. Employing the Gauss–Legendre quadrature formula, the LIRBF method approximates the integrals in Fredholm integro-differential equations accurately and efficiently, enhancing the computational efficiency of the method. Being a meshless approach, the LIRBF method does not require structured meshes or grids for discretization, providing flexibility in handling complex geometries and irregular domains, thus expanding its applicability to diverse problem sets.

2 Locally Supported IRBF

Consider a section [j] that includes ns nodes distributed along an x-grid line, as illustrated in Fig. 1. We aim to analyze the variation of the nodal function $u^{[j]}$ along this section using the integrated radial basis function (IRBF) formulation. By decomposing the second-order derivative of $u^{[j]}$ into RBFs, we integrate the RBF network twice. This process of integration gives us expressions for both the first-order derivative and the function of $u^{[j]}$ itself.

Fig. 1

LIRBF structures covering segment [j] with $n_s=3$

$$\begin{aligned} u^{{\prime \prime }^{[j]}}(x)&\approx \sum _{k=1}^{n_s} \gamma _{k} \phi ^{[2]}_{k}(x), \end{aligned}$$

(2)

$$\begin{aligned} u^{{\prime }^{[j]}}(x)&\approx \sum _{k=1}^{n_s} \gamma _{k} \phi ^{[1]}_{k}(x)+w_1, \end{aligned}$$

(3)

$$\begin{aligned} u^{[j]}(x)&\approx \sum _{k=1}^{n_s} \gamma _{k} \phi ^{[0]}_{k}(x)+w_1 x+w_2, \end{aligned}$$

(4)

where $\left\{ \gamma _{k}\right\} _{k=1}^{n_s}$ signifies the RBF weights requiring determination, while $\left\{ \phi _{k}\right\} _{k=1}^{n_s}$ indicates the given RBFs. The expressions $\phi ^{[1]}_{k}(x)=\int \phi ^{[2]}_{k} dx$ and $\phi ^{[0]}_{k}=\int \phi ^{[1]}_{k} dx$ define the functions $\phi ^{[1]}_{k}(x)$ and $\phi ^{[0]}_{k}$ as the integrals of $\phi ^{[2]}_{k}$ and $\phi ^{[1]}_{k}$, respectively. Moreover, ns is the number of collocation nodes in every stencil, $w_1$ and $w_2$ denote integration constants that are also undetermined.

Opting for the physical space instead of the network-weight space provides enhanced convenience. The RBF coefficients, comprising two integration constants, can be converted into understandable nodal variable values using the subsequent correlation equation:

$$\begin{aligned} {\bar{u}}^{[j]}={\Phi }\left( \begin{array}{c} \gamma \\ w \end{array}\right) , \end{aligned}$$

(5)

where the matrix ${\Phi }$, with dimensions $n_s \times (n_s+2)$, is introduced. Its specific form is described as follows:

$$\begin{aligned} {\Phi }=\left[ \begin{array}{lllllr} \phi ^{[0]}_{1}\left( x_1\right) &{} \phi ^{[0]}_{2}\left( x_1\right) &{} \ldots &{} \phi ^{[0]}_{n_s}\left( x_1\right) &{} x_1 &{} 1 \\ \phi ^{[0]}_{1}\left( x_2\right) &{} \phi ^{[0]}_{2}\left( x_2\right) &{} \ldots &{} \phi ^{[0]}_{n_s}\left( x_2\right) &{} x_2 &{} 1 \\ \ldots &{} \ldots &{} \ldots &{} \ldots &{} \ldots &{} \ldots \\ \phi ^{[0]}_{1}\left( x_{n_s}\right) &{} \phi ^{[0]}_{2}\left( x_{n_s}\right) &{} \ldots &{} \phi ^{[0]}_{n_s}\left( x_{n_s}\right) &{} x_{n_s} &{} 1 \end{array}\right] , \end{aligned}$$

(6)

Let ${u}^{[j]}=\left( u_{1}, u_{2}, \ldots , u_{n_s)}\right) ^T$, $\gamma =\left( \gamma _{1}, \gamma _{2}, \ldots , \gamma _{n_s}\right) ^T$, and $w=\left( w_1, w_2\right) ^T$ be defined as column vectors. In the context of this study, we consider two distinct transformation cases.

For a labeled segment represented by [j] that exclusively comprises interior points, employing Eq. (5) results in an inadequately determined system.

$$\begin{aligned} {u}^{[j]}\approx {\Phi }\left( \begin{array}{c} \gamma \\ w \end{array}\right) ={\mathfrak {C}}\left( \begin{array}{c} \gamma \\ w \end{array}\right) , \end{aligned}$$

(7)

or

$$\begin{aligned} \left( \begin{array}{c} \gamma \\ w \end{array}\right) ={\mathfrak {C}}^{-1} {u}^{[j]}, \end{aligned}$$

(8)

in which the matrix ${\mathfrak {C}}$, denoted as ${\Phi }$ in the context, serves as the transformation matrix. The utilization of the singular value decomposition (SVD) method enables the attainment of its invertibility.

In the context of a segment identified as [j], which encompasses interior as well as boundary points, the presence of coefficients $w_1$ and $w_2$ permits the introduction of an additional equation given by:

$$\begin{aligned} f={K}\left( \begin{array}{c} \gamma \\ w \end{array}\right) , \end{aligned}$$

(9)

to equation system (5). When Neumann boundary conditions are encountered, this subsystem can be employed to enforce a boundary value of the derivative at the location $x=x_N$ as

$$\begin{aligned} f&=u^{\prime } (x_N), \end{aligned}$$

(10)

$$\begin{aligned} {K}&=\left[ \begin{array}{llllll} \phi ^{[1]}_{1}\left( x_N\right)&\phi ^{[1]}_{2}\left( x_N\right)&\ldots&\phi ^{[1]}_{n_s}\left( x_N\right)&1&0 \end{array}\right] . \end{aligned}$$

(11)

The conversion system can be represented in the following formulation.

$$\begin{aligned} \left( \begin{array}{c} {u}^{[j]} \\ f \end{array}\right) \approx \left[ \begin{array}{c} {\Phi } \\ {K} \end{array}\right] \left( \begin{array}{c} \gamma \\ w \end{array}\right) ={\mathfrak {C}}\left( \begin{array}{c} \gamma \\ w \end{array}\right) , \end{aligned}$$

(12)

or

$$\begin{aligned} \left( \begin{array}{c} \gamma \\ w \end{array}\right) = {\mathfrak {C}}^{-1}\left( \begin{array}{cc} {u}^{[j]}&f \end{array}\right) ^T, \end{aligned}$$

(13)

where ${\mathfrak {C}}^{-1}$ can be computed the pseudo-inverse code in MATLAB as $\text {pinv}(C)$. The relation (8) can be recognized as a specific instance of (13), where the function f is assigned a null value. By incorporating Eq. (13) into Eqs. (2)–(4), the expressions for the second-order and first-order derivatives, as well as the function involving the variable $u^{[j]}$, are obtained in relation to the values of the nodal variables.

$$\begin{aligned} u^{{\prime \prime }^{[j]}}(x)&\approx \left( \phi ^{[2]}_{1}(x), \phi ^{[2]}_{2}(x), \ldots , \phi ^{[2]}_{n_s}(x), 0,0\right) {\mathfrak {C}}^{-1}\left( \begin{array}{cc} {u}^{[j]}&f \end{array}\right) ^T, \end{aligned}$$

(14)

$$\begin{aligned} u^{{\prime }^{[j]}}(x)&\approx \left( \phi ^{[1]}_{1}(x), \phi ^{[1]}_{2}(x), \ldots , \phi ^{[1]}_{n_s}(x), 1,0\right) {\mathfrak {C}}^{-1}\left( \begin{array}{cc} {u}^{[j]}&f \end{array}\right) ^T, \end{aligned}$$

(15)

$$\begin{aligned} u^{[j]}(x)&\approx \left( \phi ^{[0]}_{1}(x), \phi ^{[0]}_{2}(x), \ldots , \phi ^{[0]}_{n_s}(x), x, 1\right) {\mathfrak {C}}^{-1}\left( \begin{array}{cc} {u}^{[j]}&f \end{array}\right) ^T, \end{aligned}$$

(16)

or

$$\begin{aligned} \begin{aligned} u^{{\prime \prime }^{[j]}}(x)&\approx {\bar{d}}_{2 }^T {u}^{[j]}+k_{2 }(x), \\ u^{{\prime }^{[j]}}(x)&\approx {\bar{d}}_{1 }^T {u}^{[j]}+k_{1 }(x), \\ u^{[j]}(x)&\approx {\bar{d}}_{0 }^T {u}^{[j]}+k_{0 }(x). \end{aligned} \end{aligned}$$

(17)

In the given context, the variables $k_{0}, k_{1}$, and $k_{2}$ represent scalar quantities that are dependent on both x and a boundary value denoted as f. On the other hand, the vectors ${\bar{d}}_{0 }, {\bar{d}}_{1 }$ and ${\bar{d}}_{2 }$ are predefined vectors with a length of $n_s$.

By utilizing Eqs. (14) and (15) on the segment [j] with $n_s$ nodes, the second- and first-order derivatives of $u^{[j]}$ at node $x_i$ can be determined.

$$\begin{aligned} u^{{\prime \prime }^{[j]}}(x_i)&\approx \bar{{D}}_{2(ind,:)} {u}^{[j]}+{\bar{k}}_{2 (ind)}, \end{aligned}$$

(18)

$$\begin{aligned} u^{{\prime }^{[j]}}(x_i)&\approx \bar{{D}}_{1(ind,:)} {u}^{[j]}+{\bar{k}}_{1 (ind)}, \end{aligned}$$

(19)

$$\begin{aligned} u^{[j]}\left( x_i\right)&\approx \bar{{D}}_{0(ind,:)} {u}^{[j]}+{\bar{k}}_{0 (ind)}=\bar{{I}}_{(ind,:)} {u}^{[j]}, \end{aligned}$$

(20)

in which the matrices $\bar{{D}}_{1}$ and $\bar{{D}}_{2 }$ are matrices of known dimensions $n_s \times n_s$, while the vectors ${\bar{k}}_{1 }$ and ${\bar{k}}_{2 }$ are known vectors of length $n_s$. The index number ind represents the position of node $x_i$ within the local network [j]. It should be mentioned that $\bar{{D}}_{0 }$ is equivalent to the identity matrix $\bar{{I}}$, which has dimensions $n_s \times n_s$ and ${\bar{k}}_{1 }$ is a zero vector. Consequently, the shape function of the one-dimensional LIRBF exhibits the properties of the Kronecker delta function.

By meticulously combining the stencils associated with individual nodes, we can construct comprehensive matrices representing the second- and first-order derivatives. These assembled matrices provide a systematic representation of the derivative operations within the computational domain. The resulting matrices encapsulate the relationship between the nodes and enable the computation of derivative values at specific locations. The assembled matrices that the accurate estimation of derivatives are as follows:

$$\begin{aligned} u^{\prime \prime }(x)\approx U_{xx} = {{D}}_{xx} U,~~ u^{\prime }(x) \approx U_{x} = {{D}}_{x} U,~~ u\left( x\right) \approx U = {{I}} U, \end{aligned}$$

(21)

where ${D}_{xx}$ and ${D}_{x}$ are second- and first-order derivatives matrices, respectively, and I is identity matrix.

3 Solution of Integral Equations

This section introduces a numerical scheme for solving one-dimensional Fredholm integral equations. The proposed scheme utilizes the collocation method in conjunction with the Local Integrated Radial Basis Functions (LIRBF) approach.

Consider the operator ${\mathcal {I}}: C([a,b]) \rightarrow C([a,b])$ defined as

$$\begin{aligned} {\mathcal {I}} u(x)=\int _{a}^{b} K(x, s) u(s) d s. \end{aligned}$$

(22)

The integral equation (1) can be reformulated in an abstract form as

$$\begin{aligned} (L-\lambda {\mathcal {I}}) u=f, \end{aligned}$$

(23)

where L is linear differential operator. It is assumed that the kernel function K(x, s) is Riemann-integrable with respect to s for all $x \in [a,b]$. Furthermore, the following assumption is made (Atkinson 1997): $\lim _{h \rightarrow 0} w(h)=0$, where

$$\begin{aligned} w(h)=\max _{{x_1, x_2 \in [a,b]}{\left\| x_1-x_2\right\| \le h}} \int _{a}^{b}\left\| K\left( x_1, s\right) -K\left( x_1, s\right) \right\| d s, \end{aligned}$$

(24)

and consider (Atkinson 1997)

$$\begin{aligned} \max _{x \in [a,b]} \int _{a}^{b}|K(x, s)| d s<\infty . \end{aligned}$$

(25)

Theorem 1

(Geometric Series Theorem) Atkinson (1997) Consider a Banach space denoted as ${\mathcal {Y}}$. Let ${\mathcal {F}}$ be a bounded operator mapping from ${\mathcal {Y}}$ to ${\mathcal {Y}}$, where ${\mathcal {F}}$ is defined as follows:

$$\begin{aligned} \Vert {\mathcal {F}}\Vert <1, \end{aligned}$$

Subsequently, when considering the operator $I-{\mathcal {F}}$ in the context of ${\mathcal {Y}}$, it can be established that $I-{\mathcal {F}}: {\mathcal {Y}} \underset{ \text{ onto } }{{\mathop {\longrightarrow }\limits ^{1-1}}} {\mathcal {Y}}$, wherein $(I-{\mathcal {F}})^{-1}$ represents a bounded linear operator and

$$\begin{aligned} \left\| (I-{\mathcal {F}})^{-1}\right\| \leqslant \frac{1}{1-\Vert {\mathcal {F}}\Vert }. \end{aligned}$$

The series

$$\begin{aligned} (I-{\mathcal {F}})^{-1}=\sum _{j=0}^{\infty } {\mathcal {F}}^j, \end{aligned}$$

known as the Neumann series, converges within the space of bounded operators on ${\mathcal {Y}}$, given the assumption that $\Vert {\mathcal {F}}\Vert <1$. As a result of this convergence, the Neumann series yields the desired output ${\mathcal {Y}}$.

Theorem 2

Consider the bounded operator ${\mathcal {I}}$ mapping from the space C([a, b]) to C([a, b]). It is assumed that $\Vert \lambda \Vert \Vert {\mathcal {I}}\Vert < 1$. In this case, the operator $L-\lambda {\mathcal {I}}$ can be identified as a contraction operator. By virtue of the Banach contraction mapping principle Atkinson (1997), it follows that the integral equation possesses a unique solution $u(x) \in C([a,b])$ for any given function $f(x) \in C([a,b])$.

Proof

Let $u_1(x)$ and $u_2(x)$ be two solutions to the integral equation $u = L u + f(x)$, with corresponding operators $L - \lambda {\mathcal {I}}$, where $\Vert \lambda \Vert \Vert {\mathcal {I}}\Vert < 1$. Then we have:

$$\begin{aligned} \Vert u_1(x) - u_2(x)\Vert&= \Vert L u_1(x) - L u_2(x)\Vert \\&= \Vert \lambda {\mathcal {I}} u_1(x) - \lambda {\mathcal {I}} u_2(x)\Vert \\&\le \Vert \lambda \Vert \Vert {\mathcal {I}}\Vert \Vert u_1(x) - u_2(x)\Vert . \end{aligned}$$

Since $\Vert \lambda \Vert \Vert {\mathcal {I}}\Vert < 1$, we have $\Vert \lambda \Vert \Vert {\mathcal {I}}\Vert < 1$. Hence, by the Banach contraction mapping principle, $L - \lambda {\mathcal {I}}$ is a contraction mapping on C([a, b]). Therefore, the integral equation $u = L u + f(x)$ has a unique solution $u(x) \in C([a,b])$ for any given function $f(x) \in C([a,b])$. $\square$

4 Implementation of the Proposed Method

This section aims to demonstrate the application of the proposed method to solve one-dimensional Fredholm integro-differential equations, serving as an introduction to the fundamental concept of our approach. For sample, the equation under consideration can be represented as:

$$\begin{aligned} L[u(x)]=f(x)+\lambda \int _a^b K(x, s, u(s)) d s, \end{aligned}$$

(26)

with appropriate boundary conditions based on the high-order of the derivative in differential operator L.

In order to implement the LIRBF method, an initial step involves selecting a set of N nodal points $\left\{ x_i\right\}$ on the interval [a, b], where $a \leqslant x_1<x_2<\cdots <x_N \leqslant b$. The distribution of these nodes can be chosen in a regular or random manner. Subsequently, instead of considering the unknown function u, we introduce $u^h$ as a replacement, as indicated in Eq. (4). Therefore, Eq. (26) can be modified accordingly.

$$\begin{aligned} L[u^{{h}}(x)]-\lambda \int _a^b K(x, s, u^{{h}}(s)) d s=f(x), \end{aligned}$$

(27)

and more precisely for each node $x_i$

$$\begin{aligned}{} & {} \sum _{k=1}^{n_s} \gamma _{k} \phi ^{[2]}_{k}(x_i)-\lambda \int _{\alpha _i}^{\beta _i} K\left( x_i, s,\sum _{k=1}^{n_s} \gamma _{k} \phi ^{[0]}_{k}(s)+w_1 s+w_2\right) \nonumber \\{} & {} d s=f(x_i),\quad i=1,2,\dots ,N. \end{aligned}$$

(28)

or

$$\begin{aligned} {\Upsilon } \left( \begin{array}{c} {\gamma } \\ {w} \end{array}\right) -\lambda \int _{\alpha _i}^{\beta _i} K\left( x_i, s,{\Psi } \left( \begin{array}{c} {\gamma } \\ {w} \end{array}\right) \right) d s=f(x_i),\quad i=1,2,\dots ,N, \end{aligned}$$

(29)

where $\alpha _i =\min (a,x_i-\delta _i)$, $\beta _i =\min (b,x_i+\delta _i)$ and

$$\begin{aligned} {\Upsilon }= & {} \left[ \begin{array}{lllllr} \phi ^{[2]}_{1}\left( x_1\right) &{} \phi ^{[2]}_{2}\left( x_1\right) &{} \ldots &{} \phi ^{[2]}_{n_s}\left( x_1\right) &{} x_1 &{} 1 \\ \phi ^{[2]}_{1}\left( x_2\right) &{} \phi ^{[2]}_{2}\left( x_2\right) &{} \ldots &{} \phi ^{[2]}_{n_s}\left( x_2\right) &{} x_2 &{} 1 \\ \ldots &{} \ldots &{} \ldots &{} \ldots &{} \ldots &{} \ldots \\ \phi ^{[2]}_{1}\left( x_{n_s}\right) &{} \phi ^{[2]}_{2}\left( x_{n_s}\right) &{} \ldots &{} \phi ^{[2]}_{n_s}\left( x_{n_s}\right) &{} x_{n_s} &{} 1 \end{array}\right] , ~ \nonumber \\ {\Psi }= & {} \left[ \begin{array}{lllllr} \phi ^{[0]}_{1}\left( s\right)&\phi ^{[0]}_{2}\left( s\right)&\ldots&\phi ^{[0]}_{n_s}\left( s\right)&s&1 \end{array}\right] . \end{aligned}$$

(30)

Utilizing Eqs. (8) and (13), we can rewrite (29) as follows:

$$\begin{aligned}{} & {} {\Upsilon } \left( {\Phi }^{[i]}\right) ^{-1} { {u}}^{h[i]} -\lambda \int _{\alpha _i}^{\beta _i} K\left( x_i, s, {\Psi }\left( \left( {\Phi }^{[i]}\right) ^{-1} {u}^{h[i]} \right) \right) \nonumber \\{} & {} ds=f(x_i),\quad i=1,2,\dots ,N, \end{aligned}$$

(31)

Utilizing an M-point quadrature formula, characterized by the coefficients $\left\{ \xi _l\right\}$ and weights $\left\{ \omega _l\right\}$, within every interval $[\alpha _i,\beta _i]$, the integral is estimated as follows (Wazwaz 2011):

$$\begin{aligned} \int _{\alpha _i}^{\beta _i} g(s) ds \approx \frac{\beta _i-\alpha _i}{2} \sum _{l=1}^M \omega _l g\left( \vartheta _{l, i}\right) , \end{aligned}$$

(32)

in which

$$\begin{aligned} \omega _{l} & = \frac{2}{{(l + 1)P_{{M + 1}}^{\prime } \left( {\xi _{l} } \right)P_{M} \left( {\xi _{l} } \right)}}~~{\text{ and }}~~\vartheta _{{l,i}} = \frac{1}{2}\left( {\alpha _{i} + \beta _{i} } \right) \\ & \quad + \frac{1}{2}\left( {\beta _{i} - \alpha _{i} } \right)\xi _{l} , \\ \end{aligned}$$

(33)

and

$$\begin{aligned} \left\| \int _{\alpha _i}^{\beta _i} g(s) ds-\frac{\beta _i-\alpha _i}{2} \sum _{l=1}^M \omega _l g\left( \vartheta _{l, i}\right) \right\| \le \frac{2^{2 M} \delta _i^{2 M+1}}{(2 M) !} \max _{\alpha _i \le x \le \beta _i}\left\| g^{(2 M)}(s) \right\| , \end{aligned}$$

(34)

where $P_m(x)$ is the well-known Legendre polynomial of order M and $g \in C^{2 M}\left[ \alpha _i, \beta _i\right]$. By employing the numerical integration scheme (32) within the system of Eq. (31), we obtain a linear system comprising algebraic equations.

$$\begin{aligned} & \Upsilon ^{{[i]}} \left( {\Phi ^{{[i]}} } \right)^{{ - 1}} u^{{h[i]}} - \lambda \sum\limits_{{l = 1}}^{M} {\omega _{l} } K(x_{i} ,\xi _{l} )\Psi \left( {\left( {\Phi ^{{[i]}} } \right)^{{ - 1}} u^{{h[i]}} } \right) \\ & \quad = f(x_{i} ),\quad i = 1,2, \ldots ,N. \\ \end{aligned}$$

(35)

By assembling Eq. (32) for every node $x_i$, we can derive the following relation:

$$\begin{aligned} {D}_{xx}{U} -\lambda \sum _{l=1}^{M} \omega _l K(x, \xi _l) {\Psi } \left( {\Phi }\right) ^{-1} {U} =f(x),\quad x \in [a,b]. \end{aligned}$$

(36)

In this context, let us define the matrix G as an $N \times N$ matrix by

$$\begin{aligned} G & = D_{{xx}} - \lambda \left( {\omega K(x,\xi )} \right)^{T} \Psi \left( \Phi \right)^{{ - 1}} , \\ U & = \{ U_{1} ,U_{2} , \ldots ,U_{N} \} ,\quad f = \{ f_{1} ,f_{2} , \ldots ,f_{N} \} , \\ \end{aligned}$$

(37)

and equivalently

$$\begin{aligned} {G}{U}={f}. \end{aligned}$$

(38)

5 Numerical Results

In this section, some examples are given to certify the efficiency and accuracy of the presented method. All results are computed by using the MATLAB 9.6 software on an Asus laptop powered by an Intel Core i7-4510U with 8 GB of RAM and a 2.6 GHz CPU. Also in this article, we have utilized Gaussian radial basis function as follows

$$\begin{aligned} \Psi _{{ Gaussian}} = e^{(-\epsilon r)^2}, \end{aligned}$$

(39)

where $r=\sqrt{(x-x_j)^2}, j=1,\dots ,N,$ and $\epsilon$ is shape parameter that to achieve an optimal shape parameter, we use Algorithm 1 that has been introduced via Sarra (Sarra 2012).

Algorithm 1

An optimal shape parameter (Sarra 2012)

where in Algorithm 1, $\Phi$ is the interpolation matrix and $c_{Inc} = \frac{1}{n_s}$ in which $n_s$ is the number of points in the considered domain and ${\mathcal {K}}_{\min }=110$ and ${\mathcal {K}}_{\min }=1e+11$.

The accuracy of the technique has been assessed through the evaluation of error metrics as follows:

$$\begin{aligned} \left\| e\right\| _{\infty }= & {} \max _{x \in [a,b]}\left\{ \left\| u_{e x}(x)-u_{app}(x) \right\| \right\} ,\\ \Vert u_{ex}-u_{app}\Vert _1= & {} \sqrt{\int _{a}^{b} \left\| u_{ex}^2(t) - u_{app}^2(t) \right\| dt}, \end{aligned}$$

where the exact solution $u_{ex}(x)$ is estimated using the numerical solution $u_{app}(x)$ obtained through the method presented in this paper. The sparsity of the matrix, denoted as $S_{\varepsilon }$, is given by the following expression (Saray et al. 2015):

$$\begin{aligned} S_{\varepsilon }=\frac{M-M_{\varepsilon }}{M} \times 100\%, \end{aligned}$$

where M represents the total number of elements, and $M_{\varepsilon }$ corresponds to the number of non-zero elements.

To solve the problem of solving Fredholm integro-differential equations using LIRBF method, the following algorithm can be employed:

• 1. Define the Fredholm integro-differential equation to be solved.

• 2. Decompose the highest-order derivative of the function into RBFs.

• 3. Integrate the RBF basis several times to obtain expressions for the low-order derivatives and the function itself.

• 4. Utilize a meshless approach with collocation at Gauss–Lobatto quadrature points for spatial discretization.

• 5. Construct an interpolating extension of local IRBFs to approximate the unknown function within the discrete collocation method.

• 6. Apply the Gauss–Legendre quadrature formula to approximate the integrals involved and transform the problem into solving a system of linear algebraic equations.

Example 1

Our first example is the problem (Asady et al. 2005; Kurt and Sezer 2008)

$$\begin{aligned} \left\{ \begin{array}{c} y^{\prime }(x)=\int _0^1 e^{t x} y(t) \textrm{d} t+y(x)+\frac{1-e^{x+1}}{x+1}, \\ y(0)=1, \end{array}\right. \end{aligned}$$

with exact solution $y(x)=e^x$.

Table 1 Comparison of errors for proposed method and Taylor matrix method for Example 1

Table 2 Comparisons of numerical results for Example 1

The tables present a comprehensive comparison of errors for the proposed method, Taylor matrix method with $N=8$, and the exact solution for Example 1. In Table 1, the errors for different values of x and N are provided. The columns include the results from the reference (Kurt and Sezer 2008), the proposed method with $N=6$ and $N=8$, and the exact solution. The table demonstrates the accuracy of the proposed method in approximating the exact solution, with errors close to the exact values.

Table 2 further compares the numerical results for Example 1 using various methods. The columns include results from hybrid Fourier and block-pulse functions, Fourier functions, Taylor matrix method with $N=8$, $E_8(x)$ for Taylor matrix method, and the present method $E_8(x)$. The table illustrates that the present method achieves highly accurate results, with errors in the range of $10^{-7}$ to $10^{-4}$, demonstrating its effectiveness in approximating the given example. This comparison provides valuable insights into the performance of different numerical methods and highlights the accuracy and reliability of the proposed approach. We also examine the influence of the shape parameter on the proposed method in comparison to the LRBF method for Example 1. Figure 2 visually represents the impact of varying the shape parameter on the performance of both methods. The analysis of this figure depicts that the effect of the shape parameter in LIRBF method is significantly less pronounced compared to LRBF method. This observation suggests that the proposed method exhibits lower sensitivity and dependence on the shape parameter, indicating a more robust and stable behavior. Furthermore, Fig. 2 illustrates that the errors obtained across a wide range of shape parameters in the proposed method are consistently lower than those in LIRBF method. This finding underscores the efficiency and accuracy of the proposed method, particularly when faced with variations in the shape parameter.

Fig. 2

Influence of the shape parameter on the performance of LRBF and LIRBF methods for Example 1

Example 2

The second-order linear Fredholm integral-differential equations can be expressed as follows (Chen et al. 2015, 2020; Khan et al. 2022):

$$\begin{aligned} \begin{aligned} u^{\prime \prime }(x)= \int _0^1 \exp (\tau x) u(\tau ) d \tau +\frac{2x^3+(x-2)\exp (x)+x+2}{x^3}, \qquad u(0)=0, ~u(1)=0. \end{aligned} \end{aligned}$$

The exact solution to this problem is given by $u(x) = x^2-x$.

Table 3 Comparison of errors for proposed method and FMGM/OMGM approaches for Example 2

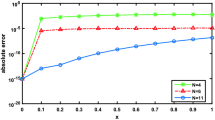
In this instance, the objective is to showcase the accuracy of approximation and computational efficiency of the proposed approach in contrast to the Fractional Multiscale Galerkin Method (FMGM) and the original multiscale Galerkin method (OMGM) (Chen et al. 2019). Table 3 succinctly presents the numerical outcomes achieved through the application of these three methods. For each designated N value, the approximated solutions arising from FMGM and OMGM are denoted as $u_{app}^{FMGM}$ and $u_{app}^{OMGM}$, correspondingly. Figure 3 shows a comparison of the proposed technique, linear Legendre multiwavelets (Khan et al. 2022), and Multi-scale Galerkin methods (Chen et al. 2015) for Example 2 in terms of maximum absolute errors. Additionally, Table 4 displays the rate of convergence for each method. Upon analyzing the data presented in Table 4, we observe that both $u_{app}^{FMGM}$ and $u_{app}^{OMGM}$ exhibit nearly the same level of accuracy and demonstrate an identical optimal convergence order of 1. However, it is noteworthy that the errors associated with the LIRBF are significantly more accurate than the OMGM and FMGM. To provide a visual representation of the computational time comparison between the three methods, we include Fig. 4, where the computing times of LIRBF, FMGM and OMGM are plotted. The figure distinctly illustrates that both computing time for LIRBF and FMGM exhibit nearly the same. However, it is noteworthy that the computational time associated with LIRBF and FMGM is significantly less than that of the OMGM. Table 5 presents the errors, condition numbers, and CPU time obtained using the presented method with various selected RBFs. These findings emphasize the superiority of the proposed method in terms of computational efficiency over the approach introduced in Chen et al. (2019).

Table 4 Comparison of computational order for FMGM, OMGM and LIRBF methods

Table 5 Errors obtained, condition number and CPU-time for the LIRBF method by several radial basis functions

Fig. 3

Comparison of the proposed technique, linear Legendre multiwavelets (Khan et al. 2022) and Multi-scale Galerkin methods (Chen et al. 2015) for Example 2 in terms of maximum absolute errors

Fig. 4

Comparison of computational times for LIRBF, FMGM, and OMGM in Example 2

In conclusion, the results presented in Tables 3 and 4 and Fig. 4 underscore the effectiveness of the IRBF in achieving comparable approximation accuracy to the OMGM while considerably reducing the computational time. The findings indicate that the proposed method offers significant advantages over the previous methods (Chen et al. 2019) and holds promise for enhancing computational efficiency in solving similar problems. Figure 3 presents a log-log plot illustrating the errors obtained by the proposed method, Multi-scale Galerkin (Chen et al. 2015), and linear Legendre multiwavelets (Khan et al. 2022) methods. The comparison allows us to discern that the proposed method exhibits higher accuracy than the existing methods in Chen et al. (2015) and Khan et al. (2022). The log-log plot visually demonstrates the convergence behavior and efficiency of the different methods in approximating the solution. It is evident that the proposed method outperforms both Multi-scale Galerkin (Chen et al. 2015) and linear Legendre multiwavelets (Khan et al. 2022) approaches in terms of error reduction and precision. We investigate the impact of the shape parameter on the proposed method relative to the LRBF method in Example 2. The visual representation in Fig. 5 illustrates the influence of varying the shape parameter on both methods. The analysis of the figure indicates that the proposed LIRBF method exhibits significantly less sensitivity to the shape parameter compared to the LRBF method, highlighting its enhanced robustness and stability. Additionally, Fig. 5 demonstrates consistently lower errors across a broad range of shape parameters in the proposed method compared to the LRBF method, emphasizing the efficiency and accuracy of the proposed approach.

Fig. 5

Influence of the shape parameter on the performance of LRBF and LIRBF methods for Example 2

Example 3

Let us consider the subsequent system of integro-differential equations (Pour-Mahmoud et al. 2005; Saray et al. 2015):

$$\begin{aligned} \begin{aligned} u_1^{\prime \prime }(x)+u_2^{\prime }(x)+\int _0^1 2 x t\left( u_1(t)-3 u_2(t)\right) d t=f_1(x), \\ u_1^{\prime }(x)+u_2^{\prime \prime }(x)+\int _0^1 3\left( 2 x+t^2\right) \left( u_1(t)-2 u_2(t)\right) d t=f_2(x), \end{aligned} \end{aligned}$$

where the functions $f_1(x)$ and $f_2(x)$ are defined as:

$$\begin{aligned} f_1(x)=\frac{3 x}{10}+3 x^2+8, \quad f_2(x)=21 x+\frac{4}{5}, \end{aligned}$$

Moreover, the system is subject to the following boundary conditions:

$$\begin{aligned} \begin{array}{ll} u_1(0)+u_1^{\prime }(0)=1, &{} u_1(1)+u_1^{\prime }(1)=10, \\ u_2(0)+u_2^{\prime }(0)=1, &{} u_2(1)+u_2^{\prime }(1)=7. \end{array} \end{aligned}$$

The exact solution to this equation is determined as follows:

$$\begin{aligned} u_1(x)=3 x^2+1, \quad u_2(x)=x^3+2 x-1. \end{aligned}$$

Table 6 Comparison of results for the IRBF method and Alpert multiwavelets method for Example 3

Fig. 6

Plots of sparse matrix

Table 6 presents the sparsity and $\Vert \cdot \Vert _{\infty }$ error for $N=6, 12, 24$ using the Lattice Interpolation Radial Basis Function (LIRBF) method, along with various thresholding parameters for implementing the Alpert multiwavelets method (Saray et al. 2015). Figure 6 illustrates the sparsity plot of the matrices ${D}_{xx}$ and ${D}_{x}$.

Fig. 7

Influence of the shape parameter on the performance of LRBF and LIRBF methods for Example 3

We explore the effect of the shape parameter on the proposed method in Example 3, comparing it to the LRBF method. The visual representation in Fig. 7 depicts the impact of varying the shape parameter on both methods. The analysis reveals that the proposed LIRBF method displays significantly lower sensitivity to the shape parameter when contrasted with the LRBF method, showcasing its improved robustness and stability. Moreover, Fig. 7 consistently shows lower errors across a wide range of shape parameters both components $u_1$ and $u_2$ in the proposed method than in the LRBF method, emphasizing the efficiency and accuracy of the proposed approach.

Example 4

Consider the following system of integro-differential equations with associated supplementary conditions (Pour-Mahmoud et al. 2005; Saray et al. 2015):

$$\begin{aligned} \begin{aligned}&u_1^{\prime \prime \prime }(x)+2 u_2^{\prime \prime }(x)+u_3^{\prime }(x)+\int _0^1(x+t)^2\left( u_1(t)+u_2(t)\right. \\&\left. +2 u_3(t)\right) d t=f_1(x), \\&u_1^{\prime }(x)+u_2^{\prime \prime }(x)+u_3(x)+\int _0^1\left( x^3+t^2+5\right) \left( 2 u_1(t)\right. \\&\left. +u_2(t)-u_3(t)\right) d t=f_2(x), \\&u_1^{\prime }(x)+u_2^{\prime }(x)+u_3^{\prime }(x)+\int _0^1\left( 5 x^2+t^2+5\right) \left( u_1(t)\right. \\&\left. -u_2(t)-u_3(t)\right) d t=f_3(x),\\&u_1(0)+u_1^{\prime }(0)+u_1^{\prime \prime }(0)=3,\\&\quad u_1(1)+u_1^{\prime }(1)+u_1^{\prime \prime }(1)=\sin (1)+4 \cos (1), \\&u_2(0)+u_2^{\prime }(0)=0, \quad u_2(1)+u_2^{\prime }(1)=-\cos (1),~~\\&u_2(0)=1, ~~ u_3(1)=8. \end{aligned} \end{aligned}$$

The objective of this system is to determine the functions $u_1(x)$, $u_2(x)$, and $u_3(x)$ that satisfy the given equations. Moreover, it is known that the exact solutions to the system are defined as:

$$\begin{aligned} u_1(x)= & {} (1+x) \sin (x), \quad u_2(x)=(1-x) \cos (x),\\{} & {} u_3(x)=(1+x)^3. \end{aligned}$$

The forcing functions $f_i$ for $i=1,2,3$ are:

$$\begin{aligned} f_1(x)&=\left( x+1\right) \sin \left( x\right) +4\sin \left( x\right) -2\left( 1-x\right) \cos \left( x\right) \\&\quad +2\cos \left( x\right) \\&\quad +3\left( x+1\right) ^2+\sin \left( 1\right) \,x^2 \\&\quad -3\cos \left( 1\right) \,x^2+\dfrac{19x^2}{2}+10\sin \left( 1\right) \,x-2\cos \left( 1\right) \,x\\&\quad +\dfrac{19x}{5}+3\sin \left( 1\right) \\&\quad +11\cos \left( 1\right) -\dfrac{43}{10},\\ f_2(x)&=3\sin \left( x\right) +\left( x+1\right) \cos \left( x\right) \\&\quad +\left( x-1\right) \cos \left( x\right) +\left( x+1\right) ^3\\&\quad +2\sin \left( 1\right) \,x^3-5\cos \left( 1\right) \,x^3-\dfrac{3x^3}{4}\\&\quad +12\sin \left( 1\right) -8\cos \left( 1\right) -\dfrac{78}{5},\\ f_3(x)&=\left( x-1\right) \sin \left( x\right) +\sin \left( x\right) \\&\quad +\left( x+1\right) \cos \left( x\right) -\cos \left( x\right) \\&\quad +3\left( x+1\right) ^2+5\sin \left( 1\right) \,x^2-5\cos \left( 1\right) \,x^2-\dfrac{75x^2}{4}\\&\quad -4\cos \left( 1\right) -\dfrac{83}{5}. \end{aligned}$$

Table 7 presents the maximum errors obtained from the proposed methods, alongside the results of the method described in Saray et al. (2015). Additionally, this table showcases the sparsity of the derivative coefficients matrices, as well as the computation time required to solve the problem using the presented method. Through a meticulous examination of the acquired outcomes, it becomes evident that, in certain instances, the errors derived from the proposed method exhibit more suitable accuracy. This observation holds great promise for the future applicability of the proposed method in solving another system of Fredholm equation, as it demonstrates the potential to yield results with high precision and in a computationally efficient manner. Investigating the shape parameter’s impact on the proposed method in Example 4 relative to the LRBF method, Fig. 8 visually demonstrates the sensitivity difference. The analysis indicates that the LIRBF method exhibits significantly lower sensitivity to the shape parameter than the LRBF method, highlighting enhanced robustness. Moreover, Fig. 8 consistently reveals lower errors across a broad range of shape parameters for three components, $u_1$, $u_2$ and $u_3$, in the proposed method compared to the LRBF method, underscoring its efficiency and accuracy.

Table 7 Comparison of results for the IRBF method and Alpert multiwavelets method for Example 4

Fig. 8

Influence of the shape parameter on the performance of LRBF and LIRBF methods for Example 4

Example 5

Consider the following fourth-order nonlinear system of integro-differential Fredholm equations of the second kind, defined for $0 < x \le 1$:

$$\begin{aligned} \begin{aligned}&u_1^{(4)}(x)+u_2^{\prime \prime }(x) u_2^{(4)}(x)+u_1(x)+ \int _0^1 \exp (x-t) u_2(t) d t = 2\exp (x)\\&\quad +\exp (-2x)+\dfrac{\exp (x+1)-1}{x+1}, \\&u_2^{(4)}(x)+\left( u_1^{\prime \prime \prime }(x)\right) ^3+u_2(x)+ \int _0^1 \exp (xt) u_1(t) d t = \exp (3x)\\&\quad +2\exp (-x)+\exp (x). \end{aligned} \end{aligned}$$

The boundary conditions for this system are specified as follows:

$$\begin{aligned} \begin{aligned} u_1(0)&= u_1^{\prime }(0) = 1, \quad u_1(1) = u_1^{\prime }(1) = \exp (1), \\ u_2(0)&= -u_2^{\prime }(0) = 1, \quad u_2(1) = -u_2^{\prime }(1) = \exp (-1). \end{aligned} \end{aligned}$$

The exact solution to this system is given by:

$$\begin{aligned} u_1 = \exp (x), \quad u_2 = \exp (-x). \end{aligned}$$

Tables 8 and 9 provide an in-depth analysis of the errors and computational performance for components $u_1$ and $u_2$, respectively. The reference method (El-Gamel and Mohamed 2022), as well as the proposed method, are scrutinized for their accuracy in solving the problem. The maximum errors, quantified by $|e|_{\infty }$, are presented for various discretization levels (N). The proposed method showcases promising accuracy, as evidenced by the lower errors compared to the reference method. The convergence rates, a crucial indicator of method performance, are reported, demonstrating the efficiency of the proposed method. Moreover, the computational time needed for each discretization level is incorporated, further confirming the efficiency of the proposed approach. Figure 9 illustrates a visual contrast in terms of the comparison between the proposed LIRBF method and the Chebyshev pseudo-spectral method as described in reference (El-Gamel and Mohamed 2022), focusing on the $\Vert e\Vert _{\infty }$ values.

Table 8 Comparison of errors and show computational performance for component $u_1$ for Example 5

Table 9 Comparison of errors and show computational performance for component $u_2$ for Example 5

Fig. 9

Comparison of $\Vert e \Vert _{\infty }$ for LIRBF and Chebyshev pseudo-spectral methods (El-Gamel and Mohamed 2022) for Example 5

Exploring the impact of the shape parameter in Example 5, we compare the proposed method to the LRBF method. The visual representation in Fig. 10 illustrates the varying shape parameter’s effect on both methods. Analysis indicates that the proposed LIRBF method exhibits significantly lower sensitivity to the shape parameter than the LRBF method, showcasing enhanced robustness. Figure 10 consistently depicts lower errors across a broad range of shape parameters for both components $u_1$ and $u_2$ in the proposed method, emphasizing its efficiency and accuracy.

Fig. 10

Influence of the shape parameter on the performance of LRBF and LIRBF methods for Example 5

Example 6

Consider the following boundary value problem with a logarithmic kernel (Assari et al. 2014a):

$$\begin{aligned} & u^{{\prime \prime }} (x) - \frac{1}{\pi }\int_{{ - \pi }}^{\pi } {\left[ {\ln \left| {2\sin \frac{{x - t}}{2}} \right|\left\{ {1 + e^{{xt}} \sin ^{2} \frac{{x - t}}{2}} \right\}} \right.} \\ & \left. {\quad + \frac{1}{{t^{2} + x^{2} + 1}}} \right]u(t)dt = f(x),~~x \in [0,5\pi ], \\ & u(0) + u^{\prime } (0) = \cosh (1) - 7\sinh (1),\quad u(5\pi ) + u^{\prime } (5\pi ) = 1, \\ \end{aligned}$$

(40)

where the function $f(x)$ has been chosen such that the exact solution is given by

$$\begin{aligned} u(x) = \cosh \left( \frac{1}{x^2+7x+1}\right) . \end{aligned}$$

Table 10 Comparison of the proposed method and exact solutions for Example 6

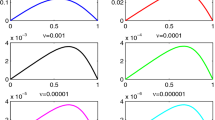
Figure 11 presents the graph of the approximation solution for Example 6 over the interval $[0, 5\pi ]$. From Table 10, it can be observed that the proposed method provides approximate solutions for different values of x with varying levels of accuracy. These approximations are compared against the exact solution, demonstrating that the proposed method closely matches the exact solution for the given example. The slight discrepancies in the results can be attributed to the finite precision of numerical computations and the approximation techniques used in the proposed method.

Fig. 11

The graph of approximation solution for Example 6 in $[0,5 \pi ]$