An improved radial basis functions method for the high-order Volterra–Fredholm integro-differential equations

Abstract

This paper is aimed at rectifying the numerical solution of linear Volterra–Fredholm integro-differential equations with the method of radial basis functions (RBFs). In this method, the spectral convergence rate can be acquired by infinitely smooth radial kernels such as Gaussian RBF (GA-RBF). These kernels are made by a free shape parameter, and the highest accuracy can often be achieved when this parameter is small, but herein the coefficient matrix of interpolation is ill-conditioned. Alternative bases can be used to improve the stability of method. One of them is based on the eigenfunction expansion for GA-RBFs which is utilized in this study. The Legendre–Gauss–Lobatto integration rule is applied to estimate the integral parts. Moreover, the error analysis is discussed. The results of numerical experiments are presented to demonstrate stable solutions with high accuracy compared to the standard GA-RBFs, the analytical solutions, and the other methods.

Introduction

The study of integro-differential equations (IDEs) arises from its abundant applications in the real world, such as finance [46], ecology and evolutionary biology [37], medicine [20], mechanics and plasma physics [2, 23, 27] and other cases. Therefore, computational methods to solve these types of equations are noteworthy by many scientists. Some methods for solving these equations include: Bessel functions [50], Wavelets [11, 42], Adomian decomposition method [25, 29], compact finite difference method [51, 52], Galerkin method [7, 35], homotopy analysis method [24, 39] and radial basis functions method [12, 21, 28, 30, 45].

Recently, the radial basis functions (RBFs) meshless method has been used as an effective technique to interpolate and approximate the solution of differential equations (DEs), and integral equations (IEs). In the RBF method, we do not mesh the geometric space of the problem, but instead use some scattered points in the desired domain. Since the RBF method uses pairwise distances between points, so it is efficient for problems with high dimensions and irregular domains. First time, Hardy introduced MQ-RBF which was motivated by the cartographic problem [26], and later Kansa utilized it to solve parabolic, hyperbolic and elliptic partial differential equations [32]. Frank [18] examined about 30 two-dimensional approaches to interpolation and demonstrated that the best ones are MQ and TPS.

Radial basis functions are classified into two main classes [8, 33]:

Class 1. Infinitely smooth RBFs.

These basis functions are infinitely differentiable and depend on a parameter, called shape parameter $\varepsilon$ (analogous Multiquadric(MQ), inverse multiquadric (IMQ) and Gaussian (GA)).

Class 2. Infinitely smooth (except at centers) RBFs.

These basis functions are not infinitely differentiable and are lacking the shape parameter. Also, these functions have less accurate than ones in Class 1. (analogous Thin Plate Splines (TPS)).

Selecting the optimal shape parameter is still an open problem. Some attempts have been made to overcome this problem. For MQ-RBF, Hardy [26] expressed $\varepsilon =0.815d$ in which $d=\frac{1}{N} \sum _{i=1}^{N} d_{i}$, N is the number of data and $d_i$ is the distance between the $i^{th}$ data point and its closest neighborhood. Franke [19] defined $\varepsilon =\frac{1.25D}{\sqrt{N}}$ where D is the diameter of the smallest circle containing all data points. Carlson and Foley [5] declared that a good value of $\varepsilon$ is independent of the number and position of the grid points. Furthermore, they employed the same value of $\varepsilon$ for MQ and IMQ RBF interpolation. Rippa [43] showed that the optimal value depends on the number and position of grid points, the approximated function, the accuracy of calculation and the kind of RBF interpolation. Moreover, Rippa introduced an algorithm based on the Leave-One-Out Cross Validation (LOOCV) method for any RBF and any dimension by minimizing a cost function. In [3], Azarboni et al. presented the Leave-Two-Out Cross Validation (LTOCV) method which is more accurate than the LOOCV one. In RBFs, when the shape parameter is small and the basis function is near to be flat, the accuracy of method increases, but in this case, the system of equations is ill-conditioned. To overcome this problem, researchers have made many efforts that have led to the production of stable methods for small values of the shape parameter, like the Contour-Pade method [17], the RBF-QR method [15, 16, 34] and the Hilbert-Schmidt SVD method [6].

Fasshauer et al. established a new procedure to calculate and evaluate Gaussian radial basis function interpolants in a stable way with a concentration on small values of the shape parameter; see [14] and references therein. Using this, Rashidinia et al. introduced an effective stable method to estimate Gaussian radial basis function interpolants which has been performed by the eigenfunction expansion [41]. This approach is based on the properties of the orthogonal eigenfunctions and their zeros. They tested various interpolations and solved the boundary value problems in one and two dimensions by applying their method.

In this paper, we focus on high-order Volterra–Fredholm integro-differential equations in the following general form

$$\begin{aligned}&\sum _{k=0}^{m} p_{k}(x) y^{(k)}(x)+\theta _{1} \int _{a}^{b} k_{1}(x, t) y^{(l_1)}(t) \mathrm {d} t\nonumber \\&\quad +\theta _{2} \int _{a}^{x} k_{2}(x, t) y^{(l_2)}(t) \mathrm {d} t=f(x), \quad a \le x\le b, \end{aligned}$$

(1)

with initial-boundary conditions

$$\begin{aligned} \sum _{k=0}^{m-1}\left( r_{j k} y^{(k)}(a)+s_{j k} y^{(k)}(b)\right) =q_{j}, \quad j=0,1,2, \ldots , m-1. \end{aligned}$$

(2)

, where $r_{j k}, s_{j k}, q_{j}, \theta _{1}, \theta _{2}, a$ and b are real constants, $m\in \mathbb {N}$, $l_1,l_2$ are two non-negative integers, $y^{(0)}(x)=y(x)$ is an unknown function, $p_{k}$ and f are known and continuous functions on [a, b] and the kernels $k_{1}$ and $k_{2}$ are known and analytical functions that have suitable derivatives on $[a, b] \times [a, b]$. With the help of Legendre–Gauss–Lobatto approximation for integrals and collocation points, we intend to develop the eigenfunction expansion method to solve (1) under the conditions (2).

The method proposed in this work transforms the main problem to a system of linear algebraic equations. By solving the resulting system, the coefficients of expansion for the solution are found. In illustrative examples, very small values for the shape parameter are employed. Numerical results show stable solutions with high accuracy and appropriate condition number compared to the standard GA-RBF method.

This paper is arranged as follows: In Sect. 2, a review of previous studies about standard RBFs interpolation and eigenfunction expansions are mentioned. The Legendre–Gauss–Lobatto nodes and weights are described in Sect. 3. In Sect. 4, the present method is explained. Section 5 is assigned to a discussion on the residual error. Numerical examples are included in Sect. 6.

The preliminaries and basic definitions

In this section, we briefly describe some basic definitions and items required in this work.

Standard RBFs interpolation method

Definition 1

[48] A function $\varPhi : \mathbb {R}^{d} \rightarrow \mathbb {R}$ is called radial basis whenever there exists a univariate function $\varphi :[0, \infty ) \rightarrow \mathbb {R}$ such that $\varPhi (x)=\varphi (r)$, where $r=\Vert x\Vert$ and $\Vert \cdot \Vert$ is usual Euclidean norm.

Definition 2

A real-valued continuous function $\varPhi : \mathbb {R}^{d} \rightarrow \mathbb {R}$ is called positive definite whenever for any N distinct points $\{x_i\}_{i=1} ^{N} \in \mathbb {R}^{d}$ and $\mathbf {G}={(g_1,g_2,\dots ,g_N)}^T \in \mathbb {R}^{N},$ we have

$$\begin{aligned} \sum _{i=1}^{N} \sum _{j=1}^{N} g_{i} g_{j} \varPhi \left( x_{i}-x_{j}\right) \ge 0. \end{aligned}$$

(3)

The function $\varPhi$ is called strictly positive definite if unequal in (3) becomes equal only for $\mathbf {G}=0$.

Definition 3

(Scattered data interpolation problem [13, 38, 47]). For given data $f_{i} \in \mathbb {R}$ at scattered data $\{x_i\}_{i=1} ^{N} \in {\mathbb {R}}^d$, we find a continuous function W such that

$$\begin{aligned} {W}\left( x_{i}\right) =f_{i}, \quad i=1,2, \ldots , N. \end{aligned}$$

(4)

One of the efficient methods for interpolating scattered points is the RBF method. An RBF approximation is presented as follows:

$$\begin{aligned} {W}(x)=\sum ^N_{i=1}{c_i\varphi (\left\| x-x_i\right\| )},\ \ \ \ \ \ \ x,x_{i}\in {\mathbb {R}}^d. \end{aligned}$$

(5)

To interpolate the given values $\{f_i\}_{i=1} ^{N}$ at scattered data set $\mathbf {x}=\{x_i\}_{i=1} ^{N},$, namely center nodes, where $\varphi \left( r\right)$ is a radial kernel.

In order to acquire unknown coefficients $\mathbf {C}={(c_1,c_2,\ldots ,c_N)}^T$, we apply the interpolation conditions (4) which is equivalent to solving the following system

$$\begin{aligned} \mathbf {AC=F}, \end{aligned}$$

(6)

so that $\mathbf {A}_{ij}=\varphi \left( \left\| x_i-x_j\right\| \right)$ and $\mathbf {F}={(f_1,f_2,\dots ,f_N)}^T$ .

If the function $\varphi$ is strictly positive definite, then the matrix $\mathbf {A}$ is positive definite and so non-singular. Therefore, the system of equations corresponding to the interpolation problem has a unique solution. Some popular choices of radial kernels are summarized in Table 1.

Table 1 Some radial functions that are strictly positive definite, infinitely smooth and depend on a free shape parameter $\varepsilon$ which controls their flatness

The following theorem is related to the convergence of RBFs interpolation:

Theorem 1

If $\left\{ x_{i}\right\} _{i=1}^{N}$ are N nodes in the convex space $\varOmega \subset \mathbb {R}^{d}$ and

$$\begin{aligned} h=\max _{x \in \varOmega } \min _{1 \le i \le N}\left\| x-x_{i}\right\| _{2}, \end{aligned}$$

when $\hat{\phi }(\eta )<c(1+|\eta |)^{-2 l+d} \text{ for } \text{ any } y(x) { \text{ satisfies } \text{ in } } \int (\hat{y}(\eta ))^{2} /\hat{ \phi }(\eta ) d \eta <\infty ,$ then

$$\begin{aligned} \left\| y_{N}^{(\alpha )}-y^{(\alpha )}\right\| _{\infty }<c h^{l-\alpha }, \end{aligned}$$

in which $\phi$ refers to RBFs and the constant c depends on RBFs, $\hat{\phi }$ and $\hat{y}$ are supposed to be the Fourier transforms of $\phi$ and y respectively, $y^{(\alpha )}$ denotes the $\alpha ^{th}$ derivative of $y, y_{N}$ is the RBFs approximation of y, d is space dimension, l and $\alpha$ are non-negative integers.

Proof

A complete proof is presented in [49, 53]. $\square$

It can be seen that not only RBFs itself but also its any order derivative has a good convergence.

An eigenfunction expansion for Gaussian RBFs

Let the Gaussian kernel be a positive definite function. So, the coefficient matrix in the system (6) is non-singular but often ill-condition. Using Mercer’s theorem, a decomposition of the matrix $\mathbf {A}$ is found which overcomes the ill-conditioning of system.

Theorem 2

(Mercer). If $X\subseteq {\mathbb {R}}^d$ be closed, then a continuous positive definite kernel $K:X\times X \rightarrow \mathbb {R}$ has an eigenfunction expansion

$$\begin{aligned} K(x, y)=\sum _{n=1}^{\infty } \lambda _{n} \varphi _{n}(x) \varphi _{n}(y), \quad x, y \in X, \end{aligned}$$

so that $\lambda _{n}$ are positive eigenvalues, $\varphi _{n}$ are orthogonal eigenfunctions in $L_{2}(X)$ and the series converges absolutely and uniformly. Moreover,

$$\begin{aligned} \lambda _{n} \varphi _{n}(x)=\int _{X} K(x, y) \varphi _{n}(y) \mathrm {d} y, \quad x \in X, n \ge 0. \end{aligned}$$

Proof

A complete explanation is given in [36, 40, 41]. $\square$

So, GA-RBFs can be written by

$$\begin{aligned} e^{-\varepsilon ^{2}\left\| x-y\right\| ^{2}}=\sum _{n=1}^{\infty } \lambda _{n} \varphi _{n}(x) \varphi _{n}(y){.} \end{aligned}$$

(7)

The eigenfunctions $\varphi _{n}$ are orthogonal with respect to the weight function $\rho (x)=\frac{\alpha }{\sqrt{\pi }} e^{-\alpha ^{2} x^{2}}$, and

$$\begin{aligned} \varphi _{n}(x) =\sqrt{\gamma _{n}} e^{-\delta ^{2} x^{2}} H_{n-1}(\alpha \beta x), \quad n=1,2, \ldots , \end{aligned}$$

(8)

where $H_{n-1}$ are Hermite polynomials of degree $n-1$ defined by the following recursion relation

$$\begin{aligned} \left\{ \begin{array}{l} H_{n+1}(x)=2 x H_{n}(x)-2 n H_{n-1}(x), \quad n \ge 0, \\ H_{-1}(x)=0, \quad H_{0}(x)=1. \end{array}\right. \end{aligned}$$

(9)

In addition,

$$\begin{aligned} \int _{\mathbb {R}} H_{n-1}^{2}(x) e^{-x^{2}} \mathrm {d} x=\sqrt{\pi } 2^{n-1} \varGamma (n), \quad n=1,2, \ldots , \end{aligned}$$

and

$$\begin{aligned} \lambda _{n}= & {} \sqrt{\frac{\alpha ^{2}}{\alpha ^{2} +\delta ^{2}+\varepsilon ^{2}}}\left( \frac{\varepsilon ^{2}}{\alpha ^{2}+\delta ^{2} +\varepsilon ^{2}}\right) ^{n-1}, \quad n=1,2, \ldots ,\\ \beta= & {} \left( 1+\left( \frac{2 \varepsilon }{\alpha }\right) ^{2}\right) ^{\frac{1}{4}}, \quad \gamma _{n}=\frac{\beta }{2^{n-1} \varGamma (n)}, \quad \\&\delta ^{2}=\frac{\alpha ^{2}}{2} \left( \beta ^{2}-1\right) {.} \end{aligned}$$

Also, by applying (8) and (9) we get

$$\begin{aligned} \left\{ \begin{array}{l} \varphi _{n+1}(x)=\alpha \beta x\sqrt{\frac{2}{n}} \varphi _{n}(x)-\sqrt{\frac{n-1}{n}} \varphi _{n-1}(x), \quad n \ge 1, \\ \varphi _{0}(x)=0, \quad \varphi _{1}(x)=\sqrt{\beta } \mathrm {e}^{-\delta ^{2} x^{2}}. \end{array}\right. \end{aligned}$$

(10)

The parameters $\varepsilon$ and $\alpha$ are called the shape and the global scale parameters, respectively. Although they are freely chosen, but they have an important effect on the accuracy of the method. For GA-RBFs, if $\alpha$ is fixed and $\varepsilon \rightarrow 0,$ then $\beta \rightarrow 1$, $\delta \rightarrow 0,$ the eigenfunctions $\varphi _{n}$ converge to the normalized Hermite polynomials $\widetilde{H}_{n}(x)= \frac{1}{\sqrt{2^{n-1} \varGamma (n)}} H_{n-1}(\alpha x)$ and the eigenvalues behave similarly $\left( \frac{\varepsilon ^{2}}{\alpha ^{2}}\right) ^{n-1} \cdot$ This content indicates that one of the sources of ill-conditioning is the eigenvalues $\lambda _{n}$ [6, 14].

The stable method for Gaussian RBF interpolation in one dimension space

By applying the assumptions mentioned before, we now interpret the interpolation by the Gaussian RBF using Mercer’s series. According to Eq. (5), the Gaussian RBF approximation is as the following form

$$\begin{aligned} {W}(x)=\sum ^N_{i=1} {c_i} e^{-\varepsilon ^{2}(x-x_i)^{2}}. \end{aligned}$$

(11)

To use Mercer’s series, we have to truncate the expansion at the finite length L. If L is selected large enough, then interpolation by the truncated expansion converges to the one based on the full series [22, 41]. So, the Gaussian kernel can be approximated as follows

$$\begin{aligned} {W}_L(x)=\sum ^N_{i=1} {c_i} \sum _{n=1}^{L} \lambda _{n} \varphi _{n}(x) \varphi _{n}(x_i)= \varPhi _{1}^{T}(x) \varLambda \varPhi _{1} \mathbf {C}, \end{aligned}$$

(12)

, where $\varPhi _{1}^{T}(x)=\left( \varphi _{1}(x), \ldots , \varphi _{N}(x)\right) , \mathbf {C}=\left( c_{1}, \ldots , c_{N}\right) ^{T},$

$$\begin{aligned} \varLambda =\left( \begin{array}{ccc} \lambda _{1} &{} &{} 0 \\ &{} \ddots &{} \\ 0 &{} &{}\lambda _{N} \end{array}\right) , \quad \quad \varPhi _{1}=\left( \begin{array}{ccc} \varphi _{1}\left( x_{1}\right) &{} \dots &{} \varphi _{1}\left( x_{N}\right) \\ \vdots &{} &{} \vdots \\ \varphi _{N}\left( x_{1}\right) &{} \dots &{} \varphi _{N}\left( x_{N}\right) \end{array}\right) . \end{aligned}$$

To obtain unknown coefficients $c_{i}$, the linear system of Eqs. (6) is written as follows

$$\begin{aligned} \mathbf {F}=\varPhi _{1}^{T} \varLambda \varPhi _{1} \mathbf {C}, \end{aligned}$$

then

$$\begin{aligned} \mathbf {C}=\varPhi _{1}^{-1} \varLambda ^{-1} \varPhi _{1}^{-T} \mathbf {F}. \end{aligned}$$

(13)

By substituting (13) into (12) we achieve

$$\begin{aligned} {W_L}(x)=\varPhi _{1}^{T}(x) \varPhi _{1}^{-T} \mathbf {F}. \end{aligned}$$

(14)

This stable interpolation function is called “interpolant with the cardinal basis” which lacks the matrix $\varLambda$ as one of the sources of ill-conditioning.

Theorem 3

[41] Let

$$\begin{aligned} {W}(x)=\sum ^N_{i=1} {c_i} \sum _{n=1}^{\infty } \lambda _{n} \varphi _{n}(x) \varphi _{n}(x_i), \end{aligned}$$

and $W_{L}$ be in the form of Eq. (12). Then,

$$\begin{aligned} \left| W(x)-W_{L}(x)\right| \le \sqrt{\frac{2}{\pi L}}\frac{NC\alpha \beta }{\sqrt{\alpha ^2+\delta ^2+\varepsilon ^2}}e^{\alpha ^2 b^2}\frac{E^L}{1-E}, \end{aligned}$$

when $L \rightarrow \infty$ then $\left| W(x)-W_{L}(x)\right| \rightarrow 0,$ , where $C= \max \lbrace |c_{j}|, j=1,\ldots , N \rbrace$, and

$$\begin{aligned} E=\frac{\varepsilon ^{2}}{\alpha ^{2}+\varepsilon ^{2}+\delta ^{2}}. \end{aligned}$$

Legendre–Gauss–Lobatto nodes and weights

Let $\{P_{i}\}_{i\ge 1}$ be Legendre polynomial functions of order i which are orthogonal with respect to the weight function $\omega (x)=1$, on the interval $[-1,1]$. These polynomials satisfy in the following formulas

$$\begin{aligned} \begin{array}{l} P_{1}(x)=1, \quad P_{2}(x)=x, \\ \\ P_{i+1}(x)=\left( \frac{2i+1}{i+1}\right) x P_{i}(x)-\left( \frac{i}{i+1}\right) P_{i-1}(x), \quad i=2,3, \ldots . \end{array} \end{aligned}$$

The Legendre–Gauss–Lobatto nodes can be found as follows

$$\begin{aligned} \begin{array}{c} \left( 1-x_{j}^{2}\right) P_{N}^{\prime }\left( x_{j}\right) =0,\\ \\ -1=x_{1}<x_{2}<\cdots <x_{N}=1, \end{array} \end{aligned}$$

(15)

, where $P_{i}^{\prime }(x)$ is the derivative of $P_{i}(x)$. No explicit formula for the nodes $\{x_{j}\}_{j=2}^{N-1}$ is known, and so they are computed numerically using subroutines [9, 10]. The integral approximation of function f on the interval $[-1,1]$ is

$$\begin{aligned} \int _{-1}^{1} f(x) d x=\sum _{j=1}^{N} w_{j} f\left( x_{j}\right) +E_{f}, \end{aligned}$$

(16)

, where $w_{j}$ are Legendre–Gauss–Lobatto weights presented in [44]

$$\begin{aligned} w_{j}=\frac{2}{N(N-1)} \frac{1}{\left( P_{N-1}\left( x_{j}\right) \right) ^{2}}, \quad j=1,2, \ldots , N, \end{aligned}$$

and $E_{f}$ is the error term specified by

$$\begin{aligned} E_{f}= & {} -\frac{{N}{(N-1)^3}2^{2N-1}[(N-2)!]^{4}}{(2N-1)[(2N-2)!]^3} f^{(2N-2)}(\zeta ), \quad \\&\zeta \in (-1,1). \end{aligned}$$

Also, if f(x) is a polynomial of degree $\le 2 N-3$ then the integration in Eq. (16) is exact.

Method of solution

The main aim of this section is to solve high-order linear Volterra–Fredholm integro-differential equations in the form (1) with the conditions (2). First of all, we consider the grid points $\{x_{i}\}_{i=1}^{N}$ into integral domain [a, b]. Then, the unknown solution of equation can be approximated by GA-RBFs as follows

$$\begin{aligned} y(x)=\varPhi _{1}^{T}(x) \varPhi _{1}^{-T} \mathbf {S}, \end{aligned}$$

(17)

, where $\mathbf {S}=\left( s(x_1), \ldots , s(x_N)\right) ^{T}$ is an unknown vector, $\varPhi _{1}^{T}(x)$ and $\varPhi _{1}$ are defined in the Sect. 2.3. By substituting Eq. (17) into Eqs. (1) and (2), we get

$$\begin{aligned}&\sum _{k=0}^{m} p_{k}(x) (\varPhi _{1}^{(k)}(x))^{T} \varPhi _{1}^{-T} \mathbf {S}\nonumber \\&\quad +\theta _{1} \int _{a}^{b} k_{1}(x, t) (\varPhi _{1}^{(l_1)}(t))^{T} \varPhi _{1}^{-T} \mathbf {S} \mathrm {d} t\nonumber \\&\quad +\theta _{2} \int _{a}^{x} k_{2}(x, t) (\varPhi _{1}^{(l_2)}(t))^{T} \varPhi _{1}^{-T} \mathbf {S} \mathrm {d} t=f(x), \end{aligned}$$

(18)

and

$$\begin{aligned}&\sum _{k=0}^{m-1}\left( r_{j k} \varPhi _{1}^{(k)}(a)) +s_{j k} \varPhi _{1}^{(k)}(b) \right) ^T\varPhi _{1}^{-T} \mathbf {S}=q_{j}, \quad \nonumber \\&j=0,1,2, \ldots , m-1. \end{aligned}$$

(19)

Now, by collocating Eq. (18) at interior points $\{x_{i}\}_{i=1}^{N-m}$ we have

$$\begin{aligned}&\sum _{k=0}^{m} p_{k}(x_i) (\varPhi _{1}^{(k)}(x_i))^{T} \varPhi _{1}^{-T} \mathbf {S}\nonumber \\&\quad +\theta _{1} \int _{a}^{b} k_{1}(x_i, t) (\varPhi _{1}^{(l_1)}(t))^{T} \varPhi _{1}^{-T} \mathbf {S} \mathrm {d} t\nonumber \\&\quad +\theta _{2} \int _{a}^{x_i} k_{2}(x_i, t) (\varPhi _{1}^{(l_2)}(t))^{T} \varPhi _{1}^{-T} \mathbf {S} \mathrm {d} t=f(x_i), \quad \nonumber \\&\quad i=1,2, \ldots , N-m. \end{aligned}$$

(20)

To use the Legendre–Gauss–Lobatto rule for Eq. (20), we apply the following transformations

$$\begin{aligned} t= & {} \frac{b-a}{2} \tau _1+\frac{b+a}{2}, \quad \tau _1 \in [-1,1], \qquad \text {for Fredholm},\\ t= & {} \frac{x_i-a}{2} \tau _2+\frac{x_i+a}{2}, \quad \tau _2 \in [-1,1], \qquad \text {for Volterra }. \end{aligned}$$

So,

$$\begin{aligned}&\sum _{k=0}^{m} p_{k}(x_i) (\varPhi _{1}^{(k)}(x_i))^{T} \varPhi _{1}^{-T} \mathbf {S}\\&\quad +\theta _{1} \frac{b-a}{2} \int _{-1}^{1} k_{1}\left( x_i, \frac{b-a}{2} \tau _1+\frac{b+a}{2}\right) \\&\quad \left( \varPhi _{1}^{(l_1)}\left( \frac{b-a}{2} \tau _1+\frac{b+a}{2}\right) \right) ^{T} \varPhi _{1}^{-T} \mathbf {S} \mathrm {d} \tau _1\\&\quad +\theta _{2} \frac{x_{i}-a}{2} \int _{-1}^{1} k_{2}\left( x_i, \frac{x_i-a}{2} \tau _2+\frac{x_i+a}{2}\right) \\&\quad \left( \varPhi _{1}^{(l_2)}\left( \frac{x_i-a}{2} \tau _2+\frac{x_i+a}{2}\right) \right) ^{T} \varPhi _{1}^{-T} \mathbf {S} \mathrm {d} \tau _2\\&\quad =f(x_i), \quad i=1,2, \dots , N-m, \end{aligned}$$

and by using (16) we write

$$\begin{aligned} \begin{array}{l} \left[ \sum _{k=0}^{m} p_{k}(x_i) \varPhi _{1}^{(k)}(x_i) \right. \left. +\theta _{1} \frac{b-a}{2} \sum _{j=1}^{M} w_{1j} k_{1}\left( x_i, \frac{b-a}{2} \tau _{1j}+\frac{b+a}{2}\right) \varPhi _{1}^{(l_1)}\left( \frac{b-a}{2} \tau _{1j}+\frac{b+a}{2}\right) \right. \\ \left. +\theta _{2} \frac{x_{i}-a}{2} \sum _{j=1}^{M} w_{2j} k_{2}(x_i, \frac{x_i-a}{2} \tau _{2j}+\frac{x_i+a}{2}) \varPhi _{1}^{(l_2)}\left( \frac{x_i-a}{2} \tau _{2j}+\frac{x_i+a}{2}\right) \right] ^T\varPhi _{1}^{-T} \mathbf {S}\\ \simeq f(x_i),\quad i=1,2, \dots , N-m, \end{array} \end{aligned}$$

(21)

, where $\tau _{\beta j}$ and $w_{\beta j}$, $(\beta =1,2)$ are the Legendre–Gauss–Lobatto nodes and weights into $[-1,1]$, respectively. Finally, an $N\times N$ system of linear algebraic equations is produced such that the $N-m$ first row is related to Eq. (21) and m remained row is related to Eq. (19). By use of the $\mathtt {linsolve}$ command in MATLAB, the value of unknown vector $\mathbf {S}$ and consequently the solution y(x) is obtained.

Error analysis

In this section, we try to find an upper bound for the residual error when the presented method is derived for (1). Suppose that y and $\tilde{y}$ are the exact solution and the approximate one, respectively. Define

$$\begin{aligned} \begin{aligned} RE(x)&=\sum _{k=0}^{m} p_{k}(x) \left( y^{(k)}(x)-\tilde{y}^{(k)}(x)\right) \\&\quad +\theta _{1} \int _{a}^{b} k_{1}(x, t) \left( y^{(l_1)}(t)-\tilde{y}^{(l_1)}(t)\right) \mathrm {d} t\\&\quad +\theta _{2} \int _{a}^{x} k_{2}(x, t) \left( y^{(l_2)}(t)-\tilde{y}^{(l_2)}(t)\right) \mathrm {d} t . \end{aligned} \end{aligned}$$

The main result of this section is formulated through the following theorem.

Theorem 4

Assume $M_{p}, M, R_{1}, R_{2}, R'_{1}, R'_{2}$ are real positive numbers and

$$\begin{aligned} \begin{aligned} E&=\frac{\varepsilon ^2}{\alpha ^2+\varepsilon ^2+\delta ^2},\\ R(N)&=\frac{{N}{(N-1)^3}2^{2N-1}[(N-2)!]^{4}}{(2N-1)[(2N-2)!]^3}. \end{aligned} \end{aligned}$$

For the residual error function, that is RE(x) , we have the following bound

$$\begin{aligned} \vert RE(x) \vert \le&M_{p} \sum _{k=0}^{m}T_{k} + \vert \theta _{1}\vert \left( \frac{b-a}{2}NR_{1}T_{l_{1}}+R(N)R'_{1} \right) \\&+\vert \theta _{2}\vert \left( \frac{b-a}{2}NR_{2}T_{l_{2}}+R(N)R'_{2} \right) , \end{aligned}$$

in which

$$\begin{aligned} T_{j}=\frac{NcM\beta \alpha e^{\alpha ^2 b^2}E^{L}}{\sqrt{\alpha ^2+\varepsilon ^2+\delta ^2} 2^{L}\left( \frac{L}{2}\right) !}\sum _{n=L+1}^{\infty } \sum _{i=0}^{j} \left( \begin{array}{c} j\\ i\\ \end{array}\right) \frac{(2\alpha \beta )^{i}n!}{\left( \frac{n-i-1}{2}\right) !}, \quad j=k,l_1,l_2. \end{aligned}$$

Proof

Using (1) one can write

$$\begin{aligned} \begin{aligned} RE(x)&=\sum _{k=0}^{m} p_{k}(x) \left( y^{(k)}(x)-\tilde{y}^{(k)}(x)\right) \\&\quad +\theta _{1} \int _{a}^{b} k_{1}(x, t) \left( y^{(l_1)}(t)-\tilde{y}^{(l_1)}(t)\right) \mathrm {d} t\\&\quad +\theta _{2} \int _{a}^{x} k_{2}(x, t) \left( y^{(l_2)}(t)-\tilde{y}^{(l_2)}(t)\right) \mathrm {d} t . \end{aligned} \end{aligned}$$

(22)

We define $e(x)= y(x)-\tilde{y}(x)$. By utilizing (16), it is obvious

$$\begin{aligned} \begin{aligned}&\int _{a}^{b} k_{1}(x, t) {e}^{(l_1)}(t) \mathrm {d} t\\&\quad =\frac{b-a}{2} \int _{-1}^{1} k_{1}\left( x, \frac{b-a}{2}z+\frac{b+a}{2}\right) {e}^{(l_1)}\\&\qquad \left( \frac{b-a}{2}z+\frac{b+a}{2}\right) \mathrm {d} z\\&\quad = \frac{b-a}{2} \sum _{j=1}^{N}{\omega }_{j}k_{1}(x, \frac{b-a}{2}z_{j}+\frac{b+a}{2}) {e}^{(l_1)}\\&\qquad \left( \frac{b-a}{2}z_{j}+\frac{b+a}{2}\right) +E_{k_{1}}, \end{aligned} \end{aligned}$$

(23)

, where there exists an $\zeta \in (-1,1)$ so that

$$\begin{aligned} E_{k_{1}}&=-\frac{{N}{(N-1)^3}2^{2N-1}[(N-2)!]^{4}}{(2N-1)[(2N-2)!]^3}\\&\quad \times \frac{\partial ^{2N-2}}{\partial {\zeta ^{2N-2}}}\left( k_{1}\left( x, \frac{b-a}{2}\zeta +\frac{b+a}{2}\right) {e}^{(l_1)}\right. \nonumber \\&\quad \left. \left( \frac{b-a}{2}\zeta +\frac{b+a}{2}\right) \right) . \end{aligned}$$

Moreover, for each $a\le x \le b$

$$\begin{aligned} \begin{aligned}&\left| \int _{a}^{x} k_{2}(x, t) {e}^{(l_2)}(t) \mathrm {d} t\right| \le \int _{a}^{b} \left| k_{2}(x, t) {e}^{(l_2)}(t)\right| \mathrm {d} t\\&\quad =\frac{b-a}{2} \int _{-1}^{1} \left| k_{2}\left( x, \frac{b-a}{2}z+\frac{b+a}{2}\right) {e}^{(l_2)}\right. \\&\qquad \left. \left( \frac{b-a}{2}z+\frac{b+a}{2}\right) \right| \mathrm {d} z\\&\quad = \frac{b-a}{2} \sum _{j=1}^{N}{\omega }^{'}_{j}\left| k_{2}\left( x, \frac{b-a}{2}z_{j}+\frac{b+a}{2}\right) {e}^{(l_2)}\right. \\&\qquad \left. \left( \frac{b-a}{2}z_{j}+\frac{b+a}{2}\right) \right| +E_{k_{2}}, \end{aligned} \end{aligned}$$

(24)

, where there exists an $\eta \in (-1,1)$ so that

$$\begin{aligned} E_{k_{2}}&=\frac{{N}{(N-1)^3}2^{2N-1}[(N-2)!]^{4}}{(2N-1)[(2N-2)!]^3}\times \frac{\partial ^{2N-2}}{\partial {\eta ^{2N-2}}}\\&\left| {k_{2}\left( x, \frac{b-a}{2}\eta +\frac{b+a}{2}\right) {e}^{(l_2)}\left( \frac{b-a}{2}\eta +\frac{b+a}{2}\right) }\right| . \end{aligned}$$

On the other hand, for every $0\le k \le m$ one obtains

$$\begin{aligned} \left| y^{(k)}(x)-\tilde{y}^{(k)}(x) \right|&= \left| \sum _{j=1}^{N}c_{j}\sum _{n=L+1}^{\infty }\lambda _{n}\varphi _{n}^{(k)}(x)\varphi _{n}(x_{j})\right| \\&\quad \le \sum _{j=1}^{N}\left| c_{j}\right| \sum _{n=L+1}^{\infty }\left| \lambda _{n}\right| \left| \varphi _{n}^{(k)}(x)\varphi _{n}(x_{j})\right| . \end{aligned}$$

If $c=\max \left\{ \left| c_{j} \right| : j=1,\ldots , N \right\}$ then we have

$$\begin{aligned} \left| e^{(k)}(x) \right| \le c\sum _{j=1}^{N}\sum _{n=L+1}^{\infty }\left| \lambda _{n} \right| \left| \varphi _{n}^{(k)}(x)\varphi _{n}(x_{j})\right| . \end{aligned}$$

(25)

Since

$$\begin{aligned} \varphi _{n}(x)=\sqrt{\frac{\beta }{2^{n-1}(n-1)!}}e^{-\delta ^{2}x^{2}}H_{n-1}(\alpha \beta x), \end{aligned}$$

we can write

$$\begin{aligned} \varphi _{n}^{(k)}(x)&=\sqrt{\frac{\beta }{2^{n-1}(n-1)!}}\sum _{i=0}^{k} \left( \begin{array}{c} k\\ i\\ \end{array}\right) \\&\quad \frac{d^{k-i}}{dx^{k-i}}e^{-\delta ^2 x^2} \frac{d^{i}}{dx^{i}}H_{n-1}(\alpha \beta x). \end{aligned}$$

Because of $\frac{d}{dx}e^{-\delta ^2 x^2}=-2\delta ^2 x e^{-\delta ^2 x^2}$, for every $0 \le i \le k$ there exists an $M_{i}>0$ on the interval [a, b] such that

$$\begin{aligned} \left| \frac{d^{k-i}}{dx^{k-i}}e^{-\delta ^2 x^2} \right| \le M_{i} e^{-\delta ^2 x^2}. \end{aligned}$$

Putting $M=\max \left\{ M_{i}:\ i=0,1, \ldots k\right\}$ enables one to conclude

$$\begin{aligned} \begin{aligned} \left| \varphi _{n}^{(k)}(x)\right|&\le M\sqrt{\frac{\beta }{2^{n-1}(n-1)!}}e^{-\delta ^2 x^2}\\&\quad \sum _{i=0}^{k} \left( \begin{array}{c} k\\ i\\ \end{array}\right) \left| \frac{d^{i}}{dx^{i}}H_{n-1}(\alpha \beta x)\right| \\&\quad = M\sqrt{\frac{\beta }{2^{n-1}(n-1)!}}e^{-\delta ^2 x^2}\\&\quad \sum _{i=0}^{k} \left( \begin{array}{c} k\\ i\\ \end{array}\right) \frac{(2\alpha \beta )^{i} n!}{(n-1-i)!}\left| H_{n-1-i}(\alpha \beta x)\right| \\ \end{aligned} \end{aligned}$$

According to the asymptotic expansion of Hermite polynomials [41],

$$\begin{aligned} H_{n}(x)&\sim e^{\frac{x^2}{2}}\frac{n!}{\left( \frac{n}{2}\right) !}\cos \left( x\sqrt{2n+1}-\frac{n\pi }{2} \right) ,\qquad \text {for large n}, \end{aligned}$$

, it is easy to see that

$$\begin{aligned} \left| \varphi _{n}^{(k)}(x)\right| \le&M\sqrt{\frac{\beta }{2^{n-1}(n-1)!}}e^{\left( \frac{\alpha ^2 \beta ^2}{2}-\delta ^2\right) x^2}\\&\times \sum _{i=0}^{k} \left( \begin{array}{c} k\\ i\\ \end{array}\right) \frac{(2\alpha \beta )^{i}n!}{\left( \frac{n-i-1}{2}\right) !}\\&\quad \left| \cos \left( x\sqrt{2n-2i-1}-\frac{\pi }{2}\left( n-1-i \right) \right) \right| . \end{aligned}$$

Let $E=\frac{\varepsilon ^2}{\alpha ^2+\varepsilon ^2+\delta ^2}<1$. From (25), we determine

$$\begin{aligned} \left| e^{(k)}(x) \right|&\le \frac{NcM\beta \alpha e^{\alpha ^2 b^2}}{\sqrt{\alpha ^2+\varepsilon ^2+\delta ^2}} \sum _{n=L+1}^{\infty } \frac{E^{n-1}}{2^{n-1} \left( \frac{n-1}{2}\right) !}\\&\quad \sum _{i=0}^{k} \left( \begin{array}{c} k\\ i\\ \end{array}\right) \frac{(2\alpha \beta )^{i} n!}{\left( \frac{n-i-1}{2}\right) !}\\&\le \frac{NcM\beta \alpha e^{\alpha ^2 b^2}E^{L}}{\sqrt{\alpha ^2+\varepsilon ^2+\delta ^2} 2^{L}\left( \frac{L}{2}\right) !}\\&\quad \sum _{n=L+1}^{\infty } \sum _{i=0}^{k} \left( \begin{array}{c} k\\ i\\ \end{array}\right) \frac{(2\alpha \beta )^{i}n!}{\left( \frac{n-i-1}{2}\right) !} . \end{aligned}$$

Subsequently, if we assume $M'=\frac{cM\beta \alpha e^{\alpha ^2 b^2}}{\sqrt{\alpha ^2+\varepsilon ^2+\delta ^2}}$ it is acquired

$$\begin{aligned} \left| e^{(k)}(x) \right| \le \frac{M'N E^{L}}{2^{L}\left( \frac{L}{2}\right) !}\sum _{n=L+1}^{\infty } \sum _{i=0}^{k} \left( \begin{array}{c} k\\ i\\ \end{array}\right) \frac{(2\alpha \beta )^{i}n!}{\left( \frac{n-i-1}{2}\right) !}=T_{k} . \end{aligned}$$

(26)

The inequality (26) shows that when $L \rightarrow \infty$ then $e^{(k)}(x)$ converges to zero. Now, suppose that

$$\begin{aligned} \begin{aligned} R_{1}&=\max _{1\le j\le N} \left| \omega _{j}k_{1}(x, \frac{b-a}{2}z_{j}+\frac{b+a}{2})\right| , \,\\ R_{2}&=\max _{1\le j\le N} \left| \omega '_{j}k_{2} \left( x, \frac{b-a}{2}z_{j}+\frac{b+a}{2}\right) \right| ,\\ R_{1}'&=\max _{x,\zeta }\frac{\partial ^{2N-2}}{\partial {\zeta ^{2N-2}}}\left| k_{1}\left( x, \frac{b-a}{2}\zeta +\frac{b+a}{2}\right) {e}^{(l_1)}\right. \\&\quad \left. \left( \frac{b-a}{2}\zeta +\frac{b+a}{2}\right) \right| ,\\ R_{2}'&=\max _{x,\eta } \frac{\partial ^{2N-2}}{\partial {\eta ^{2N-2}}}\left| k_{2}\left( x, \frac{b-a}{2}\eta +\frac{b+a}{2}\right) {e}^{(l_2)}\right. \\&\quad \left. \left( \frac{b-a}{2}\eta +\frac{b+a}{2}\right) \right| ,\\ R(N)&=\frac{{N}{(N-1)^3}2^{2N-1}[(N-2)!]^{4}}{(2N-1)[(2N-2)!]^3}.\\ \end{aligned} \end{aligned}$$

By these notations and deriving (23), (24), we realize

$$\begin{aligned} \begin{aligned}&\left| \int _{a}^{b} k_{1}(x, t) {e}^{(l_1)}(t) \mathrm {d} t \right| \\&\quad \le \frac{b-a}{2}R_{1} \frac{M'N^2 E^{L}}{2^{L}\left( \frac{L}{2}\right) !}\\&\qquad \sum _{n=L+1}^{\infty } \sum _{i=0}^{l_1} \left( \begin{array}{c} l_1\\ i\\ \end{array}\right) \frac{(2\alpha \beta )^{i}n!}{\left( \frac{n-i-1}{2}\right) !}+R_{1}'R(N),\\&\left| \int _{a}^{b} k_{2}(x, t) {e}^{(l_2)}(t) \mathrm {d} t \right| \\&\quad \le \frac{b-a}{2}R_{2} \frac{M'N^2 E^{L}}{2^{L}\left( \frac{L}{2}\right) !}\\&\qquad \sum _{n=L+1}^{\infty } \sum _{i=0}^{l_2} \left( \begin{array}{c} l_2\\ i\\ \end{array}\right) \frac{(2\alpha \beta )^{i}n!}{\left( \frac{n-i-1}{2}\right) !}+R_{2}'R(N). \end{aligned} \end{aligned}$$

(27)

If we set $M_{p}=\max \left\{ \vert p_{k}(x)\vert :\ k=0,1,\ldots , m \right\}$, by applying (22), (23) and (27) the expected result is achieved. $\square$

Numerical examples

In this section, several examples are given to assess the performance of present method. A uniform data set from size N in one dimension is considered. The number of Legendre–Gauss–Lobatto nodes is denoted by M. Assume that y and $\tilde{y}$ refer to the exact solution and the approximate one, respectively. The accuracy of method is measured by applying the absolute error, namely $\left| e(x)\right|$, the maximum absolute error $(L_{\infty } \text{ error } )$ and the Root-Mean-Square error (RMS error) overall N data points as follows:

$$\begin{aligned} L_{\infty }= & {} \max _{a \le x_i \le b}\left| e(x_{i})\right| ,\quad i=1,\dots ,N, \end{aligned}$$

(28)

$$\begin{aligned} RMS= & {} \sqrt{\frac{\sum ^N_{i=1}{e^{2}(x_{i})}}{N}}. \end{aligned}$$

(29)

All of the numerical computations are performed in MATLAB R2015a, on a laptop with an Intel(R) Core(TM) i5-6200U, CPU 2.40GHz, 8GB(RAM).

Example 1

Let us consider linear Volterra IDE of the first kind

$$\begin{aligned} \int _{0}^{x} \cos (x-t) y^{\prime \prime }(t) d t=2 \sin (x), \quad 0\le x \le 1, \end{aligned}$$

with the initial conditions $y(0)=y^{\prime }(0)=0$. The exact solution for this equation is $y(x)=x^{2}$.

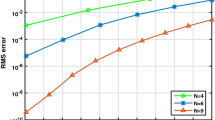
Put $M=4$, $\varepsilon =0.4$ and $\alpha =0.1$. The comparison of RMS error, $L_\infty$ error and condition number for different values of N between the present method and the standard GA-RBF one are given in Table 2. It indicates that the error values and condition numbers of present method are better than those of the standard one. Because the eigenfunctions $\varphi _{n}$ are orthogonal, so the matrix $\varPhi _{1}$ in Eq. (14) is relatively well behaved. Also, by removing the matrix $\varLambda$ into (14), as one of the sources of ill-conditioning for the small values of $\varepsilon$, the present method is more stable, and the condition number is significantly less than that of classical GA-RBF. Figure 1 displays the absolute error as a function of $x\in [0,1]$ for $N=\{4,6,11\}$ which decreases when the number of data points increases. The RMS error as a function of $\varepsilon \in [0.01,1]$ for $N=\{4,6,11\}$ is shown in Figure 2. It can be seen that for small $\varepsilon$ the RMS error value is less for $N=\{4,6\}$.

Table 2 Comparison between the present method and the standard GA-RBF one with $M=4$, $\varepsilon =0.4$ and $\alpha =0.1$ for Example 1

Fig. 1

Absolute error of present method as a function of x for different values of N for Example 1

Fig. 2

RMS error of present method as a function of $\varepsilon$ for different values of N for Example 1

Example 2

Consider first-order Volterra IDE

$$\begin{aligned} y^{\prime }=1-2 x \sin (x)+\int _{0}^{x} y(t) d t, \quad y(0)=0, \quad 0 \le x \le 1{.} \end{aligned}$$

The exact solution is $y(x)=x \cos (x)$.

We use $M=5$, $\varepsilon =0.09$ and $\alpha =1.9$. The comparison of RMS error for different values of N between the present method and the methods introduced by [4] are expressed in Table 3. It shows that the error values in the present method are better than those of [4]. Table 4 declares the RMS error results of present method, $L_\infty$ error and condition number for different values of N. Figure 3 displays the absolute error as a function of $x\in [0,1]$ for $N=\{5,8,12\}$, which decreases by increasing the number of data points. The RMS error as a function of $\varepsilon \in [0.01,2]$ for $N=\{5,8,12\}$ is shown in Fig. 4.

Table 3 Comparison between the present method and the methods of [4] with $M=5$, $\varepsilon =0.09$ and $\alpha =1.9$ for Example 2

Table 4 Numerical results with $M=5$, $\varepsilon =0.09$ and $\alpha =1.9$ for Example 2

Fig. 3

Absolute error of present method as a function of x for different values of N for Example 2

Fig. 4

RMS error of present method as a function of $\varepsilon$ for different values of N for Example 2

Example 3

Let us consider linear Fredholm IDE

$$\begin{aligned}&y^{\prime \prime }(x)+x y^{\prime }(x)-x y(x)\\&\quad =e^{x}-2 \sin (x)\\&\qquad +\int _{-1}^{1} \sin (x) e^{-t} y(t) \mathrm {d} t, \quad -1 \leqslant x \leqslant 1, \end{aligned}$$

under the initial conditions $y(0)=1$ and $y^{\prime }(0)=1 .$ Here, the exact solution is $y(x)=e^{x}$.

Assume $M=4$, $\varepsilon =0.01$ and $\alpha =1.9$. The comparison of absolute errors on the interval $[-1,1]$ between the present method and the method described by [21] are expressed in Table 5. It indicates that the absolute error values of present method for $N=13$ are better than those of described in [21] for $N=1000$. The RMS error in [21] for $N=1000$ is 2.87486e-08, whereas the RMS error of our method is 4.1029e-11 for $N=13$. Table 6 presents the RMS error results, $L_\infty$ error and condition number of present method for different values of N. Figure 5 displays the absolute error as a function of $x\in [-1,1]$ for $N=\{6,8,11,13\}$, which decreases by increasing the number of data points. The RMS error as a function of $\varepsilon \in [0.01,1.5]$ for $N=\{6,8,11,13\}$ is shown in Fig. 6.

Table 5 Comparison of the absolute errors between the present method and the method of [21] with $M=4$, $\varepsilon =0.01$ and $\alpha =1.9$ for Example 3

Table 6 Numerical results with $M=4$, $\varepsilon =0.01$ and $\alpha =1.9$ for Example 3

Fig. 5

Absolute error of present method as a function of x for different values of N for Example 3

Fig. 6

RMS error of present method as a function of $\varepsilon$ for different values of N for Example 3

Example 4

We consider eight-order Fredholm IDE with initial conditions as follows

$$\begin{aligned} y^{(8)}(x)= & {} -8 e^{x}+x^{2}+y(x)+\int _{0}^{1} x^{2} y^{\prime }(t) d t, \quad 0 \leqslant x \leqslant 1,\\ y(0)= & {} 1, y^{\prime }(0)=0, y^{\prime \prime }(0)=-1, y^{\prime \prime \prime }(0)=-2,\\ y^{(4)}(0)= & {} -3, y^{(5)}(0)=-4, y^{(6)}(0)=-5, y^{(7)}(0)=-6{.} \end{aligned}$$

The exact solution is $y(x)=(1-x) e^{x} .$

Let $M=4$, $\varepsilon =0.01$ and $\alpha =0.9$. Table 7 announces the RMS error results, $L_\infty$ error and condition number of present method for different values of N. Figure 7 portrays the absolute error as a function of $x\in [0,1]$ for $N=\{6,10,12,13\}$, which decreases by increasing the number of data points. The RMS error as a function of $\varepsilon \in [0.001,1.5]$ for $N=\{6,10,12,13\}$ is shown in Fig. 8.

Table 7 Numerical results with $M=4$, $\varepsilon =0.01$ and $\alpha =0.9$ for Example 4

Fig. 7

Absolute error of present method as a function of x for different values of N for Example 4

Fig. 8

RMS error of present method as a function of $\varepsilon$ for different values of N for Example 4

Example 5

[31] Consider linear Fredholm–Volterra IDE

$$\begin{aligned} \begin{aligned}&y^{\prime }(x)=\frac{27}{5}-\frac{1}{5} x^{6}-\frac{3}{4} x^{5}-x^{4}-\frac{1}{2} x^{3}+3 x^{2} +\frac{41}{20} x\\&\quad +\int _{-1}^{1}(x-t) y(t) \mathrm {d} t+\int _{-1}^{x} x t y(t) \mathrm {d} t, \quad -1 \leqslant x \leqslant 1, \end{aligned} \end{aligned}$$

with the initial condition $y(0)=1 .$ The exact solution of this equation is $y(x)=(x+1)^{3}$.

Put $M=5$, $\varepsilon =0.01$ and $\alpha =1.9$. Table 8 gives the RMS error results, $L_\infty$ error and condition number of present method for different values of N. Figure 9 displays the absolute error as a function of $x\in [-1,1]$ for $N=\{5,7,9,10\}$, which decreases by increasing the number of data points. The RMS error as a function of $\varepsilon \in [0.01,1.5]$ for $N=\{5,7,9,10\}$ is shown in Fig. 10.

Table 8 Numerical results with $M=5$, $\varepsilon =0.01$ and $\alpha =1.9$ for Example 5

Fig. 9

Absolute error of the presented method as a function of x for different values of N for Example 5

Fig. 10

RMS error of present method as a function of $\varepsilon$ for different values of N for Example 5

Example 6

Consider fifth-order linear Fredholm–Volterra IDE with initial conditions given by

$$\begin{aligned}&y^{(5)}(x)-x y^{(2)}(x)+x y(x)=-e^{-x}-\frac{1}{2} e^{2 x}-x^{2}\\&\quad +\frac{1}{2} \int _{0}^{1} e^{2 x+t} y(t) d t+\int _{0}^{x} x e^{t} y(t) d t, \quad 0 \leqslant x \leqslant 1,\\&\quad y(0)=y^{(2)}(0)=y^{(4)}(0)=1, \quad y^{(1)}(0)=y^{(3)}(0)=-1{.} \end{aligned}$$

The exact solution of the above equation is $y(x)=e^{-x}$.

Suppose $M=4$, $\varepsilon =0.01$ and $\alpha =1.9$. Table 9 declares the RMS error results, $L_\infty$ error and condition number of present method for different values of N. Figure 11 displays the absolute error as a function of $x\in [0,1]$ for $N=\{10,11,12,13\}$, which decreases when the number of data points increases. The RMS error as a function of $\varepsilon \in [0.01,2]$ for $N=\{10,11,12,13\}$ is demonstrated in Fig. 12.

Table 9 Numerical results with $M=4$, $\varepsilon =0.01$ and $\alpha =1.9$ for Example 6

Fig. 11

Absolute error of present method as a function of x for different values of N for Example 6

Fig. 12

RMS error of present method as a function of $\varepsilon$ for different values of N for Example 6

Conclusion

We described an improved approach of Gaussian RBFs to solve high-order linear Volterra–Fredholm integro-differential equations. The small values of $\varepsilon$ were well known to make highly accurate results, but the coefficient matrix of interpolation became ill-conditioned. We used very small values for $\varepsilon$ and employed the eigenfunction expansion for GA-RBFs. The standard RBF did not work for illustrative examples except for the first one. We did not mention the numerical results of standard RBF for those examples. In those cases, the impression of present version of RBF was seen. Generally, in Figures attributed to RMS error as a function of $\varepsilon$ for fixed N, the RMS error increased by increasing $\varepsilon$. Also, according to Figures corresponding to the absolute error as a function of x, by increasing N the absolute error rate decreased. Besides, the condition number in the present method was small and acceptable compared to the standard GA-RBF one. These were reasons for the efficiency of present method.