On Mixed Steps-Collocation Schemes for Nonlinear Fractional Delay Differential Equations

Abstract

This research deals with the numerical solution of fractional differential equations with delay using the method of steps and shifted Legendre (Chebyshev) collocation method. This article presents a new formula for the fractional derivatives (in the Caputo sense) of shifted Legendre polynomials. With the help of this tool and previous work of the authors, efficient numerical schemes for solving nonlinear continuous fractional delay differential equations are proposed. The proposed schemes transform the nonlinear fractional delay differential equations to a non-delay one by employing the method of steps. Then, the approximate solution is expanded in terms of Legendre (Chebyshev) basis functions. Furthermore, the convergence analysis of the proposed schemes is provided. Several practical model examples are considered to illustrate the efficiency and accuracy of the proposed schemes.

1 Introduction

Delay differential equations (DDEs) belong to a broader class of functional differential equations. The rate of change of the unknown function at a specific time is represented due to the values of the function at previous times. DDEs are also known as differential-difference equations. Laplace and Condorcet (Chen and Moore 2002) first studied these equations, and naturally, they appear in various fields of science and engineering (Erneux 2009). Fractional delay differential equations (FDDEs) are considered a generalization of DDEs, which contain derivatives of arbitrary fractional order. The integer order differential operator is a local operator, while the fractional-order differential operator is a non-local operator. More precisely, the next state of a system, which is modeled by fractional differential equations (FDEs) depends not only upon its present situation but also upon all of its past positions. The fractional order differential operator enables us to describe a real event more accurately than the classical integer order differential operator. Recently, FDEs and FDDEs are frequently used to model many natural phenomena in the fields of control theory (Si-Ammour et al. 2009), biology (Magin 2010; Dehghan and Salehi 2010), economy Škovránek et al. (2012), and so on.

Because of the computational complexities of fractional delay derivatives, for most of the FDEs and FDDEs, the exact solution is available. Therefore, it is necessary to employ numerical methods for solving such equations. Shakeri and Dehghan (2008) used the homotopy perturbation method for delay differential equations with integer order derivatives. The variational iteration method is considered by Saadatmandi and Dehghan (2009) to obtain the numerical solution of the generalized pantograph equation. Moghaddam and Mostaghim (2013), Parsa Moghaddam and Salamat Mostaghim (2017) introduced numerical methods in the framework of the finite difference method for solving FDDEs. They also presented a matrix approach using the fractional finite difference method for solving nonlinear FDDEs (Moghaddam and Mostaghim 2014). Prakash et al. (2016) proposed a numerical algorithm based on a modified He-Laplace method for solving nonlinear FDDEs. Wang (2013) combined the Adams-Bashforth-Moulton method with the linear interpolation method to find an approximate solution for FDDEs. Mohammed and Khlaif (2014) applied the Adomian decomposition method to get the numerical solution of FDDEs. Mousa-Abadian and Momeni-Masuleh proposed a numerical scheme for solving linear fractional delay differential systems (Mousa-Abadian and Momeni-Masuleh 2021). Their scheme employs the method of steps to handle the delay term and the Chebyshev-Tau method to construct the approximate solution. Sedaghat et al. (2012) introduced a numerical scheme using Chebyshev polynomials for solving FDDEs of pantograph type. Saeed et al. (2015) developed Chebyshev wavelet methods for solving FDDEs. Khader (2013) derived an approximate formula of the Laguerre polynomials for the numerical treatment of FDDEs. Daftardar-Gejji et al. (2015) extended a new predictor-corrector method to solve FDDEs. Parsa Moghaddam et al. (2016) developed a numerical method based on the Adams-Bashforth-Moulton method for solving variable-order FDDEs. Yaghoobi et al. (2017) devised a numerical scheme based on a cubic spline interpolation for solving variable-order FDDEs. Khosravian-Arab et al. (2017) developed new Lagrange basis functions to approximate fractional derivatives in unbounded domains. Their approach is based on the pseudo-spectral, Galerkin, and Petrov-Galerkin methods.

A numerical approach to solve nonlinear FDDEs can be a generalization of the method introduced in Ref Mousa-Abadian and Momeni-Masuleh (2021). The Chebyshev collocation method can be considered to solve nonlinear FDDEs. Of course, employing collocation methods are not restricted to use the Chebyshev basis functions, but also the Legendre basis functions can be applied. Therefore, a significant part of this article deals with the solution of nonlinear FDDEs by using a Legendre basis functions. In this paper, we derive a new formula for the fractional derivatives of shifted Legendre polynomials and then present the efficient numerical schemes for solving nonlinear FDDEs.

The remainder of this article proceeds as follows. In the next section, the properties of shifted collocation-type bases are discussed. In Sect. 3, a formula for the fractional derivatives of shifted Legendre basis functions are derived. Section 4 describes mixed steps-collocation schemes for solving nonlinear FDDEs. The convergence analysis of the proposed schemes has been done in Sect. 5. Section 6 concerns applying the proposed schemes to several nonlinear FDDEs. The conclusion is given in Sect. 7.

2 Shifted Collocation-Type Bases

The most common collocation methods are those based on Chebyshev and Legendre basis functions. Properties of shifted Chebyshev basis functions have been investigated in Ref Mousa-Abadian and Momeni-Masuleh (2021). Here, we deduce the properties of shifted Legendre basis functions. The Legendre basis $L_{{k}}(t)$ for $k=0, 1, \dots ,$ and $-1\le t\le 1$, can be defined as the solution of the following ordinary differential equation (Canuto et al. 2006):

$$\begin{aligned} \frac{d}{dt}\Big ((1-t^2)\frac{dL_{{k}}}{dt}(t)\Big )+k(k+1)L_{{k}}(t)=0, \end{aligned}$$

which satisfy $L_{{k}}(\pm 1)=(\pm 1)^k$. For $k\ge 1$, we have the following recurrence formula:

$$\begin{aligned} L_{{k+1}}(t)=\frac{2k+1}{k+1}tL_{{k}}(t)-\frac{k}{k+1}L_{{k-1}}(t), \end{aligned}$$

(1)

where $L_{{0}}(t)=1$ and $L_{{1}}(t)=t$. The shifted Legendre basis functions are defined on the interval $[\alpha ,\beta ]$ using the change of variable $t=\frac{2}{\beta -\alpha }(x-\beta )+1$. For simplicity, let us denote $L_{{k}}(\frac{2}{\beta -\alpha }(x-\beta )+1)$ by $L_{{\alpha ,\beta ,k}}(x)$. Therefore, similar to (1), the following recurrence relation can be obtained

$$\begin{aligned} L_{{\alpha ,\beta ,k+1}}(x)=\frac{2k+1}{k+1}\left( \frac{2}{\beta -\alpha }(x-\beta )+1 \right) L_{{\alpha ,\beta ,k}}(x)-\frac{k}{k+1}L_{{\alpha ,\beta ,k-1}}(x). \end{aligned}$$

The shifted Legendre basis $L_{{\alpha ,\beta ,k}}(x)$ can be presented in the following form:

$$\begin{aligned} L_{{\alpha ,\beta ,n}}(x)=\frac{1}{2^n}\sum _{k=0}^{[\frac{n}{2}]}(-1)^k\left( {\begin{array}{c}n\\ k\end{array}}\right) \left( {\begin{array}{c}2n-2k\\ n\end{array}}\right) \left( \frac{2}{\beta -\alpha }(x-\beta )+1 \right) ^{n-2k}. \end{aligned}$$

(2)

By using the identity

$$\begin{aligned} \left( \frac{2}{\beta -\alpha }(x-\beta )+1 \right) ^{n-2k}=\sum _{l=0}^{n-2k}\sum _{j=0}^{l}\frac{(-1)^{l-j}\left( {\begin{array}{c}l\\ j\end{array}}\right) \left( {\begin{array}{c}n-2k\\ l\end{array}}\right) 2^l\beta ^{l-j}}{(\beta -\alpha )^l}x^j, \end{aligned}$$

(3)

the shifted Legendre basis $L_{{\alpha ,\beta ,k}}(x)$ can be written in terms of a power series in x as

$$\begin{aligned} L_{{\alpha ,\beta ,n}}(x)=\sum _{k=0}^{[\frac{n}{2}]}\sum _{l=0}^{n-2k}\sum _{j=0}^{l}\frac{(-1)^{k-j+l}2^{l-n}\beta ^{l-j}(2n-2k)!}{(\beta -\alpha )^l(n-k)!k!(n-2k-l)!j!(l-j)!}x^j, \end{aligned}$$

(4)

which satisfy $L_{{\alpha ,\beta ,k}}(\beta )=1$ and $L_{{\alpha ,\beta ,k}}(\alpha )=(-1)^k$. The next lemma describes integer order derivatives of the shifted Legendre basis functions.

Lemma 1

For $m\le j\le n$, we have

$$\begin{aligned} D^m L_{{\alpha ,\beta ,n}}(x)= \sum _{k=0}^{[\frac{n}{2}]}\sum _{l=m}^{n-2k}\sum _{j=m}^{l}\frac{(-1)^{k-j+l}2^{l-n}(\beta -\alpha )^{-l}\beta ^{l-j}(2n-2k)!}{(n-k)!k!(n-2k-l)!(l-j)!(j-m)!}x^{j-m}. \end{aligned}$$

(5)

Proof

The proof is easily obtained from Eq. (4).

The shifted Legendre polynomials satisfy the following relation:

$$\begin{aligned} \int _{\alpha }^\beta L_{{\alpha ,\beta ,i}}(x) L_{{\alpha ,\beta ,k}}(x)\textrm{d}x=\delta _{ik}\left( k+\frac{1}{2}\right) ^{-1}, \end{aligned}$$

(6)

i.e., they are orthogonal with each other concerning the unit weight function. The shifted Legendre basis functions form an orthogonal system of polynomials, which is complete in the space of square-integrable functions, i.e., ${\mathscr {L}}^2(\alpha , \beta )$. Therefore, any $u\in {\mathscr {L}}^2(\alpha ,\beta )$ can be written as

$$\begin{aligned} u(x)=\sum _{k=0}^\infty \hat{u}_{{k}} L_{{\alpha ,\beta ,k}}(x), \end{aligned}$$

where

$$\begin{aligned} \hat{u}_{{k}}=\left( k+\frac{1}{2}\right) \int _{\alpha }^\beta u(x)L_{{\alpha ,\beta ,k}}(x)\textrm{d}x, \quad k\ge 0. \end{aligned}$$

The associated inner product and norm are given by

$$\begin{aligned} (f,g)=\int _{\alpha }^\beta f(x)g(x)\textrm{d}x \end{aligned}$$

and

$$\begin{aligned} ||f||^2_{{\mathscr {L}}^2(\alpha ,\beta )}=(f,f)=\int _{\alpha }^{\beta }|f(t)|^2\textrm{d}t. \end{aligned}$$

We define $H^m(\alpha ,\beta )$ to be the vector space of the functions $g\in {\mathscr {L}}^2(\alpha , \beta )$ such that all distributional derivatives of f of the order up to m can be represented by functions in ${\mathscr {L}}^2(\alpha , \beta )$. $H^m(\alpha ,\beta )$ is endowed with the norm

$$\begin{aligned} ||f||^2_{H^m(\alpha ,\beta )}=\sum _{k=0}^{m}\Big |\Big | \frac{\partial ^k}{\partial x^k}f(x) \Big |\Big |^2_{{\mathscr {L}}^2(\alpha ,\beta )}. \end{aligned}$$

Furthermore, the associated semi-norm is defined as follows

$$\begin{aligned} | f |^2_{H^{m:N}(\alpha ,\beta )}=\sum _{j=\min (m,N)}^{m}|| f^{(j)}||^2_{{\mathscr {L}}^2(\alpha ,\beta )}, \end{aligned}$$

where N is the number of nodal bases.

Hereafter, we will use the Gaussian integration formula to approximate integrals such as

$$\begin{aligned} \int _{\alpha }^{\beta }f(x)\textrm{d}x. \end{aligned}$$

(7)

Explicit formulas for the quadrature nodes and weights for discrete shifted Chebyshev and Legendre basis functions are Daftardar-Gejji et al. (2015)

• Chebyshev Gauss-Lobatto

  For $j=0,1,\cdots ,N$,

  $$\begin{aligned} x_{{\alpha , \beta , N, j}}=\frac{\beta -\alpha }{2}(x_{{N, j}}-1)+\beta , w_{{\alpha , \beta , N, j}}= {\left\{ \begin{array}{ll} \frac{\pi }{2N},&{}j=0, N,\\ \frac{\pi }{N},&{}j=1,\cdots ,N-1, \end{array}\right. } \end{aligned}$$

  (8)

  where

  $$\begin{aligned} x_{{N, j}}=\cos \frac{j\pi }{N}. \end{aligned}$$

• Legendre Gauss-Lobatto

  $$\begin{aligned} x_{{\alpha , \beta , 0}}=\alpha ,\, x_{{\alpha , \beta , N}}=\beta ,\, x_{{\alpha , \beta , j}} (j=1, 2, \cdots , N-1){ \text{ roots } \text{ of } } L^{'}_{{\alpha ,\beta ,N}}(x), \end{aligned}$$

  (9)

  and

  $$\begin{aligned} w_{{\alpha ,\beta ,N,j}}=\frac{2}{N(N+1)[L_{{\alpha ,\beta ,N}}(x_{{j}})]^2},\quad j=0, 1, \cdots , N. \end{aligned}$$

For any $p(x)\in \mathbb {P}_{2N+1}$, where $\mathbb {P}_{2N+1}$ is the space of polynomials of degree at most $2N+1$, we have

$$\begin{aligned} \int _\alpha ^\beta \frac{p(x)}{\sqrt{1-x^2}} \textrm{d}x&=\sum _{j=0}^Np(x_{{j}})w_{{\alpha ,\beta ,N,j}},&(\text {Chebyshev Gauss-Lobatto}), \\ {\text{ and }}\quad \int _\alpha ^\beta p(x)\textrm{d}x&=\sum _{j=0}^Np(x_{{j}})w_{{\alpha ,\beta ,N,j}},&(\text {Legendre Gauss-Lobatto}). \end{aligned}$$

3 Fractional Derivatives of Collocation Bases

The shifted Chebyshev basis functions’ fractional derivatives have been discussed in Bhrawy et al. (2017). This section continues to obtain a novel formula for fractional derivatives of shifted Legendre basis $L_{{\alpha ,\beta ,n}}(x)$ in the Caputo sense (Podlubny 1999). Similar to the shifted Chebyshev basis functions (Mousa-Abadian and Momeni-Masuleh 2021), one can find the following lemma and theorem.

Lemma 2

Let $\nu$ be a positive real number. Then, the fractional derivative of order $\nu$ of shifted Legendre polynomials $L_{{\alpha ,\beta ,n}}(x)$ can be given by

$$\begin{aligned} D^\nu L_{{\alpha ,\beta ,n}}(x)=0,\quad n=0, 1, \cdots , \lceil \nu \rceil -1. \end{aligned}$$

(10)

Theorem 1

The fractional derivative of order $\nu$ of the shifted Legendre basis functions are

$$\begin{aligned} D^\nu L_{{\alpha ,\beta ,n}}(x)=\sum _{i=0}^\infty S_\nu (n,i) L_{{\alpha ,\beta ,i}}(x), \quad n=\lceil \nu \rceil , \lceil \nu \rceil +1, \cdots , \end{aligned}$$

(11)

where the ceiling function $\lceil \nu \rceil$ stands for the smallest integer greater than or equal to $\nu$ and

$$\begin{aligned} S_\nu (n,i)=\displaystyle \sum _{k=0}^{[\frac{n}{2}]}\sum _{l=\lceil \nu \rceil }^{n-2k}\sum _{j=\lceil \nu \rceil }^{l}\frac{(-1)^{k-j+l}2^{l-n}\beta ^{l-j}(\beta -\alpha )^{-l}(2n-2k)!j!}{(n-k)!k!(n-2k-l)!j!(l-j)!\varGamma (j+1-\nu )}c_{ij}, \end{aligned}$$

(12)

in which

$$\begin{aligned} c_{{ij}}=\left(i+\frac{1}{2}\right)\int _\alpha ^\beta x^{j-\nu }L_{{\alpha ,\beta ,i}}(x)\textrm{d}x. \end{aligned}$$

(13)

Proof

As we know, the Caputo fractional derivative of $x^k$ of order $\nu$ is

$$\begin{aligned} D^\nu x^k =\left\{ \begin{array}{ll} 0,&{} k=0, 1, \cdots \text { and} \ k<\lceil \nu \rceil ,\\ \frac{\varGamma (k+1)}{\varGamma (k+1-\nu )}x^{k-\nu },&{}k=0, 1, \cdots \text { and} \ k\ge \lceil \nu \rceil . \end{array}\right. \end{aligned}$$

Considering (4), for $n=\lceil \nu \rceil , \lceil \nu \rceil +1, \cdots ,$ we obtain

$$\begin{aligned} D^\nu L_{{\alpha ,\beta ,n}}(x)=&\sum _{k=0}^{[\frac{n}{2}]}\sum _{l=0}^{n-2k} \sum _{j=0}^{l}\frac{(-1)^{k-j+l}2^{l-n}\beta ^{l-j}(\beta -\alpha )^{-l}(2n-2k)!}{(n-k)!k!(n-2k-l)!j!(l-j)!}D^\nu x^j \\ =&\sum _{k=0}^{[\frac{n}{2}]}\sum _{l=\lceil \nu \rceil }^{n-2k}\sum _{j=\lceil \nu \rceil }^{l}\frac{(-1)^{k-j+l}2^{l-n}\beta ^{l-j}(\beta -\alpha )^{-l}(2n-2k)!}{(n-k)!k!(n-2k-l)!(l-j)!\varGamma (j+1-\nu )}x^{j-\nu }. \end{aligned}$$

By expanding $x^{j-\nu }$ in terms of the shifted Legendre basis functions, we arrive at the following form:

$$\begin{aligned} x^{j-\nu } = \sum _{i=0}^\infty c_{{ij}}L_{{\alpha ,\beta ,j}}(x), \end{aligned}$$

where $c_{ij}$ is given in (13), which completes the proof. $\square$

4 Mixed Steps-Collocation Schemes

In this section, we propose new numerical schemes based on the method of steps and Legendre (Chebyshev) collocation method to solve the following nonlinear FDDE

$$\begin{aligned} \left\{ \begin{array}{lc} \sum \limits _{j=0}^{n} A_ju^{(j)}(t)+D^\nu u(t) +\sum\limits_{i=1}^l\lambda _iD^{\nu _i}u(t)=f(t,u(t),u(t-\tau )),&{}t\ge 0,\\ u(t)=\phi (t),&{} -\tau \le t\le 0,\\ u'(0)=\phi '(0)=\phi _1,&{}\\ \vdots &{}\\ u^{(\mu -1)}(0)=\phi ^{(\mu -1)}(0)=\phi _{\mu -1},&{} \end{array}\right. \end{aligned}$$

(14)

where $\lambda _i$, $A_j\in \mathbb {R}$ are constants and $A_n\ne 0$, $0<\nu _1<\nu _2<\cdots<\nu _l<\nu$, $m-1<\nu \le m$ are real constants, $D^\nu u(t)\equiv u^{\nu }(t)$ represents the Caputo fractional derivative of order $\nu$ of function u(t), $\mu =\max \{m, n\}$ and the function f is given nonlinear continuous function in u that satisfies the following Lipschitz conditions

$$\begin{aligned} |f(t,y_1,u)-f(t,y_2,u)|&\le L_1|y_1-y_2|, \end{aligned}$$

(15)

$$\begin{aligned} |f(t,y,u_1)-f(t,y,u_2)|&\le L_2|u_1-u_2|. \end{aligned}$$

(16)

Also, throughout this paper, we shall assume the initial function $\phi (t)$ to be continuous on $[-\tau ,0]$. These conditions guarantee the existence and uniqueness of the solution of the problem (14) (see, e.g., Choudhary and Daftardar-Gejji 2015; Yang and Cao 2013).

Clearly, for $t\in [0,\tau ]$, the nonlinear FDDE (14) equals the following nonlinear non-delay FDEs:

$$\begin{aligned} \left\{ \begin{array}{lc} \sum \limits _{j=0}^{n} A_ju^{(j)}(t)+D^\nu u(t)+{\sum }_{i=1}^l\lambda _iD^{\nu _i}u(t)=f(t,u(t),\phi (t-\tau )),&{}t\in (0,\tau ],\\ u(0) = \phi (0)=\phi _0,&{}\\ u'(0)=\phi '(0)=\phi _1,&{}\\ \quad \vdots &{}\\ u^{(\mu -1)}(0)=\phi ^{(\mu -1)}(0)=\phi _{\mu -1}.&{} \end{array}\right. \end{aligned}$$

(17)

One way of solving the nonlinear FDE (17) is to use shifted Chebyshev basis functions, which is an extension of the scheme presented in Ref Mousa-Abadian and Momeni-Masuleh (2021). Another way is to expand the approximate solution $u_{{N}}(t)$ in terms of truncated shifted Legendre basis functions. The latter idea leads to

$$\begin{aligned} u_{{N}}(t)=\sum _{k=0}^Na_{{k}}L_{{0,\tau ,k}}(t),\qquad t\in [0,\tau ], \end{aligned}$$

(18)

where $a_{{k}}\in \mathbb {R}$ are the unknown coefficients that find them. Thanks to Theorem 1, we can express the derivative $u^{(1)}(t)$, $u^{(2)}(t)$, $\cdots , u^{(n)}(t)$, $D^\nu u(t)$, $D^{\nu _1}u(t)$, $D^{\nu _2}u(t), \cdots , D^{\nu _l}u(t)$ in terms of unknown coefficients $a_{{k}}$.

Now, we employ the Legendre (Chebyshev) collocation method to solve (17) numerically. To do this, the following equation:

$$\begin{aligned} \sum \limits _{j=0}^{n} A_ju{{N}}^{(j)}(t)+D^\nu u_{{N}}(t)+\sum _{i=1}^l\lambda _iD^{\nu _i}u_{{N}}(t)=f(t,u_{{N}}(t),\phi (t-\tau )), \end{aligned}$$

(19)

must be satisfied with the shifted Legendre collocation nodes (9) (shifted Chebyshev collocation nodes (8)) exactly. In fact, by using (11) and (18), for $j=0, 1, \cdots , N-\mu$, we get the following equations:

$$\begin{aligned}&\sum \limits _{j=0}^{n}\sum _{k=0}^N A_ja_{{k}}L^{(j)}_{{0,\tau ,k}}(t_{{\alpha , \beta , j}})+ \sum _{k=0}^Na_{{k}}D^\nu L_{{0,\tau ,k}}(t_{{\alpha , \beta , j}})\nonumber \\&\quad +\sum _{i=1}^l\sum _{k=0}^N\lambda _ia_{{k}}D^{\nu _i}L_{{0,\tau ,k}}(t_{{\alpha , \beta , j}}) \nonumber \\&\quad =f(t_{{\alpha , \beta , j}},\sum _{k=0}^Na_{{k}}L_{{0,\tau ,k}}\left( t_{{\alpha , \beta , j}}),\phi (t_{{\alpha , \beta , j}}-\tau )\right) ,\ t_{{\alpha , \beta , j}}\ge 0, \end{aligned}$$

(20)

where $t_{{\alpha , \beta , j}}$ are the same as $x_{{\alpha , \beta , j}}$, which are defined by (9). After imposing the initial conditions

$$\begin{aligned} u_{{N}}^{(i)}(0)=\phi _i,\quad i=0, 1, \cdots , \mu -1, \end{aligned}$$

(21)

we arrive at a nonlinear system of algebraic equations. Similarly, using Theorem 1 in Ref Mousa-Abadian and Momeni-Masuleh (2021) and related shifted Chebyshev expansion; we obtain an algebraic system of nonlinear equations. The nonlinear resulting systems can be solved, for example, by Newton’s method. Therefore, the approximate solution $u_{{N}}$ in the interval $[0, \tau ]$ is now available. To obtain the approximate solution of Eq. (14) in $[\tau , 2\tau ]$, the presented procedure is used. Generally, if we want to solve Eq. (14) in the interval $[(i-1)\tau , i\tau ]$, $i\ge 1$, we should solve the following equation:

$$\begin{aligned}{} & {} \sum \limits _{j=0}^{n} A_j{_{{(i)}}}u^{(j)}(t)+D^\nu {_{{(i)}}}u(t)+\sum _{p=1}^l\lambda _p D^{\nu _p}{_{{(i)}}}u(t)\nonumber \\{} & {} \quad =f(t,{_{{(i)}}}u(t),{_{{(i-1)}}}u(t-\tau )), \end{aligned}$$

(22)

where $A_j\in \mathbb {R}$ are constants and $A_n\ne 0$; for $k\ge 1$ we have $t\in \varOmega _k=[(k-1)\tau , k\tau ]$, $u\in C^{\mu }(\varOmega _k)$, $m-1<\nu <m$, $m_p-1< \nu _p<m_p<m$, $\mu =\max \{m, n\}$, $u^{(j)}(t)=\frac{d^j}{dt^j}u(t)$, with the initial conditions

$$\begin{aligned} {_{{(i)}}}u^{(j)}(0)={_{{(i-1)}}}u^{(j)}(\tau ), \quad j=0, 1, \cdots , \mu , \end{aligned}$$

and

$$\begin{aligned} {_{{(i)}}}u(t)=u((i-1)\tau +t),\quad i\ge 1. \end{aligned}$$

Using the proposed procedure, we get the approximate solution ${_{{(i)}}}u_{{N}}$ of Eq. (22).

5 Convergence Analysis

In this section, similarly presented in Ref Ghoreishi and Yazdani (2011), we show that the obtained approximate solutions in the previous section are convergent to the exact solutions. To investigate the exponential rate of convergence of the proposed schemes, we consider the nonlinear FDDE (22) on the interval $\varOmega _i=[(i-1)\tau , i\tau ]$.

Let us define ${_{{(i)}}}e_{{N}}(t)={_{{(i)}}}u_{{N}}(t)-{_{{(i)}}}u(t)$ to be the error function of the proposed scheme, where ${_{{(i)}}}u(t)$ and ${_{{(i)}}}u_{{N}}(t)$ are the exact and Legendre (Chebyshev) collocation solution of (22) at the $i-th$ step, respectively.

Hereafter, we use the subscript w for the Legendre and Chebyshev weight functions. The orthogonal projection operator $P_{{N}}$ from ${\mathscr {L}}_{{w}}^2(\varOmega )$ onto $\mathbb {P}_{{N}}$, where $\varOmega =[\alpha , \beta ]$, satisfies

$$\begin{aligned} \forall \psi _N\in \mathbb {P}_{{N}} , \quad \int _{0}^{\tau }(f-P_{{N}}f)(r)dr=0, \end{aligned}$$

for any function f in ${\mathscr {L}}_{{w}}^2(\varOmega )$. $P_{{N}}$ belongs to $\mathbb {P}_{{N}}$.

The following inequalities for the shifted Legendre (Chebyshev) polynomials and shifted Legendre (Chebyshev)-Gauss-Lobatto nodes for $k\ge 1$ can be obtained by a similar argument provided in Ref Canuto et al. (2006)

$$\begin{aligned} || y-P_{{N}}(y)||_{H^{l}_w(\varOmega )} \le&CN^{2l-1/2-k}|y|_{H^{k:N}_w(\varOmega )}, \end{aligned}$$

(23)

where $y\in H_w^k(\varOmega )$. Now, we present the convergence theorem of the proposed schemes.

Theorem 2

Suppose that the exact solution ${_{{(i)}}}u(t)$ at the $i-th$ step of Eq. (22) is smooth enough, i.e. ${_{{(i)}}}u(t)\in H^k_w(\varOmega )$ for $i, k\ge 1$, and the corresponding mixed steps-collocation solution ${_{{(i)}}}u_{{N}}(t)$ is given by shifted Legendre or Chebyshev basis functions. Then for sufficiently large N, we have

$$\begin{aligned} ||{_{{(i)}}}e_{{N}}(t)||_{{\mathscr {L}^2_{{w}}}(\varOmega )}\le&C_1N^{-k}|{_{{(i)}}}u|_{H_{{w}}^{k:N}(\varOmega )}+C_2 N^{-3/2}|{_{{(i)}}}u|_{H_{{w}}^{1:N}(\varOmega )}\nonumber \\&+C_3N^{2(\eta _1 -1)-1/2-k}|{_{{(i)}}}u|_{H_{{w}}^{k:N}}\nonumber \\&+C_{4}N^{2(\eta _2 -1)-1/2-k}|{_{{(i)}}}u|_{H_{{w}}^{k:N}}+C_{5}N^{-3/2}, \end{aligned}$$

(24)

where

$$\begin{aligned} \eta _1= {\left\{ \begin{array}{ll} m,&{} m\le 3,\\ 3,&{} m>3, \end{array}\right. }\qquad \eta _2= {\left\{ \begin{array}{ll} m_p,&{}m_p\le 3,\\ 3,&{} m_p>3, \end{array}\right. } \end{aligned}$$

and the constants $C_i$ are independent of N and depend only on n, m, and $\nu$.

Proof

As ${_{{(i)}}}u_{{N}}(t)$ is the mixed steps-collocation solution of Eq. (22) on the interval $\varOmega _i$, it satisfies the following equation

$$\begin{aligned}&\sum _{j=0}^{n}A_j {_{{(i)}}}u_{{N}}^{(j)}(t)+P_{{N}}\left( \frac{1}{\varGamma (m-\nu )}\int _{(i-1)\tau }^{t}(t-s)^{m-\nu -1}{_{{(i)}}}u_{{N}}^{(m)}(s)\textrm{d}s\right) \\&\quad +P_{{N}}\left( \sum _{p=1}^l\frac{\lambda _p}{\varGamma (m_p-\nu _p)} \int _{(i-1)\tau }^t(t-s)^{m_p-\nu _p-1}{_{{(i)}}}u_{{N}}^{(m_p)}(s)\textrm{d}s \right) \\&\quad =P_{{N}}\left( f(t,{_{{(i)}}}u_{{N}}(t),{_{(i-1)}}u_{{N}}(t))\right) . \end{aligned}$$

By n-times integration of the above expression, we have

$$\begin{aligned}&\int _{(i-1)\tau }^{t}\int _{(i-1)\tau }^{t_n}\cdots \int _{(i-1)\tau }^{t_2}A_n{_{{(i)}}}u_{{N}}^{(n)}(t_1)\textrm{d}T\nonumber \\&\quad +\sum _{j=0}^{n-1}\int _{(i-1)\tau }^{t}\int _{(i-1)\tau }^{t_n}\cdots \int _{(i-1)\tau }^{t_2}A_j{_{{(i)}}}u_{{N}}^{(j)}(t_1)\textrm{d}T\nonumber \\&\quad +\frac{1}{\varGamma (m-\nu )}\int _{(i-1)\tau }^{t}\int _{(i-1)\tau }^{t_n}\cdots \nonumber \\&\quad \int _{(i-1)\tau }^{t_2}P_{{N}}\left( \int _{(i-1)\tau }^{t_1}(t_1-s)^{m-\nu -1}{_{{(i)}}}u_{{N}}^{(m)}(s)\textrm{d}s\right) \textrm{d}T\nonumber \\&\quad +\sum _{p=1}^l\frac{\lambda _p}{\varGamma (m_p-\nu _p)}\int _{(i-1)\tau }^{t}\int _{(i-1)\tau }^{t_n}\cdots \nonumber \\&\quad \int _{(i-1)\tau }^{t_2}P_{{N}}\left( \int _{(i-1)\tau }^{t_1}(t_1-s)^{m_p-\nu _p-1}{_{{(i)}}}u_{{N}}^{(m_p)}(s)\textrm{d}s\right) \textrm{d}T\nonumber \\&\quad =\int _{(i-1)\tau }^{t}\int _{(i-1)\tau }^{t_n}\cdots \nonumber \\&\quad \int _{(i-1)\tau }^{t_2}P_{{N}}\left( f(t_1,{_{{(i)}}}u_{{N}}(t_1),{_{(i-1)}}u_{{N}}(t_1))\right) \textrm{d}T.&\end{aligned}$$

(25)

We can rewrite each multiple integral in (25) as a single integral

$$\begin{aligned}&A_n{_{{(i)}}}u_{{N}}(t)+Q_0(t)\nonumber \\&\quad +\sum _{j=0}^{n-1}\int _{(i-1)\tau }^{t}\frac{A_j}{(n-1-j)!}(t-s)^{n-1-j} {_{{(i)}}}u_{{N}}(s)\textrm{d}s\nonumber \\&\quad +\frac{1}{\varGamma (m-\nu )}\int _{(i-1)\tau }^{t}\frac{(t-s)^{n-1}}{(n-1)!}P_{{N}}\left( \int _{(i-1)\tau }^{s}(s-s_1)^{m-\nu -1}{_{{(i)}}}u_{{N}}^{(m)}(s_1)\textrm{d}s_1 \right) \textrm{d}s\nonumber \\&\quad +\sum _{p=1}^l\frac{\lambda _p}{\varGamma (m_p-\nu _p)}\nonumber \\&\quad \int _{(i-1)\tau }^{t}\frac{(t-s)^{n-1}}{(n-1)!}P_{{N}}\left( \int _{(i-1)\tau }^{s}(s-s_1)^{m_p-\nu _p -1}{_{{(i)}}}u_{{N}}^{(m_p)}(s_1)\textrm{d}s_1 \right) \textrm{d}s \nonumber \\&\quad =\int _{(i-1)\tau }^{t}\frac{(t-s)^{n-1}}{(n-1)!}\nonumber \\&\quad P_{{N}}\left( f(s,{_{{(i)}}}u_{{N}}(s),{_{(i-1)}}u_{{N}}(s))\right) \textrm{d}s, \end{aligned}$$

(26)

where $Q_0(t)$ contains initial conditions. Similarly, the exact solution ${_{{(i)}}}u(t)$ satisfies the following relation:

$$\begin{aligned}&A_n{_{{(i)}}}u(t)+Q_0(t)+\sum _{j=0}^{n-1}\int _{(i-1)\tau }^{t}\frac{A_j}{(n-1-j)!}(t-s)^{n-1-j} {_{{(i)}}}u(s)\textrm{d}s\nonumber \\&\quad +\frac{1}{\varGamma (m-\nu )}\int _{(i-1)\tau }^{t}\frac{(t-s)^{n-1}}{(n-1)!}\nonumber \\&\quad \int _{(i-1)\tau }^{s}(s-s_1)^{m-\nu -1}{_{{(i)}}}u^{(m)}(s_1)\textrm{d}s_1\textrm{d}s\nonumber \\&\quad +\sum _{p=0}^l\frac{\lambda _p}{\varGamma (m_p-\nu _p)}\int _{(i-1)\tau }^{t} \frac{(t-s)^{n-1}}{(n-1)!}\nonumber \\&\quad \int _{(i-1)\tau }^{s}(s-s_1)^{m_p-\nu _p -1}{_{{(i)}}}u^{(m_p)}(s_1)\textrm{d}s_1\textrm{d}s \nonumber \\&\quad =\int _{(i-1)\tau }^{t}\frac{(t-s)^{n-1}}{(n-1)!}f(s, {_{{(i)}}}u(s),{_{(i-1)}}u(s))\textrm{d}s. \end{aligned}$$

(27)

Subtracting (27) from (26) leads to

$$\begin{aligned}&A_n{_{{(i)}}}e_{{N}}(t)+\sum _{j=0}^{n-1}\frac{A_j}{(n-1-j)!}\int _{(i-1)\tau }^{t}(t-s)^{n-1-j}{_{{(i)}}}e_{{N}}(s)\textrm{d}s\nonumber \\&\quad +\frac{1}{\varGamma (m-\nu )}\int _{(i-1)\tau }^{t}\frac{(t-s)^{n-1}}{(n-1)!}{_{{(i)}}}e_{P_{{N}}}\textrm{d}s \nonumber \\&\quad +\frac{1}{\varGamma (m-\nu )}\int _{(i-1)\tau }^{t}\frac{(t-s)^{n-1}}{(n-1)!}\nonumber \\&\quad \int _{(i-1)\tau }^{s}(s-s_1)^{m-\nu -1}{_{{(i)}}}e_{{N}}^{(m)}(s_1)\textrm{d}s_1\textrm{d}s\nonumber \\&\quad +\sum _{p=1}^l\frac{\lambda _p}{\varGamma (m_p-\nu _p)}\int _{(i-1)\tau }^{t}\frac{(t-s)^{n-1}}{(n-1)!}{_{{(i)}}}e_{P^p_N}\textrm{d}s\nonumber \\&\quad +\sum _{p=1}^l\frac{\lambda _p}{\varGamma (m_p-\nu _p)}\int _{(i-1)\tau }^{t}\frac{(t-s)^{n-1}}{(n-1)!}\nonumber \\&\quad \int _{(i-1)\tau }^{s}(s-s_1)^{m_p-\nu _p -1}{_{{(i)}}}e_{{N}}^{(m_p)}(s_1)\textrm{d}s_1\textrm{d}s\nonumber \\&\quad =\int _{(i-1)\tau }^{t}\frac{(t-s)^{n-1}}{(n-1)!}{_{{(i)}}}e_f(s)\textrm{d}s, \end{aligned}$$

(28)

where

$$\begin{aligned} {_{{(i)}}}e_f(s)&=P_{{N}}(f(s,{_{{(i)}}}u_{{N}}(s),{_{(i-1)}}u_{{N}}(s)))-f(s,{_{{(i)}}}u(s),{_{(i-1)}}u(s)),\\ {_{{(i)}}}e_{{P}_{{N}}}(s)&=P_{{N}}\left( \int _{(i-1)\tau }^{s}(s-s_1)^{m-\nu -1}{_{{(i)}}}u_{{N}}^{(m)}(s_1)\textrm{d}s_1\right) \\&\qquad -\int _{(i-1)\tau }^{s}(s-s_1)^{m-\nu -1}{_{{(i)}}}u_{{N}}^{(m)}(s_1)\textrm{d}s_1, \end{aligned}$$

and

$$\begin{aligned} {_{{(i)}}}e_{P^p_N}(s)&=P_{{N}}\left( \int _{(i-1)\tau }^{s}(s-s_1)^{m_p-\nu _p -1}{_{{(i)}}}u_{{N}}^{(m_p)}(s_1)\textrm{d}s_1\right) \\&\qquad -\int _{(i-1)\tau }^{s}(s-s_1)^{m_p-\nu _p -1}{_{{(i)}}}u_{{N}}^{(m_p)}(s_1)\textrm{d}s_1. \end{aligned}$$

After $(n-1)$-times integrating by parts of the fourth and sixth term on the left-hand side of (28), we get

$$\begin{aligned}&\frac{1}{\varGamma (m-\nu )}\int _{(i-1)\tau }^{t}\frac{(t-s)^{n-1}}{(n-1)!} \nonumber \\&\quad \int _{(i-1)\tau }^{s}(s-s_1)^{m-\nu -1}{_{{(i)}}}e_{{N}}^{(m)}(s_1)\textrm{d}s_1\textrm{d}s\nonumber \\&\quad =\frac{1}{\varGamma (m-\nu )\prod _{j=1}^{n-1}(m-\nu +j-1)}\nonumber \\&\quad \int _{(i-1)\tau }^{t}\int _{(i-1)\tau }^{s}(s-s_1)^{m+n-\nu -2}{_{{(i)}}}e_{{N}}^{(m)}(s_1)\textrm{d}s_1\textrm{d}s, \end{aligned}$$

(29)

and

$$\begin{aligned}&\frac{1}{\varGamma (m_p-\nu _p)}\int _{(i-1)\tau }^{t}\frac{(t-s)^{n-1}}{(n-1)!}\nonumber \\&\quad \int _{(i-1)\tau }^{s}(s-s_1)^{m_p-\nu _p-1}{_{{(i)}}}e_{{N}}^{(m_p)}(s_1)\textrm{d}s_1\textrm{d}s\nonumber \\&\quad =\frac{1}{\varGamma (m_p-\nu _p)\prod _{j=1}^{n-1}(m_p-\nu _p+j-1)}\nonumber \\&\quad \int _{(i-1)\tau }^{t}\int _{(i-1)\tau }^{s}(s-s_1)^{m_p+n-\nu _p-2}{_{{(i)}}}e_{{N}}^{(m_p)}(s_1)\textrm{d}s_1\textrm{d}s. \end{aligned}$$

(30)

Now we consider the three cases:

• (i) $m\ge 4$ and $m_p\ge 4$,

• (ii) $m\ge 4$ and $m_p\le 4$,

• (iii) $m\le 4$.

Case (i): $(m-3)$-times integrating by parts of the right-hand side of equations (29) and (30), for $n+1>\nu$, gives

$$\begin{aligned}&\frac{1}{\varGamma (m-\nu )\prod _{j=1}^{n-1}(m-\nu +j-1)} \nonumber \\&\quad \int _{(i-1)\tau }^{t}\int _{(i-1)\tau }^{s}(s-s_1)^{m+n-\nu -2}{_{{(i)}}}e_{{N}}^{(m)}(s_1)\textrm{d}s_1\textrm{d}s\nonumber \\&\quad =\frac{\prod _{j=1}^{m-3}(m+n-\nu -1-j)}{\varGamma (m-\nu )\prod _{j=1}^{n-1}(m-\nu +j-1)}\nonumber \\&\quad \int _{(i-1)\tau }^{t}\int _{(i-1)\tau }^{s}(s-s_1)^{n-\nu +1}{_{{(i)}}}e_{{N}}^{(3)}(s_1)\textrm{d}s_1\textrm{d}s, \end{aligned}$$

(31)

and

$$\begin{aligned}&\frac{1}{\varGamma (m_p-\nu _p)\prod _{j=1}^{n-1}(m_p-\nu _p+j-1)}\int _{(i-1) \tau }^{t}\nonumber \\&\quad \int _{(i-1)\tau }^{s}(s-s_1)^{m_p+n-\nu _p -2}{_{{(i)}}}e_{{N}}^{(m_p)}(s_1)\textrm{d}s_1\textrm{d}s\nonumber \\&\quad =\frac{\prod _{j=1}^{m_p-3}(m_p+n-\nu _p-1-j)}{\varGamma (m_p-\nu _p)\prod _{j=1}^{n-1}(m_p-\nu _p+j-1)}\nonumber \\&\quad \int _{(i-1)\tau }^{t}\int _{(i-1)\tau }^{s}(s-s_1)^{n-\nu _p+1}{_{{(i)}}}e_{{N}}^{(3)}(s_1)\textrm{d}s_1\textrm{d}s.&\end{aligned}$$

(32)

Substituting the right-hand side of (31) into the right-hand side of (29), we obtain

$$\begin{aligned}&\frac{1}{\varGamma (m-\nu )}\int _{(i-1)\tau }^{t}\frac{(t-s)^{n-1}}{(n-1)!} \nonumber \\&\quad \int _{(i-1)\tau }^{s}(s-s_1)^{m-\nu -1}{_{{(i)}}}e_{{N}}^{(m)}(s_1)\textrm{d}s_1\textrm{d}s \nonumber \\&\quad =\frac{\prod _{j=1}^{m-3}(m+n-\nu -1-j)}{\varGamma (m-\nu )\prod _{j=1}^{n-1}(m-\nu +j-1)} \nonumber \\&\quad \int _{(i-1)\tau }^{t}\int _{(i-1)\tau }^{s}(s-s_1)^{n-\nu +1}{_{{(i)}}}e_{{N}}^{(3)}(s_1)\textrm{d}s_1\textrm{d}s, \end{aligned}$$

(33)

and similarly, from equations (30) and (32), we have

$$\begin{aligned}&\frac{1}{\varGamma (m_p-\nu _p)}\int _{(i-1)\tau }^{t}\frac{(t-s)^{n-1}}{(n-1)!}\nonumber \\&\quad \int _{(i-1)\tau }^{s}(s-s_1)^{m_p-\nu _p -1}{_{{(i)}}}e_{{N}}^{(m_p)}(s_1)\textrm{d}s_1\textrm{d}s\nonumber \\&\quad =\frac{\prod _{j=1}^{m_p-3}(m_p+n-\nu _p-1-j)}{\varGamma (m_p-\nu _p)\prod _{j=1}^{n-1}(m_p-\nu _p+j-1)}\nonumber \\&\quad \int _{(i-1)\tau }^{t}\int _{(i-1)\tau }^{s}(s-s_1)^{n-\nu _p+1}{_{{(i)}}}e_{{N}}^{(3)}(s_1)\textrm{d}s_1\textrm{d}s.&\end{aligned}$$

(34)

Substituting (33) and (34) into (28), we arrive at

$$\begin{aligned}&|{_{{(i)}}}e_{{N}}(t)|\le \gamma _1\int _{(i-1)\tau }^{t}|{_{{(i)}}}e_{{N}}(s)|\textrm{d}s+\gamma _2\nonumber \\&\quad \int _{(i-1)\tau }^{t}|{_{{(i)}}}e_{{P}_{{N}}}(s)|\textrm{d}s+\gamma _3\int _{(i-1)\tau }^{t}\Big |s^{n-\nu +1}{_{{(i)}}}e_{{N}}^{''}(s)\Big |\textrm{d}s\nonumber \\&\quad +\gamma _4\sum _{p=1}^l\int _{(i-1)\tau }^{t}|{_{{(i)}}}e_{P^p_N}(s)|\textrm{d}s\nonumber \\&\quad +\gamma _5\sum _{p=1}^l\int _{(i-1)\tau }^{t}\Big |s^{n-\nu _p+1}{_{{(i)}}}e_{{N}}^{''}(s)\Big |\textrm{d}s\nonumber \\&\qquad +\gamma _6\int _{(i-1)\tau }^{t}|{_{{(i)}}}e_f(s)|\textrm{d}s, \end{aligned}$$

(35)

where $\gamma _i$ are independent of N and depend on n, m, $m_p$, and $\nu$. By the Gronwall lemma (Wang 2013), we get

$$\begin{aligned}&|{_{{(i)}}}e_{{N}}(t)| \le \gamma _7\int _{(i-1)\tau }^{t}|{_{{(i)}}}e_{{P}_{{N}}}(s)|\textrm{d}s+\gamma _8\int _{(i-1)\tau }^{t}\Big |s^{n-\nu +1}{_{{(i)}}}e_{{N}}^{''}(s)\Big |\textrm{d}s \\&\quad +\gamma _{9}\sum _{p=1}^l\int _{(i-1) \tau }^{t}|{_{{(i)}}}e_{P^p_N}(s)|\textrm{d}s\\&\quad +\gamma _{10}\sum _{p=1}^l\int _{(i-1)\tau }^{t}\Big |s^{n-\nu _p+1}{_{{(i)}}}e_{{N}}^{''}(s)\Big |\textrm{d}s\\&\quad +\gamma _{11}\int _{(i-1)\tau }^{t}|{_{{(i)}}}e_f(s)|\textrm{d}s, \end{aligned}$$

where $\gamma _7,\cdots ,\gamma _{11}$ are some constants related to $\gamma _1,\cdots ,\gamma _6$.

From Lipschitz conditions (15) and (16), inequality (23) and generalized Hardy’s inequality (Gogatishvill and Lang 1999), we obtain

$$\begin{aligned}&||{_{{(i)}}}e_{{N}}(t)||_{{\mathscr {L}^2_{{w}}}(\varOmega )}\le \gamma _{12} ||{_{{(i)}}}e_{{P}_{{N}}}(s)||_{{\mathscr {L}^2_{{w}}}(\varOmega )}+\gamma _{13} || s^{n-\nu +1}{_{{(i)}}}e_{{N}}^{''}(s)||_{{\mathscr {L}^2_{{w}}}(\varOmega )}\nonumber \\&\quad\quad\quad\quad\quad\quad\quad +\gamma _{14}\sum _{p=1}^l||{_{{(i)}}}e_{P^p_N}(s)||_{{\mathscr {L}^2_{{w}}}(\varOmega )}\nonumber \\&\quad\quad\quad\quad\quad\quad\quad +\gamma _{15}\sum _{p=1}^l|| s^{n-\nu _p +1}{_{{(i)}}}e_{{N}}^{''}(s)||_{{\mathscr {L}^2_{{w}}}(\varOmega )}+C_{5}N^{-3/2}, \end{aligned}$$

(36)

where $\gamma _{12},\cdots ,\gamma _{15}$ are some constants related to $\gamma _7,\cdots ,\gamma _{11}$ and are independent of N. From (23) we get

$$\begin{aligned}&||s^{n-\nu }{_{{(i)}}}e_{{N}}^{''}(s)||_{{\mathscr {L}^2_{{w}}}(\varOmega )}\le ||s^{n-\nu }||_{{\mathscr {L}^2_{{w}}}(\varOmega )}||{_{{(i)}}}e_{{N}}^{''}(s)||_{{\mathscr {L}^2_{{w}}}(\varOmega )}\nonumber \\& \qquad\qquad\qquad\qquad\quad \le \gamma _{16} ||{_{{(i)}}}e_{{N}}(s)||_{H^2_w(\varOmega )}\nonumber \\&\qquad\qquad\qquad\qquad\quad \le \gamma _{17}N^{7/2-k}|{_{{(i)}}}u|_{H^{k:N}_w(\varOmega )}, \end{aligned}$$

(37)

and

$$\begin{aligned}&||s^{n-\nu _p}{_{{(i)}}}e_{{N}}^{''}(s)||_{{\mathscr {L}^2_{{w}}}(\varOmega )}\le ||s^{n-\nu _p}||_{{\mathscr {L}^2_{{w}}}(\varOmega )}||{_{{(i)}}}e_{{N}}^{''}(s)||_{{\mathscr {L}^2_{{w}}}(\varOmega )}\nonumber \\&\qquad\qquad\qquad\qquad\quad \le \gamma _{18} ||{_{{(i)}}}e_{{N}}(s)||_{H^2_w(\varOmega )}\nonumber \\&\qquad\qquad\qquad\qquad\quad \le \gamma _{19}N^{7/2-k}|{_{{(i)}}}u|_{H^{k:N}_w(\varOmega )}, \end{aligned}$$

(38)

where $\gamma _{16},\cdots ,\gamma _{19}$ did not depend on N. From (23) we have

$$\begin{aligned} ||{_{{(i)}}}e_{P_{{N}}}(t)||_{{\mathscr {L}^2_{{w}}}(\varOmega )}&\le C_6N^{-3/2}\Big |\int _{(i-1)\tau }^{t}(t-s)^{m-\nu -1}{_{{(i)}}}u_{{N}}^{(m)}(s)\textrm{d}s\Big |_{H^{1:N}_w(\varOmega )}\nonumber \\&=C_7N^{-3/2}|D^\nu {_{{(i)}}}u_{{N}}|_{H^{1:N}_w(\varOmega )}, \end{aligned}$$

(39)

$$\begin{aligned} ||{_{{(i)}}}e_{P^p_N}(t)||_{{\mathscr {L}^2_{{w}}}(\varOmega )}&\le C_8N^{-3/2}\Big |\int _{(i-1)\tau }^{t}(t-s)^{m_p-\nu _p-1}{_{{(i)}}}u_{{N}}^{(m_p)}(s)\textrm{d}s\Big |_{H^{1:N}_w(\varOmega )}\nonumber \\&=C_9N^{-3/2}|D^{\nu _p} {_{{(i)}}}u_{{N}}|_{H^{1:N}_w(\varOmega )}. \end{aligned}$$

(40)

Linear operators $D^\nu :\mathbb {P}_N\rightarrow \mathbb {P}_N^\nu$ and $D^{\nu _p}:\mathbb {P}_N\rightarrow \mathbb {P}_N^{\nu _p}$ are bounded (see Ref Mousa-Abadian and Momeni-Masuleh (2021)) so that the constants $C_{10}$ and $C_{11}^p$ can be found such that

$$\begin{aligned} |D^\nu {_{{(i)}}}u_{{N}}|_{H^{k:N}_w(\varOmega )}\le C_{10}| {_{{(i)}}}u_{{N}}|_{H^{k:N}_w(\varOmega )}, \end{aligned}$$

(41)

and

$$\begin{aligned} |D^{\nu _p} {_{{(i)}}}u_{{N}}|_{H^{k:N}_w(\varOmega )}\le C_{11}^p| {_{{(i)}}}u_{{N}}|_{H^{k:N}_w(\varOmega )}. \end{aligned}$$

(42)

Therefore, from (39) and (41), we have

$$\begin{aligned}&||{_{{(i)}}}e_{{P}_{{N}}}(t)||_{{\mathscr {L}^2_{{w}}}(\varOmega )}\nonumber \\&\quad \le C_{12}N^{-3/2}|{_{{(i)}}}u_{{N}}(s)|_{H^{1:N}_w(\varOmega )} \le C_{12}N^{-3/2}\left( |{_{{(i)}}}e_{{N}}(s)|_{H^{1:N}_w(\varOmega )}+|{_{{(i)}}}u(s)|_{H^{1:N}_w(\varOmega )} \right) . \end{aligned}$$

(43)

Since $u_{{N}}=P_{{N}}u$, we can write

$$\begin{aligned} |{_{{(i)}}}e_{{N}}(s)|_{H^{1:N}_w(\varOmega )}=&|{_{{(i)}}}u_{{N}}(s)-{_{{(i)}}}u(s)+P_{{N}}{_{{(i)}}}u(s)-P_{{N}}{_{{(i)}}}u(s)|_{H^{1:N}_w(\varOmega )}\\ =&|{_{{(i)}}}u(s)-P_{{N}}{_{{(i)}}}u(s)|_{H^{1:N}_w(\varOmega )}. \end{aligned}$$

So that

$$\begin{aligned} ||{_{{(i)}}}e_{{P}_{{N}}}(t)||_{{\mathscr {L}^2_{{w}}}(\varOmega )}{\overset{{ (23)}}{\le }} C_{13}N^{-k} |{_{{(i)}}}u|_{H^{k:N}_w(\varOmega )}+C_{12}N^{-3/2}|{_{{(i)}}}u|_{H^{1:N}_w(\varOmega )}. \end{aligned}$$

(44)

From (40) and (42), we have

$$\begin{aligned}&||{_{{(i)}}}e_{P^p_N}(t)||_{{\mathscr {L}^2_{{w}}}(\varOmega )}\nonumber \\&\quad \le C_{14}^pN^{-3/2}|{_{{(i)}}}u_{{N}}(s)|_{H^{1:N}_w(\varOmega )} \le C_{11}^pN^{-1} \left( C_{14}N^{3/2-k}|{_{{(i)}}}u|_{H^{k:N}_w(\varOmega )} +|{_{{(i)}}}u|_{H^{1:N}_w(\varOmega )} \right) \nonumber \\&\quad {\overset{{ (23)}}{\le }} C_{15}^pN^{-k} |{_{{(i)}}}u|_{H^{k:N}_w(\varOmega )} +C_{14}^pN^{-3/2}|{_{{(i)}}}u|_{H^{1:N}_w(\varOmega )}. \end{aligned}$$

(45)

From Eqs. (36)–(45), for $m\ge 4$ and $m_p\ge 4$, we have

$$\begin{aligned} ||{_{{(i)}}}e_{{N}}(t)||_{{\mathscr {L}^2_{{w}}}(\varOmega )}\le&C_1N^{-k}|{_{{(i)}}}u|_{H_{{w}}^{k:N}(\varOmega )}+C_2 N^{-3/2}|{_{{(i)}}}u|_{H_{{w}}^{1:N}(\varOmega )}\\&+C_3N^{2(\eta _1 -1)-1/2-k}|{_{{(i)}}}u|_{H_{{w}}^{k:N}}\\&+C_{4}N^{2(\eta _2 -1)-1/2-k}|{_{{(i)}}}u|_{H_{{w}}^{k:N}}+C_{5}N^{-3/2}, \end{aligned}$$

where $C_1,\cdots , C_5$ are constants related to earlier $\gamma _i$’s and $C_i$’s.

The same argument can be applied to cases (ii) and (iii) by assuming that $n+1>\nu$, $m_p-\nu _p+n>2$, and $m-\nu +n>2$ respectively. $\square$

6 Numerical Results

In this section, we consider several practical examples that, in general, do not have an exact solution. The computational codes were conducted on an Intel (R) Core (TM) i7-6700 K processor, equipped with 8 GB of RAM. Also, We use the fix-point iteration method for solving nonlinear systems, and the stopping criterion is set to be $10^{-15}$. In all tables SLBF stands for Shifted Legendre basis functions, while SCBF represents Shifted Chebyshev basis functions.

Example 1

Consider the following FDDE

$$\begin{aligned} D^{\nu }u(t)=h(t)-u(t)-u(t-\tau ), \quad t\in (0,T], \end{aligned}$$

(46)

with the boundary condition

$$\begin{aligned} u(t)=0, \quad t\in [-\tau , 0], \end{aligned}$$

where $\tau$ is taken as a fraction of the length of time interval [0, 1]. Now, two cases for the forcing term h(t) can be considered:

Case (i):

$$\begin{aligned} h(t)= {\left\{ \begin{array}{ll} \frac{\varGamma (11)}{\varGamma (11-\nu )}t^{10-\nu }+t^{10},&{} t\in [0, \tau ],\\ \frac{\varGamma (11)}{\varGamma (11-\nu )}t^{10-\nu }+t^{10}+(t-\tau )^{10},&{} t\in (\tau ,1], \end{array}\right. } \end{aligned}$$

(47)

which corresponding exact solution is

$$\begin{aligned} u(t)= {\left\{ \begin{array}{ll} 0, &{} t\in [-\tau , 0],\\ t^{10},&{} t\in (0,1]. \end{array}\right. } \end{aligned}$$

(48)

Case (ii):

$$\begin{aligned} h(t)= {\left\{ \begin{array}{ll} \sum\limits _{j=0}^{\infty } \gamma _j\frac{\varGamma (\beta _j)}{\varGamma (\beta _j-\nu )}t^{\xi _j-\nu }+t^{\frac{13}{2}}\sin (\pi t^{\frac{4}{3}}), &{} t\in [0, \tau ],\\ \sum\limits _{j=0}^{\infty } \gamma _j\frac{\varGamma (\beta _j)}{\varGamma (\beta _j-\nu )}t^{\xi _j-\nu }+t^{\frac{13}{2}}\sin (\pi t^{\frac{4}{3}}) +(t-\tau )^{\frac{13}{2}}\sin (\pi (t-\tau )^{\frac{4}{3}}),&{} t\in (\tau ,1], \end{array}\right. } \end{aligned}$$

(49)

where

$$\begin{aligned} \gamma _j=\frac{(-1)^j}{(2j+1)!}\pi ^{2j+1},\quad \beta _j=\frac{53+16j}{6},\quad \xi _j=\frac{47+16j}{6}. \end{aligned}$$

The related exact solution is

$$\begin{aligned} u(t)=\left\{ \begin{array}{lr} 0, \quad &{} t\in [-\tau , 0],\\ t^{\frac{13}{2}}\sin (\pi t^{\frac{4}{3}}),\quad &{} t\in (0,1]. \end{array}\right. \end{aligned}$$

(50)

Zayernouri et al. (2014) used a Petrov-Galerkin spectral method to solve (46). They employed Reimann-Liouville fractional derivatives while we use Caputo’s fractional derivatives. As we know, these are related together to the following relation (Monje et al. 2010)

$$\begin{aligned} {_{{R}}}D^{\nu }u(t)=D^{\nu }u(t)+\sum _{k=0}^{m-1}\frac{t^{k-\nu }}{\varGamma (k+1-\nu )}u^{(k)}(0^+), \end{aligned}$$

where ${_{{R}}}D^{\nu }$ stands for Reimann-Liouville fractional derivative. Since $u(0)=0$, both fractional derivatives are the same, and consequently, both approximate solutions are comparable. The $\mathscr {L}^2$-Error of Case (i) and Case (ii) for $\tau =0.5$ and different N and $\nu =0.1$ are reported in Table 1. Compared to the PG spectral presented in Ref Zayernouri et al. (2014), SLBF has the same $\mathscr {L}^2$-Error as Petrov-Galerkin spectral method, while SCBF produces much less $\mathscr {L}^2$-Error in cases (i) and (ii). As one can observe, results obtained by employing SCBF, are more accurate than the others.

Table 1 $\mathscr {L}^2$-Error of Example 1 for different values of N with $\tau =0.5$ and $\nu =0.1$

Example 2

Consider the following FDDE (Zayernouri et al. 2014)

$$\begin{aligned} D^{\nu }u(t)=h(t)-A(t)u(t)-B(t)u(t-\tau ), \quad t\in (0,1], \end{aligned}$$

(51)

with the initial condition

$$\begin{aligned} u(t)=0, \quad t\in [-\tau , 0]. \end{aligned}$$

Now, two cases are taken into consideration. Case (i): Take $A(t)=B(t)=t^2-t^3$. The corresponding exact solution is given in (48). Case (ii): Put $A(t)=B(t)=\sin (\pi t)$, where the analytical solution is given in (50). The $\mathscr {L}^2$-Error of Case (i) and Case (ii) for different values of N, $\tau =0.5$ and $\nu =0.1$ are provided in Table 2. The $\mathscr {L}^2$-Error of Case (i) in both SLBF and SCFB of the current work is at least of the order $10^{-13}$ for $N\ge 11$, while it happened only when $N\ge 17$ in Ref Zayernouri et al. (2014). In Case (ii), the results are the same as the results of Zayernouri et al. (2014) when employing SLBF, while SCBF produces less $\mathscr {L}^2$-Error. Again, those results are obtained by employing SCBF are more accurate than the others.

Table 2 $\mathscr {L}^2$-Error of Example 2 for different values of N with $\tau =0.5$ and $\nu =0.1$

Example 3

Consider Houseflies model as following Moghaddam and Mostaghim (2013)

$$\begin{aligned} D^{\nu }u(t)=-du(t)+cu(t-\tau )(k-czu(t-\tau )),\quad t>0, \end{aligned}$$

(52)

with the initial condition

$$\begin{aligned} u(t)=160,\quad -\tau \le t\le 0. \end{aligned}$$

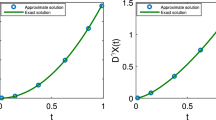
By taking $c= 1.81$, $k=0.5107$, $d=0.147$ and $z=0.000226$, numerical results of the shifted Chebyshev basis functions for different values of $\nu$, $\tau =3$ and $\tau =5$ are presented in Tables 3 and 4, respectively. Tables 5 and 6 describe the numerical results of the shifted Legendre basis functions with the same parameters. The approximate solutions are sketched in Fig. 1. Comparison between the second and third columns of Tables 3 and 4 (Tables 5 and 6) reveals that the maximum absolute error (MAE) is $2\times 10^{-6}$ for $N=15$, while the MAE reported in Ref Moghaddam and Mostaghim (2013), which employed the finite difference method was of the order $10^{-5}$ using $N=100$. Moreover, the log plots of MAE for different values of N, $\tau =3$, and $\tau =5$ are plotted in Fig. 2.

Table 3 Numerical results of Example 3 using the shifted Chebyshev basis functions with $N=15$ and $\tau =3$

Table 4 Numerical results of Example 3 using the shifted Chebyshev basis functions with $N=15$ and $\tau =5$

Table 5 Numerical results of Example 3 using the shifted Legendre basis functions with $N=15$ and $\tau =3$

Table 6 Numerical results of Example 3 using the shifted Legendre basis functions with $N=15$ and $\tau =5$

Fig. 1

Approximate solution of Example 3 using the shifted Chebyshev basis functions for $\tau =3$ (left), and$\tau =0.5$ (right) with $N=15$

Fig. 2

Log plot of MAE of Example 3 for $\tau =3$ (left), and $\tau =5$ (right) with $\nu =1$

Example 4

The following model example concerns the effect of noise on a light, which is introduced by Moghaddam and Mostaghim (2013)

$$\begin{aligned} D^{\nu }u(t)=-\frac{1}{\epsilon }u(t)+\frac{1}{\epsilon }u(t)u(t-\tau ), \quad t>0, \end{aligned}$$

(53)

with the initial condition

$$\begin{aligned} u(t)=0.9,\quad -\tau \le t\le 0. \end{aligned}$$

The obtained results of the shifted Chebyshev basis functions for various values of $\nu$ and $\tau$ with $\epsilon =0.1$ are reported in Tables 7 and 8. Also, the numerical results of the shifted Legendre basis functions are given in Tables 9 and 10. In this model example, the MAEs related to the current works are an order of $10^{-6}$ using $N=15$, while the MAE reported in Ref Moghaddam and Mostaghim (2013), which employed the finite difference method achieved this order of accuracy using $N=100$ nodes. Figure 3 shows the approximate solutions. Also, the log plots of MAE for $\tau =1$ and $\tau =3$ are plotted in Fig. 4.

Table 7 Numerical results of Example 4 using the shifted Chebyshev basis functions with $N=15$ and $\tau =1$

Table 8 Numerical results of Example 4 using the shifted Chebyshev basis functions with $N=15$ and $\tau =3$

Table 9 Numerical results of Example 4 using the shifted Legendre basis functions with $N=15$ and $\tau =1$

Table 10 Numerical results of Example 4 using the shifted Legendre basis functions with $N=15$ and $\tau =3$

Fig. 3

Approximate solution of Example 4 using the shifted Legendre basis functions for $\tau =1$ (left), and $\tau =3$ (right) with $N=15$

Fig. 4

Log plot of MAE of Example 4 for $\tau =1$ (left), and $\tau =3$ (right) with $\nu =1$

Applying relation (24) of Theorem 2 and using the fact that all the displayed norms are fixed numbers, $N^{-\frac{3}{2}}$ will be the predominant term. Therefore, we have

$$\begin{aligned} ||{_{{(i)}}}e_{{N}}(t)||_{{\mathscr {L}^2_{{w}}}(\varOmega )}\le C N^{-\frac{3}{2}}. \end{aligned}$$

(54)

Now if we calculate this expression for different values of N, we find that in (54) the value of C for model examples 1–4 is given in Table 11.

Table 11 Computed constant C in (54) for Example 1 through Example 4 for different values of N

Example 5

As a final model example, consider the following FDDE, which is introduced by Parsa Moghaddam and Salamat Mostaghim (2017)

$$\begin{aligned} D^{\nu }u(t)+\delta D^{\nu _1}u(t)=-u(t)+\frac{\mu q^2}{u^3(t)}(u(t)-\gamma u(t-\tau )), \quad t\in (0,1), \end{aligned}$$

(55)

equipped with the conditions

$$\begin{aligned} u(t)=1, \quad t\in [-\tau , 0], \quad u(1)=3, \end{aligned}$$

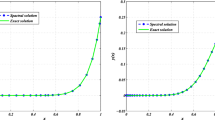
where $\delta = 0.3$, $\mu = 1$, $q = 0.4$ and $\gamma =0.2$. Computational results of the shifted Legendre basis functions with $N=15$ and $\tau =5$ are reported in Tables 13 and 12 demonstrates the results using the shifted Chebyshev basis functions. A comparison between the second and third columns of Tables 12 and 13 show that the present work and the function $\text {bvp4c}$ of the Matlab software have the same results for at least 4 decimal places. However, the MAE of the finite difference method at $t=1$ is of the order $10^{-2}$ (Parsa Moghaddam and Salamat Mostaghim 2017), but in both presented schemes we get the exact results. The graph of the numerical solutions of (55) for different values of $\nu$ and $\nu _1$ is sketched in Fig. 5. Assuming that the analytical solution of (55) has two degrees of smoothness, again the predominant term in relation (24) is $N^{-\frac{3}{2}}$. If we consider $\text {bvp4c}$ of the Matlab software as a reference solution, then the corresponding $\mathscr {L}^2$-Error constant of (54) for SLBF and SCBF is 0.39 and 1.25, respectively.

Table 12 Numerical results of Example 5 using the shifted Chebyshev basis functions with $N=15$ and $\tau =5$

Table 13 Numerical results of Example 5 using the shifted Legendre basis functions with $N=15$ and $\tau =5$

Fig. 5

Approximate solution of Example 5 using the shifted Legendre basis functions with $N=15$ and $\tau =5$

The CPU time of the above examples is reported in Table 14. As we see from the table, the CPU time of the shifted Chebyshev basis functions is less than Legendre one.

Table 14 CPU time (s) for the proposed schemes with $N=15$

7 Conclusion

In this article, a new formula for fractional derivatives of shifted Legendre polynomials is derived. All the fractional derivatives are considered in the Caputo sense. By using the formula and formula based on shifted Chebyshev polynomials for fractional derivatives (Mousa-Abadian and Momeni-Masuleh 2021), the numerical schemes for solving nonlinear FDDEs are proposed. The proposed schemes exploit the method of steps and shifted Legendre (Chebyshev) basis functions to generate an approximate solution. A mathematical analysis shows that the proposed schemes have an exponential rate of convergence. Moreover, practical examples are taken to demonstrate the effectiveness of the obtained results. MAE reveals that the approximate solution has acceptable conformity with the available literature. Further development of the proposed schemes should be concentrated on solving nonlinear fractional delay differential problems with more than one delay. It would also be interesting to extend an approximate solution in which a discontinuous nonlinear f is considered.