Numerical solution of nonlinear fractional delay integro-differential equations with convergence analysis

Abstract

In this work, a high accurate method is given for solving the nonlinear fractional delay integro-differential equations, numerically. By considering the equation before and after delay time, we first apply the delay function in the equation and propose an equivalent system. By discretization in the Jacobi-Gauss collocation points, an algebraic nonlinear system is then proposed to approximate the solution of main equation. The convergence of method is fully given in spaces $L^{\infty }_{\omega ^{\alpha ,\beta }}(I)$ and $L^{2}_{\omega ^{\alpha ,\beta }}(I)$, and the error bounds are specified for obtained approximations. Finally, some numerical examples are provided to show the capability and efficiency of method.

1 Introduction

Fractional calculus is a popular branch of mathematics that, in addition to attracting a lot of attention, also appears in various fields of science, medicine, physics, etc. Fractional differential equations (FDEs) are part of mathematical analysis that study derivative and integral operations of fractional order, and as we know, it originated in 1965 by Hopital and then several researchers have analytically and numerically examined different types of these equations. For example, Chouhan et al. [10] constructed generalized fractional Bernoulli wavelet functions to numerically solve the diffusion modelling anomalous infiltration problems using a class of nonlinear FDEs with variable order. They first generated generalized Bernoulli wavelets of fractional order and then extracted the operational integration matrices and used them to convert the FDEs into a system of algebraic equations. In [3], a new kind of wavelet method is proposed for solving the nonlinear FDEs. In this work, Alkhalissi et al. proposed this method based on a generalized Gegenbaur-Humbert polynomial and they obtained operational matrices for fractional and integer order derivatives. Finally, they used these operational matrices to obtain a system of algebraic equations. Mohammadizadeh et al. generated the two unique piecewise $C^3$-splines of six and eight degrees to approximately solve the fractional differential integro equations (FDIEs). They proved the uniqueness of the second-order solution to these equations and analysed the convergence analysis and error of their method [23]. Shokri and Mirzaei [33], performed a pseudospectral method based on Lagrange polynomials to numerically investigate the time-FDEs of multi terms. They used a semi-discrete approximate scheme to convert these equations into a system of ordinary FDEs, and also used the Mittag-Leffler function to achieve the accuracy of their method. In [2], the asymptotic optimal homotopy method was generalized to a system of FDIEs. Akbar et al. investigated these equations as test examples and used the least squares method to achieve the optimal values of auxiliary constants. Dehestani et al. [14] combined the Lucas wavelets with Gauss Legendre quadrature rule and used them to solve the fractional differential Volterra Fredholm integral equations. They obtained the operational matrices for the Lucas wavelet functions and utilized them to arrive at their numerical scheme. They also obtained an error bound for their numerical method, which showed good behavior for their method.

Delay differential equations (DDEs) are actually a type of differential equations in which the unknown function can be defined at a specific time and in terms of the function and its derivative at earlier times and places. These equations have wide applications in science and engineering. The genesis of field of DDEs can be seen in Minorsky studies (1941) when examining the motion of a ship. Since ancient times, a lot of research has been done on different types of DDEs, and we will review several numerical methods which such equations investigated. To learn more about DDEs, reader can refer to [5, 6, 8, 15,16,17,18, 20, 34, 35]. In these books, the history of the emergence of DDEs and their different types have been reviewed. Among the works that have been discussed here is the theory and applications of DDEs, various aspects of nonlinear DDEs, and various quantitative theories, including normal forms, centre manifold and Hopf bifurcation theory in finite dimension. Control systems and stability analysis methods, Hopf bifurcations and center manifold analysis, numerical computations of DDE solutions, neural systems, and stochastic DDEs are also covered. Analytical and numerical solutions, existence, uniqueness and regularity of results for very famous classes of these equations, general formulas and convergence results for discrete and continuous methods are presented.

Now, if derivative order in DDEs is fractional, a new type of DDEs, known as the fractional delay differential equations (FDDEs), will emerge. Usman et al. [36] used a new operational matrix method to solve the FDDEs. They applied these matrices to fractional derivatives and integrals using the concept of shifted Gegenbauer polynomials, and finally obtained a system of algebraic equations. In [12], Daftardar-Gejji et al. utilize a method called the new iterative method for solving the nonlinear and linear FDDEs. They obtained their corrector predictor formula by using the fractional Adams method and completed their work by investigating the error analysis of their method under Lipschitz conditions. In [22], Moghaddam et al. used Brownian motion to approximate a class of stochastic FDDEs. They applied quadrature spline of the piecewise integral quadrature to approximate the fractional integral and demonstrated the efficiency of their computational scheme by evaluating the exact solutions using statistical predictors. Agarwal et al. [1], proposed a function called the mild solution of a fractional delay integro-differential equations (FDIDEs). For the existence of mild solutions of a class of these equations, they could expressed sufficient conditions. By using this function, they were able to achieve the application of concrete in the conduction heat in materials with memory. In [31], an operational matrix was formulated for the Tau method and for approximately solving a class of FDIDEs by Shahmorad et al. Dabas and Cahuhan [13] examined the existence and uniqueness of the mild solution of a class of infinite FDIDEs. They used the fixed point technique to achieve their results by using the solution operator in a complex Banach space.

Although many numerical methods have been used to solve the types of FDDEs and FDIDE, we can still feel the absence of an efficient method for solving different classes of these equations with high convergence rate and low error. Here, we propose a new Jacobi-Gauss collocation (JGC) method for solving a class of nonlinear FDIDEs. We totally analyze the convergence of our method in the $L^{\infty }_{\omega ^{\alpha ,\beta }}(I)$ and $L^{2}_{\omega ^{\alpha ,\beta }}(I)$ spaces by generalizing the proposed technique in the work [38] for linear FDDEs. The process of implementing the method is that we first convert the original equation into an equivalent time-dependent system and then we discrete the resulting system at JGC points and arrive at a system of algebraic equations that simultaneously gives us the approximate values of the solution and its fractional derivative. By investigate the method error, we find that the error bounds of our method tend to zero by increasing the number of collocation points, and also by providing several numerical examples, we can observe the acceptable results.

This paper is organized as follows: Some basic definitions and notations are provided in Sect. 2. We state the problem and perform our numerical approach in Sect. 3. In Sect. 4, we survey the convergence and error analysis of the method in spaces $L^{\infty }_{\omega ^{\alpha ,\beta }}(I)$ and $L^{2}_{\omega ^{\alpha ,\beta }}(I)$ by giving some useful lemmas. In Sect. 5, by presenting some numerical examples, we represent the preference and advantages of proposed method. At last, we present the suggestions conclusions.

2 Preliminaries and notations

In this section, we review some of the preliminary definitions and necessary concepts including the concept of the Caputo fractional derivative, and express the definitions of Jacobi polynomials and required spaces of the issue.

Definition 1

([19, 27]) Suppose that $g(\cdot )$ is given on [a, b]. The Caputo fractional derivative of $g(\cdot )$ is expressed as follows

$$\begin{aligned} {}^C_aD^{\gamma }_tg(t)=\dfrac{1}{\Gamma (n-\gamma )}\int _a^t \dfrac{g^{(n)}(\theta )}{(t-\theta )^{(\gamma -n+1)}}d\theta ,~~t\in (a,b], \end{aligned}$$

(1)

where $n-1<\gamma <n$ is the order of Caputo derivative, n is a positive integer and $\Gamma (\cdot )$ shows the Gamma function.

Definition 2

([19, 30]) With the assumptions of definition 1, we have the Riemann-Liouville fractional integral of $g(\cdot )$ as follows

$$\begin{aligned} {}^C_aI_t^{\gamma }g(t)=\left\{ \begin{array}{ll} \dfrac{1}{\Gamma (\gamma )}\int _a^t (t-\theta )^{\gamma -1}g(\theta )d\theta ,&{} \gamma >0,\\ g(t),&{}\gamma =0. \end{array}\right. \end{aligned}$$

(2)

Remark 2.1

([27, 30]) We can express a useful relation between Caputo derivative and Riemann-Liouville fractional integral as follows

$$\begin{aligned} {}^C_aI_t^{\gamma }\left( {}^C_aD^{\gamma }_tg(t)\right) =g(t)-\sum _{k=0}^{n-1}g^{(k)}(a)\dfrac{t^k}{k!}. \end{aligned}$$

(3)

In the following, a useful relation of the fractional calculus is presented, which we use in the numerical section ([7, 20])

$$\begin{aligned} {}_a^CD_t^{\gamma }(t^q)=\left\{ \begin{array}{ll} 0,&{}q\in \mathbb {N}_0~and~q<\lceil \gamma \rceil ,\\ \dfrac{\Gamma (q+1)}{\Gamma (q-\gamma +1)}t^{q-\gamma },&{}q\in \mathbb {N}_0~and~q\ge \lceil \gamma \rceil ~or,~~ q\notin \mathbb {N}_0~and~q>\lceil \alpha \rceil -1, \end{array}\right. \end{aligned}$$

where $\mathbb {N}_0=\{0\}\cup \mathbb {N}$.

Definition 3

([32, 38]) Jacobi polynomials are a class of classical orthogonal polynomials that symbolized by $P_n^{\gamma ,\alpha }$, and they are orthogonal with respect to weight function $\omega ^{\gamma ,\alpha }(t)=(1-t)^{\gamma }(1+t)^{\alpha }$ on $I=[-1,1]$ for $\gamma ,\alpha$. We can calculated these polynomials by using the following formula

$$\begin{aligned}&P_{n+1}^{\gamma ,\alpha }=\left( a_n^{\gamma ,\alpha }t-b_n^{\gamma ,\alpha }\right) P_n^{\gamma ,\alpha }(t)-c_n^{\gamma ,\alpha }P_{n-1}^{\gamma ,\alpha },~~n\ge 1,\nonumber \\&P_0^{\gamma ,\alpha }(t)=1,~~P_1^{\gamma ,\alpha }(t)=\frac{1}{2}(\gamma +\alpha +2)t+\frac{1}{2}(\gamma -\alpha ), \end{aligned}$$

(4)

where

$$\begin{aligned}&a_n^{\gamma ,\alpha }=\dfrac{(2n+\gamma +\alpha +1)(2n+\gamma +\alpha +2)}{2(n+1)(n+\gamma +\alpha +1)},\nonumber \\&b_n^{\gamma ,\alpha }=\dfrac{(\alpha ^2-\gamma ^2)(2n+\gamma +\alpha +1)}{2(n+1)(n+\gamma +\alpha +1)(2n+\gamma +\alpha )},\nonumber \\&c_n^{\gamma ,\alpha }=\dfrac{(n+\gamma )(n+\alpha )(2n+\gamma +\alpha +2)}{(n+1)(n+\gamma +\alpha +1)(2n+\gamma +\alpha )}. \end{aligned}$$

(5)

Definition 4

([32, 38]) The $L^p_{\omega ^{\gamma ,\alpha }}(I)$-space for $1\le p\le \infty$ is defined as follows

$$\begin{aligned} L^p_{\omega ^{\gamma ,\alpha }}(I)=\{u: u~ is ~measurable~ and ~||u||_{L^p_{\omega ^{\gamma ,\alpha }}}<\infty \}, \end{aligned}$$

where

$$\begin{aligned} \left\{ \begin{array}{ll} ||u||_{L^p_{\omega ^{\gamma ,\alpha }}(I)} =\left( \int _{-1}^{1}|u(t)|^p\omega ^{\gamma ,\alpha }(t)dt\right) ^{\frac{1}{p}},&{}1\le p<\infty ,\\ ||u||_{L^{\infty }_{\omega ^{\gamma ,\alpha }}(I)}=ess~\sup _{t\in I}|u(t)|,&{}p=\infty . \end{array}\right. \end{aligned}$$

Also, $\{P_n^{\gamma ,\alpha }(t)\}_{n=0}^{\infty }$ constitute a complete orthogonal $L^2_{\omega ^{\alpha ,\beta }}(I)$ space where $\{P_n^{\gamma ,\alpha }(t)\}_{n=0}^{\infty }$ is a the set of Jacobi polynomials. We can show the inner product in $L^2_{\omega ^{\gamma ,\alpha }}(I)$ as follows

$$\begin{aligned} (f,g)_{L^2_{\omega ^{\gamma ,\alpha }}(I)}=\int _{-1}^{1}f(t)g(t)\omega ^{\gamma ,\alpha }(t)dt,~~ \forall f,g\in L^2_{\omega ^{\gamma ,\alpha }}(I). \end{aligned}$$

Definition 5

([32, 38]) The JG integration formula for JG points $\{\tau _j^{\gamma ,\alpha }\}_{j=0}^N$ and their corresponding weights $\{\omega _j^{\gamma ,\alpha }\}_{j=0}^N$ is as follows

$$\begin{aligned} \int _{-1}^{1}g(t)\omega ^{\gamma ,\alpha }(t)dt\simeq \sum _{j=0}^Ng(\tau _j^{\gamma ,\alpha })\omega _j^{\gamma ,\alpha }, \end{aligned}$$

(6)

where N is a given positive integer.

Definition 6

([32, 38]) Let $\mathcal {P}_N$ be the space of polynomials of almost N. Then, the Lagrange interpolating polynomial for any $f\in C(I)$ is defined as follows

$$\begin{aligned} I_N^{\gamma ,\alpha }f(t)=\sum _{j=0}^Nf(\tau _j^{\gamma ,\alpha })L_j(t), \end{aligned}$$

(7)

where this polynomial is satisfying in $I_N^{\gamma ,\alpha }f(\tau _j^{\gamma ,\alpha })=f(\tau _j^{\gamma ,\alpha }), 0\le j\le N$ and $L_j(t),j=0,1,\ldots ,N$ are the Lagrange interpolating basis functions associated with points $\{\tau _j^{\gamma ,\alpha }\}_{j=0}^N$.

Definition 7

([32]) We can define the Sobolev space $H^m(I)$ for $m\in \mathbb {N}$ as follows

$$\begin{aligned} H^m(I)=\left\{ f\in L^2(I):f^{(k)}\in L^2(I),~~k=0,1,\ldots , m\right\} . \end{aligned}$$

(8)

This space contains the following semi-norm and norm

$$\begin{aligned} \left\{ \begin{array}{ll} |f|_{m,I}=||f^{(m)}(\cdot )||_{L^2(I)},\\ ||f||_{m,I}=\left( \sum _{k=0}^m||f^{(k)}(\cdot )||^2_{L^2(I)}\right) ^{\frac{1}{2}}. \end{array}\right. \end{aligned}$$

(9)

Also, a Hilbert space is a space $H^m(I)$ if equipped with the inner product

$$\begin{aligned} (f,g)_{m,I}=\sum _{k=0}^m\int _{I}f^{(k)}(t)g^{(k)}(t)dt, \end{aligned}$$

(10)

and the Sobolev space of weighted Jacobi for $m\in \mathbb {N}$ can be expressed as follows

$$\begin{aligned} H^{m,N}_{\omega ^{\gamma ,\alpha }}(I):=\left\{ f:f^{(k)}(\cdot )\in L^2_{\omega ^{\gamma +k,\alpha +k}}(I), ~ k=0,1,2,\ldots ,m\right\} . \end{aligned}$$

(11)

and has the following norm

$$\begin{aligned} |f|_{H^{m,N}_{\omega ^{\gamma ,\alpha }}(I)}=\left( \sum _{k=min(m,N+1)}^m\parallel f^{(k)}\parallel ^2_{L^2_{\omega ^{\gamma ,\alpha }}(I)}\right) ^{\frac{1}{2}}. \end{aligned}$$

(12)

3 Problem statement and implementing

Now, we investigate the following nonlinear FDIDE

$$\begin{aligned} \left\{ \begin{array}{ll} {}_0^CD_t^{\gamma }X(t)=F(t,X(t),X(t-\delta ))+\int _0^t G(t,\theta ,X(\theta ),X(\theta -\delta ))d\theta ,~~ 0< t\le T,\\ X(t)=\psi (t),~~ -\delta \le t\le 0, \end{array}\right. \end{aligned}$$

(13)

where, $F,G:[0,T]\times \mathbb {R}\times \mathbb {R}\rightarrow \mathbb {R}$ and $\psi : [0,T]\rightarrow \mathbb {R}$ are given function that are continuously differentiable, $X:[0,T]\rightarrow \mathbb {R}$ is a unknown function, $0<\gamma \le 1$ and $0<\delta <T$ is a specified delay parameter.

In beginning, the above equation converts as follows

$$\begin{aligned} \left\{ \begin{array}{ll} {}_0^CD_t^{\gamma }X(t)=\left\{ \begin{array}{ll} F(t,X(t),\psi (t-\delta ))+\int _0^t G\left( t,\theta ,X(\theta ),\psi (\theta -\delta )\right) d\theta ,~~ 0< t\le \delta ,\\ F(t,X(t),X(t-\delta ))+\int _0^t G\left( t,\theta ,X(\theta ),X(\theta -\delta )\right) d\theta ,~~ \delta < t\le T, \end{array}\right. \\ X(0)=\psi (0). \end{array}\right. \end{aligned}$$

(14)

Then, we let the change of variables

$$\begin{aligned} t=\frac{T}{2}(1+z),~~ z=\frac{2t}{T}-1,~~ \theta =\frac{T}{2}(1+\vartheta ),~~\vartheta =\frac{2\theta }{T}-1,~~\bar{\delta }=\frac{2\delta }{T}-1, \end{aligned}$$

(15)

to exert the Jacobi polynomials. By defining $v(z)=X(\frac{T}{2}(1+z))$, we got $v(z-\bar{\delta }-1)=X(t-\delta )$ and then

$$\begin{aligned} \left\{ \begin{array}{lll} &{}\bar{\psi }(z-\bar{\delta })=\psi (\frac{T}{2}(z-\bar{\delta })),\\ &{}\bar{F}(z,v(z),v(z-\bar{\delta }-1))=F(\frac{T}{2}(1+z),X(\frac{T}{2}(1+z)),X(\frac{T}{2}(1+z)-\frac{T}{2}(1+\bar{\delta }))),\\ &{}\bar{G}(z,\vartheta ,v(\vartheta ),v(\vartheta -\bar{\delta }-1)=G(\frac{T}{2}(1+z),\frac{T}{2}(1+\vartheta ),X(\frac{T}{2}(1+\vartheta )),X(\frac{T}{2}(1+\vartheta ) -\frac{T}{2}(1+\bar{\delta })). \end{array}\right. \end{aligned}$$

(16)

We use the following Lemma to implementation the method

Lemma 3.1

Consider $v(z)=X\left( \dfrac{T}{2}(1+z)\right) ,~ z\in (-1,1]$ where $X:[0,T]\rightarrow \mathbb {R}$ is a given differentiable function. Then for $t=\dfrac{T}{2}(1+z)$ and any $z\in (-1,1]$, we have

$$\begin{aligned} \left\{ \begin{array}{ll} {}_0^CI_t^{\gamma }X(t)=\left( \dfrac{T}{2}\right) ^{\gamma }{}_{-1}^CI_z^{\gamma }v(z),\\ {}_0^CD_t^{\gamma }X(t)=\left( \dfrac{2}{T}\right) ^{\gamma }{}_{-1}^CD_z^{\gamma }v(z), \end{array}\right. \end{aligned}$$

(17)

where $0<\gamma \le 1$.

Proof

The proof is similar to the Lemma 1 in [26] and Theorem 4.1 in [25]. Let $z\in (-1,1]$ is given and put $t=\dfrac{T}{2}(1+z)$. For all $\tau \in (-1,z]$, define $\theta =\dfrac{t}{1+z}(1+\tau )$. So $d\theta =\dfrac{t}{1+z}d\tau$ and hence

$$\begin{aligned} {}_0^CI_t^{\gamma }X(t)&=\dfrac{1}{\Gamma (\gamma )}\int _{-1}^z\left( \left( \dfrac{T}{2}(1+z)\right) -\left( \dfrac{t}{1+z}(1+\tau )\right) \right) ^{\gamma -1}v(\tau )\left( \dfrac{t}{1+z}\right) d\tau \\&=\dfrac{1}{\Gamma (\gamma )}\int _{-1}^z\left( \dfrac{T}{2}\right) ^{\gamma -1}(z-\tau )^{\gamma -1}v(\tau )\left( \dfrac{T}{2}\right) d\tau =\left( \dfrac{T}{2}\right) ^{\gamma }\dfrac{1}{\Gamma (\gamma )}\int _{-1}^z(z-\tau )^{\gamma -1}v(\tau )d\tau \\&=\left( \dfrac{T}{2}\right) ^{\gamma }{}_{-1}^CI_z^{\gamma }v(z), \end{aligned}$$

and

$$\begin{aligned} {}_0^CD_t^{\gamma }X(t)&=\dfrac{1}{\Gamma (1- \gamma )}\int _{0}^t \dfrac{X'(\theta )}{(t-\theta )^{\gamma }}d\theta =\dfrac{1}{\Gamma (1- \gamma )}\int _{-1}^z \dfrac{\frac{1+z}{t}v'(\tau )(\frac{t}{1+z})d\tau }{(t-\frac{t}{1+z}(1+\tau ))^{\gamma }}\\&=\dfrac{1}{\Gamma (1- \gamma )}\int _{-1}^z \dfrac{v'(\tau )d\tau }{\left( \frac{T}{2}\right) ^{\gamma }(z-\tau )}=\left( \dfrac{2}{T}\right) ^{\gamma }\dfrac{1}{\Gamma (1- \gamma )}\int _{-1}^z \dfrac{v'(\tau )d\tau }{(z-\tau )}\\&=\left( \dfrac{2}{T}\right) ^{\gamma }{}_{-1}^CD_z^{\gamma }v(z). \end{aligned}$$

Now, we use the (15), (16) and (17) for converting (14) into the equivalent form below.

$$\begin{aligned} \left\{ \begin{array}{ll} {}_{-1}^CD_z^{\gamma }v(z)=\left\{ \begin{array}{ll} \left( \dfrac{T}{2}\right) ^{\gamma }\bar{F}\left( z,v(z),\bar{\psi }(z-\bar{\delta })\right) +\left( \dfrac{T}{2}\right) ^{\gamma +1}\int _{-1}^z \bar{G}\left( z,\vartheta ,v(\vartheta ),\bar{\psi }(\vartheta -\bar{\delta })\right) d\vartheta ,~~ -1< z\le \bar{\delta },\\ \left( \dfrac{T}{2}\right) ^{\gamma }\bar{F}\left( z,v(z),v(z-\bar{\delta }-1)\right) +\left( \dfrac{T}{2}\right) ^{\gamma +1}\int _{-1}^z \bar{G}\left( z,\vartheta ,v(\vartheta ),v(\vartheta -\bar{\delta }{-}1)\right) d\vartheta ,~~ \bar{\delta }{<} z\le 1, \end{array}\right. \\ v(-1)=\bar{\psi }(-1). \end{array}\right. \end{aligned}$$

(18)

Let $\Phi (z)={}_{-1}^CD_z^{\gamma }v(z)$. By (2) and (3), we have

$$\begin{aligned} \left\{ \begin{array}{ll} \Phi (z)=\left\{ \begin{array}{ll} \left( \dfrac{T}{2}\right) ^{\gamma }\bar{F}\left( z,v(z),\bar{\psi }(z-\bar{\delta })\right) +\left( \dfrac{T}{2}\right) ^{\gamma +1}\int _{-1}^z \bar{G}\left( z,\vartheta ,v(\vartheta ),\bar{\psi }(\vartheta -\bar{\delta })\right) d\vartheta ,~~ -1< z\le \bar{\delta },\\ \left( \dfrac{T}{2}\right) ^{\gamma }\bar{F}\left( z,v(z),v(z-\bar{\delta }-1)\right) +\left( \dfrac{T}{2}\right) ^{\gamma +1}\int _{-1}^z \bar{G}\left( z,\vartheta ,v(\vartheta ),v(\vartheta -\bar{\delta }-1)\right) d\vartheta ,~~\bar{\delta }< z\le 1, \end{array}\right. \\ v(z)=\dfrac{1}{\Gamma (\gamma )}\int _{-1}^z(z-\vartheta )^{\gamma -1}\Phi (\vartheta )d\vartheta +\bar{\psi }(-1),~~-1< z\le 1. \end{array}\right. \end{aligned}$$

(19)

Also we see, in the above system, there are two singular integrals. Therefore, for approximate these integrals via JG formula, we utilize $\vartheta _1(z,\tau )=\frac{1+z}{2}\tau +\frac{z-1}{2}$ and by this, we can convert the above system into the following equivalent form

$$\begin{aligned} \left\{ \begin{array}{ll} \Phi (z)=\left\{ \begin{array}{ll} \left( \dfrac{T}{2}\right) ^{\gamma }\bar{F}\left( z,v(z),\bar{\psi }(z-\bar{\delta })\right) +\left( \dfrac{T}{2}\right) ^{\gamma +1}\left( \dfrac{1+z}{2}\right) \int _{-1}^1 \bar{G}\left( z,\vartheta _1\left( z,\tau \right) ,\right. \\ \left. v(\vartheta _1\left( z,\tau \right) ),\bar{\psi }(\vartheta _1\left( z,\tau \right) -\bar{\delta })\right) d\tau \\ \qquad \qquad \qquad ,-1< z\le \bar{\delta },\\ \left( \dfrac{T}{2}\right) ^{\gamma }\bar{F}\left( z,v(z),v(z-\bar{\delta }-1)\right) +\left( \dfrac{T}{2}\right) ^{\gamma +1}\left( \dfrac{1+z}{2}\right) \int _{-1}^1 \bar{G}\left( z,\vartheta _1\left( z,\tau \right) ,\right. \\ \left. v\left( \vartheta _1(z,\tau )\right) ,v\left( \vartheta _1(z,\tau ) -\bar{\delta }-1\right) \right) d\tau \\ \qquad \qquad \qquad ,\bar{\delta }< z\le 1, \end{array}\right. \\ v(z)=\dfrac{1}{\Gamma (\gamma )}\left( \dfrac{1+z}{2}\right) ^{\gamma }\int _{-1}^1(1-\tau )^{\gamma -1}\Phi \left( \vartheta _1(z, \tau )\right) d\tau +\bar{\psi }(-1),~~-1< z\le 1. \end{array}\right. \end{aligned}$$

(20)

Assume that $\alpha =1- \gamma$ and let collocation points $\{z_i^{-\alpha ,-\alpha }\}_{i=0}^N:$ be the set of JG points with the corresponding weight function $\omega ^{-\alpha ,-\alpha }$. Define

$$\begin{aligned} v_i=v(z_i^{-\alpha ,-\alpha }),~~ \Phi _i =\Phi (z_i^{-\alpha ,-\alpha }),~~ v_N(z)=\sum _{j=0}^Nv_j L_j(z),~~\Phi _N(z)=\sum _{j=0}^N\Phi _j L_j(z). \end{aligned}$$

(21)

Therefore,

$$\begin{aligned} v_N(z-\bar{\delta } -1)=\sum _{j=0}^Nv_j L_j(z-\bar{\delta } -1). \end{aligned}$$

(22)

Now, we use the Gauss quadrature formula to approximate the integrals in (20)

$$\begin{aligned}&\int _{-1}^1 \bar{G}\left( z_i^{-\alpha ,-\alpha },\vartheta _1(z_i^{-\alpha ,-\alpha },\tau ),v\left( \vartheta _1((z_i^{-\alpha ,-\alpha },\tau )\right) ,\bar{\psi }\left( \vartheta _1(z_i^{-\alpha ,-\alpha },\tau ) -\bar{\delta }\right) \right) d\tau \nonumber \\&\quad \quad \quad \simeq \sum _{k=0}^N\bar{G}\left( z_i^{-\alpha ,-\alpha },\vartheta _1(z_i^{-\alpha ,-\alpha },\tau _k),v\left( \vartheta _1(z_i^{-\alpha ,-\alpha },\tau _k)\right) ,\bar{\psi }\left( \vartheta _1(z_i^{-\alpha ,-\alpha },\tau _k) -\bar{\delta }\right) \right) \omega _k^{0,0},\nonumber \\&\int _{-1}^1 \bar{G}\left( z_i^{-\alpha ,-\alpha },\vartheta _1(z_i^{-\alpha ,-\alpha },\tau ),v\left( \vartheta _1(z_i^{-\alpha ,-\alpha },\tau )\right) ,v\left( \vartheta _1(z_i^{-\alpha ,-\alpha },\tau ) -\bar{\delta }-1\right) \right) d\tau \nonumber \\&\quad \quad \quad \simeq \sum _{k=0}^N\bar{G}\left( z_i^{-\alpha ,-\alpha },\vartheta _1(z_i^{-\alpha ,-\alpha },\tau _k),v\left( \vartheta _1(z_i^{-\alpha ,-\alpha },\tau _k)\right) ,v\left( \vartheta _1(z_i^{-\alpha ,-\alpha },\tau _k) -\bar{\delta }-1\right) \right) \omega _k^{0,0},\nonumber \\&\int _{-1}^{1}(1-\tau )^{-\alpha }\Phi \left( \vartheta _1(z_i^{-\alpha ,-\alpha }, \tau )\right) d\tau \simeq \sum _{k=0}^N \Phi \left( \vartheta _1(z_i^{-\alpha ,-\alpha }, \hat{\tau } _k)\right) \omega _k^{-\alpha ,0}, \end{aligned}$$

(23)

where $\{\tau _k\}_{k=0}^N$ and $\{\hat{\tau }_k\}_{k=0}^N$ are two sets of JG points with respect to the weight functions $\{\omega _k^{0,0}\}_{k=0}^N$ and $\{\omega _k^{-\alpha ,0}\}_{k=0}^N$.

Finally, we achieve the following system by these relations

$$\begin{aligned} \left\{ \begin{array}{ll} \Phi _i =\left\{ \begin{array}{ll} \left( \dfrac{T}{2}\right) ^{\gamma }\bar{F}\left( z_i^{-\alpha ,-\alpha },v_i,\bar{\psi }(z_i^{-\alpha ,-\alpha }-\bar{\delta })\right) \\ \quad +\left( \dfrac{1+z_i^{-\alpha ,-\alpha }}{2}\right) \left( \dfrac{T}{2}\right) ^{\gamma +1}\sum _{k=0}^N\bar{G}\left( z_i^{-\alpha ,-\alpha },\vartheta _1(z_i^{-\alpha ,-\alpha },\tau _k),\sum _{j=0}^Nv_j L_j\left( \vartheta _1(z_i^{-\alpha ,-\alpha },\tau _k)\right) ,\right. \\ \left. \bar{\psi }\left( \vartheta _1((z_i^{-\alpha ,-\alpha },\tau _k) -\bar{\delta }\right) \right) \omega _k^{0,0},\\ \quad \quad \quad i=1,2,...,l_{\bar{\delta }},\\ \left( \dfrac{T}{2}\right) ^{\gamma }\bar{F}\left( z_i^{-\alpha ,-\alpha },v_i,\sum _{j=0}^Nv_j L_j(z_i^{-\alpha ,-\alpha }-\bar{\delta } -1)\right) +\left( \dfrac{1+z_i^{-\alpha ,-\alpha }}{2}\right) \left( \dfrac{T}{2}\right) ^{\gamma +1}\\ \quad \cdot \sum _{k=0}^N\bar{G}\left( z_i^{-\alpha ,-\alpha },\vartheta _1(z_i^{-\alpha ,-\alpha },\tau _k),\sum _{j=0}^Nv_j L_j\left( \vartheta _1(z_i^{-\alpha ,-\alpha },\tau _k)\right) ,\right. \\ \left. \sum _{j=0}^Nv_j L_j(\vartheta _1(z_i^{-\alpha ,-\alpha }, \tau _k)-\bar{\delta } -1)\right) \omega _k^{0,0},\\ \quad \quad \quad i=l_{\bar{\delta }}+1,\ldots ,N, \end{array}\right. \\ v_i=\dfrac{1}{\Gamma (\gamma )}\left( \dfrac{1+z_i^{-\alpha ,-\alpha }}{2}\right) ^{\gamma }\sum _{k=0}^N \sum _{j=0}^N\Phi _j L_j\left( \vartheta _1(z_i^{-\alpha ,-\alpha }, \hat{\tau } _k)\right) \omega _k^{-\alpha ,0}\ +\bar{\psi }(-1),~~i=1,2,\ldots ,N, \end{array}\right. \end{aligned}$$

(24)

where $\left( v_0,v_1,\ldots ,v_N\right)$ and $\left( \Phi _0,\Phi _1,\ldots ,\Phi _N\right)$ are the unknown variables and as we see, above system is a nonlinear algebraic system where $l_{\bar{\delta }}$ satisfies in $z_{l_{\bar{\delta }}}\le \bar{\delta }<z_{l_{\bar{\delta }}+1}<T$ and we show that we can simultaneously obtain the values of approximate solution and its values of fractional derivatives.

4 Convergence and error analysis

Now, we investigate the error analysis in two spaces $L^2_{\omega ^{\gamma ,\alpha }}(I)$ and $L^{\infty }_{\omega ^{\gamma ,\alpha }}(I)$. We begin our work by presenting several Lemmas.

Lemma 4.1

([9, 37]) Assume that $f\in H^{m,N}_{L^2_{\omega ^{-\alpha ,-\alpha }}(I)}$ and denote by $I_N^{-\alpha ,-\alpha }f$ its interpolation polynomial associated with the $(N+1)$ JG points $\{t_j\}_{j=0}^N$, namely, $I_N^{-\alpha ,-\alpha }f=\sum _{j=0}^Nf(t_j)L(t_j)$. Then the following relations hold for the Chebyshev weight function $\omega ^{C} =\omega ^{-\frac{1}{2},-\frac{1}{2}}$

$$\begin{aligned}{} & {} ||I_N^{-\alpha ,-\alpha }f-f||_{L^2_{\omega ^{-\alpha ,-\alpha }}(I)}\le C_{1,1}N^{-m}|f|_{H^{m,N}_{\omega ^{\gamma ,\zeta }}(I)}, \end{aligned}$$

(25)

$$\begin{aligned}{} & {} ||I_N^{-\alpha ,-\alpha }f-f||_{L^{\infty }(I)}\le \left\{ \begin{array}{ll} C_{1,1}N^{1-\alpha -m}|f|_{H^{m,N}_{\omega ^{C}}(I)},&{}0\le \alpha<\frac{1}{2},\\ C_{1,1}N^{\frac{1}{2}-m}\log N|f|_{H^{m,N}_{\omega ^{C}}(I)}, &{}\frac{1}{2}\le \alpha <1. \end{array}\right. \end{aligned}$$

(26)

Lemma 4.2

([21]) Let $\{L_j(t)\}_{j=0}^N$ be the N-th degree Lagrange basis polynomials. Then, the following relation holds for the Gauss points of the Jacobi polynomials

$$\begin{aligned} ||I_N^{\gamma ,\zeta }g||_{L^{\infty }(I)}\le \max _{t\in [-1,1]}\sum _{j=0}^N|L_j(t)|=\left\{ \begin{array}{ll} \mathcal {O}(\log N),&{}-1<\gamma ,\zeta \le -\frac{1}{2},\\ \mathcal {O}(N^{\beta +\frac{1}{2}}),&{}\beta =\max (\gamma , \zeta ),~otherwise. \end{array}\right. \end{aligned}$$

(27)

Lemma 4.3

([28, 29]) Let $||\cdot ||_{p ,q}$ be the standard norm in $C^{p ,q}(I)$ and assume that $\mathcal {L}_N$ be a linear operator from space $C^{p ,q}(I)$ into the space $\mathcal {P}_N$. Then, there exist a a constant $C_{p ,q}>0$ for $q\in (0,1)$ and a non-negative integer p and a polynomial function $\mathcal {L}_Nf\in \mathcal {P}_N$ for any function $f\in C^{p ,q}(I)$ such that

$$\begin{aligned} ||f-\mathcal {L}_Nf||_{L^{\infty }(I)}\le C_{p,q}N^{-(p +q)}||f||_{C^{p ,q}}. \end{aligned}$$

(28)

Lemma 4.4

([11]) Let $\alpha \in (0,1)$ and $K(\cdot ,\cdot )$ be a function. Also, assume that $\mathcal {J}$ be defined by

$$\begin{aligned} \mathcal {J}f(t)=\int _{-1}^t(t-\tau )^{-\alpha }K(t,\tau )f(\tau )d\tau . \end{aligned}$$

(29)

Then, we have the following relation for a positive constant $C_{2,2}$ (may depend on $||K||_{L^{\infty }(E)}$ and $||K||_{C^{0,q}}$ for $E=[-1,1]^2$) for any function $f\in C(I)$ such that

$$\begin{aligned} \dfrac{|\mathcal {J}f(t')-\mathcal {J}f(t'')|}{|t'-t''|^{q}}\le C_{2,2}\max _{t\in I}|f(t)|, \end{aligned}$$

under the assumption that $0<q <1-\alpha$, for any $t',t''\in I$ and $t'\ne t''$.

This implies that

$$\begin{aligned} \parallel \mathcal {J}f\parallel _{C^{0,q}}\le C_{2,2}\max _{t\in I}|f(t)|,\quad 0<q <1-\alpha . \end{aligned}$$

Lemma 4.5

([24]) Let $f(\cdot )$ be a bounded function. Then, due to Lagrange interpolation basis polynomials $L_j(t),j=0,1,\ldots ,N$ with respect to JGC points $\{t_j\}_{j=0}^N$, we have

$$\begin{aligned} \sup _{N}\parallel \sum _{j=0}^Nf(t_j)L_j(t)\parallel _{L^2_{\omega ^{\gamma ,\zeta }}(I)}\le C_{2,2}\max _{t\in I}|f(t)|, \end{aligned}$$

where $C_{2,2}$ is a constant which is independent of function $f(\cdot )$.

Theorem 4.1

Let $v(\cdot )$ is the smooth exact solution for nonlinear FDIDE (19). If $0<\gamma <1$, $v\in H_{\omega ^{-\alpha ,-\alpha }}^{m+1}(I)$ and $\alpha =1-\gamma$, then for the approximate solutions $v_N(\cdot )$ and $\Phi _N(\cdot )$ of (24)

$$\begin{aligned}&||E^{\gamma ,N}(z)||_{L^{\infty }(I)}\le \left\{ \begin{array}{ll} A_1^{\gamma ,N}\left( |\Phi |_{H^{m,N}_{\omega ^{-\frac{1}{2},-\frac{1}{2}}}(I)}+4MN^{\gamma -\frac{1}{2}}\left( \dfrac{T}{2}\right) ^{\gamma +1} |v|_{H^{m,N}_{\omega ^{-\frac{1}{2},-\frac{1}{2}}}(I)}\right) , &{}\dfrac{1}{2}\le \gamma<1,\\ B_1^{\gamma ,N}\left( |\Phi |_{H^{m,N}_{\omega ^{-\frac{1}{2},-\frac{1}{2}}}(I)}+4M\log N\left( \dfrac{T}{2}\right) ^{\gamma +1} |v|_{H^{m,N}_{\omega ^{-\frac{1}{2},-\frac{1}{2}}}(I)}\right) , &{}0\le \gamma <\dfrac{1}{2}, \end{array}\right. \end{aligned}$$

(30)

$$\begin{aligned}&||e^{\gamma ,N}(z)||_{L^{\infty }(I)}\le \left\{ \begin{array}{ll} D_1^{\gamma ,N}|\Phi |_{H^{m,N}_{\omega ^{-\frac{1}{2},-\frac{1}{2}}}(I)}+F_1^{\gamma ,N} |v|_{H^{m,N}_{\omega ^{-\frac{1}{2},-\frac{1}{2}}}(I)}, &{}\dfrac{1}{2}\le \gamma<1,\\ G_1^{\gamma ,N}|\Phi |_{H^{m,N}_{\omega ^{-\frac{1}{2},-\frac{1}{2}}}(I)}+H_1^{\gamma ,N} |v|_{H^{m,N}_{\omega ^{-\frac{1}{2},-\frac{1}{2}}}(I)}, &{}0\le \gamma <\dfrac{1}{2}, \end{array}\right. \end{aligned}$$

(31)

where $C_{1,1} ,C_{3,3}, C_{2,2}$ and $C_{0,q}$ are constants independent of N and

$$\begin{aligned}&M=\max (M_1,M_2), \end{aligned}$$

(32)

$$\begin{aligned}&E^{\gamma ,N}(z)=\Phi _N(z)-\Phi (z),~~e^{\gamma ,N}(z)=v_N(z)-v(z),\end{aligned}$$

(33)

$$\begin{aligned}&A_1^{\gamma ,N}=\dfrac{C_{1,1}N^{\gamma -m}}{1-4MN^{\gamma -\frac{1}{2}}\left( \dfrac{T}{2}\right) ^{\gamma +1}\left( 1+C_{1,1}C_{2,2}C_{0,q}N^{\gamma -\frac{1}{2}-q}\right) },\end{aligned}$$

(34)

$$\begin{aligned}&B_1^{\gamma ,N}=\dfrac{C_{1,1}N^{\frac{1}{2} -m}\log N}{1-4M\log N\left( \dfrac{T}{2}\right) ^{\gamma +1}\left( 1+C_{1,1}C_{2,2}C_{0,q}N^{-q}\log N\right) },\end{aligned}$$

(35)

$$\begin{aligned}&D_1^{\gamma ,N}=\dfrac{C_{1,1}N^{\gamma -m}\left( 1+C_{1,1}C_{2,2}C_{0,q}N^{\gamma -\frac{1}{2} -q}\right) }{1-4MN^{\gamma -\frac{1}{2}}\left( \dfrac{T}{2}\right) ^{\gamma +1}\left( 1+C_{1,1}C_{2,2}C_{0,q}N^{\gamma -\frac{1}{2}-q}\right) },\end{aligned}$$

(36)

$$\begin{aligned}&F_1^{\gamma ,N}=C_{1,1}N^{\gamma -m}+\left( \dfrac{C_{1,1}N^{\gamma -m}\left( 1+C_{1,1}C_{2,2}C_{0,q}N^{\gamma -\frac{1}{2} -q}\right) \left( 4MN^{\gamma -\frac{1}{2}}\left( \dfrac{T}{2}\right) ^{\gamma +1}\right) }{1-4MN^{\gamma -\frac{1}{2}}\left( \dfrac{T}{2}\right) ^{\gamma +1}\left( 1+C_{1,1}C_{2,2}C_{0,q}N^{\gamma -\frac{1}{2} -q}\right) }\right) ,\end{aligned}$$

(37)

$$\begin{aligned}&G_1^{\gamma ,N}=\dfrac{C_{1,1}N^{\frac{1}{2} -m}\log N\left( 1+C_{1,1}C_{2,2}C_{0,q}N^{-q}\log N\right) }{1-4M\log N\left( \dfrac{T}{2}\right) ^{\gamma +1}\left( 1+C_{1,1}C_{2,2}C_{0,q}N^{-q}\log N\right) },\end{aligned}$$

(38)

$$\begin{aligned}&H_1^{\gamma ,N}=C_{1,1}N^{\frac{1}{2} -m}\log N+\left( \dfrac{C_{1,1}N^{\frac{1}{2} -m}\log N\left( 1+C_{1,1}C_{2,2}C_{0,q}N^{-q}\log N\right) \left( 4M\log N\left( \dfrac{T}{2}\right) ^{\gamma +1}\right) }{1-4M\log N\left( \dfrac{T}{2}\right) ^{\gamma +1}\left( 1+C_{1,1}C_{2,2}C_{0,q}N^{-q}\log N\right) }\right) . \end{aligned}$$

(39)

Proof

By Assuming $\Phi _N(z)\simeq \sum _{j=0}^N\Phi _j L_j(z)\in \mathcal {P}_N$, we get

$$\begin{aligned} \int _{-1}^{1}(1-\tau )^{-\alpha }\Phi _N\left( \vartheta _1(z_i^{-\alpha ,-\alpha },\tau )\right) d\tau =\sum _{k=0}^N \Phi _N\left( \vartheta _1(z_i^{-\alpha ,-\alpha },\tau _k)\right) \omega _k^{-\alpha ,0}, \end{aligned}$$

where $\vartheta _1(z_i^{-\alpha ,-\alpha },\tau _k)=\dfrac{z_i^{-\alpha ,-\alpha }+1}{2}\tau _k +\dfrac{z_i^{-\alpha ,-\alpha }-1}{2}$. By approximating (19) at the JG points $\{z_i^{-\alpha ,-\alpha }\}_{i=1}^N$, we can get

$$\begin{aligned} \left\{ \begin{array}{ll} \Phi _i=\left\{ \begin{array}{ll} \left( \dfrac{T}{2}\right) ^{\gamma }\bar{F}\left( z_i^{-\alpha ,-\alpha } ,v_i,\bar{\psi }(z_i^{-\alpha ,-\alpha } -\bar{\delta })\right) +\left( \dfrac{T}{2}\right) ^{\gamma +1}\int _{-1}^{z_i^{-\alpha ,-\alpha }} \bar{G}\left( z_i^{-\alpha ,-\alpha },\vartheta ,v_N(\vartheta ),\bar{\psi }(\vartheta -\bar{\delta })\right) d\vartheta ,\\ \qquad \qquad \qquad \qquad i=1,2,,...,l_{\bar{\delta }},\\ \left( \dfrac{T}{2}\right) ^{\gamma }\bar{F}\left( z_i^{{-}\alpha ,{-}\alpha } ,v_i,v(z_i^{{-}\alpha ,{-}\alpha } {-}\bar{\delta }-1)\right) +\left( \dfrac{T}{2}\right) ^{\alpha {+}1}\int _{-1}^{z_i^{-\alpha ,-\alpha }} \bar{G}\left( z_i^{{-}\alpha ,{-}\alpha } ,\vartheta ,v_N(\vartheta ),v_N(\vartheta {-}\bar{\delta }{-}1)\right) d\vartheta ,\\ \qquad \qquad \qquad \qquad i=l_{\bar{\delta }}+1,...,N, \end{array}\right. \\ v_i=\dfrac{1}{\Gamma (\gamma )}\int _{-1}^{z_i^{-\alpha ,-\alpha }}(z_i^{-\alpha ,-\alpha }-\vartheta )^{\gamma -1}\Phi _N(\vartheta )d\vartheta +\bar{\psi }(-1), ~~ i=1,2,...,N, \end{array}\right. \end{aligned}$$

(40)

where $\alpha =1-\gamma$. We have the following by multiplying both sides of (40) by $L_i(z)$ and then summing from 0 to N

$$\begin{aligned} \left\{ \begin{array}{ll} \Phi _N(z)=\left\{ \begin{array}{ll} \left( \dfrac{T}{2}\right) ^{\gamma }I_N^{-\alpha ,-\alpha }\left( \bar{F}\left( z,v(z),\bar{\psi }(z-\bar{\delta })\right) \right) +\left( \dfrac{T}{2}\right) ^{\gamma +1}I_N^{-\alpha ,-\alpha }\left( \int _{-1}^{z} \bar{G}\left( z,\vartheta ,v_N(\vartheta ),\bar{\psi }(\vartheta -\bar{\delta })\right) d\vartheta \right) ,\\ \qquad \qquad \qquad \qquad -1< z\le \bar{\delta },\\ \left( \dfrac{T}{2}\right) ^{\gamma }I_N^{-\alpha ,{-}\alpha }\left( \bar{F}\left( z,v(z),v(z {-}\bar{\delta }{-}1)\right) \right) {+}\left( \dfrac{T}{2}\right) ^{\alpha {+}1}I_N^{{-}\alpha ,{-}\alpha }\left( \int _{{-}1}^{z} \bar{G}\left( z ,\vartheta ,v_N(\vartheta ),\right. \right. \\ \left. \left. v_N(\vartheta {-}\bar{\delta }{-}1)\right) d\vartheta \right) ,\\ \qquad \qquad \qquad \qquad \bar{\delta }< z\le 1, \end{array}\right. \\ v_N(z)=I_N^{-\alpha ,-\alpha }\left( \dfrac{1}{\Gamma (\gamma )}\int _{-1}^{z}(z-\vartheta )^{-\alpha }\Phi (\vartheta )d\vartheta \right) +I_N^{-\alpha ,-\alpha }\left( \dfrac{1}{\Gamma (\gamma )}\int _{-1}^{z}(z-\vartheta )^{-\alpha }E^{\gamma ,N}(\vartheta )d\vartheta \right) \\ +\bar{\psi }(-1), ~~ -1<z \le 1 \end{array}\right. \end{aligned}$$

(41)

We arrive to the following system by (19)

$$\begin{aligned} \left\{ \begin{array}{ll} \Phi _N(z)=\left\{ \begin{array}{ll} I_N^{-\alpha ,-\alpha }\left( \Phi (z)-\left( \dfrac{T}{2}\right) ^{\gamma +1}\int _{-1}^z \bar{G}\left( z,\vartheta ,v(\vartheta ),\bar{\psi }(\vartheta -\bar{\delta })\right) d\vartheta \right) \\ \quad \quad +\left( \dfrac{T}{2}\right) ^{\gamma +1}I_N^{-\alpha ,-\alpha }\left( \int _{-1}^{z} \bar{G}\left( z,\vartheta ,v_N(\vartheta ),\bar{\psi }(\vartheta -\bar{\delta })\right) d\vartheta \right) ,~ -1< z\le \bar{\delta },\\ I_N^{-\alpha ,-\alpha }\left( \Phi (z)-\left( \dfrac{T}{2}\right) ^{\gamma +1}\int _{-1}^z \bar{G}\left( z,\vartheta ,v(\vartheta ),v(\vartheta -\bar{\delta }-1)\right) d\vartheta \right) \\ \quad \quad +\left( \dfrac{T}{2}\right) ^{\gamma +1}I_N^{-\alpha ,-\alpha }\left( \int _{-1}^{z} \bar{G}\left( z ,\vartheta ,v_N(\vartheta ),v_N(\vartheta -\bar{\delta }-1)\right) d\vartheta \right) ,~~\bar{\delta }< z\le 1, \end{array}\right. \\ v_N(z)=I_N^{-\alpha ,-\alpha }v(z)+\dfrac{1}{\Gamma (\gamma )}I_N^{-\alpha ,-\alpha }\left( \int _{-1}^{z}(z-\vartheta )^{-\alpha }E^{\gamma ,N}(\vartheta )d\vartheta \right) , ~~ -1< z\le 1, \end{array}\right. \end{aligned}$$

(42)

where $I^{-\alpha ,-\alpha }_N$ is the Lagrange operator which defined in Lemma 4.1. Now, according to (33)

$$\begin{aligned}&E^{\gamma ,N}(z)=\left\{ \begin{array}{ll} \left( \dfrac{T}{2}\right) ^{\gamma +1}I_N^{-\alpha ,-\alpha }\left( \int _{-1}^{z} \bar{G}\left( z,\vartheta ,v_N(\vartheta ),\bar{\psi }(\vartheta -\bar{\delta })\right) d\vartheta -\int _{-1}^z \bar{G}\left( z,\vartheta ,v(\vartheta ),\bar{\psi }(\vartheta -\bar{\delta })\right) d\vartheta \right) \\ \qquad \qquad +J_1(z), ~~-1< z\le \bar{\delta },\\ \left( \dfrac{T}{2}\right) ^{\gamma +1}I_N^{-\alpha ,-\alpha }\left( \int _{-1}^{z} \bar{G}\left( z ,\vartheta ,v_N(\vartheta ),v_N(\vartheta -\bar{\delta }-1)\right) d\vartheta -\int _{-1}^z \bar{G}\left( z,\vartheta ,v(\vartheta ),\right. \right. \\ \left. \left. v(\vartheta -\bar{\delta }-1)\right) d\vartheta \right) \\ \qquad \qquad +J_1(z),~~\bar{\delta }< z\le 1, \end{array}\right. \end{aligned}$$

(43)

$$\begin{aligned}&e^{\gamma ,N}(z)=\dfrac{1}{\Gamma (\gamma )}\int _{-1}^{z}(z-\vartheta )^{-\alpha }E^{\gamma ,N}(\vartheta )d\vartheta +J_2(z)+J_3(z), ~~ -1<z\le 1 \end{aligned}$$

(44)

where

$$\begin{aligned}&J_1(z)=I_N^{-\alpha ,-\alpha }\Phi (z)-\Phi (z),~~J_2(z)=I_N^{-\alpha ,-\alpha }v(z)-v(z),\end{aligned}$$

(45)

$$\begin{aligned}&J_3(z)=\dfrac{1}{\Gamma (\gamma )}\left( I_N^{-\alpha ,-\alpha }\int _{-1}^{z}(z-\vartheta )^{-\alpha }E^{\gamma ,N}(\vartheta )d\vartheta -\int _{-1}^{z}(z-\vartheta )^{-\gamma }E^{\gamma ,N}(\vartheta )d\vartheta \right) . \end{aligned}$$

(46)

From (43), we have

$$\begin{aligned} |E^{\gamma ,N}(z)|\le \left\{ \begin{array}{ll} \left( \dfrac{T}{2}\right) ^{\gamma +1}|I_N^{-\alpha ,-\alpha }\left( \int _{-1}^{z} \bar{G}\left( z,\vartheta ,v_N(\vartheta ),\bar{\psi }(\vartheta -\bar{\delta })\right) d\vartheta -\int _{-1}^z \bar{G}\left( z,\vartheta ,v(\vartheta ),\bar{\psi }(\vartheta -\bar{\delta })\right) d\vartheta \right) |\\ \qquad \qquad +|J_1(z)|,~ -1< z\le \bar{\delta },\\ \left( \dfrac{T}{2}\right) ^{\gamma +1}|I_N^{-\alpha ,-\alpha }\left( \int _{-1}^{z} \bar{G}\left( z ,\vartheta ,v_N(\vartheta ),v_N(\vartheta -\bar{\delta }-1)\right) d\vartheta -\int _{-1}^z \bar{G}\left( z,\vartheta ,v(\vartheta ),\right. \right. \\ \left. \left. v(\vartheta -\bar{\delta }-1)\right) d\vartheta \right) |\\ \qquad \qquad +|J_1(z)|,~~\bar{\delta }\le z\le 1. \end{array}\right. \end{aligned}$$

(47)

Now, we get from triangular inequality

$$\begin{aligned} ||E^{\gamma ,N}(z)||_{L^{\infty }(I)}\le \max \left\{ L_1,L_2\right\} , \end{aligned}$$

(48)

where

$$\begin{aligned} L_1&=\left( \dfrac{T}{2}\right) ^{\gamma +1}||I_N^{-\alpha ,-\alpha }\left( \int _{-1}^{z} \bar{G}\left( z,\vartheta ,v_N(\vartheta ),\bar{\psi }(s -\bar{\delta })\right) d\vartheta -\int _{-1}^z \bar{G}\left( z,\vartheta ,v(\vartheta ),\bar{\psi }(\vartheta -\bar{\delta })\right) d\vartheta \right) ||_{L^{\infty }(I)}\nonumber \\&\quad +||J_1(z)||_{L^{\infty }(I)},\end{aligned}$$

(49)

$$\begin{aligned} L_2&=\left( \dfrac{T}{2}\right) ^{\gamma +1}||I_N^{-\alpha ,-\alpha }\left( \int _{-1}^{z} \bar{G}\left( z ,\vartheta ,v_N(\vartheta ),v_N(\vartheta -\bar{\delta }-1)\right) d\vartheta \right. \nonumber \\&\quad \left. -\int _{-1}^z \bar{G}\left( z,\vartheta ,v(\vartheta ),v(\vartheta -\bar{\delta }-1)\right) d\vartheta \right) ||_{L^{\infty }(I)}+||J_1(z)||_{L^{\infty }(I)}. \end{aligned}$$

(50)

With a similar process, we conclude from (44) that

$$\begin{aligned} ||e^{\gamma ,N}(z)||_{L^{\infty }(I)}\le ||E^{\gamma ,N}(z)||_{L^{\infty }(I)}+||J_2(z)||_{L^{\infty }(I)}+||J_3(z)||_{L^{\infty }(I)}. \end{aligned}$$

(51)

Using Lemma 4.2, the relation (48) and Lipschitz condition, we have

$$\begin{aligned} ||I_N^{-\alpha ,-\alpha }&\left( \int _{-1}^{z} \bar{G}\left( z,\vartheta ,v_N(\vartheta ),\bar{\psi }(\vartheta -\bar{\delta })\right) d\vartheta -\int _{-1}^z \bar{G}\left( z,\vartheta ,v(\vartheta ),\bar{\psi }(\vartheta -\bar{\delta })\right) d\vartheta \right) ||_{L^{\infty }(I)}\nonumber \\&\le \left\{ \begin{array}{ll} N^{\frac{1}{2}-\alpha }\max \limits _{[-1,1]}|\int _{-1}^{z} \bar{G}\left( z,\vartheta ,v_N(\vartheta ),\bar{\psi }(\vartheta -\bar{\delta })\right) d\vartheta -\int _{-1}^z \bar{G}\left( z,\vartheta ,v(\vartheta ),\bar{\psi }(\vartheta {-}\bar{\delta })\right) d\vartheta |,~~0{<}\alpha {<}\frac{1}{2},\\ \log N\max \limits _{[-1,1]}|\int _{-1}^{z} \bar{G}\left( z,\vartheta ,v_N(\vartheta ),\bar{\psi }(\vartheta -\bar{\delta })\right) d\vartheta -\int _{-1}^z \bar{G}\left( z,\vartheta ,v(\vartheta ),\bar{\psi }(\vartheta -\bar{\delta })\right) d\vartheta |,~~\frac{1}{2}<\alpha {<}1, \end{array}\right. \nonumber \\&\le \left\{ \begin{array}{ll} 2N^{\frac{1}{2}-\alpha }M_1||v_N(\vartheta )-v(\vartheta )||_{L^{\infty }(I)},~~0<\alpha<\frac{1}{2},\\ 2\log NM_1||v_N(\vartheta )-v(\vartheta )||_{L^{\infty }(I)},~~\frac{1}{2}<\alpha<1, \end{array}\right. \nonumber \\&\le \left\{ \begin{array}{ll} 2N^{\frac{1}{2}-\alpha }M_1||e^{\gamma ,N}||_{L^{\infty }(I)},~~0<\alpha<\frac{1}{2},\\ 2\log NM_1||e^{\gamma ,N}||_{L^{\infty }(I)},~~\frac{1}{2}<\alpha<1, \end{array}\right. \nonumber \\ ||I_N^{-\alpha ,-\alpha }&\left( \int _{-1}^{z} \bar{G}\left( z,\vartheta ,v_N(\vartheta ),v_N(\vartheta -\bar{\delta }-1)\right) d\vartheta -\int _{-1}^z \bar{G}\left( z,\vartheta ,v(\vartheta ),v(\vartheta -\bar{\delta }-1)\right) d\vartheta \right) ||_{L^{\infty }(I)}\nonumber \\&\le \left\{ \begin{array}{ll} N^{\frac{1}{2}-\alpha }\max \limits _{[-1,1]}|\int _{-1}^{z} \bar{G}\left( z,\vartheta ,v_N(\vartheta ),v_N(\vartheta -\bar{\delta }-1)\right) d\vartheta -\int _{-1}^z \bar{G}\left( z,\vartheta ,v(\vartheta ),v(\vartheta -\bar{\delta }-1)\right) d\vartheta |,\\ ~~0<\alpha<\frac{1}{2},\\ \log N\max \limits _{[-1,1]}|\int _{-1}^{z} \bar{G}\left( z,\vartheta ,v_N(\vartheta ),v_N(\vartheta -\bar{\delta }-1)\right) d\vartheta -\int _{-1}^z \bar{G}\left( z,\vartheta ,v(\vartheta ),v(\vartheta -\bar{\delta }-1)\right) d\vartheta |,\\ ~~\frac{1}{2}<\alpha<1, \end{array}\right. \nonumber \\&\le \left\{ \begin{array}{ll} 2N^{\frac{1}{2}-\alpha }\left( M_2||v_N(\vartheta )-v(\vartheta )||_{L^{\infty }(I)}+M_2||v_N(\vartheta -\bar{\delta }-1)-v(\vartheta -\bar{\delta }-1)||_{L^{\infty }(I)}\right) ,~~0<\alpha<\frac{1}{2},\\ 2\log N\left( M_2||v_N(\vartheta )-v(\vartheta )||_{L^{\infty }(I)}+M_2||v_N(\vartheta -\bar{\delta }-1)-v(\vartheta -\bar{\delta }-1)||_{L^{\infty }(I)}\right) ,~~\frac{1}{2}<\alpha<1, \end{array}\right. \nonumber \\&\le \left\{ \begin{array}{ll} 4N^{\frac{1}{2}-\alpha }M_2||e^{\gamma ,N}||_{L^{\infty }(I)},~~0<\alpha<\frac{1}{2},\\ 4\log NM_2||e^{\gamma ,N}||_{L^{\infty }(I)},~~\frac{1}{2}<\alpha <1. \end{array}\right. \end{aligned}$$

(52)

We have from Lemma 4.1

$$\begin{aligned}&||J_1(z)||_{L^{\infty }(I)}\le \left\{ \begin{array}{ll} C_{1,1}N^{1-\alpha -m}|\Phi |_{H^{m,N}_{\omega ^{-\frac{1}{2},-\frac{1}{2}}}(I)},&{}0\le \alpha<\frac{1}{2},\\ C_{1,1}N^{\frac{1}{2}-m}\log N|\Phi |_{H^{m,N}_{\omega ^{-\frac{1}{2},-\frac{1}{2}}}(I)},&{}\frac{1}{2}\le \alpha<1, \end{array}\right. \nonumber \\&||J_2(z)||_{L^{\infty }(I)}\le \left\{ \begin{array}{ll} C_{1,1}N^{1-\alpha -m}|v|_{H^{m,N}_{\omega ^{-\frac{1}{2},-\frac{1}{2}}}(I)},&{}0\le \alpha<\frac{1}{2},\\ C_{1,1}N^{\frac{1}{2}-m}\log N|v|_{H^{m,N}_{\omega ^{-\frac{1}{2},-\frac{1}{2}}}(I)},&{}\frac{1}{2}\le \alpha <1. \end{array}\right. \end{aligned}$$

(53)

By Lemmas 4.1, 4.3 and 4.4, we conclude that

$$\begin{aligned} ||J_3(z)||_{L^{\infty }(I)}&=||\left( I_N^{-\alpha ,-\alpha }-1\right) \mathcal {J}E^{\gamma ,N}||_{L^{\infty }(I)}\nonumber \\&=||\left( I_N^{-\alpha ,-\alpha }-1\right) \left( \mathcal {J}E^{\gamma ,N}-\mathcal {L}_N\mathcal {J}E^{\gamma ,N}\right) ||_{L^{\infty }(I)}\nonumber \\&\le \left( 1+I_N^{-\alpha ,-\alpha }\right) C_{0,q}N^{-q}||\mathcal {J}E^{\gamma ,N}||_{C^{0,q}}\nonumber \\&\le \left\{ \begin{array}{ll} C_{1,1}C_{2,2}C_{0,q}N^{\frac{1}{2}-\alpha -q}||E^{\gamma ,N}||_{L^{\infty }(I)},&{} 0\le \alpha<\frac{1}{2},\\ C_{1,1}C_{2,2}C_{0,q}N^{-q}\log N||E^{\gamma ,N}||_{L^{\infty }(I)},&{} \frac{1}{2}\le \alpha <1. \end{array}\right. \end{aligned}$$

(54)

Fig. 1

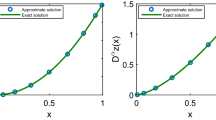
The exact and approximate solution with $\gamma =0.5$, $\delta =0.25$ and $N=5$ for Example 1

Fig. 2

The approximate solutions for $\gamma =0.5,0.7,0.9$, $\delta =0.25$ and $N=5$ for Example 1

Fig. 3

The error for $\gamma =0.8$, $\delta =0.25$ and $N=3,5,7$ for Example 1

Fig. 4

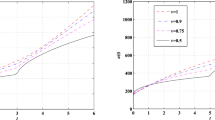
The error for $\gamma =0.9,0.99,0.999$, $\delta =0.25$ and $N=5$ for Example 1

Note that we employ the Lemma 4.4 under the following assumptions

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{1}{2}-\alpha<q<1-\eta ,&{} 0\le \alpha<\frac{1}{2},\\ 0<q<1-\alpha ,&{}\frac{1}{2}\le \alpha <1. \end{array}\right. \end{aligned}$$

(55)

Now, we give the following relations by Combining (52)-(54) in (48) and (51)

$$\begin{aligned}&||E^{\gamma ,N}(z)||_{L^{\infty }(I)}\le \left\{ \begin{array}{ll} A_1^{\gamma ,N}\left( |\Phi |_{H^{m,N}_{\omega ^{-\frac{1}{2},-\frac{1}{2}}}(I)}+4MN^{\frac{1}{2}-\alpha }\left( \dfrac{T}{2}\right) ^{\gamma +1} |v|_{H^{m,N}_{\omega ^{-\frac{1}{2},-\frac{1}{2}}}(I)}\right) , &{}\dfrac{1}{2}\le \gamma<1,\\ B_1^{\gamma ,N}\left( |\Phi |_{H^{m,N}_{\omega ^{-\frac{1}{2},-\frac{1}{2}}}(I)}+4M\log N\left( \dfrac{T}{2}\right) ^{\gamma +1} |v|_{H^{m,N}_{\omega ^{-\frac{1}{2},-\frac{1}{2}}}(I)}\right) , &{}0\le \gamma <\dfrac{1}{2}, \end{array}\right. \end{aligned}$$

(56)

$$\begin{aligned}&||e^{\gamma ,N}(z)||_{L^{\infty }(I)}\le \left\{ \begin{array}{ll} D_1^{\gamma ,N}|\Phi |_{H^{m,N}_{\omega ^{-\frac{1}{2},-\frac{1}{2}}}(I)}+F_1^{\gamma ,N} |v|_{H^{m,N}_{\omega ^{-\frac{1}{2},-\frac{1}{2}}}(I)}, &{}\dfrac{1}{2}\le \gamma<1,\\ G_1^{\gamma ,N}|\Phi |_{H^{m,N}_{\omega ^{-\frac{1}{2},-\frac{1}{2}}}(I)}+H_1^{\gamma ,N} |v|_{H^{m,N}_{\omega ^{-\frac{1}{2},-\frac{1}{2}}}(I)}, &{}0\le \gamma <\dfrac{1}{2}, \end{array}\right. \end{aligned}$$

(57)

Theorem 4.2

By considering the assumptions of Theorem 4.1, we have

$$\begin{aligned}&||E^{\gamma ,N}(z)||_{L^{2}_{\omega ^{-\alpha ,-\alpha }}(I)}\le \left\{ \begin{array}{ll} A_2^{\gamma ,N}|\Phi |_{H^{m,N}_{\omega ^{-\frac{1}{2},-\frac{1}{2}}}(I)}+B_2^{\gamma ,N}|v|_{H^{m,N}_{}(I)}, &{}\frac{1}{2}\le \gamma<1,\\ S_2^{\gamma ,N}|\Phi |_{H^{m,N}_{\omega ^{-\frac{1}{2},-\frac{1}{2}}}(I)}+Q_2^{\gamma ,N}|v|_{H^{m,N}_{\omega ^{-\frac{1}{2},-\frac{1}{2}}}(I)}, &{}0\le \gamma <\dfrac{1}{2}, \end{array}\right. \end{aligned}$$

(58)

$$\begin{aligned}&||e^{\gamma ,N}(z)||_{L^{2}_{\omega ^{-\alpha ,-\alpha }}(I)}\le \left\{ \begin{array}{ll} \left( R_2^{\gamma ,N}|\Phi |_{H^{m,N}_{\omega ^{-\frac{1}{2},-\frac{1}{2}}}(I)}+M_2^{\gamma ,N}|v|_{H^{m,N}_{\omega ^{-\frac{1}{2},-\frac{1}{2}}}(I)}\right) , &{}\dfrac{1}{2}\le \gamma<1,\\ \left( G_2^{\gamma ,N}|\Phi |_{H^{m,N}_{\omega ^{-\frac{1}{2},-\frac{1}{2}}}(I)}+F_2^{\gamma ,N}|v|_{H^{m,N}_{\omega ^{-\frac{1}{2},-\frac{1}{2}}}(I)}\right) , &{}0\le \gamma <\dfrac{1}{2}, \end{array}\right. \end{aligned}$$

(59)

where

$$\begin{aligned}&A_2^{\gamma ,N}=\dfrac{C_{1,1}N^{-m}}{1-4\left( \dfrac{T}{2}\right) ^{\gamma +1}\tilde{C}MN^{\gamma -\frac{1}{2}}}\left( 1+\dfrac{4\tilde{C}C_{2,2}\bar{C}C_{0,q}M\left( \dfrac{T}{2}\right) ^{\gamma +1}N^{2\gamma -\frac{1}{2}-q}}{1-4MN^{\gamma -\frac{1}{2}}\left( \dfrac{T}{2}\right) ^{\gamma +1}\left( 1+C_{1,1}C_{2,2}C_{0,q}N^{\gamma -\frac{1}{2} -q}\right) }\right) ,\nonumber \\ \end{aligned}$$

(60)

$$\begin{aligned}&B_2^{\gamma ,N}=\dfrac{4C_{1,1}\tilde{C}M\left( \dfrac{T}{2}\right) ^{\gamma +1}N^{\gamma -\frac{1}{2} -m}}{1-4\tilde{C}\left( \dfrac{T}{2}\right) ^{\gamma +1}MN^{\gamma -\frac{1}{2}}}\left( 1+\dfrac{4C_{2,2}\bar{C}C_{0,q} M\left( \dfrac{T}{2}\right) ^{\gamma +1}N^{2\gamma -\frac{1}{2} -q}}{1-4MN^{\gamma -\frac{1}{2}}\left( \dfrac{T}{2}\right) ^{\gamma +1}\left( 1+C_{1,1}C_{2,2}C_{0,q}N^{\gamma -\frac{1}{2} -q}\right) }\right) ,\nonumber \\ \end{aligned}$$

(61)

$$\begin{aligned}&S_2^{\gamma ,N}=\dfrac{C_{1,1}N^{-m}}{1-4\left( \dfrac{T}{2}\right) ^{\gamma +1}\tilde{C}M\log N}\left( 1+\dfrac{4MC_{2,2}\tilde{C}\bar{C}C_{0,q}\log N N^{\frac{1}{2} -q}\left( \dfrac{T}{2}\right) ^{\gamma +1}\log N}{1-4M\log N\left( \dfrac{T}{2}\right) ^{\gamma +1}\left( 1+C_{1,1}C_{2,2}C_{0,q}N^{-q}\log N\right) }\right) , \nonumber \\ \end{aligned}$$

(62)

$$\begin{aligned}&Q_2^{\gamma ,N}=\dfrac{4C_{1,1}\tilde{C}M\left( \dfrac{T}{2}\right) ^{\gamma +1} N^{-m}\log N}{1-4\left( \dfrac{T}{2}\right) ^{\gamma +1}\tilde{C}M\log N}\left( 1+\dfrac{4C_{2,2}\bar{C}C_{0,q} M\log N\left( \dfrac{T}{2}\right) ^{\gamma +1}N^{\frac{1}{2} -q}\log N}{1-\bar{C}_1M\log N\left( \dfrac{T}{2}\right) ^{\gamma +1}\left( 1+C_{1,1}C_{2,2}C_{0,q}N^{-q}\log N\right) }\right) , \end{aligned}$$

(63)

$$\begin{aligned}&R_2^{\gamma ,N}=\dfrac{C_{1,1}N^{-m}}{1-4\left( \dfrac{T}{2}\right) ^{\gamma +1}\tilde{C}MN^{\gamma -\frac{1}{2}}}\left( 1+\dfrac{4\tilde{C}C_{2,2}\bar{C}C_{0,q}M\left( \dfrac{T}{2}\right) ^{\gamma +1}N^{2\gamma -\frac{1}{2} -q}}{1-4MN^{\gamma -\frac{1}{2}}\left( \dfrac{T}{2}\right) ^{\gamma +1}\left( 1+C_{1,1}C_{2,2}C_{0,q}N^{\gamma -\frac{1}{2} -q}\right) }\right) \nonumber \\&\qquad \qquad +\dfrac{C_{1,1}C_{2,2}\bar{C}C_{0,q}N^{\gamma -m-q}}{1-4MN^{\gamma -\frac{1}{2}}\left( \dfrac{T}{2}\right) ^{\gamma +1}\left( 1+C_{1,1}C_{2,2}C_{0,q}N^{\gamma -\frac{1}{2} -q}\right) } \end{aligned}$$

(64)

$$\begin{aligned}&M_2^{\gamma ,N}=C_{1,1}N^{-m}+\dfrac{4MC_{1,1}C_{2,2}\bar{C}C_{0,q}\left( \dfrac{T}{2}\right) ^{\gamma +1}N^{2\gamma -\frac{1}{2}-m-q}}{1-4MN^{\gamma -\frac{1}{2}}\left( \dfrac{T}{2}\right) ^{\gamma +1}\left( 1+C_{1,1}C_{2,2}C_{0,q}N^{\gamma -\frac{1}{2} -q}\right) }\nonumber \\&\qquad \qquad +\dfrac{4C_{1,1}\tilde{C}M\left( \dfrac{T}{2}\right) ^{\gamma +1}N^{\gamma -\frac{1}{2}-m}}{1-4\tilde{C}\left( \dfrac{T}{2}\right) ^{\gamma +1}MN^{\gamma -\frac{1}{2}}}\left( 1+\dfrac{4C_{2,2}\bar{C}C_{0,q} M\left( \dfrac{T}{2}\right) ^{\gamma +1}N^{2\gamma -\frac{1}{2} -q}}{1-4MN^{\gamma -\frac{1}{2}}\left( \dfrac{T}{2}\right) ^{\gamma +1}\left( 1+C_{1,1}C_{2,2}C_{0,q}N^{\gamma -\frac{1}{2} -q}\right) }\right) \nonumber \\4 \end{aligned}$$

(65)

$$\begin{aligned}&G_2^{\gamma ,N}=\dfrac{C_{1,1}N^{-m}}{1-4\left( \dfrac{T}{2}\right) ^{\gamma +1}\tilde{C}M\log N}\left( 1+\dfrac{4MC_{2,2}\tilde{C}\bar{C}C_{0,q}\log N N^{\frac{1}{2} -q}\left( \dfrac{T}{2}\right) ^{\gamma +1}\log N}{1-4M\log N\left( \dfrac{T}{2}\right) ^{\gamma +1}\left( 1+C_{1,1}C_{2,2}C_{0,q}N^{-q}\log N\right) }\right) \nonumber \\&\qquad \qquad +\dfrac{C_{1,1}\bar{C}C_{2,2}C_{0,q}N^{\frac{1}{2} -m-q}\log N}{1-4M\log N\left( \dfrac{T}{2}\right) ^{\gamma +1}\left( 1+C_{1,1}C_{2,2}C_{0,q}N^{-q}\log N\right) } \end{aligned}$$

(66)

$$\begin{aligned}&F_2^{\gamma ,N}=C_{1,1}N^{-m}+\dfrac{4C_{1,1}\bar{C}C_{2,2}C_{0,q}M\log N\left( \dfrac{T}{2}\right) ^{\gamma +1}N^{\frac{1}{2} -m-q}\log N}{1-4M\log N\left( \dfrac{T}{2}\right) ^{\gamma +1}\left( 1+C_{1,1}C_{2,2}C_{0,q}N^{-q}\log N\right) }\nonumber \\&\qquad \qquad +\dfrac{4C_{1,1}\tilde{C}M\left( \dfrac{T}{2}\right) ^{\gamma +1} N^{-m}\log N}{1-4\left( \dfrac{T}{2}\right) ^{\gamma +1}\tilde{C}M\log N}\left( 1+\dfrac{4C_{2,2}\bar{C}C_{0,q} M\log N\left( \dfrac{T}{2}\right) ^{\gamma +1}N^{\frac{1}{2} -q}\log N}{1-\bar{C}_1M\log N\left( \dfrac{T}{2}\right) ^{\gamma +1}\left( 1+C_{1,1}C_{2,2}C_{0,q}N^{-q}\log N\right) }\right) . \end{aligned}$$

(67)

Proof

We conclude that from (43) and generalization of the triangular inequality

$$\begin{aligned} ||E^{\gamma ,N}(\cdot )||_{L^{2}_{\omega ^{-\alpha ,-\alpha }}(I)}\le \max \left\{ L_1',L_2'\right\} \end{aligned}$$

(68)

where

$$\begin{aligned} L_1'&=\left( \dfrac{T}{2}\right) ^{\gamma +1}||I_N^{-\alpha ,-\alpha }\left( \int _{-1}^{z} \bar{G}\left( z,\vartheta ,v_N(\vartheta ),\bar{\psi }(\vartheta -\bar{\delta })\right) d\vartheta -\int _{-1}^z \bar{G}\left( z,\vartheta ,v(\vartheta ),\bar{\psi }(\vartheta -\bar{\delta })\right) d\vartheta \right) ||_{L^{2}_{\omega ^{-\alpha ,-\alpha }}(I)}\nonumber \\ {}&\quad +||J_1(z) ||_{L^{2}_{\omega ^{-\alpha ,-\alpha }}(I)},\nonumber \\ L_2'&=\left( \dfrac{T}{2}\right) ^{\gamma +1}||I_N^{-\alpha ,-\alpha }\left( \int _{-1}^{z} \bar{G}\left( z,\vartheta ,v_N(\vartheta ),v_N(\vartheta -\bar{\delta }-1)\right) d\vartheta \right. \nonumber \\ {}&\quad \left. -\int _{-1}^z \bar{G}\left( z,\vartheta ,v(\vartheta ),v(\vartheta -\bar{\delta }-1)\right) d\vartheta \right) ||_{L^{2}_{\omega ^{-\alpha ,-\alpha }}(I)}\nonumber \\&\qquad +||J_1(z) ||_{L^{2}_{\omega ^{-\alpha ,-\alpha }}(I)}, \end{aligned}$$

(69)

and

$$\begin{aligned} ||e^{\gamma ,N}(z)||_{L^{2}_{\omega ^{-\alpha ,-\alpha }}(I)}\le ||E^{\gamma ,N}(z)||_{L^{2}_{\omega ^{-\alpha ,-\alpha }}(I)}+||J_2(z)||_{L^{2}_{\omega ^{-\alpha ,-\alpha }}(I)}+||J_3(z)||_{L^{2}_{\omega ^{-\alpha ,-\alpha }}(I)}, \end{aligned}$$

(70)

Fig. 5

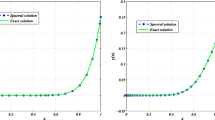
The approximate and exact solutions of Example 2 for $\gamma =0.5$, $\delta =0.25$ and $N=5$

Fig. 6

The approximate solutions of Example 2 for $\gamma =0.5,0.7,0.9$, $\delta =0.25$ and $N=5$

Fig. 7

The error of Example 2 for $\gamma =0.8$, $\delta =0.25$ and $N=4,6,8$

Fig. 8

The error of Example 2 for $\gamma =0.5,0.7,0.9$, $\delta =0.25$ and $N=5$

Fig. 9

The error of Example 2 for $\gamma =0.5$, $\delta =0.2,0.4,0.6$ and $N=5$

where $J_1(z)$, $J_2(z)$ and $J_3(z)$ are described in (45) and (46). Now, it conclude from (52) that

$$\begin{aligned} || I_N^{-\alpha ,-\alpha }&\left( \int _{-1}^{z} \bar{G}\left( z,\vartheta ,v_N(\vartheta ),\bar{\psi }(\vartheta -\bar{\delta })\right) d\vartheta -\int _{-1}^z \bar{G}\left( z,\vartheta ,v(\vartheta ),\bar{\psi }(\vartheta -\bar{\delta })\right) d\vartheta \right) || _{L^{2}_{\omega ^{-\alpha ,-\alpha }}(I)} \nonumber \\&\le \tilde{C}||I_N^{-\alpha ,-\alpha }\left( \int _{-1}^{z} \bar{G}\left( z,\vartheta ,v_N(\vartheta ),\bar{\psi }(\vartheta -\bar{\delta })\right) d\vartheta -\int _{-1}^z \bar{G}\left( z,\vartheta ,v(\vartheta ),\bar{\psi }(\vartheta -\bar{\delta })\right) d\vartheta \right) ||_{L^{\infty }(I)}\nonumber \\&\le \left\{ \begin{array}{ll} 2\tilde{C}N^{\frac{1}{2}-\alpha }M_1||e^{\gamma ,N}||_{L^{\infty }(I)},~~0<\alpha<\frac{1}{2},\\ 2\tilde{C}\log NM_1||e^{\gamma ,N}||_{L^{\infty }(I)},~~\frac{1}{2}<\alpha<1, \end{array}\right. \nonumber \\ ||I_N^{-\alpha ,-\alpha }&\left( \int _{-1}^{z} \bar{G}\left( z,\vartheta ,v_N(\vartheta ),v_N(\vartheta -\bar{\delta }-1)\right) d\vartheta -\int _{-1}^z \bar{G}\left( z,\vartheta ,v(\vartheta ),v(\vartheta -\bar{\delta }-1)\right) d\vartheta \right) ||_{L^{2}_{\omega ^{-\alpha ,-\alpha }}(I)}\nonumber \\&{\le }\tilde{C}||I_N^{{-}\alpha ,{-}\alpha }\left( \int _{-1}^{z} \bar{G}\left( z,\vartheta ,v_N(\vartheta ),v_N(\vartheta {-}\bar{\delta }-1)\right) d\vartheta {-}\int _{-1}^z \bar{G}\left( z,\vartheta ,v(\vartheta ),v(\vartheta {-}\bar{\delta }{-}1)\right) d\vartheta \right) ||_{L^{\infty }(I)}\nonumber \\&\le \left\{ \begin{array}{ll} 4\tilde{C}N^{\frac{1}{2}-\alpha }M_2||e^{\gamma ,N}||_{L^{\infty }(I)},~~0<\alpha<\frac{1}{2},\\ 4\tilde{C}\log NM_2||e^{\gamma ,N}||_{L^{\infty }(I)},~~\frac{1}{2}<\alpha <1. \end{array}\right. \end{aligned}$$

(71)

Using Lemma 4.1, we have

$$\begin{aligned}&|J_1(z)||_{L^{2}_{\omega ^{-\alpha ,-\alpha }}(I)}\le C_{1,1}N^{-m}|\Phi |_{H^{m,N}_{\omega ^{-\frac{1}{2},-\frac{1}{2}}}(I)}, \end{aligned}$$

(72)

$$\begin{aligned}&||J_2(z)||_{L^{2}_{\omega ^{-\alpha ,-\alpha }}(I)}\le C_{1,1}N^{-m}|v|_{H^{m,N}_{\omega ^{-\frac{1}{2},-\frac{1}{2}}}(I)}. \end{aligned}$$

(73)

From Lemmas 4.3 and 4.5, it follows that

$$\begin{aligned} ||J_3(z)||_{L^{2}_{\omega ^{-\alpha ,-\alpha }}(I)}&=||\left( I_N^{-\alpha ,-\alpha }-1\right) \mathcal {J}E^{\gamma ,N}||_{L^{2}_{\omega ^{-\alpha ,-\alpha }}(I)}\nonumber \\&=||\left( I_N^{-\alpha ,-\alpha }-1\right) \left( \mathcal {J}E^{\gamma ,N}-\mathcal {L}_N\mathcal {J}E^{\gamma ,N}\right) ||_{L^{2}_{\omega ^{-\alpha ,-\alpha }}(I)}\nonumber \\&\le ||I_N^{-\alpha ,-\alpha }\left( \mathcal {J}E^{\gamma ,N}-\mathcal {L}_N\mathcal {J}E^{\gamma ,N}\right) ||_{L^{2}_{\omega ^{-\alpha ,-\alpha }}(I)}+||\mathcal {J}E^{\gamma ,N}-\mathcal {L}_N\mathcal {J}E^{\gamma ,N}||_{L^{2}_{\omega ^{-\alpha ,-\alpha }}(I)}\nonumber \\&\le \bar{C}||\mathcal {J}E^{\gamma ,N}-\mathcal {L}_N\mathcal {J}E^{\gamma ,N}||_{L^{\infty }(I)}{\le }\bar{C}C_{0,q}N^{-q}||\mathcal {J}E^{\gamma ,N}||_{C^{0,q}}{\le } C_{2,2}\bar{C}C_{0,q} N^{-q}||E^{\gamma ,N}||_{L^{\infty }(I)}, \end{aligned}$$

(74)

where $C_{2,2}$, $\bar{C}$ and $C_{0,q}$ are constants, independent of N. As in Theorem 4.1, it follows that

$$\begin{aligned} ||J_3(z)||_{L^{2}_{\omega ^{-\alpha ,-\alpha }}(I)}\le \left\{ \begin{array}{ll} a_2^{\gamma ,N}\left( |\Phi |_{H^{m,N}_{\omega ^{-\frac{1}{2},-\frac{1}{2}}}(I)}+4MN^{\frac{1}{2}-\alpha }\left( \dfrac{T}{2}\right) ^{\gamma +1} |v|_{H^{m,N}_{\omega ^{-\frac{1}{2},-\frac{1}{2}}}(I)}\right) , &{}0\le \alpha<\frac{1}{2},\\ b_2^{\gamma ,N}\left( |\Phi |_{H^{m,N}_{\omega ^{-\frac{1}{2},-\frac{1}{2}}}(I)}+4M\log N\left( \dfrac{T}{2}\right) ^{\gamma +1} |v|_{H^{m,N}_{\omega ^{-\frac{1}{2},-\frac{1}{2}}}(I)}\right) , &{}\frac{1}{2}\le \alpha <1, \end{array}\right. \end{aligned}$$

(75)

where

$$\begin{aligned} a_2^{\gamma ,N}=C_{2,2}\bar{C}C_{0,q}N^{-q}A_1^{\gamma ,N},~~b_2^{\gamma ,N}=C_{2,2}\bar{C}C_{0,q}N^{-q}B_1^{\gamma ,N}, \end{aligned}$$

where q satisfies (55). The proof is completed by (68)-(75).

Fig. 10

The exact and approximate solutions of Example 3 for $\gamma =0.5$, $\delta =1$ and $N=5$

Fig. 11

The exact and approximate solutions of Example 3 for $\gamma =0.5,0.7,0.9$, $\delta =1$ and $N=5$

Fig. 12

The error of Example 3 for $\gamma =0.8$, $\delta =1$ and $N=4,6,8$

Fig. 13

The error of Example 3 for $\gamma =0.5,0.7,0.9$, $\delta =1$ and $N=5$

Fig. 14

The error of Example 3 for $\gamma =0.5$, $\delta =0.5,1,1.5$ and $N=5$

5 Numerical examples

At present, we solve several nonlinear FDIDEs by proposed method and show the efficiently of the method. For this, consider the following relations for the exact and approximate solutions $X^*(\cdot )$ and $X(\cdot )$ and the exact and approximate derivatives of fractional order ${}_0^CD_t^{\gamma }X^*(\cdot )$ and ${}^C_0D^{\gamma }_tX(\cdot )$

$$\begin{aligned} \left\{ \begin{array}{lll} E^{\gamma ,N}(t_k)=|{}^C_0D^{\gamma }_{t_k}X(t_k)-{}_0^CD_{t_k}^{\gamma }X^*(t_k)|, \quad k=1,2,...,N,\\ E^N(t_k)=|X(t_k)-X^*(t_k)|,\quad k=1,2,...,N. \end{array}\right. \end{aligned}$$

(76)

Example 1

Consider the following nonlinear FDDIE

$$\begin{aligned} \left\{ \begin{array}{ll} {}^C_0D_t^{\gamma }X(t)=X^2(t-0.25)+\int _{0}^tX(\theta )X(\theta -0.25)d\theta +\dfrac{2}{\Gamma (3-\gamma )}t^{2-\gamma } -(t-0.25)^4-\dfrac{48t^5-30t^4+5t^3}{240},\\ ~~0< t\le 1\\ X(t)=\psi (t),~~-0.25\le t\le 0, \end{array}\right. \end{aligned}$$

(77)

where $\psi (t)=t^{2}, t\le 0$. Function $X(t)=t^{2}$ is the exact solution. In the following, we show the corresponding system of (24) for this example

$$\begin{aligned} \left\{ \begin{array}{ll} \Phi _i=\left\{ \begin{array}{ll} \left( \dfrac{1}{2}\right) ^{\gamma }\Bigg [\psi ^2 \left( \dfrac{z_i^{-\alpha ,-\alpha }-0.625}{2}\right) +\dfrac{2}{\Gamma (3-\gamma )}\left( \dfrac{z_i^{-\alpha ,-\alpha }+1}{2}\right) ^{2-\gamma }-\left( \dfrac{z_i^{-\alpha ,-\alpha }+0.5}{2}\right) ^4\\ \quad -\dfrac{3(z_i^{-\alpha ,-\alpha }+1)^5-\frac{15}{8}(z_i^{-\alpha ,-\alpha }+1)^4+\frac{5}{8}(z_i^{-\alpha ,-\alpha }+1)^3}{240}\Bigg ]\\ \quad \quad +\left( \dfrac{z_i^{-\alpha ,-\alpha }+1}{2}\right) \left( \dfrac{1}{2}\right) ^{\gamma +1} \sum _{k=0}^N\sum _{j=0}^Nv_jL_j(\vartheta _1(z_i^{-\alpha ,-\alpha },\tau _k))\psi \left( \frac{1}{2}\vartheta _1(z_i^{-\alpha ,-\alpha },\tau _k)+0.3125\right) \\ \omega _k^{0,0} ~~ i=1,2,...,l_{\bar{\delta }},\\ \left( \dfrac{1}{2}\right) ^{\gamma }\Bigg [\sum _{j=0}^Nv_j L_j^2(z_i^{-\alpha ,-\alpha }-1.625)+\dfrac{2}{\Gamma (3-\gamma )}\left( \dfrac{z_i^{-\alpha ,-\alpha }+1}{2}\right) ^{2-\gamma }-\left( \dfrac{z_i^{-\alpha ,-\alpha }+0.5}{2}\right) ^4\\ \quad -\dfrac{3(z_i^{-\alpha ,-\alpha }+1)^5-\frac{15}{8}(z_i^{-\alpha ,-\alpha }+1)^4+\frac{5}{8}(z_i^{-\alpha ,-\alpha }+1)^3}{240}\Bigg ]\\ \quad \quad +\left( \dfrac{z_i^{-\alpha ,-\alpha }+1}{2}\right) \left( \dfrac{1}{2}\right) ^{\gamma +1} \sum _{k=0}^N\sum _{j=0}^Nv_j^2 L_j(\vartheta _1(z_i^{-\alpha ,-\alpha },\tau _k))L_j(\vartheta _1(z_i^{-\alpha ,-\alpha },\tau _k)-1.625)\\ \omega _k^{0,0}, ~~ i=l_{\bar{\delta }}+1,...,N,\\ \end{array}\right. \\ v_i=\dfrac{1}{\Gamma (\gamma )}\left( \dfrac{z_i^{-\alpha ,-\alpha }+1}{2}\right) ^{\gamma }\sum _{k=0}^N\sum _{j=0}^N\Phi _j L_j\left( \vartheta _1(z_i^{-\alpha ,-\alpha }, \hat{\tau }_k)\right) \omega _k^{-\alpha ,0}, \quad \quad \quad i=0,1,...,N,\\ \end{array}\right. \end{aligned}$$

(78)

where $\vartheta _1(z,\tau )=\frac{1+z}{2}\tau +\frac{z-1}{2}$. The approximate and exact solutions for $\gamma =0.5$, $\delta =0.25$ and $N=5$ are given in Fig. 1. Also, the exact and approximate solutions with $\gamma =0.5,0.7,0.9$, $\delta =0.25$ and $N=5$ are showed in Figure 2. The error for approximate solutions with $\gamma =0.8$, $\delta =0.25$ and $N=3,5,7$ is illustrate in Fig. 3. The error for approximate solutions with $\gamma =0.9,0.99,0.999$, $\delta =0.25$ and $N=5$ is provided in Fig. 4.

Example 2

Consider the following nonlinear FDIDE

$$\begin{aligned} \left\{ \begin{array}{ll} {}^C_0D_t^{\gamma }X(t)=X^2(t-\delta )+\int _0^t X^2(\theta )d\theta +\dfrac{\Gamma (2+\gamma )}{\Gamma (2)}t-(t-\delta )^{2+2\gamma }-\dfrac{t^{2\gamma +3}}{2\gamma +3},~~0< t\le 1,\\ X(t)=\psi (t),~~-\delta \le t\le 0. \end{array}\right. \end{aligned}$$

(79)

where $\psi (t)=t^{1+\gamma },-\delta \le t\le 0$. The exact solution is $X(t)=t^{1+\gamma }$. In Fig. 5, the approximate solutions with $\gamma =0.5$, $\delta =0.25$ and $N=5$ are showed. In Fig. 6, the approximate solutions for $\gamma =0.5,0.7,0.9$, $\delta =0.25$ and $N=5$ are displayed. In Fig. 7, the error of approximate solutions for $\gamma =0.8$, $\delta =0.25$ and $N=4,6,8$ are demonstrated. As we see in Figure 8, the error of approximate solutions are presented for $\gamma =0.5,0.7,0.9$, $\delta =0.25$ and $N=5$. And finally, the error of approximate solutions are displayed in Fig. 9 for $\gamma =0.5$, $\delta =0.2,0.4,0.6$ and $N=5$.

Example 3

Consider the following nonlinear FDIDE

$$\begin{aligned} \left\{ \begin{array}{ll} {}^C_0D_t^{\gamma }X(t)=-X(t)X(t-\delta )+\int _0^t X(\theta )d\theta +\dfrac{\Gamma (2\gamma +1)}{\Gamma (\gamma +1)}t^{\gamma }+t^{2\gamma }(t-\delta )^{2\gamma }-\dfrac{1}{2\gamma +1}t^{2\gamma +1},~~0< t\le 2\\ X(t)=\psi (t),~~-\delta \le t\le 0, \end{array}\right. \end{aligned}$$

(80)

where $\psi (t)=t^{2\gamma },-\delta \le t\le 0$. $X(t)=t^{2\gamma }$ is the exact solution. The approximate and exact solutions for $\gamma =0.5$, $\delta = 1$ and $N=5$ are given in Fig. 10. For $\gamma =0.5,0.7,0.9$, $\delta =1$ and $N=5$, the exact and approximate solutions are demonstrated in Fig. 11. The error with $\gamma =0.8$, $N=4,6,8$ and $\delta =1$ is presented in Fig. 12. The error of approximate solutions for $\gamma =0.5,0.7,0.9$, $\delta =1$ and $N=5$ is showed in Fig. 13. Aslo, The error with $\gamma =0.5$, $N=5$ and $\delta =0.5,1,1.5$ is showed in Fig. 14.

6 Conclusions and suggestions

In this article, we showed that Jacobi-Gauss collocation method can be implemented for solving the nonlinear fractional delay integro-differential equation with a high accuracy. By this method, a system of algebraic equations can be obtained for approximating the solution. Also, we gained the error bounds for approximations in two spaces $L^{\infty }_{\omega ^{\alpha ,\beta }}(I)$ and $L^{2}_{\omega ^{\alpha ,\beta }}(I)$, and illustrated the capability of presented method in numerical simulations.

We will extended the presented method and its convergence analysis for other types of fractional delay problems including nonlinear fractional delay singular integro-differential equations and fractional delay partial differential equations.