1 Introduction

Fractional calculus and its applications in many areas in science and engineering have attracted more intention of research communities [1–4]. As given in [5–8] point out, research carried out in recent years shows that the fractional-order differential equations are an effective tool for describing complex dynamics and many physical and engineering systems can be modeled efficiently using them.

Recent decades have witnessed a fast-growing research on developing applications of variable-order (VO) fractional calculus to diverse scientific and engineering fields. More specifically, VO formulations employed to describe the mechanics of an oscillating mass subjected to a variable viscoelasticity damper and a linear spring [9], to characterize the dynamics of van der Pol equation [10] and history of drag expression [11], to analyze elastoplastic indentation problems [12], to interpolate the behavior of systems with multiple fractional terms [13], to develop a statistical mechanics model [14], to obtain variable- order fractional noise [15] and to design new control algorithms [16, 17]. The VO operator definitions recently proposed in the literature include the Riemann–Liouville, Marchaud, Coimbra and Grunwald definitions [9, 13, 18]. There are several set of definitions for the generalized fractional integration operators among which we adopted the one proposed by Leronzo and Hartley [19], VO fractional integration with strong memory of order, stated as

$$\begin{aligned} _{0+}^{V(.)}J^{\alpha (t)}_{t}y(t)= & {} \int _{0+}^t\frac{1}{\varGamma (\alpha (t,\tau ))} (t-\tau )^{\alpha (t,\tau )-1}y(\tau ) {\mathrm {d}{\tau }},\nonumber \\&{Re}(\alpha (t,\tau ))>0. \end{aligned}$$
(1)

and VO fractional derivative in the Caputo-base, expressed as follows

$$\begin{aligned} _{0+}^{V(.)}D^{\alpha (t)}_{t}y(t)= & {} \int _{0+}^t\frac{1}{\varGamma (\kappa -\alpha (t,\tau ))} \frac{y^\kappa (\tau )\mathrm {d}{\tau }}{(t-\tau )^{\alpha (t)+1-\kappa }},\nonumber \\&{\kappa -1}<\alpha (t)<\kappa . \end{aligned}$$
(2)

where \(\kappa \in {\mathbb {Z}}^{+}, y(t)\) is \((\kappa -1)\) times continuously differentiable, \(y^{(\kappa )}(t)\) is once integrable and \(\varGamma (\cdot )\) is the gamma function.

There are three main type of VO fractional operators that characterized by changing the form of the argument of \(\alpha (t,\tau )\). The following definitions will be considered: \(\alpha (t,\tau )=\alpha (t), \alpha (t,\tau )=\alpha (\tau )\), and \(\alpha (t,\tau )=\alpha (t-\tau )\).

Definition 1.1

The VO fractional integration type 1 (V1) is given by

$$\begin{aligned} _{0+}^{V1}J^{\alpha (t)}_{t}y(t)= & {} \frac{1}{\varGamma (\alpha (t))} \int _{0+}^t(t-\tau )^{\alpha (t)-1}y(\tau ){\mathrm {d}{\tau }},\nonumber \\&{Re}(\alpha (t))>0. \end{aligned}$$
(3)

Definition 1.2

The VO fractional integration type 2 (V2) is given by

$$\begin{aligned} _{0+}^{V2}J^{\alpha (t)}_{t}y(t)= & {} \int _{0+}^t\frac{1}{\varGamma (\alpha (\tau ))}(t-\tau )^{\alpha (\tau )-1} y(\tau ){\mathrm {d}{\tau }},\nonumber \\&{Re}(\alpha (t))>0. \end{aligned}$$
(4)

Definition 1.3

The VO fractional integration type 3 (V3) is given by

$$\begin{aligned} _{0+}^{V3}J^{\alpha (t)}_{t}y(t)= & {} \int _{0+}^t\frac{1}{\varGamma (\alpha (t-\tau ))}(t-\tau )^ {\alpha (t-\tau )-1}\nonumber \\&y(\tau ){\mathrm {d}{\tau }}, \qquad {Re}(\alpha (t))>0. \end{aligned}$$
(5)

More details about these operators and their application can be found in [20, 21].

In VO fractional differential equations (VOFDEs), the order of the derivative changes with respect to either the dependent or the independent variables (or both), or parametrically with respect to an external functional behavior [22, 23]. Since the kernel of the VO operators has variable exponent, analytical solutions for the VOFDEs are more difficult to obtain. These naturally lead to rapid increasing developments of numerical methods for VOFDEs [24–27].

The VO fractional delay differential equation (VOFDDE) is a generalization of the fixed-order delay differential equation to arbitrary functional order. Compared to fractional delay differential equations (FDDEs), VOFDDEs have not received much attention, although the potential to characterize complex behavior by the functional order of differentiation or integration is clear, along with necessary background from the application area, in order to motivate our study of VOFDDEs [28–31].

In this paper, we focus our attention on VOFDDEs that formulated by means of VO integration and derivation with \(\alpha (t,\tau )=\alpha (\tau )\). The importance of this type of VO derivative was recognized recently, and there is a limited knowledge about its application. Ingman and Suzdalnitsky [32] employed type V2 and attempted to create computational algorithms involving satisfactory agreement between the experimental and theoretical distributions of the numerical data in studies of deformation and vibration of systems made from viscoelastic materials resulted in a variety of concepts and models. In [33], Sun et al. the advantage and potential applications of two VO fractional derivate definitions (types V1 and V2) are highlighted through a comparative analysis of anomalous relaxation process. In this line of thought, in [34], Moghaddam and Machado purpose a stable three-level explicit spline finite difference scheme based on the linear B-spline approximation of the time VO fractional derivative of type V2 and the Du FortFrankel algorithm for a class of nonlinear time variable-order fractional partial differential equations.

Having these ideas in mind, the rest of this paper is organized as follows. In Sect. 2, we design an efficient approach for the VO fractional integral based on cubic spline interpolation. In Sect. 3, two numerical examples are included to illustrate the effectiveness of the numerical approach. In Sect. 4, we extend numerical approach for solving a class of nonlinear VOFDDEs. Moreover, we apply the proposed method to the Hutchinson and Ikeda VOFDDEs. In Sect. 4, we outline the main conclusions.

2 Discretization of the VO fractional integral

Throughout the paper, we always assume y(t) a smooth function defined on [a, T], along with the notations \( t_j=a+jh, y(t_j)=y_j, y'(t_j)=y'_j, \alpha (t_j)=\alpha _j\) and \(\beta (t_j)=\beta _j, j=0,1,\ldots ,[(T-a)/h]\), where h denotes the uniform step size and [x] takes the integer part of x, being the maximum integer that does not exceed x.

For the time instant \(t_j, j = 1,\ldots ,N-1\), we need to calculate

$$\begin{aligned} _{a+}^{V2}J^{\alpha (t)}_{t_j}y(t)= & {} \int _{a+}^{t_j}\frac{1}{\varGamma (\alpha (\zeta ))}(t_j-\zeta )^{\alpha (\zeta )-1}y_j(\zeta ) \mathrm {d}\zeta ,\nonumber \\&{Re}(\alpha (t))>0, \end{aligned}$$
(6)

where \(\zeta \) is an auxiliary variable belong to the interval \([a,t_j]\).

We compute the integral by means of a cubic spline \(y_j(\zeta )\), with nodes and knots chosen at instants \(t_k, k = 0,1,2,\ldots ,j-1\). The cubic spline \(y_j(\zeta )\) is of the form

$$\begin{aligned} y_j(\zeta )=\sum _{k=0}^{j}N_{j,k}(\zeta )y_k+\sum _{k=0}^{j} M_{j,k}(\zeta )y'_{k+1}, \end{aligned}$$
(7)

where \(N_{j,k}(\zeta )\) and \(M_{j,k}(\zeta )\) are shape functions and in each interval \([t_{k},t_{k+1}]\), for \(1\le k\le j-1\), given by

$$\begin{aligned} N_{j,k}(\zeta )=\left\{ \begin{array}{ll} (1-2\frac{\zeta -t_{k}}{t_{k}-t_{k+1}}) (\frac{\zeta -t_{k+1}}{t_{k}-t_{k+1}})^2, &{} {t_{k-1}\le \zeta \le t_{k}} \\ (1-2\frac{\zeta -t_{k+1}}{t_{k+1}-t_{k}}) (\frac{\zeta -t_{k}}{t_{k+1}-t_{k}})^2, &{} {t_{k}\le \zeta \le t_{k+1}} \\ 0, &{} \hbox {otherwise} \end{array} \right. , \end{aligned}$$

and

$$\begin{aligned} M_{j,k}(\zeta )=\left\{ \begin{array}{ll} (\zeta -t_{k})(\frac{\zeta -t_{k+1}}{t_{k}-t_{k+1}})^2, &{} {t_{k-1}\le \zeta \le t_{k}} \\ (\zeta -t_{k+1})(\frac{\zeta -t_{k}}{t_{k+1}-t_{k}})^2, &{} {t_{k}\le \zeta \le t_{k+1}} \\ 0, &{} \hbox {otherwise} \end{array} \right. . \end{aligned}$$

For \(k=0\) and \(k=j, N_{j,k}(\zeta )\) is of the form

$$\begin{aligned} N_{j,0}(\zeta )=\left\{ \begin{array}{ll} (1-2\frac{\zeta -t_{1}}{t_{1}-t_{0}})(\frac{\zeta -t_{0}}{t_{1}-t_{0}})^2, &{} {t_{0}\le \zeta \le t_{1}} \\ 0, &{} \hbox {otherwise} \end{array} \right. , \end{aligned}$$

and

$$\begin{aligned} N_{j,j}(\zeta )=\left\{ \begin{array}{ll} (1-2\frac{\zeta -t_{j}}{t_{j}-t_{j+1}}) (\frac{\zeta -t_{j+1}}{t_{j}-t_{j+1}})^2, &{} {t_{j-1}\le \zeta \le t_{j}} \\ 0, &{} \hbox {otherwise} \end{array} \right. , \end{aligned}$$

and for \(k=0\) and \(k=j, M_{j,k}(\zeta )\) is of the form

$$\begin{aligned} M_{j,0}(\zeta )=\left\{ \begin{array}{ll} (\zeta -t_{1})(\frac{\zeta -t_{0}}{t_{1}-t_{0}})^2, &{} {t_{0}\le \zeta \le t_{1}} \\ 0, &{} \hbox {otherwise} \end{array} \right. , \end{aligned}$$

and

$$\begin{aligned} M_{j,j}(\zeta )=\left\{ \begin{array}{ll} (\zeta -t_{j})(\frac{\zeta -t_{j+1}}{t_{j}-t_{j+1}})^2, &{} {t_{j-1}\le \zeta \le t_{j}} \\ 0, &{} \hbox {otherwise} \end{array} \right. . \end{aligned}$$

Therefore, substituting (7) into (6) gives

(8)

and after some calculations, we obtain

(9)

where

$$\begin{aligned} a_{j,k}=\left\{ \begin{array}{l@{\quad }l} -6(2j+1+\alpha _0)(-1+j)^{\alpha _0+2}\\ +j^{\alpha _0}((-6\alpha _0-18)j^2+12j^3+\alpha _0^3 +6\alpha _0^2+11\alpha _0+6), &{} {k=0} \\ 6((j-k-1)^{\alpha _j+2}(2k-2j-\alpha _k-1)\\ \qquad +(j-k+1)^{\alpha _j+2}(2k-2j-\alpha _k+1+4(j-k)^{\alpha _k+3})), &{} {1\le k\le n-1} \\ 6(\alpha _j+1), &{} {k=n} \end{array} \right. , \end{aligned}$$
(10)
Fig. 1
figure 1

The numerical approximation of the VO integral of function \(y(t)=t^4\) (left) and magnitude of the \(\log _{10}\)(AE) (right), with various values of \(\alpha (t)\) and step size \(h=0.01\) in the interval \(t\in [0,5]\)

Full size image

and

$$\begin{aligned} b_{j,k}=\left\{ \begin{array}{l@{\quad }l} -(6j+2\alpha _0)(j-1)^{\alpha _0+2}+(\alpha _0^2+(-4j+5)\alpha _0+6(-1+j))j^{\alpha _0+1}, &{} {k=0} \\ 2(3k-3j-\alpha _k)(j-k-1)^{\alpha _k+2}\\ \qquad -2(3k-3j+\alpha _k)(j-k+1)^{\alpha _k+2} -8(j-k)^{\alpha _k+2}(\alpha _k+3), &{} {1\le k\le n-1} \\ -2\alpha _j, &{} {k=n} \end{array} \right. . \end{aligned}$$
(11)

Thus, we get the following discretization formula for the VO fractional integral.

Proposition 2.1

Let y(t) be a function in \(C^{4}[a,T]\) and \(Re(\alpha (t))>0\). Then

$$\begin{aligned} _{a+}^{V2}J^{\alpha (t)}_{t_j}y(t)= & {} \sum _{k=0}^{j}\frac{h^{\alpha _k}}{\varGamma (\alpha _k+4)}a_{j,k}y_k\nonumber \\&+\sum _{k=0}^{j} \frac{h^{\alpha _k+1}}{\varGamma (\alpha _k+4)}b_{j,k}y'_k+ \mathcal {E}_{V2}(t_{j}),\nonumber \\ \end{aligned}$$
(12)

where \(\mathcal {E}_{V2}(t_{j})\) is the approximation error at \(t_{j}\) and is bounded by

$$\begin{aligned} |\mathcal {E}_{V2}(t_{j})|\le \frac{(t_j-a)^{\alpha ^*}|{y^{(4)}(t_j)}|}{\varGamma (\alpha ^*+1)}O(h^4), \end{aligned}$$
(13)

where \(j=1,\ldots ,\left[ \frac{(T-a)}{h}\right] \) and

$$\begin{aligned}\alpha ^*=\left\{ \begin{array}{ll} \sup \{\alpha (t)|\alpha (t)>0,t\in {\mathbb {R}}^+\}, &{} {\texttt {if} \qquad t_{j}\le 1} \\ \inf \{\alpha (t)|\alpha (t)>0,t\in {\mathbb {R}}^+\}, &{} {\texttt {if} \qquad t_{j}>1}\\ \end{array} \right. . \end{aligned}$$

3 The numerical method based on cubic spline approximation

In this section, we consider the following initial value problem (IVP) for VOFDDE:

$$\begin{aligned} \left\{ \begin{array}{l@{\quad }l} _{0+}^{V2}D^{\alpha (t)}_{t}y(t)=f(t,y(t),y(t-\tau )), &{} {{t>0}} \\ y(t)=\phi (t), &{} {-\tau {\le }t\le 0} \end{array} \right. ,\nonumber \\ \end{aligned}$$
(14)

where \(\kappa -1<\alpha (t){\le }\kappa , \tau \) is the delay time and \(\phi (t)\) is the history function defined on the interval \(t\in [-\tau ,0]\). The existence and uniqueness of solution for Eq. (14) was investigated by Parsa et al. [35]. This form of nonlinear delayed system is a very general one and includes all well-known delayed systems such as Ikeda system [36], Mackey and Glass system [37], Hopfield delayed neural network [38], delayed Duffing system [39], Delayed Lorenz system [40], BAM neural network [36] and cellular neural network [41].

Fig. 2
figure 2

Magnitude of the \(\log _{10}\)(MAE) for approximate VO integral of function \(y(t)=t^4\) for various values of \(\alpha (t)\) and step size \(h=0.01\) in the interval \(t\in [0,T_n=0.25n]\) where \(n=1,\ldots ,20\)

Full size image
Fig. 3
figure 3

The numerical approximation of the VO integral of function \(y(t)=t^2\cos (t)\) (left) and magnitude of the \(\log _{10}\)(AE) (right), with various values of \(\alpha (t)\) and step size \(h=0.01\) in the interval \(t\in [0,5]\)

Full size image
Table 1 Comparison of MAE, ECO and E-time for approximate VO integral of function \(y(t)=t^4\) for various values of \(\alpha (t)\) and different step sizes in the interval \(t\in [0,5]\)
Full size table
Fig. 4
figure 4

Magnitude of the \(\log _{10}\)(MAE) for approximate VO integral of function \(y(t)=t^4\) for various values of \(\alpha (t)\) and step size \(h=0.01\) in the interval \(t\in [0,T_n=0.25n]\) where \(n=1,\ldots ,20\)

Full size image
Table 2 Comparison of MAE, ECO and E-time for integral VO derivative of function \(y(t)=t^2\cos (t)\) for various values of \(\alpha (t)\) and different step sizes in the interval \(t\in [0,5]\)
Full size table

It is easily noted that Eq. (14) can be transformed to Abel–Volterra integral equation

$$\begin{aligned} y(t)= & {} T_{\kappa -1}[y;0](t)+{_{0+}^{V2}J^{\alpha (t)}_{t}}f(t,y(t),\nonumber \\&y(t-\tau )), \end{aligned}$$
(15)

where

$$\begin{aligned}&T_{\kappa -1}[y;0](t)=\sum _{j=0}^{\kappa -1}\phi ^{(j)}(0)\frac{t^j}{j!},\\&_{0+}^{V2}J^{\alpha (t)}_{t}f(t,y(t), y(t-\tau ))\\&\quad =\int _{0+}^{t}\frac{1}{\varGamma (\alpha (\zeta ))} (t-\zeta )^{\alpha (\zeta ))-1} f(\zeta ,y(\zeta ),y(\zeta -\tau ))\mathrm {d}\zeta . \end{aligned}$$

For solving (15) on [0, T], the interval \([-\tau ,T]\) is divided into \(m+n\) subintervals, where m and n are integers such that \(m=\frac{\tau }{h}, n=\frac{T}{h}\) and \(t_j=jh, j=-m,-m+1,\ldots ,-1,0,1,,\ldots ,n\).

Table 3 Model 1: Comparison of MAE, for various values of \(\alpha (t)\) and \(a = 0.3, \tau =1, T = 25\) and different step sizes h
Full size table
Table 4 Model 1: Comparison of ECO, for various values of \(\alpha (t)\) and \(a=0.3, \tau =1, T=25\) and different step sizes h
Full size table

The discretized version of (15) is given as

$$\begin{aligned} y_n= & {} T_{\kappa -1}[y;0](t_n)\nonumber \\&+\int _{0+}^{t_n}\frac{1}{\varGamma (\alpha (\zeta ))} (t-\zeta )^{\alpha (\zeta ))-1}\nonumber \\&\times \,f(\zeta ,y(\zeta ), y(\zeta -\tau ))\mathrm {d}\zeta . \end{aligned}$$
(16)

Applying proposed technique in the Sect. 2 to the above equation yields

$$\begin{aligned} y_n= & {} T_{\kappa -1}[y;0](t_n)\nonumber \\&+\sum _{j=0}^{n} \frac{h^{\alpha _j}}{\varGamma (\alpha _j+4)}a_{n,j}f(t_j,y_j,y_{j-m})\nonumber \\&+\sum _{j=0}^{n}\frac{h^{\alpha _j+1}}{\varGamma (\alpha _j+4)}b_{n,j}f'(t_j,y_j,y_{j-m}) \end{aligned}$$
(17)

where the coefficients \(a_{n,j}\) and \(b_{n,j}\) are given by (10) and (11), respectively.

For this method, since both side of Eq. (17) include the unknown variable \(y_n\), and due to the nonlinearity of the functions f and \(f'\), it is difficult to derive \(y_n\). Therefore, to achieve a better approximate solution, we substitute a predicted value \(y_n\) into the right-hand side of (14).

Fig. 5
figure 5

Time response for Eq. (22), for various values of \(\alpha (t)\), with \(a=1.4, \tau =1\) and step size \(h=\frac{1}{16}\)

Full size image
Fig. 6
figure 6

Time response (left) and phase-space solution (right) for Eq. (22), with \(\alpha (t)=1, a=1.7, \tau =1\) and step size \(h=\frac{1}{16}\)

Full size image
Fig. 7
figure 7

Time response (left) and phase-space solution (right) for Eq. (22), with \(\alpha (t)=0.7, a=1.7, \tau =1\) and step size \(h=\frac{1}{16}\)

Full size image
Fig. 8
figure 8

Time response (left) and phase-space solution (right) for Eq. (22), with \(\alpha (t)=1-0.003t, a=1.7, \tau =1\) and step size \(h=\frac{1}{16}\)

Full size image
Fig. 9
figure 9

Time response (left) and phase-space solution (right) for Eq. (23), with \(\alpha (t)=1, \lambda =0, \mu =1, \tau =4, \varphi _0=2.988\) and step size \(h=\frac{1}{16}\)

Full size image
Fig. 10
figure 10

Time response (left) and phase-space solution (right) for Eq. (23), with \(\alpha (t)=0.75, \lambda =0, \mu =1, \tau =4, \varphi _0=2.988\) and step size \(h=\frac{1}{16}\)

Full size image
Fig. 11
figure 11

Time response (left) and phase-space solution (right) for Eq. (23), with \(\alpha (t)=1-0.0025t, \lambda =0, \mu =1, \tau =4, \varphi _0=2.988\) and step size \(h=\frac{1}{16}\)

Full size image

Let \(y_n^p\) be the predicted value, which can be obtained by some simple explicit method. For instance, here we use VO fractional Adams–Bashforth method to drive the predicted value

$$\begin{aligned} y_{n}^{p}=\sum _{j=0}^{\kappa -1}{\phi ^{(j)}(0) \frac{t_{n}^j}{j!}}+\sum _{j=0}^{n}c_{j,n}f(t_{j},y_{j},y_{j-m}), \end{aligned}$$
(18)

where

$$\begin{aligned} c_{j,n}= & {} \frac{h^{\alpha _j}}{\varGamma (\alpha _{j}+1)}((n-j)^{\alpha _j}-(n-j-1)^{\alpha _j}),\nonumber \\&\quad 0\le j\le n. \end{aligned}$$

Ultimately, replacing \(y_n^p\) in the right-hand side of (14) by (15) gives

$$\begin{aligned} y_{n+1}= & {} \sum _{j=0}^{\kappa -1}{\phi ^{(j)}(0)\frac{t_{n}^j}{j!}} +\frac{6(\alpha _n+1)h^{\alpha _n}}{\varGamma (\alpha _n+4)} f(t_{n},y_{n}^{p},y_{n-m})\nonumber \\&-\frac{2{\alpha _n}h^{\alpha _n}}{\varGamma (\alpha _n+4)}f'(t_{n},y_{n}^{p},y_{n-m})\nonumber \\&+\sum _{j=0}^{n-1}\frac{h^{\alpha _j}}{\varGamma (\alpha _j+4)} a_{n,j}f(t_j,y_j,y_{j-m})\nonumber \\&+\sum _{j=0}^{n-1} \frac{h^{\alpha _j+1}}{\varGamma (\alpha _j+4)}b_{n,j}f'(t_j,y_j,y_{j-m}). \end{aligned}$$
(19)
Table 5 Model 2: Comparison of MAE, for various values of \(\alpha (t)\) and \(\lambda =\mu =0.4, \tau =0.5, \varphi _0=\frac{\pi }{2}, T=25\) and different step sizes h
Full size table
Table 6 Model 2: Comparison of ECO, for various values of \(\alpha (t)\) and \(\lambda =\mu =0.4, \tau =0.5, \varphi _0=\frac{\pi }{2}, T=25\) and different step sizes h
Full size table

4 Numerical illustrative examples

In this section, we demonstrate the efficiency and accuracy of the proposed method. For this purpose, we can analyze its accuracy and computational efficiency, in the view point of the mean absolute error (MAE) defined as

$$\begin{aligned} MAE=\frac{1}{N}\sum _{i=1}^{N}AE, \end{aligned}$$
(20)

where \(AE=|y_i^N-y_{2i}^{2N}|, y_i^N\) and \(y_{2i}^{2N}\) are approximate values of y(t) in \(t_i\) and N denotes the number of interior mesh points. Furthermore, we apply the measure

$$\begin{aligned} ECO = \frac{\log (MAE)}{\log (h)}, \end{aligned}$$
(21)

where h denotes the uniform step size, for estimating the experimental convergence order (ECO). Note that an optimal step size can only be defined in relation to a given error tolerance. This pre-assigned value of the error, which is under the user control, will be regarded as the user-imposed tolerance.It is worth mentioning that all the numeric computations are performed by Maple v18 and the results were generated on a desktop PC with an AMD Athlon 64 X2 Dual Core Processor 5200+@2.6 GHz. For measuring the computational load, we obtain the elapsed time “E-time.” The E-time is independent of the CPU time, includes the simplification of data structures and shows the duration from when the process starts until the time it terminates with units in seconds.

4.1 Approximation of VO fractional integrals

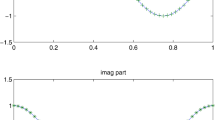
In this subsection, the efficiency and numerical accuracy of proposed method are illustrated by two test examples. We adopt a numerical discretization formula (12) to approximate the VO fractional integral for a given functions \(y(t)=t^4\) and \(y(t)=t^2\cos (t)\). Figures 1 and 3 show the VO fractional integrals of the functions \(y(t)=t^4\) and \(y(t)=t^2\cos (t)\) and the magnitude of the AEs for various values of \(\alpha (t)\) with uniform step size \(h = 0.01\) in interval \(t\in [0,5]\). The computational results presented in Tables 1 and 2 reveal that if we increase the number of mesh points, then the MAE becomes smaller and we get a better approximation. Figures 2 and 4 show that when the time interval becomes larger, the values of MAE increase for constant step size. Therefore, to control the value of MAE, it is necessary; we reduced the step size by larger time interval. Furthermore, it is clear from Tables 1 and 2 that the proposed method has a fast convergence.

4.2 Applications

Since Mackey and Glass in 1977 [37] found chaotic behavior in a delay differential equation model of blood production in patients with leukemia, chaotic time-delay systems have been employed in numerous other practical applications in engineering, biology, economy and other disciplines [42–45].

On the other hand, delay estimation has a variety of widespread applications from satellite orbit determination to radar systems and secure communications. In addition, delay estimation has a critical role in climate prediction. A good the time-delay estimate can be a means to achieve a good model, which results in a good stability analysis [46] or control design.

In this subsection, we concentrate on the two VO fractional mathematical modeling of nonlinear dynamics, Hutchinson and Ikeda equations. The dynamical behavior of the models is studied numerically for fixed-order and VO fractional derivatives. To demonstrate the accuracy and efficiency of the proposed method, we use monotonic solutions for considered models and list results in the tables. Using a phase plane analysis, both periodic and chaotically behaving solutions are found and show the effect of VO on the dynamics behavior of the models.

Model 1 The VO fractional Hutchinson equation: Hutchinson incorporated the effect of delays into the logistic equation [47, 48]. Delays bring about interesting topological changes in the population size like damped oscillations, limit cycles and even chaos [49]. We modified the Hutchinsons equation or delay logistic equation and represent as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} ^{V2}_{0+}D^{\alpha (t)}_{t}y(t)=ay(t)(1-y(t-\tau )), &{} {0<\alpha (t)\le 1, 0<t<T} \\ y(t)=0.1, &{} {-\tau \le t\le 0} \end{array} \right. ,\!\!\!\!\!\!\nonumber \\ \end{aligned}$$
(22)

where \(a>0\) is the parameter and \(\tau \) is the delay time.

For comparative study, in Tables 3 and 4 the MAE and the ECO for various values of \(\alpha (t)\) and different step sizes are listed. Decreasing the step size, one can obtain highly accuracy approximation solution to (22). Figure 5 shows the time history of the damped oscillatory solutions of (22) by using the proposed method for various values of \(\alpha (t)\) with \(a=1.4, \tau =1\) and step size \(h=\frac{1}{16}\). The results show that by using the suitable VO fractional derivative functions, \(\alpha (t)\), the amplitude of oscillation is reduced and damped gradually with time. In Figs. 6, 7 and 8, we depict the time responses and the phase-space solutions of the Eq. (22) with \(a=1.7, \tau =1\) and step size \(h=\frac{1}{16}\) for \(\alpha (t)=1, \alpha (t)=0.7\) and \(\alpha (t)=1-0.003t\), respectively.

Model 2 The VO fractional Ikeda equation: The Ikeda system [50–52] was introduced to describe the dynamics of an optical bistable resonator, and the time taken for the round trip of the light across the resonator is considered as the delay time \(\tau \). The VO fractional Ikeda equation states as

$$\begin{aligned} \left\{ \begin{array}{ll} ^{V2}_{0+}D^{\alpha (t)}_{t}y(t)=\mu \sin (y(t-\tau ))-{\lambda }y(t), &{} {0{<}\alpha (t)\le 1, 0{<}t{<}T} \\ y(t)=\varphi _0, &{} {-\tau \le t\le 0} \end{array} \right. ,\!\!\!\!\nonumber \\ \end{aligned}$$
(23)

where \(\lambda >0\) and \(\mu >0\) are the parameters and \(\tau \) is the delay time.

Physically, y(t) represents the phase lag of the electric field across the resonator, \(\mu \) is the light intensity injected into the system, \(\tau \) is the feedback delay time in the resonator and \(\lambda \) is the relaxation coefficient.

We assume that \(\alpha (t)=1-0.0025t\) and we study the dynamic behavior of Eq. (23) in the interval [0, 100]. It obvious the function \(\alpha (t)=1-0.0025t\) is decreasing function and \(\alpha (t)\in [0.75,1]\). As shown in Figs. 9, 10 and 11, decreasing value of VO function \(\alpha (t)\) from 1 to 0.75, we observe the transition from a integer-order (\(\alpha (t)=1\)) behavior to a fixed-order (\(\alpha (t)=0.75\)) behavior. MAE and ECO for Eq. (23) for various values of \(\alpha (t)\) and different step sizes h, calculated by means of proposed algorithm using embedding delay \(\tau =4\) and embedding \(\lambda =\mu =0.4\) and \(T=25\), along with the initial condition \(y(t)=\frac{\pi }{2}\) in the range \(t\in (-\tau ,0)\) are summarized in Tables 5 and 6.

5 Conclusion

In this paper, a new numerical discretization formula, based on the cubic spline interpolation for approximating the VO fractional integral, is introduced and implemented. By adopting the approximation formula, we obtained a predictor–corrector method for the numerical solution of a class of nonlinear VOFDDEs. Several illustrative VO fractional models of nonlinear dynamics are solved by new method, and the results are analyzed using phase portraits. The numerical experiments demonstrated the high accuracy and the fast convergence of the new scheme. Moreover, the results reveal that VO can act as a modulation parameter that may useful for better describing and chaos controlling of dynamic systems with time delay.