1 Introduction

Digital signature (DS) schemes are widely used in information technologies for solving different tasks of insuring information security (Rivest et al. 1978, ElGamal 1985). A particular type of the signature schemes, called blind signatures (Chaum 1983, Chaum 1988), represent a special interest for application in electronic cash systems and in electronic secret-voting systems. Specific requirements to the blind DS protocols are: (1) the signer has no access to the document during the procedure of forming the signature; (2) the signer does not have the ability to find a correlation of the signed document with the act of signing (anonymity or untraceability requirement).

A variety of different known DS schemes can be used to satisfy the first requirement. To do this, it is enough to accept the agreement that the signature to the document is formed as a signature to the hash function calculated from the document. The first requirement is a necessary condition for the feasibility of the second requirement. To implement a DS protocol satisfying the second requirement a specific method is used, that consists in using a blinding factor (or factors) during the process of the signature generation.

The participants of a blind DS protocol are the signer and the requester (client) who has prepared some electronic document for signing. Protocols of such type are supposed to be used in information technologies where the signer performs signing of many documents provided by many different clients. The intention of the requester is to obtain a genuine signature of the signer to the document in such a way that in the future, when the signed document is presented to the signatory, the latter will not be able to identify which of the clients is associated with this document.

The first blind signature protocol (Chaum 1983) was developed on the basis of the RSA signature scheme (Rivest et al. 1978) that is based on the computational difficulty of the factoring problem (FP). Subsequently, blind DS protocols based on the computational difficulty of the discrete logarithm problem (DLP) have been proposed (Camenisch 1995). In the first case the anonymity of the requester is ensured by his introducing one blinding factors into the blind signature. In the second case the anonymity is ensured by requester’s introducing two blinding factors into the blind signature. The protocols are designed so that after receiving a blind signature from the signer, the requester can possibility to remove the blinding factors, thereby obtaining a genuine signature.

Like in the case of modern DS standards and other DS schemes of wide use, which are based on computational difficulty of FP and DLP, the said blind signature protocols will be insecure in coming post-quantum era (Yan 2014, Ding and Steinwandt 2018) when quantum attacks will become possible in practice. An attack on a cryptographic scheme is called quantum, if it uses both the ordinary and quantum computers. A cryptoscheme is called post-quantum, if it performs efficiently on ordinary computers and resists quantum attacks.

Post-quantum cryptographic algorithms and protocols should be based on the computationally difficult problems that are different from the FP and the DLP, since for solving them there are known polynomial algorithms (Shor 1997, Smolin et al. 2013). Quantum method for solving FP and DLP exploits (1) extreme efficiency of performing a discrete Fourier transform of a periodic function taking on values in an explicitly given finite cyclic group and (2) reduction of each of the mentioned two problems to problem of finding a period length of a periodic function (Jozsa 1988, Ekert and Jozsa 1996).

A response to such a challenge in the field of applied and theoretical cryptography was the announcement by the US National Institute of Standards and Technology (NIST) in December 2016 of a program of adopting post-quantum cryptographic standards of public-key agreement and digital signature schemes by 2024 (NIST 2016). A worldwide competition for the development of post-quantum public-key cryptoschemes had been started as a core part of that program (NIST 2020). The NIST program does not provide for the development of post-quantum blind signature protocols. However, this task is quite important and interesting.

The present paper is devoted to development of a practical post-quantum blind signature scheme based on computational difficulty of so called hidden discrete logarithm problem (HDLP). Next Sect. 2 describes in brief the concept of HDLP as a post-quantum cryptographic primitive and finite associative algebras (FAAs) as algebraic support of the HDLP-based public key cryptoschemes. Section 3 introduces the initial HDLP-based signature scheme suitable for transformation into a blind signature scheme. A novel 4-dimensional FAA with 4-dimensional cyclicity is used as algebraic support of the developed signature scheme. Section 4 proposes a practical post-quantum blind signature protocol using four blinding factors and a public key representing a triple of 512-bit integers. Section 5 presents discussion and Sect. 6 concludes the paper.

2 Preliminaries

The HDLP appears to be one of attractive cryptographic primitives for development of practical post-quantum public-key cryptoschemes. On the base of the HDLP, public-key agreement protocols (Kuzmin et al. 2017, Moldovyan-Dmitriy 2019), commutative encryption algorithms (Modovyan-Dmitriy et al. 2020, Modovyan-Nikolay and Modovyan-Alexander 2019), and DS schemes (Modovyan-Nikolay and Abrosimov 2019, Modovyan-Nikolay and Modovyan-Alexander 2020) had been designed. To reveal the concept of HDLP, consider the definition of DLP.

The latter is usually set in a given finite cyclic group of prime order q as finding the unknown value of the integer x in the equation Y′ = G′x, where G′ is a generator of the group. The HDLP is set in a finite algebraic structure containing a very large number of different cyclic groups as different subsets of algebraic elements. One of such groups is selected at random and is secret, for example, the cyclic group generated by an element G. A random non-negative integer x < q is generated and the value Y′ = Gx is calculated. Then the values Y′ and G are mapped into the elements Y = α(Y′) and Z = β(G), where α(⋅) and β(⋅) are masking operations possessing property of mutual commutativity with the exponentiation operation. Parameters of the masking operations are secret. The HDLP consists in finding the value x when the elements Y and Z are given. Different forms of the HDLP are introduced for development of different public key. In some particular forms of the HDLP only one of the values Y′ and G is masked (Kuzmin et al. 2017, Moldovyan-Dmitriy 2010).

Finite associative algebras are used as algebraic supports of the HDLP-based cryptoschemes. An arbitrary vector A of some finite m-dimensional vector space defined over a finite field, for example over a ground field GF(p), can be written as an ordered set of elements of the field GF(p): A = (a0, a1, …, am − 1) or as a sum of its component: \(A = \sum\nolimits_{i = 0}^{m - 1} {a_{i} {\text{e}}_{i} ,}\) where ei are basis vectors; ai ∈ GF(p) are coordinated of the vector. A vector space in which, in addition to the operations of addition of vectors and multiplication of a vector by a scalar, an operation of multiplication of two vectors (the vector multiplication) is defined, which has the property of distributivity with respect to the operation of addition, is called algebra.

The vector multiplication operation \(A = \sum\nolimits_{i = 0}^{m - 1} {a_{i} {\text{e}}_{i} }\) and \(B = \sum\nolimits_{j = 0}^{m - 1} {b_{j} {\text{e}}_{j} }\) is usually determined by the rule of multiplying each component of the first vector with each component of the second vector, namely, by the following formula:

$$A \circ B = \sum\nolimits_{i = 0}^{m - 1} {\sum\nolimits_{j = 0}^{m - 1} {a_{i} b_{j} \left( {e_{i} \circ e_{j} } \right)} ,}$$
(1)

in which every product of the form \({\text{e}}_{i} \circ {\text{e}}_{j}\) must be replaced by a one-component vector λek, selected from the so-called multiplication table of basis vectors (MTBV), where λ ∈ GF(p) is called structural constant. In the case λ = 1 only basis vector ek is indicated in the MTBV. Left multiplier in the product \({\text{e}}_{i} \circ {\text{e}}_{j}\) specifies the row and the right one specifies the column, the intersection of which indicates the cell containing the value λek.

Taking into account the formula (1) one can prove that the defined vector multiplication operation is associative, if the used MTBV is such that the following equality holds true:

$$\left( {{\mathbf{e}}_{i} \circ {\mathbf{e}}_{j} } \right) \circ {\mathbf{e}}_{k} = {\mathbf{e}}_{i} \circ \left( {{\mathbf{e}}_{j} \circ \;{\mathbf{e}}_{k} } \right)$$
(2)

for all possible triples (ei, ej, ek). Note also that the defined vector multiplication and scalar multiplication by a scalar ψ are mutually commutative: ψ(A o B) = (ψA) o B = A o (ψB).

If the vector multiplication operation, defined by a MTBV, has the properties of non-commutativity and associativity, then the case of specifying a non-commutative FAA is realized. Most of the different known forms of the HDLP had been proposed for non-commutative algebras used as algebraic support of the developed cryptoschemes. The paper (Modovyan-Nikolay and Modovyan-Alexander 2019) introduced a unified method for setting non-commutative FAAs of arbitrary even dimensions m ≥ 2. The paper (Modovyan-Nikolay 2020) introduced another unified method for setting other type non-commutative FAAs of arbitrary even dimensions m > 4. For the case m > 4, the latter method defines a commutative FAA possessing multidimensional cyclicity. That 4-dimensional FAA was used in the paper (Minh et al. 2020) to define for the first time the HDLP in commutative algebras. The concept of multidimensional cyclicity was proposed in (Modovyan-Nikolay and Modovyanu-Peter 2009) as follows: a commutative finite group generated by a minimum generator system containing μ ≥ 2 elements of the same order is called a group possessing μ-dimensional cyclicity.

In present paper another form of the HDLP is set in a commutative FAA for developing a post-quantum signature scheme that is suitable for developing on its base a post-quantum blind signature protocol. Like in the case of the DS scheme from (Minh et al. 2020), the proposed form of the HDLP exploits the multidimensional structure of the commutative FAA used as algebraic support. However, the proposed form implements another criterion of post-quantum security than that implemented in (Minh et al. 2020). This difference gives possibility to design a signature scheme that is free from doubling the verification equation. Due to the last one has possibility to develop a HDLP-based blind signature protocol, in addition the signature has a smaller size. Besides, a new 4-dimensional commutative FAA is used as algebraic support of the introduced HDLP and developed signature schemes.

3 Initial Signature Scheme

3.1 The Used Algebraic Support

The 4-dimensional commutative FAA used as algebraic support is defined over the ground field GF(p) by MTBV shown as Table 1.

Table 1 Setting a 4-dimensional FAA possessing multidimensional cyclicity (λ = 4)
Full size table

Proposition 1

The vector multiplication operation defined by Table 1 is associative.

Proof

Note that the Table 1 is described by the following formula:

$$e_{i} \circ e_{j} = \left\{ {\begin{array}{*{20}c} {e_{i + j - 2\bmod 4} ,\;\;\;\;\;\;\;if\,\;i\bmod 2 = 0;} \\ {e_{i - j + 2\bmod 4} ,\;\,\,\,\,\,\,\,\,\,if\;\;i\bmod 2 = 1.} \\ \end{array} } \right.$$
(3)

Consider the product of arbitrary three vectors A, B and \(C = \sum\nolimits_{k = 0}^{m - 1} {c_{k} {\text{e}}_{k} ,}\) which is performed in correspondence with Table 1:

$$\begin{aligned} \left( {A \circ B} \right) \circ C = & \left( {\sum\limits_{i = 0}^{3} {\sum\limits_{j = 0}^{3} {a_{i} b_{j} {\text{e}}_{i} \circ {\text{e}}_{j} } } } \right) \circ \sum\limits_{k = 0}^{3} {c_{k} {\text{e}}_{k} } \\ & = \sum\limits_{i = 0}^{3} {\sum\limits_{j = 0}^{3} {\sum\limits_{k = 0}^{3} {a_{i} b_{j} c_{k} \left( {{\text{e}}_{i} \circ {\text{e}}_{j} } \right) \circ {\text{e}}_{k} } } } ; \\ \end{aligned}$$
(4.1)
$$\begin{gathered} A \circ \left( {B \circ C} \right) = \left( {\sum\limits_{i = 0}^{3} {a_{i} {\text{e}}_{i} } } \right) \circ \left( {\sum\limits_{j = 0}^{3} {\sum\limits_{k = 0}^{3} {b_{j} c_{k} {\text{e}}_{i} \circ {\text{e}}_{j} } } } \right) \hfill \\ = \sum\limits_{i = 0}^{3} {\sum\limits_{j = 0}^{3} {\sum\limits_{k = 0}^{3} {a_{i} b_{j} c_{k} {\text{e}}_{i} \circ \left( {{\text{e}}_{j} \circ {\text{e}}_{k} } \right)} } } . \hfill \\ \end{gathered}$$
(4.2)

The right parts in formulas (4.1) and (4.2) are equal, if equality (2) holds true for all possible triples of indices (i, j, k). Since the value of k does not influence on selection of one of two formulas in the right part of the expression (3), one should consider only the following four cases:

Case 1 i and j are even numbers.

$$\begin{gathered} \left\{ {\begin{array}{*{20}c} {\left( {{\text{e}}_{i} \circ {\text{e}}_{j} } \right) \circ {\text{e}}_{k} = {\text{e}}_{i + j - 2} \circ {\text{e}}_{k} = {\text{e}}_{i + j - 2 + k - 2} = {\text{e}}_{i + j + k} } \\ {{\text{e}}_{i} \circ \left( {{\text{e}}_{j} \circ {\text{e}}_{k} } \right) = {\text{e}}_{i} \circ {\text{e}}_{j + k - 2} = {\text{e}}_{i + j + k - 2 - 2} = {\text{e}}_{i + j + k} } \\ \end{array} } \right\} \Rightarrow \hfill \\ \Rightarrow \left( {{\text{e}}_{i} \circ {\text{e}}_{j} } \right) \circ {\text{e}}_{k} = {\text{e}}_{i} \circ \left( {{\text{e}}_{j} \circ {\text{e}}_{k} } \right). \hfill \\ \end{gathered}$$

Case 2 i is odd; j is even.

$$\begin{gathered} \left\{ {\begin{array}{*{20}c} {\left( {{\text{e}}_{i} \circ {\text{e}}_{j} } \right) \circ {\text{e}}_{k} = {\text{e}}_{i - j + 2} \circ {\text{e}}_{k} = {\text{e}}_{i - j + 2 - k + 2} = {\text{e}}_{i - j - k} } \\ {{\text{e}}_{i} \circ \left( {{\text{e}}_{j} \circ {\text{e}}_{k} } \right) = {\text{e}}_{i} \circ {\text{e}}_{j + k - 2} = {\text{e}}_{i - j - k + 2 + 2} = {\text{e}}_{i - j - k} } \\ \end{array} } \right\} \Rightarrow \hfill \\ \Rightarrow \left( {{\text{e}}_{i} \circ {\text{e}}_{j} } \right) \circ {\text{e}}_{k} = {\text{e}}_{i} \circ \left( {{\text{e}}_{j} \circ {\text{e}}_{k} } \right). \hfill \\ \end{gathered}$$

Case 3 i is even; j is odd.

$$\begin{gathered} \left\{ {\begin{array}{*{20}c} {\left( {{\text{e}}_{i} \circ {\text{e}}_{j} } \right) \circ {\text{e}}_{k} = {\text{e}}_{i + j - 2} \circ {\text{e}}_{k} = {\text{e}}_{i + j - 2 - k + 2} = {\text{e}}_{i + j - k} } \\ {{\text{e}}_{i} \circ \left( {{\text{e}}_{j} \circ {\text{e}}_{k} } \right) = {\text{e}}_{i} \circ {\text{e}}_{j - k + 2} = {\text{e}}_{i + j - k + 2 - 2} = {\text{e}}_{i + j - k} } \\ \end{array} } \right\} \Rightarrow \hfill \\ \Rightarrow \left( {{\text{e}}_{i} \circ {\text{e}}_{j} } \right) \circ {\text{e}}_{k} = {\text{e}}_{i} \circ \left( {{\text{e}}_{j} \circ {\text{e}}_{k} } \right). \hfill \\ \end{gathered}$$

Case 4: i and j are odd numbers.

$$\begin{gathered} \left\{ {\begin{array}{*{20}c} {\left( {{\text{e}}_{i} \circ {\text{e}}_{j} } \right) \circ {\text{e}}_{k} = {\text{e}}_{i - j + 2} \circ {\text{e}}_{k} = {\text{e}}_{i - j + 2 + k - 2} = {\text{e}}_{i - j + k} } \\ {{\text{e}}_{i} \circ \left( {{\text{e}}_{j} \circ {\text{e}}_{k} } \right) = {\text{e}}_{i} \circ {\text{e}}_{j - k + 2} = {\text{e}}_{i - j + k - 2 + 2} = {\text{e}}_{i - j + k} } \\ \end{array} } \right\} \Rightarrow \hfill \\ \Rightarrow \left( {{\text{e}}_{i} \circ {\text{e}}_{j} } \right) \circ {\text{e}}_{k} = {\text{e}}_{i} \circ \left( {{\text{e}}_{j} \circ {\text{e}}_{k} } \right). \hfill \\ \end{gathered}$$

Thus, for all possible triples (ei, ej, ek) the formula (2) holds true, i. e., the vector multiplication operation defined by Table 1 possesses the property of associativity. Proposition 1 is proven.

Proposition 2

The 4-dimensional finite algebra set by Table 1 is commutative.

Proof

Note ei o ej = ej o ei, therefore, due to formula (1) we have A o B = B o A. Proposition 2 is proven.

Proposition 3

The 4-dimensional FAA set by Table 1 contains a two-sided unit that is the vector E = (0, 0, 1, 0).

Proof Using formula (1) we have \(A \circ E = \sum\nolimits_{i = 0}^{3} {a_{i} \left( {e_{i} \circ e_{3} } \right)} = \sum\nolimits_{i = 0}^{3} {a_{i} e_{i} } = A\) and \(E \circ A = \sum\nolimits_{j = 0}^{3} {a_{j} \left( {{\varvec{e}}_{3} \circ {\varvec{e}}_{j} } \right)} = \sum\nolimits_{j = 0}^{3} {a_{j} {\varvec{e}}_{j} } = A.\) Proposition 3 is proven.

A vector A for which the vector equation A o X = E has a unique solution is called invertible vector. For a fixed invertible vector A the solution is denoted as A−1 and is called inverses of A. Evidently, A o A−1 = A−1 o A = E. To obtain invertibility condition one can consider the vector equation A o X = E can be reduced to the following system of four equations with the unknown coordinates of the vector X = (x0, x1, x2, x3):

$$\left\{ {\begin{array}{*{20}c} {a_{2} x_{0} + a_{3} x_{1} + a_{0} x_{2} + a_{1} x_{3} = 1;\;\;} \\ {\lambda a_{3} x_{0} + a_{2} x_{1} + a_{1} x_{2} + \lambda a_{0} x_{3} = 0;} \\ {\lambda a_{0} x_{0} + a_{1} x_{1} + a_{2} x_{2} + \lambda a_{3} x_{3} = 0;} \\ {a_{1} x_{0} + a_{0} x_{1} + a_{3} x_{2} + a_{2} x_{3} = 0.} \\ \end{array} } \right.$$
(5)

The main determinant of the system (5) is

$$\begin{array}{*{20}l} {\Delta = \left| {\begin{array}{*{20}c} {a_{2} } & {a_{3} } & {a_{0} } & {a_{1} } \\ {\lambda a_{3} } & {a_{2} } & {a_{1} } & {\lambda a_{0} } \\ {\lambda a_{0} } & {a_{1} } & {a_{2} } & {\lambda a_{3} } \\ {a_{1} } & {a_{0} } & {a_{3} } & {a_{2} } \\ \end{array} } \right| = a_{2} \left| {\begin{array}{*{20}c} {a_{2} } & {a_{1} } & {\lambda a_{0} } \\ {a_{1} } & {a_{2} } & {\lambda a_{3} } \\ {a_{0} } & {a_{3} } & {a_{2} } \\ \end{array} } \right| - a_{3} \left| {\begin{array}{*{20}c} {\lambda a_{3} } & {a_{1} } & {\lambda a_{0} } \\ {\lambda a_{0} } & {a_{2} } & {\lambda a_{3} } \\ {a_{1} } & {a_{3} } & {a_{2} } \\ \end{array} } \right|} \hfill \\ {\quad \quad \quad + a_{0} \left| {\begin{array}{*{20}c} {\lambda a_{3} } & {a_{2} } & {\lambda a_{0} } \\ {\lambda a_{0} } & {a_{1} } & {\lambda a_{3} } \\ {a_{1} } & {a_{0} } & {a_{2} } \\ \end{array} } \right| - a_{1} \left| {\begin{array}{*{20}c} {\lambda a_{3} } & {a_{2} } & {a_{1} } \\ {\lambda a_{0} } & {a_{1} } & {a_{2} } \\ {a_{1} } & {a_{0} } & {a_{3} } \\ \end{array} } \right|} \hfill \\ {\quad = a_{2} \left( {a_{2} \left( {a_{2}^{2} - \lambda a_{3}^{2} } \right) - a_{1} \left( {a_{1} a_{2} - \lambda a_{0} a_{3} } \right) + \lambda a_{0} \left( {a_{1} a_{3} - a_{0} a_{2} } \right)} \right)} \hfill \\ {\quad \quad \quad - a_{3} \left( {\lambda a_{3} \left( {a_{2}^{2} - \lambda a_{3}^{2} } \right) - a_{1} \left( {\lambda a_{0} a_{2} - \lambda a_{1} a_{3} } \right) + \lambda a_{0} \left( {\lambda a_{0} a_{3} - a_{1} a_{2} } \right)} \right)} \hfill \\ {\quad \quad \quad + a_{0} \left( {\lambda a_{3} \left( {a_{1} a_{2} - \lambda a_{0} a_{3} } \right) - a_{2} \left( {\lambda a_{0} a_{2} - \lambda a_{1} a_{3} } \right) + \lambda a_{0} \left( {\lambda a_{0}^{2} - a_{1}^{2} } \right)} \right)} \hfill \\ {\quad \quad \quad - a_{1} \left( {\lambda a_{3} \left( {a_{1} a_{3} - a_{0} a_{2} } \right) - a_{2} \left( {\lambda a_{0} a_{3} - a_{1} a_{2} } \right) + a_{1} \left( {\lambda a_{0}^{2} - a_{1}^{2} } \right)} \right) = .\;.\;.} \hfill \\ {\quad = \lambda^{2} \left( {a_{0}^{2} + a_{3}^{2} } \right)^{2} - 4\lambda a_{0}^{2} a_{3}^{2} + \left( {a_{1}^{2} + a_{2}^{2} } \right)^{2} - 4\lambda a_{0}^{2} a_{3}^{2} } \hfill \\ {\quad \quad \quad - 2\lambda \left( {a_{0}^{2} + a_{3}^{2} } \right)\left( {a_{1}^{2} + a_{2}^{2} } \right) + 8\lambda a_{0} a_{1} a_{2} a_{3} = .\;.\;.} \hfill \\ {\quad = \left( {\lambda a_{0}^{2} - a_{1}^{2} - a_{2}^{2} + \lambda a_{3}^{2} } \right)^{2} - 4\left( {\lambda a_{0} a_{3} - a_{1} a_{2} } \right)^{2} .} \hfill \\ \end{array}$$

The system (5) has unique solution, if Δ ≠ 0, and has no solution, if Δ = 0. Therefore, we have the following invertibility condition:

$$\left( {{\uplambda }a_{0}^{2} - a_{1}^{2} - a_{2}^{2} + \lambda a_{3}^{2} } \right)^{2} - 4\left( {{\uplambda }a_{0} a_{3} - a_{1} a_{2} } \right)^{2} \ne 0$$
(6)

and the non-invertibility condition

$$\left( {{\uplambda }a_{0}^{2} - a_{1}^{2} - a_{2}^{2} + {\uplambda }a_{3}^{2} } \right)^{2} = 4\left( {{\uplambda }a_{0} a_{3} - a_{1} a_{2} } \right)^{2} .$$
(7)

The set of all invertible vectors compose a finite commutative group called multiplicative group of the algebra.

Proposition 4

If the structural constant λ is a quadratic non-residue, then the number of non-invertible vectors in the 4-dimensional FAA set by Table 1 is equal to η = 2p2 − 1 and the order of the multiplicative group of the algebra is equal to Ω = (p2 − 1)2.

Proof

Formula (7) sets the following two cases

$${\uplambda }a_{0}^{2} - a_{1}^{2} - a_{2}^{2} + {\uplambda }a_{3}^{2} = 2{\uplambda }a_{0} a_{3} - 2a_{1} a_{2} \Rightarrow {\uplambda }\left( {a_{0} - a_{3} } \right)^{2} = \left( {a_{1} - a_{2} } \right)^{2} ;$$
$${\uplambda }a_{0}^{2} - a_{1}^{2} - a_{2}^{2} + {\uplambda }a_{3}^{2} = - 2{\uplambda }a_{0} a_{3} + 2a_{1} a_{2} \Rightarrow {\uplambda }\left( {a_{0} + a_{3} } \right)^{2} = \left( {a_{1} + a_{2} } \right)^{2} .$$

Since the structural constant λ is a quadratic non-residue, in the first case the equality holds true only if \(\left( {a_{0} - a_{3} } \right)^{2} = \left( {a_{1} - a_{2} } \right)^{2} = 0.\) This gives p2 different sets of coordinates a0, a1, a2, and a3, including (0, 0, 0, 0). In the second case the equality holds true only if \(\left( {a_{0} + a_{3} } \right)^{2} = \left( {a_{1} + a_{2} } \right)^{2} = 0.\) This gives other p2 different sets of coordinates a0, a1, a2, and a3, including (0, 0, 0, 0). Therefore, we have η = 2p2 − 1 and Ω = p4 − η = (p2 − 1)2. Proposition 4 is proven.

Proposition 5

If the structural constant λ is a quadratic residue in GF(p), then the number of non-invertible vectors in the 4-dimensional FAA set by Table 1 is equal to η = 4p3 − 6p2 + 4p2 − 1 and the order of the multiplicative group of the algebra is equal to Ω = (p − 1)4.

Proof

Since the structural constant λ is a quadratic residue, formula (7) defines the following two cases

$$\left( {a_{0} \sqrt {\uplambda } - a_{3} \sqrt {\uplambda } } \right)^{2} = \left( {a_{1} - a_{2} } \right)^{2} \Rightarrow a_{0} \sqrt {\uplambda } - a_{3} \sqrt {\uplambda } = \pm \left( {a_{1} - a_{2} } \right);$$
$$\left( {a_{0} \sqrt {\uplambda } + a_{3} \sqrt {\uplambda } } \right)^{2} = \left( {a_{1} + a_{2} } \right)^{2} \Rightarrow a_{0} \sqrt {\uplambda } + a_{3} \sqrt {\uplambda } = \pm \left( {a_{1} + a_{2} } \right).$$

Sets of coordinates (a0, a1, a2, a3) satisfying four conditions defined by the said two cases represent non-invertible vectors. The following Table 2 shows the number of vectors coordinates of which satisfy every of the conditions.

Table 2 Number of subsets of non-invertible vectors for the case when λ is a quadratic residue
Full size table

Total number of non-invertible vectors equals to \(\eta = p^{2} + p^{2} + 2p\left( {p - 1} \right)^{2} + 2p\left( {p - 1} \right)^{2} = 4p^{3} - 6p^{2} + 4p - 1.\)

The order of the multiplicative group of the algebra is equal to Ω = p4 − η = (p − 1)4. Proposition 5 is proven.

In the first case the equality holds true only if \(\left( {a_{0} - a_{3} } \right)^{2} = \left( {a_{1} - a_{2} } \right)^{2} = 0.\) This gives p2 different sets of coordinates a0, a1, a2, and a3, including (0, 0, 0, 0). In the second case the equality holds true only if \(\left( {a_{0} + a_{3} } \right)^{2} = \left( {a_{1} + a_{2} } \right)^{2} = 0.\) This gives other p2 different sets of coordinates a0, a1, a2, and a3, including (0, 0, 0, 0). Therefore, we have η = 2p2 − 1 and Ω = p4 − η = (p2 − 1)2.

Like in the case of the commutative FAA introduced in (Minh et al. 2020), the said group has a 4-dimensional (2-dimensional) cyclicity, if the structural constant λ is equal to the quadratic residue (non-residue) in the field GF(p). In the case of forming a group with 2-dimensional cyclicity, its basis includes two vectors, each of which has order equal to p2 − 1, and order of the group is equal to (p2 − 1)2. Tables 3 and 4 present some examples of vectors V having the maximum possible order for the said two cases of the value of structural constant λ, when p = 14,377,379 (q = 7,188,689).

Table 3 Vectors V having maximum order equal to p − 1 (λ is a quadratic residue)
Full size table
Table 4 Vectors V having maximum order p2 − 1 (λ is a quadratic non-residue)
Full size table

When developing the HDLP-based DS scheme in this section, we will consider the case of 4-dimensional cyclicity, when the basis of the multiplicative group Γ includes four vectors, each of which has order equal to p − 1, and order of the group is equal to (p − 1)4. It is also assumed that λ = 4 and the characteristic p of the field GF(p) is equal to a prime number having the structure p = 2q + 1, where q is a 512-bit prime. The generation of the required primes p is done by generating many different 512-bit primes q and testing the values p = 2q + 1 for primarily. Table 5 presents some examples of prime values of q of different size for which the value 2q + 1 is prime.

Table 5 Specially selected prime values of q
Full size table

3.2 Signature scheme

To develop a HDLP-base DS scheme we use the primary group of the order q4 contained in the multiplicative group of the algebra. For generating a minimum generator system < G1, G2, G3, G4 > , the probabilistic method described in (Minh et al. 2020) can be used. That method involves the generation of random four vectors of order q, which with probability about 1 − q−1 form a minimum generator system of the mentioned primary group. Suppose that the four vectors G1, G2, G3, and G4 have been produced.

Procedure for generating a public key in the developed signature scheme includes the following steps:

  1. 1.

    Generate at random three non-negative integers x < q, w < q, and μ < p, where μ is a primitive element modulo p.

  2. 2.

    Calculate the vector Y = G1x \(\circ\) G2w.

  3. 3.

    Calculate the vector Z = μG1 \(\circ\) G31/x.

  4. 4.

    Calculate the vector U = G2 \(\circ\) G3−1/w.

The produced public key represents the triple (Y, Z, U) of 4-dimensional vectors contained in three different cyclic subgroups of the primary group.

The signature generation algorithm is as follows:

  1. 1.

    Generate at random non-negative integers k < q, and ρ < p.

  2. 2.

    Compute the integer t = kwx−1 mod q.

  3. 3.

    Compute the fixator \(R = \rho G_{1}^{k} \circ G_{2}^{t}\).

  4. 4.

    Compute the first signature element e = fh(M, R), where fh is a pre-agreed 512-bit collision-resistant hash function; M is a document to be signed.

  5. 5.

    Compute the second signature element s = k − ex mod q.

  6. 6.

    Compute the third signature element d = t − ew mod q.

  7. 7.

    Compute the fourth signature element ψ = ρμ−s mod p.

This algorithm outputs the 2049-bit signature in the form of three 512-bit integers e, s, d and one 513-bit integer ψ.

The procedure for verifying the authenticity of the signature (e, s, d, ψ) to the document M is performed using the public key (Y, Z, U) as follows.

The signature verification algorithm:

  1. 1.

    Compute the vector \(R^{*} = \psi Y^{e} \circ Z^{S} \circ U^{d}\).

  2. 2.

    Compute the hash value e* = fh(M, R*).

  3. 3.

    If e* = e, then the signature is accepted as genuine one. Otherwise the signature is rejected as a false one.

Consider a signature (e, s, d, ψ) to a document M, which have been correctly computed in full correspondence with the signature generation algorithm. To prove correctness of the developed DS scheme we show that the said signature passes the verification procedure as a genuine signature:

$$\begin{array}{*{20}l} {R^* = \psi Y^{e} \circ Z^{s} \circ U^{d} } \hfill \\ {\quad \quad = \rho \mu^{ - s} G_{1}^{ex} \circ G_{2}^{ew} \circ \mu^{s} G_{1}^{s} \circ G_{3}^{s/x} \circ G_{2}^{d} \circ G_{3}^{ - d/w} } \hfill \\ {\quad \quad = \rho G_{1}^{ex} \circ G_{2}^{ew} \circ G_{1}^{k - ex} \circ G_{3}^{(k - ex)/x} } \circ\hfill \\ \circ {G_{2}^{t - ew} \circ G_{3}^{ - (t - ew)/w} } \hfill \\ {\quad \quad = \rho G_{1}^{ex} \circ G_{2}^{ew} \circ G_{1}^{k - ex} \circ G_{3}^{k/x - e} } \circ \hfill \\ \circ{G_{2}^{t - ew} \circ G_{3}^{ - t/w + e} } \hfill \\ {\quad \quad = \rho G_{1}^{ex} \circ G_{2}^{ew} \circ G_{1}^{k - ex} \circ G_{3}^{k/x - e} } \circ \hfill \\ \circ{G_{2}^{t - ew} \circ G_{3}^{ - k/x + e} = \rho G_{1}^{k} \circ G_{2}^{t} = R} \hfill \\ {\quad \quad \Rightarrow f_{h} \left( {M,R^*} \right) = f_{h} \left( {M,R} \right) \Rightarrow e^* = e} \hfill \\ \end{array}$$

One should note that the owner of the public key (Y, Z, U) has possibility to use an alternative method for computing the signature, which is the same as the described signature generation algorithm, except the steps 3 and 7. The latter in the alternative signature generation algorithm are as follows:

3. Compute the vector \(R = \rho Z^{k} \circ U^{t}\)

7. Compute the fourth signature element \(\psi = \rho \mu^{k - s} \bmod \;p.\)

Since \(Z^{k} \circ U^{t} = \mu^{k} G_{1}^{k} \circ G_{2}^{t}\), the alternative algorithm for computing a signature performs correctly and allows one to use only two 512-bit integers x and w and 513-bit integer μ as a 1537-bit private key instead of using five private values x, w, μ, G1, and G2 as 5641-bit private key.

Security of the described signature scheme is based on the particular form of the HDLP that is supposedly hard and can be defined as follows: for the given triple of vectors (Y, Z, U) find the triple of integers (x, w, μ) such that \(Y = \mu^{ - x} Z^{x} \circ U^{w}\).

Security of the proposed signature algorithm Security definition of the proposed signature scheme we formulate as follows: to forge a signature is computationally infeasible.

Like in the case of the Schnorr signature scheme (Schnorr 1991) the first signature element e is the hash-function value computed from the document M to which the fixator value R is concatenated and the right part of the verification equation (indicated in item 1 of the signature verification algorithm) is equal to R, if the signature is valid (genuine). We suppose the hash function used in the proposed signature scheme is secure and possesses no weaknesses that can be used to forge a signature. Therefore, a forging algorithm is an algorithm that computes a valid signature after computing the fixator value R and the hash value e. The fixator value R is defined by the randomization integers k < q and ρ < p.

Proposition 6

Existence of a polynomial algorithm for forging a signature means existence of a polynomial algorithm for solving the underlying HDLP.

Argumentation. The supposed forging algorithm uses no weakness of the hash function, therefore, it works equally well for different hash functions and different values of the fixator R. Suppose the forging algorithm computes two signatures (e1, s1, d1, ψ1) and (e2, s2, d2, ψ2) for two different hash functions, but the same value of the fixator R, i. e., we have two different verification equations with the same value of the left part. Therefore, one can write

$$\begin{gathered} \begin{array}{*{20}l} {R^* = \psi_{1} Y^{e_1} \circ Z^{s_1} \circ U^{d_1} = \psi_{2} Y^{e_2} \circ Z^{s_2} \circ U^{d_2} } \hfill \\ { \Rightarrow \frac{{\psi_{1} }}{{\psi_{2} }}Y^{{e_{1} - e_{2} }} \circ Z^{{s_{1} - s_{2} }} \circ U^{{d_{1} - d_{2} }} = E} \hfill \\ { \Rightarrow \frac{{\psi_{1} }}{{\psi_{2} }}G_{1}^{{x\left( {e_{1} - e_{2} } \right)}} \circ G_{2}^{{w\left( {e_{1} - e_{2} } \right)}} \circ \mu^{{s_{1} - s_{2} }} G_{1}^{{s_{1} - s_{2} }} \circ } \hfill \\ \circ {G_{3}^{{\left( {s_{1} - s_{2} } \right)/x}} \circ G_{2}^{{d_{1} - d_{2} }} \circ G_{3}^{{ - \left( {d_{1} - d_{2} } \right)/w}} = E} \hfill \\ { \Rightarrow \frac{{\psi_{1} }}{{\psi_{2} }}\mu^{{s_{1} - s_{2} }} G_{1}^{{x\left( {e_{1} - e_{2} } \right) + s_{1} - s_{2} }} \circ G_{2}^{{w\left( {e_{1} - e_{2} } \right) + d_{1} - d_{2} }} } \circ \hfill \\ \circ{G_{3}^{{\left( {s_{1} - s_{2} } \right)x^{ - 1} - \left( {d_{1} - d_{2} } \right)w^{ - 1} }} = E} \hfill \\ {} \hfill \\ \end{array} \hfill \\ \Rightarrow \left\{ {\begin{array}{*{20}c} {\frac{{\psi_{1} }}{{\psi_{2} }}\mu^{s1 - s2} \equiv 1\bmod p} \\ {x\left( {e_{1} - e_{2} } \right) + s_{1} - s_{2} \equiv 0\bmod q} \\ {w\left( {e_{1} - e_{2} } \right) + d_{1} - d_{2} \equiv 0\bmod q} \\ {\left( {s_{1} - s_{2} } \right)x^{ - 1} - \left( {d_{1} - d_{2} } \right)w^{ - 1} \equiv 0\bmod q} \\ \end{array} } \right\}. \hfill \\ \end{gathered}$$

If the value s2 − s1 is even, then repeat the forging signature procedure for another fixator value (generate new random values k and ρ and compute a new value of R), until the odd value s2 − s1 is obtained. Then one can easily get the following:

$$x = (s_{2} - s_{1} )(e_{1} - e_{2} )^{ - 1} \bmod \; q,$$
$$w = (d_{2} - d_{1} )(e_{1} - e_{2} )^{ - 1} \bmod \;q,\;{\text{and}}$$
$$\mu = (y_{1}^{ - 1} y_{2} )(s_{2} - s_{1} )^{ - 1} \bmod \;p - 1 \bmod \;p$$

Thus, taking into account that operation of finding odd-degree roots in GF(p), where p = 2q + 1, has polynomial computational complexity, one can conclude that a polynomial algorithm for forging a signature is reducible to a polynomial algorithm of solving the HDLP underlying the introduced signature scheme.

One can note that the described security proof is based on the ideas of the reductionist security proof (Pointcheval and Stern 2000, Koblitz and Menezes 2007) that was applied to the Schnorr signature algorithm (Schnorr 1991).

4 Blind signature protocol

Like in the known DLP-base signature schemes, in the developed HDLP-based signature the main contribution to the security is introduced by the exponentiation operations performed during the procedures for generating the public key, computing the signature, and verifying the signature. However, the fundamental difference of the latter is the following two points: i) when calculating the public key, the exponentiation operations are performed in two different finite cyclic groups, and 2) these two groups are hidden due to masking multiplications by the vectors G31/x and G3−1/w belonging to the third cyclic group and masking scalar multiplication by integer ψ. Due to the marked differences of the developed DS scheme, the elements of the public key (Y, Z, U) belong to three different cyclic groups.

The proposed signature verification equation \(R^{*} = \psi Y^{e} \circ Z^{S} \circ U^{d}\) includes factors of four types, therefore in the blind signature protocol based on the developed HDLP-based signature scheme one should use blinding factors of four different types: β, Yε, Zσ, and Uτ. Thus, like in the case of known DLP-based blind DS protocols (Camenisch et al. 1995, Pointcheval and Stern 2000), a requester participating in process of generating a blind signature is to execute generation of four uniformly random integers β < p, ε < q, σ < q, and τ < q, followed by computing the said four blinding factors.

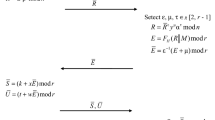
The proposed HDLP-based blind digital signature protocol includes the following steps:

  1. 1.

    The signer generates two random non-negative integers k < q and ρ < p and computes the integer t = kwx−1 mod q. Then he calculates the vector \(\overline{R}\) = ρZ k \(\circ\) U t. Then he sends the value of \(\overline{R}\) to the requester who wish to obtain a genuine signer’s signature to the document M (that is unknown to the signer).

  2. 2.

    The requester generates four uniformly random natural numbers β < p, ε < q, σ < q, and τ < q, calculates the vector \(R = \beta \overline{R} \circ Y^{\varepsilon } \circ Z^{\sigma } \circ U^{\tau }\) and the first element e of genuine signature: e = fh(M,R).

  3. 3.

    The requester then calculates the first element of the blind signature \(\;\overline{e}\) = e − ε mod q and sends it to the signer.

  4. 4.

    Using his private key (x, w, μ), the signer calculates the second \(\overline{s}\), the third \(\overline{d}\), and the fourth \({\overline{\psi }}\) elements of blind signature: \(\overline{S} = k - \overline{e} \;x\;\bmod \;q\), \(\overline{d} = t - \overline{e}\) w mod q, and \({\overline{\psi }}\) = ρ \({\upmu }^{{ - s\overline{e}}}\) mod p. He then sends the values \(\overline{s}\), \(\overline{d}\), and \({\overline{\psi }}\) to the requester.

  5. 5.

    Using the value \(\overline{s}\), \(\overline{d}\), and \({\overline{\psi }}\),the requester calculates the second s, third d and fourth ψ elements of genuine signer’s signature to the document M: s = \(\overline{s}\) + σ mod q, d = \(\overline{d}\) + τ mod q, and ψ = \({\overline{\psi }}\) β.

Procedure for verifying a signature (e, s, d, ψ) to the document M is executed using the public key (Y, Z, U) and the signature verification algorithm of the initial HDLP-based signature scheme (see Sect. 3).

The correctness of the described blind signature protocol can be proved by substituting the signature for the input of the specified verification procedure and demonstrating that it passes verification as a genuine signature.

The proof of correctness of the blind digital signature protocol based on computational difficulty of the HDLP:

$$\begin{array}{*{20}l} {R^* = \psi Y^{e} \circ Z^{s} \circ U^{d} } \hfill \\ { = \overline{\psi }\beta Y^{{\overline{e} + \varepsilon }} \circ Z^{{\overline{s} + \sigma }} \circ U^{{\overline{d} + \tau }} } \hfill \\ { = \beta \overline{\psi }Y^{{\overline{e}}} \circ Z^{{\overline{s}}} \circ U^{{\overline{d}}} \circ Y^{\varepsilon } \circ Z^{\sigma } \circ U^{\tau } } \hfill \\ { = \beta \overline{R} \circ Y^{\varepsilon } \circ Z^{\sigma } \circ U^{\tau } } \hfill \\ { \Rightarrow f_{h} \left( {M,R^*} \right) = f_{h} \left( {M,R} \right) \Rightarrow e^* = e} \hfill \\ \end{array}$$

To demonstrate that that anonymity is provided, consider a blind signature \(\;(\overline{e}\), \(\overline{s}\), \(\overline{\psi }\)) computed correctly and an arbitrary genuine signature (e, s, d, ψ).

$$\begin{gathered} \left\{ {\begin{array}{*{20}c} {R = \psi Y^{e} \circ Z^{s} \circ U^{d} } \\ {\overline{R} = \overline{\psi }Y^{{\overline{e}}} \circ Z^{{\overline{s}}} \circ U^{{\overline{d}}} } \\ \end{array} } \right\} \Rightarrow \hfill \\ R = \frac{\psi }{{\overline{\psi }}}\overline{R} \circ Y^{{e - \overline{e}}} \circ Z^{{s - \overline{s}}} \circ U^{{d - \overline{d}}} . \hfill \\ \end{gathered}$$

Thus, the signatures \(\left( {\overline{e},\overline{s},\overline{d},{\overline{\psi }}} \right)\) and (e, s, d, ψ) are connected via some random values \(\varepsilon = e - \overline{e};\;\sigma = s - \overline{s}\) and \(\tau = d - \overline{d},\) \(\beta = \psi \overline{\psi }^{ - 1}\), therefore, having a given genuine signature, the signer is unable to distinguish the blind signature associated with the given authentic signature.

5 Discussion

For the first time, the implementation of a HDLP-based signature schemes on commutative FAAs was proposed in the paper (Minh et al. 2020). The main common features of the DS schemes presented in Sect. 3 and in (Minh et al. 2020) are:

  1. (1)

    A commutative FAA multiplicative group of which has 4-dimensional cyclicity is used as algebraic support of the signature scheme;

  2. (2)

    Computational difficulty of the HDLP is used to provide resistance to quantum attacks.

These two DS schemes have a number of significant differences, which are due to the use of different criteria for ensuring post-quantum resistance. The signature scheme from (Minh et al. 2020) satisfies the general criterion of post-quantum resistance introduced in (Moldovyan-Dmitriy et al. 2020), which can be formulated as follows: the signature scheme should be constructed so that setting periodic functions based on public parameters of the scheme, which contain a period with the length depending on the value of discrete logarithm, is a computationally difficult problem.

To satisfy the said design criterion, which is oriented to ensuring resistance to the both known and possible future quantum algorithm for finding a period length of periodic functions, the signature scheme (Minh et al. 2020) uses the method of doubling the verification equation, like that described in (Moldovyan-Dmitriy et al. 2020). In that method one of the signature elements represents an element of the algebra. Because of the latter, the public key size and signature size in (Minh et al. 2020) are quite large. Besides, it is not evident how to develop a blind signature protocol on the base of the DS scheme from (Minh et al. 2020).

In the proposed signature scheme, we use a particular design criterion of post-quantum resistance that is oriented to ensuring security to the known quantum attacks (Shor 1997, Ekert and Jozsa 1996), that was used in (Moldovyan-Nikolay and Moldovyan-Alexander 2019, Moldovyan-Nikolay and Abrosimov 2019) for developing HDLP-based signature schemes on non-commutative FAAs. One can propose the following formulation of the used particular criterion: a periodic function f set on the base of public parameters of the signature scheme and containing a period with the length depending on the discrete logarithm value should take on values in different finite cyclic groups contained in the algebraic support of the signature scheme and no cyclic group can be pointed out as a preferable cyclic group for the values of the function f.

You can specify a periodic function from three integer variables i, j, and k with contains periods with the lengths (hx−1, h, hxw−1) depending on the values of x and of \(w:F(i,j,k) = Y^{i} \circ Z^{j} \circ U^{k}\). However, the values of the function F(i,j,k) lie in many different cyclic groups contained in the primary subgroup of order q3, which is generated by the minimum generator system < G1, G2, G3 > . At the same time, it is impossible to distinguish any fixed cyclic group, which with a significant probability includes the values of the function F(i, j, k). This circumstance does not allow one to apply the quantum Shor algorithm (Shor 1997) to find the length of a period of the function F(i, j, k) and then to find the values of x and of w.

The signature schemes described in Sect. 3 is characterized in the following features:

  1. 1.

    the signature scheme is set in a hidden commutative group with 2-dimensional cyclicity, therefore the discrete logarithm represents a pair of integers x and w (the hidden group is set by secret vectors G1 and G2);

  2. 2.

    the public key elements Z and U represent the masked forms of the vectors G1 and G2 representing a minimum generator system of the hidden group (the masking is performed as scalar multiplication by the integer ψ and multiplications by the vectors G31/x and G3−1/w contained in the cyclic group generated the vector G3 that together with the vectors G1 and G2 composes a minimum generator system of a primary group of order q3 which has 3-dimensional cyclicity);

  3. 3.

    the powers of the masking factors G31/x and G3−1/w are chosen so that their contribution to the left part of the verification equation is reduced to the multiplication by the unit element of the algebra (this is also due to specific generation of the signature randomization integers k and t; note also that due to the used scalar multiplication by the integer ψ the vectors Y, Z, and U compose a generator system of some group containing a primary subgroup possessing 3-dimensional cyclicity and order q3).

The developed HDLP-based signature scheme and blind signature protocol are candidates for practical post-quantum public-key cryptoschemes due to sufficiently small size of public key and signature (see Table 6).

Table 6 Comparison with some known HDLP-based signature schemes (for the case of 512-bit value p)
Full size table

The developed DS scheme and protocol use a novel 4-dimensional commutative FAA, however they can be implemented using the 4-dimensional commutative FAA described in (Minh et al. 2020).

6 Conclusion

A novel HDLP-based signature scheme on a commutative FAA is proposed and used to develop a practical post-quantum blind signature protocol. The advantages of the introduced scheme and protocol are comparatively small size of public key and signature.