Abstract
An OR-proof is a protocol that enables a user to prove the possession of a witness for one of two (or more) statements, without revealing which one. Abe and Okamoto (CRYPTO 2000) used this technique to build a partially blind signature scheme whose security is based on the hardness of the discrete logarithm problem. Inspired by their approach, we present  , an efficient blind signature scheme from OR-proofs based on lattices over modules. Using OR-proofs allows us to reduce the security of our scheme from the \(\mathsf {MLWE}\) and \(\mathsf {MSIS}\) problems, yielding a much more efficient solution compared to previous works.
, an efficient blind signature scheme from OR-proofs based on lattices over modules. Using OR-proofs allows us to reduce the security of our scheme from the \(\mathsf {MLWE}\) and \(\mathsf {MSIS}\) problems, yielding a much more efficient solution compared to previous works.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Blind signature schemes are a fundamental cryptographic primitive. First introduced by Chaum [9] in the context of an anonymous e-cash system, they have since become an essential building block in many applications such as anonymous credentials, e-voting, and blockchain protocols. They have been standardized as ISO/IEC 18370, and were deployed in real-life applications such as Microsoft’s U-Prove technology and smart card devices produced by Gemalto.
In a blind signature scheme, a user holding a message \( m \) interacts with a signer to generate a blind signature on \( m \) under the signer’s secret key. The scheme is required to satisfy two security properties called blindness and one-more unforgeability [16, 19]. Informally, the first condition means that the signer gets no information about \( m \) during the signing process, while the latter ensures that the user cannot generate signatures without interacting with the signer.
In an effort to develop practical blind signature schemes from a diverse range of assumptions (in particular, those conjectured to be secure against quantum attacks), various schemes based on lattice problems have been proposed. The first such scheme by Rückert [20] can be seen as an important step in carrying the core design of classical constructions based on the discrete logarithm problem [19] over to the lattice setting. The same design principle was then adopted in subsequent works, e.g., by Alkeilani Alkadri et al. [3, 4], where the scheme \(\mathsf {BLAZE}\) and its successor \(\mathsf {BLAZE}^{+}\) have been proposed and shown to be practical.
Recently, Hauck et al. [15] pointed out that the proof of the one-more unforgeability property, originally by Pointcheval and Stern for a discrete logarithm based construction [19] and later reproposed by Rückert for his lattice-based scheme [20], has not been adapted correctly to this new setting. Indeed, the main idea of the reduction in [19] is to select a secret key \(\textit{sk}\) and then run the forger with the related public key \(\textit{pk}\), which represents an instance of a computationally hard problem that admits more than one solution. In other words, \(\textit{pk}\) is related to more than one \(\textit{sk}\), and the forger cannot distinguish which \(\textit{sk}\) is used by the reduction. Note that it is crucial for the reduction to know a secret key because, unlike standard signature schemes, the signer cannot be simulated without one (otherwise the scheme would be universally forgeable [19]). After running the forger and obtaining an element z, the reduction rewinds the forger with the same random tape and partially different random oracle replies to obtain \(z'\). The proof in [19] then uses a subtle argument to ensure that \(z \ne z'\) with noticeable probability, which yields a solution to the underlying hard problem.
In lattice-based schemes, the hardness assumption underpinning security is usually the Short Integer Solution (\(\mathsf {SIS}\)) problem or its ring variant \(\mathsf {RSIS}\). In this context, after obtaining z and \(z'\), the reduction simply returns \(z - z'\) as a non-zero solution to \((\mathsf {R}) \mathsf {SIS}\). The problem, as discussed in [15], is that Rückert’s argument is not sufficient to ensure that \(z \ne z'\) with high probability, and further assumptions are required to guarantee that a transcript of the scheme with a given key \(\textit{sk}\) can be preserved with high probability when switching to a different valid secret key. Based on this observation, Hauck et al. [15] extended the modular framework for blind signatures from linear functions given in [14] to the lattice setting, and provided a proof that covers the missing argument.
Unfortunately, as stated by the authors themselves, their work is mostly of theoretical interest. Indeed, the solution presented in [15] entails increasing the parameter sizes, so that their framework applies and yields a correct proof. In particular, the \(\mathsf {RSIS}\)-based instantiation given in [15] has public and secret keys of size 443.75 KB and 4275 KB, respectively, and generates signatures of size 7915.52 KB. This leaves us in the regrettable position where all known (three-move) lattice-based blind signature schemes are either not backed by a correct security proof, or need impractically large parameters to achieve security.
Our Contributions. In this paper we make a significant progress towards constructing efficient and at the same time provably secure lattice-based blind signature schemes. We present  , a new blind signature scheme based on lattices over modules. Our scheme uses the OR-technique of Cramer et al. [10], a feature which allows us to sidestep the missing security argument pointed out in [15]. At a high level, an OR-proof is a Sigma protocol that proves the knowledge of a witness for one of two statements, without revealing which one. Therefore, the public key of our scheme consists of two statements (two instances of a hard lattice problem), and the secret key includes a witness for one of them. Consequently and for the first time, the hardness assumption underlying the public key does not have to “natively” admit multiple solutions, because the OR-technique already forces there to be more than one (and thus simulation of signatures is still possible).
, a new blind signature scheme based on lattices over modules. Our scheme uses the OR-technique of Cramer et al. [10], a feature which allows us to sidestep the missing security argument pointed out in [15]. At a high level, an OR-proof is a Sigma protocol that proves the knowledge of a witness for one of two statements, without revealing which one. Therefore, the public key of our scheme consists of two statements (two instances of a hard lattice problem), and the secret key includes a witness for one of them. Consequently and for the first time, the hardness assumption underlying the public key does not have to “natively” admit multiple solutions, because the OR-technique already forces there to be more than one (and thus simulation of signatures is still possible).
In particular, the public key of  consists of two instances of the Module Learning with Errors (\(\mathsf {MLWE}\)) problem, which results in a much more efficient scheme. Signing is carried out by proving the possession of the witness included in the secret key. A user interacting with the signer blinds the two transcripts generated by the signer without being able to distinguish for which instance the signer holds a witness. We capture these blinding steps in a set of algorithms and show that
consists of two instances of the Module Learning with Errors (\(\mathsf {MLWE}\)) problem, which results in a much more efficient scheme. Signing is carried out by proving the possession of the witness included in the secret key. A user interacting with the signer blinds the two transcripts generated by the signer without being able to distinguish for which instance the signer holds a witness. We capture these blinding steps in a set of algorithms and show that  is statistically blind. The one-more unforgeability of our scheme is proven in the random oracle model (ROM) assuming the hardness of both \(\mathsf {MLWE}\) and \(\mathsf {MSIS}\) (the module version of \(\mathsf {SIS}\)). The reduction creates one instance of the hard problem with a witness in order to simulate the signing oracle, and tries to solve the other instance, which is given to the reduction as input. That is, the reduction does not know a witness for its input. This is analogous to the security proof of standard lattice-based signature schemes, and hence no further conditions are required to ensure the correctness and success of the reduction with high probability. This is in contrast to previous lattice-based constructions of blind signatures, as observed in [15].
is statistically blind. The one-more unforgeability of our scheme is proven in the random oracle model (ROM) assuming the hardness of both \(\mathsf {MLWE}\) and \(\mathsf {MSIS}\) (the module version of \(\mathsf {SIS}\)). The reduction creates one instance of the hard problem with a witness in order to simulate the signing oracle, and tries to solve the other instance, which is given to the reduction as input. That is, the reduction does not know a witness for its input. This is analogous to the security proof of standard lattice-based signature schemes, and hence no further conditions are required to ensure the correctness and success of the reduction with high probability. This is in contrast to previous lattice-based constructions of blind signatures, as observed in [15].
 uses techniques from prior works in order to reduce or even remove the number of restarts inherent in lattice-based schemes. More precisely, it uses the partitioning and permutation technique introduced in [3]. Given a hash function taking values in the challenge space of the underlying Sigma protocol, it allows to blind the hash values without having to carry out any security check or potential restart. Another advantage of this technique is that it can be used to construct OR-proofs based on lattice assumptions, because it allows to use a specified challenge space that has an abelian group structure, a crucial requirement for OR-proofs. This is in contrast to the typical challenge space used in current lattice-based schemes, which consists of polynomials from the ring \(\mathbb {Z}[X]/\langle X^n + 1\rangle \) with coefficients in \(\lbrace -1, 0, 1\rbrace \) and a given Hamming weight. We also use the trees of commitments technique from [4] to remove the restarts induced by the user when blinding the signature generated by the signer. We extend this technique in
uses techniques from prior works in order to reduce or even remove the number of restarts inherent in lattice-based schemes. More precisely, it uses the partitioning and permutation technique introduced in [3]. Given a hash function taking values in the challenge space of the underlying Sigma protocol, it allows to blind the hash values without having to carry out any security check or potential restart. Another advantage of this technique is that it can be used to construct OR-proofs based on lattice assumptions, because it allows to use a specified challenge space that has an abelian group structure, a crucial requirement for OR-proofs. This is in contrast to the typical challenge space used in current lattice-based schemes, which consists of polynomials from the ring \(\mathbb {Z}[X]/\langle X^n + 1\rangle \) with coefficients in \(\lbrace -1, 0, 1\rbrace \) and a given Hamming weight. We also use the trees of commitments technique from [4] to remove the restarts induced by the user when blinding the signature generated by the signer. We extend this technique in  to reduce the potential restarts induced by the signer when computing signatures, which must be distributed independently from the secret key.
to reduce the potential restarts induced by the signer when computing signatures, which must be distributed independently from the secret key.
To demonstrate the efficiency of our scheme, we propose concrete parameters for  targeting 128 bits of security. The related key and signature sizes, the communication cost, and a comparison with the corresponding metrics for the scheme proposed by Hauck et al. [15] are given in Table 1. In summary, although our scheme requires twice as many public key and signature parts, which is inherent to using OR-proofs, it yields smaller sizes compared to the provably secure construction from [15], resulting in a more efficient scheme overall.
targeting 128 bits of security. The related key and signature sizes, the communication cost, and a comparison with the corresponding metrics for the scheme proposed by Hauck et al. [15] are given in Table 1. In summary, although our scheme requires twice as many public key and signature parts, which is inherent to using OR-proofs, it yields smaller sizes compared to the provably secure construction from [15], resulting in a more efficient scheme overall.
 and the scheme introduced in [15] in terms of key and signature sizes and communication cost. Numbers are given in kilobytes (KB). The related parameters are given in Table 3 and [15, Figure 9].
and the scheme introduced in [15] in terms of key and signature sizes and communication cost. Numbers are given in kilobytes (KB). The related parameters are given in Table 3 and [15, Figure 9].We remark that the security of our scheme can easily be extended to the stronger security notions of selective failure blindness [8] and honest-user unforgeability [21]. This is established by signing a commitment to the message instead of the message itself [12, 21]. However, and similar to [15], it is still unclear how to prove the blindness property under a maliciously generated key pair [11].
Related Work. Our construction is inspired by the work of Abe and Okamoto [1], who used OR-proofs to build partially blind signatures with security based on the hardness of the discrete logarithm problem. Observe that we cannot simply convert their scheme to the lattice setting, as this would force us to use \(\mathsf {MSIS}\) (instead of \(\mathsf {MLWE}\)) and result in an inefficient scheme. The change to \(\mathsf {MLWE}\) is possible because there is no common information to consider in our case.
Hauck et al. [15] showed that all lattice-based constructions of blind signatures from Sigma protocols (or canonical identification schemes) prior to their framework, such as [3, 20], do not have a valid security argument. Furthermore, Alkeilani Alkadri et al. [3] showed that all two-round lattice-based blind signature schemes based on preimage sampleable trapdoor functions are insecure.
Recently, Agrawal et al. [2] made a step towards practical two-round lattice-based blind signatures. They improved the two-round construction of Garg et al. [13] which is based on general complexity assumptions, and degraded it to rely on the ROM. This allows them to avoid complexity leveraging, the main source of inefficiency in [13]. However, as pointed out by the authors, there are some challenges left before this approach becomes practical. For instance, the scheme requires the homomorphic evaluation of a specific signing algorithm that relies on the ROM. In practice, this must be instantiated with a cryptographic hash function that can be evaluated homomorphically. Finding such a function is still an open problem. We refer to [2, Section 6.3] for more details and discussions on the limitations of their construction.
2 Preliminaries
Notation. We denote by \(\mathbb {N}\), \(\mathbb {Z}\), and \(\mathbb {R}\) the sets of natural numbers, integers, and real numbers, respectively. If \(k \in \mathbb {N}\), we let  . For \(q \in \mathbb {N}\), we write \(\mathbb {Z}_q\) to denote the ring of integers modulo q with representatives in
. For \(q \in \mathbb {N}\), we write \(\mathbb {Z}_q\) to denote the ring of integers modulo q with representatives in  . If n is a fixed power of 2, we define the ring
. If n is a fixed power of 2, we define the ring  and its quotient
and its quotient  . Elements in R and \(R_q\) are denoted by regular font letters. Column vectors with coefficients in R or \(R_q\) are denoted by bold lower-case letters, while bold upper-case letters are matrices. We let \(\mathbf {I}_k\) denote the identity matrix of dimension k, and \(\mathbb {T}_{\kappa }^{n}\) the subset of \(R_q\) containing all polynomials with coefficients in \(\lbrace -1, 0, 1\rbrace \) and Hamming weight \(\kappa \). The \(\ell _2\) and \(\ell _\infty \) norms of an element \(a = \sum _{i=0}^{n-1} a_{i} X^{i} \in R\) are defined by
. Elements in R and \(R_q\) are denoted by regular font letters. Column vectors with coefficients in R or \(R_q\) are denoted by bold lower-case letters, while bold upper-case letters are matrices. We let \(\mathbf {I}_k\) denote the identity matrix of dimension k, and \(\mathbb {T}_{\kappa }^{n}\) the subset of \(R_q\) containing all polynomials with coefficients in \(\lbrace -1, 0, 1\rbrace \) and Hamming weight \(\kappa \). The \(\ell _2\) and \(\ell _\infty \) norms of an element \(a = \sum _{i=0}^{n-1} a_{i} X^{i} \in R\) are defined by  and
and  , respectively. Similarly, for \(\mathbf {b}= (b_1, \ldots , b_k)^t\in R^k\), we let
, respectively. Similarly, for \(\mathbf {b}= (b_1, \ldots , b_k)^t\in R^k\), we let  and
and  . All logarithms are to base 2.
. All logarithms are to base 2.
If D is a distribution, we write  to denote that x is sampled according to D. For a finite set S, we also write
to denote that x is sampled according to D. For a finite set S, we also write  if x is chosen from the uniform distribution over S. The statistical distance between two distributions X and Y over a countable set S is defined by
if x is chosen from the uniform distribution over S. The statistical distance between two distributions X and Y over a countable set S is defined by  . For \(\varepsilon > 0\) we say that X and Y are \(\varepsilon \)-statistically close if \(\varDelta (X,Y) \le \varepsilon \).
. For \(\varepsilon > 0\) we say that X and Y are \(\varepsilon \)-statistically close if \(\varDelta (X,Y) \le \varepsilon \).
We denote the security parameter by \(\lambda \in \mathbb {N}\), and abbreviate probabilistic polynomial-time by PPT and deterministic polynomial-time by DPT. For a probabilistic algorithm \(\mathsf {A}\), we write  to denote that \(\mathsf {A}\) returns y when run on input x with access to oracle \(\mathsf {O}\), and \(y \in \mathsf {A}^{\mathsf {O}}(x)\) if y is a possible output of \(\mathsf {A}^{\mathsf {O}}(x)\). To make the randomness
to denote that \(\mathsf {A}\) returns y when run on input x with access to oracle \(\mathsf {O}\), and \(y \in \mathsf {A}^{\mathsf {O}}(x)\) if y is a possible output of \(\mathsf {A}^{\mathsf {O}}(x)\). To make the randomness  on which \(\mathsf {A}\) is run explicit, we use the notation \(y \leftarrow \mathsf {A}^{\mathsf {O}}(x; r)\). If \(\mathsf {A}\) and \(\mathsf {B}\) are interactive algorithms, we write
on which \(\mathsf {A}\) is run explicit, we use the notation \(y \leftarrow \mathsf {A}^{\mathsf {O}}(x; r)\). If \(\mathsf {A}\) and \(\mathsf {B}\) are interactive algorithms, we write  to denote the joint execution of \(\mathsf {A}\) and \(\mathsf {B}\) in an interactive protocol with private inputs a for \(\mathsf {A}\) and b for \(\mathsf {B}\), as well as private outputs x for \(\mathsf {A}\) and y for \(\mathsf {B}\). Accordingly, we write \(\mathsf {A}^{\langle \cdot , \mathsf {B}(b)\rangle ^k}(a)\) if \(\mathsf {A}\) can invoke up to k executions of the protocol with \(\mathsf {B}\).
to denote the joint execution of \(\mathsf {A}\) and \(\mathsf {B}\) in an interactive protocol with private inputs a for \(\mathsf {A}\) and b for \(\mathsf {B}\), as well as private outputs x for \(\mathsf {A}\) and y for \(\mathsf {B}\). Accordingly, we write \(\mathsf {A}^{\langle \cdot , \mathsf {B}(b)\rangle ^k}(a)\) if \(\mathsf {A}\) can invoke up to k executions of the protocol with \(\mathsf {B}\).
The random oracle model (ROM) [7] is a model of computation where all occurrences of a hash function are replaced by a random oracle \(\mathsf {H}\), i.e., a function chosen at random from the space of all functions \(\{0,1\}^* \rightarrow \{0,1\}^{\ell _{\mathsf {H}}}\) for some \(\ell _{\mathsf {H}}\in \mathbb {N}\), to which all involved parties have oracle access. This means that, for every new oracle query, \(\mathsf {H}\) returns a truly random response from \(\{0,1\}^{\ell _{\mathsf {H}}}\), and every repeated query consistently yields the same output.
Relations, Sigma Protocols, and OR-Proofs
Definition 1
A relation is a tuple  , where:
, where:
-
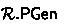 is the parameter generation algorithm which, on input the security parameter \(\lambda \in \mathbb {N}\), returns public parameters \( pp \).
is the parameter generation algorithm which, on input the security parameter \(\lambda \in \mathbb {N}\), returns public parameters \( pp \). -
 is the relation set, a collection of sets indexed by
is the relation set, a collection of sets indexed by  .
. -
 is the instance generator algorithm which, on input
is the instance generator algorithm which, on input  and \(b\in \{0,1\}\), returns a pair
and \(b\in \{0,1\}\), returns a pair  if \(b= 1\) (where \(x\) is called a yes-instance for \(\mathcal {R}\) w.r.t. \( pp \) and \(w\) a corresponding witness), and an element \(x\) if \(b= 0\) (called a no-instance for \(\mathcal {R}\) w.r.t. \( pp \)).
if \(b= 1\) (where \(x\) is called a yes-instance for \(\mathcal {R}\) w.r.t. \( pp \) and \(w\) a corresponding witness), and an element \(x\) if \(b= 0\) (called a no-instance for \(\mathcal {R}\) w.r.t. \( pp \)).
We now define the OR-relation \(\mathcal {R}_{\mathsf {OR}}\) on a relation \(\mathcal {R}\). Informally, for \(\lambda \in \mathbb {N}\) and public parameters  , a yes-instance for \(\mathcal {R}_{\mathsf {OR}}\) w.r.t. \( pp \) is a pair of values \((x_0, x_1)\), each a yes-instance for \(\mathcal {R}\) w.r.t. \( pp \). A witness for such an instance is a witness for one of the two coordinates, i.e.a pair \((d, w)\) with \(d\in \{0,1\}\) and \(w\) a witness for \(x_d\). In contrast, a no-instance for \(\mathcal {R}_{\mathsf {OR}}\) consists of a pair \((x_0, x_1)\), where at least one coordinate is a no-instance for \(\mathcal {R}\) w.r.t. \( pp \).
, a yes-instance for \(\mathcal {R}_{\mathsf {OR}}\) w.r.t. \( pp \) is a pair of values \((x_0, x_1)\), each a yes-instance for \(\mathcal {R}\) w.r.t. \( pp \). A witness for such an instance is a witness for one of the two coordinates, i.e.a pair \((d, w)\) with \(d\in \{0,1\}\) and \(w\) a witness for \(x_d\). In contrast, a no-instance for \(\mathcal {R}_{\mathsf {OR}}\) consists of a pair \((x_0, x_1)\), where at least one coordinate is a no-instance for \(\mathcal {R}\) w.r.t. \( pp \).
Definition 2
Let \(\mathcal {R}\) be a relation. The OR-relation on \(\mathcal {R}\) is the relation \(\mathcal {R}_{\mathsf {OR}}\) whose parameter generation algorithm is  , whose relation set is
, whose relation set is  , and whose instance generator
, and whose instance generator  is given in Fig. 1.
is given in Fig. 1.
Definition 3
Let \(\mathcal {R}\) be a relation. A Sigma protocol for \(\mathcal {R}\) is a tuple of algorithms  , where:
, where:
-
 is an interactive algorithm, called prover, that consists of two algorithms
is an interactive algorithm, called prover, that consists of two algorithms  , where:
, where:-
 is a PPT algorithm which, on input a set of public parameters \( pp \) and an instance-witness pair \((x, w)\), returns a message \( cm \), called the commitment, and a state
is a PPT algorithm which, on input a set of public parameters \( pp \) and an instance-witness pair \((x, w)\), returns a message \( cm \), called the commitment, and a state 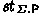 .
. -
 is a DPT algorithm which, on input a set of public parameters \( pp \), an instance-witness pair \((x, w)\), the state information
is a DPT algorithm which, on input a set of public parameters \( pp \), an instance-witness pair \((x, w)\), the state information  , and a verifier message \( ch \), outputs a message \( rp \), called the response.
, and a verifier message \( ch \), outputs a message \( rp \), called the response.
-
-
 is an interactive algorithm, called verifier, that consists of two algorithms
is an interactive algorithm, called verifier, that consists of two algorithms  , where:
, where:-
 is a PPT algorithm which, on input a set of public parameters \( pp \), an instance \(x\), and a prover message \( cm \), returns a message \( ch \) (called the challenge) sampled uniformly at random from a finite abelian group
is a PPT algorithm which, on input a set of public parameters \( pp \), an instance \(x\), and a prover message \( cm \), returns a message \( ch \) (called the challenge) sampled uniformly at random from a finite abelian group  (called the challenge space), as well as a state
(called the challenge space), as well as a state  consisting only of the received message and the sampled challenge.
consisting only of the received message and the sampled challenge. -
 is a DPT algorithm which, on input a set of public parameters \( pp \), an instance \(x\), the state information
is a DPT algorithm which, on input a set of public parameters \( pp \), an instance \(x\), the state information  , and a prover message \( rp \), outputs a pair \((b, int )\) with \(b \in \{0,1\}\) and \( int \in \mathbb {Z}\). We say that the verifier accepts the transcript if \(b = 1\), and that it rejects if \(b = 0\).
, and a prover message \( rp \), outputs a pair \((b, int )\) with \(b \in \{0,1\}\) and \( int \in \mathbb {Z}\). We say that the verifier accepts the transcript if \(b = 1\), and that it rejects if \(b = 0\).
-
-
 is a PPT algorithm, called simulator. On input a set of public parameters \( pp \), an instance \(x\), and a challenge \( ch \), it outputs a pair of messages \(( cm , rp )\).
is a PPT algorithm, called simulator. On input a set of public parameters \( pp \), an instance \(x\), and a challenge \( ch \), it outputs a pair of messages \(( cm , rp )\). -
 is a DPT algorithm, called extractor. On input a set of public parameters \( pp \), an instance \(x\), and two transcripts \(( cm , ch , rp )\) and \(( cm , ch ', rp ')\) such that \( ch \ne ch '\) and
is a DPT algorithm, called extractor. On input a set of public parameters \( pp \), an instance \(x\), and two transcripts \(( cm , ch , rp )\) and \(( cm , ch ', rp ')\) such that \( ch \ne ch '\) and  returns the same output \((1, int )\) in both cases,
returns the same output \((1, int )\) in both cases, 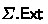 outputs a string \(w\) such that
outputs a string \(w\) such that 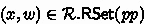 .
. -
 is a DPT algorithm, called commitment recovering algorithm. On input a set of public parameters \( pp \), an instance \(x\), a challenge \( ch \), and a response \( rp \), it returns a message \( cm \).
is a DPT algorithm, called commitment recovering algorithm. On input a set of public parameters \( pp \), an instance \(x\), a challenge \( ch \), and a response \( rp \), it returns a message \( cm \).
If \(\mathcal {R}\) is a relation, the Sigma protocols for \(\mathcal {R}\) we consider must satisfy a few properties which we briefly describe in the following. The first one is correctness, saying that an honest protocol execution is likely to be accepted by the verifier. Next, there is a variant of the zero-knowledge property, where we require that on input an instance \(x\) and a randomly chosen challenge \( ch \), the simulator be able to provide an authentic-looking transcript. Finally, we have soundness, saying that if the commitment recovering algorithm succeeds in finding a commitment, this commitment verifies for the given challenge and response.
We now consider the OR-combination of two Sigma protocols (OR-proof). It enables a prover  to show that it knows the witness of one of several statements, or that one out of many statements is true. Here, we restrict ourselves to the case where a prover holds two statements \((x_0, x_1)\) and one witness \(w\) for \(x_d\), with \(d\in \{0,1\}\). The prover’s goal is to convince the verifier that it holds a witness for one of the two statements, without revealing which one. This problem was first solved by Cramer et al. [10], and we now recall their construction.
to show that it knows the witness of one of several statements, or that one out of many statements is true. Here, we restrict ourselves to the case where a prover holds two statements \((x_0, x_1)\) and one witness \(w\) for \(x_d\), with \(d\in \{0,1\}\). The prover’s goal is to convince the verifier that it holds a witness for one of the two statements, without revealing which one. This problem was first solved by Cramer et al. [10], and we now recall their construction.
Let \(\mathcal {R}\) be a relation and \(\varSigma _0\), \(\varSigma _1\) be two Sigma protocols for \(\mathcal {R}\). The construction of [10] allows to combine \(\varSigma _0\) and \(\varSigma _1\) into a new Sigma protocol \(\varSigma _{\mathsf {OR}}= \mathsf {OR}[\varSigma _0, \varSigma _1]\) for the relation \(\mathcal {R}_{\mathsf {OR}}\). The key idea of the construction is that the prover  splits the challenge \( ch \) received by
splits the challenge \( ch \) received by  into two random parts \( ch = ch _{0} + ch _{1}\), and is able to provide accepting transcripts for both statements \(x_0\) and \(x_1\) for the respective challenge share. In more detail, for a given security parameter \(\lambda \in \mathbb {N}\), public parameters
into two random parts \( ch = ch _{0} + ch _{1}\), and is able to provide accepting transcripts for both statements \(x_0\) and \(x_1\) for the respective challenge share. In more detail, for a given security parameter \(\lambda \in \mathbb {N}\), public parameters  , and instance-witness pair
, and instance-witness pair  , the execution of \(\varSigma _{\mathsf {OR}}\) proceeds as follows:
, the execution of \(\varSigma _{\mathsf {OR}}\) proceeds as follows:
-
(a)
The prover
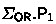 starts with computing
starts with computing 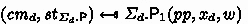 and samples a challenge
and samples a challenge  . Next, it runs
. Next, it runs 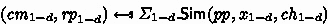 to complete the transcript of \(x_{1-d}\). In case the simulation fails (i.e. \(( cm _{1-d}, rp _{1-d}) = (\bot , \bot )\)), the prover re-runs the simulator. Finally, it sets
to complete the transcript of \(x_{1-d}\). In case the simulation fails (i.e. \(( cm _{1-d}, rp _{1-d}) = (\bot , \bot )\)), the prover re-runs the simulator. Finally, it sets  and sends \(( cm _0, cm _1)\) to the verifier
and sends \(( cm _0, cm _1)\) to the verifier  .
. -
(b)
Upon receiving the commitments \(( cm _0, cm _1)\),
 samples a random challenge from the challenge space, i.e.
samples a random challenge from the challenge space, i.e.  , and sends it to
, and sends it to  . Finally, it sets its state to
. Finally, it sets its state to  .
. -
(c)
After receiving the challenge \( ch \),
 sets \( ch _d\leftarrow ch - ch _{1-d}\) and computes a response for \(x_d\) as
sets \( ch _d\leftarrow ch - ch _{1-d}\) and computes a response for \(x_d\) as  . In case this computation fails (i.e. \( rp _d= \bot \)), it also sets \( rp _{1-d} \leftarrow \bot \). Otherwise, the prover sends the split challenges and responses to the verifier.
. In case this computation fails (i.e. \( rp _d= \bot \)), it also sets \( rp _{1-d} \leftarrow \bot \). Otherwise, the prover sends the split challenges and responses to the verifier. -
(d)
After receiving \(( ch _0, ch _1, rp _{0}, rp _{1})\) from the prover,
 accepts if and only if the shares satisfy \( ch = ch _{0} + ch _{1}\) and both transcripts verify correctly.
accepts if and only if the shares satisfy \( ch = ch _{0} + ch _{1}\) and both transcripts verify correctly.
For the remainder of the paper, we are interested in the situation where a Sigma protocol is combined with itself, i.e., we obtain a new Sigma protocol \(\varSigma _{\mathsf {OR}}= \mathsf {OR}[\varSigma , \varSigma ]\) for the relation \(\mathcal {R}_{\mathsf {OR}}\). One can show that this protocol inherits many properties of \(\varSigma \), such as correctness and special honest-verifier zero-knowledge. An important property of \(\varSigma _{\mathsf {OR}}\) is that it is witness indistinguishable, meaning that the verifier does not learn which particular witness was used to generate the proof.
Blind Signatures. We define blind signatures following the exposition of Hauck et al. [15], where the interaction between signer and user consists of three moves.
Definition 4
A blind signature scheme is a tuple of polynomial-time algorithms  where:
where:
-
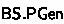 is a PPT parameter generation algorithm that, on input the security parameter \(\lambda \in \mathbb {N}\), returns a set of public parameters \( pp \). We assume that the set \( pp \) identifies the message space
is a PPT parameter generation algorithm that, on input the security parameter \(\lambda \in \mathbb {N}\), returns a set of public parameters \( pp \). We assume that the set \( pp \) identifies the message space  of the scheme.
of the scheme. -
 is a PPT key generation algorithm that, on input a set of public parameters
is a PPT key generation algorithm that, on input a set of public parameters  , returns a public/secret key pair \((\textit{pk}, \textit{sk})\).
, returns a public/secret key pair \((\textit{pk}, \textit{sk})\). -
 is an interactive algorithm, called signer, that consists of two algorithms:
is an interactive algorithm, called signer, that consists of two algorithms:-
The PPT algorithm
 takes as input a set of public parameters \( pp \) and a key pair \((\textit{pk}, \textit{sk})\), and returns the signer message \(s_{1}\) and a state
takes as input a set of public parameters \( pp \) and a key pair \((\textit{pk}, \textit{sk})\), and returns the signer message \(s_{1}\) and a state  .
. -
The DPT algorithm
 takes as input a set of public parameters \( pp \), a key pair \((\textit{pk}, \textit{sk})\), the state information
takes as input a set of public parameters \( pp \), a key pair \((\textit{pk}, \textit{sk})\), the state information 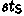 , and the user message \(u_1\), and returns the next signer message \(s_{2}\).
, and the user message \(u_1\), and returns the next signer message \(s_{2}\).
-
-
 is an interactive algorithm, called user, that consists of two algorithms:
is an interactive algorithm, called user, that consists of two algorithms:-
The PPT algorithm
 takes as input a set of public parameters \( pp \), a public key \(\textit{pk}\), a message
takes as input a set of public parameters \( pp \), a public key \(\textit{pk}\), a message  , and a signer message \(s_{1}\), and returns a user message \(u_1\) and a state
, and a signer message \(s_{1}\), and returns a user message \(u_1\) and a state 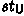 .
. -
The DPT algorithm
 takes as input a set of public parameters \( pp \), a public key \(\textit{pk}\), a message \( m \), a user state
takes as input a set of public parameters \( pp \), a public key \(\textit{pk}\), a message \( m \), a user state  , and a signer message \(s_{2}\), and outputs a signature \( sig \). We let \( sig = \bot \) denote failure.
, and a signer message \(s_{2}\), and outputs a signature \( sig \). We let \( sig = \bot \) denote failure.
-
-
 is a DPT verification algorithm that, upon receiving a set of public parameters \( pp \), a public key \(\textit{pk}\), a message \( m \), and a signature \( sig \) as input, outputs 1 if the signature is valid and 0 otherwise.
is a DPT verification algorithm that, upon receiving a set of public parameters \( pp \), a public key \(\textit{pk}\), a message \( m \), and a signature \( sig \) as input, outputs 1 if the signature is valid and 0 otherwise.
Let  . We say that \(\mathsf {BS}\) is \(\mathsf {corr}_{\mathsf {BS}}\)-correct w.r.t. \( pp \) if
. We say that \(\mathsf {BS}\) is \(\mathsf {corr}_{\mathsf {BS}}\)-correct w.r.t. \( pp \) if  validates honestly signed messages under honestly created keys with probability at least \(1-\mathsf {corr}_{\mathsf {BS}}\). The security of blind signatures is defined by the notions blindness and one-more unforgeability [16, 19].
validates honestly signed messages under honestly created keys with probability at least \(1-\mathsf {corr}_{\mathsf {BS}}\). The security of blind signatures is defined by the notions blindness and one-more unforgeability [16, 19].
Definition 5
Let \(\mathsf {BS}\) be a blind signature scheme, \(\lambda \in \mathbb {N}\) and  . We say that \(\mathsf {BS}\) is \((t, \varepsilon )\)-blind w.r.t. \( pp \) if, for every adversarial signer
. We say that \(\mathsf {BS}\) is \((t, \varepsilon )\)-blind w.r.t. \( pp \) if, for every adversarial signer  running in time at most \(t\) and working in modes \(\mathsf {find}\), \(\mathsf {issue}\), and \(\mathsf {guess}\), we have
running in time at most \(t\) and working in modes \(\mathsf {find}\), \(\mathsf {issue}\), and \(\mathsf {guess}\), we have  , where the game
, where the game  is depicted in Fig. 2. \(\mathsf {BS}\) is \(\varepsilon \)-statistically blind if it is \((t, \varepsilon )\)-blind for every \(t\).
is depicted in Fig. 2. \(\mathsf {BS}\) is \(\varepsilon \)-statistically blind if it is \((t, \varepsilon )\)-blind for every \(t\).
Definition 6
Let \(\mathsf {BS}\) be a blind signature scheme, \(\lambda \in \mathbb {N}\) and  . We say that \(\mathsf {BS}\) is \((t, q_{\mathsf {Sign}}, \varepsilon )\)-one-more unforgeable w.r.t. \( pp \) if, for every adversarial user
. We say that \(\mathsf {BS}\) is \((t, q_{\mathsf {Sign}}, \varepsilon )\)-one-more unforgeable w.r.t. \( pp \) if, for every adversarial user  running in time at most \(t\) and making at most \(q_{\mathsf {Sign}}\) signing queries, we have
running in time at most \(t\) and making at most \(q_{\mathsf {Sign}}\) signing queries, we have  , where the game
, where the game  is depicted in Fig. 2.
is depicted in Fig. 2.
Lattices and Gaussians
Definition 7
Let \(\mathcal {L}\subset \mathbb {R}^m\) be a lattice, \(\sigma \in \mathbb {R}_{>0}\), and \(\mathbf {c}\in \mathbb {R}^m\). The discrete Gaussian distribution over \(\mathcal {L}\) with standard deviation \(\sigma \) and center \(\mathbf {c}\) is the probability distribution \(D_{\mathcal {L}, \sigma , \mathbf {c}}\) which assigns to every \(\mathbf {x}\in \mathcal {L}\) the probability of occurrence given by  , where
, where  and
and  . We will omit the subscript \(\mathbf {c}\) when \(\mathbf {c}= \mathbf {0}\).
. We will omit the subscript \(\mathbf {c}\) when \(\mathbf {c}= \mathbf {0}\).
Next we recall a special version of the rejection sampling lemma related to the discrete Gaussian distribution [18, Theorem 4.6].
Lemma 8
Let \(T \in \mathbb {R}_{>0}\), and define  . Let
. Let  for some \(\alpha \in \mathbb {R}_{>0}\), and let \(h:V\rightarrow \mathbb {R}\) be a probability distribution. Then there exists a constant \(M \in \mathbb {R}_{>0}\) such that \(\exp (\frac{12}{\alpha } + \frac{1}{2\alpha ^2}) \le M\), and such that the following two algorithms are within statistical distance of at most \(2^{-100}/M\):
for some \(\alpha \in \mathbb {R}_{>0}\), and let \(h:V\rightarrow \mathbb {R}\) be a probability distribution. Then there exists a constant \(M \in \mathbb {R}_{>0}\) such that \(\exp (\frac{12}{\alpha } + \frac{1}{2\alpha ^2}) \le M\), and such that the following two algorithms are within statistical distance of at most \(2^{-100}/M\):
-
(a)
 ,
, 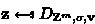 , output \((\mathbf {z}, \mathbf {v})\) with probability \(\frac{D_{\mathbb {Z}^{m}, \sigma }(\mathbf {z})}{M\cdot D_{\mathbb {Z}^{m}, \sigma , \mathbf {v}}(\mathbf {z})}\), and \(\bot \) otherwise.
, output \((\mathbf {z}, \mathbf {v})\) with probability \(\frac{D_{\mathbb {Z}^{m}, \sigma }(\mathbf {z})}{M\cdot D_{\mathbb {Z}^{m}, \sigma , \mathbf {v}}(\mathbf {z})}\), and \(\bot \) otherwise. -
(b)
 ,
,  , output \((\mathbf {z}, \mathbf {v})\) with probability 1/M, and \(\bot \) otherwise.
, output \((\mathbf {z}, \mathbf {v})\) with probability 1/M, and \(\bot \) otherwise.
Moreover, the probability that the first algorithm returns a value different from \(\bot \) is at least \(\frac{1 - 2^{-100}}{M}\).
We let \(\mathsf {Rej}\) denote an algorithm that carries out rejection sampling on \(\mathbf {z}\), where  , with \(\mathbf {v}\in \mathbb {Z}^m\) such that \(\Vert \mathbf {v}\Vert \le T\), and \(\sigma = \alpha T\). It outputs 1 if \(\mathbf {z}\) is accepted and 0 if rejected.
, with \(\mathbf {v}\in \mathbb {Z}^m\) such that \(\Vert \mathbf {v}\Vert \le T\), and \(\sigma = \alpha T\). It outputs 1 if \(\mathbf {z}\) is accepted and 0 if rejected.
Finally, we recall the definitions of the two lattice problems relevant to our work, the Module Short Integer Solution (\(\mathsf {MSIS}\)) and the decisional Module Learning With Errors ( ) problems. In both cases, we assume that there is an algorithm that, on input \(1^{\lambda }\), generates a set of public parameters \( pp \). Note that
) problems. In both cases, we assume that there is an algorithm that, on input \(1^{\lambda }\), generates a set of public parameters \( pp \). Note that  can be defined w.r.t. an arbitrary distribution; here we only focus on the case where the witness is sampled from the Gaussian distribution.
can be defined w.r.t. an arbitrary distribution; here we only focus on the case where the witness is sampled from the Gaussian distribution.
Definition 9
Let \( pp = (n, q, k_1, k_2, \beta )\), where \(n, q, k_1, k_2 \in \mathbb {Z}_{>0}\), and \(\beta \in \mathbb {R}_{>0}\). We say that the Hermite normal form of the module short integer solution problem (\(\mathsf {MSIS}\)) is \((t, \varepsilon )\)-hard w.r.t. \( pp \) if, for every algorithm \(\mathsf {A}^*\) running in time at most \(t\), we have  , where the game
, where the game  is depicted in Fig. 3.
is depicted in Fig. 3.
Definition 10
Let \( pp = (n, q, k_1, k_2, \sigma , \mathbf {A})\), where \(n, q, k_1, k_2 \in \mathbb {Z}_{>0}\), \(\sigma \in \mathbb {R}_{>0}\), and  . We say that the decisional module learning with errors problem (
. We say that the decisional module learning with errors problem ( ) is \((t, \varepsilon )\)-hard w.r.t. \( pp \) if, for every algorithm \(\mathsf {A}^*\) running in time at most \(t\), we have
) is \((t, \varepsilon )\)-hard w.r.t. \( pp \) if, for every algorithm \(\mathsf {A}^*\) running in time at most \(t\), we have  , where the game
, where the game  is depicted in Fig. 3.
is depicted in Fig. 3.
Additional Preliminaries. In the full version of this paper [5] we provide a description of the partitioning and permutation technique [3], trees of commitments technique [4], and a minor modified version of the general forking lemma [6], which is used in the security proof of  . Here, we only give the required definitions.
. Here, we only give the required definitions.
We define by  the set of signed permutation polynomials, which represent a rotation multiplied by a sign. The set \(\mathbb {T}\) has an abelian group structure with respect to multiplication in R. The inverse of any \(p = (-1)^b\cdot X^i \in \mathbb {T}\) is given by \(p^{-1} = (-1)^{1-b}\cdot X^{n-i} \in \mathbb {T}\). When constructing OR-proofs, we will use the abelian group \(\mathbb {T}^\kappa \) as the challenge space rather than \(\mathbb {T}_{\kappa }^{n}\), since the latter does not have a group structure.
the set of signed permutation polynomials, which represent a rotation multiplied by a sign. The set \(\mathbb {T}\) has an abelian group structure with respect to multiplication in R. The inverse of any \(p = (-1)^b\cdot X^i \in \mathbb {T}\) is given by \(p^{-1} = (-1)^{1-b}\cdot X^{n-i} \in \mathbb {T}\). When constructing OR-proofs, we will use the abelian group \(\mathbb {T}^\kappa \) as the challenge space rather than \(\mathbb {T}_{\kappa }^{n}\), since the latter does not have a group structure.
Let \(\mathsf {F}:\{0,1\}^{*}\rightarrow \{0,1\}^{\ell _{ {\mathsf {F}}}}\) be a cryptographic hash function, where \(\ell _{ {\mathsf {F}}}\ge 2\lambda \) for \(\mathsf {F}\) to be collision resistant. We consider the following algorithms:
-
\(\mathsf {HashTree}\) is an algorithm that computes an (unbalanced) binary hash tree of height \(h \ge 1\). On input \(\ell \le 2^h\) strings \(v_0, \ldots , v_{\ell -1}\), it returns a pair \(( root , tree )\), where \( root \) is the root of the hash tree whose leaves are hashes of \(v_0, \ldots , v_{\ell -1}\), and \( tree \) is the sequence of all the other nodes in the tree.
-
\(\mathsf {BuildAuth}\) is an algorithm that, on input an index \(0\le k \le \ell - 1\), a sequence of nodes \( tree \), and a height h, returns the authentication path \( auth \) for k.
-
\(\mathsf {RootCalc}\) is an algorithm that computes the root of a hash tree given a leaf and its authentication path.
3 BlindOR: a New Blind Signature Scheme
Sigma Protocol. In lattice-based cryptography, it is common to prove in zero-knowledge the possession of a witness \(\mathbf {s}\) with small entries such that \(\mathbf {b}=\mathbf {A}\mathbf {s}\), given a matrix \(\mathbf {A}\) and a vector \(\mathbf {b}\) over some ring (typically \(\mathbb {Z}_q\) or \(R_q\)). One approach to do so is the so-called Fiat-Shamir with Aborts technique [17]. However, rather than proving knowledge of \(\mathbf {s}\) itself, this method allows to prove knowledge of a pair \((\bar{\mathbf {s}}, \bar{c})\) satisfying \(\mathbf {b}\bar{c}=\mathbf {A}\bar{\mathbf {s}}\), where the entries of \(\bar{\mathbf {s}}\) are still small but slightly larger than those of \(\mathbf {s}\), and \(\bar{c}\) is small as well. More precisely, the Fiat-Shamir with Aborts technique allows to prove possession of a witness of the form \((\bar{\mathbf {s}}, \bar{c})\in B_1\times B_2\), where \(B_1\) and \(B_2\) are some predefined sets, even though the prover actually holds a witness of the form \((\mathbf {s},1)\in B'_1\times B_2\), where \(B'_1\subseteq B_1\). This relaxation is known to be sufficient for many cryptographic applications, e.g., digital signatures [18]. Here we extend this line of applications to blind signatures.
 is built on a variant of the Sigma protocol introduced in [17], so we briefly recall this construction before presenting our modified protocol. Given a public matrix \(\mathbf {A}\in R_q^{k_1\times k_2}\) and an instance \(\mathbf {b}\in R_q^{k_1}\), the prover holds a witness \((\mathbf {s}, 1) \in B'_1 \times B_2 \subseteq R^{k_1+k_2}\times R_q\) such that \(\mathbf {b}=[\mathbf {I}_{k_1} \,\vert \,\mathbf {A}]\cdot \mathbf {s}\pmod {q}\). An execution of the protocol allows him to prove knowledge of a witness \((\bar{\mathbf {s}}, \bar{c})\in B_1\times B_2\), with \(B'_1\subseteq B_1 \subseteq R^{k_1+k_2}\), such that \(\mathbf {b}\bar{c}=[\mathbf {I}_{k_1} \,\vert \,\mathbf {A}]\cdot \bar{\mathbf {s}}\pmod *{q}\). The commitment message is given by \(\mathbf {v}=[\mathbf {I}_{k_1} \,\vert \,\mathbf {A}]\cdot \mathbf {y}\pmod *{q}\), where \(\mathbf {y}\) is a masking vector with small entries. Upon receiving a challenge \(c\in \mathbb {T}_{\kappa }^{n}\), the response is computed as \(\mathbf {z}=\mathbf {y}+\mathbf {s}c\), and is sent to the verifier only if it follows a specified distribution, typically the Gaussian distribution \(D_{\mathbb {Z}^n, \sigma }^{k_1+k_2}\) for some \(\sigma >0\) or the uniform distribution over a small subset of \(R^{k_1+k_2}\). This ensures that \(\mathbf {y}\) masks the secret-related term \(\mathbf {s}c\) and that \(\mathbf {z}\) is independently distributed from \(\mathbf {s}\). If \(\mathbf {z}\) does not follow the target distribution, the prover restarts the protocol with a fresh \(\mathbf {y}\). The verifier accepts if \(\mathbf {v}=[\mathbf {I}_{k_1} \,\vert \,\mathbf {A}]\cdot \mathbf {z}-\mathbf {b}c\pmod {q}\) and if \(\Vert \mathbf {z}\Vert _p\) is bounded by some predefined value. Note that \(p\in \lbrace 2,\infty \rbrace \), depending on the distribution of \(\mathbf {z}\).
is built on a variant of the Sigma protocol introduced in [17], so we briefly recall this construction before presenting our modified protocol. Given a public matrix \(\mathbf {A}\in R_q^{k_1\times k_2}\) and an instance \(\mathbf {b}\in R_q^{k_1}\), the prover holds a witness \((\mathbf {s}, 1) \in B'_1 \times B_2 \subseteq R^{k_1+k_2}\times R_q\) such that \(\mathbf {b}=[\mathbf {I}_{k_1} \,\vert \,\mathbf {A}]\cdot \mathbf {s}\pmod {q}\). An execution of the protocol allows him to prove knowledge of a witness \((\bar{\mathbf {s}}, \bar{c})\in B_1\times B_2\), with \(B'_1\subseteq B_1 \subseteq R^{k_1+k_2}\), such that \(\mathbf {b}\bar{c}=[\mathbf {I}_{k_1} \,\vert \,\mathbf {A}]\cdot \bar{\mathbf {s}}\pmod *{q}\). The commitment message is given by \(\mathbf {v}=[\mathbf {I}_{k_1} \,\vert \,\mathbf {A}]\cdot \mathbf {y}\pmod *{q}\), where \(\mathbf {y}\) is a masking vector with small entries. Upon receiving a challenge \(c\in \mathbb {T}_{\kappa }^{n}\), the response is computed as \(\mathbf {z}=\mathbf {y}+\mathbf {s}c\), and is sent to the verifier only if it follows a specified distribution, typically the Gaussian distribution \(D_{\mathbb {Z}^n, \sigma }^{k_1+k_2}\) for some \(\sigma >0\) or the uniform distribution over a small subset of \(R^{k_1+k_2}\). This ensures that \(\mathbf {y}\) masks the secret-related term \(\mathbf {s}c\) and that \(\mathbf {z}\) is independently distributed from \(\mathbf {s}\). If \(\mathbf {z}\) does not follow the target distribution, the prover restarts the protocol with a fresh \(\mathbf {y}\). The verifier accepts if \(\mathbf {v}=[\mathbf {I}_{k_1} \,\vert \,\mathbf {A}]\cdot \mathbf {z}-\mathbf {b}c\pmod {q}\) and if \(\Vert \mathbf {z}\Vert _p\) is bounded by some predefined value. Note that \(p\in \lbrace 2,\infty \rbrace \), depending on the distribution of \(\mathbf {z}\).
We now turn our attention to our modified Sigma protocol, built on top of the protocol recalled above, and start by introducing the relation \(\mathcal {R}\) it is associated to. The algorithm  generates a set of public parameters of the form
generates a set of public parameters of the form

subject to the constraints given in Table 2, where the matrix \(\mathbf {A}\in R_{q}^{k_1\times k_2}\) follows the uniform distribution. In Table 3 we propose a concrete tuple of such parameters targeting 128 bits of security. The relation set is then given by

where \(\overline{\mathcal {C}}=\lbrace \mathbf {c}-\mathbf {c}'=(c_1-c'_1, \ldots , c_\kappa -c'_\kappa ) \,\vert \,\mathbf {c}, \mathbf {c}'\in \mathbb {T}^\kappa ,\ \mathbf {c}\ne \mathbf {c}'\rbrace \), and the instance generator is given in Fig. 4. The actual witness the prover possesses is of the form \((\mathbf {s},1)\), where \(\Vert \mathbf {s}\Vert \le B_s < B_z\) and \(\mathbf {b}=[\mathbf {I}_{k_1} \,\vert \,\mathbf {A}]\cdot \mathbf {s}\pmod *{q}\). The challenge space of the protocol is \(\mathbb {T}^\kappa \), and its other algorithms are given in Fig. 4.
At a high level, the protocol can be seen as a generalized version of the one given in [17] and briefly recalled above. In particular, it is optimized to work for  . Rather than computing only one commitment to a masking vector in
. Rather than computing only one commitment to a masking vector in  , the prover computes commitments to \(\omega \ge 1\) such vectors and sends them to the verifier all at once. Choosing \(\omega >1\) allows to reduce the number of restarts, since the chance of masking the secret-related term without restarting the protocol is increased. More concretely, increasing \(\omega \) allows to compute a response such that there is no need to trigger a protocol restart with some fixed probability. The masking vectors are chosen according to the Gaussian distribution \(D^{k_1+k_2}_{\mathbb {Z}^n, \sigma ^*}\). Upon receiving the challenge \(\mathbf {c}\in \mathbb {T}^\kappa \), the prover sends the first response \(\mathbf {z}\) for which rejection sampling accepts, i.e., for the masking vector \(\mathbf {y}^{(i)}\) such that \(\mathsf {Rej}( pp , \mathbf {z})=1\) and i is chosen from the uniform distribution over the set \(T\subseteq \{0, \ldots , \omega -1\}\). The random choice of the index i ensures that the simulator
, the prover computes commitments to \(\omega \ge 1\) such vectors and sends them to the verifier all at once. Choosing \(\omega >1\) allows to reduce the number of restarts, since the chance of masking the secret-related term without restarting the protocol is increased. More concretely, increasing \(\omega \) allows to compute a response such that there is no need to trigger a protocol restart with some fixed probability. The masking vectors are chosen according to the Gaussian distribution \(D^{k_1+k_2}_{\mathbb {Z}^n, \sigma ^*}\). Upon receiving the challenge \(\mathbf {c}\in \mathbb {T}^\kappa \), the prover sends the first response \(\mathbf {z}\) for which rejection sampling accepts, i.e., for the masking vector \(\mathbf {y}^{(i)}\) such that \(\mathsf {Rej}( pp , \mathbf {z})=1\) and i is chosen from the uniform distribution over the set \(T\subseteq \{0, \ldots , \omega -1\}\). The random choice of the index i ensures that the simulator  returns \((\mathbf {v}, \mathbf {z})\ne (\bot , \bot )\) with the same probability as the prover. Note that each of the \(\omega \) commitments consists of \(\kappa \) components, where \(\kappa \) defines the challenge space \(\mathbb {T}^\kappa \). This allows to use the partitioning and permutation technique in
returns \((\mathbf {v}, \mathbf {z})\ne (\bot , \bot )\) with the same probability as the prover. Note that each of the \(\omega \) commitments consists of \(\kappa \) components, where \(\kappa \) defines the challenge space \(\mathbb {T}^\kappa \). This allows to use the partitioning and permutation technique in  . To verify a transcript \((\mathbf {v}, \mathbf {c}, \mathbf {z})\), the verifier first finds out which of the \(\omega \) commitments is related to the response. The index i of the corresponding commitment is part of the verifier’s output.
. To verify a transcript \((\mathbf {v}, \mathbf {c}, \mathbf {z})\), the verifier first finds out which of the \(\omega \) commitments is related to the response. The index i of the corresponding commitment is part of the verifier’s output.
Theorem 11
Given the parameters in Table 2, the protocol depicted in Fig. 4 is a Sigma protocol for relation \(\mathcal {R}\) given in Eq. (1).
The proof is provided in the full version of this paper [5]. We remark that when constructing the Sigma protocol \(\varSigma _{\mathsf {OR}}=\mathsf {OR}[\varSigma , \varSigma ]\), where \(\varSigma \) is the protocol introduced above, we must consider the group operation defined on the challenge space \(\mathbb {T}^\kappa \). More precisely,  samples
samples  and then runs
and then runs  on \(\mathbf {c}_{1-d}\). Upon receiving a challenge \(\mathbf {c}=(c_1, \ldots , c_\kappa )\) from
on \(\mathbf {c}_{1-d}\). Upon receiving a challenge \(\mathbf {c}=(c_1, \ldots , c_\kappa )\) from  ,
,  computes \(\mathbf {c}_{d}=(c_1 c^{-1}_{1,1-d}, \ldots , c_\kappa c^{-1}_{\kappa ,1-d})\) and runs
computes \(\mathbf {c}_{d}=(c_1 c^{-1}_{1,1-d}, \ldots , c_\kappa c^{-1}_{\kappa ,1-d})\) and runs  on \(\mathbf {c}_{d}\). Therefore, we have \(\mathbf {c}=\mathbf {c}_{d}\cdot \mathbf {c}_{1-d}=(c_{1,d}c_{1,1-d}, \ldots , c_{\kappa ,d}c_{\kappa ,1-d})\).
on \(\mathbf {c}_{d}\). Therefore, we have \(\mathbf {c}=\mathbf {c}_{d}\cdot \mathbf {c}_{1-d}=(c_{1,d}c_{1,1-d}, \ldots , c_{\kappa ,d}c_{\kappa ,1-d})\).
Description of BlindOR. Let \(\mathsf {BS}\) be a blind signature scheme as defined in Sect. 2. Recall how signing and verification of such a scheme works. The signer computes and sends a commitment \( cm ^*\) to the user. The user blinds \( cm ^*\) to obtain a blind commitment \( cm \) and computes a challenge \( ch \), which is generated by evaluating a hash function \(\mathsf {H}\) on input \(( cm , m )\), i.e. \( ch =\mathsf {H}( cm , m )\) with \( m \) being a message. After that, the user unblinds \( ch \) to obtain a challenge \( ch ^*\) and sends it to the signer. The signer computes a response \( rp ^*\) and sends it back to the user. Finally, the user blinds \( rp ^*\) to obtain a blind response \( rp \) and outputs \( sig =( ch , rp )\). Verifying the validity of \( sig \) is established by computing a commitment \( cm \) corresponding to \( ch \) and \( rp \), and then checking if \( ch \) matches \(\mathsf {H}( cm , m )\). Observe that while the steps carried out by the signer are actually what a prover in a Sigma protocol does when proving the possession of a witness for a statement, the steps performed by the user consist of blinding the transcript \(( cm ^*, ch ^*, rp ^*)\) during interaction. In  , we capture these blinding steps by algorithms \(\mathsf {Com}, \mathsf {Cha}\), and \(\mathsf {Rsp}\), which we describe next.
, we capture these blinding steps by algorithms \(\mathsf {Com}, \mathsf {Cha}\), and \(\mathsf {Rsp}\), which we describe next.
For the remainder of this section we let \(\varSigma \) be the Sigma protocol depicted in Fig. 4. Furthermore, let \(h=\lceil \log (\omega \ell )\rceil \) and define the bijective mapping \(\mathsf {IntIdx}:\lbrace 0, \ldots , \omega -1\rbrace \times \lbrace 0, \ldots , \ell -1\rbrace \rightarrow \lbrace 0, \ldots , \omega \ell -1\rbrace ,\ (i,k)\mapsto k+i\ell \). \(\mathsf {IntIdx}\) converts the pair \((i,k)\) to a unique positive integer. This is used in  to build authentication paths via the algorithm \(\mathsf {BuildAuth}\). Let \( pp \) be a set of public parameters for
to build authentication paths via the algorithm \(\mathsf {BuildAuth}\). Let \( pp \) be a set of public parameters for  and \(x=\mathbf {b}\in R_q^{k_1}\) be an instance for \(\mathcal {R}\). We define the following algorithms, which are formally described in Fig. 5:
and \(x=\mathbf {b}\in R_q^{k_1}\) be an instance for \(\mathcal {R}\). We define the following algorithms, which are formally described in Fig. 5:
-
\(\mathsf {Com}\) is a PPT algorithm that, on input \( pp \), \(x\), and a commitment \( cm ^*=\mathbf {v}^*\) generated by
 , returns a blind commitment \( cm = root \) and a state \((\mathbf {p}, tree ,\mathbf {e})\).
, returns a blind commitment \( cm = root \) and a state \((\mathbf {p}, tree ,\mathbf {e})\). -
\(\mathsf {Cha}\) is a DPT algorithm that, on input \( pp \), a randomness \(\mathbf {p}\in \mathbb {T}^\kappa \), a challenge \( ch ^*=\mathbf {c}^* \in \mathbb {T}^\kappa \), and an auxiliary bit \(b\in \{0,1\}\), returns a challenge \( ch =\mathbf {c}\in \mathbb {T}^\kappa \). Observe that \(b\) determines if \(\mathbf {c}^*\) will be blinded using \(\mathbf {p}\) or using its inverse with respect to the group operation defined on \(\mathbb {T}^\kappa \).
-
\(\mathsf {Rsp}\) is a DPT algorithm that, on input \( pp \), a state \((\mathbf {p}, tree ,\mathbf {e})\), a response \( rp ^*=\mathbf {z}^*\) generated by
 , and an integer \(i\in \lbrace 0,\ldots ,\omega -1\rbrace \), returns a blind response \( rp =(\mathbf {z}, auth )\), where \( rp =(\bot ,\bot )\) is possible.
, and an integer \(i\in \lbrace 0,\ldots ,\omega -1\rbrace \), returns a blind response \( rp =(\mathbf {z}, auth )\), where \( rp =(\bot ,\bot )\) is possible. -
\(\mathsf {Rec}\) is a DPT algorithm that, on input \( pp \), the statement \(x\), a challenge \( ch \), and a response \( rp \), returns a commitment \( cm \), where \( cm =\bot \) is possible.
Note that the blinding algorithms depicted in Fig. 5 can be seen as a generalized version of the blinding steps implicitly presented in the lattice-based blind signature scheme \(\mathsf {BLAZE}^{+}\) [4]. Unlike \(\mathsf {BLAZE}^{+}\), the algorithms shown in Fig. 5 are defined for lattices over modules rather than over rings. This complies with the module structure of \(\varSigma \) and allows for more flexibility when choosing concrete parameters. Furthermore, these blinding algorithms employ the partitioning and permutation technique, which allows to use the abelian group \(\mathbb {T}^\kappa \) as a challenge space rather than the set \(\mathbb {T}_{\kappa }^{n}\), which does not have a group structure. Moreover, the algorithm \(\mathsf {Com}\) blinds \(\omega \) commitments \({\mathbf {v}^*}^{(0)}, \ldots , {\mathbf {v}^*}^{(\omega -1)}\) rather than only one commitment generated by  . More precisely, the trees of commitments technique employed in \(\mathsf {BLAZE}^{+}\) is extended to further include \(\omega \) commitments created by the prover. These \(\omega \) commitments are then combined with \(\ell \) commitments generated within \(\mathsf {Com}\) to compute the root related to a tree of \(\omega \ell \) commitments. We require \(\ell \) to be chosen large enough so that \(\mathsf {Rsp}\) returns a blind response \((\mathbf {z}, auth )=(\bot , \bot )\) with probability close to zero, e.g., \(2^{-80}\). This is crucial for
. More precisely, the trees of commitments technique employed in \(\mathsf {BLAZE}^{+}\) is extended to further include \(\omega \) commitments created by the prover. These \(\omega \) commitments are then combined with \(\ell \) commitments generated within \(\mathsf {Com}\) to compute the root related to a tree of \(\omega \ell \) commitments. We require \(\ell \) to be chosen large enough so that \(\mathsf {Rsp}\) returns a blind response \((\mathbf {z}, auth )=(\bot , \bot )\) with probability close to zero, e.g., \(2^{-80}\). This is crucial for  since otherwise, we would need an extra move between the signer and user, which would allow the user to request a restart of the signing protocol in case the algorithm \(\mathsf {IterateRej}\) returns \((\bot , \bot )\). This extra move would increase the communication complexity and force the signer to carry out almost all computations performed by the user before triggering a protocol restart. Moreover, this extra move would not allow the use of Gaussian distributed masking vectors \(\mathbf {e}\) since a blind signature could be correctly verified even if rejection sampling does not accept. This would enable the user to request a protocol restart and obtain two different signatures. The advantage of using the Gaussian distribution for masking is that it allows to generate blind signatures with a size smaller than signatures generated using masking vectors that are uniformly distributed over a small subset of R.
since otherwise, we would need an extra move between the signer and user, which would allow the user to request a restart of the signing protocol in case the algorithm \(\mathsf {IterateRej}\) returns \((\bot , \bot )\). This extra move would increase the communication complexity and force the signer to carry out almost all computations performed by the user before triggering a protocol restart. Moreover, this extra move would not allow the use of Gaussian distributed masking vectors \(\mathbf {e}\) since a blind signature could be correctly verified even if rejection sampling does not accept. This would enable the user to request a protocol restart and obtain two different signatures. The advantage of using the Gaussian distribution for masking is that it allows to generate blind signatures with a size smaller than signatures generated using masking vectors that are uniformly distributed over a small subset of R.
Next, we describe  . Let \(\varSigma _{\mathsf {OR}}=\mathsf {OR}[\varSigma , \varSigma ]\) and \(\mathsf {F}:\{0,1\}^*\rightarrow \{0,1\}^{\ell _{ {\mathsf {F}}}}\), \(\mathsf {H}:\{0,1\}^*\rightarrow \mathbb {T}^{\kappa }\) be hash functions, where \(\ell _{ {\mathsf {F}}}\ge 2\lambda \) and \(\mathbb {T}^{\kappa }\) is the challenge space of \(\varSigma \). The algorithm
. Let \(\varSigma _{\mathsf {OR}}=\mathsf {OR}[\varSigma , \varSigma ]\) and \(\mathsf {F}:\{0,1\}^*\rightarrow \{0,1\}^{\ell _{ {\mathsf {F}}}}\), \(\mathsf {H}:\{0,1\}^*\rightarrow \mathbb {T}^{\kappa }\) be hash functions, where \(\ell _{ {\mathsf {F}}}\ge 2\lambda \) and \(\mathbb {T}^{\kappa }\) is the challenge space of \(\varSigma \). The algorithm  generates and returns a set of public parameters
generates and returns a set of public parameters  . The description of the parameters is summarized in Table 2. The matrix \(\mathbf {A}\) is chosen from the uniform distribution over \(R_{q}^{k_1\times k_2}\). We remark that \( pp \) includes the public parameters of the relation \(\mathcal {R}\) for which \(\varSigma \) is defined, i.e.,
. The description of the parameters is summarized in Table 2. The matrix \(\mathbf {A}\) is chosen from the uniform distribution over \(R_{q}^{k_1\times k_2}\). We remark that \( pp \) includes the public parameters of the relation \(\mathcal {R}\) for which \(\varSigma \) is defined, i.e.,  may first run
may first run  and then generates the remaining parameters of the scheme. For simplicity, the input of the algorithms of \(\varSigma \) includes \( pp \). The remaining algorithms of
and then generates the remaining parameters of the scheme. For simplicity, the input of the algorithms of \(\varSigma \) includes \( pp \). The remaining algorithms of  are formalized in Fig. 6.
are formalized in Fig. 6.
 .
.In Table 3, we propose concrete parameters for  targeting 128 bits of security. Next, we state the correctness, blindness, and one-more unforgeability of
targeting 128 bits of security. Next, we state the correctness, blindness, and one-more unforgeability of  . We provide the description of the parameter selection as well as the proof of correctness in the full version of this paper [5].
. We provide the description of the parameter selection as well as the proof of correctness in the full version of this paper [5].
 targeting 128 bits of security.
targeting 128 bits of security.Theorem 12
Given the parameters in Table 2,  is \(\mathsf {corr}_{\mathsf {BS}}\)-correct w.r.t. \( pp \), where \(\mathsf {corr}_{\mathsf {BS}}=\delta ^*+2\varepsilon ^*+2\delta +2\varepsilon \), \(\delta ^*\) is the probability that algorithm
is \(\mathsf {corr}_{\mathsf {BS}}\)-correct w.r.t. \( pp \), where \(\mathsf {corr}_{\mathsf {BS}}=\delta ^*+2\varepsilon ^*+2\delta +2\varepsilon \), \(\delta ^*\) is the probability that algorithm  returns \(\bot \), \(\varepsilon ^*\) is the probability that algorithm
returns \(\bot \), \(\varepsilon ^*\) is the probability that algorithm  returns \((0,i)\), \(\delta \) is the probability that algorithm \(\mathsf {Rsp}\) returns \(\bot \), and \(\varepsilon \) is the probability that \(\mathsf {Rec}\) returns \(\bot \).
returns \((0,i)\), \(\delta \) is the probability that algorithm \(\mathsf {Rsp}\) returns \(\bot \), and \(\varepsilon \) is the probability that \(\mathsf {Rec}\) returns \(\bot \).
Theorem 13
Let \(\mathsf {F}:\{0,1\}^{*}\rightarrow \{0,1\}^{\ell _{ {\mathsf {F}}}}\) and \(\mathsf {H}:\{0,1\}^{*}\rightarrow \mathbb {T}^\kappa \) be two hash functions modeled as random oracles. Given the parameters in Table 2,  is \(\varepsilon \)-statistically blind w.r.t. \( pp \) in the ROM, where \(\varepsilon =\max \lbrace *\rbrace {(2n)^{-\kappa }, 2^{-100}/U}\).
is \(\varepsilon \)-statistically blind w.r.t. \( pp \) in the ROM, where \(\varepsilon =\max \lbrace *\rbrace {(2n)^{-\kappa }, 2^{-100}/U}\).
Proof
Let  be an adversarial signer in the blindness experiment
be an adversarial signer in the blindness experiment  defined in Fig. 2. Then,
defined in Fig. 2. Then,  selects two messages \( m _0, m _1\) and interacts with the honest user twice. The goal is to show that after both interactions, the messages output by the user, i.e., two blind challenges of the form \(\mathbf {c}^*\in \mathbb {T}^\kappa \) together with two blind signatures of the form \( sig =(\mathbf {c}_0, \mathbf {c}_1, \mathbf {z}_0, \mathbf {z}_1, auth _0, auth _1)\), are independently distributed and do not leak any information about the signed messages and the respective interaction.
selects two messages \( m _0, m _1\) and interacts with the honest user twice. The goal is to show that after both interactions, the messages output by the user, i.e., two blind challenges of the form \(\mathbf {c}^*\in \mathbb {T}^\kappa \) together with two blind signatures of the form \( sig =(\mathbf {c}_0, \mathbf {c}_1, \mathbf {z}_0, \mathbf {z}_1, auth _0, auth _1)\), are independently distributed and do not leak any information about the signed messages and the respective interaction.
The authentication paths \( auth _0, auth _1\) include hash values that are uniformly distributed over \(\{0,1\}^{\ell _{ {\mathsf {F}}}}\). The challenge \(\mathbf {c}^*\) as well as the signature part \((\mathbf {c}_0, \mathbf {c}_1)\) are uniformly distributed over \(\mathbb {T}^\kappa \), and hence they do not leak any information. Moreover, [3, Lemma 4] ensures that \(\mathbf {c}^*\) is independently distributed from \(\mathbf {c}=\mathbf {c}_0\cdot \mathbf {c}_1\), and  can link \(\mathbf {c}\) to the correct \(\mathbf {c}^*\) only with probability \((2n)^{-\kappa }\) over guessing. The blind vectors \(\mathbf {z}_0, \mathbf {z}_1\) have the form \(\mathbf {z}=\mathbf {e}+\sum _{j=1}^{\kappa }\mathbf {z}^*_{j}p_j\) (see Fig. 5). By Lemma 8, both vectors completely mask \(\sum _{j=1}^{\kappa }\mathbf {z}^*_{j}p_j\) and are independently distributed within statistical distance of \(2^{-100}/U\) from \(D^{k_1+k_2}_{\mathbb {Z}^n,\sigma }\).
can link \(\mathbf {c}\) to the correct \(\mathbf {c}^*\) only with probability \((2n)^{-\kappa }\) over guessing. The blind vectors \(\mathbf {z}_0, \mathbf {z}_1\) have the form \(\mathbf {z}=\mathbf {e}+\sum _{j=1}^{\kappa }\mathbf {z}^*_{j}p_j\) (see Fig. 5). By Lemma 8, both vectors completely mask \(\sum _{j=1}^{\kappa }\mathbf {z}^*_{j}p_j\) and are independently distributed within statistical distance of \(2^{-100}/U\) from \(D^{k_1+k_2}_{\mathbb {Z}^n,\sigma }\).
Finally, if a protocol restart is triggered by  , then
, then  generates fresh random elements. Therefore, the protocol restarts are independent of each other, and hence
generates fresh random elements. Therefore, the protocol restarts are independent of each other, and hence  does not get any information about the message being signed. \(\square \)
does not get any information about the message being signed. \(\square \)
Theorem 14
Let \(\mathsf {F}:\{0,1\}^*\rightarrow \{0,1\}^{\ell _{ {\mathsf {F}}}}\) and \(\mathsf {H}:\{0,1\}^*\rightarrow \mathbb {T}^\kappa \) be two hash functions modeled as random oracles. Given the parameters in Table 2,  is \((t, q_{\mathsf {Sign}}, q_{\mathsf {F}}, q_{\mathsf {H}}, \varepsilon )\)-one-more unforgeable w.r.t. \( pp \) in the ROM if
is \((t, q_{\mathsf {Sign}}, q_{\mathsf {F}}, q_{\mathsf {H}}, \varepsilon )\)-one-more unforgeable w.r.t. \( pp \) in the ROM if  is \((t', \varepsilon ')\)-hard w.r.t. \( pp _{\mathsf {MLWE}}= (n, q, k_1, k_2, \sigma ',\mathbf {A})\) and \(\mathsf {MSIS}\) is \((t'', \varepsilon '')\)-hard w.r.t. \( pp _{\mathsf {MSIS}}= (n, q, k_1, k_2+1, 2\sqrt{B_z^2+\kappa ^2})\). More precisely, if there exists a forger \(\mathsf {A}^*\) against
is \((t', \varepsilon ')\)-hard w.r.t. \( pp _{\mathsf {MLWE}}= (n, q, k_1, k_2, \sigma ',\mathbf {A})\) and \(\mathsf {MSIS}\) is \((t'', \varepsilon '')\)-hard w.r.t. \( pp _{\mathsf {MSIS}}= (n, q, k_1, k_2+1, 2\sqrt{B_z^2+\kappa ^2})\). More precisely, if there exists a forger \(\mathsf {A}^*\) against  w.r.t. \( pp \) that returns \(q_{\mathsf {Sign}}+1\) blind signatures in time \(t\) and with probability \(\varepsilon \), and after making \(q_{\mathsf {F}}, q_{\mathsf {H}}\) queries to \(\mathsf {F}, \mathsf {H}\), respectively, then \(\mathsf {A}^*\) can be used to solve
w.r.t. \( pp \) that returns \(q_{\mathsf {Sign}}+1\) blind signatures in time \(t\) and with probability \(\varepsilon \), and after making \(q_{\mathsf {F}}, q_{\mathsf {H}}\) queries to \(\mathsf {F}, \mathsf {H}\), respectively, then \(\mathsf {A}^*\) can be used to solve  w.r.t. \( pp _{\mathsf {MLWE}}\) in time \(t' \approx t\) and advantage \(\varepsilon ' \approx \varepsilon \), or \(\mathsf {A}^*\) can be used to solve \(\mathsf {MSIS}\) w.r.t. \( pp _{\mathsf {MSIS}}\) in time \(t'' \approx 2 t\) and probability
w.r.t. \( pp _{\mathsf {MLWE}}\) in time \(t' \approx t\) and advantage \(\varepsilon ' \approx \varepsilon \), or \(\mathsf {A}^*\) can be used to solve \(\mathsf {MSIS}\) w.r.t. \( pp _{\mathsf {MSIS}}\) in time \(t'' \approx 2 t\) and probability

where  .
.
Proof
First we observe that the hardness of  is required to protect against key recovery attacks, i.e., being able to determine the yes-instance of \(\mathsf {MLWE}\) included in the public key \(\textit{pk}= (\mathbf {b}_0, \mathbf {b}_1)\) allows to compute the secret key, and hence forgeries. Therefore, in what follows we assume the hardness of
is required to protect against key recovery attacks, i.e., being able to determine the yes-instance of \(\mathsf {MLWE}\) included in the public key \(\textit{pk}= (\mathbf {b}_0, \mathbf {b}_1)\) allows to compute the secret key, and hence forgeries. Therefore, in what follows we assume the hardness of  w.r.t. \( pp _{\mathsf {MLWE}}\), and construct a reduction algorithm \(\mathsf {R}\) that solves \(\mathsf {MSIS}\) w.r.t. \( pp _{\mathsf {MSIS}}\) as given in the theorem statement.
w.r.t. \( pp _{\mathsf {MLWE}}\), and construct a reduction algorithm \(\mathsf {R}\) that solves \(\mathsf {MSIS}\) w.r.t. \( pp _{\mathsf {MSIS}}\) as given in the theorem statement.
Given \( pp _{\mathsf {MSIS}}\) and a matrix \(\mathbf {A}' \in R_{q}^{k_1 \times (k_2+1)}\), \(\mathsf {R}\) chooses a bit  , and writes \(\mathbf {A}' = [\mathbf {A}\,\vert \,\mathbf {b}_{1-d}] \in R_{q}^{k_1 \times k_2} \times R_{q}^{k_1}\). Then, it generates the remaining public parameters \( pp \) of
, and writes \(\mathbf {A}' = [\mathbf {A}\,\vert \,\mathbf {b}_{1-d}] \in R_{q}^{k_1 \times k_2} \times R_{q}^{k_1}\). Then, it generates the remaining public parameters \( pp \) of  , and sets \(C = \lbrace \mathbf {c}_1, \ldots , \mathbf {c}_{q_{\mathsf {H}}}\rbrace \), where
, and sets \(C = \lbrace \mathbf {c}_1, \ldots , \mathbf {c}_{q_{\mathsf {H}}}\rbrace \), where  . Afterwards, \(\mathsf {R}\) runs
. Afterwards, \(\mathsf {R}\) runs  to obtain \((\mathbf {b}_{d}, \mathbf {s})\). Then, \(\mathsf {R}\) sets \(\textit{pk}= (\mathbf {b}_0, \mathbf {b}_1)\), \(\textit{sk}= (d,\mathbf {s})\), and runs \(\mathsf {A}^*\) on input \(( pp , \textit{pk})\). The random oracle and signing queries that \(\mathsf {A}^*\) make are answered by \(\mathsf {R}\) as follows:
to obtain \((\mathbf {b}_{d}, \mathbf {s})\). Then, \(\mathsf {R}\) sets \(\textit{pk}= (\mathbf {b}_0, \mathbf {b}_1)\), \(\textit{sk}= (d,\mathbf {s})\), and runs \(\mathsf {A}^*\) on input \(( pp , \textit{pk})\). The random oracle and signing queries that \(\mathsf {A}^*\) make are answered by \(\mathsf {R}\) as follows:
-
Random Oracle Query. \(\mathsf {R}\) maintains a list \(L_{\mathsf {H}}\) initialized by the empty set. It stores pairs of queries to \(\mathsf {H}\) and their answers. If \(\mathsf {H}\) was previously queried on some input, then \(\mathsf {R}\) looks up its entry in \(L_{\mathsf {H}}\) and returns its answer \(\mathbf {c}\). Otherwise, it picks the first unused \(\mathbf {c}\in C\) and updates the list. Furthermore, \(\mathsf {R}\) initializes an empty list \(L_{\mathsf {F}}\) to store pairs of queries to \(\mathsf {F}\) and their answers. The queries to \(\mathsf {F}\) are answered in a way that excludes collisions and chains. Excluding collisions rules out queries \(\mathbf {x}\ne \mathbf {x}'\) such that \(\mathsf {F}(\mathbf {x}) = \mathsf {F}(\mathbf {x}')\), and excluding chains guarantees that the query \(\mathsf {F}(\mathsf {F}(\mathbf {x}))\) will not be made before the query \(\mathsf {F}(\mathbf {x})\). This ensures that each node output by \(\mathsf {HashTree}\) has a unique preimage, and prevents spanning hash trees with cycles. Simulating \(\mathsf {F}\) this way is within statistical distance of at most \(\frac{q_{\mathsf {F}}^2+q_{\mathsf {F}}}{2^{\ell _{ {\mathsf {F}}}}}\) from an oracle that allows collisions and chains.
-
Signature Query. Upon receiving a signature query from \(\mathsf {A}^*\), \(\mathsf {R}\) runs the signing protocol of
 . Furthermore, \(\mathsf {R}\) updates both lists \(L_{\mathsf {H}}\) and \(L_{\mathsf {F}}\) accordingly.
. Furthermore, \(\mathsf {R}\) updates both lists \(L_{\mathsf {H}}\) and \(L_{\mathsf {F}}\) accordingly.
After \(q_{\mathsf {Sign}}\) successful invocations, \(\mathsf {A}^*\) returns \(q_{\mathsf {Sign}}+1\) pairs of distinct messages and their signatures, where one of these pairs is not generated during the interaction. If \(\mathsf {H}\) was not programmed or queried during invocation of \(\mathsf {A}^*\), then \(\mathsf {A}^*\) produces a \(\mathbf {c}\in \mathbb {T}^{\kappa }\) that validates correctly with probability \(1/|\mathbb {T}^{\kappa }|\). Therefore, the probability that \(\mathsf {A}^*\) succeeds in a forgery such that all \(q_{\mathsf {Sign}}+1\) signatures correspond to random oracle queries made by \(\mathsf {A}^*\) is at least \(\varepsilon -\frac{q_{\mathsf {Sign}}+1}{|\mathbb {T}^{\kappa }|}\).
Afterwards, \(\mathsf {R}\) guesses an index \(i^* \in [q_{\mathsf {Sign}}+1]\) such that \(\mathbf {c}_{i^*} = \mathbf {c}_{j^*}\) for some \(j^* \in [q_{\mathsf {H}}]\). Then, \(\mathsf {R}\) records the pair \(( m _{i^*}, sig _{i^*} = (\mathbf {c}_0, \mathbf {c}_1, \mathbf {z}_0, \mathbf {z}_1, auth _0, auth _1))\) and invokes \(\mathsf {A}^*\) again with the same random tape and the random oracle queries \(C' = \lbrace \mathbf {c}_1, \ldots , \mathbf {c}_{j^*-1}, \mathbf {c}'_{j^*}, \ldots , \mathbf {c}'_{q_{\mathsf {H}}}\rbrace \), where \(\mathbf {c}'_{j^*}, \ldots , \mathbf {c}'_{q_{\mathsf {H}}}\in \mathbb {T}^\kappa \) are freshly generated by \(\mathsf {R}\). After rewinding, \(\mathsf {A}^*\) returns \(q_{\mathsf {Sign}}+1\) pairs of distinct messages and their valid signatures. The potential two valid forgeries (before and after rewinding) output by \(\mathsf {A}^*\) at index \(i^*\) have the form
where \(\mathbf {c}_i = (c_{1,i}, \ldots , c_{\kappa ,i})\) and \(\mathbf {c}'_i =(*){c'_{1,i}, \ldots , c'_{\kappa ,i}}\), \(i \in \{0,1\}\). By the verification algorithm we obtain
By the forking lemma (see the full version [5]) we have \( root _0 = root '_0\), \( root _1 = root '_1\), \( m = m '\), \(\mathbf {c}\ne \mathbf {c}'\), and \(k_{1-d} = k'_{1-d}\), where \(k_{1-d}, k'_{1-d} \in \lbrace 0, \ldots , \omega \ell -1\rbrace \) are the indices included in \( auth _{1-d}, auth '_{1-d}\), respectively. Observe that simulating the hash queries to \(\mathsf {F}\) as described above ensures that both \( auth _{1-d}, auth '_{1-d}\) include the same sequence of hash values, and hence \( auth _{1-d} = auth '_{1-d}\) and \(\mathbf {w}_{1-d}=\mathbf {w}'_{1-d}\). If \(\mathbf {c}_{1-d}\ne \mathbf {c}'_{1-d}\), then we have
where \(c_{1-d}=\sum _{j=1}^\kappa c_{j,1-d}\) and \(c'_{1-d}=\sum _{j=1}^\kappa c'_{j,1-d}\). In this case, \(\mathsf {R}\) runs  on input \(( pp ,\mathbf {b}_{1-d},(\mathbf {v},\mathbf {c},\mathbf {z}),(\mathbf {v},\mathbf {c}',\mathbf {z}'))\), where
on input \(( pp ,\mathbf {b}_{1-d},(\mathbf {v},\mathbf {c},\mathbf {z}),(\mathbf {v},\mathbf {c}',\mathbf {z}'))\), where
The output of  is the pair \((\mathbf {z}_{1-d}-\mathbf {z}'_{1-d},\mathbf {c}_{1-d}-\mathbf {c}'_{1-d})\), which gives the non-trivial solution \([\mathbf {z}_{1-d}-\mathbf {z}'_{1-d}\,\vert \,c'_{1-d}-c_{1-d}]^\top \) to \(\mathsf {MSIS}\) w.r.t. \( pp _{\mathsf {MSIS}}\) and the matrix \([\mathbf {I}_{k_1}\,\vert \,\mathbf {A}\,\vert \,\mathbf {b}_{1-d}]=[\mathbf {I}_{k_1}\,\vert \,\mathbf {A}']\).
is the pair \((\mathbf {z}_{1-d}-\mathbf {z}'_{1-d},\mathbf {c}_{1-d}-\mathbf {c}'_{1-d})\), which gives the non-trivial solution \([\mathbf {z}_{1-d}-\mathbf {z}'_{1-d}\,\vert \,c'_{1-d}-c_{1-d}]^\top \) to \(\mathsf {MSIS}\) w.r.t. \( pp _{\mathsf {MSIS}}\) and the matrix \([\mathbf {I}_{k_1}\,\vert \,\mathbf {A}\,\vert \,\mathbf {b}_{1-d}]=[\mathbf {I}_{k_1}\,\vert \,\mathbf {A}']\).
Next, we analyze the success probability of \(\mathsf {R}\). The probability that \(\mathsf {R}\) answers the correct sequence of \(q_{\mathsf {Sign}}+1\) random oracle queries to \(\mathsf {H}\) that are used by \(\mathsf {A}^*\) in the forgery is at least \(1/q_{\mathsf {H}}^{q_{\mathsf {Sign}}+1}\). Since one of the \(q_{\mathsf {Sign}}+1\) pairs output by \(\mathsf {A}^*\) is by assumption not generated during the interaction with \(\mathsf {R}\), the probability of correctly guessing the index \(i^*\) corresponding to this pair is \(1/(q_{\mathsf {Sign}}+1)\). The success probability of the forking is given by \( frk \ge acc \cdot (\frac{ acc }{(q_{\mathsf {Sign}}+1)\omega \ell }-\frac{1}{|\mathbb {T}^{\kappa }|})\), where \( acc =(\varepsilon -\frac{q_{\mathsf {F}}^2+q_{\mathsf {F}}}{2^{\ell _{ {\mathsf {F}}}}}-\frac{q_{\mathsf {Sign}}+1}{|\mathbb {T}^{\kappa }|})\Big /q_{\mathsf {H}}^{q_{\mathsf {Sign}}+1}\). By Lemma 15, the probability that \(\mathbf {c}_{1-d}\ne \mathbf {c}'_{1-d}\) is given by \(\frac{1}{2}-\varepsilon '\). This deduces the probability \(\varepsilon ''\) that is given in the theorem statement. \(\square \)
Lemma 15
Assume that after rewinding the forger \(\mathsf {A}^*\) by the reduction \(\mathsf {R}\) given in Theorem 14, the two forgeries output by \(\mathsf {A}^*\) satisfy \(\mathbf {c}_{1-d} = \mathbf {c}'_{1-d}\) with probability \(1/2+\varepsilon '\), where \(d\) corresponds to the yes-instance of \(\mathsf {MLWE}\) included in the public key and \(\varepsilon '\) is noticeably greater than 0. Then, there exists a distinguisher \(\mathsf {D}^*\) that uses \(\mathsf {A}^*\) to win the experiment  with the advantage \(\varepsilon '\).
with the advantage \(\varepsilon '\).
The proof is provided in the full version of this paper [5].
References
Abe, M., Okamoto, T.: Provably secure partially blind signatures. In: Bellare, M. (ed.) CRYPTO 2000. LNCS, vol. 1880, pp. 271–286. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-44598-6_17
Agrawal, S., Yadav, A.L.: Towards practical and round-optimal lattice-based threshold and blind signatures. Cryptology ePrint Archive, Report 2021/381
Alkeilani Alkadri, N., El Bansarkhani, R., Buchmann, J.: BLAZE: practical lattice-based blind signatures for privacy-preserving applications. In: Bonneau, J., Heninger, N. (eds.) FC 2020. LNCS, vol. 12059, pp. 484–502. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-51280-4_26
Alkeilani Alkadri, N., El Bansarkhani, R., Buchmann, J.: On lattice-based interactive protocols: an approach with less or no aborts. In: Liu, J.K., Cui, H. (eds.) ACISP 2020. LNCS, vol. 12248, pp. 41–61. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-55304-3_3
Alkeilani Alkadri, N., Harasser, P., Janson, C.: BlindOR: an efficient lattice-based blind signature scheme from or-proofs. Cryptology ePrint Archive, Report 2021/1385
Bellare, M., Neven, G.: Multi-signatures in the plain public-key model and a general forking lemma. In: ACM CCS 2006
Bellare, M., Rogaway, P.: Random oracles are practical: a paradigm for designing efficient protocols. In: ACM CCS 93
Camenisch, J., Neven, G., Shelat: Simulatable adaptive oblivious transfer. In: Naor, M. (ed.) EUROCRYPT 2007. LNCS, vol. 4515, pp. 573–590. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-72540-4_33
Chaum, D.: Blind signatures for untraceable payments. In: Chaum, D., Rivest, R.L., Sherman, A.T. (eds.) Advances in Cryptology. LNCS, pp. 199–203. Springer, Boston, MA (1983). https://doi.org/10.1007/978-1-4757-0602-4_18
Cramer, R., Damgård, I., Schoenmakers, B.: Proofs of partial knowledge and simplified design of witness hiding protocols. In: Desmedt, Y.G. (ed.) CRYPTO 1994. LNCS, vol. 839, pp. 174–187. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-48658-5_19
Fischlin, M.: Round-optimal composable blind signatures in the common reference string model. In: Dwork, C. (ed.) CRYPTO 2006. LNCS, vol. 4117, pp. 60–77. Springer, Heidelberg (2006). https://doi.org/10.1007/11818175_4
Fischlin, M., Schröder, D.: Security of blind signatures under aborts. In: Jarecki, S., Tsudik, G. (eds.) PKC 2009. LNCS, vol. 5443, pp. 297–316. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-00468-1_17
Garg, S., Rao, V., Sahai, A., Schröder, D., Unruh, D.: Round optimal blind signatures. In: Rogaway, P. (ed.) CRYPTO 2011. LNCS, vol. 6841, pp. 630–648. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22792-9_36
Hauck, E., Kiltz, E., Loss, J.: A modular treatment of blind signatures from identification schemes. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019. LNCS, vol. 11478, pp. 345–375. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17659-4_12
Rückert, M.: Lattice-based blind signatures. In: Abe, M. (ed.) ASIACRYPT 2010. LNCS, vol. 6477, pp. 413–430. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-17373-8_24
Juels, A., Luby, M., Ostrovsky, R.: Security of blind digital signatures (extended abstract). In: Kaliski, B.S. (ed.) CRYPTO 1997. LNCS, vol. 1294, pp. 150–164. Springer, Heidelberg (1997). https://doi.org/10.1007/BFb0052233
Lyubashevsky, V.: Fiat-shamir with aborts: applications to lattice and factoring-based signatures. In: Matsui, M. (ed.) ASIACRYPT 2009. LNCS, vol. 5912, pp. 598–616. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-10366-7_35
Lyubashevsky, V.: Lattice signatures without trapdoors. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 738–755. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_43
Pointcheval, D., Stern, J.: Security arguments for digital signatures and blind signatures. J. Cryptology 13(3), 361–396 (2000)
Rückert, M.: Lattice-based blind signatures. In: Abe, M. (ed.) ASIACRYPT 2010. LNCS, vol. 6477, pp. 413–430. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-17373-8_24
Schröder, D., Unruh, D.: Security of blind signatures revisited. J. Cryptology, 30(2), 470–494 (2017)
Acknowledgments
We thank Marc Fischlin for helpful discussions. This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – SFB 1119 – 236615297.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 Springer Nature Switzerland AG
About this paper
Cite this paper
Alkeilani Alkadri, N., Harasser, P., Janson, C. (2021). BlindOR: an Efficient Lattice-Based Blind Signature Scheme from OR-Proofs. In: Conti, M., Stevens, M., Krenn, S. (eds) Cryptology and Network Security. CANS 2021. Lecture Notes in Computer Science(), vol 13099. Springer, Cham. https://doi.org/10.1007/978-3-030-92548-2_6
Download citation
DOI: https://doi.org/10.1007/978-3-030-92548-2_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-92547-5
Online ISBN: 978-3-030-92548-2
eBook Packages: Computer ScienceComputer Science (R0)





 is the parameter generation algorithm which, on input the security parameter
is the parameter generation algorithm which, on input the security parameter  is the relation set, a collection of sets indexed by
is the relation set, a collection of sets indexed by  .
. is the instance generator algorithm which, on input
is the instance generator algorithm which, on input  and
and  if
if 
 of the OR-relation on
of the OR-relation on  is an interactive algorithm, called prover, that consists of two algorithms
is an interactive algorithm, called prover, that consists of two algorithms  , where:
, where: is a PPT algorithm which, on input a set of public parameters
is a PPT algorithm which, on input a set of public parameters 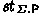 .
. is a DPT algorithm which, on input a set of public parameters
is a DPT algorithm which, on input a set of public parameters  , and a verifier message
, and a verifier message  is an interactive algorithm, called verifier, that consists of two algorithms
is an interactive algorithm, called verifier, that consists of two algorithms  , where:
, where: is a PPT algorithm which, on input a set of public parameters
is a PPT algorithm which, on input a set of public parameters  (called the challenge space), as well as a state
(called the challenge space), as well as a state  consisting only of the received message and the sampled challenge.
consisting only of the received message and the sampled challenge. is a DPT algorithm which, on input a set of public parameters
is a DPT algorithm which, on input a set of public parameters  , and a prover message
, and a prover message  is a PPT algorithm, called simulator. On input a set of public parameters
is a PPT algorithm, called simulator. On input a set of public parameters  is a DPT algorithm, called extractor. On input a set of public parameters
is a DPT algorithm, called extractor. On input a set of public parameters  returns the same output
returns the same output 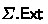 outputs a string
outputs a string 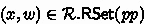 .
. is a DPT algorithm, called commitment recovering algorithm. On input a set of public parameters
is a DPT algorithm, called commitment recovering algorithm. On input a set of public parameters 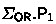 starts with computing
starts with computing 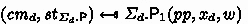 and samples a challenge
and samples a challenge  . Next, it runs
. Next, it runs 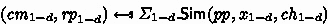 to complete the transcript of
to complete the transcript of  and sends
and sends  .
. samples a random challenge from the challenge space, i.e.
samples a random challenge from the challenge space, i.e.  , and sends it to
, and sends it to  . Finally, it sets its state to
. Finally, it sets its state to  .
. sets
sets  . In case this computation fails (i.e.
. In case this computation fails (i.e.  accepts if and only if the shares satisfy
accepts if and only if the shares satisfy  is a PPT parameter generation algorithm that, on input the security parameter
is a PPT parameter generation algorithm that, on input the security parameter  of the scheme.
of the scheme. is a PPT key generation algorithm that, on input a set of public parameters
is a PPT key generation algorithm that, on input a set of public parameters  , returns a public/secret key pair
, returns a public/secret key pair  is an interactive algorithm, called signer, that consists of two algorithms:
is an interactive algorithm, called signer, that consists of two algorithms: takes as input a set of public parameters
takes as input a set of public parameters  .
. takes as input a set of public parameters
takes as input a set of public parameters  , and the user message
, and the user message  is an interactive algorithm, called user, that consists of two algorithms:
is an interactive algorithm, called user, that consists of two algorithms: takes as input a set of public parameters
takes as input a set of public parameters  , and a signer message
, and a signer message  .
. takes as input a set of public parameters
takes as input a set of public parameters  , and a signer message
, and a signer message  is a DPT verification algorithm that, upon receiving a set of public parameters
is a DPT verification algorithm that, upon receiving a set of public parameters 
 and
and  .
. ,
, 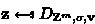 , output
, output  ,
,  , output
, output 
 and
and  .
.
 . Prover restarts
. Prover restarts  returns
returns  , returns a blind commitment
, returns a blind commitment  , and an integer
, and an integer 

 . Signer restarts the protocol if
. Signer restarts the protocol if  . Furthermore,
. Furthermore,