1 Introduction

The buoyancy-driven flow in a square cavity with differentially heated walls is one of the least pursued areas in finite element methods, although it has been an extensively explored area in finite difference methods. Physics involved in the buoyancy-driven flow inside a square domain has relevance to a variety of practical problems such as nuclear reactor insulation, ventilation of rooms, solar energy collection, crystal growth in liquids and convective heat transfer associated with boilers and electronics etc. Buoyancy-driven flows have added complexity in form of coupling between transport properties of the flow and the thermal fields. Internal flow problems like one being discussed are more complex compared to external flows due to the fact that unlike the external flows where flow outside the boundary layer can be considered unaffected by boundary layer, over here the flow outside the boundary layer forms a core surrounded by boundary layers on the four walls. The confined core and surrounding boundary layer interact and this interaction causes added complexity especially at higher Rayleigh numbers (Ra) and larger temperature differences [7, 13, 19]. Literature review shows various studies have been published on the mechanism of natural convection in a square cavity containing various fluids with different geometrical parameters and boundary conditions: De Vahl Davis [11] used a false transient approach based on a stream function–vorticity finite difference method employing forward difference and second order central difference for time and space derivatives respectively to solve natural convection in a square cavity within the Boussinesq approximation. Chenoweth and Paolucci [8] investigated the steady state flow in rectangular cavities with large temperature differences between vertical isothermal walls of rectangular cavities. They used transient form of the flow equations, simplified for low Mach numbers. Vierendeels et al. [28] solved full Navier–Stokes equations for low speed compressible flows to simulate buoyancy-driven flow inside a square domain without resorting to Boussinesq approximation or low Mach number approximation. The low Mach number stiffness was tackled by appropriate discretization and local preconditioning. Their study employing multigrid method that provides benchmark solutions for the thermally driven flows in a square cavity. A comprehensive numerical study is performed in [14] to investigate the transient heat transfer and flow characteristics of the natural convection of three different fluids in a vertical square enclosure within which a centred, square, heat-conducting body generates heat. Bhoite et al. [6] studied numerically the problem of mixed convection flow and heat transfer in a shallow enclosure with a series of block-like heat generating component for a range of Reynolds and Grashof numbers and block-to-fluid thermal conductivity ratios. They showed that higher Reynolds number tend to create a recirculation region of increasing strength at the core region and the effect of buoyancy became insignificant beyond a Reynolds number of typically 600, and the thermal conductivity ratio has a negligible effect on the velocity fields. Recently, Rahman et al. [23] analyzed mixed convection in a rectangular cavity with a heat conducting horizontal circular cylinder by using finite element method. Das and Reddy [9] studied natural convection heat transfer inside an inclined square cavity with an internal conducting block. They concluded that a block with low (high) conductivity enhances (reduces) the heat transfer and, at low values of the Rayleigh number, the angle of inclination has nominal effect on heat transfer for different values of the conductivity. Bhave et al. [5] investigated numerically the effect of an adiabatic centrally-placed solid block inside a differentially square cavity on the flow and temperature fields. Results of the study show that there exists an optimum block size which generates a heat transfer enhancement over the no-block case. Lee and Ha [15] considered the problem of natural convection in a square enclosure heated from below and cooled from above, with a heat-generating conducting square body at the center of the cavity. Results of the study give a detailed analysis for the distribution of streamlines, isotherms and Nusselt number as a function of different thermal conductivity ratios of the heating body. Raji et al. [24] investigated numerically the effect of the subdivision of an obstacle on the natural convection heat transfer in a square cavity. Results of the study show that the heat transfer and the flow intensity could be significantly reduced by increasing the number of the blocks and their relative conductivity. It is also demonstrated that, the results of the saturated porous medium are recovered when the number of blocks is large enough. Recently, Prasopchingchana et al. [22] analyzed numerically the natural convection of air in an inclined square enclosure. They concluded that the angles of the inclination of the enclosure giving the maximum average Nusselt numbers are \(\theta \approx 110^{\circ }\) for \({Ra}=10^3\) and \(\theta \approx 130^{\circ }\) for \(3\times 10^3\le {Ra}\le 10^4\).

Based on literature reviews, despite a large number of numerical studies on free convection of various fluids inside square cavities with different boundary conditions, there is a little studies on free convection in square cavities with an inside adiabatic body. This problem may be occurred in a number of technical applications such as solar collectors, heat exchangers, and cooling of electronic equipment. The adiabatic body can be considered as a model of heat transfer controller or modifier device. In a heat exchanger an adiabatic block can be a model of baffle which manages the flow rate and heat transport process. In the present paper the problem of free convection heat transfer and fluid flow in a square cavity containing air and with an adiabatic square obstacle located at its center and with a fixed temperature drop between the vertical walls, is investigated using penalty finite element method based on Galerkin weighted residuals. The results in the form of streamlines and isotherms plots, average and local Nusselt number are presented for a wide range of Rayleigh numbers and size of the adiabatic square obstacle in case of presence and absence of the obstacle. Comparison of the present results with previous experimental or numerical data will also be presented.

2 Problem Statement

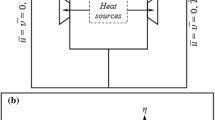
A schematic view of the square cavity with an adiabatic square obstacle located at the center is shown in Fig. 1. The height and the width of the cavity are denoted by H. An adiabatic square obstacle with the length of l is located at the center of the square cavity. Aspect ratio (dimensionless size of the adiabatic square body) is defined as \(\hbox {AR}=l\big /H\). The left wall is kept at high temperature \(T_\mathrm{h}\), while, the right wall is kept at cold temperature Tc. The horizontal top and bottom walls of the cavity are kept insulated. The length of the cavity perpendicular to its plane is assumed to be long enough; hence, the problem is considered two dimensional. The cavity is filled with air i.e. Prandtl number (Pr) is about 0.71. It is assumed that the fluid is in thermal equilibrium and there is no slip between the fluid and the walls.

Fig. 1
figure 1

A schematic view of the considered cavity

Full size image

3 Mathematical Formulation

This study assumes a Newtonian fluid with constant properties except density in body force term of the momentum equation. We considered steady state incompressible flow with thermal convection. The Boussinesq-approximation relates the density changes to the temperature changes and thereby couples temperature-field with the flow-field. The governing equations for the thermal convection flow using conservation of mass, momentum and energy can be written as:

$$\begin{aligned}&\displaystyle \frac{\partial u}{\partial x} +\frac{\partial v}{\partial y}=0, \end{aligned}$$
(1)
$$\begin{aligned}&\displaystyle u \frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y} =-\frac{1}{\rho } \frac{\partial p}{\partial x}+\nu \left( \frac{\partial ^{2}u}{\partial x^{2}}+\frac{ \partial ^{2}u}{\partial y^{2}}\right) , \end{aligned}$$
(2)
$$\begin{aligned}&\displaystyle u\frac{\partial v}{\partial x} +v\frac{\partial v}{\partial y}=-\frac{1}{\rho } \frac{\partial p}{\partial y} +\nu \left( \frac{\partial ^{2} v}{ \partial x^{2} } +\frac{\partial ^{2} v}{\partial y^{2} } \right) +g\beta \left( T-T_\mathrm{c}\right) , \end{aligned}$$
(3)
$$\begin{aligned}&\displaystyle u\frac{\partial T}{\partial x} +v\frac{\partial T}{\partial y}=\alpha \left( \frac{\partial ^{2} T}{\partial x^{2} } +\frac{\partial ^{2} T}{\partial y^{2} } \right) , \end{aligned}$$
(4)

with boundary condition:

There is no slip condition on the walls of the cavity and obstacle. \({T}(0,{y})={T_\mathrm{h}},\,{T}({H},{y})={T_\mathrm{c}},{\partial T/\partial y} =0\) on top and bottom cavity walls and \({\partial T\big /\partial n} =0\) on the adiabatic obstacle walls. Here u and v are the velocity components in x and y directions, respectively. The density is denoted by \(\rho \), pressure by p and T is the temperature. Symbols \(\nu \) and \(\alpha \) are for the kinematic viscosity and the thermal diffusivity respectively. \(\beta \) and g are the coefficient of thermal expansion and the gravitational acceleration, respectively.

Symbol n is the direction normal to the surface of the adiabatic block in Fig. 1. The Eqs. (1)–(4) were non-dimensionalized as follows:

$$\begin{aligned} x'=\frac{x}{H},\,y'=\frac{y}{H},\,u'=\frac{uH}{\alpha },\,v'=\frac{vH}{\alpha },\, T'=\frac{T-T_\mathrm{c}}{T_\mathrm{h}-T_\mathrm{c}}\quad \hbox {and}\;\, p'=\frac{pH^{2} }{\rho \alpha ^{2}}. \end{aligned}$$

where variables with \(x',\,y',\,u'\) etc. are the non-dimensionalized variables. With these non-dimensional variables we get the following non dimensional form of the governing equations where ’ has been dropped for the sake of clarity.

$$\begin{aligned}&\displaystyle \frac{\partial u}{\partial x} +\frac{\partial v}{\partial y}=0, \end{aligned}$$
(5)
$$\begin{aligned}&\displaystyle u\frac{\partial u}{\partial x} +v\frac{\partial u}{\partial y}=-\frac{\partial p}{\partial x} +Pr\left( \frac{\partial ^{2} u}{\partial x^{2} } +\frac{\partial ^{2} u}{\partial y^{2} } \right) , \end{aligned}$$
(6)
$$\begin{aligned}&\displaystyle u\frac{\partial v}{\partial x} +v\frac{\partial v}{\partial y} =-\frac{\partial p}{\partial y} +Pr\left( \frac{\partial ^{2} v}{\partial x^{2} } +\frac{ \partial ^{2} v}{\partial y^{2} } \right) +Ra\,Pr\,T, \end{aligned}$$
(7)
$$\begin{aligned}&\displaystyle u\frac{\partial T}{\partial x} +v\frac{\partial T}{\partial y}=\frac{\partial ^{2} T}{\partial x^{2} } +\frac{\partial ^{2} T}{\partial y^{2}}, \end{aligned}$$
(8)

and the boundary conditions are:

\(u=v=0\) on all walls of the cavity and obstacle. \({T}{(0,{y})}=1\), \({T}(1,{y})=0\), \({\partial T/\partial y} =0\) on top and bottom cavity walls and \({\partial T\big /\partial n}=0\) on the adiabatic obstacle walls. Here Pr and Ra are the dimensionless numbers called Rayleigh and Prandtl numbers, respectively. These are given as: \(Pr={\nu /\alpha }\) and \(Ra=\frac{g\beta \left( T_\mathrm{h}-T_\mathrm{c}\right) H^{3}Pr}{\nu ^{2}}\), respectively.

The rate of heat transfer across the walls of the cavity with and without the adiabatic obstacle in place was quantified using a wall surface Nusselt number (Nu) and averaged Nusselt number (\(N{u}_\mathrm{avg}\)) along the hot wall of the cavity. The Nusselt number is the ratio of convective to conductive heat transfer across the boundary. It can be proved that it is equal to the dimensionless temperature gradient at the surface of the wall with length H as \(Nu_{H} =-H\nabla T'\). By integrating over the surface, the averaged Nusselt number can obtained. Due to the non-dimensionalized representation of the problem, the local and the averaged Nusselt number along the left wall of the cavity can be easily defined as,

$$\begin{aligned} Nu= & {} -\frac{\partial T'}{\partial x}, \end{aligned}$$
(9)
$$\begin{aligned} Nu_\mathrm{avg}= & {} \int _{0}^{1}Nu\,\mathrm{d}y . \end{aligned}$$
(10)

4 Method of Solution

The numerical technique has been used to solve the dimensionless governing equations (5)–(8) subject to the given boundary conditions is the finite element method based on the Galerkin weighted residuals. The applications of the considered method are well described in [17, 18, 20, 21, 26, 27]. Based on the finite element method, the overall domain is discretized into a number of appropriate finite elements as a grid. Here, the given domain is composed into non-uniform biquadratic elements. The continuity equation (5) can be used as a constraint due to mass conservation and hence the pressure distribution can be obtained using this constraint as illustrated in [2, 3, 25, 26]. In order to solve Eqs. (6)–(8), a penalty finite element technique is used. The pressure p can be eliminated in Eqs. (6) and (7) using the constraint equation,

$$\begin{aligned} p=-\gamma \left( \frac{\partial u}{\partial x} +\frac{ \partial v}{\partial y} \right) , \end{aligned}$$
(11)

where \(\gamma \) is a penalty parameter [2, 3, 25, 26]. The continuity equation (5) is satisfied for large values of \(\gamma \). Typical value of \(\gamma \) that give up consistent solution is \(\gamma =10^{7}\).

With the aid of Eq. (11), the momentum balance Eqs. (6) and (7) reduce to

$$\begin{aligned} u\frac{\partial u}{\partial x} +v\frac{\partial u}{\partial y}= & {} \gamma \frac{\partial }{\partial x} \left( \frac{\partial u}{\partial x} +\frac{\partial v}{\partial y} \right) +Pr\left( \frac{\partial ^{2} u}{\partial x^{2} } +\frac{\partial ^{2} u}{\partial y^{2} } \right) , \end{aligned}$$
(12)
$$\begin{aligned} u\frac{\partial v}{\partial x} +v\frac{\partial v}{\partial y}= & {} \gamma \frac{\partial }{\partial y} \left( \frac{\partial u}{\partial x} +\frac{\partial v}{\partial y} \right) +Pr\left( \frac{\partial ^{2} v}{\partial x^{2} } +\frac{\partial ^{2} v}{\partial y^{2} } \right) +Ra\,Pr\,T. \end{aligned}$$
(13)

Expanding the velocity components (u, v) and temperature (T) by using basis set \(\left\{ \phi _{k} \right\} _{k=1}^{N}\) as,

$$\begin{aligned} u\approx & {} \sum _{k=1}^{N}\phi _{k} \left( x,y\right) \cdot u_{k},\quad v\approx \sum _{k=1}^{N}\phi _{k} \left( x,y\right) \cdot v_{k} ,\nonumber \\ T\approx & {} \sum _{k=1}^{N}\phi _{k} \left( x,y\right) \cdot T_{k} ,\quad \mathrm{for}\;\, 0\le x,\,y\le 1, \end{aligned}$$
(14)

where N is the number of nodes for each biquadratic element. Based on the Galerkin weighted residual finite element method, the weight functions are identical to the elements shape functions \(\phi _{k}\) and hence the nonlinear residual equations related to Eqs. (12), (13), and (8), respectively, at the nodes of internal element domain \(\Omega e\) are:

$$\begin{aligned} R_{i}^{(1)}= & {} \sum \nolimits _{k=1}^{N}u_{k} \iint \nolimits _{\Omega e}\left[ \left( \sum \nolimits _{k=1}^{N}\phi _{k}\cdot u_{k} \right) \frac{\partial \phi _{k}}{\partial x}+\left( \sum \nolimits _{k=1}^{N}\phi _{k}\cdot v_{k}\right) \frac{ \partial \phi _{k}}{\partial y}\right] \phi _{i}\mathrm{d}x\,\mathrm{d}y \nonumber \\&+\gamma \left[ \sum \nolimits _{k=1}^{N}u_{k} \iint \nolimits _{\Omega e}\frac{\partial \phi _{i} }{\partial x} \frac{\partial \phi _{k}}{\partial x}\mathrm{d}x\,\mathrm{d}y+\sum \nolimits _{k=1}^{N}v_{k}\iint \nolimits _{\Omega e}\frac{\partial \phi _{i} }{\partial x} \frac{\partial \phi _{k}}{\partial y}\mathrm{d}x\,\mathrm{d}y\right] \nonumber \\&+Pr\sum \nolimits _{k=1}^{N}u_{k}\iint \nolimits _{\Omega e}\left[ \frac{\partial \phi _{i} }{\partial x} \frac{\partial \phi _{k}}{\partial x} +\frac{\partial \phi _{i} }{\partial y} \frac{\partial \phi _{k} }{\partial y} \right] \mathrm{d}x\,\mathrm{d}y=0,\quad i=1,2,\ldots ,N, \nonumber \\ \end{aligned}$$
(15)
$$\begin{aligned} R_{i}^{(2)}= & {} \sum \nolimits _{k=1}^{N}v_{k} \iint \nolimits _{\Omega e}\left[ \left( \sum \nolimits _{k=1}^{N}\phi _{k}\cdot u_{k} \right) \frac{\partial \phi _{k}}{\partial x}+\left( \sum \nolimits _{k=1}^{N}\phi _{k}\cdot v_{k}\right) \frac{\partial \phi _{k}}{\partial y} \right] \phi _{i} \mathrm{d}x\,\mathrm{d}y\nonumber \\&\;+ \gamma \left[ \sum \nolimits _{k=1}^{N}u_{k} \iint \nolimits _{\Omega e}\frac{\partial \phi _{i} }{\partial y} \frac{\partial \phi _{k} }{\partial x}\mathrm{d}x\,\mathrm{d}y+\sum \nolimits _{k=1}^{N}v_{k} \iint \nolimits _{\Omega e}\frac{\partial \phi _{i} }{\partial y} \frac{\partial \phi _{k} }{\partial y}\mathrm{d}x\,\mathrm{d}y\right] \nonumber \\&\;+Pr\sum \nolimits _{k=1}^{N}v_{k}\iint \nolimits _{\Omega e}\left[ \frac{\partial \phi _{i} }{\partial x} \frac{\partial \phi _{k}}{\partial x} +\frac{\partial \phi _{i}}{\partial y} \frac{\partial \phi _{k}}{\partial y} \right] \mathrm{d}x\,\mathrm{d}y\nonumber \\&\;-Ra\,Pr\,\iint \nolimits _{\Omega e}\left( \sum \nolimits _{k=1}^{N}\phi _{k}\cdot T_{k} \right) \phi _{i}\mathrm{d}x\,\mathrm{d}y=0,\quad i=1,2,\dots ,N, \end{aligned}$$
(16)
$$\begin{aligned} R_{i}^{(3)}= & {} \sum _{k=1}^{N}T_{k}\iint \nolimits _{\Omega e}\left[ \left( \sum _{k=1}^{N}\phi _{k} \cdot u_{k} \right) \frac{\partial \phi _{k}}{\partial x}+\left( \sum _{k=1}^{N}\phi _{k}\cdot v_{k}\right) \frac{\partial \phi _{k}}{\partial y} \right] \phi _{i}\mathrm{d}x\,\mathrm{d}y\nonumber \\&+\sum _{k=1}^{N}T_{k}\iint \nolimits _{\Omega e}\left[ \frac{\partial \phi _{i} }{\partial x} \frac{\partial \phi _{k} }{\partial x} +\frac{\partial \phi _{i} }{\partial y} \frac{\partial \phi _{k} }{\partial y} \right] \mathrm{d}x\,\mathrm{d}y=0,\quad i=1,2,\dots ,N, \end{aligned}$$
(17)

Biquadratic shape functions with three point Gaussian quadrature is used to calculate the integrals in the residual equations (15)–(17). In Eqs. (15) and (16), the second integral containing the penalty parameter \(\gamma \) are evaluated with two point Gaussian quadrature (reduced integration penalty formulation [2, 3, 25, 26]). It has been found that lowering the integration order is essential to avoid ill-conditioning of the Jacobian for large values of \(\gamma \).

The non-linear residual equations are solved using Newton–Raphson method to determine the coefficients of the expansions in Eq. (14). The boundary conditions are incorporated into the assembled global system of nonlinear equations to make it determinate. \(L_{2}\) norm for the residual vectors is used for the stopping criteria of the Newton–Raphson iterative process. The process is terminated with the convergence criterion \(\sqrt{\left[ \sum \left( R_{i}^{\left( j\right) }\right) ^{2}\right] }\le 10^{-6}\).

Eight node biquadratic elements have been used with each element. Before evaluating Gauss integration, the coordinate x–y must be mapped into of the natural coordinate \(\xi -\eta \) due to the irregularity of the element shape. The transformation between (x, y) and \((\xi ,\eta )\) coordinates can be defined by

$$\begin{aligned} x=\sum _{k=1}^{8}\phi _{k} \left( \xi ,\eta \right) \cdot x_{k} ,\quad y=\sum _{k=1}^{8}\phi _{k}\left( \xi ,\eta \right) \cdot y_{k}, \end{aligned}$$
(18)

where \(\left( x_{k},y_{k}\right) \) are the x, y coordinates of the k nodal points and \(\phi _{k}\left( \xi ,\eta \right) \) is the local basis function in \(\xi -\eta \) domain. The eight basis functions used are the serendipity type illustrated in [16]. Consequently, the domain integrals in the residual equations are approximated using eight node biquadratic basis functions in \(\xi -\eta \) domain using Eq. (18) and serendipity type basis functions.

5 Stream Function Evaluation

The motion of the fluid is displayed using the stream function \(\psi \) obtained from velocity components u and v. The relationships between stream function and velocity components for two dimensional flows are [4]

$$\begin{aligned} u=\frac{\partial \psi }{\partial y},\quad v=-\frac{\partial \psi }{\partial x}, \end{aligned}$$
(19)

which yield a single equation

$$\begin{aligned} \frac{\partial ^{2} \psi }{\partial x^{2} } +\frac{\partial ^{2} \psi }{\partial y^{2} } =\frac{\partial u}{\partial y} -\frac{\partial v}{\partial x}. \end{aligned}$$
(20)

Using the above definition of the stream function, the positive sign of \(\psi \) denotes anticlockwise circulation and the clockwise circulation is represented by the negative sign of \(\psi \). Expanding the stream function \((\psi )\) using the basis set \(\left\{ \phi _{k}\right\} _{k=1}^{N}\) as \(\psi =\sum _{k=1}^{N}\phi _{k}\left( x,y\right) \cdot \psi _{k}\) and the relation for u, v from Eq. (14), the Galerkin finite element method yield the following residual equations for Eq. (20).

$$\begin{aligned} R_{i}^{(s)}= & {} \sum \nolimits _{k=1}^{N}\psi _{k} \iint \nolimits _{\Omega e}\left[ \frac{\partial \phi _{i} }{\partial x} \frac{\partial \phi _{k} }{\partial x} +\frac{\partial \phi _{i} }{\partial y} \frac{\partial \phi _{k}}{\partial y} \right] \mathrm{d}x\,\mathrm{d}y\nonumber \\&+\sum \nolimits _{k=1}^{N}u_{k} \iint \nolimits _{\Omega e}\phi _{i} \frac{\partial \phi _{k}}{\partial y}\mathrm{d}x\,\mathrm{d}y\nonumber \\&-\sum \nolimits _{k=1}^{N}v_{k} \iint \nolimits _{\Omega e}\phi _{i} \frac{\partial \phi _{k}}{\partial x}\mathrm{d}x\,\mathrm{d}y=0,\quad i=1,2,\dots ,N, \end{aligned}$$
(21)

The no-slip condition is valid at all boundaries as there is no cross flow, hence \(\psi =0\) is used as residual equations at the nodes for the boundaries.

6 Results and Discussion

In this section, results of numerical simulation of free convection fluid flow and heat transfer of a fluid in square cavities having an inside adiabatic square obstacle are presented. The study focuses on effects of the Rayleigh number and size of the adiabatic square body on the flow, temperature fields and heat transfer. The aspect ratio AR (dimensionless size) of the adiabatic square obstacle is ranging from 0 to 0.6. Computations were carried out in the Rayleigh number range of \(10^2\) to \(10^7\) and value of Prandtl number, was taken as 0.71 which is the value for air at room temperature. The results of the calculations are presented in graphical form in Figs. 2, 3, 4, 5 and 6. Isotherms and streamlines are shown in Figs. 2, 3 and 4 for different Ra values and AR-values. In case of no obstacle inside the cavity, i.e. \(\hbox {AR}=0\), the following results can be summarized. For low values of Ra a central vortex appears as the dominant characteristic of the flow. As Ra increases, the vortex tends to become elliptic and finally breaks up into two vortices at \({Ra}=10^5\). The two vortices move towards the walls, giving space for a third vortex to develop. This third vortex is very weak in comparison with the other two and, as discussed in detail by other investigators as in [10], the rotation is again clockwise owing to a very small positive temperature gradient at the centre of the cavity.

Fig. 2
figure 2

Variation of the streamlines with the aspect ratio at various Rayleigh numbers. a \(Ra=10^3\), b \(Ra=10^4\), c \(Ra=10^5, \) d \(Ra=10^6\), e \(Ra=10^7\)

Full size image
Fig. 3
figure 3

Variation of the isotherms with the aspect ratio at various Rayleigh numbers. a \(Ra=10^2\), b \(Ra=10^3\), c \(Ra=10^4, \) d \(Ra=10^5\), e \(Ra=10^6\), f \(Ra=10^7\). (Color figure online)

Full size image
Fig. 4
figure 4

Color bar of the isotherms in Fig. 3. (Color figure online)

Full size image
Fig. 5
figure 5

Variation of the local Nusselt number Nu with the aspect ratio of the adiabatic obstacle at various Rayleigh numbers. a \(Ra=10^{2}\), b \(Ra=10^{3}\), c \(Ra=10^{4}\), d \(Ra=10^{5}\), e \(Ra=10^{6}\), f \(Ra=10^{7}\). (Color figure online)

Full size image
Fig. 6
figure 6

a Distribution of u-velocity component at mid-width of cavity for \(\hbox {AR}=0\), b distribution of u-velocity component at mid-width obtained in [1] for various Ra values. (Color figure online)

Full size image

For even higher values of Ra the velocities at the centre of the cavity are very small compared with those at the boundaries where the fluid is moving fast, forming vortices at the lower right and top left corner of the cavity. The vortices become narrow, improving the stratification of the flow at the centre of the cavity.

The shape of the isotherms shows how the dominant heat transfer mechanism changes as Ra increases. For low Ra values almost vertical isotherms appear, because heat is transferred by conduction between hot and cold walls. As the isotherms depart from the vertical position, the heat transfer mechanism changes from conduction to convection. Figure 3 shows that the isotherms at the centre of the cavity are horizontal and become vertical only inside the very thin boundary layers.

For the other 3 cases, i.e. \(\hbox {AR}=0.4,0.5,0.6\), the heated fluid ascends along the hot wall, then moves horizontally, is cooled and descends at the vicinity of the cold right wall, hence a primary clockwise vortex is developed inside the cavity, regardless the aspect ratio of the adiabatic obstacle. Secondary clockwise vortices are developed in the left and right side of the adiabatic obstacle via movement of the primary vortex and existence of the obstacle. The corresponding isotherms are nearly located adjacent to the horizontal isothermal walls. Moreover uniformly distributed parallel horizontal isotherms are formed in the right and left hand side of the square obstacle.

Effects of Rayleigh number on the flow pattern and temperature distribution inside the cavity with an inside adiabatic square body with \(\hbox {AR}=0.4,0.5\) and 0.6 are depicted in Figs. 2, 3 and 4. At \({Ra}=10^3\) and for all values of AR, via domination of conduction heat transfer, the isotherms are nearly parallel with the vertical walls. From the streamlines, a single clockwise vortex is observed inside the cavity for all values of AR. The symmetric vortex demonstrates a low velocity and low intensity flow at low Rayleigh numbers.

By increase of the buoyant force via increase in the Rayleigh number, the flow intensity increases and the streamlines closes to the side walls. At \({Ra}=10^5\) and for \(\hbox {AR}=0.4\) and 0.5, two secondary vortices are developed in the lower left and upper right sides of the adiabatic obstacle. These secondary vortices will be developed for \(\hbox {AR}=0.6\) when \({Ra}=10^6\). At this value of the Rayleigh number and higher, the streamlines are located close to the isothermal side walls and distinct velocity boundary layers formed in this region. For all values of AR, inside the cavity, the secondary vortices are elongated from down to the top of the side walls of the adiabatic obstacle.

The isotherms indicate that with increase in the Rayleigh number, the effect of free convection increases and the isotherms are condensed next to the isothermal side walls. Moreover, thermal stratification is observed in the left and right sides of the obstacle. Formation of the thermal boundary layers can be observed from the isotherms at \({Ra}=10^5\) and higher. Effects of the increase in the aspect ratio of the adiabatic square obstacle on the local Nusselt number along the hot wall of the cavity at various Rayleigh numbers are illustrated in Fig. 5.

At \({Ra}=10^2\), \(10^3\) and for all aspect ratios, maximum local Nusselt number occurs at the lower end of the hot wall i.e. \({y}=0\). At this region the cold fluid faces the hot wall and hence maximum temperature gradient occurs at this region. When the fluid ascends adjacent to the hot wall the fluid temperature increases, then the temperature gradient decreases and hence the local Nusselt number decreases. For \(\hbox {AR}=0.4\) and \({Ra}=10^3\), minimum local Nusselt number occurs at the upper part of the hot wall i.e. \({y}=1\). Moreover, a uniform Nusselt number distribution is observed along whole upper half of the hot wall. At \({Ra}=10^3\), the local Nusselt number decreases as the size of the adiabatic obstacle increases. This is due to the fact that when adiabatic obstacle is located in the center of cavity, the fluid movement is damped and hence rate of free convection decreases. So, as the size of the adiabatic body increases, the reduction in the rate of heat transfer is augmented.

For \(\hbox {AR}=0.4{-}0.6\) when \({Ra}=10^2\) and for \(\hbox {AR}=0.5,\,0.6\) when \({Ra}=10^3\), the local Nusselt number decreases from down to the middle section of the hot wall and then increases by moving towards the top of the wall. In these cases, the location at which the minimum local Nusselt number occurs is about \({y}=0.5\). In general, for \({Ra}=10^2{-}10^4\), the heat transfer rate decreases with the increase of adiabatic obstacle size.

At \({Ra}=10^5\) and for all aspect ratios, maximum rate of heat transfer occurs at about \({y}=0.1\) of the hot wall. With the decrease in AR, the maximum local Nusselt number decreases for \(y<0.1\). A reverse behaviour is found for the major portion of the wall. For \(y>0.1\), the local Nusselt number decreases when the aspect ratio increases. It is because of the increase in blockage of fluid flow via increase in the adiabatic obstacle size. At \({Ra}=10^6\) and \(10^7\), the size of the obstacle does not affect the heat transfer rate significantly. This is due to the increase in the buoyant force will eliminate the effect of the increase in fluid flow blockage. It is worth mentioning that the maximum rate of heat transfer occurs at a position \(y<0.1\), and this position approaches the lower part of the hot wall as Ra increases.

Figure 6 presents a comparison between (a) the profiles for the u-component for \(\hbox {AR}=0\), i.e. without obstacle, and (b) u-component obtained in [1] at the mid-width of the cavity. From Fig. 6, it can be drawn that the present results are coinciding with the results obtained by Barakos et al. [1] at \({Ra}=10^3-10^7\). The figure shows a gradually decreasing velocity near the centre and the development of narrow boundary layers along the walls. It is clear that for high Ra, thicker boundary layers are developed. It is obvious that the velocity profile at the lower half of the vertical walls of the cavity is negative however at the upper half is positive and hence there are changes in the velocity direction. These changes correspond to slope changes of the temperature profile and lead to vortex development. Here, the boundary layer separation occurs at the point (0.5, 0) at which the portion of the boundary layer reverses in flow direction.

Again to ensure the validity and verify the accuracy of the considered numerical technique, the obtained results for Nusselt number are compared with the benchmark solutions [1, 11, 12] for a fluid of \({Pr}=0.71\) in a square cavity without obstacle. Table 1 shows this comparison that describes an excellent agreement between the present results and the benchmark solution for all values of Ra. The comparison concerns the averaged Nu along the hot wall and its maximum values and the locations where they occur.

Table 1 Comparison of maximum and averaged Nusselt number with previous works for a square cavity without obstacle and various Ra values
Full size table

7 Conclusion

In the present paper the problem of free convection of air inside differentially heated square cavity with an adiabatic square obstacle located in its center was investigated numerically using the a penalty finite element method based on Galerkin weighted residual method. A parametric study was undertaken and effects of the Rayleigh number and square obstacle aspect ratio on the fluid flow, temperature field and rate of heat transfer were investigated and the following results were obtained.

In case of no obstacle inside the cavity, the present results compare favourably with benchmark solutions and in agreement with similar ones found in the literature, for example [1, 11, 12].

In case of low Rayleigh numbers \((10^2{-}10^4)\), the rate of heat transfer decreases when the aspect ratio of the adiabatic square obstacle increases.

In case of relatively high Rayleigh numbers \((10^5{-}10^6)\), the maximum heat transfer rate increases when the aspect ratio of the adiabatic square obstacle increases.

In case of high Rayleigh numbers \((10^7)\), the increase in the size of the inside square obstacle does not affect the heat transfer rate significantly.