Computations of incompressible fluid flow around a long square obstacle near a wall: laminar forced flow and thermal characteristics

Abstract

Computations of incompressible fluid flow and heat transfer around a square obstacle with a nearby adiabatic wall have been performed in a horizontal plane. The ranges of dimensionless control parameters considered are Prandtl number (Pr) = 10–100, Reynolds number (Re) = 1–150 and gap ratio (G) = 0.25–1. The steady-flow regime is observed up to Re = 121 for G = 0.5, and beyond this Re, time-periodic regime is observed. The shift to a time-periodic regime from a steady regime occurred at greater Re than that for an unconfined square obstacle. With increasing Pr, increase in average Nusselt number values is recorded for all Re and G studied. The heat transfer augmentation is approximately 1332% at Re = 150 (Pr = 100, G = 0.25) with regard to the corresponding values at Re = 1. Lastly, a correlation for j _h factor is determined for the preceded conditions.

1 Introduction

Incompressible Newtonian fluids flow and heat transfer around a square obstacle are typical problems in fluid mechanics and are widely encountered in several engineering appliances, for instance, novel heat exchangers, evaluation of hydrodynamic forces exerted on various pipelines, probes/sensors and so forth. Additionally, the neighbourhood of a wall can have noticeable impacts on the flow and heat transfer attributes near an obstacle. Also, the interference between the wall and the obstacle directed towards the variations in both steady and unsteady forces act on the obstacle. Therefore, the current work is related to the forced flow and heat transfer from a long square obstacle close to a wall in the laminar regime. The flow over a square obstacle in close proximity to a wall is characterised by the flow control parameters (e.g. incoming fluid velocity and Reynolds number (Re)), thermal control parameters (e.g. fluid temperature and Prandtl number (Pr)) and physical dimensions (e.g. sides of a square obstacle (D) and gap ratio (G); i.e. the ratio between the gap of a square obstacle and the channel wall to the side of the square). It is also valuable to point out that the flow around a square obstacle in the neighbourhood of a wall is more complex than the free-stream square obstacle because of the interaction of the square obstacle and wall shear layers, and limited information available in the literature [1]. On the contrary, extensive literature is reported on a circular obstacle in the neighbourhood of a wall. Thus, it is advantageous to analyse pertinent studies on square and/or circular cross-section obstacles.

For a circular obstacle in the propinquity of a wall, the vortex shedding is examined for different gap heights (0.3–3) as well as Re varying from 80 to 1000 [2]. The vortex shedding mechanism at low gap spacing was evaluated, and the critical gap spacing was found to be 0.6, 0.78, 1 and 1.2 for Re = 200, 150, 100 and 78, respectively. The onset of periodicity is computed for a confined circular obstacle for Re ≤ 1800 and G ≤ 2 [3]. Shifting to a time-periodic state from a steady state has been deferred as the cylinder reaches the wall. For G = 2, the transition is between Re = 230 and 240. As the gap is decreased to 0.25, there is a fast growth in the critical Re and finally the transition arises between Re = 1500 and 1800. The effect of thermal conductivity is studied for a cylinder in the propinquity of wall for Re = 0.001–1 and G = 0.1–10 [4]. Low-conductivity wall materials (e.g. mirror, glass and perspex) have a leading impact on the heat transfer from the obstacle in the proximity of a wall. As G decreased from 5 to 0.7 at Re = 180, Strouhal number (St) rises to a maximum at a gap ratio of 0.7 [5,6,7]. Further gap reduction from 0.7 to 0.1 leads to a rapid decrease in St, with shedding finally ceasing altogether at gap ratios below 0.16. The heat transfer and fluid flow behaviours are studied for Re = 20–200 and G = 0.1–2.5 at Pr = 0.7 in [8]. The vortex shedding is entirely eliminated when the obstacle is positioned below critical gap spacing. Unlike preceded studies, the two-dimensional (2-D) flow around a rotating circular obstacle in the neighbourhood of a wall is simulated for G = 0–5 at a fixed Re = 200 [9]. Two critical values of G (e.g. G _down and G _up ) were found, which rely on the rotational rate (G _down  = 0.4 and G _up  = 1.5 for rotational rate = 0.5, and G _down  = 0.6 and G _up  = 1.5 for rotational rate = 1). Also, rotating circular cylinders in close proximity to a wall (G = 0.005) were studied for Re = 20–750 [10]. It was observed that the cylinder rolling backward can entirely eliminate the vortex shedding. The variations of wake dynamics and turbulence characteristics in the neighbourhood of a wall for G = 0.25–1 were observed in [11] and also illustrated the physics comprising the shear layer transition, stretching, breakdown and turbulence production for Re = 1440.

The separation points on a square obstacle are generally placed at the corner points and, as a result, exert significant influences on flow and heat transfer features. The presence of a wall in the neighbourhood of a square obstacle was studied numerically in [12,13,14,15,16,17,18,19,20,21,22,23,24] and the detailed discussion on the literature is now available in our recent work [1]. The two- and three-dimensional (3-D) effects were investigated on a square cylinder located at G = 0.2–4 for Re = 175, 185 and 250 [16]. At Re = 175 and 185, a slight difference was observed for 2-D and 3-D simulations but a significant variation was observed at Re = 250. The effect of forced convection heat transfer using turbulent flow model at Re = 10–50,000 was studied for G = 0.25–3 and air as a working fluid [18]. Critical points were recorded for which the transition between oscillatory flow and steady flow occurs. Furthermore, experimental practices on the flow past a square obstacle in the neighbourhood of a wall were performed at high Re [19,20,21,22,23,24].

Thus, the aforementioned discussion suggests that the majority of the prior experimental/numerical observations focused on vortex shedding from the square and/or circular obstacles for laminar and/or turbulent regime at high Re. A study [12] deals with the shear flow near a plane wall for G = 0.25, 0.5 and Re = 100, 125, 400. However, studies [1, 14, 15, 18] deal with flow and heat transfer aspects close to a plane wall taking air (Pr = 0.7) as a working fluid. Furthermore, it is to be noted that uniform inlet velocity is assumed in previous studies [15, 18] and the heat transfer is studied for Re = 100–250 at a fixed G = 0.5 in another study [14]. Our recent work [1] is limited to the mixed convection heat transfer results for Pr = 0.7 and Re up to 100 at Richardson number (Ri) = 0 to 1 and G = 0.25 to 1. However, in the current study, effects of Pr are investigated for the wider range of settings as opposed to our recent work [1]. The numerical methodology has also been validated extensively with literature [12, 14, 25,26,27,28,29,30,31]. Specifically, the novelty of the present work can be realised based on the following important issues:

• No heat-transfer observations for high Pr (>0.7) near a plane wall are available in the literature.

• The onset of vortex shedding (i.e. the shifting of unsteady periodic regime from a steady regime) is not yet explored for G = 0.5.

Thus, in the present study, an effort has been made to address these issues.

2 Problem description

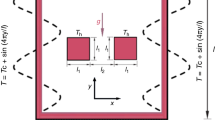
The laminar flow and heat transfer have been considered in the horizontal plane for Newtonian fluids around a long square cylinder (long in neutral direction) in the proximity of an adiabatic wall (figure 1). At inlet, the incompressible fluid is coming with a linear velocity and having a constant temperature of T _∞ ; however, the square obstacle temperature is maintained constant at T _w such that T _w  > T _∞ . The dimensionless upstream (L _u ) and downstream (L _d ) dimensions and the domain height (H) are 15, 50 and 20, respectively. These dimensions have been chosen after domain independence study, which is thoroughly discussed in section 3.

Figure 1

Schematic diagram.

The incoming fluid is assumed to be having constant fluid properties [1]. Also, the viscous dissipation term in the thermal energy equation is ignored. Additionally, the value of Richardson number is calculated using the data available in the literature [30] and it has been found that the value of Richardson number is changing here from 0.014 to 0.066 for the working fluids considered. Owing to such low values of Richardson numbers, the buoyancy effects are very weak and the forced convection mode is predominant. Hence, the impact of the mixed convection is neglected in this investigation. Thus, the continuity (Eq. 1), the components of momentum (Eqs. 2 and 3) and the energy (Eq. 4) equations in the dimensionless form for the present framework are given as

$$ \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0 $$

(1)

$$ \frac{\partial u}{\partial t} + \frac{\partial uu}{\partial x} + \frac{\partial vu}{\partial y} = - \frac{\partial p}{\partial x} + \frac{1}{\text{Re}}\left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial y^{2} }}} \right) $$

(2)

$$ \frac{\partial v}{\partial t} + \frac{\partial uv}{\partial x} + \frac{\partial vv}{\partial y} = - \frac{\partial p}{\partial y} + \frac{1}{\text{Re}}\left( {\frac{{\partial^{2} v}}{{\partial x^{2} }} + \frac{{\partial^{2} v}}{{\partial y^{2} }}} \right) $$

(3)

$$ \frac{\partial \theta }{\partial t} + \frac{\partial u\theta }{\partial x} + \frac{\partial v\theta }{\partial y} = \frac{1}{{\text{Re} \Pr }}\left( {\frac{{\partial^{2} \theta }}{{\partial x^{2} }} + \frac{{\partial^{2} \theta }}{{\partial y^{2} }}} \right) $$

(4)

The boundary settings (in non-dimensional form) can be noted as follows: At the inlet: u = y, v = 0 and $\theta = 0$, where the slope is unity [1, 12,13,14]. On the top domain side: $\partial u/\partial y = 0$, v = 0 and $\partial \theta /\partial y = 0$ [1, 12,13,14]. On the bottom domain side: u = 0, v = 0 and $\partial \theta /\partial y = 0$. On a square obstacle: u = 0, v = 0 and $\theta = 1$. At the downstream outlet: it is placed adequately distant from the square obstacle and a zero normal velocity/temperature gradient is applied such that $\partial u/\partial x = 0$, $\partial v/\partial x = 0$ and $\partial \theta /\partial x = 0$. Equations (1)–(4) with boundary conditions are solved by adopting Ansys Fluent [31] and the computational grid is constructed by making use of Ansys workbench. More numerical details about grid structure, discretisation schemes, numerical method to solve algebraic equations and convergence criteria can be found in a study by Kumar and Dhiman [1].

3 Grid, domain and time independence studies

Because this study covers the wider ranges of Pr (>0.7) and Re (up to 150) than that of Kumar and Dhiman [1], then the new details on the grid, domain and time independence studies are discussed as follows:

In this work, grids consisting of 68,300, 80,000 and 122,000 cells for G = 0.25, 0.5 and 1 respectively are used. To justify these choices of grid sizes, the grid size is examined by monitoring the engineering output control parameters; the grid dimensions of 48,528, 68,300 and 90,320 cells are applied with N = 60, 100 and 140 CVs on each side of the square obstacle, respectively. The calculations are performed for the severe values of Re (=150), Pr (=100) and G (=0.25). The maximum differences in the values of dimensionless flow and heat transfer output values, for instance, drag coefficient (C _D ), lift coefficient (C _L ) and Nusselt number ($\overline{Nu}$) for the cases of N = 60 CVs with respect to N = 100 CVs are found to be less than 1% (table 1). The corresponding maximum differences for N = 140 CVs with respect to N = 100 CVs are found to be only ~0.7%. Thus, the grid size of 68,300 cells with N = 100 CVs is utilised (table 1). Also, the consequences of change of the smallest cell dimension (δ) near the square cylinder on the output parameters are examined and the outcomes are tabulated in table 2. The results at δ = 0.008D are found to lie between the results for δ = 0.005D and 0.01D. For instance, the maximum relative change for δ = 0.005D with respect to δ = 0.008D is found to be less than 1.4%. Thus, the dimensionless grid spacing of 0.008 close to the square obstacle is used for further simulations.

Table 1 Grid dependence study for N = 60–140 CVs at Re = 150, G = 0.25 and Pr = 100.

Table 2 Grid dependence study for δ = 0.005D – 0.01D at Re = 150, G = 0.25 and Pr = 100.

The influence on the flow and heat transfer output values is examined for the upstream length (L _u ) = 10D (66,694 cells), 15D (68,300 cells) and 20D (72,128 cells) for both end values of Re (1 and 150) at Pr = 100, G = 0.25 and is documented in table 3. Table 3 also records the percentage relative deviations with L _u  = 15D. From table 3, the relative maximum differences for these parameters are noted higher for L _u  = 10D with L _u  = 15D, and the changes are noted lesser for L _u  = 20D with L _u  = 15D. Therefore, a dimensionless upstream length of 15 is employed. On the other hand, the impact of the downstream length (L _d ) is studied for three downstream lengths of 40D (65,429 cells), 50D (68,300 cells) and 60D (71,432 cells) at Re = 150, Pr = 100 and G = 0.25 (table 4). It is recorded that the values of C _D , C _L and $\overline{Nu}$ are independent of the downstream distances, and hence a dimensionless downstream distance of 50 is utilised.

Table 3 Upstream dependence study for Re = 1, 150 and Pr = 100 at G = 0.25.

Table 4 Downstream dependence study at Re = 150, G = 0.25 and Pr = 100.

The influence on the values of output parameters is investigated for the height of the computational field (H) = 10D (52,100 cells), 20D (68,300 cells) and 30D (84,500 cells) for both end values of Re (1 and 150) at Pr = 100, G = 0.25 (table 5). Table 5 also records the percentage relative deviations with H = 20D. The relative maximum differences for these parameters are noted higher for H = 10D with H = 20D, and the changes are noted fewer for H = 30D with H = 20D. Hence, a dimensionless domain height of 20 has been used for further studies.

Table 5 Domain height dependence study for Re = 1, 150 and Pr = 100 at G = 0.25.

The effect of time step (Δt) on output parameters has also been investigated for Δt = 0.0075, 0.01 and 0.0125 at Pr = 100, G = 0.25, 1 and Re = 150 (table 6). The maximum relative variations in the values of average Nusselt number are noted around 0.1% at G = 0.25; however, no variation is noted for C _D and C _L . Similarly, the time-dependence test is performed for time-periodic case at G = 1 for Pr = 100 and Re = 150 (table 6). The maximum relative deviations in the values of the parameters for Δt = 0.0075 with respect to Δt = 0.01 are found to be ~2.7%, and for Δt = 0.0125 with respect to Δt = 0.01 the changes are found to be only ~0.8%. It can be observed here that Δt = 0.0075 is not sufficient because the results, when compared with Δt = 0.01, vary significantly. However, when Δt = 0.01 is compared with an even larger time step (Δt = 0.0125), the insignificant deviation in the results has been noticed. Hence, a dimensionless time step of 0.01 has been used, which is also sufficient to resolve the unsteady cases.

Table 6 Time dependence study for Re = 150 and Pr = 100 at G = 0.25 and 1.

4 Results and discussion

The flow and heat transfer results for Pr = 10–100 at Re = 1–150 and G = 0.25–1 are presented and discussed. Mahir [16] performed the 2-D and 3-D numerical simulations to investigate the effect of flow features around a square cylinder near a plane wall. He performed computations for gap ratios of 0.2–4 and Re = 175, 185 and 250. At Re = 175 and 185, a slight difference is observed for 2-D and 3-D simulations but a major difference is observed at 250. Therefore, the 2-D assumption in the present work is believed to be justified. However, before discussing the new results, the present methodology has been validated thoroughly with literature [12, 14, 25,26,27,28,29,30,31] in section 4.1.

4.1 Validation

First, the validation of the current work is completed with the results available in [14]. For this, the time-dependent fluid flow and heat transfer investigations were conducted for Re = 100 and 125 at G = 0.5 and Pr = 0.7 (table 7). At Re = 100, it has been noted that the present C _L differs by ~5.2% compared to previous study [14]. At Re = 125, the present values of flow quantities like C _D and C _L have the maximum deviations of ~5.3% and 2.9%, respectively. The slightly larger differences in the flow output parameter values between two studies are attributed to the fact that an upstream distance of 8, downstream distance of 40, coarse grid size of 31,450 cells, implicit first-order scheme and residual of 0.5 × 10⁻⁴ were used in a study [14], but in the current work an upstream distance of 15, downstream distance of 50, fine grid size of 68,300 cells, implicit second-order scheme and residual of 10⁻¹⁵ are being used.

Table 7 Validation of present results with Bhattacharyya et al. [14] at different values of Re for G = 0.5 and Pr = 0.7.

Secondly, to gain confidence on the numerical methodology used, we have further compared various output flow parameters with reliable experimental/numerical values for confined/unconfined configurations. In a confined domain, the present results for the flow past a square obstacle, with a parabolic velocity profile at the inlet, for Prandtl number of 0.7 and blockage ratio of 25% at various values of Re are compared in figure 2 with literature [25, 26]. The difference amongst the values of C _D , St and $\overline{Nu}$ of the current study with that of literature [25, 26] is achieved less than 2%. Therefore, the present analysis has an excellent agreement with literature [25, 26]. Also, the present results for the case of unconfined flow across a square obstacle are evaluated and presented in figure 3 with literature [12, 25,26,27,28,29] for the uniform velocity inlet. The maximum variations in $\overline{Nu}$ are around 0.7% and 0.9% with regard to the study by Chatterjee and Mondal [25] and Sharma and Eswaran [26], respectively. Again, an excellent agreement of present unconfined results exists with aforementioned studies [25, 26]. However, the deviations in C _D are found within approximately 5% of those in other studies [12, 28]. Strouhal number differs by ~1.7% and 0.3% from those in another study [12, 25] for Re = 100 and 150, respectively. It is also valuable to state that the maximum variations of up to 5% are not at all unusual in the literature [32]. Furthermore, the present methodology is validated in our previous studies [1, 33]. Thus, the results found in the current work are in good agreement with the results existing in the literature and therefore can be deemed trustworthy.

Figure 2

Benchmarking of results with literature [25, 26].

Figure 3

Validation of results with experimental/numerical values [12, 25,26,27,28,29].

4.2 Fluid flow characteristics

Flow patterns around a square obstacle for the working fluid as air (Pr = 0.7) can be found in a previous study [1] at G = 0.25 to 1, while for Re up to 100. Therefore, this section covers the flow features which are not been covered in the previous study [1]. The time-averaged streamlines are plotted for Re = 100–150 at G = 0.25–1 in figure 4. The twin vortices are formed at the rear of the square cylinder (figure 4c–4i) except for Re < 150 at G = 0.25. The channel wall has a small influence on the upper vortex of the twin vortices behind the square cylinder; however, the lower vortex is more stretched towards downstream than towards the upper vortex. The upper vortex is diminished/shortened on decreasing gap ratio (or increasing wall effect). At G = 0.25, a single time-averaged vortex is observed at the rear of the square obstacle up to Re = 125. In addition, a wake is formed on the downstream channel wall and its height increases laterally on decreasing gap ratio from 1 to 0.25. On increasing Re, this wake flattens along the channel wall and hence its size increases. The flow is observed to be steady for Re up to 121 at G = 0.5. The conversion to a time-periodic regime from a steady regime is presented in figure 5a–5b by providing the temporal variation of the lift coefficient. It can be noted that the onset of the shifting to a time-periodic regime from a steady regime exists at Re = 122 for G = 0.5. Also, as the gap ratio reduces the delay in the shifting of time-periodic regime from steady regime is observed. To demarcate the (periodic) unsteady regime at differing values of Re and G, numerical analysis has been performed in the complete domain and the frequency of the vortex shedding (Strouhal number) is recorded with time. It is also valuable to state that the transition to periodic unsteady regime occurs after Re = 45 for the free stream flow past a long square obstacle [34, 35]. Analogous to the transition of time-periodic regime from a steady regime, the flow separation from the surface of the square obstacle delays with decreasing gap ratio. An asymmetric vortex is observed downstream on the bottom wall of the square obstacle at G = 0.25 for Re ≤ 150. Similarly, for G = 0.5, an asymmetric vortex is formed at Re ≤ 100 and at G = 1, an asymmetric vortex is found at Re = 1.

Figure 4

Time-averaged streamlines for (a–c) G = 0.25, (d–f) G = 0.5 and (g–i) G = 1.

Figure 5

Onset of transition from a steady to a time-periodic regime: C _L vs t plot for G = 0.5.

The variation of the time history of flow output parameters (drag and lift coefficients) is presented in figure 6 for Re > 100 at different G. In the unsteady time-periodic regime, full-domain computations are carried out until 10 cycles of almost constant amplitude are obtained for the output parameters. Moreover, these instantaneous values of the output parameters in 10 periodic cycles are employed to analyse their time-averaged values. The amplitudes of C _D and C _L increase with increase in Re and G (figure 6) because as the gap ratio increases the interaction between the lower domain wall shear layer and the shear layer of the bottom surface of the square obstacle decreases and hence the drag and lift forces are enhanced. At the same instance, the time period for a cycle increases with increase in Re, which implies that vortices are now shed with a lower frequency. However, the time period for a cycle lowers with increase in G, which implies that on going away from the wall the frequency of vortices is increasing. It is also found that the drag coefficient cycles appear with one additional pseudo peak for G = 1. The existence of two peaks in one complete time cycle is the outcome of the establishment and subsequent separation of vortices (vortex shedding) alternatively from either side of the square obstacle, that is, two rows of vortices are shed alternatively from the bottom and top surfaces of the square obstacle for the given range of G [8].

Figure 6

Time history of C _L and C _D for (a–d) G = 0.5 and (e–h) G = 1 at different values of Re.

Figure 7a shows the variation of overall drag coefficient for Re ≥ 100 and G = 0.25–1. The values of total drag coefficients show a decreasing non-linear dependence on Re for all gap spacings. Also, a simple heat transfer expression as developed in our recent work [1] can be employed to compute the in-between values of the overall drag coefficients even for the extended ranges of Re covered in this work. The deviation of the drag coefficient correlation [1] with respect to existing computed results is found to have a maximum of ~10.4% (at Re = 5), 6.3% (at Re = 125) and 9.3% (at Re = 50) for G = 0.25, 0.5 and 1, respectively. The corresponding average deviations are ~4.8%, 3.1% and 4.7% for G = 0.25, 0.5 and 1, respectively.

Figure 7

Variation of (a) C _D , (b) C _L and (c) St with Re and G.

Figure 7b presents the overall lift coefficient at Re ≥ 100 and G = 0.25–1. As observed in [1] at high Re, pressure at the top surface increases for G = 0.25 and 0.5 with increase in Re but it decreases for G = 1. The difference between the bottom and top surface pressures contributed to lift coefficient. Hence, with increasing Re, lift coefficient decreases for G = 0.25 and 0.5, and it increases for G = 1 (figure 7b). The Strouhal number values with Re (100–150) and G (0.25–1) are presented in figure 7c. It is found that the flow is time periodic for Re ≥ 122 at G = 0.5. The value of the Strouhal number increases with the rise in gap ratio. This suggests that the wavering motion rises with rising gap ratio. It can also be noted from this figure that the maximum values of the Strouhal numbers appear at Re = 100 and 125 for G = 1 and 0.5, respectively. As expected, the Strouhal number for the current flow system is higher than that for the unconfined square obstacle [13, 34, 35].

Furthermore, the pressure distribution on the lower surface of the square cylinder and the channel wall is presented to explore the effect of changing G and Re. The difference in pressure coefficient between the lower surface of the square cylinder and the channel wall (that is, in the gap region) is almost negligible at G = 0.25 (figure 8a–8d). Similarly, for G = 0.5, the difference in pressure coefficient is almost negligible at the core (at Bb) of the gap region and also negligible on moving from Bb to Cc (figure 8e–8h). At G = 1, the core of the gap region has a negligible pressure coefficient difference for Re = 1 (figure 8i). This shows that for gap ratios (0.25–0.5) and/or Re = 1, the gap region flow is unidirectional, and the core flow looks like the channel flow. This observation is also consistent with the experimental and numerical findings reported in [21] and [13], respectively. On the other hand, significant change in pressure coefficient difference can be noted at G = 1. Also, the pressure coefficient distribution on the lower surface of the square cylinder is less than that on the channel wall for Re > 1 at G = 1 (figure 8j–l).

Figure 8

Pressure coefficient variation along the lower surface of the square cylinder and the channel wall for (a–d) G = 0.25, (e–h) G = 0.5 and (i–l) G = 1.

4.3 Thermal characteristics

The temperature fields close to the wall near the square obstacle are given by isotherm contours for Pr = 10, 50 and 100 in figures 9a–9i, 10a–10i and 11a–11i for Re = 1, 100 and 150 at G = 0.25, 0.5 and 1, respectively. Similar to results at Pr = 0.7 [1], presence of the adiabatic wall causes an asymmetry in the temperature fields near the obstacle. Figures 9, 10 and 11 show that on increasing Re, the hydrodynamic boundary layer decreases, and also with increasing Pr the thermal boundary layer decreases [36]. It is also consistent with the growing values of the gap ratio at a constant Re and Pr. Figure 9 shows that due to low Re, heat transfer is interrupted by the presence of a channel wall. Hence, the temperature difference between the channel wall and the square obstacle is low. This difference in temperature increases with increasing G and/or Pr due to shrinking of isotherms. Hence, the thermal boundary layer reduces with the increase in gap ratio. Also, the temperature difference between the channel wall and the square obstacle is reduced with increasing Re.

Figure 9

Isotherm contours around a square cylinder near a wall at different values of Pr and G for Re = 1.

Figure 10

Isotherm contours around a square cylinder near a wall at different values of Pr and G for Re = 100.

Figure 11

Isotherm contours around a square cylinder near a wall at different values of Pr and G for Re = 150.

The longitudinal span of the recirculation region after the square obstacle enhances with growing Re and also the congestion of the thermal contours close to the back surface of the square obstacle increases (figures 9, 10, 11). The effective heat transfer area with the bottom wall of the square cylinder decreases with increasing G and also the wall interruption is reduced. On increasing Pr, the thermal boundary layer becomes weaker and hence the crowding of the temperature contours near the square cylinder increases (figures 9, 10, 11). The isotherms around the square cylinder also extend axially with increasing Pr.

The time history of heat transfer output parameter (Nusselt number) is generated and shown in figure 12 at Pr = 10, 100 for Re = 125, 150 and G = 0.5, 1. The amplitude of average Nusselt number increases with G. Also, it increases with Re except at G = 1 for Pr ≥ 50. The mixed trend is observed with increasing Pr. The local maximum is observed at Pr = 50 for G = 0.5. At G = 1, the local minimum is found at Pr = 50 for Re = 125 and it decreases monotonically with Pr for Re = 150. Similar to the flow output parameters, the time period for a cycle improves with increasing Re and deteriorates with increasing G. For higher Re, Pr and G (that is, Re = 150, Pr = 100 and G = 1), the Nusselt number cycles also have one additional pseudo peak (figure 12h).

Figure 12

Time history of Nusselt number for (a–d) G = 0.5 and (e–h) G = 1 at different values of Re, Pr.

The average surface Nusselt number on the surfaces of the square bar in the steady regime for Pr ≥ 10 at various values of Re and G is presented in figure 13a–13d. The local Nusselt number (Nu) at this juncture is described as $- \partial \theta /\partial n$. The average surface value on each face of the square body is computed by taking the average of the local values. In general, for an unconfined square obstacle, the front surface has the maximum Nusselt number, while the back surface has the least value of Nusselt number and the bottom and top surfaces have the same Nusselt number values [35]. For the occurrence of a square obstacle near a moving wall with uniform inlet velocity, the maximum and the minimum heat transfer rates appear along the front and back faces, respectively. The presence of a moving wall decreases the heat transfer rate along the top surface with decreasing G [15]. In linear inlet velocity, the velocity increases on moving from the bottom to the top. At low Re, the wall acts as a stationary wall and interrupts the heat transfer. Hence, the highest and the least Nusselt number values are observed on the top and bottom surfaces, respectively (figure 13). Similar results are obtained for higher gap ratio (G = 1) because at high gap ratio velocity difference plays the major role. On increasing Re, the near-wall fluid acts as a moving wall for a low gap ratio (G = 0.25). Hence, the similar results of a moving wall [15] are obtained. It is observed from figure 13 that as Pr and/or Re increases the heat transfer enhances for all the surfaces.

Figure 13

Variation of average Nusselt number of (a) front, (b) bottom, (c) rear and (d) top surfaces of 2-D square cylinder near a wall with Re, Pr and G in the steady regime.

The average cylinder Nusselt number ($\overline{Nu}$) values for different Pr (≥10) with Re and G are shown in figure 14. The $\overline{Nu}$ values are achieved by taking the mean of the average Nusselt number values on the faces. With increasing gap height, heat transfer on the front face reduces and the opposite trends are observed on the back and top surfaces; whereas a mixed trend is found on the bottom surface [1]. However, from isotherm contours, wall interruption reduces with increasing G and also the congestion of isotherms mainly in the back surface enhances with increasing G. So, the rear face increase in average Nusselt number is much higher than the decrease caused by the front surface. Hence, the $\overline{Nu}$ values increase with the increase in G. Also, the average cylinder Nusselt number rises with the rise in Pr and/or Re as the surface average Nusselt number rises with the increase in Pr and/or Re. The disparity among the values of an average cylinder Nusselt number also increases with increasing G for constant values of Re and Pr.

Figure 14

Variation of the $\overline{Nu}$ with Re and G for (a) Pr = 10, (b) Pr = 50 and (c) Pr = 100.

The heat transfer enhancement is computed for various Re, Pr and G. The enhancement in the $\overline{Nu}$ values for various Pr with respect to Pr = 0.7 is given in figure 15a–15c. Similarly, figure 15d–15f provides the enhancement in the $\overline{Nu}$ for different gap ratios against G = 0.25. The heat transfer enhancement increases with the rise in Pr (figure 15a–15c) and G (figure 15d–15g) at any Re. The maximum increase in heat transfer attained is ~660% (at Re = 30, Pr = 100 and G = 0.25) against the analogous values at Pr = 0.7, ~89% (at Re = 20, Pr = 0.7 and G = 1) against the equivalent values at G = 0.25 and ~1332% (at Re = 150, Pr = 100 and G = 0.25) against the corresponding values at Re = 1.

Figure 15

Percent enhancement in $\overline{Nu}$ with Re for (a–c) different Prandtl numbers with respect to Pr = 0.7 at G = 0.25–1 and (d–f) different gap ratios with respect to G = 0.25 at Pr = 10–100.

Furthermore, the Colburn heat transfer factor (j _h ) is presented with Re, G and Pr in figure 16a–16c, which is described as $j_{h} = \overline{Nu} /(\text{Re} \Pr^{1/3} )$. It is notable from this figure that with rising G, the j _h factor enhances; however, these results are more notorious at low Re. The j _h factor increases with rising Pr. It is also valuable to note that all the values of the j _h factor more or less coincide onto a single curve at different values of Re and G for Pr = 10–100. So, a heat transfer correlation (Eq. 5) is formulated for the given Pr range (Pr ≥ 10) at different values of Re and G covered. Based on the earlier studies [1, 33, 36, 37], this correlation is generated by applying best fit method. Also, the flow is dominated by viscous diffusion for Pr > 0.7; however, at Pr = 0.7, flow is dominated by thermal diffusion [1].

$$ j_{h} = 0.721G^{0.288} \text{Re}^{ - 0.5} $$

(5)

This correlation has the upper limit deviation of ~14.7% (at Re = 5, Pr = 10 and G = 0.25) and the mean deviation of ~5.7% with present computed values.

Figure 16

Variation of the j _h factor with Re and G for (a) Pr = 10, (b) Pr = 50 and (c) Pr = 100.

5 Conclusions

Forced convection heat transfer from a square obstacle in the neighbourhood of a wall is studied in a horizontal plane for $1 \le \text{Re} \le 150$, $10 \le \Pr \le 100$ and $0.25 \le G \le 1$. The key points of this study are as follows:

• The numerical methodology has been validated extensively.

• The fluid flow and heat transfer fields remain steady for G = 0.5 up to Re = 121. Thus, the onset of time-periodic regime is originated at Re = 122 for G = 0.5.

• In time-periodic regime, the peak amplitudes of average Nusselt number, drag and lift coefficients increase with rise in G.

• The $\overline{Nu}$ and the j _h factor are observed to rise with increasing Pr.

• The average surface Nusselt number along the front surface of the square cylinder rises gradually with increase in gap ratio and the opposite scenario is obtained for the top and rear surfaces.

• Maximum rise in heat transfer is obtained approximately 1332% at Re = 150 (Pr = 100, G = 0.25) against the analogous values at Re = 1.

• Finally, the correlation of the Colburn j _h factor has been established for the ranges covered. Also, it has been ensured that the drag coefficient correlation developed in [1] can be utilised even for the extended ranges of Re.

Investigation of forced convection heat transfer for non-Newtonian fluids would be the scope for future study at low Re for varying G and Pr.

Appendices

Notations

$C_{D}$ :

drag coefficient $\left( {\frac{{2F_{D} }}{{\rho U_{\infty }^{2} D}}} \right)$

$C_{L}$ :

lift coefficient $\left( {\frac{{2F_{L} }}{{\rho U_{\infty }^{2} D}}} \right)$

$C_{p}$ :

pressure coefficient $\left( {\frac{2\Delta p}{{\rho U_{\infty }^{2} }}} \right)$

$c_{p}$ :

specific heat (J/kg.K)

CV:

control volume

D :

side of the square obstacle (m)

$F_{D}$ :

drag force (N/m)

$F_{L}$ :

lift force (N/m)

$f$ :

frequency of vortex shedding (1/s)

G :

gap ratio $\left( {\frac{{G^{*} }}{D}} \right)$

H :

domain height (m)

h :

coefficient of local heat transfer (W/m² K)

$\bar{h}$ :

coefficient of average heat transfer (W/m² K)

j _h :

Colburn factor of heat transfer

$k$ :

thermal conductivity (W/m K)

L _d , L _u :

downstream and upstream distances, respectively (m)

n :

normal direction

N:

control volumes on a side of the square obstacle

Nu :

local Nusselt number $\left( {\frac{hD}{k}} \right)$

$\overline{Nu}$ :

average Nusselt number $\left( {\frac{{\overline{h} D}}{k}} \right)$

$p$ :

pressure $\left( {\frac{{p^{*} }}{{\rho U_{\infty }^{2} }}} \right)$

Pr:

Prandtl number $\left( {\frac{{\mu c_{p} }}{k}} \right)$

Re:

Reynolds number $\left( {\frac{{DU_{\infty } \rho }}{\mu }} \right)$

$St$ :

Strouhal number $\left( {\frac{fD}{{U_{\infty } }}} \right)$

$t$ :

time $\left( {\frac{{t^{*} }}{{\left( {{\raise0.7ex\hbox{$D$} \!\mathord{\left/ {\vphantom {D {U_{\infty } }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${U_{\infty } }$}}} \right)}}} \right)$

$T$ :

temperature (K)

$T_{\infty }$ :

inlet fluid temperature (K)

$T_{w}$ :

square obstacle temperature (K)

$U_{\infty }$ :

inlet fluid average velocity (m/s)

u*, v* :

components of velocity in x* and y* directions, respectively (m/s)

x*, y* :

axial and lateral coordinates respectively (m)

Greek symbols

$\rho$ :

fluid density (kg/m³)

$\mu$ :

dynamic viscosity (Pa.s)

$\delta$ :

smallest cell size (m)

$\theta$ :

dimensionless temperature $\left( {\frac{{T - T_{\infty } }}{{T_{w} - T_{\infty } }}} \right)$

Superscript

*:

dimensional value