Total coloring of planar graphs without adjacent short cycles

Abstract

In the study of computer science, optimization, computation of Hessians matrix, graph coloring is an important tool. In this paper, we consider a classical coloring, total coloring. Let $G=(V,E)$ be a graph. Total coloring is a coloring of $V\cup {E}$ such that no two adjacent or incident elements (vertex/edge) receive the same color. Let G be a planar graph with $\varDelta \ge 8$. We proved that if for every vertex $v\in V$, there exists two integers $i_v,j_v\in \{3,4,5,6,7\}$ such that v is not incident with adjacent $i_v$-cycles and $j_v$-cycles, then the total chromatic number of graph G is $\varDelta +1$.

1 Introduction

In graph theory, coloring is an important and classical problem. It has many applications in pattern matching, frequency assignment in optical communication networks, and so on. A vertex coloring of a graph is a coloring such that every vertex receives color, and every two adjacent vertices have different colors. A total coloring assigns each vertex or edge with a color such that no adjacent vertices receive the same color, no adjacent edges receive the same color, and no incident vertex and edge receive the same color. For a graph $G=(V,E)$, its total graph T(G) is defined to have vertex set $V \cup E$ and edge set consisting of all pairs of adjacent or incident elements in $V \cup E$. A total coloring of graph G is equivalent to a vertex coloring of T(G).

In total coloring problem, the target of total coloring is to find the minimum number of colors to do this coloring. For simplicity of speaking, if G has a total coloring with k colors, then G is said to be total-k-colorable. The total chromatic number $\chi ''(G)$ is the smallest number k such that G is total-k-colorable. Clearly, $\chi ''(G)\ge \varDelta +1$. In 1964, Behzad and Vizing gave a popular conjecture that every graph G is total-$(\varDelta +2)$-colorable, where $\varDelta$ is the maximum vertex degree of G. For short, this conjecture is referred as TCC which has attracted many researchers’ attention. Yap (1996) proved $\chi ''(K_n)=n$ if n is odd and $\chi ''(K_n)=n+1$ otherwise. Moreover, TCC is also proved for interval graph Bojarshinov (2001), series-parallel graphs Wu (2004), and so on. For a general graph, TCC hold for graphs with $\varDelta \le 5$ (see Yap 1996; Kowalik et al. 2008). Snchez-Arroyo (1989) proved that it is NP-complete to decide whether $\chi ''(G)=\varDelta +1$ for a given graph. McDiarmid and Snchez-Arroyo (1994) further proved that for every fixed $k\ge 3$, it is even NP-complete to decide whether $\chi ''(G)=k+1$ for a given k-regular bipartite graph G.

In our paper, we consider planar graph. For planar graphs, the only open case of TCC is $\varDelta =6$ (see Kostochka 1996; Sanders and Zhao 1999). Interestingly, the total chromatic number of planar graphs with large maximum degree equals the lower bound, i.e., $\chi ''(G)=\varDelta +1$. This result was proved for $\varDelta \ge 9$ in Kowalik et al. (2008). In the following, we consider the planar graph with $\varDelta \ge 8$. Some related results can be found in Du et al. (2009), Liu et al. (2009), Roussel and Zhu (2010), Shen and Wang (2009), Wang et al. (2013), and Yap (1996). In this paper we get the following theorem.

Theorem 1

Suppose G is a planar graph with $\varDelta \ge 8$. If for every vertex v, there exists two integers $i_v,j_v\in \{3,4,5,6,7\}$ such that v is not incident with adjacent $i_v$-cycles and $j_v$-cycles, then $\chi ''(G)=\varDelta +1$.

Here, we say that two cycles are adjacent if they share at least one common edge. Note that in Theorem 1, $i_v$ and $j_v$ are related to v, respectively. If $i_v=i,j_v=j$ for each vertex $v\in V$, then we can easily get one corollary.

Corollary 1

For two fixed integers i and j $(i,j\in \{3,4,5,6,7\})$, if G is a planar graph with $\varDelta \ge 8$ and without adjacent i-cycles and j-cycles, then $\chi ''(G)=\varDelta +1$.

This corollary generalizes the result for $\varDelta =8$, which has been recently proved (see Wang et al. 2014), that is $\chi ''(G)=\varDelta +1$ if G is a planar graph without adjacent cycles of size i and j, for some $i,j\in \{3,4,5\}$. Clearly, it also generalizes the result in Du et al. (2009) that if G is a planar graph with $\varDelta \ge 8$ and without adjacent triangles, then $\chi ''(G)=9$. In addition, it strengthens the results in Shen and Wang (2009), Wu and Wang (2008) and Tan et al. (2009).

In this paper, all graphs are finite, simple and undirected. Most of the notions are standard and we refer the readers to Bondy and Murty (1976). Let G be a graph. A k -vertex, $k^{-}$ -vertex or a $k^{+}$ -vertex is a vertex of degree k, at most k or at least k, respectively. Similarly, we can define a k -face, $k^{-}$ -face and a $k^{+}$ -face. We use $(v_{1},v_{2},\cdots ,v_{n})$ to denote a cycle whose vertices are consecutively $v_{1},v_{2},\cdots ,v_{n}$. If the boundary of a face f is $(v_{1},v_{2},\cdots ,v_{n})$, then f is simply referred to as a $(d(v_{1}),d(v_{2}),\cdots ,d(v_{n}))$-face. We use $n_{k}(v)$ to denote the number of k-vertices adjacent to v, use $n_{k}(f)$ to denote the number of k-vertices incident with f, and use $f_{k}(v)$ to denote the number of k-faces incident with v.

2 Reducible configurations

In Kowalik et al. (2008), Theorem 1 was proved for $\varDelta \ge 9$. So in the following we assume that $\varDelta =8$. Let $G=(V,E,F)$ be a minimal counterexample to Theorem 1 with $|V|+|E|$ as small as possible.

In this section we start the proof of Theorem 1 by obtaining structural informations about our minimal counterexample G, which shows that certain configurations are reducible, that is, they cannot occur in G. First, we shown some known properties.

• (a) G is 2-connected.

• (b) If uv is an edge of G with $d(u)\le 4$, then $d(u)+d(v)\ge \varDelta +2=10$ (see Wang et al. 2014).

• (c) The subgraph $G_{28}$ of G induced by all edges joining 2-vertices to $\varDelta$-vertices is a forest (see Wang et al. 2014).

Lemma 1

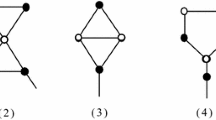
(Du et al. 2009) G has no configurations depicted in Fig. 1, where the vertices marked by $\bullet$ have no other neighbors in G and 7-v denotes the vertex with degree of 7.

Fig. 1

Reducible configurations of Lemma 1

Lemma 2

(Wang et al. 2014) Suppose $d(v)=d\ge 6$, whose adjacent vertices are consecutively $v_{1},v_{2},\cdots ,v_{d}$ and whose incident faces are consecutively $f_{1},f_{2},\cdots ,f_{d}$, where $v_i$ is incident with $f_{i-1}$ and $f_i$ $(i=1,2,\cdots ,d)$. Note that $f_{0}$ and $f_{d}$ are the same face. Let $d(v_1)=2$ and $N(v_1)=\{v,u_1\}$. Then G does not satisfy one of the following conditions, where

• (1) there exists an integer k $(2\le k\le d-1)$ such that $d(v_{k+1})=2$, $d(v_i)=3$ $(2\le i\le k)$ and $d(f_j)=4$ $(1\le j\le k)$.

• (2) there exist two integers k and $t\,(2\le k<t\le d-1)$ such that $d(v_{k})=2$, $d(v_i)=3\,(k+1\le i\le t)$, $d(f_t)=3$ and $d(f_j)=4\,(k\le j\le t-1)$.

• (3) there exist two integers k and $t\,(3\le k\le t\le d-1)$ such that $d(v_i)=3\,(k\le i\le t)$, $d(f_{k-1})=d(f_t)=3$ and $d(f_j)=4$ $(k\le j\le t-1)$.

• (4) there exists an integer k $(2\le k\le d-2)$ such that $d(v_{d})=d(v_{i})=3$ $(2\le i\le k)$, $d(f_k)=3$ and $d(f_j)=4$ $(0\le j\le k-1)$.

By Lemma 2, we can easily get the corollary as follows.

Corollary 2

(Wang et al. 2014) G does not contain the configurations depicted in Fig. 2.

Fig. 2

Reducible configurations of Corollary 2

Lemma 3

If a 6-vertex u is adjacent to one 4-vertex v and incident with one 3-cycle (u, v, s), then u is adjacent to no other 4-vertex.

Proof

Suppose u is adjacent to another 4-vertex w. By the minimality of G, $G'=G-uv$ has a total-9-coloring $\phi$. Erase the colors on v and w. Let $C(x)=\{\phi (xy): y\in N(x)\}\cup \{\phi (x)\}$, then the forbidden colors for uv is at most 9. Without loss of generality, let $C(u)=\{1,2,3,4,5,6\}$, $C(v)=\{7,8,9\}$, $\phi (u)=1$, $\phi (us)=5$, $\phi (vs)=7$, $\phi (uw)=6$. Then $C(w)\setminus \phi (uw)=\{7,8,9\}$. Otherwise, without loss of generality, if $7\not \in C(w)$, we can recolor uw with 7 and color uv with 6. By proper coloring the 4-vertices v and w, we get a total-9-coloring of G, a contradiction. In the following, change the colors of us and vs, that is, recolor us with 7, recolor vs with 5. Then color 5 does not appear in C(u). So recolor uw with 5, color uv with 6, by proper coloring the 4-vertices v and w, we get a total-9-coloring of G, a contradiction. $\square$

3 Discharging

We shall complete the proof of Theorem 1 by using the discharging method. This is an important and interesting tool in the proof of the coloring of planar graphs. By Euler’s formula $|V|-|E|+|F|=2$, we have

$$\begin{aligned} \sum _{v\in V}(2d(v)-6)+\sum _{f\in F}(d(f)-6)=-6(|V|-|E|+|F|)=-12<0 \end{aligned}$$

We define c(x) to be the initial charge. Let $c(v)=2d(v)-6$ for each $v\in V$ and $c(f)=d(f)-6$ for each $f\in F$. So $\sum _{x\in V\cup F}c(x)=-12<0$. Then we apply the following rules to redistribute the initial charge that leads to a new charge $c'(x)$.

(R1):

From each 8-vertex to each of its adjacent 2-vertices, transfer 1.

(R2):

From each 4-vertex to each of the k-faces incident with it, where $3\le {k}\le 5$, transfer $\frac{1}{2}$.

(R3):

From each 5-vertex v to each of the k-faces incident with it, where $3\le {k}\le 5$, transfer

$\frac{4}{5}$,:

   if $k=3$ and $f_3(v)=5$;

$\frac{7}{8}$,:

   if $k=3$ and $f_3(v)=4$;

$\frac{7}{6}$,:

   if $k=3$ and $f_3(v)=3$;

$\frac{5}{4}$,:

   if $k=3$ and $f_3(v)\le 2$;

$\frac{1}{2}$,:

   if $k=4$;

$\frac{1}{5}$,:

   if $k=5$.

(R4):

From each 6-vertex v to each of the k-faces f incident with it, transfer

$\frac{5}{4}$,:

   if $k=3$ and $n_{4}(f)=1$;

$\frac{11}{10}$,:

   if $k=3$ and $n_{5}(f)=1$ or $n_{5}(f)=2$;

1 ,:

   if $k=3$ and $n_{6^+}(f)\ge 3$;

$\frac{1}{2}$,:

   if $k=4$;

$\frac{1}{3}$,:

   if $k=5$.

(R5):

From each $7^{+}$-vertex to each of the k-faces f incident with it, transfer

$\frac{3}{2}$,:

   if $k=3$ and $n_{3}(f)=1$;

$\frac{5}{4}$,:

   if $k=3$ and $n_{3}(f)=0$;

1 ,:

   if $k=4$ and $n_{3^-}(f)=2$;

$\frac{3}{4}$,:

   if $k=4$, $n_{3^-}(f)=1$ and $n_{4}(f)=1$ or $n_{5}(f)=1$;

$\frac{2}{3}$,:

   if $k=4$, $n_{3^-}(f)=1$ and $n_{6^+}(f)=3$;

$\frac{1}{2}$,:

   if $k=4$ and $n_{3^-}(f)=0$ ;

$\frac{1}{3}$,:

   if $k=5$.

The rest of this paper is to check that $c'(x)\ge 0$ for all $x\in V\cup F$ which will be the desired contradiction.

Final charge of faces. Let $f\in F$. Suppose $d(f)=3$. Then $c(f)=d(f)-6=-3$. If $n_{3^-}(f)=1$, then $n_{7^+}(f)=2$ by (b), and $c'(f)= -3+\frac{3}{2}\times 2=0$ by (R5). If $n_{4}(f)=1$, then $c'(f)= -3+\frac{5}{4}\times 2+\frac{1}{2}=0$ by (R2), (R4) and (R5). If $n_{5}(f)=1$, then $n_{6^+}(f)=2$ and $c'(f)\ge -3+\frac{11}{10}\times 2+\frac{4}{5}=0$. If $n_{5}(f)=2$ and one 5-vertex incident with f is incident with at least four 3-faces, then the other 5-vertex incident with f is incident with at most three 3-faces. So $c'(f)= -3+\min \{\frac{4}{5}+\frac{7}{6}+\frac{11}{10},\frac{7}{8}+\frac{7}{6}+\frac{11}{10}\}>0$. If $n_{5}(f)=2$ and no 5-vertex incident with f is incident with at least four 3-faces, then $c'(f)\ge -3+\frac{7}{6}\times 2+\frac{11}{10}=\frac{13}{30}>0$. If $n_{5}(f)=3$, then the number of 5-vertices incident with f and incident with five 3-faces is at most one, so $c'(f)= -3+\min \{\frac{4}{5}+\frac{7}{6}\times 2, \frac{7}{8}+\frac{7}{6}\times 2, \frac{7}{6}\times 3\}=\frac{2}{15}>0$. If $n_{6^+}(f)=3$, then $c'(f)= -3+1\times 3=0$. Suppose $d(f)=4$. Then $c(f)=d(f)-6=-2$. If $n_{3^-}(f)=2$, then $n_{7^+}(f)=2$ by (b), and $c'(f)= -2+1\times 2=0$ by (R5). If $n_{3^-}(f)=1$ and $n_{4}(f)=1$, then $c'(f)=-2+\frac{1}{2}+\frac{3}{4}\times 2=0$. If $n_{3^-}(f)=1$ and $n_{5}(f)=1$, then $c'(f)=-2+\frac{1}{2}+\frac{3}{4}\times 2=0$. If $n_{3^-}(f)=1$ and $n_{6^+}(f)=3$, then $c'(f)=-2+\frac{2}{3}\times 3=0$. If $n_{3^-}(f)=0$, then $c'(f)=-2+\frac{1}{2}\times 4=0$. Suppose $d(f)=5$. Then $c(f)=d(f)-6=-1$ and $n_{5^+}(f)\ge 3$. If $n_5(f)=0$, then $c'(f)\ge -1+\frac{1}{3}\times 3=0$. Otherwise, $n_5(f)\ge 1$ and $c'(f)\ge -1+\min \{\frac{1}{5}\times 5, \frac{1}{5}+\frac{1}{3}\times 3,\frac{1}{5}\times 4+\frac{1}{3}\}=0$. Suppose $d(f)\ge 6$. Then $c(f)=d(f)-6\ge 0$.

Final charge of vertices. Let $v\in V$. Note that G has no vertex of degree one. Suppose $d(v)=2$. Then $c(v)=2d(v)-6=-2$ and $n_{8}(v)=2$. So $c'(v)=-2+1\times 2=0$ by (R1). Suppose $d(v)=3$. Then clearly $c'(v)=c(v)=0$. Suppose $d(v)=4$. Then $c(v)=2$ and v sends at most $\frac{1}{2}$ to each of its incident faces. So $c'(v)\ge 2-\frac{1}{2}\times 4=0$ by (R2). Suppose $d(v)=5$. Then $c(v)=4$, and $n_{4^-}(v)=0$. If $f_3(v)=5$, then $c'(v)=4-\frac{4}{5}\times 5=0$ by (R3). If $f_3(v)=4$, then $c'(v)\ge 4-\frac{7}{8}\times 4-\frac{1}{2}=0$. Suppose $f_3(v)=3$. Then v is incident with at most one 4-face. If $f_4(v)=1$, then $f_5(v)=0$ and so $c'(v)\ge 4-\frac{7}{6}\times 3-\frac{1}{2}=0$. If $f_4(v)=0$, then $c'(v)\ge 4-\frac{7}{6}\times 3-\frac{1}{5}\times 2=\frac{1}{10}>0$. If $f_3(v)\le 2$, then $c'(v)\ge 4-\frac{5}{4}\times 2-\frac{1}{2}\times 3=0$. Suppose $d(v)=6$. Then we have $c(v)=6$, $n_{3^-}(v)=0$, and $f_3(v)\le 5$. By lemma 2, v is incident with at most two 3-faces each of which receives $\frac{5}{4}$ from v. If $f_3(v)=5$, then $f_{6^+}(v)=1$ and $c'(v)\ge 6-\frac{5}{4}\times 2-\frac{11}{10}\times 3=\frac{1}{5}>0$. If $f_3(v)\le 4$, then $c'(v)\ge 6-\frac{5}{4}\times 2-\frac{11}{10}\times 2-\frac{1}{2}\times 2=\frac{3}{10}>0$.

Suppose $d(v)=7$. Then $c(v)=8$, $n_{2}(v)=0$, and $f_3(v)\le 5$. We also known v is incident with at most two 3-faces each of which receives $\frac{3}{2}$ from v. Moreover, if v is incident with one 3-face which incident with a 3-vertex, then v is adjacent to no other 3-vertex. If $f_3(v)=5$, then $c'(v)\ge 8-\frac{3}{2}\times 2-\frac{5}{4}\times 3-\frac{1}{2}\times 2=\frac{1}{4}>0$. If $f_3(v)=4$, then $c'(v)\ge 8-\frac{3}{2}\times 2-\frac{5}{4}\times 2-\frac{3}{4}\times 3=\frac{1}{4}>0$. If $f_3(v)=3$, then $c'(v)\ge 8-\frac{3}{2}\times 2-\frac{5}{4}-\frac{3}{4}\times 4=\frac{3}{4}>0$. If $f_3(v)\le 2$, then $c'(v)\ge 8-\frac{3}{2}\times 2-1\times 5=0$.

In the following, we consider the vertex of degree 8. Suppose $d(v)=8$, whose adjacent vertices are consecutively $v_{1},v_{2},\cdots ,v_{8}$ and whose incident faces are consecutively $f_{1},f_{2},\cdots ,f_{8}$, where $v_i$ is incident with $f_{i-1}$ and $f_i$ $(i=1,2,\cdots ,8)$. Note that $f_{0}$ and $f_{8}$ are the same face. We also have $c(v)=2\times 8-6=10$.

Lemma 4

Suppose $d(v)=8$ and $v_{1},v_{2},\cdots ,v_{k-1},v_k$ be the consecutively adjacent vertices of v for $k\ge 3$. If $d(v_1)=d(v_k)=2$, $d(v_j)\ge 3$ for all $j=2,3,\cdots ,k-1$, and $\min \{d(f_2),d(f_3),\cdots ,d(f_{k-2})\}\ge 3$, then v sends at most $\frac{3}{2}+(k-3)\times \frac{5}{4}$(in total) to $f_1,f_2,\cdots ,f_{k-1}$.

Proof

Firstly, we have $\min \{d(f_1),d(f_{k-1})\}\ge 4$ by Lemma 1. Suppose $\min \{d(f_1)$ $,d(f_{k-1})\}\ge 5$. Then v is not incident with two 3-faces which are incident with a common 3-vertex, and the 3-face incident with v needs more charge than the 4-face incident with v. So v sends at most $\frac{1}{3}\times 2+(k-3)\times \frac{5}{4}$(in total) to $f_1,f_2,\cdots ,f_{k-1}$, which is less than $\frac{3}{2}+(k-3)\times \frac{5}{4}$. Suppose $\min \{d(f_1)$ $,d(f_{k-1})\}=4$ and $\max \{d(f_1)$ $,d(f_{k-1})\}\ge 5$. Then v sends at most $\frac{1}{3}+1+(k-3)\times \frac{5}{4}$(in total) to $f_1,f_2,\cdots ,f_{k-1}$, which is less than $\frac{3}{2}+(k-3)\times \frac{5}{4}$. Suppose $d(f_1)=d(f_{k-1})=4$. If $\min \{d(f_2), d(f_3),$ $\cdots , d(f_{k-2})\}\ge 5$, then v sends at most $1\times 2+(k-3)\times \frac{1}{3}$(in total) to $f_1,f_2,\cdots ,f_{k-1}$, which is less than $\frac{3}{2}+(k-3)\times \frac{5}{4}$. If $\min \{d(f_2), d(f_3),$ $\cdots , d(f_{k-2})\}=4$ and $\max \{d(f_2), d(f_3),$ $\cdots , d(f_{k-2})\}\ge 5$, then v sends at most $1\times 2+(k-5)\times 1+\frac{3}{4}+\frac{1}{3}$(in total) to $f_1,f_2,\cdots ,f_{k-1}$, which is less than $\frac{3}{2}+(k-3)\times \frac{5}{4}$ for $k\ge 3$. If $d(f_2)=d(f_3)=\cdots = d(f_{k-2})=4$, then v sends at most $1\times 2+(k-5)\times 1+\frac{3}{4}\times 2$(in total) to $f_1,f_2,\cdots ,f_{k-1}$, which is less than $\frac{3}{2}+(k-3)\times \frac{5}{4}$ for $k\ge 3$. In the following, suppose $\min \{d(f_2),d(f_3),\cdots ,d(f_{k-2})\}=3$. Since v needs to sends at least $\frac{5}{4}$ to each of its incident 3-faces and sends at most 1 to each of its incident 4-faces, we suppose $d(f_2)=d(f_3)=\cdots =d(f_{k-2})=3$. Then there are at most two 3-faces, that is $f_2,f_{k-2}$, which may be need receive $\frac{3}{2}$ from v. Suppose there is exactly one 3-face from $f_2,f_{k-2}$ which needs receive $\frac{3}{2}$ from v. Then $\max \{d(f_1),d(f_{k-1})\}\ge 5$. So v sends at most $\frac{3}{2}+(k-4)\times \frac{5}{4}+\frac{3}{4}+\frac{1}{3}$(in total) to $f_1,f_2,\cdots ,f_{k-1}$. Suppose each of $f_2$ and $f_{k-2}$ needs receive $\frac{3}{2}$ from v. Then $\min \{d(f_1),d(f_{k-1})\}\ge 5$. So v sends at most $\frac{3}{2}\times 2+(k-5)\times \frac{5}{4}+\frac{1}{3}\times 2$(in total) to $f_1,f_2,\cdots ,f_{k-1}$. Suppose none of $f_2$ and $f_{k-2}$ needs receive $\frac{3}{2}$ from v. Then v sends at most $\frac{3}{2}+(k-3)\times \frac{5}{4}$(in total) to $f_1,f_2,\cdots ,f_{k-1}$. $\square$

Suppose $n_2(v)=8$. Then clearly $f_{6^+}(v)=8$ and v sends each of its adjacent 2-vertices at most 1 by R1. So $c'(v)=10-1\times 8=2$. Suppose $n_2(v)=7$. Then $f_{6^+}(v)\ge 6$, $f_{4}(v)\le 2$ and $f_3(v)=0$. So $c'(v)\ge 10-1\times 7-1\times 2=1$. Suppose $n_2(v)=6$. Then $f_3(v)\le 1$. If $f_3(v)=1$, then $f_{6^+}(v)\ge 5$ and $c'(v)\ge 10-1\times 6-\frac{3}{2}-1\times 2=\frac{1}{2}>0$. Otherwise, $f_3(v)=0$, $f_{6^+}(v)\ge 4$ and $c'(v)\ge 10-1\times 6-1\times 4=0$. Suppose $n_2(v)=5$. Then $f_3(v)\le 2$. If $f_3(v)=2$, then $f_{6^+}(v)\ge 4$ and $c'(v)\ge 10-1\times 5-\frac{3}{2}\times 2-1\times 2=0$. If $f_3(v)=1$, then $f_{6^+}(v)\ge 3$ and $f_{4}(v)\le 4$. We also known there are at least two 4-faces each of which needs receive $\frac{3}{4}$ from v. So $c'(v)\ge 10-1\times 5-\frac{3}{2}-1-\frac{3}{4}\times 2=0$. If $f_3(v)=0$, then $f_{6^+}(v)\ge 2$, $f_{4}(v)\le 6$ and none of 4-faces incident with v needs receive 1 from v. So $c'(v)\ge 10-1\times 5-\frac{3}{4}\times 6=\frac{1}{2}>0$.

Fig. 3

$n_2(v)=4$

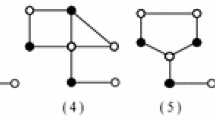
Suppose $n_2(v)=4$. Then there are eight possibilities in which 2-vertices are located. They are shown as configurations in Fig. 3. In Fig. 3(1), by Lemma 4, $c'(v)\ge 10-4-\frac{3}{2}-\frac{5}{4}\times 3=\frac{3}{4}>0$. In Fig. 3(2), $c'(v)\ge 10-4-\frac{3}{2}-\frac{5}{4}\times 2-\frac{3}{2}=\frac{1}{2}>0$. In Fig. 3(3) and (7), $c'(v)\ge 10-4-(\frac{3}{2}+\frac{5}{4})\times 2=\frac{1}{2}>0$. In Fig. 3(4), $c'(v)\ge 10-4-\frac{3}{2}-\frac{5}{4}\times 2-\frac{3}{2}=\frac{1}{2}>0$. In Fig. 3(5-6), $c'(v)\ge 10-4-\frac{3}{2}-\frac{5}{4}-\frac{3}{2}\times 2=\frac{1}{4}>0$. In Fig. 3(8), $c'(v)\ge 10-4-\frac{3}{2}\times 4=0$.

Fig. 4

$n_2(v)=3$

Suppose $n_2(v)=3$. Then there are five possibilities in which 2-vertices are located. They are shown as configurations in Fig. 4. In Fig. 4(1), by Lemma 4, $c'(v)\ge 10-3-\frac{3}{2}-\frac{5}{4}\times 4=\frac{1}{2}>0$. In Fig. 4(2), $c'(v)\ge 10-3-\frac{3}{2}-\frac{5}{4}\times 3-\frac{3}{2}=\frac{1}{4}>0$. In Fig. 4(3), $c'(v)\ge 10-3-\frac{3}{2}-\frac{5}{4}\times 2-\frac{3}{2}-\frac{5}{4}=\frac{1}{4}>0$. In Fig. 4(4), $c'(v)\ge 10-3-\frac{3}{2}-\frac{5}{4}\times 2-\frac{3}{2}\times 2=0$. In Fig. 4(5), $c'(v)\ge 10-3-(\frac{3}{2}+\frac{5}{4})\times 2-\frac{3}{2}=0$.

Fig. 5

$n_2(v)=2$

Suppose $n_2(v)=2$. Then there are four possibilities in which 2-vertices are located. They are shown as configurations in Fig. 5. In Fig. 5(1), by Lemma 4, $c'(v)\ge 10-2-\frac{3}{2}-\frac{5}{4}\times 5=\frac{1}{4}>0$. In Fig. 5(2), $c'(v)\ge 10-2-\frac{3}{2}-\frac{5}{4}\times 4-\frac{3}{2}=0$. In Fig. 5(3), $c'(v)\ge 10-2-\frac{3}{2}-\frac{5}{4}\times 3-\frac{3}{2}-\frac{5}{4}=0$. In Fig. 5(4), $c'(v)\ge 10-2-(\frac{3}{2}+\frac{5}{4}\times 2)\times 2=0$.

Suppose $n_2(v)=1$, let u be a 2-vertex adjacent to v and uv is not incident with a 3-cycle. Then $f_3(v)\le 5$. Suppose $f_3(v)=5$. Then v is incident with at least two $6^+$-faces or at least one $7^+$-face. So $c'(v)\ge 10-1-\frac{3}{2}\times 3-\frac{5}{4}\times 2-1\times 2=0$. Suppose $f_3(v)=4$. Then v is incident with at least two $5^+$-faces or at least one $6^+$-face. So $c'(v)\ge 10-1-\frac{3}{2}\times 4-1\times 3=0$. Suppose $f_3(v)=3$. Then v is incident with at least one $5^+$-face. So $c'(v)\ge 10-1-\frac{3}{2}\times 3-1\times 4-\frac{1}{3}=\frac{1}{6}>0$. Suppose $f_3(v)\le 2$. Then $c'(v)\ge 10-1-\frac{3}{2}\times 2-1\times 6=0$.

Suppose uv is incident with a 3-cycle. Then $f_3(v)\le 6$, v is incident with at most one 3-face which need receive $\frac{3}{2}$ from v and other 3-faces each of which receive $\frac{5}{4}$ from v. Suppose $f_3(v)=6$. Then v is incident with at least one $6^+$-face and $c'(v)\ge 10-1-\frac{3}{2}-\frac{5}{4}\times 5-1=\frac{3}{4}>0$. Suppose $f_3(v)=5$. Then $c'(v)\ge 10-1-\frac{3}{2}-\max \{\frac{5}{4}\times 4+\frac{3}{4}\times 2+1, \frac{5}{4}\times 4+2\times 2+\frac{1}{3}\}=0$. Suppose $f_3(v)=4$. Then v is incident with at least one $5^+$-face and $c'(v)\ge 10-1-\frac{3}{2}-\frac{5}{4}\times 3-1\times 3-\frac{1}{3}=\frac{5}{12}>0$. Suppose $f_3(v)\le 3$. Then $c'(v)\ge 10-1-\frac{3}{2}-\frac{5}{4}\times 2-1\times 5=0$.

Suppose $n_2(v)=0$. Then $f_3(v)\le 6$. Suppose $f_3(v)=6$. Then v is incident with at least one $6^+$-face and $c'(v)\ge 10-\frac{3}{2}\times 6-1=0$. Suppose $f_3(v)=5$. Then v is incident with at least one $5^+$-face and $c'(v)\ge 10-\frac{3}{2}\times 5-1\times 2-\frac{1}{3}=\frac{1}{6}>0$. Suppose $f_3(v)\le 4$. Then $c'(v)\ge 10-\frac{3}{2}\times 4-1\times 4=0$.

Hence we complete the proof of Theorem 1.